Наклонная дальность

Рисунок 1. К пояснению различия наклонной и горизонтальной дальности

Рисунок 1. К пояснению различия наклонной и горизонтальной дальности
Наклонная дальность
Когда идет речь об измерении дальности до цели при помощи радиолокатора, различают два понятия:
наклонная дальность цели и горизонтальная дальность цели.
Наклонная дальность цели R — это длина линии,
по которой электромагнитная волна распространяется от антенны радиолокатора до цели.
Очевидно, что это будет отрезок почти прямой линии, поскольку электромагнитная волна в
свободном пространстве распространяется по прямой с возможными искривлениями за счет атмосферной рефракции.
Этот отрезок будет иметь наклон по отношению к горизонтальной плоскости, равный углу места цели ε.
Именно поэтому такую дальность называют наклонной.
При отображении радиолокационной информации на фоне карт местности, как правило, оперируют горизонтальной дальностью цели,
которая представляет собой проекцию наклонной дальности на горизонтальную плоскость.
На Рисунке 1 поясняется разница между наклонной и горизонтальной дальностью цели.
Здесь показаны два самолета, летящие один точно над другим.
Следовательно, они будут иметь одинаковую горизонтальную дальность.
Однако на основе простейших геометрических знаний понятно, что находящийся выше самолет будет иметь большую наклонную дальность,
что и отображается на индикаторе радиолокатора, фрагмент которого изображен в нижней части Рисунка 1.
Разница между измеренной (наклонной) и горизонтальной дальностью в современных радиолокаторах учитывается в программном обеспечении,
реализующем соответствующий алгоритм пересчета.
Таким радиолокатором является, например,
AN-FPS-117 .
Упомянутое программное обеспечение должно быть специально адаптировано к географическим координатам позиции радиолокатора.
Пересчет связан с достаточно сложными
вычислениями,
и требует также
информации о погоде
для коррекции значений используемых в расчетах данных.
К сожалению, в более старых
двухкоординатных радиолокаторах,
таких как
ASR-E ,
все еще используемых в системах управления воздушным движением, такой пересчет не выполняется.
Поэтому оператор должен знать и автоматически учитывать в своей работе то, что самолет, летящий на большом удалении,
на индикаторе радара будет отображаться на дальности, которая больше, чем его истинная дальность!
Тем не менее, для большинства радиолокаторов ошибки за счет отсутствия пересчета относительно невелики.
Такие ошибки становятся более ярко выраженными для бортовых радиолокаторов с синтезированными апертурами.
Вычисление горизонтальной дальности

Рисунок 2. Геометрия задачи расчета горизонтальной дальности (без учета кривизны Земли)

Рисунок 2. Геометрия задачи расчета горизонтальной дальности (без учета кривизны Земли)

Рисунок 2. Геометрия задачи расчета горизонтальной дальности (без учета кривизны Земли)
Горизонтальная дальность цели — это дальность между точкой на Земле, где находится радиолокатор и проекцией точки,
в которой находится цель, на поверхность Земли (горизонтальную плоскость).
Информация о том, над какой именно топографической точкой точно находится обнаруженный самолет, часто бывает очень важна.
Для этого
электронная карта
тем или иным образом отображается на экране индикатора.
Вычисление действительной горизонтальной (используют также термин «топографической») дальности является достаточно сложным в радиолокаторе.
Исходя из схемы, приведенной на Рисунке 2, вычисление топографической дальности можно выполнить по формуле:
Rtopogr. = R · cos ε
Однако, данная формула будет справедлива только для сравнительно небольших расстояний,
для которых поверхность Земли может быть представлена плоскостью с незначительной погрешностью.
Влияние кривизны поверхности Земли на расчет топографической дальности поясняется с помощью Рисунка 3.
Видно, что действительная топографическая дальность зависит от следующих величин:
- измеренной наклонной дальности;
- действительной высоты цели;
- радиуса земной поверхности в области, соответствующей зоне действия радиолокатора.

Рисунок 3. Геометрия задачи расчета горизонтальной (топографической) дальности с учетом кривизны Земли

Рисунок 3. Геометрия задачи расчета горизонтальной (топографической) дальности с учетом кривизны Земли

Рисунок 3. Геометрия задачи расчета горизонтальной (топографической) дальности с учетом кривизны Земли
Для расчета можно воспользоваться математическими соотношениями, которые выводятся при помощи Рисунка 3.
Рассмотрим треугольник с вершинами в точках: центр Земли, позиция радиолокатора и точка, в которой находится цель.
Стороны и углы при вершинах такого треугольника связаны между собой теоремой косинусов:
R2 = re2 + (re + H)2 — 2re(re + H) · cos α
(здесь re эквивалентный радиус Земли).
В предположении сферической поверхности Земли топографическая дальность может быть вычислена как длина дуги
окружности радиуса re,
стягивающей угол α:
360° · Rtopogr. = α · 2π re
Заметим, что при использовании такого приближения необходимо отдельно учитывать влияние
атмосферной рефракции,
под действием которой траектория распространения электромагнитной волны становится отличной от прямолинейной.
Степень ее искривления зависит от следующих величин:
- длины волны излучаемого сигнала;
- барометрического давления;
- температуры воздуха;
- атмосферной влажности.
Таким образом, модель обстановки, формируемая на индикаторе радиолокатора, будет неточной,
если при обработке и отображении радиолокационных данных не учитывается соотношение между наклонной и топографической дальностью.
Это, к сожалению всегда имеет место в случае двухкоординатных радиолокаторов,
поскольку в составе измеряемых ими данных отсутствует значение высоты цели, необходимое для выполнения пересчета!
Задача решается
по формуле (рис. 41)
![]()
где
Н
—
высота полета;
ВУ
—
вертикальный угол.
Порядок
решения
(шкалы 4
и 5):
— передвигая
движок, установить индекс
![]() против
против
деления шкалы 5,
соответствующего высоте полета Н (рис.
42);
— установить
визирку по шкале 4
на деление, соответствующее заданному
вертикальному углу ВУ;


— отсчитать
по визирке на шкале 5
искомое значение горизонтальной
дальности ГД.
Пример:
Дано:
Н
= 8300
м;
ВУ = 28°.
Находим: ГД
— 4400
м.
12. Расчет горизонтальной дальности по высоте и наклонной дальности.
Задача решается
по формулам (рис. 43)
ГД
= (НД)sinВУ;
![]()
![]()
где
Н
—
высота полета;
НД
—
наклонная дальность;
ГД
—
горизонтальная дальность;
α
— вспомогательный угол;
ВУ
—
вертикальный угол (ВУ = 90° — α).

Порядок
решения
(шкалы 3,
4
и 5):
— передвигая
движок, установить индекс
![]()
на деление шкалы 5,
соответствующее наклонной дальности
НД
(рис.
44, а);
— установить
визирку по шкале 5 на деление, соответствующее
высоте полета Н;
— отсчитать по
визирке на шкале 3 вспомогательный угол
а;
— перевести
визирку на деление шкалы 3, соответствующее
вертикальному углу (90° — α);
— отсчитать
по визирке на шкале 5
искомую горизонтальную дальность ГД.
Пример.
Дано:
НД
=
22,8 км;
Н
— 10
км
Находим:
α
= 26°; ВУ = (90° — α)
= 64°, затем ГД
=
20,5 км.
При
малых углах α для большей точности
расчета можно задачу определения ГД
решать
по второй формуле, используя шкалу
тангенсов.
Порядок решения:
— определить
значение вспомогательного угла а так,
как указано выше;
— установить
визирку по шкале 5
на деление, соответствующее Н
(рис.
44, б);
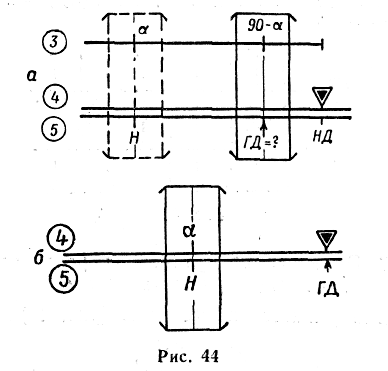
— передвигая
движок, подвести под визирку деление
шкалы 4,
соответствующее значению α;
— отсчитать
против индекса
![]()
по шкале 5
искомое значение ГД.
Решение
задачи по третьей формуле выполняется
по шкалам 5
и 6,
как правило, во время предварительной
подготовки.
Порядок решения:
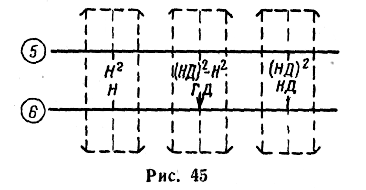
— устанавливая
визирку по шкале 6
последовательно на деления, соответствующие
значению НД
и
Н (рис. 45), отсчитать квадраты этих
значений по визирке на шкале 5
и затем, найдя разность полученных
квадратов этих значений (НД)2
— Н2,
установить
ее на шкале 5;
— отсчитать
при помощи визирки по шкале 6
искомое значение горизонтальной
дальности ГД.
Пример.
Дано:
НД
=. 28
км;
Н
— 9
км.
Находим:
(НД)2
= 784; т
=
81, затем (НД)2
— Н2
= 703 и ГД
— 26,6км.
13. Определение путевой скорости при помощи круговых систем.
Задача решается
по формуле (рис. 46)
![]()
где
ψ
—
угол станций;
ΔR —
изменение дальности от станции скорости
за время t.
Порядок
решения
(шкалы 1,
2
и 3);
— установить
визирку по шкале 1
на деление, соответствующее значению
ΔR (рис. 47);
— передвигая
движок, подвести под визирку деление
шкалы 2,
соответствующее значению t;
— перевести
визирку до совмещения риски с индексом
![]() ;
;
— передвигая
движок, подвести под визирку деление
шкалы 3,
соответствующее углу ψ;
— отсчитать
по шкале 1
против индекса
![]()
искомое
значение путевой скорости W.
Пример.
Дано:
ψ
= 41°; ΔR = 4000л; t
=
30 сек.
Находим:
W
= 735
км/час.

Соседние файлы в папке навигация
- #
- #
- #
- #
- #
Радиолокация и радионавигация
УДК 621.396.969.1
Ю. Г. Булычев, А. А. Мозоль
Ростовский военный институт ракетных войск
В. Н. Вернигора ФГУП «ВНИИ “Гоадиент”» (г. Ростов на Дону) В. А. Морковкин, А. Г. Нечаенко
Ростовская академия сервиса Южно-Российского государственного
университета экономики и сервиса
Метод оперативного определения наклонной дальности до цели по двум измерениям пеленга
Развит оперативный метод определения наклонной дальности до цели по двум последовательным во времени измерениям пеленгов автономной угломерной системы с использованием априорной информации о вероятных значениях скорости и ускорения. Дана оценка эффективности метода. Приведен пример использования метода.
Наклонная дальность, оценка, оперативность
В настоящее время для некоторых измерительных комплексов (например, комплексов радиоэлектронного подавления (РЭП)) весьма актуальна задача оперативного приближенного определения наклонной дальности до цели по минимальному количеству измерений пеленга, получаемых автономной угломерной системой [1]-[3]. Такая задача возникает, например на этапе ранжирования потока целей по ориентировочной дальности, т. е. по дальности, определенной с точностью, пригодной для решения задачи ранжирования целей при проведении РЭП. При этом рассматриваются цели с частично известными параметрами [4], когда заданы тип траектории, значения скорости и ускорения, а также тактико-технические характеристики сопровождаемых целей.
К комплексам РЭП не предъявляется повышенных требований к точности определения дальности до цели (как это имеет место, например, для дальномерных систем). Для них в первую очередь важна оперативность формируемых оценок этого параметра. Это позволяет отказаться от высокоточных статистических методов оценивания (метода наименьших квадратов, максимума правдоподобия, максимума апостериорной плотности вероятности и др. [5]) и использовать методы косвенного оценивания на базе несложных конечных формул.
В работах [4], [6] дальность определяется автономной угломерной системой по трем и более измерениям пеленга на цель, движущуюся прямолинейно и равномерно с известной скоростью. Однако использование более двух измерений пеленга снижает оперативность решения целевых задач измерительных комплексов, функционирующих в реальном времени.
Целью настоящей статьи является развитие оперативного метода определения наклонной дальности по двум последовательным во времени измерениям пеленгов. Метод основывается на допущениях о прямолинейном движении цели с известными значениями © Булычев Ю. Г., Мозоль А., А. Вернигора В. Н., Морковкин В. А., Нечаенко А. Г., 2009 57
Ц2
ЛБ
Ц1
01
Rl
R2
Да12
скорости и ускорения, а также об известной мощности принимаемых автономной угломерной системой сигналов.
Геометрия задачи представлена на рис. 1, где точка 0 соответствует геометрическому центру автономной угломерной системы; ЛБ – линия барражирования цели; точки Ц1 и Ц2 указывают положения цели в моменты измерения пеленга на нее 11 и ^ соответственно; ^ и Й2 – расстояния от угломерной системы до цели в моменты ^ и ¿2 соответственно; Р – угол, образуемый пеленгом на цель в момент времени ¿1 и линией движения цели; Да^ – угол между пеленгами, измеренными из точки 0 на цель в моменты времени ¿1 и ¿2 .
Предполагается, что цель движется прямолинейно, причем проходимое расстояние описывается математической моделью:
Рис. 1
N – 0)
* (‘ ) = Е-V (‘ – ¿о)’; ‘ * ¿о. Л i!
1=1
(1)
где
* (‘ )= 0 &
N е {1, 2, …} ; ¿о – начальный момент времени, а все величины -0′) в
г=¿0
модели (1) полагаются известными.
Известны также время Дгl2 = ¿2 – ¿1 пролета цели между точками Ц1 и Ц2, угол
Да12 и величины Ql2 = ^р /р и Q2l = ^ 1!р (р и Р2 – мощности сигналов, принимаемых автономной угломерной системой в моменты времени ¿1 и ¿2 соответственно).
Требуется развить оперативный метод определения наклонной дальности до цели и проанализировать точностные характеристики метода с учетом основных случайных факторов в рамках нормального закона распределения.
Из рис. 1 определим расстояние между Ц1 и линией визирования, направленной в
точку Ц2:
|ц1,0^ = Я1 sin Да12. (2)
На основании (1) найдем расстояние, пройденное целью:
Р
0
N s (i )
i=1
(3)
С учетом (2) и (3) имеем
Р1Д2 =
N S(i )
i ^
i =1
– (Ri sin Ла12 ) .
С другой стороны,
Из (4) и (5) вытекает, что
N S(i)
i ^ л4
i =1
Р1Д2 = R2 – R1cos Ла12 .
– (Ri sin Ла12 )2 = (R2 – Ri cos Ла12 )2 .
(4)
(5)
(6)
Известно [7], что мощность Р сигнала на входе автономной угломерной системы обратно пропорциональна квадрату дальности до цели R : Р = дК , где д – коэффициент пропорциональности, сложным образом зависящий от условий наблюдения цели и в общем случае изменяющийся во времени. Для моментов времени ^ и ^ имеем
=1^1Р1 ) ; = д(Ч); К2 =1^2Р2 ) ; Д2 = д(Н).
На практике интервал времени Д^2 весьма мал. Поэтому можно принять неизменность на данном интервале коэффициента: ^ = Д2 = Д. Тогда получим формулу для отношения дальностей:
Ril R2 =( P2I Pi )
12
С учетом (6) и (7) имеем
N S (i) i =i
îi2 {s
= Ri2 i sin2 Ла12 +
(Pi/P2 )V2 – cos Лап
(7)
(8)
■J/2
Преобразовав выражение в фигурных скобках и введя обозначения Qi2 =(Pi/р)
2
и Ci2 = Qi2 – 2cos +1, с учетом (8) получим искомую формулу для наклонной
дальности в момент времени ti :
Ri =
N S(i) i=i
C
-i/2 i2
(9)
Учтя, что Да,12 = Д«21, по аналогии с (9) получим формулу для наклонной дальности в момент времени 12 :
R2 =
N S (i) i=i
C
-V2 2i ,
(iO)
2
2
2
где с21 = Q221 – 2 Да12Q21 +1.
Выражения (9) и (10) позволяют определить дальность до цели по двум последовательным во времени измерениям пеленга и относительной мощности измеряемого сигнала.
Выражения (9), (10) не дают решения при С12 < 0 и С21 < 0 соответственно. Рассмотрение уравнений С12 < 0 и С21 < 0 показывает, что они не имеют решений в области вещественных чисел относительно Ql2 и Q2l соответственно. Ситуации С12 = 0 (С21 = 0) возможны при одновременном выполнении двух условий: Да^ = 0 и Ql2 = 1 (Q2l = 1) . Первое из них означает движение цели по линии визирования (отсутствие параллакса). Второе выполняется при столь медленном движении цели, что за время Дгl2 она не сместилась на расстояние, достаточное для существенного изменения приходящей мощности сигнала. Совпадение этих условий означает, что автономная угломерная станция не в состоянии различить два измерения и, естественно, оказывается неработоспособной. Однако такие ситуации могут рассматриваться, скорее, как частный случай. Во всех остальных случаях выражения (9), (10) пригодны для определения наклонной дальности в рамках развития рассматриваемого метода.
Формулы (9), (10) дают детерминированные решения при наличии достоверной информации о типе цели и некоторых ее характеристиках. Перейдем к рассмотрению этих решений в условиях априорной неопределенности.
Учтем случайный характер основных параметров, входящих в формулы для наклонной дальности, полагая их нормально распределенными некоррелированными случайными величинами. Для нахождения дисперсии ошибки определения дальности воспользуемся широко распространенным на практике принципом линеаризации (первым приближением [4]—[6]). Кроме того, по аналогии с [4] ограничимся случаем прямолинейного равномерного движения цели.
Учитывая общность (9) и (10), при дальнейшем рассмотрении введем обозначения: 2) для N1 и Я2 ‘; Ql2(21) для Ql2 и Q2l, С^(21) для Су2 и С21, имея в виду, что в каждом конкретном случае в выражениях должны использоваться либо индексы, стоящие вне скобок, либо индексы в скобках. Рассмотрим Я( 2) как функции случайных некоррелированных аргументов V, Да^, Ql2(21) (V – скорость цели): Я(2)=ф(^, Да^, Ql2(21)) = = Ф1(2). С учетом метода линеаризации искомые дисперсии ошибок определения наклонной дальности находятся по формуле
^2) = |>1(2)/^ +|>1(2)/5Да12]2 °Да12 +|>1(2)/^12(21)]2 ^21), (11)
2 2 2
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
где ау, ада12 , ^ ^ – дисперсии ошибок определения скорости, угла Да^ и величин Ql2( 21) соответственно.
Частные производные в (11) с учетом (9), (10) находятся по формулам
дф!( 2)/дУ = Д^12С]-)1(/221);
3/2 —32
дФ1(2)/дДа12 =С12(21)sin Да12012(21) ^ Г (12)
32 32
дФ1(2)/дС?12(21) = ‘ С12(21) [cos Да12 — Q12(21)] ^
Подставив (12) в (11), окончательно получим формулу для дисперсий ошибок определения наклонной дальности в моменты времени 11 и ^ соответственно:
2) =Д^122С—21(21) Х
I 2 . 2/-<—2 Х|°2 + v С12(21)
Даl2Ql22(21)^Да12 +[c0S Да12 — Q12(21)]2 0312(21) }). (13)
Формула (13) позволяет исследовать потенциальные возможности развитого метода для различных условий пеленгационно-мощностных измерений. Используемое при ее выводе условие некоррелированности случайных величин V, Да^, Ql2( 21) не является принципиальным. В случае их коррелированности достаточно в правую часть формулы (13) добавить слагаемое, учитывающее соответствующие коэффициенты корреляции между случайными величинами.
Для анализа эффективности развитого метода применим два подхода: первый, основанный на расчетах по формуле (13), и второй, основанный на статистическом моделировании с использованием датчиков случайных чисел.
Расчетами по (13) определялись среднеквадратические отклонения оценок наклонной дальности до цели ащ^ . Статистическим моделированием формировались значения
1 N –
1 ^ г, п
ошибок определения расстояния до цели: 5Я12) = Я12) — Я*2) , где Я^2) = — ^ 2) –
^ п=1
результирующая оценка наклонной дальности, полученная на основе развитого метода по результатам усреднения по N = 100 реализациям; Я*( 2) – истинные значения наклонной
формулам Я* = д/ х2 + у2 ; Я2* = ^ЩуД^^совР ;
дальности, вычисленные по формулам Я=д/ х” + _ 2 * ” *
причем ЯЦ 2) – единичные оценки, соответствующие п-му эксперименту, получаемые с использованием формул (9), (10); х, у – горизонтальная и вертикальная координаты цели относительно точки 0 в момент 11 соответственно; Р = агс% [(Н—у )/х ] + аrctg [У1/Х];
Н = 50 км – высота пролета цели над точкой 0, в которой расположена автономная угломерная станция.
При построении единичных и результирующих оценок с помощью датчиков случай-
ных чисел формировались ошибки измерений ДаП2, Qn2(21), Дvn; п = 1, 100 со средне-квадратическими отклонениями Од^ , Од^^^ , Оду = 3 м/с соответственно.
Расчеты и моделирование проведены для следующей модели движения цели:
Х(
Xг) = х: + Ухг; у (г) = у: + ; V = ^+ угу ; Аа12 = arccos (Я2 + – V2 А^)/2ЯЯ
г2 = Аг12; 312 = Я2/ Я1; 621 = Я1/ Я2 (vx, Vy – проекции вектора скорости V на горизонтальную и вертикальную оси координат
соответственно) при начальных условиях ¿1 = 0; г > 0; Х1 = 1 км, V = 200 м/с, ^ = 3 м/с.
На рис. 2 представлены зависимости о^ (А^2), а^ (А^2) (рис. 2, а) и бЯ1 (А^2), 8Я2 (А^12) (рис. 2, б) для начальных условий У1 = 60 км, од^ = 032! = 0.009, 0Аа^ = 5″.
На рис. 3 представлены аналогичные зависимости для начальных условий У1 = 50 км, 0б12 = 02*1 = °.°45, 0Аа12 = I5″ .
На рис. 4 представлены аналогичные зависимости для начальных условий У1 = 40 км,
0Й2 =0321 = °.°9, 0Аа12 = 30″ .
Анализ результатов расчетов и моделирования (рис. 2-4) показывает, что расчетные и модельные оценки подтверждают работоспособность метода для различных условий наблюдения цели.
Развитый в настоящей работе метод позволяет оценить значение наклонной дальности до цели по двум измерениям пеленга при известных значениях скорости и ускорения, а также мощности принимаемых автономной угломерной системой сигналов для рассматриваемых моментов измерений. Важнейшим отличием метода от традиционных подходов к решению задачи определения наклонной дальности является его оперативность при удовлетворительных точностных значениях оценки.
8Я, км
0.3
о я , км
1.6
1.5 _
1.4 °Я2
1.3 1
5 10
0.2
0.1
0
15 20
а
о я , км
0.5
0.3
0.1
Рис. 2
бЯ, км
0.4
0.3 0.2
15 20
а
Аг12 Рис. 3
25 А/12
б
б
СТ R, км
5R, км
2.8
1.4
0
0.25
5
10
15
20 25 А/
5
10
15
20 25 А/12
а
б
Рис. 4
С точки зрения технической реализации метод целесообразно применять в измерительных комплексах РЭП на этапах ранжирования целей, когда важную роль играет оперативность определения оценки ориентировочной дальности.
1. Палий А. И. Радиоэлектронная борьба. М.: Воениздат, 1981. 350 с.
2. Основы маневрирования кораблей / под ред. М. И. Скворцова. М.: Воениздат, 1996. 248 с.
3. Хвощ В. А. Тактика подводных лодок. М.: Воениздат, 1989. 264 с.
4. Мельников Ю. П., Попов С. В. Определение дальности при пеленговании объекта с частично известными параметрами движения // Радиотехника. 2003. № 4. С. 71-75.
5. Жданюк Б. Ф. Основы статистической обработки траекторных измерений. М.: Сов. радио, 1978. 384 с.
6. Булычев Ю. Г., Коротун А. А., Манин А. П. Идентификация параметров траекторий по измерениям подвижного пеленгатора // Радиотехника. 1990. № 1. С. 16-19.
7. Справочник по радиолокации / пер. с англ.; под ред. К. Н. Трофимова. М.: Сов. радио, 1976. Т. 4. 376 с.
J. G. Bulychev, А. А. Mozol Rostov military institute of rocket troops V. N. Vernigora
FSUE ARSRI “Gradient” (Rostov-on-Don) V. А. Morkovkin, А. G. Nechaenko
Rostov academy of service of the south Russian state university of economics and service
A method of the operative estimation of the slant range to the target according to two bearing measurements
Список литературы
Operative method of slant target range estimation according to two bearing measurements independent by goniometric system with using of the a priori information about probable values of speed and acceleration is developed. Method efficiency estimation is given. The example of method using is resulted.
Slant range, estimation, operativeness
Статья поступила в редакцию 16 июня 2009 г.
The slant range is the distance between the two points, from radar to the target. The geocenter is the description of the universe where the earth is in the center. The angle between the horizontal plane and the line of sight is called as elevation angle. Here is the online Satellite Slant Range Calculator to calculate slant range satellite communication. Enter the inputs values, the tool will update you the distance between the geocentric & satellite and slant range of the satellite.
Calculate Slant Range Satellite Communication
The slant range is the distance between the two points, from radar to the target. The geocenter is the description of the universe where the earth is in the center. The angle between the horizontal plane and the line of sight is called as elevation angle. Here is the online Satellite Slant Range Calculator to calculate slant range satellite communication. Enter the inputs values, the tool will update you the distance between the geocentric & satellite and slant range of the satellite.
Code to add this calci to your website 

Formula:
r = h + B
D = √ [(B x Cos(ε))2 + r2 – B2] – (B x Cos(ε))
Where,
h = Distance Between GND Station and Satellite
B = Distance Between Geocenter and Ground Station
ε = Elevation Angle
r = Distance Between Geocenter and Satellite
D = Satellite Slant Range
Example:
Calculate the satellite slant range based on the Distance Between GND Station and Satellite of 1000 km, Distance Between Geocenter and Ground Station of 200 km and the elevation angle of 45°.
Solution:
r = h + B
= 1000 + 200
= 1200 km
D = √ [(B x Cos(ε))2 + r2 – B2] – (B x Cos(ε))
= √ [(200 x Cos(45))2 + 12002 – 2002] – (200 x Cos(45))
= 1082.807 km
По
формуле (2.1.20) определяется выигрыш в отношении сигнал/шум, обеспечиваемый ЧМ
приемником при найденных выше параметрах ЧМ сигнала, а по формуле (2.1.19)
полагая, что введение линейных предыскажений обеспечит выигрыш в
отношении сигнал/шум, можно найти точное отношение сигнал/шум на входе
приемника:
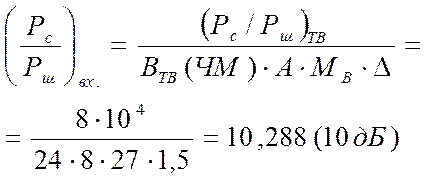 (2.1.21)
(2.1.21)
5. Распределение
полученного отношения сигнал / шум по двум участкам линии связи с тем, чтобы
выделить долю запаса, определяемую коэффициентом b, для линии ИСЗ – Земля.
a = b / (b – 1.) (2.1.22)
Принимаем b=1,2
а =
1,2/(1,2 – 1) = 6
4.2. РАСЧЕТ ВЧ ЧАСТИ РАДИОЛИНИИ ИСЗ – ЗЕМЛЯ.
4.2.1 Определяем необходимые параметры:
d – дальность ИСЗ от земной станции,
Gпр.з., – коэффициент усиления приемной антенны
земной станции;
Gпер.б – коэффициент усиления передающей
антенны ИСЗ в главном направлении,
Lдоп – полную величина потерь энергии сигнала на линии связи,
Тз – эквивалентная
шумовая температура всей земной приемной станции.
4.2.2 В любой точке земной
поверхности положение луча антенны ЗС характеризуется двумя угловыми
величинами: азимутом ![]() и
и
углом места ![]() .
.
Угол
места (угол возвышения) – это угол между направлением на спутник и проекцией
этого направления на плоскость, касательную к поверхности Земли.
Азимут
– это угол между направлением на север и проекцией направления на ИСЗ на
касательную плоскость.
Положение
точки ЗС на земной поверхности характеризуют:
долгота
![]() – угол между
– угол между
плоскостью Гринвичского меридиана и плоскостью меридиана, проходящего через
точку ЗС,
 широта
широта ![]() – угол между радиусом Земли, проведенным в
– угол между радиусом Земли, проведенным в
точку ЗС и плоскостью экватора.
Плоскость Плоскость орбиты экватора Зем ли
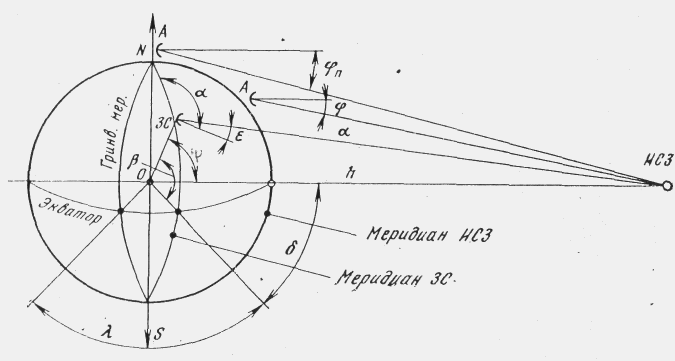
Рис. 2.3
Схема
расположения ИСЗ связи для расчета азимута и угла места
антенны приемной
станции
Обозначения, применяемые на данной
схеме (рис.2.3):![]() –
–
долгота ЗС; ![]() –
–
разница долготы ЗС и ИСЗ;![]() – широта места ЗС;
– широта места ЗС; ![]() – угол места;
– угол места; ![]() – азимут;
– азимут;![]() – угол деклинации;
– угол деклинации;![]() – угол деклинации на полюсе;
– угол деклинации на полюсе;
d – наклонная даль6ность; h – высота орбиты.
4.2.3 Определяем наклонную дальность
для ЗС в Санкт-Петербурге.
ИСЗ – Интелсат, долгота λИСЗ
= 600.
Санкт-Петербург:
Широта – β = 590
Долгота – λ = 300.
Определим азимут ЗС на ИСЗ.
При определении азимута![]() необходимо учитывать,
необходимо учитывать,
что в северном полушарии возможны варианты:
Если ЗС западнее ИСЗ, то ![]() , если ЗС восточнее ИСЗ, то
, если ЗС восточнее ИСЗ, то ![]() , где
, где 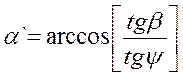 , а
, а ![]() .
.
Так
как ЗС западнее ИСЗ, то ![]() . Где δ = λЗС – λИСЗ.
. Где δ = λЗС – λИСЗ.
Тогда:
δ = λЗС – λИСЗ = 300 – 600 = – 300
![]()
![]()
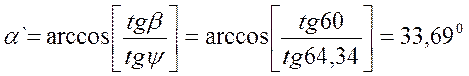
Азимут:
![]()
Определяем наклонную
дальность ![]() :
: 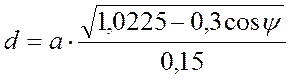 , где а = 6370
, где а = 6370
км (радиус Земли).
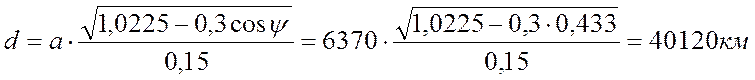
При нахождении угла места ![]() используем выражение:
используем выражение:
 ,
,
Тогда:
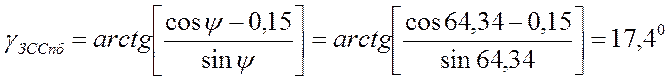
Произведем
аналогичные вычисления для ЗС, находящейся в городе Хабаровск.
Хабаровск: Широта – β = 480
Долгота – λ = 1350.
Определим азимут ЗС на ИСЗ.
Так как ЗС восточнее ИСЗ, то ![]()
где 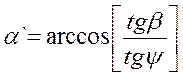 ,
, ![]() , δ = λЗС – λИСЗ.
, δ = λЗС – λИСЗ.
Тогда: δ = λЗС – λИСЗ = 1350 – 600
= 950
![]()
![]()

Азимут:
![]()
Определяем наклонную
дальность ![]() :
: 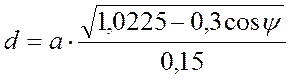 , где а = 6370
, где а = 6370
км (радиус Земли).

При нахождении угла места ![]() используем выражение:
используем выражение:
 ,
,
Тогда: 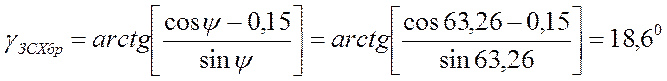
4.2.4 Определение
коэффициента усиления передающей антенны ИСЗ в главном направлении для
заданного значения ширины диаграммы направленности бортовой антенны ![]()
![]() = 5о, приняв q = 0,5:
= 5о, приняв q = 0,5:
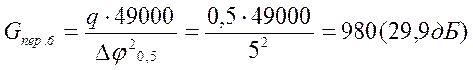 (2.2.1)
(2.2.1)
4.2.5 Определение диаметра передающей антенны ИСЗ
производится из расчета действующей площади антенны, которая определяется как
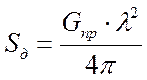 ,
,
м. (2.2.2)
Частота передачи, согласно исходных
данных, fИСЗ-ЗС = 4 ГГц, тогда длина волны в метрах: 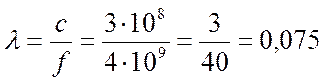 , тогда площадь равна:
, тогда площадь равна: 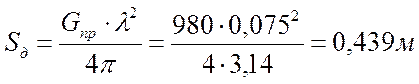
А для антенн с круглой апертурой
диаметром DA выполняется
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
