Асимптоты графика функции
Часто задание на нахождение асимптот функции встречается в курсе математического анализа, в частности при решении задач на тему исследования функции. Для того, чтобы успешно ответить на вопрос: как найти асимптоты функции? необходимо уметь вычислять пределы, понимать что они собой представляют, знать основные методы решения пределов. Если всё это вы умеете на должном уровне, тогда найти асимптоты для вас не будет проблемой. Итак, что такое асимптота? Асимптота это линия, к которой бесконечно приближается ветвь графика функции. Чтобы было наглядно, посмотрите на изображения представленные ниже.
Обратите внимание, что соприкосновения между асимптотой и графиками нет, и не должно быть. Асимптота бесконечно приближается к графику функции. Давайте рассмотрим какие виды асимптоты функции бывают и как их находить, но о последнем будет рассказано далее.
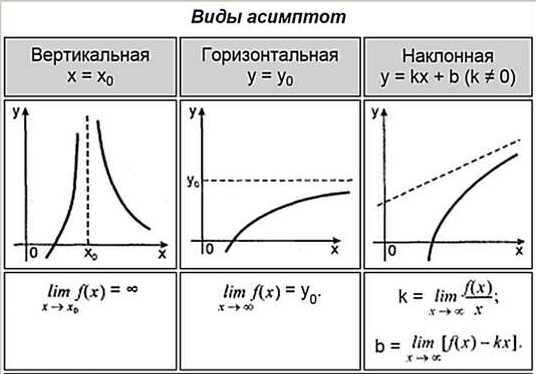
Из таблицы узнаем, что асимптоты у функции бывают трех видов: вертикальные, горизонтальные, наклонные. Каждую найти асимптоту функции нужно по своему. Для этого нужны лимиты. Сколько бывает асимптот всего у функции? Ответ: ни одной, одна, две, три… и бесконечно много. У каждой функции по разному.
Вертикальные асимптоты
Чтобы найти данный вид асимптот необходимо найти область определения заданной функции и отметить точки разрыва. В этих точках предел функции будет равен бесконечности, а это значит, что функция в этой точке бесконечно приближается к линии асимптоты.
Горизонтальные асимптоты
Необходимо устремить аргумент лимита функции к бесконечности. Если предел существует и равен числу, то горизонтальная асимптота будет найдена и равна $ y=y_0 $ как показано во втором столбце таблицы
Наклонные асимптоты
Наклонная асимптота представляется в виде $ y = kx+b $. Где $ k $ – это коэффициент наклона асимптоты. Сначала находится коэффициент $ k $, затем $ b $. Если какой либо из них равен $ infty $, тогда наклонной асимптоты нет. А если $ k = 0 $, то получаем горизонтальную асимптоту. Так что для экономии времени лучше сразу находить наклонную асимптоту, а горизонтальная проявится сама собой в случае её существования.
Примеры решений
| Пример 1 |
| Найти все асимптоты графика функции $$ f(x) = frac{5x}{3x+2} $$ |
| Решение |
|
Для начала решения найдем вертикальные асимптоты, но прежде найдем область определения функции $ f(x) $. По определению знаменатель не должен быть равен нулю. Поэтому имеем, $ 3x+2 neq 0; 3x neq -2; x neq -frac{2}{3} $. Получили точку разрыва $ x = -frac{2}{3} $. Вычислим в ней предел функции и убедимся окончательно, что вертикальная асимптота это $ x = -frac{2}{3} $. $$ limlimits_{{x rightarrow -frac{2}{3}}} frac{5x}{3x+2} = (-frac{10}{infty}) = -infty $$. Теперь найдем горизонтальные асимптоты, но прежде рассчитаем коэффициенты $ k $ и $ b $. $$ k = limlimits_{x rightarrow infty} frac{f(x)}{x} =limlimits_{x rightarrow infty} frac{5}{3x+2}=frac{5}{infty}=0 $$ Так как $ k = 0 $, то мы уже понимаем то, что наклонных асимптот нет, а есть горизонтальные. Найдем теперь коэффициент $ b $. $$ b = limlimits_{x rightarrow infty} [f(x)-kx] = limlimits_{x rightarrow infty} frac{5x}{3x+2} = frac{infty}{infty} =frac{5}{3} $$ Подставляем найденные коэффициенты в формулу $ y = kx + b $, получаем, что $ y = frac{5}{3} $ – горизонтальная асимптота. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ y = frac{5}{3} $$ |
| Пример 2 |
| Найти все асимптоты графика функции $ f(x) = frac{1}{1-x} $ |
| Решение |
|
Найдем область определения данного примера, чтобы определить вертикальные асимптоты. $ 1-x neq 0; x neq 1; $. Точка разрыва $ x = 1 $, а это значит что это и есть вертикальная асимптота. Найдем для доказательства предположения предел в этой точке. $$ limlimits_{x rightarrow 1} frac{1}{1-x} = frac{1}{0} = infty $$ Приступим к поиску наклонных асимптот. $$ k = limlimits_{x rightarrow infty}frac{f(x)}{x}=limlimits_{x rightarrow infty}frac{1}{x(1-x)} = frac{1}{infty}=0 $$ $$ b =limlimits_{x rightarrow infty}[f(x)-kx]=limlimits_{x rightarrow infty}frac{1}{1-x} = frac{1}{infty}=0 $$ Итого, $ y=0 $ – горизонтальная асимптота. |
| Ответ |
| $$ y=0 $$ |
| Пример 3 |
| Найти все асимптоты графика функции $ f(x) = frac{x^3}{3x^2+5} $ |
| Решение |
|
Замечаем, что знаменатель не обращается в ноль при любом значении икса. А это значит, что нет точек разрыва и следовательно нет вертикальных асимптот. Остается найти горизонтальные асимптоты. $$ k = limlimits_{x rightarrow infty} frac{f(x)}{x} =limlimits_{x rightarrow infty}frac{x^2}{3x^2+5} =limlimits_{x rightarrow infty} frac{2x}{6x} = frac{1}{3} $$ Так как $ k $ конечное число, не равное $ 0 $ или бесконечности, то существует наклонная асимптота. Вычислим недостающее число $ b $. $$ b =limlimits_{x rightarrow infty} [f(x)-kx] =limlimits_{x rightarrow infty} [frac{x^3}{3x^2+5}-frac{x}{3}] =limlimits_{x rightarrow infty} -frac{5x}{3(3x^2+5)}= $$ $$ = -frac{5}{3}limlimits_{x rightarrow infty} frac{x}{3x^2+5} =-frac{5}{3}limlimits_{x rightarrow infty} frac{1}{6x} =-frac{5}{3}frac{1}{infty} = 0 $$ $ y =frac{1}{3}x $ – наклонная асимптота к функции с углом наклона одна третья. |
| Ответ |
| $$ y =frac{1}{3}x $$ |
| Пример 4 |
| Найти асимптоты $ f(x) = xe^{-x} $ |
| Решение |
|
Нет точек разрыва, а это значит, нет вертикальных асимптот. $$ k=limlimits_{x rightarrow infty} frac{1}{e^x} = frac{1}{infty} = 0 $$ $$ b=limlimits_{x rightarrow infty} frac{x}{e^x} =limlimits_{x rightarrow infty} frac{1}{e^x} = frac{1}{infty} = 0 $$ $ y = 0 $ – горизонтальная асимптота |
| Ответ |
| $$ y = 0 $$ |
Если в задачах даются элементарные функции, то заранее известно сколько и есть ли асимптоты. Например, у параболы, кубической параболы, синусоиды вообще нет никаких. У графиков функций таких как логарифмическая или экспоненциальная есть по одной. А у функций тангенса и котангенса бесчисленное множество асимптот, но арктангенс и арккатангенс имеет по две штуки.
Во всех приведенных примерах пределы вычислялись с помощью правило Лопиталя, которое очень ускоряет процесс вычисления и создает меньше ошибок.
Построение графика
функции значительно облегчается, если
знать его асимптоты.
Определение.
Асимптотой
кривой называется прямая, расстояние
до которой от точки, лежащей на кривой,
стремится к нулю при неограниченном
удалении от начала координат этой точки
по кривой (рис.5.10).
Асимптоты бывают
вертикальные (параллельные оси Оу),
горизонтальные (параллельные оси Ох)
и наклонные.
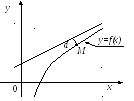
Рис. 5.10
Вертикальные асимптоты
Определение.
Прямая
![]() называетсявертикальной
называетсявертикальной
асимптотой графика
функции
![]() ,
,
если выполнено одно из условий:
![]() или
или
![]() (рис.5.11)
(рис.5.11)

Рис. 5.11
Вертикальные
асимптоты, уравнение которых х=x0
, следует
искать в точках, где функция терпит
разрыв второго рода, или на концах ее
области определения, если концы не равны
![]() .
.
Если таких точек нет, то нет и вертикальных
асимптот.
Например, для
кривой
![]() ,
,
вертикальной асимптотой будет прямая![]() ,
,
так как![]() ,
,![]() .
.
Вертикальной асимптотой графика функции![]() является прямая
является прямая![]() (осьОу),
(осьОу),
поскольку
![]() .
.
Горизонтальные асимптоты
Определение.
Если при
![]() (
(![]() )
)
функция![]() имеет конечный предел, равный числуb:
имеет конечный предел, равный числуb:
 ,
,
то прямая
![]() есть горизонтальная асимптота графика
есть горизонтальная асимптота графика
функции![]() .
.
Например, для
функции
![]() имеем
имеем
![]() ,
,
![]() .
.
Соответственно,
прямая
![]() − горизонтальная асимптота для правой
− горизонтальная асимптота для правой
ветви графика функции![]() ,
,
а прямая![]() − для левой ветви.
− для левой ветви.
В том случае, если
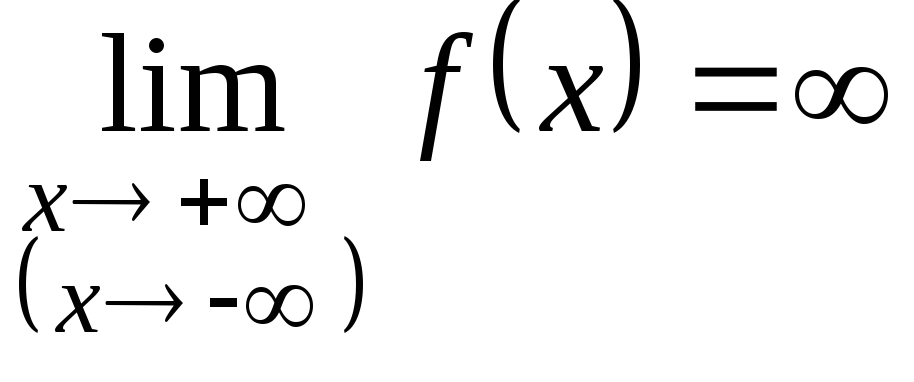 ,
,
график функции не
имеет горизонтальных асимптот, но может
иметь наклонные.
Наклонные асимптоты
Определение.
Прямая
![]() называетсянаклонной
называетсянаклонной
асимптотой
графика функции
![]() при
при![]() (
(![]() ),
),
если выполняется равенство
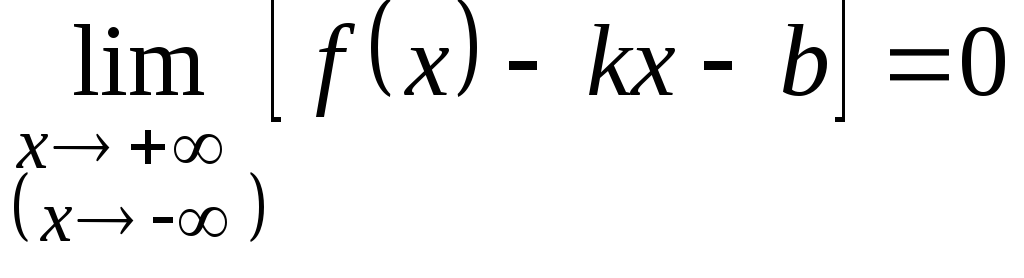 .
.
Наличие наклонной
асимптоты устанавливают с помощью
следующей теоремы.
Теорема.
Для того, чтобы
график функции
![]() имел при
имел при![]() (
(![]() )
)
наклонную асимптоту![]() ,
,
необходимо и достаточно, чтобы существовали
конечные пределы
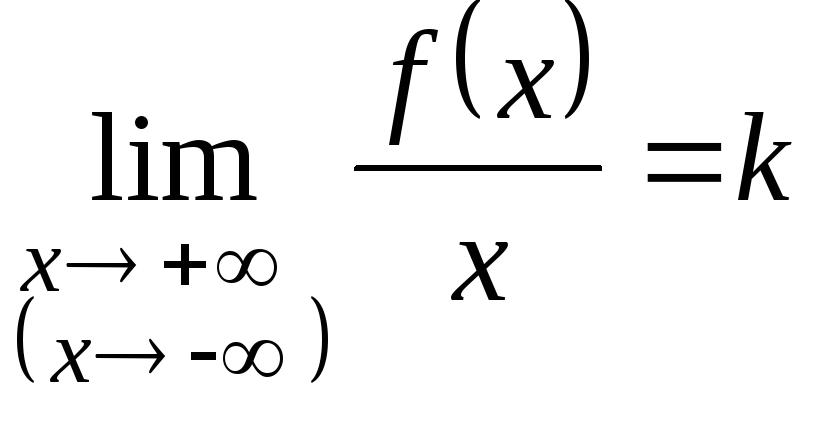 и
и
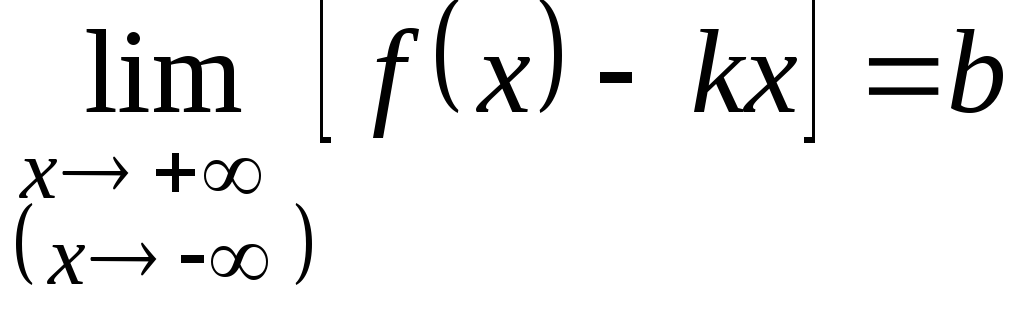 .
.
Если хотя бы один
из этих пределов не существует или равен
бесконечности, то кривая
![]() наклонной асимптоты не имеет.
наклонной асимптоты не имеет.
Замечания.
1. При отыскании
асимптот следует отдельно рассматривать
случаи
![]() и
и![]() .
.
2. Если
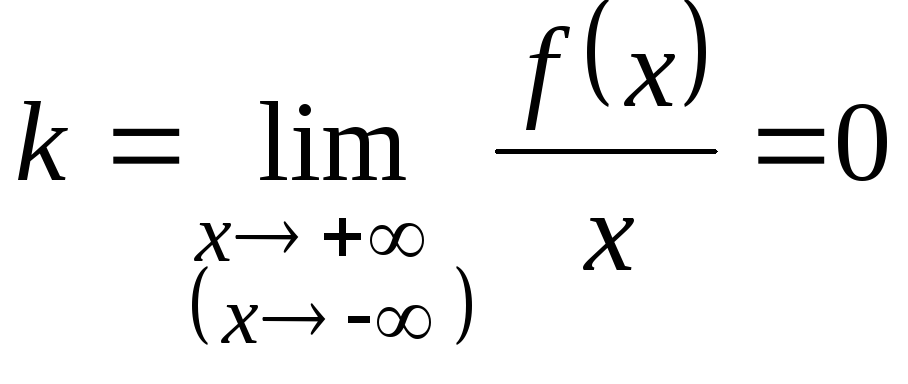 и
и
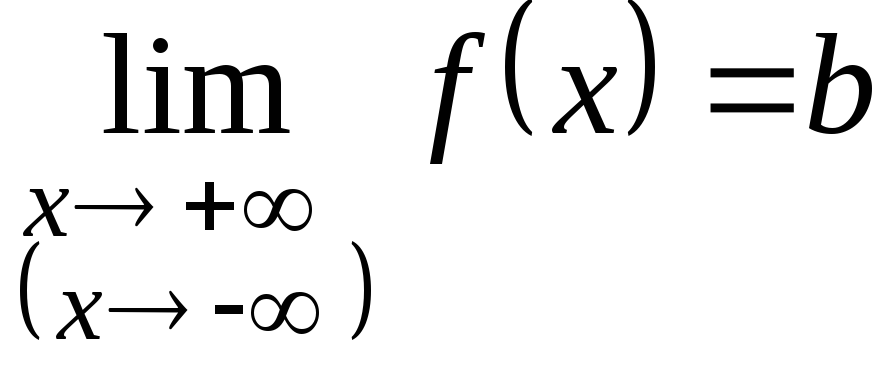 ,
,
то график функции
![]() имеет горизонтальную асимптоту
имеет горизонтальную асимптоту![]() .
.
3. Если
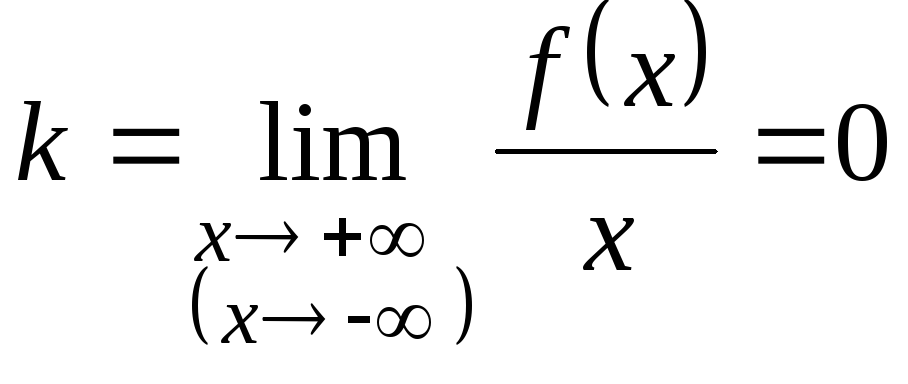 и
и
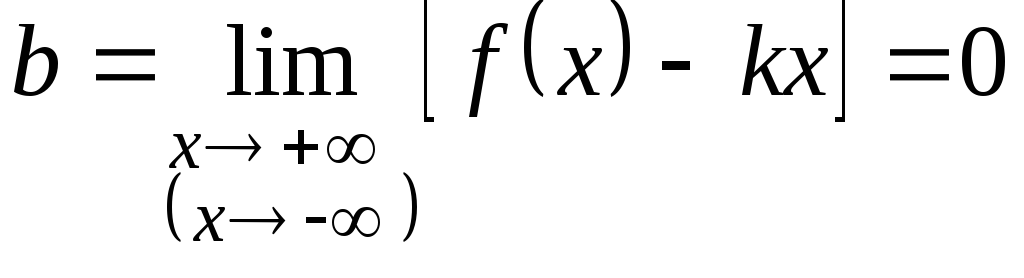 ,
,
то прямая
![]() (осьОх)
(осьОх)
является горизонтальной асимптотой
графика функции
![]() .
.
Из замечаний
следует, что горизонтальную асимптоту
можно рассматривать как частный случай
наклонной асимптоты при
![]() .
.
Поэтому при отыскании асимптот графика
функции рассматривают лишь два случая:
1) вертикальные
асимптоты,
2) наклонные
асимптоты.
Пример
Найти асимптоты
графика функции
![]() .
.
![]() .
.
1)
![]() − точка разрыва второго рода:
− точка разрыва второго рода:
![]() ,
,
![]() .
.
Прямая
![]() − вертикальная асимптота.
− вертикальная асимптота.
2)
![]() ,
,
![]() ,
,
![]() .
.
Прямая
![]() − горизонтальная асимптота. Наклонной
− горизонтальная асимптота. Наклонной
асимптоты нет.
5.6. Общая схема исследования функции и построение графика
В предыдущих
параграфах было показано, как с помощью
производных двух первых порядков
изучаются общие свойства функции.
Пользуясь результатами этого изучения,
можно составить представление о характере
функции и, в частности, построить ее
график.
Исследование
функции
![]() целесообразно проводить по следующей
целесообразно проводить по следующей
схеме.
-
Найти область
определения функции. -
Исследовать
функцию на четность и нечетность. -
Исследовать
функцию на периодичность. -
Найти точки
пересечения графика функции с осями
координат. -
Найти интервалы
знакопостоянства функции (интервалы,
на которых
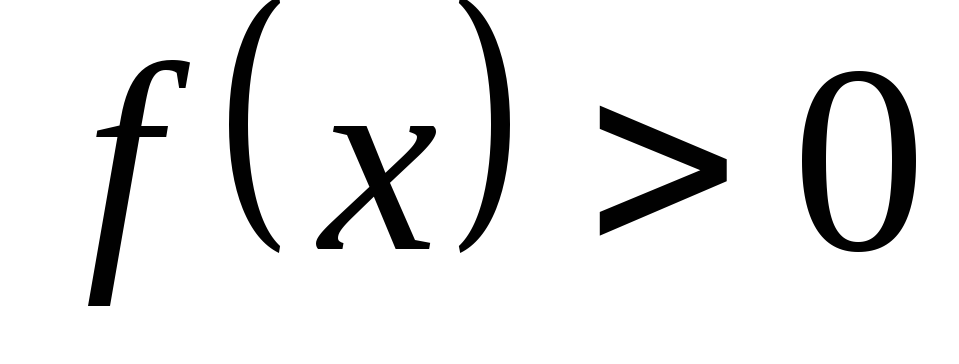 или
или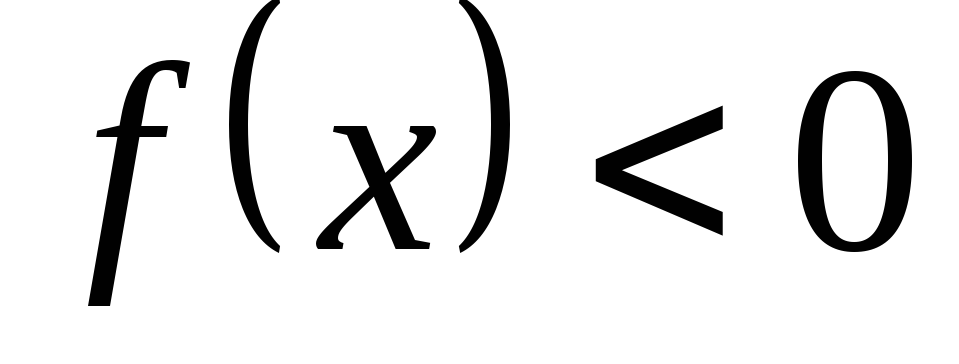 ).
). -
Найти асимптоты
графика функции. -
Найти интервалы
монотонности и точки экстремума функции. -
Найти интервалы
выпуклости и вогнутости и точки перегиба
графика функции. -
Построить график
функции.
Пример
Исследовать функцию
![]() и построить ее график.
и построить ее график.
-
Область определения
функции
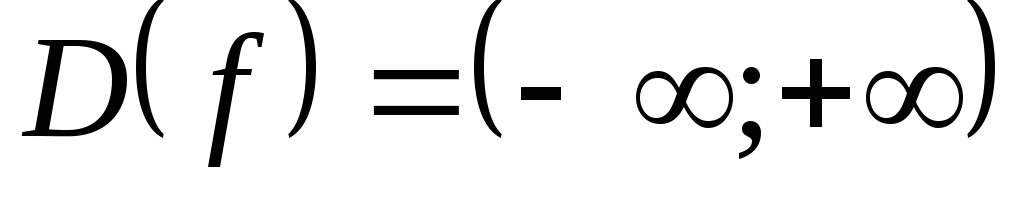 .
. -
Функция нечетная:
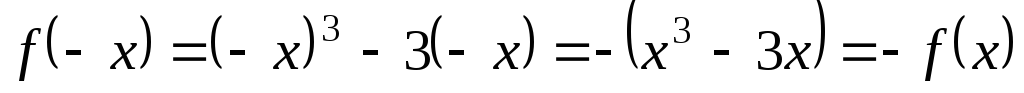 .
.
График функции симметричен относительно
начала координат -
Функция
непериодическая. -
Точки пересечения
с осями координат:
С осью Оу:
![]() ,
,
точка![]() .
.
С осью Ох:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
-
Точки
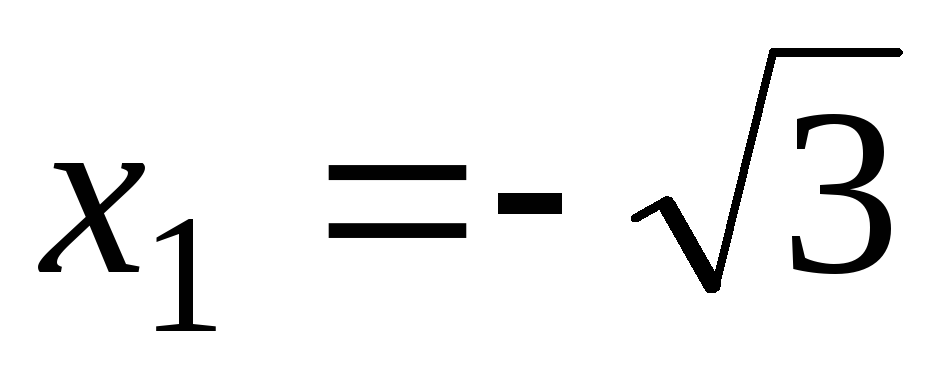 ,
,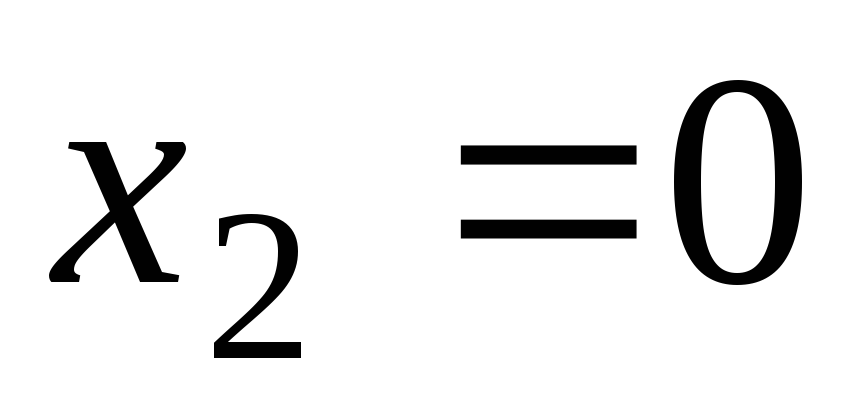 и
и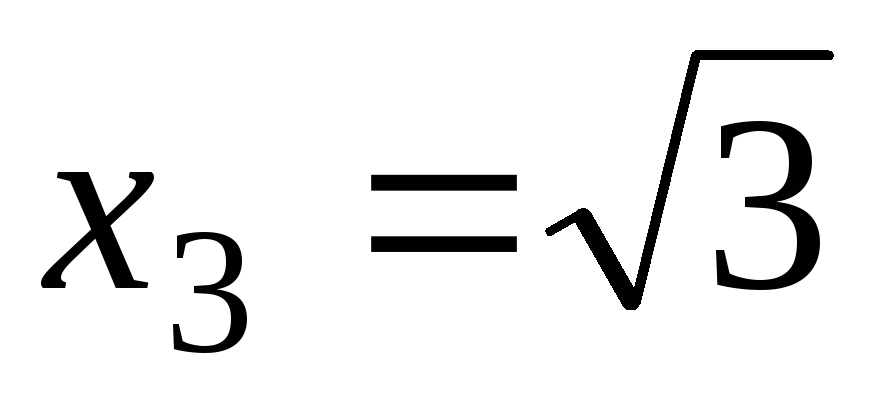 разбивают осьОх
разбивают осьОх
на четыре интервала.
![]() при
при
![]() ;
;
![]() при
при
![]() ;
;
![]() при
при
![]() ;
;
![]() при
при
![]() .
.
-
Так как функция
является непрерывной, то ее график не
имеет вертикальных асимптот.
![]() .
.
Наклонной и
горизонтальной асимптот нет.
-
 ,
,
![]() ,
,
![]() ,
,![]() − критические точки.
− критические точки.
![]() для
для
![]() «↑»,
«↑»,
![]() для
для
![]() «↓»,
«↓»,
![]() для
для
![]() «↑».
«↑».
Сведем данные в
таблицу.
|
х |
|
-1 |
|
1 |
|
|
|
+ |
0 |
− |
0 |
+ |
|
|
↑ (возрастает) |
mах 2 |
↓ (убывает) |
min -2 |
↑ (возрастает) |
![]() ,
,
![]() ;
;
точка
![]() − максимум;
− максимум;
точка
![]() − минимум.
− минимум.
-
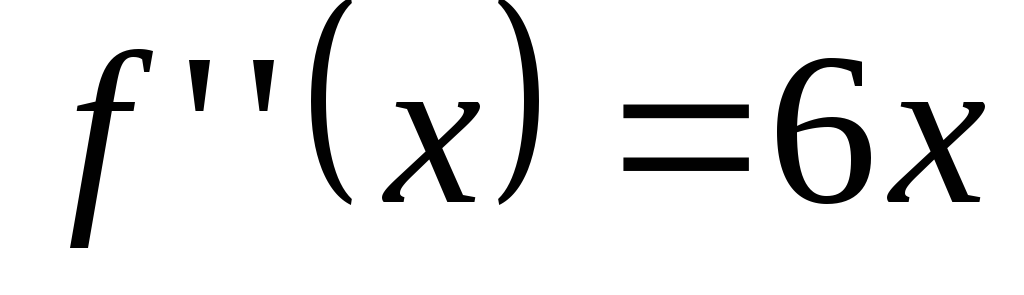 ,
,
 ,
,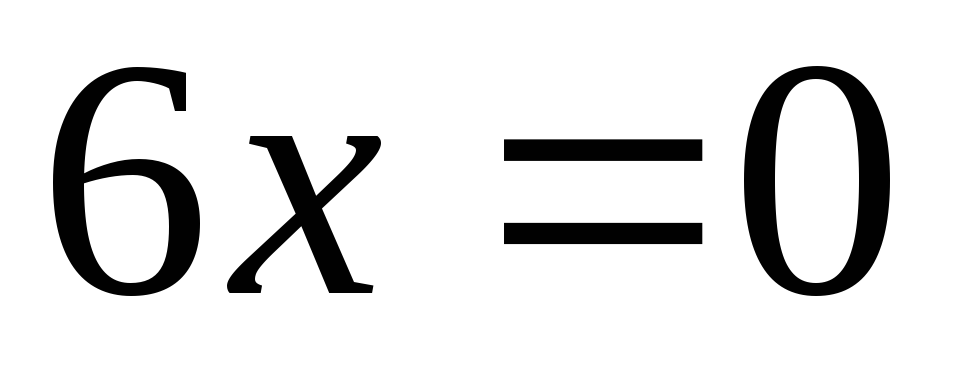 ,
, .
.
![]() при
при
![]() «
«![]() »;
»;
![]() при
при
![]() «
«![]() ».
».
|
х |
|
0 |
|
|
|
− |
0 |
+ |
|
|
(выпуклый) |
0 (точка перегиба) |
(вогнутый) |
Точка
![]() − точка перегиба.
− точка перегиба.
-
График функции
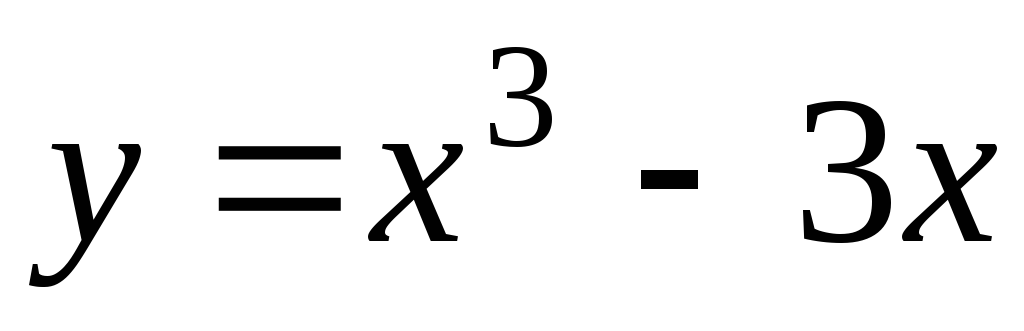 (рис.5.12)
(рис.5.12)

Рис. 5.12
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Понятие асимптоты
- Вертикальная асимптота
- Горизонтальная асимптота
- Наклонная асимптота
- Алгоритм исследования асимптотического поведения функции
- Примеры
п.1. Понятие асимптоты
Асимптота прямая, расстояние от которой до точки кривой стремится к нулю при удалении точки вдоль ветви кривой на бесконечность.
Различают вертикальные, горизонтальные и наклонные асимптоты.
Например:
п.2. Вертикальная асимптота
Вертикальная асимптота кривой (y=f(x)) имеет вид: (x=a)
где (a) – точка разрыва 2-го рода функции (f(x)), для которой хотя бы один односторонний предел существует и равен бесконечности.
Таким образом, практически каждой точке разрыва 2-го рода (см. §40 данного справочника) соответствует вертикальная асимптота.
Вертикальных асимптот может быть сколько угодно, в том числе, бесконечное множество (например, как у тангенса – см. §6 данного справочника).
Например:
Исследуем непрерывность функции (y=frac{1}{(x-1)(x+3)})
ОДЗ: (xne left{-3;1right})
(left{x_0=-3, x_1=1right}notin D) – точки не входят в ОДЗ, подозрительные на разрыв.
Исследуем (x_0=-3). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -3 -0}frac{1}{(x-1)(x+3)}=frac{1}{(-3-0-1)(-3-0+3)}=frac{1}{-4cdot(-0)}=+infty\ lim_{xrightarrow -3 +0}frac{1}{(x-1)(x+3)}=frac{1}{(-3+0-1)(-3+0+3)}=frac{1}{-4cdot(+0)}=-infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_0=-3) – точка разрыва 2-го рода.
Исследуем (x_1=1). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 1 -0}frac{1}{(x-1)(x+3)}=frac{1}{(1-0-1)(1-0+3)}=frac{1}{-0cdot 4}=-infty\ lim_{xrightarrow 1 +0}frac{1}{(x-1)(x+3)}=frac{1}{(1+0-1)(1+0+3)}=frac{1}{+0cdot 4}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_1=1) – точка разрыва 2-го рода.
Вывод: у функции (y=frac{1}{(x-1)(x+3)}) две точки разрыва 2-го рода (left{x_0=-3, x_1=1right}), соответственно – две вертикальные асимптоты с уравнениями (x=-3) и (x=1).
п.3. Горизонтальная асимптота
Горизонтальная асимптота кривой (y=f(x)) имеет вид: (y=b)
где (b) – конечный предел функции (f(x)) на бесконечности: (b=lim{xrightarrow pminfty}f(x), bneinfty)
Число горизонтальных асимптот не может быть больше двух.
Например:
Исследуем наличие горизонтальных асимптот у функции (y=frac{1}{(x-1)(x+3)})
Ищем предел функции на минус бесконечности: begin{gather*} lim_{xrightarrow -infty}frac{1}{(x-1)(x+3)}=frac{1}{(-infty)(-infty)}=+0 end{gather*} На минус бесконечности функция имеет конечный предел (b=0) и стремится к нему сверху (о чем свидетельствует символическая запись +0).
Ищем предел функции на плюс бесконечности: begin{gather*} lim_{xrightarrow +infty}frac{1}{(x-1)(x+3)}=frac{1}{(+infty)(+infty)}=+0 end{gather*} На плюс бесконечности функция имеет тот же конечный предел (b=0) и также стремится к нему сверху.
Вывод: у функции (y=frac{1}{(x-1)(x+3)}) одна горизонтальная асимптота (y=0). На плюс и минус бесконечности функция стремится к асимптоте сверху.
Итоговый график асимптотического поведения функции (y=frac{1}{(x-1)(x+3)}): 
п.4. Наклонная асимптота
Наклонная асимптота кривой (y=f(x)) имеет вид: (y=kx+b) begin{gather*} k=lim_{xrightarrow pminfty}frac{f(x)}{x}, kne 0, kneinfty\ b=lim_{xrightarrow pminfty}(f(x)=kx) end{gather*}
Число наклонных асимптот не может быть больше двух.
Например:
Исследуем наличие наклонных асимптот у функции (y=frac{x^2+3}{x-1})
Найдем угловой коэффициент: begin{gather*} k_1=lim_{xrightarrow -infty}frac{y}{x}=lim_{xrightarrow -infty}frac{x^2+3}{x(x-1)}= lim_{xrightarrow -infty}frac{x^2+3}{x^2-x}=left[frac{infty}{infty}right]= lim_{xrightarrow -infty}frac{x^2left(1+frac{3}{x^2}right)}{x^2left(1-frac 1xright)}=\ =lim_{xrightarrow -infty}frac{1+frac{3}{x^2}}{1-frac1x}=frac{1+0}{1-0}=1\ k_2=lim_{xrightarrow +infty}frac{y}{x}=lim_{xrightarrow +infty}frac{x^2+3}{x(x-1)}=k_1=1 end{gather*} На плюс и минус бесконечности отношение функции к аргументу имеет один и тот же конечный предел (k=1).
Найдем свободный член: begin{gather*} b=lim_{xrightarrow pminfty}(y-kx)=lim_{xrightarrow pminfty}left(frac{x^2+3}{x-1}-1cdot xright)= lim_{xrightarrow pminfty}left(frac{x^2+3-x(x-1)}{x-1}right)=\ =lim_{xrightarrow pminfty}frac{x+3}{x-1}=left[frac{infty}{infty}right]=lim_{xrightarrow pminfty}frac{xleft(1+frac3xright)}{xleft(1-frac1xright)}=frac{1+0}{1-0}=1 end{gather*} Вывод: у функции (y=frac{x^2+3}{x-1}) одна наклонная асимптота (y=x+1). Функция стремится к асимптоте на плюс и минус бесконечности.
Чтобы построить график асимптотического поведения, заметим, что у функции (y=frac{x^2+3}{x-1}), очевидно, есть вертикальная асимптота x=1. При этом: begin{gather*} lim_{xrightarrow -1-0}frac{x^2+3}{x-1}=-infty, lim_{xrightarrow -1+0}frac{x^2+3}{x-1}=+infty end{gather*}
График асимптотического поведения функции (y=frac{x^2+3}{x-1}): 
п.5. Алгоритм исследования асимптотического поведения функции
На входе: функция (y=f(x))
Шаг 1. Поиск вертикальных асимптот
Исследовать функцию на непрерывность. Если обнаружены точки разрыва 2-го рода, у которых хотя бы один односторонний предел существует и бесконечен, сопоставить каждой такой точке вертикальную асимптоту. Если таких точек не обнаружено, вертикальных асимптот нет.
Шаг 2. Поиск горизонтальных асимптот
Найти пределы функции на плюс и минус бесконечности. Каждому конечному пределу сопоставить горизонтальную асимптоту. Если оба предела конечны и равны, у функции одна горизонтальная асимптота. Если оба предела бесконечны, горизонтальных асимптот нет.
Шаг 3. Поиск наклонных асимптот
Найти пределы отношения функции к аргументу на плюс и минус бесконечности.
Каждому конечному пределу k сопоставить наклонную асимптоту, найти b. Если только один предел конечен, у функции одна наклонная асимптота. Если оба значения k конечны и равны, и оба значения b равны, у функции одна наклонная асимптота. Если оба предела для k бесконечны, наклонных асимптот нет .
На выходе: множество всех асимптот данной функции.
п.6. Примеры
Пример 1. Исследовать асимптотическое поведение функции и построить схематический график:
a) ( y=frac{4x}{x^2-1} )
1) Вертикальные асимптоты
Точки, подозрительные на разрыв: (x=pm 1)
Односторонние пределы в точке (x=-1) begin{gather*} lim_{xrightarrow -1-0}frac{4x}{(x+1)(x-1)}=frac{4(-1-0)}{(-1-0+1)(-1-0-1)}=frac{-4}{-0cdot(-2)}=-infty\ lim_{xrightarrow -1+0}frac{4x}{(x+1)(x-1)}=frac{4(-1+0)}{(-1+0+1)(-1+0-1)}=frac{-4}{+0cdot(-2)}=+infty end{gather*} Точка (x=-1) – точка разрыва 2-го рода
Односторонние пределы в точке (x=1) begin{gather*} lim_{xrightarrow -1-0}frac{4x}{(x+1)(x-1)}=frac{4(1-0)}{(1-0+1)(1-0-1)}=frac{4}{2cdot(-0)}=-infty\ lim_{xrightarrow -1+0}frac{4x}{(x+1)(x-1)}=frac{4(1+0)}{(1+0+1)(1+0-1)}=frac{4}{2cdot(+0)}=+infty end{gather*} Точка (x=1) – точка разрыва 2-го рода
Функция имеет две вертикальные асимптоты (x=pm 1)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin{gather*} b_1=lim_{xrightarrow -infty}frac{4x}{x^2-1}=left[frac{infty}{infty}right]=lim_{xrightarrow -infty}frac{x^2cdot frac4x}{x^2(1-frac{1}{x^2})}=lim_{xrightarrow -infty}frac{frac4x}{1-frac{1}{x^2}}=frac{-0}{1}=-0\ b_2=lim_{xrightarrow +infty}frac{4x}{x^2-1}=left[frac{infty}{infty}right]=lim_{xrightarrow +infty}frac{frac4x}{1-frac{1}{x^2}}=frac{+0}{1}=+0 end{gather*} Функция имеет одну горизонтальную асимптоту (y=0). На минус бесконечности функция стремится к асимптоте снизу, не плюс бесконечности – сверху.
3) Наклонные асимптоты
Ищем угловые коэффициенты: begin{gather*} k=lim_{xrightarrow pminfty}frac{4x}{x(x^2-1)}=lim_{xrightarrow pminfty}frac{4}{x^2-1}=frac{4}{infty}=0 end{gather*} Наклонных асимптот нет.
График асимптотического поведения функции (y=frac{4x}{x^2-1})
б) ( y=e^{frac{1}{x+3}} )
1) Вертикальные асимптоты
Точка, подозрительная на разрыв: (x=-3)
Односторонние пределы: begin{gather*} lim_{xrightarrow -3-0}e^{frac{1}{x+3}}=e^{frac{1}{-3-0)+3}}=e^{frac{1}{-0}}=e^infty=0\ lim_{xrightarrow -3+0}e^{frac{1}{x+3}}=e^{frac{1}{-3+0)+3}}=e^{frac{1}{+0}}=e^{+infty}=+infty end{gather*} Точка (x=-3) – точка разрыва 2-го рода
Функция имеет одну вертикальную асимптоту (x=2)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin{gather*} b_1=lim_{xrightarrow -infty}e^{frac{1}{x+3}}=e^0=1\ b_2=lim_{xrightarrow +infty}e^{frac{1}{x+3}}=e^0=1\ b=b_1=b_2=1 end{gather*} Функция имеет одну горизонтальную асимптоту (y=1). Функция стремится к этой асимптоте на минус и плюс бесконечности.
3) Наклонные асимптоты
Ищем угловые коэффициенты: begin{gather*} k_1=lim_{xrightarrow -infty}frac{e^{frac{1}{x+3}}}{x}=frac{e^0}{-infty}=0\ k_2=lim_{xrightarrow +infty}frac{e^{frac{1}{x+3}}}{x}=frac{e^0}{+infty}=0 end{gather*} Наклонных асимптот нет.
График асимптотического поведения функции (y=e^{frac{1}{x+3}})
в) ( y=frac{x^3+x^2+x+1}{x^2-1} )
Заметим, что ( frac{x^3+x^2+x+1}{x^2-1}=frac{x^2(x+1)+(x+1)}{(x+1)(x-1)}=frac{(x^2)(x+1)}{(x+1)(x-1)}=frac{x^2+1}{x-1} ) $$ y=frac{x^3+x^2+x+1}{x^2-1}Leftrightarrow begin{cases} y=frac{x^2+1}{x-1}\ xne -1 end{cases} $$ График исходной функции совпадает с графиком функции (y=frac{x^2+1}{x-1}), из которого необходимо выколоть точку c абсциссой (x=-1).
1) Вертикальные асимптоты
Точки, подозрительные на разрыв: (x=pm 1)
Односторонние пределы в точке (x=-1) begin{gather*} lim_{xrightarrow -1-0}frac{x^3+x^2+x+1}{x^2-1}=lim_{xrightarrow -1-0}frac{x^2+1}{x-1}=frac{2}{-2}=-1\ lim_{xrightarrow -1+0}frac{x^3+x^2+x+1}{x^2-1}=lim_{xrightarrow -1-0}frac{x^2+1}{x-1}=frac{2}{-2}=-1 end{gather*} Точка (x=-1) – точка разрыва 1-го рода, устранимый разрыв («выколотая» точка).
Односторонние пределы в точке (x=1) begin{gather*} lim_{xrightarrow 1-0}frac{x^3+x^2+x+1}{x^2-1}=lim_{xrightarrow 1-0}frac{x^2+1}{x-1}=frac{2}{1-0-1}=frac{2}{-0}=-infty\ lim_{xrightarrow 1-0}frac{x^3+x^2+x+1}{x^2-1}=lim_{xrightarrow 1-0}frac{x^2+1}{x-1}=frac{2}{1+0-1}=frac{2}{+0}=+infty end{gather*} Точка (x=1) – точка разрыва 2-го рода
Функция имеет одну вертикальную асимптоту (x=1)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin{gather*} b_1=lim_{xrightarrow -infty}frac{x^2+1}{x-1}=left[frac{infty}{infty}right]=lim_{xrightarrow -infty}frac{x^2left(1+frac{1}{x^2}right)}{x^2left(frac1x-frac{1}{x^2}right)}=frac{1+0}{-0-0}=-infty\ b_2=lim_{xrightarrow +infty}frac{x^2+1}{x-1}=left[frac{infty}{infty}right]=lim_{xrightarrow +infty}frac{x^2left(1+frac{1}{x^2}right)}{x^2left(frac1x-frac{1}{x^2}right)}=frac{1+0}{0-0}=+infty end{gather*} Оба предела бесконечны.
Функция не имеет горизонтальных асимптот.
3) Наклонные асимптоты
Ищем угловые коэффициенты: begin{gather*} k_1=lim_{xrightarrow -infty}frac{x^2+1}{x(x-1)}=left[frac{infty}{infty}right]=lim_{xrightarrow -infty}frac{x^2left(1+frac{1}{x^2}right)}{x^2left(1-frac1xright)}=frac{1+0}{1-0}=1\ k_2=lim_{xrightarrow +infty}frac{x^2+1}{x(x-1)}=left[frac{infty}{infty}right]=lim_{xrightarrow +infty}frac{x^2left(1+frac{1}{x^2}right)}{x^2left(1-frac1xright)}=frac{1+0}{1-0}=1\ k=k_1=k_2=1 end{gather*} У функции есть одна наклонная асимптота с (k=1).
Ищем свободный член: begin{gather*} b=lim_{xrightarrow infty}(y-kx)= lim_{xrightarrow infty}left(frac{x^2+1}{x-1}-2right)= lim_{xrightarrow infty}frac{x^2+1-x^2+x}{x-1}= lim_{xrightarrow infty}frac{x+1}{x-1}=left[frac{infty}{infty}right]=\ =lim_{xrightarrow infty}frac{xleft(1+frac1xright)}{xleft(1-frac1xright)}=frac{1+0}{1-0}=1 end{gather*} Функция имеет одну наклонную асимптоту (y=x+1).
График асимптотического поведения функции (y=frac{x^3+x^2+x+1}{x^2-1})
г*) ( y=xe^{frac{1}{2-x}} )
1) Вертикальные асимптоты
Точка, подозрительная на разрыв: (x=2)
Односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}xe^{frac{1}{2-x}}=(2-0)e^{frac{1}{2-(2-0)}}=2e^{frac{1}{+0}}=2e^{+infty}=+infty\ lim_{xrightarrow 2+0}xe^{frac{1}{2-x}}=(2+0)e^{frac{1}{2-(2+0)}}=2e^{frac{1}{-0}}=2e^{-infty}=-infty end{gather*} Точка (x=2) – точка разрыва 2-го рода.
Функция имеет одну вертикальную асимптоту (x=2)
2) Горизонтальные асимптоты
Пределы функции на бесконечности: begin{gather*} b_1=lim_{xrightarrow -infty}xe^{frac{1}{2-x}}=-inftycdot e^0=-infty\ b_2=lim_{xrightarrow +infty}xe^{frac{1}{2-x}}=+inftycdot e^0=+infty end{gather*} Оба предела бесконечны.
Функция не имеет горизонтальных асимптот.
3) Наклонные асимптоты
Ищем угловые коэффициенты: begin{gather*} k_1=lim_{xrightarrow -infty}frac{xe^{frac{1}{2-x}}}{x}=lim_{xrightarrow -infty}e^{frac{1}{2-x}}=e^0=1\ k_2=lim_{xrightarrow +infty}frac{xe^{frac{1}{2-x}}}{x}=lim_{xrightarrow +infty}e^{frac{1}{2-x}}=e^0=1\ k=k_1=k_2=1 end{gather*} У функции есть одна наклонная асимптота с (k=1).
Ищем свободный член: begin{gather*} b=lim_{xrightarrow infty}(y-kx)= lim_{xrightarrow infty}left(xe^{frac{1}{2-x}}-xright)=lim_{xrightarrow infty}xleft(e^{frac{1}{2-x}}-1right)=left[inftycdot 0right] end{gather*} Используем одно из следствий второго замечательного предела (см. §39 данного справочника): begin{gather*} lim_{xrightarrow 0}frac{e^x-1}{x}=1\ b=lim_{xrightarrow infty}xleft(e^{frac{1}{2-x}}-1right)= left[ begin{array}{l} t=frac{1}{2-x}\ trightarrow 0\ x=2-frac1t=frac{2t-1}{t} end{array} right]=\ =lim_{trightarrow 0}left(left(frac{2t-1}{t}right)(e^t-1)right)=lim_{trightarrow 0}(2t-1)cdot lim_{trightarrow 0}frac{e^t-1}{t}=-1cdot 1=-1 end{gather*} Функция имеет одну наклонную асимптоту (y=x-1).
График асимптотического поведения функции (y=xe^{frac{1}{2-x}})

Для гиперболы 
Асимпто́та, или аси́мптота[1] (от др.-греч. ἀσύμπτωτος — несовпадающая, не касающаяся кривой с бесконечной ветвью) — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность[2]. Термин впервые появился у Аполлония Пергского, хотя асимптоты гиперболы исследовал ещё Архимед[3].
Затухающие колебания. 

Пример асимптоты для кривой в пространстве. Спираль бесконечно приближается к прямой
Виды асимптот графиков[править | править код]
Вертикальная[править | править код]
Прямая вида 
.
Вертикальных асимптот может быть любое количество.
Прямая не может быть вертикальной асимптотой, если функция непрерывна в точке 
Горизонтальная и наклонная[править | править код]

На графике функции x+1/x, ось y (x = 0) и линия y=x являются асимптотами.
Наклонная асимптота — прямая вида 
.
При этом, если выполняется первое условие, то говорят, что эта прямая является асимптотой при 

Если 
Замечание 1: Число наклонных асимптот у функции не может быть больше двух: одна при 

Замечание 2: Некоторые источники включают требование, чтобы кривая не пересекала эту прямую в окрестности бесконечности[5].
Замечание 3: В некоторых случаях, таких как алгебраическая геометрия, асимптота определена, как прямая, которая является «касательной» к кривой на бесконечности[5].

Функция y=arctgx с двумя горизонтальными асимптотами
Нахождение асимптот[править | править код]
Порядок нахождения асимптот[править | править код]
- Нахождение точек разрыва, выбор точек, в которых есть вертикальная асимптота (прямой проверкой, что предел в этой точке есть бесконечность).
- Проверка, не являются ли конечными пределы
и
. Если да, то существует горизонтальная асимптота
при
и
соответственно.
- Нахождение двух пределов
- Нахождение двух пределов
, если хотя бы один из пределов в пункте 3 или 4 не существует (или равен
), то наклонной асимптоты при
(или
) не существует.
Наклонная асимптота — выделение целой части[править | править код]

Также наклонную асимптоту можно найти, выделив целую часть. Например:
Дана функция 
Разделив нацело числитель на знаменатель, получим: 
При 

и 
Свойства[править | править код]
- Среди конических сечений асимптоты имеют только гиперболы. Асимптоты гиперболы как конического сечения параллельны образующим конуса, лежащим в плоскости, проходящей через вершину конуса параллельно секущей плоскости[6]. Максимальный угол между асимптотами гиперболы для данного конуса равен углу раствора конуса и достигается при секущей плоскости, параллельной оси конуса.
См. также[править | править код]
- Асимптотическая кривая
Примечания[править | править код]
- ↑ Двойное ударение указано в Советском энциклопедическом словаре. В словарях XIX и первой половины XX века (например, в кн.: Словарь иностранных слов / Под ред. И. В. Лёхина и проф. Ф. Н. Петрова. — М.: Гос. изд-во иностр. и нац. словарей, 1955. — С. 77. — 856 с.) указывался единственный вариант ударения «асимпто́та».
- ↑ Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 1. Архивная копия от 13 ноября 2013 на Wayback Machine
- ↑ Математический энциклопедический словарь Архивная копия от 1 августа 2013 на Wayback Machine — М.: Советская энциклопедия, 1988. — 847 с.
- ↑ Кудрявцев Л. Д. Курс математического анализа. — 5-е изд. — М.: «Дрофа», 2003. — Т. 1. — С. 374-375. — 704 с. — ISBN 5-7107-4119-1.
- ↑ 1 2 «Asymptotes» by Louis A. Talman
- ↑ Taylor C. Geometrical Conics; Including Anharmonic Ratio and Projection, With Numerous Examples. — Cambridge: Macmillan, 1863. — С. 170.
Литература[править | править код]
- Рашевский П. К. Курс дифференциальной геометрии, 4-е изд. М., 1956.
- Графики функций: Справочник / Вирченко Н. А., Ляшко И. И., Швецов К. И. — Киев: Наук. думка, 1979, — 320 с.
Ссылки[править | править код]
- Асимптота // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Асимптота / Э. Г. Позняк // Ангола — Барзас. — М. : Советская энциклопедия, 1970. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 2).
Содержание:
Понятие асимптоты:
Асимптота кривой — это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность.
Вертикальные асимптоты 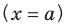
 — вертикальная асимптота, если при
— вертикальная асимптота, если при 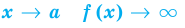
Вертикальная асимптота 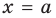 может быть в точке
может быть в точке 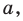 если точка
если точка 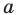 ограничивает открытые (или полуоткрытые) промежутки области определения данной функции и вблизи точки
ограничивает открытые (или полуоткрытые) промежутки области определения данной функции и вблизи точки 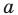 значения функции стремятся к бесконечности.
значения функции стремятся к бесконечности.
Примеры вертикальных асимптот графиков функций
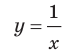
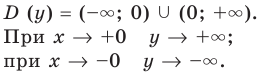
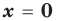 — вертикальная асимптота (
— вертикальная асимптота (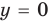 — также асимптота, но горизонтальная)
— также асимптота, но горизонтальная)
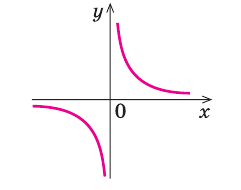
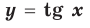
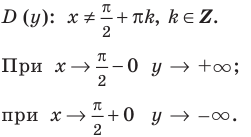
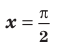 — вертикальная асимптота
— вертикальная асимптота
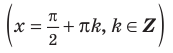
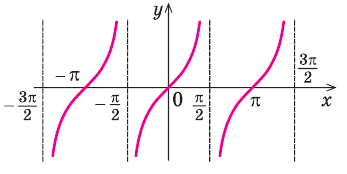
Наклонные и горизонтальные асимптоты 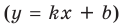
I. Если  — дробно рациональная функция, у которой степень числителя на единицу больше степени знаменателя (или равна ей), то выделяем целую часть дроби и используем определение асимптоты.
— дробно рациональная функция, у которой степень числителя на единицу больше степени знаменателя (или равна ей), то выделяем целую часть дроби и используем определение асимптоты.
Примеры:
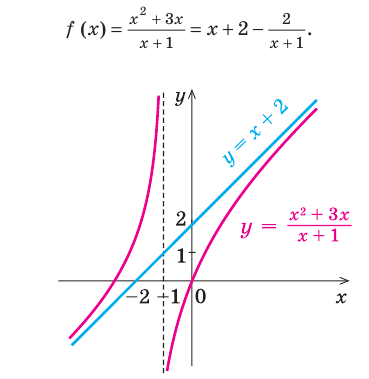
При  тогда
тогда  Следовательно,
Следовательно, 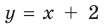 — наклонная асимптота (также
— наклонная асимптота (также 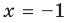 — вертикальная асимптота)
— вертикальная асимптота)
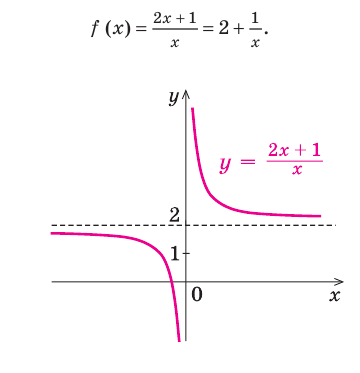
При 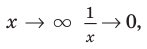 тогда
тогда 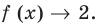 Следовательно,
Следовательно, 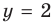 — горизонтальная асимптота (также
— горизонтальная асимптота (также 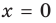 — вертикальная асимптота)
— вертикальная асимптота)
II. В общем случае уравнения наклонных и горизонтальных асимптот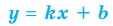 можно получить с использованием формул
можно получить с использованием формул
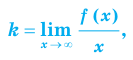
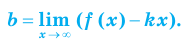
Понятие асимптоты
Если кривая 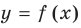 имеет бесконечную ветвь, то асимптотой такой кривой называют прямую, к которой эта ветвь неограниченно приближается. Другими словами, асимптота кривой — это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность.
имеет бесконечную ветвь, то асимптотой такой кривой называют прямую, к которой эта ветвь неограниченно приближается. Другими словами, асимптота кривой — это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность.
Асимптоты могут быть вертикальными, горизонтальными или наклонными.
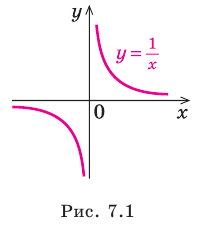
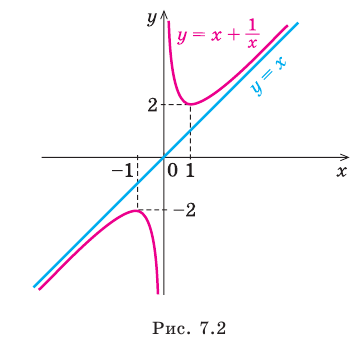
Например, для графика функции 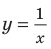 (рис. 7.1) асимптотами будут оси координат, поскольку при
(рис. 7.1) асимптотами будут оси координат, поскольку при 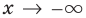 и при
и при 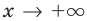 график функции приближается к прямой
график функции приближается к прямой 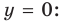 ось
ось 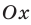 — горизонтальная асимптота. Когда функция стремится к
— горизонтальная асимптота. Когда функция стремится к 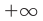 (или
(или 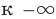 ), то кривая приближается к прямой
), то кривая приближается к прямой 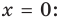 ось
ось 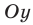 — вертикальная асимптота.
— вертикальная асимптота.
Если рассмотреть функцию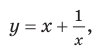 то при
то при 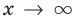 выражение
выражение 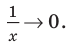 Вследствие этого график функции
Вследствие этого график функции 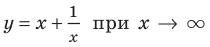 приближается к прямой
приближается к прямой 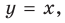 поэтому эта прямая будет наклонной асимптотой графика функции
поэтому эта прямая будет наклонной асимптотой графика функции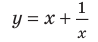 (рис. 7.2) (график этой функции имеет также и вертикальную асимптоту
(рис. 7.2) (график этой функции имеет также и вертикальную асимптоту 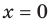 ).
).
Следует отметить, что не любая кривая имеет асимптоту, поэтому не у каждого графика функции будет асимптота. Но исследование функции на наличие у ее графика асимптот позволяет уточнить свойства функции и поведение ее графика.
Вертикальные асимптоты
Если прямая 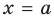 — вертикальная асимптота, то по определению около точки
— вертикальная асимптота, то по определению около точки  кривая должна иметь бесконечную ветвь, то есть предел данной функции при
кривая должна иметь бесконечную ветвь, то есть предел данной функции при  (слева или справа) должен равняться бесконечности (
(слева или справа) должен равняться бесконечности (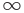 ). Исходя из непрерывности элементарных функций, которые рассматривались в школьном курсе математики, такими точками могут быть только точки, ограничивающие открытые (или полуоткрытые) промежутки области определения данной функции.
). Исходя из непрерывности элементарных функций, которые рассматривались в школьном курсе математики, такими точками могут быть только точки, ограничивающие открытые (или полуоткрытые) промежутки области определения данной функции.
Например, у функции 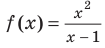 область определения
область определения 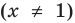 имеет разрыв в точке
имеет разрыв в точке  (область определения:
(область определения: 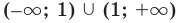 и точка 1 ограничивает открытые промежутки области определения). Можно предположить, что прямая
и точка 1 ограничивает открытые промежутки области определения). Можно предположить, что прямая  будет вертикальной асимптотой. Для того чтобы убедиться в этом, необходимо проверить, будет ли функция стремиться к бесконечности около точки 1 (слева или справа). Для этого рассмотрим
будет вертикальной асимптотой. Для того чтобы убедиться в этом, необходимо проверить, будет ли функция стремиться к бесконечности около точки 1 (слева или справа). Для этого рассмотрим
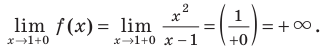
Аналогично 
Таким образом, прямая  является вертикальной асимптотой, поскольку при стремлении функции к бесконечности ее график неограниченно приближается к прямой
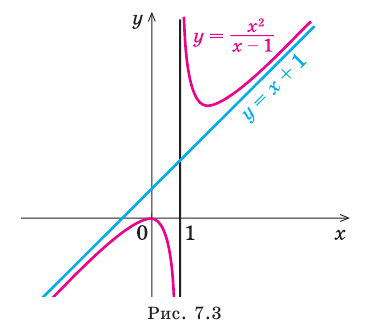
является вертикальной асимптотой, поскольку при стремлении функции к бесконечности ее график неограниченно приближается к прямой  (рис. 7.3).
(рис. 7.3).
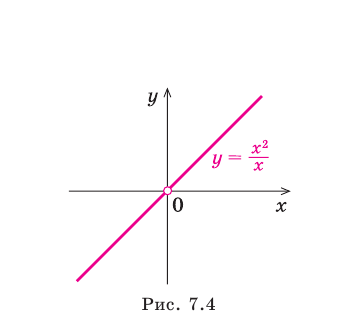
Отметим, что не всегда в точке разрыва области определения функция будет иметь вертикальную асимптоту. Например, функция 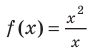 имеет область определения
имеет область определения 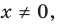 поэтому прямая
поэтому прямая 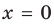 «подозрительна» на вертикальную асимптоту. Но
«подозрительна» на вертикальную асимптоту. Но 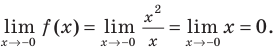 Аналогично
Аналогично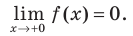 Следовательно, около прямой
Следовательно, около прямой 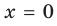 функция
функция 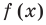 не стремится к бесконечности, и поэтому прямая
не стремится к бесконечности, и поэтому прямая 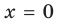 не является асимптотой графика данной функции (рис. 7.4).
не является асимптотой графика данной функции (рис. 7.4).
Наклонные и горизонтальные асимптоты
Наклонные и горизонтальные асимптоты довольно просто находятся для графиков дробно-рациональных функций, у которых степень числителя на единицу больше степени знаменателя (или равна степени знаменателя). Для этого достаточно выделить целую часть заданной дроби и использовать определение асимптоты.
Например, еще раз рассмотрим функцию 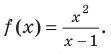 Выделим целую часть:
Выделим целую часть: 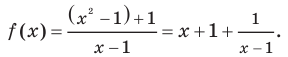
При 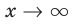 выражение
выражение 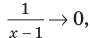 то есть график нашей функции будет х -1 неограниченно приближаться к прямой
то есть график нашей функции будет х -1 неограниченно приближаться к прямой 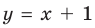 при
при 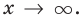 Из этого следует, что наклонной асимптотой графика данной функции* будет прямая
Из этого следует, что наклонной асимптотой графика данной функции* будет прямая 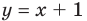 (рис. 7.3).
(рис. 7.3).
Рассмотрим, как находятся наклонные и горизонтальные асимптоты в общем случае.
Пусть наклонной (или горизонтальной) асимптотой графика функции 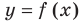 является прямая
является прямая  По определению асимптоты при
По определению асимптоты при 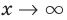 график функции
график функции 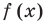 неограниченно приближается к прямой
неограниченно приближается к прямой 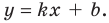 Другими словами, при
Другими словами, при 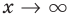 с любой точностью будет выполняться равенство
с любой точностью будет выполняться равенство
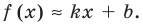 (1)
(1)
Эта равенство не нарушится, если обе его части разделить на 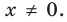 Получим:
Получим: 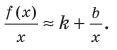 При
При 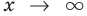 отношение
отношение 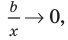 поэтому отношение
поэтому отношение 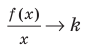 при
при 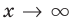 , то есть
, то есть
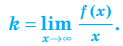 (2)
(2)
Возвращаясь к формуле (1), получаем, что при 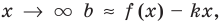 то есть
то есть
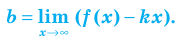 (3)
(3)
Формулы (2) и (3) дают возможность находить наклонные и горизонтальные асимптоты для графика любой функции 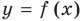 (при условии, что они существуют).
(при условии, что они существуют).
Отметим, что если у графика функции 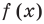 есть горизонтальная асимптота, то ее уравнение будет
есть горизонтальная асимптота, то ее уравнение будет 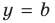 (в этом случае
(в этом случае 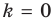 ). Но при
). Но при 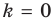 из формулы (3) получаем
из формулы (3) получаем 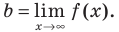 Следовательно, если существует число
Следовательно, если существует число 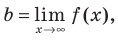 то график функции
то график функции 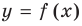 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 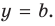
- Заказать решение задач по высшей математике
Пример:
Пользуясь общими формулами, найдите наклонную асимптоту графика функции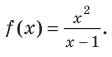
Решение:
Будем искать наклонную асимптоту в виде 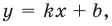 где
где 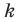 и
и 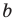 находятся по формулам (2) и (3):
находятся по формулам (2) и (3):
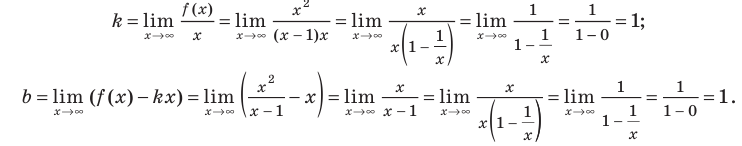
Асимптотой графика данной функции будет прямая 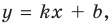 то есть прямая
то есть прямая 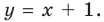
Пример:
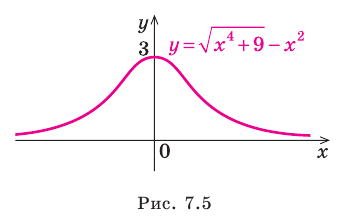
Найдите асимптоты графика функции 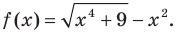
Решение:
Область определения функции: 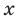 — любое действительное число, то есть
— любое действительное число, то есть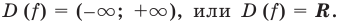 На всей области определения эта функция непрерывна, поэтому вертикальных асимптот график функции не имеет. Будем искать наклонные и горизонтальные асимптоты в виде
На всей области определения эта функция непрерывна, поэтому вертикальных асимптот график функции не имеет. Будем искать наклонные и горизонтальные асимптоты в виде 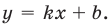 Тогда
Тогда
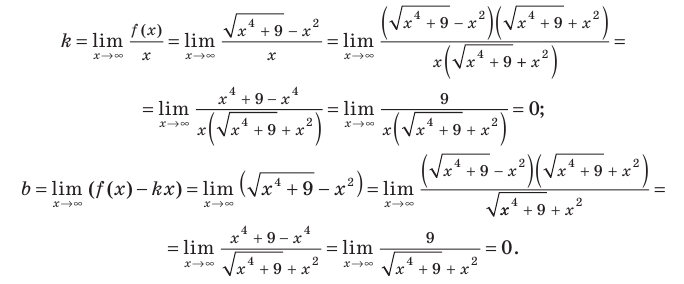
Таким образом, заданная функция имеет только горизонтальную асимптоту 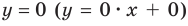 (рис. 7.5).
(рис. 7.5).
Иногда график функции  может иметь разные асимптоты при
может иметь разные асимптоты при 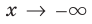 и при
и при 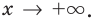 в этом случае при использовании формул (2) и (3) приходится отдельно находить значения
в этом случае при использовании формул (2) и (3) приходится отдельно находить значения 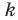 и
и 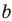 при
при 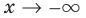 и при
и при 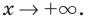
Как найти асимптоты графика функции
При исследовании поведения функции на бесконечности или вблизи точек разрыва часто оказывается, что расстояние между точками графика функции и точками некоторой прямой стремится к нулю при неограниченном удалении точек графика от начала координат. Прямая, к которой стремится кривая в бесконечно удаленной точке, называется асимптотой графика. Различают вертикальные и наклонные асимптоты. Прямая 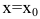 называется вертикальной асимптотой графика функции y=f(x), если хотя бы один из односторонних пределов в точке
называется вертикальной асимптотой графика функции y=f(x), если хотя бы один из односторонних пределов в точке 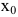 равен бесконечности:
равен бесконечности: 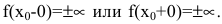 Такие асимптоты существуют только в точках разрыва второго рода.
Такие асимптоты существуют только в точках разрыва второго рода.
Внимание! Непрерывные на множестве действительных чисел функции вертикальных асимптот на имеют.
Для того чтобы график функции y=f(x) имел наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали конечные пределы
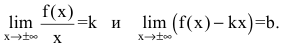
Частным случаем наклонной асимптоты (k=0) является горизонтальная асимптота.
Пример:
Найти асимптоты графика функции 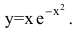
Решение:
Функция 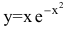 непрерывна в области определения
непрерывна в области определения 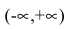 как элементарная. Следовательно, вертикальных асимптот нет. Найдем наклонные асимптоты y=kx+b:
как элементарная. Следовательно, вертикальных асимптот нет. Найдем наклонные асимптоты y=kx+b:
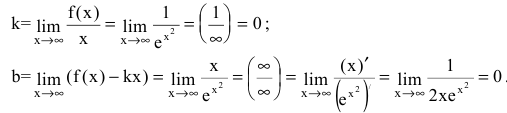
Получаем горизонтальную асимптоту y=0.
Общее исследование функции и построение графика
С помощью производной функции можно провести ее полное исследование и построить график этой функции. При этом рекомендуется использовать следующую схему.
- Найти область определения функции D(f).
- Исследовать функцию на четность
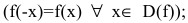 нечетность
нечетность 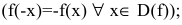 периодичность
периодичность 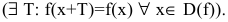
- Исследовать функцию на непрерывность, найти точки разрыва.
- Найти асимптоты графика функции.
- Исследовать функцию на монотонность, найти точки экстремума.
- Найти интервалы выпуклости и вогнутости, точки перегиба функции.
- Используя результаты проведенного исследования, построить график функции (можно вычислить координаты точек пересечения с осями координат).
Пример:
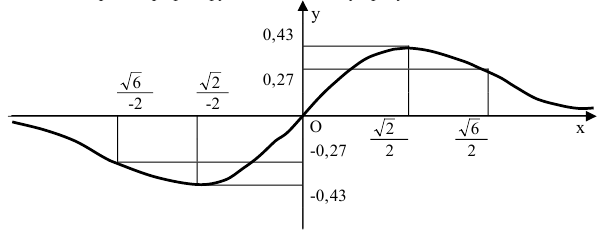
Провести полное исследование функции 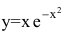 и построить ее график.
и построить ее график.
Решение:
Область определения функции – вся числовая прямая: 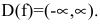
Функция непериодическая. Она нечетная, т.к. область определения симметрична относительно начала координат и 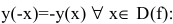
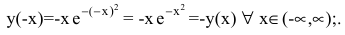
Следовательно, график функции симметричен относительно начала координат и достаточно исследовать функцию для 
Функция непрерывна в области определения как композиция основных элементарных функций. Поскольку 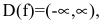 точек разрыва нет.
точек разрыва нет.
Строим график функции, используя результаты исследования.
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
- Иррациональные уравнения
- Иррациональные неравенства
- Производная в математике
- Как найти производную функции



