Загрузить PDF
Загрузить PDF
В статистике абсолютная частота показывает, какое количество раз конкретное значение появляется в наборе данных. В отличие от нее, накопительная частота показывает сумму (или нарастающий итог) всех частот вплоть до текущей точки в наборе данных. Не беспокойтесь, если поначалу это кажется не совсем понятным: возьмите ручку и лист бумаги, и вы быстро во всем разберетесь!
-

1
Отсортируйте набор данных. «Набор данных» — это просто изучаемый вами список числовых значений. Отсортируйте его так, чтобы числа располагались по возрастанию.[1]
- Пример: предположим, список чисел представляет собой количество книг, которые каждый студент прочитал за последний месяц. После сортировки у вас получился следующий набор чисел: 3, 3, 5, 6, 6, 6, 8.
-

2
Посчитайте абсолютную частоту каждой величины. Частота значения показывает, сколько раз данное значение появляется в наборе данных. Это число можно называть абсолютной частотой, чтобы не путать его с накопительной частотой. Наиболее простой способ заключается в том, чтобы составить таблицу. Вверху левой колонки напишите «Значение» (или укажите, что измеряется данными числами). Вверху второй колонки напишите «Частота». Заполните таблицу для всех значений из списка.[2]
- Пример: вверху левой колонки напишите «Количество книг», а вверху правой колонки — «Частота».
- Во второй строке напишите первое количество прочитанных книг, то есть число 3.
- Посчитайте, сколько раз число 3 встречается в списке данных. В списке есть два числа 3, поэтому во второй строке колонки «Частота» запишите цифру 2.
- Повторите данную процедуру для всех значений списка, пока не заполните таблицу:
- 3 | Ч = 2
- 5 | Ч = 1
- 6 | Ч = 3
- 8 | Ч = 1
-

3
Найдите накопительную частоту для первого значения. Накопительная частота отвечает на вопрос «сколько раз встречается в списке данное значение или меньшая величина?». Всегда начинайте с наименьшего значения в наборе данных. Поскольку в нашем примере нет меньших значений, для данной величины накопительная частота равна абсолютной.[3]
-
Пример: наименьшее значение равно 3. Количество прочитавших 3 книги студентов составляет 2. Никто из студентов не прочитал меньшее число книг, поэтому накопительная частота равна 3. Впишите это значение в третью колонку таблицы:
- 3 | F = 2 | НЧ=2
-
Пример: наименьшее значение равно 3. Количество прочитавших 3 книги студентов составляет 2. Никто из студентов не прочитал меньшее число книг, поэтому накопительная частота равна 3. Впишите это значение в третью колонку таблицы:
-

4
Найдите накопительную частоту для следующей величины. Перейдите к следующему значению списка. Выше мы определили, сколько раз встречается в списке наименьшая величина. Чтобы определить накопительную частоту для второго значения списка, необходимо прибавить его абсолютную частоту к накопительной частоте предыдущего значения. Иными словами, следует взять последнюю накопительную частоту и прибавить к ней абсолютную частоту данной величины.[4]
-
Пример:
- 3 | Ч = 2 | НЧ = 2
- 5 | Ч = 1 | НЧ = 2+1 = 3
-
Пример:
-

5
Повторите процедуру для остальных значений. Постепенно продвигайтесь к более высоким числам. При этом каждый раз прибавляйте текущую абсолютную частоту к последней накопительной частоте.
-
Пример:
- 3 | Ч = 2 | НЧ = 2
- 5 | Ч = 1 | НЧ = 2 + 1 = 3
- 6 | Ч = 3 | НЧ = 3 + 3 = 6
- 8 | Ч = 1 | НЧ = 6 + 1 = 7
-
Пример:
-

6
Проверьте полученные результаты. В итоге вы сложите абсолютные частоты всех значений списка. Конечная накопительная частота должна соответствовать числу значений в списке. Есть два способа проверить, так ли это:
- Сложите абсолютные частоты всех значений: 2 + 1 + 3 + 1 = 7, в результате у вас получится накопительная частота.
- Посчитайте число значений в наборе данных. В нашем примере список имел следующий вид: 3, 3, 5, 6, 6, 6, 8. В этом списке семь величин, и итоговая накопительная частота также равна 7.
Реклама
-

1
Поймите разницу между дискретными и непрерывными данными. Дискретные данные можно посчитать, они не дробятся на более мелкие составляющие. Непрерывные данные часто не поддаются конечному счету, между двумя произвольными величинами обязательно найдутся другие возможные значения. Ниже приведена пара примеров:[5]
- Количество собак является дискретным множеством. Нет такого понятия, как половина собаки.
- Глубина снега представляет собой непрерывное множество. Она возрастает постепенно и непрерывно, а не на дискретные величины. Если вы измерите глубину снега в сантиметрах, то точное значение может оказаться, например, 20,6 сантиметра.
-

2
Разбейте непрерывные данные на интервалы. Наборы непрерывных данных часто имеют большое количество значений. Если попробовать представить такой набор описанным выше методом, таблица получится слишком длинной и малопонятной. В этом случае удобно разбить данные на отдельные интервалы. Эти интервалы должны быть одинаковой длины (например, 0—10, 11–20, 21–30 и так далее) независимо от того, сколько значений попадает в каждый интервал. Ниже приведена возможная таблица для непрерывного набора данных:[6]
- Набор данных: 233, 259, 277, 278, 289, 301, 303
- Таблица (в первой колонке интервал значений, во второй частота, в третьей накопительная частота):
- 200–250 | 1 | 1
- 251–300 | 4 | 1 + 4 = 5
- 301–350 | 2 | 5 + 2 = 7
-

3
Постройте линейный график. После того как вы рассчитаете накопительную частоту, возьмите лист миллиметровой бумаги. Отложите по горизонтальной оси (ось x) значения из набора данных, а по вертикальной (ось y) — накопительную частоту, и постройте график. Это значительно облегчит последующие вычисления.[7]
- Например, если набор данных включает числа от 1 до 8, отложите по горизонтальной оси 8 делений. Над каждым делением отметьте точкой соответствующее ему значение накопительной частоты. Соедините получившиеся точки линией.
- Если какое-либо значение не встречается, его абсолютная частота составляет 0. В этом случае прибавьте 0 к последней величине накопительной частоты и поставьте точку на том же уровне, что и в предыдущий раз.
- Поскольку накопительная частота всегда растет с продвижением к большим значениям, с перемещением вправо линия будет оставаться на той же самой высоте или подниматься. Если в какой-то точке линия опустилась вниз, значит, вы допустили ошибку (например, вместо накопительной частоты взяли абсолютную).
-

4
Найдите по графику медиану. Медиана — это значение, расположенное точно посередине набора данных. Половина значений находится выше медианы, а вторая половина расположена ниже нее. Медиану можно найти по графику следующим образом:
- Посмотрите на последнее значение в самом правом конце графика. Для него величина y соответствует суммарной накопительной частоте, которая равна общему числу точек в наборе данных. Предположим, эта величина равна 16.
- Умножьте эту величину на ½ и найдите соответствующее значение на оси y. В нашем примере получится 8. Найдите число 8 на оси y.
- Найдите точку на линии графика, значение y которой соответствует найденной величине. Проведите от цифры 8 на оси y горизонтальную прямую и определите точку ее пересечения с линией графика. Именно эта точка делит набор данных точно пополам.
- Найдите значение x в данной точке. Проведите из точки вертикальную прямую до пересечения с осью x. Точка пересечения определит медиану для изучаемого набора данных. Например, если получилось 65, значит половина данных расположена ниже 65, а вторая половина лежит выше этого значения.
-

5
Найдите по графику квартили. Квартили делят набор данных на четыре части. Эта процедура очень похожа на определение медианы. Единственное различие заключается в нахождении значений y:
- Чтобы определить величину y для нижнего квартиля, умножьте максимальное значение накопительной частоты на ¼. В результате вы получите значение x, ниже которого будет лежать ровно ¼ всех данных.
- Чтобы найти величину y для верхнего квартиля, умножьте максимальное значение накопительной частоты на ¾. В результате вы получите значение x, ниже которого будет лежать ¾, а выше — ¼ всех данных.
Реклама
Советы
- С помощью интервалов можно представлять любые большие, в том числе и дискретные наборы данных.
Реклама
Об этой статье
Эту страницу просматривали 72 908 раз.
Была ли эта статья полезной?
-
Пользуясь формулой, вычисляем накопленные частоты интервалов. В частности,
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
-
Вычисляем частости
интервалов. Например,
![]() ;
;
![]() ;
;
![]() .
.
-
Вычисляем
накопленные частости интервалов. -
Данные вычислений
заносим в табл. 2
Таблица 2
|
№ интервала |
Границы |
Частота |
Накопленная |
Частость |
Накопленная |
|
1 |
5 |
3 |
3 |
0,06 |
0,06 |
|
2 |
7 |
9 |
12 |
0,18 |
0,24 |
|
3 |
9 |
17 |
29 |
0,34 |
0,58 |
|
4 |
11 |
10 |
39 |
0,20 |
0,78 |
|
5 |
13 |
7 |
46 |
0,14 |
0,92 |
|
6 |
15 |
4 |
50 |
0,08 |
1 |
Распределение
типа сведенного в табл. 2 представляет
собой интервальный
вариационный ряд.
Анализ вариационных
рядов упрощается при их графическом
представлении. Наряду с гистограммой
и полигоном частот можно построить
полигон
накопленных частостей (кумулята)
График получается
при соединении точек прямыми отрезками.
Координаты точек соответствуют верхним
границам интервалов и
накопленным частотам. Если по оси ординат
откладывать накопленные частости, то
полученный график называется полигоном
накопленных частостей.
Если ряд не интервальный, то по оси
![]()
откладывают значения измеряемого
признака, а по оси
![]()
соответствующие накопленные частоты
или частости. На рис.2 изображен полигон
накопленных частостей для примера 3.

На
практике соседние точки чаще всего
соединяют кривыми линиями (рис. 3).
1 .3. Статистические характеристики вариационного ряда
Для
полноты картины анализа выборки
рассматривают статистические
характеристики
вариационного ряда. С этой целью оценивают
следующие качества ряда:
-
центральную
тенденцию выборки; -
вариацию.
Центральную
тенденцию выборки оценивают такими
статистическими характеристиками, как
-
мода;
-
медиана;
-
среднее
арифметическое значение.
К
характеристикам вариации относят:
-
размах;
-
дисперсию;
-
среднее
квадратическое отклонение; -
коэффициент
вариации; -
ошибку
выборочного среднего.
Модой
называется значение признака, наиболее
часто встречающееся в выборке. Мода
обозначается
![]() .
.
Если значения выборки сгруппированы в
интервальный вариационный ряд, то
выбирается модальный
интервал с
наибольшей частотой.
Медиана
это такое значение признака, при котором
одна половина значений признака меньше
ее, а другая половина
больше (медиана делит вариационный ряд
пополам). Медиана обозначается
![]() .
.
Для отыскания медианы выборку ранжируют,
то есть значения признака располагают
в порядке возрастания или убывания. В
ранжированной выборке ранг (порядковый
номер в выборке)
![]()
медианы определяют по формуле:
![]()
, где
![]()
объем выборки.
При
![]()
нечетном ранг
![]()
целое число, и медианой считают следующее
значение:
![]() .
.
При
![]()
четном ранг
![]()
число не целое, представимое в виде
![]() ,
,
где
![]()
целое. В таком случае медианой считают
значение
![]() .
.
Среднее
арифметическое неупорядоченной
выборки вычисляют по формуле:
 .
.
В случае интервального
вариационного ряда формула приобретает
вид:
 ,
,
где
![]()
частота
![]() -го
-го
интервала,
![]()
среднее арифметическое значение этого
интервала.
Размах вариации
– это разность
между максимальным и минимальным
значениями выборки:
![]() .
.
Дисперсией
называется
средний квадрат отклонений значений
признака от среднего арифметического
и вычисляется по формуле:
![]() .
.
Средним
квадратическим отклонением называется
положительный квадратный корень из
дисперсии:
 ,
,
Среднее квадратическое
отклонение имеет ту же единицу измерения,
что и варьирующий признак. Оно характеризует
степень отклонения значений признака
от его среднего арифметического значения
в абсолютных единицах.
Для
сравнения варьируемости двух или
нескольких выборок, имеющих разные
единицы измерения, используют коэффициент
вариации. Коэффициент
вариации
это относительный показатель, равный
отношению среднего квадратического
отклонения к среднему арифметическому
значению:
![]() .
.
Принято
считать, что если
![]() ,
,
то варьируемость малая,
![]()
средняя,
![]()
большая.
Отклонения
выборочных коэффициентов от параметров
в генеральной совокупности называются
ошибками
параметров. Эти ошибки возникают в силу
того, что выборочная совокупность
представляет генеральную совокупность
только приближенно. Если взять несколько
вариантов выборок объемом
![]()
из одной и той же генеральной совокупности
и вычислить для каждой из них среднее
арифметическое, то окажется, что средние
арифметические выборок варьируют вокруг
среднего арифметического для генеральной
совокупности
![]()
в
![]()
раз меньше, чем отдельные варианты. На
этом основании в качестве стандартной
ошибки выборочного среднего
принимают величину
![]() .
.
Чтобы
подчеркнуть точность оценки среднего
выборочного, его чаще всего записывают
в виде: ![]() .
.
Пример 4.
В качестве оценки силовой подготовки
учащихся 5 класса произведен тест на
количество подтягиваний на перекладине.
Данные теста
следующие: 9, 9, 10, 11, 8, 7, 10, 7, 9, 11, 7, 8, 9, 8, 9.
Требуется вычислить
моду, медиану, среднее арифметическое
значение, размах вариации, дисперсию,
среднее квадратическое отклонение,
коэффициент вариации и ошибку выборочного
среднего данной выборки.
Решение.
Непосредственным подсчетом убеждаемся,
что значение
![]()
встречается в выборке чаще других (5
раз), следовательно,
![]() .
.
Для
вычисления медианы производим ранжировку
заданной выборки:
7, 7, 7, 8, 8, 8, 9, 9, 9, 9,
9, 10, 10, 11, 11
Объем выборки
![]()
число нечетное, поэтому ранг медианы
вычисляем по формуле:
![]() ,
,
то есть медианой
является 8-е значение выборки),
![]() .
.
Среднее арифметическое
значение выборки находим, пользуясь
формулой:

Крайние значения
ряда) определяют минимальное и максимальное
значения выборки
![]() ,
,
![]() .
.
Согласно определению, размах вариации
равен:
![]() .
.
Для удобства
вычисления дисперсии составляем таблицу.
Пользуясь суммой значений последней
колонки и формулой, находим: ![]() .
.
|
|
|
|
|
|
1 |
9 |
0,2 |
0,04 |
|
2 |
9 |
0,2 |
0,04 |
|
3 |
10 |
1,2 |
1,44 |
|
4 |
11 |
2,2 |
4,84 |
|
5 |
8 |
-0,8 |
0,64 |
|
6 |
7 |
-1,8 |
3,24 |
|
7 |
10 |
1,2 |
1,44 |
|
8 |
7 |
-1,8 |
3,24 |
|
9 |
9 |
0,2 |
0,44 |
|
10 |
11 |
2,2 |
4,24 |
|
11 |
7 |
-1,8 |
3,24 |
|
12 |
8 |
-0,8 |
0,64 |
|
13 |
9 |
0,2 |
0,04 |
|
14 |
8 |
-0,8 |
0,64 |
|
15 |
9 |
0,2 |
0,04 |
|
|
132 |
24,4 |
Вычислим среднее
квадратическое отклонение:
![]() .
.
Коэффициент
вариации:
![]() ,
,
откуда делаем вывод
результаты тестирования имеют средний
коэффициент вариации.
Ошибку выборочного
среднего арифметического находим:
![]() .
.
Наконец, записываем:
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в EXCEL
- Синтаксис функции
- Пример
- Как рассчитать относительную частоту в Excel
- Пример: относительные частоты в Excel
- Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)
- Как посчитать абсолютную частоту в excel
- Как посчитать абсолютную частоту в excel
- Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в EXCEL
- Синтаксис функции
- Пример
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в EXCEL
history 9 апреля 2013 г.
Функция ЧАСТОТА( ) , английская версия FREQUENCY() , вычисляет частоту попадания значений в заданные пользователем интервалы и возвращает соответствующий массив чисел.
Функцией ЧАСТОТА() можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в определенные интервалы (См. Файл примера )
Синтаксис функции
ЧАСТОТА ( массив_данных ; массив_интервалов )
Массив_данных — массив или ссылка на множество ЧИСЛОвых данных, для которых вычисляются частоты.
Массив_интервалов — массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных».
Функция ЧАСТОТА() вводится как формула массива после выделения диапазона смежных ячеек, в которые требуется вернуть полученный массив распределения (частот). Т.е. после ввода формулы необходимо вместо нажатия клавиши ENTER нажать сочетание клавиш CTRL+SHIFT+ENTER .
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве « массив_интервалов ». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения (см. пример ниже).
Пример
Пусть в диапазоне А2:А101 имеется исходный массив чисел от 1 до 100.
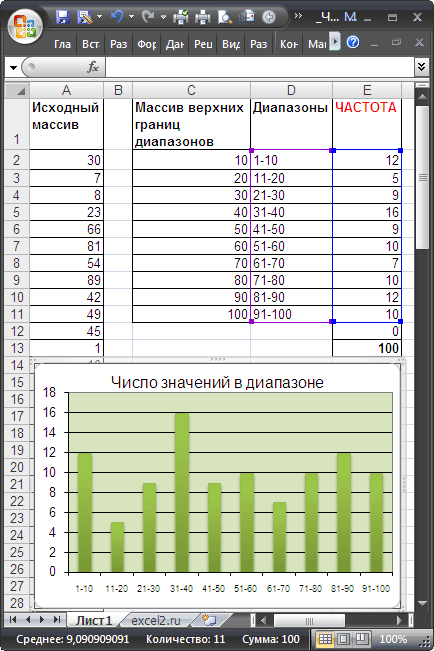
Подсчитаем количество чисел, попадающих в интервалы 1-10; 11-20; . 91-100.
Сформируем столбце С массив верхних границ диапазонов (интервалов). Для наглядности в столбце D сформируем текстовые значения соответствующие границам интервалов (1-10; 11-20; . 91-100).
Для ввода формулы выделим диапазон Е2:Е12 , состоящий из 11 ячеек (на 1 больше, чем число верхних границ интервалов). В Строке формул введем =ЧАСТОТА($A$2:$A$101;$C$2:$C$11) . После ввода формулы необходимо нажать сочетание клавиш CTRL+SHIFT+ENTER . Диапазон Е2:Е12 заполнится значениями:
- в Е2 — будет содержаться количество значений из А2:А101 , которые меньше или равны 10;
- в Е3 — количество значений из А2:А101 , которые меньше или равны 20, но больше 10;
- в Е11 — количество значений из А2:А101 , которые меньше или равны 100, но больше 90;
- в Е12 — количество значений из А2:А101 , которые больше 100 (таких нет, т.к. исходный массив содержит числа от 1 до 100).
Примечание . Функцию ЧАСТОТА() можно заменить формулой = СУММПРОИЗВ(($A$5:$A$104>C5)*($A$5:$A$104 (См. Файл примера )
Источник
Как рассчитать относительную частоту в Excel
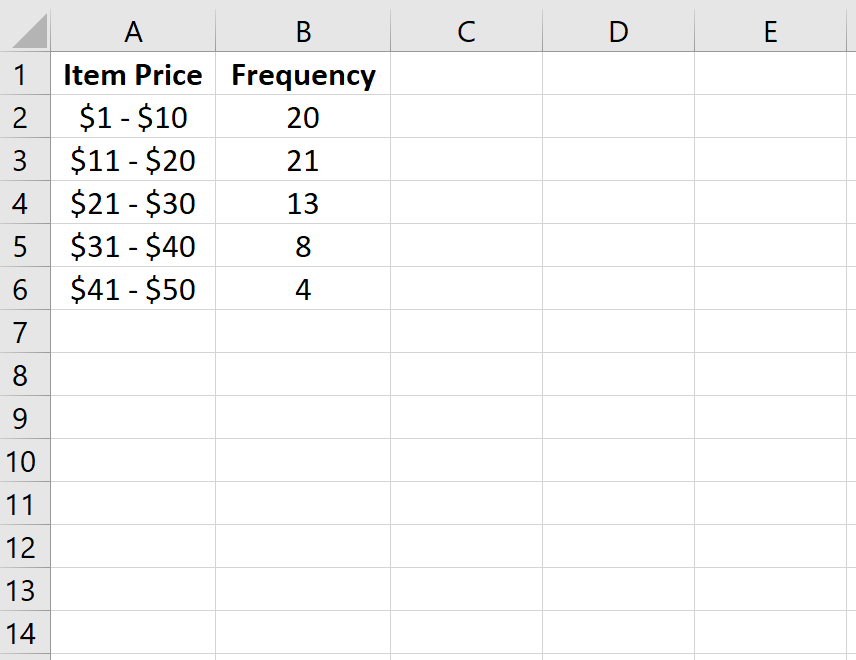
Таблица частот — это таблица, в которой отображается информация о частотах. Частоты просто говорят нам, сколько раз произошло определенное событие.
Например , в следующей таблице показано, сколько товаров было продано магазином в разных ценовых диапазонах за данную неделю:
| Цена товара | Частота | | — | — | | $1 – $10 | 20 | | $11 – $20 | 21 | | 21 – 30 долларов США | 13 | | $31 – $40 | 8 | | $41 — $50 | 4 |
В первом столбце отображается ценовой класс, а во втором столбце — частота этого класса.
Также можно рассчитать относительную частоту для каждого класса, которая представляет собой просто частоту каждого класса в процентах от целого.
| Цена товара | Частота | Относительная частота | | — | — | — | | $1 – $10 | 20 | 0,303 | | $11 – $20 | 21 | 0,318 | | 21 – 30 долларов США | 13 | 0,197 | | $31 – $40 | 8 | 0,121 | | $41 — $50 | 4 | 0,061 |
Всего было продано 66 штук. Таким образом, мы нашли относительную частоту каждого класса, взяв частоту каждого класса и разделив ее на общее количество проданных товаров.
Например, было продано 20 товаров по цене от 1 до 10 долларов. Таким образом, относительная частота класса $1 – $10 составляет 20/66 = 0,303 .
Затем был продан 21 предмет в ценовом диапазоне от 11 до 20 долларов. Таким образом, относительная частота класса $11 – $20 составляет 21/66 = 0,318 .
В следующем примере показано, как найти относительные частоты в Excel.
Пример: относительные частоты в Excel
Сначала мы введем класс и частоту в столбцах A и B:
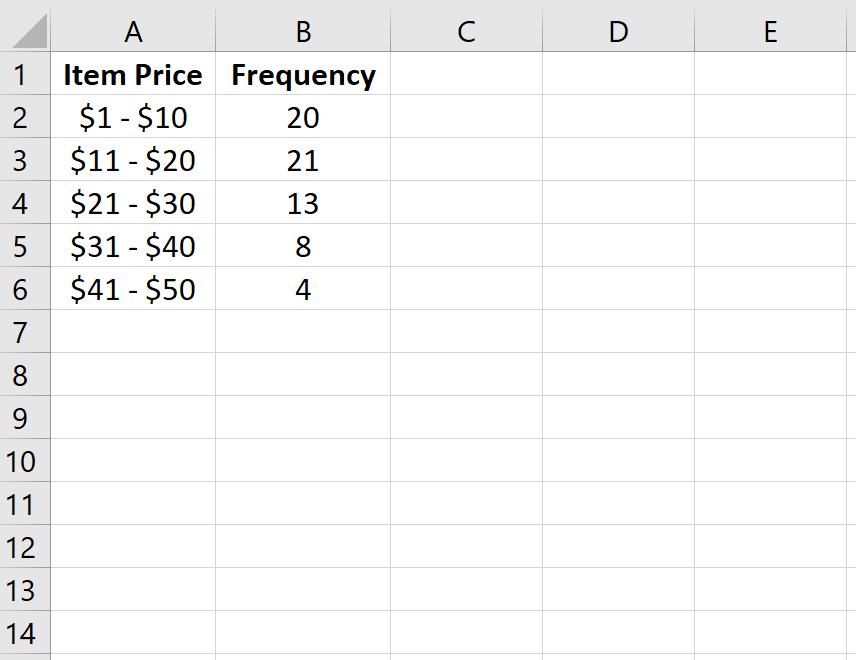
Далее мы рассчитаем относительную частоту каждого класса в столбце C. В столбце D показаны формулы, которые мы использовали:
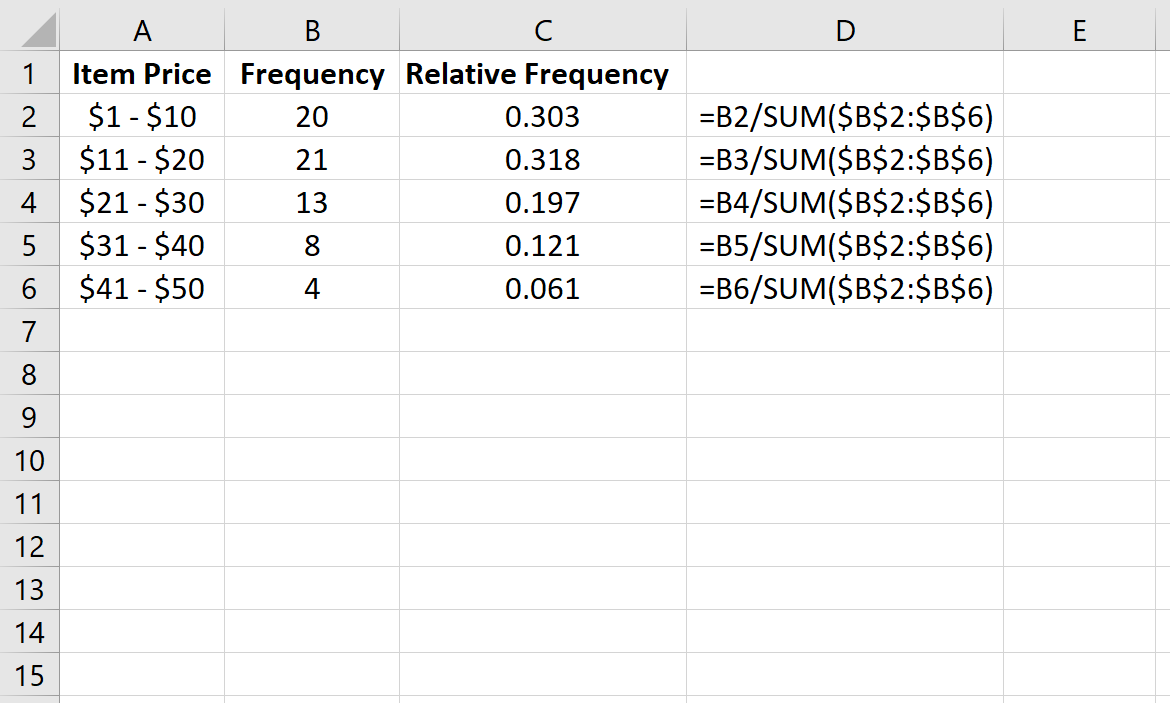
Мы можем проверить правильность наших расчетов, убедившись, что сумма относительных частот равна 1:
Мы также можем создать гистограмму относительной частоты для визуализации относительных частот.
Просто выделите относительные частоты:

Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить столбец» или «Гистограмма» :
Автоматически появится гистограмма относительной частоты:
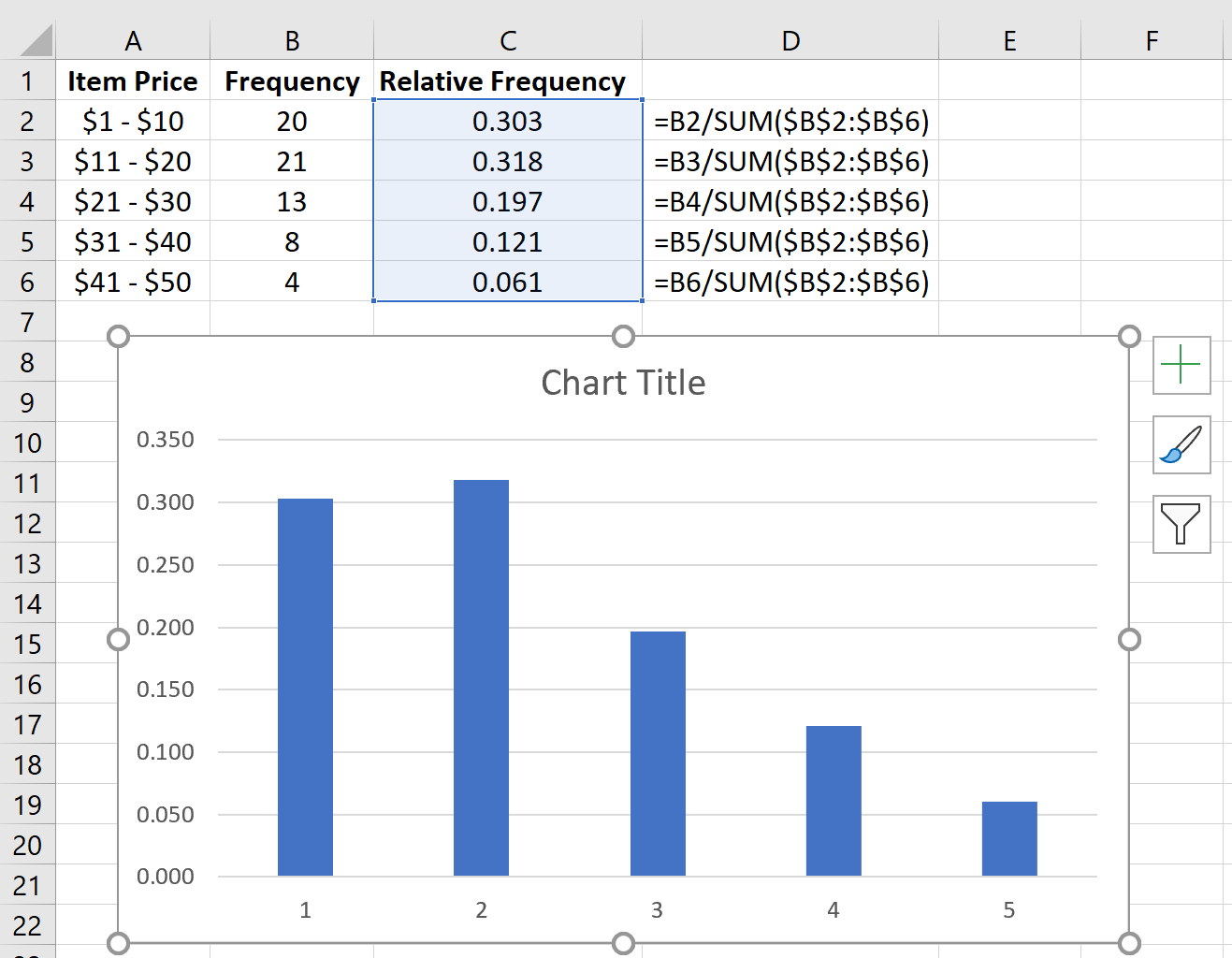
Измените метки оси X, щелкнув правой кнопкой мыши диаграмму и выбрав Выбрать данные.В разделе « Ярлыки горизонтальной (категории) оси » нажмите « Изменить » и введите диапазон ячеек, содержащий цены на товары. Нажмите OK , и новые метки осей появятся автоматически:
Источник
Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)
При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы «от и до» (в статистике их называют «карманы»). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:
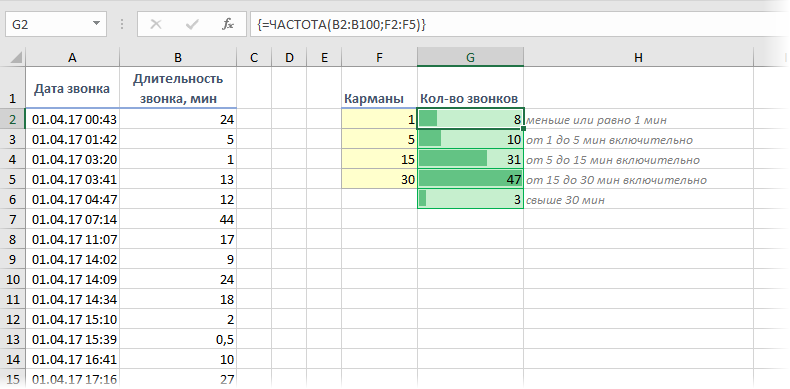
Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY) . Ее синтаксис прост:
=ЧАСТОТА( Данные ; Карманы )
- Карманы — диапазон с границами интервалов, попадание в которые нас интересует
- Данные — диапазон с исходными числовыми значениями, которые мы анализируем
Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.
Для использования функции ЧАСТОТА нужно:
- заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
- выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5)
- ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива
Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.
Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:
Источник
Как посчитать абсолютную частоту в excel
Как посчитать абсолютную частоту в excel
1. Построение вариационного ряда
Нужно выделить ячейки содержащие результаты эксперимента, и воспользоваться операцией сортировка по возрастанию (либо с панели инструментов, либо через главное меню Данные>Сортировка), и в появившемся окне сообщения – «обнаружены данные выходящие за пределы выделенного диапазона» выбрать действие – «сортировать в пределах указанного выделения»
2. Построение группировочного статистического ряда
Добавьте и заполните, введя соответствующие формулы, две таблицы:
Таблица №1
Для вычисления минимального и максимального элемента воспользуйтесь встроенными в Excel статистическими формулами (главное меню – вставка – функция…) МИН и МАКС.
Таблица №2
начало промежутка
конец промежутка
Середина промежутка
Абсолютная частота
Относи-тельная частота
Накопленная частота
1
2
Для вычисления абсолютной частоты нужна статистическая функция ЧАСТОТА. При её использовании нужно выполнить следующие действия:
а) выделить весь диапазон ячеек, в которых будет располагаться результат подсчёта частот (т.е. это ячейки под заголовком Абсолютная частота в количестве равном числу промежутков)
b) не снимая выделения, поставить курсор в строку формул и нажать на кнопку вставка функции (чуть левее курсора) или Главное меню – вставка – формула.
с) выбрать функцию ЧАСТОТА
d) ввести Массив_данных – диапазон, содержащий элементы выборки (в файле 2.xls это ячейки) B2:B101
e) ввести Массив_интервалов – диапазон ячеек под заголовком Начало промежутка начиная со строчки, соответствующей промежутку под номером 2 до строчки, соответствующей последнему промежутку.
f) нажмите на кнопку ОК и после закрытия окна для ввода аргументов функции ЧАСТОТА поставьте курсор обратно в строку формул.
g) Нажмите на три кнопки Ctrl+Shift+Enter (сначала на первые две, а потом, не отпуская их, нажмите на Enter).
Примечание. Формулу вычисления абсолютной частоты необходимо ввести как формулу массива. Нажатие комбинации клавиш CTRL+SHIFT+ENTER позволяет определить формулу как формулу массива. Если формула не будет введена как формула массива, единственное значение будет равно 1.
В результате изначально выделенный диапазон будет содержать абсолютные частоты попадания во все промежутка. Проверьте, что сумма всех абсолютных частот равна общему числу элементов выборки (100).
3. Построение гистограммы группировочного статистического ряда
В качестве элементов группировочного ряда надо взять середины промежутков и приведённые частоты.
Для построения гистограммы выполните следующие действия:
- Главное меню: Вставка – Диаграмма.
- Тип: точечная.
- Диапазон данных: выделите ячейки содержащие значения абсолютных частот.
- Ряд: Значения по X: укажите диапазон ячеек содержащий значения середины промежутков.
- Готово.
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в EXCEL
history 9 апреля 2013 г.
- Группы статей
- Формулы массива
- Подсчет Чисел
Функция ЧАСТОТА( ) , английская версия FREQUENCY() , вычисляет частоту попадания значений в заданные пользователем интервалы и возвращает соответствующий массив чисел.
Функцией ЧАСТОТА() можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в определенные интервалы (См. Файл примера )
Синтаксис функции
ЧАСТОТА ( массив_данных ; массив_интервалов )
Массив_данных — массив или ссылка на множество ЧИСЛОвых данных, для которых вычисляются частоты.
Массив_интервалов — массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных».
Функция ЧАСТОТА() вводится как формула массива после выделения диапазона смежных ячеек, в которые требуется вернуть полученный массив распределения (частот). Т.е. после ввода формулы необходимо вместо нажатия клавиши ENTER нажать сочетание клавиш CTRL+SHIFT+ENTER .
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве « массив_интервалов ». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения (см. пример ниже).
Пример
Пусть в диапазоне А2:А101 имеется исходный массив чисел от 1 до 100.

Подсчитаем количество чисел, попадающих в интервалы 1-10; 11-20; . 91-100.
Сформируем столбце С массив верхних границ диапазонов (интервалов). Для наглядности в столбце D сформируем текстовые значения соответствующие границам интервалов (1-10; 11-20; . 91-100).
Для ввода формулы выделим диапазон Е2:Е12 , состоящий из 11 ячеек (на 1 больше, чем число верхних границ интервалов). В Строке формул введем =ЧАСТОТА($A$2:$A$101;$C$2:$C$11) . После ввода формулы необходимо нажать сочетание клавиш CTRL+SHIFT+ENTER . Диапазон Е2:Е12 заполнится значениями:
- в Е2 — будет содержаться количество значений из А2:А101 , которые меньше или равны 10;
- в Е3 — количество значений из А2:А101 , которые меньше или равны 20, но больше 10;
- в Е11 — количество значений из А2:А101 , которые меньше или равны 100, но больше 90;
- в Е12 — количество значений из А2:А101 , которые больше 100 (таких нет, т.к. исходный массив содержит числа от 1 до 100).
Примечание . Функцию ЧАСТОТА() можно заменить формулой = СУММПРОИЗВ(($A$5:$A$104>C5)*($A$5:$A$104 (См. Файл примера )
Источник
В статистике абсолютная частота – это название, данное количеству раз, когда определенное значение появляется в заданном наборе данных. Накопленная частота отличается: она представляет собой сумму (или промежуточный итог) всех частот до текущей точки в наборе данных. Не волнуйтесь, если это звучит как технический жаргон – вам будет легче следовать, если у вас есть ручка и бумага.
шаги
Метод 1 из 2: Базовая совокупная частота

Шаг 1. Отсортируйте набор данных
«Набор данных» состоит только из группы чисел, которую вы в настоящее время изучаете. Отсортируйте их в порядке возрастания, от наименьшего к наибольшему.
Пример: в наборе данных указано количество книг, прочитанных каждым студентом за последний месяц. После сортировки значений это будет выглядеть так: 3, 3, 5, 6, 6, 6, 8

Шаг 2. Подсчитайте абсолютную частоту каждого значения
Частота значения равна тому, сколько раз оно встречается в ряду (вы можете назвать эту переменную «абсолютной частотой», когда вам нужно избежать путаницы с накопленной частотой). Самый простой способ узнать это – создать таблицу. Напишите «Значение» (или описание того, что означает этот термин) в начале первого столбца. Напишите «Частота» вверху второго столбца. Заполните таблицу для каждого конкретного значения.
- Пример: напишите «Количество книг» вверху первого столбца и «Частота» вверху второго столбца.
- Во второй строке напишите первое значение в поле «Количество книг»: 3.
- Подсчитайте, сколько 3 в наборе данных. Поскольку есть две тройки, напишите 2 в поле «Частота» в той же строке.
-
Повторяйте эту процедуру для каждого значения, пока не закончите таблицу:
- 3 | F = 2
- 5 | F = 1
- 6 | F = 3
- 8 | F = 1

Шаг 3. Найдите совокупную частоту первого значения
Накопленная частота отвечает на вопрос «сколько раз появляется это или меньшее значение?». Всегда начинайте с наименьшего значения в наборе данных. Поскольку нет меньших чисел, ответ всегда будет равняться накопленной частоте этого значения.
-
Пример: Наше наименьшее значение – 3. Количество студентов, прочитавших 3 книги, равно 2. Никто не прочитал меньше, поэтому совокупная посещаемость будет равна 3. Добавьте это число в первую строку таблицы:
3 | F = 2 | CF = 2

Шаг 4. Найдите совокупную частоту следующего значения
Перейти к следующему значению в нашей таблице. Мы только что выяснили, во сколько раз появлялись меньшие значения. Чтобы найти кумулятивную частоту этого числа, нам просто нужно добавить его абсолютную частоту к текущему итоговому значению. Другими словами, возьмите последнюю найденную совокупную частоту и прибавьте ее к абсолютной частоте этого значения.
-
Пример:
-
3 | F = 2 | CF =
Шаг 2.
-
5 | F =
Шаг 1. | CF
Шаг 2
Шаг 1. = 3
-

Шаг 5. Повторите процедуру для остальных значений
Продолжайте двигаться к все более и более высоким значениям. В каждом из них прибавьте последнюю накопленную частоту к абсолютной частоте следующего значения.
-
Пример:
-
3 | F = 2 | CF =
Шаг 2.
-
5 | F = 1 | CF = 2 + 1 =
Шаг 3.
-
6 | F = 3 | CF = 3 + 3 =
Шаг 6.
-
8 | F = 1 | CF = 6 + 1 =
Шаг 7.
-

Шаг 6. Проверьте свою работу
Когда закончите, вы добавите, сколько раз появлялась каждая переменная. Окончательная совокупная частота должна равняться общему количеству точек данных в вашем пуле. Проверить, что было сделано, можно двумя способами:
- Сложите все отдельные частоты: 2 + 1 + 3 + 1 = 7, это наша окончательная совокупная частота.
- Подсчитайте количество точек данных. В нашем списке было 3, 3, 5, 6, 6, 6, 8. Всего 7 пунктов, и это число является нашей окончательной совокупной частотой.
Метод 2 из 2: расширенное использование

Шаг 1. Разберитесь с концепцией дискретных и непрерывных данных
Дискретные данные поступают в счетных единицах, поэтому найти часть единицы невозможно. Непрерывные данные описывают что-то бесчисленное, с измерениями, которые могут находиться в любом месте между выбранными вами единицами. Вот некоторые примеры:
- Количество собак: конфиденциальные данные. Полусобаки не бывает.
- Высота снежного покрова: непрерывные данные. Снег накапливается постепенно, а не по одной единице за раз. Если попробовать измерить его в сантиметрах, то можно найти сугроб глубиной 14,2 сантиметра.

Шаг 2. Сгруппируйте непрерывные данные по амплитуде
Непрерывные наборы данных часто содержат большое количество уникальных переменных. Если вы попытаетесь использовать описанный выше метод, вы заметите, что таблица будет очень длинной и сложной для понимания. Вместо этого выражайте каждую строку в таблице как диапазон значений. Важно сохранить каждую амплитуду в идентичных измерениях (например, 0 ~ 10, 11 ~ 20, 21 ~ 30 и т. Д.), Независимо от того, сколько значений содержится в каждом из них. Вот пример непрерывного набора данных, преобразованного в таблицу:
- Набор данных: 233, 259, 277, 278, 289, 301, 303.
-
Таблица (первый столбец: значение, второй столбец: частота, третий столбец: совокупная частота):
- 200–250 | 1 | 1
- 251–300 | 4 | 1 + 4 = 5
- 301–350 | 2 | 5 + 2 = 7

Шаг 3. Составьте линейный график.
После того, как вы рассчитали накопленную частоту, возьмите лист миллиметровой бумаги. Нарисуйте линейный график с осью X, содержащей значения из вашего набора данных, и осью Y – накопленными данными частоты. Это значительно упростит следующие расчеты.
- Например, если набор данных находится в диапазоне от 1 до 8, нарисуйте ось x с отмеченными восемью единицами. На каждом значении оси x нарисуйте точку на оси y, которая равна соответствующей накопленной частоте. Соедините каждую пару соседних точек линией.
- Если для определенного значения нет точек данных, его абсолютная частота равна 0. Добавление 0 к накопленной частоте не изменит его значение. Итак, нарисуйте точку с тем же значением y, что и предыдущая.
- Поскольку накопленная частота всегда увеличивается со значениями, линейный график всегда должен оставаться плоским или повышаться при движении вправо. Если в любой точке линия спускается вниз, возможно, вы неправильно использовали абсолютные значения частоты.

Шаг 4. Найдите на графике медиану
Медиана – это значение прямо в центре набора данных. Половина значений будет выше медианы, а половина – ниже. Узнайте здесь, как найти его на своем графике:
- Посмотрите на последнюю точку в правом углу графика. Значение y представляет собой общую накопленную частоту, то есть количество точек в наборе данных. Допустим, это значение равно 16.
- Умножьте это значение на ½ и найдите результат по оси y. В нашем примере половина 16 равна 8. Найдите значение 8 на оси ординат.
- Найдите точку на графике, соответствующую этому значению. Переместите палец от значения 8 по оси y и остановитесь, коснувшись линии графика. Это точная точка, до которой считается половина ваших точек данных.
- Теперь найдите ось абсцисс. Переместите палец вниз, чтобы найти значение оси X, которое представляет собой медианное значение набора данных. Если это значение равно 65, например, половина набора данных ниже 65, а половина – выше.

Шаг 5. Найдите квартили на графике
Квартили делят данные на четыре части, что аналогично поиску медианы. Единственное отличие состоит в том, как находятся значения y.
- Чтобы найти значение для нижнего квартиля оси Y, возьмите максимальную накопленную частоту и умножьте ее на. Результат указывает точку, ниже которой находится ¼ данных.
- Чтобы найти значение в верхнем квартиле оси Y, умножьте максимальную накопленную частоту на ¾. Результат указывает на точку, которая точно разделяет нижних данных от ¼ более высоких данных.

Содержание
- Формулы
- Прочие накопленные частоты
- Как получить накопленную частоту?
- Как заполнять частотную таблицу
- Таблица частотности
- Кумулятивное частотное распределение
- пример
- Предлагаемое упражнение
- Ответить
- Ссылки
В накопленная частота представляет собой сумму абсолютных частот f, от самой низкой до той, которая соответствует определенному значению переменной. В свою очередь, абсолютная частота – это количество раз, когда наблюдение появляется в наборе данных.
Очевидно, переменная исследования должна быть сортируемой. А поскольку накопленная частота получается сложением абсолютных частот, получается, что накопленная частота до последних данных должна совпадать с их суммой. В противном случае в расчетах будет ошибка.

Обычно накопленная частота обозначается как Fя (или иногда nя), чтобы отличить ее от абсолютной частоты fя и важно добавить для него столбец в таблице, с помощью которой организованы данные, известной как таблица частот.
Это упрощает, среди прочего, отслеживание того, сколько данных было подсчитано до определенного наблюдения.
А Фя он также известен как абсолютная совокупная частота. Если разделить на общие данные, мы получим относительная совокупная частота, окончательная сумма которых должна быть равна 1.
Формулы
Кумулятивная частота данного значения переменной Xя представляет собой сумму абсолютных частот f всех значений, меньших или равных ей:
Fя = f1 + f2 + f3 +… Fя
Путем сложения всех абсолютных частот получается общее количество данных N, то есть:
F1 + F2 + F3 +…. + Fп = N
Предыдущая операция кратко записывается с помощью символа суммирования ∑:
∑ Fя = N
Прочие накопленные частоты
Также могут накапливаться следующие частоты:
-Относительная частота: получается делением абсолютной частоты fя между общими данными N:
Fр = fя / N
Если относительные частоты сложить от самой низкой к той, которая соответствует определенному наблюдению, мы получим совокупная относительная частота. Последнее значение должно быть равно 1.
-Процент кумулятивной относительной частоты: накопленная относительная частота умножается на 100%.
F% = (fя / N) x 100%
Эти частоты полезны для описания поведения данных, например, при нахождении показателей центральной тенденции.
Как получить накопленную частоту?
Чтобы получить накопленную частоту, необходимо упорядочить данные и организовать их в таблице частот. Процедура иллюстрируется следующей практической ситуацией:
-В интернет-магазине, который продает сотовые телефоны, отчет о продажах определенного бренда за март месяц показал следующие значения за день:
1; 2; 1; 3; 0; 1; 0; 2; 4; 2; 1; 0; 3; 3; 0; 1; 2; 4; 1; 2; 3; 2; 3; 1; 2; 4; 2; 1; 5; 5; 3
Переменная – это количество телефонов, проданных за день и это количественно. Данные, представленные таким образом, не так легко интерпретировать, например, владельцы магазина могут быть заинтересованы в том, чтобы узнать, есть ли какая-либо тенденция, например, дни недели, когда продажи этого бренда выше.
Подобную информацию и многое другое можно получить, представив данные в упорядоченном виде и указав частоты.
Как заполнять частотную таблицу
Для расчета накопленной частоты данные сначала упорядочиваются:
0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5
Затем строится таблица со следующей информацией:
-Первый столбец слева с количеством проданных телефонов от 0 до 5 в порядке возрастания.
-Второй столбец: абсолютная частота, то есть количество дней, в течение которых было продано 0 телефонов, 1 телефон, 2 телефона и т. Д.
-Третий столбец: накопленная частота, состоящая из суммы предыдущей частоты и частоты данных, которые необходимо учитывать.
Этот столбец начинается с первых данных в столбце абсолютной частоты, в данном случае это 0. Для следующего значения сложите его с предыдущим. Это продолжается до тех пор, пока не будут достигнуты последние накопленные данные частоты, которые должны совпадать с общими данными.
Таблица частотности
В следующей таблице показаны переменная «количество телефонов, проданных за день», ее абсолютная частота и подробный расчет накопленной частоты.

На первый взгляд, можно сказать, что у рассматриваемого бренда один или два телефона почти всегда продаются в день, поскольку максимальная абсолютная частота составляет 8 дней, что соответствует этим значениям переменной. Только за 4 дня месяца они не продали ни одного телефона.
Как уже отмечалось, таблицу легче изучить, чем изначально собранные индивидуальные данные.
Кумулятивное частотное распределение
Кумулятивное распределение частот – это таблица, в которой показаны абсолютные частоты, совокупные частоты, совокупные относительные частоты и совокупные процентные частоты.
Хотя есть преимущество организации данных в таблице, подобной предыдущей, если количество данных очень велико, может оказаться недостаточно для их организации, как показано выше, потому что, если частот много, их все равно трудно интерпретировать.
Проблему можно решить, построив Распределение частоты по интервалам, полезная процедура, когда переменная принимает большое количество значений или если это непрерывная переменная.
Здесь значения сгруппированы в интервалы равной амплитуды, называемые класс. Классы характеризуются наличием:
-Предел класса: – крайние значения каждого интервала, их два, верхний предел и нижний предел. Как правило, верхняя граница относится не к интервалу, а к следующему, а нижняя – к.
-Классовый знак: является средней точкой каждого интервала и принимается в качестве его репрезентативного значения.
-Ширина класса: Он рассчитывается путем вычитания значения самого высокого и самого низкого данных (диапазона) и деления на количество классов:
Ширина класса = Диапазон / Количество классов
Подробное описание частотного распределения приведено ниже.
пример
Этот набор данных соответствует 40 баллам за тест по математике по шкале от 0 до 10:
0; 0;0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9;10; 10.
Распределение частот может быть выполнено с определенным количеством классов, например 5 классами. Следует иметь в виду, что при использовании многих классов данные нелегко интерпретировать, и смысл группировки теряется.
А если, наоборот, они сгруппированы в очень немногие, то информация размывается и часть ее теряется. Все зависит от количества имеющихся у вас данных.
В этом примере рекомендуется иметь две оценки в каждом интервале, поскольку будет 10 оценок и будет создано 5 классов. Ранг – это вычитание между высшим и низшим классом, ширина класса составляет:
Ширина класса = (10-0) / 5 = 2
Слева интервалы закрыты, а справа открыты (кроме последнего), что обозначено скобками и круглыми скобками соответственно. Все они одинаковой ширины, но это не обязательно, хотя и является наиболее распространенным.
Каждый интервал содержит определенное количество элементов или абсолютную частоту, а в следующем столбце – накопленная частота, с которой переносится сумма. В таблице также указана относительная частота fр (абсолютная частота между общим количеством данных) и относительная частота в процентах fр ×100%.

Предлагаемое упражнение
Одна компания ежедневно звонила своим клиентам в течение первых двух месяцев года. Данные следующие:
6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 18, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 20, 13, 17, 14, 26, 7, 12, 24, 7
Сгруппируйте по 5 классам и составьте таблицу с частотным распределением.
Ответить
Ширина класса:
(26-6)/5 = 4
Пожалуйста, попытайтесь понять это, прежде чем увидите ответ.

Ссылки
- Беренсон, М. 1985. Статистика для управления и экономики. Interamericana S.A.
- Деворе, Дж. 2012. Вероятность и статистика для техники и науки. 8-е. Издание. Cengage.
- Левин, Р. 1988. Статистика для администраторов. 2-й. Издание. Прентис Холл.
- Вероятность и статистика. Ширина интервала классов. Получено с: pedroprobabilidadyestadistica.blogspot.com.
- Шпигель, М. 2009. Статистика. Серия Шаум. 4-й Издание. Макгроу Хилл.
- Уолпол, Р. 2007. Вероятность и статистика для инженерии и науки. Пирсон.
