- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Параллельные прямые
- Теорема о накрест лежащих углах
Теорема
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Дано: 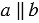 , АВ – секущая,
, АВ – секущая,  1 и
1 и  2 – накрест лежащие (Рис.1).
2 – накрест лежащие (Рис.1).
Доказать:  1 =
1 = 2.
2.
Доказательство:
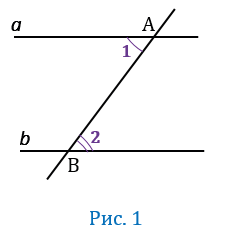
Предположим,что углы 1 и 2 не равны друг другу. Отложим от луча АВ угол РАВ, равный углу 2, так, чтобы  РАВ и
РАВ и  2 были накрест лежащими углами при пересечении прямых АР и
2 были накрест лежащими углами при пересечении прямых АР и 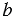 секущей АВ (Рис.2).
секущей АВ (Рис.2).
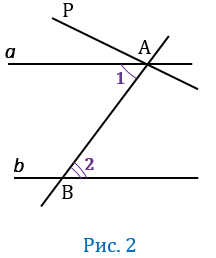
По построению накрест лежащие углы РАВ и 2 равны, значит АР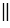
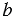 (по признаку параллельности двух прямых). То есть мы получили, что через точку А проходят две прямые
(по признаку параллельности двух прямых). То есть мы получили, что через точку А проходят две прямые 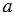 и АР, параллельные прямой
и АР, параллельные прямой 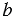 . Но это противоречит аксиоме параллельных прямых. Значит наше предположение неверно и
. Но это противоречит аксиоме параллельных прямых. Значит наше предположение неверно и  1 =
1 =  2. Что и требовалось доказать.
2. Что и требовалось доказать.
Следствие
Дано: 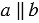 ,
, 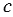
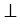
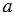 (Рис.3).
(Рис.3).
Доказать: 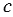
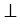
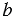 .
.
Доказательство:
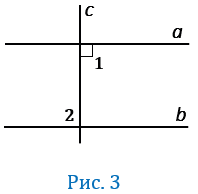
Прямая 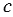 пересекает прямую
пересекает прямую 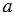 , при этом
, при этом 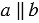 , значит
, значит 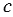 пересекает и прямую
пересекает и прямую 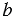 (смотри следствие 20 из аксиомы параллельных прямых). При пересечении параллельных прямых
(смотри следствие 20 из аксиомы параллельных прямых). При пересечении параллельных прямых 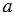 и
и 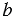 секущей
секущей 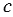 образуются равные накрест лежащие углы:
образуются равные накрест лежащие углы:  1 =
1 = 2 (по теореме о накрест лежащих углах). По условию
2 (по теореме о накрест лежащих углах). По условию 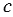
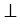
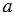 , т.е.
, т.е.  1 = 900, значит и
1 = 900, значит и  2 = 900 , т.е.
2 = 900 , т.е. 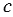
 . Что и требовалось доказать.
. Что и требовалось доказать.
Советуем посмотреть:
Параллельные прямые
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Аксиомы геометрии
Аксиома параллельных прямых
Теорема о соответственных углах
Теорема об односторонних углах
Теорема об углах с соответственно параллельными сторонами
Теорема об углах с соответственно перпендикулярными сторонами
Параллельные прямые
Правило встречается в следующих упражнениях:
7 класс
Задание 210,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 216,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 245,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 379,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 425,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 625,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 626*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 861,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 888,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1069,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Когда секущая пересекает пару параллельных линий, образуются накрест лежащие углы. Накрест лежащие углы равны друг другу.
Один из способов найти накрест лежащие углы – нарисовать зигзагообразную линию на рисунке, (d) и (e) , (c) и (f) являются накрест лежащими углами.
Пример 1: На приведенной ниже рисунке определите значения углов (b, c, d, e, f, g , h).
Решение:
- (b + 60° =180° ⇒ b = 180° – 60° = 120°)
- (b) и (c) – вертикальные углы. Поэтому (c = b = 120°)
- (d) и (60°) вертикальные углы. Поэтому (d = 60°)
- (e = d = 60°)
- (f+ 60° =180° ⇒ f = 180° – 60° = 120°)
- (g) и (f-)вертикальные углы. (g = f = 120°)
- (h) и (e-)вертикальные углы. Поэтому (h = e = 60°)
Ответ: (b = 120°, c = 120°, d = 60°, e = 60°, f = 120°, g = 120° , h = 60°)
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
На этой странице вы узнаете:
- Какими бывают углы?
- По каким признакам можно сказать, что треугольники равны?
- Что такое коэффициент подобия?
- Какие бывают многоугольники?
- Какими формулами пользоваться, чтобы найти площадь фигуры?
- Что такое окружность и из чего она состоит?
- Когда можно вписать окружность в многоугольник, а когда около него можно её описать?
Прямая, отрезок, луч, углы
Квадрат, круг, треугольник. Несомненно, вы знаете о таких геометрических фигурах, эти фигуры относятся к разделу геометрии, который называется планиметрия. Планиметрия – это наука о изучении геометрических фигур на плоскости. Точки, прямые, отрезки, лучи и углы являются основой этого раздела геометрии. Давайте их и рассмотрим.
Прямая – это линия, не имеющая ни начала, ни конца, такая линия может быть бесконечной.
Отрезок – это часть прямой, ограниченная с обеих сторон.
Луч – это отрезок, ограниченный только с одной стороны.
Угол – это фигура, образованная двумя лучами, исходящими из одной точки, измеряется в градусах.
Рассмотрим части угла:
Углы бывают четырёх видов:
Смежные и вертикальные углы
Смежные углы – это углы, имеющие одну общую сторону, а две другие стороны этих углов лежат на одной прямой.
Смежные углы в сумме дают 180°.
Вертикальные углы – это углы, вершиной которых является одна и та же точка, стороны одного такого угла являются продолжениями сторон другого угла.
Рассмотрим углы при параллельных прямых
Накрест лежащие углы – это углы, образованные при пересечении двух параллельных прямых секущей и лежащие по разные стороны от секущей между параллельным прямыми. Такие углы всегда равны.
Внутренние односторонние углы – это углы, образованные при пересечении двух параллельных прямых секущей и лежащие по одну сторону от секущей между параллельным прямыми. Сумма этих углов 1800.
Соответственные углы — это углы, образованные при пересечении двух параллельных прямых секущей и лежащие по одну сторону от секущей так, что один угол находится между двумя прямыми относительно одной прямой, а другой угол прилегает к другой прямой с внешней стороны. Эти углы равны.
Пусть a || b, а с – секущая
Тогда 3 и 6, 4 и 5 накрест лежащие; 3 и 5, 4 и 6 внутренние односторонние; 1 и 5, 2 и 6, 3 и 7, 4 и 8 соответственные
Треугольники, их виды и признаки их равенства
Сумма углов любого треугольника равна 180°
Для треугольников также верно следующее утверждение: каждая сторона треугольника меньше суммы двух других его сторон
Элементы треугольника:
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Также медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины (в треугольнике медиана показана как BM)
Биссектриса – это отрезок, делящий угол на два равных угла. Также центром вписанной в треугольник окружности является точка пересечения биссектрис углов треугольника (в треугольнике биссектриса показана как BD)
Высота – это перпендикуляр, опущенный из вершины на одну из сторон треугольника. Также высоты или их продолжения пересекаются в одной точке, которая называется ортоцентром (в треугольнике высота показана как ВН)
Средняя линия – это отрезок, соединяющий середины сторон. Средняя линия треугольника параллельна основанию, и по длине она равна половине основания. Средняя линия трапеции равна половине суммы оснований и параллельна основаниям.
Виды треугольников:
У равностороннего треугольника все стороны равны и углы по 600.
У равнобедренного треугольника равны только две стороны и углы при основании. Медиана, проведенная в нём к основанию, также является биссектрисой и высотой.
У прямоугольного треугольника один угол равен 900 и сумма двух других углов тоже равна 900. Сторона, лежащая напротив прямого угла в таком треугольнике, называется гипотенузой, а две другие — катетами. Катет, лежащий напротив угла 300, равен половине гипотенузы. Медиана, проведённая в прямоугольном треугольнике из вершины прямого угла, равна половине гипотенузы
Признаки равенства треугольников:
- Треугольники равны по двум сторонам и углу между ними
АВ = А1В1
АС = А1С1
Угол ВАС = угол В1А1С1
- Треугольники равны по стороне и двум прилежащим к ней углам
АВ = А1В1
Угол ВАС = угол В1А1С1
Угол АВС = угол А1В1С1
- Треугольники равны по трём сторонам
АВ = А1В1
АС = А1С1
ВС = В1С1
Давайте теперь разберёмся, что значит подобие:
Если треугольники похожие, но отличаются только размером, тогда поможет подобие треугольников
Коэффициент подобия – это число, в которое отличаются стороны треугольников
Если АВС подобен А1В1С1, тогда верно равенство, где к – коэффициент подобия
Если треугольники подобны, тогда отношение их площадей равно квадрату коэффициента подобия
Признаки подобия треугольников:
- По двум сторонам и углу между ними
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами, равны, то такие треугольники подобны
- По двум углам
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны
- По трём сторонам
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны
Площадь треугольника
Площадь треугольника, если известна высота и основание, к которому она проведена

Площадь треугольника с двумя известными сторонами и углом между ними

Площадь прямоугольного треугольника с известными катетами

Площадь правильного треугольника, если известна только сторона

Формула Герона позволяет вычислить площадь треугольника, если известны его стороны
Площадь треугольника, когда известен полупериметр и радиус вписанной окружности

Площадь треугольника, когда известны стороны и радиус описанной окружности

Многоугольник
Многоугольник – это часть плоскости, ограниченная замкнутой ломаной линией
Многоугольники бывают выпуклые и невыпуклые
Многоугольник является выпуклым, если он находится в одной полуплоскости относительно прямой, содержащей любую его сторону
Для нахождения площади любого выпуклого четырёхугольника существует формула:
Виды многоугольников:
- Параллелограмм – это четырёхугольник, у которого стороны попарно параллельны
Свойства параллелограмма:
- Противоположные стороны равны
- Противоположные углы равны
- Диагонали делятся точкой пересечения пополам
Формулы площади
- Прямоугольник – это четырехугольник, у которого все углы прямые
Свойства прямоугольника:
- Диагонали равны
- Противоположные стороны параллельны и равны
- Угол между сторонами прямой
- Сумма углов 360 градусов
Формула площади
Квадрат – это частный случай прямоугольника
Свойства квадрата:
- Диагонали взаимно перпендикулярны и равны
- Диагонали делят углы квадрата пополам
- Все стороны равны
- Угол между сторонами прямой
- Сумма углов 360 градусов
Формулы площади
- Трапеция – это четырёхугольник с двумя параллельными сторонами (основаниями), а две другие стороны у него не параллельны
Трапеция может быть произвольной, равнобедренной или прямоугольной.
Общие свойства трапеции:
- Сумма углов, прилежащих к боковой стороне, равна 180 градусов
- Средняя линия равна полусумме оснований
- Отрезок, соединяющий середины диагоналей, равен полуразности её оснований
Свойства равнобедренной трапеции:
- Углы при основании равны
- Диагонали равны
Формулы площади
- Ромб – это параллелограмм, у которого все стороны равны
Свойства ромба:
- Противоположные углы равны
- Все стороны равны
- Диагонали делятся точкой пересечения пополам
- Диагонали перпендикулярны друг другу
- Диагонали являются биссектрисами углов
Формулы площади
Окружность
Окружность – это замкнутая прямая на плоскости, все точки которой равноудалены от центра (например, обруч)
Дуга – это часть окружности, заключённая между двумя точками, лежащими на этой окружности
В окружности можно провести радиус, диаметр и хорду
Радиус – расстояние от центра до окружности
Диаметр – прямая, соединяющая две точки на окружности и проходящая через центр окружности
Хорда – прямая, соединяющая две любых точки окружности
Также в окружности есть два вида углов
Вписанный угол – угол, у которого вершина лежит на окружности, а стороны угла пересекают её. Такой угол равен половине дуги, на которую опирается
Центральный угол – угол, у которого вершина находится в центре окружности, а стороны угла пересекают её. Данный угол равен дуге, на которую опирается
Окружность, вписанная в четырёхугольник
Чтобы вписать окружность в четырёхугольник, суммы длин противоположных сторон четырёхугольника должны быть равны
a + c = b + d
Окружность, вписанная в прямоугольный треугольник
У вписанной в прямоугольный треугольник окружности радиус вычисляется по формуле r
Окружность, описанная около четырёхугольника
Чтобы описать окружность около четырёхугольника, необходимо и достаточно выполнения одного из условий:
- Сумма противоположных углов треугольника равна 180 градусов
- Вписанные углы, опирающиеся на одну хорду, равны
Окружность, описанная около прямоугольного треугольника
- Диаметр окружности равен гипотенузе вписанного треугольника
- Радиус описанной окружности равен половине гипотенузы
R=c/2, где c-диаметр
Теорема синусов:
Отношения длин сторон треугольника к синусам противолежащих углов равны между собой, а также равны двум радиусам описанной окружности

Фактчек
Равенство треугольников можно определить по одному из трёх признаков равенства треугольников (по двум сторонам и углу между ними, по стороне и прилежащим к ней углам, по трем сторонам).
- Признаки подобия немного отличаются от признаков равенства треугольников (по двум сторонам и углу между ними, по двум углам, по трём сторонам), по ним определяется отношение соответственных сторон одного треугольника к сторонам другого.
- Для нахождения площади выпуклого четырёхугольника есть универсальная формула
S = ½* d1* d2 *sin α , где d 1, d 2 — длины диагоналей четырехугольника, α — угол между диагоналями четырехугольника.
- Окружность можно вписать в четырёхугольник, если суммы его противоположных сторон равны, а описать окружность около четырёхугольника можно, если пара противоположных углов в сумме даёт 180 градусов.
- Так же стоит помнить, что в теореме синусов равны не только отношения противолежащих сторон к синусам углов, но и каждое такое отношение равно двум радиусам описанной окружности.
Проверь себя
Задание 1.
Чему равен отрезок соединяющий середины диагоналей в трапеции с основаниями а и b?
1. (a + b) / 2
2. (a — b) / 2
3. a-b
4. a+b
Задание 2.
В прямоугольном треугольнике один из катетов равен половине гипотенузы, чему равен угол напротив этого катета?
1. 90°
2. 60°
3. 30°
4. 20°
Задание 3.
Чему равен вписанный угол, опирающийся на хорду равную 84 градусам?
1. 42°
2. 21°
3. 84°
4. 90°
Задание 4.
Чему равен радиус описанного прямоугольного треугольника с катетами 3 и 4?
1. 5
2. 1,5
3. 2,5
4. 2
Задание 5.
Из каких длин сторон треугольника нельзя получить треугольник?
1. 4 16 12
2. 5 6 9
3. 3. 41 18 24
4. 17 14 28
Ответы: 1. — 2; 2. — 2; 3. — 1; 4. — 3; 5. — 1.
Углы при пересечении двух прямых
Если какие-нибудь две прямые пересечены третьей прямой, то пересекающая их прямая называется секущей по отношению к прямым, которые она пересекает.
При пересечении двух прямых третьей, образуется два вида углов: внешние и внутренние.

На рисунке изображены две прямые a и b, пересекаемые прямой c. Прямая c по отношению к прямым a и b является секущей. Синим цветом на рисунке обозначены внешние углы (∠1, ∠2, ∠7 и ∠8), а красным — внутренние углы (∠3, ∠4, ∠5 и ∠6).
Также при пересечении двух прямых третьей, образовавшиеся углы получают попарно следующие названия:
Углы при пересечении параллельных прямых
Если секущая пересекает две параллельные прямые линии, то:
- внутренние накрест лежащие углы равны;
- сумма внутренних односторонних углов равна 180°;
- соответственные углы равны;
- внешние накрест лежащие углы равны;
- сумма внешних односторонних углов равна 180°.
Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы
Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть
Конечно, углы и , и — тоже вертикальные.
Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .
Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.
Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть
Углы и (а также и , и , и ) называются соответственными.
Соответственные углы равны, то есть
Углы и (а также и , и , и ) называют накрест лежащими.
Накрест лежащие углы равны, то есть
Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.
Ты нашел то, что искал? Поделись с друзьями!
1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .
 Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.
Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.
Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.
Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .
Периметр параллелограмма — это сумма всех его сторон, то есть
2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.
Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .
3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
 Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.
Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.
Давайте посмотрим на чертеж. По условию, , то есть .
Углы и — односторонние при параллельных прямых и секущей, следовательно,
Геометрия. Урок 2. Углы
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Углы
Понятие угла
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Стороны угла – лучи, которые образуют угол.
Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.
Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠ A O B или ∠ B O A , но ни в коем случае не ∠ O A B , ∠ O B A , ∠ A B O , ∠ B A O .
Величину угла измеряют в градусах. ∠ A O B = 24 ° .
Виды углов:
Биссектриса угла
Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.
Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.
O D – биссектриса угла ∠ A O B . Она делит этот угол на два равных угла.
∠ A O D = ∠ B O D = ∠ A O B 2
Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон O A и O B угла ∠ A O B .
Углы, образованные при пересечении двух прямых
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.
Свойство: сумма смежных углов равна 180 ° .
( 1 ) и ( 3 )
( 2 ) и ( 4 )
называются вертикальными .
По свойству вертикальных углов:
∠ C O D = ∠ A O B
∠ B O D = ∠ A O C
( 1 ) и ( 2 )
( 2 ) и ( 3 )
( 3 ) и ( 4 )
( 4 ) и ( 1 )
называются смежными .
По свойству смежных углов:
∠ C O D + ∠ D O B = 180 ° ∠ D O B + ∠ B O A = 180 ° ∠ B O A + ∠ A O C = 180 ° ∠ A O C + ∠ C O D = 180 °
Углы, образованные при пересечении двух прямых секущей
Прямая, пересекающая две заданные прямые, называется секущей этих прямых.
Существует пять видов углов, которые образуются при пересечении двух прямых секущей.
( 1 ) и ( 5 )
( 2 ) и ( 6 )
( 3 ) и ( 7 )
( 4 ) и ( 8 )
называются соответственными .
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).
( 3 ) и ( 5 )
( 4 ) и ( 6 )
называются внутренними односторонними .
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).
( 1 ) и ( 7 )
( 2 ) и ( 8 )
называются внешними односторонними .
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).
( 3 ) и ( 6 )
( 4 ) и ( 5 )
называются внутренними накрест лежащими .
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).
( 1 ) и ( 8 )
( 2 ) и ( 7 )
называются внешними накрест лежащими .
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).
Если прямые, которые пересекает секущая, параллельны , то углы имеют следующие свойства:
- Соответственные углы равны.
- Внутренние накрест лежащие углы равны.
- Внешние накрест лежащие углы равны.
- Сумма внутренних односторонних углов равна 180 ° .
- Сумма внешних односторонних углов равна 180 ° .
Сумма углов многоугольника
Сумма углов произвольного n -угольника вычисляется по формуле:
S n = 180 ° ⋅ ( n − 2 )
где n – это количество углов в n -угольнике.
Пользуясь этой формулой, можно вычислить сумму углов для произвольного n -угольника.
Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 °
Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 °
Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 °
Так можно продолжать до бесконечности.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунках изображены примеры правильных многоугольников:



Чтобы найти величину угла правильного n -угольника , необходимо сумму углов этого многоугольника разделить на количество углов.
α n = 180 ° ⋅ ( n − 2 ) n
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с углами
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/ugly-pri-parallelnyx-pryamyx/
[/spoiler]
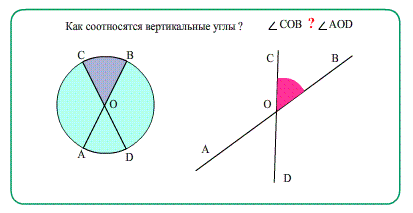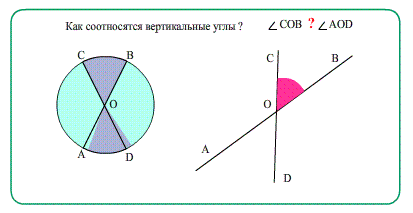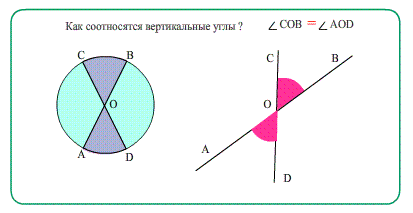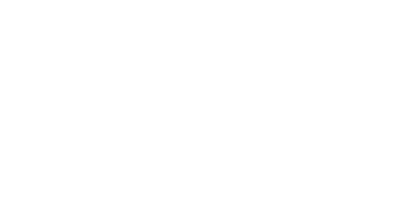
Пересечение двух параллельных прямых секущей
Параллельными называются пара прямых, которые при продолжении не пересекаются.
Когда две паралелльные прямые $a$ и $b$ пересекаются секущей $c$ , то образуется много разнообразных углов.
Некоторые пары углов имеют свои имена – названия:
пара накрест лежащие углы : ∠3 и ∠5, ∠4 и ∠6;
пара односторонние углы : ∠4 и ∠5, ∠3 и ∠6;
пара соответственные углы : ∠1 и ∠5, ∠4 и ∠8, ∠2 и ∠6, ∠3 и ∠7.
Свойства:
- накрест лежащие углы равны: 3 = 5, 4 = 6.
- соответственные углы равны: 1 = 5, 4 = 8, 2 = 6, 3 = 7.
- сумма односторонних углов равна 180 градусов: 3 + 6 = 180 градусов, 4 + 5 = 180 градусов.

_____________________________________________________________________________________
Теорема Если две параллельные линии пересекаются третьей (Секущей), тогда выполняется следующее:
ТеоремаТеорема * накрест лежащие углы равны ;
ТеоремаТеорема * соответственные углы равны ;
ТеоремаТеорема * сумма односторонних углов 180 град. ;
ТеоремаТеорема * вертикальные равны ∠3 = ∠1, ∠8 = ∠6 .
_____________________________________________________________________________________
Теорема Если две прямые перпендикулярны (обе одновременно) к третьей, то они параллельны друг другу.
_____________________________________________________________________________________
Теорема Если две прямые не параллельны друг другу, то равенства для сумм углов не выполняются: 3 + 6 < 180 ; 4 + 5 > 180 .
_____________________________________________________________________________________
Теорема Если одна прямая параллельна второй, а вторая параллельна третьей, то первая прямая так же параллельна третьей.
_____________________________________________________________________________________
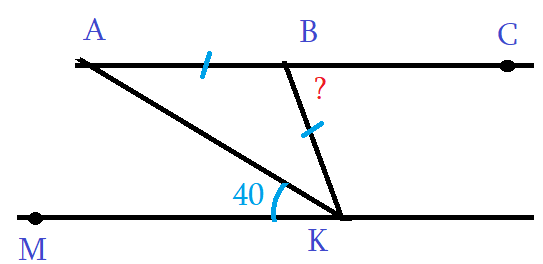
Задача 1: На рисунке АС и МК параллельны, отрезки АВ = ВК равные. Дан угол ∠АКМ = 40°. Найти ∠КВС.
- Решение: АС ║ МК параллельны, АК – секущая, $Rightarrow$ ∠АКМ и ∠КАВ накрест лежащие, $Rightarrow$ ∠КАВ = 40°.
- ∆АВК – равнобедренный, АВ = ВК $Rightarrow$ углы у основания ∠КАВ = ∠АКВ значит, $Rightarrow$ ∠АКВ = 40°.
- Значит, углы ∠АКВ = ∠АКМ равные. Угол ∠МКВ состоит из частей, аддитивность, ∠МКВ = ∠АКВ + ∠АКМ = 80°.
- АС ║ МК параллельны, АК – секущая, $Rightarrow$ ∠ВКМ и ∠КВС накрест лежащие, $Rightarrow$ Ответ: ∠КВС = 80°.
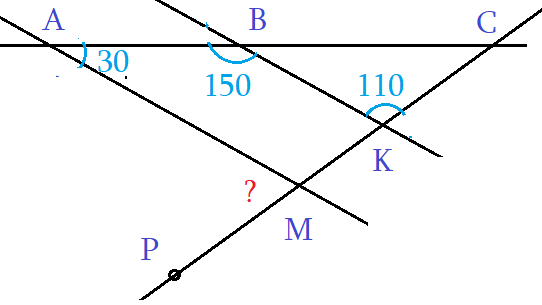
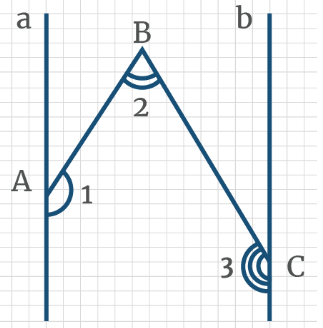
Задача 2: На рисунке, даны углы ∠ВАМ = 30°, ∠АВК = 150°, ∠ВКС = 110°. Найти ∠АМР.
- Решение: Углы ∠ВАМ и ∠АВК – односторонные от секущей АВ. Их сумма ∠ВАМ + ∠АВК = 180°.
- Сумма односторонных 180°? … по теореме “о параллельных”, прямые АМ и ВК должны быть параллельными. АМ ║ ВК.
- Теперь: АМ ║ ВК, СР – секущая. Односторонные углы равные, ∠ВКС = ∠АМК. Значит, ∠АМК = 110°.
- Наконец, углы ∠АМК и ∠АМР – смежные. Значит, ∠АМК + ∠АМР = 180°. $Rightarrow$ ∠АМР = 180° – ∠АМК = 70°.
- Ответ: ∠АМР = 70°. Замечание: “надо видеть все секущие к параллельным, и углы к ним”.
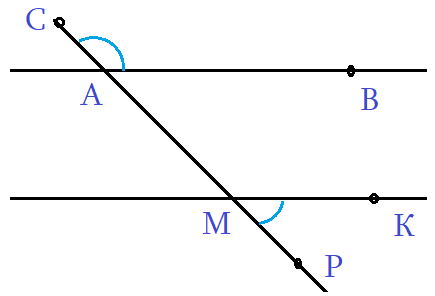
Задача 3: На рисунке, АВ параллельно МК, угол ∠РМК составляет треть угла ∠САВ. Найти эти углы.
- Решение: Дано: отношение углов ∠РМК : ∠САВ = 1 : 3. Выразим: ∠САВ = 3∠РМК
- Как связаны искомые углы по рисунку? ∠САВ и ∠МАВ – смежные, значит ∠МАВ = 180° – ∠САВ.
- Углы ∠МАВ и ∠РМК односторонные углы при параллельных АВ ║ МК и секущей РС. Значит, ∠МАВ = ∠РМК
- Из двух равенств получаем ∠РМК = 180° – ∠САВ. Вспомним ∠САВ = 3∠РМК, подставим: ∠РМК = 180° – 3∠РМК
- ∠РМК = 45°, значит ∠САВ = 3∠РМК = 135°. Ответ: 45°, 135°
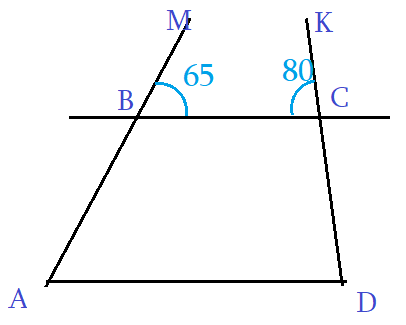
Задача 4: На рисунке, АD параллельно ВС, угол ∠МВС = 65°, ∠ВСК = 80°. Найти четырехугольника АВСD.
- Трапеция АВСD: Четырехугольник с двумя параллельными сторонами называется трапецией. АD ║ ВС.
- Решение: Угол трапеции ∠АВС смежен с ∠МВС, значит ∠АВС = 180° – ∠МВС = 115°.
- Аналогично, угол трапеции ∠ВСD смежный к углу ∠ВСК, значит ∠ВСD = 180° – ∠ВСК = 100°.
- АМ секущая к АD ║ ВС $Rightarrow$ ∠ВАD и ∠МВС соответственные, значит равные ∠ВАD = ∠МВС = 65°.
- Аналогично, КD секущая к АD ║ ВС $Rightarrow$ ∠АDС и ∠ВСК соответственные, значит равные ∠АDС = ∠ВСК = 80°.
- Ответ: Углы трапеции ∠ВАD = 65° ∠АВС = 115° ∠ВСD = 100° ∠АDС= 80°
Задача 4, продолжение, “углы в трапеции”: Пусть углы любые: ∠МВС = х, ∠ВСК = у.
- Такими же рассуждениями о смежных и односторонных, получим: ∠А = х ∠В = 180° – х ∠С = 180° – у ∠D = у
- Видно: ∠А + ∠В = 180° ∠С + ∠D = 180°. Сумма углов при боковой стороне трапеции 180° . Односторонные!
- Видно: ∠А + ∠В + ∠С + ∠D = 180°. Сумма всех углов трапеции равна 360°. . Как у четырехугольника?
Факты, Следствия из теорем о углах при параллельных и секущей к ним:
- В параллелограмме и трапеции диагонали образуют со сторонами равные накрест лежащие углы. Что секущая?
- В паралеллограмме сумма углов у одной стороны равен 180 град. – внутренные односторонные. Что секущая?
- В трапеции сумма углов у боковых сторон равен 180 град. – внутренные односторонные. Что секущая?
- Еще о углах: Диаметры в окружности при пересечении образуют равные вертикальные углы.
- Сумма углов треугольника 180 градусов . Достроить параллельную, увидеть секущую!
Интерактивные Упражнения:
Задачи из сайта https://resh.edu.ru :
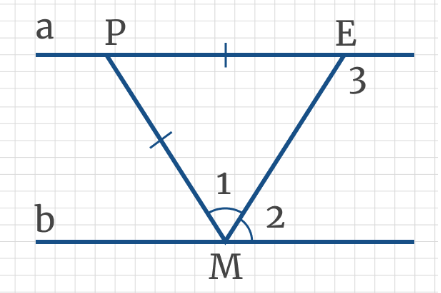
Задача 1: Установите соответствие между углами и их градусными мерами, если ∠РМЕ = 50°, а ∠1 = ∠2 и РМ = РЕ.
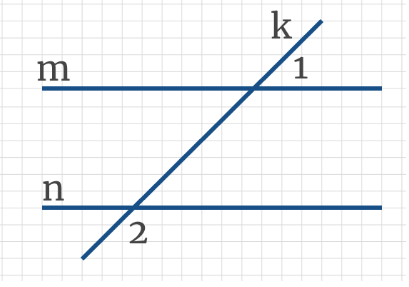
Задача 2: На рисунке через параллельные прямые m и n проведена секущая k, угол 1 составляет 50% угла 2. Найдите угол 1.
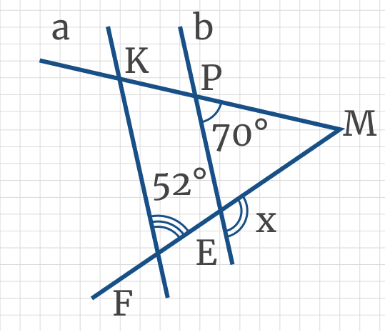
Задача 3: По рисунку найдите градусную меру неизвестного угла х. Параллельные прямые а и b пересечены секущими МК и МF.
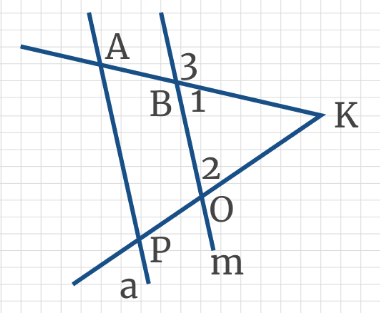
Задача 4: Прямые а и m параллельны. АК и КР – секущие, ∆ВКО – равнобедренный. ∠3 = 120°. Чему равен ∠2?
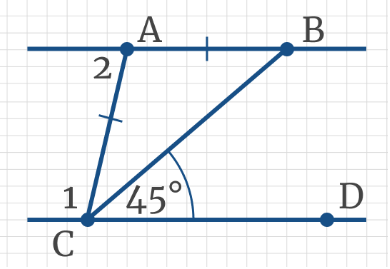
Задача 5: На рисунке прямые AB║CD, при этом AB = AC, ∠BCD = 45°. Найдите угол 2
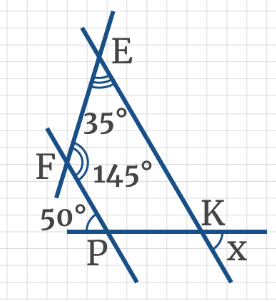
Задача 6: Прямые FP и EK параллельны, чему равна градусная мера угла x?
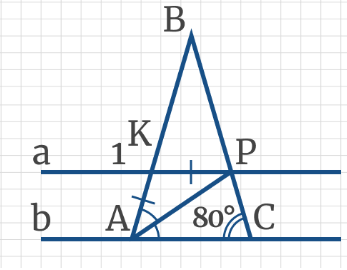
Задача 7: Через параллельные прямые а и b проведены секущие ВА и ВС, так что АВ = ВС, при этом ∠ВСА = 80°. Найдите градусную меру угла 1.
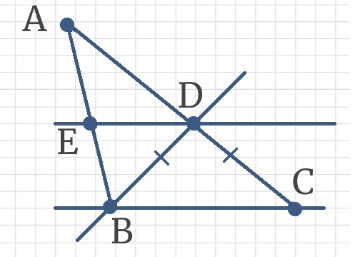
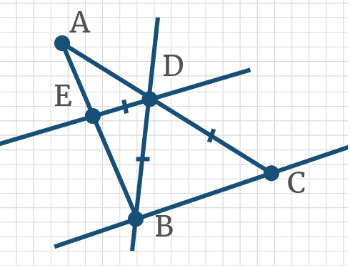
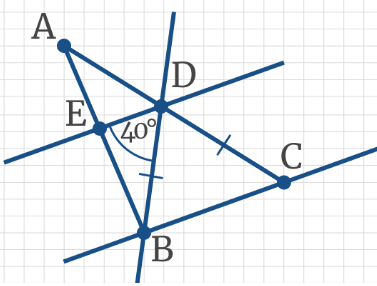
Задача 8: В треугольнике АВС BD – секущая к параллельным прямым BC и DE, при этом ВD = DC, ∠BDE = 40°. Чему равен угол ADВ?
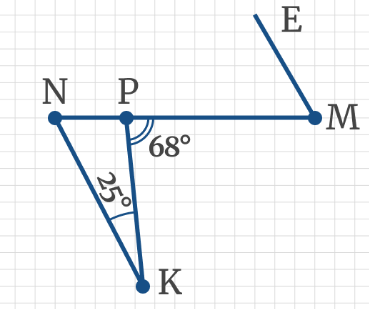
Задача 9: Прямые KN и ME параллельны. По рисунку найдите угол ЕМР, если сумма углов треугольника равна 180°.
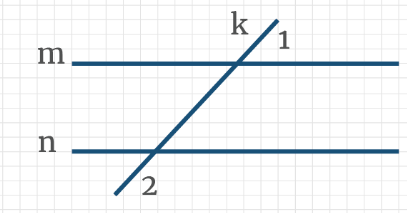
Задача 10: На рисунке через параллельные прямые m и n проведена секущая k, угол 1 составляет 20 % угла 2. Найдите угол 1.
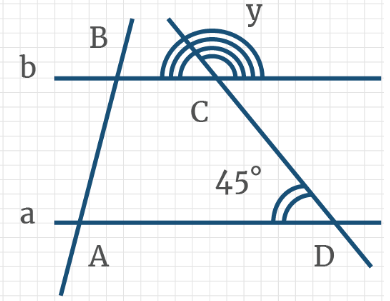
Задача 11: Прямые a и b параллельны. Основываясь на рисунке, определите, чему равна градусная мера угла y.
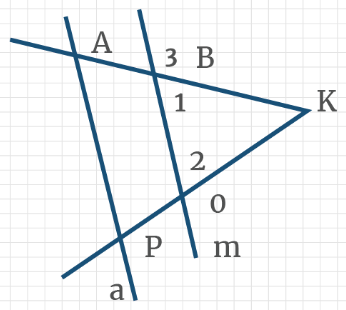
Задача 12: ∆ВКО – равнобедренный. ∠3 = 110°. Чему равен ∠2?
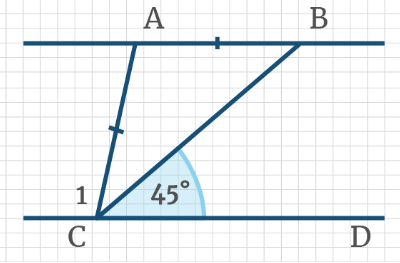
Задача 13: На рисунке AB║CD, при этом AB=AC, ∠BCD = 45°. Найдите угол BAC.
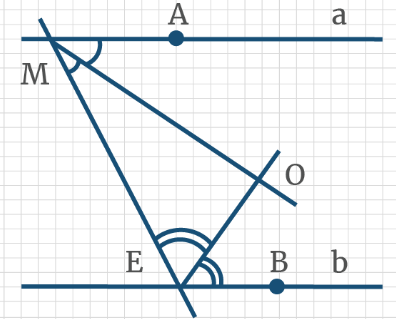
Задача 14: На рисунке прямые а║b, при этом MO и ЕО – биссектрисы углов М и Е соответственно, пересекаются в точке О. Чему равна градусная мера угла МОЕ?
Задача 15: Дан треугольник АВС. BD – секущая к параллельным прямым BC и DE, при этом ВD = DC, ∠BDE = 50°. Чему равен угол ADE?
Задача 16: Прямые а и b параллельны. Чему равна градусная мера суммы углов 1, 2, 3?
Задача 17: Проведена секущая к прямым BC и DE, при этом ВD = DC, BC || DE, ∠BDE = 40°. Чему равен ∠ADE?
Задача 18: Один из односторонних углов при двух параллельных прямых и секущей на 66º меньше другого. Найдите меньший из односторонних углов.
Задача 19: Сумма пары накрест лежащих углов, образованных при пересечении параллельных прямых секущей, равна 110°. Найдите, чему равен один накрест лежащий угол.
Задача 20: “углы в параллелограмме и трапеции”:
-
один из углов параллелограмма 40. найти остальные
-
найти углы параллелограмма, если известно, что сумма двух 80. (100, 160)
-
найти углы параллелограмма, если известно, что разность двух 70. (110, 130)
-
Диагональ параллелограмма состовляет с одной из сторон углы 25 и 35. найти все углы параллелограмма
-
Углы параллелограмма относятся как 2:3 найти все углы
-
Чему равны углы равнобедренной трапеции, если разность противолежащих 40
