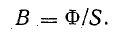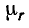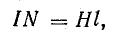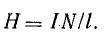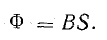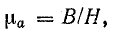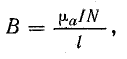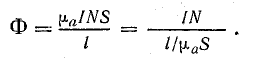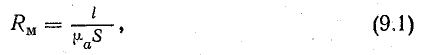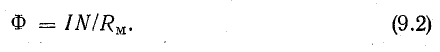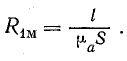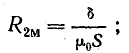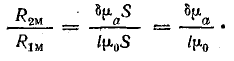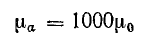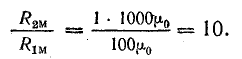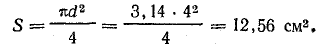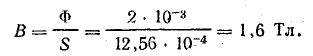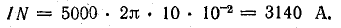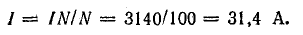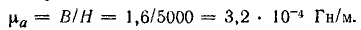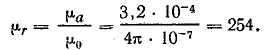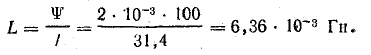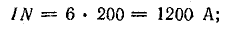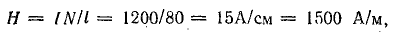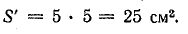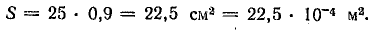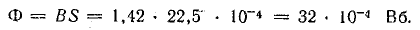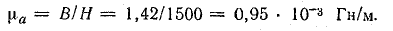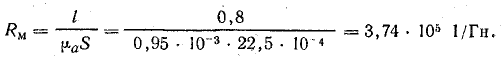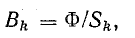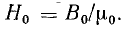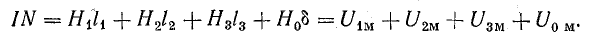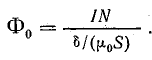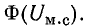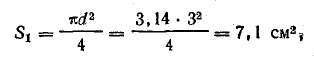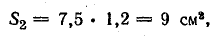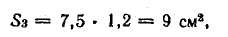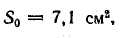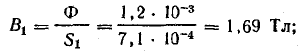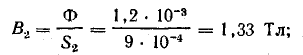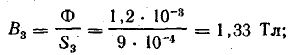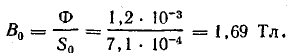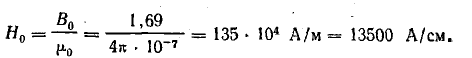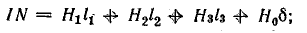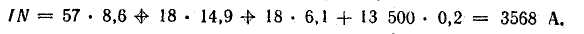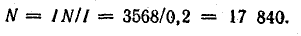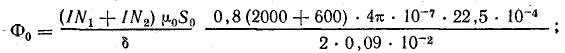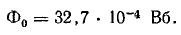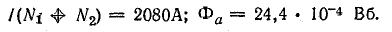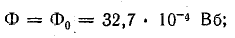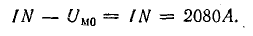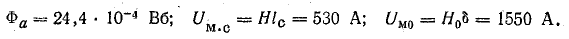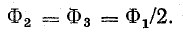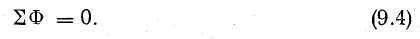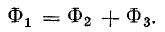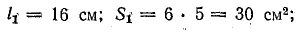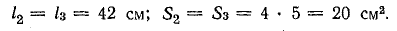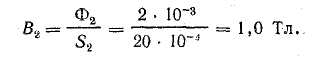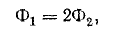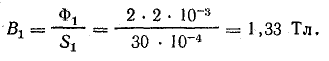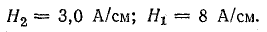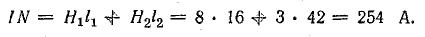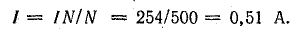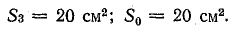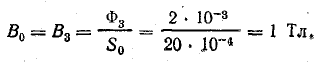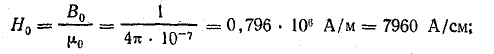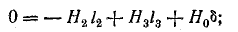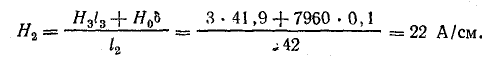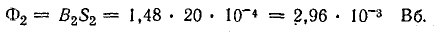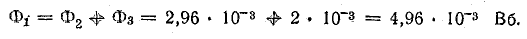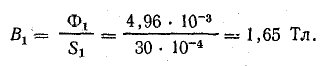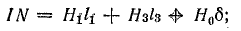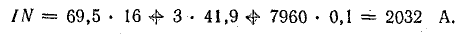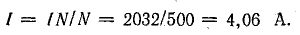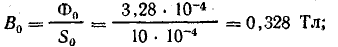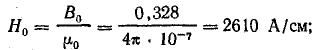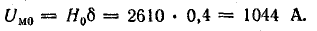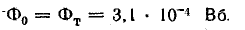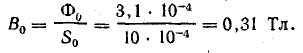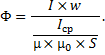Содержание:
Магнитные цепи:
В конструкцию многих электротехнических устройств (электрических машин, трансформаторов, электрических аппаратов, измерительных приборов и т. д.) входят магнитные цепи.
Магнитной цепью называется часть электротехнического устройства, содержащая ферромагнитные тела, в которой при наличии намагничивающей силы возникает магнитный поток и вдоль которой замыкаются линии магнитной индукции. Источниками намагничивающей силы могут быть катушки с токами, постоянные магниты.
В конструктивном отношении магнитные цепи выполняют неразветвленными и разветвленными; применение того или иного вида цепи определяется в основном назначением электромагнитного устройства.
Расчет неразветвленной однородной магнитной цепи
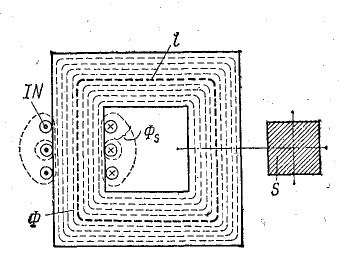
В неразветвленной магнитной цепи (рис. 9.1, 9.2) магнитный поток во всех участках один и тот же.
При расчете и конструировании магнитной цепи электромагнитного устройства решаются вопросы, связанные с выбором размеров, формы, материалов. Эти вопросы изучают в специальных курсах.
Здесь рассмотрим расчет для существующей или сконструированной магнитной цепи, размеры и материалы которой, а также расположение обмоток с токами известны. При этом решают задачи двух типов.
Прямая задача:
По заданному магнитному потоку в цепи требуется определить намагничивающую силу, необходимую для создания этого потока.
Рассмотрим решение этой задачи для неразветвленной однородной магнитной цепи (см. рис. 9.1) без учета потоков рассеяния.
1. По заданному магнитному потоку и известной площади S поперечного сечения сердечника находят магнитную индукцию:
2. Определяют напряженность магнитного поля Н в сердечнике. Зависимость В(Н) — характеристика намагничивания — для стали нелинейная, а магнитная проницаемость
Рис. 9.1. Неразветвленная однородная магнитная цепь
Рис. 9.2. Неразветвленная неоднородная магнитная цепь
Обычно напряженность магнитного поля определяют по кривой намагничивания данного сорта стали (см. рис. 8.30 и приложение 4).
3. Находят намагничивающую силу по закону полного тока [см. формулу (8.41)]:
где l — длина магнитопровода, подсчитанная по средней линии без учета закруглений, причем условно принимается, что эта средняя линия во всех точках совпадает с линией магнитной индукции.
Обратная задача:
По заданной намагничивающей силе требуется найти магнитный поток в магнитопроводе.
1. Определяют напряженность магнитного поля в сердечнике:
2. По кривой намагничивания данного сорта стали находят магнитную индукцию В.
3. Определяют магнитный поток:
Для конкретных величин В и Н, определенных в ходе решения задачи, можно подсчитать статическую магнитную проницаемость данного сорта стали по формуле (8.37):
тогда магнитная индукция
магнитный поток
Обозначив знаменатель этого выражения через Rм:
получим
Магнитное сопротивление
Выражение (9.2) по форме напоминает закон Ома для электрической цепи: на месте тока стоит магнитный поток, на месте э. д. с. — намагничивающая сила (ее называют еще магнитодвижущей силой — м. д. с.). Величину Rм называют магнитным сопротивлением. Выражение магнитного сопротивления сердечника по форме аналогично выражению для определения сопротивления проводника электрическому току. Нужно отметить, что формулы для электрической и магнитной цепей похожи только написанием. Никакого физического подобия явлений в электрической и магнитной цепях не существует.
Расчет магнитных цепей обычно проводят без определения магнитного сопротивления. Это понятие используют в некоторых случаях при качественном рассмотрении явлений в магнитных цепях. Пользуясь им, найдем, как должна измениться намагничивающая сила катушки, если в стальном сердечнике (см. рис. 9.1) сделать хотя бы незначительный воздушный зазор, а магнитный поток при этом должен остаться таким же.
Предположим, что в стальном сердечнике длиной l = 100 мм имеется воздушный зазор δ = 1 мм.
Магнитное сопротивление сердечника
Магнитное сопротивление сердечника с воздушным зазором равно сумме сопротивлений двух участков.
Сопротивление стальной части магнитной цепи при той же магнитной индукции останется практически без изменения, так как уменьшение длины ее очень незначительно (≈ 1 %).
Сопротивление воздушного зазора
Предположим, что относительная магнитная проницаемость стали 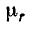
и
Магнитное сопротивление воздушного зазора оказывается в 10 раз больше сопротивления стального сердечника.
Отсюда следует, что для обеспечения того же магнитного потока при наличии воздушного зазора в 1 мм нужно иметь намагничивающую силу примерно в 10 раз большую, чем при его отсутствии. Эта разница оказывается во много раз большей для сердечников из специальных сплавов, для которых величина 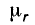
Поэтому во всех случаях, когда по условиям работы электромагнитного устройства без воздушного зазора обойтись нельзя, следует по возможности его сокращать.
Задача 9.1.
В сердечнике кольцевой формы из электротехнической стали нужно получить магнитный поток Ф = 2 • 10-3 Вб. Определить: 1) ток в обмотке, имеющей N = 100 витков; 2) магнитную проницаемость стали при заданном потоке в сердечнике; 3) индуктивность катушки.
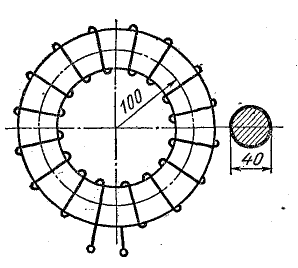
Размеры сердечника заданы в миллиметрах на рис. 9.3.
Рис. 9.3. К задаче 9.1
Решение. Площадь сечения сердечника
Считая магнитную индукцию по сечению сердечника постоянной, найдем ее величину по заданному потоку:
По кривой намагничивания (см.рис. 8.30) определим напряженность магнитного поля: H = 50 А/см = 5000 А/м.
Намагничивающая сила, необходимая для создания заданного потока,
Ток в обмотке
Магнитная проницаемость стали при найденных величинах В и H
Относительная магнитная проницаемость
Индуктивность катушки
Задача 9.3.
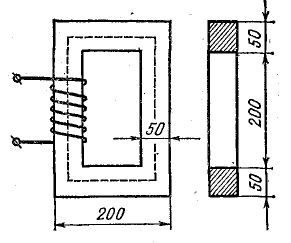
Определить магнитный поток и магнитное сопротивление сердечника (рис. 9.4), размеры которого заданы в миллиметрах, если в катушке с числом витков N = 200 ток I = 6 А. Сердечник изготовлен из электротехнической стали 1511, причем 10% его сечения занимает изоляция между листами.
Рис. 9.4. К задаче 9.3
Решение. Намагничивающая сила и напряженность поля
где I — длина замкнутого сердечника по средней линии; согласно размерам, указанным на чертеже, l = 80 см = 0,8 м.
Магнитная индукция по характеристике намагничивания электротехнической стали 1511 В = 1,42 Тл.
Полная площадь сечения сердечника
Активная площадь
Магнитный поток
Магнитная проницаемость при заданной величине намагничивающей силы
Магнитное сопротивление
Расчет неразветвленной неоднородной магнитной цепи
Неоднородная магнитная цепь состоит из нескольких участков, отличающихся в общем случае длиной, поперечным сечением и материалом. Чаще всего встречаются магнитные цепи, у которых кроме участков из ферромагнитных материалов имеются воздушные зазоры.
Прямая задача:
При решении прямой задачи размеры и материалы каждого участка цепи известны, а магнитный поток задан; определяют намагничивающую силу. Порядок решения прямой задачи такой же, как и для однородной цепи, но магнитную индукцию и напряженность поля определяют для каждого участка; при этом потоки рассеяния в расчет не принимают.
Магнитная индукция k-го участка
где Sk — площадь поперечного сечения k-го участка.
По магнитной индукции определяют напряженность поля: для участков из ферромагнитных материалов — по кривым намагничивания; для воздушных зазоров и других участков из неферромагнитных материалов — по формуле
Далее составляют уравнение согласно закону полного тока:
где Нk — напряженность магнитного поля k-го участка (принимают ее одинаковой во всех точках этого участка); lk — длина k-то участка, взятая по средней линии; Нklk — магнитное напряжение к-то участка (далее магнитное напряжение будем обозначать Um); 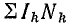
Намагничивающую силу считают положительной в левой части уравнения (9.3), если ее направление, определенное по правилу буравчика, совпадает с направлением обхода магнитного контура. Магнитное напряжение в правой части уравнения считают положительным, если направление магнитного потока совпадает с направлением обхода контура.
Для магнитной цепи (см. рис. 9.2) развернутое уравнение (9.3) имеет вид
Обратная задача:
Обратную задачу — определение магнитного потока по заданным намагничивающим силам — нельзя решить так же просто, как для однородной цепи, так как нельзя сразу установить распределение магнитного напряжения между участками.
Нельзя воспользоваться формулой (9.2), так как магнитное сопротивление участка из ферромагнитного материала зависит от величины 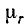
Задачу можно решить методом последовательных приближений.
При наличии в цепи воздушного зазора первое значение магнитного потока можно взять, считая магнитное сопротивление воздушного зазора равным сопротивлению всей магнитной цепи.
Основанием для такого выбора является то, что даже малый воздушный зазор имеет магнитное сопротивление, значительно большее, чем вся остальная часть цепи, выполненная из ферромагнитных материалов.
Пренебрегая в первом приближении магнитным сопротивлением ферромагнитной части цепи, получим поток
Определить магнитный поток можно, построив кривую намагничивания цепи в целом. Для этого нужно задаться произвольно несколькими величинами магнитного потока и определить соответствующие им величины намагничивающей силы.
Рис. 9.5. Кривая намагничивания магнитной цепи
Рис. 9.6. К расчету неразветвленной неоднородной магнитной цепи (обратная задача)
По результатам расчета строится кривая намагничивания цепи (рис. 9.5). По кривой находят магнитный поток, соответствующий заданной намагничивающей силе.
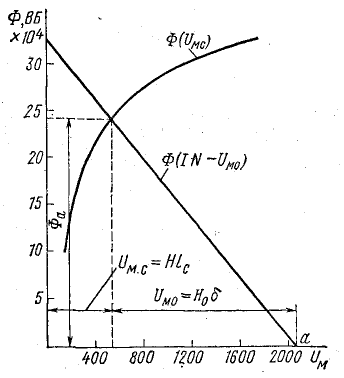
Возможен и другой путь графо-аналитического решения обратной задачи (рис. 9.6). По взятым произвольно нескольким величинам магнитного потока находят величины 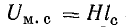
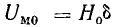
На оси абсцисс находят точку a, соответствующую заданной намагничивающей силе IN, из которой влево проводят прямую Ф(IN — Uм0).
В точке пересечения этих графиков по оси ординат находят искомый поток, а по оси абсцисс — величины Uм.с = Нlс и Uм0 = Н0δ.
Задача 9.5.
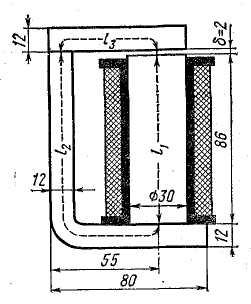
Магнитная цепь электромагнитного реле клапанного типа, изготовленная из стали, имеет поток Ф = 1,2 • 10-3 Вб. Определить число витков катушки реле, необходимое для возбуждения созданного магнитного потока при токе в катушке 0,2 А. Ярмо и якорь реле прямоугольного сечения 7,5 x 1,2 см, сердечник круглого сечения диаметром 3 см. Другие размеры показаны на рис. 9.2.
Решение. Магнитная цепь реле делится на однородные участки:
а) сердечник круглого сечения
длина l1 = 8,6 см;
б) ярмо прямоугольного сечения
длина l2 = 14,9 см (см. рис. 9.2);
в) якорь прямоугольного сечения
длина l3 = 6,1 см;
г) воздушный зазор, сечение которого принимаем равным сечению сердечника, пренебрегая некоторым увеличением его за счет выпучивания линий магнитной индукции:
длина δ = 0,2 см.
Магнитная индукция в участках цепи:
Напряженность магнитного поля в стальных участках определена по кривой намагничивания литой стали, которая принята такой же и для кованой стали: Н1 = 57 А/см; Н2 = 18 А/см; Нз = 18 А /см.
В воздушном зазоре
Составляем уравнение по закону полного тока:
Число витков обмотки
Задача 9.7.
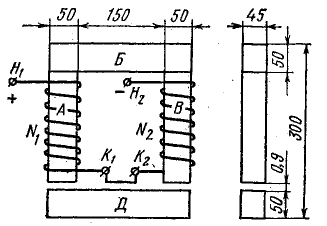
Две катушки N1 = 2000 и N2 = 600 витков насажены на стержни сердечника из электротехнической стали 1211. Размеры магнитной цепи показаны на рис. 9.7. Определить магнитный поток при токе в катушках I = 0,8 А и при соединении концов катушек по схеме: К1 соединен с К2 напряжение приложено к зажимам Н1 и Н2.
Решение. Магнитная цепь рис. 9.7 имеет шесть участков, размеры которых найдены из чертежа:
а) воздушный зазор — δ01 = 0,09 см, S01 = 5 • 4,5 = 22,5 см2;
б) стержень А — l1 = 20 см, S1 = 22,5 см2;
в) ярмо Б — l2 = 25 см, S2 = 22,5 см2;
г) стержень В — lз = 20 см, S3 = 22,5 см2;
д) воздушный зазор — δ02 = 0,09 см, S02 = 22,5 см2;
е) якорь Д — l0 = 25 см, S6 = 22,5 см2.
Рис. 9.7. К задаче 9.7
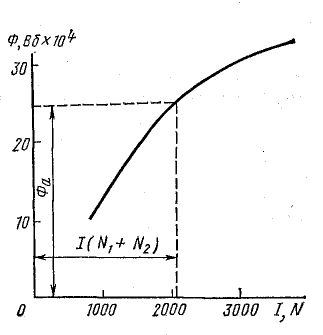
Задаемся несколькими величинами магнитного потока, причем наибольший возможный поток найдем в предположении, что магнитное сопротивление создают только воздушные зазоры [см. формулы (9.1), (9.2)]:
При определении потока учтено, что катушки включены согласно, поэтому их намагничивающие силы сложены.
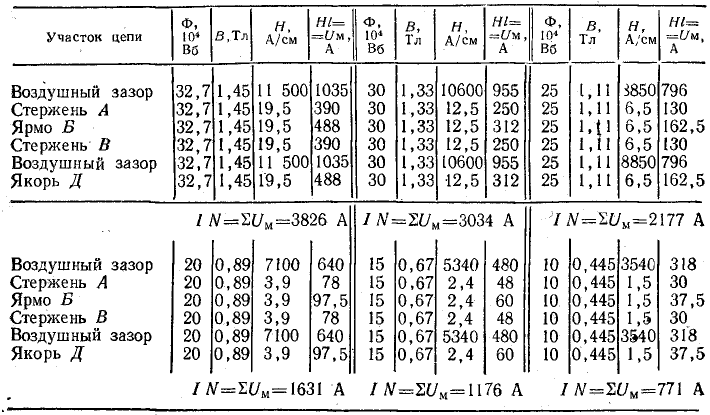
Для полученного потока найдем намагничивающую силу с учетом стальной части магнитной цепи. Последовательность решения та же, что и при решении задачи 9.5. Результаты расчета для Ф0 и других величин потока сведены в табл. 9.1.
Таблица 9.1
Зависимость Ф(IN) построена на рис. 9.5.
По этой кривой определяем искомый поток, соответствующий намагничивающей силе:
Для графо-аналитического способа определения потока по типу рис. 9.6 из табл. 9.1 выпишем величины Ф и Нlc в табл. 9.2.
Таблица 9.2
Зависимости Ф(Um.c) и Ф(IN — Um0) показаны на рис. 9.6, причем прямая Ф(IN — Um0) построена по двум точкам. При IN — Um0 = 0
при Ф = 0
В точке пересечения графиков определяем искомый магнитный поток, а также величины Hlc = Um.c и H0δ = Um0, соответствующие этому потоку:
Расчет разветвленной магнитной цепи
В разветвленной магнитной цепи магнитные потоки в общем случае различны в разных ветвях (рис. 9.8).
Разветвленные магнитные цепи делятся на симметричные и несимметричные.
Рис. 9.8. Разветвленная симметричная магнитная цепь
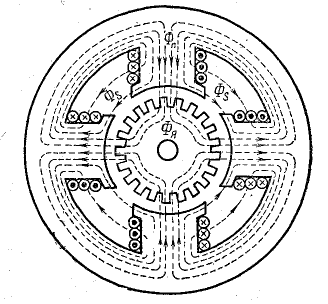
Рис. 9.9. Магнитная цепь четырехполюсной электрической машины
Симметричную магнитную цепь мысленно можно разделить на неразветвленные цепи таким образом, что во всех участках выделенной цепи магнитный поток будет один и тот же. Кроме того, предполагается симметричное расположение намагничивающих сил (рис. 9.8, 9.9).
Если указанные условия симметрии не соблюдаются, то магнитная цепь относится к несимметричным (рис. 9.10).
Узловые и контурные уравнения магнитной цепи
Симметричная магнитная цепь (см. рис. 9.8) состоит из двух одинаковых контуров. Средний стержень вместе с катушкой (источником намагничивающей силы) входит в оба контура.
Место соединения среднего стержня с ярмом является узлом магнитной цепи, в котором магнитный поток Ф1, делится на два равных потока, если магнитное сопротивление обоих контуров одинаково:
Расчет разветвленной симметричной цепи из-за равенств потоков симметричных контуров сводится к расчету одного контура, который выполняют в том же порядке, что и расчет неразветвленной цепи.
В аналогичной несимметричной магнитной цепи поток в узле делится на неравные части, но для любого узла пригодно уравнение
Для схемы рис. 9.8 это уравнение в развернутом виде записывают так:
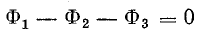
При составлении такого уравнения учитывают направления потоков: направленные к узлу и направленные от узла потоки берутся с разными знаками.
Для каждого контура магнитной цепи можно также составить уравнение по закону полного тока.
Предположим, что все участки магнитной цепи выполнены из материалов с постоянными значениями магнитной проницаемости. Каждый участок и вся цепь имеют линейную зависимость магнитного потока от магнитного напряжения Ф(Uм).
Рис. 9.10. Разветвленная несимметричная магнитная цепь
Рис. 9.11. К расчету разветвленной магнитной цепи графическим методом
Определив для каждого участка магнитное сопротивление Rм, магнитную цепь можно представить соответствующей схемой замещения, в которую войдут постоянные магнитные сопротивления участков и намагничивающие силы.
На рис. 9.11, а показана схема замещения магнитной цепи (см. рис. 9.8). Пренебрегая потоками рассеяния, расчет магнитной цепи можно выполнить аналогично расчету электрической цепи, решая систему линейных уравнений, составленных для узлов (см. формулу (9.4)] и контуров [см. формулу (9.3)].
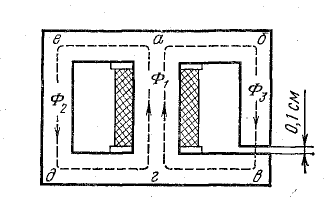
Графический расчет разветвленной цепи
Элементы схем замещения магнитных цепей, осуществляемых на практике (кроме элементов, соответствующих воздушным зазорам), имеют нелинейные характеристики Ф(Uм), так как магнитная проницаемость ферромагнитных материалов зависит от напряженности поля. Нелинейными являются и магнитные цепи в целом.
Аналогия с электрической цепью указывает на возможность графического расчета нелинейной магнитной цепи в порядке. Первый этап расчета состоит в построении характеристик Ф(Uм) для каждого участка цепи в общей системе координат. Для этого используются характеристики намагничивания материалов, из которых изготовлена магнитная цепь. Например, чтобы построить характеристику Ф3(U3м), нужно ряд величин напряженности поля Н3, взятых из характеристики намагничивания материала третьего участка магнитной цепи, умножить на длину этого участка (H3l3 = U3м), а соответствующие им величины магнитной индукции умножить на площадь S3 этого участка (В3S3 = Ф3).
По полученным значениям U3м и Ф3 строят график Ф3(U3м) (рис. 9.11, б). Магнитные сопротивления R2м и R3м соединены параллельно. Поэтому магнитные напряжения второго и третьего участков одинаковы: U2м = U3м = U2.3м.
Сумма магнитных потоков этих участков равна магнитному потоку первого участка (сопротивление R1м): Ф1 = Ф2 + Ф3.
Складывая магнитные потоки Ф2 и Ф3 для ряда значений магнитного напряжения, получим кривую Ф1 (U2.3м).
На рис. 9.11, б это показано для одного значения Uм.п.Отрезки 4-3 и 4-2 в масштабе магнитных потоков выражают потоки Ф3 и Ф2. Сумма этих отрезков, равная отрезку 4-1, выражает магнитный поток Ф1П. Магнитное сопротивление R1м и сопротивление, эквивалентное R2м и R3м, соединены последовательно. Поэтому намагничивающая сила всей цепи IN равна сумме магнитных напряжений U1м и U2.3м: IN = U1м + U2.3м. Магнитные же потоки участков цепи с сопротивлениями R1м и R2.3м одинаковы.
Складывая магнитные напряжения U1м и U2.3м для ряда значений магнитного потока, получим кривую Ф1(IN). На рис. 9.11, б это показано для одного значения Ф1п. Отрезки 7-6 и 7-1 в масштабе магнитных напряжений выражают магнитные напряжения U1м и U2.3м. Сумма этих отрезков дает отрезок 7-5, выражающий намагничивающую силу IN.
Выполнив указанные построения, нетрудно решить различные задачи расчета магнитной цепи.
Задача 6.9.
Катушка, имеющая 500 витков, расположена на среднем стержне магнитопровода, изготовленного из стали 1511 (см. рис. 9.8). Определить ток в катушке, если в крайнем стержне поток Ф2 = Ф3 = 2 • 10-3Вб. Рассеяние потока не учитывается.
Решение. В данной симметричной цепи можно наметить два одинаковых в магнитном отношении контура: а-б-в-г-а и а-е-д-г-а. В каждом из них по два участка:
Рассматривая один из контуров, решим задачу в порядке, принятом для неразветвленной цепи:
Магнитный поток в среднем стержне в два раза больше, чем в крайних:
По кривым намагничивания стали 1511 находим:
По закону полного тока,
Ток в катушке
Задача 9.10.
В крайнем стержне магнитопровода, взятого по условию задачи 9.9, имеется воздушный зазор δ = 0,1 см. Определить, как нужно изменить ток в катушке, чтобы сохранить прежнюю величину потока в этом стержне (см. рис. 9.10).
Решение. При наличии воздушного зазора в одном крайнем стержне магнитная цепь становится несимметричной.
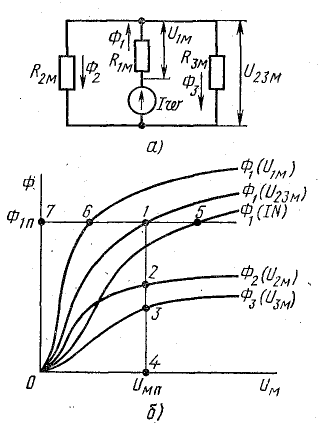
В контуре а-е-д-г-а сохранились те же участки; в контуре а-б-в-г-а: l1 = 16 см; l3 = 41,9 см; δ = 0,1 см; S1 = 30 см2;
Магнитная индукция в воздушном зазоре и крайнем стержне 6-в
Напряженность поля
по кривой намагничивания стали 1511 Н3 = 3 А/см.
В магнитной цепи можно наметить третий контур (а-б-в-г-д-е-а). Для этого контура, по закону полного тока,
Магнитная индукция на участке l2 по кривой намагничивания В2 = 1,48 Тл. Магнитный поток на участке l2
Магнитный поток в среднем стержне (участок l1) определим на основании первого закона Кирхгофа для узла а:
Магнитная индукция на этом участке
Напряженность поля Н1 = 69,5 А/см.
Для одного из контуров, включающего средний стержень, например а-б-в-г-а, по закону полного тока,
Ток в катушке
Вывод. Для того чтобы сохранить в крайнем стержне такой же магнитный поток при наличии воздушного зазора δ = 0,1 см, требуется увеличить ток в катушке почти в восемь раз по сравнению с тем случаем, когда зазор отсутствует.
Постоянные магниты
В измерительных приборах, электрической аппаратуре и других устройствах в качестве источников намагничивающей силы широко применяют постоянные магниты.
На рис. 9.12 схематично изображены магнитные системы магнито-электрического измерительного прибора (а) и поляризованного реле (б).
Эти системы, как и большинство им подобных, имеют несколько участков: 1) из магнитно-твердого материала— постоянного магнита 1; 2) из магнитно-мягкого материала 2, служащего магнитопроводом, и воздушного зазора 3, форма и размеры которого определяются конструкцией и назначением устройства.
При расчете магнитной цепи с постоянным магнитом требуется определить магнитный поток и индукцию в воздушном зазоре или по заданному потоку найти оптимальные размеры постоянного магнита (наименьшие объем и габариты).
Характеристики размагничивания постоянных магнитов
Величины остаточной магнитной индукции Вг и коэрцитивной силы Hс характеризуют материал постоянного магнита: чем они больше, тем выше его качество. Как известно, на петле гистерезиса Вг соответствует Н = 0, а при В = 0 Н = Нс.
Рис. 9.12. Магнитные цепи с постоянными магнитами
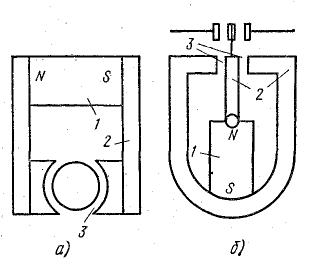
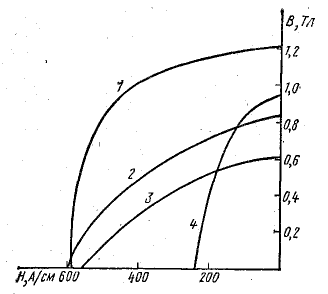
Рис. 9.13. Характеристики размагничивания постоянных магнитов:
1 — АНКО-4; 2 — АНКО-2; З-АН-2; 4 — сталь с 30% СО
Промежуточные магнитные состояния определяются частью петли магнитного гистерезиса, лежащей во второй четверти, — характеристикой размагничивания (рис. 9.12). Эта характеристика используется при расчете постоянных магнитов.
Согласно закону полного тока, сумма магнитных напряжений участков магнитной цепи (рис. 9.12) равна нулю, так как внешняя намагничивающая сила (ампер-витки) отсутствует:
где Uм.т — магнитное напряжение постоянного магнита; 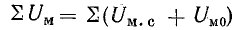
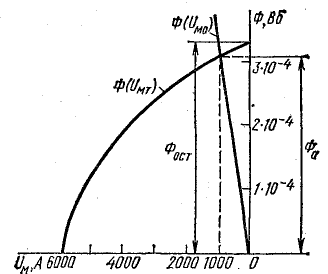
Левая и правая части равенства (9.5) связаны с магнитной индукцией и потоком определенными зависимостями: Фт(Uм.т) — кривая размагничивания постоянного магнита (по форме повторяет кривую размагничивания материала, из которого выполнен постоянный магнит); Фм(Uм.с) — кривая намагничивания части конструкции устройства, изготовленной из магнитно-мягкого материала; Ф0(Uм0) — прямая, проходящая через начало координат и повторяющая в других масштабах зависимость
Определение магнитного потока в магнитной цепи с постоянным магнитом
Пренебрегая потоком рассеяния 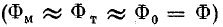
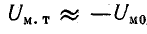
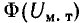
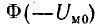
В этом случае искомый магнитный поток Ф0 определяется точкой их пересечения (рис. 9.14).
Магнитная индукция в воздушном зазоре
Из равенства (9.5) следует, что напряженности поля в воздушном зазоре и магните направлены в противоположные стороны.
При отсутствии воздушного зазора (постоянный магнит замкнут) остаточная индукция имеет величину Вг, а при наличии зазора будет меньше Вг (рис. 9.14). Воздушный зазор создает эффект размагничивания магнита.
Рис. 9.14. К расчету магнитной цепи с постоянным магнитом
Задача 9.12.
Определить магнитный поток и индукцию в воздушном зазоре постоянного магнита (см. рис. 9.12, а), если магнит, изготовленный из сплава АНКО-2, имеет длину lт = 10 см; SТ = 4 см2. Полюса и цилиндрический сердечник изготовлены из магнитно-мягкой стали, имеют общую длину lм = 15 см; воздушный зазор между полюсом и сердечником δ = 0,2 см с каждой стороны и площадь S = 10 см2. Характеристика размагничивания сплава АНКО-2 представлена на рис. 9.13.
Решение. Построим зависимость магнитного потока в магните от магнитного напряжения Ф(Uм.т).
Для этого, согласно кривой 2 на рис. 9.13, берем величины В и Н, подсчитываем Ф и Uм.т и результаты подсчета сводим в табл. 9.3.
Для тех же величин магнитного потока определим Uм0 = Н0δ для воздушного зазора. Величинами Hсlс для участков из стали пренебрегаем из-за их незначительной величины.
Т а б л и ц а 9.3
Для потока Ф = 3,28 • 10-4 Вб
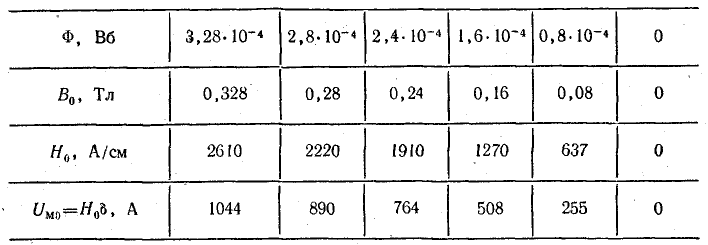
Результаты подсчетов сводим в табл. 9.4.
Таблица 9.4
Зависимости Ф(Uм.т) и Ф(Uм0) построены на рис. 9.14. В точке пересечения этих графиков находим магнитный поток:
Магнитная индукция в воздушном зазоре
- Энергия магнитного поля
- Синусоидальные Э.Д.С. и ток
- Электрические цепи с взаимной индуктивностью
- Резонанс в электрических цепях
- Электромеханические аналогии
- Индуктивно связанные электрические цепи
- Фильтры и топологические методы анализа линейных электрических цепей
- Электрическое поле и его расчёт
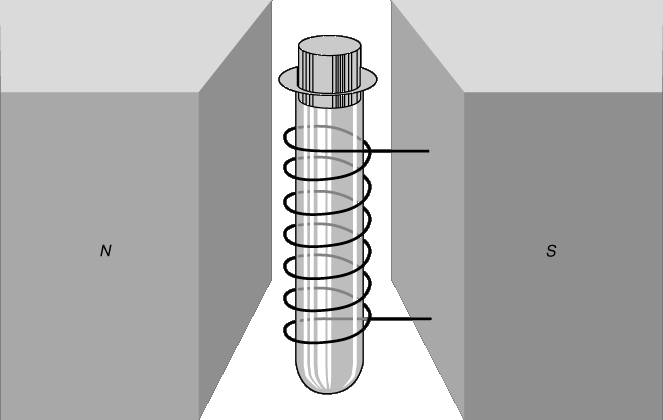
- Магнитные полюса и магнитное поле.
- Гальванометр.
- Намагничивающая сила и напряженность магнитного поля.
- Магнитная проницаемость и ее роль в магнетизме.
- Теории магнетизма.
- МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
- Измерение магнитных свойств.
- Расчет магнитных свойств.
МАГНИТЫ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА. Простейшие проявления магнетизма известны очень давно и знакомы большинству из нас. Однако объяснить эти, казалось бы, простые явления на основе фундаментальных принципов физики удалось лишь сравнительно недавно.
Существуют магниты двух разных видов. Одни – так называемые постоянные магниты, изготовляемые из «магнитно-твердых» материалов. Их магнитные свойства не связаны с использованием внешних источников или токов. К другому виду относятся так называемые электромагниты с сердечником из «магнитно-мягкого» железа. Создаваемые ими магнитные поля обусловлены в основном тем, что по проводу обмотки, охватывающей сердечник, проходит электрический ток.
Магнитные полюса и магнитное поле.
Магнитные свойства стержневого магнита наиболее заметны вблизи его концов. Если такой магнит подвесить за среднюю часть так, чтобы он мог свободно поворачиваться в горизонтальной плоскости, то он займет положение, примерно соответствующее направлению с севера на юг. Конец стержня, указывающий на север, называют северным полюсом, а противоположный конец – южным полюсом. Разноименные полюса двух магнитов притягиваются друг к другу, а одноименные взаимно отталкиваются.
Если к одному из полюсов магнита приблизить брусок ненамагниченного железа, то последний временно намагнитится. При этом ближний к полюсу магнита полюс намагниченного бруска будет противоположным по наименованию, а дальний – одноименным. Притяжением между полюсом магнита и индуцированным им в бруске противоположным полюсом и объясняется действие магнита. Некоторые материалы (например, сталь) сами становятся слабыми постоянными магнитами после того, как побывают около постоянного магнита или электромагнита. Стальной стержень можно намагнитить, просто проведя по его торцу концом стержневого постоянного магнита.
Итак, магнит притягивает другие магниты и предметы из магнитных материалов, не находясь в соприкосновении с ними. Такое действие на расстоянии объясняется существованием в пространстве вокруг магнита магнитного поля. Некоторое представление об интенсивности и направлении этого магнитного поля можно получить, насыпав на лист картона или стекла, положенный на магнит, железные опилки. Опилки выстроятся цепочками в направлении поля, а густота линий из опилок будет соответствовать интенсивности этого поля. (Гуще всего они у концов магнита, где интенсивность магнитного поля наибольшая.)
М.Фарадей (1791–1867) ввел для магнитов понятие замкнутых линий индукции. Линии индукции выходят в окружающее пространство из магнита у его северного полюса, входят в магнит у южного полюса и проходят внутри материала магнита от южного полюса обратно к северному, образуя замкнутую петлю. Полное число линий индукции, выходящих из магнита, называется магнитным потоком. Плотность магнитного потока, или магнитная индукция (В), равна числу линий индукции, проходящих по нормали через элементарную площадку единичной величины.
Магнитной индукцией определяется сила, с которой магнитное поле действует на находящийся в нем проводник с током. Если проводник, по которому проходит ток I, расположен перпендикулярно линиям индукции, то по закону Ампера сила F, действующая на проводник, перпендикулярна и полю, и проводнику и пропорциональна магнитной индукции, силе тока и длине проводника. Таким образом, для магнитной индукции B можно написать выражение
где F – сила в ньютонах, I – ток в амперах, l – длина в метрах. Единицей измерения магнитной индукции является тесла (Тл).
См. также ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ.
Гальванометр.
Гальванометр – чувствительный прибор для измерения слабых токов. В гальванометре используется вращающий момент, возникающий при взаимодействии подковообразного постоянного магнита с небольшой токонесущей катушкой (слабым электромагнитом), подвешенной в зазоре между полюсами магнита. Вращающий момент, а следовательно, и отклонение катушки пропорциональны току и полной магнитной индукции в воздушном зазоре, так что шкала прибора при небольших отклонениях катушки почти линейна.
Намагничивающая сила и напряженность магнитного поля.
Далее следует ввести еще одну величину, характеризующую магнитное действие электрического тока. Предположим, что ток проходит по проводу длинной катушки, внутри которой расположен намагничиваемый материал. Намагничивающей силой называется произведение электрического тока в катушке на число ее витков (эта сила измеряется в амперах, так как число витков – величина безразмерная). Напряженность магнитного поля Н равна намагничивающей силе, приходящейся на единицу длины катушки. Таким образом, величина Н измеряется в амперах на метр; ею определяется намагниченность, приобретаемая материалом внутри катушки.
В вакууме магнитная индукция B пропорциональна напряженности магнитного поля Н:
где m0 – т.н. магнитная постоянная, имеющая универсальное значение 4pЧ10–7 Гн/м. Во многих материалах величина B приблизительно пропорциональна Н. Однако в ферромагнитных материалах соотношение между B и Н несколько сложнее (о чем будет сказано ниже).
На рис. 1 изображен простой электромагнит, предназначенный для захвата грузов. Источником энергии служит аккумуляторная батарея постоянного тока. На рисунке показаны также силовые линии поля электромагнита, которые можно выявить обычным методом железных опилок.
Крупные электромагниты с железными сердечниками и очень большим числом ампер-витков, работающие в непрерывном режиме, обладают большой намагничивающей силой. Они создают магнитную индукцию до 6 Тл в промежутке между полюсами; эта индукция ограничивается лишь механическими напряжениями, нагреванием катушек и магнитным насыщением сердечника. Ряд гигантских электромагнитов (без сердечника) с водяным охлаждением, а также установок для создания импульсных магнитных полей был сконструирован П.Л.Капицей (1894–1984) в Кембридже и в Институте физических проблем АН СССР и Ф.Биттером (1902–1967) в Массачусетском технологическом институте. На таких магнитах удавалось достичь индукции до 50 Тл. Сравнительно небольшой электромагнит, создающий поля до 6,2 Тл, потребляющий электрическую мощность 15 кВт и охлаждаемый жидким водородом, был разработан в Лосаламосской национальной лаборатории. Подобные поля получают при криогенных температурах.
Магнитная проницаемость и ее роль в магнетизме.
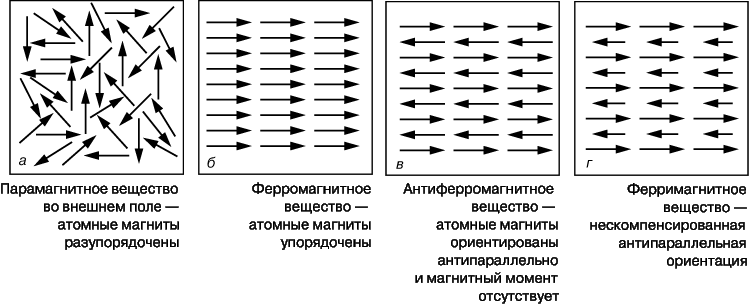
Магнитная проницаемость m – это величина, характеризующая магнитные свойства материала. Ферромагнитные металлы Fe, Ni, Co и их сплавы обладают очень высокими максимальными проницаемостями – от 5000 (для Fe) до 800 000 (для супермаллоя). В таких материалах при сравнительно малых напряженностях поля H возникают большие индукции B, но связь между этими величинами, вообще говоря, нелинейна из-за явлений насыщения и гистерезиса, о которых говорится ниже. Ферромагнитные материалы сильно притягиваются магнитами. Они теряют свои магнитные свойства при температурах выше точки Кюри (770° С для Fe, 358° С для Ni, 1120° С для Co) и ведут себя как парамагнетики, для которых индукция B вплоть до очень высоких значений напряженности H пропорциональна ей – в точности так же, как это имеет место в вакууме. Многие элементы и соединения являются парамагнитными при всех температурах. Парамагнитные вещества характеризуются тем, что намагничиваются во внешнем магнитном поле; если же это поле выключить, парамагнетики возвращаются в ненамагниченное состояние. Намагниченность в ферромагнетиках сохраняется и после выключения внешнего поля.
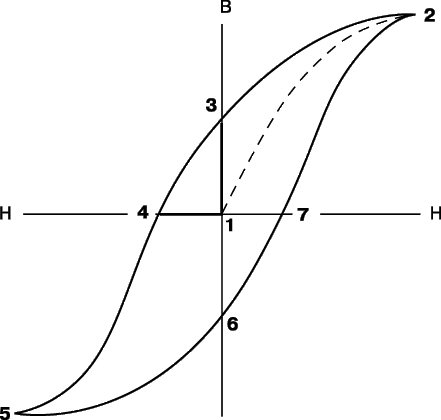
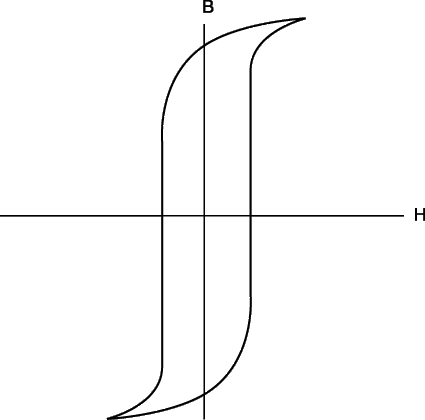
На рис. 2 представлена типичная петля гистерезиса для магнитно-твердого (с большими потерями) ферромагнитного материала. Она характеризует неоднозначную зависимость намагниченности магнитоупорядоченного материала от напряженности намагничивающего поля. С увеличением напряженности магнитного поля от исходной (нулевой) точки (1) намагничивание идет по штриховой линии 1–2, причем величина m существенно изменяется по мере того, как возрастает намагниченность образца. В точке 2 достигается насыщение, т.е. при дальнейшем увеличении напряженности намагниченность больше не увеличивается. Если теперь постепенно уменьшать величину H до нуля, то кривая B(H) уже не следует по прежнему пути, а проходит через точку 3, обнаруживая как бы «память» материала о «прошлой истории», откуда и название «гистерезис». Очевидно, что при этом сохраняется некоторая остаточная намагниченность (отрезок 1–3). После изменения направления намагничивающего поля на обратное кривая В (Н) проходит точку 4, причем отрезок (1)–(4) соответствует коэрцитивной силе, препятствующей размагничиванию. Дальнейший рост значений (–H) приводит кривую гистерезиса в третий квадрант – участок 4–5. Следующее за этим уменьшение величины (–H) до нуля и затем возрастание положительных значений H приведет к замыканию петли гистерезиса через точки 6, 7 и 2.
Магнитно-твердые материалы характеризуются широкой петлей гистерезиса, охватывающей значительную площадь на диаграмме и потому соответствующей большим значениям остаточной намагниченности (магнитной индукции) и коэрцитивной силы. Узкая петля гистерезиса (рис. 3) характерна для магнитно-мягких материалов – таких, как мягкая сталь и специальные сплавы с большой магнитной проницаемостью. Такие сплавы и были созданы с целью снижения обусловленных гистерезисом энергетических потерь. Большинство подобных специальных сплавов, как и ферриты, обладают высоким электрическим сопротивлением, благодаря чему уменьшаются не только магнитные потери, но и электрические, обусловленные вихревыми токами.
Магнитные материалы с высокой проницаемостью изготовляются путем отжига, осуществляемого выдерживанием при температуре около 1000° С, с последующим отпуском (постепенным охлаждением) до комнатной температуры. При этом очень существенны предварительная механическая и термическая обработка, а также отсутствие в образце примесей. Для сердечников трансформаторов в начале 20 в. были разработаны кремнистые стали, величина m которых возрастала с увеличением содержания кремния. Между 1915 и 1920 появились пермаллои (сплавы Ni с Fe) с характерной для них узкой и почти прямоугольной петлей гистерезиса. Особенно высокими значениями магнитной проницаемости m при малых значениях H отличаются сплавы гиперник (50% Ni, 50% Fe) и му-металл (75% Ni, 18% Fe, 5% Cu, 2% Cr), тогда как в перминваре (45% Ni, 30% Fe, 25% Co) величина m практически постоянна в широких пределах изменения напряженности поля. Среди современных магнитных материалов следует упомянуть супермаллой – сплав с наивысшей магнитной проницаемостью (в его состав входит 79% Ni, 15% Fe и 5% Mo).
Теории магнетизма.
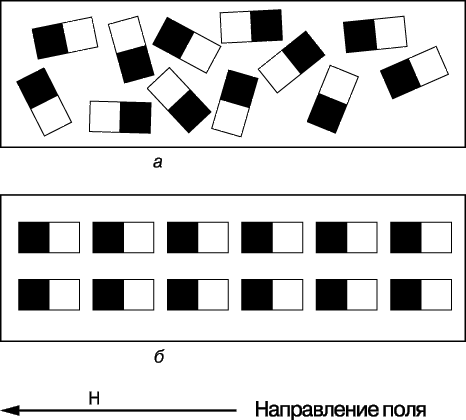
Впервые догадка о том, что магнитные явления в конечном счете сводятся к электрическим, возникла у Ампера в 1825, когда он высказал идею замкнутых внутренних микротоков, циркулирующих в каждом атоме магнита. Однако без какого-либо опытного подтверждения наличия в веществе таких токов (электрон был открыт Дж.Томсоном лишь в 1897, а описание структуры атома было дано Резерфордом и Бором в 1913) эта теория «увяла». В 1852 В.Вебер высказал предположение, что каждый атом магнитного вещества представляет собой крошечный магнит, или магнитный диполь, так что полная намагниченность вещества достигается, когда все отдельные атомные магниты оказываются выстроенными в определенном порядке (рис. 4,б). Вебер полагал, что сохранять свое упорядочение вопреки возмущающему влиянию тепловых колебаний этим элементарным магнитам помогает молекулярное или атомное «трение». Его теория смогла объяснить намагничивание тел при соприкосновении с магнитом, а также их размагничивание при ударе или нагреве; наконец, объяснялось и «размножение» магнитов при разрезании намагниченной иглы или магнитного стержня на части. И все же эта теория не объясняла ни происхождения самих элементарных магнитов, ни явлений насыщения и гистерезиса. Теория Вебера была усовершенствована в 1890 Дж.Эвингом, заменившим его гипотезу атомного трения идеей межатомных ограничивающих сил, помогающих поддерживать упорядочение элементарных диполей, которые составляют постоянный магнит.
Подход к проблеме, предложенный когда-то Ампером, получил вторую жизнь в 1905, когда П.Ланжевен объяснил поведение парамагнитных материалов, приписав каждому атому внутренний нескомпенсированный электронный ток. Согласно Ланжевену, именно эти токи образуют крошечные магниты, хаотически ориентированные, когда внешнее поле отсутствует, но приобретающие упорядоченную ориентацию после его приложения. При этом приближение к полной упорядоченности соответствует насыщению намагниченности. Кроме того, Ланжевен ввел понятие магнитного момента, равного для отдельного атомного магнита произведению «магнитного заряда» полюса на расстояние между полюсами. Таким образом, слабый магнетизм парамагнитных материалов обусловлен суммарным магнитным моментом, создаваемым нескомпенсированными электронными токами.
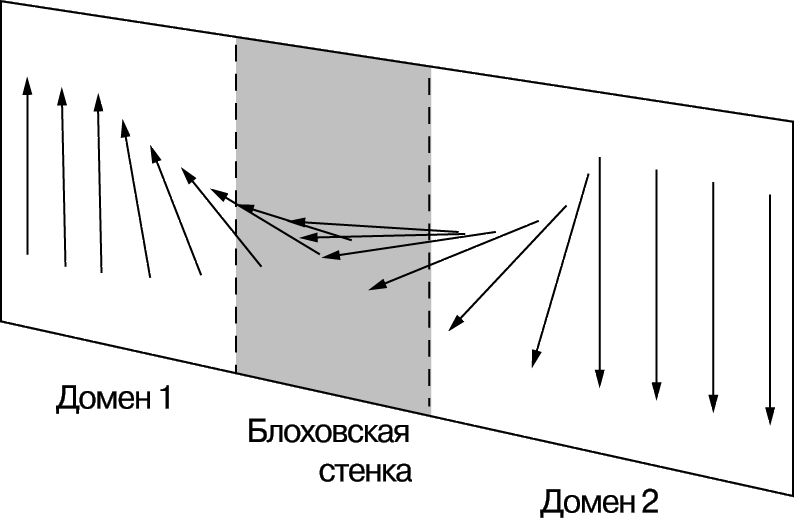
В 1907 П.Вейс ввел понятие «домена», ставшее важным вкладом в современную теорию магнетизма. Вейс представлял домены в виде небольших «колоний» атомов, в пределах которых магнитные моменты всех атомов в силу каких-то причин вынуждены сохранять одинаковую ориентацию, так что каждый домен намагничен до насыщения. Отдельный домен может иметь линейные размеры порядка 0,01 мм и соответственно объем порядка 10–6 мм3. Домены разделены так называемыми блоховскими стенками, толщина которых не превышает 1000 атомных размеров. «Стенка» и два противоположно ориентированных домена схематически изображены на рис. 5. Такие стенки представляют собой «переходные слои», в которых происходит изменение направления намагниченности доменов.
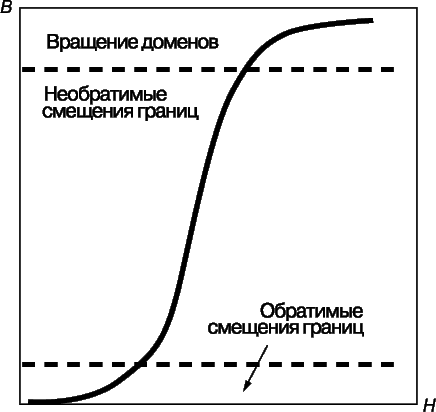
В общем случае на кривой первоначального намагничивания можно выделить три участка (рис. 6). На начальном участке стенка под действием внешнего поля движется сквозь толщу вещества, пока не встретит дефект кристаллической решетки, который ее останавливает. Увеличив напряженность поля, можно заставить стенку двигаться дальше, через средний участок между штриховыми линиями. Если после этого напряженность поля вновь уменьшить до нуля, то стенки уже не вернутся в исходное положение, так что образец останется частично намагниченным. Этим объясняется гистерезис магнита. На конечном участке кривой процесс завершается насыщением намагниченности образца за счет упорядочения намагниченности внутри последних неупорядоченных доменов. Такой процесс почти полностью обратим. Магнитную твердость проявляют те материалы, у которых атомная решетка содержит много дефектов, препятствующих движению междоменных стенок. Этого можно достичь механической и термической обработкой, например путем сжатия и последующего спекания порошкообразного материала. В сплавах алнико и их аналогах тот же результат достигается путем сплавления металлов в сложную структуру.
Кроме парамагнитных и ферромагнитных материалов, существуют материалы с так называемыми антиферромагнитными и ферримагнитными свойствами. Различие между этими видами магнетизма поясняется на рис. 7. Исходя из представления о доменах, парамагнетизм можно рассматривать как явление, обусловленное наличием в материале небольших групп магнитных диполей, в которых отдельные диполи очень слабо взаимодействуют друг с другом (или вообще не взаимодействуют) и потому в отсутствие внешнего поля принимают лишь случайные ориентации (рис. 7,а). В ферромагнитных же материалах в пределах каждого домена существует сильное взаимодействие между отдельными диполями, приводящее к их упорядоченному параллельному выстраиванию (рис. 7,б). В антиферромагнитных материалах, напротив, взаимодействие между отдельными диполями приводит к их антипараллельному упорядоченному выстраиванию, так что полный магнитный момент каждого домена равен нулю (рис. 7,в). Наконец, в ферримагнитных материалах (например, ферритах) имеется как параллельное, так и антипараллельное упорядочение (рис. 7,г), итогом чего оказывается слабый магнетизм.
Имеются два убедительных экспериментальных подтверждения существования доменов. Первое из них – так называемый эффект Баркгаузена, второе – метод порошковых фигур. В 1919 Г.Баркгаузен установил, что при наложении внешнего поля на образец из ферромагнитного материала его намагниченность изменяется небольшими дискретными порциями. С точки зрения доменной теории это не что иное, как скачкообразное продвижение междоменной стенки, встречающей на своем пути отдельные задерживающие ее дефекты. Данный эффект обычно обнаруживается с помощью катушки, в которую помещается ферромагнитный стерженек или проволока. Если поочередно подносить к образцу и удалять от него сильный магнит, образец будет намагничиваться и перемагничиваться. Скачкообразные изменения намагниченности образца изменяют магнитный поток через катушку, и в ней возбуждается индукционный ток. Напряжение, возникающее при этом в катушке, усиливается и подается на вход пары акустических наушников. Щелчки, воспринимаемые через наушники, свидетельствует о скачкообразном изменении намагниченности.
Для выявления доменной структуры магнита методом порошковых фигур на хорошо отполированную поверхность намагниченного материала наносят каплю коллоидной суспензии ферромагнитного порошка (обычно Fe3O4). Частицы порошка оседают в основном в местах максимальной неоднородности магнитного поля – на границах доменов. Такую структуру можно изучать под микроскопом. Был предложен также метод, основанный на прохождении поляризованного света сквозь прозрачный ферромагнитный материал.
Первоначальная теория магнетизма Вейса в своих основных чертах сохранила свое значение до настоящего времени, получив, однако, обновленную интерпретацию на основе представления о нескомпенсированных электронных спинах как факторе, определяющем атомный магнетизм. Гипотеза о существовании собственного момента у электрона была выдвинута в 1926 С.Гаудсмитом и Дж.Уленбеком, и в настоящее время в качестве «элементарных магнитов» рассматриваются именно электроны как носители спина.
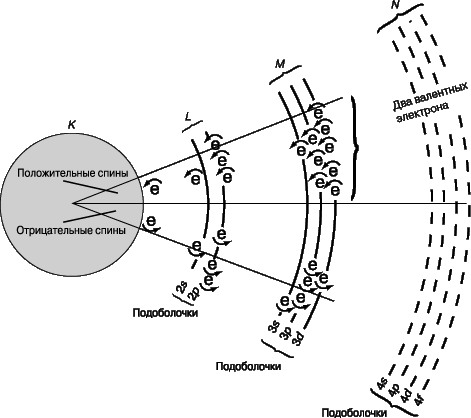
Для пояснения этой концепции рассмотрим (рис. 8) свободный атом железа – типичного ферромагнитного материала. Две его оболочки (K и L), ближайшие к ядру, заполнены электронами, причем на первой из них размещены два, а на второй – восемь электронов. В K-оболочке спин одного из электронов положителен, а другого – отрицателен. В L-оболочке (точнее, в двух ее подоболочках) у четырех из восьми электронов положительные, а у других четырех – отрицательные спины. В обоих случаях спины электронов в пределах одной оболочки полностью компенсируются, так что полный магнитный момент равен нулю. В M-оболочке ситуация иная, поскольку из шести электронов, находящихся в третьей подоболочке, пять электронов имеют спины, направленные в одну сторону, и лишь шестой – в другую. В результате остаются четыре нескомпенсированных спина, чем и обусловлены магнитные свойства атома железа. (Во внешней N-оболочке всего два валентных электрона, которые не дают вклада в магнетизм атома железа.) Сходным образом объясняется магнетизм и других ферромагнетиков, например никеля и кобальта. Поскольку соседние атомы в образце железа сильно взаимодействуют друг с другом, причем их электроны частично коллективизируются, такое объяснение следует рассматривать лишь как наглядную, но весьма упрощенную схему реальной ситуации.
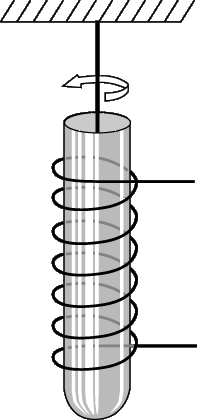
Теорию атомного магнетизма, основанную на учете спина электрона, подкрепляют два интересных гиромагнитных эксперимента, один из которых был проведен А.Эйнштейном и В.де Гаазом, а другой – С.Барнеттом. В первом из этих экспериментов цилиндрик из ферромагнитного материала подвешивался так, как показано на рис. 9. Если по проводу обмотки пропустить ток, то цилиндрик поворачивается вокруг своей оси. При изменении направления тока (а следовательно, и магнитного поля) он поворачивается в обратном направлении. В обоих случаях вращение цилиндрика обусловлено упорядочением электронных спинов. В эксперименте Барнетта, наоборот, так же подвешенный цилиндрик, резко приведенный в состояние вращения, в отсутствие магнитного поля намагничивается. Этот эффект объясняется тем, что при вращении магнетика создается гироскопический момент, стремящийся повернуть спиновые моменты по направлению собственной оси вращения.
За более полным объяснением природы и происхождения короткодействующих сил, упорядочивающих соседние атомные магнитики и противодействующих разупорядочивающему влиянию теплового движения, следует обратиться к квантовой механике. Квантово-механическое объяснение природы этих сил было предложено в 1928 В.Гейзенбергом, который постулировал существование обменных взаимодействий между соседними атомами. Позднее Г.Бете и Дж.Слэтер показали, что обменные силы существенно возрастают с уменьшением расстояния между атомами, но по достижении некоторого минимального межатомного расстояния падают до нуля.
МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
Одно из первых обширных и систематических исследований магнитных свойств вещества было предпринято П.Кюри. Он установил, что по своим магнитным свойствам все вещества можно разделить на три класса. К первому относятся вещества с резко выраженными магнитными свойствами, подобными свойствам железа. Такие вещества называются ферромагнитными; их магнитное поле заметно на значительных расстояниях (см. выше). Во второй класс попадают вещества, называемые парамагнитными; магнитные свойства их в общем аналогичны свойствам ферромагнитных материалов, но гораздо слабее. Например, сила притяжения к полюсам мощного электромагнита может вырвать из ваших рук железный молоток, а чтобы обнаружить притяжение парамагнитного вещества к тому же магниту, нужны, как правило, очень чувствительные аналитические весы. К последнему, третьему классу относятся так называемые диамагнитные вещества. Они отталкиваются электромагнитом, т.е. сила, действующая на диамагнетики, направлена противоположно той, что действует на ферро- и парамагнетики.
Измерение магнитных свойств.
При изучении магнитных свойств наиболее важное значение имеют измерения двух типов. Первый из них –измерения силы, действующей на образец вблизи магнита; так определяется намагниченность образца. Ко второму относятся измерения «резонансных» частот, связанных с намагничением вещества. Атомы представляют собой крошечные «гироскопы» и в магнитном поле прецессируют (как обычный волчок под влиянием вращающего момента, создаваемого силой тяжести) с частотой, которая может быть измерена. Кроме того, на свободные заряженные частицы, движущиеся под прямым углом к линиям магнитной индукции, действует сила, как и на электронный ток в проводнике. Она заставляет частицу двигаться по круговой орбите, радиус которой дается выражением
R = mv/eB,
где m – масса частицы, v – ее скорость, e – ее заряд, а B – магнитная индукция поля. Частота такого кругового движения равна
где f измеряется в герцах, e – в кулонах, m – в килограммах, B – в теслах. Эта частота характеризует движение заряженных частиц в веществе, находящемся в магнитном поле. Оба типа движений (прецессию и движение по круговым орбитам) можно возбудить переменными полями с резонансными частотами, равными «естественным» частотам, характерным для данного материала. В первом случае резонанс называется магнитным, а во втором – циклотронным (ввиду сходства с циклическим движением субатомной частицы в циклотроне).
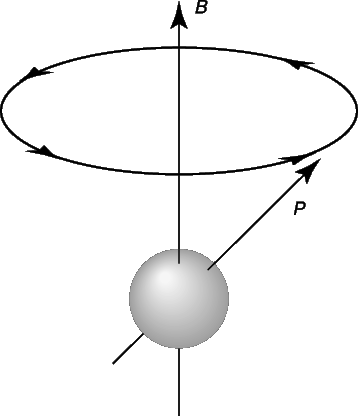
Говоря о магнитных свойствах атомов, необходимо особо остановиться на их моменте импульса. Магнитное поле действует на вращающийся атомный диполь, стремясь повернуть его и установить параллельно полю. Вместо этого атом начинает прецессировать вокруг направления поля (рис. 10) с частотой, зависящей от дипольного момента и напряженности приложенного поля.
Прецессия атомов не поддается непосредственному наблюдению, поскольку все атомы образца прецессируют в разной фазе. Если же приложить небольшое переменное поле, направленное перпендикулярно постоянному упорядочивающему полю, то между прецессирующими атомами устанавливается определенное фазовое соотношение и их суммарный магнитный момент начинает прецессировать с частотой, равной частоте прецессии отдельных магнитных моментов. Важное значение имеет угловая скорость прецессии. Как правило, это величина порядка 1010 Гц/Тл для намагниченности, связанной с электронами, и порядка 107 Гц/Тл для намагниченности, связанной с положительными зарядами в ядрах атомов.
Принципиальная схема установки для наблюдения ядерного магнитного резонанса (ЯМР) представлена на рис. 11. В однородное постоянное поле между полюсами вводится изучаемое вещество. Если затем с помощью небольшой катушки, охватывающей пробирку, возбудить радиочастотное поле, то можно добиться резонанса на определенной частоте, равной частоте прецессии всех ядерных «гироскопов» образца. Измерения сходны с настройкой радиоприемника на частоту определенной станции.
Методы магнитного резонанса позволяют исследовать не только магнитные свойства конкретных атомов и ядер, но и свойства их окружения. Дело в том, что магнитные поля в твердых телах и молекулах неоднородны, поскольку искажены атомными зарядами, и детали хода экспериментальной резонансной кривой определяются локальным полем в области расположения прецессирующего ядра. Это и дает возможность изучать особенности структуры конкретного образца резонансными методами.
Расчет магнитных свойств.
Магнитная индукция поля Земли составляет 0,5Ч10–4 Тл, тогда как поле между полюсами сильного электромагнита – порядка 2 Тл и более.
Магнитное поле, создаваемое какой-либо конфигурацией токов, можно вычислить, пользуясь формулой Био – Савара – Лапласа для магнитной индукции поля, создаваемого элементом тока. Расчет поля, создаваемого контурами разной формы и цилиндрическими катушками, во многих случаях весьма сложен. Ниже приводятся формулы для ряда простых случаев. Магнитная индукция (в теслах) поля, создаваемого длинным прямым проводом с током I (ампер), на расстоянии r (метров) от провода равна
Индукция в центре кругового витка радиуса R с током I равна (в тех же единицах):
Плотно намотанная катушка провода без железного сердечника называется соленоидом. Магнитная индукция, создаваемая длинным соленоидом c числом витков N в точке, достаточно удаленной от его концов, равна
Здесь величина NI/L есть число ампер (ампер-витков) на единицу длины соленоида. Во всех случаях магнитное поле тока направлено перпендикулярно этому току, а сила, действующая на ток в магнитном поле, перпендикулярна и току, и магнитному полю.
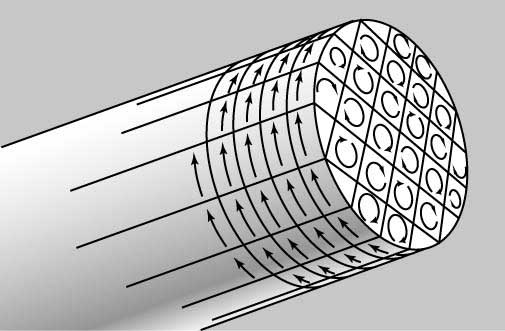
Поле намагниченного железного стержня сходно с внешним полем длинного соленоида с числом ампер-витков на единицу длины, соответствующим току в атомах на поверхности намагниченного стержня, поскольку токи внутри стержня взаимно компенсируются (рис. 12). По имени Ампера такой поверхностный ток называется амперовским. Напряженность магнитного поля Ha, создаваемая амперовским током, равна магнитному моменту единицы объема стержня M.
Если в соленоид вставлен железный стержень, то кроме того, что ток соленоида создает магнитное поле H, упорядочение атомных диполей в намагниченном материале стержня создает намагниченность M. В этом случае полный магнитный поток определяется суммой реального и амперовского токов, так что B = m0(H + Ha), или B = m0(H + M). Отношение M/H называется магнитной восприимчивостью и обозначается греческой буквой c ; c – безразмерная величина, характеризующая способность материала намагничиваться в магнитном поле.
Величина B/H, характеризующая магнитные свойства материала, называется магнитной проницаемостью и обозначается через ma, причем ma = m0m, где ma – абсолютная, а m – относительная проницаемости,
В ферромагнитных веществах величина c может иметь очень большие значения –до 104ё106. Величина c у парамагнитных материалов немного больше нуля, а у диамагнитных – немного меньше. Лишь в вакууме и в очень слабых полях величины c и m постоянны и не зависят от внешнего поля. Зависимость индукции B от H обычно нелинейна, а ее графики, т.н. кривые намагничивания, для разных материалов и даже при разных температурах могут существенно различаться (примеры таких кривых приведены на рис. 2 и 3).
Магнитные свойства вещества весьма сложны, и для их глубокого понимания необходим тщательный анализ строения атомов, их взаимодействий в молекулах, их столкновений в газах и их взаимного влияния в твердых телах и жидкостях; магнитные свойства жидкостей пока наименее изучены.
Рассмотрим
в начале намагничивающую силу однофазной
обмотки.
а
)
Намагничивающая сила однофазной обмотки.
Рассмотрим
в начале простой случай, 2-х полюсную
обмотку однослойную 2Р = 2, Р = 1 с полным
шагом у = = q
= 1, т.е. катушка и будет фаза намагничивающая
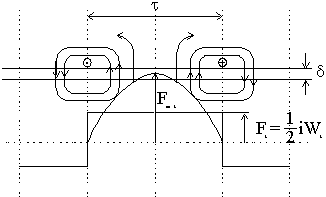
сила катушки F = iWk,
а на полюс Fk
=1/2iWk,
так как любая магнитная силовая линия
сцеплена с одним и тем током i
и число витков W, то н.с.
на полюсном делении будет в пространстве
постоянной, т.е. в пространстве
намагничивающая сила катушки имеет
форму прямоугольника, а во времени
изменяется по синусоидальному закону,
т.к.
максимум
Первая
пространственная гармоника
;
Амплитуда
намагничивающей силы катушечной группы
однослойной обмотки
Амплитуда
намагничивающей силы катушечной группы
двухслойной обмотки с укороченным шагом
Намагничивающая
сила фазы для двухслойной обмотки
Ч
аще
используют амплитуду н.с. на один полюс
или
Запишем
закон изменения н.с. однофазной обмотки.
Для
оси фазы
Намагничивающая
сила
в любой точке пространства и в любой
момент времени определится
,
или
Это
выражение пульсирующей волны
намагничивающей силы фазы. Более удобно
иметь дело с вращающейся намагничивающей
силой, но с постоянной амплитудой.
Заменим пульсирующую н.с. двумя бегущими
волнами, используя тригонометрическую
формулу
,
отсюда
,
тогда
– прямая волна,
– обратная волна.
Представим
графически, что пульсирующая волна
равна сумме двух бегущих волн в разные
стороны с постоянной амплитудой. Условием
бегущей волны является постоянство
аргумента при синусе, т.е. для прямой
волны
,
продифференцируем
,

,
число оборотов
,
об/сек,
в минуту
.
Для
обратной волны
,
.
Итак,
пульсирующую н.с. фазы разложили на две
бегущие волны, которые двигаются с
постоянной амплитудой в разные стороны
с синхронной скоростью.
б)
Намагничивающая сила трехфазной обмотки.
Намагничивающая
сила обмотки является базой для
определения потока.
Запишем
намагничивающие силы для трех фаз в
виде пульсирующих волн, а затем разложим
их на прямую и обратную волну, затем их
сложим, то получим намагничивающую силу
трехфазной обмотки

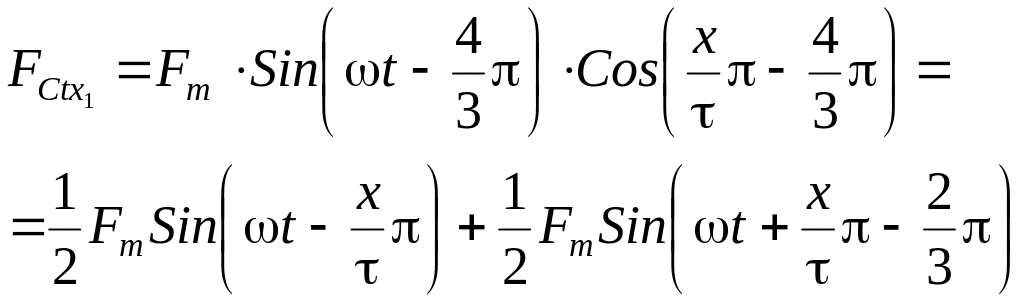
+0,
сумма
обратных волн равна 0, т.к. сдвиг на
и
Намагничивающая
сила трехфазной обмотки есть сумма
прямых волн, что это бегущая волна,
которая двигается вдоль зазора с
синхронной скоростью и с постоянной
амплитудой. Эта н.с. создает вращающееся
магнитное поле, которое движется вдоль
зазора с синхронной скоростью и постоянной
амплитудой.
Покажем
графически, что три пульсирующие волны
трех фаз создают в любой момент времени
бегущую волну с постоянной амплитудой.

Для
изменения направления движения волны
необходимо поменять чередование фаз,
т.е. сменить любые две фазы.
в)
Намагничивающие силы высших гармоник
Вопрос
о высших гармонических намагничивающих
сил очень сложен. Высшие гармоники могут
быть пространственные и временные. Мы
рассматриваем пространственные высшие
гармоники, вызванные расположением
самой обмотки в пространстве.
Амплитуда
намагничивающей силы
гармоники запишется
Высшие гармоники
намагничивающих сил однофазной обмотки
Пульсирующая волна.
,
разложим на две бегущие волны
Здесь
тоже будет прямая и обратная волна.
Скорость прямой волны
,
;
;
Скорость обратной волны
т.е.
скорость н.с.
гармоники в раз
меньше основной гармоники.
Высшие
гармоники намагничивающих сил трехфазной
обмотки
Если
намагничивающие силы высших гармоник
трех фаз разложить на прямую и обратную
волну, а затем их сложить, то будет видно,
что высшие гармоники н.с. будут вести
себя по-разному.
-
Гармоники четные
исчезнут, т.к. гармоники симметричны
оси абсцисс. -
Гармоники кратные
3-м выпадут. = 3, т.к.
– для всех трех фаз будет иметь Cos одного
и того же угла, а сумма же амплитуд
сдвинутых на уголи
с одинаковыми амплитудами равна нулю.
Другие
гармоники будут вести себя по разному,
одни будут вращаться в одну сторону,
другие в другую при одном чередовании
фаз.
Гармоники
порядка
,
где а = 1, 2, 3. = 5, 11,
17 … которым соответствует выражение
Эти
гармоники будут вращаться в обратную
сторону по отношению к н.с. первой
гармоники.
Посмотрим
чередование фаз.

|
Для первой гармоники A1 |
A5 – B5 |
A7 – B7 |
Гармоники
порядка
,
= 7, 13, 19 будут
вращаться в сторону первой гармоники.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
29.03.201529.88 Mб18Электрические машины. Вольдек А.И..pdf
- #
- #
- #
Магнитной цепью или магнитопроводом называется путь, по которому замыкается магнитный поток. Этот путь может проходить целиком по воздуху.
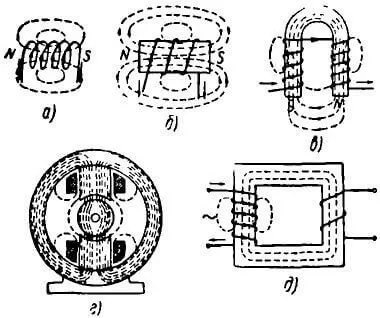 |
| Рисунок 1. Примеры магнитных цепей |
На рисунке 1, а показан соленоид. Магнитная цепь здесь проходит через воздух. Магнитное сопротивление воздуха очень велико, поэтому даже при большой намагничивающей силе магнитный поток мал.
Для увеличения магнитного потока в состав магнитной цепи вводят ферромагнитные материалы (обычно литая или электротехническая сталь), имеющие меньшее магнитное сопротивление.
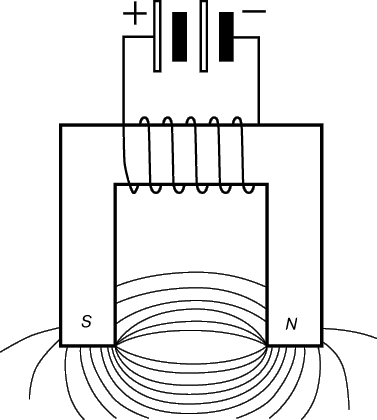
На рисунке 1, б представлен прямой электромагнит с разомкнутым сердечником. Магнитные линии только небольшую часть своего пути проходят по стальному сердечнику, большую же часть своего пути они проходят по воздуху. Полюсы электромагнита определяются при помощи “правила буравчика”.
Подковообразный электромагнит, изображенный на рисунке 1, в, представляет магнитную цепь с лучшими условиями для прохождения магнитного потока. При такой конструкции поток большую часть пути проходит по стали и меньшую часть от полюса N до полюса S по воздуху.
На рисунке 1, г представлена конструкция магнитной цепи, применяемая в электромашиностроении и приборостроении. Между полюсами электромагнита помещается стальной якорь. Большую часть своего пути магнитные линии проходят по стали и только очень малую часть (от нескольких долей миллиметра до 2–3 мм) проходят по двум воздушным промежуткам.
Трансформаторы имеют замкнутый стальной сердечник (рисунок 1, д). Сердечники трансформаторов собираются из нескольких частей, но во время сборки принимают меры к тому, чтобы воздушные зазоры между отдельными частями практически были равны нулю.
До сих пор мы не говорили о том, что магнитный поток, созданный намагничивающей силой, не весь замыкается по тому пути, который ему предназначен. Помимо рабочего магнитного потока, существует магнитный поток рассеяния, который замыкается вне того места, где используется рабочий поток. На рисунке 1, б, в, г, д показаны потоки рассеяния.
Таким образом, общий магнитный поток, который должна создать обмотка возбуждения электромагнита, равен сумме рабочего потока и потока рассеяния.
Расчет магнитной цепи, казалось бы, можно производить по формуле:
Но если вспомнить, что относительная магнитная проницаемость µ для ферромагнитных тел непостоянна и зависит от многих причин, то становится ясно, что этой формулой можно пользоваться лишь в том случае, когда в состав магнитной цепи входят только немагнитные тела (в том числе и воздух), для которых µ есть заранее заданная величина.
На практике для расчета магнитных цепей предпочитают пользоваться графическими методами решения.
Расчет магнитной цепи производят в следующем порядке. Задаются необходимой величиной магнитного потока. Разбивают магнитную цепь на участки, имеющие одинаковые поперечные сечения и однородный материал, и для каждого участка определяют величину магнитной индукции по формуле:
Затем по кривым намагничивания для данного материала находят для каждого значения магнитной индукции величину напряженности H. Если в магнитной цепи встречаются воздушные зазоры, то зависимость B0 и H0 определяется по формуле:
Здесь B0 выражено в Вб/м², µ0 – в Гн/м, H0 – в А/см .
Если индукция выражена в гауссах, а напряженность в А/см, то зависимость между B0 и H0 будет:
H0 = 0,8 × B0 .
Определив величину H для каждого участка, находим по закону полного тока величину намагничивающей силы по формуле:
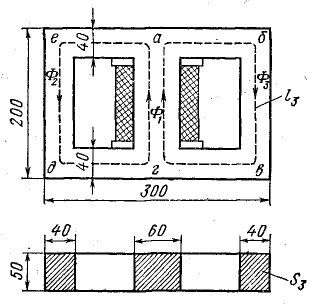
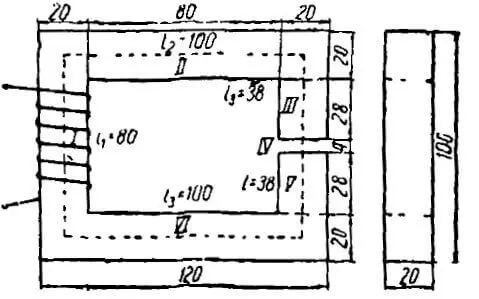
Пример. Найти намагничивающую силу обмотки электромагнита, изображенного на рисунке 2. Размеры даны в миллиметрах. Материал сердечника – электротехническая сталь. В сердечнике необходимо создать магнитный поток 60 000 Мкс. Магнитным рассеянием пренебрегаем.
Рисунок 2. К примеру расчета магнитной цепи
Проводим среднюю линию по все длине магнитной цепи. Разбиваем цепь на пять участков и определяем длину каждого участка.
Так как магнитный поток во всех участках одинаков и площадь поперечного сечения всех участков магнитной цепи (2 × 2 см), то магнитная индукция везде также будет одинакова.
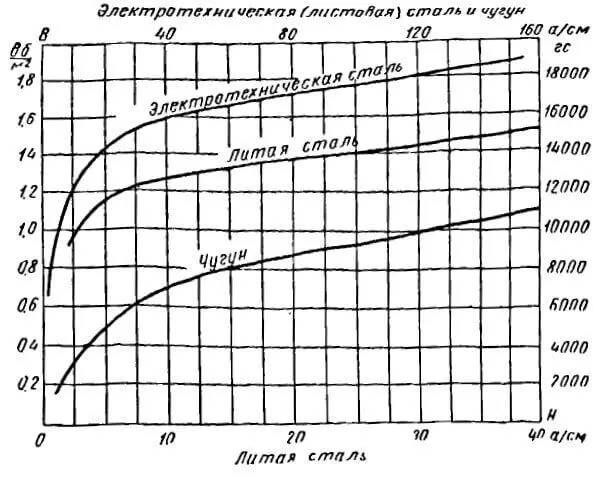
По кривой намагничивания (рисунок 3) для электротехнической стали по индукции 15000 Гс находим напряженность магнитного поля H = 30 А/см. Для воздушного зазора имеем:
H0 = 0,8 × 15000 = 12000 А/см .
Рисунок 3. Кривые намагничивания электротехнической стали, литой стали и чугуна
Умножая величины напряженности на длины соответствующих участков, получаем произведения H × l для этих участков.
Результаты вычислений записываем в таблицу (таблица 1).
Таблица 1
| Номера участков | Материал | B | l | H | H × l |
| Гс | см | А/см | А | ||
| I II и VI III и V IV |
Электротехническая сталь То же То же Воздух |
15000 15000 15000 15000 |
8 10 × 2 3,8 × 2 0,4 |
30 30 30 12000 |
240 600 228 4800 |
I × w = ∑ (H × l) = 5868 А .
Интересно отметить, что если на участках из электротехнической стали I, II, III, V и VI общей протяженностью 35,6 см (8 + 20 + 7,6 см) для проведения магнитного потока необходима намагничивающая сила 1068 А (240 + 600 + 228 А), то на воздушный зазор длиной всего 4 мм (в 89 раз меньше длины пути стали) нужна намагничивающая сила 4800 А. Отсюда становится понятной необходимость создания магнитных цепей с минимальными воздушными зазорами.
Источник: Кузнецов М. И., “Основы электротехники” – 9-е издание, исправленное – Москва: Высшая школа, 1964 – 560с.