Как найти напор в гидравлике

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 июля 2015 года; проверки требуют 17 правок.

Напо́р (более точно по́лный напо́р) (в гидравлике и гидромеханике) — физическая величина, равная удельной энергии потока жидкости в рассматриваемой точке^[1]. Обычно рассматривается для течений несжимаемой жидкости в поле сил тяжести и определяется из уравнения Бернулли^[1] соотношением:

${displaystyle H=z+{frac {p}{rho g}}+{frac {v^{2}}{2g}},}$

где $z$ — вертикальная координата рассматриваемой точки относительно некоторого выбранного уровня (отсчитываемая вверх, против направления силы тяжести), $p$ — давление в жидкости, $g$ — ускорение свободного падения, $v$ — модуль скорости жидкости. Единица напора в Международной системе единиц (СИ) — метр, в системе СГС — сантиметр.

Пьезометрическим напором называют величину^[2]

${displaystyle H=z+{frac {p}{rho g}},}$

которую удобно использовать в гидрологических измерениях, т.к. эта величина с точностью до постоянного слагаемого равна высоте столба жидкости в колене водяного манометра.

Входящие в выражение для полного напора слагаемые имеют специальные названия:

При стационарном течении несжимаемой идеальной (невязкой) жидкости в силу интеграла Бернулли полный напор сохраняется вдоль линии тока. При течении реальных жидкостей вдоль линии тока напор уменьшается за счёт диссипативных процессов (вязкого трения). Разность напора в двух поперечных сечениях потока реальной жидкости называется потерянным напором (гидравлическими потерями, утратами напора).

Понятие о напоре используется при проектировании гидротехнических сооружений и решении многих задач гидравлики и гидродинамики. При использовании метода электрогидравлических аналогий гидравлический напор аналогичен электрическому напряжению (в то время как подача или расход аналогичны силе тока). Потерянный напор аналогичен падению напряжения.

См. также[править | править код]

Миллиметр водяного столба
Давление

Примечания[править | править код]

↑ ¹ ² Напор // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 242. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
↑ ¹ ² ³ ⁴ Полубаринова-Кочина П.Я. Теория движения грунтовых вод. — М.: Наука, 1977. — С. 30. — 664 с.

Источник

(кг/м³) – плотность

(н/м³) – удельный вес

ГИДРОСТАТИКА

р – давление или сжимающие напряжение (н/м² = Па)

Свойства:

Давление всегда направлено к поверхности по внутренней нормали.

Действует одинаково по всем направлениям (не зависит от угла наклона площадки)

Основное уравнение гидростатики:

р_А = р_о + р_в; р_в = h·γ

р_А–абсолютное давление;

р_о–давление действующее на поверхность жидкости;

р_в– весовое давление, т.е. давление столба жидкости.

р_в = h·γ

h – глубина расположения точки;

γ – удельный вес жидкости.

При атмосферном давлении на поверхности:

р_А = р_а + р_изб; р_изб = h_изб·γ

р_а – атмосферное давление;

р_изб – избыточное давление.

Выводы:

Закон Паскаля. Давление действующее на поверхность жидкости передается во все ее точки без изменения.
Любая горизонтальная плоскость проведенная в жидкости, является плоскостью равного давления.
Можем измерять величину давления эквивалентной ему высотой столба жидкости.

р = h·γ, отсюда h = р/γ

Например давление величиной в 1 атм. р = 1 кгс/см² соответствует

h = 10 м вод. столба

Сила давления жидкости на плоскую поверхность

Р = р_сS = h_сγS (н)

р_с = h_сγ – давление в центре тяжести при атмосферном давлении на поверхности

р_с = h_сγ + р_М, либо р_с = h_сγ – р_ВАК

h_с – глубина расположения центра тяжести поверхности (м);

S – площадь поверхности (м²).

Потенциальная энергия покоящейся жидкости величина постоянная, т.е. одинаковая для всех точек жидкости

Удельная энергия (напор) Э = Е/G = Е/mg (м)

Z + h_п = Н_ГС = Э = const

Z – геометрический напор;

h_п – пьезометрический напор;

Н_ГС –гидростатический напор или полная удельная потенциальная энергия жидкости.

ГИДРОДИНАМИКА

Уравнение неразрывности

Q = V₁ω₁ = V₂ω₂ = const

Q – расход жидкости (м³/с);

V – средняя скорость потока (м/с);

Ω – площадь живого сечения потока (м²).

V_i = Q / ω_i – средняя скорость потока

Уравнение Бернулли для идеальной жидкости (при действии сил давления и сил тяжести)

где z – геометрический напор, м;

P/γ – приведенная пьезометрическая высота (если Р – абсолютное давление) или пьезометрическая высота (если Р – избыточное давление), м;

V²/2g – скоростной напор, м.

– гидростатический напор,

удельная потенциальная энергия жидкости

Н_ГС = Э – гидродинамический напор или полная удельная энергия

Уравнение Бернулли для реальной жидкости (с учетом сил трения (вязкости)).

Σh = h_пот = h_ℓ + h_м – потери энергии при движении жидкости от 1 до 2 сечений (м);

α= Е_КД/Е_КУ – коэффициент кинетический энергии (коэффициент Кориолиса);

h_ℓ – потери по длине.

(м)

λ – коэффициент гидравлического трения f(R_е·Δ);

h_м – потери на местных сопротивлениях.

(м)

РЕЖИМЫ ДВИЖЕНИЯ

Число (критерий) Рейнольдса

Для кругло-цилиндрических труб

(м)

R_Г – гидравлический радиус;

ω – площадь живого сечения потока (м²);

Х – смоченный периметр.

Ламинарный режим: Rе < Rе_кр ≈ 2320

Эпюра скорости при ламинарном движении.

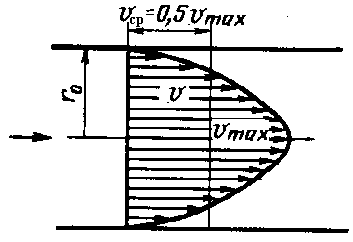
u_max = 2V; α = 2; λ = f(Rе); λ = 64/Rе; h_ℓ = f (V^1…1,4)

Турбулентный режим: Rе > Rе_кр

Профиль скорости при турбулентном движении

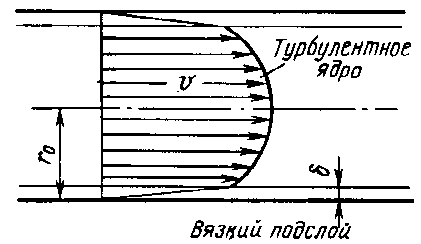
Толщина ламинарной пленки δ уменьшается с увеличением скорости V (числа Рейнольдса)

u ≈ V; α = 1…1,4

В турбулентном режиме имеется три вида трения:

Гидравлически гладкие русла

λ = f(Rе) λ = 0,3164/Rе^0,25

Смешанное трение

λ = f(Rе;Δ)

Шероховатое трение, квадратичная область турбулентного режима

λ = f (Δ); λ = 0,11(Δ /d)^0,25

h_ℓ = f (V^1,7…2)

СКОРОСТЬ ДВИЖЕНИЯ (ИСТЕЧЕНИЯ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ

(м/с)

– коэффициент скорости

Н_о – действующий (расчетный напор (м)

Расход жидкости

(м³/с)

μ = φε – коэффициент расхода;

ω – площадь проходного (живого) сечения потока (м²);

Н_о – действующий напор (м).

Источник

From Wikipedia, the free encyclopedia

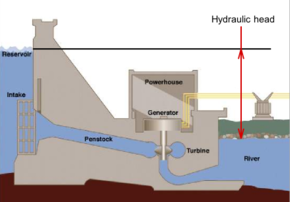
Available difference in hydraulic head across a hydroelectric dam, before head losses due to turbines, wall friction and turbulence

Fluid flows from the tank at the top to the basin at the bottom under the pressure of the hydraulic head.

Measuring hydraulic head in an artesian aquifer, where the water level is above the ground surface

Hydraulic head or piezometric head is a specific measurement of liquid pressure above a vertical datum.^[1]^[2]

It is usually measured as a liquid surface elevation, expressed in units of length, at the entrance (or bottom) of a piezometer. In an aquifer, it can be calculated from the depth to water in a piezometric well (a specialized water well), and given information of the piezometer’s elevation and screen depth. Hydraulic head can similarly be measured in a column of water using a standpipe piezometer by measuring the height of the water surface in the tube relative to a common datum. The hydraulic head can be used to determine a hydraulic gradient between two or more points.

“Head” in fluid dynamics[edit]

In fluid dynamics, head is a concept that relates the energy in an incompressible fluid to the height of an equivalent static column of that fluid. From Bernoulli’s principle, the total energy at a given point in a fluid is the energy associated with the movement of the fluid, plus energy from static pressure in the fluid, plus energy from the height of the fluid relative to an arbitrary datum. Head is expressed in units of distance such as meters or feet. The force per unit volume on a fluid in a gravitational field is equal to ρg where ρ is the density of the fluid, and g is the gravitational acceleration. On Earth, additional height of fresh water adds a static pressure of about 9.8 kPa per meter (0.098 bar/m) or 0.433 psi per foot of water column height.

The static head of a pump is the maximum height (pressure) it can deliver. The capability of the pump at a certain RPM can be read from its Q-H curve (flow vs. height).

A common misconception is that the head equals the fluid’s energy per unit weight, while, in fact, the term with pressure does not represent any type of energy (in the Bernoulli equation for an incompressible fluid this term represents work of pressure forces). Head is useful in specifying centrifugal pumps because their pumping characteristics tend to be independent of the fluid’s density.

There are generally four types of head:

Velocity head is due to the bulk motion of a fluid (kinetic energy).

${displaystyle h_{v}={tfrac {1}{2}}rho v^{2}/rho g={frac {1}{2}}{frac {v^{2}}{g}}}$

Note that ${displaystyle rho gh_{v}}$ is equal to the dynamic pressure for irrotational flow.
Elevation head is due to the fluid’s weight, the gravitational force acting on a column of fluid. The elevation head is simply the elevation (h) of the fluid above an arbitrarily designated zero point:

${displaystyle h_{e}=rho gh/rho g}$
Pressure head is due to the static pressure, the internal molecular motion of a fluid that exerts a force on its container. It is equal to the pressure divided by the force/volume of the fluid in a gravitational field:

${displaystyle h_{p}=p/rho g}$
Resistance head (or friction head or Head Loss) is due to the frictional forces acting against a fluid’s motion by the container. For a continuous medium, this is described by Darcy’s law which relates volume flow rate (q) to the gradient of the hydraulic head through the hydraulic conductivity K:

${displaystyle mathbf {q} =-Knabla h}$

while in a piped system head losses are described by the Hagen–Poiseuille equation and the Bernoulli Equation.

Components of hydraulic head[edit]

After free falling through a height $h$ in a vacuum from an initial velocity of 0, a mass will have reached a speed

${displaystyle v={sqrt {{2g}{h}}}}$

where $g$ is the acceleration due to gravity. Rearranged as a head:

${displaystyle h={frac {v^{2}}{2g}}.}$

The term $frac{v^{2}}{2 g}$ is called the velocity head, expressed as a length measurement. In a flowing fluid, it represents the energy of the fluid due to its bulk motion.

The total hydraulic head of a fluid is composed of pressure head and elevation head.^[1]^[2] The pressure head is the equivalent gauge pressure of a column of water at the base of the piezometer, and the elevation head is the relative potential energy in terms of an elevation. The head equation, a simplified form of the Bernoulli principle for incompressible fluids, can be expressed as:

${displaystyle h=psi +z}$

where

In an example with a 400 m deep piezometer, with an elevation of 1000 m, and a depth to water of 100 m: z = 600 m, ψ = 300 m, and h = 900 m.

The pressure head can be expressed as:

${displaystyle psi ={frac {P}{gamma }}={frac {P}{rho g}}}$

where
$P$ is the gauge pressure (Force per unit area, often Pa or psi),

Fresh water head[edit]

The pressure head is dependent on the density of water, which can vary depending on both the temperature and chemical composition (salinity, in particular). This means that the hydraulic head calculation is dependent on the density of the water within the piezometer. If one or more hydraulic head measurements are to be compared, they need to be standardized, usually to their fresh water head, which can be calculated as:

${displaystyle h_{mathrm {fw} }=psi {frac {rho }{rho _{mathrm {fw} }}}+z}$

where

Hydraulic gradient[edit]

The hydraulic gradient is a vector gradient between two or more hydraulic head measurements over the length of the flow path. For groundwater, it is also called the Darcy slope, since it determines the quantity of a Darcy flux or discharge. It also has applications in open-channel flow where it is also known as stream gradient and can be used to determine whether a reach is gaining or losing energy. A dimensionless hydraulic gradient can be calculated between two points with known head values as:

${displaystyle i={frac {dh}{dl}}={frac {h_{2}-h_{1}}{mathrm {length} }}}$

where

$i$ is the hydraulic gradient (dimensionless),
$dh$ is the difference between two hydraulic heads (length, usually in m or ft), and
$dl$ is the flow path length between the two piezometers (length, usually in m or ft)

The hydraulic gradient can be expressed in vector notation, using the del operator. This requires a hydraulic head field, which can be practically obtained only from numerical models, such as MODFLOW for groundwater or standard step or HEC-RAS for open channels. In Cartesian coordinates, this can be expressed as:

${displaystyle nabla h=left({frac {partial h}{partial x}},{frac {partial h}{partial y}},{frac {partial h}{partial z}}right)={frac {partial h}{partial x}}mathbf {i} +{frac {partial h}{partial y}}mathbf {j} +{frac {partial h}{partial z}}mathbf {k} }$

This vector describes the direction of the groundwater flow, where negative values indicate flow along the dimension, and zero indicates ‘no flow’. As with any other example in physics, energy must flow from high to low, which is why the flow is in the negative gradient. This vector can be used in conjunction with Darcy’s law and a tensor of hydraulic conductivity to determine the flux of water in three dimensions.

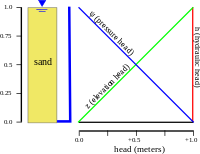
Hydraulic head in groundwater[edit]

Relation between heads for a hydrostatic case and a downward flow case.

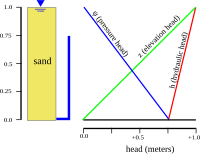
The distribution of hydraulic head through an aquifer determines where groundwater will flow. In a hydrostatic example (first figure), where the hydraulic head is constant, there is no flow. However, if there is a difference in hydraulic head from the top to bottom due to draining from the bottom (second figure), the water will flow downward, due to the difference in head, also called the hydraulic gradient.

Atmospheric pressure[edit]

Even though it is convention to use gauge pressure in the calculation of hydraulic head, it is more correct to use total pressure (gauge pressure + atmospheric pressure), since this is truly what drives groundwater flow. Often detailed observations of barometric pressure are not available at each well through time, so this is often disregarded (contributing to large errors at locations where hydraulic gradients are low or the angle between wells is acute.)

The effects of changes in atmospheric pressure upon water levels observed in wells has been known for many years. The effect is a direct one, an increase in atmospheric pressure is an increase in load on the water in the aquifer, which increases the depth to water (lowers the water level elevation). Pascal first qualitatively observed these effects in the 17th century, and they were more rigorously described by the soil physicist Edgar Buckingham (working for the United States Department of Agriculture (USDA)) using air flow models in 1907.

Head loss[edit]

In any real moving fluid, energy is dissipated due to friction; turbulence dissipates even more energy for high Reynolds number flows. This dissipation, called head loss, is divided into two main categories, “major losses” associated with energy loss per length of pipe, and “minor losses” associated with bends, fittings, valves, etc. The most common equation used to calculate major head losses is the Darcy–Weisbach equation. Older, more empirical approaches are the Hazen–Williams equation and the Prony equation.

For relatively short pipe systems, with a relatively large number of bends and fittings, minor losses can easily exceed major losses. In design, minor losses are usually estimated from tables using coefficients or a simpler and less accurate reduction of minor losses to equivalent length of pipe, a method often used for shortcut calculations of pneumatic conveying lines pressure drop.^[3]

Notes[edit]

^ ^a ^b Mulley, Raymond (2004), Flow of Industrial Fluids: Theory and Equations, CRC Press, ISBN 978-0849327674, 410 pages. See pp. 43–44.
^ ^a ^b Chanson, Hubert (2004), Hydraulics of Open Channel Flow: An Introduction, Butterworth–Heinemann, ISBN 978-0750659789, 650 pages. See p. 22.
^ “Pipe equivalent length (Pneumatic conveying)”.

References[edit]

Bear, J. 1972. Dynamics of Fluids in Porous Media, Dover. ISBN 0-486-65675-6.
for other references which discuss hydraulic head in the context of hydrogeology, see that page’s further reading section

Источник

Гидростатический напор

Рассмотрим основное
уравнение гидростатики в виде:

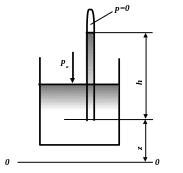
Здесь z
надо рассматривать, как высоту выбранной
точки над условной плоскостью сравнения
0-0 (см
рис.). Координата z
называется геометрической высотой.
Величина

представляет ту высоту, на которую
поднимается жидкость в пьезометре, если
бы верхний его конец находился под
нулевым давлением. Обозначим

.
Тогда

(6)

называют полным
гидростатическим напором, который
представляет собой сумму двух высот z
и

– пьезометрическая высота.

Преобразуем (6):

(7)

Величина H_p
называется гидростатическим напором,
а величину

– пьезометрическим напором.

Выражениям (6) и
(7) можно придать энергетический смысл.
Рассмотрим частицу массой m.
Ее потенциальная энергия относительно
плоскости 0-0
равна mgz.
Под действием давления частица может
подняться на высоту

,
т.е. обладает потенциальной энергией
давления, равной:

Полный запас
потенциальной энергии частицы:

где е_п
– удельная полная потенциальная энергия.
Значит z
– удельная потенциальная энергия
положения частицы, р/
– удельная потенциальная энергия
давления.

Последнее равенство
называется энергетическим законом
покоящейся жидкости.

Рассматриваются
в полных курсах случаи относительного
покоя: равноускоренное движение, и
вращательное движение.

Закон Паскаля

Основное уравнение
гидростатики является аналитическим
выражением закона Паскаля.

Для двух точек 1
и 2
покоящейся жидкости имеем:

Если в точке 1
давление изменится на величину р,
то и в точке 2
оно должно изменится на эту же величину,
чтобы не нарушилось равенство.

Возьмем уравнение
гидростатики в форме:

Если давление на
свободной поверхности изменится на р,
то и в любой точке жидкости оно изменится
на эту же величину:

.

Закон Паскаля:
любое изменение давления в какой-либо
точке покоящейся жидкости, не нарушающее
ее равновесия, передается в остальные
ее точки без изменения.

Закон Паскаля
указывает на способность жидкости
передавать усилие на расстоянии, что
широко используется в технике. На законе
Паскаля основана работа гидравлических
домкратов, прессов, мультипликаторов,
тормозов, объемного гидропривода, систем
гидропневмоавтоматики и т.п.

Сила давления жидкости на плоскую стенку

Р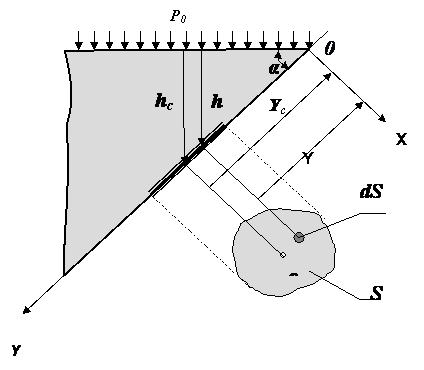
ассмотрим
произвольную площадку ds,
расположенную на плоской наклонной
стенке сосуда с жидкостью на расстоянии
Y
от оси X,
и определим силы, действующие на эту
площадку. Сила от давления, действующего
на элементарную площадку ds,
будет описываться формулой:

Если проинтегрировать
это выражение по площади, можно определить
полную силу, действующую на всю площадь
целиком:

Из рисунка ясно,
что в последнем выражении

.
Подставив значение h
в предыдущее выражение, будем иметь:

Из теоретической
механики известно, что интеграл

есть
ни что иное, как статический момент
площади S
относительно оси 0X.
Он равен произведению этой площади на
координату её центра тяжести, т.е. можно
записать

где Y_с
– расстояние от оси X
до центра тяжести площади S.
В формуле S
– площадь
рассматриваемой площадки.

Подставив формулу
момента в выражение силы, получим:

Учтем, что

– глубина положения центра тяжести
площадки и

– избыточное давление жидкости в центре
тяжести площадки, тогда

где р_с
является абсолютным давлением в центре
тяжести рассматриваемой произвольной
площадки. Таким образом, можно сделать
вывод: полная сила давления жидкости
на плоскую стенку равна произведению
её площади на величину гидростатического
давления в центре тяжести этой стенки.
Однако необходимо учесть, что эта сила
не сконцентрирована в точке, а распределена
по площади. И распределение это
неравномерно. По этой причине для
расчётов, кроме величины силы действующей
на наклонную площадку, необходимо знать
точку приложения равнодействующей.

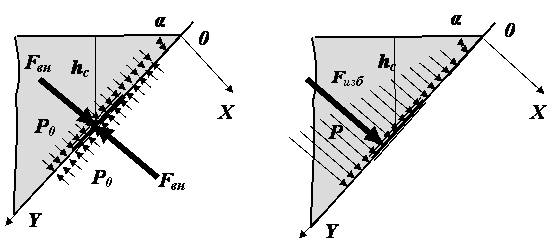
Давление
р₀
передаётся всем точкам площадки
одинаково. Следовательно, равнодействующая
F_вн
этого давления будет приложена в центре
тяжести площадки S.
При этом надо учитывать, что в большинстве
случаев это давление действует и со
стороны жидкости и с наружной стороны
стенки.

Д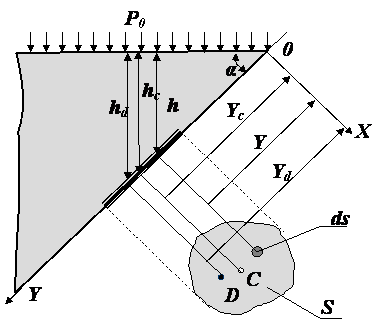
авление
р
увеличивается с увеличением глубины.
При этом величина равнодействующей
этой силы F_изб
известна и равна:

,
а точку её приложения необходимо
определить.

Для нахождения
центра избыточного давления жидкости
применим уравнение механики, согласно
которому момент равнодействующей силы
относительно оси 0X
равен сумме моментов составляющих сил,
т.е.

где Y_D
– координата
точки приложения силы F_изб,
Y
– текущая глубина.

Преобразуем

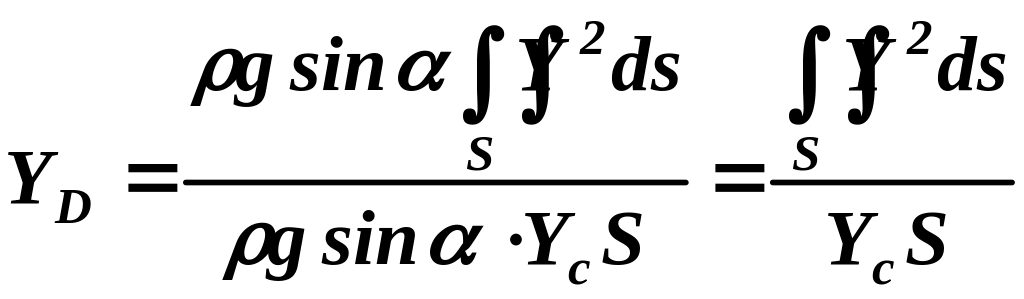
Интеграл в числителе
дроби является статическим моментом
инерции площади S
относительно оси 0X
и обычно обозначается J_x

Из теоретической
механики известно, что статический
момент площади относительно оси вращения
равен сумме собственного момента инерции
(момента инерции этой площади относительно
оси проходящей через её центр тяжести
и параллельной первой оси) и произведению
этой площади на квадрат расстояния от
оси вращения до центра её тяжести

С учётом последнего
определения Y_D
окончательно можно выразить в виде:

Таким образом,
разница в положениях Y
(глубинах) центра тяжести площадки (т.
C)
и центра давления (т. D)
составляет:

В итоге можно
сделать следующие выводы. Если внешнее
давление действует на стенку с обеих
сторон, то найденная точка D
будет являться центром давления. Если
внешнее давление со стороны жидкости
выше давления с противоположной стороны
(например, атмосферного), то центр
давления находится по правилам механики
как точка приложения равнодействующей
двух сил: силы, создаваемой внешним
давлением, и силы, создаваемой весом
жидкости. При этом, чем больше внешнее
давление, тем ближе располагается центр
давления к центру тяжести.

В гидроприводе
технологического оборудования внешние
давления в десятки и сотни раз превышают
давления, вызванные высотой столба
жидкости. Поэтому в расчётах гидравлических
машин и аппаратов положение центров
давления принимаются совпадающими с
центрами тяжести. Графическим изображением
изменения гидростатического давления
вдоль плоской стенки служат эпюры
давления
(см. рис.). Площадь эпюры выражает силу
давления, а центр тяжести эпюры – это
точка, через которую проходит
равнодействующая сила давления. При
построении эпюр учитывают, что давление
направлено нормально к стенке, а уравнение

,
характеризующее распределение
гидростатического давления по глубине,
является уравнением прямой. Чтобы
построить эпюры давления на вертикальную
стенку, откладывают в выбранном масштабе
давление по горизонтальному направлению,
совпадающему с направлением сил давления
(на поверхности жидкости и у дна), соединив
концы этих отрезков прямой линией.

Рис. Примеры
построения эпюр давления на стенку:

Эпюра абсолютного
гидростатического давления представляет
собой трапецию, а эпюра избыточного —
треугольник (рис. а).

Если плоская
стенка, на которую действует жидкость,
наклонена к горизонту под углом 
(рис. б),
то основное уравнение гидростатики
принимает следующий вид:

Таким образом,
эпюры абсолютного и избыточного
гидростатического давления на наклонную
стенку представляют собой соответственно
наклонную трапецию и наклонный
треугольник.

Если плоская
стенка, на которую с двух сторон оказывает
воздействие жидкость, вертикальна, то
на нее будут действовать параллельные
и противоположно направленные силы
гидростатического давления. Эпюра
гидростатического давления на вертикальную
стенку представляет собой вертикальную
трапецию.

Эпюра гидростатического
давления на горизонтальное дно резервуара
представляет собой прямоугольник, так
как при постоянной глубине избыточное
давление на дно постоянно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
17.03.2016298.61 Кб10262598.rtf
#

Источник

Напор (гидравлика)

Напо́р, в гидравлике и гидродинамике — давление жидкости, выражаемое высотой столба жидкости над выбранным уровнем отсчёта. Выражается в линейных единицах.

Полный запас удельной энергии потока (полный напор) определяется уравнением Бернулли и включает в себя:

высоту рассматриваемой точки над плоскостью отсчёта (гидростатический напор),
давление жидкости, обусловленное скоростью потока (скоростной напор).

Вдоль потока напор уменьшается. Разность напора в двух поперечных сечениях потока реальной жидкости называется потерянным напором.

Понятие о напоре используется при проектировании гидротехнических сооружений и решении многих задач гидравлики и гидродинамики. В электронно-гидравлической аналогии (см. en:Hydraulic analogy) гидравлический напор аналогичен электрическому напряжению (в то время как скорость потока аналогична силе тока). Потеряный напор аналогичен падению напряжения или разности потенциалов.

Wikimedia Foundation.
2010.

Смотреть что такое “Напор (гидравлика)” в других словарях:

Напор — (в гидравлике и гидромеханике) величина давления жидкости (или газа), выражаемая высотой столба жидкости (газа) над выбранным уровнем отсчёта; измеряется в линейных единицах (метрах). Либо же энергия, отнесенная к единице веса… … Википедия
Гидравлика — I см. Газовое производство. II есть учение о движении жидкостей, приноровленное к практическим целям. Искусство управлять движением вод в естественных и искусственных руслах и резервуарах, а также пользоваться течением воды и ветром для… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Напор — в гидравлике, линейная величина, выражающая удельную (отнесённую к единице веса) энергию потока жидкости в данной точке. Полный запас удельной энергии потока Н (полный Н.) определяется Бернулли уравнением: где z высота… … Большая советская энциклопедия
Подземная гидравлика — (подземная гидродинамика) наука о движении нефти, воды, газа и их смесей (флюидов) через горные породы, имеющие пустоты, которые могут представлять собой поры или трещины. Теоретической основой ПГ является теория фильтрации, описывающая… … Википедия
СО 34.21.308-2005: Гидротехника. Основные понятия. Термины и определения — Терминология СО 34.21.308 2005: Гидротехника. Основные понятия. Термины и определения: 3.10.28 аванпорт: Ограниченная волнозащитными дамбами акватория в верхнем бьефе гидроузла, снабженная причальными устройствами и предназначенная для размещения … Словарь-справочник терминов нормативно-технической документации
Основное уравнение гидростатики — Основным законом (уравнением) гидростатики называется уравнение[1]: , где гидростатическое давление (абсолютное или избыточное) в произвольной точке жидкости, плотность жидкости, ускорение свободного падения … Википедия
Закон Бернулли — является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости: Здесь плотность жидкости, скорость потока, высота, на которой находится рассматриваемый… … Википедия
ВОДОСНАБЖЕНИЕ — ВОДОСНАБЖЕНИЕ. I. Водоснабжение населенных мест. Цель и назначение водоснабжения. В. организованное и регулярное доставление массовому потребителю воды установл. качества и в определенном количестве, обеспечивающем с той или иной полнотой… … Большая медицинская энциклопедия
Гидравлический уклон — Гидравлический уклон это величина, характеризующая собой потерю напора на единицу длины русла. При постоянной скорости течения и одинаковой высоте русла (то есть, при горизонтальном русле) гидравлический уклон может быть определён по… … Википедия
ГИДРОАЭРОМЕХАНИКА — раздел механики, изучающий движение жидкостей и газов в условиях, при которых не имеют практического значения различия в сжимаемости. Такой единый подход возможен, поскольку благодаря своей текучести жидкие и газообразные среды ведут себя… … Энциклопедия Кольера

Источник

См. также[править | править код]

Примечания[править | править код]

“Head” in fluid dynamics[edit]

Components of hydraulic head[edit]

Fresh water head[edit]

Hydraulic gradient[edit]

Hydraulic head in groundwater[edit]

Atmospheric pressure[edit]

Head loss[edit]

See also[edit]

Notes[edit]

References[edit]

Гидростатический напор

Закон Паскаля

Сила давления жидкости на плоскую стенку

Напор (гидравлика)

Смотреть что такое “Напор (гидравлика)” в других словарях:

Добавить комментарий Отменить ответ

См. также[править | править код]

Примечания[править | править код]

“Head” in fluid dynamics[edit]

Components of hydraulic head[edit]

Fresh water head[edit]

Hydraulic gradient[edit]

Hydraulic head in groundwater[edit]

Atmospheric pressure[edit]

Head loss[edit]

See also[edit]

Notes[edit]

References[edit]

Гидростатический напор

Закон Паскаля

Сила давления жидкости на плоскую стенку

Напор (гидравлика)

Смотреть что такое “Напор (гидравлика)” в других словарях:

Вам также может понравиться

Как найти работу python без опыта

Как составить бизнес план по экономике 11 класс

Как найти свой фотографий на порно сайтах

Добавить комментарий Отменить ответ