Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 июля 2015 года; проверки требуют 17 правок.

Напо́р (более точно по́лный напо́р) (в гидравлике и гидромеханике) — физическая величина, равная удельной энергии потока жидкости в рассматриваемой точке[1]. Обычно рассматривается для течений несжимаемой жидкости в поле сил тяжести и определяется из уравнения Бернулли[1] соотношением:
где 



Пьезометрическим напором называют величину[2]
которую удобно использовать в гидрологических измерениях, т.к. эта величина с точностью до постоянного слагаемого равна высоте столба жидкости в колене водяного манометра.
Входящие в выражение для полного напора слагаемые имеют специальные названия:
При стационарном течении несжимаемой идеальной (невязкой) жидкости в силу интеграла Бернулли полный напор сохраняется вдоль линии тока. При течении реальных жидкостей вдоль линии тока напор уменьшается за счёт диссипативных процессов (вязкого трения). Разность напора в двух поперечных сечениях потока реальной жидкости называется потерянным напором (гидравлическими потерями, утратами напора).
Понятие о напоре используется при проектировании гидротехнических сооружений и решении многих задач гидравлики и гидродинамики. При использовании метода электрогидравлических аналогий гидравлический напор аналогичен электрическому напряжению (в то время как подача или расход аналогичны силе тока). Потерянный напор аналогичен падению напряжения.
См. также[править | править код]
- Миллиметр водяного столба
- Давление
Примечания[править | править код]
- ↑ 1 2 Напор // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 242. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ 1 2 3 4 Полубаринова-Кочина П.Я. Теория движения грунтовых вод. — М.: Наука, 1977. — С. 30. — 664 с.
From Wikipedia, the free encyclopedia
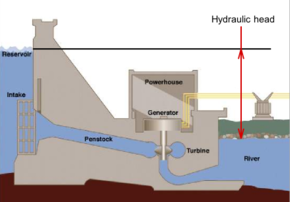
Available difference in hydraulic head across a hydroelectric dam, before head losses due to turbines, wall friction and turbulence
Fluid flows from the tank at the top to the basin at the bottom under the pressure of the hydraulic head.

Measuring hydraulic head in an artesian aquifer, where the water level is above the ground surface
Hydraulic head or piezometric head is a specific measurement of liquid pressure above a vertical datum.[1][2]
It is usually measured as a liquid surface elevation, expressed in units of length, at the entrance (or bottom) of a piezometer. In an aquifer, it can be calculated from the depth to water in a piezometric well (a specialized water well), and given information of the piezometer’s elevation and screen depth. Hydraulic head can similarly be measured in a column of water using a standpipe piezometer by measuring the height of the water surface in the tube relative to a common datum. The hydraulic head can be used to determine a hydraulic gradient between two or more points.
“Head” in fluid dynamics[edit]
In fluid dynamics, head is a concept that relates the energy in an incompressible fluid to the height of an equivalent static column of that fluid. From Bernoulli’s principle, the total energy at a given point in a fluid is the energy associated with the movement of the fluid, plus energy from static pressure in the fluid, plus energy from the height of the fluid relative to an arbitrary datum. Head is expressed in units of distance such as meters or feet. The force per unit volume on a fluid in a gravitational field is equal to ρg where ρ is the density of the fluid, and g is the gravitational acceleration. On Earth, additional height of fresh water adds a static pressure of about 9.8 kPa per meter (0.098 bar/m) or 0.433 psi per foot of water column height.
The static head of a pump is the maximum height (pressure) it can deliver. The capability of the pump at a certain RPM can be read from its Q-H curve (flow vs. height).
A common misconception is that the head equals the fluid’s energy per unit weight, while, in fact, the term with pressure does not represent any type of energy (in the Bernoulli equation for an incompressible fluid this term represents work of pressure forces). Head is useful in specifying centrifugal pumps because their pumping characteristics tend to be independent of the fluid’s density.
There are generally four types of head:
- Velocity head is due to the bulk motion of a fluid (kinetic energy).
Note that
is equal to the dynamic pressure for irrotational flow.
- Elevation head is due to the fluid’s weight, the gravitational force acting on a column of fluid. The elevation head is simply the elevation (h) of the fluid above an arbitrarily designated zero point:
- Pressure head is due to the static pressure, the internal molecular motion of a fluid that exerts a force on its container. It is equal to the pressure divided by the force/volume of the fluid in a gravitational field:
- Resistance head (or friction head or Head Loss) is due to the frictional forces acting against a fluid’s motion by the container. For a continuous medium, this is described by Darcy’s law which relates volume flow rate (q) to the gradient of the hydraulic head through the hydraulic conductivity K:
while in a piped system head losses are described by the Hagen–Poiseuille equation and the Bernoulli Equation.
Components of hydraulic head[edit]
After free falling through a height 
where 
The term 
The total hydraulic head of a fluid is composed of pressure head and elevation head.[1][2] The pressure head is the equivalent gauge pressure of a column of water at the base of the piezometer, and the elevation head is the relative potential energy in terms of an elevation. The head equation, a simplified form of the Bernoulli principle for incompressible fluids, can be expressed as:
where
In an example with a 400 m deep piezometer, with an elevation of 1000 m, and a depth to water of 100 m: z = 600 m, ψ = 300 m, and h = 900 m.
The pressure head can be expressed as:
where

Fresh water head[edit]
The pressure head is dependent on the density of water, which can vary depending on both the temperature and chemical composition (salinity, in particular). This means that the hydraulic head calculation is dependent on the density of the water within the piezometer. If one or more hydraulic head measurements are to be compared, they need to be standardized, usually to their fresh water head, which can be calculated as:
where
Hydraulic gradient[edit]
The hydraulic gradient is a vector gradient between two or more hydraulic head measurements over the length of the flow path. For groundwater, it is also called the Darcy slope, since it determines the quantity of a Darcy flux or discharge. It also has applications in open-channel flow where it is also known as stream gradient and can be used to determine whether a reach is gaining or losing energy. A dimensionless hydraulic gradient can be calculated between two points with known head values as:
where
is the hydraulic gradient (dimensionless),
is the difference between two hydraulic heads (length, usually in m or ft), and
is the flow path length between the two piezometers (length, usually in m or ft)
The hydraulic gradient can be expressed in vector notation, using the del operator. This requires a hydraulic head field, which can be practically obtained only from numerical models, such as MODFLOW for groundwater or standard step or HEC-RAS for open channels. In Cartesian coordinates, this can be expressed as:
This vector describes the direction of the groundwater flow, where negative values indicate flow along the dimension, and zero indicates ‘no flow’. As with any other example in physics, energy must flow from high to low, which is why the flow is in the negative gradient. This vector can be used in conjunction with Darcy’s law and a tensor of hydraulic conductivity to determine the flux of water in three dimensions.
Hydraulic head in groundwater[edit]
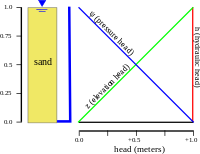
|
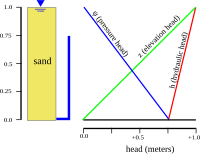
|
The distribution of hydraulic head through an aquifer determines where groundwater will flow. In a hydrostatic example (first figure), where the hydraulic head is constant, there is no flow. However, if there is a difference in hydraulic head from the top to bottom due to draining from the bottom (second figure), the water will flow downward, due to the difference in head, also called the hydraulic gradient.
Atmospheric pressure[edit]
Even though it is convention to use gauge pressure in the calculation of hydraulic head, it is more correct to use total pressure (gauge pressure + atmospheric pressure), since this is truly what drives groundwater flow. Often detailed observations of barometric pressure are not available at each well through time, so this is often disregarded (contributing to large errors at locations where hydraulic gradients are low or the angle between wells is acute.)
The effects of changes in atmospheric pressure upon water levels observed in wells has been known for many years. The effect is a direct one, an increase in atmospheric pressure is an increase in load on the water in the aquifer, which increases the depth to water (lowers the water level elevation). Pascal first qualitatively observed these effects in the 17th century, and they were more rigorously described by the soil physicist Edgar Buckingham (working for the United States Department of Agriculture (USDA)) using air flow models in 1907.
Head loss[edit]
In any real moving fluid, energy is dissipated due to friction; turbulence dissipates even more energy for high Reynolds number flows. This dissipation, called head loss, is divided into two main categories, “major losses” associated with energy loss per length of pipe, and “minor losses” associated with bends, fittings, valves, etc. The most common equation used to calculate major head losses is the Darcy–Weisbach equation. Older, more empirical approaches are the Hazen–Williams equation and the Prony equation.
For relatively short pipe systems, with a relatively large number of bends and fittings, minor losses can easily exceed major losses. In design, minor losses are usually estimated from tables using coefficients or a simpler and less accurate reduction of minor losses to equivalent length of pipe, a method often used for shortcut calculations of pneumatic conveying lines pressure drop.[3]
See also[edit]
- Borda–Carnot equation
- Dynamic pressure
- Minor losses in pipe flow
- Total dynamic head
- Stage (hydrology)
- Head (hydrology)
Notes[edit]
- ^ a b Mulley, Raymond (2004), Flow of Industrial Fluids: Theory and Equations, CRC Press, ISBN 978-0849327674, 410 pages. See pp. 43–44.
- ^ a b Chanson, Hubert (2004), Hydraulics of Open Channel Flow: An Introduction, Butterworth–Heinemann, ISBN 978-0750659789, 650 pages. See p. 22.
- ^ “Pipe equivalent length (Pneumatic conveying)”.
References[edit]
- Bear, J. 1972. Dynamics of Fluids in Porous Media, Dover. ISBN 0-486-65675-6.
- for other references which discuss hydraulic head in the context of hydrogeology, see that page’s further reading section
Измерить водяное давление, используя манометр, – простая задача. Но что делать, если данного прибора дома не оказалось?
Даже в этом случае с довольно высокой точностью можно совершить интересующие замеры. Далее представлены 3 доступных и несложных способа.
Содержание
- Можно ли узнать без использования измерителя?
- Точность измерения водонапора при отсутствии прибора
- Определение напора с использованием шланга
- Как проверить с помощью метода расхода?
- С помощью математического метода
- Полезное видео
- Заключение
Можно ли узнать без использования измерителя?
Такое измерение действительно возможно: бытовая смекалка, математические знания и использование нехитрых конструкций – всё это позволяет получить довольно точные показатели давления.
Точность измерения водонапора при отсутствии прибора
 Точность показателей расчётов водяного давления в трубах дома будет упираться в точные физические данные трубопровода.
Точность показателей расчётов водяного давления в трубах дома будет упираться в точные физические данные трубопровода.
Если реальные характеристики измерены максимально верно, то и математический расчёт будет достаточно точным.
Примерные же данные предоставят возможность рассчитать давление только на приблизительном уровне.
Знание водонапорных нормативов позволят перейти к практике измерения водяного напора дома. Далее рассматриваются 3 метода, как рассчитать показатели давления, не имея манометра.
Определение напора с использованием шланга
Рассматриваемый метод позволяет измерять водяное давление в точке подключения к сантех. прибору, предоставляя возможность не использовать специальных устройств, но выдавая некоторую погрешность.
Совет! Чтобы получить более точное входное давление воды, его нужно измерить на водорозетке (то есть трубе) подвода воды к санузлу. Обычно он располагается на небольшом расстоянии от распределительного узла.
Для метода №1 потребуется прозрачный ПВХ шланг или же трубка ПВХ длиной порядка 2 метров. Диаметр должен составлять ровно столько, сколько нужно для подключения шланга к крану водонапора.
Расчёт интересующих показателей проводится по схеме, представленной ниже:
- Один конец шланга подключается к точке разбора, его нужно выставить и, если возможно, зафиксировать в вертикальном положении.
- Кран открывается, при этом трубка должна заполниться до уровня, который соответствует низу крана (этот уровень называется нулевым).
- Отверстие сверху надёжно закрывается. После этого нужно будет сделать запись следующих показателей:
- Общую длину от уровня ноля до закрытого заглушкой конца.
- Длину шланга между значением уровня воды под давлением и закрытым заглушкой концом.
Теперь можно воспользоваться следующей формулой:
Р = Ратм. х Но/Н1
Здесь:
- P – интересующее нас водопроводное давление,
- Paтм – давление до пуска воды (т.е. давление, которое установлено в комнате). Оно равно почти всегда приблизительно 1 атмосфере, для расчётов можно использовать это значение,
- Но – исходная длина воздушного столба,
- Н1 – длина воздушного столба после открывания крана на полную мощность.
Например, Paтм=1 атмосфера, Но=50 сантиметров, Н1=40 сантиметров. Тогда: P=1*50/40 = 1,25 атмосферы.
Как проверить с помощью метода расхода?
 Производить расчёт можно и с помощью таблиц значений, но результат не будет радовать точностью.
Производить расчёт можно и с помощью таблиц значений, но результат не будет радовать точностью.
Поэтому лучшим вариантом будет проведение расчётов на месте, учитывая при этом и скорость потоков воды, и материал трубопровода системы, и иные свойства трубопровода.
Самой простой формулой для расчёта расходуемой жидкости будет являться:
Q=П*d^2/4*v, где:
- Q — интересующий нас расход воды (литр в секунду).
- v — скорость потока (m/c).
- d – диаметр трубы (в см).
- П – «число Pi» — константа из математики, приблизительно 3,14.
К примеру, есть: d=4, v=2. В таком случае: Q=3,14*4^2/4*2=3,14*8=25 литров в секунду.
Применять эту формулу можно при поиске иных неизвестных. В случае, когда известен диаметр вместе с расходом воды, можно определять её скорость. Либо, если известна скорость и известен расход, можно высчитать диаметр.
С помощью математического метода
 Потребуется взять трехлитровую банку и секундомер. После открытия крана в полную силу необходимо подставить под поток банку, включив при этом таймер.
Потребуется взять трехлитровую банку и секундомер. После открытия крана в полную силу необходимо подставить под поток банку, включив при этом таймер.
Этот метод имеет значительные погрешности, поэтому довольно приблизительный.
Но можно отметить, что наполнение трёхлитровой банки не должно происходить дольше 10 секунд, иначе показатель считается ниже нормы.
Установленные эксплуатационные и технические нормы говорят, что ёмкость должна быть заполнена за 5-7 секунд. Они учитываются, если трубы не имеют сужений по трассе и если кран не имеет сетки-фильтра.
Получается, что за 5 секунд налилось 3 литра воды. То есть, за 1 секунду налилось 600 мл. Этот показатель давления воды считается очень хорошим.
Если же ёмкость объёмом 3 литра наполнилась водой за 20 секунд, то выходит, что скорость наполнения уже 150 мл в секунду. Этот показатель очень мал. Если наполнение произошло за 3 секунды, то расход равен 1 литр в секунду – это очень высокий показатель.
Внимание! За сутки давление воды успевает несколько раз незначительно измениться. Поэтому для получения достоверных данных необходимо производить измерения несколько раз, включая период, когда разбор воды достигает пикового значения.
Полезное видео
В видео ролике еще один способ измерения напора воды:
Заключение
При следовании вышеуказанным инструкциям каждый человек в домашних условиях, даже если у него нет специальных приборов, может сам обеспечить себе комфорт в пользовании водой.
Самостоятельное измерение давления воды без использования манометра уже не является невыполнимой задачей: 3 вышеуказанных несложных метода это доказывают.
Введение

Транспортировка жидкостей всегда занимала существенное место в человеческой деятельности. Вода нужна, например, для приготовления пищи и орошения. Даже сегодня наше общество не может существовать без многих способов подачи воды, с которыми мы сталкиваемся на каждом шагу.
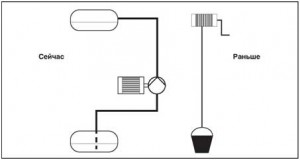
Первым средством, применявшимся для доставки воды по назначению, была лохань или ведро. Чтобы поднять воду со дна колодца, применялись веревка и примитивный ворот. Сегодня наиболее распространенным средством доставки жидкостей являются насосы с электрическим приводом. Для различных целей применяется множество различных типов подобных насосов. В частности, стали очень распространены центробежные насосы благодаря таким своим преимуществам как:
- высокая надежность
- простота конструкции
- низкая стоимость
- универсальное применение
В этом пособии мы хотим дать читателю рекомендации по правильному выбору насоса для решения конкретной задачи и объяснить ему физические законы, действующие при работе центробежного насоса.
Физические условия
Чтобы выбрать оптимальный насос для решения конкретных задач, необходимо учитывать следующие физические условия.
1. Характеристики жидкости
- плотность (“тяжесть” жидкости)
- давление насыщенных паров (температура кипения)
- температура
- вязкость (“густоту” жидкости)
2. Объем, который необходимо подать (расход)
3. Высота всасывания:разница в уровне между насосом и точкой забора жидкости
4. Высота нагнетания: разница в уровне между насосом и наивысшей точкой, в которую подается жидкость
5. Потери давления на всасывании (потери на трение)
6. Потери давления в напорном трубопроводе (потери на трение)
7. Конечное избыточное давление
8. Начальное избыточное давление
Когда все эти данные известны, можно определить режим работы насоса и выбрать его оптимальную модель.
Характеристики жидкости
Для выбора оптимального насоса необходимо иметь полную информацию о характеристиках той жидкости, которая должна подаваться потребителю.
Естественно, что “более тяжелая” жидкость потребует больше затрат энергии при перекачивании данного объема. Чтобы описать, насколько одна жидкость “тяжелее” другой, используется такое понятие, как “плотность” или “удельный вес”; этот параметр определяется как масса (вес) единицы объема жидкости и обычно обозначается как “ρ” (греческая буква “ро”). Измеряется в килограммах на кубометр (кг/м3).
Любая жидкость при определенных температуре и давлении стремится испариться (температура или точка начала кипения); повышение давления вызывает повышение температуры и наоборот. Таким образом, при более низком давлении (даже возможно при вакууме), которое может иметь место со стороны всасывания насоса, жидкость будет иметь более низкую температуру кипения. Если она близка или в особенности ниже текущей температуры жидкости, возможно образование пара и возникновение кавитации в насосе, что в свою очередь может иметь отрицательные последствия для его характеристик и способно вызвать серьезные повреждения (смотрите главу о кавитации).
Вязкость жидкости вызывает потери на трение в трубах. Численное значение этих потерь можно получить у изготовителя конкретного насоса.
Необходимо учитывать, что вязкость “густых” жидкостей, таких как масло, с ростом температуры падает.
Расход воды
Он определяется как объем, который должен быть подан за указанное время, и обозначается как “Q”. Применяемые единицы измерения: как правило, это литры в минуту (л/мин) для насосов небольшой мощности/ производительности, кубометры в час (м3/ч) для насосов средней производительности и, наконец, кубометры в секунду (м3/с) для самых мощных насосов.
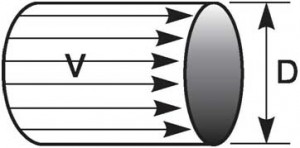
Размеры поперечного сечения трубопровода определяются объемом, который должен быть подан потребителю при данной скорости потока жидкости “v”:
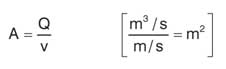
![]()
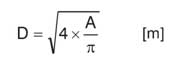

Геодезическая (статическая) высота всасывания
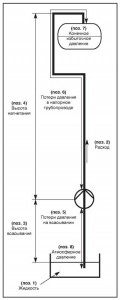
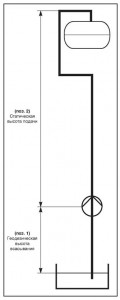
Она определяется как разница в геодезическом уровне между впускным патрубком насоса и свободной поверхностью жидкости в наиболее низко расположенном резервуаре, измеряется в метрах (м) (рис. 3, поз. 1).
Статическая высота подачи (статический напор)
Она определяется как разница в геодезическом уровне между выпускным патрубком и наивысшей точкой гидросистемы, в которую необходимо подать жидкость (рис. 3, поз. 2).
Потери давления на всасывании
Это потери на трение между жидкостью и стенками трубопровода и зависят от вязкости жидкости, качества шероховатости поверхности стенок трубопровода и скорости потока жидкости. При увеличении скорости потока в 2 раза потери давления возрастают во второй степени (рис. 4, поз. 1).
Информацию о потерях давления в трубопроводе, коленах, фитингах и т.п. при различных скоростях потока можно получить у поставщика.
Потери давления в напорном трубопроводе
Смотрите описание, приведенное выше (рис. 4, поз. 2).

Конечное избыточное давление
Это давление, которое необходимо иметь в той точке, куда должна подаваться жидкость (рис. 5, поз. 1).
Начальное избыточное давление
Это давление на свободной поверхности жидкости в месте водозабора. Для открытого резервуара или бака это просто атмосферное (барометрическое) давление (рис. 5, поз. 2).

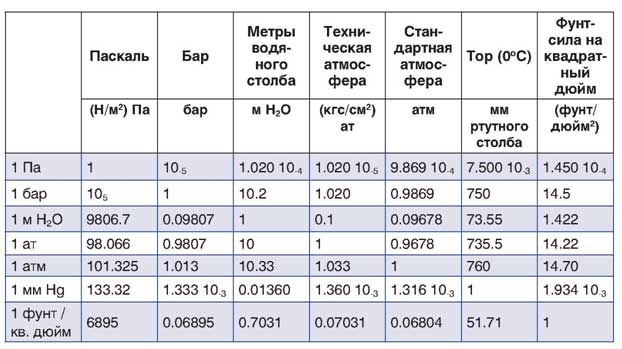
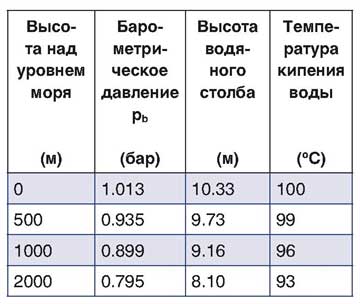
Связь между напором и давлением
Как можно видеть из рис. 6, столб воды высотой 10 м оказывает такое же давление, что и столб ртути (Hg) высотой 0,7335 м. Умножив высоту столба (напор) на плотность жидкости и ускорение свободного падения (g), получим давление в ньютонах на квадратный метр (Н/м2) или в паскалях (Па). Поскольку это очень незначительная величина, в практику эксплуатации насосов ввели единицу измерения, равную 100000 Па, названную баром.

Уравнение на рис. 6 можно решить в метрах высоты столба жидкости:
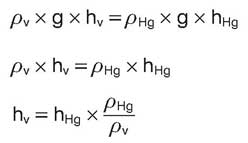
Таким образом, высоту столба жидкостей с различной вязкостью можно привести к эквивалентной высоте водяного столба. На рис. 7 приводятся коэффициенты преобразования для множества различных единиц измерения давления.
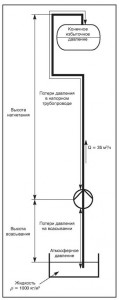
Ниже показан пример расчета общего гидравлического напора со схемой установки насоса.
Гидравлическая мощность (Phyd) насоса определяет объем жидкости, подаваемой при данном напоре за данное время, и может быть рассчитана с помощью следующей формулы:

Пример
Объем в 35 м3 воды за час должен быть перекачан из колодца глубиной 4 м в бак, размещенный на высоте 16 м относительно уровня установки насоса; конечное давление в баке должно быть 2 бара. Потери напора на трение во всасывающем трубопроводе принимаются равными 0,4 м, а в напорном трубопроводе составляют 1,3 м включая потери в коленах.
Плотность воды предположительно составляет 1000 кг/м3 и значение ускорения свободного падения 9,81 м/с2.
Решение:
Общий напор (H):
Высота всасывания – 4,00 м
Потери напора на всасывании – 0,40 м
Высота нагнетания – 16,00 м
Потери давления в напорном трубопроводе – 1,30 м
Конечное давление: – 2 бара*~20,40м
Минус 1 атм**~ -9,87 м
Общий напор – 32,23 м
Гидравлическая мощность определяется по формуле:
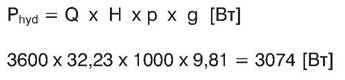
* В данном примере конечное избыточное давление дано как абсолютное давление, т.е. как давление, измеренное относительно абсолютного вакуума.
** Если конечное избыточное давление дано как абсолютное, то начальное избыточное давление необходимо вычесть, поскольку это давление “помогает” насосу всасывать жидкость.
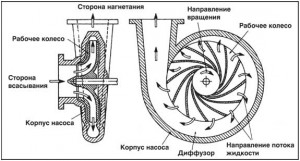
Вода через всасывающий патрубок насоса попадает на вход рабочего колеса и под действием вращающихся лопаток испытывает положительное ускорение. В диффузоре кинетическая энергия потока преобразуется в потенциальную энергию давления. В многоступенчатых насосах поперечное сечение диффузора со встроенными неподвижными лопатками называют “направляющим аппаратом”.
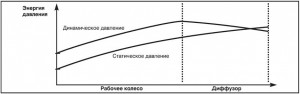
Из схемы на рис. 10 видно, что потенциальная энергия в виде давления в насосе растет в направлении от всасывающего к напорному патрубку, поскольку гидродинамическое давление, создаваемое рабочим колесом (кинетическая энергия скорости потока), преобразуется в потенциальную энергию давления в диффузоре.
Рабочие характеристики насоса
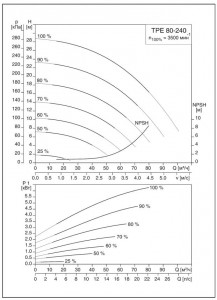
На рис. 11 представлена типичная эксплуатационная характеристика центробежного насоса “Q/H”.
Из нее видно, что максимальное давление нагнетания достигается, когда подача насоса равна нулю, т.е. когда напорный патрубок насоса закрыт. Как только поток в насосе возрастает (увеличивается объем перекачиваемой жидкости), высота нагнетания падает.
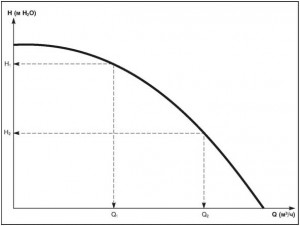
Точная характеристика зависимости подачи Q от напора H определяется изготовителем опытным путем на испытательном стенде. Например (рис. 11), при напоре H1 насос будет подавать объем Q1 и аналогично при H2 – Q2.
Эксплуатационная характеристика насоса
Как уже было показано выше, потери напора на трение в трубопроводе зависят от качества шероховатости поверхности стенок трубопровода, и квадрата скорости потока жидкости и, конечно же, от протяженности трубопровода. Потери давления на трение можно представить на графике “H/Q” как кривую характеристики гидросистемы. В случае замкнутых систем, таких как системы центрального отопления, текущая высота нагнетания может не учитываться, поскольку она уравновешивается положительным напором со стороны всасывающего патрубка.
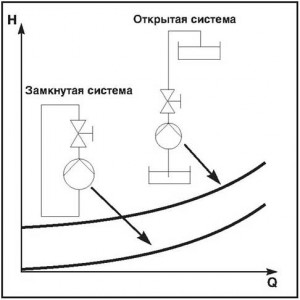
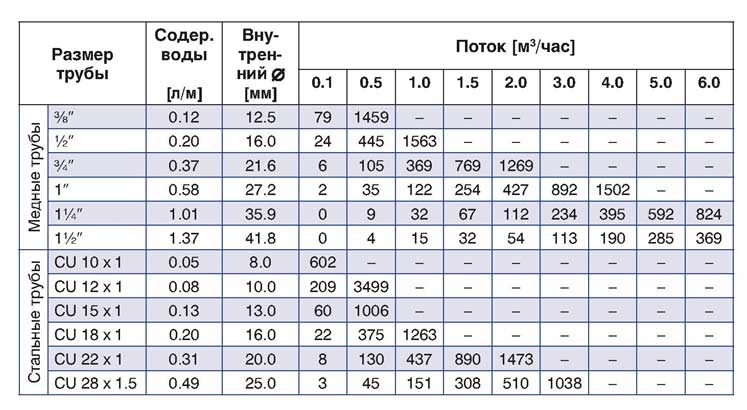
Потери давления [Па/м] при температуре t = 60°C. Рекомендуемые потери в трубах – не более 150 Па/м.
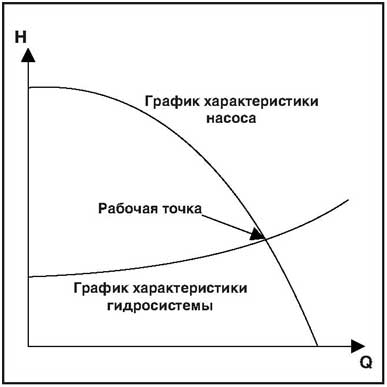
Рабочая точка
Рабочая точка – это точка пересечения графика характеристики насоса с графиком характеристики гидросистемы. Понятно, что любые изменения в гидросистеме, например изменение проходного сечения клапана при его открытии или образование отложений в трубопроводе, сказываются на характеристики гидросистемы, в результате чего положение рабочей точки изменяется. Аналогичным образом изменения в насосе, например износ рабочего колеса или изменении частоты вращения, вызовут возникновение новой рабочей точки.
Последовательно включенные насосы
Многоступенчатые насосы можно рассматривать как пример последовательно включенных одноступенчатых насосов. Конечно, в этом случае невозможно разобщить отдельные ступени, что иногда бывает желательно при проверке состояния насоса.
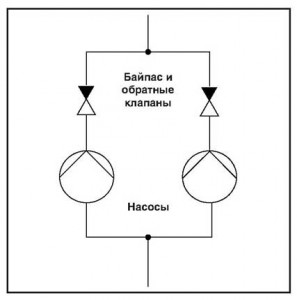
Поскольку неработающий насос создает существенное сопротивление, необходимо предусмотреть байпасную линию и обратный клапан (рис. 14).
Для работающих последовательно насосов общий напор (рис. 15) при любой заданной подаче определяется суммой значений высоты нагнетания каждого отдельного насоса.
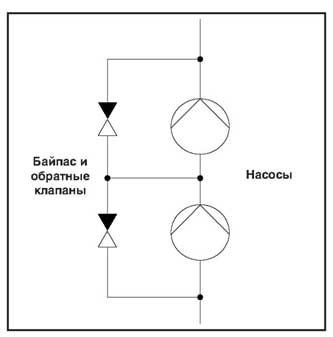
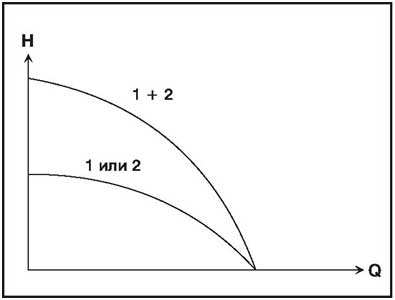
Параллельно включенные насосы.
Такая схема монтажа используется с целью обеспечения контроля состояния насосов или для обеспечения эксплуатационной безопасности, когда требуется наличие вспомогательного или резервного оборудования (например, сдвоенные насосы в отопительной системе). В этом случае также необходимо устанавливать обратные клапаны для каждого из насосов, чтобы предотвратить образование противотока через один из неработающих насосов. Этим требованиям в сдвоенных насосах удовлетворяет переключающий клапан типа заслонки.
Для параллельно работающих насосов общая подача (рис. 17) определяется как сумма значений подачи отдельных насосов при постоянном напоре.
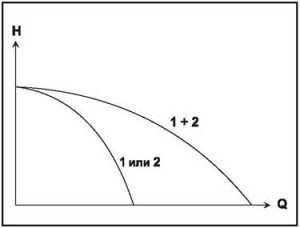
КПД насоса
КПД насоса показывает, какая часть механической энергии, переданной насосу через его вал, преобразовалась в полезную гидравлическую энергию.
![]()
На КПД влияют:
- форма корпуса насоса;
- форма рабочего колеса и диффузора;
- качество шероховатости поверхности;
- уплотнительные зазоры между всасывающей и напорной полостями насоса.
Чтобы потребитель имел возможность определить КПД насоса в конкретной рабочей точке, большинство изготовителей насосного оборудования прилагают к диаграммам рабочих характеристик насоса диаграммы с графиками характеристик КПД (рис. 18).
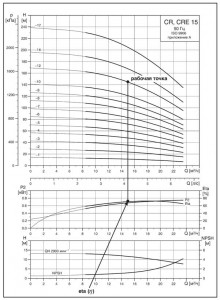
Типовые закономерности
Приведенные далее типовые закономерности демонстрируют теоретическое влияние диаметра (d) рабочего колеса на напор, подачу и потребляемую мощность.
Напор пропорционален диаметру во второй степени:
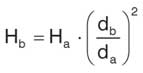
Согласно этой закономерности, удвоение диаметра повысит напор в 4 раза.
Подача пропорциональна диаметру в третьей степени:
![]()
Согласно этой закономерности, удвоение диаметра повысит подачу в 8 раза.
Потребляемая мощность пропорциональна диаметру в пятой степени:
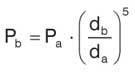
Согласно этой закономерности, удвоение диаметра повысит потребляемую мощность в 32 раза.
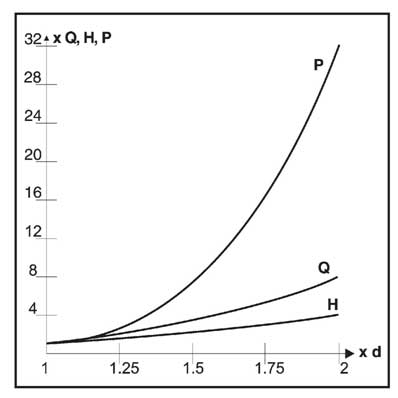
Типовые закономерности
Приведенные далее типовые закономерности демонстрируют теоретическое влияние частоты вращения (n) рабочего колеса на напор, подачу и потребляемую мощность.
Подача пропорциональна частоте вращения:
![]()
Согласно этой закономерности, удвоение частоты вращения в два раза повысит подачу.
Напор пропорционален квадрату частоты вращения:
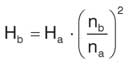
Согласно этой закономерности, удвоение частоты вращения в 4 раза повысит напор.
Потребляемая мощность пропорциональна частоте вращения в третьей степени:
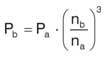
Согласно этой закономерности, удвоение частоты вращения в 8 раз повысит потребляемую мощность.
Потребляемая мощность
P1: Мощность, потребляемая электродвигателем из электросети.
У электродвигателей, непосредственно присоединенных к валу насосов, как это имеет место в приводе циркуляционных насосов, максимальное значение потребляемой мощности указывается на фирменной табличке с техническими данными.
P1 также можно определить по следующей формуле:
![]()
(3-фазные электродвигатели)
![]()
(1-фазные электродвигатели)
где:
V = напряжение (В)
I = сила тока (A)
cos ϕ = коэффициент мощности (-)
P2: мощность на валу электродвигателя.
В случае, когда электродвигатель и насос являются отдельными узлами (включая стандартные и погружные электродвигатели), на фирменной табличке указывается максимальная мощность на валу электродвигателя.
P3: Мощность, потребляемая насосом
Текущая нагрузка электродвигателя может быть определена по кривой мощности насоса. В случае непосредственного присоединения электродвигателя к валу насосов: P3 = P2.
P4: Мощность насоса (Phydraulic)
Значение мощности насоса определяется по формуле:
![]()

Адаптация насосов к переменным режимам эксплуатации
Потери давления в гидросистеме рассчитываются для определенных специфических условий эксплуатации. На практике характеристика гидросистемы почти никогда не совпадает с теоретической из-за коэффициентов запаса прочности, закладываемых в гидросистему.
Рабочая точка гидросистемы с насосом – это всегда точка пересечения графика характеристики насоса с графиком характеристики гидросистемы, следовательно, подача обычно бывает больше, чем требуется для новой гидросистемы.
Такое несоответствие может создать проблемы в гидросистеме. В отопительных контурах может возникать шум, вызванный потоком, в конденсатных системах – кавитация, а в некоторых случаях неоправданно большая подача приводит к потерям энергии.
Вследствие этого возникает необходимость смещения рабочей точки (точки пересечения графиков обоих характеристик) путем регулировки насоса и подстройки гидросистемы. На практике применяют один из указанных ниже способов:
- Изменение характеристики гидросистемы путем прикрытия дроссельного клапана (дросселирование) (рис. 22).
- Изменение характеристики насоса за счет уменьшения наружного диаметра (путем механической обработки) его рабочего колеса (рис. 23).
- Изменение характеристики насоса путем регулировки частоты вращения (рис. 24).
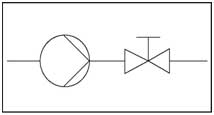
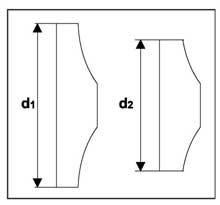
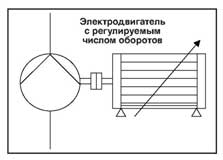
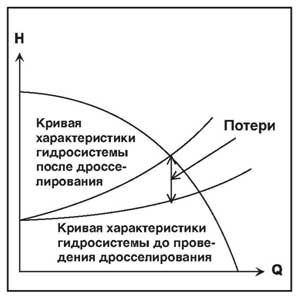
Регулирование подачи с помощью дроссельного клапана
Уменьшение проходного сечения дроссельного клапана в гидросистеме вызывает повышение потерь давления (гидродинамического напора Hdyn), делая кривую характеристики гидросистемы более крутой, в результате чего рабочая точка смещается в направлении более низкой подачи (смотрите рис. 25).
В результате снижается потребляемая мощность, поскольку центробежные насосы имеют характеристику мощности, которая уменьшается при уменьшении подачи. Однако потери мощности при дроссельном регулировании в гидросистеме с высоким значением потребляемой мощности будут значительны, поэтому в таких случаях необходимо проводить специальные расчеты для оценки рентабельности метода регулирования подачи с помощью дроссельного клапана.
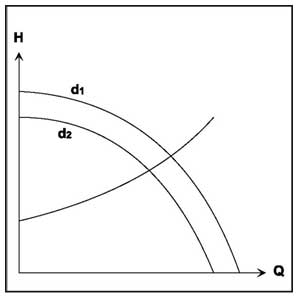
Модификация рабочего колеса
В тех случаях, когда снижение производительности насоса и напора требуется постоянно, наиболее оптимальным решением может стать уменьшение наружного диаметра рабочего колеса.
При этом протачивают по наружному диаметру либо все рабочее колесо, либо только торцы лопаток. Чем больше будет занижение наружного диаметра, тем ниже станет КПД насоса.
Снижение КПД обычно бывает более значительно в тех насосах, которые работают на высоких оборотах. У низкооборотных насосов оно не столь заметно, в особенности, если уменьшение наружного диаметра незначительно.
Когда уменьшение наружного диаметра незначительно, то с достаточно высокой степенью точности можно воспользоваться следующими соотношениями:
![]()
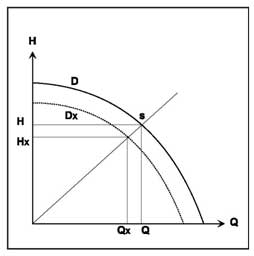
На рис. 27 представлен способ определения заниженного диаметра Dx с помощью диаграммы характеристики “H/Q” в линейных координатах. Начало координат (Q = 0, H = 0) соединяется с новой рабочей точкой (Qx, Hx) прямой линией, продолженной до пересечения с характеристикой имеющегося насоса (Q, H) в точке “s”. После этого новый диаметр (Dx) рассчитывается по следующей формуле:
![]()
![]()
Однако эти зависимости недействительны в случае необходимости значительного снижения производительности насоса. В таком случае рекомендуется проводить занижение рабочего колеса в несколько этапов. Сначала занижение диаметра рабочего колеса выполняется до размера, несколько превышающего значение Dx, рассчитываемое как указывалось выше. После этого насос подвергается испытаниям, после которых можно определить окончательный диаметр.
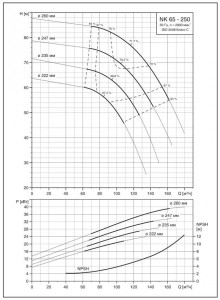
В серийном производстве этого можно избежать. Имеются графики рабочих характеристик для насосов, оборудованных рабочими колесами с различным занижением наружного диаметра (смотрите рис. 28), непосредственно по которым можно рассчитать значение Dx, используя вышеуказанные формулы.
Регулирование частоты вращения
Изменение частоты вращения вызовет изменения в рабочих характеристиках центробежного насоса. Воспользуемся типовыми закономерностями, указанными ранее:
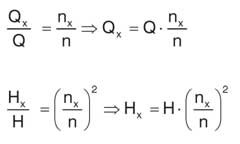
Кавитация
Наиболее часто встречающиеся при эксплуатации насосов проблемы связаны с условиями всасывания на входе гидросистемы и почти всегда они бывают вызваны слишком низким гидростатическим давлением (подпором) на входе насоса.
Причина этого может корениться либо в выборе насоса с неоптимальными для данных условий эксплуатации параметрами, либо в ошибках, допущенных при проектировании гидросистемы.
Вращение рабочего колеса отбрасывает жидкость к поверхности корпуса насоса, в результате чего со стороны всасывающей полости рабочего колеса возникает разряжение. Это вызывает подсос жидкости через всасывающий клапан и трубопровод, которая поступает к рабочему колесу, где она опять отбрасывается к поверхности корпуса насоса. Разряжение на входе насоса зависит от разницы между уровнем положения впускного отверстия и поверхности перекачиваемой жидкости, от потерь давления на трение во всасывающем клапане и трубопроводе, а также от плотности самой жидкости.
Это разряжение ограничено давлением насыщенного пара жидкости при данной температуре, т.е. давлением, при котором будут образовываться пузырьки пара. Любая попытка снизить гидростатическое давление до величины, меньшей чем давление насыщенного пара, приведет к тому, что жидкость отреагирует на это образованием пузырьков пара, поскольку она начнет закипать.
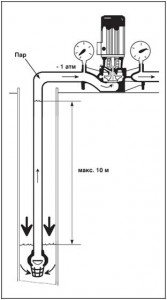
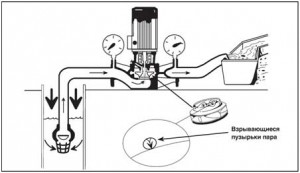
В насосе кавитация возникает тогда, когда давление с той стороны лопаток рабочего колеса, которая обращена в сторону всасывающей полости (обычно вблизи впускного отверстия насоса), падает ниже давления насыщенного пара жидкости, вызывая образование пузырьков газа. Будучи перенесенными в области высокого давления в рабочем колесе, эти пузырьки разрушаются (взрываются), а возникающая при этом волна давления может вызвать повреждение насоса (рис. 31).
Это повреждение, которое может возникнуть в течение нескольких минут или через несколько лет, настолько серьезно, что может отрицательно подействовать не только на насос, но и на электродвигатель. Наиболее уязвимыми деталями при этом являются подшипники, сварные швы и даже поверхности рабочего колеса.
Масштабы повреждений рабочего колеса зависят от характеристик материала, из которого оно изготовлено; например, из таблицы видно, что при одних и тех же условиях ущерб для рабочего колеса из нержавеющей стали составляет всего лишь 5% от ущерба, причиненного рабочему колесу из чугуна.
Потеря в массе различных материалов
(при сравнении за основу взят чугун = 1,0):
| Нержавеющая сталь: | 0,05 |
| Чугун: | 1,0 |
| Бронза: | 0,5 |
| Бронзовые сплавы: | 0,1 |
С явлением кавитации связаны также повышенный уровень шума, падение напора и нестабильность эксплуатации. Зачастую повреждение остается не выявленным до тех пор, пока насос и электродвигатель не будут подвергнуты разборке.
Расчеты по устранению опасности кавитации
Кавитационный запас Hmax насоса, необходимый для устранения опасности кавитации, рассчитывается следующим образом:
Hmax = Hb – Hfs – NPSH – Hv – Hs
Hmax: Кавитационный запас насоса (смотрите рис. 33). Если он положительный, насос может работать при данной высоте всасывания. Если он отрицательный, для работы насоса необходимо создать условия, при которых он станет положительным.
Hb: Атмосферное давление со стороны насоса; это – теоретически максимальная высота всасывания.
![]()
Это значение Hb зависит от плотности жидкости и значения “g” со стороны насоса (рис. 32).
Hfs: Потери давления на трение во всасывающем клапане и присоединенном трубопроводе также зависят от плотности жидкости.
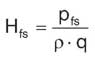
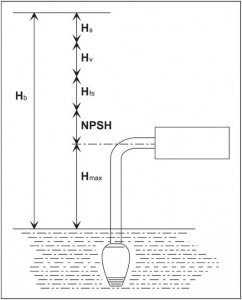
NPSH: Net Positive Suction Head
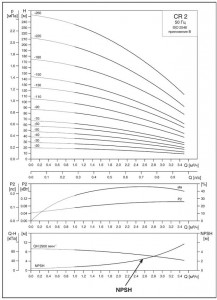
Этот параметр отражает минимальное давление на всасывании, необходимое для безаварийной эксплуатации. Он характеризует потери давления на трение на участке от всасывающего патрубка насоса до той точки первого рабочего колеса, в которой давление минимально, и определяет гидравлические условия, при которых насос не в состоянии всасывать цельный водяной столб высотой 10,33 м. Таким образом, значение NPSH будет расти с ростом подачи, что можно видеть из графика характеристики на рис. 35 конкретного насоса.
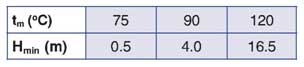
Для циркуляционных насосов график NPSH не используется; вместо этого на рис. 34 представлена таблица с указанием минимального давления на всасывании, необходимого при различных значениях температуры рабочей жидкости.
Hv: Этот параметр отражает давление насыщенного пара перекачиваемой жидкости. Он включен в уравнение, поскольку при более высокой температуре жидкость начинает испаряться быстрее. Hv также зависит от плотности жидкости:
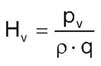
Hs: Этот параметр представляет собой запас прочности, который должен определяться в конкретных условиях в зависимости от степени надежности и достоверности применяемой методики расчета. На практике его берут равным 0,5-1 м. В случае присутствия в воде газа это значение часто выбирают равным 2 м.
Как избежать кавитации
Данная аргументация основана на приведенной выше формуле:
Hmax = Hb – Hfs – NPSH – Hv – Hs
и учитывает влияние каждого из членов уравнения.
Hmax: Насос всегда необходимо устанавливать как можно ниже или потребуется поднять уровень жидкости со стороны всасывания. Последний способ часто бывает наиболее дешевым решением. Положительное давление на всасывании, создаваемое насосом (если таковой имеется) или расширительным бачком, должно поддерживаться как можно более высоким.
Hb: Этот показатель является постоянным при перекачивании определенной жидкости в данном месте.
Hfs: Всасывающий трубопровод должны быть как можно более коротким и иметь минимальное количество колен, клапанов, вентилей и фитингов.
NPSH: Следует выбирать насос с наименьшим потребным NPSH.
Hv: Этот параметр может снижаться при падении температуры жидкости (температуры окружающей среды).
Hs: Устанавливается индивидуально.
Наиболее простой способ избежать кавитации – это снизить подачу насоса путем частичного закрытия нагнетательного (или напорного) клапана; в результате этого понизится требуемое значение NPSH и Hfs, следовательно возрастет значение Hmax.
Альтернативная методика расчета для устранения опасности кавитации
Многие предпочитают преобразовать формулу в функции NPSH следующим образом:
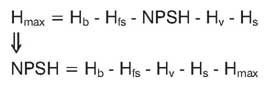
Это дает имеющееся значение NPSHavailable для данной гидросистемы, которое затем можно сравнить с требуемым значением NPSHrequired, указанным на графиках рабочих характеристик соответствующего насоса.
Таким образом, если
NPSHavailable≥NPSHrequired
кавитации удается избежать.
Однако если
NPSHavailable≤NPSHrequired
то опасность возникновения кавитации сохраняется.
Расшифровка обозначений:
“ – “ означает “от – до“; “ / “ означает, что электродвигатель может подключаться двумя разными вариантами;
“ D “ обозначение соединения обмоток электродвигателя по схеме «треугольник»;
“ Y “ обозначение соединения обмоток электродвигателя по схеме «звезда».
1 х 220-230 / 240 V
- Двигатель может быть подключен в однофазную сеть переменного тока напряжением U = 1 x 220-230В.
- Двигатель может быть подключен в однофазную сеть переменного тока напряжением U = 1 x 240В.
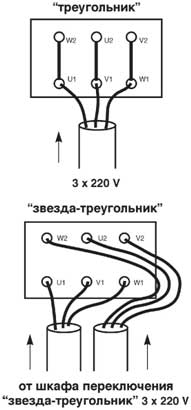
3 х 220–240D / 380–415Y V
- Двигатель может быть подключен в трехфазную сеть переменного тока напряжением U = 3 x 380-415В по схеме «звезда».
- Двигатель может быть подключен в трехфазную сеть переменного тока напряжением U = 3 x 220-240В по схеме «треугольник» (например в Бельгии, в Норвегии, в Италии, во Франции).
- Двигатель может быть подключен в трехфазную сеть переменного тока напряжением U = 3 x 220-240В по схеме «звезда-треугольник».
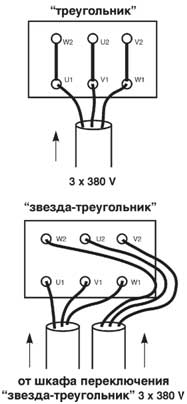
3 х 380–415D V
- Двигатель может быть подключен в трехфазную сеть переменного тока напряжением U = 3 x 380-415В по схеме «треугольник».
- Двигатель может быть подключен в трехфазную сеть переменного тока напряжением U = 3 x 380-415В по схеме «звезда-треугольник».
Теория перекачивания жидкостей” в PDF
PumpTheory-91830082-0908.pdf 824
SHA1: 2456233c5e083b549a564ace008c667f83980783
2020-04-15
Что такое напор насоса
В быту люди часто используют выражение “сильный напор”, открыв кран в ванной или вентиль в саду, увидев большое количество жидкости говорят – “сильный напор”. То есть воспринимают большое количество жидкости, как высокий напор, с точки зрения гидравлики это не совсем верно, разберемся почему.

Напор – удельная энергия потока
Для того, чтобы было удобно сравнивать характеристики потоков жидкости в механике жидкости газа было использовано понятие удельной энергии, если речь идет о жидкости то удобно использовать значение удельной энергии на единицу веса жидкости. Вот эту удельную энергию и называют напором.
Напор – это энергия потока жидкости, отнесенная к единице веса. Если речь идет о напоре, создаваемым насосом, то это удельная энергия передаваемая от насоса к жидкости. Для того, чтобы вычислить напор на выходе насоса необходимо измерить расход жидкости и давление в линии нагнетания насоса.
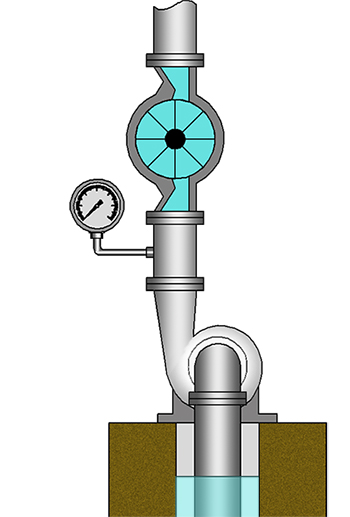
Измеряют напор в метрах, а сам он учитывает как кинетическую так и потенциальную энергию потока, отнесенную к единице веса.
Как определяется напор?
Величина полного напора определяется как сумма:
- геометрического напора – энергии положения, z
- пьезометрического напора – энергии давления, p/ρg – p – статическое давление в центре сечения, ρ – плотность, g – ускорение свободного падения,
- скоростного напора – кинетической энергии, αV2/2g – средняя скорость в живом сечении, α – коэффициент кинетической энергии (в большинстве инженерных расчетах принимают α≈1).
z + p/(ρg) + αV2/2g = Н
Сумму пьезометрического и геометрического напоров называют – статическим.
Hст + αV2/2g = Н
Получается, что напор учитывает это не только количество жидкости вытекающее из трубы, но величину давления, высоту на которую нужно поднять жидкость. У насоса способного поднять жидкость на большую высоту при не очень высоком расходе может быть больший напор, чем у насоса который качает большое количество жидкости, но не преодолевает значительного сопротивления.
Читайте также:


Все новости