Индуктированная электродвижущая сила (ЭДС) возникает в следующих случаях:
- Когда движущийся проводник пересекает неподвижное магнитное поле или, наоборот, перемещающееся магнитное поле пересекает неподвижный проводник; или когда проводник и магнитное поле, двигаясь в пространстве, перемещаются один относительно другого;
- Когда переменное магнитное поле одного проводника, действуя на другой проводник, индуктирует в нем ЭДС (взаимоиндукция);
- Когда изменяющееся магнитное поле индуктирует в енм самом ЭДС (самоиндукция).
Таким образом, всякое изменение во времени величины магнитного потока, пронизывающего замкнутый контур (виток, рамку), сопровождается появлением в проводнике индуктированной ЭДС.
Как было отмечено в статье “Явление электромагнитной индукции”, направление ЭДС магнитной индукции зависит от направления движения проводника и от направления магнитного поля.
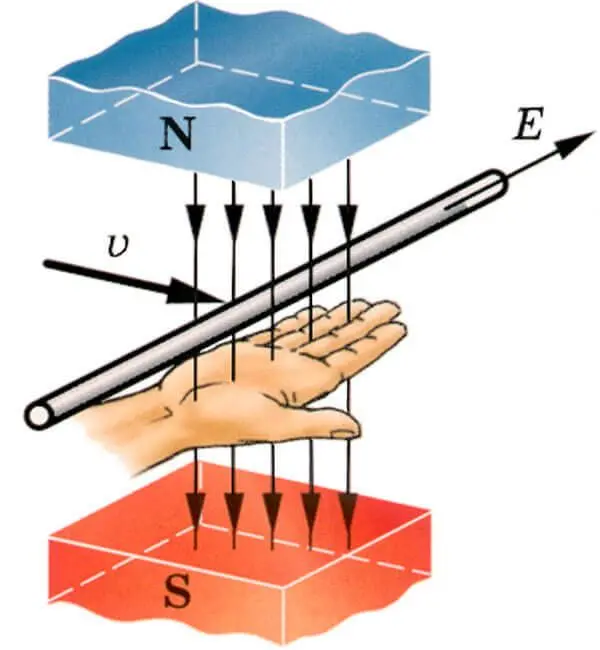
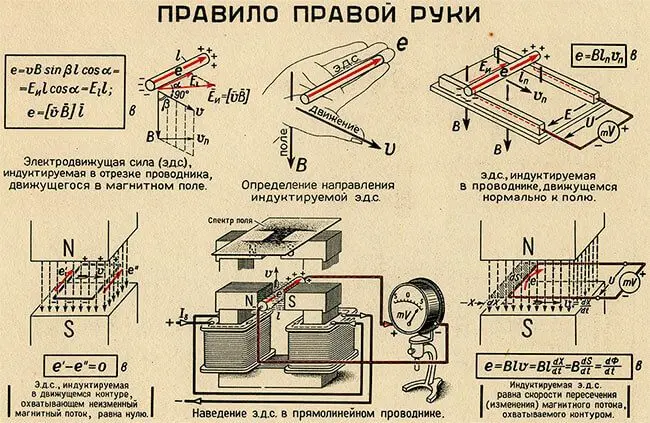
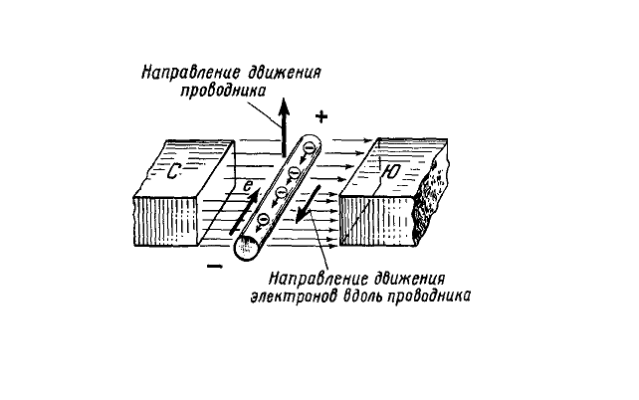
Для определения направления индуктированной ЭДС в проводнике служит “правило правой руки”. Оно заключается в следующем: если мысленно расположить правую руку в магнитном поле вдоль проводника так, чтобы магнитные линии, выходящие из северного полюса, входили в ладонь, а большой отогнутый палец совпадал с направлением движения проводника, то четыре вытянутых пальца будут указывать направление индуктированной ЭДС в проводнике (рисунок 1).
Рисунок 1. Определение направления ЭДС индукции в проводнике по “правилу правой руки”
В случаях, когда проводник остается неподвижным, а магнитное поле движется, для определения направления индуктированной ЭДС нужно предположить, что поле остается неподвижным, а проводник движется в сторону, обратную движению поля, и применить “правило правой руки”.
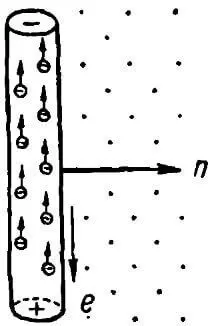 |
| Рисунок 2. Электромагнитная индукция в проводнике |
Явление индуктированной ЭДС можно также объяснить при помощи электронной теории.
Поместим проводник в магнитное поле. Свободные электроны проводника будут находиться в беспорядочном тепловом движении. Положительные и отрицательные заряды равномерно расположены по всему объему проводника и взаимно нейтрализуют друг друга. Будем перемещать проводник с определенной скоростью в однородном магнитном поле в направлении n (рисунок 2) перпендикулярно вектору магнитной индукции. Магнитные линии, показанные точками, направлены из-за плоскости чертежа к читателю.
На электрические заряды проводника в этом случае будет действовать сила, под действием которой свободные электроны получат добавочную составляющую скорости и будут двигаться вдоль проводника.
В то время как положительные заряды, связанные с кристаллической решеткой проводника, относительно проводника не смещаются, движущиеся вместе с проводником свободные электроны могут перемещаться относительно него.
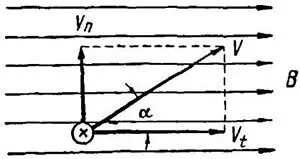 |
| Рисунок 3. Разложение скорости движения проводника в магнитном поле |
В нашем примере электроны движутся от нижнего края проводника к его верхнему краю, что соответствует направлению тока сверху вниз. Направление индуктированной ЭДС и тока в проводнике, как легко убедиться, согласуется с правилом правой руки.
Величина ЭДС индукции магнитного поля в проводнике зависит:
- от величины индукции B магнитного поля, так как чем гуще расположены магнитные индукционные линии, тем больше число их пересечет проводник за единицу времени (секунду);
- от скорости движения проводника v в магнитном поле, так как при большой скорости движения проводник может больше пересечь индукционных линий в секунду;
- от рабочей (находящейся в магнитном поле) длины проводника l, так как длинный проводник может больше пересечь индукционных линий в секунду;
- от величины синуса угла α между направлением движения проводника и направлением магнитного поля (рисунок 3).
Раскладываем вектор скорости движения проводника в магнитном поле на две составляющие: vn – составляющую нормальную к направлению поля (vn = v × sin α) и vt – тангенциальную составляющую (vt = v × cos α), которая не принимает участия в создании ЭДС, так как при движени под воздействием тангенциальной составляющей проводник двигался бы параллельно вектору B и не пересекал бы линии магнитной индукции.
Формула ЭДС индукции дает возможность определить ее величину:
e = B × l × v × sin α (В) .
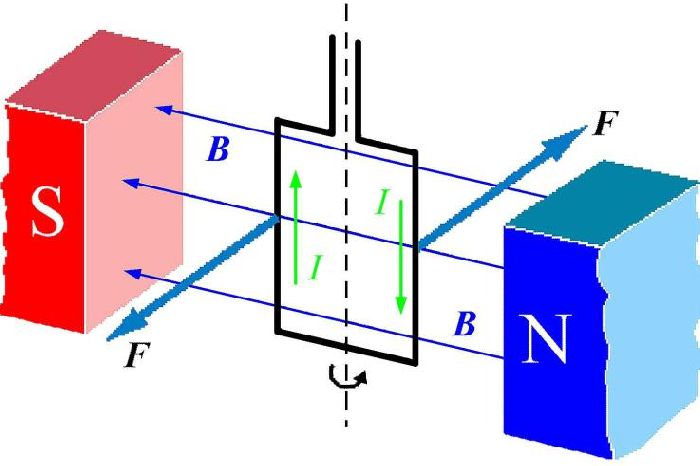
Познакомившись с явлением электромагнитной индукции, рассмотрим еще раз процесс преобразования электрической энергии в механическую.
Рисунок 4. Преобразование электрической энергии в механическую
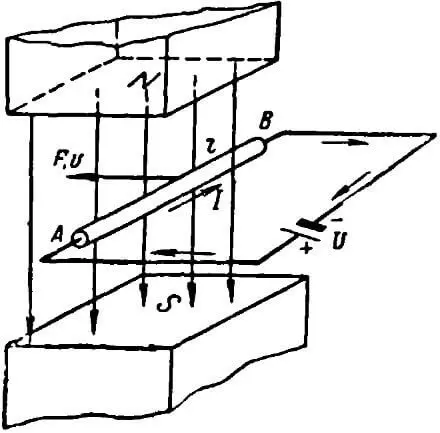
Пусть прямолинейный проводник АВ (рисунок 4), по которому проходит ток от источника напряжения, помещен во внешнее магнитное поле. Если проводник неподвижен, то энергия источника напряжения расходуется исключительно на нагрев проводника:
A = U × I × t = I² × r × t (Дж) .
Затрачиваемая мощность будет равна:
Pэл = U × I = I² × r (Вт) ,
откуда определяем ток в цепи:
| (1) |
Однако нам известно, что проводник с током, помещенный в магнитное поле, будет испытывать силу со стороны поля, стремящуюся перемещать проводник в магнитном поле в направлении, определяемом правилом левой руки. При своем движении проводник будет пересекать магнитные силовые линии поля и в нем по закону электромагнитной индукции возникнет индуктированная ЭДС. Направление этой ЭДС, определенное по правилу правой руки, будет обратным току I. Назовем ее обратной ЭДС Eобр. Величина Eобр согласно закону электромагнитной индукции будет равна:
Eобр = B × l × v (В) .
По второму закону Кирхгофа для замкнутой цепи имеем:
U – Eобр = I × r
или
откуда ток в цепи
| (3) |
Сравнивая выражения (1) и (3), видим, что в проводнике, движущемся в магнитном поле, при одних и тех же значениях U и r ток будет меньше, чем при неподвижном проводнике.
Умножая полученное выражение (2) на I, получим:
U × I = Eобр × I + I² × r .
Так как Eобр = B × l × v, то
U × I = B × l × v × I + I² × r .
Учитывая, что B × l × I = F и F × v = Pмех, имеем:
U × I = F × v + I² × r
или
P = Pмех + Pэм .
Последнее выражение показывает, что при движении проводника с током в магнитном поле мощность источника напряжения преобразуется в тепловую и механическую мощности.
Источник: Кузнецов М. И., “Основы электротехники” – 9-е издание, исправленное – Москва: Высшая школа, 1964 – 560с.
как определить направление ЭДС в генераторе и электромагнитной силы в электродвигателе?? ? ОЧЕНЬ НАДО!!!
Знаток
(353),
на голосовании
9 лет назад
Голосование за лучший ответ
romfil
Знаток
(495)
9 лет назад
эдс возникает в проводниках под действием изменяющихся магнитных полей, в которых находятся эти проводники. Направление эдс индукции в проводнике, перемещающемся в магнитном поле, может быть определено по правилу правой руки, которое формулируется так: Если правую руку расположить ладонью к северному полюсу так, чтобы большой отогнутый палец показывал направление движения проводника, то четыре пальца будут указывать направление эдс индукции. 
Величина эдс индукции, возникающей в замкнутом проводнике, пропорциональна скорости изменения магнитного потока, пронизывающего контур этого проводника.
Величина и направление ЭДС индукции (в день науки)
Величина ЭДС
индукции зависит от количества силовых линий поля, пересекающих проводник в
единицу времени, т. е. от скорости движения проводника в поле.
Величина
индуктированной ЭДС находится в прямой зависимости от скорости движения
проводника в магнитном поле.
Величина
индуктированной ЭДС зависит также и от длины той части проводника, которая
пересекается силовыми линиями поля. Чем большая часть проводника пересекается
силовыми линиями поля, тем большая ЭДС индуктируется в проводнике. И, наконец,
чем сильнее магнитное поле, т. е. чем больше его индукция, тем большая ЭДС
возникает в проводнике, пересекающем это поле.
Итак, величина
ЭДС индукции, возникающей в проводнике при его движении в магнитном поле, прямо
пропорциональна индукции магнитного поля, длине проводника и скорости его
перемещения.
Зависимость
эта выражается формулой Е = Blv,
где Е — ЭДС
индукции; В — магнитная индукция; I — длина проводника; v — скорость движения
проводника.
Следует
твердо помнить, что в проводнике, перемещающемся в магнитном поле, ЭДС
индукции возникает только в том случае, если этот проводник пересекается
магнитными силовыми линиями поля. Если же проводник перемещается вдоль
силовых линий поля, т. е. не пересекает, а как бы скользит по ним, то никакой
ЭДС в нем не индуктируется. Поэтому приведенная выше формула справедлива только
в том случае, когда проводник перемещается перпендикулярно магнитным силовым
линиям поля.
Направление
индуктированной ЭДС (а также и тока в проводнике) зависит от того, в какую
сторону движется проводник. Для определения направления индуктированной ЭДС
существует правило правой руки.
Если держать
ладонь правой руки так, чтобы в нее входили магнитные силовые линии поля, а
отогнутый большой палец указывал бы направление движения проводника, то
вытянутые четыре пальца укажут направление действия индуктированной ЭДС и
направление тока в проводнике.
Правило правой руки
Электромагнитная индукция
Содержание
- Явление электромагнитной индукции
- Магнитный поток
- Закон электромагнитной индукции Фарадея
- Правило Ленца
- Самоиндукция
- Индуктивность
- Энергия магнитного поля
- Основные формулы раздела «Электромагнитная индукция»
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ):
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec{B} ) ЭДС электромагнитной индукции равна:
где ( alpha ) – угол между векторами ( vec{B} ) и ( vec{v} ).
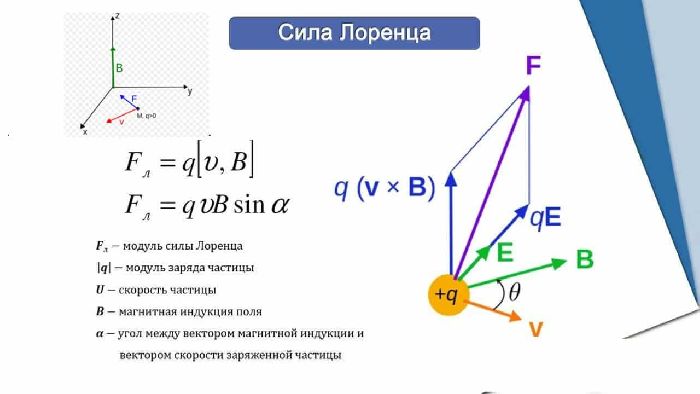
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_{is} ), возникающая в катушке с индуктивностью ( L ), по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec{B} ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ), создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3.1 (62.61%) 92 votes
ЭДС индукции в движущихся проводниках

4.5
Средняя оценка: 4.5
Всего получено оценок: 116.
4.5
Средняя оценка: 4.5
Всего получено оценок: 116.
ЭДС индукции возникает в контуре при изменении магнитного потока через него. Более редким случаем магнитной индукции является движение уединенного проводника в магнитном поле. Кратко рассмотрим ЭДС индукции в движущихся проводниках.
Механизм индукции в движущемся проводнике
Из курса физики в 11 классе известно, что электрический ток — это движение носителей заряда. Если магнитный поток через контур изменяется, то в контуре возникает вихревое электрическое поле, благодаря которому и движутся носители и возникает электрический ток. Однако это не единственный способ создать в проводнике движение зарядов.
Вторым способом создания в проводнике движущихся зарядов является использование силы Лоренца. Если эта сила начнет действовать на носители заряда в проводнике, то в нем возникнет ЭДС и электрический ток.
Сила Лоренца действует только на движущиеся заряды. Следовательно, если проводник, в котором есть носители заряда, начнет двигаться в магнитном поле, то на заряды начнет действовать сила, и они придут в движение — в проводнике возникнет ЭДС.
Заметим, что ЭДС, возникающая в этом случае в проводнике, имеет иную причину, по сравнению с изменением магнитного потока через контур. Если при изменении потока причиной возникновения ЭДС является вихревое электрическое поле, то в движущемся проводнике причиной ЭДС является сила Лоренца.
ЭДС индукции в движущемся проводнике
Вычислим ЭДС индукции в проводнике длиной $l$, который движется с постоянной скоростью $v$ так, что вектор магнитной индукции $overrightarrow B$ однородного поля перпендикулярен проводнику и направлен под углом $alpha$ к скорости движения проводника.
По формуле силы Лоренца ее величина равна:
$$F=|q|Bvsinalpha$$
Компонента этой силы, направленная вдоль проводника, совершает положительную работу, которая на пути $l$ равна:
$$А=Fl=|q|Bvlsinalpha$$
Заметим, что вторая компонента силы Лоренца совершает равную по модулю отрицательную работу. Поэтому суммарная работа силы Лоренца равна нулю.
ЭДС по определению равна отношению работы, совершенной полем по переносу зарядом, к величине этого заряда. Следовательно:
$$mathscr{E} = {Aover q}=Bvlsinalpha$$
Движение контура в магнитном поле
Формулу ЭДС индукции в движущихся проводниках можно применить к прямоугольному контуру, разбив его на четыре элементарных проводника (по числу сторон). В этом случае ЭДС, возникающие в противоположных сторонах контура, будут направлены в противоположные стороны. В результате суммарная ЭДС в контуре будет равна нулю. Следовательно, при движении контура в однородном магнитном поле ток в нем возникнуть не может.
Этот же вывод можно сделать и из закона электромагнитной индукции. Если контур движется в однородном магнитном поле, то магнитный поток, пронизывающий его, не изменяется, следовательно, ЭДС индукции, возникающая в нём, равна нулю.
Единственная возможность создать ЭДС в контуре, движущемся в однородном магнитном поле, это совершить его поворот таким образом, чтобы ЭДС возникала за счет изменения компоненты $sinalpha$. Действительно, такой поворот будет изменять магнитный поток через контур, а значит, в нём будет возникать ЭДС индукции.
Что мы узнали?
В уединенном проводнике, движущемся в однородном магнитном поле, возникает ЭДС индукции. Эта ЭДС обусловлена возникновением силы Лоренца, действующей на заряды внутри проводника. В рамке, движущейся без вращения в однородном магнитном поле, ЭДС на противоположных сторонах имеет разные направления, поэтому ток по рамке в этих условиях не течет.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-
Кронг Кронг
10/10
Оценка доклада
4.5
Средняя оценка: 4.5
Всего получено оценок: 116.
А какая ваша оценка?