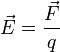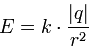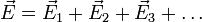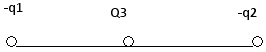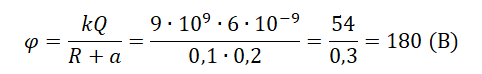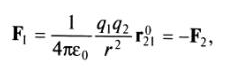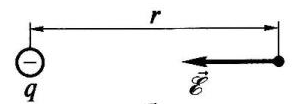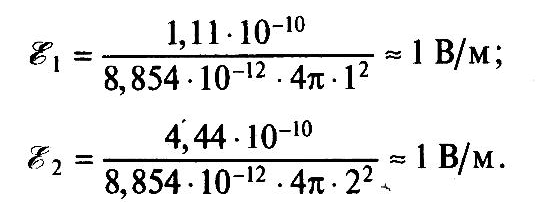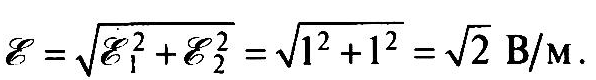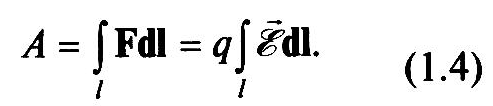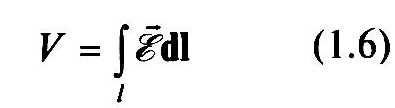В этой статье мы обсудим электрическое поле, создаваемое заряженными частицами в точке, и направление поля, а также несколько фактов.
Электрическое поле в точке представляет собой результирующее поле, создаваемое всеми заряженными частицами, окружающими эту точку, и интенсивность поля прямо пропорциональна заряду источника и расстоянию от точки до источника.
Как найти электрическое поле в точке?
Электрическое поле, создаваемое заряженной частицей, может быть притягивающим или отталкивающим в зависимости от заряда частицы.
Электрическое поле в любой точке вокруг этой области, образованной заряженной частицей, прямо пропорционально заряду, который она несет, и обратно пропорционально расстоянию между зарядом и рассматриваемой точкой.
Электрическое поле в точке из-за наличия заряда q1 просто задается соотношением
Где д1 это заряд, создающий электрическое поле
r – расстояние, разделяющее заряд и точку
В случае, если в точке P присутствует заряд, мы знаем, что электрическая сила между двумя заряженными частицами равна
Где д1 заряженная частица
И д2 частица в точке P в электрическом поле, образованном частицей q1
r – расстояние, разделяющее две частицы
То же самое изображено на диаграмме ниже
Направление электрического поля показано на диаграмме, так как частица в точке P заряжена противоположно, электрическая сила является силой притяжения.
Тогда электрическое поле, создаваемое частицей q1 в точке P есть
Это формула для расчета электрического поля в любой точке, присутствующей в поле, развиваемом заряженной частицей.
Задача 1: Каково электрическое поле в точке, вызванной зарядом 5 Кл, находящимся на расстоянии 5 см?
Данный:
q1= 5C
г=5 см=0.05 м
Электрическое поле, обусловленное зарядом q1=5С
9 * 109*5С/(0.05)2
45 * 109/ 0.0025
18 * 1012N / C
Электрическое поле в точке равно 18*1012N / C
Как найти результирующее электрическое поле в точке?
Суммарное электрическое поле в точке представляет собой сумму всех электрических полей, действующих в точке.
Чистое электрическое поле можно рассчитать, сложив все электрические поля, действующие в точке, электрические поля могут быть притягивающими или отталкивающими в зависимости от заряда, который генерирует электрическое поле.
Рассмотрим следующую диаграмму, показывающую частицы с различным зарядом q1, д2, д3, а q4 окружён точкой P, отстоящей на разное расстояние r1, г2, г3и г4 соответственно от точки.
Теперь здесь электрическое поле из-за заряда q1 is
Точно так же электрическое поле заряда q2 is
Электрическое поле, обусловленное зарядом q3 is
Электрическое поле, обусловленное зарядом q4 is
Тогда суммарное электрическое поле в точке P равно
Если имеется «n» зарядов, то суммарное электрическое поле в точке, обусловленное всеми зарядами, равно
Как найти напряженность электрического поля в точке?
Напряженность электрического поля — это напряженность поля и потенциал поля в точке.
Электростатическую силу можно рассчитать как отношение электростатической силы к заряду, на который действует сила или же заряд создает электрическое поле в определенной точке, отстоящей на некоторое расстояние.
Задача 2: Какова напряженность электрического поля в точке, удаленной на расстояние 0.25 м от заряда +2С?
Данный: д=+2С
r = 0.25 м
У нас есть,
= 9 * 109*2/(0.25)2
9 * 109* 2/0.0625
228 * 109N / C
Следовательно, электрическое поле в точке на расстоянии 0.25 м от заряда +2C равно 228*109N / C
Как найти напряженность электрического поля в точке?
Его можно рассчитать как отношение электрической силы, действующей в точке на единицу заряда частицы, и дается соотношением E=F/q
Чем больше электростатическая сила, действующая на заряды или в точке исходной частицей, тем больше будет напряженность электрического поля пространства, создаваемого заряженной частицей. Напряженность поля будет максимальной, когда расстояние между точкой и источником будет минимальным и если заряд источника несет более высокий заряд.
Как найти направление электрического поля в точке?
Мы можем найти направление электрического поля в точке, введя пробный заряд в электрическое поле.
В основном, направление положительно заряженной частицы — радиально наружу, тогда как направление поля отрицательно заряженной частицы — радиально внутрь.
При введении точечного заряда в область электрического поля заряд будет демонстрировать внезапный дрейф и выравниваться в направлении поля, что указывает направление электрического поля, создаваемого зарядом источника.
Если мы поместим положительный пробный заряд в поле, то направление электрического поля будет таким, как показано на диаграмме ниже:
А что касается отрицательного точечного заряда, направление электрического поля излучается внутрь, как показано ниже:
Если мы поместим два противоположно заряженных носителя в электрическое пространство, то направление поля будет направлено от положительно заряженной частицы к отрицательному носителю заряда.
Если в поле поместить два заряда с одинаковыми зарядами, то на каждый из зарядов будет действовать сила отталкивания. Предположим, у нас есть два положительных заряда, тогда сила отталкивания будет оказывать силу толкания друг на друга.
Как найти величину электрического поля в точке?
Величина электрического поля в точке – это чистая электрическая сила, действующая на единицу заряда в этой точке.
Величина электрического поля рассчитывается по формуле
и величина поля всегда положительна независимо от знака заряда.
Каковы величина и направление электрического поля в точке, удаленной от источника заряда на расстоянии 15 см, имеющего заряд -15 мКл?
Данный: q=-15мКл
г=15 см=0.15 м
= 9 * 109Nm2C-2 *[-15*10-6]/(0.15)2
= 135 * 103/ 0.0225
= 6 * 106N / C
Величина электрического поля 6*106N / C
Электрическое поле в точке на экваториальной линии
Экваториальная линия — это линия, перпендикулярная осевой линии диполя, соединяющая два противоположно заряженных носителя.
Рассмотрим точку «P» на экваториальной линии, электрическое поле в точке P из-за заряда –q равно
А электрическое поле в точке P из-за заряда +q равно
Величина обоих электрических полей одинакова,
Мы можем рассчитать результирующее электрическое поле в точке P, применив закон параллелограмма сложения векторов.
[E1]=[Е2]
Э=2Э1Cosθ—-(5)
Подставляя значение для «E», мы имеем,
Из треугольника APO находим значение Cosθ как
Cosθ=l/√r2=l2
Используя это в приведенном выше уравнении,
р=2ql
Для г>>>XNUMX,
Электрическое поле в точке на осевой линии диполя
Диполь образуется за счет разделения противоположных зарядов на некотором расстоянии.
Осевая точка — это центральная точка между двумя зарядами, образующими электрические диполи, наша цель — найти электрическое поле на этой осевой линии, соединяющей точку в середине двух зарядов.
Рассмотрим два заряда +q и –q и осевую точку между ними, расположенную в точке «О». Расстояние между двумя зарядами равно 2l. Пусть “p” будет точкой на осевой линии.
Напряженность электрического поля в точке P из-за заряда +q равна
E=1/4π∈0*к/(рл)2
А напряженность электрического поля в точке P из-за заряда -q равна
Следовательно, результирующее электрическое поле в точке P на осевой линии диполя E=E1+E2
q/4π∈0*q(1/(рл)2-1/(р+XNUMX)2)
q/4π∈0(4рл/(р2-l2)2)
Мы знаем, что
Электрический момент
Следовательно,
Если г>>>XNUMX, то
Электрическое поле в точке на экваториальной плоскости
Рассмотрим экваториальную плоскость, стоящую в осевой точке «О». Величина электрического поля в точке «P» на плоскости равна из-за зарядов +q и –q.
Суммарное электрическое поле в точке равно
Из уравнения (6) мы знаем, что
Полное электрическое поле противоположно электрическому диполю, поэтому результирующее электрическое поле отрицательно.
Для больших расстояний, т.е. r>>a,
Следовательно, электрическое поле в экваториальной плоскости равно
Электрическое поле в точке на оси заряженного кольца.
Рассмотрим однородно заряженное кольцо радиуса r и небольшой заряженный элемент dq на кольце. Пусть P — точка, лежащая на центральной оси заряженного кольца на расстоянии l от его центра. Пусть θ — угол, образованный осью и линией, соединяющей точку P и элемент заряда.
Суммарное электрическое поле создается всеми зарядами вокруг кольца. Поле, перпендикулярное оси, равно нулю, поэтому единственная составляющая электрического поля, которая принимается во внимание, – это x-компонента.
Элемент электрического поля
Из диаграммы
Следовательно,
Интегрируя это уравнение
Оно равно напряжению электрического поля в точке на оси, идущей от центра заряженного кольца.
Для больших расстояний r>>>l,
Это уравнение дает электрическое поле в точке на оси заряженного кольца, имеющей большой радиус.
Электрическое поле в точке, обусловленное точечным зарядом
Рассмотрим исходный заряд Q, создающий электрическое поле
Пусть q — пробный заряд, помещенный в это поле на расстоянии r от исходного заряда.
Электрическая сила между двумя произведенными теперь зарядами равна
Электрическое поле, создаваемое точечным зарядом, равно E=F/q.
Что равно
Q может быть положительным или отрицательным в зависимости от заряда, который он несет.
Электрическое поле в точке, обусловленное двумя зарядами
Если есть два заряда Q1 и Q2 разделены некоторым расстоянием ‘r’, тогда электрическая сила между ними равна
Электрическое поле, обусловленное зарядом Q1 в точке P есть
Электрическое поле, обусловленное зарядом Q2 в точке P есть
Суммарное электрическое поле в точке равно
Электрическое поле в точке зависит от количества зарядов, окружающих ее, и от электрической силы, действующей на эту точку.
Напряженность электрического поля в точке между двумя параллельными листами
Рассмотрим два параллельных листа с плотностью заряда +σ и –σ, разделенных некоторым расстоянием.
Линии электрического поля будут проходить от положительно заряженной пластины к отрицательно заряженной пластине. Электрическое поле перпендикулярно плоскому листу, а величина электрического поля равна
Пусть P будет точкой между двумя параллельными листами. Величина электрического поля одинакова и имеет то же направление, что показано на рисунке между двумя пластинами, поэтому результирующее электрическое поле в точке P равно
Это напряженность электрического поля в точке между двумя заряженными пластинами. В любой точке за пределами этого параллельного слоя заряда напряженность электрического поля равна нулю.
Часто задаваемые вопросы
Если результирующая электростатическая сила между двумя зарядами +3C и -2C помещена в точки A и B соответственно, разделенные расстоянием 10 фм, то каково расстояние от точки A, где напряженность электрического поля равна нулю?
Данный: q1=+3С
q2=-2С
d=10 фм
ds=(10-s) FM
Пусть электрическое поле, создаваемое зарядом q1,Eb а электрическое поле, создаваемое зарядом q2 быть Еb
Точка, в которой напряженность электрического поля равна нулю,
Решение этого уравнения с помощью квадратичной формулы
Разделение не может быть отрицательным, поэтому исключая другую часть и учитывая только положительный член уравнения, мы находим
Следовательно, расстояние от точки А, где напряженность электрического поля равна нулю, равно
ds= 10-4.5=5.5 фм
Узнайте больше о Являются ли линии электрического поля перпендикулярными?
Как определить направление вектора напряженности электрического поля
Содержание
- Характеристика электрического поля
- Силовые линии
- Что называется напряженностью электрического поля
Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будет действовать кулоновская сила; значит, в пространстве, окружающем электрические заряды, существует силовое поле. Согласно представлениям современной физики, поле реально существует и наряду с веществом является одной из форм существования материи, посредством которого осуществляются определенные взаимодействия между макроскопическими телами или частицами, входящими в состав вещества. В данном случае говорят об электрическом поле — поле, посредством которого взаимодействуют электрические заряды. Мы рассматриваем электрические поля, которые создаются неподвижными электрическими зарядами и называются электростатическими.
Для обнаружения и опытного исследования электростатического поля используется пробный точечный положительный заряд — такой заряд, который не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле). Если в поле, создаваемое зарядом Q, поместить пробный заряд Q, то на него действует сила F, различная в разных точках поля, которая, согласно закону Кулона, пропорциональна пробному заряду Q. Поэтому отношение F/Q не зависит от Q и характеризует электростатическое поле в той точке, где пробный заряд находится. Эта величина называется напряженностью и является силовой характеристикой электростатического поля.
Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:
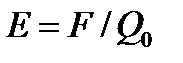
Напряженность поля точечного заряда в вакууме
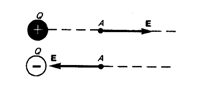
Единица напряженности электростатического поля — ньютон на кулон (Н/Кл): 1 Н/Кл — напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н; 1 Н/Кл= 1 В/м, где В (вольт) — единица потенциала электростатического поля. Графически электростатическое поле изображают с помощьюлиний напряженности — линий, касательные к которым в каждой точке совпадают с направлением вектора Е (рис.).

Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, условились проводить их с определенной густотой: число линий напряженности, пронизывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Е. Тогда число линий напряженности, пронизывающих элементарную площадку dS, нормаль n которой образует угол a с вектором Е, равно Е dS cosa = EndS, где Еп—проекция вектора Е на нормаль n к площадке dS (рис.).
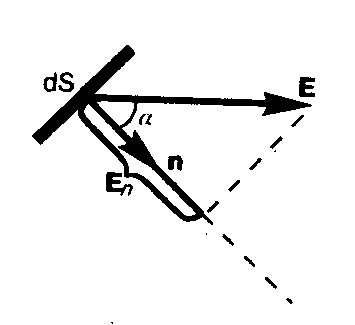
Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверхность

где интеграл берется по замкнутой поверхности S. Поток вектора Е является алгебраической величиной: зависит не только от конфигурации поля Е, но и от выбора направления n. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т. е. нормаль, направленная наружу области, охватываемой поверхностью.
К кулоновским силам применим принцип независимости действия сил, т. е. результирующая сила F, действующая со стороны поля на пробный заряд Q, равна векторной сумме сил Fi, приложенных к нему со стороны каждого из зарядов Qi: 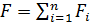
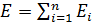
Принцип суперпозиции позволяет рассчитать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.
Принцип суперпозиции применим для расчета электростатического поля электрического диполя. Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+Q,–Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Согласно принципу суперпозиции, напряженность Е поля диполя в произвольной точке 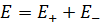
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 — 

Разделы: Физика
Цель урока: дать понятие напряжённости электрического поля и ее определения в любой точке поля.
- формирование понятия напряжённости электрического поля; дать понятие о линиях напряжённости и графическое представление электрического поля;
- научить учащихся применять формулу E=kq/r 2 в решении несложных задач на расчёт напряжённости.
Электрическое поле – это особая форма материи, о существовании которой можно судить только по ее действию. Экспериментально доказано, что существуют два рода зарядов, вокруг которых существуют электрические поля, характеризующиеся силовыми линиями.
Графически изображая поле, следует помнить, что линии напряженности электрического поля:
- нигде не пересекаются друг с другом;
- имеют начало на положительном заряде (или в бесконечности) и конец на отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
- между зарядами нигде не прерываются.
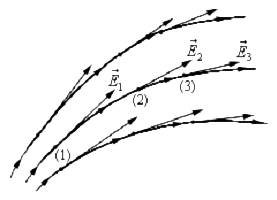
Рис.1
Силовые линии положительного заряда:
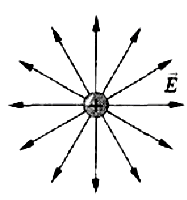
Рис.2
Силовые линии отрицательного заряда:
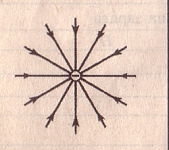
Рис.3
Силовые линии одноименных взаимодействующих зарядов:
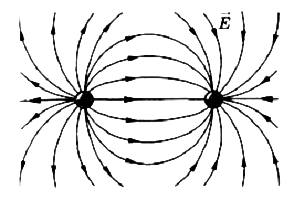
Рис.4
Силовые линии разноименных взаимодействующих зарядов:
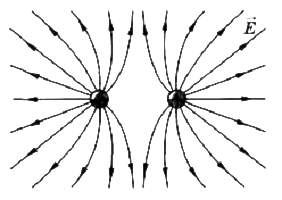
Рис.5
Силовой характеристикой электрического поля является напряженность, которая обозначается буквой Е и имеет единицы измерения 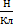

В результате преобразования формулы закона Кулона и формулы напряженности имеем зависимость напряженности поля от расстояния, на котором она определяется относительно данного заряда
где: k – коэффициент пропорциональности, значение которого зависит от выбора единиц электрического заряда.
В системе СИ 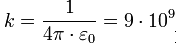
где ε – электрическая постоянная, равная 8,85·10 -12 Кл 2 /Н·м 2 ;
q – электрический заряд (Кл);
r – расстояние от заряда до точки в которой определяется напряженность.
Направление вектора напряженности совпадает с направлением силы Кулона.
Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным. В ограниченной области пространства электрическое поле можно считать приблизительно однородным, если напряженность поля внутри этой области меняется незначительно.
Общая напряженность поля нескольких взаимодействующих зарядов будет равна геометрической сумме векторов напряженности, в чем и заключается принцип суперпозиции полей:
Рассмотрим несколько случаев определения напряженности.
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный положительный заряд между ними, тогда в данной точке будут действовать два вектора напряженности, направленные в одну сторону:
Е31 – напряженность точечного заряда 3 со стороны заряда 1;
Е32 – напряженность точечного заряда 3 со стороны заряда 2.
Согласно принципу суперпозиции полей общая напряженность поля в данной точке равна геометрической сумме векторов напряженности Е31 и Е32.
Напряженность в данной точке определяется по формуле:
где: r – расстояние между первым и вторым зарядом;
х – расстояние между первым и точечным зарядом.
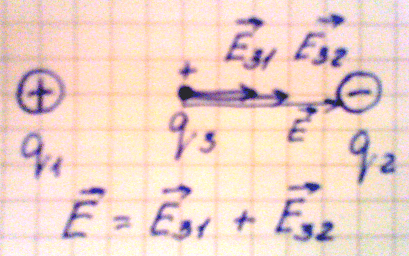
Рис.6
2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной на расстояние а от второго заряда. Если учесть, что поле первого заряда больше, чем поле второго заряда, то напряженность в данной точке поля равна геометрической разности напряженности Е31 и Е32.
Формула напряженности в данной точке равна:
Е = kq1/(r + a) 2 – kq2/a 2
Где: r – расстояние между взаимодействующими зарядами;
а – расстояние между вторым и точечным зарядом.
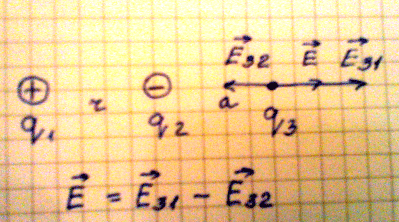
Рис.7
3. Рассмотрим пример, когда необходимо определить напряженность поля в некоторой удаленности и от первого и от второго заряда, в данном случае на расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные заряды отталкиваются , а разноименные притягиваются, имеем два вектора напряженности исходящие из одной точки, то для их сложения можно применить метод противоположному углу параллелограмма будет являться суммарным вектором напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:
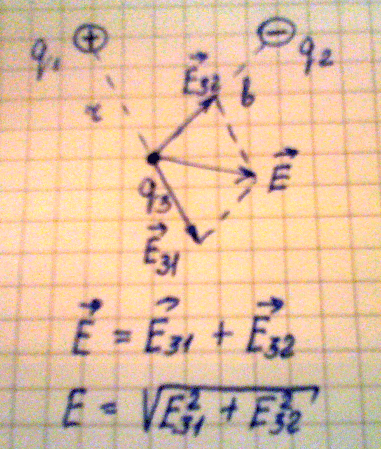
Рис.8
Исходя из данной работы, следует, что напряженность в любой точке поля можно определить, зная величины взаимодействующих зарядов, расстояние от каждого заряда до данной точки и электрическую постоянную.
4. Закрепление темы.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: электрическое поле – это ….
3. Как направлены силовые линии напряженности данного заряда?
4. Определить знаки зарядов:
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: напряженностью называется …
3. Как направлены силовые линии напряженности данного заряда?
4. Определить заряды.
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
1. Два заряда q1 = +3·10 -7 Кл и q2 = −2·10 -7 Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите напряженность поля в точке С, расположенной на линии, соединяющей заряды, на расстоянии 0,05 м вправо от заряда q2.
2. В некоторой точке поля на заряд 5·10 -9 Кл действует сила 3·10 -4 Н. Найти напряженность поля в этой точке и определите величину заряда, создающего поле, если точка удалена от него на 0,1 м.
По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля.
Характеристика электрического поля
Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле:
E → = F → q , где F → — сила, действующая со стороны поля на неподвижный (пробный) заряд q . Его значение должно быть настолько мало, чтобы отсутствовала возможность искажать поле, напряженность которого с его помощью и измеряют. По уравнению видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный пробный заряд.
У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным.
Силовые линии
Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий.
Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.
Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться.
Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:
E → = ∑ i = 1 n E → i .
Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле:
Интегрирование E → = ∫ d E → проводится по области распределения зарядов. Если их распределение идет по линии ( τ = d q d l — линейная плотность распределения заряда), то интегрирование E → = ∫ d E → тоже. Когда распределение зарядов идет по поверхности и поверхностная плоскость обозначается как σ = d q d S , тогда интегрируют по поверхности.
Интегрирование по объему выполняется, если имеется объемное распределение заряда:
ρ = d q d V , где ρ — объемная плотность распределения заряда.
Что называется напряженностью электрического поля
Напряженность поля в диэлектрике равняется векторной сумме напряженностей полей, которые создают свободные E 0 → и связанные E p → заряды:
Зачастую бывают случаи, когда диэлектрик изотропный. Тогда запись напряженности поля имеет вид:
E → = E 0 → ε , где ε обозначает относительную диэлектрическую проницаемость среды в рассматриваемой точке поля.
Отсюда следует, что по выражению E → = E 0 → ε имеется однородный изотропный диэлектрик с напряженностью электрического поля в ε меньше, чем в вакууме.
Напряженность электростатического поля системы точечных зарядов равняется:
E → = 1 4 π ε 0 ∑ i = 1 n q i ε r i 3 r i → .
В системе СГС напряженность поля точечного заряда в вакууме:
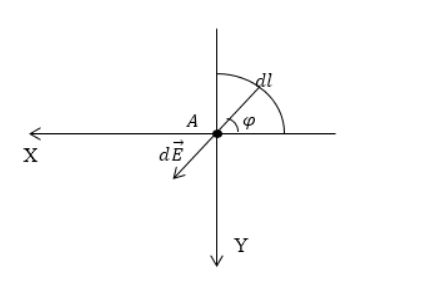
Дан равномерно распределенный заряд по четверти окружности радиуса R с линейной плотностью τ . Необходимо найти напряженность поля в точке А , являющейся центром окружности.
Решение
Произведем выделение на заряженной части окружности элементарного участка d l , который будет создавать элемент поля в точке А . Следует записать выражение для напряженности, то есть для d E → . Тогда формула примет вид:
d E → = d q R 3 R → R .
Проекция вектора d E → на ось О х составит:
d E x = d E cos φ = d q cos φ R 2 .
Произведем выражение d q через линейную плотность заряда τ :
d q = τ d l = τ · 2 πRdR .
Необходимо использовать d q = τ d l = τ · 2 πRdR для преобразования d E x = d E cos φ = d q cos φ R 2 :
d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,
где 2 π d R = d φ .
Далее перейдем к нахождению полной проекции E x при помощи интегрирования d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,
по d φ с изменением угла 0 ≤ φ ≤ 2 π .
E x = ∫ 0 2 π τ cos φ d φ R = τ R ∫ 0 2 π cos φ d φ = τ R sin φ 0 2 π = τ R .
Перейдем к проекции вектора напряженности на О у :
d E y = d E sin φ = τ R sin φ d φ .
Следует проинтегрировать с изменяющимся углом π 2 ≤ φ ≤ 0 :
E y ∫ π 2 0 τ R sin φ d φ = τ R ∫ π 2 0 sin φ d φ = — τ R cos φ π 2 0 = — τ R .
Произведем нахождение модуля вектора напряженности в точке А , применив теорему Пифагора:
E = E x 2 + E y 2 = τ R 2 + — τ R 2 = τ R 2 .
Ответ: E = τ R 2 .
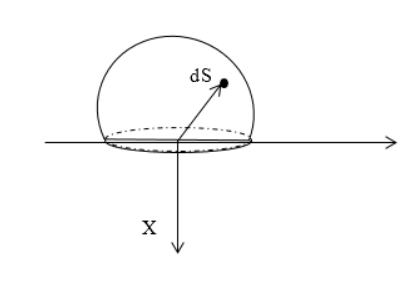
Найти напряженность электростатического поля равномерно заряженной полусферы с радиусом R . Поверхностная плотность заряда равняется σ .
Решение
Следует выделить на поверхности заряженной сферы элементарный заряд d q , располагаемый на элементе площади d S . Запись, используя сферические координаты d S , равняется:
d S = R 2 sin θ d θ d φ ,
при 0 ≤ φ ≤ 2 π , 0 ≤ θ ≤ π 2 .
Элементарная напряженность поля точечного заряда в системе С И :
d E → = d q 4 π ε 0 R 3 R → R .
Необходимо спроецировать вектор напряженности на О х :
d E x = d q cos θ 4 π ε 0 R 2 .
Произведем выражение заряда через поверхностную плотность заряда:
Подставим d q = σ d S в d E x = d q cos θ 4 π ε 0 R 2 , используя d S = R 2 sin θ d θ d φ , проинтегрируем и запишем:
E x = σ R 2 4 π ε 0 R 2 ∫ 0 2 π d φ ∫ 0 π 2 cos θ sin θ d θ = σ 4 π ε 0 2 π · 1 2 = σ 4 ε 0 .
Отсюда следует, что E = E x .
Ответ: напряженность полусферы в центре равняется E = σ 4 ε 0 .
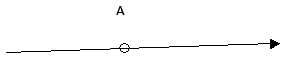
Указать направление вектора напряженности электрического поля, созданного в точке
Условие задачи:
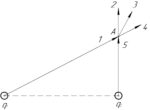
Задача №6.2.53 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
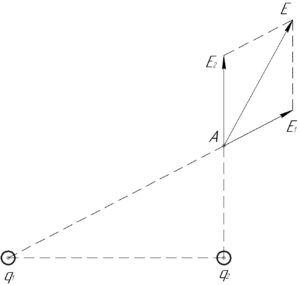
Направление этих полей показано на схеме к решению. По правилу параллелограмма сумма векторов (overrightarrow {{E_1}}) и (overrightarrow {{E_2}}) будет направлена как в случае 3, показанном на схеме к условию.
Ответ: 3.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.2.52 Три равных по величине и знаку заряда q расположены в вакууме вдоль одной прямой
6.2.54 Точечный положительный заряд создаёт на расстоянии 10 см электрическое поле
6.2.55 На каком расстоянии от поверхности шара напряженность электрического поля
Пожалуйста, поставьте оценку
( 2 оценки, среднее 5 из 5 )
Любые заряженные тела создают вокруг себя электростатическое поле. Рассмотрим особенности электростатического поля, создаваемого точечным зарядом и заряженной сферой.
Электростатическое поле точечного заряда
Направление силовых линий электростатического поля точечного заряда
Модуль напряженности не зависит от значения пробного заряда q0:
E=FKq0=kQq0r2q0=kQr2
Модуль напряженности точечного заряда в вакууме:
E=kQr2
Модуль напряженности точечного заряда в среде:
E=kQεr2
Сила Кулона:
−FKулона=q−E
Потенциал не зависит от значения пробного заряда q0:
φ=Wpqo=±kQq0rq0=±kQr
Потенциал точечного заряда в вакууме:
φ=±kQr
Потенциал точечного заряда в среде:
φ=±kQεr
Внимание! Знак потенциала зависит только от знака заряда, создающего поле.
Эквипотенциальные поверхности для данного случая — концентрические сферы, центр которых совпадает с положением заряда.
Работа электрического поля по перемещению точечного заряда:
A12=±q(φ1−φ2)
Пример №1. Во сколько раз увеличится модуль напряженности электрического поля, созданного точечным зарядом Q в некоторой точке, при увеличении значения этого заряда в 5 раз?
Модуль напряженности электрического поля, созданного точечным зарядом, определяется формулой:
E=kQεr2
Формула показывает, что модуль напряженности и электрический заряд — прямо пропорциональные величины. Следовательно, если заряд, который создает поле, увеличится в 5 раз, то модуль напряженности создаваемого поля тоже увеличится в 5 раз.
Электростатическое поле заряженной сферы
Направление силовых линий электростатического поля заряженной сферы:
Модуль напряженности электростатического поля заряженной сферы:
| Внутри проводника (расстояние меньше радиуса сферы, или r < R) |
E=0 |
| На поверхности проводника (расстояние равно радиусу сферы, или r = R) |
E=kQR2 |
| Вне проводника (расстояние больше радиуса сферы, или r > R) |
E=kQr2=kQ(R+a)2 a — расстояние от поверхности сферы до изучаемой точки. r — расстояние от центра сферы до изучаемой точки. |
Сила Кулона:
−FK=q−E
Потенциал:
| Внутри проводника и на его поверхности (r < R или r = R) |
φ=±kQR |
| Вне проводника (r > R) |
φ=±kQr=±φ=±kQR+a |
Пример №2. Определить потенциал электростатического поля, создаваемого заряженной сферой радиусом 0,1 м, в точке, находящейся на расстоянии 0,2 м от этой сферы. Сфера заряжена положительна и имеет заряд, равный 6 нКл.
6 нКл = 6∙10–9 Кл
Так как сфера заряжена положительно, то потенциал тоже положителен:
Задание EF18107
Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F. Чему станет равен модуль этих сил, если один заряд увеличить в n раз, другой заряд уменьшить в n раз, а расстояние между ними оставить прежним?
Ответ:
а) F
б) nF
в) Fn
г) n2F
Алгоритм решения
1.Записать исходные данные.
3.Применить закон Кулона к обоим зарядам для 1 и 2 случая.
4.Установить, как меняется сила, с которой заряды действуют друг на друга.
Решение
Запишем исходные данные:
• Первая пара зарядов: q1 и q2.
• Вторая пара зарядов: q1’ = nq1 и q2’=q2/n.
• Расстояние между зарядами: r1 = r2 = r.
Закон Кулона:
FK=k|q1||q2|r2
Применим закон Кулона к парам зарядов. Закон Кулона для первой пары:
FK1=k|q1||q2|r2
Закон Кулона для второй пары:
FK2=k|nq1|∣∣q2n∣∣r2=k|q1||q2|r2
Коэффициент n сократился. Следовательно, силы, с которыми заряды взаимодействуют друг с другом, не изменятся:
FK1=FK2
После изменения зарядов модуль силы взаимодействия между ними останется равным F.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18591
Ответ:
а) ↘
б) →
в) ↖
г) ↓
Алгоритм решения
1.Сделать чертеж. Обозначить все силы, действующие на центральный точечный заряд со стороны остальных точечных зарядов.
2.Найти равнодействующую сил геометрическим способом.
Решение
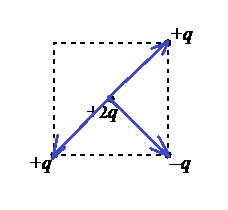
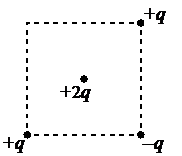
Сделаем чертеж. В центр помещен положительный заряд. Он будет отталкиваться от положительных зарядов и притягиваться к отрицательным:
Модули всех векторов сил, приложенных к центральному точечному заряду равны, так как модули точечных зарядов, расположенных в вершинах квадрата равны, и находятся они на одинаковом расстоянии от этого заряда.
Складывая векторы геометрически, мы увидим, что силы, с которыми заряд +2q отталкивается от точечных зарядов +q, компенсируют друг друга. Поэтому на заряд действует равнодействующая сила, равная силе, с которой он притягивается к отрицательному точечному заряду –q. Эта сила направлена в ту же сторону (к нижней правой вершине квадрата).
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22574
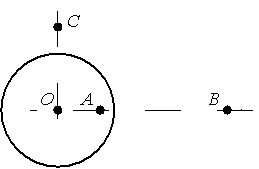
Установите соответствие между физическими величинами и их значениями.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать формулы для нахождения напряженности электростатического поля внутри и снаружи заряженной сферы.
2.Определить величину напряженности поля в указанных точках.
3.Установить соответствие между величинами и их значениями.
Решение
Внутри заряженной сферы напряженность электростатического поля равна 0. Поэтому напряженность в точке А равна 0.
EA=0
Снаружи заряженной сферы напряженность электростатического поля равна:
E=kQr2=kQ(R+a)2
Найдем напряженность электростатического поля в точке В, которая находится на расстоянии 3R от центра заряженной сферы:
EB=kQr2=kQ(3R)2=kQ9R2
Чтобы выразить EB через Eс, найдем напряженность электростатического поля в точке С, которая находится на расстоянии 3R/2 от центра заряженной сферы:
EС=kQr2=kQ(32R)2=4kQ9R2
Найдем отношение EB к Eс:
EBEС=kQ9R2÷4kQ9R2=kQ9R2·9R24kQ=14
Следовательно:
EB=EС4
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 7.4k
-
Основные
свойства и характеристики
электрического
поля
Электрическое
поле (статическое)
— поле
неподвижных,
электрически
заряженных тел,
заряды
которых не изменяются
во времени.
Электрическое
поле обнаруживается
как силовое
взаимодействие заряженных тел.
При
этом различают положительные
и отрицательные заряды.
(виды
зарядов)
Заряды
одного знака отталкиваются друг от
друга, разного знака притягиваются.
(взаимодействие
зарядов)
В
основе описания свойств электрического
поля лежит закон Кулона, установленный
опытным путем.
Закон
Кулона.
Между
покоящимися точечными зарядами действует
сила, пропорциональная произведению
зарядов, обратно пропорциональная
квадрату расстояния между ними и
направленная по прямой от одного заряда
к другому (рис.
1.1):

(1.1)
где
F,
—
сила, действующая на заряд q
r2
— квадрат
расстояния
между зарядами q1
и
q2
F2
—
сила, действующая на заряд q2
r021
—
единичный вектор, направленный от
второго заряда к первому;
е0
= 8,854 • 10-12
Ф/м — электрическая
постоянная.
Точечными
зарядами
можно
считать заряженные тела, размеры которых
малы по сравнению с расстоянием между
ними.
Основные
единицы
измерения:
силы
в международной системе
единиц (СИ)
—
ньютон
(Н);
заряда
— кулон
(Кл):
1
Кл = 1 А • с;
длины
— метр
(м).
Основными
величинами, характеризующими электрическое
поле,
являются
напряженность,
электрический
потенциал
и
разность
потенциалов, или напряжение
Напряженностью
электрического
поля
называется
мера интенсивности его сил, равная
отношению силы F,
действующей
на пробный положительный
точечный заряд q,
вносимый
в рассматриваемую точку поля, к значению
заряда

Так
же как и сила F, напряженность электрического
поля ε
—
векторная величина, т.е. характеризуется
значением и направлением действия.
Основная
единица
измерения напряженности электрического
поля в СИ
— вольт
на метр (В/м).
Из
формулы (1.1) следует, что напряженность
электрического поля точечного заряда
q
на
расстоянии r
от
него равна
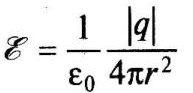
и
направлена от точки расположения заряда
к точке, где определяется напряженность,
если заряд положительный (рис. 1.2, а),

1.2, а
и
в противоположную сторону, если заряд
отрицательный (рис. 1.2, б).
1.2
б
Если
зарядов, создающих электрическое поле,
несколько, то напряженность в
любой точке поля
равна
геометрической
сумме
напряженностей
от каждого из них в отдельности.
(напряженность
электростатического поля нескольких
зарядов)
Пример
1.1.
Определить
значение и направление действия
напряженности электрического поля в
точке А,
расположенной
на расстояниях
r1
=
1м и r2
=
2м
от точечных зарядов
q1=
1,11
• 10-10
Кл и q2
=
-4,44-
10-10
Кл
(рис. 1.3).
Решение.
По
формуле (1.3) определяем напряженности
электрического поля в точке А
от
действия “точечных зарядов q1=
и q2
Направления
векторов напряженности
совпадают
с
направлениями действия сил на пробный
положительный точечный заряд, если его
расположить в точке А.
Напряжённость
результирующего электрического поля
в точке А
направлена
вдоль гипотенузы прямоугольного
треугольника, катетами которого являются
векторы напряженностей
и имеет значение
Можно
говорить о поле
вектора
и
изображать это поле линиями
вектора — силовыми
линиями.
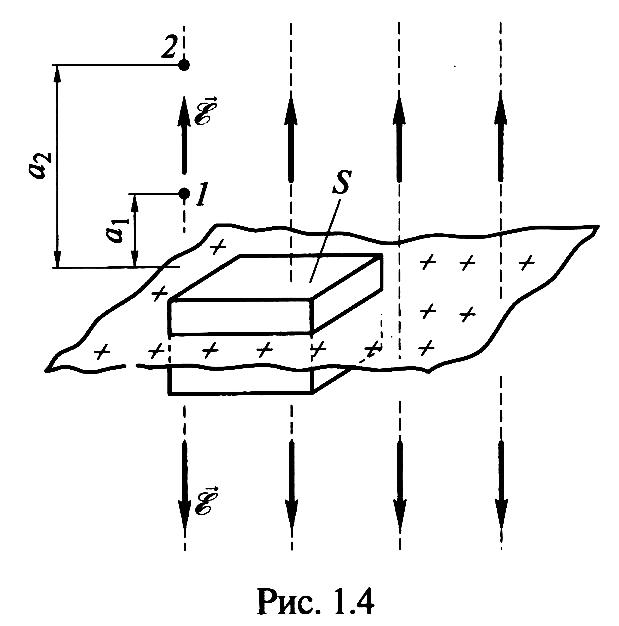
Если
напряженность электрического поля во
всех точках одинакова, то поле
однородное,
например
поле равномерно заряженной плоской
пластины бесконечных размеров (рис.
1.4),
а
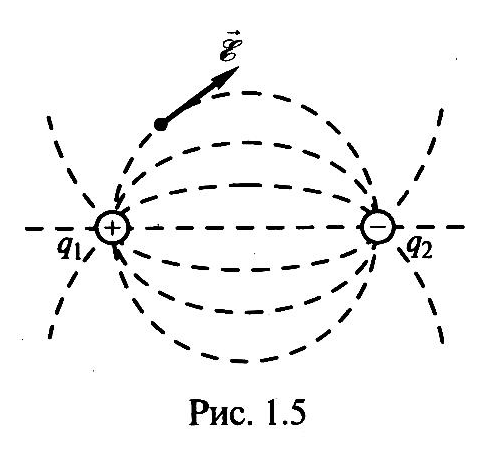
если различна, то поле
неоднородно,
например поле двух точечных зарядов
(рис. 1.5).
При
перемещении вдоль произвольного участка
длиной
заряда q
в
электрическом поле под
действием сил поля F
совершается
работа
При
этом работа
по переносу заряда вдоль произвольного
замкнутого
контура
равна
нулю.
Действительно,
так как все свойства поля определяются
относительным расположением зарядов,
то перенос заряда по замкнутому контуру
и возвращению в исходную точку означает
первоначальные распределение зарядов
и запас энергии. Это означает также, что
с учетом (1.4) циркуляция вектора
напряженности равна нулю
Условие
(1.5) позволяет характеризовать электрическое
поле в каждой точке функцией ее координат
— электрическим
потенциалом.
Электрический
потенциал в
данной
точке
электрического поля
с учетом (1.4) численно
равен работе, которую могут совершить
силы электрического поля при переносе
единичного положительного заряда из
данной точки в точку, потенциал которой
принят равным нулю.
Разность
потенциалов двух
точек 1 и 2,
или напряжение
между
точками 1 и 2, электрического поля
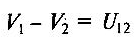
численно
равна работе, которую могут совершить
силы электрического поля при переносе
единичного положительного заряда из
точки 1
в точку 2.
Единица
измерения электрического потенциала
в СИ
— вольт
(В).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #