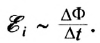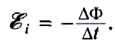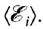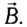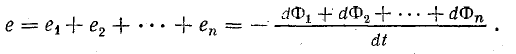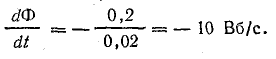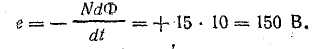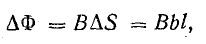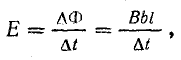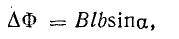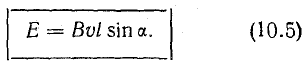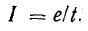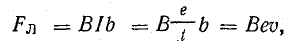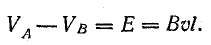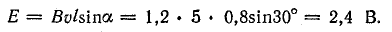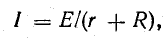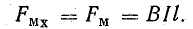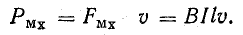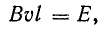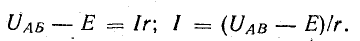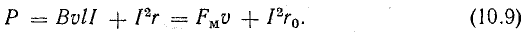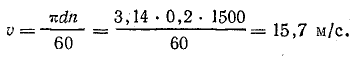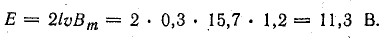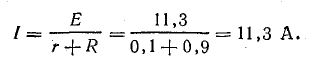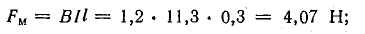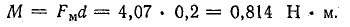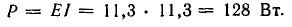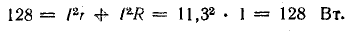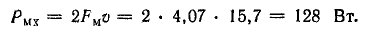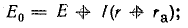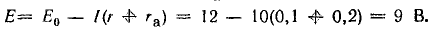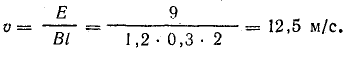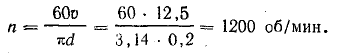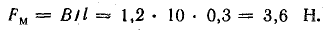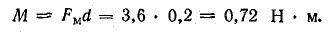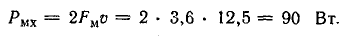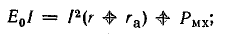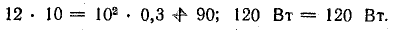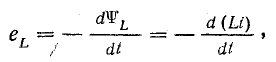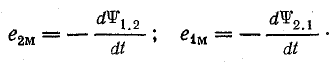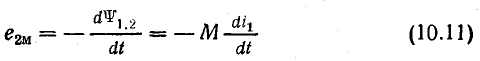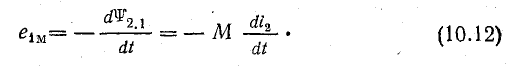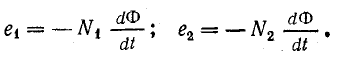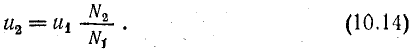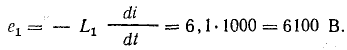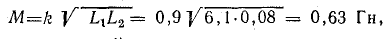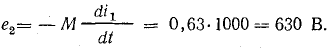Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.
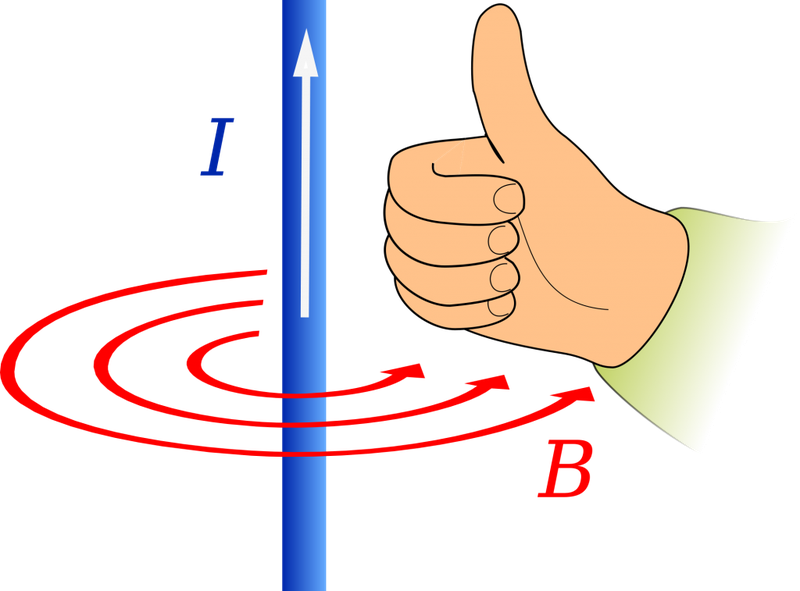
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
Сила Ампера
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
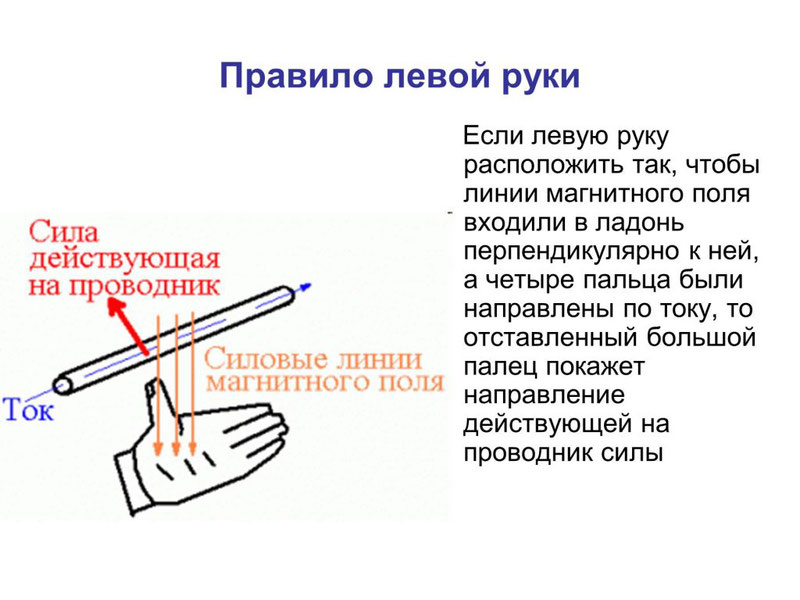
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
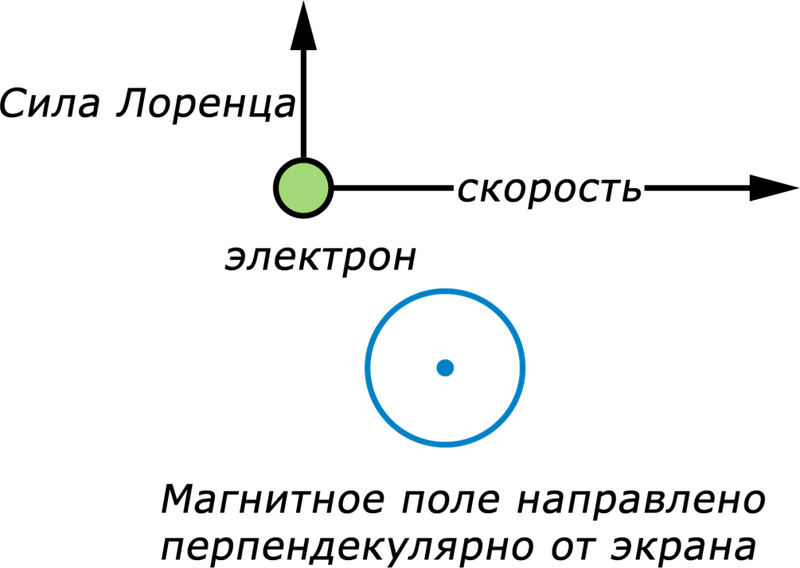
Сила Лоренца
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
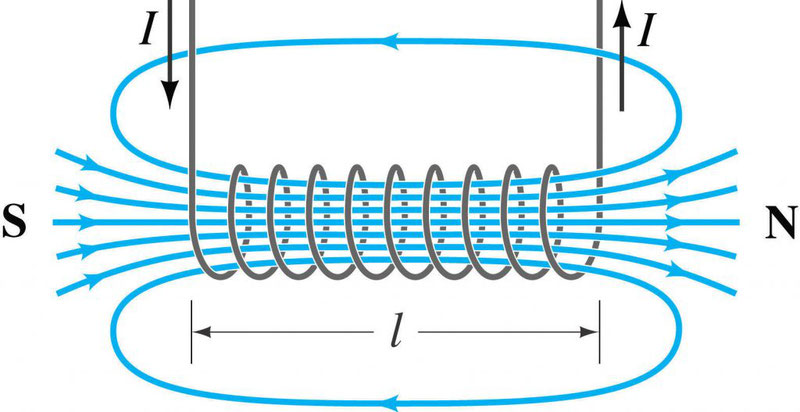
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Магнитный поток и ЭДС
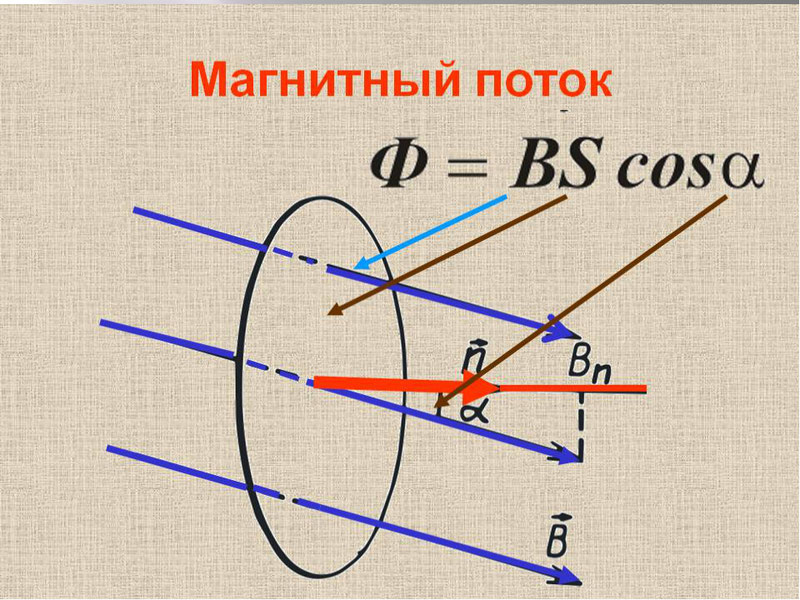
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
Формула для ЭДС самоиндукции:
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
Объемная плотность энергии поля:
Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.
Электромагнитная индукция
Содержание
- Явление электромагнитной индукции
- Магнитный поток
- Закон электромагнитной индукции Фарадея
- Правило Ленца
- Самоиндукция
- Индуктивность
- Энергия магнитного поля
- Основные формулы раздела «Электромагнитная индукция»
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ):
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec{B} ) ЭДС электромагнитной индукции равна:
где ( alpha ) – угол между векторами ( vec{B} ) и ( vec{v} ).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_{is} ), возникающая в катушке с индуктивностью ( L ), по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec{B} ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ), создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3.2 (63.33%) 96 votes
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Электромагни́тная инду́кция — явление возникновения электрического тока, электрического поля или электрической поляризации при изменении магнитного поля во времени или при движении материальной среды в магнитном поле[1]. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года[2]. Он обнаружил, что электродвижущая сила (ЭДС), возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Закон Фарадея[править | править код]
Согласно закону электромагнитной индукции Фарадея (в СИ):
где
— электродвижущая сила, действующая вдоль произвольно выбранного контура,
— магнитный поток через поверхность, ограниченную этим контуром.
Знак «минус» в формуле отражает правило Ленца , названное так по имени физика Э. Х. Ленца:
- Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
где
— электродвижущая сила,
— число витков,
— магнитный поток через один виток,
— потокосцепление катушки.
Векторная форма[править | править код]
Закон Фарадея можно записать либо в дифференциальной форме:
(в системе СИ)
или
(в системе СГС),
либо в эквивалентной интегральной форме:
(СИ)
или
(СГС).
Здесь 




Закон Фарадея в такой форме описывает лишь ту часть ЭДС, которая возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учёте последнего см. ниже).
- В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)[3].
Если же, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство 

- Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год[4] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п. к формуле
в случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)[5]. В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.
- Однако возможность (пусть с некоторыми оговорками, уточняющими область применимости) совпадающей формулировки «правила потока» с законом электромагнитной индукции нельзя назвать чисто случайной. Дело в том, что, по крайней мере для определённых ситуаций, это совпадение оказывается очевидным проявлением принципа относительности. А именно, например, для случая относительного движения катушки с присоединённым к ней вольтметром, измеряющим ЭДС, и источника магнитного поля (постоянного магнита или другой катушки с током), в системе отсчёта, связанной с первой катушкой, ЭДС оказывается равной именно циркуляции электрического поля, тогда как в системе отсчёта, связанной с источником магнитного поля (магнитом), происхождение ЭДС связано с действием силы Лоренца на движущиеся с первой катушкой носители заряда. Однако та и другая ЭДС обязаны совпадать, поскольку вольтметр показывает одну и ту же величину, независимо от того, для какой системы отсчёта мы её рассчитали.
Потенциальная форма[править | править код]
При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:
(в случае отсутствия безвихревого поля, то есть тогда, когда электрическое поле порождается полностью только изменением магнитного, то есть электромагнитной индукцией).
В общем случае, при учёте и безвихревого (например, электростатического) поля имеем:
Подробнее
Поскольку вектор магнитной индукции по определению выражается через векторный потенциал так:
то можно подставить это выражение в
получая
и, поменяв местами дифференцирование по времени и пространственным координатам (ротор):
Отсюда, поскольку 

То есть в случае отсутствия безвихревой части можно записать
а в общем случае
История[править | править код]
В 1820 году Ханс Кристиан Эрстед показал, что протекающий по цепи электрический ток вызывает отклонение магнитной стрелки. Если электрический ток порождает магнетизм, то с магнетизмом должно быть связано появление электрического тока. Эта мысль захватила английского ученого М. Фарадея. «Превратить магнетизм в электричество», — записал он в 1822 году в своём дневнике. Многие годы он настойчиво ставил различные опыты, но безуспешно, и только 29 августа 1831 года наступил триумф: он открыл явление электромагнитной индукции. Установка, на которой Фарадей сделал своё открытие, состояла из кольца из мягкого железа примерно 2 см шириной и 15 см диаметром. На каждой половине кольца было намотано много витков медной проволоки. Цепь одной обмотки замыкала проволока, в её витках находилась магнитная стрелка, удаленная настолько, чтобы не сказывалось действие магнетизма, созданного в кольце. Через вторую обмотку пропускался ток от батареи гальванических элементов. При включении тока магнитная стрелка совершала несколько колебаний и успокаивалась; когда ток прерывали, стрелка снова колебалась. Выяснилось, что стрелка отклонялась в одну сторону при включении тока и в другую, когда ток прерывался. М. Фарадей установил, что «превращать магнетизм в электричество» можно и с помощью обыкновенного магнита.
В это же время американский физик Джозеф Генри также успешно проводил опыты по индукции токов, но пока он собирался опубликовать результаты своих опытов, в печати появилось сообщение М. Фарадея об открытии им электромагнитной индукции.
М. Фарадей стремился использовать открытое им явление, чтобы получить новый источник электричества.
См. также[править | править код]
- Взаимоиндукция
- Самоиндукция
- Индуктивность
- Закон электромагнитной индукции Фарадея
Примечания[править | править код]
- ↑ Миллер М. А., Пермитин Г. В. Электромагнитная индукция // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 537—538. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
- ↑ Faraday, Michael; Day, P. The philosopher’s tree: a selection of Michael Faraday’s writings (англ.). — CRC Press, 1999. — P. 71. — ISBN 978-0-7503-0570-9.
- ↑
Это уравнение Максвелла может быть переписано в эквивалентном виде(здесь просто производная по t внесена под знак интеграла). В таком виде уравнение также может быть включено в систему уравнений Максвелла, причем оговорка о неподвижности контура интегрирования теряет актуальность, так как производная теперь не действует на границу области (на пределы интегрирования), а само интегрирование в любом случае полагается «мгновенным». В принципе, в таком виде это уравнение также могут называть законом Фарадея (чтобы отличить его от других уравнений Максвелла), пусть в таком виде оно и не совпадает прямо с его обычной формулировкой (но эквивалентно ей в своей области применимости).
- ↑ М. Лившиц. Закон электромагнитной индукции или «правило потока»? // Квант. — 1998. — № 3. — С. 37—38.
- ↑ Такой отказ объясняется тем, что, в отличие от закона для циркуляции электрического поля, выполняющегося всегда, «правило» корректно работает лишь для случаев, когда контур, в котором вычисляется ЭДС, совпадает физически с проводником (то есть совпадает их движение; в противном же случае правило может не работать (самый известный пример — униполярная машина Фарадея; контур, который в этом случае трудно определить, но кажется довольно очевидным, что он не меняется; во всяком случае, довольно затруднительно указать разумное определение для контура, который бы в этом случае менялся), то есть проявляется парадокс, что для «закона природы» недопустимо.
Ссылки[править | править код]
- Про электромагнитную индукцию в «Школе для электрика»
- Электромагнитная индукция (учебный видеофильм)
В этой статье мы рассмотрим, что такое правило Ленца и какого его практическое применение. Это правило позволяет быстро определить направление индукционного тока. На самом деле, правило Ленца тесно связано с принципом сохранения энергии — об этом также читайте в этой статье.
Формулировка
Правило Ленца обычно формулируется следующим образом:
Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.
Википедия
Давайте расшифруем это предложение.
Давайте расшифруем это предложение. Давайте начнем с причины. Причиной протекания индукционного тока является изменяющийся поток магнитной индукции B через поверхность, охватываемую контуром, в котором должен протекать электрический ток.
Противодействие причине здесь заключается в том, что когда поток увеличивается, магнитное поле Bind, создаваемое индукционным током, направлено так, чтобы уменьшить поток. И наоборот, когда поток уменьшается, индуцированное магнитное поле направлено так, чтобы усилить поток. В общем, если поле B перпендикулярно плоской поверхности, охватывающей замкнутый проводник, то
Когда ФB уменьшается, то Вind параллельно В.
Когда ФB увеличивается, то Bind антипараллельно B.
В более общем случае необходимо задать условие для углов между этими векторами.
Как только мы установили, как направлен вектор магнитной индукции Bind (внутри контура), мы должны связать индукционный ток с этим вектором и определить его направление.
Пример правила Ленца в действии
Теперь мы покажем правило Ленца в действии; вот конкретный пример.
В магнитном поле, создаваемом прямолинейным проводником с током, имеется круговой контур (кольцо), лежащий в одной плоскости с проводником (рис. 2а.). Ток в прямолинейном проводнике течет вверх. В каком направлении будет течь электрический ток в кольце, если мы прижмем его к проводнику?
Ток в прямолинейном проводнике создает вокруг себя магнитное поле. Для определения направления вектора магнитной индукции в кольце мы используем хорошо известный метод правой руки. Мы располагаем большой палец так, как направлен электрический ток, а пальцы покажут нам магнитное поле, «оборачивающееся» вокруг этого электрического тока. Справа от проводника, где находится кольцо, линии поля идут «внутрь», как показано на рис. 2б.
Сближение кольца вызывает увеличение потока магнитного поля, проникающего через кольцо (увеличивается значение магнитной индукции B). Согласно правилу Ленца, ток в кольце должен протекать таким образом, чтобы вектор магнитного поля Bind, создаваемого этим током, был направлен противоположно вектору, вызывающему явление индукции B. То есть, вектор Bind направлен «в нашу сторону». (рис. 2в).
Снова применим правило правой руки. На этот раз мы укажем большим пальцем вектор индукции Bind, а остальные пальцы покажут нам направление индукционного тока. Он будет протекать против часовой стрелки.
Правило Ленца и закон сохранения энергии
То, что «скрывается» под правилом Ленца — это фундаментальный принцип сохранения энергии в физике. Вы узнаете об этом, прочитав данный подраздел.
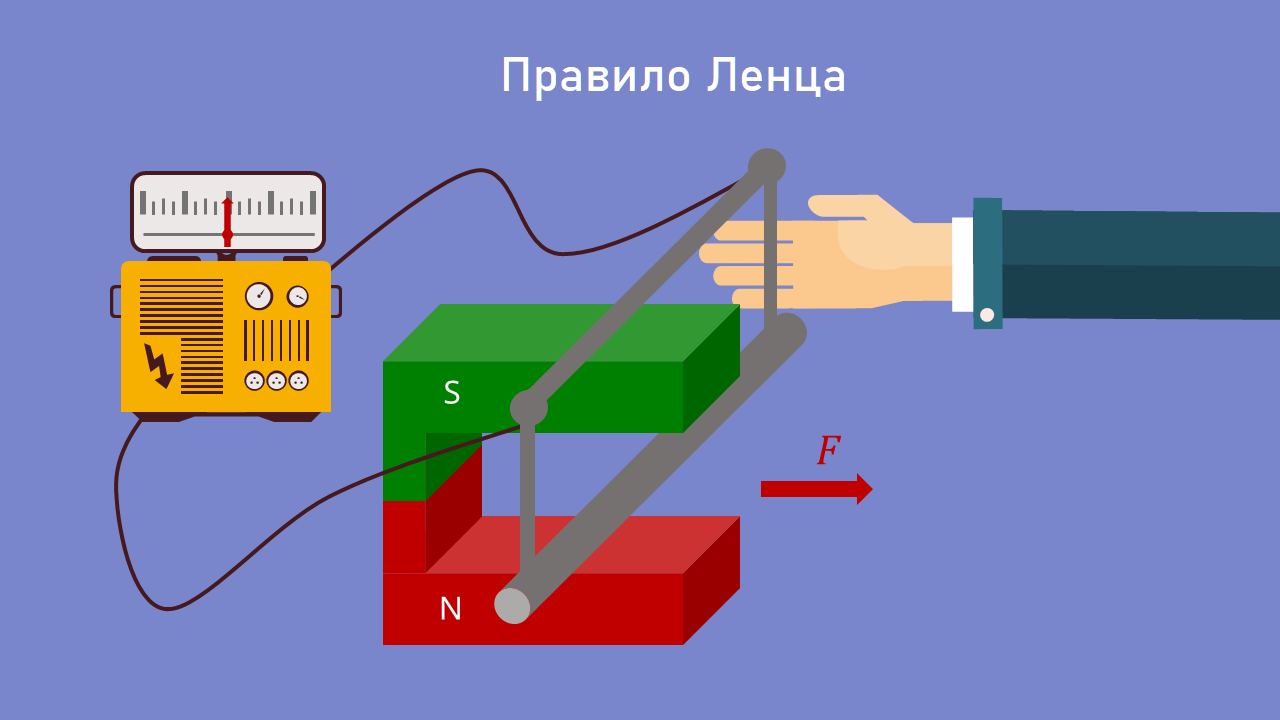
Посмотрите на следующую экспериментальную установку (см. рисунок 3).
Для эксперимента подвесьте качели проводника в магнитном поле подковообразного магнита. Подковообразный магнит располагается так, чтобы северный полюс находился внизу, а южный — вверху. Вы подключаете проводник к амперметру вне магнитного поля, поэтому во всей цепи нет источника.
В эксперименте мы теперь перемещаем качели проводника в направлении, перпендикулярном силовым линиям магнитного поля, в нашем случае «из подковообразного магнита». Для перемещения качающегося проводника нужна сила F. Когда частицы движутся в магнитном поле, действует сила Лоренца, происходит разделение зарядов, а значит, и возникает индукционный ток. Это можно наблюдать по отклонению стрелки амперметра.
Для определения направления индукционного тока применяется правило левой руки. Большой палец указывает направление, в котором электроны перемещаются под действием силы F, т.е. «из подковы». Ваш указательный палец указывает направление магнитного поля, от северного к южному полюсу. Наконец, средний палец указывает направление, в котором электроны притягиваются силой Лоренца. На конце проводника, в сторону которого указывает ваш средний палец, образуется избыток электронов и это приводит к изменению направления тока.
Однако, в силу правила Ленца, точно в тот же момент должна действовать противодействующая сила F‘, направленная в противоположную сторону от причины F. Эта противодействующая сила создается индукционным током, который, так сказать, пытается восстановить исходное состояние.
Вы можете еще раз проверить направление силы F‘ с помощью правила левой руки. На этот раз большой палец указывает направление движения электронов. Итак, в проводнике, который перемещается под действием силы F внутри магнита , большой палец направлен в плоскость рисунка, а указательный палец снова направлен от северного полюса к южному. Затем средний палец указывает направление силы F’. Это направление согласуется с правилом Ленца и действует в направлении, противоположном направлению движения проводника. Чтобы проиллюстрировать это, мы провели эти рассуждения одно за другим. В реальном эксперименте, однако, все это происходит параллельно.
Можно также сравнить правило Ленца с поведением детей (аналог индукционного тока). Когда их родители (аналог причины) говорят им что-то, они сначала хотят сделать прямо противоположное. Если вы будете помнить об этой мнемонике, вы гарантированно не забудете правило Ленца.
Сохранение энергии для индукции также может быть соблюдено только с помощью правила Ленца.
Чтобы проверить это, вы можете провести следующий мысленный эксперимент. Если бы сила из F‘ была направлена в противоположную сторону, то есть равна силе F, раскачивание качелей ускорялось бы все больше и больше. И это без добавления дополнительной энергии извне. Таким образом, можно было бы создать вечный двигатель, что противоречит закону сохранения энергии.
Применение
Правило Ленца необходимо для многих применений в технике. Например, в вихретоковом тормозе. Этот тормоз не изнашивается, поскольку отсутствует трение. Тормозная сила генерируется магнитными полями. Например, такие тормоза есть у поездов и грузовиков. Электродвигатели также работают по этому принципу.
Правило Ленца защитит вас, даже если в вашу машину ударит молния. Клетка Фарадея также основана на этом принципе.
Все металлодетекторы, которые вы знаете по аэропортам или магазинам, работают одинаково. Они генерируют магнитное поле с помощью катушки. Если в магнитном поле находится металлический предмет, в нем индуцируются вихревые токи. Согласно правилу Ленца, эти токи направлены таким образом, что противодействуют причине возникновения тока. Поэтому магнитное поле детектора становится слабее. Это также уменьшает ток в металлодетекторе, эта разница измеряется, что приводит, например, к сигналу тревоги.
Металлодетекторы также используются в некоторых светофорах, только здесь катушка расположена в асфальте под машинами. Таким образом, светофор, так сказать, замечает, что автомобиль ждет, и по возможности переключает его на зеленый. Как видите, правило Ленца важно для многих областей электротехники, а также в повседневной жизни.
Список использованной литературы
- Мякишев Г. Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений. – М.: Просвещение, 2010.
- Касьянов В. А. Физика. 11 кл.: Учеб. для общеобразоват. учреждений. – М.: Дрофа, 2005.
- Сивухин Д. В. § 64. Электромагнитная индукция // Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 265. — 688 с.
Закон электромагнитной индукции:
Вам уже известно, что электрический ток, или движущиеся заряды, создают в окружающем пространстве магнитное поле. А возможен ли обратный процесс, при котором с помощью магнитного поля в замкнутом проводнике будет создан электрический ток?
Именно такой вопрос заинтересовал выдающегося английского физика Майкла Фарадея, который в 1821 г. в своем дневнике поставил перед собой задачу: «Превратить магнетизм в электричество». Через 10 лет упорного труда эта задача была им успешно решена. В августе 1831 г. Фарадей сделал фундаментальное открытие в области электромагнитных явлений.
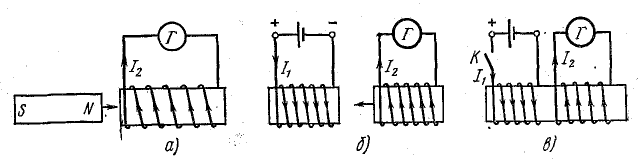
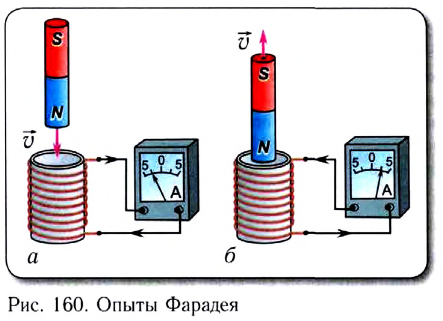
При проведении опытов Фарадей обнаружил, что при введении постоянного магнита в катушку (рис. 160, а) или при выведении из нее (рис. 160, б) стрелка гальванометра в цепи катушки отклонялась, т. е. в цепи возникал кратковременный электрический ток. Изменение направления движения магнита приводило к отклонению стрелки гальванометра в противоположную сторону (см. рис. 160).
Таким образом, при изменении индукции магнитного поля, пронизывающей витки катушки, в замкнутой цепи возникает электрический ток, называемый индукционным. Следовательно, в цепи появился источник тока. Можно сделать вывод о том, что изменение индукции магнитного поля в пределах площади, ограниченной контуром, приводит к появлению в контуре ЭДС, называемой электродвижущей силой индукции.
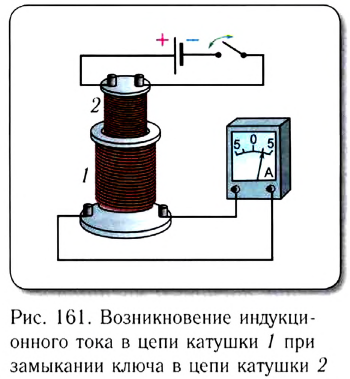
Фарадей наблюдал возникновение индукционного тока в цепи исследуемой катушки 1 не только при перемещении постоянного магнита, но и в том случае, если замыкали (размыкали) ключ в цепи, содержащей катушку 2, расположенную внутри катушки 1 (рис. 161 ).
Индукционный ток возникал в катушке 1 также при перемещении контура с током 2 в непосредственной близости от исследуемой катушки.
Таким образом, в результате серии экспериментов Фарадей установил, что возникновение индукционного тока в замкнутом контуре достигается при изменении магнитного потока через него.
Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.
Эксперименты Фарадея позволили установить закон электромагнитной индукции (закон Фарадея), количественно определяющий ЭДС индукции в контуре:
- ЭДС электромагнитной индукции
возникающая в замкнутом контуре, прямо пропорциональна скорости изменения магнитного потока через него:
Как видно из приведенного соотношения, ЭДС индукции не зависит от материала проводника, его сопротивления, температуры и от носителей тока, а определяется только характером изменения магнитного поля.
Для объяснения возникновения ЭДС в неподвижном замкнутом контуре при изменении магнитного поля внутри него английский ученый Джеймс Клерк Максвелл предложил такую гипотезу: изменяющееся магнитное поле создает в окружающем пространстве электрическое поле, которое и приводит свободные заряды проводника в движение, т. е. создает индукционный ток. На основе этой гипотезы Максвелл создал теорию электромагнитного поля, подтвердившуюся на опыте. Согласно этой теории при изменении магнитного поля в некоторой области пространства обязательно возникает электрическое поле с замкнутыми силовыми линиями. Причем это происходит даже при отсутствии проводящего контура, например в вакууме.
Таким образом, явление электромагнитной индукции в более широком понимании заключается нс только в возникновении индукционного тока, или ЭДС индукции 
Русский физик Эмилий Ленц в 1833 г. сформулировал правило (правило Ленца), позволяющее установить направление индукционного тока в цепи:
возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.
Согласно этому правилу в формуле, выражающей закон Фарадея, следует ставить знак «минус».
Максвелл в 1873 г. дал современную формулировку закона электромагнитной индукции:
- ЭДС индукции в замкнутом проводящем контуре равна скорости изменения пронизывающего его магнитного потока, взятой с противоположным знаком:
Знак «минус» в законе электромагнитной индукции (в формуле для 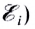
Отметим, что в таком виде закон применим только, когда скорость изменения магнитного потока постоянна. В общем случае эта формула дает среднее значение ЭДС индукции
Покажем, что если бы правило Ленца не выполнялось, то взаимодействие индукционного тока с внешними полями приводило бы к неограниченному росту энергии системы без подвода ее извне, т. е. к нарушению закона сохранения энергии.
Действительно, ток, возникающий за счет ЭДС индукции, сам является источником магнитного поля. Если бы индуцированное магнитное поле «помогало» расти магнитному потоку через контур, то тем самым увеличивался бы индукционный ток, что вызывало бы еще большее увеличение первоначального магнитного поля. Это сопровождалось бы еще большим изменением магнитного потока через контур, и так до бесконечности.
В результате сила индукционного тока и связанная с ним энергия возрастали бы неограниченно, что является нарушением закона сохранения энергии.
Для наглядной демонстрации правила Ленца используется прибор, состоящий из двух колец (замкнутого и незамкнутого), уравновешенных для уменьшения трения на игольчатой опоре (рис. 162).
При введении постоянного магнита в замкнутое кольцо оно «уходит» от него, а при выведении — «догоняет» магнит. Разрезанное кольцо никак не «реагирует» на движения магнита, поскольку в нем не может возникнуть индукционный ток.
Рассмотрим более подробно движение постоянного магнита вблизи проводящего кольца.
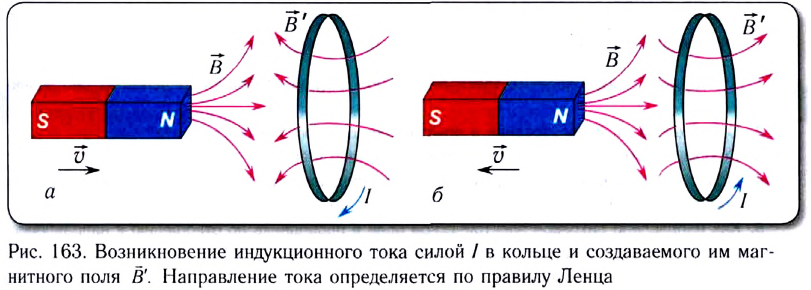
При движении магнита вправо магнитный поток через кольцо увеличивается (рис. 163, а). В соответствии с правилом Ленца индукционный ток силой I создает магнитное поле 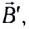
Движение магнита влево приводит к уменьшению магнитного потока через кольцо. Возникающий индукционный ток силой I создает поле 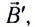
щее изменению начального магнитного потока, т. е. стремится сохранить начальную величину магнитного потока (рис. 163, б).
Таким образом, замкнутый контур как бы «сопротивляется» изменению пронизывающего его магнитного потока. Следовательно, возникновение индукционного тока можно рассматривать как проявление инерции системы.
В то же время возникновение индукционного тока в замкнутом контуре при изменении магнитного потока через него означает, что заряженные частицы пришли в движение под действием каких-то сил. Это не могут быть силы Лоренца, поскольку они действуют только на движущиеся заряды. Какие же силы заставляют двигаться электроны в покоящемся проводнике при изменении индукции магнитного поля?
Эти силы имеют электрическую природу, но по своим свойствам отличаются от электростатических сил (сил Кулона). При электромагнитной индукции возникает вихревое электрическое поле, действующее на заряженные частицы.
В отличие от потенциального электростатического поля, создаваемого неподвижными электрическими зарядами, вихревое электрическое поле, возникающее вследствие изменения магнитного поля, непотенциально. Это означает, что работа сил этого поля по замкнутой траектории не равна нулю, и они являются сторонними силами в замкнутом контуре при возникновении индукционного тока. Следовательно, работа сил вихревого электрического поля по перемещению единичного заряда по замкнутому контуру определяет ЭДС электромагнитной индукции.
Подчеркнем, что вихревое электрическое поле, возникающее при изменении магнитного поля, существует независимо от того, имеется или нет в этом месте замкнутый проводящий контур. Проводящий контур является лишь своеобразным индикатором, обнаруживающим наличие этого вихревого поля.
В отличие от электростатического вихревое электрическое поле имеет замкнутые силовые линии. Это связано с тем, что источниками электростатического поля являются электрические заряды, а источником вихревого электрического поля — переменное во времени магнитное поле.
Индукционные токи, возникающие в массивных проводниках под действием переменного магнитного поля, называются токами Фуко или вихревыми токами. В соответствии с законом Джоуля — Ленца они приводят к нагреванию проводников (выделению теплоты) и переходу энергии системы во внутреннюю энергию. Токи Фуко эффективно используются на практике: в плавильных печах, в установках для закалки металлических деталей, в сушильных установках, в медицине.
Открытие Фарадеем явления электромагнитной индукции позволило создать мощные генераторы электрического тока и положило начало промышленному производству электроэнергии, без которой невозможно представить существование современного общества.
Электромагнитная индукция
Электромагнитная индукция — это одно из явлений, на которых основаны электротехника и радиотехника.
Для оценки важности этого явления достаточно назвать взаимное преобразование механической и электрической энергии, передачу и распределение электрической энергии, передачу и прием информации.
Знание явления и закона электромагнитной индукции необходимо при изучении электрических цепей переменного тока.
Закон электромагнитной индукции
Явление электромагнитной индукции открыл в 1831 г. английский физик М. Фарадей и на основе этого открытия сформулировал один из важнейших физических законов — закон электромагнитной индукции.
Явление электромагнитной индукции
Явление электромагнитной индукции можно продемонстрировать следующими опытами. Внутрь цилиндрической катушки, концы которой соединены с гальванометром, с определенной скоростью вводится постоянный магнит. Стрелка гальванометра отклоняется, обнаруживая электрический ток в катушке (рис. 10.1, а). При удалении магнита от катушки стрелка гальванометра отклоняется в обратную сторону.
Гальванометр обнаруживает ток в катушке, если перемещать ее относительно другой катушки с током, которую назовем первичной (рис. 10.1, б). На рис. 10.1, в показаны две катушки, расположенные на одном сердечнике. Одна из них присоединена к источнику электрической энергии через ключ, вторая замкнута через гальванометр.
Электрические катушки между собой не связаны, но при замыкании ключа наблюдается отклонение стрелки гальванометра в одну сторону, при размыкании — в другую.
Несмотря на внешнее различие опытов, их одинаковый результат дает основание полагать, что непосредственная причина возникновения электрического тока в цепи вторичной катушки в этих опытах одинакова.
Действительно, во всех рассмотренных опытах изменяется потокосцепление вторичной катушки: в первых двух случаях — благодаря изменению положения ее в магнитном поле, в третьем случае — в связи с увеличением тока в первичной катушке после замыкания ключа и уменьшением его после размыкания.
Возбуждение электродвижущей силы в контуре при изменении потокосцепления этого контура называется электромагнитной индукцией.
Под действием индуктированной э.д.с. в замкнутом контуре возникает индуктированный электрический ток. Возникновение тока означает, что во вторичный контур передается энергия, которая при наличии сопротивления в цепи превращается в тепло. В первых двух опытах электрическая энергия возникла за счет механической работы при перемещении постоянного магнита (рис. 10.1, а) или катушки (рис. 10.1, б). В третьем опыте обе катушки неподвижны, т. е. механическая работа не совершается. Электрическая энергия во вторичной катушке возникает за счет энергии источника, включенного в цепи первичной катушки. В этом случае электрическая энергия передается из одной цепи в другую посредством магнитного поля.
Рис. 10.1. Опыты для наблюдения электромагнитной индукции
Преобразование энергии из одного вида в другой посредством магнитного поля или изменение энергии поля количественно определяются через абсолютное значение изменения потокосцепления. Явление электромагнитной индукции, сопровождающее эти процессы, связано со скоростью изменения потокосцепления.
Закон электромагнитной индукции
Закон электромагнитной индукции устанавливает количественное выражение для индуктированной э. д. с.
Электродвижущая сила, индуктируемая в замкнутом контуре при изменении сцепленного с ним магнитного потока, равна скорости изменения потокосцепления, взятой с отрицательным знаком:
В этой форме закон электромагнитной индукции был дан Максвеллом.
В катушке, имеющей несколько витков, общая э. д. с. зависит от числа витков N. Если все витки катушки сцеплены с одинаковым магнитным потоком, то э. д. с. будет в N раз больше:
В общем случае витки катушки могут быть сцеплены с разными потоками, тогда ее общая э. д. с. определяется алгебраической суммой э. д. с. отдельных витков:
В числителе последнего выражения дана алгебраическая сумма изменений потокосцепления отдельных витков катушек, т. е. изменение общего потокосцепления.
Таким образом, э. д. с. катушки определяется скоростью изменения ее общего потокосцепления и общая формула закона электромагнитной индукции имеет вид
Правило Ленца
В 1833 г. проф. Петербургского университета Э. X. Ленц установил общее правило для определения направления индуктированного тока и электромагнитных сил, возникающих в результате взаимодействия магнитного поля с индуктированным током.
Если магнитный поток, сцепленный с проводящим замкнутым контуром, изменяется, в контуре возникают явления электрического и механического характера, препятствующие изменению магнитного потока.
Рис. 10.2. Схемы, поясняющие правило Ленца
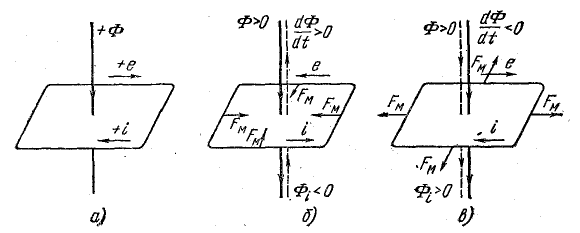
Правило Ленца отражает проявления электромагнитной инерции в системах контуров с токами. Этому правилу соответствует знак минус в формулах, выражающих закон электромагнитной индукции [см. (10.1) — (10.3)], если принять положительными направления магнитного потока и индуктированной в контуре э.д.с., удовлетворяющие правилу правого буравчика (рис. 10.2, а).
Предположим, что положительный магнитный поток, сцепленный с контуром, увеличивается. Приращение потока dФ и скорость его изменения dФ/dt положительны (dФ > 0, dФ/dt > 0). Индуктированная в контуре э. д. с., согласно правилу Ленца, направлена против выбранного положительного направления, т. е. отрицательна (е < 0) (рис. 10.2, б). Индуктированный в контуре ток i (направление его совпадает с направлением э. д. с.) создает вторичный магнитный поток Фi, который, согласно правилу буравчика, действует против основного потока Ф, т.е. препятствует его увеличению. Одновременно в контуре возникают электромагнитные силы, стягивающие контур (направление силы определяется правилом левой руки).
Тенденция к уменьшению поверхности, ограниченной контуром, направлена в данном случае на уменьшение основного потока.
При уменьшении основного магнитного потока (dФ < 0 и dФ/dt < 0) индуктированная э. д. с. положительна (е > 0), т. е. совпадает с выбранным положительным направлением (рис. 10.2, в). Индуктированный в контуре ток i создает вторичный магнитный поток, совпадающий по направлению с основным потоком. Вторичный магнитный поток, возникновение которого можно рассматривать как реакцию системы контуров с токами на изменение ее магнитного состояния, в данном случае препятствует уменьшению основного магнитного потока. Возникающие при этом электромагнитные силы стремятся расширить контур с током, т. е. увеличить магнитный поток, сцепленный с ним.
Факторы, противодействующие изменению магнитного потока, тем сильнее, чем быстрее изменяется поток.
Электромагнитная инерция в системах контуров с токами подобна механической инерции в системах движущихся тел: при всяком изменении скорости возникают силы инерции, препятствующие этому изменению.
Задачи
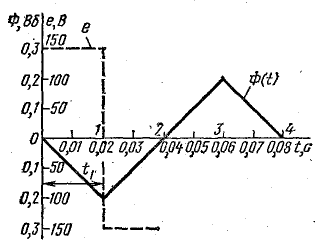
Задача 10.1. Магнитный поток, создаваемый током в катушке, изменяется по графику рис. 10.3. Построить график э. д. с., индуктированной в катушке с числом витков N = 15, если наибольшая величина потока Фm = 0,2 Вб.
Рис. 10.3. К задаче 10.1
Решение. Э. д. с: в катушке определяют по формуле (10.2), где dФ/dt — скорость изменения магнитного потока. На участке 0-1 отрицательный магнитный поток в течение t1 = 0,02 с растет от нуля до Фm = 0,2 Вб по линейному закону, поэтому скорость изменения потока постоянна и отрицательна:
При постоянной скорости изменения магнитного потока э. д. с. будет постоянной:
Знак э. д. с. определим по правилу Ленца.
Условно-положительные направления магнитного потока и индуктированной э. д. с. в катушке показаны на рис. 10.4, а.
На участке 0-1 кривой Ф(t) отрицательный магнитный поток увеличивается. Направления магнитного потока и тока в катушке, соответствующие этому отрезку времени, отмечены на рис. 10.4, б. Индуктированная э. д. с. препятствует росту магнитного потока, т. е. направлена против тока, создающего поток (пунктирные стрелки). В данном случае э. д. с. положительна, так как ее направление совпадает с условно-положительным направлением.
Рис. 10.4. К задаче 10.1
На участке 1-2 отрицательный магнитный поток уменьшается с той же скоростью, с какой он раньше увеличивался. Индуктированная э. д. с., сохраняя свою величину 150 В, препятствует уменьшению потока, т. е. направлена, так же как ток в катушке (рис. 10.4, в), против условно-положительного направления. Из формулы (10.2) также следует, что э. д. с. отрицательна.
Наведение э.д.с. в проводнике, движущемся в магнитном поле
В проводнике, движущемся в магнитном поле так, что он пересекает линии магнитной индукции, индуктируется электродвижущая сила. Это явление — разновидность электромагнитной индукции.
Выражение э.д.с. в проводнике, движущемся в магнитном поле
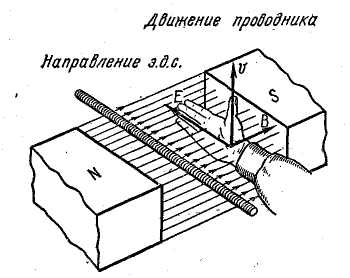
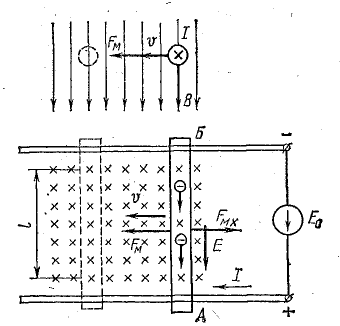
Рассмотрим отрезок АБ прямолинейного проводника, который движется, пересекая под прямым углом линии магнитной индукции равномерного поля с магнитной индукцией В.
На рис. 10.6, а показан проводник АБ, который катится в направлении механической силы Fмх по металлическим шинам, соединенным между собой через сопротивление R.
Проводник АБ, отрезки шин и сопротивление образуют замкнутый проводящий контур. При перемещении проводника на расстояние b с постоянной скоростью v магнитный поток, сцепленный с этим контуром, увеличивается за счет увеличения площади поверхности, ограниченной контуром.
Приращение магнитного потока
где l — длина части проводника АБ, находящейся в магнитном поле.
Абсолютная величина э. д. с. в контуре
где Δt — время, в течение которого проводник АБ переместился на расстояние b; b/Δt = v — скорость движения проводника; поэтому
Рис. 10.6. Движение прямого провода в магнитном поле
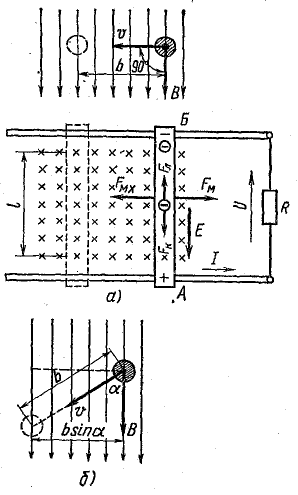
Если проводник будет перемещаться под углом α < 90° к направлению магнитной индукции поля (рис. 10.6, б), то приращение магнитного потока за время Δt при той же скорости v будет
вы м
э. д. с. в контуре
При α = 90° из (10.5) можно получить формулу (10.4), по которой подсчитывается наибольшая величина э. д.с. при данных величинах B, v, l. При α = 0 (проводник движется вдоль линий магнитной индукции) э. д. с. равна нулю.
Силы Лоренца
Выражение (10.4) для индуктированной э. д. с. можно получить, используя формулу (8.4) и выражение (2.1) применительно к одному электрону:
Магнитное поле действует на заряженные частицы только в проводнике АВ, который движется в магнитном поле. На другие части проводящего контура (шины и сопротивление R) оно не действует, так как они находятся вне поля и к тому же неподвижны. Учитывая это, рассмотрим один проводник АБ, несвязанный с остальной частью контура.
Свободные электроны вещества проводника АБ, находящегося в магнитном поле, одновременно перемещаются относительно проводника (внутреннее перемещение, например тепловое) и вместе с ним со скоростью v под действием внешней силы Fмх, приложенной к проводнику.
В данном случае рассмотрим ту составляющую общей скорости электронов, которая связана с движением проводника.
Электромагнитная сила, действующая на каждый электрон (Fл — сила Лоренца), согласно правилу левой руки, направлена вдоль проводника, а по величине определяется выражением (8.4):
где b — путь, пройденный электроном вместе с проводником за время t.
Скапливаясь на одном конце проводника, электроны создают избыточный отрицательный заряд, а на другом конце образуется такой же по величине положительный заряд.
Разделение зарядов в проводнике приводит к возникновению электрического поля и взаимодействию разделенных частиц. Силы электрического поля Fк (силы Кулона) являются силами притяжения частиц, поэтому они направлены против сил магнитного поля (сил Лоренца Fл).
Если проводник движется с постоянной скоростью, то электромагнитные силы не меняются, а силы электрического поля растут по мере накопления зарядов на концах проводника.
Разделение зарядов прекращается при равенстве электромагнитных и электрических сил: Fл = Fк.
Равенство сил означает наличие между концами проводника установившейся разности потенциалов или электрического напряжения:
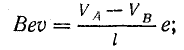
Действие магнитного поля на свободные электроны проводника при его движении является причиной возникновения электродвижущей силы, которая называется э.д.с. электромагнитной индукции.
Магнитогидродинамический генератор
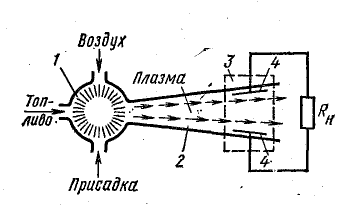
Силовое действие магнитного поля на движущие заряженные частицы используется для прямого преобразования тепловой энергии в электрическую. Такое преобразование происходит в магнитогидродинамическом генераторе (МГД-генераторе), принципиальная схема которого показана на рис. 10.7.
В камере сгорания 1 горит топливо и образуется газ, нагретый до высокой температуры 2500—2800°С. Для ионизации в раскаленный газ вводится в небольшом количестве присадка (пары солей щелочных металлов калия, натрия или цезия) и так образуется электропроводная плазма. Плазма направляется в канал-сопло 2, где приобретает большую скорость (несколько тысяч метров в секунду), а в конце канала она пролетает в сильном магнитном поле, образованном электромагнитом 3.
Магнитное поле действует на движущиеся заряженные частицы (электроны, ионы) с силой, направленной перпендикулярно направлению движения плазмы (правило левой руки). Часть из них достигает стенок канала, где смонтированы электроды 4, которые заряжаются — один положительно, другой отрицательно, т. е. образуется э. д. с. магнитогидродинамического генератора.
К электродам присоединен потребитель электрической энергии и в образованной цепи устанавливается электрический ток.
Рис. 10.7. Схема магнитогидродинамического генератора
Рис. 10.8. К правилу правой руки
В Советском Союзе с 1971 г. действует первая в мире опытно-промышленная установка с МГД-генератором мощностью 25 тыс. кВт, ведутся работы по созданию промышленной установки мощностью порядка 1 млн. кВт.
При высокой температуре топливо в МГД-генераторе сгорает более полно, чем в топках паровых котлов, что способствует увеличению к. п. д. и существенно сокращает вредные выбросы в атмосферу.
Правило правой руки
Если проводник АБ входит в замкнутый проводящий контур, как на рис. 10.6, то благодаря действию э. д. с. индукции в контуре установится постоянное перемещение электронов — электрический ток.
Направление индуктированной э. д. с. и тока в проводнике АБ можно определить по направлению движения электронов: ток направлен против движения электронов, т. е. от минуса к плюсу.
В практике для определения направления индуктированной э. д. с. применяют правило правой руки (рис. 10.8): если расположить правую руку так, чтобы большом палец, отогнутый перпендикулярно остальным четырем, показывал направление движения проводника, а линии магнитной индукции входили в ладонь, то вытянутые четыре пальца покажут направление э. д. с. электромагнитной индукции.
Все изложенное о возникновении индуктированной э. д. с. в проводнике справедливо и в том случае, когда проводник остается неподвижным, а движется система магнитных полюсов, так что линии магнитной индукции пересекают проводник. В этом случае, определяя направление э. д. с. по правилу правой руки, нужно считать проводник движущимся в направлении, противоположном направлению движения магнитных полюсов.
Задачи
Задача 10.4. В равномерном магнитном поле, магнитная индукция которого В = 1,2 Тл, движется проводник, пересекая линии магнитной индукции под углом α = 30°.
Определить э. д. с. в проводнике, если его длина l = 80 см, а скорость движения v = 5 м/с.
Решение. При α = 30°
Взаимное преобразование механической и электрической энергии
Электромеханическое действие магнитного поля и электромагнитная индукция используются для преобразования механической энергии в электрическую и обратно.
Устройства, при помощи которых эти преобразования осуществляются, называются электрическими машинами. Машина для преобразования механической энергии в электрическую называется генератором, а для обратного преобразования — двигателем.
Конструкции, принципы и режимы работы различных электрических машин изучаются в специальном курсе.
Здесь в общем виде рассмотрим принципы взаимного преобразования механической и электрической энергии.
Принцип преобразования механической энергии в электрическую
Проводник АБ (см. рис. 10.6) движется с постоянной скоростью за счет механической энергии какого-либо первичного двигателя — источника механической энергии.
Механическая мощность движения проводника
где Fмх — сила, действующая на проводник со стороны первичного двигателя.
Благодаря электромагнитной индукции в проводнике возникают э. д. с. и ток
где r — сопротивление проводника АБ (внутреннее сопротивление источника электрической энергии); R — сопротивление внешней части цепи, включая сопротивление приемника, и части шин, входящей в контур.
В данном случае проводник АБ является источником э. д. с., электрическая мощность которого Р = ЕI.
Величину Р часто называют электромагнитной мощностью. С появлением тока в проводнике АБ возникает электромагнитная сила Fм, действующая в направлении, перпендикулярном направлению тока. Применяя правило левой руки, можно убедиться в том, что электромагнитная сила Fм направлена против силы Fмх.
Следовательно, внешняя сила Fмх в данном случае движущая, а Fм — тормозная.
При постоянной скорости v (установившееся движение) движущая и тормозная силы равны:
Подставляя выражения силы в формулу (10.6), получим
Так как
то
Следовательно, механическая мощность первичного двигателя равна электрической мощности источника.
Выражение (10.7) показывает, что при движении проводника в магнитном поле в направлении механической силы происходит полное преобразование механической энергии в электрическую.
Напряжение на концах проводника UАБ является одновременно напряжением на внешней части цепи, которое меньше э. д. с. на величину внутреннего падения напряжения:
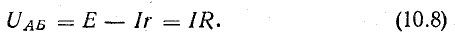
Преобразование электрической энергии в механическую
Обратное преобразование электрической энергии в механическую можно показать на том же проводнике АБ, изменив несколько электрическую цепь, в которую он входит (рис. 10.9). Вместо приемника электрической энергии в цепь входит источник электрической энергии с э. д. с. E0.
Если на концах проводника АБ обеспечить и поддерживать напряжение UАБ больше, чем его э. д. с. Е, ток в нем изменит направление на обратное [согласно формуле (10.8), ток меняет знак]. Такое состояние в цепи достигается благодаря наличию э. д. с. Е0 источника электрической энергии.
Рис. 10.9. К вопросу о преобразовании электрической энергии в механическую
Считая направление тока на рис. 10.9 положительным, его величину найдем согласно второму закону Кирхгофа:
В этом случае э. д. с. индукции в проводнике направлена против тока и является противо-э. д. с.
Встречное направление э. д. с. и тока является признаком потребления электрической энергии в данном устройстве и преобразования ее в другой вид энергии. Действительно, с изменением направления тока изменяется на противоположное и направление электромагнитной силы Fм. Оно совпадает теперь с направлением скорости движения проводника. Сила Fм становится движущей. Теперь противодействие оказывает механическая сила Fмх (например, сила трения).
Составим баланс мощностей для рассматриваемой электрической цепи.
Проводник АБ является приемником электрической энергии. Его электрическая мощность P = UАБI. Так как 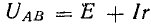
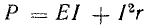
Учитывая выражение (10.4), запишем
Первое слагаемое в этой сумме определяет механическую мощность движущегося проводника, а второе — мощность тепловых потерь в проводнике АБ в соответствии с законом Ленца — Джоуля.
В связи с тем что механическая энергия возникает как результат действия сил магнитного поля, может создаться впечатление, что движение проводника происходит за счет энергии магнитного поля. В действительности же в механическую преобразуется электрическая энергия источника, что и подтверждается уравнением (10.9). Магнитное поле здесь является лишь посредником при преобразовании энергии. Последнее замечание относится и к обратному преобразованию энергии — механической в электрическую.
Задачи
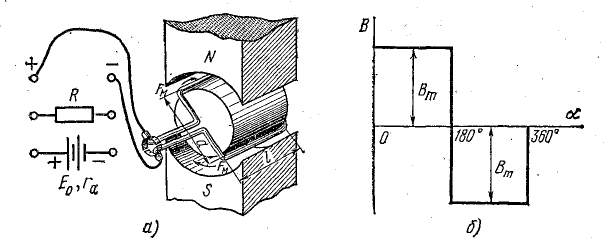
Задача 10.8. Виток медного провода в виде рамки, укрепленный на стальном цилиндре — роторе длиной l = 30 см и диаметром d = 20 см (рис. 10.10, а), вращается с частотой n = 1500 об/мин в радиальном магнитном поле. Концы рамки присоединены к двум половинкам разрезанного медного кольца (коллектора), вращающегося вместе с ротором. К щеткам, наложенным на коллектор, присоединен приемник энергии с сопротивлением R = 0,9 Ом; сопротивление самой рамки и соединительных проводов r = 0,1 Ом. График распределения магнитной индукции в воздушном зазоре показан на рис. 10.10, б, где Вm = 1,2 Тл.
Рис. 10.10. К задачам 10.8, 10.9
Определить: 1) величину и направление силы, действующей на провода рамки; 2) механический момент, развиваемый двигателем, вращающим рамку; 3) электрическую мощность в рамке.
Решение. Определим э. д. с., индуктированную в рамке, по формуле (10.4). Предварительно найдем линейную скорость проводника:
Учитывая, что рамка имеет два проводника, в которых индуктируются э. д. с., суммарную э. д. с. витка найдем по формуле
Ток в цепи
Тормозная сила, действующая на одну сторону рамки, и механический момент:
Этот момент, будучи тормозным, при постоянной частоте вращения равен движущему моменту двигателя.
Электрическая мощность, развиваемая в рамке,
Баланс электрической мощности
Механическая мощность двигателя
Выводы. 1. Механическая энергия, подводимая к рамке от первичного двигателя, полностью превращается в электрическую, что подтверждается равенством механической и электрической мощностей.
2. Электрическая энергия, полученная в рамке, превращается в тепло в самой рамке (I2r = 12,8 Вт) и в приемнике (I2R = 115,2 Вт).
Задача 10.9. Устройство, описанное в задаче 10.8, переведено в режим двигателя. Для этого вместо приемника энергии в цепь включили аккумуляторную батарею с э. д. с. Е0 = 12 В и внутренним сопротивлением rа = 0,2 Ом.
Определить окружное усилие, вращающий момент и скорость рамки и составить баланс мощностей, если ток в цепи установился равным 10 А.
Решение. Определим э. д. с. в рамке согласно второму закону Кирхгофа:
Линейная скорость вращения рамки
Частота вращения
Окружное усилие на цилиндре
Вращающий момент
Механическая мощность
Баланс мощностей: мощность батареи равна сумме механической мощности и мощности потерь в электрической цепи:
Э.Д.С. Самоиндукции и взаимоиндукции
При изменении собственного потокосцепления в контуре или катушке наводится э. д. с. самоиндукции eL, а при изменении взаимного потокосцепления — э. д. с. взаимоиндукции.
Э.д.с. самоиндукции
Изменение собственного потокосцепления обычно является следствием изменения тока
или
Э. д. с. самоиндукции пропорциональна скорости изменения тока di/dt. Она противодействует изменению тока, т. е. при увеличении тока препятствует его росту, а при уменьшении задерживает его падение (правило Ленца).
Чем быстрее изменяется ток, тем больше противодействие его росту или падению. Однако это противодействие зависит не только от скорости изменения тока, но и от конструкции электромагнитного устройства, что в формуле (10.10) выражается множителем L, т. е. индуктивностью этого устройства.
Если изменение тока в катушке является следствием изменения приложенного к ней напряжения, то э. д. с. самоиндукции направлена против приложенного напряжения, когда ток растет, и совпадает по направлению с напряжением, когда ток уменьшается.
Подобно массе, характеризующей инертность в механической системе, индуктивность характеризует инертность в электромагнитной системе.
Э.д.с. взаимоиндукции
Для системы магнитно-связанных катушек (см. рис. 8.21) э. д. с. взаимоиндукции
Изменение взаимного потокосцепления может быть следствием изменения тока в одной из катушек или изменения коэффициента связи.
Предположим, что изменяется ток i1 в первой катушке. Э. д. с. взаимоиндукции е2м во второй катушке пропорциональна скорости изменения этого тока:
Аналогично, при изменении тока i2 э. д. с. взаимоиндукции
В том и другом случае коэффициентом пропорциональности является взаимоиндуктивность системы М.
Правило Ленца в применении к такой системе указывает на то, что изменение тока в одной катушке встречает противодействие со стороны другой катушки.
Из выражения (10.11) видно, что э. д. с. взаимоиндукции е2м, а следовательно, и индуктированный ток i2 имеют знак, противоположный скорости изменения тока i1. Это значит, что при увеличении тока i1 и его магнитного потока Ф1.2 индуктированный ток i2 создает магнитный поток Ф2.1, направленный встречно потоку Ф1.2; при уменьшении i1 поток Ф2.1 направлен согласно с уменьшающимся потоком Ф1.2.
Рис. 10.11. Схема трансформатора
Аналогичное рассуждение можно привести из выражения (10.12). Направление магнитных потоков в обоих случаях, как обычно, определяется по правилу буравчика.
Взаимоиндуктивность, так же как и индуктивность, характеризует электромагнитную инерцию, но в системе катушек (контуров), имеющих магнитную связь.
Принцип действия трансформатора
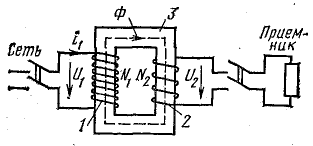
Наглядным примером практического использования явления взаимоиндукции является работа трансформатора. Трансформатор — статический электромагнитный аппарат для изменения величины напряжения или тока.
Принципиальная схема трансформатора (рис. 10.11) имеет магнитопровод 3 из электротехнической стали и две обмотки на магнитопроводе: первичную 1 с числом витков N1 и вторичную 2 с числом витков N2. Обмотки выполняют из медного провода.
Первичной обмоткой трансформатор включается в сеть переменного напряжения U1 и в ней возникает ток i1. К вторичной обмотке подключается приемник электрической энергии.
Рассмотрим трансформатор с разомкнутой цепью вторичной обмотки, т. е. в режиме холостого хода.
При переменном токе в первичной обмотке создается переменный магнитный поток Ф, который замыкается по стальному сердечнику и образует потокосцепление с обеими обмотками. Таким образом, в трансформаторе обмотки электрически между собой не связаны, а связаны переменным магнитным потоком.
В обеих обмотках наводится э. д. с.:
Отношение э. д. с.
Отношение чисел витков обмоток трансформатора называется коэффициентом трансформации.
Отношение э. д. с. при холостом ходе можно заменить отношением напряжений на зажимах обмоток, учитывая, что u2 = е2 и u1 ≈ е1 (u1 > е1 на величину падения напряжения в обмотке, которое при холостом ходе мало).
Следовательно,
Отсюда видно, что при N2 > N1 (u2 > u1) трансформатор повышает, а при N2 < N1 (u2 < u1) — понижает напряжение.
Если к вторичной обмотке подключить приемник энергии, то в ее цепи возникнет ток i2 и в приемник будет поступать электрическая энергия из сети через трансформатор. При этом передача энергии из первичной обмотки во вторичную осуществляется посредством магнитного поля.
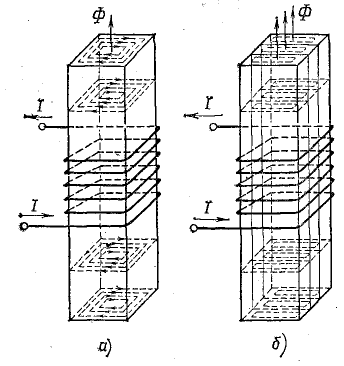
Вихревые токи
Рассмотрим металлический сердечник внутри катушки с переменным током (рис. 10.12, а). При отмеченном направлении тока магнитный поток в сердечнике направлен вдоль оси сердечника вверх.
Металлический сердечник можно мысленно разделить на ряд замкнутых на себя слоев, ось которых совпадает с осью сердечника. Каждый такой слой представляет собой замкнутый виток, в котором переменным потоком индуктируются э. д. с. и ток, направленные в плоскостях, перпендикулярных оси магнитного потока.
Рассматривая совокупность таких замкнутых контуров, можно представить себе в теле сердечника вихревые токи, замыкающиеся вокруг оси магнитного потока. Направление вихревых токов определяется правилом Ленца.
При увеличении магнитного потока вихревые токи направлены по часовой стрелке, если смотреть на сердечник сверху. Вихревые токи в соответствии с законом Ленца — Джоуля сопровождаются выделением тепла в сердечнике. Это явление используется на практике для нагревания металлов (плавления стали, нагрева под закалку и других целей).
В сердечниках электрических машин, трансформаторов и электрических аппаратов тоже возникают вихревые токи. Но здесь они нежелательны, потому что увеличивают общие потери энергии в устройствах и вызывают дополнительный их нагрев.
Для уменьшения потерь энергии сердечники устройств переменного тока собираются из листовой электротехнической стали (толщина 0,35 мм), листы которой изолируются друг от друга специальным лаком.
Уменьшение вихревых токов таким способом достигается благодаря тому, что контуры, по которым в сплошном сердечнике замыкаются вихревые токи, оказываются разрезанными на части, изолированные друг от друга (рис. 10.12, б). Кроме того, ослабление вихревых токов достигается увеличением удельного электрического сопротивления материала сердечников. Для этого в электротехническую сталь вводится присадка кремния до 4 %.
Рис. 10.12. К вопросу о вихревых токах
Задачи
Задача 10.11. Обмотки трансформатора имеют индуктивность L1 = 6,1 Гн; L2 = 0,08 Гн и коэффициент магнитной связи k = 0,9. Определить э. д. с., наведенную в обеих обмотках при увеличении тока в первой обмотке со скоростью 1000 А/с.
Решение. Э. д. с. самоиндукции в первой обмотке
Для определения э. д. с. во второй обмотке найдем взаимную индуктивность
обмоток:
- ЭДС индукции в движущемся проводнике
- Производство, передача и потребление электрической энергии
- Условия равновесия тел в физике
- Равновесие тел в физике
- Электромагнитная индукция в физике
- Правило Ленца для электромагнитной индукции
- Магнитные свойства вещества
- Явление самоиндукции
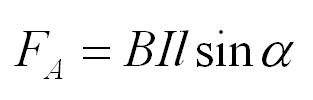
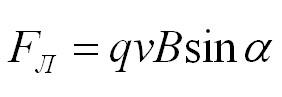
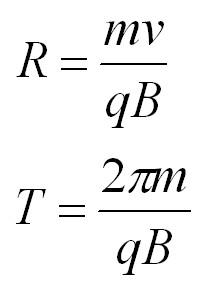
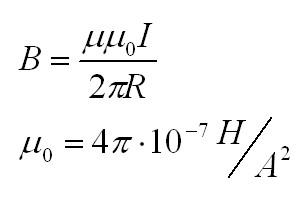
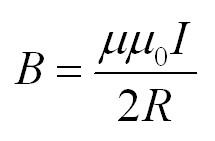
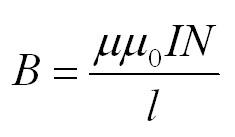
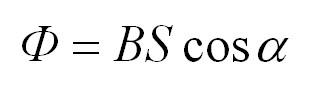
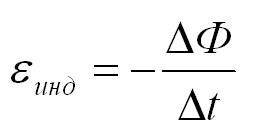
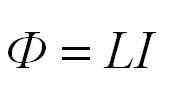
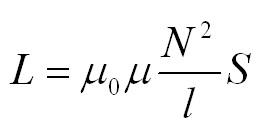
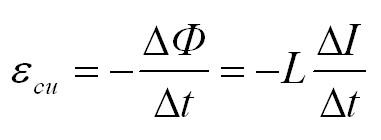
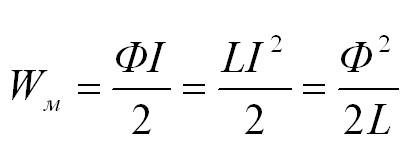
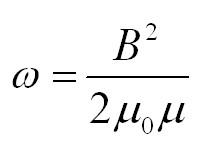











































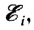 возникающая в замкнутом контуре, прямо пропорциональна скорости изменения магнитного потока через него:
возникающая в замкнутом контуре, прямо пропорциональна скорости изменения магнитного потока через него: