как определить направление электронов в проводнике?
Профи
(529),
закрыт
6 лет назад
Андрей Винк
Искусственный Интеллект
(151251)
6 лет назад
Разрываешь проводник и опускаешь два конца (да не своих, дурень!!!) в стакан с соленой водой.
С одного пойдут пузырьки — это пердячий пар, с которым электроны сопротивление преодолевают.
Оттуда и бегут, вестимо.
яя чячяПрофи (529)
6 лет назад
а может наоборот, откуда ты это взял? может они летят в воде, и разгоняются, а как о проводник шлёпаются, разбивают молекулы воды. тоже не знаешь…
Сцуко
Мудрец
(13683)
6 лет назад
Не совсем понятен вопрос.
Если тебе известна полярность подключения проводника? Или если не известна?
Если известно, где на провод подан положительный потенциал, а где – отрицательный, так тогда сам подумай . Если электроны – это отрицательные заряды, то они должны двигатся от отрицательного потенциала к положительному по всем законам электростатики (отрицательные заряды притягиваются к плюсу).
Если тебе неизвестно, как провод подключен (где + а где -), но ты уверен, что там постоянный ток, то можно с помощью компаса (намагниченной стрелки), т. к. любой движущийся заряд создаёт вокруг себя магнитное поле. Ну и существуют так называемые “линии магнитного поля”. Их можно измерить намагниченной стрелкой, например. Ну и по “правилу буравчика” (или “правилу левой руки, =) кроме шуток, правда так называется) найти направление тока электронов в проводнике.
Не благодари. =)
яя чячяПрофи (529)
6 лет назад
и не буду благодарить, тыж так и не ответил. вот есть у тебя батарейка, визуально и плюс и минус выглядят одинаково, есть например диоды, маркировка их не определена, ты визуально не знаешь где катод анод, есть механический прерыватель рэле, есть трансформатор, пусть на железе, или на феррите, есть неполярный конденсатор, любой по напряжению, есть провода, есть компас, есть огонь свечи, если хочешь и снег. как определишь? что сделаешь? других приборов никаких нет.
Закон движения электрона в магнитном поле
Содержание:
- Каково движение электрона в магнитном поле
-
Как найти скорость
- Траектория движения
- Период обращения электрона в магнитном поле
- Отклонение электронов в магнитном поле
- Примеры решения задач
Каково движение электрона в магнитном поле
Известно, что магниты представляют собой металлы, обладающие свойством к притяжению прочих магнитов и металлических предметов определенного состава. Во внутренней области таких объектов сгенерировано магнитное поле, действие которого можно наблюдать в реальных условиях. Эффект проявляется по-разному, то есть магнит отталкивает или притягивает предметы.
Роль источника, формирующего магнитное поле, играют заряженные частицы, которые пребывают в движении. Если перемещение зарядов обладает определенным направлением, то такой процесс называют электрическим током. Таким образом, легко сделать вывод об образовании магнитного поля, благодаря наличию электричества.
Электрический ток ориентирован по перемещению зарядов со знаком плюс и направлен противоположно относительно передвижения частиц, которые заряжены отрицательно. Если предположить, что имеется некая трубка в форме кольца с потоком воды, то какой-то ток примет противоположное ему направление. Электрический ток записывают с помощью буквы I.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если рассматривать металлические предметы, то в них образование тока связано с перемещением отрицательных зарядов. На наглядном изображении продемонстрировано передвижение частиц, заряженных отрицательно, то есть электронов, в левую сторону. В то время как электричество ориентировано в правую сторону.
Источник: habr.com
В начале исследований электричества ученые не обладали информацией о природе и свойствах носителей электрического тока. При рассмотрении аналогичного проводника слева, как на рисунке выше, можно заметить, что ток перемещается от наблюдателя, а магнитное поле окружает его по часовой стрелке.
Источник: habr.com
Эксперимент можно продолжить, используя компас. При размещении прибора около проводника, изображенного на схеме, произойдет разворот стрелки перпендикулярно относительно рассматриваемого проводника, параллельно по отношению к силовым линиям магнитного поля, то есть параллельно кольцевой стрелке, обозначенной черным цветом на изображении.
Представим, что имеется некий шарообразный предмет, заряженный положительно. Заряд со знаком плюс обусловлен недостаточным количеством электронов. Данному шарику можно задать направление путем подбрасывания вперед. В таком случае вокруг объекта сформируется аналогичное предыдущему примеру магнитное поле кольцевого типа, которое закручивается вокруг шарика по направлению часовой стрелки.
Источник: habr.com
В данном случае заряженные частицы перемещаются в определенном направлении. Таким образом, целесообразно сделать вывод о наличии электрического тока. В результате при возникновении электричества вокруг него формируется магнитное поле. Передвигающийся заряд, либо какое-то количество таких частиц, формирует около себя «тоннель» в виде магнитного поля. При этом стенки «тоннеля» более плотные около перемещающейся заряженной частицы.
Удаляясь от перемещающегося заряда, напряженность, то есть сила генерируемого магнитного поля, слабеет. В результате компасная стрелка меньше реагирует на него. Закон, согласно которому напряженность рассматриваемого поля распределяется около источника, аналогичен закономерности формирования электрического поля вокруг заряда. Таким образом, величина напряженности и квадрат расстояния до источника находятся в обратной пропорциональной зависимости.
Рассмотрим следующую ситуацию, когда шарик с положительным зарядом движется по траектории в форме круга. В таком случае кольцевые линии магнитных полей, сформированных вокруг предмета, складываются. В итоге получается магнитное поле, обладающее перпендикулярным направлением относительно плоскости, в рамках которой происходит движение заряженного шарика.
Источник: habr.com
Заметим, что «тоннель» магнитного поля, образованный около заряженного объекта, сворачивается, и получается кольцо, которое схоже по форме с бубликом. Аналогичную ситуацию можно наблюдать в процессе сворачивания в кольцо проводника с электричеством. Тогда проводник, деформированный так, что получается катушка с множеством витков, называют электромагнитом. Около подобного предмета формируются магнитные поля за счет перемещающихся в нем зарядов, то есть электронов.
При условии вращения шарика с зарядом вокруг собственной оси возникает магнитное поле по аналогии с тем, что образовано у нашей планеты, которое ориентировано вдоль оси вращательного движения. Тогда имеет место возникновение кругового электрического тока, который определяют как ток, провоцирующий образование магнитного поля во время перемещения по круговой траектории заряженной частицы относительно оси шарика.
Источник: habr.com
В этом случае процесс аналогичен перемещению шарика по кругу. Отличие состоит в том, что радиус орбиты движения уменьшен до величины радиуса шарообразного объекта. Вышеизложенные выводы имеют смысл и тогда, когда заряд шарика имеет знак минуса, а магнитное поле ориентировано противоположно.
Описанный выше эффект удалось выявить экспериментальным путем Роуланду и Эйхенвальду. Исследователи фиксировали магнитные поля около дисков, обладающих зарядом и совершающих вращательные движения. Вблизи этих объектов замечали отклонения компасной стрелки. Ознакомиться с наглядным представлением опыта можно на рисунке ниже:
Источник: habr.com
На изображении отмечены направления магнитных полей, которые зависят от положительного или отрицательного заряда дисков, расположенных в системе. По рисунку заметно, как эти направления меняются при смене знака заряда. Если диск, не обладающий зарядом, привести во вращательное движение, то магнитное поле отсутствует. Стационарные заряды также не образуют вокруг себя поля.
Как найти скорость
В плане изучения интересен процесс перемещения зарядов в пространственной области при наличии магнитного и электрического поля. Применительно к такой ситуации целесообразно воспользоваться соотношением для силы Лоренца, которая представляет собой суммарную величину сил, оказывающих воздействие на заряд, перемещающийся в электрическом и магнитном полях.
Представим, что заряд равен q и перемещается со скоростью (overrightarrow{v}) в условиях однородного магнитного поля, индукция которого составляет (overrightarrow{В}), а также в присутствии электрического поля с определенной напряженностью (overrightarrow{N}). Запишем силу воздействия электрического поля на заряд по модулю:
(Fэ = qE)
Этот компонент силы Лоренца принято называть электрической составляющей. Применительно к магнитному полю, на перемещающийся заряд воздействует магнитная составляющая силы Лоренца. Модуль определяют по закономерности Ампера. Представим, что проводник, по которому течет электричество, расположен в однородном магнитном поле. Вдоль этого объекта перемещаются заряды. Проанализирует ситуацию на отрезке данного проводника, который в длину составляет (triangle l), а площадь его поперечного сечения равна S.
Источник: иванов-ам.рф
Формула для вычисления силы тока, протекающего по проводнику:
(I = qnυS)
Зная, что:
(F_{А} = BItriangle l sin alpha)
Получим следующее выражение:
(FA = BqnvSΔtriangle l sin alpha)
Здесь (N = nStriangle l) обозначает количество зарядов, входящих в объем (Striangle l).
Исходя из записанной формулы, несложно выразить скорость движения заряда с учетом второго закона Ньютона:
(v = frac{qBR}{m})
Траектория движения
Изучить направление, в котором перемещаются заряженные частицы в магнитном поле, целесообразно на примере простейшего случая. При этом происходит движение заряда в однородном магнитном поле с индукцией, которая является перпендикуляром исходной скорости заряженной частицы. Схематично передвижение заряда изображено на рисунке:
Источник: иванов-ам.рф
В связи со стабильным значением модуля скорости заряда, не меняется модуль магнитной составляющей силы Лоренца по аналогии. Исходя из того, что рассматриваемая сила является перпендикуляром к скорости, можно заключить наличие центростремительного ускорения у перемещающейся частицы. Данная величина также не меняется по модулю, что позволяет сделать вывод о постоянстве радиуса кривизны R рассматриваемой траектории. Таким образом, подтверждается ранее выведенная формула скорости:
(v = frac{qBR}{m})
Период обращения электрона в магнитном поле
Запишем математическое соотношение, позволяющее выразить период обращения заряженной частицы в магнитном поле:
(T=frac{2 cdot{pi}cdot r}{upsilon};)
(r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B}.)
Отклонение электронов в магнитном поле
Из предыдущего анализа движения заряда известно, что процесс сопровождается воздействием на частицу, перемещающуюся в магнитном поле, силы Лоренца. Данная сила определяется величиной и знаком рассматриваемой частицы, а также зависит от быстроты ее перемещения и индукции магнитного поля. В итоге траектория, по которой движется заряд, изменяется. Опытным путем явление можно наблюдать с помощью системы магнитного поля и электронного луча осциллографа.
В ходе эксперимента необходимо выключить горизонтальную развертку луча и с помощью рукояток отрегулировать положение луча по вертикали и горизонтали. В результате последовательных манипуляций луч окажется направленным непосредственно в центральную область экрана. Следует расфокусировать образованное световое пятно, увеличивая яркость до максимально возможного значения. Если поместить рядом с прибором постоянный магнит, то можно наблюдать смещение пятна вбок, как изображено на рисунке:
Источник: duckproxy.com
Изменение положение пятна наблюдается в процессе приближения или удаления магнита от осциллографа. Таким образом, справедливо сделать вывод о том, что смещение пятна зависит от величины индукции магнитного поля. Если перевернуть магнит, то направление индукции изменится, а пятно на экране переместится в противоположную сторону.
Примеры решения задач
Задача 1
Созданы условия для движения электрона в однородном магнитном поле. Индукция данного поля составляет (B=4cdot {10}^{-3} {Тл}). Требуется вычислить, чему равен период обращения рассматриваемой отрицательно заряженной частицы.
Решение
В первую очередь следует записать данные из условия задачи. Так как речь в задании идет об электроне, то следует выписать справочные величины заряда и массы:
({q}_{e}=-1.6cdot {10}^{-19} {Кл})
({m}_{e}=9.1cdot {10}^{-31} {кг})
Вспомним формулу для расчета период обращения заряженной частицы в магнитном поле из ранее пройденного теоретического материала:
(T=frac{2 cdot{pi}cdot r}{upsilon}; r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B})
Подставим численные значения и получим:
(T=frac{2 cdot 3.14 cdot 9.1cdot {10}^{-31},text{кг}}{|-1.6cdot {10}^{-19},text{Кл}| cdot 4cdot {10}^{-3},text{Тл}}=8.9cdot {10}^{-9},с)
Ответ: период обращения электрона в магнитном поле равен (8.9cdot {10}^{-9} с).
Задача 2
Имеется однородное магнитное поле, величина индукции которого составляет (10^{-3} Тл) . В это поле попадает отрицательно заряженная частица по направлению перпендикулярно относительно линий магнитной индукции и под углом (alpha=frac{pi}{4}) к границе рассматриваемого поля. Скорость электрона по модулю соответствует (10^{6} м/с). В направлении оси абсциссы и ординаты поле не имеет границ. Известно, что заряд частицы к ее массе относится как (frac{е}{m}=1,76cdot 10^{11} Кл/кг). Необходимо вычислить расстояние, на котором от точки взлета электрон покинет поле.
Решение
Изобразим схематично условие задания:
Источник: иванов-ам.рф
В данном случае целесообразно применить правило левой руки, чтобы определить направление силы Лоренца с учетом отрицательного заряда наблюдаемой частицы. Схематично это представлено на рисунке выше. В условиях воздействия магнитного поля электрон подвержен действию магнитной составляющей силы Лоренца. В результате отрицательно заряженная частица будет перемещаться по дуге окружности. Следует вычислить радиус этой окружности. Воспользуемся вторым законом Ньютона:
(moverrightarrow{a}=overrightarrow{F_{л}})
Поскольку центростремительное ускорение:
(а = frac{v^{2}}{R})
В результате получим, что:
(frac{mv^{2}}{R}=evB Rightarrow R=frac{mv}{eB})
При рассмотрении (triangle O^{,}OC) можно сделать вывод:
(OC = frac{l}{2} = R sin alpha)
Тогда:
(l = 2R sin alpha = 2frac{mv sin alpha}{eB})
При подстановке численных значений получим:
(l = frac{2cdot 10^{6} cdot sin frac{pi}{4}}{1,76 cdot 10^{11}cdot 10^{-3} } = 0,008м = 8 мм)
Ответ: 8 мм.
Содержание:
- Движение электронов в атомах
- Распределение электронов в атомах
- Электронные формулы атомов
- Образование ионов
- Составление формул соединений
Движение электронов в атоме – это когда электрон в атоме находится в постоянном движении вокруг ядра. Но у такого движения отсутствует определенная траектория. Это выглядит примерно так, как показано на рисунке снизу. В каждый момент времени электрон находится в определенной точке околоядерного пространства.
На странице -> решение задач по химии собраны решения задач и заданий с решёнными примерами по всем темам химии.
Движение электронов в атомах
Электронное облако — модель движения электрона в атоме; область пространства, в каждой точке которой может находиться данный электрон. … Размер зависит от энергии электрона. Чем больше энергия электрона, тем больше по размеру его орбиталь, и тем дальше он находится от ядра.
Распределение электронов в атомах
Вспомните! Атом, молекула. Строение атома
Из курса 7 класса мы узнали, что атом является сложной системой, состоящей из ядра и электронов (рис. 1). Выясним теперь закономерности расположения электронов вокруг ядра. Число электронов равно заряду ядра атома (атомному номеру элемента). Однако
электроны притягиваются к ядру не с одинаковой силой, так как обладают различным запасом энергии и поэтому находятся на разном расстоянии от ядра.
Электроны с близкими значениями энергии располагаются на одинаковом расстоянии от ядра. Эти расстояния называются энергетическими уровнями. Их обозначают буквой n и нумеруют по мере удаления от ядра: 1, 2, 3, 4, 5, 6, 7. Значение n определяется номером периода, в котором расположен элемент. Максимальное число электро-
нов на каждом энергетическом уровне (емкость энергетического уровня)
определяется формулой 
энергетического уровня. Если n = 1, N = 2; n = 4, 
Электроны, расположенные ближе к ядру, сильнее притягиваются к
нему. По мере отдаления от ядра энергия связи уменьшается. Радиус r показывает удаленность каждого энергетического уровня от ядра.
Электроны заселяют пространство вокруг ядра поэтапно, образуя энергетические уровни (рис. 2). Почему так важно знать, как располагаются электроны в атоме? Потому что от строения электронных оболочек элемента зависят его физические и химические свойства (табл. 1). Потому что при непосредственном участии электронов атомов происходят образование и разрыв химических связей, т. е. протекают химические реакции. Скорость движения электрона очень велика, и определить его положение в пространстве в определенный момент времени невозможно. В одном месте пространства его можно обнаружить часто, в другом – редко. Область пространства, в которой вероятность нахождения электронов максимальна, называется электронным облаком, или орбиталью (s, p, d, f).
Форма электронных облаков различная: сферическая обозначается буквой s (s-облако); гантелеобразная – р-облако, причем р-облака ориентированы взаимно перпендикулярно вдоль трех осей x, y, z (рис. 3).
s-oблако может располагаться в пространстве симметрично точке пере-
сечения осей координат, поэтому его обозначают одной ячейкой 
может располагаться вдоль трех осей x, y, z, поэтому их обозначают
или тремя ячейками 
Электроны вращаются не только вокруг ядра, но и вокруг своей оси, как
Земля вокруг Солнца и своей оси.
Вращение электрона вокруг своей оси называют спином (от англ. spin – волчок). Электроны могут вращаться по часовой стрелке или против нее. На каждой орбитали могут располагаться только два разнонаправленных электрона. Поэтому при составлении электронно-графических формул атомов электроны изображают в ячейке двумя разнонаправленными стрелками
Электронное облако, энергетический уровень, электронная формула, ячейка, спин.
Электронные формулы атомов
Теперь перейдем к рассмотрению электронных формул атомов. Начнем с первого элемента в таблице Менделеева – атома водорода. У атома водорода имеется один электрон, который расположен на s-подуровне первого энергетического уровня, поэтому электронная формула атома водорода 

В Периодической системе атомы водорода и гелия расположены в 1-м периоде, т. е. у этих элементов запас энергии электронов одинаковый, поэтому они находятся на одном энергетическом уровне. Согласно формуле 
Следующий: литий – элемент 2-го периода. У лития имеются два энергетических уровня вокруг ядра, внутренний повторяет электронное строение атома гелия. Два его электрона находятся на первом энергетическом уровне, третий электрон – на втором. Во 2-м периоде п = 2,

У атома неона второй энергетический уровень заполнен электронами, т. е.
второй слой завершен.
Такая закономерность повторяется на третьем энергетическом уровне – от натрия до аргона. У элементов этого периода строение внутренних двух уровней повторяет структуру неона (табл. 2).
У атома аргона завершается третий энергетический уровень. Элементы, у которых внешний энергетический уровень завершен, обладают инертностью.
После аргона в таблице расположен калий. У атома калия следующий электрон образует новый, четвертый энергетический уровень, а внутренние три уровня повторяют электронное строение аргона (табл. 1).
При сравнении электронной структуры элементов 2-го и 3-го периодов заметно, что число электронов на внешнем энергетическом уровне у атомов лития, натрия и калия одинаковое 
Такие сходства в структурах внешних уровней наблюдаются у элементов, расположенных в одной группе, например, у фтора и хлора 7 электронов. У неона и аргона на внешних энергетических уровнях по 8 электронов.
Каждый период (кроме 1-го) начинается с щелочного металла и заканчивается инертным газом. По периодам слева направо число электронов увеличивается от 1 до 8, электроны внешнего энергетического уровня слабее притягиваются к ядру. У элементов главных (А) подгрупп электроны внешнего энергетического уровня являются валентными, т. е. определяют валентность элемента (табл. 3).
Рассмотренные 20 элементов являются элементами главных подгрупп, их очередные электроны помещаются на внешних s– и р-подуровнях, поэтому их называют s– и р-элементами.
К s-элементам относятся элементы главных подгрупп I и II группы; к р-элементам – элементы главных подгрупп III–VIII группы. Объединение элементов в одну группу объясняется одинаковым числом у них валентных электронов.
Ознакомившись с электронным строением атома, мы можем дать следующее определение периодов и групп в Периодической системе:
Периодами называются горизонтальные ряды элементов с одинаковым числом энергетических уровней, начинающиеся со щелочного металла и заканчивающиеся инертным газом (кроме 1-го периода).
Группами называются вертикальные ряды элементов с одинаковым числом валентных электронов.
Электронная формула, электронно-графическая формула, s-, р-элементы.
Лабораторный опыт №1
изготовление моделей атомов
Цель работы: изготовить модели атомов.
Оборудование: разноцветный пластилин, шаростержневые модели атомов.
Ход работы
Атомы элементов можно смоделировать с помощью разноцветного пластилина (рис. 4, 5).
Смоделируйте атомы: водорода, углерода, серы, йода, кислорода, железа. Подберите цвета пластилина или готовых шариков таким образом, чтобы цвета соответствовали простым веществам: водород –бесцветный (можно белый); углерод – черный; сера –желтая; йод – темно-красный; кислород – бесцветный (можно голубой или синий, т.к. сжиженный кислород голубого цвета); железо – серый.

Образование ионов
Вспомните! Cтроение атома, завершенный слой, электронная конфигурация элемента
После ознакомления с электронным строением атомов можно приступить к изучению способности элементов образовывать химические соединения.
Каждый период в системе заканчивается инертным газом. Как вы думаете, почему они так инертны? Для выяснения этого вопроса рассмотрим электронные структуры этих элементов. Нам известно строение атомов 

У других элементов химическая активность определяется именно этой недостроенностью внешнего электронного слоя. Они могут завершить внешние электронные слои путем отдачи или присоединения электронов при образовании соединений (рис. 7).

Если элемент отдает электрон, он превращается в положительно заряженную частицу, а если принимает электрон — в отрицательно заряженную частицу, которые называются ионами, т. е. имеют завершенный энергетический уровень.
А это зависит от двух факторов:
1) от электронного строения атомов;
2) от радиуса атомов.
Заряды ионов пишутся арабскими цифрами сверху
над символом элемента, знак заряда указывается после
числового значения: например:
У элементов, расположенных в начале периодов, на внешней орбитали электронов мало (1–3). Поэтому они легко отдают эти электроны, принимая при этом электронное строение инертного газа, которым заканчивается предыдущий период. А у элементов, расположенных в конце периодов, число электронов на внешнем уровне больше, поэтому они легко принимают электроны. При этом они принимают конфигурацию инертного газа, которым заканчивается данный период. По периодам число электронов на внешнем электронном уровне (валентные электроны) постепенно увеличивается. Слева направо увеличиваются заряды ядер атомов. То есть в этом направлении усиливается способность принимать электрон.
Напишем формулы валентных электронов элементов III периода. Определим число неспаренных электронов и число электронов, недостающих до завершения энергетического уровня (табл.4).
Рассмотрим, как заряжаются атомы элементов при образовании соединения с изменением их электронных структур.
Для завершения внешнего слоя атому хлора недостает лишь одного электрона, поэтому он принимает один электрон от атома магния, превращаясь при этом в отрицательно заряженный ион.
А у атома магния на внешнем слое имеются два электрона, он отдает каждому атому хлора по одному электрону, т. е. требуется два атома хлора.
Как изменяются эти свойства по группам? Число валентных электронов одинаковое у элементов, расположенных в одной группе. А число электронных слоев, т. е. атомных радиусов в этом направлении, увеличивается. По этой причине усиливается способность отдать электрон 
Способность элемента отдать электрон характеризует металлические а принимать — неметаллические свойства.
Для выяснения этого вопроса рассмотрим электронное строение и значения атомных радиусов элементов IA и VIIA групп (табл. 5).
По периодам слева направо металлические свойства ослабевают, неметаллические свойства постепенно усиливаются;
По группам сверху вниз усиливаются металлические свойства.
Ионы, условия образования положительно и отрицательно заряженных ионов.
Составление формул соединений
По пройденным материалам вы знаете, что атомы являются электронейтральными частицами. Потому что количество электронов, которые вращаются вокруг ядра, численно равно заряду ядра, точно так же, абсолютные значения положительно и отрицательно заряженных частиц, составляющих молекулу, будут равны. Поэтому и молекула электронейтральна.
Теперь попытаемся составить формулу обыкновенной поваренной соли. В состав этого вещества входят элементы натрий и хлор в виде ионов. А образование этих ионов вам знакомо из предыдущего параграфа. Теперь обратим внимание на числовые значения зарядов данных ионов:
При образовании иона натрия заряд ядра превышает на единицу общее количество электронов, которые вращаются вокруг ядра.
А при образовании ионов хлора, наоборот, общее количество электронов становится больше на единицу, чем заряд ядра.
При написании формул бинарных (состоящих из двух элементов) соединений мы должны придерживаться такого правила:
В молекулах бинарных соединений положительно заряженная частица
пишется (в основном) на первом месте, отрицательная – на втором.
В соединениях, состоящих из элементов металла и неметалла, частицы атомов металла всегда положительно заряжены, а неметаллы – отрицательно.
Тогда формула поваренной соли выглядит так: NaCl (хлорид натрия).
В название бинарных соединений к международному или сокращенному названию элемента добавляется окончание ид, 


Далее рассмотрим составление формулы хлорида магния:
Используя правило «нулевой суммы», составим такое уравнение:
+2 + (–1)х = 0 ⇒ х = 2, следовательно, формула вещества:
І. Рассмотрим примеры составления формул и определения зарядов элементов соединений по этому способу.
Пример 1. Составьте формулу оксида трехвалентного элемента.
1. Напишем схему формулы оксида трехвалентного элемента –
2. Укажем заряды элементов в этом соединении: 
3. Находим значение наименьшего кратного абсолютных значений зарядов атомов элементов (3 · 2 = 6).
4. Разделив значение наименьшего кратного на абсолютное значение зарядов элементов, запишем их как индексы при них:
6 : 3 = 2, 6 : 2 = 3; х = 2, у = 3;
тогда формула оксида
Алгебраическая сумма зарядов элементов в соединении равна нулю.
+3 · 2 = +6; –2 · 3 = –6; +6 + (–6) = 0
II. Если дана формула вещества, можно определить заряды элементов в
соединении.
Пример 2. Определите заряд фосфора (V) в его оксиде.
1. 
2. В соответствии с вышеуказанным правилом, составляем уравнение с
одним неизвестным:
2х + 5 · (–2) = 0; 2х = +10; х = +5

Метод «нулевой суммы»
ДЕЛАЕМ ВЫВОДЫ:
- 1. Электроны заселяют пространство вокруг ядра поэтапно, образуя энергетические уровни.
- 2. Область пространства, в которой вероятность нахождения электронов максимальна, называется электронным облаком, или орбиталью. Формы s-облаков – сферическая, а р-облаков – гантелеобразная.
- 3. Изображение электронов в атоме с помощью электронных облаков и распределение по уровням и подуровням называется электроннографической формулой.
- 4. Если элемент отдает электрон, он превращается в положительно заряженную частицу, а если принимает электрон – в отрицательно заряженную частицу. Эти заряженные частицы называются ионами.
- 5. Алгебраическая сумма зарядов элементов в соединении равна нулю.
Услуги по химии:
- Заказать химию
- Заказать контрольную работу по химии
- Помощь по химии
Лекции по химии:
- Основные понятия и законы химии
- Атомно-молекулярное учение
- Периодический закон Д. И. Менделеева
- Химическая связь
- Скорость химических реакций
- Растворы
- Окислительно-восстановительные реакции
- Дисперсные системы
- Атомно-молекулярная теория
- Строение атома в химии
- Простые вещества
- Химические соединения
- Электролитическая диссоциация
- Химия и электрический ток
- Чистые вещества и смеси
- Изменения состояния вещества
- Атомы. Молекулы. Вещества
- Воздух
- Химические реакции
- Закономерности химических реакций
- Периодическая таблица химических элементов
- Относительная атомная масса химических элементов
- Химические формулы
- Формулы веществ и уравнения химических реакций
- Химическая активность металлов
- Количество вещества
- Стехиометрические расчёты
- Энергия в химических реакциях
- Вода
- Необратимые реакции
- Кинетика
- Химическое равновесие
- Разработка новых веществ и материалов
- Зеленая химия
- Термохимия
- Правило фаз Гиббса
- Диаграммы растворимости
- Законы Рауля
- Растворы электролитов
- Гидролиз солей и нейтрализация
- Растворимость электролитов
- Электрохимические процессы
- Электрохимия
- Кинетика химических реакций
- Катализ
- Строение вещества в химии
- Строение твердого тела и жидкости
- Протекание химических реакций
- Комплексные соединения
Лекции по неорганической химии:
- Важнейшие классы неорганических соединений
- Водород и галогены
- Подгруппа кислорода
- Подгруппа азота
- Подгруппа углерода
- Общие свойства металлов
- Металлы главных подгрупп
- Металлы побочных подгрупп
- Свойства элементов первых трёх периодов периодической системы
- Классификация неорганических веществ
- Углерод
- Качественный анализ неорганических соединений
- Металлы и сплавы
- Металлы и неметаллы
- Производство металлов
- Переходные металлы
- Элементы 1 (1А), 2 IIA и 13 IIIA групп и соединения
- Элементы 17(VIIA), 16(VIA) 15(VA), 14(IVA) групп и их соединения
- Важнейшие S -элементы и их соединения
- Важнейшие d элементы и их соединения
- Важнейшие р-элементы и их соединения
- Производство неорганических соединений и сплавов
- Главная подгруппа шестой группы
- Главная подгруппа пятой группы
- Главная подгруппа четвертой группы
- Первая группа периодической системы
- Вторая группа периодической системы
- Третья группа периодической системы
- Побочные подгруппы четвертой, пятой, шестой и седьмой групп
- Восьмая группа периодической системы
- Водород
- Кислород
- Озон
- Водород
- Галогены
- Естественные семейства химических элементов и их свойства
- Химические элементы и соединения в организме человека
- Геологические химические соединения
Лекции по органической химии:
- Органическая химия
- Углеводороды
- Кислородсодержащие органические соединения
- Азотсодержащие органические соединения
- Теория А. М. Бутлерова
- Соединения ароматического ряда
- Циклические соединения
- Карбонильные соединения
- Амины и аминокислоты
- Химия живого вещества
- Синтетические полимеры
- Органический синтез
- Элементы 14(IVA) группы
- Азот и сера
- Растворы кислот и оснований
Сила Лоренца
Сила Лоренца действующая на электрон
В частном случае носителем заряда является электрон. Тогда в формулу (5) в качестве Q следует подставить
[ е = – 1.602 cdot 10^{-19} enspace Кл. ]
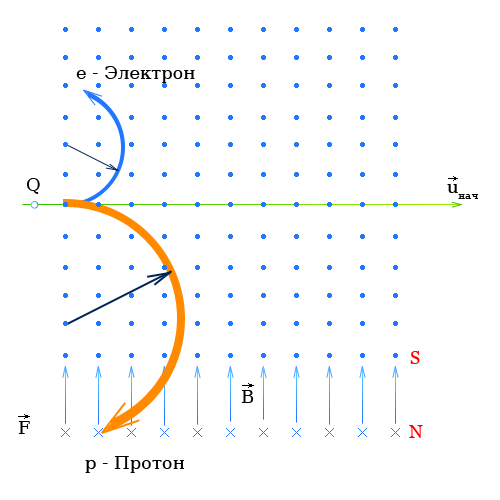
При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.
Сила Лоренца действующая на электрон и протон
Величина и направление силы Лоренца определяются соотношением
[ vector{F_{L}}= e vector{v} × vector{B} ]
где $vector{v}$, $vector{B}$ и $vector{F}$ образуют правую систему.
Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:
[ F_{L} = e v B ]
Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины.
Поэтому электрон движется в магнитном поле по окружности.
Вычислить, найти силу Лоренца действующую на электрон или протон
Радиус траектории электрона в магнитном поле
Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.
Если
| r | радиус круговой траектории электрона, | метр |
|---|---|---|
| me | 9,11 · 10-31 кг — масса электрона, | кг |
| e | 1,602 · 10-19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость электрона, | м/с |
| B | магнитная индукция, | Тесла |
то, приравнивая обе силы, получаем
[ evB = frac{m_{e} v^{2}}{r} ]
и, следовательно,
[ r = frac{m_{e} v}{eB} ]
Сила Лоренца действующая на протон
Электрический заряд протона равен по модулю заряду электрона, но имеет положительный знак.
[ p = + 1.602 cdot 10^{-19} enspace Кл. ]
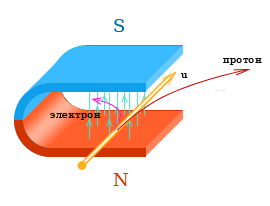
При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.
Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.
Сила Лоренца действующая на протон
Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.
Радиус траектории протона в магнитном поле
Если
| r | радиус круговой траектории протона, | метр |
|---|---|---|
| mp | 1,67 · 10-27 кг — масса протона, | кг |
| p | 1,602 · 10-19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость протона, | м/с |
| B | магнитная индукция, | Тесла |
Радиус траектории для протона будет вычисляться по аналогичной формуле
[ r = frac{m_{p} v}{p B} ]
Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц
Сила Лоренца |
стр. 667 |
|---|
Спин (spin – вращение) это наиболее простая вещь на которой можно продемонстрировать отличия квантовой механики от классической. Из определения кажется, что связан он с вращением, но не надо представлять себе электрон или протон вращающимися шариками. Как и в случае многих других устоявшихся научных терминов было доказано что это не так, но терминология уже устоялась. Электрон – точечная частица (нулевого радиуса). А спин отвечает за магнитные свойства. Если электрически заряженная частица движется по кривой траектории (в том числе вращается), то образуется магнитное поле. Электромагниты так работают – электроны движутся по проводам катушки. Но спин отличается от классического магнита. Вот неплохая анимация:
Если магнитики пропускать через неоднородное магнитное поле (обратите внимание на различную форму северного и южного полюсов магнита, задающего поле), то в зависимости от ориентации магнитика (его вектора магнитного момента) они будут притягиваться (отталкиваться) от полюса с большей концентрацией силовых линий магнитного поля (заостренный полюс магнита). В случае перпендикулярной ориентации магнитик вообще никуда не отклонится и попадет в центр экрана.
Пропуская электроны мы будем наблюдать только отклонение вверх или вниз на одно и то же расстояние. Это пример квантования (дискретности). Спин электрона может принимать только одно из двух значений относительно заданной оси ориентации магнита – «вверх» или «вниз». Поскольку электрон мысленно представить себе нельзя (у него нет ни цвета, ни формы, ни даже траектории движения), как и во всех подобных анимациях цветные шарики не отражают реальность, но суть думаю понятна.
Если электрон отклонился вверх, то говорят, что его спин направлен «вверх» (+1/2 условно обозначают) относительно оси магнита. Если вниз, то -1/2. И казалось бы спин можно описать обычным вектором, указывающим направление. У тех электронов, где он был направлен вверх, они и отклонятся вверх в магнитном поле, а у которых вниз – те соответственно вниз. Но не все так просто! Электрон отклоняется вверх (вниз) на одно и тоже расстояние относительно любой ориентации магнита. На видео выше можно было бы менять не ориентацию пропускаемых магнитиков, а поворачивать сам магнит, создающий магнитное поле. Эффект в случае обычных магнитиков был бы тот же. Что будет в случае электронов – в отличие от магнитиков они всегда будут отклонятся на одно и тоже расстояние вверх или вниз.
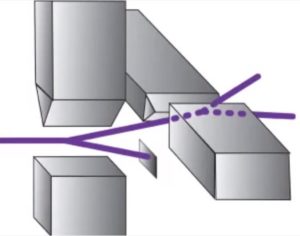
Если, например, пропустить вертикально расположенный классический магнитик через два перпендикулярно ориентированных друг относительно друга магнита, то отклоняясь вверх в первом, он не отклонится во втором вообще никак – его вектор магнитного момента будет перпендикулярен линиям магнитного поля. На видео выше это тот случай когда магнитик попадает в центр экрана. Электрон же обязан куда-нибудь отклонится.
Если мы будем пропускать через второй магнит только электроны со спином вверх, как на рисунке, то окажется что часть из них оказались еще и со спином вверх (вниз) относительно другой перпендикулярной оси. Вправо и влево фактически, но спин измеряют относительно выбранной оси, поэтому «вверх» и «вниз» общепринятая терминология вместе с указанием оси. Вектор не может быть направлен сразу вверх и вправо. Делаем вывод, что спин – это не классический вектор, прикрепленный к электрону наподобие вектора магнитного момента магнитика. Более того, зная, что спин электрона направлен вверх после прохождения первого магнита (отклоняющиеся вниз блокируем), невозможно предсказать куда он отклонится во втором случае: вправо или влево.
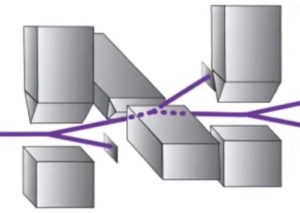
Ну и можно еще чуть-чуть усложнить эксперимент – блокировать электроны, отклонившиеся влево и пропустить через третий магнит, ориентированный как и первый.
И мы увидим, что электроны будут отклонятся как вверх, так и вниз. То есть электроны, попадающие во второй магнит все имели спин вверх относительно ориентации первого магнита, а потом часть из них стала вдруг со спином вниз относительно той же самой оси.
Странно! Если через такую конструкцию пропускать классические магнитики, повернутые под одним и тем же произвольно выбранным углом, то они всегда будут попадать в конце в одну и ту же точку экрана. Это называется детерминизмом. Повторив эксперимент при полном соответствии начальных условий мы должны получить тот же результат. В этом заключается основа предсказательной силы науки. Даже наша интуиция основана на повторяемости результатов в схожих ситуациях. В квантовой механике предсказать куда отклонится конкретно взятый электрон в общем случае невозможно. Хотя в некоторых ситуациях есть исключения: если поставить два магнита с одинаковой ориентацией, то если электрон отклонится вверх в первом, то он точно отклонится вверх и во втором. А если магниты повернуты на 180 градусов друг относительно друга и в первом электрон отклонился, например, вниз, то во втором он точно отклонится вверх. И наоборот. Сам по себе спин не меняется. Это уже хорошо)
Какие из всего этого можно сделать общие выводы.
- Многие величины, которые могли принимать любые значения в классической механике, могут иметь только некоторые дискретные (квантованные) значения в квантовой теории. Помимо спина энергия электронов в атомах является ярким примером.
- Объектам микромира нельзя приписать никакие классические характеристики до момента измерения. Нельзя полагать, что спин имел какое-то определенное направление до того как мы посмотрели куда отклонился электрон. Это общее положение и оно касается всех измеряемых величин: координат, скорости и т.п. Квантовая механика субъективна. Она утверждает, что объективный, не зависимый ни от кого классический мир, просто не существует. Теорема Белла наиболее наглядно демонстрирует данный факт. Роль субъекта (наблюдателя) в квантовой механике чрезвычайно важна.
- Процесс измерения затирает (делает неактуальной) информацию о предыдущем измерении. Если спин оказался направлен вверх относительно оси y, то неважно, что раньше он был направлен вверх относительно оси x, он может оказаться и спином вниз относительно той же самой оси x впоследствии. Опять же данное обстоятельство касается не только спина. Например, если электрон обнаружен в точке с координатами (x, y, z) это в общем случае не значит, что он был в этой точке до этого. Данный факт известен под названием «коллапс волновой функции».
- Есть такие физические величины значения которых невозможно знать одновременно. Например, нельзя измерить спин относительно оси x и одновременно относительно перпендикулярной ей оси y. Если мы попытаемся сделать это одновременно, то магнитные поля двух повернутых магнитов наложатся и мы вместо двух разных осей получим одну новую и измерим спин относительно нее. Последовательно измерять тоже не удастся вследствие предыдуще изложенного вывода №3. Это тоже общий принцип. Например, координату и импульс (скорость) тоже нельзя измерить одновременно с большой точностью — знаменитый принцип неопределенности Гейзенберга.
- Предсказать результат единичного измерения невозможно в принципе. Квантовая механика позволяет лишь вычислять вероятности того или иного события. Например, можно посчитать, что в опыте на первой картинке при ориентации магнитов 90° друг к другу 50% отклонится влево и 50% вправо. Предсказать куда отклонится конкретно взятый электрон нельзя. Данное общее обстоятельство известно как «правило Борна» и является центральным в Копенгагенской интерпретации.
- Детерминированные классические законы выводятся из вероятностных квантовомеханических за счет того, что в макроскопическом объекте очень много частиц и вероятностные флуктуации усредняются. Например, если в опыте на первой картинке пропускать вертикально ориентированный классический магнитик, то 50% составляющих его частиц будут «тянуть» его вправо, а 50% влево. В итоге он никуда не отклонится. При других ориентациях углов магнита меняется процентное соотношение, что в итоге и влияет на отклоняемое расстояние. Квантовая механика позволяет рассчитать конкретные вероятности и как следствие из нее можно вывести формулу для отклоняемого расстояния в зависимости от угла ориентации магнитика, получаемую обычно из классической электродинамики. Так классическая физика выводится и является следствием квантовой.
Да, описанные действия с магнитиками называются эксперимент Штерна-Герлаха.
Существует видеоверсия данного поста в части 2 и части 3 элементарного введения в квантовую механику.
Вторая статья цикла про спин электрона: Электроны в магнитном поле.