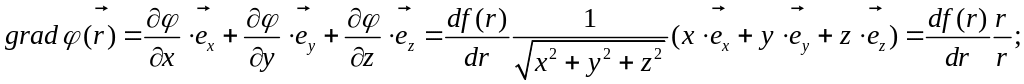Как найти направление градиента поля

Градиент скалярного поля

Если в каждой точке

пространства задан скаляр

– это скалярное
поле. Если
в каждой точке

пространства задан вектор

– это векторное
поле.

Если скалярное
поле

задается в ДСК,
то это означает, что скалярная функция
трех переменных

.
При рассмотрении локального поведения

часто используется порождаемое
им векторное поле

,
называемое градиентом
скалярного поля.

Одно из альтернативных
определений этой величины использует
понятие производной
по направлению,
заданному единичным вектором

.

Градиентом
скалярного поля

в точке

называется вектор

, (2.1)

величина которого
определяется производной по направлению
единичного вектора

нормали к поверхности уровня

,
проходящей через точку

,
в сторону возрастания значений

.

Напомним, что
нормалью к поверхности
S
в точке P
называется
прямая, проходящая через точку P
и перпендикулярная к касательной
плоскости к S
в этой точке.

Компоненты этого
вектора в ДСК

можно получить, используя приводимое
ранее выражение

.

Следовательно, в
ДСК
выражение для градиента скалярного
поля

имеет вид:

(2.2)

Полный дифференциал

от

определяется как приращение значения
этой величины при изменении радиус-вектора

на бесконечно малое приращение

(2.3)

Следовательно,

, (2.4)

где

– угол между векторами градиент

и

.
Следовательно, направление
вектора

– это направление скорейшего роста
скалярного поля в данной точке, а модуль
градиента – это скорость роста поля в
этом направлении.

Экстремальные
точки скалярного поля
– это точки, при смещении из которых с
точностью до членов, линейных по смещению,
поле остается неизменным. Из этого
определения вытекает, что частные
производные

в этих точках равны нулю, а возникающую
из этого условия систему трех уравнений
можно использовать для нахождения
экстремальных
точек

.
По этой же причине в этих точках

.

Указания по
решению задач

2.1. Для заданных
ниже функций найти градиент, точки
экстремума, направление наискорейшего
роста в заданной точке (x₀,
y₀,
z₀),
а также уравнение плоскости, касательной
к поверхности постоянного значения
функции в этой точке:

2.1.1.


;

2.1.2.

;

2.1.3.


;

2.1.4.

;

2.1.5.

.

Указание.
Пусть

=

(2.1.3). Для
нахождения компонент вектора градиента
и точек экстремума

вычислим:

Запишем систему
уравнений, определяющих
точки экстремума:

Решение полученной
системы определяет точку экстремума

с координатами

Выражение для
векторного поля градиента имеет вид:

,

а в точке

:

.

Для нахождения
уравнение плоскости, касательной к
поверхности постоянного значения

в точке

воспользуемся определяющим ее выражением
(1.22), в котором компоненты вектора

заменим на соответствующие значения
компонент вектора

:

.

2.2. Найти компоненты
вектора градиент:

2.2.1.

,
где

.

Указание.
В данной задаче

=

.

Следовательно:

Аналогично: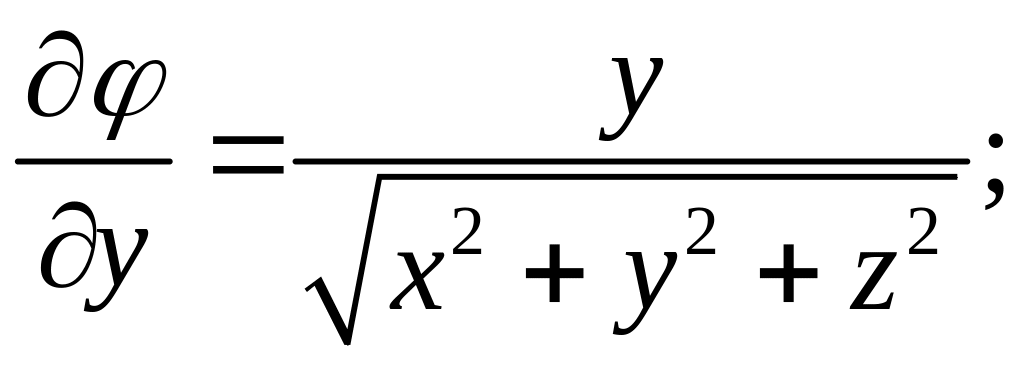

и

Подставляя найденные
выражения в (2.2), получим:

Ответ:

.

2.2.2.

,
где

;

Указание.
Решение данной задачи аналогично решению
предыдущей. Следует лишь учесть, что в
соответствии с определением, данным
при постановке задачи, вектор

.

Итак:
=

.

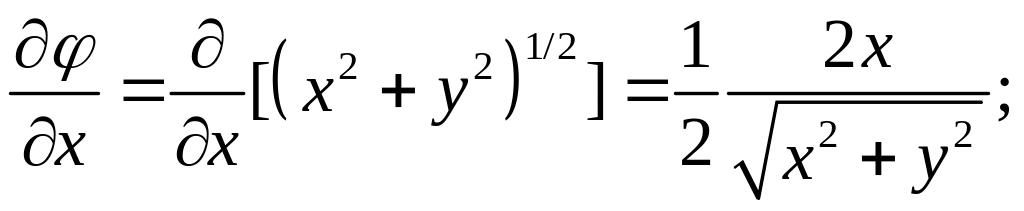
Следовательно:

Аналогично:

а

Подставляя найденные
выражения в (2.2), получим:

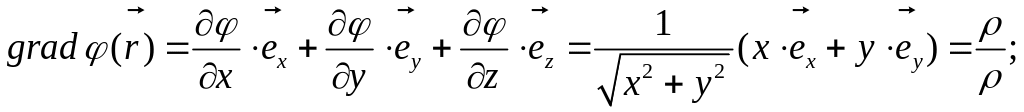
Ответ:

.

2.2.3.

;

2.2.4.

;

2.2.5.

,
где

— постоянный вектор,

;

2.2.6.

,
где


— постоянный
вектор,

;

2.2.7.

;

Указание.
В данной задаче

=

.

Следовательно:

Аналогично: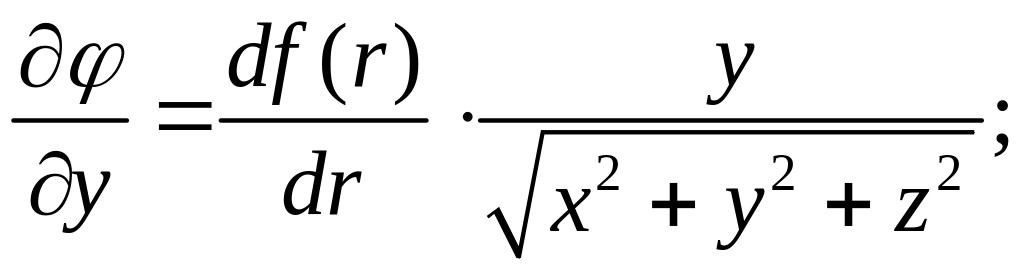

и

Подставляя найденные
выражения в (2.2), получим:

Ответ:

.

2.2.8.

;

2.2.9.

,
где

— постоянный вектор;

2.2.10.

;

2.2.11.


;

Указание.
В данной задаче

=

.

Следовательно:

Аналогично: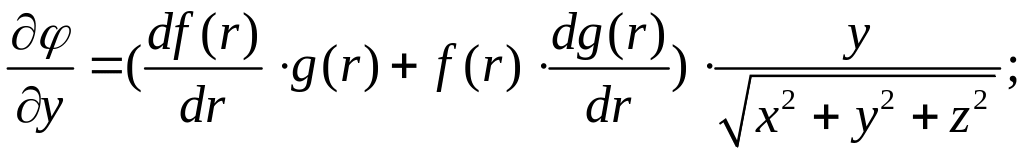

и

Подставляя найденные
выражения в (2.2), получим:

Ответ:

.

2.2.12.

,
где

— постоянный вектор.

Указание.
В данной задаче

=

=

.

Следовательно:

Аналогично:

и

Подставляя найденные
выражения в (2.2), получим:

Ответ:

.

2.2.13.

,
где

и

— постоянные векторы;

Указание.
В данной задаче

=



=

.

,

где

компонента векторного произведения на
ось x.

Примечание:
Полученный результат можно получить
быстрее, переписав, используя свойство
векторного произведения по отношению
к циклической перестановке векторов,
выражение для

в виде:

=
=
=

Следовательно:

Подставляя найденные
выражения в (2.2), получим:

Ответ:

.

2.2.14.

;

2.2.15.

;

2.2.16.

;

2.2.17.

;

2.2.18.

;

2.2.19.

;

2.2.20.

;

2.2.21.

2.2.22.

2.2.23.

2.3.1. Написать
уравнение прямой, проходящей через
точку А(3,
2, 1) в направлении наискорейшего роста
функции

,
r=|
|

Указание.
Уравнение
прямой, проходящей через точку

и параллельной вектору

,
определяется выражением (1.23a).
Направление
наискорейшего роста функции

в точке

определяется
вектором градиента этой функции в этой
точке.

В соответствии с
этими замечаниями найдем вначале
векторное поле градиента предложенной
функции.

В данной задаче

=

.

.

Следовательно:

Аналогично:

и

Подставляя найденные
выражения в (2.2), получим:

.

Для определения
значения вектора градиента в точке А(3,
2, 1) введем
радиус-вектор

,
вычислим его длину

и подставим в полученное выражение для
градиента:

Сократив записанное
уравнение на неравный нулю множитель,
получим искомое уравнение прямой.

Ответ:

.

2.3.2. Написать
уравнение плоскости, касательной к
поверхности постоянного значения
функции (x²+y²-3z)
в точке А(-1,
2, -1).

2.3.3. Найти угол
между направлениями наискорейшего
роста функций (x²+2y²–z²)
и r=|
|
в точке А(-1,
1, 1).

2.3.4. Найти силу,
действующую на частицу в точке А(-1,
-2, -1), если потенциальная энергия равна
(2x+y²–z).

Указание.
По определению,
если задана
потенциальная энергия

,
сила

,
действующую на частицу в точке

,
определяется выражением

.

2.3.5. Написать
уравнение плоскости, проходящей через
точку А(1,
1, 2), которая является плоскостью,
касательной к поверхности постоянного
значения функции

в этой точке.

— радиус-вектор,

— постоянный вектор с координатами (1,
2, 0).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Краткая теория

Градиентом называется вектор, направление которого указывает направление максимально быстрого возрастания функции f(x). Нахождение этой векторной величины связано с определением частных производных функции. Производная по направлению это скалярная величина и показывает скорость изменения функции при движении вдоль направления, заданного некоторым вектором.

Пример решения задачи

Условие задачи

Даны функция
, точка
и вектор
. Найти:

Решение задачи

Нахождение градиента функции

1) Найдем градиент
функции в точке
:

Искомый градиент:

Нахождение производной по направлению вектора

2) Найдем производную
в направлении вектора
:

где
-угол,
образованный вектором и осью

Искомая производная в
точке
:

На цену сильно влияет срочность решения (от суток до нескольких часов). Онлайн-помощь на экзамене/зачете осуществляется по предварительной записи.

Заявку можно оставить прямо в чате, предварительно скинув условие задач и сообщив необходимые вам сроки решения. Время ответа – несколько минут.

Понятие производной по направлению

рассматривается для функций двух и трёх переменных.
Чтобы понять смысл производной по направлению, нужно сравнить производные по определению

Следовательно,

Теперь можем найти производную по направлению данной функции по её формуле:

А сейчас – домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько
иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру
.

Пример 2.
Найти производную функции
в точке M
0
(1; 2)
по направлению вектора
, где M
1

–
точка с координатами (3; 0)
.

Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере –
в виде разложения по ортам координатных осей
, но эта хорошо знакомая тема из самого начала векторной алгебры.

Пример 3.
Найти производную функции
в точке M
0
(1; 1; 1)
по направлению вектора
.

Решение. Найдём направляющие косинусы вектора

Найдём частные производные функции в точке M
0

:

Следовательно, можем найти производную по направлению данной функции по её формуле:

.

Градиент функции

Градиент функции нескольких переменных в точке M
0

характеризует направление максимального роста этой функции в точке M
0

и
величину этого максимального роста.

Как найти градиент?

Нужно определить вектор, проекциями которого на оси координат

являются значения частных
производных
,
,
этой функции в соответствующей точке:

.

То есть, должно получиться представление вектора по ортам координатных осей
, в котором на каждый
орт умножается соответствующая его оси частная производная.

ГРАДИЕНТ ФУНКЦИИ
и = f(x, у,
z), заданной в некоторой обл. пространства (X Y Z),
есть вектор
с проекциями обозначаемый символами: grad где i, j, k
– координатные орты. Г. ф. – есть функция точки (х, у,
z), т. е. он образует векторное поле. Производная в направлении Г. ф. в данной точке достигает наибольшего значения и равна:
Направление градиента есть направление наибыстрейшего возрастания функции. Г. ф. в данной точке перпендикулярен поверхности уровня, проходящей через эту точку. Эффективность использования Г. ф. при литологических исследованиях была показана при изучении эоловых отл. Центральных Каракумов.

Геологический словарь: в 2-х томах. – М.: Недра
.
Под редакцией К. Н. Паффенгольца и др.
.
1978
.

Смотреть что такое “ГРАДИЕНТ ФУНКЦИИ” в других словарях:

Эта статья о математической характеристике; о способе заливки см.: Градиент (компьютерная графика) … Википедия

– (лат.). Разность в барометрических и термометрических показаниях в разных местностях. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ГРАДИЕНТ разность в показаниях барометра и термометра в один и тот же момент… … Словарь иностранных слов русского языка


градиент
– Изменение значения некоторой величины на единицу расстояния в заданном направлении. Топографический градиент — это изменение высоты местности на измеренном по горизонтали расстоянии. Тематики релейная защита EN gradient of the differential protection tripping characteristic … Справочник технического переводчика


Градиент
– вектор, направленный в сторону наискорейшего возрастания функции и равный по величине ее производной в этом направлении: где символами ei обозначены единичные векторы осей координат (орты) … Экономико-математический словарь


Одно из основных понятий векторного анализа и теории нелинейных отображений. Градиентом скалярной функции векторного аргумента из евклидова пространства Е n наз. производная функции f(t).по векторному аргументу t, то есть n мерный вектор с… … Математическая энциклопедия


Градиент физиологический
– – величина, отражающая изменение к либо показателя функции в зависимости от другой величины; напр., градиент парциального давления разность парциальных дав лений, определяющая диффузию газов из альвеол (акцинусов) в кровь и из крови в… … Словарь терминов по физиологии сельскохозяйственных животных


I Градиент (от лат. gradiens, род. падеж gradientis шагающий) Вектор, показывающий направление наискорейшего изменения некоторой величины, значение которой меняется от одной точки пространства к другой (см. Поля теория). Если величина… … Большая советская энциклопедия


Градиент
– (от лат. gradiens шагающий, идущий) (в математике) вектор, показывающий направление наискорейшего возрастания некоторой функции; (в физике) мера возрастания или убывания в пространстве или на плоскости какой либо физической величины на единицу… … Начала современного естествознания

Книги

• Методы решения некоторых задач избранных разделов высшей математики. Практикум , Клименко Константин Григорьевич, Левицкая Галина Васильевна, Козловский Евгений Александрович. В данном практикуме рассматриваются методы решения некоторых типов задач из таких разделов общепринятого курса математического анализа, как предел и экстремум функции, градиент и производная…

Лекция
15.
«Дифференцирование функции
нескольких переменных»

Градиент
функции двух переменных и производная
по направлению.

Определение
.
Градиентом функции

называется
вектор

.

Как
видно из определения градиента функции,
компонентами вектора градиента являются
частные производные функции.

Пример.


Вычислить градиент функции

в
точке A(2,3).

Решение.
Вычислим частные производные функции.

В
общем виде градиент функции имеет вид:

=

Подставим
координаты точки A(2,3)
в выражения частных производных

В
градиент функции в
точке A(2,3)
имеет вид:

Аналогично
можно определить понятие градиента
функции трех переменных:

Определение
.
Градиентом функции от трех переменных

называется
вектор

Иначе,
этот вектор может быть записан следующим
образом:

Определение

производной по направлению.

Пусть
задана функция двух переменных

и
произвольный вектор

Рассмотрим
приращение этой функции, взятое вдоль
данного вектора

Т.е.
вектор
коллинеарный по отношению к вектору
.
Длина приращения аргумента

Производной
по некоторому направлению называется
предел отношения приращения функции
вдоль данного направления на длину
приращения аргумента, когда длина
приращения аргумента стремиться к 0.

Формула
для вычисления производной по направлению
.

Исходя
из определения градиента, производную
функции по направлению, можно посчитать
следующим образом.

некоторый
вектор. Вектор с тем же направлением,
но единичной

длины назовем

Координаты
этого вектора вычисляются следующим
образом:

Из
определения производной по направлению
,
производная по направлению
может быть вычислена по следующей
формуле:

Правая
часть этой формулы представляет собой
скалярное произведение двух векторов

Поэтому,
производную по направлению можно
представить в виде следующей формулы:

Из
этой формулы следует несколько важных
свойств вектора градиента.

Первое
свойство градиента следует из того
очевидного факта,
что скалярное произведение двух векторов
принимает наибольшее значение, когда
вектора совпадают по направлению. Второе
свойство следует из того, что скалярное
произведение перпендикулярных векторов
равно нулю. Кроме того, из первого
свойства следует геометрический смысл
градиента – градиент это вектор, вдоль
направления, которого производная по
направлению наибольшая. Так как
производная по направлению определяет
тангенс угла наклона касательной к
поверхности функции, то градиент
направлен вдоль наибольшего наклона
касательной.

Пример
2.

Для
функции (из примера 1)

Вычислить
производную по направлению

в
точке A(2,3).

Решение.
Для вычисления производной по направлению
надо вычислить вектор градиента в
указанной точке и единичный вектор
направления
(т.е.
нормализовать вектор
).

Вектор
градиента был вычислен в примере 1:

Вычисляем
единичный вектор направления:

Вычисляем
производную по направлению:

#2.
Максимум и минимум функции нескольких
переменных.

Определение.

Функция

Имеет
максимум в точке
(т. е. при
и
),
если

Определение.

Совершенно аналогично говорят, что
функция

Имеет
минимум в точке
(т. е. при
и
),
если

для
всех точек
,
достаточно близких к точке
и отличных от нее.

Максимум
и минимум функции называются экстремумами
функции, т. е. говорят, что функция имеет
экстремум в данной точке, если эта
функция имеет максимум или минимум в
данной точке.

Например,
функция

Имеет
очевидный минимум z
= -1 при x
= 1 и y
= 2.

Имеет
максимум в точке
при x
= 0 и y
= 0.

Теорема.

(необходимые условия экстремума).

Если
функция
достигает экстремума при
,
,
то каждая частная производная первого
порядка от z
или обращается в нуль при этих значениях
аргументов, или не существует.

Замечание.

Эта теорема не является достаточной
для исследования вопроса об экстремальных
значениях функции. Можно привести
примеры функций, которые в некоторых
точках имеет нулевые частные производные,
но не имеет экстремума в этих точка.

Пример.

Функции, которая имеет нулевые частные
производные, но не имеет экстремума.

В
самом деле:

Достаточные
условия экстремума.

Теорема.

Пусть в некоторой области, содержащей
точку
,
функция
имеет непрерывные
частные производные до третьего порядка
включительно; пусть, кроме того, точка
является
критической точкой функции
,
т.е.

Тогда
при
,

Пример 3.2. Исследовать
на максимум и на минимум функцию

Найдем
критические точки, т.е. точки, в которых
первые частные производные равны нулю
или не существуют.

Сначала вычисляем
сами частные производные.

Приравниваем
частные производные нулю и решаем
следующую систему линейных уравнений

Умножаем второе
уравнение на 2 и складываем с первым.
Получится уравнение только от y.

Находим
и подставляем
в первое уравнение

Преобразуем

Следовательно,
точка ()
является критической.

Вычислим
вторые производные второго порядка и
подставим в них координаты критической
точки.

В нашем случае,
подставлять значения критических точек
не надо, так как вторые производные
являются числами.

В итоге имеем:

Следовательно,
найденная критическая точка, является
точкой экстремума. Более того, так как

то эта точка
минимума.

1 0
Градиент направлен по нормали к поверхности уровня (или к линии уровня, если поле плоское).

2 0
Градиент направлен в сторону возрастания функции поля.

3 0
Модуль градиента равен наибольшей производной по направлениювданной точке поля:

Эти свойства дают инвариантную характеристику градиента. Они говорят о том, что вектор gradU указывает направление и величину наибольшего изменения скалярного поля в данной точке.

Замечание 2.1.
Если функция U(x,y) есть функция двух переменных, то вектор

лежит в плоскости oxy.

Пусть U=U(x,y,z) и V=V(x,y,z) дифференцируемых в точке М 0 (x,y,z) функции. Тогда имеет место следующие равенства:

а) grad()= ; б) grad(UV)=VgradU+UgradV;

в) grad(U V)=gradU gradV; г) г) grad = , V ;

д) gradU( = gradU, где , U=U() имеет производную по .

Пример 2.1.
Дана функция U=x 2 +y 2 +z 2 . Определить градиент функции в точке М(-2;3;4).

Решение.
Согласно формуле (2.2) имеем

Поверхностями уровня данного скалярного поля являются семейство сфер x 2 +y 2 +z 2 , вектор gradU=(-4;6;8) есть нормальный вектор плоскостей.

Пример 2.2.
Найти градиент скалярного поля U=x-2y+3z.

Решение.
Согласно формуле (2.2) имеем

Поверхностями уровня данного скалярного поля являются плоскости

x-2y+3z=С; вектор gradU=(1;-2;3) есть нормальный вектор плоскостей этого семейства.

Пример 2.3.
Найти наибольшую крутизну подъема поверхности U=x y в точке М(2;2;4).

Решение.
Имеем:

Пример 2.4.
Найти единичный вектор нормали к поверхности уровня скалярного поля U=x 2 +y 2 +z 2 .

Решение.
Поверхности уровня данного скалярного Поля-сфера x 2 +y 2 +z 2 =С (С>0).

Градиент направлен по нормали к поверхности уровня, так что

Определяет вектор нормали к поверхности уровня в точке М(x,y,z). Для единичного вектора нормали получаем выражение

Пример 2.5.
Найти градиент поля U= , где и постоянные векторы, r –радиус вектор точки.

Решение.
Пусть

Тогда: . По правилу дифференцирования определителя получаем

Следовательно,

Пример 2.6.
Найти градиент расстояния , где P(x,y,z) – изучаемая точка поля, P 0 (x 0 ,y 0 ,z 0) – некоторая фиксированная точка.

Решение.
Имеем – единичный вектор направления .

Пример 2.7.
Найти угол между градиентами функций в точке М 0 (1,1).

Решение.
Находим градиенты данных функций в точке М 0 (1,1), имеем

; Угол между gradU и gradV в точке М 0 определяется из равенства

Отсюда =0.

Пример 2.8.
Найти производную по направлению, радиус- вектор равен

Решение.
Находим градиент этой функции:

Подставляя (2.5) в (2.4), получим

Пример 2.9.
Найти в точке М 0 (1;1;1) направление наибольшего изменения скалярного поля U=xy+yz+xz и величину этого наибольшего изменения в этой точке.

Решение.
Направление наибольшего изменения поля указывается вектором grad U(M). Находим его:

И, значит, . Это вектор определяет направление наибольшего возрастания данного поля в точке М 0 (1;1;1). Величина наибольшего изменения поля в этой точке равна

Пример 3.1.
Найти векторные линии векторного поля где -постоянный вектор.

Решение.
Имеем так что

Умножим числитель и знаменатель первой дроби на х, второй-на у, третий- на z и сложим почленно. Используя свойство пропорций, получим

Отсюда xdx+ydy+zdz=0, а значит

x 2 +y 2 +z 2 =A 1 , A 1 -const>0. Умножив теперь числитель и знаменатель первой дроби (3.3) на с 1 , второй –на с 2 , третий на с 3 и сложив почленно, получим

Откуда с 1 dx+c 2 dy+c 3 dz=0

И, следовательно, с 1 x+c 2 y+c 3 z=A 2 . A 2 -const.

Искомые уравнения векторных линий

Эти уравнения показывают, что векторные линии получаются в результате пересечения сфер, имеющих общий центр в начале координат, с плоскостями, перпендикулярными вектору . Отсюда следует, что векторные линии являются окружностями, центры которых находятся на прямой, проходящей через начало координат в направлении вектора с. Плоскости окружностей перпендикулярны указанной прямой.

Пример 3.2.
Найти векторную линию поля проходящую через точку (1,0,0).

Решение.
Дифференциальные уравнения векторных линий

Отсюда имеем . Решая первое уравнение . Или если ввести параметр t, то будем иметь В этом случае уравнение принимает вид или dz=bdt, откуда z=bt+c 2 .

Линейной формойОтносительно вектораНазывают скалярное произведе

Ние вектораНа некоторый векторНе зависящий от-радиус-

Вектор точки– вектор, соединяющий точки

Скалярное полеНазывается дифференцируемым в точкеИз области

Если приращение поляВ этой точке можно представить в виде

(29.3)

Где– расстояние между точками

Градиентом дифференцируемого в точкеСкалярного поля называют векторИз (29.3). Обозначение:

Если поле дифференцируемо в каждой точке области, то оно дифференцируемо в. В этом случае

При заданной декартовой системе координат

Свойства градиента:

Если– базис в ортогональной криволинейной системе координат

, то

Где– параметры Ламе, определенные формулой

(29.6)

В цилиндрической системе координат  в сферической системе координат

Дифференциалом скалярного поляНазывают скалярное произведение

Пусть _ – единичный вектор, указывающий направлениеВ точкеОбласти– произвольная точка, отличная отИ такая, что вектор коллинеарен вектору

Предел– расстояние между

ТочкамиI, если он существует, называют производной поляВ точ

КеПо направлениюИ обозначают символом

Где

4

ИЛИ

Если е имеет направление, то

Пример 29.3. Найти величину и направление градиента скалярного поля В точке

Находим частные производные функции к  их значения в точке:

По формуле (29.4) получаем

Величину градиента находим по формуле (29.5):

Пример 29.4. Найти производную поляВ точке

По направлению вектора iОбразующего с координатными осями острые углы Установить характер изменения поля в данном направлении. Частные производные функцииВ точкеИмеют значения:

По условию задачиПоскольку

, а угол– острый, то. По

Формуле (29.7) находим

Так какСкалярное полеВозрастает в данном направлении.

< Предыдущая		Следующая >