Явление электромагнитной индукции заключается в том, что в результате изменения во времени магнитного потока, который пронизывает замкнутый проводящий контур, в контуре возникает электрический ток. Открыто это явление было физиком из Великобритании Максом Фарадеем в 1831 году.
Формула магнитного потока
Введем обозначения, необходимые нам для записи формулы. Для обозначения магнитного потока используем букву Ф, площади контура – S, модуля вектора магнитной индукции – B, α – это угол между вектором B→ и нормалью n→ к плоскости контура.
Магнитный поток, который проходит через площадь замкнутого проводящего контура, можно задать следующей формулой:
Φ=B·S·cos α,
Проиллюстрируем формулу.
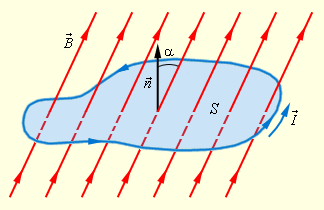
Рисунок 1.20.1. Магнитный поток через замкнутый контур. Направление нормали n→ и выбранное положительное направление l→ обхода контура связаны правилом правого буравчика.
За единицу магнитного потока в СИ принят 1 вебер (Вб). Магнитный поток, равный 1 Вб, может быть создан в плоском контуре площадью 1 м2 под воздействием магнитного поля с индукцией 1 Тл, которое пронизывает контур по направлению нормали.
1 Вб=1 Тл·м2
Закон Фарадея
Изменение магнитного потока приводит к тому, что в проводящем контуре возникает ЭДС индукции δинд. Она равна скорости, с которой происходит изменение магнитного потока через ограниченную контуром поверхность, взятой со знаком минус. Впервые экспериментально установил это Макс Фарадей. Он же записал свое наблюдение в виде формулы ЭДС индукции, которая теперь носит название Закона Фарадея:
Закон Фарадея:
δинд=-∆Φ∆t
Правило Ленца
Согласно результатам опытов, индукционный ток, который возникает в замкнутом контуре в результате изменения магнитного потока, всегда направлен определенным образом. Создаваемое индукционным током магнитное поле препятствует изменению вызвавшего этот индукционный ток магнитного потока. Ленц сформулировал это правило в 1833 году.
Проиллюстрируем правило Ленца рисунком, на котором изображен неподвижный замкнутый проводящий контур, помещенный в однородное магнитное поле. Модуль индукции увеличивается во времени.
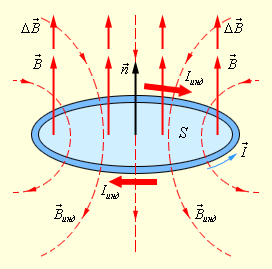
Рисунок 1.20.2. Правило Ленца
Здесь ∆Φ∆t>0, а δинд<0 < 0. Индукционный ток Iинд протекает навстречу выбранному положительному направлению l→ обхода контура.
Благодаря правилу Ленца мы можем обосновать тот факт, что в формуле электромагнитной индукции δинд и ∆Φ∆t противоположны по знакам.
Если задуматься о физическом смысле правила Ленца, то это частный случай Закона сохранения энергии.
Причины возникновения индукционного тока в движущихся и неподвижных проводниках
Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две:
- Изменение магнитного потока вследствие перемещения всего контура или отдельных его частей в магнитном поле, которое не изменяется со временем;
- Изменение магнитного поля при неподвижном контуре.
Перейдем к рассмотрению этих случаев подробнее.
Перемещение контура или его частей в неизменном магнитном поле
При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δинд можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила.
На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B→ направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью.
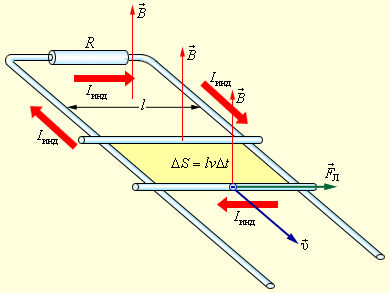
Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Отражена составляющая силы Лоренца, которая действует на свободный электрон
На свободные заряды подвижной части контура воздействует сила Лоренца. Основная составляющая силы Лоренца в данном случае направлена вдоль проводника и связана с переносной скоростью зарядов υ→. Модуль этой сторонней силы равен:
FЛ=eυ→B.
Работа силы FЛ на пути l равна:
A=FЛ·l=eυBl.
По определению ЭДС:
δинд=Ae=υBl.
Значение сторонней силы для неподвижных частей контура равно нулю. Для соотношения δинд можно записать другой вариант формулы. Площадь контура с течением времени изменяется на ΔS=lυΔt. Соответственно, магнитный поток тоже будет с течением времени изменяться: ΔΦ=BlυΔt.
Следовательно,
δинд=∆Φ∆t.
Знаки в формуле, которая связывает δинд и ∆Φ∆t, можно установить в зависимости от того, какие направления нормали и направления контура будут выбраны. В случае выбора согласованных между собой по правилу правого буравчика направлений нормали n→ и положительного направления обхода контура l→ можно прийти к формуле Фарадея.
При условии, что сопротивление всей цепи – это R, то по ней будет протекать индукционный ток, который равен Iинд=δиндR. За время Δt на сопротивлении R выделится джоулево тепло:
∆Q=RIинд2∆t=υ2B2l2R∆t
Парадокса здесь нет. Мы просто не учли воздействие на систему еще одной силы. Объяснение заключается в том, что при протекании индукционного тока по проводнику, расположенному в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, которая связана с относительной скоростью движения зарядов вдоль проводника. Благодаря этой составляющей появляется сила Ампера FА→.
Для рассмотренного выше примера модуль силы Ампера равен FA =IBl. Направление силы Ампера таково, что она совершает отрицательную механическую работу Aмех. Вычислить эту механическую работу за определенный период времени можно по формуле:
Aмех=-Fυ∆t=-IBlυ∆t=-υ2B2l2R∆t
Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.
Изменение магнитного поля при неподвижном контуре
Вихревое электрическое поле – это электрическое поле, которое вызывается изменяющимся магнитным полем.
В отличие от потенциального электрического поля работа вихревого электрического поля при перемещении единичного положительного заряда по замкнутому проводящему контуру равна δинд в неподвижном проводнике.
В неподвижном проводнике электроны могут приводиться в движение только под действием электрического поля. А возникновение δинд нельзя объяснить действием силы Лоренца.
Первым, кто ввел понятие вихревого электрического поля, был английский физик Джон Максвелл. Случилось это в 1861 году.
Фактически, явления индукции в подвижных и неподвижных проводниках протекают одинаково. Так что в этом случае мы тоже можем использовать формулу Фарадея. Отличия касаются физической причины возникновения индукционного тока: в движущихся проводниках δинд обусловлена силой Лоренца, в неподвижных – действием на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
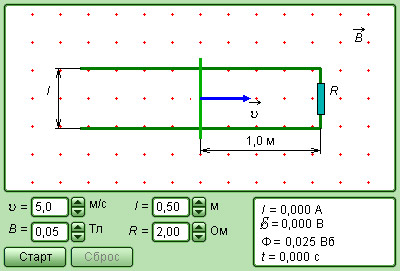
Рисунок 1.20.4. Модель электромагнитной индукции
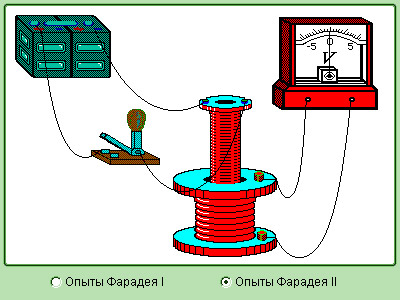
Рисунок 1.20.5. Модель опытов Фарадея
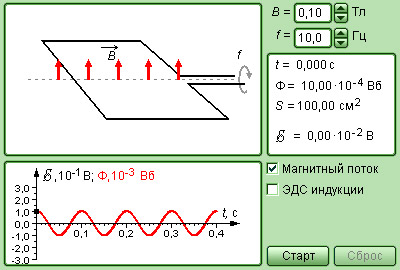
Рисунок 1.20.6. Модель генератора переменного тока
Направление индукционного тока
При внесении в катушку магнита в ней возникает
индукционный ток. Если к катушке присоединить гальванометр, то можно заметить,
что направление тока будет зависеть от того приближаем ли мы магнит или удаляем
его.
Магнит будет взаимодействовать с катушкой либо
притягиваясь, либо отталкиваясь от нее. Это будет возникать вследствие того,
что катушка с проходящим по ней током, будет подобна магниту с двумя полюсами.
Направление индуцируемого тока будет определять, где у катушки будет находиться
какой из полюсов.
Если приближать к катушке магнит, то в ней будет
возникать индукционный ток такого направления, что катушка обязательно будет
отталкиваться от магнита. Если мы будет удалять магнит от катушки, то при этом
в катушке возникнет такой индукционный ток, что она будет притягиваться к
магниту.
Стоит отметить, что не важно каким полюсом мы
подносим или убираем магнит, всегда при подносе катушка будет отталкиваться, а
при удалении притягиваться. Различие состоит в том, что при приближении магнита
к катушке магнитный поток, который будет пронизывать катушку, увеличивается,
так как у полюса магнита кучность линий магнитной индукции увеличивается. А при
удалении магнита, магнитный поток, пронизывающий катушку, будет уменьшаться.
Узнать направление индукционного тока можно. Для
этого существует правило Ленца. Оно основано на законе сохранения.
Рассмотрим следующий опыт.

Имеется катушка с подключенным к ней
гальванометром. К одному и краев катушки начинаем подносить магнит, например,
северным полюсом. Количество линий, которые будут пронизывать поверхность
каждого витка катушки, будет увеличиваться. Следовательно, будет увеличиваться
и значение магнитного потока.
Так как должен выполняться закон сохранения,
должно возникнуть магнитное поле, которое будет препятствовать изменению
магнитного потока. В нашем случае магнитный поток увеличивался, следовательно,
ток должен течь в таком направлении, чтобы линии вектора магнитной индукции,
создаваемые катушкой, были направлены в противоположном направлении линиям
магнитной индукции, создаваемым магнитом.
То есть они должны в нашем случае быть направлены
вверх. Теперь воспользуемся правилом буравчика. Направляем большой палец правой
руки по необходимому нам направлению линий магнитной индукции, то есть – вверх.
Тогда остальные пальцы укажут, в какую сторону должен быть направлен
индукционный ток. В нашем случае, слева на право.
Аналогичный процесс происходит при удалении
магнита. Убираем магнит, магнитный поток уменьшается, следовательно, должно
возникнуть поле которое будет увеличивать магнитный поток. То есть поле линии
магнитной индукции, которого будут сонаправлены с линиями магнитной индукции,
создаваемыми постоянным магнитом. В нашем случае эти лини направлены вниз.
Опять пользуемся правилом буравчика и определяем направление индукционного
тока.
Правило Ленца.
Согласно правилу Ленца возникающий в
замкнутом контуре индукционный ток своим магнитным полем противодействует тому
изменению магнитного потока, которым он вызван. Более кратко это правило можно
сформулировать следующим образом: индукционный ток направлен так, чтобы
препятствовать причине, его вызывающей.
Применять правило Ленца для нахождения направления
индукционного тока в контуре надо так:
1. Определить
направление линий магнитной индукции вектора В внешнего
магнитного поля.
2. Выяснить,
увеличивается ли поток вектора магнитной индукции этого поля через поверхность,
ограниченную контуром (ΔФ >
0), или уменьшается (ΔФ <
0).
3. Установить
направление линий магнитной индукции вектора В’ магнитного
поля индукционного тока. Эти линии должны быть согласно правилу Ленца
направлены противоположно линиям магнитной индукции вектора В’ при ΔФ > 0
и иметь одинаковое с ними направление при ΔФ <
0.
4. Зная
направление линий магнитной индукции вектора В’, найти
направление индукционного тока, пользуясь правилом буравчика.
Направление индукционного тока
определяется с помощью закона сохранения энергии. Индукционный ток во всех
случаях направлен так, чтобы своим магнитным полем препятствовать изменению
магнитного потока, вызывающего данный индукционный ток.
Вихревое
электрическое поле.
Причина возникновения электрического тока в
неподвижном проводнике – электрическое поле.
Всякое изменение магнитного поля порождает
индукционное электрическое поле независимо от наличия или отсутствия замкнутого
контура, при этом если проводник разомкнут, то на его концах возникает разность
потенциалов; если проводник замкнут, то в нем наблюдается индукционный ток.
Индукционное электрическое поле является вихревым.Направление силовых линий вихревого электрического поля совпадает
с направлением индукционного тока
Индукционное электрическое поле имеет совершенно
другие свойства в отличии от электростатического поля.
|
электростатическое поле |
индукционное электрическое поле (вихревое электрическое |
|
1. |
1. |
|
2. силовые |
2. силовые |
|
3. |
3. |
|
4. работа |
4. работа |
Электромагнитная индукция

Содержание
- Явление электромагнитной индукции
- Магнитный поток
- Закон электромагнитной индукции Фарадея
- Правило Ленца
- Самоиндукция
- Индуктивность
- Энергия магнитного поля
- Основные формулы раздела «Электромагнитная индукция»
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):


Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ):

При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec{B} ) ЭДС электромагнитной индукции равна:

где ( alpha ) – угол между векторами ( vec{B} ) и ( vec{v} ).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_{is} ), возникающая в катушке с индуктивностью ( L ), по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec{B} ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ), создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3.2 (63.4%) 94 votes
В этой статье мы рассмотрим, что такое правило Ленца и какого его практическое применение. Это правило позволяет быстро определить направление индукционного тока. На самом деле, правило Ленца тесно связано с принципом сохранения энергии — об этом также читайте в этой статье.

Формулировка
Правило Ленца обычно формулируется следующим образом:
Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.
Википедия
Давайте расшифруем это предложение.
Давайте расшифруем это предложение. Давайте начнем с причины. Причиной протекания индукционного тока является изменяющийся поток магнитной индукции B через поверхность, охватываемую контуром, в котором должен протекать электрический ток.
Противодействие причине здесь заключается в том, что когда поток увеличивается, магнитное поле Bind, создаваемое индукционным током, направлено так, чтобы уменьшить поток. И наоборот, когда поток уменьшается, индуцированное магнитное поле направлено так, чтобы усилить поток. В общем, если поле B перпендикулярно плоской поверхности, охватывающей замкнутый проводник, то
Когда ФB уменьшается, то Вind параллельно В.
Когда ФB увеличивается, то Bind антипараллельно B.
В более общем случае необходимо задать условие для углов между этими векторами.
Как только мы установили, как направлен вектор магнитной индукции Bind (внутри контура), мы должны связать индукционный ток с этим вектором и определить его направление.
Пример правила Ленца в действии
Теперь мы покажем правило Ленца в действии; вот конкретный пример.
В магнитном поле, создаваемом прямолинейным проводником с током, имеется круговой контур (кольцо), лежащий в одной плоскости с проводником (рис. 2а.). Ток в прямолинейном проводнике течет вверх. В каком направлении будет течь электрический ток в кольце, если мы прижмем его к проводнику?

Ток в прямолинейном проводнике создает вокруг себя магнитное поле. Для определения направления вектора магнитной индукции в кольце мы используем хорошо известный метод правой руки. Мы располагаем большой палец так, как направлен электрический ток, а пальцы покажут нам магнитное поле, «оборачивающееся» вокруг этого электрического тока. Справа от проводника, где находится кольцо, линии поля идут «внутрь», как показано на рис. 2б.

Сближение кольца вызывает увеличение потока магнитного поля, проникающего через кольцо (увеличивается значение магнитной индукции B). Согласно правилу Ленца, ток в кольце должен протекать таким образом, чтобы вектор магнитного поля Bind, создаваемого этим током, был направлен противоположно вектору, вызывающему явление индукции B. То есть, вектор Bind направлен «в нашу сторону». (рис. 2в).

Снова применим правило правой руки. На этот раз мы укажем большим пальцем вектор индукции Bind, а остальные пальцы покажут нам направление индукционного тока. Он будет протекать против часовой стрелки.
Правило Ленца и закон сохранения энергии
То, что «скрывается» под правилом Ленца — это фундаментальный принцип сохранения энергии в физике. Вы узнаете об этом, прочитав данный подраздел.
Посмотрите на следующую экспериментальную установку (см. рисунок 3).
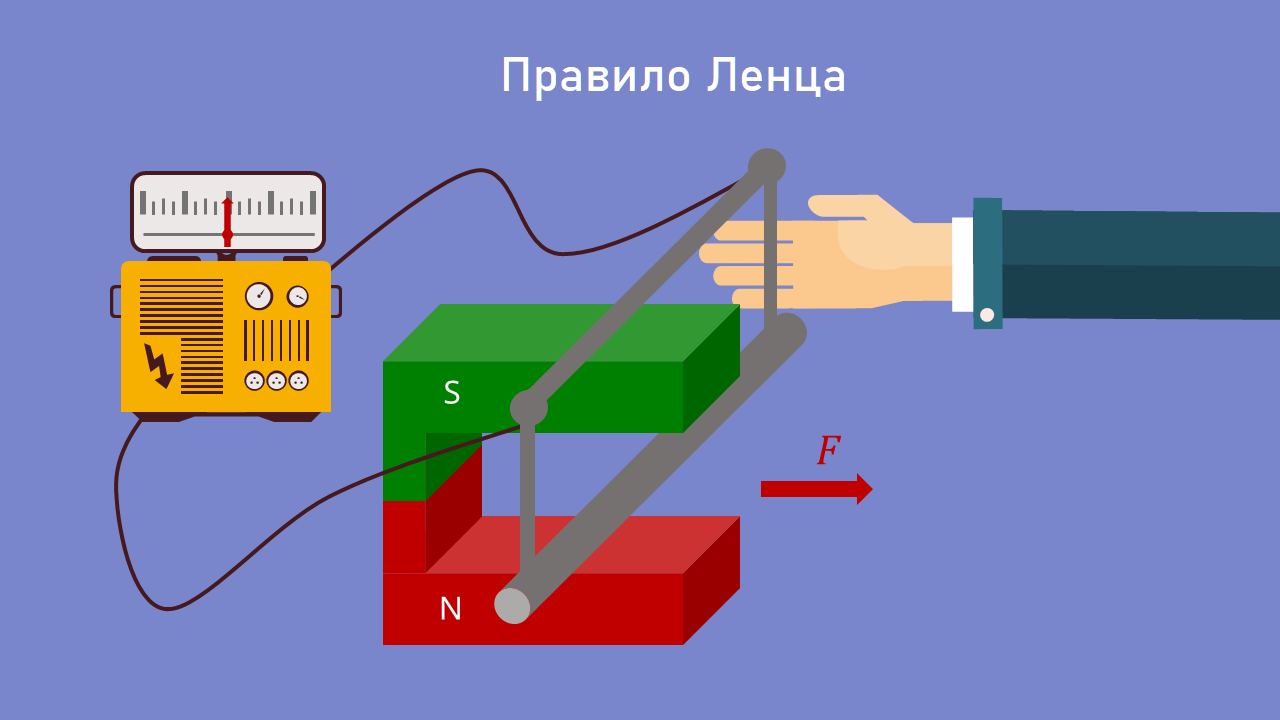
Для эксперимента подвесьте качели проводника в магнитном поле подковообразного магнита. Подковообразный магнит располагается так, чтобы северный полюс находился внизу, а южный — вверху. Вы подключаете проводник к амперметру вне магнитного поля, поэтому во всей цепи нет источника.
В эксперименте мы теперь перемещаем качели проводника в направлении, перпендикулярном силовым линиям магнитного поля, в нашем случае «из подковообразного магнита». Для перемещения качающегося проводника нужна сила F. Когда частицы движутся в магнитном поле, действует сила Лоренца, происходит разделение зарядов, а значит, и возникает индукционный ток. Это можно наблюдать по отклонению стрелки амперметра.
Для определения направления индукционного тока применяется правило левой руки. Большой палец указывает направление, в котором электроны перемещаются под действием силы F, т.е. «из подковы». Ваш указательный палец указывает направление магнитного поля, от северного к южному полюсу. Наконец, средний палец указывает направление, в котором электроны притягиваются силой Лоренца. На конце проводника, в сторону которого указывает ваш средний палец, образуется избыток электронов и это приводит к изменению направления тока.
Однако, в силу правила Ленца, точно в тот же момент должна действовать противодействующая сила F‘, направленная в противоположную сторону от причины F. Эта противодействующая сила создается индукционным током, который, так сказать, пытается восстановить исходное состояние.
Вы можете еще раз проверить направление силы F‘ с помощью правила левой руки. На этот раз большой палец указывает направление движения электронов. Итак, в проводнике, который перемещается под действием силы F внутри магнита , большой палец направлен в плоскость рисунка, а указательный палец снова направлен от северного полюса к южному. Затем средний палец указывает направление силы F’. Это направление согласуется с правилом Ленца и действует в направлении, противоположном направлению движения проводника. Чтобы проиллюстрировать это, мы провели эти рассуждения одно за другим. В реальном эксперименте, однако, все это происходит параллельно.
Можно также сравнить правило Ленца с поведением детей (аналог индукционного тока). Когда их родители (аналог причины) говорят им что-то, они сначала хотят сделать прямо противоположное. Если вы будете помнить об этой мнемонике, вы гарантированно не забудете правило Ленца.
Сохранение энергии для индукции также может быть соблюдено только с помощью правила Ленца.
Чтобы проверить это, вы можете провести следующий мысленный эксперимент. Если бы сила из F‘ была направлена в противоположную сторону, то есть равна силе F, раскачивание качелей ускорялось бы все больше и больше. И это без добавления дополнительной энергии извне. Таким образом, можно было бы создать вечный двигатель, что противоречит закону сохранения энергии.
Применение
Правило Ленца необходимо для многих применений в технике. Например, в вихретоковом тормозе. Этот тормоз не изнашивается, поскольку отсутствует трение. Тормозная сила генерируется магнитными полями. Например, такие тормоза есть у поездов и грузовиков. Электродвигатели также работают по этому принципу.
Правило Ленца защитит вас, даже если в вашу машину ударит молния. Клетка Фарадея также основана на этом принципе.
Все металлодетекторы, которые вы знаете по аэропортам или магазинам, работают одинаково. Они генерируют магнитное поле с помощью катушки. Если в магнитном поле находится металлический предмет, в нем индуцируются вихревые токи. Согласно правилу Ленца, эти токи направлены таким образом, что противодействуют причине возникновения тока. Поэтому магнитное поле детектора становится слабее. Это также уменьшает ток в металлодетекторе, эта разница измеряется, что приводит, например, к сигналу тревоги.
Металлодетекторы также используются в некоторых светофорах, только здесь катушка расположена в асфальте под машинами. Таким образом, светофор, так сказать, замечает, что автомобиль ждет, и по возможности переключает его на зеленый. Как видите, правило Ленца важно для многих областей электротехники, а также в повседневной жизни.
Список использованной литературы
- Мякишев Г. Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений. – М.: Просвещение, 2010.
- Касьянов В. А. Физика. 11 кл.: Учеб. для общеобразоват. учреждений. – М.: Дрофа, 2005.
- Сивухин Д. В. § 64. Электромагнитная индукция // Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 265. — 688 с.
