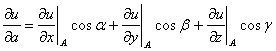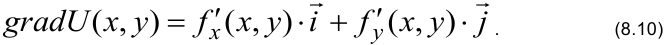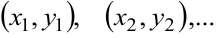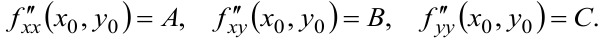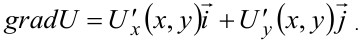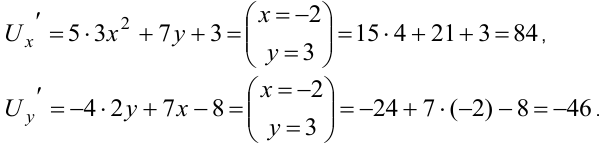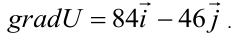Как найти направление наибольшего возрастание функции

Приветствую всех. Сегодня на занятии хотелось бы затронуть немало важную тему, связанную одновременно с дифференциальным исчислением и векторной алгеброй. Мы постараемся как можно меньше углубляться в теоретические тезисы и побольше сделаем упор на решение практических задач. Незамедлительно начнём.

Определение слова “градиент” в математике нужно усвоить.

Градиент – это вектор показывающий направление наибольшего возрастания функции. Модуль вектора градиента показывает скорость изменения функции.

Запишем формулу для нахождения вектора градиента:

При нашем раскладе можно с теорией закончить, этого будет достаточно.

Разберём простенький примерчик для начала.

Никто ведь не забыл как брать частные производные? Если подзабыли, ссылочка (на статью) будет в конце урока.

Было слишком уж просто для нас, возьмём что-нибудь посложнее.

Такого плана примеры уже устно не решишь, хотя… Нет, всё же возможно.

Не будем перенапрягаться сильно, рассмотрим последний пример и пойдём отдыхать.

Берёмся за дело.

Не отчаиваемся что уже конец практики, у вас всегда есть возможность найти похожие задачки в интернете или взять в библиотеке задачник по высшей математике. Практикуйтесь, практикуйтесь, и ещё раз практикуйтесь. Спасибо за внимание.

Другие темы:

Пусть
функцияu(x,y,z)
определена в некоторой области D.
Возьмём в этой области некоторую точку
P(x,y,z)
и рассмотрим некоторый луч,исходящий
из неё Направление этого луча зададим
углами,
которые он образует с осямиox
, oy
и oz.
Пусть точка P(x1
y1
z1)
– некоторая другая точка, расположенная
на этом же луче. Рассмотрим вектор
1.
Обозначим
=.

С
одной стороны
=,

а
с другой стороны координаты вектора
есть его проекции на координатные оси.
Поэтому

Так
как координаты x,y,z
однозначно характеризуют точку P
в

области
D,
то можно писать u(x,y,z)=
u(P)
– и есть функция точки P.
Точку P1
можно рассматривать как приращённую
относительно (.) P,

т.е.
есть
приращение аргумента функцииu(P).
Тогда соответствуещее приращение
функции
u(P)
= u()
– u(P).

Составим
отношение
и
перейдём к пределу при.

Определение:конечный
предел, если он существует,

(1)

называется
производной от функции u(x,y,z)=u(P)
по направлению
в(.)P.
Этот предел
обозначают символом
или(x,y,z).
Как видно, величина производной по
направлению зависит от точки P,
где она вычисляется, и от направления
,
в котором берётся, т.е. от углов.
Если (.)P
фиксированная, то производная зависит
лишь от направления. В частном случае,
если направление
совпадает
с положительным направлением осиox,
т.е.

, то предел (1) есть просто частная
производная функции u(x,y,z)
по x

Аналогично,
если
совпадает сoy
или oz
,то
будет
совпадать с частными производнымииКак
известно, частные производные,

характеризуют скорость изменения
функции u(x,y,z)
в направлении координатных осей.
Производная же
характеризует скорость изменения
функции в направлении луча.

Модуль
определяет величину скорости изменения
функции, знак

–
характер изменения ( увеличение или
уменьшение ).

Как вычислять
производную по направлению в общем
случае? Оказы-

вается справедливой

Теорема:
если
функция u(x,y,z)
дифференцируема в (.) P(x,y,z),то
её

производная
по любому направлениюсуществует
в этой точке и равна,
(2) ,

где
-направляющие
косинусы луча.

Доказательство.
Т.к. по условию
u(x,y,z)
дифференцируема, то её полное приращение
можно записать в виде

,
где через

обозначена
величина бесконечно малая высшего
порядка малости по сравнению с б.м.в.
Т.к.

.

Составим
отношение
.

Перейдём
к пределу при
.
Учтём что;вычисляются

в(.)
P
и есть числа, потому отне
зависят-тоже.
Но тогда

,т.е.
(2).

Из
(2) видно снова, что еслисовпадает
с осьюox,
тои потомуи аналогично, еслисовпадёт
с осямиoy
и oz
. Из (2) видно так же, что при изменении
направления дифференцирования по лучу
на противоположноезнакизменяется на противоположный :

.
.

Замечание:
Если всё
происходит на плоскости ,

то
направление луча
вполне
определяется заданием одного угла.

Тогда

и потому.
()

§11 Градиент функции. В выражении производной по направлению

множители
можно рассматри

вать
как проекции на координатные оси

единичного
вектора луча

рассмотрим
вектор, проекции которого на

координатные
оси равны значениям частных производных

в
выбранной точке P(x,y,z).
Этот вектор носит особое название –
градиент
функции.
Обозначают его одним из символов: grad
u
или
.
Значокназывается
оператором«Набла
», читается
«Набла u».
Введён
английским математиком Гамильтоном.

Определение:
Градиентом
функции u(x,y,z)
называется вектор, проекциями которого
служат значения частных производных
этой

Функции,
т.е.
grad
u.

Из
определения видно, что проекции графика
на координатные оси зависят от точки
P(x,y,z)
и изменяются с изменением её координат.
Тем самым каждоё точке из области
определения функции u(x,y,z)
соответствует определённый вектор –
градиент этой функции. Из определения
градиента и выражения производной по
направлению
видно, чтоgrad
u,
т.е. производная функции по направлению
равна скалярному произведению градиента
функции на единичный вектор направления.
Но
grad u

–
угол между градиентом и лучом
,

но
тогда
,
т.е. производная функции по направлению
равна проекцииy
градиента функции на направление
дифференцирования. Отсюда видно, что
наибольшее значение производная
достигает, когда

,т.е..
И равно это наибольшее значениеgrad
u.Таким
образом,
grad
u
иесть наибольшее возможное значение
производной
в данной точкеP,
а направление grad
u
совпадает с направлением луча из точки
P,
вдоль которого функция и меняется
быстрее всего, т.е. направление градиента
есть направление быстрейшего изменения
функции u(x,y,z).
Между градиентом и поверхностями уровня
функции есть определённая связь.

Теорема:
Направление
градиента функции u(x,y,z)
в каждой точке совпадает с направлением
нормали к поверхности уровня этой
функции, проходящей через эту точку.

Доказательство.
Возьмём любую точку из области определения
функции
.
Уравнение поверхности уровня, проходящей
через точкубудет

Уравнение
нормали к этой поверхности в точке

будет

,

т.е.
координаты направляющего вектора
нормали
.
Но это и значит, чтоgrad
u
является таким вектором (у него такие
же координаты).

Замечание:
в случае
плоскости для функции
поверхности
уровня есть линии уровня иgrad
u
лежит в плоскости XOY.
По теореме grad
u
в каждой точке перпендикулярен линии
уровня, проходящей через эту точку.
Проводя линии уровня и отмечая в различных
точках вектор
,
мы получим графическое изображение
поля, определяемого функцеий.
В том направлении, где линии уровня
расположены гуще, поля изменяютя быстрее.
Аgrad
u
показывает величину и точное направление
наибыстрейшего изменения.

Основные
свойства градиента функции (–
оператора).

1. ;

2. ;

3.

доказательство
этих свойств аналогичные. Докажем 3.

или
u
– градиент сложной функции равен
производной функции по промежуточному
аргументу, умноженный на его градиент.
Действительно
Эти
свойства показывают, что свойства
градиента похожи на свойства производных
функций.

Пример:
С какой наибольшей скоростью может
возрастать функция
при переходе точкичерез?

Решение.
Согласно теории наибольшая скорость
возрастания функции в

будет
в направлении градиента и величина
скорости равна модулю градиента в этой
точке.

,

grad
u.

Построив
вектор, реально получим направление
наибольшего возрастания функции, его
величина в точке
будетu.

Градиент функции

Градиент — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины u. Другими словами, направление градиента есть направление наибыстрейшего возрастания функции.

Назначение сервиса. Онлайн калькулятор используется для нахождения градиента функции нескольких переменных. (см. пример) При этом решаются следующие задачи:

• нахождение частных производных функции, запись формулы градиента, вычисление наибольшой скорости возрастания функции в указанной точке;
• вычисление градиента в точке A, нахождение производной в точке A по направлению вектора a;
• нахождение полного дифференциала функции.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Решение со всеми исходными формулами сохраняется в формате Word.

Полный дифференциал для функции двух переменных: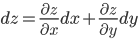

Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=dxf(x,y,z)dx+dyf(x,y,z)dy+dzf(x,y,z)dz

Алгоритм нахождения градиента

1. Вычисление частных производных по формуле:

   

2. Вычисление частных производных в точке A.
3. Нахождение направляющих углов вектора a.
4. Вычисление производной в точке A по направлению вектора a по формуле;

   
5. Наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

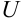
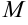
Наибольший интерес представляет вопрос о направлении быстрейшего возрастания функции в точке . Вопрос просто решается с помощью вектора -градиента функции .

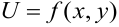
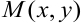
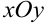
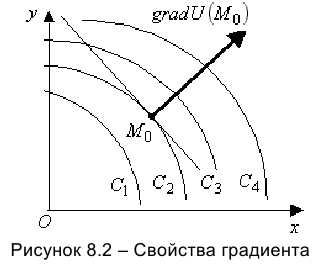
Градиентом функции в данной точке называется вектор, расположенный в плоскости с началом в точке

Основное свойство градиента: направление градиента функции в точке является направлением быстрейшего возрастания функции, его модуль равен наибольшей скорости возрастания 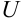в заданной точке.

Другое свойство градиента: он перпендикулярен касательной линии уровня, проходящей через точку начала градиента.

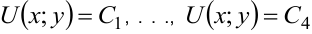
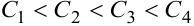
Иллюстрация свойств градиента — на рисунке 8.2. Показаны линии уровня , причем .

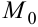
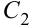
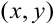
Через точку , лежащую на линии с уровнем проведены касательная и градиент, которые перпендикулярны друг другу. Градиент направлен в сторону возрастания функции .

8.6 Экстремум функции двух переменных. Необходимые и достаточные условия экстремума

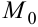
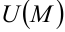
Точка называется точкой максимума функции , если значение функции в этой точке больше, чем её значение в любой другой точке некоторой (хотя бы малой) окрестности точки . Аналогично (с заменой «больше» на «меньше») определяется точка минимума функции.

Точки минимума и максимума объединяются под общим названием точки экстремума.

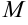
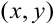
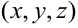
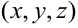
Для функции двух переменных точка имеет две координаты для функции трёх переменных — три координаты . При этом окрестностью точки является открытый шар с центром в этой точке.

Поиск критических точек, т.е. точек в которых может быть экстремум функции 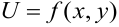, производится при помощи необходимого условия экстремума:

Решение системы (8.12) определяет координаты критических точек

Однако необходимого условия мало для существования точек экстремума.

Нужно провести исследование критических точек с использованием достаточных условий экстремума.

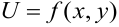
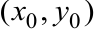
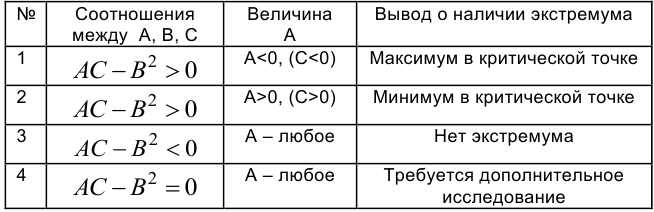
Для функции двух переменных введём обозначения для вторых частных производных в критической точке :

Достаточные условия приводим в таблице 4.

Таблица 4 — Достаточные условия экстремума функции двух переменных

Пример:

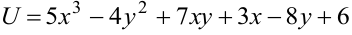
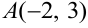
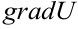
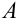
Дана функция и точка . Найти градиент функции в заданной точке .

Решение:

Используем формулу градиента

Определяем частные производные и вычисляем их при .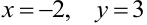

При вычислении частной производной по одной из переменных вторая переменная считается постоянной величиной.

Значения частных производных подставляем в формулу градиента:

Ответ: .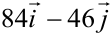

Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:

Высшая математика для 1 курса

Возможно вам будут полезны эти страницы:

Направление – наибольшее возрастание

Cтраница 1

Вектор градиента определяет направление наибольшего возрастания функции качества. Поэтому этот метод оптимален в том смысле, что он стимулирует движение рабочей точки в наилучшем направлении к цели.
 [2]

Направление градиента совпадает с направлением наибольшего возрастания функции, поэтому подбор приращений Ду, До, , Ар необходимо осуществлять по направлению градиента.
 [3]

Таким образом, выражение (8.24) дает направление наибольшего возрастания целевой функции ZO ( W) в точках гребня.
 [4]

Если в точке М0 узнать величины частных производных, то будет определено направление наибольшего возрастания ф-ции и, следовательно, противоположное ему направление наибольшего убывания: ф-ции в данной точке.
 [6]

Если в точке Л / 0 узнать величины частных производных, то будет определено направление наибольшего возрастания ф-ции и, следовательно, противоположное ему направление наибольшего убывания ф-ции в данной точке.
 [8]

Таким образом, градиентом физической величины называется ее изменение, приходящееся на единицу расстояния в направлении наибольшего возрастания. Следовательно, градиент есть вектор, направленный в сторону наибольшего возрастания физической величины.
 [9]

Распространение тепла в твердом диэлектрике обусловлено напряженностью температурного поля G – d – Q-jdn, где п – координата в направлении наибольшего возрастания температуры. Тепловой поток ( выраженный в ваттах), проходящий в единицу времени через поверхность 5, равен P – kGS, где k – коэффициент внутренней тепловодности диэлектрика.
 [10]

Он показывает направление наибольшего возрастания функции в данной точке, которое всегда перпендикулярно проходящей через нее линии ( поверхности) уровня.
 [11]

Затем строим линию уровня lOxj 5х2 0 и вектор ( 10 5), которые взаимно перпендикулярны. Нетрудно показать, что вектор дает направление наибольшего возрастания линейной функции.
 [12]

Этот метод, по сравнению с другими, имеет преимущества в отношении сходимости, которая в этом случае меньше зависит от ряда факторов. Метод основывается на использовании свойства вектора градиента указывать направление наибольшего возрастания функции в данной точке. В процессе применения метода используют, как его разновидность, также решение системы нелинейных уравнений и нахождение минимума функции переменных, участвующих в задаче.
 [13]

Действительно, наилучшим направлением при этом было бы направление вектора-градиента целевой функции в точке оврага WOBp – Проблема овражного поиска возникает по той причине, что практически при локальном поиске находится не точка оврага WOBp, а некоторая точка W, принадлежащая малой окрестности точки WOBp. При узких оврагах направления вектора-градиента в точках W и WOBp существенно различаются и, следовательно, направление наибольшего возрастания целевой функции при овражном поиске неизвестно.
 [14]

Линии равного уровня функции минимума ZO ( W) показаны полужирными. Нетрудно установить, что точка Э является точкой максимума функции ZO ( W), ее образно можно представить как вершину горы. Очевидно, что направлением наибольшего возрастания функции минимума в точке гребня, например в точке А будет направление, касательное к линии гребня в этой точке. Но это направление не совпадает с градиентными направлениями ни функции z2, ни функции z3 в точке А, так как эти направления ортогональны линиям равного уровня.
 [15]

Страницы:  

   1

   2