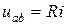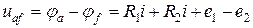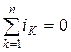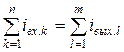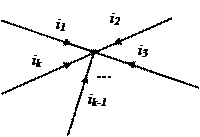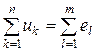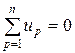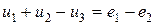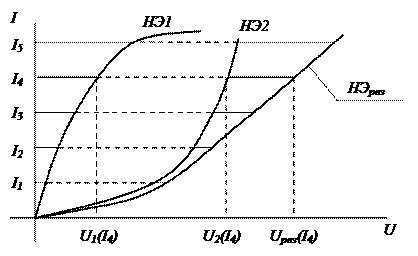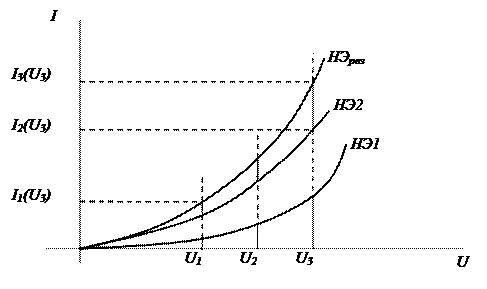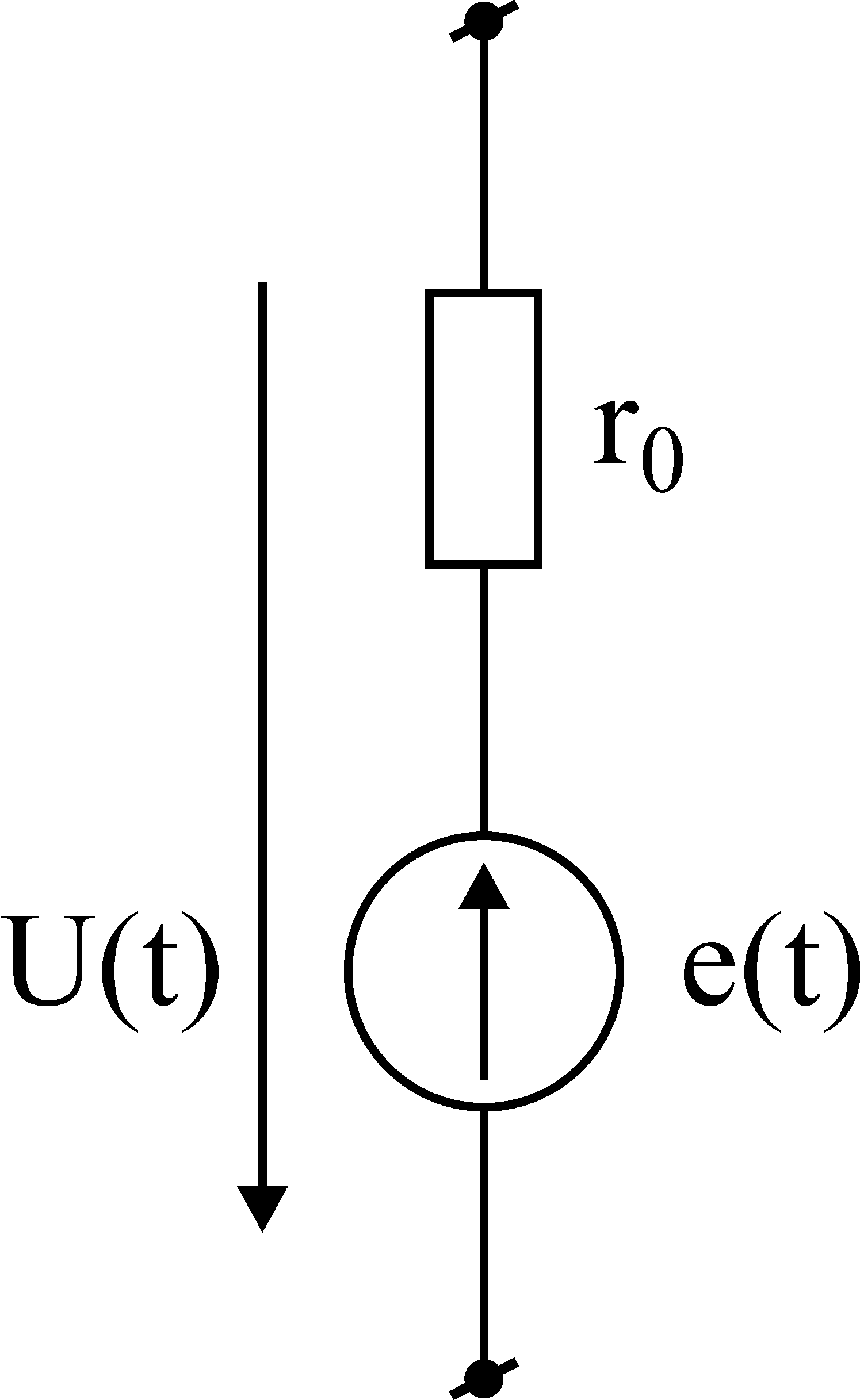Для расчета электрической цепи применяют два закона Кирхгофа. (Скорее их можно отнести не к законам, а к правилам. Но в большинстве учебников пишут именно о “законах” Кирхгофа. Поэтому и здесь будем обращаться к законам).
Первый закон Кирхгофа
Первый закон Кирхгофа применяют к узлам электрической цепи и выражают баланс токов в них. Первый закон Кирхгофа гласит:
Алгебраическая сумма токов сходящихся в узле электрической цепи равна 0.
Под словом “алгебраическая” имеется в виду, что учитывается знак перед током: “плюс” или “минус”.
В общем виде первый закон Кирхгофа можно записать как:
Для примера возьмем узел, в котором протекают токи, указанные стрелками (далее рассмотрим это все на конкретных схемах).
Токи, втекающие и вытекающие из узла, берутся с противоположными знаками. Втекающие в узел токи берутся со знаком, например, “+”, а вытекающие с “-“ (можно вытекающие брать с “+”, а втекающие с “-“). Главное, чтобы втекающие и вытекающие токи отличались по знаку.
Будем считать токи положительными, если они втекают в узел, а вытекающие из узла – отрицательными. Тогда первый закон Кирхгофа для узла, представленного на рисунке 2, запишется:
I1-I2+I3+I4=0
Это выражение можно записать и в следующем виде:
I2=I1+I3+I4;
Ток I2 мы перенесли за знак равенства, его знак поменялся на противоположный (был с “минусом”, стал с “плюсом”).
Остальные токи мы не переносим, поэтому их знаки не меняются.
Согласно последнему выражению, первый закон Кирхгофа можно сформулировать по-другому:
Сумма токов, втекающих (подходящих) в узел, равна сумме токов, вытекающих (отходящих) из узла.
Все это говорит о том, что в узле эти токи не остаются и заряд в узле не накапливается.
Для более полного понимания, представим электрическую цепь (схему электрической цепи), для которой запишем первый закон Кирхгофа.
Запишем для этой цепи первый закон Кирхгофа для узла “a” (о том, как определить количество уравнений по первому и второму законам Кирхгофа, рассмотрим в конце ).
I1+I2-I3=0 или I3=I1+I2.
Второй закон Кирхгофа
Этот закон применяется к контурам электрической цепи и выражает баланс напряжений в них. Второй закон Кирхгофа звучит так:
Алгебраическая сумма ЭДС в замкнутом контуре (с учетом направления обхода контура) равна алгебраической (учитывается знак “+” или “-“) сумме падений напряжений на всех сопротивлениях (элементах) этого контура.
Для того, чтобы правильно составить уравнения по второму закону Кирхгофа, нужно пользоваться следующим правилом:
ЭДС берется со знаком “+”, если ее действие совпадает с направлением обхода контура. Напряжение на элементе контура берется со знаком “+”, если направление тока через данный элемент совпадает с направлением обхода контура. Если не совпадает направление обхода контура с направлением тока через элемент, то напряжение этого элемента берется со знаком “-“.
Запишем второй закон Кирхгофа для цепи, представленной ниже:
Выбираем направление обхода контура по часовой стрелке. В данном случае направление тока и направление обхода контура совпадают, поэтому I·R1 и I·R2 взяли со знаком “+”. А также совпадает направление обхода контура и действие ЭДС, поэтому ЭДС также записали со знаком “+”.
Возьмем еще один пример.
Запишем для этой цепи второй закон Кирхгофа. Обход выбираем по часовой стрелке (указали обход контура на схеме круговой стрелкой внутри контура). Как видим, направление обхода контура и направление тока I1 совпадают, а ток I2 направлен напротив обхода контура.
Следовательно, падение напряжения на резисторе R1 запишется со знаком “+”, т. е. +I1·R1. А падение напряжения на R2 запишется со знаком “-“, т. е. –I2·R2.
Направление действия ЭДС совпадает с обходом контура, поэтому ЭДС E берем со знаком “+”.
Запишем второй закон Кирхгофа для этой цепи:
I1·R1-I2·R2=E
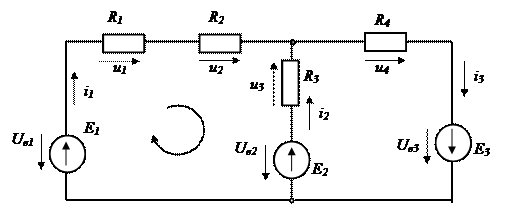
Ну и напоследок рассмотрим сложную электрическую цепь, состоящую из нескольких источников и резисторов.
Введем произвольно направление токов в ветвях, а также укажем на схеме в виде круговых стрелок направление обхода контуров.
Токи в ветвях направили произвольно, обход контура выбрали по часовой стрелке, а также узлы в этой схеме обозначили буквами a и b. Для того, чтобы понять, как и сколько уравнений по первому и второму законам Кирхгофа нужно составить для данной цепи, необходимо посчитать количество ветвей, узлов и независимых контуров.
Подробно вышесказанные понятия электрической цепи мы рассмотрим в следующих статьях. А пока вкратце.
Узел – это место соединения трех и более ветвей в электрической цепи (в данном случае таких узлов два. Это узлы “a” и “b”.
Ветвь – это участок электрической цепи, который образуется одним или несколькими последовательно соединенными элементами и через все эти элементы протекает один и тот же ток.
Контур – это любой замкнутый путь электрической цепи, проходящий по двум или нескольким ветвям.
Так же есть такое понятие как независимый контур.
Независимый контур должен включать в себя хотя бы одну ветвь, не входящую в другие контуры.
На рисунке 9 будет три контура, два из которых независимые. Если контур 1 независимый, контур 2 независимый(таким образом все три ветви этой схемы цепи вошли в эти независимые контуры). Тогда контур 3 уже независимым не будет, поскольку все ветви “заняты” остальными двумя контурами.
Или если контур 1 независимый (он включает в себя ветви с элементами E и R1). Контур 3 независимый (он включает в себя ветви с элементом E и ветвь с элементом R3. Элемент R3 ранее не входил в первый независимый контур), поэтому контур 3 считается независимым.
Получается, что все ветви “заняты”. Тогда контур 2 независимым уже не будет, поскольку в него не входят ветви или ветвь ранее не входящую в другие контура. Все ветви вошли в ранее независимые контуры 1 и 3.
В цепи на рисунке 9, в общем случае, три ветви, два узла и два независимых контура. Общее количество уравнений по законам(правилам) Кирхгофа составляется столько, сколько ветвей в схеме цепи за вычетом количества ветвей, где есть источник тока (именно источник тока, а не ЭДС). В нашей схеме нет источников тока, следовательно, составляются три уравнения по законам Кирхгофа. Теперь осталось определить, сколько уравнений нужно составить по первому и второму законам Кирхгофа. Общее количество уравнений будет три. Формула для определения количества уравнений по первому закону Кирхгофа следующая:
N1з.к.=Ny-1, где Ny – количество узлов.
Ny=2, тогда
N1.з.к.=Ny-1=2-1=1
Т. е. по первому закону Кирхгофа составляется одно уравнение для данной цепи, а общее количество уравнений – три. Таким образом, мы получаем, что по второму закону Кирхгофа нужно составить два уравнения. Или для определения количества уравнений по второму закону Кирхгофа есть формула:
N2.з.к.=Nв-(Ny-1), где Nв – количество ветвей
Nв=3, тогда:
N2.з.к.=3-(2-1)=2
По второму закону Кирхгофа составляется два уравнения. Составим систему, состоящую из трех уравнений. Одно уравнение по первому закону Кирхгофа (это уравнение составляется для любого узла a или b) и двух уравнений по второму закону Кирхгофа для двух любых независимых контуров, например, составим для контуров 1 и 2.
Неизвестными в данной системе являются токи I1, I2 и I3. Решая данную систему, находят эти неизвестные.
О том, как решаются задачи с более сложными цепями, мы поговорим в следующих статьях.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток – простыми словами;
Куда течет ток и как определить его направление
Содержание
- 1 Природа электрического тока
- 2 Виды токов
- 3 Как определяется направление электротока
- 4 Видео по теме
Чтобы правильно рассчитать параметры конкретной электрической цепи, нужно знать, как определяется направление тока. Это невозможно сделать без понимания природы электрического тока и тех правил, которым он подчиняется.
Природа электрического тока
Атомы состоят из ядер и вращающихся вокруг них электронов. У последних заряд отрицательный. Ядро включает в себя частицы, заряженные положительно (протоны), и нейтральные (нейтроны). Обычно атом не имеет заряда, однако если по каким-то причинам электроны покидают орбиту, то он теряет свою нейтральность и становится ионом, заряженным положительно.
Движущиеся электроны создают электрический ток. Он возникает при наличии упорядоченного перемещения зарядов. Сила тока в цепи выражается количеством электронов, переместившихся через фиксированное поперечное сечение проводника за единицу времени. Эта величина обозначается символом «I». Он применяется уже много десятилетий. Такое обозначение является традиционным.
В радиосхемах обычно рассматривается движение зарядов по проводникам или по полупроводникам. Особенностью металлов считается то, что электроны отрываются от атомов относительно легко. Они движутся под действием электрополя, которое образуется благодаря разности потенциалов на клеммах источника электротока. Определить, каково направление электрического тока можно по правилу Ампера.
Виды токов
Сила постоянного тока с течением времени не изменяется. В этом случае после включения заряд перемещается по проводнику с одной и той же скоростью. Поэтому определение направления тока осуществляется по простым правилам.
В электротехнике распространено использование переменного тока. В этом случае речь идёт о его циклическом изменении, которое происходит по синусоидальному закону. При этом электрический ток меняет и направление, и величину.
Например, в нашей сети электропитания ток имеет частоту 50 Гц и соответствует амплитуде изменения напряжения 220 В. Но в различных странах используется бытовая электросеть с другими параметрами. При этом направление силы тока будет всегда меняться циклически.
Иногда дополнительно выделяют пульсирующий ток. Он сохраняет свой знак, но периодически меняет абсолютную величину. Также возможно существование электротока, который носит произвольный характер. В таком случае силу и направление тока предсказать невозможно.
Надо заметить, что в проводниках движение электронов существует всегда. Оно становится направленным под действием электрополя. Однако и при этом движение в значительной степени сохраняет хаотичность. Просто при перемещении электронов возникает преимущественное направление тока. Оно выражено тем сильнее, чем больше прилагаемая разность потенциалов. Определить направление тока в проводнике можно по обычному правилу.
Ток может возникать не только в твёрдых телах, но и в газах или жидкостях. В первом случае атомы привязаны друг к другу, поэтому свободно перемещаться могут только электроны. В газах и жидкостях атомы способны так же свободно двигаться, как и электроны.
Как определяется направление электротока
Чтобы узнать, в каком направлении течет ток, нужно составить электрическую цепь. Простейшая схема предусматривает наличие источника тока, нагрузки (это может быть лампа накаливания) и проводов. Если последние правильно соединить, лампочка загорится.
Фактически наличие тока означает, что электроны перемещаются от отрицательной клеммы батареи через всю цепь к положительной. После попадания внутрь источника тока, благодаря химическим процессам, эти частицы попадут на отрицательную клемму и далее опять пройдут через цепь в определенном ранее направлении.
Физиками принято направление тока условно от отрицательного полюса к положительному. Электроны, переместившиеся к положительному полюсу, начинают вновь двигаться к отрицательному полюсу. Затем они перемещаются по цепи.
Явление электрического тока было открыто до того, как наука смогла его объяснить. В то время не было еще известно о существовании электронов. Поэтому направление движения тока принято случайным образом — от положительной клеммы источника тока к отрицательной. С тех пор в электротехнике сохраняется именно такое правило.
Впервые определение электрического тока дал французский учёный Жан-Мари Ампер. Ученый в своих работах обосновал, какое есть истинное направление электротока. Основанием для его определения послужил довольно простой эксперимент.
Приведённый на рисунке аппарат заправляется водой. В указанных на схеме местах расположены положительная и отрицательная клеммы источника тока. При пропускании электротока часть молекул воды распадается на кислород и водород. Первый выделяется там, где источник имеет положительный потенциал (на аноде), второй — отрицательный (на катоде).
Рассматривая происходящие процессы, Ампер понял, что за направление тока следует считать то движение зарядов, которое идет от кислородного электрода к водородному. Проще говоря, направление тока определяется движением электронов от плюса к минусу. Этот опыт был проведён в первой половине девятнадцатого века.
Теперь известно, что на самом деле за направление электрического тока принимается перемещение электронов, которое противоположно указанному Ампером. Этот факт был установлен в 1897 году. Но чтобы не вносить множество изменений, ученые принимают решение оставить направление от плюса к минусу и в дальнейшем использовать только его.
Нужно подчеркнуть, что указанное противоречие относится лишь к току, проходящему в проводниках. Однако он может существовать в жидкостях и газах. В таких случаях направление движения положительных ионов будет совпадать с тем, которое принимает Ампер.
В большинстве случаев в веществах присутствуют носители зарядов как положительные, так и отрицательные и они могут перемещаться. Их соотношение зависит от конкретного вещества. Например, в проводниках количество перемещающихся электронов намного больше, чем носителей положительных зарядов.
Видео по теме
1.2 Положительные направления тока и напряжения
Электрический ток в проводящей среде есть упорядоченное движение электрических зарядов. Известно, что электрический ток проводимости в металлах, так же как и ток переноса в электровакуумных приборах, представляет собой перемещение отрицательно заряженных частиц (электронов), а ток проводимости в электролитах и газах — перемещение как положительно, так и отрицательно заряженных частиц (ионов).
Электрическому току приписывается направление. Хотя в общем случае ток представляет собой движение электрических зарядов того и другого знака в разные стороны, однако, за направление тока принимают направление перемещения положительных зарядов; это направление противоположно направлению движения отрицательных зарядов.
Численно ток определяется как предел отношения количества электричества, переносимого заряженными частицами сквозь рассматриваемое поперечное сечение проводника за некоторый промежуток времени, к этому промежутку времени, когда последний стремится к нулю. Следовательно, если обозначить через q количество электричества, прошедшего через рассматриваемое сечение проводника за время t, то мгновенное значение тока, т. е. значение его в любой момент времени t, определится как производная q по t
Здесь q = q+ + q-, где q+ и q- — положительный и отрицательный заряды, переместившиеся в противоположные стороны за время t. В Международной системе единиц ток i измеряется в амперах (А), заряд q — в кулонах (К) или амперсекундах (А×с), время t — в секундах (с).
Электрический ток может быть постоянным (неизменяющимся) или переменным, т.е. изменяющимся в зависимости от времени.
Направление тока характеризуется знаком тока. Понятия положительный ток или отрицательный ток имеют смысл, только если сравнивать направление тока в проводнике с некоторым заранее выбранным ориентиром — так называемым положительным направлением.
Источник
ПОЛОЖИТЕЛЬНЫЕ НАПРАВЛЕНИЯ ТОКА И НАПРЯЖЕНИЯ
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ЗАКОНЫ, ЭЛЕМЕНТЫ
И ПАРАМЕТРЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ
Электрической цепью называется совокупность устройств, предназначаемых для прохождения электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий напряжения и тока. В общем случае электрическая цепь состоит из источников и приемников электрической энергии и промежуточных звеньев (проводов, аппаратов), связывающих источники с приемниками.
Источниками электрической энергии являются гальванические элементы, аккумуляторы, термоэлементы, генераторы и другие устройства, в которых происходит процесс преобразования химической, молекулярно-кинетической, тепловой, механической или другого вида энергии в электрическую. К источникам можно отнести и приемные антенны, в которых в отличие от перечисленных выше устройств не происходит изменения вида энергии.
Приемниками электрической энергии, или так называемой нагрузкой, служат электрические лампы, электронагревательные приборы, электрические двигатели и другие устройства, в которых электрическая энергия превращается в световую, тепловую, механическую и т. п. К нагрузкам относятся и передающие антенны, излучающие электромагнитную энергию в пространство.
Расчеты электрических цепей и исследования процессов, происходящих в них, основываются на различных допущениях и некоторой идеализации реальных объектов электрических цепей. Под элементами в теории электрических цепей подразумеваются обычно не физически существующие составные части электротехнических и радиотехнических устройств, а их идеализированные модели, которым теоретически приписываются определенные электрические и магнитные свойства так, что они в совокупности приближенно отображают явления, происходящие в реальных устройствах.
В теории электрических цепей различают активные и пассивные элементы.
Активными элементами считаются источники электрической энергии: источники напряжения и источники тока. К пассивным элементам электрических цепей относятся сопротивления, индуктивности и емкости. Соответственно различают активные и пассивные цепи; активные цепи содержат источники электрической энергии, пассивные же цепи состоят только из пассивных элементов.
ПОЛОЖИТЕЛЬНЫЕ НАПРАВЛЕНИЯ ТОКА И НАПРЯЖЕНИЯ
Электрический ток в проводящей среде есть упорядоченное движение электрических зарядов. Известно, что электрический ток проводимости в металлах, так же как и ток переноса в электровакуумных приборах, представляет собой перемещение отрицательно заряженных частиц (электронов), а ток проводимости в электролитах и газах — перемещение как положительно, так и отрицательно заряженных частиц (ионов).
Электрическому току приписывается направление. Хотя в общем случае ток представляет собой движение электрических зарядов того и другого знака в разные стороны, однако, за направление тока принимают направление перемещения положительных зарядов; это направление противоположно направлению движения отрицательных зарядов.
Численно ток определяется как предел отношения количества электричества, переносимого заряженными частицами сквозь рассматриваемое поперечное сечение проводника за некоторый промежуток времени, к этому промежутку времени, когда последний стремится к нулю. Следовательно, если обозначить через q количество электричества, прошедшего через рассматриваемое сечение проводника за время t, то мгновенное значение тока, т. е. значение его в любой момент времени t, определится как производная q по t
Здесь q = q+ + q—, где q+ и q— — положительный и отрицательный заряды, переместившиеся в противоположные стороны за время t.
В Международной системе единиц ток i измеряется в амперах (А), заряд q — в кулонах (К) или ампер-секундах (А×с), время t — в секундах (с).
Электрический ток может быть постоянным (неизменяющимся) или переменным, т.е. изменяющимся в зависимости от времени.
Направление тока характеризуется знаком тока. Понятия положительный ток или отрицательный ток имеют смысл, только если сравнивать направление тока в проводнике с некоторым заранее выбранным ориентиром — так называемым положительным направлением.
Положительное направление тока выбирается произвольно; оно обычно указывается стрелкой. Если в результате расчета тока, выполненного с учетом выбранного положительного направления, ток имеет знак плюс (i > 0), то это означает, что его направление совпадает с выбранным положительным направлением. В противном случае, когда ток отрицателен (i
Дата добавления: 2015-12-16 ; просмотров: 5579 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Напряжение участке электрической цепи



Участок электрической цепи, по которому проходит ток одного и того же значения называют ветвью .
Место соединения трех и более ветвей называют узлом .
Замкнутую электрическую цепь, образованную одной или несколькими ветвями называют контуром .
Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.
На рис. 2.1 изображен участок цепи, содержащий только резистивный элемент, крайние точки которого обозначены буквами a и b. Пусть ток 
Следовательно, потенциал точки а (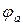
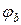

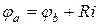
В соответствии с определением напряжение между точками а и b
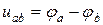
т. е. напряжение на сопротивлении равно произведению тока, протекающего по резистивному элементу, на значение его сопротивления. Последнее выражение называют законом Ома для участка цепи.
В электротехнике разность потенциалов на концах резистивного элемента (сопротивления) называют либо напряжением на сопротивлении, либо падением напряжения. Положительное направление падения напряжения на каком-либо участке (направление отсчета этого напряжения), указываемое на рисунках стрелкой, совпадает с положительным направлением отсчета тока, протекающего по данному сопротивлению.
Рассмотрим вопрос о напряжении на участке цепи, содержащем не только резистивный элемент, но и ЭДС. На рис. 2.2 показан участок цепи, в которой существует ток 
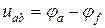
Выразим потенциал точки а через потенциал точки f. При перемещении от точки f к точке d встречно направлению ЭДС источника Е2 (рис. 2.2) потенциал точки d оказывается ниже (меньше), чем потенциал точки f, на значение ЭДС 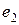
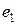
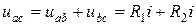
Таким образом с учетом вышеизложенного:
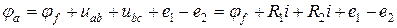
напряжение на участке цепи между точками a и f равно:
В общем случае напряжение на участке цепи равно сумме падений напряжения на резистивных элементах цепи и сумме ЭДС источников.
Положительное направление напряжения 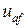
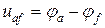
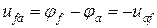
Законы Кирхгофа
Первый закон Кирхгофа (уравнение электрического состояния для узла) можно сформулировать двояко:
1) алгебраическая сумма токов, входящих в любой узел схемы (рис.2.3,а), равна нулю:
2) сумма токов, входящих в любой узел схемы (рис.2.3,б), равна сумме токов выходящих из этого узла:
Физически первый закон Кирхгофа означает, что движение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.
Второй закон Кирхгофа (уравнение электрического состояния контура) также можно сформулировать двояко:
1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:
(в каждую из сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним);
2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю:
Напряжения участков цепи включают и падения напряжения на резистивных элементах и напряжения на источниках ЭДС.
Для левого контура схемы рис.2.4
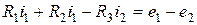
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.
Параллельное и последовательное соединение двухполюсников
Последовательное соединение резистивных элементов
Результирующее падение напряжения на цепи (рис. 2.5) из n последовательно включенных резистивных элементов:

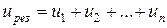
В цепи существует общий ток 
Для линейных резистивных элементов:
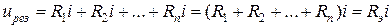
где эквивалентное сопротивление цепи из n последовательно соединенных резистивных элементов:
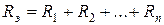
Для нелинейных резистивных элементов НЭ1 и НЭ2 результирующая ВАХ эквивалентного резистивного элемента определяется графическим способом (рис. 2.6).
В интересующем диапазоне токов (соответствующем участку ВАХ нелинейного элемента) задаются несколькими значениями токов (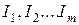
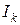
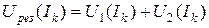
На уровне каждой из ординат откладывают найденные значения абсцисс 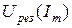
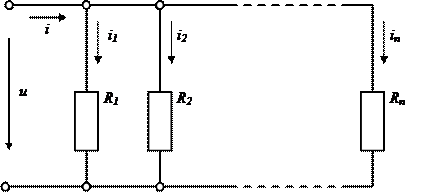
Параллельное соединение резистивных элементов
При параллельном соединении двухполюсных элементов (рис. 2.7) на их полюсах будет общее падение напряжения 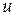
Общий ток 
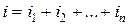
Для линейных двухполюсных элементов ток через k-тый резистивный элемент 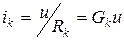
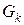
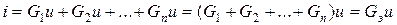
где эквивалентная проводимость 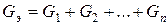
В частном случае для двух элементов эквивалентная проводимость 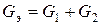
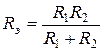
Для нелинейных резистивных элементов НЭ1 и НЭ2 результирующая ВАХ эквивалентного резистивного элемента определяется графическим способом (рис. 2.8).
В интересующем диапазоне напряжений (соответствующем участку ВАХ нелинейного элемента) задаются несколькими значениями напряжений (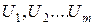
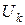
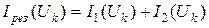
На уровне каждой из абсцисс откладывают найденные значения ординат 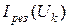
Последовательное и параллельное соединение линейных индуктивных элементов
При последовательном соединении n линейных индуктивных элементов их результирующая индуктивность определяется
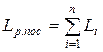
При параллельном соединении n линейных индуктивных элементов их результирующая индуктивность определяется
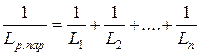
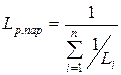
Последовательное и параллельное соединение линейных емкостных элементов
При последовательном соединении n линейных емкостных элементов их результирующая емкость определяется
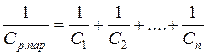
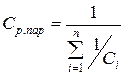
При параллельном соединении n линейных емкостных элементов их результирующая емкость определяется
Источник
Электрический
ток в общем случае представляет собой
движения электрических зарядов
отрицательного и положительного знаков
в разные стороны.
Численно
ток определяется
как придел отношения количества
электричества, переносимого заряженными
частицами сквозь рассматриваемое
поперечное сечение проводника за
некоторый промежуток времени, к этому
времени, при условии, что данный промежуток
времени стремится к нулю:
где
q
– количество электричества, прошедшее
через рассматриваемое сечение проводника
за время t.
Количество
электричества (заряд) измеряется в
Кулонах [K],
промежуток времени в секундах [сек], а
единицей измерения тока служит Ампер
[A].
Электрическому
току приписывают направление.
За
положительное
направление тока принимают направление
перемещения положительных зарядов от
точки высшего потенциала к точке
меньшего потенциала.
Направление
тока характеризуется знаком тока.
Понятия положительный или отрицательный
ток имеют смысл, если сравнивать
направление тока в проводнике с некоторым
заранее выбранным направлением – так
называемым положительным направлением
тока.
Положительное
направление тока выбирается произвольно
и указывается стрелкой.
Рассмотрим
пассивный участок электрической цепи
с выбранным положительным направлением
тока:
При
протекании тока от точки 1 к точке 2
подразумевается, что потенциал точки
1 выше потенциала точки 2.
Под
напряжением
на данном участке подразумевается
разность электрических потенциалов
точек 1 и 2.
Единица
измерения напряжения Вольт [B].
При
условии, что 1
больше 2
U12
= 1
– 2
будет положительным.
Порядок
индексов при напряжении означают его
выбранное положительное направление.
Чаще
всего положительное направление
напряжения выбирают совпадающим с
положительным направлением тока и
указывают стрелкой.
4. Источник напряжения и источник тока.
В
теории электрических цепей используют
понятия идеальные источники электрической
энергии: источник напряжения и источник
тока.
Им приписывают
следующие свойства:
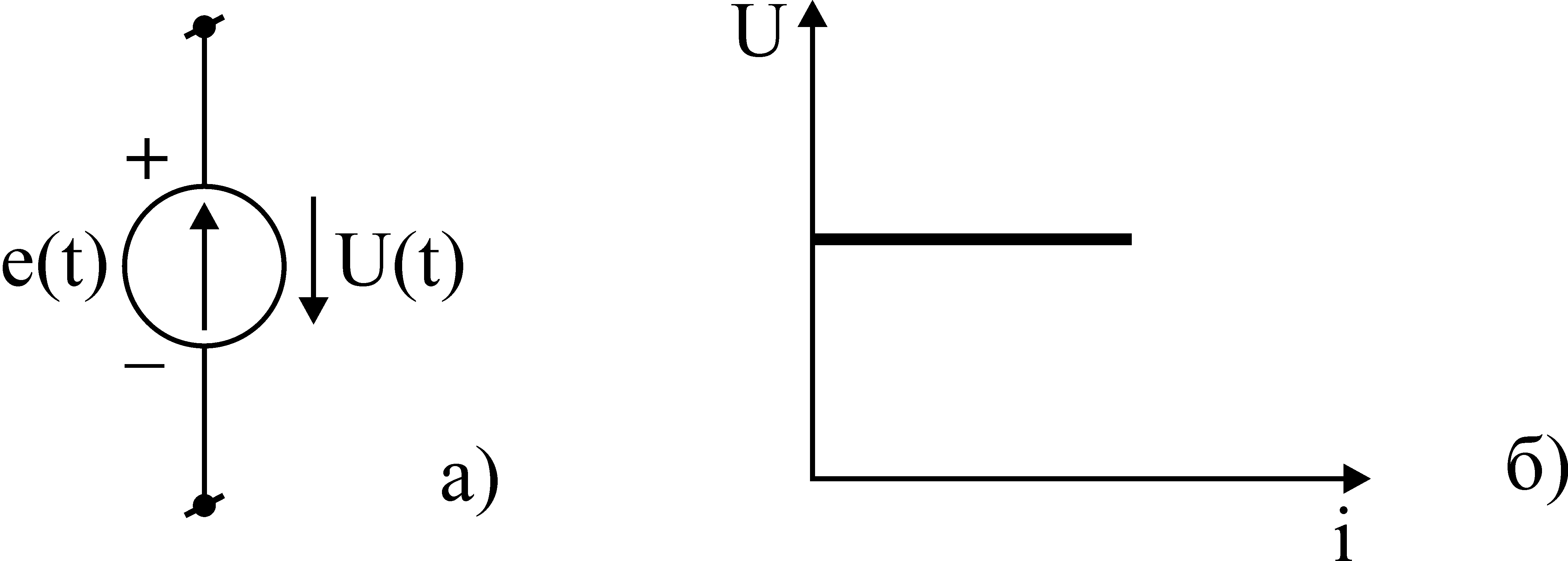
Источник
напряжения
представляет собой активный элемент с
двумя зажимами, напряжение на котором
не зависит от тока, проходящего через
источник
Рис.2. Идеальный
источник напряжения и
его
вольтамперная характеристика(BAX).
Предполагается,
что внутри идеального источника
напряжения пассивные сопротивление,
индуктивность и емкость отсутствуют
и, следовательно, прохождение тока не
вызывает падения напряжения.
Упорядоченное
перемещение положительных зарядов в
источнике напряжения от меньшего
потенциала к большему возможно за счет
работы сторонних сил, которые присущи
источнику.
Величина
работы, производимой данными сторонними
силами по перемещению единицы
положительного заряда от отрицательного
полюса источника напряжения к
положительному по полюсу, называется
электродвижущей
силой (э.д.с.)
источника
и обозначается e(t).
На
рис.2(а) указано направление напряжения
на зажимах идеального источника, которое
всегда равно э.д.с. источника по величине
и противоположно ей по направлению.
Идеальный
источник напряжения называют еще
источником
бесконечной
мощности.
Это – теоретическое понятие. Величина
тока в пассивной цепи зависит от
параметров этой цепи и e(t).
Если зажимы идеального источника
напряжения замкнуть накоротко, то ток
цепи должен быть теоретически равен
бесконечности. В действительности при
замыкании зажимов источника ток имеет
конечное значение, так как реальный
источник обладает внутренним
сопротивлением.
Обычно
внутренние параметры источника конечной
мощности незначительны по сравнению с
параметрами внешней цепи и в некоторых
случаях (по условию задачи) могут вообще
не учитываться. Внутреннее сопротивление
источника напряжения на схемах замещения
изображается последовательно соединенным
с самим источником.
Рис.3. Источник
напряжения конечной мощности.
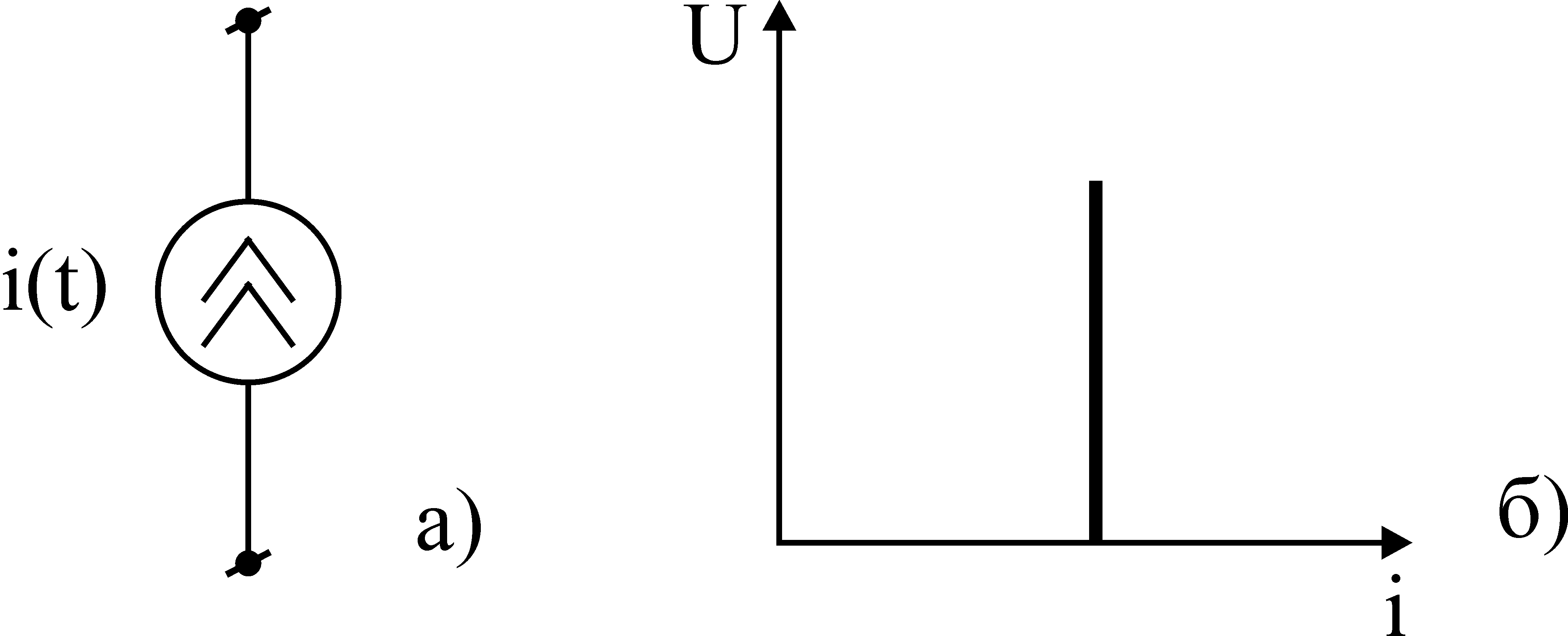
Источник
тока
представляет собой активный элемент,
ток которого не зависит от напряжения
на его зажимах.
Рис.4. Идеальный
источник тока и его вольтамперная
характеристика.
Предполагается,
что внутренне сопротивление идеального
источника тока равно бесконечности, и
поэтому параметры внешней цепи, от
которых зависит напряжение на зажимах
источника тока, не влияют на ток источника.
При
увеличении напряжения внешней цепи,
присоединенной к источнику тока,
напряжение на его зажимах, и следовательно,
мощность возрастают. Поэтому идеальный
источник тока теоретически так же
рассматривается как источник
бесконечной мощности.
Источник
тока конечной мощности изображен на
рис.5. g0
– внутренняя проводимость источника.
Она характеризует внутренние параметры
источника и ограничивает мощность,
отдаваемую в цепь.
Рис.5. Источник
тока конечной мощности.
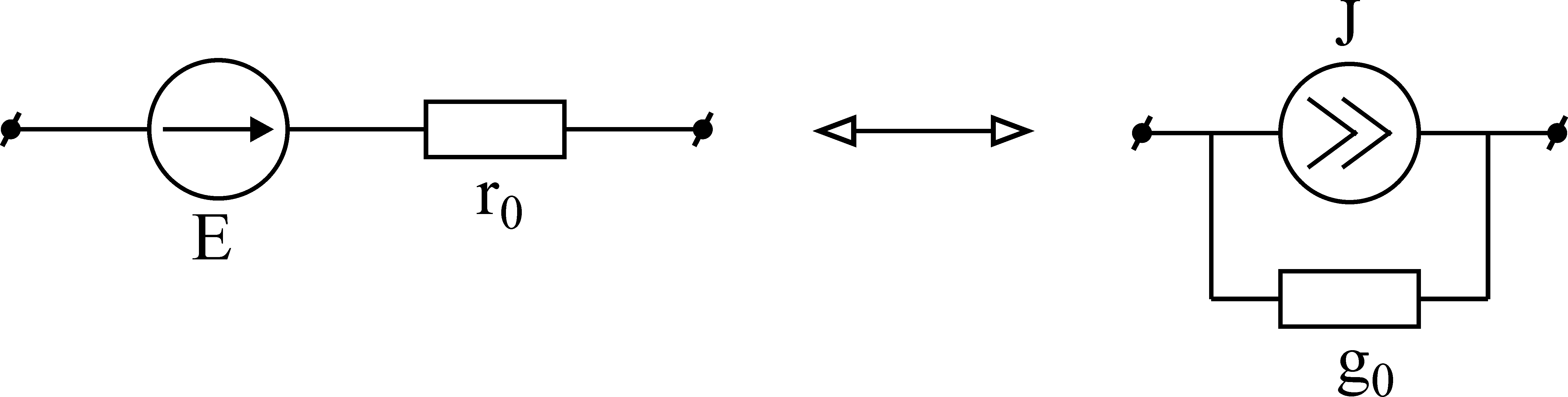
Часто
при решении задач методом эквивалентных
преобразований возникает необходимость
заменить реальный источник напряжения
эквивалентным источником тока или
наоборот. Преобразование осуществляется
по схеме и формулам рис.6.
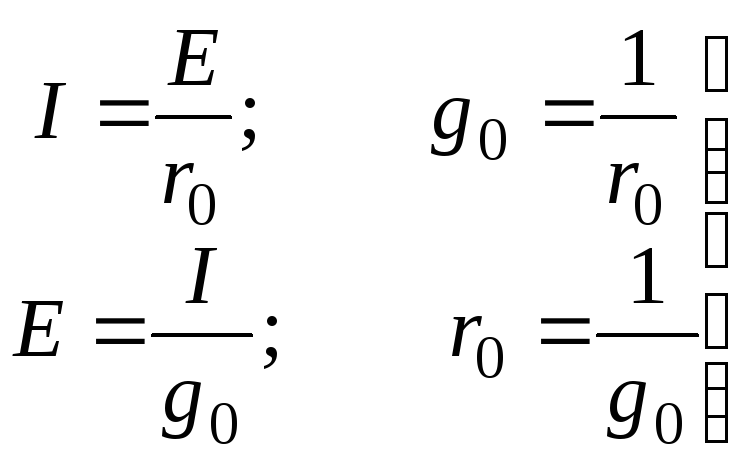
Рис.6. Преобразования
источников конечной мощности.
Соседние файлы в папке тэц
- #
- #
- #
- #
Применение закона Ома к расчету линейных электрических цепей постоянного тока
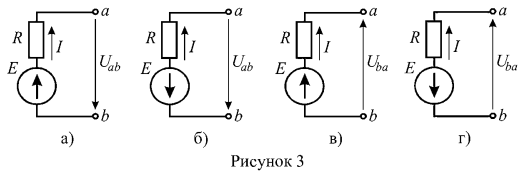
1. Найти ток ветви (рисунок 3), если: U=10 В, Е=20 В, R=5 Ом.
Решение:
Так как все схемы рисунка 3 представляют собой активные ветви, то для определения токов в них используем закон Ома обобщенный закон Ома. Рассмотрим рисунок 3 а: направление ЭДС совпадает с произвольно выбранным условно положительным направлением тока, следовательно, в формуле обобщенного закона Ома величина ЭДС учитывается со знаком «плюс». Направление напряжения не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;
Аналогично определяются токи в схемах б, в, г рисунка 3:
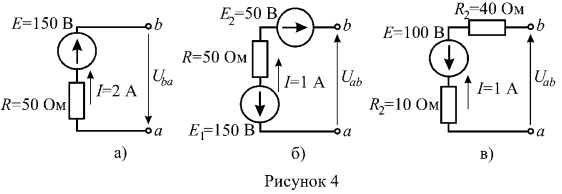
2. Найти напряжение между зажимами нетвей (рисунок 4).
Решение:
Участок цепи, изображенный на рисунке 4 а содержит источник ЭДС, т.е. является активным, поэтому воспользуемся обобщенным законом Ома:
откуда выразим напряжение на зажимах:
Аналогично определяются напряжения на зажимах участков, изображенных на рисунках 4 б и 4 в.
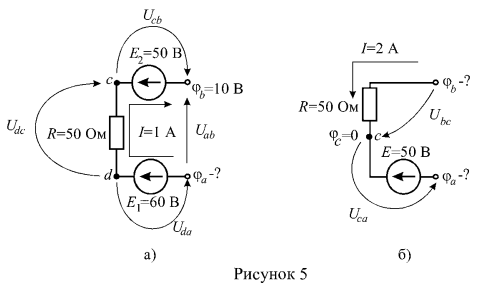
3. Определить неизвестные потенциалы точек участка цени (рисунок 5).
Решение:
Для схемы рисунка 5 а запишем обобщенный закон Ома:
откуда выразим напряжение на зажимах ветви:
Если представить напряжение как разность потенциалов:
тогда при известных параметрах цепи, токе и потенциале определим потенциал
:
Эту же задачу можно решить другим способом. Напряжение на зажимах источника ЭДС , без учета внутреннего сопротивления источника, по величине равно
и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):
и тогда, зная потенциал , определим потенциал точки С:
Потенциал точки d больше потенциала точки С на величину падения напряжения на сопротивлении R:
тогда
Потенциал точки а определяем с учетом направления напряжения на зажимах источника ЭДС
. Напряжение
направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):
откуда следует, что
или
Рассмотрим решение задачи для схемы рисунка 5 б. При известном потенциале точки С, параметрах элементов и токе, определим потенциалы крайних точек участка цепи . Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:
откуда следует
Напряжение на участке с — а, равное по величине Е, направлено от точки с большим потенциалом к точке с меньшим потенциалом:
4. В цепи (рисунок 6) известны величины сопротивлений резистивных элементов: , входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением
. Определить величину сопротивления резистора
.
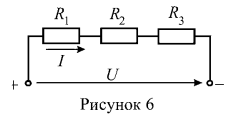
Согласно закону Джоуля-Ленца, мощность на резистивном элементе определяется:
или, согласно закону Ома:
По известному значению мощности на резистивном элементе и величине сопротивления этого элемента определим ток в ветви:
По закону Ома напряжение на зажимах определится:
тогда величина сопротивления резистивного элемента:
5. Определить показания вольтметров цепи (рисунок 7), если .
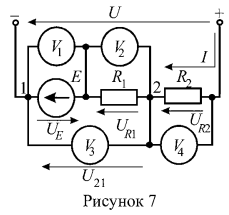
Ток в цепи определим по закону Ома:
Вольтметр показывает напряжение на источнике ЭДС Е:
Вольтметры показывают величину падения напряжения на резистивных элементах
:
Вольтметр , показывает напряжение на участке 2 — 1
, которое определим как алгебраическую сумма напряжений
:
6. Ток симметричной цепи (рисунок 8) , внутреннее сопротивлении источника ЭДС
. Определить ЭДС Е и мощность источника энергии.
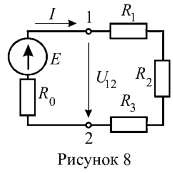
Напряжение на зажимах 1 — 2 определим по закону Ома для пассивной ветви:
Величину ЭДС источника энергии определим из выражения закона Ома для активной ветви:
Мощность, развиваемая источником энергии, определится: