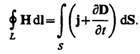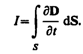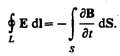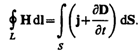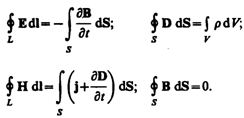Магнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.
Основные свойства магнитного поля
- Магнитное поле порождается электрическим током (движущимися зарядами).
- Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
- Магнитное поле существует независимо от нас, от наших знаний о нем.
Вектор магнитной индукции
Определение
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как→B. Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B=FAmaxIl
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Напряженность магнитного поля
Определение
Вектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как →H. Единица измерения — А/м.
→H=→Bμμ0
μ — магнитная проницаемость среды (у воздуха она равна 1), μ0 — магнитная постоянная, равная 4π·10−7 Гн/м.
Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: →H↑↑→B.
Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.
- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора →B магнитной индукции.
Отсюда следует, что:
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции →B направлен вверх.
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции →B направлен вниз.
Способы обозначения направлений векторов:
| Вверх | |
| Вниз | |
| Влево | |
| Вправо | |
| На нас перпендикулярно плоскости чертежа |  |
| От нас перпендикулярно плоскости чертежа |  |
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?
Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
Магнитное поле прямолинейного тока
Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.
Вид сверху:
Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:
Правило буравчика (правой руки)
Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.
Модуль вектора магнитной индукции на расстоянии r от оси проводника:
B=μμ0I2πr
Модуль напряженности:
H=I2πr
Магнитное поле кругового тока
Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.
Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:
Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.
Модуль вектора магнитной индукции в центре витка, радиус которого равен R:
B=μμ0I2R
Модуль напряженности в центре витка:
H=I2R
Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?
Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.
Магнитное поле электромагнита (соленоида)
Определение
Соленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.
Число витков в соленоиде N определяется формулой:
N=ld
l — длина соленоида, d — диаметр проволоки.
Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.
Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции →B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.
Модуль вектора магнитной индукции в центральной области соленоида:
B=μμ0INl=μμ0Id
Модуль напряженности магнитного поля в центральной части соленоида:
H=INl=Id
Алгоритм определения полярности электромагнита
- Определить полярность источника.
- Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
- Определить направление вектора магнитной индукции.
- Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).
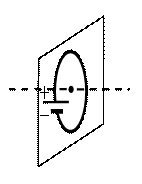
Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.
Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов. Он покажет направление линий магнитной индукции внутри соленоида. Проделав это, увидим, что линии магнитной индукции направлены вправо. Следовательно, они выходят из В, который будет являться северным полюсом. Тогда А будет являться южным полюсом.
Задание EF17530
Ответ:
а) вертикально вверх в плоскости витка
б) вертикально вниз в плоскости витка
в) вправо перпендикулярно плоскости витка
г) влево перпендикулярно плоскости витка
Алгоритм решения
1.Определить правило, по которому можно определить направление вектора магнитной индукции в данном случае.
2.Применить выбранное правило и определить направление вектора магнитной индукции относительно рисунка.
Решение
По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора →B магнитной индукции мы будем использовать правило правой руки.
Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.
Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18109
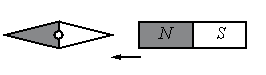
Ответ:
а) повернётся на 180°
б) повернётся на 90° по часовой стрелке
в) повернётся на 90° против часовой стрелки
г) останется в прежнем положении
Алгоритм решения
- Вспомнить, как взаимодействуют магниты.
- Определить исходное положение полюсов.
- Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.
Решение
Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18266
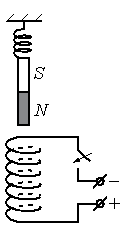
Алгоритм решения
- Определить направление тока в соленоиде.
- Определить полюса соленоида.
- Установить, как будет взаимодействовать соленоид с магнитом.
- Установить, как будет себя вести магнит после замыкания электрической цепи.
Решение
Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.
Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.
Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 22.3k
Напряженность магнитного поля
Напряженность магнитного поля, то есть силу магнитного поля оценивают по густоте магнитных силовых линий в данной точке поля. Напряженность магнитного поля обозначают в формулах буквой Н. Напряженность магнитного поля показывает число силовых линий магнитного поля, проходящих через 1 см2 поперечного сечения поля.
Магнитные силовые линии, пронизывающие какую-либо площадку, называются магнитным потоком через эту площадку. Магнитный поток через данную площадку будет, следовательно, тем больше, чем больше силовых линий проходит через нее. Магнитный поток обозначают буквой Ф.
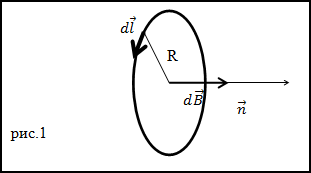
Направление магнитных силовых линий связано с направлением тока в проводнике. Наиболее простым способом определения направления магнитных силовых линий является использование правила буравчика (рисунок 1).
Рисунок 1. Определение направления магнитных силовых линий по правилу буравчика.
Правило буравчика состоит в следующем: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения буравчика совпадает с направлением магнитных силовых линий.
Интерактивная демонстрация правила буравчика. Нажать на выключатель!
Рисунок 2. Интерактивная демонстрация определения направления линий напряженности магнитного поля с помощью правила буравчика.
Для подачи тока нажмите на выключатель
Для изменения направления тока нажмите на источник напряжения
Придадим проводнику с током форму кольца (рисунок 2). Пользуясь правилом буравчика, мы легко установим, что магнитные силовые линии, создаваемые всеми участками проводника, имеют внутри кольца одинаковое направление. Значит, внутри кольца магнитное поле будет сильнее, чем снаружи.
Рисунок 3. Напряженность магнитного поля в витке с током.
Изготовим из проводника цилиндрическую спираль и пропустим по ней электрический ток (рисунок 3). Ток по всем виткам будет проходить в одном и том же направлении. Это будет равносильно тому, что мы поместим ряд кольцевых проводников на одну общую ось. Проводник, имеющий такую форму, называется соленоидом или катушкой.
Рисунок 4. Напряженность магнитного поля в катушке.
Пользуясь правилом буравчика, мы легко установим, что магнитные силовые линии, создаваемые всеми витками катушки, имеют внутри нее одинаковое направление. Значит, внутри катушки будет более сильное магнитное поле, чем внутри одного витка. Между соседними витками катушки магнитные силовые линии направлены навстречу друг другу, и поэтому магнитное поле в этих местах будет очень ослаблено. Снаружи же катушки направление всех магнитных силовых линий будет одинаковым.
Магнитное поле катушки тем сильнее, чем больше сила тока, проходящего по ее виткам, и чем теснее, т. е. ближе друг к другу, расположены витки. Из двух катушек с одинаковым током и одинаковым числом витков более сильное поле имеет катушка, у которой витки расположены ближе друг к другу, т. е. катушка, имеющая меньшую осевую длину.
Произведение силы тока в амперах на число витков, носит название ампервитков и характеризует магнитное действие электрического тока, то есть магнитодвижущую силу.
Пользуясь этим термином, можно сказать, что магнитное поле катушки тем сильнее, чем больше ампервитков приходится на единицу ее осевой длины.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Напряженность магнитного поля. Закон полного тока
Понятие
напряженности магнитного поля построено
на формальной аналогии полей неподвижных
зарядов и неподвижных намагниченных
тел. Такая аналогия часто оказывается
весьма полезной, т.к. позволяет перенести
в теорию магнитного поля методы,
разработанные для электростатических
полей.
Напряженность
магнитного поля первоначально была
введена в форме закона Кулона через
понятие магнитной массы, аналогичной
электрическому заряду, как механическая
сила взаимодействия двух точечных
магнитных масс в однородной среде,
которая пропорциональна произведению
этих масс и обратно пропорциональна
квадрату расстояния между ними
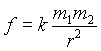
где m1 и m2 –
взаимодействующие магнитные массы; r –
расстояние между точками, в которых
магнитные массы считаются
сосредоточенными; k –
коэффициент, зависящий от свойств среды
и системы единиц измерения.
Сила f направлена
по прямой, соединяющей центры магнитных
масс.
Магнитные
массы одного знака отталкиваются, а
противоположного – притягиваются.
Для
количественной характеристики магнитного
поля можно воспользоваться механической
силой, действующей на положительный
полюс пробного магнита, в той точке, где
он расположен в пространстве. Напряженностью
магнитного поля называется
отношение механической силы, действующей
на положительный полюс пробного магнита,
к величине его магнитной массы или
механическая сила, действующая на
положительный полюс пробного магнита
единичной массы в данной точке поля.
Напряженность
изображается вектором H,
имеющим направление вектора механической
силы f.
|
|
(1) |
Если
определить напряженность во всех точках
магнитного поля, то можно построить
линии, направление касательных к которым
в каждой точке поля будет совпадать с
направлением напряженности. Такие линии
называются линиями напряженности
илисиловыми
линиями.
Можно
также ввести понятие о силовой трубке магнитного
поля аналогично тому, как это было
сделано для магнитного потока.Силовые
линии,
в отличие от линий индукции магнитного
поля, начинаются на положительных
магнитных массах и заканчиваются на
отрицательных, т.е. прерываются.
Для изотропной среды
существует связь между индукцией и
напряженностью магнитного поля
|
|
(1) |
Последнее
соотношение можно использовать для
определения магнитной
проницаемости как
отношения индукции к напряженности
магнитного поля.
П
помещении в магнитное поле вещества в
нем происходят процессы ориентации
различных структур, обладающих дипольным
магнитным моментом. Так электроны,
перемещаясь по орбитам, образуют
элементарные токи и соответствующие
магнитные поля или магнитные диполи
(рис. 1 а)). Кроме этого, электроны создают
магнитный момент за счет вращения вокруг
собственной оси, называемый спиновым
магнитным моментом.
Магнитный
диполь можно характеризовать
вектором магнитного
момента,
численно равным произведению величины
элементарного тока на площадь контура,
ограниченного этим током в пространстве
m = is,
и
направленным по нормали к площади
контура.
Геометрическая
сумма всех магнитных моментов образует
магнитный момент тела
M = m,
который
обычно соотносят с объемом вещества V и
называют намагниченностью или
интенсивностью намагничивания
|
|
(1) |
Единицу
измерения намагниченности можно
определить из выражения (1) [J]
= [M/V]
= Ам2/м3 =
А/м.
Вектор
намагниченности совпадает с направлением
вектора напряженности и связан с ним
линейной зависимостью
|
|
(2) |
Безразмерный
коэффициент называется магнитной
восприимчивостью вещества.
Для
магнитного поля, существующего в
некоторой среде, можно представить
магнитную индукцию в виде суммы двух
составляющих, индукции B0 ,
соответствующей вакууму, и дополнительной
индукции Bн,
создаваемой намагниченностью вещества
|
|
(3) |
где 0 –
магнитная проницаемость вакуума; а и =1+ –
соответственно абсолютная и относительная
магнитные проницаемости вещества.
В
зависимости от значения все
вещества разделяются на диамагнитные
парамагнитные и ферромагнитные.
К диамагнетикам относятся
вещества, у которых <0
и <1,
т.е. их магнитная проницаемость меньше
чем у вакуума. Наиболее сильно диамагнитные
свойства выражены у висмута, у
которого =0,99983.
У парамагнетиков >0
и >1.
Например, у платины относительная
магнитная проницаемость составляет
1,00036.
Особую
группу веществ, представляющих большой
интерес с практической точки зрения,
составляют ферромагнетики,
у которых >>1
и составляет величину порядка 104 106.
Определение
напряженности магнитного поля через
магнитные силы и массы не вполне адекватно
физической картине явлений в магнитном
поле, т.к., в отличие от электрического
заряда, не существует массы или заряда
магнитного. На практике удобнее
пользоваться явлениями, связывающими
между собой электрический ток и магнитное
поле.
П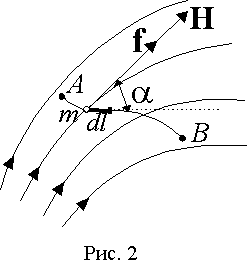
некая точечная магнитная масса m перемещается
по произвольному пути из точки A в
точку B магнитного
поля (рис. 2). Действующая на магнитную
массу механическая сила f в
любой точке поля направлена по касательной
к силовой линии и равна f=mH ,
где H –
напряженность поля.
Работа
по перемещению массы m по
пути AB равна
|
|
(4) |
где –
угол между направлением вектора H и
касательной к направлению перемещения.
В этом выражении линейный
интеграл вектора напряженности магнитного
поля, взятый вдоль некоторого пути AB,
называетсямагнитодвижущей
силой (МДС) F,
действующей вдоль этого пути
|
|
(5) |
т.е. магнитодвижущая
сила численно равна работе по перемещению
единичной магнитной массы по заданному
пути.
Рассмотрим
теперь перемещение магнитной массы m по
замкнутому пути в магнитном поле витка
с постоянным значением тока i.
Сначала
допустим, что существует только
воздействие со стороны поля витка на
массу m (рис.
3 а)).
В
соответствии с выражением (4), работа
перемещения по замкнутому пути будет
равна
|
|
(6) |
Теперь
предположим, что мы перемещаемся по
тому же замкнутому контуру, но воздействие
существует только со стороны магнитной
массы m на
виток с током (рис. 3 б)). При анализе
электромагнитной силы было установлено,
что элементарная
работа по
перемещению отрезка проводника с
током i в
магнитном поле равна dA = idФ
= idN,
где – число линий индукции магнитного
поля, пересекаемых при перемещении.
Если
магнитная масса m переместится
по изображенному на рисунке контуру,
то виток пересечет все исходящие из нее
линии индукции и работа по перемещению,
с учетом того, что полный магнитный
поток перемещаемой массы численно равен
ее значению, будет равна
|
|
(7) |
Но
на основании закона сохранения
энергии A1 = A2 ,
отсюда
|
|
(8) |
Очевидно,
что задачу можно дополнить другими
контурами (витками) с токами. Однако, в
этом случае ее можно рассмотреть по
отдельности, для каждого витка. Тогда
в правой части выражения (8) окажется
алгебраическая сумма всех токов,
охваченных контуром интегрирования
|
|
(9) |
Полученное
выражение называется законом
полного тока. Линейный
интеграл вектора напряженности магнитного
поля, взятый по замкнутому контуру,
равен полному (суммарному) электрическому
току, проходящему через поверхность,
ограниченную этим контуром или МДС
вдоль замкнутого контура равна полному
току, охватываемому этим током.
Закон
полного тока является одним из важнейших
законов, устанавливающим неразрывную
связь между электрическим током и
магнитным полем. Из него следует,
что любая
магнитная линия обязательно охватывает
электрический ток и, наоборот, электрический
ток всегда окружен магнитным полем.
Причем, не являются исключением из этого
закона и постоянные магниты, т.к. в них
магнитные линии создаются элементарными
микроскопическими токами, также входящими
в правую часть выражения (9).
Переход
магнитного потока из одной среды в
другую сопровождается некоторыми
явлениями на границе раздела этих сред.
Пусть
магнитный поток переходит из среды с
магнитной проницаемостью 1 в
среду с магнитной проницаемостью 2 (рис.
4). Из условия непрерывности магнитного
потока следует, что при переходе из
одной среды в другую через границу
раздела площадью S он
должен сохраняться, т.е. Ф1 =
Ф2 .
Но магнитный поток для изотропной среды
можно представить через индукцию в виде
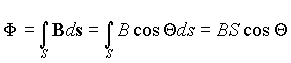
где –
угол между направлением вектора индукции
и нормалью к поверхности границы раздела
сред, а произведение Bcos –
проекция вектора индукции на нормаль
или нормальная проекция.
Отсюда
– Ф1= B1Scos 1=
Ф2= B2Scos 2 или
|
B1cos 1 = B2cos |
(10) |
>
т.е. при
переходе из одной среды в другую магнитная
индукция изменяет свое значение, но
сохраняет нормальную проекцию.
В
изотропной среде векторы индукции и
напряженности магнитного поля совпадают
по направлению, поэтому и углы с нормалью
векторов H1 и H2 будут
такими же как у векторов B1 и B2 (рис.
4 б)). Выделим вблизи поверхности раздела
замкнутый прямоугольный контур abcd так,
чтобы его противоположные стороны
длиной l располагались
в разных средах на бесконечно малом
расстоянии от границы (рис. 4 б)).Найдем
линейный интеграл от вектора напряженности
поля вдоль этого контура и по закону
полного тока приравняем его нулю, т.к.
внутри контура отсутствует электрический
ток:

Отсюда
–
|
H1sin 1 = H2sin2. |
(11) |
Это
означает, что при
переходе из одной среды в другую вектор
напряженности магнитного поля сохраняет
тангенциальную составляющую,
т.е. проекцию на границу раздела сред.
Если
разделить выражение (10) на выражение
(11), то мы получим соотношение, связывающее
углы векторов с нормалью и магнитные
проницаемости.
|
|
(12) |
Из
выражения (12) следует, что при большом
отличии магнитных проницаемостей
( 1/ 2=1000),
например, при выходе магнитного потока
из ферромагнетика в воздушную среду
почти параллельно границе раздела
( 1=87 ),
угол с нормалью вектора индукции составит
около 1 ,
т.е. можно
считать, что магнитные
линии в воздухе нормальны к поверхностям
тел из ферромагнетиков.
46. Магнитные моменты электронов и атомов.
Гиромагнитное отношение.
Рассматривая
действие магнитного поля на проводники
с током и на движущиеся заряды, мы не
интересовались процессами, происходящими
в веществе. Свойства среды учитывались
формально с помощью магнитной
проницаемости . Для
того чтобы разобраться в магнитных
свойствах сред и их влиянии на магнитную
индукцию, необходимо рассмотреть
действие магнитного поля на атомы и
молекулы вещества.
Опыт
показывает, что все вещества, помещенные
в магнитное поле, намагничиваются.
Рассмотрим причину этого явления с
точки зрения строения атомов и молекул,
положив в основу гипотезу Ампера,
согласно которой в любом теле существуют
микроскопические токи, обусловленные
движением электронов в атомах и молекулах.
Для
качественного объяснения магнитных
явлений с достаточным приближением
можно считать, что электрон движется в
атоме по круговым орбитам. Электрон,
движущийся по одной из таких орбит,
эквивалентен круговому току, поэтому
он обладает орбитальным
магнитным моментом (см.
(109.2)) pm=ISn,
модуль которого
(131.1)
где I=e — сила
тока, —
частота вращения электрона по
орбите, S — площадь
орбиты. Если электрон движется по часовой
стрелке (рис. 187), то ток направлен против
часовой стрелки и вектор рm (в
соответствии с правилом правого винта)
направлен перпендикулярно плоскости
орбиты электрона, как указано на рисунке.
С
другой стороны, движущийся по орбите
электрон обладает механическим моментом
импульса Le,
модуль которого, согласно (19.1),
(131.2)
где v =
2, r2 =
S. Вектор Le (его
направление также определяется по
правилу правого винта) называется орбитальным
механическим моментом электрона.
Из
рис. 187 следует, что направления рm и Le,
противоположны, поэтому, учитывая
выражения (131.1) и (131.2), получим
(131.3)
где
величина
(131.4)
называется гиромагнитным
отношением орбитальных моментов (общепринято
писать со знаком «–», указывающим на
то, что направления моментов противоположны).
Это отношение, определяемое универсальными
постоянными, одинаково для любой орбиты,
хотя для разных орбит значения v и r различны.
Формула (131.4) выведена для круговой
орбиты, но она справедлива и для
эллиптических орбит.
Экспериментальное
определение гиромагнитного отношения
проведено в опытах Эйнштейна и де Гааза*
(1915), которые наблюдали поворот свободно
подвешенного на тончайшей кварцевой
нити железного стержня при его намагничении
во внешнем магнитном поле (по обмотке
соленоида пропускался переменный ток
с частотой, равной частоте крутильных
колебаний стержня). При исследовании
вынужденных крутильных колебаний
стержня определялось гиромагнитное
отношение, которое оказалось
равным –(e/m). Таким
образом, знак носителей, обусловливающих
молекулярные токи, совпадал со знаком
заряда электрона, а гиромагнитное
отношение оказалось в два раза бо2льшим,
чем введенная ранее величина g (см.
(131.4)). Для объяснения этого результата,
имевшего большое значение для дальнейшего
развития физики, было предположено, а
впоследствии доказано, что кроме
орбитальных моментов (см. (131.1) и (131.2))
электрон обладает собственным
механическим моментом импульса Les,
называемым спином.
Считалось, что спин обусловлен вращением
электрона вокруг своей оси, что привело
к целому ряду противоречий. В настоящее
время установлено, что спин является
неотъемлемым свойством электрона,
подобно его заряду и массе. Спину
электрона Les,
соответствует собственный
(сотовый) магнитный момент рms,
пропорциональный Les и
направленный в противоположную сторону:
(131.5)
*В.
И. де Гааз (1878—1960) — нидерландский физик.
Величина gs называется гиромагнитным
отношением спиновых моментов.
Проекция
собственного магнитного момента на
направление вектора В может
принимать только одно из следующих двух
значений:
где ħ=h/(2) (h—постоянная
Планка), b—магнетон
Бора, являющийся
единицей магнитного момента электрона.
В
общем случае магнитный момент электрона
складывается из орбитального и спинового
магнитных моментов. Магнитный момент
атома, следовательно, складывается из
магнитных моментов входящих в его состав
электронов и магнитного момента ядра
(обусловлен магнитными моментами
входящих в ядро протонов и нейтронов).
Однако магнитные моменты ядер в тысячи
раз меньше магнитных моментов электронов,
поэтому ими пренебрегают. Таким образом,
общий магнитный момент атома
(молекулы) pa равен
векторной сумме магнитных моментов
(орбитальных и спиновых) входящих в атом
(молекулу) электронов:
(131.6)
Еще
раз обратим внимание на то, что при
рассмотрении магнитных моментов
электронов и атомов мы пользовались
классической теорией, не учитывая
ограничений, накладываемых на движение
электронов законами квантовой механики.
Однако это не противоречит полученным
результатам, так как для дальнейшего
объяснения намагничивания веществ
существенно лишь то, что атомы обладают
магнитными моментами.
Гиромагни́тное
отноше́ние (магнитомехани́ческое
отноше́ние)
— отношение дипольного магнитного
момента элементарной
частицы (или
системы элементарных частиц) к
её механическому
моменту.
В
системе СИ единицей
измерения гиромагнитного
отношения является с·А·кг−1 = с−1·Тл−1.
Часто подразумевается, что гиромагнитное
отношение измеряется в единицах q/2mc,
где с — скорость
света, q и m — заряд и масса частицы,
соответственно. В этом случае оно
выражается безразмерной
величиной.
Для
различных состояний атомной системы
гиромагнитное отношение определяется
формулой:
где g — множитель
Ланде, γ0 — единица
гиромагнитного отношения:
где e — элементарный
заряд, me —
масса электрона, с —
скорость света.
В
случае ядер,
за единицу гиромагнитного отношения
принимают величину:
где mp —
масса протона.
Согласно классической
теории,
гиромагнитное отношение является
коэффициентом пропорциональности между
угловой скоростью прецессии магнитного
момента, помещённого во внешнее магнитное
поле,
и вектором магнитной индукции.
В квантовой
теории гиромагнитным
отношением определяется величина
расщепления уровней в эффекте
Зеемана.
47. Диамагнетизм и парамагнетизм.
Всякое
вещество является магнетиком,
т. е. оно способно под действием магнитного
поля приобретать магнитный момент
(намагничиваться). Для понимания механизма
этого явления необходимо рассмотреть
действие магнитного поля на движущиеся
в атоме электроны.
Ради
простоты предположим, что электрон в
атоме движется по круговой орбите. Если
орбита электрона ориентирована
относительно вектора В произвольным
образом, составляя с ним угол (рис.
188), то можно доказать, что она приходит
в такое движение вокруг В,
при котором вектор магнитного момента рm,
сохраняя постоянным угол ,
вращается вокруг вектора В с
некоторой угловой скоростью. Такое
движение в механике называется прецессией.
Прецессию вокруг вертикальной оси,
проходящей через точку опоры, совершает,
например, диск волчка при замедлении
движения.
Таким
образом, электронные орбиты атома под
действием внешнего магнитного поля
совершают прецессионное движение,
которое эквивалентно круговому току.
Так как этот микроток индуцирован
внешним магнитным полем, то, согласно
правилу Ленца, у атома появляется
составляющая магнитного поля, направленная
противоположно внешнему полю. Наведенные
составляющие магнитных полей атомов
(молекул) складываются и образуют
собственное магнитное поле вещества,
ослабляющее внешнее магнитное поле.
Этот эффект получил название диамагнитного
эффекта,
а вещества, намагничивающиеся во внешнем
магнитном поле против направления поля,
называются диамагнетиками.
В
отсутствие внешнего магнитного поля
диамагнетик немагнитен, поскольку в
данном случае магнитные моменты
электронов взаимно компенсируются, и
суммарный магнитный момент атома (он
равен векторной сумме магнитных моментов
(орбитальных и спиновых) составляющих
атом электронов) равен нулю. К диамагнетикам
относятся многие металлы (например, Bi, Ag, Au,
Сu),
большинство органических соединений,
смолы, углерод и т. д.
Так
как диамагнитный эффект обусловлен
действием внешнего магнитного поля на
электроны атомов вещества, то диамагнетизм
свойствен всем веществам. Однако наряду
с диамагнитными веществами существуют
и парамагнитные —
вещества, намагничивающиеся во внешнем
магнитном поле по направлению поля.
У
парамагнитных веществ при отсутствии
внешнего магнитного поля магнитные
моменты электронов не компенсируют
друг друга, и атомы (молекулы) парамагнетиков
всегда обладают магнитным моментом.
Однако вследствие теплового движения
молекул их магнитные моменты ориентированы
беспорядочно, поэтому парамагнитные
вещества магнитными свойствами не
обладают. При внесении парамагнетика
во внешнее магнитное поле
устанавливается преимущественнаяориентация
магнитных моментов атомов по полю (полной
ориентации препятствует тепловое
движение атомов). Таким образом,
парамагнетик намагничивается, создавая
собственное магнитное поле, совпадающее
по направлению с внешним полем и
усиливающее его. Этот эффект называется
парамагнитным. При ослаблении внешнего
магнитного поля да нуля ориентация
магнитных моментов вследствие теплового
движения нарушается и парамагнетик
размагничивается. К парамагнетикам
относятся редкоземельные элементы, Pt,
Аl и
т.д. Диамагнитный эффект наблюдается и
в парамагнетиках, но он значительно
слабее парамагнитного и поэтому остается
незаметным.
Из
рассмотрения явления парамагнетизма
следует, что его объяснение совпадает
с объяснением ориентационной (дипольной)
поляризации диэлектриков с полярными
молекулами, только электрический момент
атомов в случае поляризации надо заменить
магнитным моментом атомов в случае
намагничения.
Подводя
итог качественному рассмотрению
диамагнетизма и парамагнетизма, еще
раз отметим, что атомы всех веществ
являются носителями диамагнитных
свойств. Если магнитный момент атомов
велик, то парамагнитные свойства
преобладают над диамагнитными и вещество
является парамагнетиком; если магнитный
момент атомов мал, то преобладают
диамагнитные свойства и вещество
является диамагнетиком.
48. Ферромагнетики и их свойства. Магнитный
гистерезис. Домены. Применение
ферромагнетиков.
Ферромагнетики —
вещества (как правило, в твёрдом
кристаллическом или аморфном состоянии),
в которых ниже определённой
критической температуры (точки
Кюри)
устанавливается дальний ферромагнитный
порядок магнитных моментов атомов или ионов (в
неметаллических кристаллах) или моментов
коллективизированных электронов (в
металлических кристаллах). Иными словами,
ферромагнетик — такое вещество,
которое, при температуре ниже точки
Кюри, способно обладать намагниченностью
в отсутствие внешнего магнитного поля.
Последние исследования в области физики
показали, что некоторые ферромагнетики,
при создании определенных условий,
могут приобретать парамагнетическиесвойства
при температурах, которые существенно
выше точки Кюри. Поэтому ферромагнетики,
наряду со многими другими магнетическими
веществами, остаются, как оказалось,
плохо изученными веществами до сих пор.
Ферромагнетики
имеют наибольшее практическое применение,
хотя их и не так много в природе. Железный
или стальной сердечник в катушке во
много раз усиливает создаваемое этой
катушкой поле, не увеличивая силу тока
в катушке. Это экономит электроэнергию.
Сердечники трансформаторов, генераторов,
электродвигателей и других устройств
изготавливают из ферромагнетиков. При
выключении внешнего магнитного поля
ферромагнетик остаётся намагниченным,
то есть создаёт магнитное поле в
окружающем его пространстве. Упорядоченная
ориентация элементарных токов не
исчезает при выключении внешнего
магнитного поля. Благодаря этому
существуют постоянные магниты. Постоянные
магниты находят широкое применение в
электроизмерительных приборах,
громкоговорителях, телефонах, в
устройствах звукозаписи, магнитных
компасах и т.д. Большое распространение
получили ферриты – ферромагнитные
материалы, не проводящие электрического
тока. Они представляют собой химические
соединения оксидов железа с оксидами
других веществ. Первый из известных
человеку ферромагнитных материалов –
магнитный железняк – является феррито
Магнитный
гистерезис —
явление зависимости вектора
намагничивания и
вектора напряженности
магнитного поля в
веществе не только от приложенного
внешнего поля, но и от предыстории
данного образца. Магнитный гистерезис
обычно проявляется вферромагнетиках — Fe, Co, Ni и
сплавах на их основе. Именно магнитным
гистерезисом объясняется
существованиепостоянных
магнитов.
Явление
магнитного гистерезиса наблюдается не
только при изменении поля H по
величине и знаку, но также и при его
вращении (гистерезис магнитного
вращения), что соответствует отставанию
(задержке) в изменении направления M с
изменением направления H.
Гистерезис магнитного вращения возникает
также при вращении образца относительно
фиксированного направления H.
Домен —
макроскопическая область в магнитном
кристалле, в которой ориентация вектора
спонтанной однороднойнамагниченности[1] или вектора
антиферромагнетизма[2] (при температуре ниже точки
Кюри или Нееля соответственно)
определенным образом повернута или
сдвинута относительно направлений
соответствующего вектора в соседних
доменах. Домены существуют
в ферро- и антиферромагнитных, сегнетоэлектрических кристаллах и
других веществах, обладающих
спонтанным дальним
порядком.
Помимо
рассмотренных двух классов веществ —
диа- и парамагнетиков,
называемых слабомагнитными веществами,
существуют еще сильномагнитные
вещества — ферромагнетики —
вещества, обладающие спонтанной
намагниченностью, т. е. они намагничены
даже при отсутствии внешнего магнитного
поля. К ферромагнетикам кроме основного
их представителя — железа (от него и
идет название «ферромагнетизм») —
относятся, например, кобальт, никель,
гадолиний, их сплавы и соединения.
Ферромагнетики
помимо способности сильно намагничиваться
обладают еще и другими свойствами,
существенно отличающими их от диа- и
парамагнетиков. Если для слабомагнитных
веществ зависимость J от Н линейна
(см. (133.6) и рис. 192), то для ферромагнетиков
эта зависимость, впервые изученная в
1878 г. методом баллистического гальванометра
для железа русским физиком А.Г. Столетовым
(1839—1896), является довольно сложной. По
мере возрастания Ннамагниченность J сначала
растет быстро, затем медленнее и, наконец,
достигается так называемое магнитное
насыщение Jнас,
уже не зависящее от напряженности поля.
Подобный характер зависимости J от Н можно
объяснить тем, что по мере увеличения
намагничивающего поля увеличивается
степень ориентации молекулярных
магнитных моментов по полю, однако этот
процесс начнет замедляться, когда
остается все меньше и меньше
неориентированных моментов, и, наконец,
когда все моменты будут ориентированы
по полю, дальнейшее увеличение J прекращается
и наступает магнитное насыщение.
Магнитная
индукция B= 0 (H+J)
(см. (133.4)) в слабых полях растет быстро
с ростом H вследствие
увеличения J, а
в сильных полях, поскольку второе
слагаемое постоянно (J=Jнас), В растет
с увеличением Н по
линейному закону (рис. 193).
Существенная
особенность ферромагнетиков — не только
большие значения (например,
для железа — 5000, для сплава супермаллоя
— 800 000!), но и зависимость от Н (рис.
194). Вначале растет
с увеличением Н, затем,
достигая максимума, начинает уменьшаться,
стремясь в случае сильных полей к 1
( =B/(0H)
= 1 + J/H, поэтому
при J = Jнас = const с
ростом Н отношение J/H 0, 1).
Характерная
особенность ферромагнетиков состоит
также в том, что для них зависимость J от H (а
следовательно, и В от Н)
определяется предысторией намагничения
ферромагнетика. Это явление получило
название магнитного
гистерезиса.
Если намагнитить ферромагнетик до
насыщения (точка 1,
рис. 195), а затем начать уменьшать
напряженность Н намагничивающего
поля, то, как показывает опыт,
уменьшение J описывается
кривой 1—2, лежащей
выше кривой 1—0. При Н =
0 J отличается
от нуля, т. е. в ферромагнетике
наблюдается остаточное
намагничение Jос.
С наличием остаточного намагничения
связано существование постоянных
магнитов. Намагничение
обращается в нуль под действием
поля Нс, имеющего
направление, противоположное полю,
вызвавшему намагничение. Напряженность Нс
называется коэрцитивной
силой.
При
дальнейшем увеличении противоположного
поля ферромагнетик перемагничивается
(кривая 3—4), и
при Н
= –Hнас достигается
насыщение (точка 4).
Затем ферромагнетик можно опять
размагнитить (кривая 4—5—6)
и вновь перемагнитить до насыщения
(кривая 6—7).
Таким
образом, при действии на ферромагнетик
переменного магнитного поля
намагниченность J изменяется
в соответствии с кривой 1—2—3—4—5—6—1,которая
называется петлей
гистерезиса (от
греч. «запаздывание»). Гистерезис
приводит к тому, что намагничение
ферромагнетика не является однозначной
функцией Н, т.е.
одному и тому же значению Н соответствует
несколько значений J.
Различные
ферромагнетики дают разные гистерезисные
петли. Ферромагнетики с малой (в пределах
от нескольких тысячных до 1—2 А/см)
коэрцитивной силойНс (с
узкой петлей гистерезиса) называются мягкими,
с большой (от нескольких десятков до
нескольких тысяч ампер на сантиметр)
коэрцитивной силой (с широкой петлей
гистерезиса) — жесткими.
Величины Нс, Jос и max определяют
применимость ферромагнетиков для
тех или иных практических целей. Taк,
жесткие ферромагнетики (например,
углеродистые и вольфрамовые стали)
применяются для изготовления постоянных
магнитов, а мягкие (например, мягкое
железо, сплав железа с никелем) — для
изготовления сердечников трансформаторов.
Ферромагнетики
обладают еще одной существенной
особенностью: для каждого ферромагнетика
имеется определенная температура,
называемая точкой
Кюри,
при которой он теряет свои магнитные
свойства. При нагревании образца выше
точки Кюри ферромагнетик превращается
в обычный парамагнетик. Переход вещества
из ферромагнитного состояния в
парамагнитное, происходящий в точке
Кюри, не сопровождается поглощением
или выделением теплоты, т.е. в точке Кюри
происходит фазовый переход II рода.
Наконец,
процесс намагничения ферромагнетиков
сопровождается изменением его линейных
размеров и объема. Это явление получило
названиемагнитострикции.
Величина и знак эффекта зависят от
напряженности Н намагничивающего
поля, от природы ферромагнетика и
ориентации кристаллографических осей
по отношению к полю.
49. Основы теории Максвелла для
электромагнитного поля. Ток смещения.
Введение
Максвеллом понятия тока смещения привело
его к завершению созданной им
макроскопической теории электромагнитного
поля, позволившей с единой точки зрения
не только объяснить электрические и
магнитные явления, но и предсказать
новые, существование которых было
впоследствии подтверждено.
В
основе теории Максвелла лежат рассмотренные
выше четыре уравнения:
1.
Электрическое поле может быть как
потенциальным (ЕQ),
так и вихревым (ЕB), поэтому
напряженность суммарного поля Е = ЕQ + ЕB.
Так как циркуляция вектора ЕQ равна
нулю (см. (137.3)), а циркуляция
вектора ЕB определяется
выражением (137.2), то циркуляция вектора
напряженности суммарного поля
Это
уравнение показывает, что источниками
электрического поля могут быть не только
электрические заряды, но и изменяющиеся
во времени магнитные поля.
2.
Обобщенная теорема о циркуляции
вектора Н (см.
(138.4)):
Это
уравнение показывает, что магнитные
поля могут возбуждаться либо движущимися
зарядами (электрическими токами), либо
переменными электрическими полями.
3.
Теорема Гаусса для поля D (см.
(89.3)):
(139.1)
Если
заряд распределен внутри замкнутой
поверхности непрерывно с объемной
плотностью , то
формула (139.1) запишется в виде
4.
Теорема Гаусса для поля В (см.
(120.3)):
Итак, полная
система уравнений Максвелла в интегральной
форме:
Величины,
входящие в уравнения Максвелла, не
являются независимыми и между ними
существует следующая связь (изотропные
несегнетоэлектрические и неферромагнитные
среды):
где 0 и 0 —
соответственно электрическая и магнитная
постоянные, и — соответственно
диэлектрическая и магнитная
проницаемости, —
удельная проводимость вещества.
Из
уравнений Максвелла вытекает, что
источниками электрического поля могут
быть либо электрические заряды, либо
изменяющиеся во времени магнитные поля,
а магнитные поля могут возбуждаться
либо движущимися электрическими зарядами
(электрическими токами), либо переменными
электрическими полями. Уравнения
Максвелла не симметричны относительно
электрического и магнитного полей. Это
связано с тем, что в природе существуют
электрические заряды, но нет зарядов
магнитных.
Для
стационарных полей (E=const и B=const)
уравнения Максвелла примут
вид
т.е.
источниками электрического поля в
данном случае являются только электрические
заряды, источниками магнитного — только
токи проводимости. В данном случае
электрические и магнитные поля независимы
друг от друга, что и позволяет изучать
отдельно постоянные электрическое
и магнитное поля.
Воспользовавшись
известными из векторного анализа
теоремами Стокса и Гаусса
можно
представить полную
систему уравнении Максвелла в
дифференциальном форме (характеризующих
поле в каждой точке пространства):
Если
заряды и токи распределены в пространстве
непрерывно, то обе формы уравнений
Максвелла — интегральная и дифференциальная
— эквивалентны. Однако если имеются
поверхности разрыва – поверхности, на
которых свойства среды или полей меняются
скачкообразно, то интегральная форма
уравнений является более общей.
Уравнения
Максвелла в дифференциальной форме
предполагают, что все величины в
пространстве и времени изменяются
непрерывно. Чтобы достичь математической
эквивалентности обеих форм уравнений
Максвелла, дифференциальную форму
дополняют граничными
условиями, которым
должно удовлетворять электромагнитное
поле на границе раздела двух сред.
Интегральная форма уравнений Максвелла
содержит эти условия. Они были рассмотрены
раньше:
(первое
и последнее уравнения отвечают случаям,
когда на границе раздела нет ни свободных
зарядов, ни токов проводимости).
Уравнения
Максвелла — наиболее общие уравнения
для электрических и магнитных полей
в покоящихся
средах. Они
играют в учении об электромагнетизме
такую же роль, как законы Ньютона в
механике. Из уравнений Максвелла следует,
что переменное магнитное поле всегда
связано с порождаемым им электрическим
полем, а переменное электрическое поле
всегда связано с порождаемым им магнитным,
т. е. электрическое и магнитное поля
неразрывно связаны друг с другом — они
образуют единое электромагнитное
поле.
Теория
Максвелла, являясь обобщением основных
законов электрических и магнитных
явлений, не только смогла объяснить уже
известные экспериментальные факты, что
также является важным ее следствием,
но и предсказала новые явления. Одним
из важных выводов этой теории явилось
существование магнитного поля токов
смещения, что позволило Максвеллу
предсказать существование электромагнитных
волн — переменного электромагнитного
поля, распространяющегося в пространстве
с конечной скоростью. В дальнейшем было
доказано, что скорость распространения
свободного электромагнитного поля (не
связанного с зарядами и токами) в вакууме
равна скорости света с =
3108 м/с.
Этот вывод и теоретическое исследование
свойств электромагнитных волн привели
Максвелла к созданию электромагнитной
теории света, согласно которой свет
представляет собой также электромагнитные
волны. Электромагнитные волны на опыте
были получены немецким физиком Г. Герцем
(1857—1894), доказавшим, что законы их
возбуждения и распространения полностью
описываются уравнениями Максвелла.
Таким образом, теория Максвелла была
экспериментально подтверждена.
К
электромагнитному полю применим только
принцип относительности Эйнштейна,
так как факт распространения
электромагнитных волн в вакууме во всех
системах отсчета с одинаковой
скоростью с не
совместим с принципом относительности
Галилея.
Согласно принципу
относительности Эйнштейна,
механические, оптические и электромагнитные
явления во всех инерциальных системах
отсчета протекают одинаково, т. е.
описываются одинаковыми уравнениями.
Уравнения Максвелла инвариантны
относительно преобразований Лоренца:
их вид не меняется при переходе от одной
инерциальной системы отсчета к другой,
хотя величины Е,
В, D,
Н в
них преобразуются по определенным
правилам.
Из
принципа относительности вытекает, что
отдельное рассмотрение электрического
и магнитного полей имеет относительный
смысл. Taк,
если электрическое поле создается
системой неподвижных зарядов, то эти
заряды, являясь неподвижными относительно
одной инерциальной системы отсчета,
движутся относительно другой и,
следовательно, будут порождать не только
электрическое, но и магнитное поле.
Аналогично, неподвижный относительно
одной инерциальной системы отсчета
проводник с постоянным током, возбуждая
в каждой точке пространства постоянное
магнитное поле, движется относительно
других инерциальных систем, и создаваемое
им переменное магнитное поле возбуждает
вихревое электрическое поле.
Таким
образом, теория Максвелла, ее
экспериментальное подтверждение, а
также принцип относительности Эйнштейна
приводят к единой теории электрических,
магнитных и оптических явлений,
базирующейся на представлении об
электромагнитном поле.
Согласно
Максвеллу, если всякое переменное
магнитное поле возбуждает в окружающем
пространстве вихревое электрическое
поле, то должно существовать и обратное
явление: всякое изменение электрического
поля должно вызывать появление в
окружающем пространстве вихревого
магнитного поля. Для установления
количественных соотношений между
изменяющимся электрическим полем и
вызываемым им магнитным полем Максвелл
ввел в рассмотрение так называемый ток
смещения.
Рассмотрим
цепь переменного тока, содержащую
конденсатор (рис. 196). Между обкладками
заряжающегося и разряжающегося
конденсатора имеется переменное
электрическое поле, поэтому, согласно
Максвеллу, через конденсатор «протекают»
токи смещения, причем в тех участках,
где отсутствуют проводники.
Найдем
количественную связь между изменяющимся
электрическим и вызываемым им магнитным
полями. По Максвеллу, переменное
электрическое поле в конденсаторе в
каждый момент времени создает такое
магнитное поле, как если бы между
обкладками конденсатора существовал
ток смещения, равный току в подводящих
проводах. Тогда можно утверждать, что
токи проводимости (I)
и смещения (Iсм)
равны: Iсм =I.
Ток
проводимости вблизи обкладок конденсатора
(138.1)
(поверхностная
плотность заряда на
обкладках равна электрическому
смещению D в
конденсаторе (см. (92.1)). Подынтегральное
выражение в (138.1) можно рассматривать
как частный случай скалярного
произведения когда
и dS взаимно
параллельны. Поэтому для общего случая
можно записать
Сравнивая
это выражение с (см.
(96.2)), имеем
(138.2)
Выражение
(138.2) и было названо Максвеллом плотностью
тока смещения.
Рассмотрим,
каково же направление векторов плотностей
токов проводимости и смещения j и jсм.
При зарядке конденсатора (рис. 197, а) через
проводник, соединяющий обкладки, ток
течет от правой обкладки к левой; поле
в конденсаторе усиливается;
следовательно, >0,
т. е. вектор направлен
в ту же сторону, что и D.
Из рисунка видно, что направления
векторов и j совпадают.
При разрядке конденсатора (рис.
197, б) через
проводник, соединяющий обкладки, ток
течет от левой обкладки к правой; поле
в конденсаторе ослабляется;
следовательно, <0,
т. е. вектор направлен
противоположно вектору D.
Однако вектор направлен
опять так же, как и вектор j.
Из разобранных примеров следует, что
направление вектора j,
а следовательно, и вектора jсм,
совпадает с направлением вектора ,
как это и следует из формулы (138.2).
Подчеркнем,
что из всех физических свойств, присущих
току проводимости, Максвелл приписал
току смещения лишь одно — способность
создавать в окружающем пространстве
магнитное поле. Таким образом, ток
смещения (в вакууме или веществе) создает
в окружающем пространстве магнитное
поле (линии индукции магнитных полей
токов смещения при зарядке и разрядке
конденсатора показаны на рис. 197 штриховыми
линиями).
В
диэлектриках ток смещения состоит из
двух слагаемых. Так как, согласно
(89.2), D=0E+P,
где Е –
напряженность электростатического
поля, а Р —
поляризованность, то плотность тока
смещения
(138.3)
где 0— плотность
тока смещения в вакууме, — плотность
тока поляризации —
тока, обусловленного упорядоченным
движением электрических зарядов в
диэлектрике (смещение зарядов в
неполярных молекулах или поворот диполей
в полярных молекулах). Возбуждение
магнитного поля токами поляризации
правомерно, так как токи поляризации
по своей природе не отличаются от токов
проводимости. Однако то, что и другая
часть плотности тока смещения ,
не связанная с движением зарядов, а
обусловленная только изменением
электрического поля во времени, также
возбуждает магнитное поле,
является принципиально
новым утверждением Максвелла.
Даже в вакууме всякое изменение во
времени электрического поля приводит
к возникновению в окружающем
пространстве магнитного поля.
Следует
отметить, что название «ток смещения»
является условным, а точнее —
исторически сложившимся, так как ток
смещения по своей сути — это изменяющееся
со временем электрическое поле. Ток
смещения поэтому существует не только
в вакууме или диэлектриках, но и внутри
проводников, по которым проходит
переменный ток. Однако в данном случае
он пренебрежимо мал по сравнению с током
проводимости. Наличие токов смещения
подтверждено экспериментально А.А.
Эйхенвальдом, изучавшим магнитное поле
тока поляризации, который, как следует
из (138.3), является частью тока смещения.
Максвелл
ввел понятие полного тока, равного
сумме токов проводимости (а также
конвекционных токов) и смещения. Плотность
полного тока
Введя
понятия тока смещения и полного тока,
Максвелл по-новому подошел к рассмотрению
замкнутости цепей переменного тока.
Полный ток в них всегда замкнут, т. е. на
концах проводника обрывается лишь ток
проводимости, а в диэлектрике (вакууме)
между концами проводника имеется ток
смещения, который замыкает ток
проводимости.
Максвелл
обобщил теорему о циркуляции вектора Н (см.
(133.10)), введя в ее правую часть полный
ток Iполн = jполнdS сквозь
поверхность S, натянутую
на замкнутый контур L. Тогда обобщенная
теорема о циркуляции вектора Н запишется
в виде
(138.4)
Выражение
(138.4) справедливо всегда, свидетельством
чего является полное соответствие
теории и опыта.
50. Уравнение Максвелла для электромагнитного
поля в интегральной форме.
Введение
Максвеллом понятия тока смещения привело
его к завершению созданной им
макроскопической теории электромагнитного
поля, позволившей с единой точки зрения
не только объяснить электрические и
магнитные явления, но и предсказать
новые, существование которых было
впоследствии подтверждено.
В
основе теории Максвелла лежат рассмотренные
выше четыре уравнения:
1.
Электрическое поле может быть как
потенциальным (ЕQ),
так и вихревым (ЕB), поэтому
напряженность суммарного поля Е = ЕQ + ЕB.
Так как циркуляция вектора ЕQ равна
нулю (см. (137.3)), а циркуляция
вектора ЕB определяется
выражением (137.2), то циркуляция вектора
напряженности суммарного поля
Это
уравнение показывает, что источниками
электрического поля могут быть не только
электрические заряды, но и изменяющиеся
во времени магнитные поля.
2.
Обобщенная теорема о циркуляции
вектора Н (см.
(138.4)):
Это
уравнение показывает, что магнитные
поля могут возбуждаться либо движущимися
зарядами (электрическими токами), либо
переменными электрическими полями.
3.
Теорема Гаусса для поля D (см.
(89.3)):
(139.1)
Если
заряд распределен внутри замкнутой
поверхности непрерывно с объемной
плотностью , то
формула (139.1) запишется в виде
4.
Теорема Гаусса для поля В (см.
(120.3)):
Итак, полная
система уравнений Максвелла в интегральной
форме:
Величины,
входящие в уравнения Максвелла, не
являются независимыми и между ними
существует следующая связь (изотропные
несегнетоэлектрические и неферромагнитные
среды):
где 0 и 0 —
соответственно электрическая и магнитная
постоянные, и — соответственно
диэлектрическая и магнитная
проницаемости, —
удельная проводимость вещества.
Из
уравнений Максвелла вытекает, что
источниками электрического поля могут
быть либо электрические заряды, либо
изменяющиеся во времени магнитные поля,
а магнитные поля могут возбуждаться
либо движущимися электрическими зарядами
(электрическими токами), либо переменными
электрическими полями. Уравнения
Максвелла не симметричны относительно
электрического и магнитного полей. Это
связано с тем, что в природе существуют
электрические заряды, но нет зарядов
магнитных.
Для
стационарных полей (E=const и B=const)
уравнения Максвелла примут
вид
т.е.
источниками электрического поля в
данном случае являются только электрические
заряды, источниками магнитного — только
токи проводимости. В данном случае
электрические и магнитные поля независимы
друг от друга, что и позволяет изучать
отдельно постоянные электрическое
и магнитное поля.
Воспользовавшись
известными из векторного анализа
теоремами Стокса и Гаусса
Содержание:
- Определение и формула напряженности магнитного поля
- Закон Био-Савара-Лапласа
- Единицы измерения
- Примеры решения задач
Определение и формула напряженности магнитного поля
Определение
Напряженностью магнитного поля $bar{H}$ называют
векторную физическую величину, направленную по касательной к силовым линиям поля, являющуюся характеристикой магнитного поля, равную:
$$bar{H}=frac{bar{B}}{mu_{0}}-bar{J}(1)$$
где $bar{B}$ – вектор магнитной индукции,
$mu_{0}=4 pi cdot 10^{-7}$ Гн/м(Н/А2)- магнитная постоянная,
$bar{j}$ – вектор намагниченности среды в исследуемой точке поля.
Для магнитного поля в вакууме напряженность магнитного поля определяется выражением:
$$bar{H}=frac{bar{B}}{mu_{0}}$$
В изотропной среде формула (1) преобразуется к виду:
$$bar{H}=frac{bar{B}}{mu_{0} mu}$$
где $mu$ – скалярная величина, называемая
относительной магнитной проницаемостью среды (или просто магнитной проницаемостью). В изотропной среде векторы напряженности
магнитного поля и магнитной индукции совпадают по направлению.
Иногда напряженность магнитного поля $d bar{H}$ определяют как
векторную величину, направленную по касательной к силовой линии поля, по модулю равной отношению силы (dF), с которой поле
воздействует на единичный элемент тока (dl), который расположен перпендикулярно полю в вакууме, к магнитной постоянной:
$$d H=frac{d F}{mu_{0} I d l}$$
Закон Био-Савара-Лапласа
Это важнейший в электромагнетизме закон. Он определяет вектор напряженности $d bar{H}$
в произвольной точке магнитного поля, которое создает в вакууме элементарный проводник длинны dl с постоянным током I:
$$d bar{H}=frac{1}{4 pi} frac{I}{r^{3}} d bar{l} times bar{r}(5)$$
где $d bar{l}$ – вектор элемента проводника, который по модулю равен длине
проводника, направление совпадает с направлением тока; $bar{r}$ – радиус–вектор,
который проводят от рассматриваемого элементарного проводника к точке рассмотрения поля;
$r=|bar{r}|$ .
Вектор $d bar{H}$ – перпендикулярен плоскости, в которой находятся
векторы $d bar{l}$ и
$bar{r}$, и направлен так, что из его конца вращение вектора
$d bar{l}$ по кратчайшему пути до совмещения с вектором
$bar{r}$ происходило по часовой стрелке. Для нахождения направления вектора
$d bar{H}$ можно использовать правило буравчика (Буравчик (винт) вращаем так,
чтобы его поступательное движение совпадало с направлением тока, тогда направление, по которому вращается ручка винта, совпадает с направлением
вектора напряженности поля, которое создает рассматриваемый ток).
Закон Био-Савара-Лапласа дает возможность вычислять величину полной напряженности магнитного поля, которое создает ток, текущий по проводнику любой формы.
Для нахождения полной напряженности магнитного поля, которое создает в исследуемой точке ток I, который течет по проводнику l, следует
векторно суммировать все элементарные напряженности $d bar{H}$, порождаемые
элементами проводника и найденные по формуле (4).
Единицы измерения
Основной единицей измерения момента силы в системе СИ является: [H]=А/м
Примеры решения задач
Пример
Задание. Чему равна напряженность (H) в центре кругового витка (R – радиус витка) с током I.
Решение. Каждый элементарный ток витка магнитное поле в центре окружности, напряженность которого направлена по
положительной нормали к плоскости контура витка (рис.1). Поэтому, если элементарную напряженность поля найти по закону Био-Савара –
Лапласа, то векторное сложение элементарных полей можно будет заменить на алгебраическое.
В соответствии с законом Био-Савара – Лапласа dH равно:
$$d bar{H}=frac{1}{4 pi} frac{I}{r^{3}} d bar{l} times bar{r}(1.1)$$
Применяя выражение (1.1) к нашему случаю, получим:
$$d H=frac{1}{4 pi} frac{I d l}{R^{2}}(1.2)$$
Возьмем интеграл по контуру, получим:
$$H=oint_{L} frac{1}{4 pi} frac{I d l}{R^{2}}=frac{1}{4 pi} I cdot frac{2 pi R}{R^{2}}=frac{I}{2 R}$$
Ответ. $H=frac{I}{2 R}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
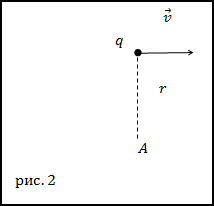
Задание. Какова напряженность магнитного поля, которую создает электрон, движущийся прямолинейно и равномерно со
скоростью v? Если точка, в которой исследуется поле, находится на расстоянии r от электрона на перпендикуляре к вектору скорости,
если перпендикуляр провести через мгновенное положение частицы.
Решение. Сделаем рисунок.
Напряженность магнитного поля будем искать, применяя закон Био – Савара – Лапласа:
$$d bar{H}=frac{1}{4 pi} frac{I}{r^{3}} d bar{l} times bar{r}(2.1)$$
Учтем, что:
$$I d l=S j d l(2.2)$$
Если все заряды одинаковы (q), то плотность тока равна:
$$bar{j}=q n bar{v}(2.3)$$
заряд отрицательный, следовательно, направления векторов
$bar{j}$ и
$bar{v}$ противоположны. n – концентрация зарядов. Подставим формулу (2.3)
в (2.2), результат в (2.1) получаем:
$$d bar{H}=frac{1}{4 pi} frac{S q n d l}{r^{3}} bar{v} times bar{r}(2.4)$$
где dN=Sdln – количество заряженных частиц в отрезке dl. В таком случае, напряженность поля, которое создает один заряд:
$$bar{H}=frac{d bar{H}}{d N}=frac{1}{4 pi} frac{q}{r^{3}} bar{v} times bar{r}(2.4)$$
По условию задачи $bar{v} perp bar{r}$ , значит модуль напряжённости магнитного поля в точке А (рис.2) будет равен:
$$H=frac{1}{4 pi} frac{q v}{r^{2}}$$
Ответ. $H=frac{1}{4 pi} frac{q v}{r^{2}}$
Читать дальше: Формула напряженности электрического поля.
Магнитное поле играет очень большую роль в электротехнике и электронике. Без магнитного поля не функционировали бы герконы, электромагнитные реле, соленоиды, катушки индуктивности, дроссели, трансформаторы, двигатели, динамики, генераторы электрической энергии да и вообще много чего.
Природа магнетизма
Согласно одной из легенд, когда-то давным-давно жил в Греции пастух по имени Магнес. И вот шел он как-то со своим стадом овец, присел на камень и обнаружил, что конец его посоха, сделанный из железа, стал притягиваться к этому камню. С тех пор стали называть этот камень магнетит в честь Магнеса. Этот камень представляет из себя оксид железа.
Если такой камень положить на деревянную доску на воду или подвесить на нитке, то он всегда выстраивался в определенном положении. Один его конец всегда показывал на СЕВЕР, а другой — на ЮГ.
Этим свойством камня пользовались древние цивилизации. Поэтому, это был своего рода первый компас. Потом уже стали обтачивать такой камень и делать из разные фигурки. Например, так выглядел китайский древний компас, ложка которого была сделана из того самого магнетита. Ручка у этой ложки всегда показывала на ЮГ.
Ну а далее дело шло за практичностью и маленькими габаритами. Из магнетита вытачивали маленькие стрелки, которые подвешивали на тонкую иглу посередине. Так стали появляться первые малогабаритные компасы.
Древние цивилизации, конечно, не знали еще что такое север и юг. Поэтому, одну сторону магнетита они назвали северным полюсом (North), а противоположный конец — южным (South). Названия на английском очень легко запомнить, если кто смотрел американский мультфильм «Южный парк», он же Сауз (South) парк).
Магнитные линии и магнитный поток
Вокруг магнита экспериментальным путем были обнаружены магнитные силовые линии. Эти магнитные линии создают так называемое магнитное поле.
Как вы могли заметить на рисунке, концентрация магнитных силовых линий на самых краях магнита намного больше, чем в его середине. Это говорит о том, что магнитное поле является более сильным именно на краях магнита, а в его середине практически равна нулю. Направлением магнитных силовых линий считается направление от севера к югу.
Ошибочно считать, что магнитные силовые линии начинают свое движение от северного полюса и заканчивают свой век на южном. Это не так. Магнитные линии — они замкнуты и непрерывны. В магните это будет выглядеть примерно так.
Если приблизить два разноименных полюса, то произойдет притягивание магнитов
Если же приблизить одноименными полюсами, то произойдет их отталкивание
Итак, ниже важные свойства магнитных силовых линий.
- Магнитные линии не поддаются гравитации.
- Никогда не пересекаются между собой.
- Всегда образуют замкнутые петли.
- Имеют определенное направление с севера на юг.
- Чем больше концентрация силовых линий, тем сильнее магнитное поле.
- Слабая концентрация силовых линий указывает на слабое магнитное поле.
Магнитные силовые линии, которые образуют магнитное поле, называют также магнитным потоком.
Итак, давайте рассмотрим два рисунка и ответим себе на вопрос, где плотность магнитного потока будет больше? На рисунке «а» или на рисунке «б»?
Видим, что на рисунке «а» мало силовых магнитных линий, а на рисунке «б» их концентрация намного больше. Отсюда можно сделать вывод, что плотность магнитного потока на рисунке «б» больше, чем на рисунке «а».
В физике формула магнитного потока записывается как
где
Ф — магнитный поток, Вебер
В — плотность магнитного потока, Тесла
а — угол между перпендикуляром n (чаще его зовут нормалью) и плоскостью S, в градусах
S — площадь, через которую проходит магнитный поток, м2
Что же такое 1 Вебер? Один вебер — это магнитный поток, который создается полем индукцией 1 Тесла через площадку 1м2 расположенной перпендикулярно направлению магнитного поля.
Напряженность магнитного поля
Формула напряженности
Слышали ли вы когда-нибудь такое выражение: «напряженность между ними все росла и росла». То есть по сути напряженность — это что-то невидимое, какая-то сдерживающая сила, энергия. Здесь почти все то же самое. Напряженностью магнитного поля также часто называют силой магнитного поля. Напряженность магнитного поля напрямую зависит от плотности магнитного потока и выражается формулой
где
H — напряженность магнитного поля, Ампер/метр
B — плотность магнитного потока, Тесла
μ0 — магнитная постоянная = 4π × 10-7 Генри/метр или если написать по человечески 1,2566 × 10-6 Генри/метр.
PS.
Эта формула работает только тогда, когда между витками катушки находится воздух, либо вакуум. Более крутая формула выглядит вот так.
где
μ — это относительная магнитная проницаемость.
У разных веществ она разная
Напряженность магнитного поля проводника с током
Итак, имеем какой-либо проводник, по которому течет электрический ток.
Для того, чтобы вычислить напряженность магнитного поля на каком-то расстоянии от проводника при условии, что проводник находится в воздушном пространстве либо в вакууме, достаточно воспользоваться формулой
где
H — напряженность магнитного поля, Ампер/метр
I — сила тока, текущая через проводник, Ампер
r — расстояние до точки, в которой измеряется напряженность, метр
Магнитное поле проводника с током
Оказывается, если через какой-либо проводник пропустить электрический ток, то вокруг проводника образуется магнитное поле.
Здесь можно вспомнить знаменитое правило буравчика, но для наглядности я лучше буду использовать правило самореза, так как почти все хоть раз в жизни ввинчивали либо болт, либо саморез.
Ввинчиваем по часовой стрелке — саморез идет вниз. В нашем случае он показывает направление электрического тока. Движение наших рук показывает направление линий магнитного поля. Все то же самое, когда мы начинаем откручивать саморез. Он начинает вылазить вверх, то есть в нашем случае показывает направление электрического тока, а наша рука в этом время рисует в воздухе направление линий магнитного поля.
Также часто в учебниках физики можно увидеть, что направление электрического тока от нас рисуют кружочком с крестиком, а к нам — кружочком с точкой. В этом случае опять представляем себе саморез и уже в голове увидим направление магнитного поля.
Как думаете, что будет если мы сделаем вот такую петельку из провода? Что изменится в этом случае?
Давайте же рассмотрим этот случай более подробно. Так в этой плоскости оба проводника создают магнитное поле, то по идее они должны отталкиваться друг от друга. Но если они хорошо закреплены, то начинается самое интересное. Давайте рассмотрим вид сверху, как это выглядит.
Как вы можете заметить, в области, где суммируются магнитные силовые линии плотность магнитного потока прям зашкаливает.
Соленоид
А что если сделать много-много таких петелек? Взять какую-нибудь круглую бобину, намотать на нее провод и потом убрать бобину. У нас должно получится что-то типа этого.
Если подать постоянное напряжение на такую катушку, магнитные силовые линии будут выглядеть вот так.
Вы только посмотрите, какая бешеная плотность магнитного потока внутри такой катушки! Получается, что от каждой петельки магнитное поле суммируется, что в итоге дает такую плотность магнитного потока. Такую катушку также называют катушкой индуктивности или соленоидом.
Вот также схема, показывающая как магнитные силовые линии складываются в соленоиде.
Плотность магнитного потока зависит от того, какая сила тока проходит через соленоид. Чтобы увеличить плотность магнитного потока, достаточно поверх витков намотать еще больше витков и вставить сердечник из специального материала — феррита.
Если в электрических цепях есть такое понятие, как ЭДС — электродвижущая сила, то и в магнитных цепях есть свой аналог — МДС — магнитодвижущая сила. Магнитодвижущая сила выражается в виде тока, протекающего через катушку из N витков и выражается в Амперах-витках.
где
I — это сила тока в катушке, Амперы
N — количество витков катушки, штуки)
Также советую посмотреть очень простое и интересное видео про магнитное поле.
Похожие статьи по теме «магнитное поле»
Катушка индуктивности
Трансформатор
Электромагнитное реле
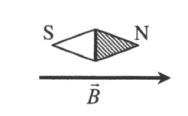
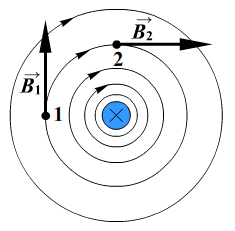
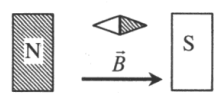
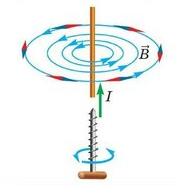
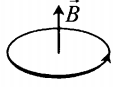
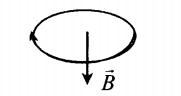

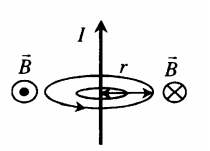
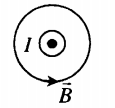
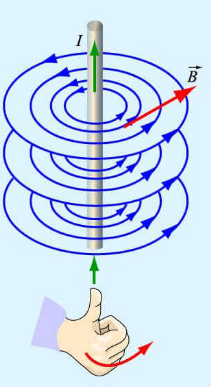
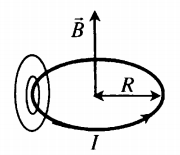
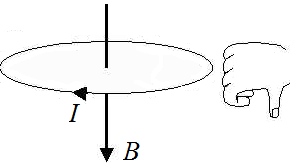
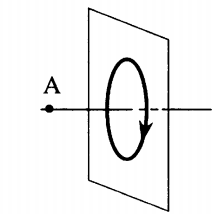
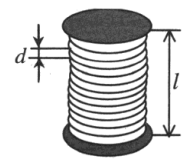
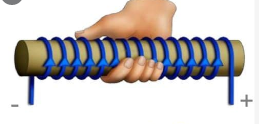
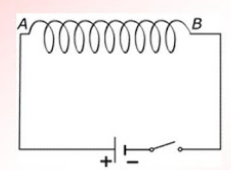



 .
.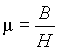 .
. .
.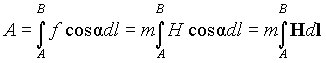 ,
,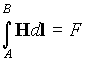 ,
,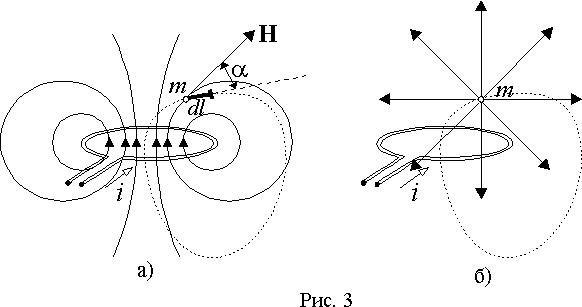

 .
.