Сила Лоренца
На проводник с током в магнитном поле действует сила Ампера. Однако магнитное поле способно взаимодействовать и с отдельными электрическими зарядами. Рассмотрим кратко эту тему, узнаем, как определить направление и величину силы, действующей на заряд в магнитном поле.
Взаимодействие магнитного поля с зарядами
Опыты показывают, что магнитное поле никак не влияет на покоящийся электрический заряд. Почему же магнитное поле взаимодействует с проводником с электрическим током, который представляет собой движущиеся электрические заряды ?
Причина в движении зарядов. Магнитное поле не взаимодействует с зарядом, пока его скорость в этом поле равна нулю. Однако, как только заряд начинает двигаться, сразу же возникает сила, направленная перпендикулярно вектору скорости заряда.
Это приводит к интересному результату. Из механики известно, что если материальная точка движется под действием силы, направленной перпендикулярно вектору скорости, то ее траектория представляет собой окружность. Именно это и происходит с движущимися заряженными частицами в однородном магнитном поле. Заряженные частицы под действием магнитного поля движутся по окружностям.
Рис. 1. Движение заряженной частицы в магнитном поле.
Сила Лоренца
Сила, которая возникает при движении заряда в магнитном поле, называется силой Лоренца. Именно силы Лоренца, действующие на отдельные заряды в проводнике, приводят к появлению общей силы Ампера. Поэтому формулу силы Лоренца можно получить из закона Ампера.
Сила Ампера равна:
$$F_A= IB Δl sin alpha$$
Величина тока, идущая в проводнике, прямо пропорциональна величине заряда носителей $q$, их концентрации $n$, скорости их движения $v$ и площади поперечного сечения проводника $S$:
$$I = qnvS$$
Подставляя это выражение в предыдущую формулу, получим:
$$ F_A = qnvSBΔl sin alpha$$
Сила Ампера действует на проводник в результате сложения сил Лоренца, действующих на каждый из зарядов в проводнике. То есть для получения силы Лоренца, действующей на отдельный носитель, надо величину силы Ампера поделить на число носителей. Число носителей $N$ равно произведению концентрации носителей на объем проводника:
$$N=nSΔl$$
Следовательно, сила Лоренца равна:
$$F_L = {F_A over N}= qvB sin alpha$$
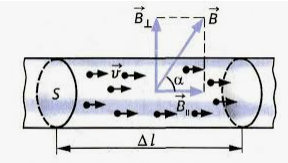
Как и в случае силы Ампера, угол $alpha $ — это угол между направлением движения носителя заряда (вектором скорости) и вектором магнитной индукции.
Направление силы Лоренца определяется точно так же, как и направление силы Ампера: с помощью мнемонического правила левой руки. Если расположить левую руку так, чтобы четыре пальца были направлены по направлению движения положительного заряда (против направления для отрицательного), а перпендикулярная составляющая индукции $B_{perp}$ входила в ладонь, то большой палец покажет направление силы Лоренца.
Рис. 2. Правило левой руки.
Получается, что сила Лоренца всегда направлена перпендикулярно движению заряженной частицы. А это значит, что сила Лоренца не совершает работу и, следовательно, не меняет кинетическую энергию частицы. Она меняет лишь направление ее движения.
Примером использования силы Лоренца является отклоняющая система кинескопов. Отклоняющие системы в телевизорах с кинескопами представляют собой электрические катушки, создающие меняющееся магнитное поле. Под действием этого поля на электроны, вылетающие из электронной пушки, начинает действовать сила Лоренца, они отклоняются и направляются в нужную в данный момент точку экрана.
Рис. 3. Отклоняющая система кинескопа.
Что мы узнали?
Сила Лоренца — это сила, действующая со стороны магнитного поля на движущийся электрический заряд. Сила Лоренца направлена перпендикулярно скорости движения частицы, и для определения этого направления используется правило левой руки. В однородном магнитном поле траектории заряженных частиц, движущихся под действием силы Лоренца, представляют собой окружности.
Для школьников (в помощь желающим лучше понять физику).
Сила Ампера
Сила Ампера – это сила, с которой магнитное поле действует на проводник с током.
Опытным путём найдено, что на прямой провод с током со стороны магнитного поля действует сила:
Из формулы видно, что сила Ампера пропорциональна индукции магнитного поля, току в проводнике, длине проводника и зависит от расположения проводника в магнитном поле:
Или действие магнитного поля на проводник определяется лишь перпендикулярной составляющей индукции магнитного поля.
Когда проводник расположен вдоль поля, сила Ампера равна нулю.
Для нахождения направления силы Ампера удобно пользоваться правилом л е в о й р у к и: левую руку располагаем так, чтобы силовые линии магнитного поля входили в ладонь, четыре вытянутых пальца направляем по току, тогда отставленный большой палец покажет направление силы Ампера.
На рисунке ниже показан проводник с током, помещённый в однородное магнитное поле, направленное к нам. Тогда, согласно правилу левой руки, сила Ампера, действующая на проводник с током, направлена вправо.
Сила Лоренца
Сила Лоренца – это сила, с которой магнитное поле действует на движущийся заряд.
Выражение для силы Лоренца (как и для силы Ампера) получено опытным путём:
Опять представим ток в прямом проводе. Воспользуемся тем же рисунком, на котором показана сила Ампера.
Ток в проводнике есть направленное движение свободных электронов.
На рисунке ток по проводнику течёт вверх, а свободные электроны, под действием сил электрического поля внутри проводника, двигаются вниз.
На каждый электрон действует сила Лоренца.
Направление силы Лоренца тоже находится по правилу л е в о й р у к и: левую руку располагаем так, чтобы силовые линии магнитного поля входили в ладонь, четыре вытянутых пальца направляем против скорости движения электрона или по направления тока в проводе (так как за направление тока условились принимать направленное движение положительных зарядов), тогда большой отогнутый палец покажет направление силы Лоренца, действующей на каждый свободный электрон в проводе. Её направление совпадает с направлением сила Ампера.
Сложение сил Лоренца, действующих на каждый электрон в отдельности, даёт силу Ампера (видим, как выражения для этих сил похожи друг на друга).
Чтобы представить свободные электроны и их движение в металлическом проводнике, надо вспомнить строение металла.
А именно, металлический проводник имеет кристаллическое строение. В узлах кристаллической решётки металла находятся ионы (атомы, от которых оторвались валентные электроны).
Если по металлу проходит ток, то свободные электроны двигаются между ионами упорядоченно, взаимодействуя с ними.
Магнитное поле, в котором находится проводник с током или движущийся заряд, создаётся или постоянным магнитом, или электромагнитом, или током.
Т а к и м о б р а з о м, силы взаимодействия между током в проводе и магнитным полем сводятся к силам Лоренца.
Возникающие силы Лоренца действуют на весь проводник, так как движущиеся в проводнике электроны взаимодействуют с атомами проводника (возникает своего рода “трение” между ними).
Наличие этого взаимодействия (“трения”) между упорядоченно движущимися электронами и атомами твёрдого металла, демонстрируется следующим опытом.
Между полюсами подковообразного магнита 2 может вращаться медный диск 1, кромка которого погружена в жёлоб с ртутью 3, служащий для подведения тока от батареи к кромке диска. Второй полюс батареи соединён с осью диска.
При замыкании ключа, благодаря “трению”, диск начинает вращаться. При изменении направления тока или направления магнитного поля направление вращения диска изменится на обратное. Как это происходит?
При прохождении тока электроны двигаются вдоль радиуса диска между центром диска и точкой соприкосновения диска с ртутью.
Сила Лоренца стремится отклонить электроны в перпендикулярном направлении. Вследствие “трения” между электронами и атомами металла весь диск приходит во вращение.
Направление вращения можно установить, пользуясь правилом левой руки.
Задачи
Задача 1.
По проводнику течёт ток, сила которого равна 10 А. Площадь поперечного сечения проводника 5 квадратных сантиметров, а число свободных электронов в одном кубическом сантиметре проводника составляет 10 в двадцать третьей степени. Определить направленную скорость электронов, считая её одинаковой для всех электронов.
Решение
За 1 с через поперечное сечение А проводника пройдут все те электроны, которые содержатся в показанном на рисунке объёме, равном произведению площади поперечного сечения проводника на длину части проводника, равную произведению скорости на 1 с.
Следовательно, сила тока равна произведению указанного объёма на концентрацию электронов и на заряд одного электрона
Ответ: найдена скорость направленного движения электронов в проводнике.
Можно было бы продолжить решение этой задачи, представив, что рассмотренный в задаче проводник с током силой
находится в магнитном поле.
Зная магнитную индукцию этого поля, могли бы найти силу Ампера, действующую на участок проводника с током, изображённом на рисунке выше.
Затем, разделив силу Ампера на число электронов участка провода
смогли бы найти силу, действующую на один движущийся электрон, то есть смогли бы найти силу Лоренца.
Задача 2.
Электрический ток в металлических проводниках представляет собой движение свободных электронов, сталкивающихся с ионами, из которых построена кристаллическая решётка металла, и отдающих при этом ионам ту энергию, которую они приобрели до соударения. Почему же металлический проводник, по которому идёт ток, не испытывает никаких механических сил в направлении движения электронов?
Ответ.
Электрическое поле в металле, вызывающее движение электронов, действует с одинаковой силой и на электроны и на ионы решётки, но силы эти направлены в противоположные стороны. Сила, действующая на электроны, вызывает их ускоренное движение. Под действием поля электроны приобретают энергию, которую они при столкновении отдают ионам. При этом средняя сила, с которой электроны действуют на проводник, сталкиваясь с ионами решётки, равна той силе, с которой электрическое поле действует непосредственно на ионы решётки, но противоположна ей по направлению. Поэтому металлический проводник, по которому идёт ток, не испытывает никаких механических сил в направлении движения электронов.
Таким образом, рассмотрев теорию и задачи к ней, мы убедились, что взаимодействие тока в проводнике с магнитным полем сводится к силам Лоренца.
Действие силы Лоренца на свободно движущуюся заряженную частицу, влетающую в магнитное поле, подробно рассмотрено с решением ряда задач в Занятии 67 и в статье “Поведение электрона в электрическом и магнитном полях”
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Для школьников предлагаются подборки материала по темам:
!. Механика. Кинематика. Равномерное прямолинейное движение.
2. Равнопеременное прямолинейное движение.
Предыдущая запись: Действие магнитного поля на контур с током.
Следующая запись: Зарядка конденсатора. Зарядный и разрядный ток проводимости.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
Сила Лоренца — сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.
Модуль силы Лоренца обозначается как FЛ. Единица измерения — Ньютон (Н).
Модуль силы Лоренца численно равен отношению модуля силы F, действующий на участок проводника длиной l, к числу N заряженных частиц, упорядоченно движущихся на этом участке проводника:
FЛ=FN
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка ∆l и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля →B можно считать неизменным в пределах этого отрезка проводника.
Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (число зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:
I=qnvS
Модуль силы, действующей со стороны магнитного поля на выбранные элемент тока, равен:
F=|I|ΔlBsinα
Подставляя сюда выражение, полученное для силы тока, получим:
F=|qnvS|ΔlBsinα=|q|nvSΔlBsinα
Учтем, что число заряженных частиц в рассматриваемом объеме равно произведению величины этого объема на концентрацию самих частиц:
N=nSΔlB
Тогда:
F=|q|vNBsinα
Следовательно, на каждый движущийся заряд действует сила Лоренца, равная:
FЛ=FN=|q|vNBsinαN=|q|vBsinα
α — угол между вектором скорости движущегося заряда и вектором магнитной индукции.
Пример №1. Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45o к вектору магнитной индукции.
FЛ=|q|vBsinα=0,005·200·0,3·√22≈0,2 (Н)
Направление силы Лоренца
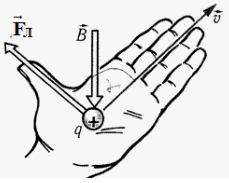
Сила Лоренца перпендикулярна вектору магнитной индукции и вектору скорости движущегося заряда. Ее направление определяется с помощью правила левой руки:
Если левую руку расположить так, чтобы составляющая магнитной индукции →B, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.
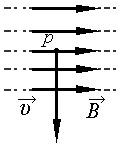
Пример №2. Протон p имеет скорость →v, направленную горизонтально вдоль прямого длинного проводника с током I (см. рисунок). Куда направлена действующая на протон сила Лоренца?
В точке, в которой находится протон, вектор магнитной индукции направлен в сторону от наблюдателя. Это следует из правила буравчика. Теперь применим правило левой руки. Для этого четыре пальца левой руки направим в сторону движения протона — вправо. Ладонь развернем в сторону наблюдателя, чтобы линии магнитной индукции входили в нее перпендикулярно. Теперь отставим на 90 градусов большой палец. Он показывает вверх. Следовательно, сила Лоренца, действующая на протон, направлена вверх.
Работа силы Лоренца
Поскольку вектор силы Лоренца направлен перпендикулярно скорости движения заряда, угол между перемещением этого заряда и этой силы равен 90о. Работа любой силы определяется формулой:
A=Fscosα
Но так как косинус 90о равен 0, сила Лоренца не совершает работу. Это значит, что сила Лоренца не влияет на модуль скорости перемещения заряда. Но она может менять вектора его скорости.
Полная сила, действующая на заряд
При решении задач, в которых заряженная частица находится одновременно в электрическом и магнитном полях, нужно учитывать, что не нее действует сразу две силы. Со стороны магнитного поля — сила Лоренца. Со стороны электрического поля — сила →Fэл, действующая на неподвижный заряд, помещенный в данную точку поля. Она равна произведению этого заряда на напряженность электрического поля:
→Fэл=q→E
Следовательно, полная сила, действующая на заряд, равна:
→F=→Fэл+→Fл=q→E+|q|→v→Bsinα
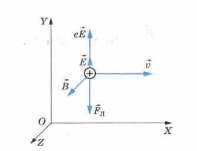
Пример №3. В пространстве, где существует одновременно однородное и постоянное электрическое и магнитное поля, по прямолинейной траектории движется протон. Известно, что напряженность электрического поля равна →E. Какова индукция →B магнитного поля?
Прямолинейное движение протона возможно в двух случаях:
- Вектор →E направлен вдоль траектории движения протона. Тогда вектор →B также должен быть направлен вдоль этой траектории, и его модуль может быть любым, так как магнитное поле на частицу действовать не будет.
- Векторы →E, →B и →v взаимно перпендикулярны, и сила, действующая на протон со стороны электрического поля, равна по модулю и противоположна по направлению силе Лоренца, действующей на протон со стороны магнитного поля (см. рисунок).
Заряд протона равен модулю заряда электрона — e. Сложим силы, действующие на протон по оси ОУ:
e→E+→FЛ=0
В скалярной форме:
eE−evB=0
Следовательно:
B=Ev
Задание EF17621
Протон ускоряется постоянным электрическим полем конденсатора, напряжение на обкладках которого 2160 В. Затем он влетает в однородное магнитное поле и движется по дуге окружности радиуса 20 см в плоскости, перпендикулярной линиям магнитной индукции. Каков модуль вектора индукции магнитного поля? Начальной скоростью протона в электрическом поле пренебречь. Ответ выразить в мТл, округлив до десятых.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения силы Лоренца.
3.Выразить модуль вектора магнитной индукции.
4.Определить недостающие величины.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Напряжение на обкладках конденсатора: U = 2160 В.
• Радиус окружности, по которой движется протон в однородном магнитном поле: R = 20 см.
• Масса протона: m = 1,673·10–27 кг.
• Заряд протона: q = 1,6·10–19 Кл.
20 см = 0,2 м
Сила Лоренца определяется формулой:
FЛ=|q|vBsinα
По условию задачи протон движется перпендикулярно вектору магнитной индукции. Поэтому синус угла между вектором скорости и вектором магнитной индукции будет равен 1. А протон имеет положительный заряд. Тогда:
FЛ=qvB
Сила Лоренца сообщает протону центростремительное ускорение, равное:
a=v2R
Применим второй закон Ньютона:
F=ma
qvB=mv2R
Отсюда модуль вектора магнитной индукции равен:
B=mv2qvR=mvqR
Энергия заряда, движущегося в электрическом поле, определяется формулой:
W=qU
Но энергию заряда также можно выразить как кинетическую энергию движения:
W=Eк=mv22
Приравняем правые части выражений и получим:
qU=mv22
Отсюда ускорение протона равно:
v=√2qUm
Конечная формула для определения модуля вектора магнитной индукции:
B=mvqR=mqR√2qUm=√2UmqR2
Ответ: 33,6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17600
а) влево
б) вправо
в) к нам
г) от нас
Алгоритм решения
- Определить, каким способом можно найти направлений силы Лоренца, действующей на протон.
- Применить правила и найти направление силы Лоренца.
Решение
Силу Лоренца, действующую на заряженную частицу, можно найти с помощью правила левой руки. Для этого мысленно расположим четыре пальца левой руки в сторону, совпадающей с направлением движения положительной частицы (протона). Относительно рисунка пальца будут направлены вниз. Теперь развернем ладонь так, чтобы в нее входили линии магнитной индукции. Теперь отклоним на 90 градусов большой палец. Он будет направлен от плоскости рисунка к нам. Это и есть направление силы Лоренца, действующей на протон.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17749
Протон в однородном магнитном поле движется по окружности. Чтобы в этом поле двигалась по окружности с той же скоростью α-частица, радиус окружности, частота обращения и энергия α-частицы по сравнению с протоном должны:
- увеличиться
- уменьшиться
- не измениться
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
1.Записать формулу для определения силы Лоренца.
2.Установить, от чего зависят перечисленные в таблице физические величины.
3.Определить характер их изменения при изменении заряда.
Решение
Сила Лоренца определяется формулой:
FЛ=|q|vBsinα
Если вместо протона взять альфа-частицу, то заряд увеличится вдвое, так как альфа-частица содержит 2 протона. Сила Лоренца прямо пропорционально зависит от величины заряда. Следовательно, она тоже увеличится вдвое. Скорость движения заряда по условию задачи остается постоянной, как и модуль вектора магнитной индукции.
Сила Лоренца будет сообщать альфа-частице центростремительное ускорение, равное:
a=v2R
Применим второй закон Ньютона:
F=ma
|q|vBsinα=mv2R
Отсюда:
|q|Bsinα=mvR
R=mv|q|Bsinα
Заряд альфа-частицы больше заряда протона вдвое. Она также содержит 2 нейтрона, поэтому ее масса примерно в 4 раза больше массы протона. Следовательно, радиус движения альфа-частицы увеличится примерно вдвое.
Частота обращения альфа-частицы связана с ее линейной скоростью формулой:
v=2πRν
Так как скорость остается постоянной, то при увеличении радиуса частота обращения должна уменьшиться.
Энергия альфа-частицы будет больше, чем у протона, вращающегося с той же скоростью. Это связано с тем, что ее кинетическая энергия будет примерно в 4 раза больше (так как во столько раз больше ее масса).
Ответ: 121
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.9k
Мари Ампер доказал, что при наличии электрического тока в проводнике, оказавшемся в магнитном поле, он взаимодействует с силами этого поля. Учитывая то, что электрический ток – это не что иное, как упорядоченное движение электронов, можно предположить, что электромагнитные поля подобным образом действуют также на отдельно взятую заряженную частицу. Это действительно так. На точечный заряд действует сила Лоренца, модуль которой можно вычислить по формуле.
Определение и формула
Хендрик Лоренц доказал, что электромагнитная индукция взаимодействует с заряженными частицами. Эти взаимодействия приводят к возникновению силы Лоренца. Рассматриваемая сила возникает под действием магнитной индукции. Она перпендикулярна вектору скорости движущейся частицы (см. рис. 1). Необходимым условием возникновения этой силы является движение электрического заряда.
Обратите внимание на расположение векторов (рисунок слева, вверху). Векторы, указывающие направления скорости и силы Лоренца, лежат в одной плоскости XOY, причём они расположены под углом 90º. Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости.
По закону Ампера:
Учитывая, что
(здесь j – плотность тока, q – единичный заряд, n – количество зарядов на бесконечно малую единицу длины проводника, S – сечение проводника, символом v обозначен модуль скорости движущейся частицы), запишем формулу Ампера в виде:
Так, как nSdl – общее число зарядов в объёме проводника, то для нахождения силы, действующей на точечный заряд, разделим выражение на количество частиц:
Модуль F вычисляется по формуле:
Из формулы следует:
- Сила Лоренца приобретает максимальное значение, если угол α прямой.
- Если точечный заряд, например, электрон, попадает в среду однородного магнитного поля, обладая некой начальной скоростью, перпендикулярной к линиям электромагнитной индукции, тогда вектор F будет перпендикулярен к вектору скорости. На точечный заряд будет действовать центробежная сила, которая заставит его вращаться по кругу. При этом работа равняется нулю (см. рис.2).
- Если угол между вектором индукции и скоростью частицы не равняется 90º, тогда заряд будет двигаться по спирали. Направление вращения зависит от полярности заряда (рис. 3).
Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).
Траекторию движения частицы правильно называть винтовой линией. Радиус этой винтовой линии (циклотронный радиус) определяется перпендикулярной к полю составной начальной скорости частицы. Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле. Эта составная направлена параллельно к электромагнитным линиям.
В чём измеряется?
Размерность силы Лоренца в международной системе СИ – ньютон (Н). Разумеется, модуль силы Лоренца настолько крохотная величина, по сравнению с ньютоном, что её записывают в виде К×10-n Н, где 0<К<1, а n – порядок числа 10.
Когда возникает?
Магнитные поля не реагируют на неподвижный электрический заряд, так же как не действует сила Ампера на обесточенный проводник.
Для возникновения силы Лоренца необходимо выполнить три условия:
- У частицы должен быть отрицательный или положительный заряд.
- Заряженная частица должна находиться в магнитном поле.
- Частица должна быть в движении, то есть вектор v ≠ 0.
Если хотя бы одно из условий не выполняется, сила Лоренца не возникает.
Формула силы Лоренца при наличии магнитного и электрического полей
Рассмотрим случай, когда заряженная частица находится в движении в двух полях одновременно (в электрическом и магнитном), тогда на заряд подействуют две составляющие:
Тогда:
Поскольку эту формулу вывел Лоренц, то её также называют именем учёного-физика.
Направление силы Лоренца
Мы уже упоминали, что направление возникшей силы Лоренца, кроме магнитных параметров, определяется (в том числе) полярностью заряда. Если бы мы имели возможность наблюдать заряженную элементарную частицу, пребывающую в магнитном поле, то по вектору её перемещения можно было бы определить направление вектора силы F.
Но на практике наблюдать элементарные заряды очень сложно из-за крохотных размеров. Поэтому для определения этого направления применяют способ, известен, как правило левой руки (рис. 4).
Ладонь необходимо развернуть так, чтобы вектор индукции входил в неё. В случае с положительным зарядом, вытянутые пальцы располагают по движению частицы. (для отрицательного заряда пальцы направляют в противоположную сторону). Большой палец под прямым углом указывает искомое направление.
Если известна ориентация вектора скорости частицы, то определить направления остальных векторов можно, применяя правило правой руки, которое понятно из рисунка 5.
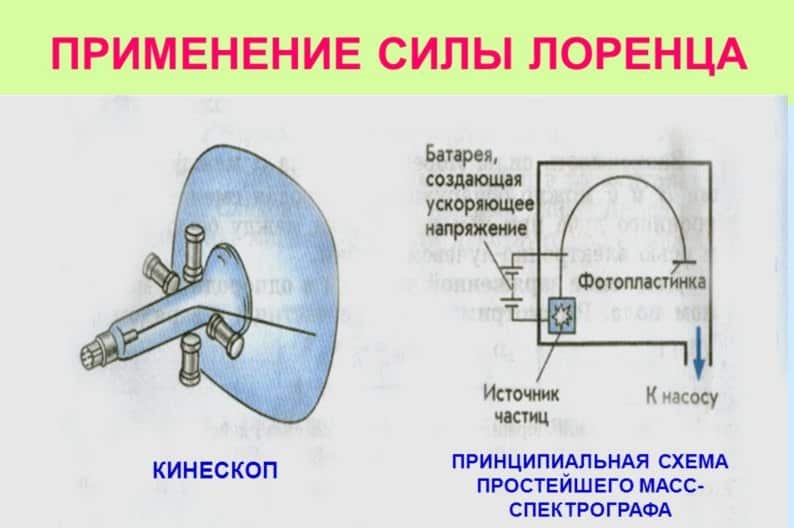
Применение на практике
Практическое значение работ Лоренца мы можем наблюдать в электронно-лучевых трубках. Там поток электронов движется в магнитном поле, изменением которого задаётся траектория электронного пучка.
Данный принцип управления траекторией электронного пучка использовался в старых моделях телевизоров Рис. 6). Электроны под воздействием магнитных полей очерчивали линии на люминофоре кинескопа, рисуя изображения на экране.
На рисунке справа изображена схема масспектрографа – прибора для разделения заряженных частиц по величине их зарядов.
Ещё один пример – бесконтактный электромагнитный метод определения скорости течения (вязкости) электропроводных жидкостей. Методика может быть применима к расплавленным металлам, например к алюминию. Бесконтактный способ определения вязкости очень полезен при работе с агрессивными жидкими электропроводными веществами (рис. 7).
Работа ускорителей была бы невозможной без участия силы Лоренца. В этих устройствах заряженные частицы удерживаются и разгоняются до околосветовых скоростей благодаря электромагнитам, расположенным вдоль кольцевой трассы.
Мощная электронная лампа – Магнетрон также работает на принципе взаимодействия электронов с магнитными полями, которые направляют высокочастотное излучение в нужном направлении. Магнетрон является основной рабочей деталью микроволновых печей.
На основании действия силы Лоренца создано много других устройств, используемых на практике.
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
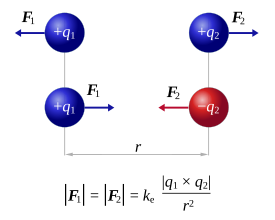
Зако́н Куло́на — физический закон, описывающий взаимодействие между двумя неподвижными точечными электрическими зарядами в вакууме. Сила, с которой заряд 

,
где 




Также под законом Кулона понимается формула для вычисления электрического поля точечного заряда, вместе с её обобщением на произвольное распределение зарядов в пространстве:
.
Здесь 




Закон Кулона в классической электродинамике[править | править код]
Установление и формулировки закона[править | править код]
Закон открыт Шарлем Кулоном в 1785 году. Проведя большое количество опытов с металлическими шариками, Кулон дал такую формулировку закона:
Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними.
Современная формулировка[1]:
Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.
В векторном виде в формулировке Ш. Кулона закон записывается как
,
где 




Условия применимости[править | править код]
Для того, чтобы закон был верен, необходимы:
- точечность зарядов, то есть расстояние между заряженными телами должно быть много больше их размеров. Здесь две оговорки: а) существует обобщение закона Кулона на случай тел конечных размеров; б) можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;
- их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;
- расположение зарядов в вакууме.
В отдельных ситуациях, с корректировками, закон может быть применен также для взаимодействий зарядов в среде и для движущихся зарядов[2]. Но в общем случае при наличии неоднородных диэлектриков он неприменим, поскольку помимо заряда 

Выражения в разных системах единиц[править | править код]
В СГСЭ единица измерения заряда выбрана таким образом, что коэффициент 
В Международной системе единиц (СИ) одной из основных единиц является единица силы электрического тока — ампер, а единица заряда — кулон — производная от него. Величина ампера определена таким образом, что k = c2·10−7 Гн/м = 8,9875517873681764⋅109 Н·м2/Кл2 (или Ф−1·м). В СИ коэффициент k записывается в виде:
,
где 
В случае среды, заполненной бесконечным однородным изотропным диэлектрическим веществом, в знаменатель формулы закона Кулона добавляется диэлектрическая проницаемость среды ε. Тогда
(в СГСЭ)
(в СИ).
Закон Кулона и уравнения Максвелла[править | править код]
Закон Кулона и принцип суперпозиции для электрических полей в вакууме полностью равносильны уравнениям Максвелла для электростатики 




Исторически закон Кулона был одним из эмпирических законов, служивших предпосылками для формулирования уравнения Максвелла. Однако при современном изложении учения об электромагнетизме этот закон (равно как и, скажем, закон Ампера) нередко позиционируется как следствие уравнений Максвелла, которым придаётся статус фундаментальных аксиом.
Вывод закона Кулона из уравнений Максвелла[править | править код]
Уравнение Максвелла 
,
где 










Обобщение на случай распределения заряда[править | править код]
Если на заряд 






,
где радиус-вектором 





Если же не только заряд 

.
Закон Кулона и расчёт электрического поля[править | править код]
Взаимодействие двух зарядов может быть истрактовано как взаимодействие одного из зарядов с электрическим полем, создаваемым другим зарядом. Это становится виднее, если соответствующим образом перегруппировать сомножители в выражении для силы:
.
Тем самым закон Кулона фактически становится основой для вычисления поля. Так же, как и при рассмотрении силы, возможно обобщение последнего равенства на случай распределения зарядов.
Для нахождения поля 



,
где заряд 





Если всё пространство заполнено однородным диэлектриком с проницаемостью 





Аналогии в других областях классической физики[править | править код]
Закон Кулона совершенно аналогичен по форме закону всемирного тяготения. При этом функцию гравитационных масс выполняют электрические заряды[4] разных знаков.
Магнитостатическими аналогами закона Кулона являются закон Ампера (в части нахождения сил взаимодействия) и закон Био — Савара — Лапласа (в части расчёта по́ля).
Об открытии и исторической значимости закона[править | править код]
Впервые исследовать экспериментально закон взаимодействия электрически заряженных тел предложил[5] Г. В. Рихман в 1752—1753 гг. Он намеревался использовать для этого сконструированный им электрометр-«указатель». Осуществлению этого плана помешала его трагическая гибель.
В 1759 г. профессор физики Санкт-Петербургской академии наук Ф. Эпинус, занявший кафедру Рихмана после его гибели, впервые предположил[6], что заряды должны взаимодействовать обратно пропорционально квадрату расстояния. В 1760 г. появилось краткое сообщение[7] о том, что Д. Бернулли в Базеле установил квадратичный закон с помощью сконструированного им электрометра. В 1767 г. Пристли в своей «Истории электричества»[8] отметил, что опыт Франклина, обнаружившего отсутствие электрического поля внутри заряженного металлического шара, может означать, что «сила электрического притяжения подчиняется тем же законам, что и сила тяжести, а следовательно, зависит от квадрата расстояния между зарядами»[9]. Шотландский физик Джон Робисон утверждал (1822), что в 1769 г. обнаружил, что шары с одинаковым электрическим зарядом отталкиваются с силой, обратно пропорциональной квадрату расстояния между ними, и таким образом предвосхитил открытие закона Кулона (1785)[10].
Примерно за 11 лет до Кулона, в 1771 г., закон взаимодействия зарядов был экспериментально открыт Г. Кавендишем, однако результат не был опубликован и долгое время (свыше 100 лет) оставался неизвестным. Рукописи Кавендиша были вручены Дж. Максвеллу лишь в 1874 г одним из потомков Кавендиша на торжественном открытии Кавендишской лаборатории и опубликованы в 1879 г.[11].
Сам Кулон занимался исследованием кручения нитей и изобрел крутильные весы. Он открыл свой закон, измеряя с помощью них силы взаимодействия заряженных шариков.
Закон Кулона является первым открытым количественным и сформулированным на математическом языке фундаментальным законом для электромагнитных явлений. С открытия закона Кулона началась современная наука об электромагнетизме[12].
Закон Кулона в квантовой механике[править | править код]
В квантовой механике закон Кулона формулируется не при помощи понятия силы, как в классической механике, а при помощи понятия потенциальной энергии кулоновского взаимодействия. В случае, когда рассматриваемая в квантовой механике система содержит электрически заряженные частицы, к оператору Гамильтона системы добавляются слагаемые, выражающие потенциальную энергию кулоновского взаимодействия, так, как она вычисляется в классической механике[13]. Это утверждение не следует из остальных аксиом квантовой механики, а получено путём обобщения опытных данных.
Так, оператор Гамильтона атома с зарядом ядра Z имеет вид:
Здесь m — масса электрона, е — его заряд, 


Закон Кулона с точки зрения квантовой электродинамики[править | править код]
Согласно квантовой электродинамике, электромагнитное взаимодействие заряженных частиц осуществляется путём обмена виртуальными фотонами между частицами. Принцип неопределённости для времени и энергии допускает существование виртуальных фотонов на время между моментами их испускания и поглощения. Чем меньше расстояние между заряженными частицами, тем меньшее время нужно виртуальным фотонам для преодоления этого расстояния и следовательно, тем большая энергия виртуальных фотонов допускается принципом неопределенности. При малых расстояниях между зарядами принцип неопределённости допускает обмен как длинноволновыми, так и коротковолновыми фотонами, а при больших расстояниях в обмене участвуют только длинноволновые фотоны. Таким образом, с помощью квантовой электродинамики можно вывести закон Кулона[15][16].
Степень точности закона Кулона[править | править код]
Закон Кулона — экспериментально установленный факт. Его справедливость неоднократно подтверждалась всё более точными экспериментами. Одним из направлений таких экспериментов является проверка того, отличается ли показатель степени r в законе от 2. Для поиска этого отличия используется тот факт, что[], какова бы ни была форма полости или проводника[17].
Такие опыты впервые провел Кавендиш и повторил Максвелл в усовершенствованном виде, получив для максимального отличия показателя в степени от двух величину 
Эксперименты, проведённые в 1971 г. в США Э. Р. Уильямсом, Д. Е. Фоллером и Г. А. Хиллом, показали, что показатель степени в законе Кулона равен 2 с точностью до 
Для проверки точности закона Кулона на внутриатомных расстояниях У. Ю. Лэмбом и Р. Резерфордом в 1947 г. были использованы измерения относительного расположения уровней энергии водорода. Было установлено, что и на расстояниях порядка атомных 10−8 см, показатель степени в законе Кулона отличается от 2 не более чем на 10−9[20][21].
Коэффициент 
Поправки к закону в квантовой электродинамике[править | править код]
На небольших расстояниях (порядка комптоновской длины волны электрона):
м[22],
где 



Например, выражение для потенциала точечного заряда 
[23]:
где 


На расстояниях порядка 

В сильных внешних электромагнитных полях, составляющих заметную долю от поля пробоя вакуума (порядка 

Закон Кулона и поляризация вакуума[править | править код]
Явление поляризации вакуума в квантовой электродинамике заключается в образовании виртуальных электронно-позитронных пар. Облако электронно-позитронных пар экранирует электрический заряд электрона. Экранировка растет с ростом расстояния от электрона, в результате эффективный электрический заряд электрона 





где
— постоянная тонкой структуры;
см — классический радиус электрона[26][27].
Эффект Юлинга[править | править код]
Явление отклонения электростатического потенциала точечных зарядов в вакууме от значения закона Кулона известно как эффект Юлинга, который впервые вычислил отклонения от закона Кулона для атома водорода. Эффект Юлинга даёт поправку к лэмбовскому сдвигу 27 МГц[28][29].
Закон Кулона и сверхтяжёлые ядра[править | править код]
В сильном электромагнитном поле вблизи сверхтяжёлых ядер с зарядом 
См. также[править | править код]
- Электростатика
- Электрическое поле
- Дальнодействие
- Закон Био — Савара — Лапласа
- Закон притяжения
- Шарль Огюстен де Кулон
- Кулон (единица измерения)
- Принцип суперпозиции
- Уравнения Максвелла
Примечания[править | править код]
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — С. 17. — 656 с. — ISBN 5-9221-0227-3.
- ↑ Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 8-е, стереотипное. — М.: Физматлит, 2001. — С. 132. — («Теоретическая физика», том II). — ISBN 5-9221-0056-4.
- ↑ Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 4 «Электростатика», п. 1 «Статика», с. 70-71;
- ↑ Ландсберг Г. С. Элементарный учебник физики. Том II. Электричество и магнетизм. — М.: Наука, 1964. — Тираж 100 000 экз. — С. 33.
- ↑ Novi Comm. Acad. Sc. Imp. Petropolitanae, v. IV, 1758, p. 301.
- ↑ Эпинус Ф. Т. У. Теория электричества и магнетизма. — Л.: АН СССР, 1951. — 564 с. — (Классики науки). — 3000 экз. Архивировано 17 ноября 2012 года.
- ↑ Abel Socin (1760) Acta Helvetica, vol. 4, pages 224-225.
- ↑ J. Priestley. The History and present state of Electricity with original experiments. London, 1767, p. 732.
- ↑ Уиттекер Э. История теории эфира и электричества. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 76. — 512 с. — ISBN 5-93972-070-6.
- ↑ John Robison, A System of Mechanical Philosophy (London, England: John Murray, 1822), vol. 4. На стр. 68 Робисон заявляет, что в 1769 он обнародовал свои измерения силы, действующей между сферами с одинаковым зарядом, и описывает также историю исследований в этой области, отмечая имена Эпинуса, Кавендиша и Кулона. На стр. 73 Архивная копия от 1 декабря 2016 на Wayback Machine автор пишет, что сила изменяется как x−2,06.
- ↑ ‘Филонович С. Р. Кавендиш, Кулон и электростатика. — М.: Знание, 1988. — С. 48.
- ↑ Спиридонов О. П. Универсальные физические постоянные.— М.: Просвещение.— 1984.— с. 52-53;
- ↑ Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — М., 2002. — С. 74. — («Теоретическая физика», том III).
- ↑ Бете Х. Квантовая механика. — Пер. с англ., под ред. В. Л. Бонч-Бруевича. — М.: Мир, 1965. — С. 11.
- ↑ Пайерлс Р. Е. Законы природы. пер. с англ. под ред. проф. Халатникова И. М. , Государственное издательство физико-математической литературы, М., 1959, тир. 20000 экз., 339 с., Гл. 9 «Электроны при высоких скоростях», п. «Силы при больших скоростях. Другие трудности», c. 263
- ↑ Окунь Л. Б.
… z Элементарное введение в физику элементарных частиц Архивная копия от 25 ноября 2010 на Wayback Machine, М., Наука, 1985, Библиотечка «Квант», вып. 45, п. «Виртуальные частицы», с. 57.
- ↑ Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 5 «Применения закона Гаусса», п. 10 «Поле внутри полости проводника», с. 106—108;
- ↑ Калашников С. Г.,
Электричество, М., ГИТТЛ, 1956, гл. III «Разность потенциалов», п. 34 «Точная проверка закона Кулона», с. 68—69; «Добавления», 1. «Теория опытов Кавендиша и Максвелла», с. 642—645; - ↑ E. R. Williams, J. E. Faller, H. A. Hill «New Experimental Test of Coulomb’s Law: A Laboratory Upper Limit on the Photon Rest Mass», Phys. Rev. Lett. 26, 721—724 (1971);
- ↑ W. E. Lamb, R. C. Retherford. Fine Structure of the Hydrogen Atom by a Microwave Method (англ.) // Physical Review. — 1947. — Vol. 72, no. 3. — P. 241—243.
- ↑ 1 2 Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 5 «Применения закона Гаусса», п. 8 «Точен ли закон Кулона?», с. 103;
- ↑ CODATA Архивная копия от 11 февраля 2012 на Wayback Machine (the Committee on Data for Science and Technology)
- ↑ Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П. Квантовая электродинамика. — Издание 3-е, исправленное. — М.: Наука, 1989. — С. 565—567. — 720 с. — («Теоретическая физика», том IV). — ISBN 5-02-014422-3.
- ↑ Neda Sadooghi. Modified Coulomb potential of QED in a strong magnetic field (англ.). Архивировано 18 января 2015 года.
- ↑ Окунь Л. Б. Физика элементарных частиц. Изд. 3-е, М.: «Едиториал УРСС», 2005, ISBN 5-354-01085-3, ББК 22.382 22.315 22.3о, гл. 2 «Гравитация. Электродинамика», «Поляризация вакуума», с. 26-27;
- ↑ «Физика микромира», гл. ред. Д. В. Ширков, М., «Советская энциклопедия», 1980, 528 с., илл., 530.1(03), Ф50, ст. «Эффективный заряд», авт. ст. Д. В. Ширков, стр. 496;
- ↑ Яворский Б. М. «Справочник по физике для инженеров и студентов вузов» / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев, 8-e изд., перераб. и испр., М.: ООО «Издательство Оникс», ООО «Издательство Мир и образование», 2006, 1056 стр.: илл., ISBN 5-488-00330-4 (ООО «Издательство Оникс»), ISBN 5-94666-260-0 (ООО «Издательство Мир и образование»), ISBN 985-13-5975-0 (ООО «Харвест»), УДК 530(035) ББК 22.3, Я22, «Приложения», «Фундаментальные физические постоянные», с. 1008;
- ↑ Uehling E. A ., Phys. Rev., 48, 55, (1935)
- ↑ Швебер С., Бете Г., Гофман Ф. Мезоны и поля. Том 1 Поля гл. 5 Свойства уравнения Дирака п. 2. Состояния с отрицательной энергией c. 56, гл. 21 Перенормировка, п. 5 Поляризация вакуума с 336
- ↑ Мигдал А. Б. Поляризация вакуума в сильных полях и пионная конденсация// Успехи физических наук Т. 123— в. 3.— 1977 г., ноябрь.— с. 369—403;
Литература[править | править код]
- Филонович С. Р. Судьба классического закона. — М.: Наука, 1990. — 240 с., ISBN 5-02-014087-2 (Библиотечка «Квант», вып. 79), тир. 70500 экз.
Ссылки[править | править код]
- Закон Кулона (видеурок, программа 10 класса)




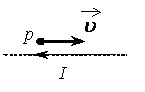
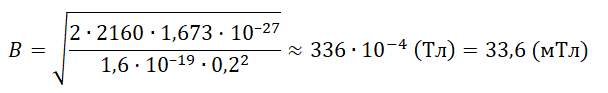


















![{displaystyle {vec {F}}_{12}={frac {1}{4pi varepsilon _{0}}}cdot {frac {q_{1}q_{2}({vec {r}}_{2}-{vec {r}}_{1})}{|{vec {r}}_{2}-{vec {r}}_{1}|^{3}}}=q_{2}cdot left[{frac {1}{4pi varepsilon _{0}}}cdot {frac {q_{1}({vec {r}}_{2}-{vec {r}}_{1})}{|{vec {r}}_{2}-{vec {r}}_{1}|^{3}}}right]=q_{2}cdot E_{1}({vec {r}}_{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0e25ba88f2895320a718c679386b044aa2eaa04)








