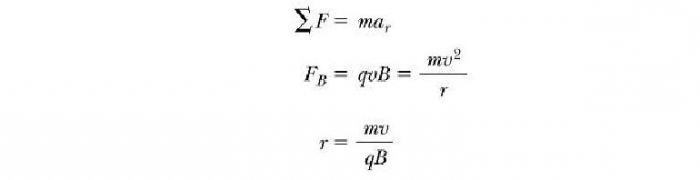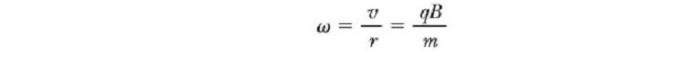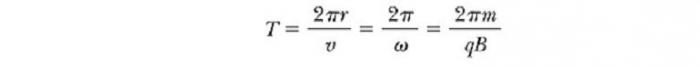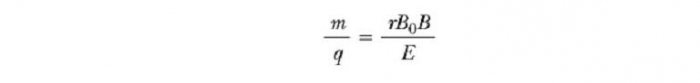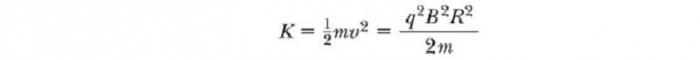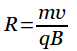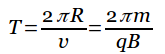Как найти направление скорости частицы

Как найти скорость частицы

Часто при изучении школьного курса электромагнетизма или при научных исследованиях возникает необходимость установить скорость, с которой двигалась какая-нибудь элементарная частица, например, электрон или протон.

Допустим, дана следующая задача: электрическое поле с напряженностью Е и магнитное поле с индукцией В, возбуждены перпендикулярно друг другу. Перпендикулярно им, равномерно и прямолинейно движется заряженная частица с зарядом q и скоростью v. Требуется определить ее скорость.

Решение очень простое. Если частица по условиям задачи движется равномерно и прямолинейно, значит, ее скорость v постоянная. Таким образом, в соответствии с первым законом Ньютона, величины действующих на нее сил взаимно уравновешены, то есть в сумме они равны нулю.

Какие силы действуют на частицу? Во-первых, электрическая составляющая силы Лоренца, которая вычисляется по формуле: Fэл = qE. Во-вторых, магнитная составляющая силы Лоренца, которую вычисляют по формуле: Fм = qvBSinα. Поскольку по условиям задачи частица движется перпендикулярно магнитному полю, угол α = 90 градусам, и соответственно, Sinα = 1. Тогда магнитная составляющая силы Лоренца Fм = qvB.

Электрическая и магнитная составляющие уравновешивают друг друга. Следовательно, величины qE и qvB численно равны. То есть Е = vB. Следовательно, скорость частицы вычисляется по такой формуле: v = E/B. Подставив в формулу значения Е и В, вы вычислите искомую скорость.

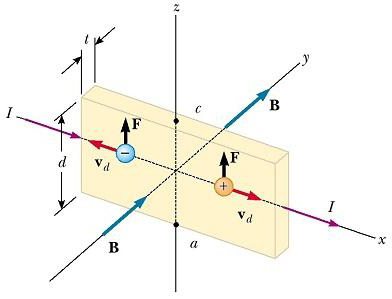
Или, например, у вас такая задача: частица с массой m и зарядом q, двигаясь со скоростью v, влетела в электромагнитное поле. Его силовые линии (как электрические, так и магнитные) параллельны. Частица влетала под углом α к направлению силовых линий и после этого началась двигаться с ускорением а. Требуется вычислить, с какой скоростью она двигалась первоначально. Согласно второму закону Ньютона, ускорение тела с массой m вычисляется по формуле: a = F/m.

Массу частицы вы знаете по условиям задачи, а F – результирующая (суммарная) величина сил, действующих на нее. В данном случае на частицу действуют электрическая и магнитная оставляющие силы Лоренца: F = qE + qBvSinα.

Но поскольку силовые линии полей (по условию задачи) параллельны, то вектор электрической силы перпендикулярен вектору магнитной индукции. Следовательно, суммарная сила F вычисляется по теореме Пифагора: F = [(qE)^2 + (qvBSinα)^2]^1/2

Преобразуя, получите: am = q[E^2 +B^2v^2Sin^2α]^1/2. Откуда: v^2 = (a^2m^2 – q^2E^2)/(q^2B^2Sin^2α). После вычисления и извлечения квадратного корня, получите искомую величину v.

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

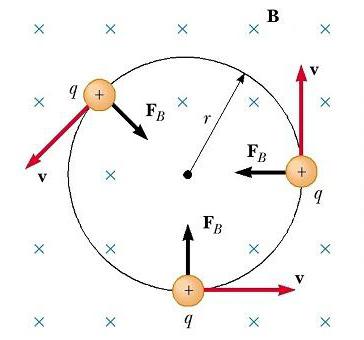
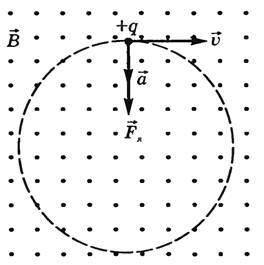
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

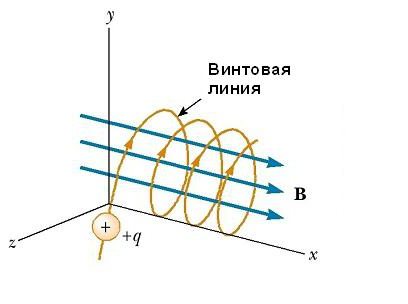
Движение частицы под углом к вектору магнитного поля

Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

Неоднородное магнитное поле: как в нем движутся частицы

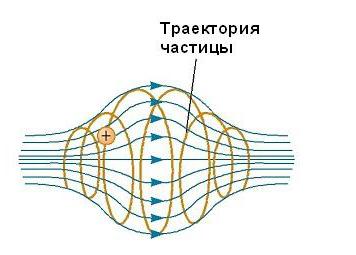
Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

Как Земля влияет на движение космических частиц

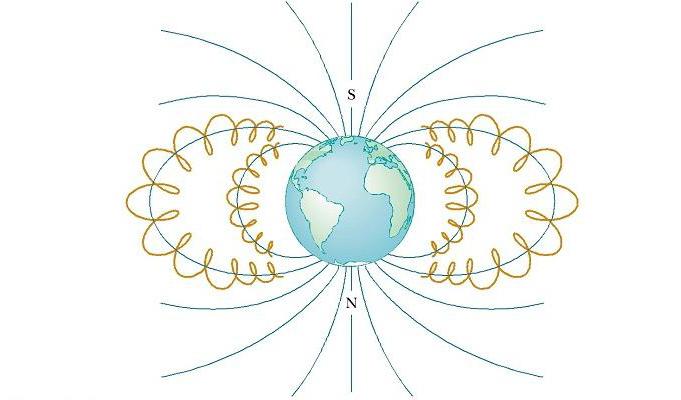
Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

Селектор скоростей

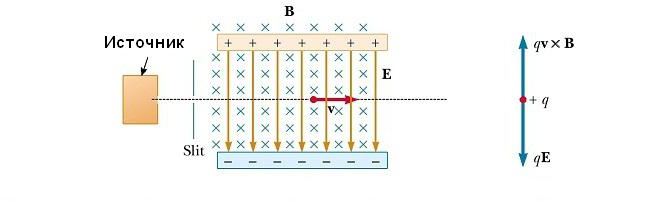
Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

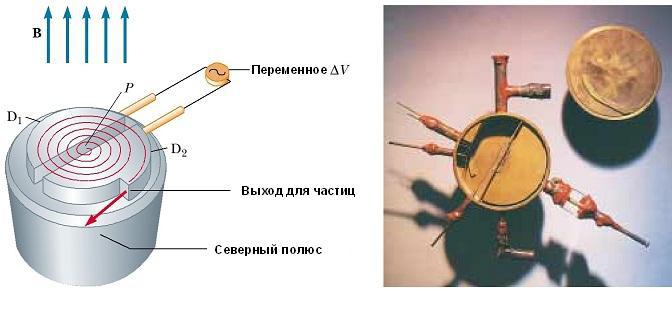
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т — время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один «удар» через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы — ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Физика. 10 класс

§ 30. Сила Лоренца. Движение заряженных частиц в магнитном поле

Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих частиц. Таким образом, силу Ампера можно рассматривать как результат сложения сил, действующих на отдельные движущиеся заряженные частицы. Как можно определить силу, действующую со стороны магнитного поля на заряженную частицу, движущуюся в этом поле?

Сила Лоренца. Силу, которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца в честь выдающегося нидерландского физика Хендрика Антона Лоренца ( 1853–1928 ).

Модуль силы Лоренца можно определить по формуле , где N — общее число свободных заряженных одинаковых частиц на прямолинейном участке проводника длиной Δl ( рис. 167 ). Если модуль заряда одной частицы q, а модуль суммарного заряда всех частиц Nq, то согласно определению силы тока , где Δt — промежуток времени, за который заряженная частица проходит участок проводника длиной Δl. Тогда

Поскольку – модуль средней скорости упорядоченного движения заряженной частицы в стационарном * электрическом поле внутри проводника, то формулу для определения модуля силы Лоренца можно записать в виде:

где α — угол между направлениями индукции магнитного поля и скорости упорядоченного движения заряженной частицы.

Из формулы (30.1) следует, что сила Лоренца максимальна в случае, когда заряженная частица движется перпендикулярно направлению индукции магнитного поля (α = 90°). Когда частица движется вдоль линии индукции поля (α = 0° или α = 180°), сила Лоренца на неё не действует. Сила Лоренца зависит от выбора инерциальной системы отсчёта, так как в разных системах отсчёта скорость движения заряженной частицы может отличаться.

Направление силы Лоренца, действующей на заряженную частицу, как и направление силы Ампера, определяют по правилу левой руки (рис. 168): если левую руку расположить так, чтобы составляющая индукции магнитного поля, перпендикулярная скорости движения частицы, входила в ладонь, а четыре пальца были направлены по движению положительно заряженной частицы (против движения отрицательно заряженной частицы), то отогнутый на 90° в плоскости ладони большой палец укажет направление действующей на частицу силы Лоренца.

Сила Лоренца перпендикулярна как направлению скорости движения частицы, так и направлению индукции магнитного поля.

На рисунке 169 представлены направления индукции магнитного поля, скорости движения частицы в данный момент времени и силы Лоренца , действующей на частицу со стороны магнитного поля. Определите знак заряда частицы.

* Электрическое поле, создаваемое и поддерживаемое источником тока в течение длительного промежутка времени и обеспечивающее постоянный электрический ток в проводнике, называют стационарным электрическим полем. ↑

Движение заряженных
частиц в магнитном поле.

На
заряженную частицу в электростатическом
поле действует кулоновская сила, которую
можно найти, зная напряженность поля в
данной точке:  .
Эта сила сообщает ускорение

  

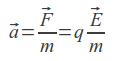
где
m — масса заряженной частицы. Как видно,
направление ускорения будет совпадать
с направлением  ,
если заряд частицы положителен (q > 0),
и будет противоположно  ,
если заряд отрицателен (q<0).

Если
электростатическое поле однородное
(  =
const), то ускорение  a= const и частица
будет совершать равноускоренное
движение (при
отсутствии других сил).

Вид
траектории частицы зависит от начальных
условий. Если вначале заряженная частица
покоилась  или
ее начальная скорость сонаправлена с
ускорением , то частица будет совершать
равноускоренное прямолинейное движение
вдоль поля и ее скорость будет расти.
Если  ,
то частица будет тормозиться в этом
поле.

Если
угол между начальной скоростью и
ускорением острый 0 < α < 90° (или тупой),
то заряженная
частица  будет
двигаться по параболе.  

Во
всех случаях при движении заряженной
частицы будет изменяться модуль скорости,
а следовательно, и кинетическая энергия
частицы.

1.  Заряженная
частица влетает в магнитное поле со
скоростью , направленной вдоль поля
 или противоположно  направлению
магнитной индукции поля  .

В
этих случаях сила Лоренца     и
частица будет продолжать двигаться
равномерно прямолинейно.

2.
Заряженная частица движется перпендикулярно
линиям магнитной индукции

тогда
сила Лоренца  ,
следовательно, и сообщаемое ускорение
будут постоянны по модулю и перпендикулярны
к скорости частицы.

В
результате частица
будет двигаться по окружности ,
радиус которой можно найти на основании
второго закона Ньютона:

  

Отношение
     —
называют удельным зарядом частицы.

  

Период
вращения частицы

то
есть период вращения не зависит от
скорости частицы и радиуса траектории.

3.
Скорость заряженной частицы направлена
под углом  к вектору.

  

Движение
частицы можно представить в виде
суперпозиции равномерного прямолинейного
движения вдоль поля со скоростью  и
движения по окружности с постоянной по
модулю скоростью  в плоскости,
перпендикулярной полю.

Радиус
окружности определяется аналогично
предыдущему случаю, только надо  заменить
 на  ,
то есть

В
результате сложения этих движений
возникает движение по винтовой линии,
ось которой параллельна магнитному
полю. Шаг винтовой линии

Направление,
в котором закручивается спираль, зависит
от знака заряда частицы.

Если
скорость заряженной частицы составляет
угол α с направлением вектора
   неоднородного
магнитного поля, индукция которого
возрастает в направлении движения
частицы, тο R и h уменьшаются с ростом B.
На этом основана фокусировка заряженных
частиц в магнитном поле.

Если
на движущуюся заряженную частицу помимо
магнитного поля с индукцией  действует
одновременно и электростатическое поле
с напряженностью , то равнодействующая
сила, приложенная к частице, равна
векторной сумме электрической силы и
силы Лоренца:  .
Характер движения и вид траектории
зависят в данном случае от соотношения
этих сил и от направления электростатического
и магнитного полей.

Соседние файлы в папке fizika

• #
• #
• #
• #
• #
• #
• #
• #
• #

Основываясь на определении скорости, мы можем утверждать, что скорость является вектором. Она непосредственно выражается через вектор-перемещения, отнесенный к промежутку времени, и должна обладать всеми свойствами вектора перемещения.

Направление вектора скорости, так же как направление физически малого вектора перемещения, определяется по чертежу траектории. В этом можно наглядно убедиться на простых примерах.

Если к вращающемуся точильному камню прикоснуться железной пластинкой, то снимаемые им опилки приобретут скорость тех точек камня, к которым прикасалась пластинка, и затем улетят в направлении вектора этой скорости. Все точки камня движутся по окружностям. Во время опыта хорошо видно, что отрывающиеся раскаленные частички-опилки уходят по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек вращающегося точильного камня.

Обратите внимание на то, как расположены выходные трубы у кожуха центробежного водяного насоса или у сепаратора для молока. В этих машинах частицы жидкости заставляют двигаться по окружностям и затем дают им возможность выйти в отверстие, расположенное в направлении вектора той скорости, которую они имеют в момент выхода. Направление вектора скорости в этот момент совпадает с направлением касательной к траектории движения частиц жидкости. И выходная труба тоже направлена по этой касательной.

Точно так же обеспечивают выход частиц в современных ускорителях электронов и протонов при ядерных исследованиях.

Итак, мы убедились, что направление вектора скорости определяется по траектории движения тела. Вектор скорости всегда направлен вдоль касательной к траектории в той точке, через которую проходит движущееся тело.

Для того чтобы определить, в какую сторону вдоль касательной направлен вектор скорости и каков его модуль, нужно обратиться к закону движения. Допустим, что закон движения задан графиком, показанным на рис. 1.54. Возьмем приращение длины пути соответствующее малому вектору по которому определяется вектор скорости. Вспомним, что Знак указывает

Рис. 1.54.

направление движения по траектории, а следовательно, определяет ориентировку вектора скорости вдоль касательной. Очевидно, что через модуль этого приращения длины пути будет определяться модуль скорости.

Таким образом, модуль вектора скорости и ориентировку вектора скорости вдоль касательной к траектории можно определить из соотношения

Здесь является алгебраической величиной, знак которой указывает, в какую сторону по касательной к траектории направлен вектор скорости.

Итак, мы убедились, что модуль вектора скорости может быть найден по графику закона движения. Отношение определяет угол наклона а касательной на этом графике. Наклон касательной на графике закона движения будет тем больше, чем больше т. е. чем больше в выбранный момент скорость движения.

Еще раз обратим внимание на то, что для полного определения скорости требуется одновременное знание траектории и закона движения. Чертеж траектории позволяет определить направление скорости, а график закона движения — ее модуль и знак.

Если теперь мы обратимся снова к определению механического движения, то убедимся в том, что после введения понятия скорости для полного описания любого движения больше ничего не требуется. Используя понятия радиус-вектора, вектора перемещения, вектора скорости, длины пути, траектории и закона движения, можно получить ответы на все вопросы, связанные с определением особенностей любого движения. Все эти понятия взаимосвязаны друг с другом, причем знание траектории и закона движения позволяет найти любую из этих величин.

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Движение частицы под углом к вектору магнитного поля

Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у² + ν_z²).

Неоднородное магнитное поле: как в нем движутся частицы

Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

Заряженная частица стартует с одного конца винтовой линии, накрученной вдоль силовых линий, и движется вдоль нее, пока не достигнет другого конца, где она поворачивает свой ​​путь обратно. Эта конфигурация известна как “магнитная бутылка”, поскольку заряженные частицы могут быть захвачены в нее. Она была использована, чтобы ограничить плазму, газ, состоящий из ионов и электронов. Такая схема плазменного заключения может выполнять ключевую роль в контроле ядерного синтеза, процессе, который представит нам почти бесконечный источник энергии. К сожалению, “магнитная бутылка” имеет свои проблемы. Если в ловушке большое число частиц, столкновения между ними вызывают утечку их из системы.

Как Земля влияет на движение космических частиц

Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

Селектор скоростей

Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Для положительного q магнитная сила F_B=qv х В направлена вверх, а электрическая сила qE – вниз. Когда величины двух полей выбраны так, что qE = qvB, то частица движется по прямой горизонтальной линии через область поля. Из выражения qE = qvB мы находим, что только частицы, имеющие скорость v=E/B, проходят без отклонения через взаимно перпендикулярные электрическое и магнитное поля. Сила F_B, действующая на частицы, движущиеся со скоростью большей, чем v=E/B, оказывается больше электрической, и они отклоняются вверх. Те же из них, которые движутся с меньшей скоростью, отклоняются вниз.

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т – время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один “удар” через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы – ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Однородное поле B приложено в направлении у. Если носителями заряда являются электроны, движущиеся вдоль оси х со скоростью дрейфа v_d, то они испытывают направленную вверх (с учетом отрицательного q) магнитную силу F_B = qv_d х B, отклоняются вверх и накапливаются на верхнем краю плоского проводника, в результате чего появляется избыток положительного заряда на нижнем краю. Это накопление заряда на краях увеличивается до тех пор, пока электрическая сила, появившаяся в результате разделения зарядов, не уравновешивает магнитную силу, действующую на носители. Когда это равновесие будет достигнуто, электроны больше не отклоняются вверх. Чувствительный вольтметр или потенциометр, подключенный к верхней и нижней граням проводника, может измерить разность потенциалов, известную как ЭДС Холла.

бюджетное
профессиональное образовательное учреждение Вологодской области «Череповецкий
металлургический колледж имени академика И.П. Бардина»

                                                                                                  
Для всех специальностей

Изучение треков заряженных частиц

Методические рекомендации и лабораторная работа по дисциплине «Физика»
для студентов I курса

Разработчик  Изотова
Е.А.,

преподаватель
колледжа

Череповец

2017

Изучение треков заряженных частиц. Методические рекомендации и
лабораторная работа  по дисциплине «Физика» для студентов I
курса. /Разработчик Изотова Е.А./ – Череповец: БПОУ ВО «ЧМК» Череповецкий металлургический колледж, 2017. – 10 с.

РАССМОТРЕНО:

на заседании цикловой
комиссии

«Математические и
естественнонаучные дисциплины»

« »                          2017
г., протокол №

председатель ПЦК

__________________
И.А.Масыгина

(подпись)

Содержание

1	Цель работы ………………………………………………………………….	4
2	Средства обучения …………….…………………………………………….	4
3	Теоретические сведения и методические рекомендации по выполнению лабораторной работы ………………………………………………………..	4
4	Задание ………………………………………………………………………	7
5	Ход выполнения лабораторной работы ……………………………………	7
6	Контрольные вопросы ………………………………………………………	9
7	Рекомендации по оформлению отчета по лабораторной работе …………	9
	Литература ……………………………………………………………………	10

Лабораторная работа

Изучение треков заряженных частиц

1         
Цель работы

Получить элементарные навыки в чтении
фотографий движения заряженных частиц, сфотографированных в камере Вильсона.

2         
Средства обучения:

·       
лабораторное оборудование:
фотографии треков заряженных частиц, прозрачная бумага, линейка;

·       
методические рекомендации
по выполнению лабораторной работы, учебник, калькулятор.

3         
Теоретические
сведения и методические рекомендации по выполнению лабораторной работы

В начале ХХ века были разработаны методы исследования явлений атомной
физики и созданы приборы, позволившие не только выяснить основные вопросы
строения атомов, но и наблюдать превращения химических элементов. В 1911 г.
английский ученый Ч. Вильсон построил прибор, с помощью которого можно видеть и
фотографировать траектории заряженных частиц. Этот прибор можно назвать «окном»
в микромир, т.е. мир элементарных частиц и состоящих из них систем. Камера
Вильсона представляет собой геометрически закрытый сосуд, заполненный парами
воды или спирта близкими к насыщению.

При резком отпускании поршня вызванном уменьшением давления; под
поршнем, пар в камере адиабатически расширяется. Вследствие этого происходит
охлаждение и пар становится  перенасыщенным. Это неустойчивое состояние пара и
пар легко конденсируется. Центрами конденсации становятся ионы, которые
образуют в рабочем пространстве пролетавшая частица. Если частица проникает в
камеру непосредственно перед расширением или сразу после него, то на ее пути
возникают капельки воды. Эти капельки образуют видимый след пролетевшей частицы
– трек.

Треки дают богатую информацию о частице:

·         
трек толще у той частицы,
которая имеет больший заряд;

·         
треки показывают
траекторию движения заряженной частицы.

·         
если частицы имеют одинаковые
заряды, то трек толще у той, которая имеет меньшую скорость. Отсюда очевидно,
что к концу движения трек частицы толще, чем в начале, так как скорость частицы
уменьшается вследствие потери  энергии на ионизацию атомов среды;

·         
пробег частицы зависит от
ее энергии и плотности среды.

·         
треки заряженных частиц в
камере Вильсона представляют собой цепочки микроскопических капелек жидкости
(воды или спирта), образовавшиеся вследствие конденсации пересыщенного пара
этой жидкости на ионах, расположенных вдоль траектории заряженной частицы; в
пузырьковой камере – цепочки микроскопических пузырьков пара перегретой
жидкости, образовавшихся на ионах; в фотоэмульсии – цепочки зерен
металлического серебра, образовавшиеся на ионах.

·         
длина трека зависит от
начальной энергии заряженной частицы и плотности окружающей среды: она тем
больше, чем больше энергия частицы и чем меньше плотность среды.

·         
толщина трека зависит от
заряда и скорости частицы: она тем больше, чем больше заряд частицы и чем
меньше ее скорость.

·         
при движении частицы в
магнитном поле трек ее получается искривленным.радиус кривизны трека зависит от
массы, заряда, скорости частицы и модуля индукции магнитного поля: он тем
больше, чем больше масса и скорость частицы и чем меньше ее заряд и модуль
индукции магнитного поля.

·         
по изменению радиуса
кривизны трека можно определить направление движения частицы и изменение ее
скорости: начало ее движения и скорость больше там, где больше радиус кривизны
трека.

·         
треки частиц в
фотоэмульсии короче и толще, чем треки в камере вильсона и пузырьковой камере,
и имеют неровные края.

Если камера Вильсона помещена в
магнитное поле, то на движущиеся в ней заряженные частицы действует сила
Лоренца:

                                                                                       ,                 (1)

где F_Л – сила Лоренца, Н;

      q –
Заряд частицы, Кл;

      V –
Скорость частицы, м/с;

      B –
Индукция магнитного поля, Тл.

Правило левой руки позволяет показать, что F_Л ^ V, следовательно, является центростремительной
силой:

                                                                                              ,              
(2)

где F_л –  сила Лоренца, Н;

      m – масса,
кг;

      V –
Скорость, м/с;

      R –
радиус кривизны трека, м.

Используя формулы  1 и 2 можно
определить радиус кривизны трека частицы:

                                                                                              ,                
(3)

Если частица имеет скорость много меньше скорости света, то
кинетическая энергия определяется по формуле 4:

                                                                                    ,               
(4)

где Е – кинетическая
энергия частицы, Дж.

Из полученных формул можно сделать
выводы, которые можно использовать для анализа фотографий треков частиц:

·         
радиус кривизны трека
зависит от массы, скорости, заряда частицы. Радиус тем меньше, чем меньше масса
и скорость частицы и чем больше ее заряд, отклонения от прямолинейного движения
больше в том случае, когда энергия частицы меньше;

·         
так как скорость частицы к
концу пробега уменьшается, то уменьшается и радиус кривизны трека. По изменению
радиуса кривизны можно определить направление движение частицы, начало  ее
движения там, где кривизна трека меньше;

·         
измерив, радиус кривизны
трека и зная другие величины, можно вычислить для частицы отношение ее заряда к
массе: .

Так для протона:

                                                            
 Кл/кг

для ядра гелия (a-частицы):

                                                             
 Кл/кг

для электрона:

                                                             
 Кл/кг

·       
эти отношения служат
важнейшей характеристикой частицы,  и позволяют идентифицировать частицу, т.е.
установить идентичность известной частицы;

·       
если в камере Вильсона
произошла реакция распада ядра атома, то по трекам -продуктов распада – можно установить
какое ядро распалось.

      Направление
вектора магнитной индукции определяют, пользуясь правилом левой руки: 1)
четыре вытянутых пальца расположить по направлению движения положительной
частицы; 2) отогнутый на 90⁰ большой палец – в направлении радиуса
кривизны трека и силы Лоренца; 3) линии магнитной индукции  вектора В будут
входить в ладонь левой руки.

4         
Задание

4.1 По фотографии заряженных частиц ( рисунок 1) определить радиусы
треков I в
начале и в конце его и III в
начале трека.

4.2 Ответить на систему вопросов к трекам частиц по рисунку 1.

5          
Ход выполнения лабораторной работы

      5.1 На фотографии рисунка 1 видны
траектории ядер легких элементов (последнии 22 см пробега). Ядра двигались в
магнитном поле с индукцией  В=2,17
Тл, направленням перпендикулярно фотографии. Начальные скорости всех ядер одинаковы и перепендикулярны линиям магнитного поля.

                            I                       III

Рисунок 1- Фотография
треков заряженных частиц в камере Вильсона.

5.2 Определите направление вектора индукции B магнитного поля.

5.3 Объясните почему траектории частиц
представляют собой дуги окружностей?

5.4 Какова причина различия в кривизне траекторий
разных ядер?

5.5Почему кривизна каждой траектории изменятся от
начала к концу пробега частицы?

5.6 Объясните причины различия в толщине треков
разных ядер. Почему трек каждой частицы толще в конце пробега, чем в начале
его?

5.7 Измерьте радиусы
кривизны трека частицы I примерно в начале и в конце пробега.

5.8 Определите на
сколько изменилась энергия частицы за время пробега по               формуле 5.
Известно, что частица I идентифицирована, как протон:

                                                                              ,              
(5)

где DЕ – изменение энергии, Дж;

       В – магнитная индукция, Кл;

       q– заряд протона, Кл;

       m– масса протона, кг;

      r, r-радиусы кривизны трека, м.

·       
Радиусы кривизны
определяют следующим образом. Наложите на фотографию листок прозрачной бумаги и
переведите на нее треки                   I, III. Начертите, как показано на рисунке 2, две
хорды и восстановите к этим хордам серединные перпендикуляры. На пересечении серединных
перпендикуляров лежит центр окружности, ее радиус измерьте линейкой.

Рисунок 2-Определение радиуса кривизны трека

5.9                        
 Измерьте радиус кривизны
река частицы III  вначале ее пробега. Вычислите для частицы III
отношение заряда к ее массе по формуле 6:

                                                       
                                     ,                (6)

    По
полученному отношению определите, какая частица оставила след.

5.10                    
Результаты вычислений и
измерений занесите в таблицу.

Таблица 1- Результаты
измерений и вычислений

Радиус кривизны трека 1 частицы в начале пробега	Радиус кривизны 1частицы в конце пробега	Заряд протона	Масса протона	модуль магнитной индукции	Изменение энергии 1 частицы	Отношение заряда 3 частицы к ее массе	Радиус кривизны трека 3 частицы в начале пробега
r1	r2	q1	m1	B	ΔE	q3/m3	r3
м	м	Кл	кг	Тл	Дж	Кл/кг	м
		1,6.10-19	1,67.10-27	2,17

5.11                    
Вычисления

5.11.1 Вычислите изменение
энергии протона по формуле:

       

      5.11.2 Вычислите
отношение заряда к массе для третьей частицы по формуле 6.

     5.11.3 Определите по полученному отношению какая
частица оставила трек III.

5.12 Сделайте вывод.     В выводе укажите, что можно
определить по  треку                        частицы , чему равно изменение
энергии I частицы , какие частицы оставили трек в камере Вильсона.

5.13 Ответьте на
контрольные вопросы.

6       
 Контрольные
вопросы

5.1Какие методы наблюдения и регистрации элементарных
частиц вы знаете?

5.2Можно ли с помощью камеры Вильсона регистрировать
незаряженные частицы?

5.3Какие преимущества имеет пузырьковая камера по
сравнению с камерой Вильсона?

5.4 В чем преимущество метода толстослойных
фотоэмульсий и кто из ученых впервые его применил?

5.5Как направлен вектор магнитной индукции в начале
трека?

     7  
Рекомендации по оформлению отчета по лабораторной работе

Отчет по
работе оформляется в соответствии с едиными требованиями, принятыми в колледже
и должен включать:

·             
вид работы;

·             
название работы;

·             
цель работы;

·             
оборудование;

·             
ход работы;

·             
алгоритм выполнения работы;

·             
расчеты;

·             
вывод.

Литература

1.     
Дик Ю.И., Кабардин О.Ф.,. Орлов В.А
и др. Руководство по проведению лабораторных работ по физике для средних
специальных  учебных заведений. –  М.: Просвещение, 2002.

2.     
Учебники 11класс›–11–klass–miakishev…

3.     
Буров В. А., Дик Ю. И., Зворыкин Г. Г. и
др.Фронтальные лабораторные занятия по физике в 7-11 классах
общеобразовательных учреждений. – М.: Просвещение, 1996.