Закон движения электрона в магнитном поле
Содержание:
- Каково движение электрона в магнитном поле
-
Как найти скорость
- Траектория движения
- Период обращения электрона в магнитном поле
- Отклонение электронов в магнитном поле
- Примеры решения задач
Каково движение электрона в магнитном поле
Известно, что магниты представляют собой металлы, обладающие свойством к притяжению прочих магнитов и металлических предметов определенного состава. Во внутренней области таких объектов сгенерировано магнитное поле, действие которого можно наблюдать в реальных условиях. Эффект проявляется по-разному, то есть магнит отталкивает или притягивает предметы.
Роль источника, формирующего магнитное поле, играют заряженные частицы, которые пребывают в движении. Если перемещение зарядов обладает определенным направлением, то такой процесс называют электрическим током. Таким образом, легко сделать вывод об образовании магнитного поля, благодаря наличию электричества.
Электрический ток ориентирован по перемещению зарядов со знаком плюс и направлен противоположно относительно передвижения частиц, которые заряжены отрицательно. Если предположить, что имеется некая трубка в форме кольца с потоком воды, то какой-то ток примет противоположное ему направление. Электрический ток записывают с помощью буквы I.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если рассматривать металлические предметы, то в них образование тока связано с перемещением отрицательных зарядов. На наглядном изображении продемонстрировано передвижение частиц, заряженных отрицательно, то есть электронов, в левую сторону. В то время как электричество ориентировано в правую сторону.
Источник: habr.com
В начале исследований электричества ученые не обладали информацией о природе и свойствах носителей электрического тока. При рассмотрении аналогичного проводника слева, как на рисунке выше, можно заметить, что ток перемещается от наблюдателя, а магнитное поле окружает его по часовой стрелке.
Источник: habr.com
Эксперимент можно продолжить, используя компас. При размещении прибора около проводника, изображенного на схеме, произойдет разворот стрелки перпендикулярно относительно рассматриваемого проводника, параллельно по отношению к силовым линиям магнитного поля, то есть параллельно кольцевой стрелке, обозначенной черным цветом на изображении.
Представим, что имеется некий шарообразный предмет, заряженный положительно. Заряд со знаком плюс обусловлен недостаточным количеством электронов. Данному шарику можно задать направление путем подбрасывания вперед. В таком случае вокруг объекта сформируется аналогичное предыдущему примеру магнитное поле кольцевого типа, которое закручивается вокруг шарика по направлению часовой стрелки.
Источник: habr.com
В данном случае заряженные частицы перемещаются в определенном направлении. Таким образом, целесообразно сделать вывод о наличии электрического тока. В результате при возникновении электричества вокруг него формируется магнитное поле. Передвигающийся заряд, либо какое-то количество таких частиц, формирует около себя «тоннель» в виде магнитного поля. При этом стенки «тоннеля» более плотные около перемещающейся заряженной частицы.
Удаляясь от перемещающегося заряда, напряженность, то есть сила генерируемого магнитного поля, слабеет. В результате компасная стрелка меньше реагирует на него. Закон, согласно которому напряженность рассматриваемого поля распределяется около источника, аналогичен закономерности формирования электрического поля вокруг заряда. Таким образом, величина напряженности и квадрат расстояния до источника находятся в обратной пропорциональной зависимости.
Рассмотрим следующую ситуацию, когда шарик с положительным зарядом движется по траектории в форме круга. В таком случае кольцевые линии магнитных полей, сформированных вокруг предмета, складываются. В итоге получается магнитное поле, обладающее перпендикулярным направлением относительно плоскости, в рамках которой происходит движение заряженного шарика.
Источник: habr.com
Заметим, что «тоннель» магнитного поля, образованный около заряженного объекта, сворачивается, и получается кольцо, которое схоже по форме с бубликом. Аналогичную ситуацию можно наблюдать в процессе сворачивания в кольцо проводника с электричеством. Тогда проводник, деформированный так, что получается катушка с множеством витков, называют электромагнитом. Около подобного предмета формируются магнитные поля за счет перемещающихся в нем зарядов, то есть электронов.
При условии вращения шарика с зарядом вокруг собственной оси возникает магнитное поле по аналогии с тем, что образовано у нашей планеты, которое ориентировано вдоль оси вращательного движения. Тогда имеет место возникновение кругового электрического тока, который определяют как ток, провоцирующий образование магнитного поля во время перемещения по круговой траектории заряженной частицы относительно оси шарика.
Источник: habr.com
В этом случае процесс аналогичен перемещению шарика по кругу. Отличие состоит в том, что радиус орбиты движения уменьшен до величины радиуса шарообразного объекта. Вышеизложенные выводы имеют смысл и тогда, когда заряд шарика имеет знак минуса, а магнитное поле ориентировано противоположно.
Описанный выше эффект удалось выявить экспериментальным путем Роуланду и Эйхенвальду. Исследователи фиксировали магнитные поля около дисков, обладающих зарядом и совершающих вращательные движения. Вблизи этих объектов замечали отклонения компасной стрелки. Ознакомиться с наглядным представлением опыта можно на рисунке ниже:
Источник: habr.com
На изображении отмечены направления магнитных полей, которые зависят от положительного или отрицательного заряда дисков, расположенных в системе. По рисунку заметно, как эти направления меняются при смене знака заряда. Если диск, не обладающий зарядом, привести во вращательное движение, то магнитное поле отсутствует. Стационарные заряды также не образуют вокруг себя поля.
Как найти скорость
В плане изучения интересен процесс перемещения зарядов в пространственной области при наличии магнитного и электрического поля. Применительно к такой ситуации целесообразно воспользоваться соотношением для силы Лоренца, которая представляет собой суммарную величину сил, оказывающих воздействие на заряд, перемещающийся в электрическом и магнитном полях.
Представим, что заряд равен q и перемещается со скоростью (overrightarrow{v}) в условиях однородного магнитного поля, индукция которого составляет (overrightarrow{В}), а также в присутствии электрического поля с определенной напряженностью (overrightarrow{N}). Запишем силу воздействия электрического поля на заряд по модулю:
(Fэ = qE)
Этот компонент силы Лоренца принято называть электрической составляющей. Применительно к магнитному полю, на перемещающийся заряд воздействует магнитная составляющая силы Лоренца. Модуль определяют по закономерности Ампера. Представим, что проводник, по которому течет электричество, расположен в однородном магнитном поле. Вдоль этого объекта перемещаются заряды. Проанализирует ситуацию на отрезке данного проводника, который в длину составляет (triangle l), а площадь его поперечного сечения равна S.
Источник: иванов-ам.рф
Формула для вычисления силы тока, протекающего по проводнику:
(I = qnυS)
Зная, что:
(F_{А} = BItriangle l sin alpha)
Получим следующее выражение:
(FA = BqnvSΔtriangle l sin alpha)
Здесь (N = nStriangle l) обозначает количество зарядов, входящих в объем (Striangle l).
Исходя из записанной формулы, несложно выразить скорость движения заряда с учетом второго закона Ньютона:
(v = frac{qBR}{m})
Траектория движения
Изучить направление, в котором перемещаются заряженные частицы в магнитном поле, целесообразно на примере простейшего случая. При этом происходит движение заряда в однородном магнитном поле с индукцией, которая является перпендикуляром исходной скорости заряженной частицы. Схематично передвижение заряда изображено на рисунке:
Источник: иванов-ам.рф
В связи со стабильным значением модуля скорости заряда, не меняется модуль магнитной составляющей силы Лоренца по аналогии. Исходя из того, что рассматриваемая сила является перпендикуляром к скорости, можно заключить наличие центростремительного ускорения у перемещающейся частицы. Данная величина также не меняется по модулю, что позволяет сделать вывод о постоянстве радиуса кривизны R рассматриваемой траектории. Таким образом, подтверждается ранее выведенная формула скорости:
(v = frac{qBR}{m})
Период обращения электрона в магнитном поле
Запишем математическое соотношение, позволяющее выразить период обращения заряженной частицы в магнитном поле:
(T=frac{2 cdot{pi}cdot r}{upsilon};)
(r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B}.)
Отклонение электронов в магнитном поле
Из предыдущего анализа движения заряда известно, что процесс сопровождается воздействием на частицу, перемещающуюся в магнитном поле, силы Лоренца. Данная сила определяется величиной и знаком рассматриваемой частицы, а также зависит от быстроты ее перемещения и индукции магнитного поля. В итоге траектория, по которой движется заряд, изменяется. Опытным путем явление можно наблюдать с помощью системы магнитного поля и электронного луча осциллографа.
В ходе эксперимента необходимо выключить горизонтальную развертку луча и с помощью рукояток отрегулировать положение луча по вертикали и горизонтали. В результате последовательных манипуляций луч окажется направленным непосредственно в центральную область экрана. Следует расфокусировать образованное световое пятно, увеличивая яркость до максимально возможного значения. Если поместить рядом с прибором постоянный магнит, то можно наблюдать смещение пятна вбок, как изображено на рисунке:
Источник: duckproxy.com
Изменение положение пятна наблюдается в процессе приближения или удаления магнита от осциллографа. Таким образом, справедливо сделать вывод о том, что смещение пятна зависит от величины индукции магнитного поля. Если перевернуть магнит, то направление индукции изменится, а пятно на экране переместится в противоположную сторону.
Примеры решения задач
Задача 1
Созданы условия для движения электрона в однородном магнитном поле. Индукция данного поля составляет (B=4cdot {10}^{-3} {Тл}). Требуется вычислить, чему равен период обращения рассматриваемой отрицательно заряженной частицы.
Решение
В первую очередь следует записать данные из условия задачи. Так как речь в задании идет об электроне, то следует выписать справочные величины заряда и массы:
({q}_{e}=-1.6cdot {10}^{-19} {Кл})
({m}_{e}=9.1cdot {10}^{-31} {кг})
Вспомним формулу для расчета период обращения заряженной частицы в магнитном поле из ранее пройденного теоретического материала:
(T=frac{2 cdot{pi}cdot r}{upsilon}; r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B})
Подставим численные значения и получим:
(T=frac{2 cdot 3.14 cdot 9.1cdot {10}^{-31},text{кг}}{|-1.6cdot {10}^{-19},text{Кл}| cdot 4cdot {10}^{-3},text{Тл}}=8.9cdot {10}^{-9},с)
Ответ: период обращения электрона в магнитном поле равен (8.9cdot {10}^{-9} с).
Задача 2
Имеется однородное магнитное поле, величина индукции которого составляет (10^{-3} Тл) . В это поле попадает отрицательно заряженная частица по направлению перпендикулярно относительно линий магнитной индукции и под углом (alpha=frac{pi}{4}) к границе рассматриваемого поля. Скорость электрона по модулю соответствует (10^{6} м/с). В направлении оси абсциссы и ординаты поле не имеет границ. Известно, что заряд частицы к ее массе относится как (frac{е}{m}=1,76cdot 10^{11} Кл/кг). Необходимо вычислить расстояние, на котором от точки взлета электрон покинет поле.
Решение
Изобразим схематично условие задания:
Источник: иванов-ам.рф
В данном случае целесообразно применить правило левой руки, чтобы определить направление силы Лоренца с учетом отрицательного заряда наблюдаемой частицы. Схематично это представлено на рисунке выше. В условиях воздействия магнитного поля электрон подвержен действию магнитной составляющей силы Лоренца. В результате отрицательно заряженная частица будет перемещаться по дуге окружности. Следует вычислить радиус этой окружности. Воспользуемся вторым законом Ньютона:
(moverrightarrow{a}=overrightarrow{F_{л}})
Поскольку центростремительное ускорение:
(а = frac{v^{2}}{R})
В результате получим, что:
(frac{mv^{2}}{R}=evB Rightarrow R=frac{mv}{eB})
При рассмотрении (triangle O^{,}OC) можно сделать вывод:
(OC = frac{l}{2} = R sin alpha)
Тогда:
(l = 2R sin alpha = 2frac{mv sin alpha}{eB})
При подстановке численных значений получим:
(l = frac{2cdot 10^{6} cdot sin frac{pi}{4}}{1,76 cdot 10^{11}cdot 10^{-3} } = 0,008м = 8 мм)
Ответ: 8 мм.
Электрон из состояния
покоя разгоняется в однородном электростатическом поле, модуль напряженности
которого 3,0 МВ/м. Определите модуль скорости электрона через 1,0 нс после
начала движения.
Решение.
В качестве физической
системы рассмотрим электрон. Если пренебречь взаимодействием электрона с
гравитационным, электрическим и магнитными полями Земли, а также предположить,
что он движется в вакууме, то разгон происходит только под действием
ускоряющего поля.
Поэтому движение электрона в инерциальной системе отсчета
можно описать вторым законом Ньютона и кинематическими законами
равноускоренного прямолинейного движения.
В качестве тела отсчета
возьмем лабораторию, ось OX направим в сторону
движения (т.е. против поля), выбрав начало координат в точке, из которой
электрон начал двигаться. Если спроецировать векторы, изображающие
соответствующие величины, на ось OX, с учетом того, что v0 = 0, получим:
ma
= eE, x = at2/2, v = at.
Откуда искомая скорость
v = eEt/m.
Подставив числовые
значения заряда и массы электрона, а также значения E и t, получим v = 5,3•108 м/с,
что больше скорости света в вакууме.
Так как ни в какой
системе отсчета тело не может двигаться со скоростью превышающей скорость света
в вакууме, то полученное значение скорости не может быть ответом задачи. Причиной
ошибки явилось неявно сделанное предположение о том, что движение электрона
может быть описано законами классической механики.
Изменение импульса тела
равно импульсу силы, действующей на него, т.е. Dp = FDt, не только в
классической, но и в релятивистской механике. Причем пот релятивистских
скоростях движения импульс тела p = gmv.
С учетом этого,
применительно к ситуации, описанной в задаче, теорему об изменении импульса
можно записать в виде: D(gmv)=eEDt.
Принимаем во внимание,
что Dv = v –
v0 = v, Dt = t – t0 = t (т.е. в момент времени t0 = 0 скорость v0 = 0).
Откуда находим модуль
искомой скорости электрона v.
Ответ: v = 2,6•108 м/с.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
Электрон движется в однородном магнитном поле с индукцией 0,1 Тл по окружности
Условие задачи:
Электрон движется в однородном магнитном поле с индукцией 0,1 Тл по окружности. Определить угловую скорость вращения электрона.
Задача №8.2.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
На электрон, движущийся в магнитном поле, действует сила Лоренца (F_Л), которую определяет следующая формула:
Здесь (B) – индукция магнитного поля, (upsilon) – скорость электрона, (e) – модуль заряда электрона, (alpha) – угол между вектором скорости и вектором магнитной индукции. Так как другого не сказано в условии, то (alpha=90^circ).
Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда, как в нашем случае), то большой палец, оставленный на 90°, покажет направление силы Лоренца. В нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца направлена вправо.
Сила Лоренца (F_Л) сообщает электрону центростремительное ускорение (a_ц), поэтому из второго закона Ньютона следует, что:
Центростремительное ускорение (a_ц) можно определить через скорость (upsilon) и радиус кривизны траектории (R) по формуле:
Подставим (3) в (2), тогда:
Приравняем правые части (1) и (4):
Известно, что угловая скорость (omega) равна отношению линейной скорости (upsilon) к радиусу кривизны (R), поэтому:
[Besin alpha = omega ]
Выразим из этого уравнения искомую угловую скорость электрона (omega):
Масса электрона (m_e) равна 9,1·10 -31 кг, а его заряд (e) (вернее модуль заряда) равен 1,6·10 -19 Кл. Численный ответ равен:
Ответ: 1,76·10 10 рад/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Шпаргалка по общей электронике и электротехнике.
5. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ.
В некоторых электровакуумных приборах используется движение электронов в магнитном поле.
Рассмотрим случай, когда электрон влетает в однородное магнитное поле с начальной скоростью v0, направленной перпендикулярно магнитным силовым линиям. В этом случае на движущийся электрон действует так называемая сила Лоренца F, которая перпендикулярна вектору нО и вектору напряженности магнитного поля Н. Величина силы F определяется выражением: F= еv0Н.
При v0 = 0 сила Рравна нулю, т. е. на неподвижный электрон магнитное поле не действует.
Сила F искривляет траекторию электрона в дугу окружности. Поскольку сила F действует под прямым углом к скорости нО, она не совершает работы. Энергия электрона и его скорость не изменяются по величине. Происходит лишь изменение направления скорости. Известно, что движение тела по окружности (вращение) с постоянной скоростью получается благодаря действию направленной к центру центростремительной силы, которой именно и является сила F.
Направление поворота электрона в магнитном поле в соответствии с правилом левой руки удобно определяется по следующим правилам. Если смотреть в направлении магнитных силовых линий, то электрон движется по часовой стреле. Иначе говоря, поворот электрона совпадает с вращательным движением винта, который ввинчивается по направлению магнитных силовых линий.
Определим радиус r окружности, описываемой электроном. Для этого воспользуемся выражением для центростремительной силы, известным из механики: F = mv20/r. Приравняем его значению силы F = еv0Н: mv20/r = еv0Н. Теперь из этого уравнения можно найти радиус: r= mv0/(еН).
Чем больше скорость электрона v0, тем сильнее он стремится двигаться прямолинейно по инерции и радиус искривления траектории будет больше. С другой стороны, с увеличением Н растет сила F, искривление траектории возрастает и радиус окружности уменьшается.
Выведенная формула справедлива для движения в магнитном поле частиц с любыми массами и зарядом.
Рассмотрим зависимость rот mи е. Заряженная частица с большей массой mсильнее стремится лететь по инерции прямолинейно и искривление траектории уменьшится, т. е. rстанет больше. А чем больше заряд е, тем больше сила F и тем сильнее искривляется траектория, т. е. ее радиус становится меньше.
Выйдя за пределы магнитного поля, электрон дальше летит по инерции по прямой линии. Если же радиус траектории мал, то электрон может описывать в магнитном поле замкнутые окружности.
Таким образом, магнитное поле изменяет только направление скорости электронов, но не ее величину, т. е. между электроном и магнитным полем нет энергетического взаимодействия. По сравнению с электрическим полем действие магнитного поля на электроны является более ограниченным. Именно поэтому магнитное поле применяется для воздействия на электроны значительно реже, нежели электрическое поле.
Найти угловую скорость вращения электрона вокруг ядра
UptoLike
В первом приближении можно считать, что электрон в атоме водорода движется по круговой орбите с линейной скоростью v. Найти угловую скорость ω вращения электрона вокруг ядра и его нормальное ускорение аn. Считать радиус орбиты r = 0,5·10 -10 м и линейную скорость электрона на этой орбите v = 2,2·10 6 м/с.

ОПРЕДЕЛЕНИЯ
- векторная величина, характеризующая быстроту вращения твердого тела
- движение вокруг своей оси по окружности
- стабильная отрицательно заряженная элементарная частица с зарядом 1,6·10 -19 Кл и массой 9·10 -31 кг
- положительно заряженная массивная центральная часть атома, состоящая из протонов и нейтронов
самая малая частица химического элемента, она является носителем его свойств. Состоит атом из электронов и положительно заряженного ядра. У атома размеры порядка 10 -10 м, а порядок энергии связи внешних электронов равен 10 эВ.
[spoiler title=”источники:”]
http://ur-consul.ru/Bibli/SHpargalka-po-obshchyeyi-elyektronikye-i-elyektrotyekhnikye.5.html
http://zzapomni.com/katalog/1-54-nayti-uglovuyu-skorost-vrashcheniya-elektrona-vokrug-yadra
[/spoiler]
Скорость движения электронов
Уже упоминалось, что электроны движутся в направлении анода ускоренно, и это без всяких преувеличений соответствует действительности. В тот момент, когда электрон покидает область катода, его скорость теоретически принимается равной нулю, однако, он, находясь в постоянном электрическом поле анода, начинает двигаться ускоренно, и приобретает энергию, пропорциональную ускоряющему напряжению:
е — заряд электрона, принимается равным ≈ 1,602 х 10 -19 Кл;
те — масса электрона, принимается равной ≈ 9,11 х 10 -31 кг;
Решая это уравнение относительно скорости электрона υ, получим следующее выражение:
В науке часто используется отношение заряда электрона к его массе, е/те, которое имеет приближенное значение 1,7588 х 10 11 Кл/кг. При приложении к аноду относительно катода напряжения 100 В электрон достигнет поверхности анода, имея скорость порядка 6 х 10 б м/с.
Если использовать предыдущее выражение и подставить в него ускоряющее напряжение 512 кВ, (величина, соответствующая, например, напряжению в дальних линиях электропередач), то получится, что скорость электрона может превысить скорость света, что, естественно, является невозможным. Причина заключается в том, что приведенное упрощенное выражение справедливо только для массы покоя электрона, однако, при движении с околосветовыми скоростями масса электрона возрастает, требуя бесконечно большого значения напряжения для ускорения электрона до околосветовых скоростей. С учетом этих условий необходимо использовать более сложное уравнение, предложенное Элли (Alley) и Этвудом (Atwood):
в котором с — скорость света в вакууме, примерно равна 2,998 х 10 8 м/с.
В качестве домашнего примера действие принципа относительности можно продемонстрировать на цветном телевизоре. Для исправного цветного кинескопа напряжение на втором аноде составляет порядка 25 кВ, поэтому скорость электрона в момент удара о поверхность кинескопа составляет более 300 млн км/час, однако более простое уравнение предсказывает скорость, на 3,5% более высокую.
В рентгеновских медицинских установках мишень бомбардируется электронами, имеющими очень высокую скорость, так как для возникновения рентгеновского излучения скорость электрона при соударении должна значительно превышать 300 млн км в час. Поэтому в кинескопах домашних телевизоров и мониторов (для снижения интенсивности рентгеновского излучения) не используется ускоряющее напряжение, превышающее 25 кВ, хотя при этом можно было бы обеспечить более высокую четкость и фокусировку изображения.
Необходимо учесть, что расстояние между анодом и катодом не входит в каждое из уравнений, хотя теоретически бесконечное расстояние позволило бы бесконечно возрасти времени, во время которого происходит ускорение движения, и даже при сравнительно небольших ускорениях скорость при ударе могла бы оказаться значительной.
Очень многие явления, происходящие внутри электронных ламп, могут быть поняты при понимании процессов, происходящих при ускоренном движении электрона в электрическом поле анода, приобретении им кинетической энергии и процессах передачи энергии электрона при ударе, когда он достигает анода.
Все сказанное выше вполне справедливо для обсуждения скорости движения ускоренных положительным полем электронов, подлетающих к аноду. Однако в области катода картина совсем иная. Дело в том, что кинетическая энергия электронов, преодолевших работу выхода из металла и покинувших катод, оказывается различной. Таким образом, отрываясь от катода, электроны начинают движение к аноду с различными начальными скоростями. Они невелики, но при детальном рассмотрении их нельзя считать одинаковыми, как это предполагалось выше, когда рассматривался ускоренный поток электронов, подлетающих к аноду. Как будет показано ниже, управление электронным потоком в триодах и более сложных электронных лампах осуществляется как раз вблизи катода. Из физической статистики известно, что из-за различных кинетических энергий, скорости электронов, вылетающих из катода распределены по так называемому закону распределения Максвелла. Однако, для дальнейших рассуждений наиболее важным фактом является тот факт, что электроны, вылетающие из катода, обладают различными кинетическими энергиями.
Источник
Электрон в электрическом поле
Движение электрона в электрическом поле является одним из важнейших для электротехники физических процессов. Разберемся как это происходит в вакууме. Сначала рассмотрим пример движения электрона от катода к аноду в однородном электрическом поле.

На приведенном ниже рисунке изображена ситуация, когда электрон покидает отрицательный электрод (катод) с пренебрежимо малой начальной скоростью (стремящейся к нулю), и попадает в однородное электрическое поле, присутствующее между двумя электродами.
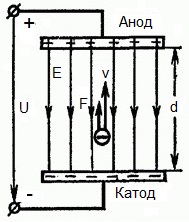
К электродам приложено постоянное напряжение U, а электрическое поле обладает соответствующей напряженностью E. Расстояние между электродами равно d. В данном случае на электрон со стороны поля будет действовать сила F, пропорциональная заряду электрона и напряженности поля:
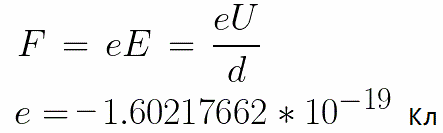
Поскольку электрон обладает отрицательным зарядом, то эта сила будет направлена против вектора E напряженности поля. Соответственно электрон будет в данном направлении электрическим полем ускоряться.
Ускорение a, которое испытывает электрон, пропорционально величине действующей на него силы F и обратно пропорционально массе электрона m. Поскольку поле однородно, ускорение для данной картины можно выразить так:
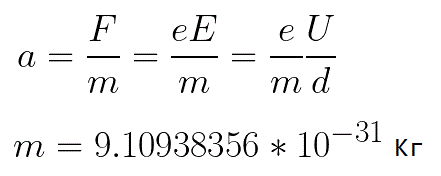
В этой формуле отношение заряда электрона к его массе есть удельный заряд электрона — величина, являющаяся физической константой:
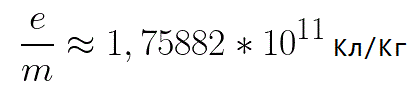
Итак, электрон находится в ускоряющем электрическом поле, ибо направление начальной скорости v0 совпадает с направлением силы F со стороны поля, и электрон движется поэтому равноускоренно. Если никаких препятствий нет, то он пройдет путь d между электродами и попадет на анод (положительный электрод) с некой скоростью v. В момент когда электрон достигнет анода, его кинетическая энергия будет соответственно равна:
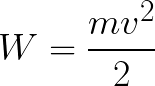
Поскольку на всем пути d электрон ускорялся силами электрического поля, то данную кинетическую энергию он приобрел в результате работы, которую совершила сила, действующая со стороны поля. Эта работа равна:
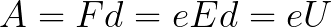
Тогда кинетическая энергия, которую приобрел электрон двигаясь в поле, может быть найдена следующим образом:
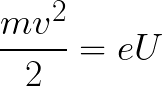
То есть это есть ни что иное, как работа сил поля по ускорению электрона между точками с разностью потенциалов U.
В подобных ситуациях для выражения энергии электрона удобно использовать такую единицу измерения как «электронвольт», равную энергии электрона при напряжении в 1 вольт. А поскольку заряд электрона является константой, то и 1 электронвольт — также постоянная величина:
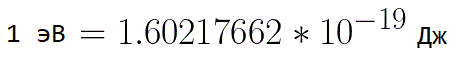
Из предыдущей формулы можно легко определить скорость электрона в любой точке на его пути при движении в ускоряющем электрическом поле, зная лишь разность потенциалов которую он прошел ускоряясь:
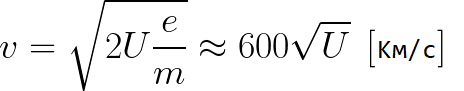
Как мы видим, скорость электрона в ускоряющем поле зависит лишь от разности потенциалов U между конечной и стартовой точками его пути.
Представим, что электрон начал движение от катода с пренебрежимо малой скоростью, а напряжение между катодом и анодом равно 400 вольт. В этом случае в момент достижения анода его скорость будет равна:
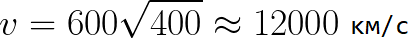
Тут же легко можно определить время, за которое электрон пройдет расстояние d между электродами. При равноускоренном движении из состояния покоя средняя скорость находится как половина конечной скорости, тогда время ускоренного полета в электрическом поле будет равно:
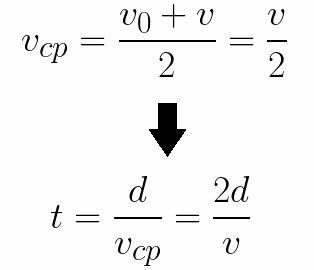
Теперь рассмотрим пример когда электрон движется в тормозящем однородном электрическом поле. То есть поле направлено как и прежде, но электрон начинает двигаться наоборот — от анода к катоду.
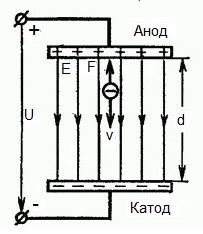
Предположим что электрон покинул анод с какой-то начальной скоростью v и изначально стал двигаться в направлении катода. В этом случае сила F, действующая на электрон со стороны электрического поля, будет направлена против вектора электрической напряженности Е — от катода к аноду.
Она станет уменьшать начальную скорость электрона, то есть поле будет замедлять электрон. Значит электрон в данных условиях станет двигаться равномерно равнозамедленно. Ситуация описывается так: «электрон движется в тормозящем электрическом поле».
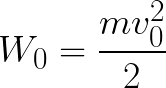
От анода электрон начал двигаться с отличной от нуля кинетической энергией, которая при торможении начинает уменьшаться, поскольку энергия теперь расходуется на преодоление силы, действующей со стороны поля навстречу электрону.
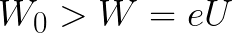
Если начальная кинетическая энергия электрона, когда он покинул анод, сразу была больше энергии, которую необходимо затратить полю на ускорение электрона при движении от катода к аноду (как в первом примере), то электрон пройдет расстояние d и в итоге все же достигнет катода несмотря на торможение.
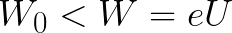
Если же начальная кинетическая энергия электрона меньше данной критической величины, то электрон не достигнет катода. В определенный момент он остановится, затем начнет равноускоренное движение обратно — к аноду. В итоге поле вернет ему энергию, которая израсходовалась в процессе торможения.
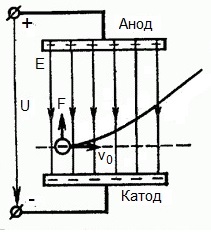
А что если электрон влетает на скорости v0 в область действия электрического поля под прямым углом? Очевидно, сила со стороны поля в этой области направлена для электрона от катода к аноду, то есть против вектора напряженности электрического поля E.
Значит электрон теперь имеет две составляющие движения: первая — со скоростью v0 перпендикулярно полю, вторая — равноускоренно под действием силы со стороны поля, направленной к аноду.
Получается, что влетев в область действия поля, электрон движется по параболической траектории. Но вылетев за пределы области действия поля, электрон продолжит равномерное движение по инерции по прямолинейной траектории.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Движение электронов в ускоряющем поле
Движение электронов в однородном электрическом поле
Движение электронов в электромагнитном поле.
Основным процессом во всех электронных приборах является взаимодействие движущихся электронов с электрическим полем. Электрон представляет собой частицу материи с отрицательным зарядом, значение которого равно e=1,6•10 -19 Кл (Кулон). Масса неподвижного электрона m=9,1•10 -28 г. С возрастанием скорости масса электрона увеличивается. Теоретически, при скорости электрона равной скорости света с=3•10 8 м/с, его масса должна стать бесконечно большой. В обычных электронных приборах скорость электрона не превышает 0,1 от скорости света, в связи с чем, массу электрона в РЭА принимают постоянной и равной массе неподвижного электрона.
Электрическое поле в электронных приборах может быть однородным и неоднородным. Наиболее простыми для изучения являются закономерности движения электронов в однородном электрическом поле. В зависимости от угла между вектором скорости электрона и вектором напряженности электрического поля, электрическое поле может ускорять, тормозить движение электрона, или делать его траекторию криволинейной.
На рис. 1 изображено в виде силовых линий (линий напряженности) однородное электрическое поле между двумя электродами, например между катодом и анодом диода. Если разность потенциалов между электродами U, а расстояние – d, то напряженность поля E=U/d/ Для однородного поля Е – постоянная величина.
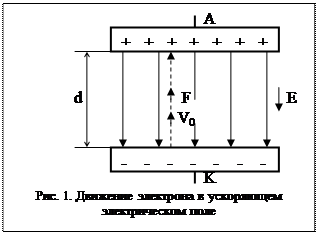
Пусть из электрода, имеющего более низкий потенциал (из К) вылетает электрод с кинетической энергией W0 и начальной скоростью V0, направленной вдоль силовых линий поля. Поле ускоряет движение электрона. Напряженность поля численно равна силе, действующей на единичный положительный заряд. Поэтому сила действия на электрон равна F=-e•E. Знак минус поставлен потому, что сила F направлена в сторону противоположную вектору Е. Под действием силы F электрон получает ускорение a=F/m. Двигаясь прямолинейно, электрон приобретает максимальную скорость V и кинетическую энергию W в конце своего пути, т.е. при ударе об электрод А. Таким образом, в ускоряющем электрическом поле кинетическая энергия электрона возрастает за счет работы электрического поля по перемещению электрона. В соответствии с законом сохранения энергии увеличение кинетической энергии электрона W-W0 , равно работе поля, которая определяется произведением перемещаемого заряда е на пройденную им разность потенциалов U:
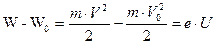 .
.
Если начальная скорость электрона равна нулю, то
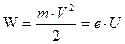 .
.
Эта же формула применяется, если V0 неизвестна, но известно, что она много меньше конечной скорости V (V0 -3 мкс=1нс.
Время пролета электрона определяет одну из важнейших характеристик электронных приборов – их быстродействие. В следствие неоднородности электрического поля в электронных приборах расчет времени пролета в них электронов более сложен.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник

