Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.
Скорость при прямолинейном равномерном движении
Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.
Векторный способ записи скорости при равномерном прямолинейном движении:![]()
s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение.
Проекция скорости на ось ОХ:
![]()
sx — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы).
Знак модуля скорости зависит от направления вектора скорости и оси координат:
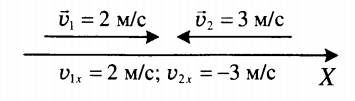
Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.
Дополнительные единицы измерения
- 1 км/ч (километр в час) = 1000 м/3600 с.
- 1 км/мин (километр в минуту) = 1000 м/60 с.
- 1 км/с (километр в секунду) = 1000 м/с.
- 1 м/мин (метр в минуту) = 1 м/60 с.
- 1 см/с (сантиметр в секунду) = 0,01 м/с.
Спидометр — прибор для измерения модули скорости тела.
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:
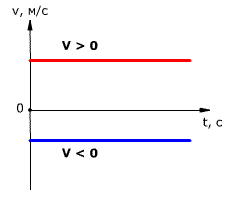
Определение направления движения по графику скорости
- Если график скорости лежит выше оси времени, тело движется в направлении оси ОХ.
- Если график скорости лежит ниже оси времени, тело движется против оси ОХ.
- Если график скорости совпадает с осью времени, тело покоится.
Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.
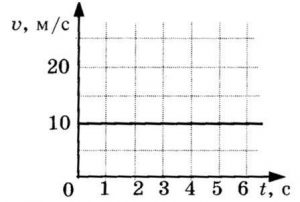
График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:
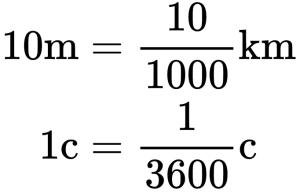
Теперь нужно разделить километры на часы:
![]()
Перемещение и координаты тела при равномерном прямолинейном движении
Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.
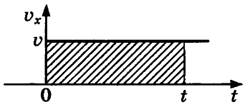
При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:
![]()
Вектор перемещения равен произведению вектора скорости на время движения:
![]()
Внимание!
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.
Формула проекции перемещения:
![]()
График проекции перемещения
График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:
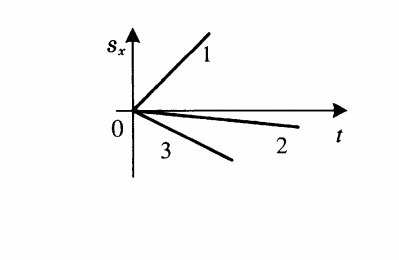
Определение направления движения по графику проекции перемещения
- Если луч лежит выше оси времени, тело движется в направлении оси ОХ.
- Если луч лежит ниже оси времени, тело движется против оси ОХ.
- Если луч совпадает с этой осью, тело покоится.
Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси sx.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси sx меньше.
График координаты
График координаты представляет собой график зависимости координаты от времени. Выглядит он так:
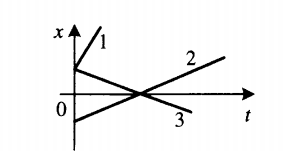
Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид:![]()
Определение направления движения тела по графику координаты
- Если с течением времени координата увеличивается (график идет снизу вверх), тело движется в направлении оси ОХ. На картинке выше этому соответствуют графики тел 1 и 2.
- Если с течением времени координата уменьшается (график идет сверху вниз), тело движется противоположно направлению оси ОХ. На картинке выше этому соответствует график тела 3.
- Если координата не изменяется, тело покоится.
Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.
Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.
Пример №2. График зависимости координаты тела от времени имеет вид:
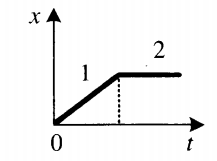
Изучите график и на его основании выберите два верных утверждения:
- На участке 1 скорость тела постоянна, а на участке 2 равна нулю.
- Проекция ускорения тела на участке 1 положительна, а на участке 2 — отрицательна.
- На участке 1 тело движется равномерно, а на участке 2 оно покоится.
- На участке 1 тело движется равноускорено, а на участке 2 оно движется равномерно.
- Проекция ускорения тела на участке 1 отрицательна, а на участке 2 — положительна.
На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?
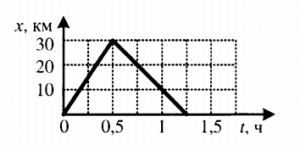
Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:
1,5 – 0,5 = 1 (час).
Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:
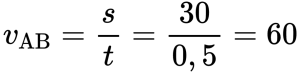
Скорость во время движения от В к А равна:
![]()
Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.
Задание EF17553
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…

Алгоритм решения
- Выбрать любой временной интервал.
- Выбрать для временного интервала начальные и конечные пути для каждого из графиков.
- Записать формулу скорости и вычислить ее для 1 и 2 тела.
- Найти n — отношение скорости второго тела к скорости первого тела
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
- Для графика 1: начальный путь s10 = 0 м. Конечный путь равен s1 = 80 м.
- Для графика 2: начальный путь s20 = 0 м. Конечный путь равен s2 = 120 м.
Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

Ответ: 1,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18768
На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.
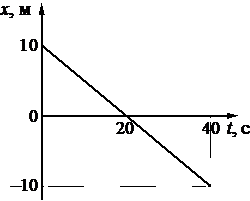
Какой из графиков соответствует зависимости от времени для проекции υx скорости этого тела на ось Ox?
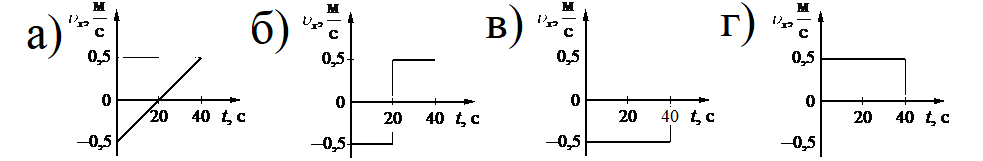
Алгоритм решения
- Записать уравнение координаты при равномерном прямолинейном движении.
- Выразить из уравнения проекцию скорости.
- Определить начальную и конечную координаты, а также время, в течение которого двигалось тело.
- Вычислить проекцию скорости.
- Выбрать соответствующий график.
Решение
Уравнение координаты при равномерном прямолинейном движении имеет вид:
![]()
Отсюда проекция скорости равна:
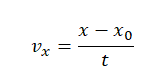
Начальная координата xo = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.
Вычисляем проекцию скорости:
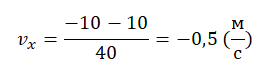
Этому значению соответствует график «в».
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18831
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50 с.

Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1 и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s1 и s2, а затем сложим их:

s1 + s2 = 100 + 100 = 200 (м)
Ответ: 200
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.6k
Как определить направление скорости
Скорость – характеристика движения тела, характеризующая быстроту его передвижения, то есть, расстояние, пройденное им за единицу времени. Этот параметр является векторным, а значит, имеет не только величину, но и направление. Определять направление скорости требуется в целом ряде физических задач.
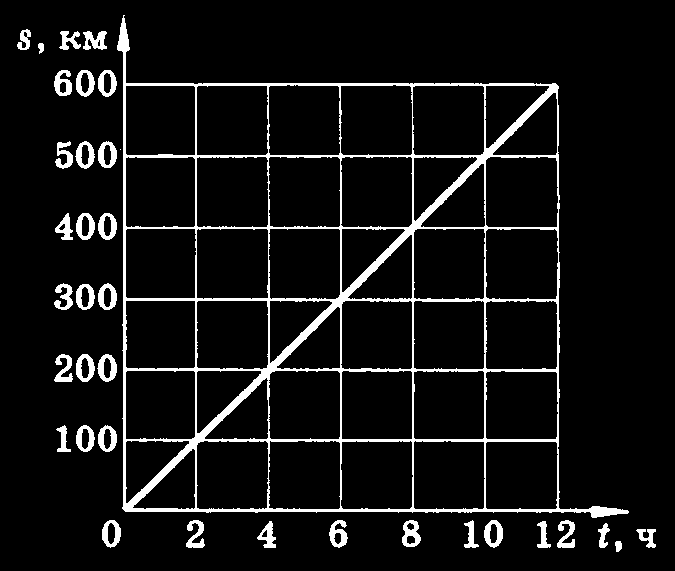
Инструкция
Скорость является одной из характеристик движения материальной точки. Она выражает расстояние, пройденное этой точкой за определенный промежуток времени. Различают среднюю и мгновенную скорость, а также равномерное и неравномерное движение.При равномерном движении скорость не меняется с течением времени, что облегчает определение направления этой скорости векторным путем. Вектор средней скорости представляет собой отношение приращения радиус-вектора к промежутку времени:[v]=?r/?tНаправление радиус-вектора ?r совпадает с направлением средней скорости, как показано на рис.1, поскольку точка перемещается из пункта М в пункт М1. Это условие соблюдается только при равномерном движении точки.
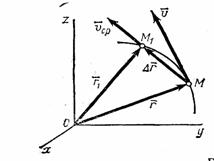
Мгновенная скорость рассчитывается при ?t, стремящемся к нулю. Это векторная величина, равная первой производной радиус-вектора по времени. Рассчитывается она следующим образом:v =|lim ?r/?t|=ds/dt
?t>0Вектор мгновенной скорости направлен по касательной к траектории движения MM1. Интегрируя последнее выражение по ds, получим:s=v?dt=v*(t2-t1)=v*tПоследняя формула применяется в случае равномерного движения, когда в условии задачи дан промежуток времени.
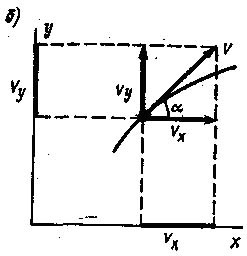
Направление скорости может быть вычислено только координатным способом, поскольку это – векторная величина.Если в задаче заданы координаты x и y, а также указаны указаны проекции vx и vy, может быть определено как численное значение скорости, так и ее направление. Вектор скорости v в данном случае является диагональю квадрата, образованного двумя проекциями. Вследствие этого, скорость равна:v= sqrt(vx^2+vy^2), где tg?=vx/vy (см. рис.2)Следует учитывать, что в реальных условиях на движущееся тело действует целый ряд факторов: трение, гравитация и т.п. В одних задачах действием этих факторов можно пренебречь, в других по крайней мере некоторые из них необходимо учитывать в обязательном порядке.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.
Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.
Будем отдельно рассматривать:
- движение без ускорения (равномерное), и
- движение с ускорением (неравномерное).
1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: (vec{a} =0).
2). Неравномерное движение — скорость меняется и появляется ускорение.
Пусть ускорение есть и, оно не изменяется: (vec{a} =const). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:
- Равноускоренное движение — скорость тела увеличивается.
- Равнозамедленное движение — скорость уменьшается.
Примечание: Когда изменяется скорость, всегда появляется ускорение!
Движение будем изображать графически, используя две перпендикулярные оси.
На графиках будем откладывать:
- по горизонтали — время в секундах.
- по вертикали — координаты тела, или проекции скорости и ускорения.
Для каждого вида движения получим три графика. Графики будем называть так:
- x(t) – зависимость координаты от времени;
- v(t) – зависимость проекции скорости от времени;
- a(t) – зависимость проекции ускорения от времени.
Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.
Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют
Пусть тело покоится на оси Ox – (рис 1а).
Точкой (x_{0}) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
[x=x_{0}]

Рис.1. Тело покоится, график координаты x(t) — горизонтальная прямая рис. б).
Скорость «v» и ускорение «a» — это прямые, лежащие на оси Ox. График скорости – рис. в). График ускорения – рис. г)
Скорость и ускорение неподвижного тела равны нулю:
[vec{v}=0]
[vec{a}=0]
Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.
Скорость не меняется — движение равномерное
Разберём равномерное движение в направлении оси (рис. 2а).
Начальная координата тела – это точка (x_{0}), а конечная координата — точка (x) на оси Ox. В точку «x» тело переместится к конечному времени «t».
Красной стрелкой обозначено направление, в котором тело движется.
Примечание: Тело движется туда, куда направлен вектор его скорости.

Рис.2. Тело движется равномерно в направлении оси Ox – рис а). Зависимость координаты от времени – это возрастающая прямая x(t) – рис. б). График скорости в) – это горизонтальная прямая, а график ускорения г) лежит на оси времени, так как ускорение равно нулю
Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).
Уравнение, описывающее изменение координаты выглядят так:
[ x = x_{0} + v cdot t ]
Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:
[ v = v_{0} = const ]
Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:
[ a = 0 ]
Равномерное движение в направлении противоположном оси
Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).

Рис.3. Тело движется равномерно противоположно направлению оси Ox – рис. а). Такому движению соответствуют: убывающая зависимость координаты от времени – рис б), отрицательная проекция скорости на ось – рис. в) и, нулевое ускорение – рис. г)
Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.
Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.
Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.
А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.
Равноускоренное движение в направлении оси, скорость увеличивается
Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.

Рис.4. Тело движется равноускорено – рис. а) по направлению оси Ox. Изменение координаты от времени x(t) описывается правой ветвью параболы – рис. б), график v(t) скорости изображен наклонной возрастающей прямой – рис. в), а график неизменного ускорения a(t) – рис. г) изображается горизонтальной прямой, лежащей выше оси времени
Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.
Уравнение, которое описывает квадратичное изменение координаты, выглядит так:
[ x = frac{a}{2}cdot t^{2} + v_{0} cdot t + x_{0} ]
Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:
[ v = v_{0} + a cdot t ]
Ускорение есть (рис. 4г) и оно не меняется:
[ a = const ]
Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.
Примечания:
1). Координата «x» будет изменяться:
- по линейному закону, когда скорость не меняется — остается одной и той же.
- по квадратичному закону, когда скорость будет изменяться (расти, или убывать).
2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.
3). Квадратичный закон – это уравнение второй степени, на графике — парабола.
4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.
Равноускоренное движение против оси
Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).
Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).

Рис.5. Тело движется равноускорено противоположно оси Ox – рис. а). Координата меняется параболически – рис. б), ветвь правая, так как скорость растет. Скорость — рис. в), и ускорение — рис. г), направлены против оси Ox, их графики лежат ниже оси времени
Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).
Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec{v}) и (vec{a}) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.
Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.
Скорость уменьшается — движение равнозамедленное
Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).

Рис.6. Тело движется равнозамедленно по оси Ox – рис. а), его координата растет по левой ветви параболы – рис. б), график скорости — убывающая наклонная прямая – рис. в), ускорение направлено против оси Ox, горизонтальный график ускорения — рис. г) лежит ниже оси времени
Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).
Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).
А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).
Равнозамедленное движение против оси
Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).
Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).

Рис.7. Тело движется равнозамедлено против оси Ox – рис. а), его координата убывает по левой ветви параболы – рис. б), скорость отрицательная и уменьшается к нулю, график скорости — наклонная прямая – рис. в), ускорение направлено по оси Ox, горизонтальный график ускорения — рис. г) лежит выше оси времени
Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).
Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.
Выводы
1). Все, что лежит:
- выше оси t – положительное;
- ниже оси t – отрицательное;
- на горизонтальной оси t – равно нулю.
2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).
3). Если скорость не меняется, ускорения нет.
- График x(t) координаты – это прямая линия.
- График v(t) скорости – горизонтальная прямая.
- График a(t) ускорения лежит на оси t.
4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.
- График x(t) координаты – это правая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.
- График x(t) координаты – это левая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
Скачать конспект “Использование графиков”
К_1.05 ИСПОЛЬЗОВАНИЕ ГРАФИКОВ
Содержание
§1. АНАЛИЗ ГРАФИКОВ КИНЕМАТИЧЕСКИХ ВЕЛИЧИН
– КАЧЕСТВЕННЫЕ ХАРАКТЕРИСТИКИ
Конспект – К_1.05 Использование графиков

1.1°. Определение характера движения – равномерное или не равномерное
Форма графика говорит нам о виде движения – равномерное или равно-переменное.

1.2°. Определение особых точек.
“Чтение” любого кинематического графика необходимо начинать с поиска “особых точек”. Такими точками являются точки пересечения с осями (в большинстве случаев), а так же точки перегибов и изломов.
Пересечение с вертикальной осью даст нам начальные значения параметров

Пересечение графика скорости с горизонтальной осью даст нам “точку остановки”

Перегибы и изломы так же позволяют определить где находится (на оси времени) точка остановки.

Мы много внимания уделяем точке остановки, так как это точка где происходит ИЗМЕНЕНИЕ характера движения.
Например, до точки остановки тело двигалось вверх, значит после точки остановки оно будет двигаться вниз, если до точки остановки тело двигалось замедленно, то после точки остановки тело будет двигаться ускоренно.
1.3°. Определение характера изменения скорости – ускоренное или замедленное. Правило ТРОЛЛЕЙБУСА.

Правило ТРОЛЛЕЙБУСА заключается в следующем:
– если тело приближается к точке остановки – оно замедляется
– если тело удаляется от точки остановки – оно ускоряется.
1.4° Направления вектора скорости и перемещения по графику КООРДИНАТЫ
Чтобы определить направление движения с помощью графика КООРДИНАТЫ необходимо отследить как изменяется координата с течением времени.

посмотреть анимацию
Например , если с течением времени координата уменьшается (Δx<0) , то это означает, что тело движется в направлении противоположном OX
1.5° Направления вектора скорости и перемещения по графику СКОРОСТИ
Чтобы определить направление движения с помощью графика СКОРОСТИ необходимо обратить внимание на то в какой полуплоскости находится график

Стрелки показывают куда смотреть
1.5° Направления вектора ускорения по графику КООРДИНАТЫ
Чтобы определить направление движения с помощью графика КООРДИНАТЫ необходимо отследить как направлены ветви графика,
если вверх – ускорение положительно
если вниз, ускорение отрицательно

1.6° Направления вектора ускорения по графику СКОРОСТИ
Что бы определить знак ускорения по графику СКОРОСТИ нужно вспомнить как определяется ускорение. А определяется оно следующим образом:

где Vx – конечная скорость, Vxo – начальная скорость тела
Следовательно, глядя на график скорости нам нужно отследить как ИЗМЕНЯЕТСЯ СКОРОСТЬ, а именно
если проекция скорости уменьшается – ускорение отрицательно.
если проекция скорости возрастает со временем – ускорение положительно.
На рисунке ниже ускорение отрицательно, так как V2x < V1x.

§2. АНАЛИЗ ГРАФИКОВ КИНЕМАТИЧЕСКИХ ВЕЛИЧИН
– КОЛИЧЕСТВЕННЫЕ ХАРАКТЕРИСТИКИ
2.1°. Определение перемещения по графику КООРДИНАТЫ
Проекция перемещения по графику координаты всегда определяется на основании формулы
|
|
(1.01) |
где Xк – конечная координата Xн – начальная координата движения

При этом не имеет значение насколько сложен график, является ли движение, равномерным или равнопеременным, замедленным или ускоренным и т.д. Посмотреть пример (анимация)
2.2°. Определение пути по графику КООРДИНАТЫ
Определение пути является более сложной операцией по сравнению с нахождением перемещения.
Что бы правильно найти путь на заданном участке движения необходимо понимать, что
- путь равен перемещению, только если направление движения не изменяется
- с течением времени путь только возрастает (путь это ДЛИНА траектории)
Соответственно, если дан график движения, состоящего из участков с различными направлениями, необходимо:
- разделить все движение на участки с одинаковым направлением движения (однородные участки).
- найти перемещение на каждом участке (по формуле 1.01).
- просуммировать модули всех перемещений.
Пример

В примере путь на всем участке движения будет определятся как
|
|
(1.02) |
2.3°. Определение перемещения по графику СКОРОСТИ
Значение перемещения определяется как ПЛОЩАДЬ ФИГУРЫ, одной из сторон которого является часть графика, одной стороной часть оси ОХ и двумя другими являются перпендикуляры опущенные из точек соответствующим заданным моментам времени.

В данном случае, на промежутке Δt перемещение будет равно площади трапеции

Пример более сложного случая
2.4°. Определение пути по графику СКОРОСТИ
Так же как и на графике координаты, разбиваем все движение на однородные участки (т.е. участки где движение однонаправленно).

Каждому участку при этом будет соответствовать своя площадь. Затем что бы найти путь сумируем все площади
|
|
(2.01) |
2.5° Определение скорости по графику КООРДИНАТЫ (для равномерного движения)

Что бы найти значение проекции скорости. Необходимо показать на графике некоторый промежуток времени Δt и соответствующее ему перемещение, тогда проекцию скорости можно будет найти как
|
|
(3.01) |
Отметим что это действие позволяет определить не только модуль проекции, но и ее знак, а значит и направление.
Отметим так же что отношение в формуле (3.01) не что иное как тангенс угла альфа.
|
|
(3.02) |
Следовательно угол наклона графика координаты при равномерном движении характеризует величину скорости тела. Чем боьше угол наклона (по отношению к горизонтали), тем больше скорость тела.
2.6° Определение ускорения по графику СКОРОСТИ
В с соответствии проекция ускорения может быть найдена как
|
|
(3.03) |
Поэтому что бы найти ускорение с помощью графика скорости, необходимо показать на графике промежуток времени Δt и соответствующее ему изменение скорости ΔV.

Их отношение и будет значением проекции вектора ускорения.
При нахождении изменения скорости принципиально ВАЖНО! отнимать от КОНЕЧНОГО значения НАЧАЛЬНОЕ, а не наоборот.
Из рисунка видно, что отношение a = ΔV / Δt это тангенс угла α. Таким образом, математическое понятие тангенса имеет в данном случае физический смысл БЫСТРОТЫ ИЗМЕНЕИЯ скорости.
|
|
(3.04) |
2.7° Построение уравнения движения по точкам графика КООРДИНАТЫ
Если мы располагаем информацией о конкретных точках графика (знаем координаты точек), мы можем построить уравнение движения соответствующее данному графику.
Идея заключается в том что бы РАСПИСАТЬ эти точки с помощью искомого уравнения движения.
Проиллюстрируем на примере.
Пусть дан следующий график

Для которого известны две точки А(4;2) и В(7;6) , а так же известно начальное значение координаты X0 = 0.
Подставим известные значения времени и координаты точки А в уравнение координаты и то же самое проделаем для точки В.
Получим следующую систему уравнений

Решая эту систему, найдем начальное значение проекции ускорения и скорости (ax= -5/12 , Vx = 29/12).
Следовательно уравнение координаты для заданного движения будет иметь вид

Голосование за лучший ответ
Аглая Шниц
Искусственный Интеллект
(115735)
3 года назад
направления скорости бывают разнообразные.
размерность задачи (1-, 2-, 3-хмерная)? дан график зависимости чего от чего?
DECMHENKOПрофи (717)
3 года назад

Аглая Шниц
Искусственный Интеллект
(115735)
ну, будем считать, что движение одномерное, по оси Ох
————о————->
1:
скорость постоянная -> равномерное движение
скорость отрицательная -> движение влево (в сторону уменьшения координат оси Ох)
2:
график наклонная прямая -> движение равноускоренное
до 1.25 с скорость положительная -> движение равнозамедленное вправо (в сторону увеличения координат оси Ох)
после 1.25 с скорость отрицательная -> движение равноускоренное влево (в сторону уменьшения координат оси Ох)
Константин Петров
Искусственный Интеллект
(150220)
3 года назад
пути математика неисповедимы – ВСЁ зависит от того, что математику захочется “доказать”
наиболее частый вариант = математик берет значение скорости ИЗ НЕВЕДОМОГО БУДУЩЕГО
в самом деле, поди проверь каково оно, это будущее
зато с математика взятки гладки
таков, например, ошибочный математический анализ
стоит взять ФАКТИЧЕСКИЕ ЗНАЧЕНИЯ скорости, как математический анализ тут же опровергается
так что….
NiemandИскусственный Интеллект (202930)
3 года назад
Костяня, нешто ты производные брать научилсо?!
Константин Петров
Искусственный Интеллект
(150220)
взять производную может любой дурак
даже Niemand
лично я про иное
производная = мошенничество
мошенники не смогли защитить ошибочный матанализ
только вот ты паскудишь иногда
Сергей Смолицкий
Искусственный Интеллект
(216209)
3 года назад
Если принять, что на изображенном графике Х – координата тела, то на кривой 2 тело неподвижно и находится в точке, отстоящей на 20 метров от начала координат в сторону, обратную положительному направлению движения. На графике 1 тело движется с постоянной скоростью, равной по модулю приблизительно 30 м/с в сторону, обратную положительному направлению движения. Точка начала движения имеет координату +33 м, через 1,1 сек тело миновало точку начала координат.







