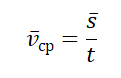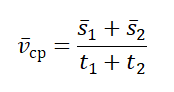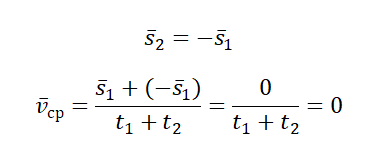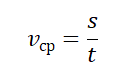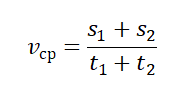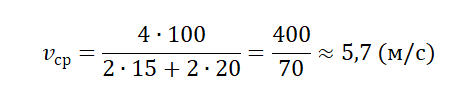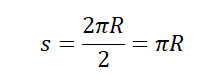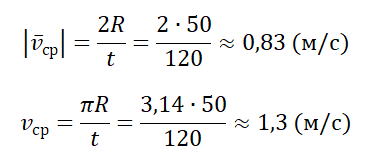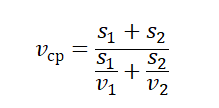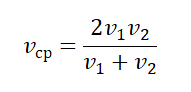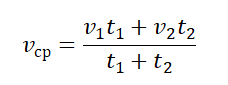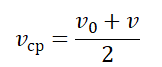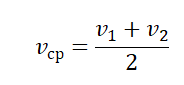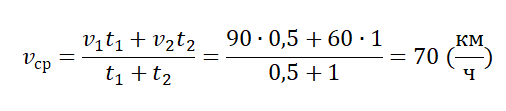Как найти направление средней скорости - Сайт, где вы сможете решить свои вопросы

Как определить направление скорости

Скорость – характеристика движения тела, характеризующая быстроту его передвижения, то есть, расстояние, пройденное им за единицу времени. Этот параметр является векторным, а значит, имеет не только величину, но и направление. Определять направление скорости требуется в целом ряде физических задач.

Инструкция

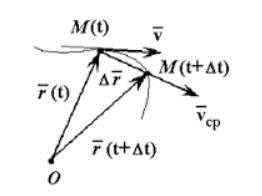
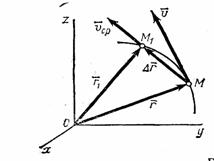
Скорость является одной из характеристик движения материальной точки. Она выражает расстояние, пройденное этой точкой за определенный промежуток времени. Различают среднюю и мгновенную скорость, а также равномерное и неравномерное движение.При равномерном движении скорость не меняется с течением времени, что облегчает определение направления этой скорости векторным путем. Вектор средней скорости представляет собой отношение приращения радиус-вектора к промежутку времени:[v]=?r/?tНаправление радиус-вектора ?r совпадает с направлением средней скорости, как показано на рис.1, поскольку точка перемещается из пункта М в пункт М1. Это условие соблюдается только при равномерном движении точки.

Мгновенная скорость рассчитывается при ?t, стремящемся к нулю. Это векторная величина, равная первой производной радиус-вектора по времени. Рассчитывается она следующим образом:v =|lim ?r/?t|=ds/dt
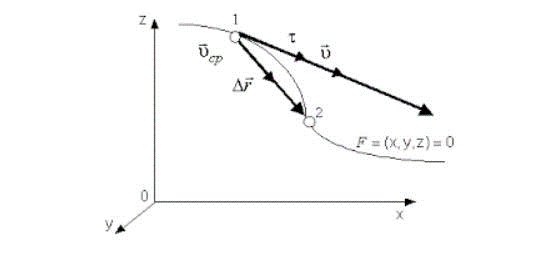
?t>0Вектор мгновенной скорости направлен по касательной к траектории движения MM1. Интегрируя последнее выражение по ds, получим:s=v?dt=v*(t2-t1)=v*tПоследняя формула применяется в случае равномерного движения, когда в условии задачи дан промежуток времени.

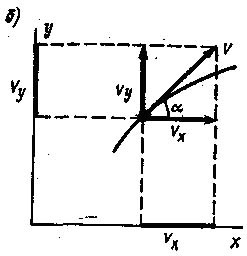
Направление скорости может быть вычислено только координатным способом, поскольку это – векторная величина.Если в задаче заданы координаты x и y, а также указаны указаны проекции vx и vy, может быть определено как численное значение скорости, так и ее направление. Вектор скорости v в данном случае является диагональю квадрата, образованного двумя проекциями. Вследствие этого, скорость равна:v= sqrt(vx^2+vy^2), где tg?=vx/vy (см. рис.2)Следует учитывать, что в реальных условиях на движущееся тело действует целый ряд факторов: трение, гравитация и т.п. В одних задачах действием этих факторов можно пренебречь, в других по крайней мере некоторые из них необходимо учитывать в обязательном порядке.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Определение

Скорость — это термин, который характеризует изменение заданной координаты в движении.

В ситуации, когда координаты изменяют свое положение относительно оси, следовательно, их материальная точка будет находится в процессе движения.

Средняя скорость — это величина векторного типа, которая имеет определенное числовое равенство относительно перемещения совершаемого в конкретную единицу времени, и направлена совместно я с векторным перемещением.

Средняя скорость – довольно простое понятие в разделе кинематика.

Определение

Следовательно, средняя скорость – это конкретная величина, которая равна отношению пройденного пути, к величине времени, за которое данный путь пройден телом.

[v_{mathrm{cp}}=frac{S}{t}]

Основные моменты, на которые следует уделить внимание при определении средней скорости:

Необходимое время, которое учитывается, когда тело в процессе движения может делать кратковременные остановки;
Определение правильной величины средней скорость тела, которое начинает движение в пункте А и оканчивает его в пункте В. Но в процессе движения, может повернуть несколько раз обратно, а затем снова продолжает движение в заданном направлении, двигаясь в пункт В.

Модуль для определения средней скорости движения вычисляется по следующей формуле: V=s/t.

Определение

Мгновенная скорость — это некий числовой предел, к которому стремится показатель средней скорости.

Мгновенная скорость, как правило, характеризует заданное движение точки в конкретный и определенный момент времени.

Для любой категории характерно бесконечное количество точек. Потому что каждый временной интервал включает в себя бесконечное количество мгновений.

Когда сам временной интервал стремится к нулевому значению, то он автоматически преобразуется в мгновение.

Формула

Мгновение скорости можно определить по следующей формуле: v=s/Δt
где:
v – скорость мгновения, м/с
s – движение, перемещение тела, м ( если Δt→0 )
Δt – временной интервал, который стремится к нулевому значению, с.

Стоит отметить, что мгновенная скорость – это величина, которая изображена как вектор. Она равняется отношению движения к временному интервалу. А именно: промежуток времени, за который данное перемещение происходит, при условии, что временной интервал стремится к нулевому значению.

Временной интервал движения тела – это всегда скляр с положительным значением. Поэтому мгновенная скорость и ее векторное значение, всегда сонаправлено с перемещением, которое имеет значение стремящееся к нулю.

Нет времени решать самому?

Наши эксперты помогут!

Направление и перемещение действия средней и мгновенной скорости относительно координатной оси

Средняя скорость всегда направлена вместе с перемещением:

Для мгновенной скорости характерно движение в конкретный момент времени.

Направление векторной скорости, которая обозначается как: υ расположено по касательной, относительно криволинейной траектории.

Так как непрерывное малое перемещение однозначно совпадает с бесконечно малым элементом траектории.

Примеры решения задач по определению мгновенной и средней скорости

Пример №1:

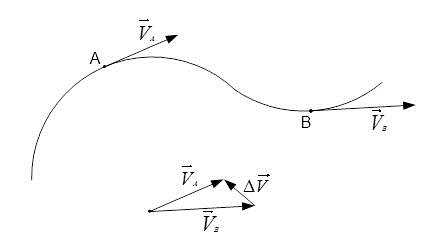
Имеет ли способность мгновенная скорость, изменять свое значение только относительно направления, при этом не меняя модульную величину.

Используя основные термины и формулы, решим данную задачу. При решении необходимо рассмотреть пример:

Движение тела происходит по криволинейной траектории. На ней необходимо обозначить начальный и конечный пункты, а именно: точки А и В.
Далее нужно обозначить основное направление мгновенной скорости в заданных ранее точках.
Следует помнить, что мгновенная скорость имеет направление относительно касательной по траектории.
Расстояние и скорость имеют одинаковые значения по модулю и, следовательно, равны 5 м/с.

[left|vec{V}_{A}right|=left|vec{V}_{B}right|=5 frac{м}{c}]

Следующее равенство вида: [vec{V}_{A}=vec{V}_{B}] будет неверным. Так как скорость – является векторной величиной. Поэтому очень важно задать не только числовое значение, но направление по которому будет осуществляться движение.

В случае, когда [vec{V}_{A}=vec{V}_{B}] можно составить равенство следующего вида:[vec{V}_{A}-vec{V}_{B}=0] однако определив вектор разности значений [Delta vec{V}], можно сделать вывод, что его значение не равно нулевому.

Следовательно, [vec{V}_{A} neq vec{V}_{B}], другими словами мгновенная скорость может быть равна нулевому значению и быть равной по модулю. Однако, при этом различаться по основному направлению движения.

Пример №2:

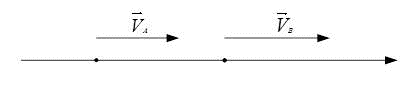
Возможно ли изменение по модульному значению мгновенной скорости, но при этом направление остается неизменным.

Алгоритм решения:

Рассмотрев рисунок, который приведен выше, можно сделать вывод, что:

в точке А и в точке В направление движения мгновенной скорости одинаково;
рассматриваемое тело, которое осуществляет движение, делает это с равным ускорением, следовательно:

[vec{V}_{A}=vec{V}_{B}]

Источник

Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.

Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.

Средняя векторная скорость

Определение и формулы

Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.

v_ср — средняя векторная скорость, s — перемещение тела, совершенное за время t

Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.

Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:

Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.

Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:

Средняя скалярная скорость

Определение и формулы

Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.

v_ср — средняя путевая скорость, s — путь, пройденный телом за время t

Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:

Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.

У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:

Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:

v_ср=v_ср, если путь равен модулю перемещения. Так бывает в случае равномерного прямолинейного движения.
v_ср>v_ср, если путь больше модуля перемещения. Так бывает в случае неравномерного прямолинейного или любого криволинейного движения.

Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.

Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:

Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:

Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:

Полезные советы и формулы

Если известны значения отдельных участков пути и скорости на этих участках, средняя скорость равна:

Если известны скорости на первой и второй половине пути (s₁=s₂), средняя скорость равна:

Если известно время прохождения отдельных участков пути и скорости движения на этих участках, средняя скорость равна:

Если тело движется прямолинейно и равноускорено, его средняя скорость равна половине суммы начальной и конечной скорости:

Если известны скорости тела за равные промежутки времени, его средняя скорость равна:

Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.

Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:

Алиса Никитина | Просмотров: 5.6k

Источник

Физическое понятие «скорость» является неоднозначным термином: зависимость от расстояния и времени позволяет ввести два понятия скорости, так как в физике используются векторные (перемещение) и скалярные (модуль перемещения, пройденный путь, время) величины.

1. Отношение вектора перемещения (vec{S}) к интервалу времени (Delta{t}) определяет среднюю (по времени) скорость:

(vec{v}_{ср}=frac{vec{S}}{Delta{t}}) ((1)).

Направление вектора средней (по времени) скорости определяется согласно математической формуле ((1)) определения данной физической величины (сравни математическое выражение (vec{a}) (=) (frac{vec{b}}{2}) и формулу ((1))):

Длина вектора (vec{v}_{ср}) не связана с длиной вектора (vec{S}), так как данные физические величины имеют разные размерности (единицы измерения).

Числовое значение данной физической величины в случае равномерного прямолинейного движения является постоянным (рис. (1)):

υx=const

.

Примечание: «const» — «постоянный» (сокращение от латинского).

Рис. (1). Изменение координаты точки при равномерном движении

2. При движении тела с постоянной скоростью и его возврате в исходное положение с той же скоростью значение средней (по времени) скорости будет равно нулю.

Отношение пути (l) (длины траектории) к интервалу времени (Delta{t}) определяет средний модуль скорости (среднюю путевую скорость):

(overline{v}=frac{l}{Delta{t}}) ((2)).

Обозначение: черта над символом ((overline{v})) обозначает среднее значение этой величины.

Именно физическое понятие «средняя путевая скорость» используется при описании движения в ситуациях следующего типа: «спортсмен/турист… пробежал/прошёл… дистанцию/расстояние… со средней скоростью <…> м/с».

Источники:

Источник

Средняя скорость при равноускоренном движении

Чтобы определить среднюю путевую скорость, нужно разделить весь путь на все время. Это справедливо и для равноускоренного движения. Модуль средней скорости по перемещению определяется как модуль перемещения, деленный на все время движения. Также перемещение – векторная величина, и имеет направление, следовательно, можно определить и угол, под которым средняя скорость будет направлена к горизонту.

Задача 1. Тело падает без начальной скорости с высоты м. Найти среднюю скорость падения на второй половине пути.

Чтобы определить среднюю скорость, нужно разделить путь, пройденный телом, на время его движения.

Длина первой половины пути – .

Тогда можно записать, что , где – время прохождения телом первой половины пути, его можно найти:

Полное время падения тоже легко определить:

Тогда определим время, за которое тело прошло вторую половину пути:

Определим среднюю скорость:

Ответ: средняя скорость на второй половине пути равна 25,6 м/c.

Задача 2. Тело брошено со скоростью м/с вертикально вверх с высоты м над поверхностью земли. Определить среднюю скорость и среднюю путевую скорость за время полета.

Так как найти надо среднюю путевую и среднюю скорость по перемещению, то необходимо знать как путь, так и перемещение тела. Очевидно, что точку старта и точку финиша тела разделяет высота , с которой тело было сброшено, так как в конце оно окажется на земле. Итак, – это перемещение тела.

Чтобы определить путь, потребуется найти высоту, до которой тело смогло подняться. Путь тела тогда будет равен

Максимальная высота подъема тела равна , следовательно,

Также для определения средней скорости надо знать время движения тела. Это время будет складываться из времени взлета и времени падения .

Время взлета найдем из условия равенства нулю скорости тела:

Время падения тоже легко определить, зная, что тело падало с высоты :

Теперь, зная время взлета и время падения, можем определить общее время движения тела:

Осталось разделить путь на это время – и получим среднюю путевую скорость:

Средняя скорость по перемещению равна (или модуль средней скорости):

Задача 3. Мячик брошен с высоты м над поверхностью земли с начальной скоростью м/с под углом к горизонту. Найти модуль и направление его средней скорости за все время полета.

В этой задаче необходимо, по сути, определить вектор средней скорости тела по перемещению: его длину (модуль) и направление. Очевидно, для этого потребуется знать, как далеко тело улетело и сколько на это понадобилось времени. Мы помним, что проекция скорости тела на горизонтальную ось остается неизменной во времени и равной . Если удастся найти время полета тела – то мы узнаем, как далеко оно шлепнулось о землю.