Как найти направление тока в резисторе

Чтобы сформулировать закон Кирхгофа для электрической цепи, потребовалось ввести новые термины в теорию – узлы, ветви и контур. Ветвями называют любой тип двухполюсной цепи. Узлом называют точку, в которой соединяются несколько ветвей. Эти элементы принадлежат одному электрическому контуру. Законы представляют собой различные соотношения между величинами тока на разных участках цепи. С их помощью можно провести расчет величины постоянных или переменных токов при помощи формул, созданный этим ученым.

В данной статье будет рассказано про законы Кирхгофа, как они могут использоваться на практике и как правильно провести расчеты, связанные с ними.

Законы Кирхгофа

Закон Ома устанавливает зависимость между силой тока, напряжением и сопротивлением для простейшей электрической цепи, представляющей собой один замкнутый контур. В практике встречаются более сложные (разветвленные) электрические цепи, в которых имеются несколько замкнутых контуров и несколько узлов, к которым сходятся токи, проходящие по отдельным ветвям. Значе­ния токов и напряжений для таких цепей можно находить при помощи законов Кирхгофа.

Первый закон

Первый закон Кирхгофа устанавливает зависимость между то­ками для узлов электрической цепи, к которым подходит несколько ветвей. Согласно этому закону алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:

?I = 0 (16)

При этом токи, направленные к узлу, берут с одним знаком (например, положительным), а токи, направленные от узла,— с противоположным знаком (отрицательным). Например, для узла А

I1 + I2 + I3 – I4 – I5 = 0 (17)

Преобразуя это уравнение, получим, что сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла:

I1 + I2 + I3 = I4 + I5 (17′)

В данном случае имеет место полная аналогия с распределением потоков воды в соединенных друг с другом трубопроводах.

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.

Второй закон Кирхгофа устанавливает зависимость между э. д. с. и напряжением в замкнутой электрической цепи. Согласно этому закону во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур:

?E = ?IR (18)

При составлении формул, характеризующих второй закон Кирхгофа, значения э. д. с. E и падений напряжений IR считают положительными, если направления э. д. с. и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления э. д. с. и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие э. д. с. и падения напряжения считают отрицательными.

Рассмотрим в качестве примера электрическую цепь, в которой имеются два источника с электродвижущими силами E1 и E2, внутренними сопротивлениями Ro1, Ro2 и два приемника с сопротивлениями R1 и R2. Применяя второй закон Кирхгофа для «этой цепи и выбирая направление ее обхода по часовой стрелке, получим:

E1 – E2 = IR01 + IR02 + IR1 + IR.

При этом э. д. с. E1 и ток I совпадают с выбранным направлением обхода контура и считаются положительными, а э. д. с. Е2, противоположная этому направлению, считается отрицательной. Если в электрической цепи э. д. с. источников электрической энергии при обходе соответствующего контура направлены навстречу друг другу (см. рис. 24, а), то такое включение называют встречным. В этом случае на основании второго закона Кирхгофа ток I = (E1-E2)/(R1+R2+R01+R02).

Встречное направление э. д. с. имеет место, например, на э. п. с.при включении электродвигателей постоянного тока (их можно рассматривать как некоторые источники э. д. с.) в две параллельные группы, а также при параллельном включении аккумуляторов в батарее.

Если же э. д. с. источников электрической энергии имеют по контуру одинаковое направление (рис. 24, б), то такое включение называют согласным и ток I = (E1-E2)/(R1+R2+R01+R02). В некоторых случаях такое включение недопустимо, так как ток в цепи резко возрастает.

Если в электрической цепи имеются ответвления (рис. 24, в), то по отдельным ее участкам проходят различные токи I1 и I2. Согласно второму закону Кирхгофа E1-E2=I1R01+I1R1-I2R2-I2R02-I2R3+I1R4.

При составлении этого уравнения э. д. с. Е1 и ток I1 считаются положительными, так как совпадают с принятым направлением обхода контура, э. д. с. Е2 и ток I2 — отрицательными.

Алгебраическая сумма разностей потенциалов.

Закон напряжения по Густаву Кирхгофу — второй закон этого автора, используемый для анализа электрической схемы. Вторым законом Кирхгофа утверждается, что для последовательного замкнутого контура алгебраическая сумма всех напряжений по кругу любой замкнутой цепи равна нулю. Утверждение обусловлено тем, что контур цепи является замкнутым проводящим путём, где потери энергии исключаются. Другими словами, алгебраическая сумма разностей потенциалов замкнутого контура теоретически равняется нулю:

ΣV = 0

Следует обратить внимание: под термином «алгебраическая сумма» имеется в виду учёт полярностей и признаков источников ЭДС, а также падения напряжений по кругу контура. Эта концепция закона Кирхгофа, известная как «сохранение энергии», как движение по кругу замкнутого контура или схемы, утверждает логику возврата к началу цепи и к первоначальному потенциалу без потери напряжения по всему контуру.

Следовательно, любое падение напряжения по кругу контура теоретически равно потенциалу любых источников напряжения, встречающихся на этом пути.

Отсюда следует вывод: применяя Второй закон Кирхгофа к определенному элементу электрической схемы, важно обращать особое внимание на алгебраические знаки падений напряжения на элементах (источниках ЭДС), иначе вычисления оборачиваются ошибкой.

Одиночный контурный элемент — резистор

Простым примером с резистором предположим — ток протекает в том же направлении, что и поток положительного заряда. В этом случае поток тока через резистор протекает от точки A до точки B. Фактически — от положительной клеммы до отрицательной клеммы. Таким образом, поскольку движение положительного заряда отмечается в направлении аналогичном направлению течения тока, на резистивном элементе зафиксируется падение потенциала, которое приведет к падению минусового потенциала на резисторе (— I * R).

Если же поток тока от точки B до точки A протекает в противоположном направлении относительно потока положительного заряда, тогда через резистивный элемент отметится рост потенциала, поскольку имеет место переход от минусового потенциала к потенциалу плюсовому, что даёт падение напряжения (+ I * R). Таким образом, чтобы правильно применить закон Кирхгофа по напряжению к электрической цепи, необходимо точно определить направление полярности. Очевидно, знак падения напряжения на резисторе зависит от направления тока, протекающего через резистор.

Направление потока тока по замкнутому контуру допустимо определять либо по часовой стрелке, либо против часовой стрелки, и любой вариант допустим к выбору. Если выбранное направление отличается от фактического направления тока, соответствие закону Кирхгофа получится корректным и действительным, но приведет к результату, когда алгебраический расчёт будет иметь знак минус. Чтобы лучше понять эту концепцию, логично рассмотреть ещё один пример с одним контуром цепи на соответствие Второму Закону Кирхгофа.

Одиночный контур электрической цепи

Второй закон Кирхгофа утверждает — алгебраическая сумма разностей потенциалов любого замкнутого контура равна нулю. Демонстрационная схема действия Второго закона Кирхгофа для замкнутого контура с двумя резисторами и одним источником ЭДС. Если принять условие, что два резистора R1 и R2 соединены последовательно, оба элемента являются частью одного контура. Соответственно, одинаковый ток протекает через каждый из резисторов.

Таким образом, падение напряжения на резисторе R1 = I * R1 и падение напряжения на резисторе R2 = I * R2, дают напряжение по Второму закону Кирхгофа:

V = I * Rs

где: Rs = R1 + R2.

Очевидно: применение Второго закона Кирхгофа к одиночному замкнутому контуру даёт формулу эквивалентного или полного сопротивления для последовательной цепи. Допустимо расширить эту формулу, чтобы найти значения падений потенциалов по кругу контура:

I = V / Rs

Vr1 = V * (R1 / R1 + R2)

Vr2 = V * (R2 / R1 + R2)

Есть три резистора номинальным сопротивлением 10, 20, 30 Ом, соответственно. Все три резистивных элемента соединены последовательно к 12-вольтовому аккумулятору.

Требуется рассчитать:

• общее сопротивление,
• ток цепи,
• ток через каждый резистор,
• падение напряжения на каждом резисторе.

Рассчитаем общее сопротивление:

Ro = R1 + R2 + R3  =  10Ω + 20Ω + 30Ω = 60Ω

Ток цепи:

I = V / Ro = 12 / 60 = 0,2A (200 мА)

Ток через каждый резистор:

I * R1 = I * R2 = I * R3 = 0,2A (200 мА)

Падение потенциала на каждом из резисторов:

VR1 = I * R1 = 0.2 * 10 = 2В

VR2 = I * R2 = 0.2 * 20 = 4В

VR3 = I * R3 = 0.2 * 30 = 6В

Таким образом, Второй закон Кирхгофа справедлив, учитывая что индивидуальные падения напряжения, отмеченные по кругу замкнутого контура, в итоге составляют сумму напряжений.

Вывод

Теория второго закона Кирхгофа, также известного как закон сохранения потенциала, особенно полезна для работы с последовательными схемами. Последовательные схемы действуют как делители потенциала, а цепь делителя потенциала — это важный узел многих электрических (электронных) схем.

Второй закон

Для расчетов сложных электрических цепей с несколькими источниками энергии используют второй закон Кирхгофа, который может быть сформулирован так: во всяком замкнутом электрическом контуре алгебраическая сумма всех э. д. с. равна алгебраической сумме падений напряжения в сопротивлениях, включенных последовательно в эту цепь, т. е.

E1 + E2 + E3 + . . . = I1r1 + I2r2 + I3r3 + . . .

При этом положительными следует считать э. д. с. и токи, направление которых совпадает с направлением обхода контура.
Если в электрическую цепь включены два источника энергии, э. д. с. которых совпадает по направлению (рис. 20, а), то э. д. с. всей цепи равна сумме э. д. с. этих источников, т. е. E = E1 + E2. Если же в цепи э. д. с. источников имеют противоположные направления, то результирующая э. д. с. равна разности э. д. с. этих источников, т. е.

E = E1 – E2.

При последовательном включении в электрическую цепь нескольких источников энергии с различным направлением э. д. с. общая э. д. с. равна алгебраической сумме э. д. с. всех источников. При суммировании э. д. с. одного направления берут со знаком плюс, а э. д. с. противоположного направления — со знаком минус. При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.

Замкнутая цепь обозначена буквами а, б, в и г. Ввиду наличия ответвлений в точках а, б, в, г токи I1, I2, I3 и I4, отличаясь по силе, могут иметь различные направления.
Для такой цепи в соответствии со вторым законом Кирхгофа можно написать:

E1 – E2 – E3 = I1(r01 + r1) – I2(r02 + r2) – I3(r03 + r3) + I4r4,

где r01, r02, r03 — внутренние сопротивления источников энергии,
r1, r2, r3, r4 — сопротивления приемников энергии.
В частном случае при отсутствии ответвлений и последовательном соединении проводников общее сопротивление равно сумме всех сопротивлений.
Если внешняя цепь источника энергии с внутренним сопротивлением r состоит, например, из трех последовательно соединенных проводников с сопротивлениями, соответственно равными r1, r2, r3, то на основании второго закона Кирхгофа можно написать следующее равенство:

E = I r + I r1 + I r2 + I r3.

При нескольких источниках тока в левой части этого равенства была бы алгебраическая сумма э. д. с. этих источников.

Друзья, не забывайте подписываться на обновления блога, ведь чем больше читателей подписано на обновления, тем больше я понимаю что  делаю что-то важное и полезное и это чертовски мотивирует на новые статьи и материалы.

Решение. 1. Обозначим стрелками токи, проходящие через каждый резистор с учетом их направления

1. Обозначим стрелками токи, проходящие через каждый резистор с учетом их направления. (рисунок 13 а).

2. Определим общее эквивалентное сопротивление цепи, метод подсчета которого для цепи со смешанным соединением резисторов сводится к последовательному упрощению схемы.

Сопротивления R ₂ и R ₃ соединены параллельно Найдем общее сопротивление при таком соединении:

приводя к общему знаменателю, получим

Схема имеет вид 13б . Теперь резисторы R_{23 ,} R_{1 ,} R_4. соединены последовательно, их общее сопротивление

Это общее сопротивление, включенное в цепь вместо четырех сопротивлений ( рисунок 13в ) при таком же значении напряжения не изменит тока в цепи. Поэтому сопротивление чаще называется общим эквивалентным сопротивлением цепи.

3. По закону Ома для внешнего участка цепи определим ток

4. Найдем токи, проходящие через все резисторы. Через резистор R _I, проходит ток I _I =1 А. Через резистор R ₄ проходит ток I ₄ = 1 А

Для определения токов, проходящих через резисторы, R ₂ и R ₃, нужно найти напряжение на параллельном участке U ₂₃. Это напряжение можно определить двумя способами:

U ₂₃ = I· R₂₃ = 11·6 = 66 В или

По закону Ома для параллельного участка цепи найдем

I ₂ = U ₂₃ / R₂ = 66 / 10 = 6,6 А, I ₃ = U ₂₃ / R₃ = 66 / 15 = 4,4 А или, применяя первый закон Кирхгофа, получим

I ₃ = I — I ₂ = 11 — 6,6 = 4,4 А

5. Найдем общую мощность цепи:

Р = U ·I = 110 · 11 = 1210 Вт = 1,21 кВт

6. Определим расход энергии:

W = Р· t = 1,21 · 10 = 12,1 кВт ч ·

7. Выполним проверку решения задачи описанными ранее способами:

а) проверим баланс мощности

11 2 · 3 +6,6 2 ·10 + 4,4 2 ·15 + 11 2 · 1 = 1210 Вт

б) для узловой точки а применим первый закон Кирхгофа:

в) составим уравнение по второму закону Кирхгофа, обходя контур цепи по часовой стрелке,

3.2 Указания к решению задачи 2

Решение этой задачи требует знания основных понятий об однофазном переменном токе, мгновенных и действующих значений токов, напряжений и ЭДС, периоде и частоте изменений переменных синусоидальных величин, начальной фазе и сдвиге фаз между током и напряжением . Необходимо также понимать физические процессы в неразветвленных цепях однофазного тока с последовательным соединением активного, индуктивного и емкостного сопротивлении, знать формулы для расчета таких цепей.

Индексы буквенных обозначений в задачах соответствуют индексам сопротивлений. Так, например Р _I – активная мощность первого сопротивления; U _А1 – напряжение на первом активном сопротивлении; U _L2 — напряжение на втором индуктивном сопротивлении и т. д.

Рассмотрим пример по расчету неразветвленных цепей переменного тока.

Задача

В неразветвленной цепи переменного тока с сопротивлениями (рисунок 14) R ₁ = R ₂ = 2 Ом, Х _L1 = 4 Ом , Х _L2 = 5 Ом, Х _С1 = 4 Ом,

Х _С2 =2 Ом, подведенное напряжение U = 220 В.

Определить: Z (полное сопротивление цепи), Сos φ, Sin φ, S, P

и Q (полную, активную и реактивную мощности), I (ток цепи). Построить в масштабе векторную диаграмму.

Дата добавления: 2015-04-16 ; просмотров: 6 ; Нарушение авторских прав

Источник

Все про резисторы

Резистор – это самая распространенная деталь в электронике. Он гасит лишнее напряжение, ограничивает ток, изменяет и фильтрует сигналы. Резисторы применяются везде, от процессоров, где их миллионы, до энергетических систем. где их размеры с напольный шкаф.

Свойства в теории и практике

Основное свойство этой радиодетали – это сопротивление. Измеряется в омах (Ом).

Разберем для начала понятие активного сопротивления. Оно так называется потому, что есть у всех материалов (даже у сверхпроводников, пусть и 0,00001 Ом). И именно оно является основным у резисторов.

Что говорит теория

В теории у резистора есть постоянное сопротивление, которое на зависит от внешних условий (температуры, давления, напряжения и т.п.).

График зависимости тока от напряжения прямолинеен.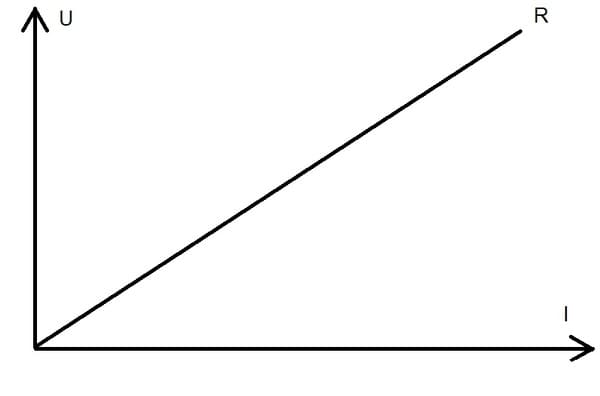

В идеальных и математических условиях у резистора только активное сопротивление. По типам бывают нелинейные и линейные резисторы.

Что на самом деле

На самом у всех резисторов непрямолинейная зависимость тока от напряжения. То есть, его сопротивление тоже зависит от внешних условий, конкретно от температуры.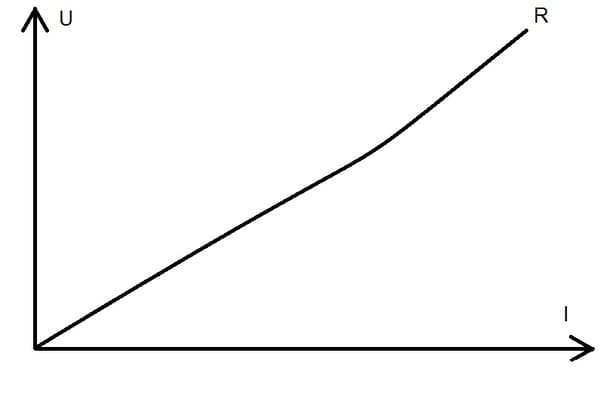

Конечно, эта зависимость не такая, как у полупроводников, но она есть. И самое главное, у этой радиодетали есть емкость и индуктивность. Помимо активного сопротивления, есть еще и реактивное.

Реактивное сопротивление отличается от активного тем, что оно по разному пропускает электрический ток на разных частотах.

Например, для постоянного тока сопротивление 200 Ом, а если есть высокие значения индуктивности, то на частотах выше 2 кГц, сопротивление будет уже 250 Ом.

Еще существует специальные типы резисторов с более выраженной нелинейной вольт-амперной характеристикой. Если у обычных резисторов вольт-амперный график чуть-чуть не линейный, то у такого типа деталей он лавинообразный.

У них сопротивление резко зависит от внешних условий, не так. как у обычных:

• Терморезистор. Повышает или понижает сопротивление из-за влияния температуры;
• Варистор. Изменяет свои свойства в зависимости от приложенного напряжения;
• Фоторезистор. Уменьшается сопротивление, если на него действует свет;
• Тензорезистор. При деформировании (сжатии, механических воздействиях) изменяет свое сопротивление.

Кроме того, еще одна особенность активного сопротивления – выделение тепла, когда проходит электрический ток. Когда протекает электрический ток замкнутой цепи, электроны ударяются об атомы. И поэтому выделяется тепло. Тепло измеряется в мощности. Она рассчитывается исходя из напряжения и тока.

Одна из популярных функций резисторов это снижение напряжения и ограничения тока. Например, если через резистор проходит ток 0,25 А и на нем есть падение напряжения 1 В, то мощность, которая будет на нем рассеиваться это 0,25 Вт.

И из-за этого и существуют резисторы с разной рассеиваемой мощностью. Нельзя ставить резистор 0,125 Вт на место 1 Вт. Он начнет греться, трескаться, чернеть. А потом и сгорит. Потому, что не рассчитан на такую мощность.

Обозначения на схемах

На схемах в Европе и СНГ обознается прямоугольником и латинской букой R. Согласно ГОСТу, на отечественных схемах не указывается номинал сопротивления, а только номер детали (R). Однако, если под изображением детали указано число, например 120, оно по умолчанию читается как 120 Ом.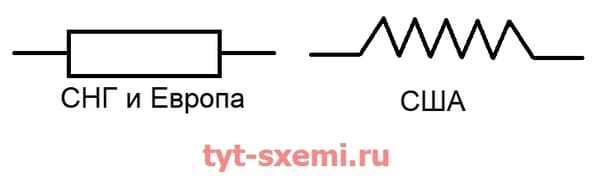

В таблице примеры обозначений детали.

Основное обозначение
0,125 Вт
0,25 Вт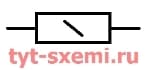
0,5 Вт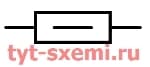
1 Вт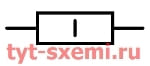
2 Вт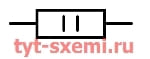
5 Вт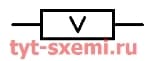
Переменный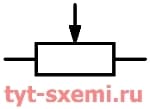
Подстроечный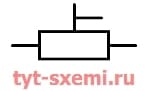

Типы включения и примеры использования

Основные типы включения это последовательные и параллельные соединения.

Последовательно сопротивление рассчитывается просто. Достаточно все сложить.

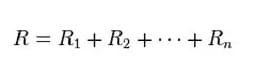
При последовательном соединении напряжение распределяется по резисторам согласно их сопротивлениям.

Это второе правило Кирхгофа. Например, напряжение 12 В, а пара резисторов по 1 кОм.

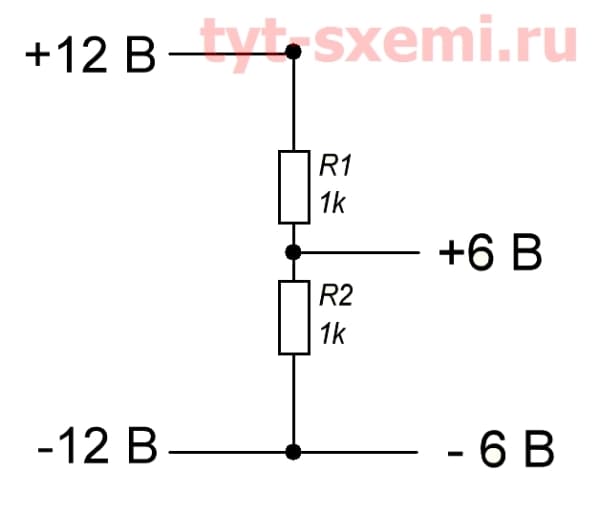
Соответственно, на каждом из них по 6 В. Это простой пример делителя напряжения. Здесь пара деталей делит напряжение, и благодаря этому можно получить необходимое напряжение.

Однако, если вы хотите использовать делитель напряжения для питания цепи, то должны помнить, что нужно согласовать сопротивления. В этой схеме сопротивление 1 кОм. Если вы подключите к ней нагрузку меньше этого сопротивления, то она не получит напряжения на свои выводы в полном объеме. Поэтому, все схемы с делителями напряжения должны быть рассчитаны и согласованы друг с другом.

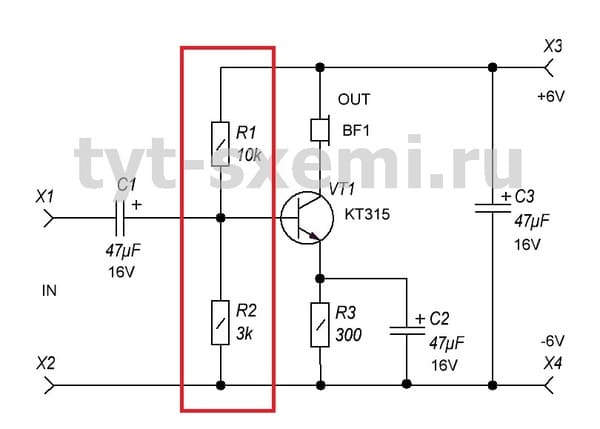Здесь R1 и R2 образуют делитель напряжения, они выполняют роль делителя напряжения. Между этими двумя резисторами и базой транзистором протекает ток, который открывает транзистор.

Это необходимо для того, чтобы он работал без искажений.

Параллельное включение

При параллельном соединении радиодеталей, общее сопротивление цепи снижается. Если два резистора по 1 кОм соединены параллельно, то общее будет равно меньше 0,5 кОм, т.е. сопротивление цепи (эквивалентное) равно половине самого наименьшего.

В таком соединении наблюдается первое правило Кирхгофа. В точку соединения направляется ток в 1 А, а в узле он расходится на два направления по 0,5 А.

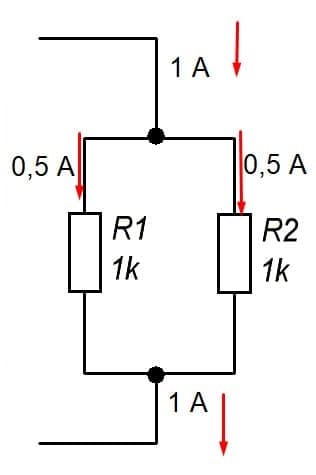
Формулы расчета

Для двух резисторов: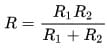

Для более: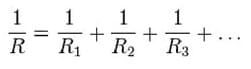

Для тока параллельное соединение — это как вторая дорога или обходной путь. Еще такой тип соединения называют шунтированием. В качестве примера можно привести амперметр. Чтобы увеличить его шкалу показаний, достаточно подключить параллельно резистору еще один шунтирующий.

Его сопротивление рассчитывается по формуле:

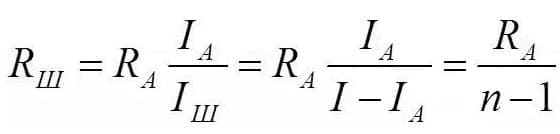
Эквивалентное соединение

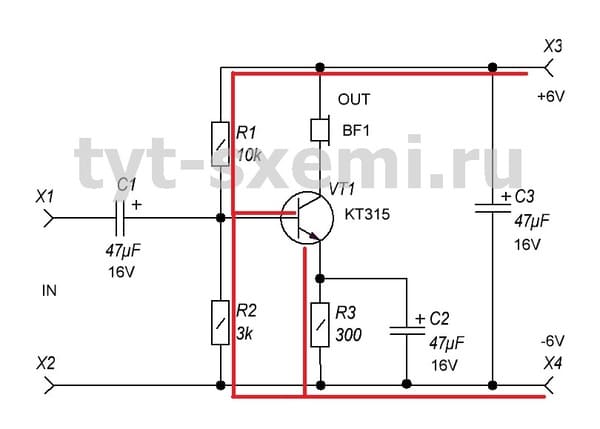
В схеме усилителя к эмиттеру транзистора VT1 подключена пара из резистора R3 и конденсатора C2.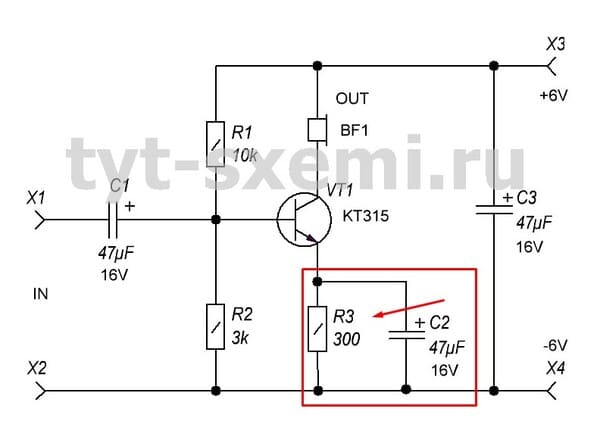

В этом случае VT1 и R3 подключены последовательно друг к другу. Зачем это надо? Когда усилитель работает, транзистор начинает нагреваться и его сопротивление снижается. R3, как и в случае со светодиодом, не позволяет транзистору перегреваться. Он балансирует общее сопротивление, чтобы транзистор не вносил искажения в сигнал. Это называется режим термостабилизации.

А конденсатор C2 подключен к R3 параллельно. И это нужно для того, чтобы при нормальном режиме работы усилителя, переменный сигнал прошел без потерь. Так работает параллельный фильтр.

Фильтры и резисторы

С помощью резисторов и конденсаторов можно делать фильтры. Так называются RC фильтры.

Эта пара может разделять сигнал на постоянные и переменные составляющие.

В качестве примера рассмотрим ФНЧ и ФВЧ.

В схеме фильтра низких частот конденсатор C1 забирает на себя высокочастотные токи. Его сопротивление для них намного меньше, чем у нагрузки. Он шунтирует нагрузку. Таким образом, можно получить низкую частоту, отделив от нее все высокие составляющие.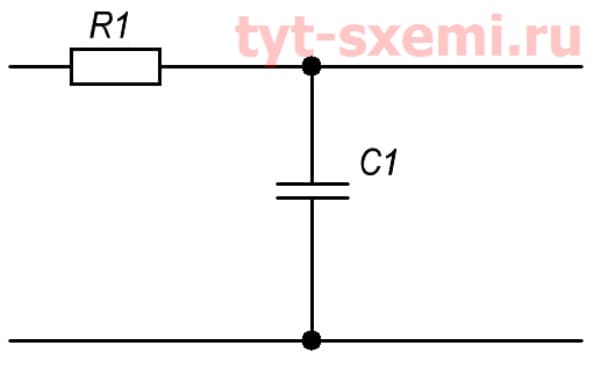
В фильтре высоких частот наоборот. Высокие частоты свободно проходят через C1, и если в сигнале есть низкочастотные, то они пойдут через R1.

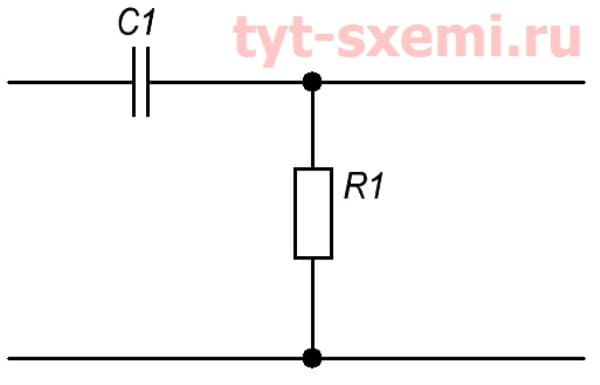
Такие фильтры бывают разные по конструкции. П образные, Г образные и т.п. Конкуренцию резистору может составить катушка индуктивности или дроссель. У них меньше активное сопротивление, но реактивное больше. Благодаря этому снижаются потери от активного сопротивления.

Источник

Последовательное и параллельное соединение

Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей — проводников.

Для начала давайте вспомним, что такое проводник? Проводник — это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:

формула сопротивление проводника

ρ – это удельное сопротивление, Ом × м

R – сопротивление проводника, Ом

S – площадь поперечного сечения, м 2

l – длина проводника, м

Более подробно об этом я писал здесь.

Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.

Последовательное соединение проводников

Сопротивление при последовательном соединении проводников

Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

последовательное соединение резисторов

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

формула при последовательном соединении резисторов

Пример

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

Решение

То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор R_AB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор R_AB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R₁ , R₂ , R₃ , то получится, что через них течет та же самая сила тока, которая текла через резистор R_AB .

сила тока через последовательное соединение проводников

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R₁ течет такая же сила тока, как и через резистор R₂ и такая же сила тока течет через резистор R₃ .

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае R_AB =R₁ + R₂ + R₃ = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения U_R1 , U_R2 , U_R3 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.

параллельное соединение резисторов

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление R_AB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников

Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.

Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что

Если бы у нас еще были резисторы, соединенные параллельно, то для них

В этом случае, сила тока в цепи будет равна:

Задача

Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение

Воспользуемся формулами, которые приводили выше.

Если бы у нас еще были резисторы, соединенные параллельно, то для них

Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи

2-ой способ найти I

Чтобы найти R_общее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть R_общее = 1,25 Ом.

I=U/R_общее = 10/1,25=8 Ампер.

Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.

Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.

Источник

Решение.
Покажем схему соединения (рис).
Для цепи применим правила Кирхгофа:
Первое правило – сумма токов, подходящих к узлу, равна сумме токов, выходящих из узла.
Второе правило – в любом замкнутом контуре сложной цепи сумма действующих ЭДС равна сумме падений напряжения на сопротивлениях этого контура, причем электродвижущие силы берем со знаком плюс, если они повышают потенциал по направлению обхода (переходим от минуса к плюсу), и со знаком минус если понижают. Падение напряжения считаем положительным, если направление токов, проходящих через сопротивление, совпадает с направлением обхода, и со знаком минус, если понижают.
Покажем направления токов стрелками. Для силы токов справедливо условие:

I₂ = I + I₁, I =  I₂ – I₁  (1).

Выбираем положительное направление обхода контура по часовой стрелке.   На основании второго правила Кирхгофа для замкнутого контура запишем формулы на зажимах источников токов:

[ {{xi }_{1}}={{I}_{1}}cdot {{R}_{1}}-Rcdot I (2), -{{xi }_{2}}=-Rcdot I-{{I}_{2}}cdot {{R}_{2}} (3). ]

Выразим токи I₁ и I₂ из уравнений (2) и (3) и подставим в (1):

[ {{I}_{1}}=frac{{{xi }_{1}}+Rcdot I}{{{R}_{1}}}, {{I}_{2}}=frac{{{xi }_{2}}-Rcdot I}{{{R}_{2}}}, I=frac{{{xi }_{2}}-Rcdot I}{{{R}_{2}}}-frac{{{xi }_{1}}+Rcdot I}{{{R}_{1}}} (4) ]

Решим уравнение (4) и найдем ток в резисторе:

[ begin{align}
  & I=frac{{{xi }_{2}}}{{{R}_{2}}}-frac{Rcdot I}{{{R}_{2}}}-frac{{{xi }_{1}}}{{{R}_{1}}}-frac{Rcdot I}{{{R}_{1}}}, Icdot (1+frac{R}{{{R}_{2}}}+frac{R}{{{R}_{1}}})=frac{{{xi }_{2}}}{{{R}_{2}}}-frac{{{xi }_{1}}}{{{R}_{1}}}, \
 & I=frac{{{xi }_{2}}cdot {{R}_{1}}-{{xi }_{1}}cdot {{R}_{2}}}{{{R}_{2}}cdot R+{{R}_{1}}cdot R+{{R}_{1}}cdot {{R}_{2}}}, I=frac{4cdot 20-1,7cdot 40}{40cdot 6+20cdot 6+20cdot 40}=0,01. \
end{align} ]

I = 0,01 А.
Ответ: 0,01 А.