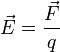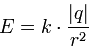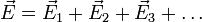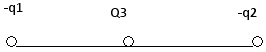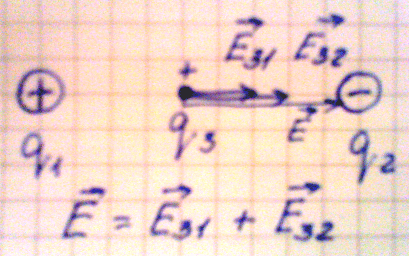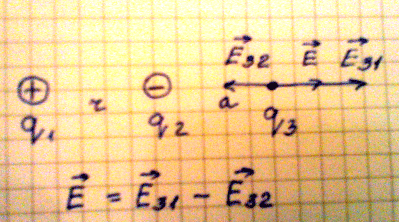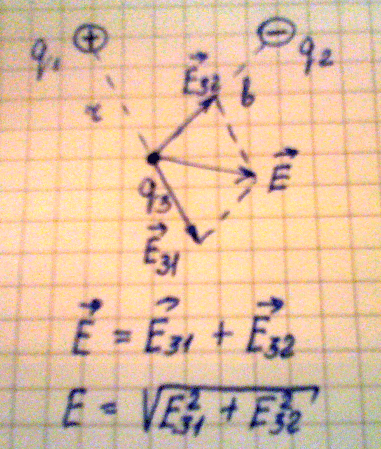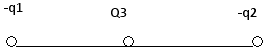Как определить направление вектора напряженности электрического поля
Содержание
- Характеристика электрического поля
- Силовые линии
- Что называется напряженностью электрического поля
Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будет действовать кулоновская сила; значит, в пространстве, окружающем электрические заряды, существует силовое поле. Согласно представлениям современной физики, поле реально существует и наряду с веществом является одной из форм существования материи, посредством которого осуществляются определенные взаимодействия между макроскопическими телами или частицами, входящими в состав вещества. В данном случае говорят об электрическом поле — поле, посредством которого взаимодействуют электрические заряды. Мы рассматриваем электрические поля, которые создаются неподвижными электрическими зарядами и называются электростатическими.
Для обнаружения и опытного исследования электростатического поля используется пробный точечный положительный заряд — такой заряд, который не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле). Если в поле, создаваемое зарядом Q, поместить пробный заряд Q, то на него действует сила F, различная в разных точках поля, которая, согласно закону Кулона, пропорциональна пробному заряду Q. Поэтому отношение F/Q не зависит от Q и характеризует электростатическое поле в той точке, где пробный заряд находится. Эта величина называется напряженностью и является силовой характеристикой электростатического поля.
Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:
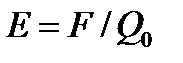
Напряженность поля точечного заряда в вакууме
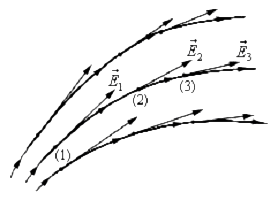
Единица напряженности электростатического поля — ньютон на кулон (Н/Кл): 1 Н/Кл — напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н; 1 Н/Кл= 1 В/м, где В (вольт) — единица потенциала электростатического поля. Графически электростатическое поле изображают с помощьюлиний напряженности — линий, касательные к которым в каждой точке совпадают с направлением вектора Е (рис.).

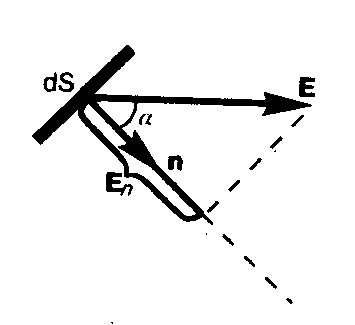
Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, условились проводить их с определенной густотой: число линий напряженности, пронизывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Е. Тогда число линий напряженности, пронизывающих элементарную площадку dS, нормаль n которой образует угол a с вектором Е, равно Е dS cosa = EndS, где Еп—проекция вектора Е на нормаль n к площадке dS (рис.).
Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверхность

где интеграл берется по замкнутой поверхности S. Поток вектора Е является алгебраической величиной: зависит не только от конфигурации поля Е, но и от выбора направления n. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т. е. нормаль, направленная наружу области, охватываемой поверхностью.
К кулоновским силам применим принцип независимости действия сил, т. е. результирующая сила F, действующая со стороны поля на пробный заряд Q, равна векторной сумме сил Fi, приложенных к нему со стороны каждого из зарядов Qi: 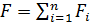
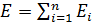
Принцип суперпозиции позволяет рассчитать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.
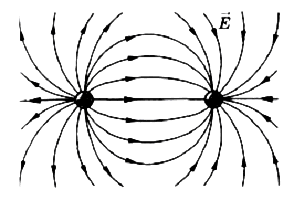
Принцип суперпозиции применим для расчета электростатического поля электрического диполя. Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+Q,–Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Согласно принципу суперпозиции, напряженность Е поля диполя в произвольной точке 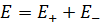
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 — 

Разделы: Физика
Цель урока: дать понятие напряжённости электрического поля и ее определения в любой точке поля.
- формирование понятия напряжённости электрического поля; дать понятие о линиях напряжённости и графическое представление электрического поля;
- научить учащихся применять формулу E=kq/r 2 в решении несложных задач на расчёт напряжённости.
Электрическое поле – это особая форма материи, о существовании которой можно судить только по ее действию. Экспериментально доказано, что существуют два рода зарядов, вокруг которых существуют электрические поля, характеризующиеся силовыми линиями.
Графически изображая поле, следует помнить, что линии напряженности электрического поля:
- нигде не пересекаются друг с другом;
- имеют начало на положительном заряде (или в бесконечности) и конец на отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
- между зарядами нигде не прерываются.
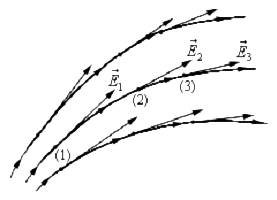
Рис.1
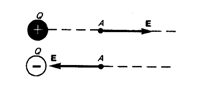
Силовые линии положительного заряда:
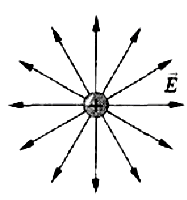
Рис.2
Силовые линии отрицательного заряда:
Рис.3
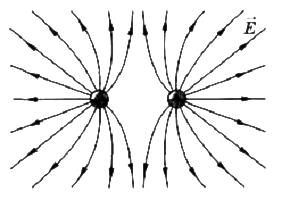
Силовые линии одноименных взаимодействующих зарядов:
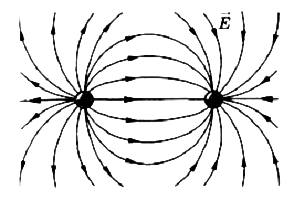
Рис.4
Силовые линии разноименных взаимодействующих зарядов:
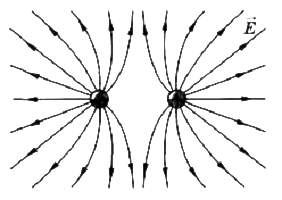
Рис.5
Силовой характеристикой электрического поля является напряженность, которая обозначается буквой Е и имеет единицы измерения 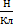

В результате преобразования формулы закона Кулона и формулы напряженности имеем зависимость напряженности поля от расстояния, на котором она определяется относительно данного заряда
где: k – коэффициент пропорциональности, значение которого зависит от выбора единиц электрического заряда.
В системе СИ 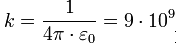
где ε – электрическая постоянная, равная 8,85·10 -12 Кл 2 /Н·м 2 ;
q – электрический заряд (Кл);
r – расстояние от заряда до точки в которой определяется напряженность.
Направление вектора напряженности совпадает с направлением силы Кулона.
Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным. В ограниченной области пространства электрическое поле можно считать приблизительно однородным, если напряженность поля внутри этой области меняется незначительно.
Общая напряженность поля нескольких взаимодействующих зарядов будет равна геометрической сумме векторов напряженности, в чем и заключается принцип суперпозиции полей:
Рассмотрим несколько случаев определения напряженности.
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный положительный заряд между ними, тогда в данной точке будут действовать два вектора напряженности, направленные в одну сторону:
Е31 – напряженность точечного заряда 3 со стороны заряда 1;
Е32 – напряженность точечного заряда 3 со стороны заряда 2.
Согласно принципу суперпозиции полей общая напряженность поля в данной точке равна геометрической сумме векторов напряженности Е31 и Е32.
Напряженность в данной точке определяется по формуле:
где: r – расстояние между первым и вторым зарядом;
х – расстояние между первым и точечным зарядом.
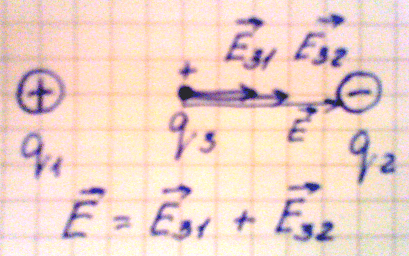
Рис.6
2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной на расстояние а от второго заряда. Если учесть, что поле первого заряда больше, чем поле второго заряда, то напряженность в данной точке поля равна геометрической разности напряженности Е31 и Е32.
Формула напряженности в данной точке равна:
Е = kq1/(r + a) 2 – kq2/a 2
Где: r – расстояние между взаимодействующими зарядами;
а – расстояние между вторым и точечным зарядом.
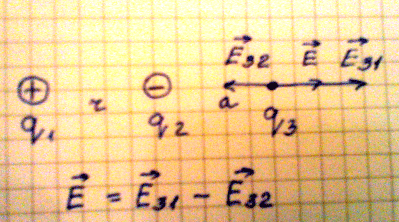
Рис.7
3. Рассмотрим пример, когда необходимо определить напряженность поля в некоторой удаленности и от первого и от второго заряда, в данном случае на расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные заряды отталкиваются , а разноименные притягиваются, имеем два вектора напряженности исходящие из одной точки, то для их сложения можно применить метод противоположному углу параллелограмма будет являться суммарным вектором напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:
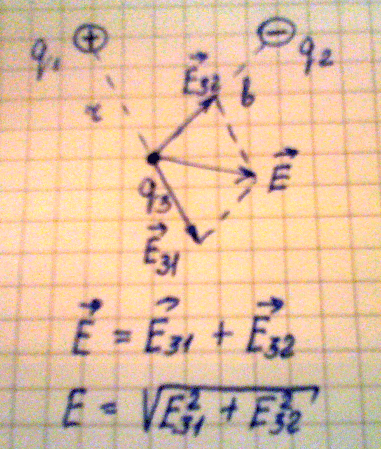
Рис.8
Исходя из данной работы, следует, что напряженность в любой точке поля можно определить, зная величины взаимодействующих зарядов, расстояние от каждого заряда до данной точки и электрическую постоянную.
4. Закрепление темы.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: электрическое поле – это ….
3. Как направлены силовые линии напряженности данного заряда?
4. Определить знаки зарядов:
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: напряженностью называется …
3. Как направлены силовые линии напряженности данного заряда?
4. Определить заряды.
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
1. Два заряда q1 = +3·10 -7 Кл и q2 = −2·10 -7 Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите напряженность поля в точке С, расположенной на линии, соединяющей заряды, на расстоянии 0,05 м вправо от заряда q2.
2. В некоторой точке поля на заряд 5·10 -9 Кл действует сила 3·10 -4 Н. Найти напряженность поля в этой точке и определите величину заряда, создающего поле, если точка удалена от него на 0,1 м.
По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля.
Характеристика электрического поля
Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле:
E → = F → q , где F → — сила, действующая со стороны поля на неподвижный (пробный) заряд q . Его значение должно быть настолько мало, чтобы отсутствовала возможность искажать поле, напряженность которого с его помощью и измеряют. По уравнению видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный пробный заряд.
У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным.
Силовые линии
Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий.
Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.
Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться.
Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:
E → = ∑ i = 1 n E → i .
Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле:
Интегрирование E → = ∫ d E → проводится по области распределения зарядов. Если их распределение идет по линии ( τ = d q d l — линейная плотность распределения заряда), то интегрирование E → = ∫ d E → тоже. Когда распределение зарядов идет по поверхности и поверхностная плоскость обозначается как σ = d q d S , тогда интегрируют по поверхности.
Интегрирование по объему выполняется, если имеется объемное распределение заряда:
ρ = d q d V , где ρ — объемная плотность распределения заряда.
Что называется напряженностью электрического поля
Напряженность поля в диэлектрике равняется векторной сумме напряженностей полей, которые создают свободные E 0 → и связанные E p → заряды:
Зачастую бывают случаи, когда диэлектрик изотропный. Тогда запись напряженности поля имеет вид:
E → = E 0 → ε , где ε обозначает относительную диэлектрическую проницаемость среды в рассматриваемой точке поля.
Отсюда следует, что по выражению E → = E 0 → ε имеется однородный изотропный диэлектрик с напряженностью электрического поля в ε меньше, чем в вакууме.
Напряженность электростатического поля системы точечных зарядов равняется:
E → = 1 4 π ε 0 ∑ i = 1 n q i ε r i 3 r i → .
В системе СГС напряженность поля точечного заряда в вакууме:
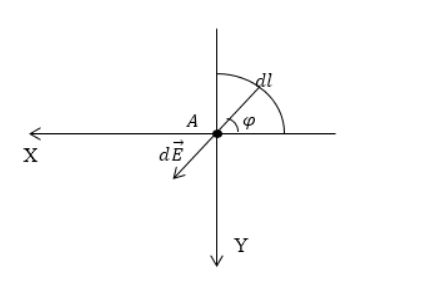
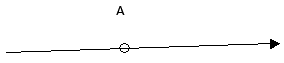
Дан равномерно распределенный заряд по четверти окружности радиуса R с линейной плотностью τ . Необходимо найти напряженность поля в точке А , являющейся центром окружности.
Решение
Произведем выделение на заряженной части окружности элементарного участка d l , который будет создавать элемент поля в точке А . Следует записать выражение для напряженности, то есть для d E → . Тогда формула примет вид:
d E → = d q R 3 R → R .
Проекция вектора d E → на ось О х составит:
d E x = d E cos φ = d q cos φ R 2 .
Произведем выражение d q через линейную плотность заряда τ :
d q = τ d l = τ · 2 πRdR .
Необходимо использовать d q = τ d l = τ · 2 πRdR для преобразования d E x = d E cos φ = d q cos φ R 2 :
d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,
где 2 π d R = d φ .
Далее перейдем к нахождению полной проекции E x при помощи интегрирования d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,
по d φ с изменением угла 0 ≤ φ ≤ 2 π .
E x = ∫ 0 2 π τ cos φ d φ R = τ R ∫ 0 2 π cos φ d φ = τ R sin φ 0 2 π = τ R .
Перейдем к проекции вектора напряженности на О у :
d E y = d E sin φ = τ R sin φ d φ .
Следует проинтегрировать с изменяющимся углом π 2 ≤ φ ≤ 0 :
E y ∫ π 2 0 τ R sin φ d φ = τ R ∫ π 2 0 sin φ d φ = — τ R cos φ π 2 0 = — τ R .
Произведем нахождение модуля вектора напряженности в точке А , применив теорему Пифагора:
E = E x 2 + E y 2 = τ R 2 + — τ R 2 = τ R 2 .
Ответ: E = τ R 2 .
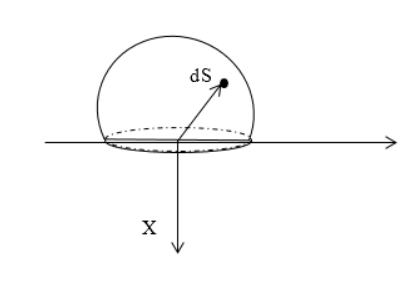
Найти напряженность электростатического поля равномерно заряженной полусферы с радиусом R . Поверхностная плотность заряда равняется σ .
Решение
Следует выделить на поверхности заряженной сферы элементарный заряд d q , располагаемый на элементе площади d S . Запись, используя сферические координаты d S , равняется:
d S = R 2 sin θ d θ d φ ,
при 0 ≤ φ ≤ 2 π , 0 ≤ θ ≤ π 2 .
Элементарная напряженность поля точечного заряда в системе С И :
d E → = d q 4 π ε 0 R 3 R → R .
Необходимо спроецировать вектор напряженности на О х :
d E x = d q cos θ 4 π ε 0 R 2 .
Произведем выражение заряда через поверхностную плотность заряда:
Подставим d q = σ d S в d E x = d q cos θ 4 π ε 0 R 2 , используя d S = R 2 sin θ d θ d φ , проинтегрируем и запишем:
E x = σ R 2 4 π ε 0 R 2 ∫ 0 2 π d φ ∫ 0 π 2 cos θ sin θ d θ = σ 4 π ε 0 2 π · 1 2 = σ 4 ε 0 .
Отсюда следует, что E = E x .
Ответ: напряженность полусферы в центре равняется E = σ 4 ε 0 .
Вектор напряженности электрического поля — что из себя представляет
В 1831 году Майкл Фарадей установил закон электромагнитной индукции, обнаружив, что меняющееся во времени магнитное поле порождает электрическое. Выяснилось, что первично электромагнитное поле, а электрические и магнитные поля — различные его проявления. Позже Максвеллу удалось найти систему уравнений, которым подчиняется электромагнитное поле.
Определение
Напряженность поля — векторная величина, которая характеризует его в конкретной точке.
Основная характеристика
Пространство около электрического заряда отличается от пустоты, даже если заряд находится в вакууме. В этом случае говорят о присутствии поля, способного действовать на любой другой заряд. Взаимозависимость силы воздействия точечных зарядов и их величины описывает закон Кулона.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Поэтому для описания поля обычно прибегают к понятию силы, с которой оно действует на положительный заряд, равный единице: такую характеристику называют напряженностью и обозначают (overrightarrow{Е}). Она равна отношению силы к величине заряда, на который та воздействует.
Таким образом, вектор напряженности электрического поля является его силовой характеристикой. Единица ее измерения — вольт на метр или в ньютон на кулон.
Определение параметров электрического поля
Зная величину внесенного в поле заряда q, можно рассчитать силу в каждом конкретном случае:
(overrightarrow{F} = q timesoverrightarrow{Е})
Согласно закону Кулона, напряженность поля вокруг неподвижного точечного заряда q описывается выражением:
(overrightarrow{Е} = k times frac{q}{r^{2}} times frac{overrightarrow{r}}{r})
(k) равен (frac{1}{4pi epsilon_{0}})
(epsilon_{0}) — электрическая постоянная, равная (8,85times 10^{-12}) Ф/м.
Для вычисления напряженности всего поля нужно сложить напряженности полей отдельных зарядов, т. е. воспользоваться принципом суперпозиции:
(overrightarrow{Е} = overrightarrow{Е_{1}} + overrightarrow{Е_{2}})
Если во всех точках поля напряженность одинакова, оно считается однородным. Если она различается — неоднородным.
Какое направление имеет вектор, как определить
Напряженность по направлению совпадает с силой, с которой поле воздействует на единичный заряд. Если оно создано положительным зарядом, происходит отталкивание: вектор направлен от заряда во внешнее пространство. Если отрицательным зарядом, вектор будет направлен к нему.
Также напряженность тесно связана с напряжением — вектор напряженности всегда направлен в сторону уменьшения потенциала, а сама она равна его градиенту, т. е. скорости его изменения. К эквипотенциальной поверхности вектор напряженности перпендикулярен в каждой точке.
Направленное колебание векторов напряженности в электромагнитной волне называется поляризацией. Она бывает круговой, эллиптической и линейной — в зависимости от формы кривой, вычерчиваемой концом вектора амплитуды. Круговая или эллиптическая поляризация может быть правой или левой, что определяется направлением вращения вектора.
Чтобы описать поляризацию волны, компоненты вектора напряженности выражают с помощью параметров Стокса, интерпретируя их, как координаты точек, расположенных на сфере, называемой сферой Пуанкаре.
Поток вектора напряженности, применение теоремы Гаусса
Суть теоремы, сформулированной Карлом Фридрихом Гауссом, сводится к следующему: если представить, что заряды окружены замкнутой поверхностью S, тогда поток вектора напряженности электрического поля через элементарную площадку (triangle S) можно записать как:
(triangle Ф = Еcosalphatriangle S)
(alpha) здесь — угол между нормалью к площадке и (overrightarrow{Е}).
Тогда поток через площадку (S) описывается формулой:
(Ф = Е_{n}S)
(Е_{n}) здесь — модуль нормальной составляющей поля (overrightarrow{Е}), произведение вектора (overrightarrow{Е}) на нормаль (overrightarrow{n}) к данной площадке.
Определение
Поток векторного поля через поверхность — интеграл второго рода по поверхности S.
Теорема
Полный поток вектора электрического поля через произвольно выбранную замкнутую поверхность равняется сумме потоков от всех зарядов, распределенных внутри нее случайным образом, и пропорционален величине этого заряда:
(Ф = oint_S E times dS = 4pi Q = frac{Q}{epsilon_{0}})
Поскольку взаимодействия между зарядами не имеют значения, расчеты значительно упрощаются. С помощью теоремы Гаусса можно рассчитать поле любого числа зарядов, но это реализуемо только в случае их симметричного расположения, когда можно выбрать поверхность, через которую получится рассчитать поток напряженности.
Как определить направление вектора напряженности
Заряженные тела могут воздействовать друг на друга без соприкосновения через электрическое поле. Поле, которое создается неподвижными электрическими частицами, называется электростатическим.
Инструкция
Если в электрическое поле, создаваемое зарядом Q, поместить еще один заряд Q0, то оно будет воздействовать на него с определенной силой. Это характеристика называется напряженностью электрического поля E. Она представляет собой отношение силы F, с которое поле действует на положительный электрический заряд Q0 в определенной точке пространства, к значению этого заряда: E = F/Q0.
В зависимости от конкретной точки пространства, значение напряженности поля E может меняться, что выражается формулой Е = Е (x, y, z, t). Поэтому напряженность электрического поля относится к векторным физическим величинам.
Поскольку напряженность поля зависит от силой, действующей на точечный заряд, то вектор напряженности электрического поля E одинаков с вектором силы F. Согласно закону Кулона, сила, с которой взаимодействуют две заряженные частицы в вакууме, направлена по прямой линии, которая соединяет эти заряды.
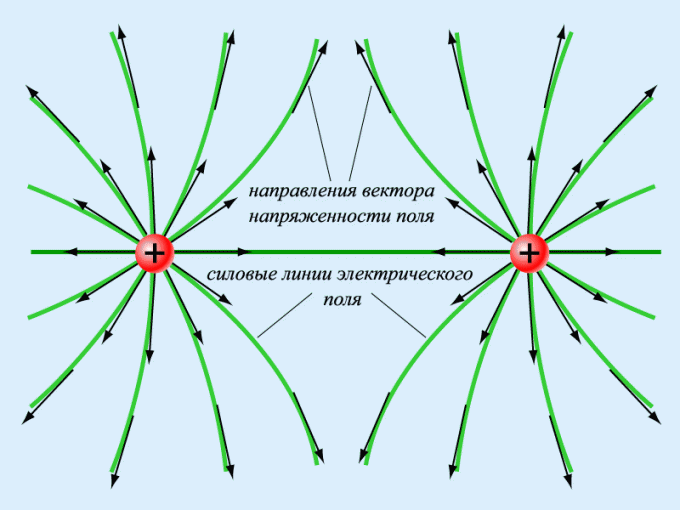
Майкл Фарадей предложил наглядно изображать напряженность поля электрического заряда с помощью линий напряженности. Эти линии совпадают с вектором напряженности во всех точках по касательной. На чертежах их принято обозначать стрелками.
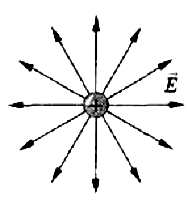
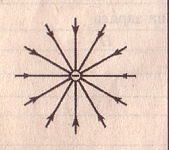
В том случае, если электрическое поле однородно и вектор его напряженности постоянен по своему модулю и направлению, то линии напряженности параллельны с ним. Если электрическое поле создается положительно заряженным телом, линии напряженности направлены от него, а в случае с отрицательно заряженной частицей – по направлению к нему.
Обратите внимание
Вектор напряженности имеет лишь одно направление в каждой точке пространства, поэтому линии напряженности никогда не пересекаются.
Источники:
- Напряженность электрического поля
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Г
электростатическое поле изображают с
помощьюлиний
напряженности —
линий, касательные к которым в каждой
точке совпадают с направлением вектора
Е
(рис. 119). Линиям напряженности
приписывается направление, совпадающее
с направлением вектора напряженности.
Так как в каждой данной точке пространства
вектор напряженности имеет лишь одно
направление, то линии напряженности
никогда не пересекаются. Для однородного
поля (когда
вектор напряженности в любой точке
постоянен по
в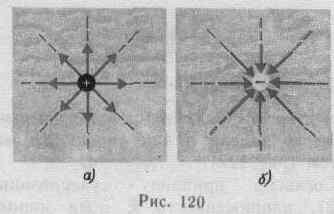
и направлению) линии напряженности
параллельны вектору напряженности.
Если поле создается точечным зарядом,
то линии напряженности — радиальные
прямые, выходящие из заряда, если он
положителен (рис. 120, а), и входящие в
него, если заряд отрицателен (рис. 120,
б). Вследствие большой наглядности
графический способ представления
электрического поля широко применяется
в электротехнике.
Чтобы
с помощью линий напряженности можно
было характеризовать не только
направление, но и значение напряженности
электростатического поля, условились
проводить их с определенной густотой
(см. рис. 119): число линий напряженности,
пронизывающих единицу площади поверхности,
перпендикулярную линиям напряженности,
должно быть равно модулю вектора Е.
Тогда число линий напряженности,
пронизывающих элементарную площадку
dS,
нормаль n
которой образует угол
с вектором Е,
равно ЕdScos=
Еп
dS,
где
Еn
— проекция
вектора Е
на нормаль n
к площадке dS
(рис. 121). Величина
dФE=EndS
= EdS
называется
потоком вектора напряженности через
площадку dS.
Здесь dS
== dSn
— вектор, модуль которого равен dS,
а направление совпадает с направлением
нормали n
к площадке.
Выбор
направления вектора n
(а следовательно, и dS)
условен, так как его можно направить
в любую сторону.
Единица потока
вектора напряженности электростатического
поля— 1 В•м..
Для
произвольной замкнутой поверхности
S
поток
вектора Е
через эту поверхность
5.Теорема Остроградского-Гаусса для электростатического поля.
Вычисление
напряженности поля системы электрических
зарядов с помощью принципа суперпозиции
электростатических полей можно
значительно упростить, используя
выведенную немецким ученым К. Гауссом
(1777—1855) теорему, определяющую поток
вектора напряженности электрического
поля через произвольную замкнутую
поверхность.
В
вектора напряженности сквозь сферическую
поверхность радиусаr,
охватывающую
точечный заряд Q,
находящийся в ее центре (рис. 124),
Этот результат
справедлив для замкнутой поверхности
любой формы. Действительно, если
окружить сферу (рис. 124) произвольной
замкнутой поверхностью, то каждая линия
напряженности, пронизывающая сферу,
пройдет и сквозь эту поверхность.
Е
замкнутая поверхность произвольной
формы охватывает заряд (рис. 125), то при
пересечении любой выбранной линии
напряженности с поверхностью она то
входит в нее, то выходит из нее. Нечетное
число пересечений при вычислении
потока в конечном счете сводится к
одному пересечению, так как поток
считается положительным, если линии
напряженности выходят из поверхности,
и отрицательным для линий, входящих
в поверхность.
Если замкнутая поверхность не
охватывает заряда, то поток сквозь нее
равен нулю, так как число линий
напряженности, входящих в поверхность,
равно числу линий напряженности,
выходящих из нее.
Таким
образом, для поверхности любой формы,
если она замкнута и заключает в себя
точечный заряд Q,
поток
вектора Е
будет равен Q/0,
т. е.
Знак
потока совпадает со знаком заряда Q.
Рассмотрим
общий случай произвольной поверхности,
окружающей n
зарядов.
В соответствии с принципом суперпозиции
(80.2) напряженность Е
поля, создаваемого всеми зарядами,
равна сумме напря-женностей Еi,
создаваемых каждым зарядом в
отдельности:;.
Поэтому
Согласно
(81.1), каждый из интегралов, стоящий под
знаком суммы, равен Qi/0.
Следовательно,
Формула
(81.2) выражает теорему Гаусса
для электростатического поля в вакууме:
поток
вектора напряженности электростатического
поля в вакууме сквозь произвольную
замкнутую поверхность равен
алгебраической сумме заключенных внутри
этой поверхности зарядов, деленной
на 0.
Эта теорема выведена математически
для векторного поля любой природы
русским математиком М. В. Остроградским
(1801 —1862), а затем независимо от него
применительно к электростатическому
полю — К. Гауссом.
В общем случае
электрические заряды могут быть
«размазаны» с некоторой
объемной
плотностью =dQ/dV,
различной
в
разных местах пространства. Тогда
суммарный заряд, заключенный внутри
замкнутой поверхности S,
охватывающей некоторый объем V,
Используя
формулу (81.3), теорему Гаусса (81.2) можно
записать так:
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.
Задачи урока:
- формирование понятия напряжённости электрического поля; дать понятие о
линиях напряжённости и графическое представление электрического поля; - научить учащихся применять формулу E=kq/r2 в решении
несложных задач на расчёт напряжённости.
Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.
Графически изображая поле, следует помнить, что линии напряженности
электрического поля:
- нигде не пересекаются друг с другом;
- имеют начало на положительном заряде (или в бесконечности) и конец на
отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями; - между зарядами нигде не прерываются.
Рис.1
Силовые линии положительного заряда:
Рис.2
Силовые линии отрицательного заряда:
Рис.3
Силовые линии одноименных взаимодействующих зарядов:
Рис.4
Силовые линии разноименных взаимодействующих зарядов:
Рис.5
Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
или
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда
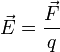
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда
где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.
В системе СИ
Н·м2/Кл2,
где ε0 – электрическая
постоянная, равная 8,85·10-12 Кл2/Н·м2;
q – электрический заряд (Кл);
r – расстояние от заряда до точки в которой определяется напряженность.
Направление вектора напряженности совпадает с направлением силы Кулона.
Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.
Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:
Рассмотрим несколько случаев определения напряженности.
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:
Е31 – напряженность точечного заряда 3 со стороны заряда 1;
Е32 – напряженность точечного заряда 3 со стороны заряда 2.
Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е31 и Е32.
Напряженность в данной точке определяется по формуле:
Е = kq1/x2 + kq2/(r – x)2
где: r – расстояние между первым и вторым зарядом;
х – расстояние между первым и точечным зарядом.
Рис.6
2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е31 и Е32.
Формула напряженности в данной точке равна:
Е = kq1/(r + a)2 – kq2/a2
Где: r – расстояние между взаимодействующими зарядами;
а – расстояние между вторым и точечным зарядом.
Рис.7
3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:
Е = (Е312 +Е322)1/2
Следовательно:
Е = ((kq1/r2 )2 + (kq2/b2)2)1/2
Рис.8
Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.
4. Закрепление темы.
Проверочная работа.
Вариант № 1.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: электрическое поле – это ….
3. Как направлены силовые линии напряженности данного заряда?
4. Определить знаки зарядов:
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Вариант № 2.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: напряженностью называется …
3. Как направлены силовые линии напряженности данного заряда?
4. Определить заряды.
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Задачи на дом:
1. Два заряда q1 = +3·10-7 Кл и q2 = −2·10-7
Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите
напряженность поля в точке С, расположенной на линии, соединяющей заряды, на
расстоянии 0,05 м вправо от заряда q2.
2. В некоторой точке поля на заряд 5·10-9 Кл действует сила 3·10-4
Н. Найти напряженность поля в этой точке и определите величину заряда,
создающего поле, если точка удалена от него на 0,1 м.