Как найти направляющие векторы косинуса

Содержание:

• Формула
• Примеры вычисления направляющих косинусов вектора

Формула

Чтобы найти направляющие косинусы вектора $bar{a}$, заданного на
плоскости своими координатами $bar{a}=left(a_{x} ; a_{y}right)$ нужно воспользоваться формулами:

$$cos alpha=frac{a_{x}}{|bar{a}|}=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}}}, quad cos beta=frac{a_{y}}{|bar{a}|}=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}}}$$

То есть необходимо соответствующую
координату вектора поделить на его
длину.

В случае если вектор задан в пространстве $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$, имеют место
следующие формулы для нахождения направляющих косинусов этого вектора:

$$begin{aligned} cos alpha=frac{a_{x}}{|bar{a}|}=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} &, text { cos } beta=frac{a_{y}}{|bar{a}|}=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} \ cos gamma=frac{a_{z}}{|bar{a}|}=& frac{a_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} end{aligned}$$

Примеры вычисления направляющих косинусов вектора

Читать дальше: как найти угол между векторами.

Направляющие косинусы вектора.

Навигация по странице:

• Определение направляющих косинусов
• Формулы для направляющих косинусов
  • для плоских задач
  • для пространственных задач
• Примеры задач с направляющими косинусами вектора
  • плоские задачи
  • пространственные задачи

Определение направляющих косинусов

Определение. Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.

Направляющие косинусы однозначно задают направление вектора.

Основное соотношение. Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора.

Соответственно, координаты единичного вектора равны его направляющим косинусам.

Свойство направляющих косинусов. Сумма квадратов направляющих косинусов равна единице.

Формулы вычисления направляющих косинусов вектора

Формула вычисления направляющих косинусов вектора для плоских задач

В случае плоской задачи (рис. 1) направляющие косинусы вектора a = {a_x ; a_y} можно найти воспользовавшись следующей формулой

cos α =	ax	;	cos β =	ay
|a|	|a|

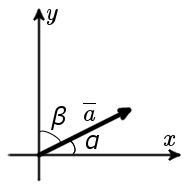рис. 1

Формула вычисления направляющих косинусов вектора для пространственных задач

В случае пространственной задачи (рис. 2) направляющие косинусы вектора a = {a_x ; a_y ; a_z} можно найти воспользовавшись следующей формулой

cos α =	ax	;	cos β =	ay	;	cos γ =	az
|a|	|a|	|a|

Свойство:

cos² α + cos² β + cos² γ = 1

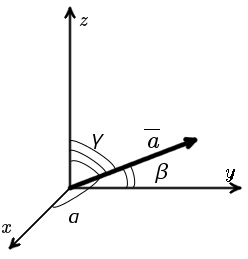рис. 2

Примеры задач с направляющими косинусами вектора

Примеры плоских задач с направляющими косинусами вектора

Пример 1. Найти направляющие косинусы вектора a = {3; 4}.

Решение:

Найдем модуль вектора a:
|a| = √3² + 4² = √9 + 16 = √25 = 5.

Найдем направляющие косинусы вектора a:

cos α =	ax	=	3	= 0.6
|a|	5

cos β =	ay	=	4	= 0.8
|a|	5

Ответ: направляющие косинусы вектора cos α = 0.6, cos β = 0.8.

Пример 2. Найти значение векора a если его длина равна 26, а направляющие косинусы cos α = 5/13, cos β = -12/13.

Решение:

a_x = |a| · cos α = 26 ·

513

= 10
a_y = |a| · cos β = 26 · (-

1213

) = -24

Ответ: a = {10; -24}.

Примеры пространственных задач с направляющими косинусами вектора

Пример 3. Найти направляющие косинусы вектора a = {2; 4; 4}.

Решение:

Найдем модуль вектора a:
|a| = √2² + 4² + 4² = √4 + 16 + 16 = √36 = 6.

Найдем направляющие косинусы вектора a:

cos α =	ax	=	2	=	1
|a|	6	3

cos β =	ay	=	4	=	2
|a|	6	3

cos γ =	az	=	4	=	2
|a|	6	3

Ответ: направляющие косинусы вектора cos α = 13, cos β = 23, cos γ = 23.

Пусть
дан вектор
(_х,_у,_z).

Обозначим
углы наклона этого вектора к осям Ох,
Оу иOz соответственно
буквами
,и.Три числа cos
,
cos
и
cosпринято называть направляющими
косинусами вектора
.
Полагая=
(1;0; 0)получаем из (9)

Аналогично

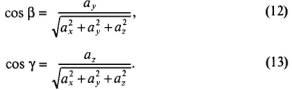
Из
формул (11) – (13) следует:

1)
сos²
+ cos²
+
cos²
= 1,

т.е.
сумма квадратов направляющих
косинусов любого ненулевого вектора
равна единице;

т.е.
направляющие косинусы
этого вектора пропорциональны его
соответствующим проекциям.

Примечание.
Из формул (11)-(13) видно, что проекции
любого единичного вектора
на
оси координат соответственно совпадают
с его направляющими косинусами и,
следовательно,

Пример.
Найти направляющие косинусы вектора
(1;
2; 2). По формулам (11)-(13) имеем

4. Векторное произведение двух векторов и его основные свойства.

Определение.
Векторным произведением двух векторов
иназывается
новый вектор,
модуль которого равен площади
параллелограмма, построенного на
векторахи,
приведенных к общему началу, и который
перпендикулярен к перемножаемым векторам
(иначе говоря, перпендикулярен к плоскости
построенного на них параллелограмма)
и направлен в такую сторону, чтобы
кратчайший поворот отквокруг
полученного векторапредставлялся
происходящим против часовой стрелки,
если смотреть из конца вектора(рис.
40).

Если
векторы
иколлинеарны,
то их векторное произведение считается
равным нулевому вектору. Из этого
определения следует, что

||
= ||
|| sin,

где
–
угол между векторамии(0).
Векторное произведение векторовиобозначается
символом

х
или
[]
или [,].

Выясним
физический смысл векторного произведения.
Если вектор
изображает
приложенную в некоторой точкеМ силу,
а векторидет
из некоторой точкиО в точкуМ, то
вектор=[]
представляет собой момент силыотносительно
точкиО.

Свойства
векторного произведения

1
. При перестановке
сомножителей векторное произведение
меняет знак, т.е.

х
=
-(x).

2.

()х=х()=(х),где–
скаляр.

3.
Векторное произведение
подчиняется распределительному закону,
т.е.

(+)
x=x+x.

4.
Если векторное произведение
двух векторов равно нулевому вектору,
то либо равен нулевому вектору хотя бы
один из перемножаемых векторов
(тривиальный случай), либо равен нулю
синус угла между ними, т.е. векторы
коллинеарны.

Обратно,
если два ненулевых вектора
коллинеарны, то их векторное произведение
равно нулевому вектору.

Таким
образом, для того чтобы
два ненулевых вектора
ибыли
коллинеарны, необходимо и достаточно,
чтобы их векторное произведение равнялось
нулевому вектору.

Отсюда,
в частности, следует, что векторное
произведение вектора на самого себя
равно нулевому вектору:

х
=0

(хеще
называют векторным
квадратом вектора
.

5. Смешанное произведение трех векторов и его основные свойства.

Пусть
даны три вектора
,и.
Представим себе, что векторумножается
векторно наи
полученный векторхумножается
скалярно на вектор,
тем самым определяется число (х).
Оно называется илисмешанным
произведениемтрех векторов,и.

Для
краткости смешанное произведение (х)будем обозначатьили
().

Выясним
геометрический смысл смешанного
произведения
.
Пусть рассматриваемые векторыинекомпланарны.
Построим параллелепипед на векторах,икак
на ребрах.

Векторное
произведение
xесть
вектор(=),
численно равный площади параллелограммаOADB(основание построенного
параллелепипеда), построенного на
векторахии
направленный перпендикулярно к плоскости
параллелограмма (рис. 41).

Скалярное
произведение (x)=есть
произведение модуля вектораи
проекции векторана(см.
п. 1, (2)).

Высота
построенного параллелепипеда есть
абсолютная величина этой проекции.

Следовательно,
произведение |
|по
абсолютной величине равно произведению
площади основания параллелепипеда на
его высоту, т.е. объему параллелепипеда,
построенного на векторах,
и.

Рис.42

При
этом важно отметить, что скалярное
произведение
дает
объем параллелепипеда иногда с
положительным, а иногда с отрицательным
знаком. Положительный знак получается,
если угол между векторамииострый;
отрицательный – если тупой. При остром
угле междуивекторрасположен
по ту же сторону плоскостиOADB,
что и вектор и, следовательно, из конца
векторавращение
откбудет
видно так же, как и из конца вектора,
т.е. в положительном направлении (против
часовой стрелки).

При
тупом угле между
векторрасположен
по другую сторону плоскостиOADB,
чем вектор,
и, следовательно, из конца векторавращение
откбудет
видно в отрицательном направлении (по
часовой стрелке). Иными словами,
произведениеположительно,
если векторы,иобразуют
систему, одноименную с основной Oxyz
(взаимно расположены так же, как оси Ox,
Oy, Oz), и оно отрицательно, если векторы,образуют
систему, разноименную с основной.

Таким
образом, смешанное
произведение
есть
число,абсолютная
величина которого выражает объем
параллелепипеда,построенного
на векторах
,как
на ребрах.

Знак
произведения положителен, если векторы
,,образуют
систему, одноименную с основной, и
отрицателен в противном .

Отсюда
следует, что абсолютная величина
произведения
=(х)останется той же, в каком бы порядке мы
ни брали сомножители,,.
Что касается знака, то он будет в одних
случаях положительным, в других –
отрицательным; это зависит от того,
образуют ли наши три вектора, взятые в
определенном порядке, систему, одноименную
с основной, или нет. Заметим, что у нас
оси координат расположены так, что они
следуют одна за другой против часовой
стрелки, если смотреть во внутреннюю
часть (рис. 42). Порядок следования не
нарушается, если мы начнем обход со
второй оси или с третьей, лишь бы он
совершался в том же направлении, т.е.
против часовой стрелки. При этом множители
переставляются в круговом порядке
(циклически). Таким образом, получаем
следующее свойство:

Смешанное
произведение не меняется при круговой
(циклической) перестановке его
сомножителей. Перестановка двух соседних
сомножителей меняет знак произведения

=
==-()=-()=-().

Наконец,
из геометрического смысла смешанного
произведения непосредственно следует
следующее утверждение.

Необходимым
и достаточным условием  компланарности
векторов
,,является равенство нулю
их смешанного произведения:

=0(14)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #

  18.04.2015421.31 Кб24бп.rtf

• #
• #
• #
• #
• #
• #
• #
• #
• #

Перейти к содержанию

В начале вспомним, что представляет собой вектор.

Одной из характеристик положения вектора в пространстве и его направления являются его направляющие косинусы.

Рассмотрим подробнее, что это такое.

Пусть дана система координат $OX, OY, OZ$.

Рассмотрим произвольный вектор $vec{a}$, берущий начало из центра координат, назовём его ${vec OM}$. Спроектируем этот вектор на оси координат. Для этого через точку $M$ проведём плоскости, параллельные координатным, а точки пересечения этих плоскостей с координатными осями назовём $M_1, M_2$ и $M_3$.

Тогда проекции $vec {OM}$ на координатные оси будут равны $vec {OM_1}=vec{a_x}, vec {OM_2}=vec {M_1N}=vec{a_y}$ и $vec {OM_3}=vec {NM}=vec{a_z}$.

В таком случае вектор $vec{a}$ можно выразить через сумму векторов:

$vec{a}= vec {OM_1} + vec {OM_2} + vec {OM_3}$.

Через единичные векторы данное равенство можно переписать так:

$vec{a}=vec{a_x} cdot i + vec{a_y} cdot j + vec{a_z} cdot k$.

Эту формулу называют разложением вектора по координатным единичным векторам-ортам. Здесь $vec{a_x}, vec{a_y}, vec{a_z}$ — координаты вектора, чаще всего их записывают как равенство вида $vec{a}={ a_x; a_y; a_z }$.

Через проекции вектора на оси координат можно выразить его модуль или проще говоря, длину через теорему о длине диагонали параллелипипеда:

$|vec{a}|^2= a_x^2 + a_y^2 + a_z^2 left(1right)$ или $|vec{a}|^2= sqrt{a_x^2 + a_y^2 + a_z^2}$.

Пусть углы вектора с осями координат $OX, OY, OZ$ равны соответственно $α, β, γ$. Тогда каждую проекцию на соответствующую ось можно записать так:

$vec{a_x}=|vec{a}| cdot cos α$;

$vec{a_y}=|vec{a}| cdot cos β$;

$vec{a_z}=|vec{a}| cdot cos γ$.

Выразим косинусы:

$cos α = frac{a_x}{|a|}$;

«Вычислить направляющие косинусы вектора» 👇

$cos β = frac{a_y}{|a|}$;

$cos γ = frac{a_y}{|a|}$.

Таким образом мы получили с вами направляющие косинусы вектора $vec{a}$. Подставим эти равенства в выражение $(1)$ и сократим на $|a|$:

$cos^2 α + cos^2 β + cos^2 γ = 1$.

Сумма квадратов направляющих косинусов ненулевого вектора равна единице. Из этого выражения можно сделать вывод, что направляющие косинусы являются координатами единичного направляющего вектора для вектора $vec{a}$.