Как найти направляющий вектор двух прямых

С понятием прямой линии тесно связано понятие ее направляющего вектора. Часто в задачах бывает удобнее рассматривать его вместо самой прямой. В рамках данного материала мы разберем, что же такое направляющий вектор прямой в пространстве и на плоскости, и расскажем, для чего можно его использовать.

В первом пункте мы сформулируем определение и покажем основные понятия на иллюстрациях, дополнив их конкретными примерами направляющего вектора. Далее мы посмотрим, как прямая и направляющие векторы взаимодействуют в прямоугольной системе координат и как можно вычислить координаты этого вектора, если мы знаем уравнение прямой. Все правила, как всегда, будут проиллюстрированы примерами решений задач.

Что такое направляющий вектор прямой

Для того чтобы понять эту тему, нам нужно хорошо представлять, что такое вообще прямая и как она может размещаться в пространстве и на плоскости. Кроме того, важно вспомнить ранее изученное понятие вектора. Об этом мы уже писали в отдельном материале. Если нужно, найдите и перечитайте эти статьи.

Сформулируем, что такое направляющий вектор.

Направляющим вектором прямой является любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.

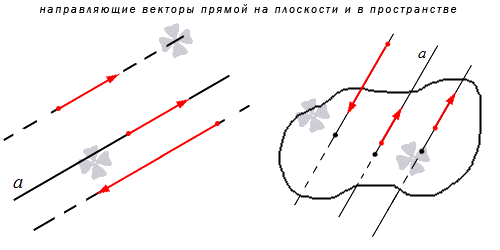
Получается, что у каждой прямой есть бесконечное множество направляющих векторов. При этом все они будут являться коллинеарными в силу озвученного определения, ведь они лежат на одной прямой или параллельной ей другой прямой. Выходит, что если a→ является направляющий вектором прямой a, то другой направляющий вектор мы можем обозначить как t·a→ при любом значении t, соответствующем действительному числу.

Также из определения выше можно сделать вывод, что направляющие векторы двух параллельных прямых будут совпадать: если прямые a и a1 являются параллельными, то вектор a→ будет направляющим и для a, и для a1.

Третий вывод, следующий из определения: если у нас есть направляющий вектор прямой a, то он будет перпендикулярным по отношению к любому нормальному вектору той же прямой.

Приведем пример направляющего вектора: в прямоугольной системе координат для осей Ox, Oy и Oz направляющими будут координатные векторы i→, j→ и k→.

Как вычислить координаты направляющего вектора по уравнениям прямой

Допустим, что у нас есть некая прямая с направляющими векторами, лежащая в прямоугольной системе координат. Сначала мы разберем случай с плоской декартовой системой Oxy, а потом с системой Oxyz, расположенной в трехмерном пространстве.

1. Прямую линию в Oxy можно описать с помощью уравнения прямой на плоскости. В этом случае координаты направляющих векторов будут соответствовать направляющим векторам исходной прямой. А если нам известно уравнение прямой, как вычислить координаты ее направляющего вектора? Это легко сделать, если мы имеем дело с каноническим или параметрическим уравнением.

Допустим, у нас есть канонический случай уравнения, которое имеет вид x-x1ax=y-y1ay. С его помощью на плоскости задана прямая с направляющим вектором a→=(ax, ay).

Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой.

Приведем пример задачи.

Если же прямая описана уравнением параметрического типа, то нам нужно смотреть на коэффициенты при параметре. Они будут соответствовать координатам нужного нам направляющего вектора.

Теперь разберем случай, как найти координаты вектора, если прямая задана общим уравнением вида Ax+By+C=0. Если A=0, то исходное уравнение можно переписать как By+C=0. Оно определяет прямую, которая будет параллельна оси абсцисс. Значит, в качестве ее направляющего вектора мы можем взять координатный вектор i→=1, 0.

А если B=0, то уравнение прямой мы можем записать как Ax+C=0. Описываемая им прямая будет параллельна оси ординат, поэтому ее координатный вектор j→=0, 1 также будет направляющим. Рассмотрим конкретную задачу.

А как быть в случае, если ни один коэффициент в Ax+By+C=0 не будет равен 0? Тогда мы можем использовать несколько разных способов.

1. Мы можем переписать основное уравнение так, чтобы оно превратилось в каноническое. Тогда координаты вектора можно будет взять из его значений.

2. Можно вычислить отдельно начальную и конечную точку направляющего вектора. Для этого надо будет взять координаты двух любых несовпадающих точек исходной прямой.

3. Третий способ заключается в вычислении координат любого вектора, который будет перпендикулярен нормальному вектору этой прямой n→=A, B.

Самым простым является первый подход. Проиллюстрируем его на примере задачи.

К общему виду легко свести и такие типы уравнений, как уравнение прямой в отрезках xa+yb=1 и  уравнение прямой с угловым коэффициентом y=k·x+b, так что если они встретились вам в задаче на нахождение координат направляющего вектора, то можно также использовать этот подход.

Далее мы разберем, как найти эти координаты, если прямая у нас задана не в плоскости, а в пространстве.

Таким образом, для вычисления координат направляющего вектора нужно взять числа из знаменателей или коэффициентов при параметре в соответствующем уравнении.  

Рассмотрим конкретную задачу.

Разберем  еще один случай. Как вычислить нужные координаты, если прямая задана уравнением двух пересекающихся плоскостей вида A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0?

Есть два способа. Можно записать это уравнение в параметрическом виде, где будут видны нужные координаты. Но можно использовать и другой способ. Объясним его.

Вспомним, что такой нормальный вектор плоскости. Он по определению будет лежать на прямой, перпендикулярной исходной плоскости. Значит, любой направляющий вектор прямой, которая в ней находится, будет перпендикулярен ее любому нормальному вектору.

Направляющий вектор прямой, образованной пересечением двух плоскостей A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0, будет перпендикулярен нормальным векторам n1→=(A1, B1, C1) и n2→=(A2, B2, C2). То есть в качестве направляющего вектора мы может взять произведение векторов n1→=(A1, B1, C1) и n2→=(A2, B2, C2).

n1→×n2→=i→j→k→A1B1C1A2B2C2 – это и есть направляющий вектор прямой, по которой пересекаются исходные плоскости.

Решим задачу, в которой применяется этот подход.

В конце статьи отметим, что умение вычислять направляющий вектор пригодится для решения многих задач, таких, как сопоставление двух прямых, доказательство их параллельности и перпендикулярности, вычисление угла между пересекающимися или скрещивающимися прямыми и др.

расположение
прямых

Пусть L– прямая, для которой необходимо
составить уравнения,– произвольная точка этой прямой.

1. Если известны
координаты направляющего вектора
прямойLи некоторой
фиксированной ее точкито уравнение

(15.12)

где
– радиус-вектор точки– радиус-вектор произвольной точки,называетсявекторно-параметрическим
уравнением прямойL.
В координатной форме уравнение
(15.12) равносильно трем параметрическим
уравнениям:

(15.13)

Система (15.13)
определяет параметрические уравнения
прямой L.

По исходной
информации получаем также канонические
уравнения прямой L:

(15.14)

2. Пусть известны
две точки
илежащие на прямойL.
Тогда векторыколлинеарны, и можно записать уравнения
прямой, проходящей через две точки:

(15.15)

3. В пространстве
прямую можно задать как линию пересечения
двух плоскостей:

(15.16)

В уравнениях
плоскостей (15.16) коэффициенты при
переменных не являются пропорциональными
(иначе плоскости либо параллельны, либо
совпадают).

О взаимном
расположении двух прямых в пространстве
можно судить по их направляющим векторам.

Угол между
прямымиможно определить через
косинус угла между направляющими
векторами.

Прямые параллельны
при условии коллинеарности их
направляющих векторов (координаты
пропорциональны).

Угол
между прямыми прямой
при условии
перпендикулярности их направляющих
векторов (скалярное произведение равно
0).

Прямые лежат в
одной плоскости при условии компланарности
их направляющих векторов и вектора
гдеМ₁иМ₂– точки
этих прямых (смешанное произведение
равно 0).

Расстояние
от точки М₀
до прямой L
вычисляется
по формуле

(15.17)

где
– направляющий вектор;М₁–
точка прямой.

Эту формулу можно
использовать и для нахождения расстояния
между параллельными прямыми.

Если прямые L₁иL₂являются
скрещивающимися, то расстояние между
ними определяют по формуле

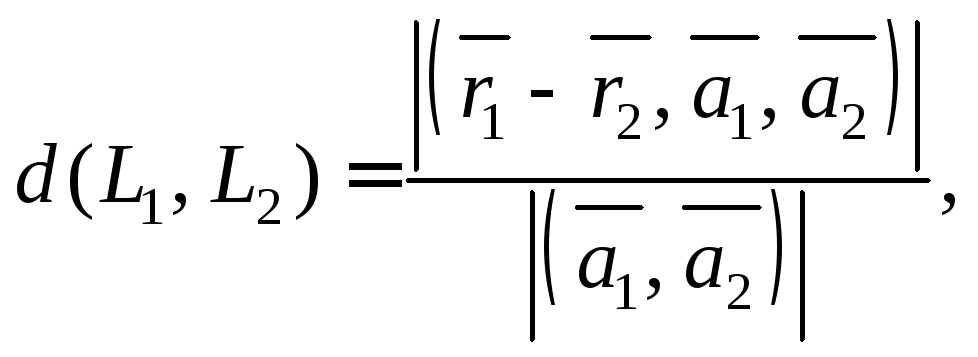(15.18)

где
и– радиус-векторы точекипринадлежащих прямымL₁иL₂соответственно,
а векторыи– направляющие векторы этих прямых.

Пример
1. Составить
канонические уравнения прямой, проходящей
через:

1) точку
параллельно вектору

2) две
заданные точки
и

Решение.
1) Пусть
– произвольная точка искомой прямой.
Тогдат. е. их координаты пропорциональны..
Согласно (15.14) получаем уравнения

которые
и представляют собой канонические
уравнения прямой.

2)
Пусть
– произвольная точка прямой. Тогда,
используя уравнение (15.15) для нашего
случая, имеем:

откуда

Это и есть искомый
результат.

Пример
2. Записать
канонические уравнения прямой, заданной
системой уравнений двух плоскостей

Решение.
Для перехода к каноническим уравнениям
прямой обычно поступают следующим
образом. Подбирают какую-либо точку
фиксируя числовое значение одной из
координат и решая систему двух линейных
уравнений с двумя неизвестными. Затем
находят направляющий векторпрямойL
как векторное произведение нормальных
векторов плоскостей, задающих прямую
L.
Реализуем этот подход на данном примере.

Имеем
– нормальный вектор плоскости– нормальный вектор плоскости

Тогда
вектор
является направляющим вектором прямойL.
Определим его координаты:

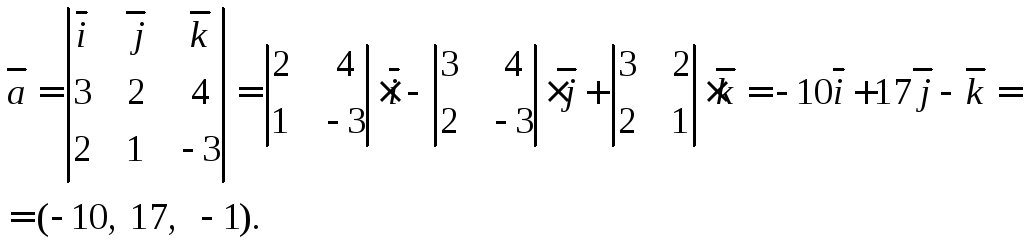
Для
нахождения точки
зафиксируем одно из координатных
значений, например,Тогда, подставив в заданные общие
уравнения значениеимеем:

или
т. е.

Таким
образом, получаем искомые канонические
уравнения заданной прямой L:

З
а м е ч а н и е. Для нахождения точки
можно
сначала решить систему в общем виде, а
потом выбрать частное решение, а в
качестве
взятьгде

Пример
3.
Доказать, что прямые L₁
и L₂
параллельны, и найти расстояние между
ними, если они заданы параметрическими
уравнениям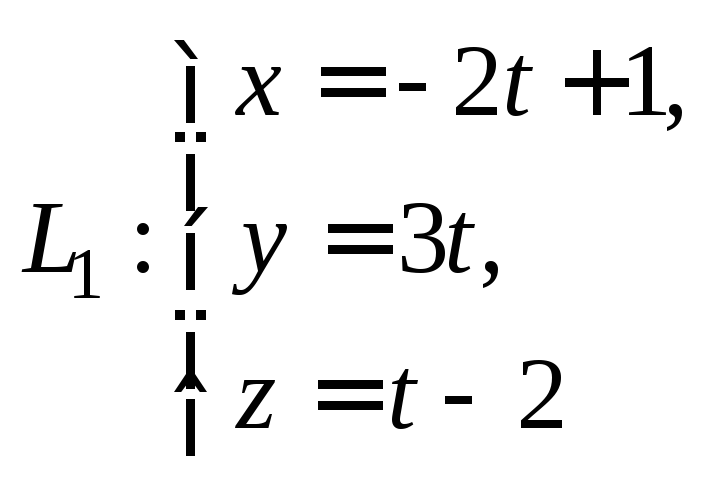и:

и

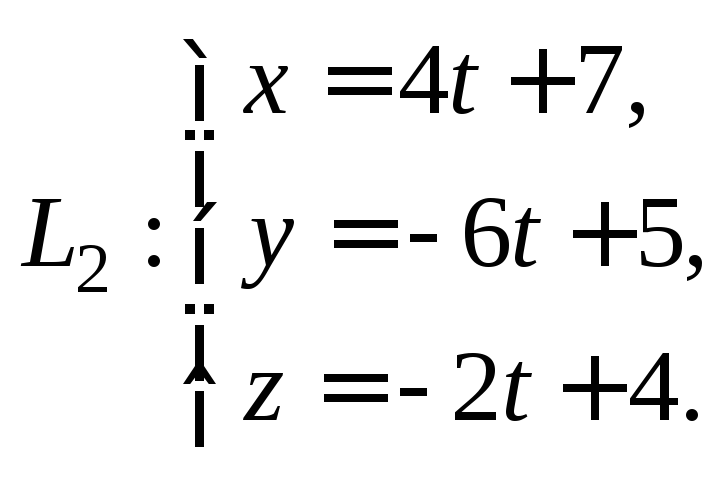
Решение.
Прямая L₁
имеет направляющий вектор
аL₂
– вектор
причемтак как
Значит,

Найдем
расстояние
между ними, используя формулу расстояния
(15.17) от точки до прямой. В параметрических
уравнениях заданных прямых полагаемимеемТогда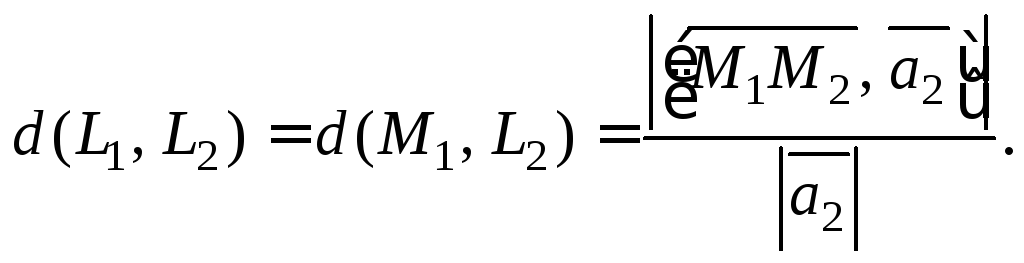

Вычисляем векторное
произведение:

После этого находим
длины нужных векторов:

Значит,

Пример
4. Доказать,
что прямые L₁
и L₂
пересекаются, и найти координаты точки
пересечения, если они заданы параметрическими
уравнениям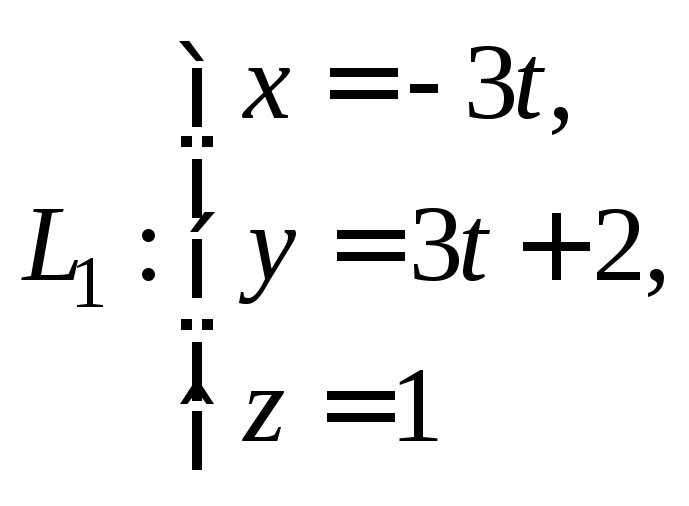и:

и

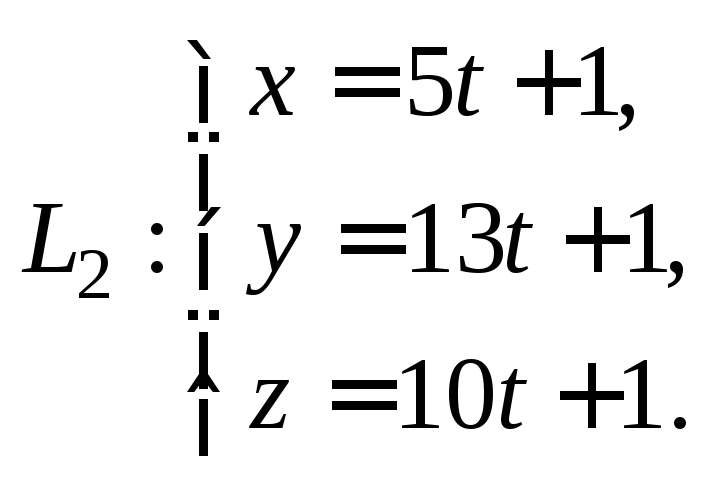
Решение.
Координаты направляющего вектора прямой
равны соответственно числовым
коэффициентам при t,
т. е.
При этомЗначит

Прежде
всего определим, лежат ли прямые в одной
плоскости, т. е. являются ли векторы
икомпланарными (здесь).
Найдем для этого их смешанное произведение:

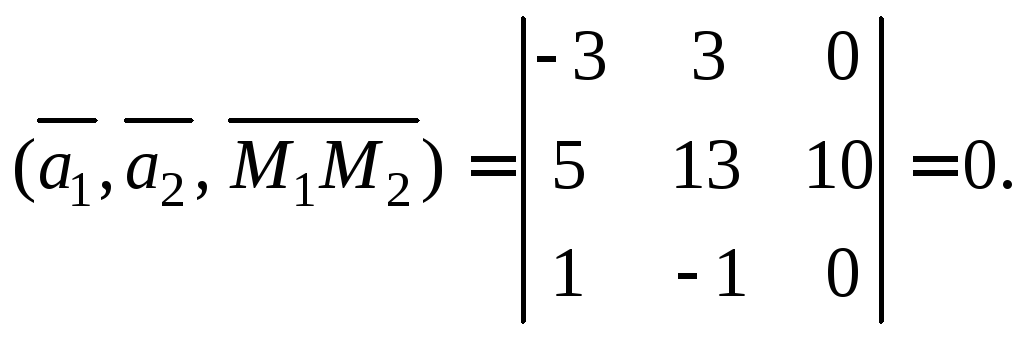
Значит,
прямые лежат в одной плоскости и не
параллельны. Следовательно, они
пересекаются.

Найдем
точку их пересечения

Поскольку
тото

Получаем,
что при подстановке
в уравнение прямой

Значит,
Итак,– точка пересечения заданных прямых.

Пример
5.
Доказать, что прямые L₁
и L₂
скрещиваются, найти расстояние между
ними, если они заданы параметрическими
уравнениям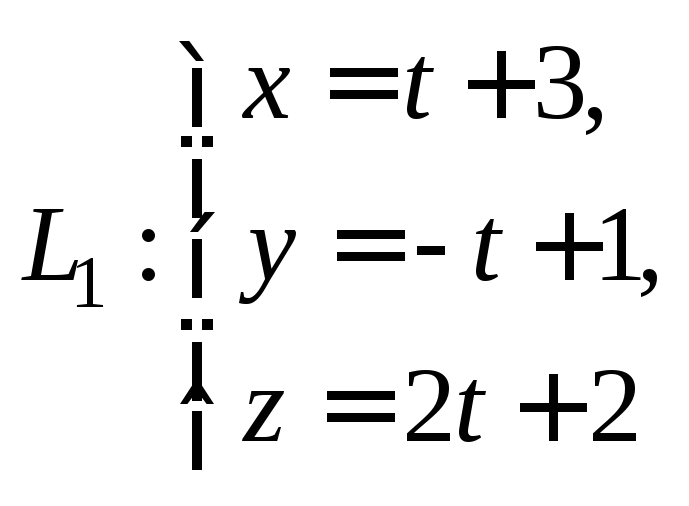и:

и

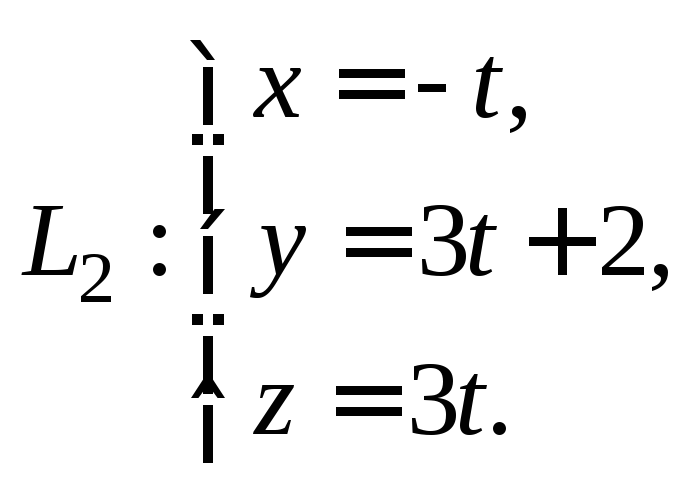
Решение.
Направляющий вектор прямой L₁
есть
а прямойL₂
– вектор
причемЗначитОпределим, пересекаются ли прямые. Так
както условием пересечения прямых служит
компланарность векторовиНайдем смешанное произведение этих
векторов:

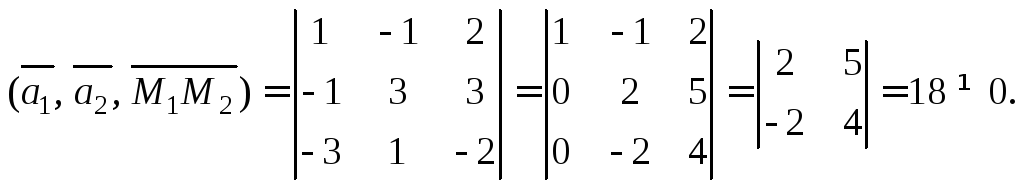(15.19)

Значит,
указанные векторы, а вместе с ними и
прямые L₁
и L₂,
не лежат
в одной плоскости.

Прямые
L₁
и L₂
скрещиваются,
так как они не пересекаются и не
параллельны. Найдем расстояние между
ними по формуле (15.18), используя (15.19):

Определяем
координаты:

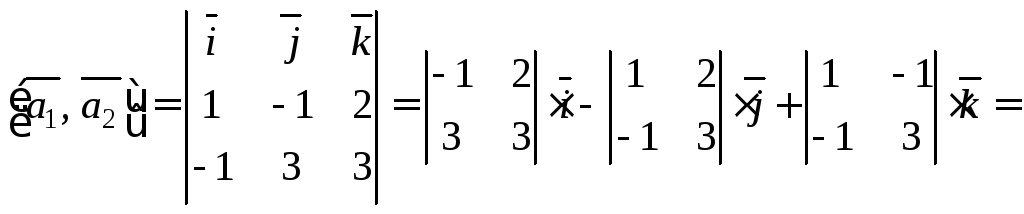
Тогда

Получаем:

Задания

Соседние файлы в папке Часть 3

• #
• #
• #
• #
• #
• #
• #
• #

2.5.1. Взаимное расположение двух прямых

Рассмотрим две прямые, уравнения которых заданы в общем виде:

Тот случай, когда зал подпевает хором. Две прямые могут:

1) совпадать;

2) быть параллельными: ;

3) или пересекаться в единственной точке: .

Справка:  – это математический знак пересечения.

Как определить взаимное расположение двух прямых?

Начнём с первого случая:

1) Две прямые совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства

Рассмотрим прямые  и составим три уравнения из соответствующих коэффициентов: . Из каждого уравнения следует, что , следовательно, данные прямые совпадают.

И действительно, если все коэффициенты уравнения  умножить на –1 (сменить знаки), и все коэффициенты уравнения  сократить на 2, то получится одно и то же уравнение:  – вспоминаем, что это «эталонный» вид общего уравнения прямой.

Второй случай, когда прямые параллельны:

2) Две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных  и   пропорциональны: , но

В качестве примера рассмотрим прямые . Сначала проверяем пропорциональность соответствующих коэффициентов при переменных :

Однако совершенно очевидно, что .

Вывод:

И третий случай, когда прямые пересекаются:

3) Две прямые пересекаются, тогда и только тогда, когда их коэффициенты при переменных  и  НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства

Так, оставим систему для прямых :

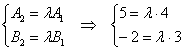
Из первого уравнения следует, что , а из второго уравнения: , значит, система несовместна (нет решений). Таким образом, коэффициенты при переменных  не пропорциональны.

Вывод: прямые пересекаются

В практических задачах можно использовать только что рассмотренную схему решения, но существует и более «цивилизованная» упаковка:

Задача 74

Выяснить взаимное расположение прямых:

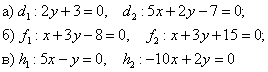
Решение основано на исследовании направляющих векторов прямых:

а) Из уравнений  найдём направляющие векторы прямых: .

Вычислим определитель, составленный из координат данных векторов:
, значит, векторы  не коллинеарны и прямые  пересекаются.

Вопрос: всё ли вам понятно? Если нет, то используйте три ссылки выше. Ну а остальные перепрыгивают камень и следуют дальше, прямо к Кащею Бессмертному =)

б) Найдем направляющие векторы прямых :
 – прямые имеют один и тот же направляющий вектор, значит, они либо параллельны, либо совпадают (тут и определитель считать не надо).

Очевидно, что коэффициенты при переменных  пропорциональны и .

Выясним, справедливо ли равенство :

Таким образом,

в) Найдем направляющие векторы прямых :

Вычислим определитель, составленный из координат данных векторов:
, следовательно, направляющие векторы коллинеарны и прямые либо параллельны, либо совпадают.

Коэффициент пропорциональности «лямбда» можно узнать прямо соотношения коллинеарных направляющих векторов . Впрочем, можно и через коэффициенты самих уравнений: .

Теперь выясним, справедливо ли равенство . Оба свободных члена нулевые, поэтому:

Полученное значение  удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).

Таким образом, прямые совпадают.

Ответ:

Очень скоро вы научитесь (или даже уже научились) решать рассмотренную задачу устно и буквально в считанные секунды – присмотрелись к уравнениям, и всё понятно.

2.5.2. Как найти прямую, параллельную данной?

2.4. Параметрические уравнениЯ прямой

| Оглавление |



Автор: Aлeксaндр Eмeлин

Рассмотрим прямую $L$, заданную точкой $M_0$, лежащей на ней, и направляющим вектором $overline{S}$ с координатами $(l;m)$, при этом вектор $overline{S}$ — ненулевой. Обозначим на прямой произвольную точку $M$ с координатами $(x, y)$, не совпадающую с точкой $M_0$. Радиус-векторы этих точек назовём $overline{r_0}$ и $overline{r}$. Вектор $overline{MM_0}$ при этом будет колинеарен вектору $overline{S}$.

Вектор $overline{r}$ можно выразить через сумму векторов $overline{MM_0}$:

$overline{r} = overline{r_0} + overline{MM_0}left(1right).$

Вектор $overline{MM_0}$ лежит на прямой $L$, поэтому он по условию является параллельным направляющему вектору $overline{S}$ и связан с ним соотношением $overline{MM_0}= toverline{S}left(2right)$, где $t$ — множитель, являющийся скалярной величиной и зависящий от позиции точки $M$ на прямой.

Учитывая равенство $(2)$, формулу $(1)$ можно переписать следующим образом:

Возможны следующие варианты задания уравнения прямой на плоскости:

• Общее уравнение прямой;
• Уравнение с угловым коэффициентом;
• Через параметрические уравнения;
• Каноническое уравнение;
• С помощью двух точек, через которые проходит прямая.

Для каждого из этих вариантов подходит свой способ нахождения направляющего вектора.

Направляющий вектор из канонического уравнения прямой и через две точки

Каноническое уравнение прямой выглядит так:

$frac{x-x_0}{l}= frac{y-y_0}{m}left(4right)$

Из канонического уравнения выразить координаты направляющего вектора проще всего: достаточно выписать знаменатели из уравнения следующим образом:

$overline{S}=(l; m)$.

Уравнение прямой, проходящей через 2 точки, имеет вид, очень похожий на каноническое уравнение:

$frac{x-x_1}{x_2 – x_1}= frac{y-y_1}{y_2-y_1}left(5right)$, где $(x_1; y_1)$ и $(x_2; y_2)$ — координаты точек, через которые проходит прямая.

В этом случае координаты направляющего вектора $overline{S}$ равны $((x_2 – x_1); (y_2-y_1))$.

Направляющий вектор из параметрических уравнений

Параметрические уравнения имеют следующий вид:
$begin{cases} x=x_0 + lt \ y=y_0 + mt end{cases}$

Для того чтобы выразить координаты направляющего вектора из параметрических уравнений, нужно выписать коэффициенты, стоящие перед параметром $t$, т.е. $overline{S}=(l; m)$.

Координаты направляющего вектора из общего уравнения

Общее уравнение имеет следующий вид:

$Ax + By + C = 0left(6right)$

Для того чтобы получить координаты направляющего вектора, нужно от общего уравнения прямой перейти к каноническому.

Сделаем это в общей форме.

Сначала перенесём часть $By + C$ в правую часть:

$Ax = – By – C$

Теперь разделим всё на $A$:

$x=-frac{By}{A} – frac{C}{A}$

А после этого всё уравнение разделим на $B$:

$frac{x}{B}=-frac{y}{A} – frac{C}{AB}$

$frac{x}{B} = frac{y + frac{C}{B}}{-A}left(7right)$

Из вышеизложенного следует, что координаты направляющего вектора $overline{S}$ будут равны $(B; -A)$.

Координаты направляющего вектора из уравнения с угловым коэффициентом

Уравнение с угловым коэффициентом имеет вид:

$y = kx + b$

Для того чтобы получить из него координаты направляющего вектора, необходимо сначала привести его к общему виду, для этого переносим всё в левую часть:

$y – kx – b= 0$

Затем нужно воспользоваться алгоритмом для общего уравнения.

Уравнение с угловым коэффициентом, приведённое к каноническому, выглядит так:

$frac{x}{1}=frac{y-b}{k}$,

то есть координаты направляющего вектора в данном случае будут $overline{S}= (1;k)$.