Составим уравнение прямой проходящей через две точки A(2; 1) и B(0; 2).
Составим каноническое уравнение прямой
Воспользуемся формулой канонического уравнения прямой
Подставим в формулу координаты точек:
В итоге получаем каноническое уравнение прямой:
Составим параметрическое уравнение прямой
Воспользуемся формулой параметрического уравнения прямой:
где:
– направляющий вектор прямой, в качестве которого можно взять вектор ;
– координаты точки лежащей на прямой, в качестве которых можно взять координаты точки A.
В итоге получим параметрическое уравнение прямой:
На этой странице вы найдете два калькулятора, которые строят уравнение прямой по координатам двух точек, принадлежащих этой прямой.
Первый калькулятор находит уравнение прямой с угловым коэффициентом, то есть уравнение в форме . Также он строит график и отдельно выводит угловой коэффициент и значение y в месте пересечения прямой с осью ординат.
Второй калькулятор находит параметрические уравнения прямой, то есть систему уравнений вида . Он также строит график и отдельно выводит направляющий вектор.
Формулы расчета можно найти под калькуляторами.
Уравнение прямой с угловым коэффициентом по двум точкам
Первая точка
Вторая точка
Значение y в точке пересечения с осью ординат
Точность вычисления
Знаков после запятой: 2
Параметрическое уравнение прямой
Первая точка
Вторая точка
Параметрическое уравнение для x
Параметрическое уравнение для y
Точность вычисления
Знаков после запятой: 2
Уравнение прямой с угловым коэффициентом
Найдем уравнение прямой с угловым коэффициентом по двум известным точкам и
.
Нам надо найти угловой коэффициент a и y координату точки пересечения прямой с осью ординат b.
Мы можем составить следующие уравнения для двух точек относительно a и b
Вычитаем первое из второго
Откуда
b можно найти как
Таким образом, как только мы нашли а, для расчета b достаточно только подставить значения или
в выражение выше.
Параметрическое уравнение прямой
Найдем параметрическое уравнение прямой по двум известным точкам и
.
Нам надо найти компоненты направляющего вектора.
Этот вектор описывает величину и направление воображаемого движения по прямой от первой до второй точки.
Имея направляющий вектор, легко записать параметрические уравнения прямой
Обратите внимание, что если , то
и если
, то
Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.
Прямая – это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнения прямой, проходящей через две точки могут быть следующих видов:
- каноническое уравнение,
- параметрическое уравнение,
- общее уравнение прямой,
- уравнение прямой с угловым коэффициентом,
- уравнение прямой в полярных координатах и другие.
Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.
Каноническое уравнение прямой на плоскости
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
xa и ya – координаты первой точки A,
xb и yb – координаты второй точки B
Параметрическое уравнение прямой на плоскости
{begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases}}
xa, ya – координаты точки, лежащей на прямой,
{l;m} – координаты направляющего вектора прямой,
t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Каноническое уравнение прямой в пространстве
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a} = dfrac{z-z_a}{z_b-z_a}}
xa, ya и za – координаты первой точки A,
xb, yb и zb – координаты второй точки B
Параметрическое уравнение прямой в пространстве
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a \ z=n cdot t + z_a end{cases} }
xa, ya и za – координаты точки, лежащей на прямой,
{l;m;n} – координаты направляющего вектора прямой,
t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Пример нахождения уравнения прямой, проходящей через две точки
Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).
Каноническое уравнение прямой
Каноническое уравнение прямой, проходящей через две точки имеет вид {dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
Подставим в формулу координаты точек A и B: {dfrac{x-1}{3-1} = dfrac{y-2}{8-2}}
Получаем каноническое уравнение прямой: {dfrac{x-1}{2} = dfrac{y-2}{4}}
Уравнение прямой с угловым коэффициентом
Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}
Параметрическое уравнение прямой
Параметрическое уравнение прямой имеет вид:
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases} }
где {x_a, y_b} – координаты точки, лежащей на прямой, {{l;m}} – координаты направляющего вектора прямой, t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)}.
Найдем координаты направляющего вектора:
overline{AB} = {x_b – x_a; y_b – y_a} = {3-1; 8-2} = {2; 6}
Получаем параметрическое уравнение:
begin{cases} x=2 t + 1 \ y=6 t + 2 end{cases}
Используем калькулятор для проверки полученного ответа.
Уравнение прямой как результат пересечения плоскостей
| Коэффициенты первой плоскости | |
| Коэффициенты второй плоскости | |
| Уравнение первой плоскости |
| Уравнение второй плоскости |
| Уравнение прямой как пересечение двух плоскостей |
Определяем уравнение прямой в пространстве если нам известны общие уравнения двух плоскостей.
Обновление от 13 октября 2019 года: Используется алгоритм описанный в статье ФРС. Фундаментальное решение системы уравнений
Если первая плоскость задана уравнением вида
а другая плоскость уравнением вида
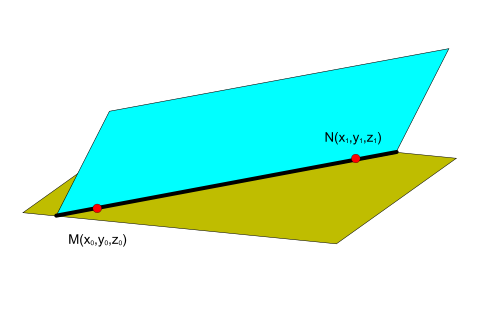
и они перескаются, то уравнение полученной прямой можно найти по двум точкам, принадлежащих одновременно этим плоскостям.
Прямая в пространстве, проходящая через две точки )
)
(cfrac{x-x_0}{x_1-x_0}=cfrac{y-y_0}{y_1-y_0}=cfrac{z-z_0}{z_1-z_0})
B принципе этого достаточно что бы решить уравнение. Положим что z=0 ( можно брать любое число, но с нулем оно как то удобнее) тогда уравнения плоскости приобретают вид
Получили систему линейных уравнений которая легко решается.
Определили таким образом точку
Теперь пусть z=1 и решаем систему
и получаем вторую точку
Эти две точки принадлежат обеим плоскостям и значит уравнение прямой имеет вид
(cfrac{x-x_0}{x_1-x_0}=cfrac{y-y_0}{y_1-y_0}=cfrac{z}{1})
Есть еще второй способ, использующий вектора. Рассмотрим и его.
Если известна точка в пространстве )
то уравнение прямой имеет вид
(cfrac{x-x_0}{m}=cfrac{y-y_0}{n}=cfrac{z-z_0}{p})
Узнав координаты точки )
Для этого вычислим векторное произведение
(begin{pmatrix}i&j&k\A_1&B_1&C_1\A_2&B_2&C_2end{pmatrix}=im+jn+kp)
и подставив вычисленные значения в уравнение
(cfrac{x-x_0}{m}=cfrac{y-y_0}{n}=cfrac{z-z_0}{p})
мы узнаем уравнение прямой в пространстве, как пресечение двух плоскостей.
Созданный онлайн калькулятор позволяет автоматически находить уравнение прямой по двум заданным общим уравнениям плоскостей.
Условие параллельности плоскостей
Две плоскости заданные уравнениями вида
лишь тогда параллельны, когда верным становится соотношение
(cfrac{A_1}{A_2}=cfrac{B_1}{B_2}=cfrac{C_1}{C_2})
Калькулятор онлайн.
Вычисление расстояния от точки до прямой
Этот калькулятор онлайн вычисляет расстояние от точки до прямой заданной в каноническом виде (для трехмерного случая):
$$ frac{x-x_0}{l} = frac{y-y_0}{m} = frac{z-z_0}{n} $$
и в виде общего уравнения прямой (для двухмерного случая):
$$ Ax+By+C=0 $$
а точка задана своими координатами.
Онлайн калькулятор для вычисления расстояния от точки до прямой не просто даёт ответ задачи, он приводит подробное решение с
пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Правила ввода чисел
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac{2}{3} )
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac{5}{7} )
Наши игры, головоломки, эмуляторы:
Немного теории.
Уравнения прямой
Линию в пространстве можно рассматривать как пересечение двух поверхностей и определять заданием двух
уравнений. В частности, каждую прямую линию можно рассматривать как пересечение двух плоскостей и соответственно этому определять
заданием двух уравнений первой степени.
Пусть заданы некоторая прямоугольная система координат Oxyz и произвольная прямая L. Обозначим через ( pi_1 ), и ( pi_2 ) две
различные плоскости, пересекающиеся по прямой L, заданные соответственно уравнениями
$$ left{ begin{array}{l} A_1x + B_1y + C_1z + D_1 = 0 \ A_2x + B_2y + C_2z + D_2 = 0 end{array} right. tag{1} $$
Два уравнения вида (1) совместно определяют прямую L в том и только в том случае, когда плоскости ( pi_1 ), и ( pi_2 ) не
параллельны и не совпадают друг с другом, т.е. нормальные векторы этих плоскостей ( N_1(A_1;B_1;C_1) ) и ( N_2(A_2;B_2;C_2) ) не
коллинеарны (коэффициенты A1, B1, C1 не пропорциональны коэффициентам A2, B2,
C2).
Уравнения (1) называются общими уравнениями прямой.
Канонические уравнения прямой.
Для решения задач уравнения (1) не всегда удобны, поэтому используют специальный вид уравнений прямой.
Пусть дана какая-нибудь прямая L и ненулевой вектор ( vec{a} ), лежащий на данной прямой или параллельный ей.
Вектор а называется направляющим вектором данной прямой. Выведем уравнения прямой, проходящей через данную точку
( M_0(x_0;y_0;z_0) ) и имеющей данный направляющий вектор ( vec{a}(l;m;n) )
Пусть ( M(x;y;z) ) — произвольная точка. Она лежит на прямой тогда и только тогда, когда вектор
( vec{M_0M}(x-x_0; y-y_0; z-z_0) ) коллинеарен направляющему вектору ( vec{a}(l;m;n) ), т.е. когда координаты
вектора ( vec{M_0M} ) пропорциональны координатам вектора ( vec{a} ):
$$ frac{x-x_0}{l} = frac{y-y_0}{m} = frac{z-z_0}{n} tag{2} $$
Уравнения (2) и являются искомыми. Они называются каноническими уравнениями прямой.
Для того чтобы составить канонические уравнения (2), если прямая L задана уравнениями (1), необходимо:
1) найти какую-нибудь точку ( M_0(x_0;y_0;z_0) in L ); для этого следует задать числовое значение одной из неизвестных
координат ( x_0, ; y_0, ; z_0 ) и подставить его вместо соответствующей переменной в уравнения (1), после этого две другие
координаты определяются в результате совместного решения уравнений (1);
2) найти направляющий вектор ( vec{a}(l;m;n) ). Так как прямая L определена пересечением плоскостей ( pi_1 ) и ( pi_2 ), то
она перпендикулярна каждому из нормальных векторов ( vec{N_1} ) и ( vec{N_2} ). Поэтому в качестве
вектора ( vec{a} ) можно взять любой вектор, перпендикулярный векторам ( vec{N_1} ) и ( ; vec{N_2} ),
например их векторное произведение ( vec{a}= vec{N_1} times vec{N_2} ). Так как координаты векторов
( vec{N_1} ) и ( vec{N_2} ) известны:
( vec{N_1}(A_1;;B_1;;C_1), ;; vec{N_2}(A_2;;B_2;;C_2) ) , то по теореме найдем координаты вектора ( vec{a} ):
( vec{a} = left{ begin{vmatrix} B_1 & C_1 \ B_2 & C_2 end{vmatrix} ; ; ;
begin{vmatrix} C_1 & A_1 \ C_2 & A_2 end{vmatrix} ; ; ; begin{vmatrix} A_1 & B_1 \ A_2 & B_2 end{vmatrix} right} =
(l; m; n) )
Параметрические уравнения прямой
Иногда прямую полезно задавать не в виде канонических уравнений (2), а иначе. Пусть прямая L задана уравнениями (2). Обозначим
через t каждое из равных отношений. Тогда
$$ frac{x-x_0}{l} = frac{y-y_0}{m} = frac{z-z_0}{n} = t $$
откуда
$$ x=x_0+lt, ;; y=y_0+mt, ;; z=z_0+nt tag{3} $$
Равенства (3) называются параметрическими уравнениями прямой L, проходящей через точку ( M_0(x_0;y_0;z_0) ) и имеющей
направляющий вектор ( vec{a}(l;m;n) ). В уравнениях (3) t рассматривается как произвольно изменяющийся параметр
( (-infty < t < +infty ) ) ; x, y, z – как функции от t. При изменении t величины x, y, z изменяются, так что точка
( M(x;y;z) ) движется по данной прямой.
Параметрические уравнения удобны в тех случаях, когда требуется найти точку пересечения прямой с плоскостью. В самом деле,
пусть непараллельные плоскость ( pi ) и прямая ( L ) заданы соответственно уравнениями
( Ax + By + Cz + D = 0 )
( x=x_0+lt, ;; y=y_0+mt, ;; z=z_0+nt )
Для определения точки пересечения прямой и плоскости подставим выражения для x, y, z из уравнений L в уравнение ( pi ).
В результате преобразований получаем
$$ t= -frac{Ax_0 + By_0 + Cz_0 + D }{Al+Bm+Cn} $$
причем знаменатель дроби не равен нулю, так как плоскость не параллельна прямой. Подставляя найденное значение t в уравнения прямой,
находим искомую точку ( M(x;y;z) ) пересечения прямой ( L ) с плоскостью ( pi ).
Угол между прямыми
Рассмотрим две прямые ( L_1 ) и ( L_2 ), заданные соответственно уравнениями
$$ frac{x-x_1}{l_1} = frac{y-y_1}{m_1} = frac{z-z_1}{n_1} $$
$$ frac{x-x_2}{l_2} = frac{y-y_2}{m_2} = frac{z-z_2}{n_2} $$
При любом расположении прямых ( L_1 ) и ( L_2 ) в пространстве один из двух углов между ними равен углу ( varphi ) между их
направляющими векторами ( vec{a_1}(l_1;m_1;n_1) ) и ( vec{a_2}(l_2;m_2;n_2) ), а второй угол равен ( 180^circ – varphi ).
Угол ( varphi ) вычисляется по следующей формуле:
$$ cos varphi = frac{l_1 l_2 + m_1 m_2 + n_1 n_2}{sqrt{l_1^2 + m_1^2 + n_1^2} ; sqrt{l_2^2 + m_2^2 + n_2^2} } $$
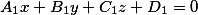
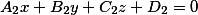
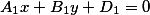
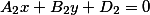
)
=0)
=0)
)
)


