Содержание:
- Цилиндры
- Упражнение
- Поверхности второго порядка
- Сфера и ее уравнение
- Цилиндрические поверхности
- Цилиндры второго порядка
- Эллипсоид
- Гиперболоиды
- Параболоиды
- Конические поверхности
- Поверхность вращения
- Понятие о поверхности второго порядка
- Общее уравнение поверхности второго порядка, основные определения
- Цилиндрические и конические поверхности
- Исследование формы поверхностей второго порядка методом сечений
Поверхностью второго порядка в пространстве 

Рассмотрим частные виды поверхностей второго порядка. Сфера с центром в точке 





Раскрыв скобки и перенеся 




По этой ссылке вы найдёте полный курс лекций по высшей математике:
Цилиндры
Цилиндрической называется поверхность, описываемая прямой, остающейся параллельной некоторому направлению и пересекающей данную линию. Последняя называется направляющей цилиндрической поверхности, а сама прямая — образующей. Пусть, например, образующие цилиндрической поверхности параллельны оси 

в плоскости 





Ясно, что абсциссы и ординаты точек 



Итак, уравнение (2.55) на плоскости
определяет эллипс, а в пространстве
— эллиптический цилиндр с образующей, параллельной
направляющей которого является указанный эллипс.
Возможно вам будут полезны данные страницы:
Упражнение
Изобразите самостоятельно:
1) гиперболический цилиндр с уравнением 

2) параболический цилиндр с уравнением 
Поверхности второго порядка
Определение. Поверхности второго порядка называют геометрическое место точек пространства, декартовые координаты которых удовлетворяют уравнению второй степени.
Сфера и ее уравнение
Сферой называют геометрическое место точек пространства, равноудаленное от заданной точки – центра сферы.
Если центром сферы является точка 

Если центр сферы находится в начале координат 

Цилиндрические поверхности
Поверхность называется цилиндрической, если она образуется прямой (образующая), параллельно к заданной прямой 

Если образующая цилиндрической поверхности параллельна оси 


тогда уравнение цилиндрической поверхности будет:
Уравнение 



Цилиндры второго порядка
а) Эллиптичным цилиндром называется поверхность (рис. 2.25), каноничное уравнение которой имеет вид:
Если 
б) Гиперболичным цилиндром называется поверхность, уравнение которой имеет вид (рис. 2.26):
в) Параболическим цилиндром называется поверхность, каноничное уравнение которой имеет вид (рис. 2.27):
Эллипсоид
Эллипсоидом называется поверхность, каноничное уравнение которой имеет вид (рис. 2.28):


Гиперболоиды
а) однополосный гиперболоид.
Однополосным гиперболоидом (рис. 2.29) называется поверхность, каноническое уравнение которой имеет вид :

Параболоиды
а) Эллиптическим параболоидом (рис. 2.31) называется
б) Гиперболичным параболоидом (рис. 2.32) называется поверхность, каноничное уравнение которой имеет вид:
Конические поверхности
конической поверхностью называется поверхность, которая описана прямой, что проходит через точку – вершину конуса – и что
Уравнение конуса (рис. 2.33) второго порядка имеет вид:
Поверхность вращения
Пусть в плоскости 







Аналогично правила будут иметь место и по отношению к поверхностям, которые образуют обращение плоских линий около других координатных осей.
Примеры: 1) уравнение поверхности, что образуются вращением эллипса 


2) уравнение поверхности, что образуются вращением гиперболы



Примеры решения задач:
Задача 2.126
Обозначить координаты центра сферы и ее радиус:
Решение. Предоставим заданное уравнение в виде (2.43), для этого: 1) объединяем в группы члены, которые содержат одноименные координаты;
2) выделим в группах полные квадраты. Получим:
Соизмеряя с (2.43), получим 

Задача 2.127
Эллипс с полуосями 5 и 3 вращается около своей большей оси. которая совпадает с началом координат. Сложить уравнение поверхности, что описывает эллипс при вращении.
Решение. Сложим каноническое уравнение эллипса с центром в начале координат, который размещен в плоскости
чтобы получить уравнение поверхности, которая образована вращением в плоскости 




Задача 2.128
Сложим уравнение конуса с вершиной в начале координат и направляющей:
Решение. Канонические уравнения образующих, что проходят через вершину 

Исключим 




подставим полученные значения 


Задача 2.129
Какие поверхности обозначаются уравнениями:
Решение. Каждое из уравнений содержит только две переменные 


В пространстве же каждое из них обозначается цилиндрическую поверхность с образующими, что параллельны оси 





Задача 2.130
Гипербола с полуосями 3 и 4 вращается около своей мнимой оси, которая совпадает с осью 
Решение. Сложим каноничное уравнение гиперболы с центром в начале координат, что находятся в плоскости
Чтобы сложить уравнение поверхности, образованной вращением гиперболы, что находится в уравнение гиперболы вместо 

Следует, получим однополосный гиперболоид вращения:
Понятие о поверхности второго порядка
Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению.
Общее уравнение поверхности второго порядка, основные определения
Поверхностью второго порядка называется множество точек пространства 


где 



Уравнение (10.27) называют общим уравнением поверхности второго порядка. Вид поверхности и ее расположение относительно координатных плоскостей зависит от значений параметров в (10.27).
Если не существует ни одной точки 
Поверхность называется вырожденной, если ее общее уравнение описывает точку, одну или две плоскости. К примеру:



При изучении поверхностей второго порядка решаются две взаимно обратные основные задачи:
1) по известным геометрическим свойствам точек поверхности составить уравнение соответствующей поверхности;
2) по известным уравнением поверхности установить геометрические свойства ее точек.
Примером решения первой основной задачи является построение уравнения сферы (9.2). Уравнение других важнейших поверхностей рассматриваются ниже.
Цилиндрические и конические поверхности
Цилиндрической поверхностью, или просто цилиндром, называется поверхность, образованная движением прямой, перемещается параллельно самой себе вдоль фиксированной линии (кривой). Подвижную прямую называют образующей, а фиксированную кривую – направляющей цилиндрической поверхности. Направляющей может быть любая сомкнутая или разомкнутая линия.
Цилиндром второго порядка называется цилиндрическая поверхность, направляющей которой является кривая второго порядка: эллипс (круг), гипербола, парабола. Название цилиндра определяется названием его направляющей. Если образующая параллельна одной из координатных осей, а направляющая лежит в плоскости, перпендикулярной этой оси, то уравнение цилиндра совпадает с уравнением направляющей. При геометрической интерпретации изображается, как правило, часть поверхности между двумя плоскостями, перпендикулярными образующей.
К примеру:



Рис. 10.9
Отсутствие переменной 


Если в уравнениях эллипса и гиперболы положить 
Конической поверхностью, или конусом, называется поверхность, образованная движением прямой, проходящей через заданную точку, вдоль фиксированной кривой. Подвижную прямую называют образующей, заданную точку – вершиной, а фиксированную кривую – направляющей конуса. Если образующей является кривая второго порядка, то поверхность называется конусом второго порядка.
На рис. 10.10 изображен конус второго порядка, определяется уравнением
Рис. 10.10
с вершиной в начале координат, направляющей которого является эллипс
в плоскости
Поверхность симметрична относительно начала координат, а координатные плоскости является ее плоскостями симметрии. Множество точек поверхности с неотъемлемыми (неположительные) аппликатами называется верхней (нижней) полостью конуса.
Если направляющей конуса является круг 
Эллипс, парабола, гипербола – кривые второго порядка – можно получить сечением прямого кругового конуса плоскостями, которые не проходят через его вершину (рис. 10.11). А именно: если плоскость пересекает только одну полость конуса и непараллельных одной из его образующих, то кривой сечения является эллипс; в частном случае – круг;
если секущая плоскость параллельна одной из образующих конуса, то результат сечения – парабола;
если плоскость сечения пересекает обе полости конуса, то кривой сечения является гипербола.
Рис. 10.11
Исследование формы поверхностей второго порядка методом сечений
Приведенные выше уравнения поверхностей второго порядка складывались по геометрическим свойствам их точек в соответствии с определений поверхностей. Для решения обратной задачи (по данным уравнением поверхности определить ее вид) применяется метод сечений, суть которого заключается в следующем:
1) анализируют поверхность, устанавливая за ее уравнением линии пересечения (сечения) данной поверхности координатными плоскостями параллельными им;
2) синтезируют определенные на предыдущем шаге геометрические свойства поверхности, что позволяет представить вид поверхности и изобразить ее.
Продемонстрируем применение метода сечений к исследованию уравнения эллиптического параболоида:
Исследование предполагает такие шаги:
1) найдем линии пересечения поверхности (10.28) с плоскостью 

Если:
а) 


б) 

в) 
то есть сечением поверхности плоскостями, параллельными 

2) установим линию пересечения поверхности с плоскостью 
Это уравнение параболы, расположенной в плоскости 

Рис. 10.12
3) определим (аналогичным образом) сечение поверхности плоскостью 



4) изображаем согласно рассмотренным выше соответствующие линии (рис. 10.12), что позволяет составить представление о форме исследуемой поверхности. Наконец намечаем обвод – линию, получается как множество точек прикосновения к поверхности прямых, параллельных выбранном направления проектирования.
Аналогично осуществляется построение параболоида 

Поверхностью вращения называется поверхность, для которой каждый из ее сечений плоскостью, перпендикулярной одной из координатных осей или произвольной оси 


Уравнения поверхностей, симметричные относительно координатных осей или / и координатных плоскостей, называют каноническими, или стандартными.
В заключение отметим, что приведенные сведения используются при изучении интегрирования функций двух переменных и является фундаментом для более глубокого изучения теории поверхностей второго порядка.
Далее в таблице 10.1 приводятся канонические уравнения и изображения важнейших поверхностей второго порядка.
Важнейшие поверхности второго порядка Таблица 10.1
Лекции:
- Уравнения с одной переменной
- Найдите координаты точки пересечения графиков
- Геометрический смысл производной в точке
- Двойной интеграл: примеры решения
- Асимптотическое поведение функций. Сравнение бесконечно малых функций
- Координаты вектора
- Определение производной
- Первый замечательный предел: пример решения
- Метод вариации постоянных
- Система показательных уравнений
Здание Планетария Тихо Браге, Копенгаген, его крыша является примером цилиндрического сечения
Цили́ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Связанные определения[править | править код]
- Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей).
- Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями, ограничивающими цилиндр, называются основаниями этого цилиндра.
- Часть цилиндрической поверхности, находящаяся между плоскостями оснований, называется боковой поверхностью цилиндра.
- Высотой цилиндра называется отрезок, высекаемый плоскостями его оснований на прямой, перпендикулярной им, или длина этого отрезка.
Типы цилиндров[править | править код]
- Прямым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), прямая между которыми перпендикулярна плоскостям этих оснований. Данная прямая называется осью цилиндра.
- Косым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), отрезок между которыми не перпендикулярен плоскостям этих оснований.
- Круговым называется цилиндр с окружностью в роли направляющей.
- Цилиндром вращения, или прямым круговым цилиндром (часто под цилиндром подразумевают именно его) называется цилиндр, который можно получить вращением (то есть тело вращения) прямоугольника вокруг одной из его сторон, содержащая которую прямая в таком случае будет осью этого цилиндра и его осью симметрии.
- Цилиндр, основания которого являются эллипсами, параболами или гиперболами, называют соответственно эллиптическим, параболическим и гиперболическим; последние два имеют бесконечный объём.
- Призма также является разновидностью цилиндра — с основанием в виде многоугольника.
- Равносторонним называется цилиндр вращения, диаметр основания которого равен его высоте[1].
Свойства[править | править код]
- Если плоскость основания цилиндра параллельна плоскости направляющей, то граница этого основания будет по форме совпадать с направляющей кривой.
Площадь поверхности цилиндра[править | править код]
Площадь боковой поверхности[править | править код]
К вычислению площади боковой поверхности цилиндра
Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.
Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой 

В частности, для прямого кругового цилиндра:
, и
, здесь и далее
— радиус основания цилиндра.
Для наклонного цилиндра площадь боковой поверхности равна длине образующей, умноженной на периметр сечения, перпендикулярного образующей:
Простой формулы, выражающей площадь боковой поверхности косого цилиндра через параметры основания и высоту, в отличие от объёма не существует. Для наклонного кругового цилиндра можно воспользоваться приближёнными формулами для периметра эллипса, а затем умножить полученное значение на длину образующей.
Площадь полной поверхности[править | править код]
Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.
Для прямого кругового цилиндра:

Объём цилиндра[править | править код]
Для наклонного цилиндра существуют две формулы:
- Объём равен длине образующей, умноженной на площадь сечения цилиндра плоскостью, перпендикулярной образующей.
,
- Объём равен площади основания, умноженной на высоту (расстояние между плоскостями, в которых лежат основания):
,
- где
— длина образующей, а
— угол между образующей и плоскостью основания. Для прямого цилиндра
.
Для прямого цилиндра 


Для кругового цилиндра:

где d — диаметр основания.
Примечания[править | править код]
- ↑ Математический справочник
Цилиндрические поверхности
Определение.
Цилиндрической
поверхностью
называется множество параллельных
прямых (образующих), проходящих через
все точки некоторой линии, называемой
направляющей.

Пусть цилиндрическая
поверхность задана таким образом в
прямоугольной системе координат OXYZ,
что образующие этой
поверхности
параллельны оси OZ, а направляющая лежит
в плоскости OXY и задается уравнением:
F(x,у)
=0
Если
взять произвольную точку M(z,y,z) на
цилиндрической поверхности, то ее
проекция на плоскость OXY есть точка
M1(х1,у1,0).
Так как точки M и М1
лежат на образующей, то х1=х,
у1=у.
А так как точка М1
лежит на направляющей, то координаты
точки М1,
а, значит, и точки M, удовлетворяют
уравнению F(x,у)=0.
Итак, уравнению удовлетворяют координаты
любой точки
цилиндрической
поверхности. Следовательно, уравнение
F(x,у)=0
– искомое
уравнение цилиндрической поверхности.
Если в прямоугольной системе координат
OXYZ направляющая является кривой второго
порядка, задаваемой каноническим
уравнением вида F(x,у)=0, а образующие
параллельны оси OZ, то цилиндрическими
поверхностями второго порядка будут:
-
х2+y2=z2
—
прямой круговой цилиндр;
2)
–
эллиптический цилиндр;
3)
–гиперболический
цилиндр;
4) у2=2рх
– параболический
цилиндр.
Заметим,
что характерной чертой уравнения
рассматриваемых цилиндрических
поверхностей, является отсутствие в
этих уравнениях одной из переменных.
Конические поверхности
Определение.
Конической
поверхностью
называется множество прямых (образующих),
проходящих через некоторую точку
(вершину)
и пересекающих некоторую линию
(направляющую).
Коническая
ПВП —
коническая поверхность с направляющей,
являющейся КВП.

Если
вершина совпадает с началом прямоугольной
системы координат OXY, а направляющей
служит эллипс:
То
уравнение конической поверхности имеет
вид:
– уравнение
конической поверхности

Поверхности вращения
Определение.
Поверхность называется поверхностью
вращения,
если она вместе с каждой своей точкой
содержит и всю окружность, полученную
вращением этой точки вокруг некоторой
фиксированной прямой, называемой осью
вращении.
Пусть
на плоскости YOZ задана кривая линия l
уравнением вида
F(y,z)=0
Тогда
уравнение поверхности вращения,
образованной вращением кривой l вокруг
оси OZ имеет вид:
Эллипсоид
Гиперболоид.
Однополостный
гиперболоид:
Каноническое
уравнение двухполоcного
гиперболоида
имеет вид:
Параболоид
Эллиптический
параболоид.
z=ах2+by2
(а,b>0).
Гиперболический
параболоид.
z=-ax2+by2
(a,b>0)
Литература:
1.
Александров П.С. Курс аналитической
геометрии и линейной алгебры. – М: Наука,
1979.
2.
Биркгоф Г., Барти Т. Современная прикладная
алгебра. – М.: Мир, 1976.
3.
Бузланов А.В., Монахов В.С. Лабораторные
работы по курсу «Алгебра и теория чисел».
– Гомель: Ротапринт ГГУ им. Ф. Скорины,
1991.
4.
Бузланов А.В., Каморников С.Ф., Кармазин
А.П. Лабораторные работы по курсу «Алгебра
и теория чисел» (раздел «Линейная
алгебра») для студентов математического
факультета. Часть I, II, III. – Гомель:
Ротапринт ГГУ им. Ф. Скорины, 1990, 1991.
5.
Бурдун А.А., Мурашко Е.А., Толкачёв М.М.,
Феденко А.О. Сборник задач по алгебре и
аналитической геометрии. – Мн.:
Университетское, 1989.
6.
Ильин В.А., Позняк Э.Г. Аналитическая
геометрия. – М.: Наука, 1982.
7.
Ильин В.А., Позняк Э.Г. Линейная алгебра.
– М.: Наука, 1974.
8.
Курош А.Г. Курс высшей алгебры. – М.:
Наука, 1968.
9.
Милованов М.В., Тышкевич Р.И., Феденко
А.С. Алгебра и аналитическая геометрия.
Часть I, II. – Мн.: Вышэйшая школа, 1984, 1987.
10. Рублёв А.Н. Курс
линейной алгебры и аналитической
геометрии. – М.: Вышэйшая школа, 1972.
Учебное
издание
ХОДАЛЕВИЧ
АЛЕКСАНДР ДМИТРИЕВИЧ
БОРОДИЧ
РУСЛАН ВИКТОРОВИЧ
РЫЖИК
ВАЛЕНТИНА НИКОЛАЕВНА
Соседние файлы в папке Методички
- #
09.03.20161.58 Mб24~WRL3761.tmp
- #
- #
- #
6.2. Цилиндрические поверхности
Или цилиндры. Под цилиндром также понимают геометрическое тело.
И это не совсем то, что обычно подразумевает обыватель – класс цилиндрических поверхностей не ограничивается чёрным цилиндром на голове:
Задача 167
Построить поверхность, заданную уравнением
…что за дела?! Не опечатка ли здесь? Вроде как дано уравнение эллипса…

Нет, здесь не опечатка и все дела происходят именно в пространстве! Исследуем предложенную поверхность тем же методом, что использовали для плоскостей. Перепишем уравнение в виде , из которого следует, что «зет» принимает любые значения. Зафиксируем
и построим в плоскости
эллипс
. Так как «зет» принимает все значения, то построенный эллипс непрерывно «тиражируется» вверх и вниз до бесконечности.
Данная поверхность называется эллиптическим цилиндром. Эллипс (на любой высоте) называется направляющей цилиндра, а параллельные прямые, проходящие через каждую точку эллипса называются образующими цилиндра (которые в прямом смысле слова его и образуют).
Ось является осью симметрии поверхности (но не её частью!).
Координаты любой точки, принадлежащей данной поверхности, обязательно удовлетворяют уравнению .
Пространственное неравенство задаёт «внутренность» бесконечной «трубы», включая саму цилиндрическую поверхность, и, соответственно, противоположное неравенство
определяет множество точек вне цилиндра.
В практических задачах наиболее популярен частный случай, когда направляющей цилиндра является окружность:
Задача 168
Построить поверхность, заданную уравнением
Бесконечную «трубу» изобразить невозможно, поэтому художества ограничиваются, как правило, «обрезком».

Сначала удобно построить окружность радиуса в плоскости
, а затем ещё пару окружностей сверху и снизу.
Полученные окружности (направляющие цилиндра) аккуратно соединяем 4 параллельными прямыми (образующими цилиндра):
Не забываем использовать пунктир для невидимых нам линий!
Координаты любой точки, принадлежащей данному цилиндру, удовлетворяют уравнению . Координаты любой точки, лежащей строго внутри «трубы», удовлетворяют неравенству
, а неравенство
задаёт множество точек внешней части. Для лучшего понимания рекомендую рассмотреть несколько конкретных точек пространства и убедиться в этом самостоятельно.
Часто эту поверхность некорректно называют круговым цилиндром. Круглым! Круговой цилиндр, строго говоря – есть тело, по той причине, что его направляющей является круг. И тело, кстати, определяется неравенством .
Задача 169
Построить поверхность и найти её проекцию на плоскость
Перепишем уравнение в виде , из которого следует, что «икс» принимает любые значения. Зафиксируем
и в плоскости
изобразим окружность
– с центром в начале координат, единичного радиуса. Так как «икс» непрерывно принимает все значения, то построенная окружность порождает цилиндр с осью симметрии
. Рисуем ещё одну окружность (направляющую цилиндра) и аккуратно соединяем их прямыми (образующими цилиндра). Местами получились накладки, но что делать, такой уж наклон:

На этот раз я ограничился кусочком цилиндра на промежутке и это не случайно. На практике зачастую и требуется изобразить лишь небольшой фрагмент поверхности.
Тут, к слову, получилось 6 образующих – две дополнительные прямые «закрывают» поверхность с левого верхнего и правого нижнего углов.
Теперь разбираемся с проекцией цилиндра на плоскость . Многие читатели понимают, что такое проекция, но, тем не менее, проведём очередную физкульт-пятиминутку:
Пожалуйста, встаньте и склоните голову над чертежом так, чтобы остриё оси смотрело перпендикулярно вам в лоб. То, чем с этого ракурса кажется цилиндр – и есть его проекция на плоскость
. А кажется он бесконечной полосой, заключенным между прямыми
, включая сами прямые. Данная проекция – это в точности область определения функций
(верхний «жёлоб» цилиндра),
(нижний «жёлоб»).
Давайте заодно проясним ситуацию и с проекциями на другие координатные плоскости. Пусть лучи солнца светят на цилиндр со стороны острия и вдоль оси . Тенью (проекцией) цилиндра на плоскость
является аналогичная бесконечная полоса – часть плоскости
, ограниченная прямыми
(
– любое), включая сами прямые.
А вот проекция на плоскость несколько иная. Если смотреть на цилиндр из острия оси
, то он спроецируется в окружность (не круг!) единичного радиуса
, с которой мы начинали построение.
Задача 170
Построить поверхность и найти её проекции на координатные плоскости
Это задача для самостоятельного решения. Если условие не очень понятно, возведите обе части в квадрат и проанализируйте результат – выясните, какую именно часть цилиндра задаёт функция . Используйте методику построения, неоднократно применявшуюся выше. Краткое решение, чертёж и комментарии в конце книги.
Цилиндрические поверхности могут быть смещены относительно координатных осей, например:
– данное уравнение (по знакомым мотивам линий 2-го порядка) задаёт цилиндр единичного радиуса с линией симметрии, проходящей через точку
параллельно оси
.
Однако на практике подобные цилиндры попадаются довольно редко, и совсем уж невероятно встретить «косую» относительно координатных осей цилиндрическую поверхность.
Параболические цилиндры
Как следует из названия, направляющей такого цилиндра является парабола.
Задача 171
Построить поверхность и найти её проекции на координатные плоскости.
Не мог удержаться от этого примера =)
Решение: идём проторенной тропой. Перепишем уравнение в виде , из которого следует, что «зет» может принимать любые значения. Зафиксируем
и построим обычную параболу
на плоскости
, предварительно отметив тривиальные опорные точки
. Поскольку «зет» принимает все значения, то построенная парабола непрерывно «тиражируется» вверх и вниз до бесконечности. Откладываем такую же параболу, скажем, на высоте (в плоскости)
и аккуратно соединяем их параллельными прямыми (образующими цилиндра):
Напоминаю полезный технический приём: если изначально нет уверенности в качестве чертежа, то линии сначала лучше прочертить тонко-тонко карандашом. Затем оцениваем качество эскиза, выясняем участки, где поверхность скрыта от наших глаз, и только потом придаём нажим грифелю.
Теперь вторая часть задания, отыскание проекций:
1) Проекцией цилиндра на плоскость является парабола
.
2) Проекция цилиндра на плоскость представляет собой полуплоскость
, включая ось
3) И, наконец, проекцией цилиндра на плоскость является вся плоскость
.
Тренируемся самостоятельно:
Задача 172
Построить параболические цилиндры:
а) , ограничиться фрагментом поверхности в ближнем полупространстве;
б) на промежутке
В случае затруднений не спешим и рассуждаем по аналогии с предыдущими примерами, благо, технология досконально отработана. Не критично, если поверхности будут получаться немного корявыми – важно правильно отобразить принципиальную картину.
Я и сам особо не заморачиваюсь над красотой линий – если получился сносный чертёж «на троечку», обычно не переделываю. В образце решения, кстати, использован ещё один приём, позволяющий улучшить качество чертежа 😉
Гиперболические цилиндры
Направляющими таких цилиндров являются гиперболы.

Этот тип поверхностей, по моим наблюдениям, встречается значительно реже, и поэтому я ограничился единственным схематическим чертежом гиперболического цилиндра .
Принцип рассуждения здесь точно такой же – обычная «школьная» гипербола из плоскости
непрерывно «размножается» вверх и вниз до бесконечности.
Переходим к следующей поверхности:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Содержание:
Поверхностью называется совокупность последовательных положений некоторой линии
Закон перемещения линии
На Рис.8.1 закон перемещения линии 
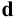
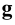
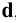
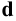
Если образующая 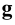
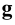
В дальнейшем будем рассматривать только линейчатые поверхности с одной направляющей. К ним относятся конические, цилиндрические и многогранные поверхности.
Коническая поверхность (Рис.8.2, а) однозначно определяется прямолинейной образующей 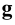
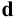
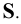
Цилиндрическая поверхность (см. Рис.8.2, б) получается в случае, когда все прямолинейные образующие пересекаются в несобственной точке
Плоскость (см. Рис.8.2, в) является частным случаем цилиндрической или конической поверхности, когда и образующая и направляющая являются прямыми и все образующие пересекаются в несобственной точке 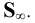
Что такое поверхность
Поверхность – абстрактная фигура, не имеющая толщины. Она ограничивает какое-либо тело, состоящее из металла, пластмассы и т.д. Тело – конечно, а поверхность может быть бесконечна. Например, шар ограничен сферой; боковой поверхностью конуса является коническая поверхность.
Способы задания поверхности
Существует несколько способов задания поверхности, в том числе: кинематический, аналитический и графический.
Внедрение в инженерную практику компьютерных технологий обусловило совместное использование графических и аналитических методов задания поверхностей.
С точки зрения аналитической геометрии:
Поверхность – непрерывное множество точек, координаты которых связаны в декартовой системе координат уравнением вида 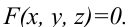
Поверхность – совокупность непрерывных последовательных положений линий, движущихся в пространстве по определенному закону.
Эта движущаяся линия называется образующей, а линия, по которой она движется – направляющей.
Поверхность считается заданной, если по одной проекции точки, принадлежащей ей, можно построить вторую проекцию. Совокупность независимых условий, необходимых и достаточных для однозначного определения поверхности, называется определителем поверхности: 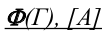
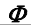
- (Г) – геометрическая часть определителя поверхности – совокупность геометрических фигур, образующих поверхность;
- [A] – алгоритмическая часть определителя поверхности – закон перемещения образующей.
Например, определитель конической поверхности имеет следующий вид:
где 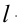
- а – направляющая;
- S – точка пересечения образующих.
Алгоритмическая часть определителя читается следующим образом:
Любая образующая 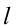
На чертеже поверхность может быть задана:
- Набором элементов, определяющих эту поверхность.
- Очерком поверхности.
- Каркасом поверхности.
Очерком поверхности называется проекции контура поверхности на плоскости проекций.
Каркасный способ задания поверхности предполагает, что поверхность можно определить как двупараметрическое множество точек с одной стороны, а, с другой, поверхность – однопараметрическое множество линий.
Каркасом (точечным или линейным) называется множество точек или линий, определяющих поверхность.
Каркасным способом задаются такие сложные поверхности с образующими переменного вида, которые нельзя описать математически.
Классификация поверхностей
Существует множество различных подходов к классификации поверхностей. Однако главными из них являются следующие критерии:
1. Закон образования поверхности:
- –поверхности закономерные – если закон их образования известен и может быть выражен математически;
- – незакономерные.
2. Вид образующей:
- – поверхности линейные –образующая прямая линия;
- – поверхности нелинейные (криволинейные) –образующая кривая линия.
3. Закон движения образующей:
- – поверхности переноса – с поступательным движением образующей;
- – поверхности вращения – с вращательным движением образующей;
- – винтовые поверхности – с винтовым движением образующей.
4. Постоянность (вариабильность) формы образующей:
- – поверхности с образующей постоянной формы;
- – поверхности с образующей переменной формы.
5. Возможность развертывания поверхности:
- – Развертываемые – поверхности, совмещаемые с плоскостью без складок и разрывов:
- – неразвертываемые.
Очевидно, что любую поверхность можно классифицировать одновременно по нескольким признакам.
Например, цилиндрическая поверхность вращения:
- линейчатая закономерная развертываемая поверхность вращения;
- циклическая поверхность переноса окружности постоянного радиуса;
- алгебраическая поверхность второго порядка.
Из всего множества поверхностей в кратком курсе начертательной геометрии мы будем рассматривать только гранные поверхности и поверхности вращения.
Поверхность
Поверхность – это наружная сторона предмета, или граница, отделяющая геометрическое тело от внутреннего пространства или другого тела (толковый словарь русского языка под редакцией Д.Н. Ушакова).
Поверхность можно рассматривать как непрерывную совокупность последовательных положений линий, перемещающихся в пространстве по определенному закону. Движущуюся линию в этом случае называют образующей поверхности, а линии (а иногда и точки), определяющие закон ее перемещения, – направляющими.
Виды способов задания поверхности
Аналитический
Поверхность рассматривается как геометрическое место точек, координаты которых удовлетворяют некоторому заданному уравнению вида F (x, y, z ) = 0 (рис. 6.1). Порядок уравнения соответствует порядку поверхности. Порядок поверхности можно определить и геометрически, как порядок кривой, по которой плоскость пересекает поверхность, или как число точек пересечения прямой с поверхностью.
Рис. 6.1. Аналитические поверхности:
Аналитический способ задания поверхности находит широкое применение в практике, особенно если требуется исследовать свойства поверхности.
Кинематический
Кинематическую поверхность можно рассматривать как непрерывную совокупность последовательных положений линии, перемещающейся в пространстве по некоторым неподвижным линиям. Таким образом, на любой кинематической поверхности можно выделить два семейства линий: семейство образующих и семейство направляющих. Направляющие и образующие обладают следующим свойством: никакие две линии одного семейства не пересекаются между собой, но каждая линия одного семейства пересекает все линии другого.
Рассмотрим формирование конической поверхности (рис. 6.2). Такая поверхность образована движением прямой образующей l, постоянно проходящей через точку S и во всех своих положениях пересекающей некоторую направляющую кривую m. Если направляющая m – окружность, каждая точка которой равноудалена от вершины S, образуется прямой круговой конус.
Совокупность точек, линий и различных условий, определяющих закон перемещения образующей, называют также определителем поверхности. Например, определителем конуса вращения могут быть ось и образующая или вершина и направляющая линия. Определителем цилиндра вращения может быть ось и образующая (прямая или кривая) или ось и направляющая (окружность). Окружность может быть и направляющей линией цилиндра и его образующей. В начертательной геометрии все поверхности рассматриваются как кинематические, то есть образованные непрерывным перемещением в пространстве какой – либо линии или поверхности.
Рис. 6.2. Образование конической поверхности:
S – вершина конической поверхности;
m – направляющая;
l1, l2… In – последовательные положения образующей
Каркасный
Поверхности, к которым нельзя применить математические закономерности или поверхности с произвольными образующими называются скульптурными или поверхностями произвольных форм (рис. 6.3). Такие поверхности обычно задают достаточно плотной сетью линий и точек, принадлежащих этим поверхностям. Совокупность таких линий называется каркасом поверхности. При этом точки, лежащие между линиями каркаса, определяются приближенно.
Одним из наиболее распространенных в промышленности методов конструирования поверхностей является метод конструирования с помощью непрерывного каркаса. Метод каркасного конструирования используется при изготовлении кузовов автомобилей, самолетов и в судостроении, для выполнения штампов при изготовлении поверхностей из листового материала, в топографии, горном и дорожном деле.
Рис. 6.3. Скульптурная поверхность
Классификация поверхностей
1. По способу задания:
- • аналитические;
- • кинематические;
- • скульптурные (поверхности произвольных форм).
2. По закону движения образующей:
- • с поступательным движением образующей;
- • с вращательным движением образующей;
- • с винтовым движением образующей.
3. По виду образующей:
- • поверхности с прямолинейной образующей или линейчатые поверхности;
- • поверхности с криволинейной образующей.
4. По закону изменения формы образующей:
- • поверхности с образующей постоянного вида;
- • поверхности с образующей переменного вида.
5. По признаку развертывания:
- • развертывающиеся поверхности – можно совместить с плоскостью без разрывов и складок. Сюда относятся поверхности всех многогранников, цилиндрические, конические, торсовые.
- • неразвертывающиеся – нельзя совместить с плоскостью без разрывов и складок. Сюда относятся все остальные поверхности.
Наибольшее распространение в технике получили поверхности вращения, сдвига и винтовые.
Поверхности вращения
Поверхности вращения – поверхности, образованные вращением произвольной образующей вокруг неподвижной оси (рис. 6.4,а). Направляющей поверхности вращения является окружность постоянного (цилиндр) или переменного радиуса (конус, сфера). Нормальное – перпендикулярное оси вращения сечение любой поверхности вращения, представляет собой окружность с центром на ее оси.
Рис. 6.4. Поверхность вращения:
а – основные линии на поверхности вращения;
б – представление поверхности вращения в виде сети
Направляющие называют также параллелями поверхности вращения. Плоскости параллелей перпендикулярны к оси поверхности. Наибольшую из параллелей называют экватором поверхности, наименьшую – горлом. Плоскости, проходящие через ось поверхности вращения, называют меридиональными, а линии, по которым они пересекают поверхность -меридианами. Поверхность вращения можно представить параллелями или меридианами поверхности, а также сетью, состоящей из параллелей и меридианов (рис. 6.4,б).
Поверхность вращения называют закрытой, если меридиональное сечение поверхности является замкнутой кривой линией, пересекающей ось поверхности в двух точках.
При вращении вокруг оси плоской или пространственной алгебраической кривой n – го порядка образуется алгебраическая поверхность вращения, в общем случае, 2n-го порядка. Если кривая второго порядка вращается вокруг своей оси, то она образует поверхность второго порядка.
В зависимости от вида образующей различают:
Торовые поверхности – поверхности, образованные вращением окружности или дуги окружности:
Рис. 6.5. Торовые поверхности:
а – сфера; б – открытый тор (кольцо); в – закрытый тор; г – глобоид
- Сфера образуется вращением окружности вокруг оси, проходящей через ее центр (рис. 6.5,а).
- Тор образуется вращением окружности вокруг оси, лежащей в плоскости этой окружности и не проходящей через ее центр (тор является поверхностью четвертого порядка). Различают открытый тор, образованный вращением окружности вокруг оси, которая не пересекает образующую (рис. 6.5, б) и закрытый тор, образованный вращением окружности вокруг оси, которая пересекает образующую окружность или касается ее (рис. 6.5,в).
- Глобоид образуется вращением окружности достаточно большого радиуса вокруг оси, которая не пересекает образующую (рис. 6.5,г).
- Эллипсоид вращения образуется вращением эллипса вокруг его оси. Если за ось вращения принята большая ось эллипса, эллипсоид вращения называют вытянутым (рис. 6.6. а),если малая – сжатым или сфероидом (рис. 6.6,б). Земной шар, например, по форме близок к сфероиду.
Параболоид вращения образуется вращением параболы вокруг ее оси (рис. 6.7, а). Параболоиды вращения используются в качестве отражающей поверхности в прожекторах и фарах автомобилей для получения параллельного светового пучка.
Рис. 6.7. Поверхности вращения:
а – параболоид;
б – однополостной гиперболоид;
в – двуполостной гиперболоид;
Гиперболоид вращения образуется вращением гиперболы. Различают однополостный гиперболоид (рис. 6.7,б), образованный вращением гиперболы вокруг ее мнимой оси, и двуполостный гиперболоид (рис. 6.7,в), образованный вращением гиперболы вокруг ее действительной оси.
Конус вращения (прямой круговой конус) образуется вращением вокруг оси кривой 2-го порядка, распадающейся на две пересекающиеся прямые (рис. 6, а).
Рис. 6.8. Поверхности вращения:
а – конус; б – цилиндр
Цилиндр вращения (прямой круговой цилиндр) образуется вращением вокруг оси кривой 2-го порядка, распадающейся на две параллельные прямые (рис. 6.8,б).
Поверхности сдвига
Поверхности сдвига или так называемые поверхности экструдий -поверхности, образованные смещением произвольной образующей вдоль произвольной направляющей (рис. 6.9, 6.10). Образующие и направляющие поверхности сдвига могут быть как постоянного, так и переменного вида.
Рис. 6.9. Поверхности сдвига:
а – наклонный цилиндр; б – наклонный конус
Рис. 6.10. Поверхности сдвига, применяемые в технике:
а – коническое зубчатое колесо; б – швеллер; в – змеевик
Винтовые поверхности
Винтовые поверхности – поверхности, образованные вращением произвольной образующей вокруг неподвижной оси с одновременным смещением в осевом (поверхность цилиндрической резьбы, рис. 6.11,а) или осевом и радиальном направлении (коническая пружина, рис. 6.11,б). Направляющей винтовой поверхности является винтовая линия.
Рис. 6.11. Винтовые поверхности:
а – поверхность трапециидальной резьбы;
б – поверхность конической пружины
Изображение поверхностей на комплексном чертеже
На комплексном чертеже изображается очерк поверхности, а также наиболее важные линии и точки на поверхности.
Рис. 6.12. Образование очерка поверхности
Очерк поверхности – линия, которая ограничивает проекцию поверхности. Для получения очерка поверхности проводят множество проецирующих лучей в направлении проецирования s, касательных к данной поверхности. Точки касания поверхности и проецирующих лучей образуют линию l, называемую контурной линией. Совокупность проецирующих лучей образует проецирующую цилиндрическую поверхность, проекция которой и представляет собой очерк l’ данной поверхности на соответствующей плоскости проекций П‘ (рис. 6.12). Очерк поверхности можно определить и как проекцию контурной линии на заданную плоскость проекций. Очерк поверхности является границей видимости поверхности.
Построение очерков конических поверхностей
Фронтальный очерк поверхности наклонного конуса представляет собой равнобедренный треугольник A2B2S2. Горизонтальный очерк поверхности наклонного конуса с круговым основанием состоит из дуги окружности основания и касательных, проведенных из проекции вершины конуса (рис. 6.13).
Рис. 6.13. Построение очерка поверхности наклонного конуса с круговым основанием
Для построения касательных на П1 вершину конуса S нужно соединить с центром окружности основания O1. Затем отрезок делится пополам и строится вспомогательная окружность радиусом O’1S1. Точки C1 и D1 пересечения вспомогательной окружности и окружности основания и являются точками касания. Угол O 1 D 1 S 1 – прямой.
Фронтальный очерк поверхности прямого кругового конуса, ось которого является фронталью, представляет собой равнобедренный треугольник A2B2S2 (см. рис. 6.14).Горизонтальный очерк состоит из части эллипса и двух касательных к нему прямых. Эллипс можно построить по двум осям малой А 1 B 1 и большой C1C1‘, равной диаметру окружности основания конуса (см. пп. 12.4.1,рис. 12.11).
Рис. 6.14. Построение очерка поверхности прямого кругового конуса
Для определения прямых (SD) и (SD’), касательных к эллипсу, используется произвольная вспомогательная сфера с центром О(О1О2) на оси конуса, касательная к его поверхности. Из произвольной точки О(О1О2) на оси конуса восстанавливаются перпендикуляры (О2M2)и (О2N2) на образующие (S2A2)и (S2B2). Линия (M2N2)-проекция линии касания конуса и вспомогательной сферы. Затем определяются фронтальные проекции случайных точек искомых касательных K2 и K’2 как точки пересечения полученной линии (MN) и экватора вспомогательной сферы. Далее определяются горизонтальные проекции K1 и K’1 на горизонтальной проекции экватора вспомогательной сферы. Прямые (S 1 K1)и (S 1 K’ 1)касаются эллипса в точках D 1 и D’ 1.
Построение очерков цилиндрических поверхностей
Для построения фронтального очерка поверхности наклонного цилиндра с круговым основанием (рис. 6.15) строятся проекции верхнего и нижнего оснований – (A2B2) и (A’2B’2)u очерковые образующие (A2A2) и (B2B’2).
Для построения горизонтального очерка строят окружности верхнего и нижнего оснований, затем через центры окружностей проводятся перпендикуляры (C 1 D 1)и (C’ 1 D’ 1) к оси цилиндра.
Рис. 6.15. Построение очерка наклонного цилиндра с круговым основанием
Определение поверхности
Поверхности в геометрии рассматриваются либо как двумерные множества точек, либо как одномерные множества линий. Второе определение наиболее соответствует конструированию поверхностей с использованием кинематического метода.
Этот подход (в соответствии с рисунком 8.1) предполагает формирование поверхности в результате перемещения одной кривой U (образующей) по другой кривой V (направляющей).
В общем случае понятия направляющей и образующей чисто условные.
Перемещение кривой V по кривой U сформирует ту же самую поверхность.
Наложение условий на форму кривых и условия перемещения позволяет формировать практически любые поверхности.
Рисунок 8.1 – Образование поверхности
Традиционно рассматривают поверхности простые, описываемые единым уравнением, и составные, состоящие из отсеков простых.
Изучение многообразия поверхностей, образуемых кинематическим способом, требует их систематизации. Это особенно важно в автоматизированном проектировании при создании информационных систем или так называемых банков данных.
Очевидно, что невозможно разработать единую, приемлемую для всех, систематизацию (классификацию) поверхностей. Сложность состоит в том, что трудно выделить единый признак классификации. Например, вполне естественно в основу систематизации положить вид образующей и закон ее перемещения.
По виду образующей различают линейчатые (образующая — прямая), циклические (образующая — окружность) и другие поверхности.
Возможна классификация и по закону перемещения образующей — поверхности вращения, параллельного переноса, винтовые и т.д. Очевидно, что при этом некоторые поверхности могут быть отнесены одновременно к различным классам. Например, цилиндрическая поверхность вращения является линейчатой и поверхностью вращения.
Все это и определило отказ от традиционного рассмотрения в пособии различного рода классификаций поверхностей.
Задание поверхности на чертеже
Для изображения поверхности на чертеже необходимо выяснить проекции каких элементов поверхности необходимо задать для того, чтобы получить обратимый чертеж.
Поверхность считается заданной, если относительно любой точки (на чертеже), можно дать однозначный ответ на вопрос: «Принадлежит ли эта точка рассматриваемой поверхности?». Другими словами, если по одной проекции точки, принадлежащей поверхности, можно построить ее вторую проекцию.
Поверхности на чертеже моделируются соответствиями, также как и плоскость, которая моделируется взаимнооднозначным соответствием — родством (раздел 3).
Возможны два способа задания таких соответствий: аналитический и графический.
При аналитическом задании, в общем случае, поверхность может быть определена уравнением в неявном виде F(x,y,z) = 0, в явном виде z =f(x,y), или параметрической форме х = X(u,v), у= Y(u,v), z = Z(u,v). Параметры u и v получили название криволинейных координат (рисунок 8.1).
Рисунок 8.2-Линейчатый каркас
Графическое задание также предусматривает несколько вариантов. Один из них непосредственно вытекает из аналитического способа.
Табулирование уравнений, задающих поверхность, позволяет получить либо двухпараметрическое множество точек, либо два однопараметрических семейства линий. Эти семейства определяют, так называемый каркас поверхности (точечный или линейчатый). Изображение этих каркасов на чертеже позволяет говорить о каркасном задании поверхности (рисунок 8.2).
Еще один, самый распространенный, графический способ — задание поверхности (отсека) очерками.
При проецировании произвольной поверхности на плоскость проекций некоторые из проецирующих прямых будут касаться этой поверхности и образовывать некоторую проецирующую (цилиндрическую для параллельного проецирования поверхность
Линия касания этих поверхностей называется контурной линией, а ее проекция на соответствующую плоскость – очерком.
В соответствии с рисунком 8.3 поверхность прямого кругового конуса на комплексном чертеже задана своими очерками (горизонтальным очерком 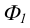
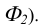
Рисунок 8.3 – Прямой круговой конус
Рисунок 8.4 – Сфера
Пользуются при задании кинематических поверхностей и понятием определителя. Под определителем кинематической поверхности понимают совокупность независимых условий, однозначно определяющих эту поверхность. Условиями могут быть: задание образующей поверхности, закон ее изменения (в случае переменной образующей), закон движения образующей и др. Некоторые из них могут быть выражены графически. Например, сфера Ф может быть представлена как поверхность вращения: Ф[i,I] (рисунок 8.4).
Условиями, включенными в определитель поверхности и определяющими ее форму, могут быть также параметры формы.
Одна и та же поверхность может быть образована несколькими способами. Поэтому она может иметь разные определители.
Все рассмотренные способы задания поверхности связаны между собой и при решении многих задач приходится переходить от одного способа задания к другому.
Точка и линия на поверхности
Обобщение определений на принадлежность точки и линии плоскости позволяет утверждать следующее:
- точка лежит на поверхности, если она лежит на линии, лежащей на поверхности;
- линия лежит на поверхности в том случае, если все ее точки лежат на поверхности.
Рисунок 8.5 – Точка на конусе
Рисунок 8.6 – Винтовая коническая линия
В соответствии с рисунком 8.5 и данным выше определением точка А лежит на поверхности конуса, заданного очерками 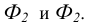
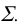
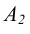
Рисунок 8.6 иллюстрирует винтовую линию l на поверхности конуса Ф, построенную по точкам.
При построении точек, лежащих на поверхностях, выбираются такие линии, лежащие на них, которые легко могут быть построены (прямые, окружности).
Конструирование поверхностей
Как уже отмечалось выше, поверхности должны отвечать определенной совокупности независимых условий (виду образующей, закону ее изменения и движения и т.д.). Все это и определяет подход к выполнению чертежей поверхностей.
Конструирование поверхностей вращения
Поверхности вращения – одни из самых распространенных, что обусловлено простотой изображения на чертеже и воспроизведения в материале.
Поверхность вращения – это поверхность, образованная вращением линии (образующей) l вокруг прямой, называемой осью поверхности i (в соответствии с рисунком 8.7).
Рисунок 8.7 – Поверхность вращения
Обычно при изображении поверхности на чертеже ось вращения выбирается перпендикулярной одной из плоскостей проекции. Окружности, по которым перемещаются все точки образующей l, называют параллелями поверхности.
Кривые, полученные в сечении поверхности плоскостями, проходящими через ось вращения, называются меридианами. Меридиан лежащий в плоскости параллельной плоскости проекции называется главным меридианом.
Параллели и меридианы поверхности вращения образуют ее непрерывный каркас, так что через любую точку поверхности проходят единственные параллель и меридиан.
Параллель с минимальным радиусом называется горловиной или горлом, а с максимальным радиусом – эквитором.
Некоторые поверхности вращения традиционно носят свои собственные названия.
Поверхности, образованные вращением прямой линии, параллельной оси вращения, называют прямыми круговыми цилиндрами (рисунок 8.8).
Рисунок 8.8 – Прямой круговой цилиндр, конус вращения, параболоид вращения
Поверхности, образованные вращением прямой линии пересекающей ось вращения в точке S (вершине конуса), называют конусами вращения (рисунок 8.8).
Рисунок 8.9 – Сфера и тор
Другие поверхности вращения, если образующая имеет собственное название, называют по ее имени при условии, что ось вращения совпадает с осью симметрии кривой. Например, параболоид вращения (рисунок 8.8).
Особняком здесь стоит окружность. Если ось вращения совпадает с осью симметрии окружности, то такую поверхность называют сферой, если же нет, то – тором (рисунок 8.9).
Конструирование поверхностей плоскопараллельного переноса
Еще один тип поверхностей, часто используемых в практике, – это поверхности плоскопараллельного переноса. В некоторых векторных графических пакетах (AutoCAD, CorelDraw и др.) эти поверхности называют поверхностями сдвига, что не совсем верно.
Поверхность “заметается” плоской образующей l, которая перемещается в пространстве по плоской направляющей m, оставаясь параллельной самой себе (рисунок 8.10).
Рисунок 8.10-Поверхность плоскопараллельного переноса
По этой схеме могут быть получены такие поверхности, как цилиндр общего вида (рисунок 8.10), плоскость (образующая и направляющая прямые линии), параболический параболоид (рисунок 8.11) и другие.
Конструирование линейчатых поверхностей
Линейчатые поверхности образуются при движении прямой линии (образующей) по заданному закону. Закон движения обычно задается направляющими. В качестве направляющих обычно рассматривают линии. Хотя направляющими могут быть и поверхности (образующая перемещается, касаясь этой поверхности), и другие геометрические элементы.
Например, коническая поверхность образуется при движении прямолинейной образующей, проходящей через фиксированную точку (вершину) и пересекающей направляющую кривую. Коническая поверхность с несобственной вершиной называют цилиндрической поверхностью.
Из определения линейчатой поверхности следует, что ее образующая в каждый момент времени должна занимать строго определенное положение. Такое возможно только при наличии трех направляющих. Поэтому линейчатые поверхности называются еще поверхностями с тремя направляющими. Действительно, взяв на направляющей а произвольную точку A, мы можем провести через нее, по крайней мере, одну образующую l, пересекающую другие две направляющие b, с. Точка А и направляющая b определяют коническую поверхность 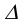
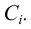

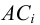
Эти направляющие – а, b, с – и входят в определитель линейчатой поверхности с тремя направляющими, что символически записывается так: Ф(а, b,с).
Среди линейчатых поверхностей выделяют поверхности с плоскостью параллелизма. Их также называют поверхностями Каталана. Образующие l этих поверхностей пересекают направляющие кривые а, b и параллельны плоскости параллелизма Г— собственному представителю несобственной направляющей прямой
В зависимости от вида направляющих а, b поверхность с плоскостью параллелизма называется цилиндроидом, коноидом или косой плоскостью.
Цилиндроидом называется линейчатая поверхность с плоскостью параллелизма, у которой направляющие — кривые линии.
Каркас образующих цилиндроида на комплексном чертеже строится весьма просто, если в качестве плоскости параллелизма принята одна из плоскостей проекций или проецирующая плоскость. На рисунке 8.13 построен каркас образующих цилиндроида с направляющими а, b и параллельными плоскости параллелизма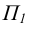
Рисунок 8.13 – Цилиндроид
Рисунок 8.14 – Коноид
Коноидом называется линейчатая поверхность с плоскостью параллелизма, имеющая одну криволинейную и вторую прямолинейную направляющие.
На чертеже коноид задается аналогично цилиндроиду. Построение каркаса образующих не отличается от цилиндроида.
На рисунке 8.14 приведен чертеж коноида, получившего в инженерной практике название «прямой клин». Направляющими коноида являются эллипс а и прямая /?, плоскость параллелизма zOy. Эта поверхность несет на себе каркас эллипсов в плоскостях параллельных
Косой плоскостью называется линейчатая поверхность с плоскостью параллелизма и прямолинейными направляющими (рисунок 8.15).
Она больше известна под названием гиперболического параболоида, так как несет на себе каркас не только прямых, но и гипербол и парабол. Из аналитической геометрии известно, что гиперболический параболоид содержит два семейства прямолинейных образующих, параллельных двум плоскостям параллелизма.
Линейчатая поверхность, образованная множеством касательных к пространственной кривой, получила называние торсовой или поверхностью с ребром возврата (рисунок 8.15). Направляющая кривая t поверхности называется ребром возврата. Примером торсовой поверхности может служить хорошо известная коническая поверхность, у которой ребро возврата выродилось в точку (вершину конуса).
Рисунок 8.15 – Косая плоскость и поверхность с ребром возврата
Многогранники
Многогранником называется тело, ограниченное плоскими многоугольниками. Поверхность, ограничивающая многогранник, — составная. Элементами этой поверхности являются вершины, ребра и грани; совокупность всех ребер многогранника называют его сеткой. Многогранник называется выпуклым, если весь он лежит по одну сторону от плоскости любой его грани; тогда грани его — тоже выпуклые многоугольники.
Построение ограничивающей поверхности многогранника сводится к построению проекций ее сетки.
Среди всего многообразия многогранников наибольший практический интерес представляют призмы, пирамиды, а также правильные выпуклые многогранники.
Чертеж призмы приведен на рисунке 8.16. Гранями призмы служат четырехугольные отсеки плоскостей. Все ребра призмы параллельны между собой. Вопрос о принадлежности точки и линии поверхности сводится к определению принадлежности этих элементов плоским граням.
Пирамида (рисунок 8.17) ограничена составной поверхностью, у которой грани представлены треугольниками.
Все ребра пирамиды пересекаются в одной точке S, которую называют вершиной пирамиды.
Поверхность призмы можно рассматривать, как поверхность пирамиды, у которой вершина — несобственная точка
Рисунок 8.16 – Призма
Рисунок 8.17 – Пирамида
Циклические и непрерывно-топографические поверхности
Циклической поверхностью называется поверхность, образованная непрерывным каркасом круговых сечений (рисунок 8.18). Циклическая поверхность несет на себе, по крайней мере, одно семейство круговых образующих. Циклическая поверхность является частным видом поверхностей подобных сечений.
Рисунок 8.18 – Поверхность подобных сечений
Для однозначного определения поверхности подобных сечений должны быть заданы три линии a,t,b где, а — линия определяющая параметрическое семейство плоскостей, перпендикулярных этой линии; t — линия центров окружностей; b – линия, определяющая величины радиусов окружностей.
Примером таких поверхностей, имеющих круговые сечения, т. е. представляющим собой разновидность циклических поверхностей, могут служить эллиптический цилиндр, конус вращения, эллипсоид, однополостной и двуполостной гиперболоиды и др.
Кинематические поверхности сложной формы традиционно называют поверхностями зависимых линий. Типичным представителем поверхностей зависимых линий являются топографические поверхности.
Топографическими называют поверхности, заданные дискретным множеством линий уровня (рисунок 8.19). Такое представление поверхностей широко распространено в топографии, строительстве, военном деле и др. На ранних этапах развития авиации, автомобилестроения и судостроения сложные поверхности самолетов, автомобилей и судов задавались также в виде дискретного множества линий уровня. Получали сетчатый каркас поверхности, состоящий из трех семейств линий уровня: батоксов (вертикальных линий), горизонталей и поперечных сечений (шпангоутов).
Рисунок 8.19 — Топографическая поверхность
Вопросы о принадлежности точки пространства для таких поверхностей решаются однозначно только на линиях каркаса поверхности.
В геометрии выделяют непрерывно топографические поверхности, образованные непрерывным множеством линий уровня. Эти поверхности широко применяют в авиации, судостроении, автомобилестроении, архитектуре и др.
Определитель, такой поверхности, состоит из проекций однопараметрического семейства линий уровня в какой-либо одной плоскости проекций и закона распределения линий семейства в пространстве (рисунок 8.20).
Рисунок 8.20 – Непрерывно топографическая поверхность
Порядок конструирования такой поверхности следующий: в одной из плоскостей проекций задается однопараметрическое семейство линий q.
Затем в пространстве выбирается распределяющая линия m.
И последнее: устанавливается взаимно однозначное соответствие между точками «распределяющей» линии т и каждой линией семейства
Пересечение поверхности плоскостью
При пересечении поверхности плоскостью получается плоская фигура, которую называют сечением. Построение сечения поверхности плоскостью целесообразно начать с пересечения многогранников плоскостью.
Многогранником называют пространственную фигуру, ограниченную рядом плоскостей, имеющих форму многоугольников. Стороны многоугольников образуют рёбра, а плоскости – грани.
Проекциями сечения многогранников в общем случае являются многоугольники, вершины которых принадлежат рёбрам, а стороны – граням многогранника. Поэтому задачу по определению сечения многогранника плоскостью можно решать способом рёбер или способом граней. Способ рёбер заключается в нахождении точек встречи прямой (ребро многогранника) с плоскостью. Способ граней сводится к построению линии пересечения двух плоскостей (грань многогранника и секущая плоскость). Какому способу отдать предпочтение, нужно решать в каждом конкретном случае отдельно. Рассмотрим примеры построения многогранников плоскостью.
Пример 1 Построить проекции сечения прямой призмы плоскостью общего положения (см. Рис.8.3).
В случае рёбра призмы ABCDEF перпендикулярны плоскости 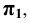
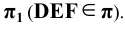
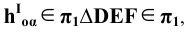
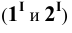
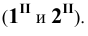
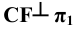
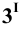
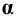
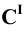
Фронтальная проекция точки 3 определяется из условия принадлежности её плоскости 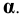
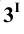
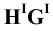
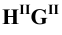
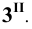
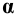
Необходимо отметить, что если бы плоскость 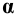
Пример 2 Построить сечение трёхгранной пирамиды горизонтально – проецирующей плоскостью (см. Рис.8.4).
При таком расположении секущей плоскости 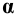
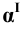
Пример 3 Построить проекции сечения наклонной пирамиды плоскостью общего положения (см. Рис.8.5). Определить истинную величину фигуры сечения.
В данном случае целесообразно методом перемены плоскостей проекций преобразовать плоскость 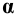
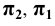
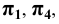
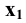
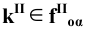
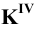
Далее строим проекцию пирамиды на плоскость 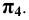
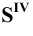
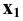
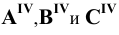
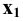
Фронтальная проекция сечения пирамиды плоскостью Р принадлежит следу 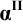
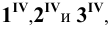
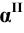
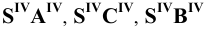
Чтобы определить истинную величину фигуры сечения, необходимо произвести замену плоскости 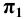
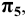
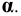
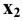
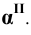
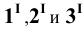
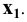
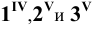
При нахождении точек сечения поверхности вращения плоскостью целесообразно применять способ вспомогательных секущих плоскостей, которые пересекают поверхность по окружностям или по образующим. Построение проекций сечения начинают с отыскания проекций характерных (опорных) точек. К ним относятся точки, проекции которых расположены на проекциях контурных (очерковых) образующих поверхности, так как в этих точках изменяется видимость проекций линии пересечения. Характерными будут также точки перехода линии пересечения с боковой поверхности тела на его основание ( если плоскость пересекает основание) и точки, проекции которых являются наивысшими наинизшими. Рассмотрим некоторые приме-
Пример 4 Построить проекции сечения прямого и кругового цилиндра плоскостью общего положения (см. Рис.8.6).
Построение начнём с отыскания характерных точек. Проекции точек линии пересечения, расположенных на контурных образующих, найдём с помощью вспомогательной фронтальной плоскости 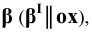
Плоскость 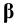
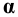
Точка 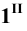
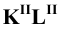
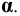
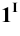
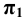
Вторая контурная образующая в пределах заданной поверхности с плоскостью 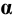
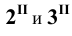
Наивысшая и наинизшая точки проекции сечения на плоскости а определяются с помощью вспомогательной горизонтально – проецирующей плоскости 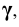
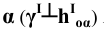
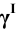
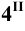
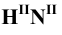
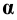
Промежуточные точки 5 и 6 линии сечения строим с помощью вспомогательной плоскости 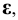
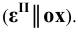
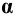
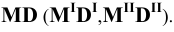
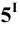
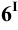
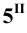
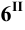
Соединяя фронтальные проекции 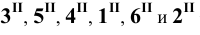
В нашем случае (см. Рис.8.7) плоскость 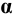
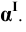
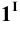
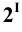
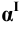
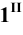
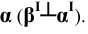
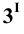
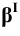
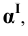
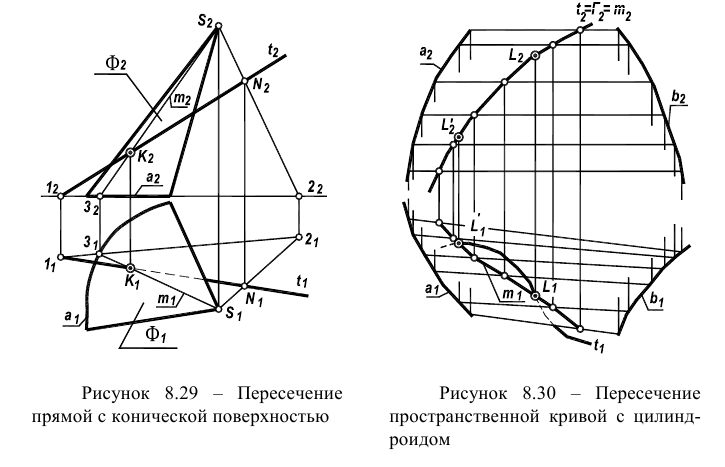
Пример 6 Построить проекции сечения поверхности прямого кругового конуса плоскостью 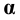
Построение начинаем с нахождения точек 1 и 2, расположенных на очерковых образующих. Для этого проводим вспомогательную плоскость 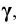
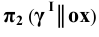
Она пересекает плоскость 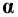
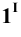
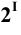
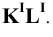
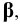

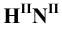
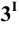
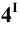
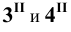
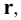
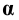
На пересечении 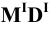
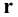
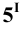
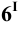
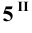
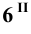
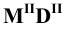
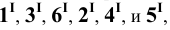
Пример 7 Построить проекции сечения поверхности конуса плоскостью, проходящей через его вершину (Рис.8.9).
Факт принадлежности точки S (вершина конуса) плоскости 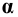
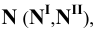
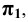
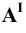
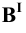
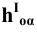
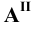
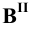
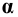
Пример 8 Построить проекции сечения поверхности сферы горизонтально-проецирующей плоскостью 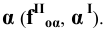
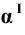
Горизонтальные проекции точек 1 и 2 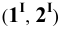
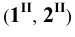
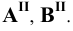
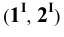
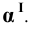
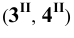
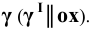
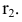
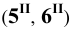
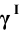
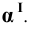
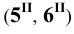
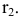
Пример 9 Построить проекции сечения поверхности сферы плоскостью общего положения 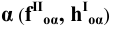
Развёртка поверхностей
Рассмотрим развёртки поверхностей вращения и многогранников. Под развёрткой многогранной поверхности понимают плоскую фигуру, составленную из граней этой поверхности, совмещённых с одной плоскостью. Существуют три способа построения развёртки многогранных поверхностей:
- способ нормального сечения
- способ раскатки
- способ треугольников Рассмотрим все три способа на примерах.
Пример 10 Построить развёртку поверхности прямой трёхгранной призмы ABCDEF (Рис.8.12).
Построение начинаем с пересечения призмы ABCDEF плоскостью 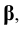
Так как плоскость 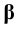
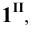
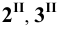
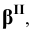
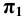
Для построения развёртки необходимо определить истинную величину рёбер и сторон треугольника, получившегося в сечении призмы плоскость 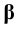
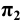
Далее в свободном месте чертежа проводим прямую и от произвольной точки 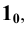
На развёртку нанесена точка К из условия:
Пример 11 Построить развёртку поверхности наклонной призмы с основанием в плоскости 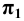
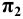
Развёртку боковой поверхности заданной призмы будем строить последовательным вращением всех её граней, которое представляет перекатывание призмы по фронтальной плоскости, проходящей через одно из рёбер призмы. Во избежание наложения развёртки на изображение призмы начинаем вращать её вокруг ребра FC. При вращении грани FCBE вокруг ребра FC точки В и Е перемещаются по окружности в плоскостях, перпендикулярных к ребру FC. Фронтальные проекции 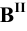
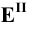
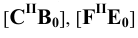
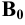
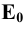
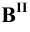
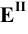
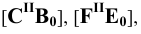
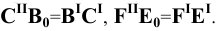
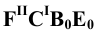
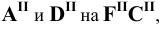
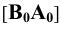
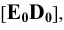

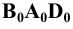
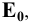
Изображение точки К на боковой поверхности построено из условия:
Если рёбра призмы не параллельны ни одной из плоскостей проекций, то этот общий случай методом перемены плоскостей проекций приводят к рассмотренному ранее частному случаю.
Пример 12 Построить развёртку поверхности трёхгранной пирамиды с основанием в плоскости 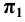
В данном случае в истинную величину проецируется на плоскость 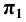
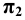
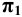
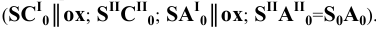
Для этого на произвольной прямой откладываем отрезок 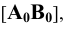
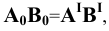
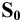
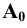
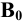
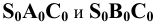
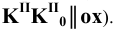
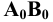
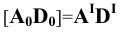
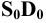
Развёртка поверхности вращения является чаще всего приближённой. Это объясняется тем, что при развёртке поверхности последнюю, как правило, аппроксимируют поверхностями вписанных или описанных многогранников. Поэтому при графическом выполнении развёртки приходится спрямлять кривые, принадлежащие поверхности, что ведёт к потере точности.
Пример 13 Построить развёртку поверхности прямого кругового конуса
В данном случае развёртка боковой поверхности представляет круговой сектор, радиус которого равен длине образующей 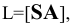
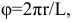
Пример 14 Построить развёртку боковой поверхности наклонного конуса с круговым основанием (Рис.8.16).
Окружность основания заменяем многоугольником со сторонами 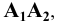
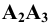
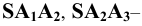
Определив способом вращения длину отрезка 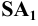
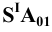
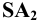
Соединив построенные точки и т. д. плавной кривой, получаем развёртку боковой поверхности наклонного конуса. Для получения полной развёртки поверхности конуса необходимо достроить его основание.
Пересечение линии с поверхностью
В общем случае для решения задачи по определению положения точек пересечения (встречи) линии с поверхностью необходимо выполнить ряд построений:
- заключить данную линию во вспомогательную поверхность ( плоскость);
- определить линии пересечения вспомогательной поверхности (плоскости) с заданной;
- отметить точки, в которых пересекаются полученные линии с заданной.
С целью упрощения записи целесообразно использовать символику, приведённую в таблице:
Пример 15 Определить точки пересечения прямой MN с поверхностью I прямой призмы (Рис.8.17).
В соответствии с записанным ранее алгоритмом заключаем прямую MN в горизонтально проецирующую плоскость 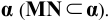
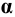
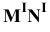
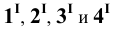
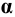
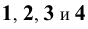
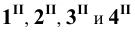
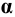
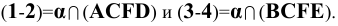
Пример 16 Определить точки пересечения прямой MN с поверхностью I наклонной призмы (Рис.8.18).
Решение начинаем с заключения прямой MN во фронтально – проецирующую плоскость 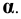
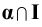
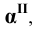
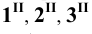
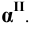
Горизонтальные проекции 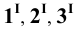
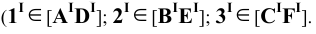
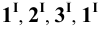
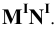
Пример 17 Определить точки пересечения прямой MN с поверхностью I пирамиды (Рис.8.19).
Заключаем прямую MN во фронтально -проецирующую плоскость 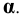
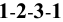
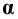
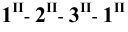
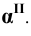
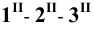
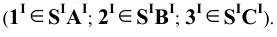
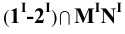
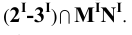
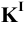
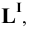
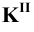
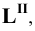
Пример 18 Определить точки пересечения прямой MN с поверхностью 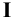
Заключаем прямую MN в плоскость 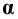
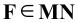
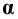
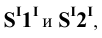
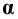
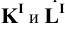
Фронтальные проекции 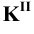
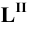
Пример 19 Определить точки пересечения прямой MN с поверхностью I наклонного цилиндра (Рис.8.21).
Заключаем прямую MN в плоскость 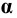
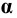
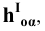
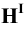
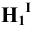
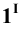
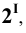
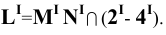
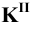
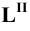
Взаимное пересечение поверхностей
Две поверхности пересекаются по линии, точки которой принадлежат одновременно обеим поверхностям. Способ построения линии пересечения двух поверхностей состоит в следующем:
- заданные поверхности пересекаются вспомогательной поверхностью (плоскостью), удобной для решения задачи;
- находят линии пересечения вспомогательной поверхности (плоскости) с каждой из данных;
- отмечают точки, в которых пересекаются полученные линии пересечения.
Повторив названные операции k раз, получим множество точек, образующих искомую линию пересечения двух поверхностей.
Рассмотрим примеры построения линии пересечения двух поверхностей.
Пример 20 Построить линию пересечения двух I и II, оси которых пересекаются под прямым углом (Рис.8.22).круговых цилиндров
Решение задачи начинаем с нахождения высших 1 и 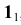
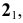
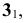
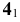
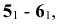
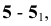
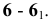
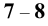
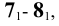
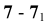
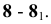
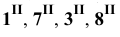
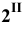
Построение линии пересечения поверхностей многогранников может быть осуществлено двумя способами. По первому способу определяют точки, в которых рёбра одной поверхности пересекают грани другой и наоборот: рёбра второй поверхности пересекают грани первой. Затем через найденные точки в определённой последовательности проводят ломаную линию, представляющую собой линию пересечения данных поверхностей. Второй способ состоит в определении отрезков прямых, по которым греши одной поверхности пересекают грани другой. Эти отрезки являются звеньями ломаной линии, получаемой при пересечении заданных поверхностей между собой.
Пример 21 Построить линию пересечения прямой трёхгранной призмы I с трёхгранной пирамидой II (Рис.8.23).
При решении данной задачи применим первый способ нахождения линии пересечения. В нашем случае трёхгранная пирамида как бы «входит» в одну грань и «выходит» из другой грани. Для нахождения точек пересечения ребра SC пирамиды с гранями призмы заключаем его во вспомогательную горизонтально – проецирующую плоскость 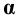
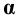
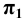
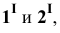
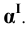
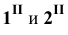
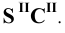
Пример 22 Построить линию пересечения наклонной призмы I и пирамиды II (Рис.8.24).
Для определения точек пересечения рёбер пирамиды с гранями призмы заключаем рёбра во фронтально – проецирующие плоскости 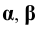
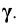
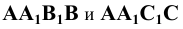
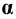
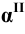
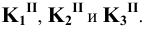
Отмечаем точки 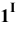
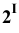
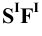
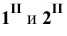
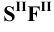
В такой же последовательности построены точки встречи рёбер SE и SD пирамиды с гранями призмы (точки 3, 4, 5 и 6).
С целью получения точек пересечения рёбер призмы с гранями пирамиды ребра призмы заключаем во фронтально – проецирующие плоскости 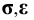
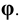
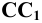
– находим фронтальные проекции 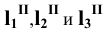
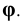
– отмечаем точки 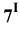
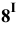
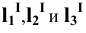
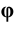
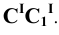
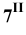
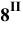
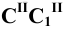
Проведя аналогичные построения для рёбер 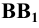
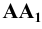
Соединяем полученные точки пересечения. При этом необходимо учитывать следующее обстоятельство. Так как каждое звено искомой пространственной ломаной является линией пересечения граней двух различных многогранников, то соединять прямыми можно лишь точки, которые одновременно принадлежат одним и тем же граням пересекающимся многогранников. Таким образом на Рис 8.22 построены замкнутые ломаные 2-8-4-6-7-2 и 1-3-5-1. При этом точки 2 и 8 первой ломаной соединены потому, что они лежат в общих для них гранях SEF пирамиды 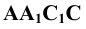
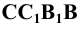
Отметим видимость звеньев построенной ломаной. При этом видимым будет звено, по которому пересекаются две видимые грани. Если хотя бы одна из граней невидима, то и звено искомой линии, расположенное на этой грани, будет невидимым. Поэтому звено 2-8 показано видимым, а звено 8-4 невидимым.
Пример 23 Построить линию пересечения поверхности I правильной призмы с поверхностью II кругового цилиндра (Рис.8.25).
Построения начинаем с нахождения точек 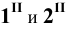
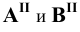
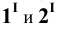
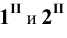
Затем определяем точки 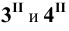
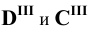
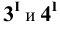
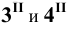
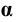
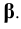
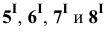
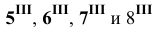
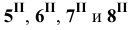
Найденные фронтальные проекции 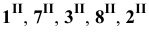
Геометрические тела – призма и пирамида
Многогранником называют геометрическое тело, поверхность которого ограничена плоскостями (гранями). Многогранник называют четырех-, пяти-, шестигранником и т. д. по количеству граней (включая основания), образующих его поверхность. На чертеже многогранник задают проекциями его граней и ребер (ребро – линия пересечения граней).
Рассмотрим призму и пирамиду – геометрические многогранники (тела), которые часто применяются при формообразовании различных деталей. Основанием призмы и пирамиды может быть любой многоугольник, по количеству сторон которого призму и пирамиду называют треугольной, четырехугольной и т. д. Такое название более соответствует изображению этих многогранников на чертеже, по которому определяется многоугольник основания, что позволяет создать в воображении соответствующий пространственный образ.
Призма как геометрическое тело имеет два параллельных основания, боковые грани и параллельные ребра. Призму называют правильной, если ее основаниями являются правильные многоугольники, вписанные в окружность. Призму называют прямой, если ее ребра перпендикулярны основанию, и наклонной, если ребра не перпендикулярны основанию.
Пирамида как геометрическое тело имеет одно основание и вершину, объединяющую все ее ребра. Пирамиду называют правильной, если ее основанием является правильный многоугольник, вписанный в окружность, а высота пирамиды проходит через центр этой окружности (то есть пирамида прямая).
Пирамида может быть наклонной, если основание высоты не лежит в центре окружности, в которую вписан многоугольник основания пирамиды. Пирамида со срезанной вершиной имеет два основания и называется усеченной.
Построение проекций прямой правильной призмы
На рис. 7.1 показан пример построения проекций (очерков) прямой правильной призмы высотой Н с треугольником в основании, вписанном в окружность заданного диаметра; основания призмы параллельны горизонтальной плоскости проекций Н.
Для построения проекций призмы требуется выполнить графоаналитические действия в следующем порядке:
1-е действие. Построить горизонтальную проекцию призмы по заданному основанию, которая представляет собой треугольник с обозначенными вершинами А’, В’ и С’, вписанный в окружность заданного диаметра 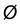
2-е действие. Выполнить графический анализ построенной горизонтальной проекции призмы:
2.1. Плоскость треугольника A’B’C’ – это горизонтальные натуральные проекции совпадающих параллельных оснований призмы, которые являются горизонтальными плоскостями уровня (//H).
2.2. Боковые стороны A’B’, B’C’ и C’A’ треугольника A’B’C’ – это горизонтальные проекции боковых граней призмы, которые спроецировались (выродились) в отрезки прямых линий, так как:
- – задняя грань АВ – фронтальная плоскость (//V);
- – передние грани ВС и СА – горизонтально-проецирующие плоскости (
H).
2.3. Вершины А’, В’ и С’ треугольника А’В’С’ – это горизонтальные проекции ребер, которые спроецировались (выродились) в точки, так как являются горизонтально-проецирующими прямыми (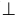
3-е действие. Построить фронтальную проекцию (очерк) призмы, которая представляет собой прямоугольник, ограниченный:
- – по заданной высоте h горизонтальными отрезками A”B”C”– проекциями оснований (//H);
- – слева – проекцией A” ребра А, построенного по вертикальной линии связи;
- – справа – проекцией B” ребра B;
- – фронтальная проекция C” ребра C – вертикальный отрезок, совпадающий с осью симметрии фронтальной проекции призмы.
4-е действие. Выполнить графический анализ построенной фронтальной проекции призмы:
4.1. Прямоугольники A”C”C”A” и C”B”B”C” – искаженные проекции передних видимых боковых граней призмы.
4.2. Прямоугольник A”B”B”A” – натуральная величина невидимой задней грани призмы.
5-е действие. Построить профильную проекцию (очерк) призмы:
5.1. Задать на горизонтальной проекции призмы положение базовой линии, проходящей через заднюю грань АВ(А’В’), относительно которой, как от базы отсчета (б.о.), можно определить координату y для любой точки на поверхности призмы.
5.2. На поле чертежа справа от фронтальной проекции выбрать положение базовой оси z, относительно которой, как от базы отсчета (б.о.), можно построить по координатам y профильные проекции любой точки на поверхности призмы.
5.3. Профильная проекция призмы представляет собой прямоугольник, ограниченный:
- – по высоте H горизонтальными отрезками – проекциями оснований;
- – слева – вертикальным отрезком совпадающих проекций A”‘ и B”‘ ребер A и B, расположенным на выбранной базовой оси z;
- – справа – вертикальной линией С”‘ ребра C, построенного по координате yc.
6-е действие. Выполнить графический анализ построенной профильной проекции призмы.
6.1. Совпадающие прямоугольники A'”C'”C'”B'” и B'”C'”C'”B'” – искаженные проекции передних боковых граней призмы AC и BC.
6.2. Отрезок A'”-A'” (B'”-B'”) слева – вырожденная проекция задней грани призмы AB.
Построение горизонтальных и профильных проекций точек, лежащих на поверхности призмы
Принадлежность точек поверхности призмы определяется их принадлежностью ребрам и граням этой призмы.
На рис. 7.1 показан пример построения горизонтальных и профильных проекций точек D, E, G и K, лежащих на боковой поверхности призмы и заданных фронтальными проекциями:
– горизонтальные проекции D’ и F’ точек D и F, лежащих на ребрах A и C совпадают с горизонтальными проекциями этих ребер – точками А(А’) и С(С’);
- – горизонтальные проекции G’ и K’ точек G и K, лежащих на гранях АС и ВС, определяются соответственно на сторонах A’ C’ и B’C’ треугольника A’B’C’, которые являются вырожденными проекциями этих граней;
- – профильные проекции точек D и E построены по их принадлежности ребрам призмы A и С: D”‘ лежит на A”‘; E”‘ лежит на C”‘;
- – профильные проекции точек G и K построены по координатам “y”: G”‘ – определяется координатой yG; K”‘ – определяется координатой yK и на профильной проекции невидима, поскольку лежит на невидимой грани BC (взята в скобки).
!!! Запомните характерные признаки очерков призмы на чертеже – два прямоугольника и многоугольник основания.
Построение проекций правильной пирамиды
На рис. 7.2 показан пример построения проекций правильной пирамиды высотой Н с треугольником в основании, вписанном в окружность заданного диаметра 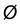
Для построения проекций пирамиды требуется выполнить графоаналитические действия в следующем порядке:
1-е действие. Построить горизонтальную проекцию пирамиды по заданному основанию, которая представляет собой треугольник, вписанный в окружность заданного диаметра 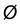
2-е действие. Выполнить графический анализ построенной горизонтальной проекции пирамиды:
2.1. Плоскость треугольника А’В’С’ – горизонтальная невидимая натуральная проекция основания пирамиды, которая является горизонтальной плоскостью уровня (//H).
2.2. Треугольники A’S’C’, A’S’B’ и B’S’C’ – горизонтальные искаженные проекции боковых граней пирамиды.
3-е действие. Построить фронтальную проекцию пирамиды, которая представляет собой треугольник, ограниченный:
- – снизу – горизонтальным отрезком A”B” – проекцией основания пирамиды (//H);
- – по заданной высоте пирамиды Н – вершиной S(S”);
- – слева – проекцией ребра SA(S”A”) (прямая общего положения);
- – справа – проекцией ребра SB(S”B”) (прямая общего положения).
Фронтальная проекция ребра SC(S”C”) (профильная прямая) совпадает с осью симметрии фронтальной проекции пирамиды.
4-е действие. Выполнить графический анализ построенной фронтальной проекции пирамиды:
4.1. Треугольники S”A”C” и S”C”B” – искаженные видимые проекции боковых передних граней пирамиды.
4.2. Треугольник S”A”B” – искаженная невидимая проекция задней невидимой грани пирамиды.
5-е действие. Построить профильную проекцию пирамиды:
5.1. Задать на горизонтальной проекции пирамиды базовую линию на стороне А’В’ основания, относительно которой, как базы отсчета (б.о.), можно определить координату y для любой точки на поверхности пирамиды.
5.2. На поле чертежа справа от фронтальной проекции выбрать положение базовой оси Z, относительно которой, как базы отсчета (б.о.), можно построить по координатам y профильные проекции любой точки на поверхности пирамиды.
5.3. Профильная проекция пирамиды представляет собой треугольник с вершинами A”‘(≡B”‘), S”‘ и C”‘:
- – точки А и В основания лежат на базовой линии, поэтому их профильные A”‘ и B”‘ проекции совпадают с выбранной базовой осью Z;
- – вершину пирамиды S”‘ построить по координате Ys на горизонтальной линии связи;
- – точку основания С”‘ построить по координате Yc.
6-е действие. Выполнить графический анализ построенной профильной проекции пирамиды:
6.1. Совпадающие треугольники S'”A'”C'” (видимый) и S'”B'”C'” (невидимый) – искаженные проекции передних боковых граней пирамиды (плоскости общего положения).
6.2. Отрезок S'”A'”(≡S'”B”‘) – вырожденная проекция задней грани пирамиды (профильно-проецирующая плоскость).
Построение проекций точек, лежащих на поверхности пирамиды
На рис. 7.2 показан пример построения горизонтальных и профильных проекций точек M, N, P и K, лежащих на поверхности пирамиды и заданных фронтальными проекциями M”, N”, P” и K”.
1. Построение горизонтальных проекций точек, лежащих на поверхности пирамиды:
- – горизонтальная проекция M’ точки М, лежащей на ребре пирамиды SA, определяется на горизонтальной проекции S’A’ этого ребра;
- – горизонтальные проекции точек N, P и K построены на вспомогательных прямых, проведенных через их заданные фронтальные проекции N”, P” и K” параллельно основанию пирамиды.
Рассмотрим графический алгоритм для построения горизонтальных проекций точек, лежащих на гранях пирамиды (на примере заданной точки P(P”)), действия которого определяются теоремами о принадлежности точки и прямой плоскости.
Графический алгоритм:
1-е действие. Провести через точку P(P”) на поверхности пирамиды вспомогательную линию d(d”), параллельную основанию пирамиды, которая пересекает ребро SA(S”A”) по вспомогательной точке 1(1″).
2-е действие. Построить горизонтальную проекцию точки 1(1′) по ее принадлежности ребру SA(S’A’).
3-е действие. Через построенную точку 1(1′) провести горизонтальную проекцию d(d’) вспомогательной линии параллельно стороне A’C’ основания пирамиды.
4-е действие. Построить по линии связи горизонтальную проекцию P’ точки Р по ее принадлежности вспомогательной линии d(d’).
Повторить действия графического алгоритма и построить аналогично горизонтальные проекции N’ и K’ точек N и K.
Проекции точек на поверхности пирамиды можно строить также с помощью вспомогательных прямых, проходящих через ее вершину. Смотри построение проекции точки K(K’) с помощью вспомогательной прямой m(m”,m’) (рис. 7.2).
2. Построение профильных проекций точек, лежащих на поверхности пирамиды:
- – профильные проекции заданных точек M и N построены по их принадлежности ребрам пирамиды:
- – M”‘ – по принадлежности ребру SA(S”‘A”‘);
- – N”‘ – по принадлежности ребру SC(S”‘C”‘);
- – профильные проекции точек Р и К построены по координатам y: P”‘ – определяется координатой yP; К”‘ – определяется координатой yK (на профильной проекции K”” невидима, так как лежит на невидимой грани SBC (взята в скобки).
!!! Запомните характерные признаки очерков пирамиды на чертеже – два треугольника и многоугольник основания. Для усеченной пирамиды – две трапеции и многоугольник основания!
Построение проекций призмы и пирамиды со срезами плоскостями частного положения
Любая плоскость пересекает поверхность призмы и пирамиды по замкнутым ломаным линиям, вершины которых лежат в точках пересечения ребер, граней и оснований многогранника с плоскостями срезов.
Следовательно, построение срезов на проекциях гранных поверхностей сводится к построению проекций точек, лежащих на поверхности призмы или пирамиды.
Построение проекций призмы со срезами плоскостями частного положения
На рис. 7.3 показан пример построения проекций прямой правильной треугольной призмы высотой H со срезами, выполненными плоскостями частного положения – фронтально-проецирующей плоскостью α и профильной плоскостью β. Для упрощения графических описаний взята призма без срезов из предыдущего примера (см. рис. 7.1), горизонтальная, фронтальная и профильная проекции которой уже построены.
Для построения проекций призмы со срезами следует выполнить предлагаемый графический алгоритм, определяющий порядок действий при решении всех подобных задач:
1-е действие. Построить тонкими линиями на поле чертежа горизонтальную, фронтальную и профильную проекции заданной прямой правильной треугольной призмы без срезов, а затем выполнить на ее фронтальной проекции срезы плоскостями частного положения по заданному условию: фронтально-проецирующей плоскостью α(αV) и профильной плоскостью β(βV).
2-е действие. Обозначить на фронтальной проекции призмы характерные точки пересечения плоскостей срезов с ребрами, гранями и основанием призмы:
- – точки 1(1″) и 2(2″) – лежат на ребрах призмы А(A”) и С(C”);
- – совпадающие точки 3(3″) и 4(4″) – лежат на гранях призмы и определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскостей срезов α и β;
- – совпадающие точки 5(5″) и 6(6″) – лежат на верхнем основании призмы и определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскости β с верхним основанием призмы.
3-е действие. Достроить горизонтальную проекцию призмы со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек, и определить видимость плоскостей срезов:
3.1. Плоскость среза α определяет четырехугольник 1′-2′-3′-4′:
- – точка 1(1′) лежит на ребре А(A’);
- – точка 2(2′) лежит на ребре С(C’);
- – совпадающие точки 3(3′) и 5(5′) лежат на передней грани СВ(C’B’);
- – совпадающие точки 4(4′) и 6(6′) лежат на задней грани АВ(А’В’).
Четырехугольник 1′-2′-3′-4′ – искаженная по величине видимая горизонтальная проекция фронтально-проецирующей плоскости среза α.
3.2. Плоскость среза β определяет совпадающие проекции отрезков 5′-6′ и 3′-4′:
- – отрезок 5′-6′(3′-4′) – горизонтальная, вырожденная в линию, видимая проекция профильной плоскости среза β (проекция прямоугольника).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции призмы для определения ее очерка и внутреннего контура:
4.1. Горизонтальный очерк определяет треугольник АВС(А’В’С’).
4.2. Внутренний контур определяет видимый отрезок 5′-6′(3′-4′).
5-е действие. Достроить профильную проекцию призмы, построив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов:
5.1. Плоскость среза α определяет видимый и искаженный по величине четырехугольник 1″‘-2″‘-3″‘-4″‘ :
- – точка 1(1″‘) – лежит на ребре А(A”‘);
- – точка 2(2″‘) – лежит на ребре С(C”‘);
- – точка 3(3″‘) – построена по координате y3;
- – точка 4(4″‘) – лежит на задней грани АВ(А'”В'”), которая спроецировалась в прямую.
5.2. Плоскость среза β определяет видимая натуральная проекция прямоугольника 3″‘-4″‘-6″‘-5″‘:
- – точки 3(3″‘) и 4(4″‘) – уже построены, так как линия пересечения плоскостей среза 3-4 принадлежит плоскости α и плоскости β;
- – точка 6(6″‘) – лежит на задней грани АВ;
- – точка 5(5″‘) – построена по координате y5(≡y3).
6-е действие. Выполнить графический анализ построенной профильной проекции призмы для определения ее очерка и внутреннего контура.
6.1. Профильный очерк определяют:
- – слева – профильная проекция ребра В(B”‘), совпадающая с проекцией грани АВ(А”‘B”‘);
- – справа – участок C”‘2″‘ ребра С и ломаная линия 2″‘-3″‘-5″;
- – снизу – отрезок А”‘(B”‘) – C”‘ нижнего основания призмы;
- – сверху – отрезок 5″‘-6″‘ – линия пересечения плоскости β с верхним основанием призмы (участок основания).
6.2. Внутренний контур определяют видимые отрезки 1″‘-2″‘ и 3″‘-4″‘.
7-е действие. Оформить чертеж призмы, обведя сплошными толстыми линиями очерки и видимые линии внутреннего контура каждой ее проекции (оставить на чертеже тонкими сплошными линиями очерки проекции призмы без срезов и линии построения).
Построение проекций пирамиды со срезами плоскостями частного положения
На рис. 7.4 показан пример построения проекций правильной треугольной пирамиды со срезами, выполненными плоскостями частного положения: фронтально-проецирующей плоскостью α и профильной плоскостью β. Для упрощения графических описаний взята пирамида без срезов из предыдущего примера (см. рис. 7.2), фронтальная, горизонтальная и профильная проекции которой уже построены.
Для построения проекций пирамиды со срезами следует выполнить предлагаемый графический алгоритм, определяющий порядок действий при решении всех подобных задач.
1-е действие. Построить тонкими линиями на поле чертежа горизонтальную, фронтальную и профильную проекции заданной правильной треугольной пирамиды без срезов, а затем выполнить на ее фронтальной проекции срезы фронтально-проецирующей плоскостью α(αV) и профильной плоскостью β(βV).
2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с ребрами и гранями пирамиды:
- – точка 1(1″) – на ребре SА(S”A”);
- – точка 2(2″) – на ребре SС(S”C”);
- – совпадающие точки 3(3″) и 4(4″) – на гранях SАВ(S”A”B”) и SВC(S”B”C”) определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскостей срезов α и β;
- – точка 5(5″) – на ребре SВ(S”B”).
3-е действие. Достроить горизонтальную проекцию пирамиды со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек, и определить видимость плоскостей срезов.
3.1. Плоскость среза α определяет четырехугольник 1-2′ -3′-4′:
- – точка 1(1′) – на ребре SА(S’A’);
- – точка 2(2′) – на ребре SC(S’C’) (построена на вспомогательной линии m//AC), см. рис. 7.4);
- – точки 3(3′) и 4(4′) лежат на гранях пирамиды и построены с помощью вспомогательной линии n //BC;
- – четырехугольник 1′-2′-3′-4′ – горизонтальная, искаженная по величине видимая проекция фронтально-проецирующей плоскости α.
3.2. Плоскость среза β определяет отрезок 3′-5′-4′ – вырожденная в видимую линию горизонтальная проекция профильной плоскости β:
- – точка 5(5′) – на ребре SВ(S’B’);
- – точки 3(3′) и 4(4′) – построены.
4-е действие. Выполнить графический анализ построенной горизонтальной проекции пирамиды со срезами для определения ее очерка и внутреннего контура.
4.1. Горизонтальный очерк определяет треугольник A’B’C’ основания пирамиды.
4.2. Внутренний контур определяют:
- – видимый отрезок A’1′ – участок ребра SA;
- – видимый отрезок B’5′ – участок ребра SB;
- – видимый отрезок C’2′ – участок ребра SC;
- – видимый четырехугольник 1′-2′-3′-4′.
5-е действие. Достроить профильную проекцию пирамиды, построив проекции плоскостей срезов по профильным проекциям обозначенных точек и определить видимость плоскостей срезов.
5.1. Плоскость среза α определяет видимый четырехугольник 1′”-2″‘-3″‘-4″‘:
- – точка 1(1″‘) – лежит на ребре SA(S”‘A'”);
- – точка 2(2″‘) – лежит на ребре SC(S”‘C”‘);
- – точка 3(3″‘) – построена по координате Y3;
- – точка 4(4″‘) – лежит на задней грани SAB(S'”A”‘B”‘), вырожденной в линию;
- – четырехугольник 1″‘-2″‘-3″‘-4″‘ – искаженная по величине видимая проекция фронтально-проецирующей плоскостью α.
5.2. Плоскость среза β определяет видимая натуральная проекция треугольника 3″‘-4″‘-5″‘:
- – точки 3(3″‘) и 4(4′”) – уже построены (отрезок 3-4 – линия пересечения плоскостей среза α и β);
- – точка 5(5″‘) – лежит на ребре SB(S”‘B”‘);
- – отрезок 3″‘-5″‘//S”‘C”‘.
6-е действие. Выполнить графический анализ построенной профильной проекции пирамиды со срезами для определения ее очерка и внутреннего контура.
6.1. Профильный очерк определяют:
- – слева – отрезок B”‘5″‘ – участок ребра S”‘B”‘;
- – справа – отрезок C”‘2″‘ – участок ребра S”‘C”‘ и ломаная линия 2′”-3″‘-5″;
- – снизу – горизонтальная линия проекции основания ABC(A”‘B”‘C”‘).
6.2. Внутренний контур определяют:
- – видимый отрезок 1″‘-2′”;
- – видимый отрезок 3″‘-4′” (линия пересечения плоскостей α и β).
7-е действие. Оформить чертеж пирамиды, выполнив сплошными толстыми линиями очерки и видимые линии внутреннего контура каждой ее проекции (тонкими линиями оставить на чертеже очерки проекции пирамиды без срезов и вспомогательные линии построения).
Поверхности вращения
Поверхностью вращения называют поверхность, образованную вращением некоторой линии (образующей поверхности) вокруг неподвижной прямой, называемой осью вращения. При этом образующая, вращаясь вокруг оси вращения, может пересекать окружность, называемую направляющей поверхности. Образующей поверхности вращения может быть кривая или прямая линия. Поверхность вращения называют линейчатой, если ее образующей является прямая линия, и криволинейной, если образующая – кривая линия.
На рис. 7.5 показана поверхность вращения общего вида, образующая которой (кривая линия) вращается вокруг горизонтально-проецирующей оси i. Все точки образующей вращаются вокруг оси i по окружностям соответствующего радиуса, которые называют параллелями поверхности. На фронтальную и профильную проекции поверхности эти параллели проецируются в прямые линии, перпендикулярные оси вращения. На горизонтальную проекцию параллели проецируются в виде окружностей. Некоторые параллели имеют определенные общепринятые наименования:
- – горло поверхности – параллель наименьшего (минимального) радиуса;
- – экватор – параллель наибольшего (максимального) радиуса.
Проекции поверхности вращения:
- – горизонтальная проекция, то есть ее горизонтальный очерк, определяется окружностью экватора k(k’);
- – фронтальная проекция, то есть ее фронтальный очерк, образуется замкнутой линией главного фронтального меридиана m(m”), полученного при пересечении этой поверхности фронтальной плоскостью уровня α(αH), проходящей через ось вращения i;
- – профильная проекция, то есть ее профильный очерк, образуется замкнутой линией главного профильного меридиана n(n”‘), полученного при пересечении этой поверхности профильной плоскостью уровня β(βH), проходящей через ось вращения i.
Построение проекций точек на поверхности вращения
Принадлежность точки поверхности вращения определяется ее принадлежностью параллели, по которой точка вращается вокруг оси вращения.
Проекции точек, лежащих на экваторе или на главных фронтальном и профильном меридианах поверхности, строятся по их принадлежности этим характерным линиям.
На рис. 7.5 показан пример построения невидимой фронтальной проекции характерной точки B (B’;B”-?), лежащей на экваторе k, по ее заданной горизонтальной проекции B (B’) и построение профильной проекции характерной точки C(C”;C”‘-?), лежащей на главном профильном меридиане “n”, по ее заданной фронтальной проекции.
Для построения проекций точки A(A”; A”-?; A”‘-?), заданной своей фронтальной проекцией и не лежащей на характерных линиях поверхности, требуется выполнить следующий графический алгоритм:
1-е действие. Провести через заданную фронтальную проекцию точки A(A”) параллель, которая имеет радиус RA.
2-е действие. Провести на горизонтальной проекции поверхности окружность-параллель радиусом RA.
3-е действие. Построить по вертикальной линии связи горизонтальную видимую проекцию точки A(A’) по ее принадлежности построенной параллели радиусом RA.
4-е действие. Построить профильную проекцию точки A(A”‘) на горизонтальной линии связи по координате YA (лежит на невидимой части поверхности, проекция взята в скобки).
Видимость точек на проекциях поверхности вращения
На рис. 7.5 показаны границы видимости поверхности для каждой проекции по направлению взгляда на плоскости проекций H, V и W.
Видимость точек на проекциях поверхности определяется этими границами, то есть видимостью части поверхности на каждой проекции: если часть поверхности является по направлению взгляда на соответствующую плоскость проекций видимой, то точка на этой проекции будет также видимой.
На рис. 7.5 видно, что горизонтальная проекция B’ заданной точки B, лежащей на экваторе, расположена на невидимой части поверхности при взгляде на фронтальную плоскость проекций V. Следовательно, ее фронтальная проекция B” лежит на экваторе, но будет невидимой (проекция взята в скобки). Профильная проекция B”‘ точки будет видимой, так как точка лежит на видимой для профильной проекции части поверхности (см. взгляд по стрелке на плоскость W). Поскольку заданная фронтальная проекция точки C, лежащей на фронтальной проекции n(n”) главного профильного меридиана, не взята в скобки, значит, она лежит на видимой для фронтальной проекции части поверхности и профильная проекция точки C(C”‘) должна лежать на профильной проекции главного меридиана n(n”‘) справа от оси вращения. Горизонтальная же проекция точки С (на рисунке не построена) по направлению взгляда на горизонтальную плоскость проекций H будет невидима, так как расположена под экватором. Соответственно профильная проекция точки A(A”‘) будет невидимой, так как лежит на невидимой для профильной проекции части поверхности.
!!! К поверхностям вращения относятся две линейчатые поверхности с прямолинейными образующими – цилиндр и конус, а также поверхности с криволинейными образующими – сфера (образующая – окружность), эллипсоид (образующая – эллипс), одно- и двуполостные гиперболоиды (гипербола), параболоид (парабола), торовые (окружность). Все перечисленные виды поверхностей вращения, кроме торовых, являются поверхностями второго порядка (по порядку образующей или направляющей).
Торовые поверхности вращения относятся к поверхностям четвертого порядка (по произведению порядков двух окружностей – образующей и направляющей).
Геометрические тела – цилиндр конус
Цилиндрическая поверхность вращения – прямой круговой цилиндр
Цилиндрическая поверхность вращения – это линейчатая поверхность, образованная параллельным перемещением прямолинейной образующей вокруг оси вращения, которая пересекает криволинейную направляющую окружность. Геометрическое тело, ограниченное цилиндрической поверхностью вращения (боковой поверхностью) и двумя параллельными секущими плоскостями (основаниями), перпендикулярными оси вращения, называют цилиндром.
Цилиндр называют круговым, поскольку направляющей является окружность, перпендикулярная оси цилиндра.
Цилиндр называют прямым, если ось вращения цилиндра перпендикулярна его основаниям.
Прямой круговой цилиндр по положению относительно плоскостей проекций называют проецирующим, если его боковая поверхность (или ось вращения) перпендикулярна какой-либо плоскости проекций:
- – горизонтально-проецирующим, если боковая поверхность перпендикулярна горизонтальной плоскости проекций (
H);
- – фронтально-проецирующим, если боковая поверхность перпендикулярна фронтальной плоскости проекций (
V);
- – профильно-проецирующим, если боковая поверхность перпендикулярна профильной плоскости проекций (
W).
Построение проекций прямого кругового цилиндра
На рис. 7.6 показан пример построения проекций прямого кругового горизонтально-проецирующего цилиндра заданной высоты Н с горизонтальными основаниями заданного радиуса R.
Для построения проекций цилиндра требуется выполнить графо-аналитические действия в следующем порядке.
1-е действие. Построить горизонтальную проекцию (очерк) цилиндра по заданному условию, которая представляет собой окружность заданного радиуса R.
2-е действие. Выполнить графический анализ построенной горизонтальной проекции цилиндра.
2.1. Окружность является горизонтальной проекцией боковой поверхности, так как образующие этого цилиндра – горизонтально-проецирующие прямые.
2.2. Круг заданного радиуса R – совпадающие горизонтальные проекции оснований цилиндра, лежащих в горизонтальных плоскостях уровня.
2.3. Обозначить вырожденные в точки проекции характерных образующих цилиндра A(A’), B(B’), C(C’) и D(D’), которые будут определять очерки фронтальной и профильной проекций цилиндра.
3-е действие. Построить фронтальную проекцию (очерк) цилиндра, которая представляет собой прямоугольник, ограниченный:
- – слева и справа вертикальными отрезками – характерными очерковыми образующими A(A”) и B(B”);
- – по заданной высоте H – горизонтальными отрезками, которые являются проекциями оснований цилиндра, лежащих в горизонтальных плоскостях уровня;
- – фронтальные проекции характерных образующих C(C”) и D(D”) совпадают с осью вращения цилиндра i(i”).
4-е действие. Построить профильную проекцию (очерк) цилиндра.
4.1. Задать на окружности горизонтальной проекции цилиндра положение базовой линии (б.о.), совпадающей с горизонтальной линией оси этой окружности, то есть проходящей через ось вращения i(i’).
4.2. Выбрать положение базовой оси z (б.о.), которая будет совпадать с вертикальной осью i(i”‘) вращения на профильной проекции цилиндра.
4.3. Профильная проекция цилиндра представляет собой прямоугольник, ограниченный:
- – слева и справа вертикальными отрезками – характерными очерковыми образующими C(C”‘) и D(D”‘), построенными по координате yD = yc = R;
- – по заданной высоте H – горизонтальными отрезками, которые являются проекциями оснований;
- – профильные проекции характерных образующих A(A”‘) и B(B”‘) совпадают с осью вращения цилиндра i(i”‘).
!!! Запомните характерные признаки очерков прямого кругового цилиндра на чертеже – окружность и два прямоугольника.
Построение проекций точек, лежащих на поверхности цилиндра
Принадлежность точки поверхности цилиндра определяется ее принадлежностью образующей этого цилиндра.
На рис. 7.6 показан пример построения горизонтальных и профильных проекций точек E, F, G и K, лежащих на образующих боковой поверхности цилиндра, по их заданным фронтальным проекциям:
Горизонтальные проекции E’, F’, G’ и K’ заданных точек лежат на окружности радиуса R, которая является проекцией его боковой поверхности.
Профильные проекции точек строятся по их принадлежности образующим цилиндра:
- – точка E(E'”) – лежит на характерной образующей A(A”‘) – видимая;
- – две точки F(F”‘) – лежат на характерных образующих D(D”‘) и C(C”‘);
- – точка G(G”‘) – построена по координате yG, так как лежит не на характерной образующей (видимая);
- – точка K(K”‘) – построена по координате yK (невидимая).
Цилиндрические сечения:
- Плоскость пересекает поверхность цилиндра по образующим, если она расположена параллельно оси вращения цилиндра (см. плоскость α на рис. 7.7).
- Плоскость пересекает поверхность цилиндра по эллипсу, если она расположена к оси вращения цилиндра под углом φ, отличным от прямого (см. плоскость β(βV) на рис. 7.7).
- Плоскость пересекает поверхность цилиндра по окружности, если она перпендикулярна оси вращения цилиндра (окружности оснований).
Построение проекций цилиндра со срезами плоскостями частного положения.
На рис. 7.7 показан пример построения проекций прямого кругового горизонтально-проецирующего цилиндра со срезами профильной плоскостью α и фронтально-проецирующей плоскостью β.
Для построения проекций цилиндра со срезами следует выполнить предлагаемый графический алгоритм, определяющий порядок действий при решении всех подобных задач:
1-е действие. Построить на чертеже тонкими линиями по заданному диаметру и заданной высоте горизонтальную, фронтальную и профильную проекции прямого кругового горизонтально-проецирующего цилиндра без срезов, а затем выполнить на ее фронтальной проекции заданные по условию срезы профильной плоскостью α(αV) и фронтально-проецирующей плоскостью β(βV).
2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основаниями цилиндра и выполнить графический анализ сечений.
2.1. Профильная плоскость α(αV), проекцией которой является вертикальный отрезок, расположена параллельно оси цилиндра и пересекает его поверхность по прямоугольнику 1-2-2-1(1″-2″-2″-1″):
- – точки 1(1″) – лежат на нижнем основании цилиндра и определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскости среза α с основанием цилиндра;
- – точки 2(2″) – определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскостей среза α и β.
2.2. Фронтально-проецирующая плоскость β(βV), проекцией которой является наклонный отрезок, расположена к оси цилиндра под углом, отличным от прямого, и пересекает его поверхность по неполному эллипсу 2-3-4(2″-3″-4″):
- – точки 3(3″) – лежат на характерных образующих D(D”) и C(C”);
- – точки 4(4″) – лежат на верхнем основании и определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскости среза β с верхним основанием цилиндра.
3-е действие. Достроить горизонтальную проекцию цилиндра со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек, и определить видимость плоскостей срезов.
3.1. Плоскость среза α определяет видимый отрезок 2′-2′ вырожденной в линию проекции профильной плоскости β, обозначенные точки которой лежат на окружности боковой поверхности цилиндра.
3.2. Плоскость среза β определяет искаженный по величине неполный видимый эллипс 2-3-4(2′-3′-4′), обозначенные точки которого совпадают с окружностью боковой поверхности цилиндра.
!!! Поскольку горизонтальная проекция имеет вертикальную симметрию относительно базовой оси (б.о.), точки обозначены на одной ее половине (нижней).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции для определения ее очерка и внутреннего контур.
4.1. Горизонтальный очерк определяет часть окружности основания и отрезок 2′-2′. 4.2. Внутренний контур определяется видимым отрезком 4′-4′.
5-е действие. Достроить профильную проекцию цилиндра со срезами, построив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов.
5.1. Плоскость среза α определяет:
- – видимая натуральная проекция прямоугольника 1″‘-2″‘-2″‘-1″‘:
- – образующие 1-2(1″‘-2″‘) – построены по координате y1= y2;
- – отрезок 1-1(1″‘-2″‘) – совпадает с проекцией нижнего основания цилиндра;
- – отрезок 2-2(2″‘-2″‘) – профильная проекция линии пересечения плоскостей срезов α и β.
5.2. Плоскость среза β определяет искаженная по величине видимая проекция неполного эллипса 2″‘-3″‘-4′”, ограниченная видимыми линиями пересечения плоскостей среза 2″‘-2″‘ (построена) и линией 4″‘-4″‘ пересечения плоскости среза β с верхним основанием цилиндра:
- – точки 2(2″‘) – построены;
- – точки 3(3″‘) – лежат на характерных образующих C(C”‘) и D(D”‘);
- – точки 4(4″‘) – построены по координате y4;
- – необозначенные промежуточные точки построены по координате y.
6-е действие. Выполнить графический анализ построенной профильной проекции цилиндра для определения ее очерка и внутреннего контура.
6.1. Профильный очерк определяют:
- – слева и справа – участки C”‘-3″‘ и D”‘-3″‘ очерковых образующих С и D и участки 3″‘-4″‘ эллипса; – снизу – проекция нижнего основания цилиндра;
- – сверху – отрезок 4″‘-4″‘ – профильная проекция линии пересечения верхнего основания с плоскостью среза β.
6.2. Внутренний контур определяют:
- – видимые участки эллипса 2″‘-3″‘;
- – отрезок 2″‘-2″‘ – видимая линия пересечения плоскостей среза α и β;
- – видимые участки 1″‘-2″‘ образующих, по которым плоскость среза α пересекает поверхность цилиндра.
7-е действие. Оформить чертеж цилиндра, выполнив сплошными толстыми линиями очерки и видимые линии внутреннего контура всех проекций цилиндра (оставить сплошными тонкими линиями полные очерки проекций и линии построения).
На рис. 7.8 показан частный случай сечения цилиндра фронтально-проецирующей плоскостью δ(δV), расположенной к его оси под углом φ = 45°. В этом случае на профильную проекцию цилиндра эллипс, полученный в сечении, проецируется в виде окружности!
Коническая поверхность вращения – прямой круговой конус
Коническая поверхность вращения – это линейчатая поверхность, образованная вращением прямолинейной образующей, которая пересекает криволинейную направляющую (окружность) и проходит через неподвижную точку оси вращения, называемую вершиной.
Конусом называют геометрическое тело, ограниченное конической поверхностью и плоскостью основания, пересекающего все его образующие.
Конус называют прямым, если ось вращения перпендикулярна его основанию. Конус называют круговым, так как направляющей является окружность. Конус с двумя параллельными основаниями, то есть конус со срезанной вершиной, называют усеченным.
Построение проекций прямого кругового конуса
На рис. 7.9 показан пример построения проекций прямого кругового конуса с горизонтально-проецирующей осью вращения i, заданной высотой H и основанием радиусом R.
Для построения проекций конуса требуется выполнить графо-аналитические действия в следующем порядке:
1-е действие. Построить горизонтальную проекцию очерка прямого кругового конуса по заданному условию, которая представляет собой окружность заданного радиуса R с вершиной S(S’), совпадающей с осью вращения i(i’).
2-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса.
2.1. Круг радиуса R является невидимой проекцией основания конуса.
2.2. Круг радиуса R с вершиной конуса S(S’) является видимой проекцией боковой поверхности конуса.
2.3. Обозначить на горизонтальной проекции характерные образующие конуса SA(S’A’), SB(S’B’), SC(S’C’) и SD(S’D’), которые будут определять очерки фронтальной и профильной проекций конуса.
3-е действие. Построить фронтальную проекцию (очерк) конуса, которая представляет собой треугольник SAB(S”A”B”) заданной высоты H, ограниченный:
- – слева и справа проекциями боковых очерковых образующих S”A” и S”B”;
- – горизонтальным отрезком AB(A”B”), который является проекцией основания конуса;
Фронтальные проекции характерных образующих SC(S”C”) и SD(S”D”) совпадают с осью конуса i(i”).
4-е действие. Построить профильную проекцию (очерк) конуса:
4.1. Задать на окружности горизонтальной проекции конуса положение базовой линии (б.о.), совпадающей с горизонтальной линией оси этой окружности.
4.2. Выбрать положение базовой оси Z (б.о.), которая будет совпадать с вертикальной осью i(i”‘) вращения на профильной проекции конуса.
4.3. Профильная проекция конуса представляет собой треугольник SCD(S”‘C”‘D”‘), ограниченный:
- – слева и справа очерковыми образующими S”‘C”‘ и S”‘D”‘, построенными по координате YC=YD=R;
- – вершиной S”‘, лежащей на базовой оси Z;
- – горизонтальным отрезком – проекцией основания;
- – профильные проекции характерных образующих SA(S”‘A'”) и SB(S'”B'”) совпадают с осью вращения конуса i(i”‘).
!!! Запомните характерные признаки очерков прямого кругового конуса на чертеже – окружность основания и два треугольника.
!!! Характерные признаки очерков прямого кругового усеченного конуса – окружность основания и две равнобокие трапеции.
Построение проекций точек, лежащих на поверхности конуса
Принадлежность точки поверхности конуса определяется ее принадлежностью образующей поверхности и принадлежностью круговым параллелям (окружностям), по которой точка вращается вокруг оси конуса. Следовательно, проекции точки можно строить либо по принадлежности образующей, либо по принадлежности круговой параллели.
На рис. 7.9 показан пример построения горизонтальных и профильных проекций точек E, F, G и K, заданных фронтальными проекциям E”, F”, G” и K” по их принадлежности круговым параллелям.
1. Построение горизонтальных проекций заданных точек:
- – горизонтальная проекция E’ характерной точки E, лежащей на характерной образующей конуса SA, определяется на горизонтальной проекции S’A’ этой образующей;
- – горизонтальные проекции точек F, G и K построены на вспомогательных круговых параллелях, проведенных через заданные фронтальные проекции точек.
Рассмотрим графический алгоритм для построения горизонтальных проекций точек, лежащих на боковой поверхности конуса (на примере заданной точки F (F”)), по их принадлежности круговым параллелям.
Графический алгоритм I:
1-е действие. Провести фронтальную проекцию вспомогательной круговой параллели m(m”) через заданную фронтальную проекцию точки F(F”): проекция параллели – это прямая, перпендикулярная оси конуса и параллельная его основанию.
2-е действие. Провести окружность горизонтальной проекции параллели m(m’) полученным радиусом RF.
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки F(F’) на горизонтальной проекции параллели m(m’).
Повторить действия графического алгоритма I и построить аналогично горизонтальные проекции G’ и K’ точек G и K.
Построение профильных проекций заданных точек. Точки E(E”‘) и F(F”‘) построены по принадлежности характерным образующим:
- – точка E(E”‘) – лежит на видимой характерной образующей SA(S”‘A”‘), совпадающей с осью конуса;
- – точка F(F”‘) – лежит на характерной образующей SD(S”‘D”‘);
- – точки G(G”‘) и K(K”‘) – построены по координатам y:
- – точка G(G”‘) – по координате yG (видимая);
- – точка K(K”‘) – по координате yK (невидимая).
На рис. 7.10 показан пример построения горизонтальной и профильной проекции точки Р(Р’-?, Р'”-?) по ее принадлежности образующей a(a”,a’).
Построение горизонтальной проекции точки P(P’) по принадлежности образующей выполняется по графическому алгоритму II:
1-е действие. Провести через вершину конуса S(S”) и заданную невидимую фронтальную проекцию точки P(P”) вспомогательную образующую a(a”).
2-е действие. Построить горизонтальную проекцию образующей a(a’), проходящей через вершину конуса S(S’) и вспомогательную точку 1(1′), лежащую на основании конуса.
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки P(P’) по ее принадлежности образующей a(a’).
Построение профильной проекции невидимой точки P(P”‘) выполняется по принадлежности образующей a(a'”), построенной по координате ya.
На этом же рисунке 7.10 показано построение фронтальной и профильной проекции точки T(T’, T”-?, T'”-?) по ее заданной горизонтальной проекции. Построение выполнено по приведенным алгоритмам I и II, но в обратном порядке:
1-е действие. Провести на горизонтальной проекции конуса радиусом RT окружность вспомогательной параллели n(n’) или вспомогательную образующую b(b’), на которых лежит горизонтальная проекция точки T(T’).
2-е действие. Построить фронтальные проекции вспомогательной параллели n(n”) или вспомогательной образующей b(b”):
- – параллель n(n”) провести через вспомогательную точку 2(2″) на образующей SA(S”A”) параллельно основанию конуса;
- – образующую b(b”) провести через вспомогательную точку 3(3″) на основании конуса и вершину конуса S(S”).
3-е действие. Построить по вертикальной линии связи фронтальную проекцию точки T(T”) по ее принадлежности либо параллели n(n”), либо образующей b(b”).
Конические сечения
Рассмотрим пять возможных случаев расположения секущей плоскости относительно оси конуса и его образующих, определяющих форму линии ее пересечения с поверхностью конуса (математические доказательства не приводятся).
1-й случай. Если секущая плоскость проходит через вершину конуса, то эта плоскость пересекает коническую поверхность по двум образующим S3 (фронтально-проецирующая плоскость α(αV), рис. 7.11).
2-й случай. Если секущая плоскость расположена перпендикулярно оси конуса, то эта плоскость пересекает коническую поверхность по окружности (горизонтальная плоскость β(βV), рис. 7.11).
3-й случай. Если секущая плоскость расположена параллельно одной образующей конуса, то эта плоскость пересекает коническую поверхность по параболе (фронтально-проецирующая плоскость γ(γV) параллельна одной образующей SA, рис. 7.12).
4-й случай. Если секущая плоскость расположена параллельно двум образующим конуса, то эта плоскость пересекает коническую поверхность по гиперболе (фронтальная плоскость δ(δV) параллельна двум образующим SA и SB, рис. 7.13).
5-й случай. Если плоскость пересекает все образующие конуса под углом, отличным от прямого (или иначе не параллельна ни одной образующей конуса), то эта плоскость пересекает коническую поверхность по эллипсу (фронтально-проецирующая плоскость ε(εV), рис. 7.14).
Рассмотрим построение на проекциях конуса линий пересечения для всех пяти случаев сечений.
1-й и 2-й случаи. На рис. 7.11 показано построение проекций прямого кругового конуса с вырезом, образованным сечениями конической поверхности фронтально-проецирующей плоскостью α(αV), проходящей через вершину конуса (1-й случай), и горизонтальной плоскостью β(βV), расположенной перпендикулярно оси конуса (2-й случай).
Плоскость α пересекает поверхность конуса по образующим SE, горизонтальные и профильные проекции которых строятся с помощью вспомогательной точки E, лежащей на основании конуса.
Плоскость β пересекает поверхность конуса по окружности радиуса Rβ, ограниченной линией 3-3 пересечения плоскостей выреза.
Построение горизонтальной и профильной проекций конуса с вырезом и оформление очерков этих проекций видно из чертежа.
3-й случай. На рис. 7.12 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью γ(γV), расположенной параллельно одной образующей конуса SA.
Плоскость γ пересекает поверхность конуса по параболе, горизонтальная и профильная проекции которой строятся по отмеченным характерным точкам 1, 2 и 3 и промежуточной точке (не обозначена).
Построение проекций этих точек выполнено по их принадлежности:
- – точка 1(1′,1″) – лежит на проекциях характерной образующей SB(S’B’, S”‘B”‘);
- – точки 2(2′,2″) – лежат на проекциях характерных образующих SD и SC, горизонтальные проекции которых построены с помощью параллели радиусом R2 (алгоритм I);
- – точки 3(3′,3″) – лежат на окружности основания конуса: горизонтальные проекции этих точек определяются по линии связи на горизонтальной проекции окружности основания, а их профильные проекции построены по координате Y3;
- – проекции промежуточной точки построены по ее принадлежности соответствующей параллели (профильные проекции – по координате Y).
Оформление очерков проекций видно из чертежа.
4-й случай. На рис. 7.13 показано построение проекций конуса со срезом фронтальной плоскостью δ(δH), расположенной параллельно двум образующим конуса SA и SB.
Плоскость δ пересекает поверхность конуса по гиперболе, фронтальная проекция которой строится по отмеченным точкам 1, 2 и 3 по их принадлежности параллелям (обратный алгоритм I), а профильная проекция гиперболы проецируется в вертикальную линию и совпадает с вырожденной проекцией плоскости среза δ(δW).
Оформление очерков проекций видно из чертежа.
На рис. 7.13 на профильной проекции конуса показано положение секущей плоскости δ1(δ1W) под углом φ1 к оси конуса. При 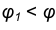
5-й случай. На рис. 7.14 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью ε(εV), пересекающей все образующие конуса под углом φ к оси, отличным от прямого.
Плоскость ε пересекает поверхность конуса по эллипсу, горизонтальная и профильная проекции которого построены по проекциям отмеченных характерных точек 1, 2, 4 и промежуточных точек 3, взятых на середине отрезка 1-4, который является совпадающей проекцией эллипса и его большой оси. Точки 3 определяют проекции малой оси эллипса и построены на горизонтальной проекции конуса по радиусу параллели, а на профильной проекции по координате Y3 (алгоритм I).
Оформление очерков проекций видно из чертежа.
!!! Количество взятых промежуточных точек должно быть минимальным, но достаточным, чтобы построить на проекциях конуса формы кривых второго порядка (параболы, гиперболы и эллипса), которые выполняют на чертеже по построенным характерным и промежуточным точкам с помощью лекала.
Построение проекций прямого конуса со срезами плоскостями частного положения
На рис. 7.15 показан пример построения проекций прямого кругового конуса со срезами фронтально-проецирующей плоскостью α и профильной плоскостью β.
Для построения проекций конуса со срезами следует выполнить графический алгоритм, определяющий порядок действий при решении всех подобных задач.
Графический алгоритм:
1-е действие. Построить на чертеже тонкими линиями по заданному радиусу основания R и высоте H фронтальную, горизонтальную и профильную проекции конуса без срезов, а затем выполнить на его фронтальной проекции заданные срезы фронтально-проецирующей плоскостью α(αV) и профильной плоскостью β(βV).
2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основанием конуса и выполнить графический анализ сечений.
2.1. Фронтально-проецирующая плоскость α(αV) параллельна одной образующей конуса SA(S”A”) и пересекает его поверхность по участку параболы 1-2-3(1″-2″-3″), которая проецируется в отрезок и ограничена вырожденной в точку фронтально-проецирующей линией пересечения 3-3(3″-3″) плоскостей срезов α и β.
2.2. Профильная плоскость β(βV) параллельна двум образующим конуса SC(S”C”) и SD(S”D”) и пересекает его поверхность по участку гиперболы 3-4(3″-4″), которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов α и β(3-3) и плоскости β с основанием конуса (4-4).
3-е действие. Достроить горизонтальную проекцию конуса со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек и определить видимость плоскостей срезов:
3.1. Плоскость среза α определяет видимая горизонтальная проекция участка параболы 1-2-3(1′-2′-3′), построенной по горизонтальным проекциям обозначенных точек:
- – точка 1(1′) лежит на образующей SB (S’B’);
- – точки 2(2′) и 3(3′) построены по принадлежности соответствующим параллелям (алгоритм I).
3.2. Плоскость среза β определяет вертикальный видимый отрезок 4′-4′ вырожденной в линию проекции профильной плоскости, точки 4(4′) которой лежат на очерковой окружности основания конуса.
!!! Поскольку горизонтальная проекция имеет вертикальную симметрию, точки обозначены на одной ее половине (нижней).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса для определения ее очерка и внутреннего контура.
4.1. Горизонтальный очерк определяют участок окружности и отрезок 4′-4′. 4.2. Внутренний контур определяет видимый участок параболы 3′-2′-1′.
5-е действие. Достроить профильную проекцию конуса со срезами, построив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов.
5.1. Плоскость среза α определяет видимый участок параболы 1-2-3(1′”2″‘-3″‘), построенный по профильным проекциям обозначенных точек:
- – точка 1(1′”) – лежит на характерной образующей SB(S'”B”‘);
- – точки 2(2′”) – лежат соответственно на характерных образующих SC(S'”C”‘) и SD(S'”D”‘);
- – точки 3(3′”) – построены по координате y3.
5.2. Плоскость среза β определяют видимые участки гиперболы 3-4(3″‘-4″‘), ограниченные видимым отрезком 3″‘-3″‘ (построен) и видимым отрезком 4-4(4″‘-4″‘), точки которого построены по координате y4.
6-е действие. Выполнить графический анализ построенной профильной проекции конуса для определения ее очерка и внутреннего контура.
6.1. Профильный очерк определяют:
- – слева – участок C”‘-2″‘ образующей SC;
- – справа – участок D”‘-2″‘ образующей SD;
- – сверху – участок параболы 1″‘-3″‘;
- – снизу – проекция основания конуса.
6.2. Внутренний контур определяют:
- – видимые участки параболы 2″‘-3″‘;
- – видимый отрезок 3″‘-3″‘ пересечения плоскостей срезов α и β;
- – видимые участки гиперболы 3″‘-4″‘.
7-е действие. Оформить чертеж конуса выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой его проекции (оставить сплошными тонкими линиями полные очерки проекций и линии построения).
Сферическая поверхность – шар
При вращении окружности вокруг ее диаметра образуется поверхность вращения, называемая сферой. Сферическая поверхность – геометрическое место точек, равноудаленных от ее центра. Сфера – единственная геометрическая поверхность, которая имеет бесконечное число осей, проходящих через ее центр, что удобно использовать при построении проекций точек на ее поверхности и при решении различных позиционных задач с геометрическими формами, в образование которых входит сфера.
Геометрическое тело, ограниченное сферой, называют шаром.
- Чертежи на заказ
Проекции шара и проекции его очерковых окружностей
Все три очерка шара – фронтальный, горизонтальный и профильный – представляют собой окружности одного диаметра с центром в точке О(О’,О”,О”‘) – это характерный признак проекций шара на чертеже (рис. 7.16). Каждая точка на поверхности шара описывает вокруг соответствующей оси окружности, называемые параллелями.
Фронтальный очерк шара – окружность n(n”) – называется главным фронтальным меридианом, который лежит во фронтальной плоскости уровня β(βH), и его горизонтальная проекция n’ – это горизонтальная прямая, а профильная проекция n”‘ – вертикальная прямая, проходящие через центр шара.
Горизонтальный очерк шара – это окружность k(k’), то есть экватор шара, лежащий в горизонтальной плоскости уровня α(αV), и его фронтальная k” и профильная k”‘ проекции – горизонтальные прямые, проходящие через центр шара.
Профильный очерк шара – это окружность m(m”‘) главного профильного меридиана, лежащего в профильной плоскости δ(δH), и его фронтальная m” и горизонтальная m’ проекции – вертикальные прямые, проходящие через центр шара.
!!! Запомните характерные признаки шара на чертеже – три очерковые окружности одного диаметра.
Построение проекций точек на поверхности шара
На рис. 7.16 показаны примеры построения проекций точек, лежащих на характерных очерковых окружностях шара.
Точка A(A”), заданная своей фронтальной проекцией, лежит на главном фронтальном меридиане n(n”); ее горизонтальная проекция A’ и профильная проекция A”‘ определяются на соответствующих проекциях этого меридиана по линиям связи.
Точки B1(B1‘) и B2(B2‘), заданные своими горизонтальными проекциями, лежат на экваторе шара k(k’); фронтальные проекции точек совпадают и определяются на фронтальной проекции экватора k(k”) по линии связи (B2” – невидимая), а профильные проекции B1“‘ и B2“‘ построены по координатам yB1 = yB2 и лежат на профильной проекции k (k”‘) экватора.
Точка C(C”‘), заданная своей профильной проекцией, лежит на главном профильном меридиане m(m'”); ее фронтальная проекция C(C”) определяется по линии связи на фронтальной проекции m(m”) профильного меридиана, а горизонтальная невидимая проекция C(C’) построена по координате yC и лежит на горизонтальной проекции профильного меридиана m(m’).
!!! Видимость проекций точки на проекциях шара определяется видимостью той части поверхности шара, на которой лежит точка, и определяется указанными границами видимости при взгляде на каждую плоскость проекций.
На рис. 7.17 показаны примеры построения проекций точек D и E, лежащих на поверхности шара, недостающие проекции которых построены с использованием различных осей вращения (без координат y).
Точка D задана видимой фронтальной проекцией D”.
Для построения ее горизонтальной проекции D(D’) нужно использовать горизонтально-проецирующую ось вращения i1 и выполнить следующие графические действия (алгоритм I):
1-е действие. Провести через фронтальную проекцию точки D(D”) прямую, перпендикулярную оси i(i”) – это проекция круговой параллели радиусом RD, по которой точка D вращается вокруг оси i1.
2-е действие. Провести горизонтальную проекцию этой параллели: окружность радиусом RD с центром в точке O(O’).
3-е действие. Построить по линии связи горизонтальную (видимую) проекцию точки D(D’) на этой параллели.
Точка E задана невидимой горизонтальной проекцией E’.
Для построения ее фронтальной проекции E(E”) нужно использовать фронтально-проецирующую ось i2 и выполнить следующие графические действия (алгоритм II):
1-е действие. Провести через горизонтальную проекцию точки E(E’) прямую, перпендикулярную оси i2(i2‘) – это проекция круговой параллели радиусом RE, по которой точка E вращается вокруг оси i2.
2-е действие. Провести фронтальную проекцию этой параллели: окружность радиусом RE с центром в точке O(O”).
3-е действие. Построить по вертикальной линии связи фронтальную видимую проекцию точки E(E”) на этой параллели.
Для построения профильных проекций заданных точек D и E нужно использовать профильно-проецирующую ось i3 и выполнить следующие графические действия (алгоритм III):
1-е действие. Провести через фронтальную проекцию точки D(D”) и горизонтальную проекцию точки E(E’) прямые, перпендикулярные оси i3(i3“,i3‘), – это проекции круговых параллелей с радиусами RD1 и RE1 (расположены вертикально), по которым точки D и E вращаются вокруг оси i3.
2-е действие. Провести профильные проекции этих параллелей: окружности радиусами RD1 и RE1 с центром в точке O(O”‘).
3-е действие. Построить по горизонтальным линиям связи профильные проекции точек D(D'”) и E(E”‘) на соответствующих параллелях (профильная проекция точки D(D'”) невидимая).
Построение проекций шара со срезами плоскостями частного положения
Всякая плоскость пересекает поверхность шара по окружностям (круговым параллелям). В зависимости от расположения секущих плоскостей относительно плоскостей проекций H, V и W окружности сечений могут проецироваться либо в окружности, либо в эллипсы.
На рис. 7.18 показан пример построения проекций шара со срезами горизонтальной плоскостью α(αV) и профильной плоскостью β(βV).
Окружность сечения шара горизонтальной плоскостью α(αV) проецируется в окружность (круговую параллель) радиусом Rα на горизонтальную проекцию шара, а профильная проекции этой окружности – горизонтальная прямая. В качестве оси вращения для построения горизонтальной проекции окружности сечения взята горизонтально-проецирующая ось i1.
Окружность сечения шара профильной плоскостью β проецируется в окружность (круговую параллель) радиусом Rβ на профильную проекцию шара (невидимая окружность), а горизонтальная проекция этой окружности – вертикальная прямая. В качестве оси вращения для построения параллели Rβ взята профильно-проецирующая ось i3.
На этом же рисунке показано расположение проекции характерных точек 1, 2, 3, 4, 5 и 6, лежащих в плоскостях сечений на характерных очерковых окружностях шара:
- – точки 1, 3, 4 и 6 лежат на главном фронтальном меридиане шара n и их проекции определяются на проекциях этого меридиана;
- – точки 5 лежат на экваторе шара k и их проекции определяются на проекциях экватора;
- – точки 2 лежат на профильном меридиане m и их проекции определяются на проекциях этого меридиана.
Оформление очерков проекций ясно из чертежа.
На рис. 7.19 показан пример построения проекций шара со срезом фронтально-проецирующей плоскостью γ(γV). Фронтальная проекция окружности сечения шара плоскостью γ совпадает с вырожденной в линию фронтальной проекцией плоскости γ, а на горизонтальную и профильную проекции шара эта окружность сечения проецируется в эллипсы.
Проекции шара со срезом построены по проекциям точек, обозначенных на фронтальной проекции сечения.
Горизонтальная проекция шара со срезом в виде эллипса построена по горизонтальным проекциям обозначенных точек:
- – точки 1(1′) и 5(5′) – лежат на проекции n(n’) главного фронтального меридиана;
- – точки 2(2′) – лежат на проекции m(m’) профильного меридиана и построены на параллели радиусом R2 (ось вращения i1, алгоритм I);
- – точка 4(4′) – лежит на проекции k(k’) экватора;
- – точки 3 – отмечены на перпендикуляре к плоскости сечения γ и определяют положение большой оси эллипса 3-3; точки 3(3′) построены по принадлежности своей параллели (алгоритм I); малая ось эллипса – линия 5′-1′.
Построенные видимые горизонтальные проекции точек соединить плавной кривой эллипса с помощью лекала.
Очерк горизонтальной проекции определяет его экватор вправо от точек 4(4′).
Профильная проекция шара со срезом в виде эллипса построена по профильным проекциям обозначенных точек:
- – точки 1(1″‘) и 5(5″‘) – лежат на n(n'”) главного меридиана;
- – точки 2(2″‘) – лежат на проекции m(m”‘) профильного меридиана;
- – точки 3 (3″‘) и 4(4″‘) – построены или по принадлежности соответствующим относительно оси вращения i3 параллелям (алгоритм III, отмечена параллель R4).
Построенные видимые проекции точек соединить плавной кривой эллипса.
Очерк профильной проекции определяет профильный меридиан m(m”‘) от точек 2(2″‘) вниз.
Торовая поверхность – тор
Поверхность, получаемая при вращении образующей окружности m (или ее дуги) вокруг оси i, лежащей в плоскости этой окружности, но не проходящей через ее центр, называется торовой. Образующая окружность m вращается вокруг оси тора i по направляющей окружности радиусом R (рис. 7.20, а, б, в, г).
Геометрическое тело, ограниченное торовой поверхностью, называют тором.
Тор называют открытым (круговое кольцо), если образующие окружности m в осевом сечении не пересекаются и не касаются друг друга, то есть 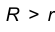
Тор называют замкнутым, если образующие окружности m касаются, то есть R = r. Проекции замкнутого тора показаны на рис. 7.20, б.
Тор называют самопересекающимся, если образующие окружности пересекаются, то есть 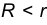
На рис. 7.20, г показаны проекции глобоида – это геометрическое тело, образованное как открытый тор, но материализующее полость (отверстие) в открытом торе.
Построение проекций открытого тора
На рис. 7.21 показан пример построения фронтальной, горизонтальной и профильной проекций половины открытого тора с фронтально-проецирующей осью i.
Фронтальную проекцию (очерк) тора определяют:
- – максимальная и минимальная круговые окружности-параллели n1(n1“) и n2(n2“), по которым диаметральные точки N1 и N2 образующей окружности m вращаются вокруг оси тора i;
- – окружности-параллели t1(t1“) и t2(t2“) диаметральных точек T1 и T2, которые совпадают между собой и совпадают с проекцией направляющей окружности радиусом R тора (выполняются на чертеже тонкой штрихпунктирной линией);
- – две горизонтальные прямые m(m”) – проекции образующих окружностей m, полученных в сечениях тора горизонтальной плоскостью α(αV), проходящей через ось вращения тора.
Горизонтальную проекцию (очерк) тора определяют:
- – совпадающие проекции n1(n1‘) и n2(n2‘) окружностей-параллелей фронтального очерка проецируются в прямую линию, перпендикулярную оси i(i’) тора, и совпадают с горизонтальной осью симметрии проекции;
- – две образующие окружности m(m’), лежащие в плоскости среза α(αV), которые проецируются в натуральную величину и видимыми являются только их половины;
- – две горизонтальные линии, в которые проецируются окружности параллели t1(t1‘) и t2(t’), полученные при вращении диаметральных точек T1 и T2 (перпендикулярны оси вращения i(i’).
Профильную проекцию(очерк) тора определяют:
- – совпадающие проекции n1(n1“‘) и n2(n2“‘) окружностей-параллелей фронтального очерка проецируются в прямую вертикальную линию и совпадают с осью симметрии проекции;
- – окружность mβ, лежащая в профильной плоскости β (половина ее – невидимая);
- – прямая горизонтальная линия совпадающих проекций образующих окружностей m(m”‘), лежащих в плоскости среза α(αV);
- – две вертикальные прямые – проекции окружностей-параллелей t1(t1“‘) и t2(t2“‘).
!!! Запомните характерные признаки проекций открытого тора на чертеже.
Построение проекций точек, лежащих на поверхности тора
Точки на поверхности тора лежат на круговых параллелях, по которым они вращаются вокруг его оси i.
1. Точки, лежащие на характерных очерковых окружностях тора n1 и n2, t1 и t2 и m строятся по их принадлежности этим окружностям.
На рис. 7.21 показаны примеры построения проекций точек по одной заданной проекции.
Например, горизонтальные и профильные проекции точек A и B, заданных своими фронтальными проекциями A” и B”, лежат на очерковых окружностях n1 и n2 и определяются на проекциях этих окружностей (горизонтальные проекции точек совпадают); профильная проекция B(B”‘) – невидимая.
Горизонтальные и профильные проекции точек C1 и C2, заданных своими фронтальными совпадающими проекциями, лежат на окружностях t1 и t2 и определяются на проекциях этих окружностей.
2. Проекции точек D1 и D2 (невидимая), заданных своими совпадающими фронтальными проекциями D1” и D2” и не лежащие на характерных окружностях тора, строятся по следующему графическому алгоритму (алгоритм I):
1-е действие. Провести вспомогательную круговую параллель радиусом RD через заданные фронтальные проекции точек D1(D1“)≡D2(D2“) .
2-е действие. Провести горизонтальные прямые – проекции этих параллелей – перпендикулярно оси вращения i(i’), используя вспомогательные точки 1(1″,1′), лежащие на проекциях образующей окружности m(m1“,m2‘).
3-е действие. Построить по линии связи видимые горизонтальные проекции точек D(D1‘) и D(D2‘) на проекциях этих вспомогательных параллелей.
4-е действие. Профильные видимые проекции точек D1(D1‘”) и D2(D2‘”) построить по координатам yD.
Проекции точек E1 и E2 (невидимая), заданных своими совпадающими горизонтальными проекциями E1(E1′) ≡E2(E2′) и не лежащие на характерных окружностях тора, строятся по “обратному” алгоритму II:
1-е действие. Провести на горизонтальной проекции тора прямую, перпендикулярную оси вращения тора i(i’) – это горизонтальные совпадающие проекции вспомогательных круговых параллелей радиусами RE1 и RE2 для точек E1 и E2.
2-е действие. Построить радиусами RE1 и RE2 фронтальные проекции этих параллелей: RE2 – параллель на внутренней поверхности тора, а RE1 – параллель на наружной поверхности тора.
3-е действие. Построить по линии связи фронтальные проекции точек E1(E”1) и E2(E”2) на проекциях этих вспомогательных параллелей.
4-е действие. Профильные невидимые проекции точек E1(E”1) и E2(E”2) построить по координатам yE.
Сечения тора плоскостями частного положения
Тор является поверхностью вращения 4-го порядка (образующая и направляющая окружности 2-го порядка – порядки умножаются) и кривые его сечений также являются кривыми 4-го порядка (кроме круговых сечений).
Тор имеет две системы круговых сечений:
- – первая система парных круговых сечений получается во всех плоскостях, проходящих через ось i, тора на той его проекции, на которую ось i проецируется в точку – смотри сечение во фронтально-проецирующей плоскости α(αV) на фронтальной проекции тора (сечение по образующим окружностям m);
- – вторая система круговых сечений получается в плоскостях β(βH), перпендикулярных оси тора – смотри сечение во фронтальной плоскости уровня βH на горизонтальной проекции тора (сечение по круговым параллелям тора).
Тор имеет также третью систему сечений плоскостями уровня, параллельными оси его вращения i.
На рис. 7.22 показаны формы кривых в различных сечениях открытого тора плоскостями уровня (ось тора i 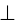
На рис. 7.22, а сечения проведены параллельно оси тора i(i”) на его фронтальной проекции и являются горизонтальными плоскостями уровня.
В зависимости от расстояния t секущей плоскости до оси тора на его поверхности получается 4 вида кривых, объединенных общим названием – кривые Персея (геометр древней Греции).
1-е сечение. Плоскость сечения на расстоянии t1 от оси тора образует на его поверхности кривую линию – овал с двумя осями симметрии (для плоскостей между точками A и B, то есть 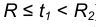
2-е сечение. Плоскость сечения на расстоянии t2 от оси тора образует на его поверхности волнообразную кривую (для плоскостей между точками B и C, то есть 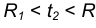
3-е сечение. Плоскость сечения на расстоянии t3 от оси тора образует на его поверхности двухлепестковую кривую (для плоскости, проходящей через точку C, то есть t3 = R1).
4-е сечение. Плоскость сечения на расстоянии t4 от оси тора образует на его поверхности два овала с одной осью симметрии (для плоскостей ниже точки C и не проходящих через ось вращения тора i(i”), то есть когда 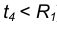
На рис. 7.22, б изображена фронтальная и горизонтальная проекции открытого тора, у которого R = 2r (частный случай). Кривые сечений этого тора называют овалами Кассини, а двухлепестковая кривая в сечении 3 называется лемнискатой Бернулли.
Построение проекций открытого тора со срезами плоскостями частного положения
На рис. 7.23 показан пример построения проекций отрытого тора с комбинированным срезом фронтально-проецирующей плоскостью α(αV) и горизонтальной плоскостью β(βV).
Для построения проекций тора со срезами следует выполнить предлагаемый графический алгоритм, определяющий порядок действий при решении всех подобных задач:
1-е действие. Построить на чертеже тонкими линиями по заданным размерам фронтальную, горизонтальную и профильную проекции тора без срезов, а затем выполнить на его фронтальной проекции (или любой другой) заданные по условию срезы фронтально-проецирующей плоскостью α(αV) и горизонтальной плоскостью β(βV).
2-е действие. Обозначить на фронтальной проекции характерные точки и выполнить графоаналитический анализ сечений:
2.1. Фронтально-проецирующая плоскость α(αV) пересекает поверхность тора по участку волнообразной кривой 1-2-3 (сечение 2), часть которой ограничена вырожденной в точку фронтально-проецирующей линией пересечения 3-3 плоскостей среза α и β.
2.2. Горизонтальная плоскость β(βV) пересекает поверхность тора по участку двухлепестковой кривой 3-4-5 (сечение 3).
!!! Поскольку горизонтальная проекция тора имеет вертикальную симметрию, точки обозначены на одной его половине (нижней).
3-е действие. Достроить горизонтальную проекцию тора, построив проекции плоскостей срезов по горизонтальным проекциям отмеченных точек и определить видимость плоскостей срезов.
3.1. Горизонтальная проекция видимого участка волнообразной кривой в плоскости α построена по проекциям обозначенных точек 1(1′), E(E’), 2(2′) и 3(3′) по их принадлежности характерным n1, t1 и t2 (точки 1 и 2) и вспомогательным (точки Е и 3) параллелям.
3.2. Горизонтальная проекция видимого участка двухлепестковой кривой в плоскости β построена по проекциям обозначенных точек 3(3′), 4(4′), D(D’) и 5(5′) по их принадлежности характерным t1, t2 и n1 (точки 4 и 5) и вспомогательным (точки D) параллелям (точки 3(3′) уже построены).
3.3. Видимый отрезок 3-3(3′-3′) – горизонтальная проекция линии пересечения плоскостей срезов α и β, ограничивающая участки кривых в плоскостях срезов.
4-е действие. Выполнить графический анализ построенной горизонтальной проекции тора для определения ее очерка и внутреннего контура.
4.1. Горизонтальный очерк определяют:
- – видимые половины окружностей m(m’);
- – участки очерковых параллелей t1(t1‘) и t2(t2‘), не существующие между точками 4(4′) и 2(2’);
- – участки кривых 4′-3′ и 3′-2′.
4.2. Внутренний контур определяют:
- – невидимые половины окружностей m(m’);
- – видимые участки кривых 4’D’-5′ и 2’E’-1′;
- – видимый отрезок 3′-3′ пересечения плоскостей срезов α и β.
5-е действие. Достроить профильную проекцию тора, построив проекции плоскостей срезов по профильным проекциям обозначенных точек и определить видимость плоскостей срезов:
5.1. Профильная проекция видимого участка волнообразной кривой построена по проекциям обозначенных точек 1(1′”), E(E”‘), 2(2′”) и 3(3′”) по их принадлежности характерным параллелям n1, t1 и t2 (точки 1(1′”) и 2(2′”)) и по координатам y (точки E(E”‘) – yE, 3(3′”) – y3).
5.2. Профильная проекция горизонтальной плоскости среза β проецируется в видимый горизонтальный отрезок 4″‘-4″‘ (точки 4(4″‘) – на очерковых линиях t1 и t2).
6-е действие. Выполнить графический анализ построенной профильной проекции тора для определения ее очерка и внутреннего контура:
6.1. Профильный очерк определяют:
- – слева и справа – проекции очерковых параллелей t1(t1‘) и t2(t2‘) до точек 2(2′”);
- – сверху – видимый участок 2′”-E”‘-1′” волнообразной кривой;
- – снизу – видимые совпадающие проекции образующих окружностей m(m'”).
6.2. Внутренний контур определяют:
- – видимый горизонтальный отрезок 4″‘-4′” (проекция плоскости среза β);
- – видимые участки 2″‘-4′” волнообразной кривой;
- – невидимая часть окружности mW(mW“‘) между точками 2″‘.
7-е действие. Оформить чертеж тора, выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой проекций (оставить тонкими линиями полные очерки проекций и линии построений).
Структуризация материала седьмой лекции в рассмотренном объеме схематически представлена на рис. 7.24 (лист 1). На последующих листах 2–6 компактно приведены иллюстрации к этой схеме для визуального закрепления основной части изученного материала при повторении (рис. 7.25–7.29).
Поверхности и частные случаи гранных и кривых поверхностей
Геометрические тела
Гранные поверхности
Прямая правильная призма
Правильная пирамида
Поверхности вращения
Прямой круговой цилиндр
Прямой круговой конус. Конические сечения.
Шар.
Тор.
Замкнутый тор.
Самопересекающийся тор (тороид).
Глобоид.
Сечения открытого тора. Кривые Персея.
Построение сечений поверхности открытого тора плоскостями частного положения
Прочие поверхности вращения
Однополостной гиперболоид
Двухполостной гиперболоид
а
Вытянутый/сжатый эллипсоид
Параболоид
Поверхности и способы их образования
Поверхности, к которым нельзя применить математические закономерности, обычно задают достаточно плотной сетью линий, принадлежащих этим поверхностям. Совокупность таких линий называют дискретной (состоящих из отдельных элементов) сетью, или дискретным каркасом поверхности.
При кинематическом способе задания поверхность рассматривается как совокупность всех положений движущейся линии. Линию, производящую поверхность, в каждом ее положении называют образующей. Образующая линия может быть прямой или кривой Кинематическая поверхность представляет собой геометрическое место линий, движущихся в пространстве по некоторому закону. Следовательно, для задания поверхности могут быть использованы три основных способа: аналитический, каркасный и кинематический.
Поверхность, которая может быть образована прямой линией, называется линейчатой поверхностью. Линейчатая поверхность представляет собой геометрическое место прямых линий. Поверхность, для которой только кривая линия может быть образующей, называется нелинейчатой поверхностью.
Пример линейчатой поверхности дан на рис. 9.1. Поверхность образована прямой линией 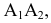
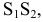
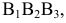
Примером нелинейчатой поверхности может быть сфера (шаровая поверхность).
Поверхности вращения
В числе кривых поверхностей – линейчатых и нелинейчатых – имеются широко распространенные в практике поверхности вращения. Поверхностью вращения называют поверхность, полученную от вращения какой-либо образующей линии 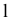
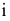
При вращении вокруг оси каждая точка образующей 
Линии, получаемые при пересечении поверхности вращения плоскостями, проходящими через ось, называют меридианами поверхности. Меридиан, расположенный во фронтальной плоскости 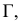
Различают поверхности вращения с прямолинейной и криволинейной образующей.
К поверхностям вращения с прямолинейной образующей относятся цилиндрическая и коническая поверхности вращения.
Наиболее распространенными поверхностями вращения с криволинейной образующей являются поверхности вращения второго порядка, т.е. получаемые при вращении алгебраических кривых, описываемых уравнениями второй степени, вокруг их осей. Это сфера, эллипсоид, параболоид и гиперболоид вращения.
Цилиндрической поверхностью вращения называется поверхность, образованная прямой линией (образующей), которая перемещается, оставаясь параллельной оси вращения. Боковая поверхность прямого кругового цилиндра (рис. 9.3) образована движением отрезка 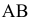
Коническая поверхность вращения представляет собой поверхность, образующая прямая которой пересекает ось вращения в точке, называемой вершиной конуса. Боковая поверхность прямого кругового конуса (рис. 9.4) образована вращением образующей 
Сферой называется поверхность, образованная вращением окружности вокруг одного из ее диаметров. На все плоскости проекций сфера проецируется в круг с радиусом, равным радиусу сферы (рис. 9.5).
Эллипсоидом вращения называется поверхность, образованная вращением эллипса вокруг одной из его осей.
Параболоид вращения образуется вращением параболы вокруг ее оси
Однополостной гиперболоид вращения образуется при вращении гиперболы вокруг ее мнимой оси, а двухполостной – при вращении вокруг действительной оси.
Тором называется поверхность, образованная вращением вокруг оси, лежащей в плоскости этой окружности и не проходящей через ее центр. Тор относится к поверхностям вращения четвертого порядка.
Точки и прямые линии, принадлежащие поверхности
Положение точки на поверхности вращения определяется при помощи окружности, проходящей через эту точку на поверхности вращения
Это не исключает возможности применения прямолинейных образующих в случае линейчатых поверхностей вращения.
Если на одной из проекций поверхность проецируется в линию, построение проекций точек, принадлежащих этой поверхности, производится с помощью линий связи.
Примеры построения проекций точек, принадлежащих поверхностям прямого кругового цилиндра, конуса н сферы показаны на рис. 9.6,9.7, 9.8.
Определение недостающих проекций точек 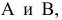
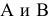
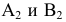
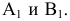
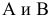
Если на поверхности конуса задана одна проекция точки 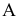
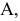
В первом случае (рис. 9.7, а) проводят фронтальную проекцию 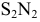
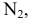
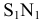
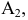
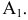
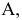
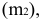
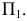
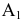
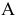
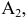
Если заданная фронтальная проекция 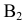
Если точка 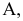
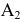
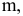
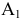
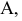
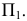
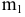
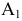
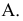
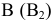
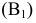
Линию на поверхности можно рассматривать как множество точек. Поэтому построение проекций линии, принадлежащей поверхности, сводится к построению проекций ряда точек, принадлежащих этой линии.
Пересечение плоскости и линии с поверхностью
В пересечении поверхностей вращения плоскостью получаются различные плоские кривые линии, проекции которых строятся по проекциям ряда точек, определяемых соответствующими способами. При этом следует стремиться определить, прежде всего, так называемые характерные (опорные) точки фигуры сечения – верхние и нижние, т.е. точки, наиболее и наименее удаленные от плоскостей проекций, и левые н правые, т.е. точки, лежащие на крайних образующих поверхностей. После этого определяется ряд промежуточных точек, которые затем соединяются с характерными плавной кривой линией.
В пересечении кругового цилиндра плоскостью в зависимости от положения секущей плоскости могут получаться: окружность, если секущая плоскость перпендикулярна оси вращения цилиндра (рис. 9.9); эллипс, если секущая плоскость наклонена к оси цилиндра под углом, отличным от прямого (рис. 9.10); прямоугольник, если секущая плоскость параллельна оси цилиндра (рис. 9.11).
Проекции фигуры сечения цилиндра плоскостью могут быть построены аналогично проекциям фигуры сечения призмы плоскостью. Для этого в цилиндр вписывается многогранная призма, находятся точки встречи ребер этой призмы с секущей плоскостью, которые соединяются плавной кривой линией. В случае, когда цилиндр прямой, построение проекций фигуры сечения может быть выполнено по-другому.
На рис. 9.12 показано построение проекций фигуры сечения прямого кругового цилиндра плоскостью общего положения 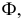
Так как цилиндр прямой, горизонтальные проекции фигуры сечения и самого цилиндра будут совпадать. Как отмечалось выше, в сечении будет получаться эллипс. Для нахождения точек, ограничивающих большую ось эллипса (нижшей и высшей), необходимо в плоскости треугольника 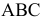
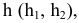
Затем через ось цилиндра перпендикулярно 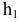
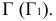
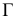
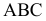
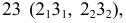
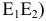
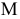
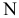
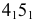
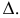
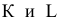
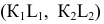
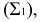
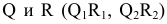
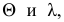
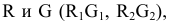
В пересечении кругового конуса плоскостью в зависимости от положения секущей плоскости могут получиться: окружность, если секущая плоскость перпендикулярна оси вращения конуса (рис. 9.13); эллипс, если секущая плоскость наклонена к оси вращения конуса под углом, отличным от прямого и пересекает все образующие конуса (рис. 9.14); гипербола, если секущая плоскость параллельна двум образующим конуса (рис. 9.15); парабола, если секущая плоскость параллельна одной образующей конуса (рис. 9.16); треугольник, если секущая плоскость проходит через вершину конуса (рис. 9.17).
Проекции фигуры сечения конуса плоскостью можно построить ана логично проекциям фигуры сечения пирамиды плоскостью (в конус в пи сывается многогранная пирамида, рис. 9.18).
Построение линии пересечения плоскости с конической поверхностью выполняется в следующем порядке. Основание конуса делится на равномерное число частей, в нашем примере 12, проводятся горизонтальные проекции 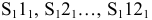
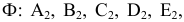
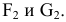
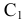
На фронтальной проекции большая ось эллипса 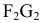
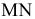
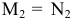
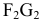
Построение горизонтальной проекции малой оси эллипса выполнено с помощью горизонтальной плоскости уровня 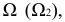
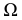
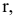
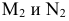
На рис. 9.19 показано построение сечения конуса плоскостью общего положения, заданной следами.
Построение проекций сечения начато с нахождения точек, ограничивающих большую ось эллипса (высшая и низшая точки сечения). Для этого проведена вспомогательная секущая плоскость 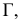
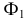
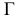
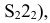
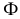
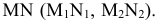
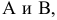
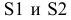
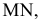
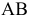
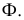
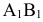
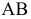
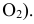
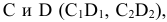
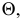
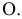

Точки, лежащие на очерке фронтальной проекции конуса и определяющие границы видимости линии пересечения, получены при помощи вспомогательной секущей плоскости 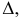
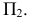

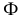
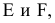
Промежуточные точки линии пересечения удобно построить, использовав горизонтальные секущие плоскости, аналогично построению точек, ограничивающих малую ось эллипса.
Задачу можно решить, использовав метод замены плоскостей проекций, с помощью которого можно привести условие к виду, приведенному на рис. 9.1S.
Для построения точек пересечения прямой с какой-либо поверхностью необходимо провести через данную прямую вспомогательную секущую плоскость; затем найти линию пересечения вспомогательной плоскости с данной поверхностью и, наконец, определить точки пересечения линии с данной прямой. Эти точки и будут искомыми точками пересечения прямой с поверхностью.
Вспомогательную плоскость, проводимую через прямую при пересечении ею какой-либо поверхности, следует выбирать так, чтобы получались простейшие сечения.
В некоторых случаях показ вспомогательной плоскости излишен. Например, точки встречи прямой 1 с поверхностью прямого кругового цилиндра, имеющего вертикальную ось (рис. 9.20), определяют следующим образом
Горизонтальная проекция цилиндрической поверхности представляет собой окружность, поэтому горизонтальные проекции всех точек, расположенных на цилиндрической поверхности, в том числе и двух искомых точек встречи, будут расположены на этой же окружности
Фронтальные проекции 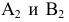
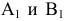
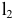
На рис. 9.21 построена точка пересечения горизонтально-проецирующей прямой с поверхностью кругового конуса. В этом случае также нет необходимости применять вспомогательную плоскость. Горизонтальная проекция 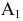
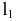
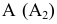
На рнс. 9.22 показано построение точек встречи прямой общего положения 1 с конической поверхностью.
В данном случае целесообразно через прямую 1 провести вспомогательную плоскость общего положения, проходящую через вершину конуса, которая пересечет поверхность по образующим. Такую плоскость зададим следующим образом. Через произвольно взятую на прямой 1 точку 
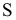
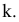
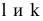
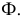
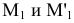
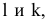
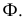
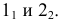
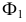
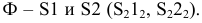
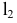
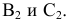
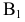
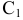
На рис. 9.23 показано построение точек пересечения поверхности наклонного цилиндра с круговым основанием с прямой линией 1. Для этого через прямую 1 проведем вспомогательную плоскость 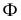
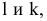
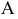
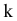
Возьмем небольшую часть поверхности и точку на ней. Если через эту точку на поверхности проведем кривые и касательные к ним прямые, то последние оказываются в одной плоскости Эту плоскость называют касательной к плоскости в данной ее точке.
Рассмотрим несколько примеров построения касательной плоскости к поверхностям
На рис. 9.24 показано построение плоскости, касательной к сфере в точке
Плоскость, касательная к сфере, перпендикулярна радиусу, проведенному в точке касания. Поэтому, проведя радиус 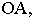
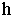
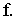
В рассмотренном примере касательная плоскость имеет с поверхностью одну общую точку.
На рис. 9.25 показано построение плоскости, касательной к цилиндру в точке 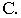
Данная поверхность линейчатая. Поэтому через точку 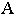
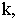
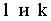
Способ вспомогательных секущих плоскостей
Линия пересечения двух поверхностей есть линия, принадлежащая обеим поверхностям. Следовательно, для построения линии пересечения поверхностей необходимо найти общие точки для данных поверхностей.
Линию пересечения поверхностей можно построить, применяя вспомогательные секущие плоскости (посредники), пересекающие данные поверхности по каким-либо линиям Взяв достаточное количество вспомогательных поверхностей, можно найти достаточное количество точек искомой линии.
Сформулируем общее правило построения линии пересечения поверхностей:
- – выбираем вид вспомогательных поверхностей;
- – строим линии пересечения вспомогательных поверхностей с заданными поверхностями;
- – находим точки пересечения построенных линий и соединяем их между собой.
В качестве вспомогательных поверхностей выбирают такие, линии пересечения которых с заданными поверхностями проецируются в графически простые линии – прямые, окружности, т.к. при этих условиях задача решается проще и точнее. В качестве вспомогательных поверхностей можно использовать плоскости или сферы
Рассмотрим применение вспомогательных секущих плоскостей на примере построения линии пересечения сферы с конусом вращения (рис. 10.1). При построении точек линии пересечения поверхности вначале находят те точки, которые называют характерными или опорными. Основания заданных поверхностей, представленных окружностями, принадлежат горизонтальной плоскости проекций 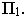
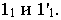
Проведенная фронтальная плоскость уровня 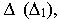
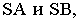
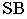
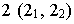
Промежуточные точки найдем при помощи горизонтальных плоскостей уровня 
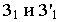
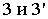
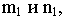
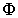
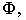
Число вспомогательных секущих плоскостей, а, следовательно, и промежуточных точек линии пересечения зависит от требуемой точности решения
Относительно горизонтальной плоскости проекций видимой является заданная половинка сферы и коническая боковая поверхность. Следовательно, видима и вся горизонтальная проекция линии пересечения этих поверхностей.
Относительно фронтальной плоскости проекций видимой является часть 1, 4, 3, 2, фронтальная проекция линии пересечения, расположенная на видимых (передних) участках заданных поверхностей, а часть 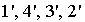
Заданные поверхности симметричны относительно фронтальной плоскости уровня 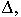
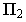
На чертеже одноименные проекции точек 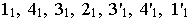
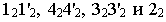
Как отмечалось выше, для нахождения промежуточных точек, принадлежащих линии пересечения, были использованы горизонтальные плоскости уровня.
Фронтальные плоскости уровня, кроме проходящей через ось конической поверхности плоскости 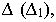
Проецирующие плоскости будут давать в пересечении сложные для построения на чертеже линии, поэтому их также нецелесообразно применять в качестве вспомогательных секущих плоскостей. Например, горизонтально-проецирующие плоскости, проходящие через ось заданной конической поверхности, будут пересекать ее по образующим, а сферу – по окружностям. Но эти окружности будут проецироваться на плоскость 
После сравнения всех возможных вариантов в качестве вспомогательных секущих плоскостей были выбраны горизонтальные плоскости уровня, т.к. их применение дает наиболее простые графические построения на чертеже.
На рис. 10.2 приведено построение линии пересечения кругового конуса с вертикальной осью с фронтально-проецирующим цилиндром.
Характерные точки 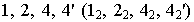
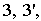
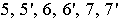
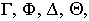
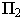
На рис. 10.3 приведено построение линии пересечения кругового цилиндра с вертикальной осью и сферы
Ход решения задачи аналогичен описанному выше. В качестве вспомогательных секущих плоскостей использованы фронтальные плоскости уровня, которые пересекают сферу по окружностям, а цилиндр – по прямолинейным образующим. Опорные точки 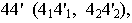
Способом вспомогательных секущих плоскостей можно воспользоваться для построения линии взаимного пересечения многогранной поверхности с поверхностью вращения.
На рис. 10.4 приведено построение линии пересечения трехгранной призмы и конуса.
В качестве вспомогательных секущих плоскостей приняты горизонтальные плоскости уровня Каждая секущая плоскость пересекает конус по окружности, радиус которой равен расстоянию от оси до образующей. Строим горизонтальные проекции окружностей и на их пересечении с проекциями ребер призмы находим проекции 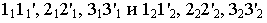
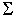
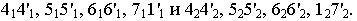
Линией пересечения грани 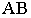
На рис. 10.5 приведено построение линии пересечения конуса и трехгранной призмы, грани которой являются горизонтально-проецирующими плоскостями.
Боковые грани призмы пересекаются с поверхностью конуса по гиперболам Построим точки, принадлежащие линиям пересечения, на каждой грани. Ребра 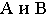
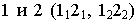
которое пересекает боковую поверхность конуса, проведем через ребро 
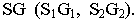
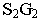
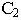
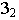
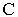
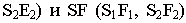
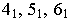
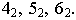
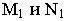
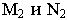
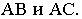
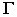
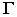
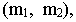
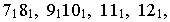
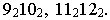
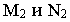
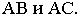
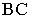
При помощи плоскости 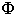
Частные случаи пересечения поверхностей второго порядка
При взаимном пересечении поверхностей второго порядка получается в некоторых случаях распадение .шиш пересечения на две плоские кривые второго порядка. Это бывает в тех случаях, когда обе пересекающиеся поверхности вращения (цилиндр и конус, два конуса и т.п.) описаны вокруг общей для них сферы В примерах, приведенных на рис. 11.1, а и 11.1, б, пересечение происходит по эллипсам
На рис. 11.2 показаны два цилиндра равного диаметра с пересекающимися осями. Из точки пересечения осей может быть проведена сфера, вписанная в оба цилиндра. Обе поверхности пересекаются по линии, состоящей из двух эллипсов.
Изображенные на рис. 11.1 и 11.2 кривые пересечения поверхностей проецируются на фронтальную плоскость проекций в виде прямолинейных отрезков, т.к. общая плоскость симметрии для каждой пары рассмотренных поверхностей расположена параллельно плоскости
Указанные выше построения основаны на следующих положениях:
- поверхности второго порядка, имеющие двойное соприкосновение, пересекаются между собой по двум кривым второго порядка, причем плоскости этих кривых проходят через прямую, определяемую точками прикосновения;
- две поверхности второго порядка, описанные около третьей поверхности второго порядка (или в нее вписанные), пересекаются между собой по двум кривым второго порядка. Это положение известно под названием теоремы Монжа.
Соосные поверхности вращения (т.е. поверхности с общей осью) пересекаются по окружностям. На рис. 11.3 даны три примера: а) цилиндр и сфера (см рис. 11.3, а); б) конус и сфера (см рнс. 11.3, б); в) две сферы (см рис 11.3, в).
Способ сфер
С помощью вспомогательных сферических поверхностей удобно строить линии пересечения двух поверхностей вращения с общей плоскостью симметрии, параллельной одной из плоскостей проекций.
При этом возможны два случая:
- если оси поверхностей вращения пересекаются, то для построения линии пересечения этих поверхностей применяют семейство концентричных сфер;
- если оси поверхностей вращения не пересекаются, то используют эксцентрические сферы
План решения задачи способом концентрических сфер следующий:
- принимая точку пересечения осей заданных поверхностей за центр, строим вспомогательные сферы – посредники;
- определяем окружности, по которым пересекаются сферы-посред-ники с каждой из заданных поверхностей;
- находим общие точки пересечения полученных окружностей.
Эти точки и принадлежат искомой линии пересечения поверхностей.
На рис. 11.4 построена линия пересечения двух конусов вращения, оси которых пересекаются, образуя общую фронтальную плоскость симметрии.
В данном случае применены вспомогательные сферы, проведенные из одного и того же центра – точки 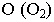
Точки пересечения фронтальных проекций очерковых образующих 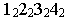
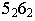
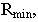
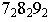
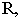
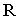
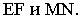
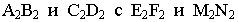
Изменяя радиус 
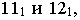
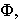
Пример построения линии пересечения двух поверхностей вращения способом эксцентрических сфер приведен на рис. 11.5 (открытый тор пересекается с конусом вращения).
Поверхности имеют одну общую плоскость симметрии. Оси пересекающихся поверхностей вращения между собой не пересекаются. Поверхности заданы фронтальными отрезками.
При построении линии пересечения поверхностей прежде всего определяем точки 1 и 2 пересечения очерковых образующих поверхностей. Затем через ось вращения тора проводим фронтально-проецирующую плоскость 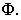
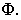
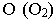
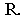
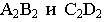
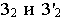
Аналогично определяют другие промежуточные точки линии пересечения поверхностей. Вспомогательные сферы имеют различные центры, находящиеся на оси конуса вращения.
Построение развертки поверхности простейших геометрических тел
Построение разверток имеет большое практическое значение, так как позволяет изготавливать разнообразные изделия из листового материала путем изгибания.
Разверткой поверхности называется фигура, полученная совмещением поверхности без складок и разрывов с плоскостью чертежа.
Не все поверхности можно совместить с плоскостью чертежа, поэтому те поверхности, которые можно совместить без разрывов и складок с плоскостью, называются развертывающимися, а поверхности, которые не могут быть совмещены с плоскостью, называются неразвертывающимися
К развертывающимся поверхностям относятся все многогранники, конические и цилиндрические поверхности.
Построение развертки поверхностей прямых призмы, цилиндра, конуса выполняется просто, без применения каких-либо специальных приемов. Для построения их разверток надо знать натуральную величину ребер, образующих и оснований
На рис. 12.1 – 12.4 показано построение разверток поверхностей простейших геометрических тел.
Развертка поверхности прямой трехгранной призмы (см. рис. 12.1) состоит из трех прямоугольников, которые являются боковыми гранями, и двух треугольников – оснований призмы.
Развертка поверхности прямого кругового цилиндра (см. рис. 12.2) состоит из прямоугольника, высота которого равна высоте цилиндра, а ширина – длине окружности, равной окружности оснований цилиндра.
Развертка поверхности трехгранной пирамиды (см. рис. 12.3) представляет собой три треугольника – боковые грани – и еще один треугольник – основание пирамиды
Натуральную величину ребер находят одним из методов преобразования. В данном случае применяется способ вращения вокруг оси, перпендикулярной плоскости проекций 
Развертка поверхности прямого кругового конуса (см. рис. 12.4) представляет собой сектор, радиус которого равен длине образующей конуса.
Угол
где 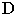
Построение развертки наклонных призматических, цилиндрических и конических поверхностей
Дня построения развертки наклонных поверхностей применяют различные способы:
- а) способ раскатки;
- б) способ нормального сечения;
- в) способ триангуляции (треугольников).
Способ раскатки используют в том случае, когда основание призмы или цилиндра на одной из плоскостей проекций изображается в натуральную величину, а ребра или образующие поверхностей параллельны другой плоскости проекций, т.е. также имеют натуральную величину.
Способ раскатки основан на последовательном совмещении всех граней призмы с плоскостью проекций. Для определения натуральной величины граней используется вращение грани вокруг одной из ее сторон как линии уровня.
На рис. 12.5 дано построение развертки поверхности наклонной трехгранной призмы способом раскатки.
Ребра призмы параллельны плоскости проекций 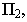
Дня построения развертки необходимо повернуть каждую грань призмы вокруг бокового ребра до положения, при котором она станет параллельной фронтальной плоскости проекций.
Раскатка боковой поверхности призмы начата с грани 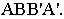
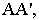
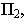
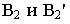
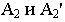
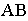
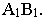
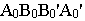
Далее вращают следующую грань 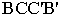
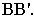
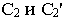
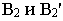
Параллелограмм 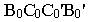
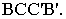
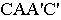
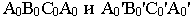
На рис. 12.6 дано построение развертки наклонного цилиндра способом раскатки.
Так как образующие цилиндра занимают общее положение и поэтому не имеют натуральную величину, то необходимо выполнить следующие построения:
- сначала заменяют фронтальную плоскость проекций
на новую
выбирая ее так, чтобы образующие цилиндра на новую плоскость проекций проецировались в натуральную величину. Для этого новую ось проекций проводят параллельно образующим цилиндра;
- делят окружность основания цилиндра на
равных частей (см. рис. 12.6);
- заменяют цилиндрическую поверхность призматической, т.е. вписывают в цилиндр восьмигранную призму. Для этого через точки деления окружности основания проводят прямолинейные образующие цилиндра – ребра призмы;
- за плоскость развертки принимают фронтальную плоскость, проходящую через ребро
призмы, которое будет являться осью вращения граней призмы Дальнейшие построения аналогичны выполненным на рис. 12.5.
Способ нормального сечения применим в том случае, когда ребра призмы или образующие цилиндра параллельны одной из плоскостей проекций, т.е. проецируются на нее в натуральную величину.
На рис. 12.7 дано построение развертки поверхности трехгранной наклонной призмы способом нормального сечения
Построения выполняют в следующем порядке:
- призму пересекают нормальной (перпендикулярной к ее ребрам) плоскостью
Так как ребра призмы параллельны фронтальной плоскости проекций и на нее проецируются в натуральную величину, то нормальная плоскость будет являться фронтально-проецирующей плоскостью;
- строят проекции и определяют натуральную величину нормального сечения. На рис. 12.7 фронтальная проекция фигуры нормального сечения
совпадает со следом плоскости
Натуральную величину фигуры сечения
строят способом плоскопараллельного перемещения. Для этого плоскость
располагают параллельно горизонтальной плоскости проекций, чтобы фигура сечения проецировалась на плоскость проекций
в натуральную величину;
- натуральную величину фигуры нормального сечения на свободном поле чертежа разворачивают в прямую линию
и через вершины сечения перпендикулярно линии
проводят прямые;
- на перпендикулярах по обе стороны откладывают длины соответствующих отрезков ребер призмы Их величины измеряют от линии сечения до оснований в обе стороны и откладывают на перпендикулярах. Полученные точки
соединяют отрезками прямых;
- пристраивают к полученной фигуре основания. Их строят по трем сторонам.
На рис. 12.8 построена развертка поверхности наклонного цилиндра с круговым основанием.
Образующие цилиндра параллельны плоскости проекций 
- делят основание цилиндра на 12 частей;
- проводят через точки деления основания образующие;
- проводят плоскость
перпендикулярную к образующим цилиндра;
- находят натуральную величину нормального сечения. В данном примере она найдена способом плоскопараллельного перемещения;
- на свободном попе чертежа натуральную величину линии сечения разворачивают в прямую линию
- через точки деления проводят перпендикулярно прямой
отрезки, на которых откладывают длины образующих от линии сечения до оснований. Длину образующих берут на фронтальной плоскости проекций;
- полученные точки соединяют плавной кривой. Образованная фигура является разверткой боковой поверхности наклонного цилиндра.
Сущность способа триангуляции (треугольников) состоит в том, что каждая грань многогранника разбивается диагональю на два треугольника, далее определяют натуральную величину всех сторон треугольников, которые последовательно в натуральную величину вычерчиваются на свободном поле чертежа.
На рис. 12.9 дано построение развертки поверхности наклонной призмы
Построение выполняют в следующем порядке:
- каждую грань
разбивают диагоналями на два треугольника. Затем определяют натуральную величину всех сторон треугольников, одной из сторон любого треугольника будет являться ребро призмы, второй – диагональ, а третьей -сторона основания наклонной призмы. Основание призмы принадлежит плоскости проекций
поэтому проецируется на нее в натуральную величину;
- все ребра призмы одинаковые, поэтому находят натуральную величину одного из ребер
призмы любым из способов преобразования В данном случае применяют способ вращения вокруг прямой, перпендикулярной плоскости проекций
и проходящей через точку
- находят натуральную величину диагоналей способом плоско параллельного перемещения;
- на свободном попе чертежа последовательно в натуральную величину вычерчиваются треугольники
по трем сторонам;
- для построения полной развертки поверхности наклонной призмы клюбой грани пристраивают два основания
На рис. 12.10 дано построение развертки поверхности наклонного конуса.
Построение развертки конической поверхности выполняется так же. как в случае построения развертки боковой поверхности пирамиды – способом триангуляции (треугольников).
Для этого заменяют поверхность конуса вписанной восьмигранной или двенадцатигранной пирамидой. Определяют длину всех образующих любым из методов преобразования, а затем строят треугольники в определенном порядке так, чтобы они примыкали друг к другу. Фигура 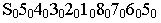
Для построения развертки боковой поверхности наклонного усеченного конуса (рис. 12.11) выполняют следующие построения:
- вписывают в конус многогранную усеченную пирамиду;
- разбивают диагоналями каждую грань вписанной пирамиды на два треугольника;
- определяют натуральную величину всех сторон треугольников (натуральную величину ребер и диагоналей) способом плоскопараллельного перемещения. Нижнее и верхнее основания конуса на горизонтальную плоскость проекций проецируются в натуральную величину.
Построение развертки поверхности сферы
Построение развертки поверхности сферы выполняется способом вспомогательных цилиндров (рис. 12.12). Этот способ заключается в следующем: заданная поверхность сферы разбивается с помощью меридианов на равные между собой части или доли. Каждая доля заменяется цилиндрической поверхностью, которая касательна к поверхности сферы в точках главного меридиана доли.
Развертка поверхности сферы выполняется в следующем порядке:
- поверхность сферы деляг на 6 частей горизонтально-проецирующими плоскостями, которые являются меридианами;
- описывают вокруг сферы цилиндрическую поверхность, ось которой проходит через центр сферы перпендикулярно
таким образом, часть сферы заменяют частью цилиндрической поверхности. На горизонтальную плоскость проекций она проецируется в виде треугольника
а на фронтальную – в виде дуги окружности;
- делят фронтальную проекцию дуги окружности на 6 равных частей Величина отрезков
будет натуральной на плоскости проекций
Строят горизонтальные проекции образующих, проходящих через соответствующие точки деления;
- находят натуральную величину образующих
на плоскости проекций
так как образующие параллельны горизонтальной плоскости проекций;
- для построения развертки главный меридиан разворачивают в прямую линию и на ней откладывают вверх и вниз отрезки, равные
а через полученные точки откладывают вправо и влево отрезки, равные
- соединив плавной кривой концы отрезков, получают развертку одной доли, т.е.
части поверхности сферы. Полная развертка поверхности сферы будет состоять из шести одинаковых долей.
Поверхности и позиционные задачи
Вопрос о принадлежности точки и линии поверхности был рассмотрен выше. Остановимся на задачах по определению линии пересечения поверхностей и точек пересечения линии с поверхностью.
Сечение поверхности плоскостью
Начнем с рассмотрения пересечения многогранника плоскостью.
Для построения сечения существуют два подхода: фиксируются точки пересечения ребер многогранника с секущей плоскостью или определяются линии пересечения граней с секущей плоскостью.
Рисунок 8.21 – Сечение призмы плоскостью
Рисунок 8.22 -Сечение пирамиды плоскостью
В сечении четырехгранной призмы плоскостью получается четырехугольник (рисунок 8.21). Вершины этого четырехугольника можно рассматривать, как точки пересечения ребер призмы с плоскостью Р.
В силу того, что призма занимает положение проецирующей поверхности, все ее ребра суть проецирующие прямые (в соответствии с рисунком 8.21 – горизонтально – проецирующие). И задача сводится к отысканию точек пересечения (1, 2, 3 и 4) проецирующих прямых (ребер) с плоскостью Р. Объединение соответствующих проекций позволяет получить проекции плоского сечения.
Аналогично может быть получено сечение пирамиды плоскостью. Например, пирамиды ABCS плоскостью общего положения Р (рисунок 8.22).
В силу того, что ребра пирамиды являются линиями общего (BS и CS) и частного (AS) положения, задача сводится к отысканию точек пересечения прямых с плоскостью Р.
Объединение соответствующих проекций позволяет получить проекции плоского сечения
Представление поверхностей вращения, как многогранников с бесчисленным числом сторон, приводит к мысли о том, что сечение поверхности вращения плоскостью может быть получено аналогичным же образом.
Сечением такого цилиндра плоскостью будет эллипс, в случае прохождения плоскости через ось вращения вырожденный (две параллельные прямые).
Рисунок 8.23 – Сечение цилиндра плоскостью общего положения
Рассмотрим возможность построения сечения проецирующего цилиндра плоскостью общего положения Р (рисунок 8.23). В силу начальных условий, одна проекция сечения уже определена 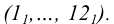
Большая ось эллипса лежит в горизонтально проецирующей плоскости Q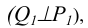
Варианты вида линий пересечения конуса плоскостью рассмотрены выше (в разделе 7.4). Здесь (рисунок 8.24) рассматривается механизм построения линии на поверхности конуса. Пусть конус вращения пересекается плоскостью общего положения Р. В соответствии с рисунком 7.5, в сечении должна получиться замкнутая кривая — эллипс.
Крайние точки кривой (3,4), лежат на очерковых образующих, и могут быть найдены, как точки их (образующих) пересечения с плоскостью Р.
Большая ось эллипса (1,2) определится аналогично предыдущей задаче. Она лежит в горизонтально-проецирующей плоскости Q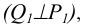
Рисунок 8.24 – Сечение конуса плоскостью общего положения
Промежуточные точки определятся во вспомогательных плоскостях 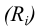
Сопряженная ’’малая” ось эллипса 56 может быть получена в плоскости R, проходящей через точку О, середину отрезка 12 (большая ось эллипса).
В общем случае промежуточные точки могут быть найдены и другим способом.
Подводя итог рассмотренным решениям, можно отметить, что линии пересечения строятся по точкам, которые на поверхности можно зафиксировать, введя дополнительные плоскости. Этот подход и определяет общую методику построения линии пересечения поверхностей.
Способ секущих плоскостей
Этот способ применяют для построения линии пересечения поверхностей, позволяющих получать (одновременно) во вводимых секущих плоскостях, графически простые линии (прямые или окружности). Это утверждение может быть проиллюстрировано на примере пересечения цилиндра 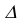
Рисунок 8.25 – Метод секущих плоскостей
Здесь в качестве вспомогательных секущих плоскостей выступают горизонтальные плоскости уровня 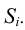
Характерные точки А, В линии пересечения определяют в пересечении фронтальных очерков. Текущие точки линии пересечения определятся как результат пересечения соответствующих окружностей и прямых в секущих плоскостях Sj.
Способ секущих сфер
Этот способ базируется на том, что две соосные поверхности вращения пересекаются по окружности, лежащей в плоскости, перпендикулярной общей оси вращения.
Сфера будет соосна с любой поверхностью вращения, если ее центр ле-
жит на оси вращения этой поверхности (рисунок 8.26). Это и определяет возможность использовать сферу в качестве вспомогательной секущей поверхности.
Условиями применения сферы в этом качестве следующие: рассматриваются поверхности вращения, их оси должны пересекаться в одной точке – центре секущих сфер.
При этом желательно, чтобы плоскость, образованная пересечением осей, была бы параллельна одной из плоскостей проекции.
Линия пересечения двух цилиндров Ф и А 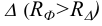
Линия пересечения распадается на две ветви, нижнюю и верхнюю, построение которых аналогично (рисунок 8.27).
Фронтальные проекции характерных точек линии пересечения 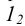
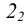
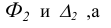
Низшая точка линии пересечения (3) определяется введением сферы 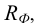
С цилиндром 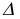
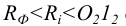
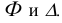
Пересечение многогранников
Построение линии пересечения многогранников можно свести к двум вариантам: определению точек пересечения ребер одного из многогранников с гранями другого и определению линий пересечения граней обоих многогранников.
Рассмотрим построение линии пересечения двух призм: прямой призмы Ф и наклонной призмы 
Грани прямой призмы Ф представляют собой проецирующие плоскости, что позволяет однозначно определить горизонтальную проекцию линии пересечения, точки 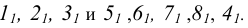
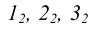
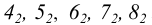
Точки 7 и 8 определятся введением через точку Е дополнительной секущей плоскости 
Пересечение линии и поверхности
Задача формулируется так: построить точки пересечения 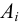
Решение для частного случая рассматривалось выше в (разделе 4.3), как задача по определению точки пересечения прямой и плоскости.
В общем случае выполняется следующее:
Проиллюстрируем все это на примере построения точек пересечения прямой t с конической поверхностью Ф (рисунок 8.29).
Прямую t целесообразно отнести к плоскости общего положения Г 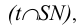
На первом этапе строится линия 12 пересечения плоскости Г с плоскостью основания конической поверхности. Затем определяется положение линии т.
Пересечение образующей m и линии t и определит решение – точку К.
Для общего случая решение задачи на пересечение цилиндроида с пространственной кривой выглядит следующим образом (рисунок 8.30).
Кривая t заключается во фронтально проецирующую цилиндрическую поверхность Г’ которая пересекает цилиндроид Ф по кривой т. Так как 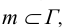
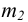
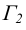
Горизонтальная проекция 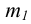
Приведенное решение является типовым. В ряде случаев для более точного построения линии пересечения данной и вспомогательной поверхностей или для упрощения построений целесообразно использовать другие виды вспомогательных поверхностей.
- Изображения и обозначения на чертежах
- Отображение пространственных объектов на плоскость
- Моделирование линии на эпюре Монжа
- Моделирование плоскости на эпюре Монжа
- Образование проекций
- Точка и прямая
- Прямая линия
- Плоскость
 — эллиптический цилиндр с образующей, параллельной
— эллиптический цилиндр с образующей, параллельной 




















































































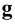
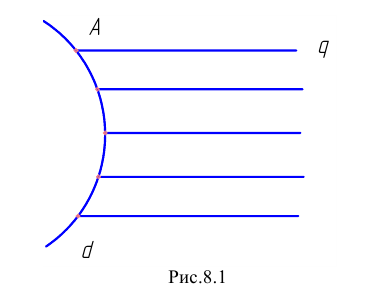
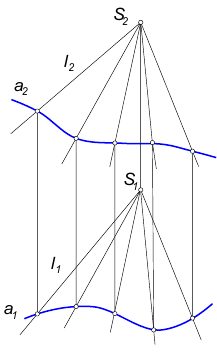
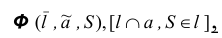
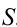
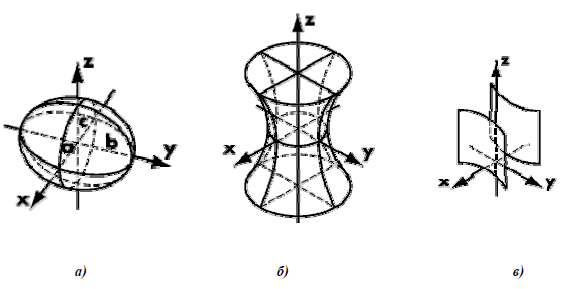
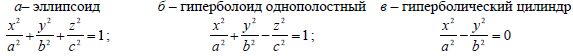
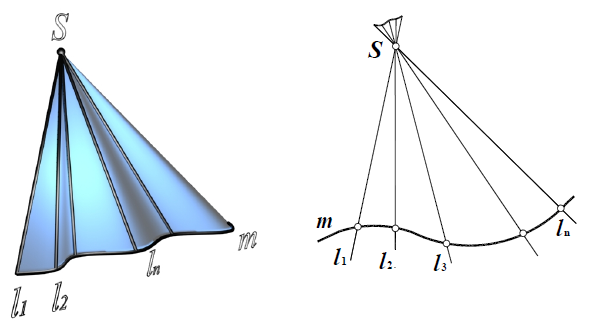

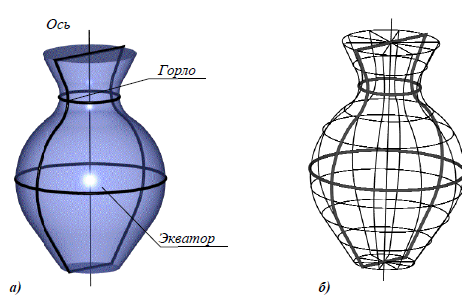
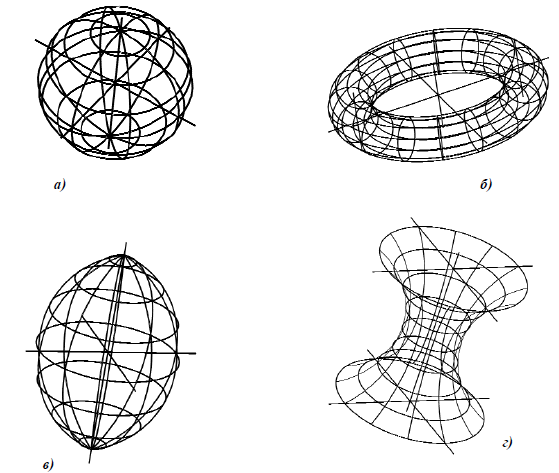
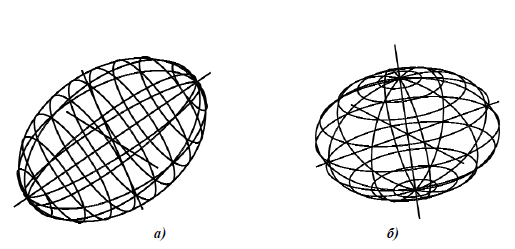
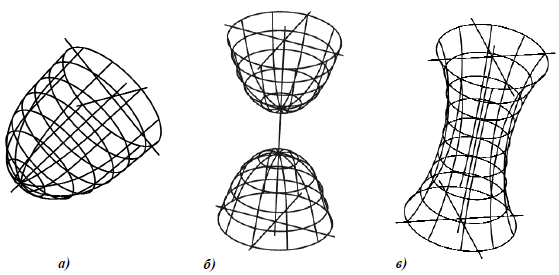
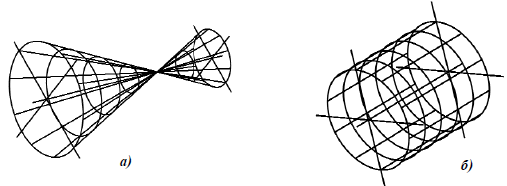
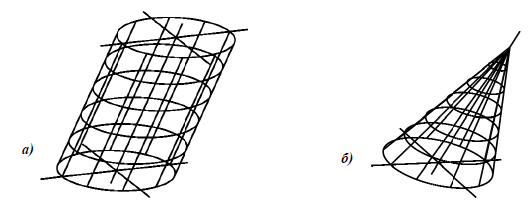
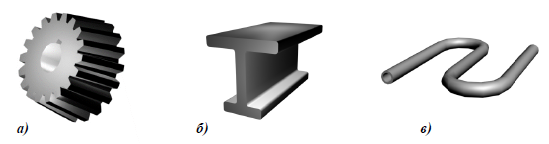

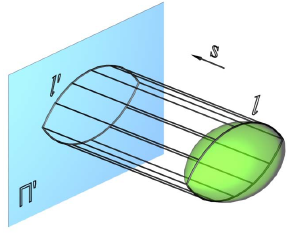
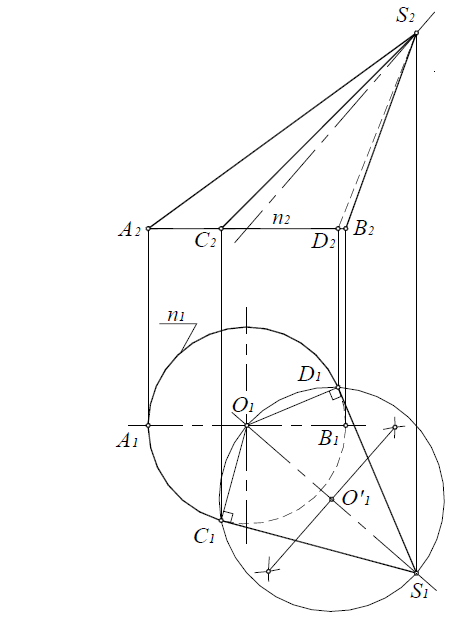
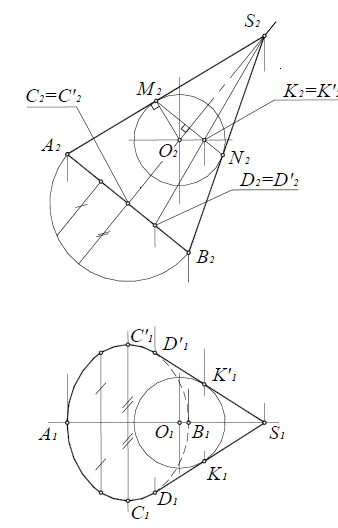
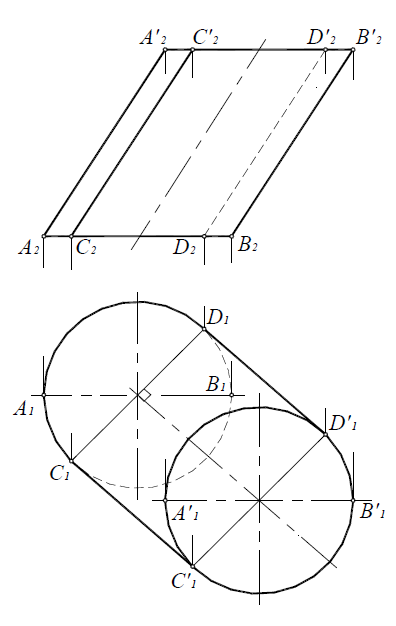
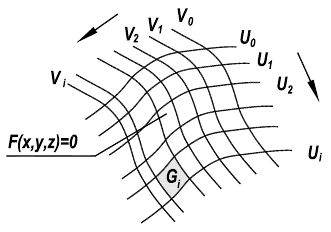
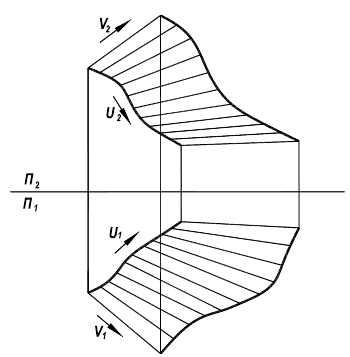
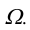
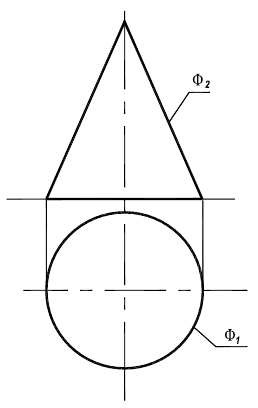
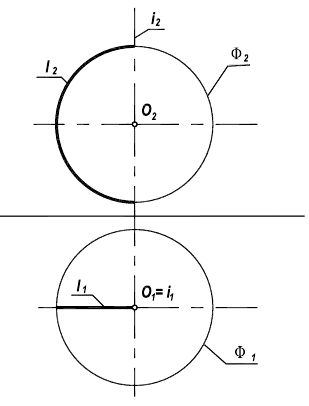
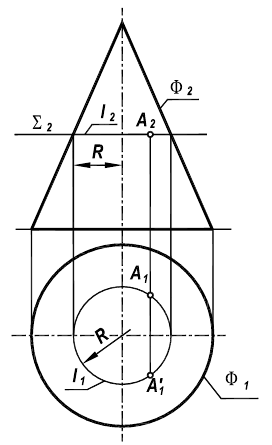
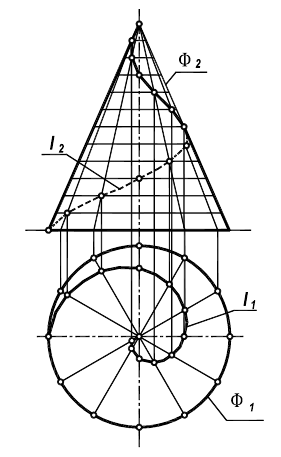
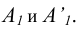
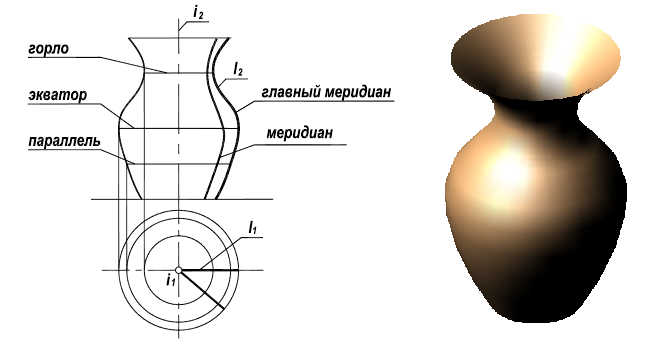
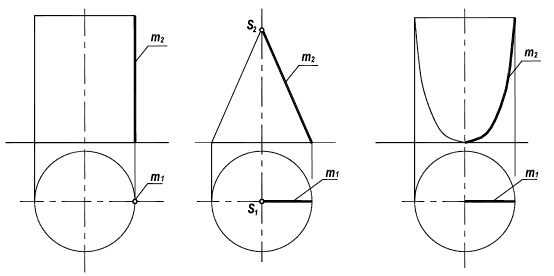
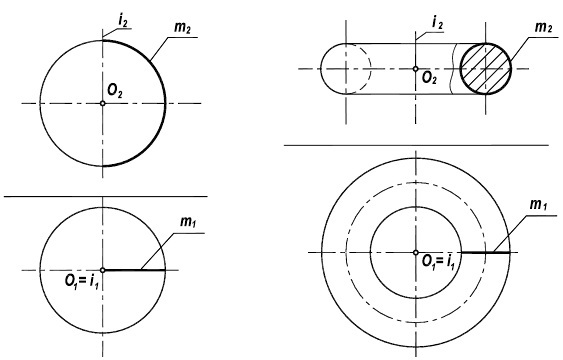
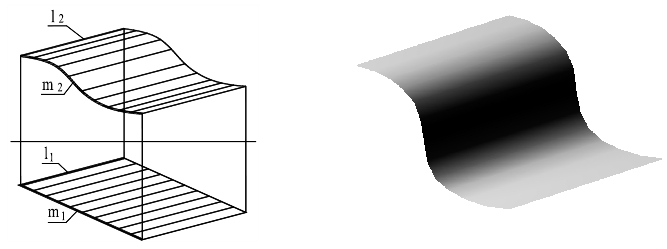
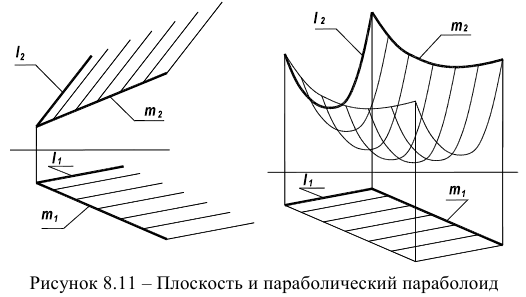
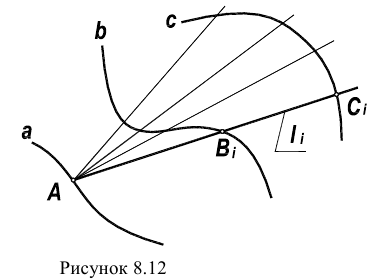
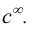
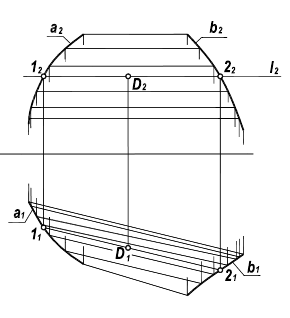
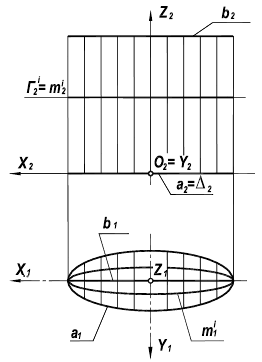
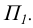
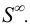
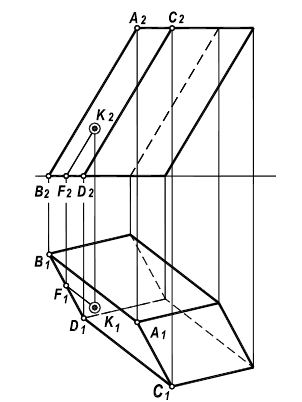
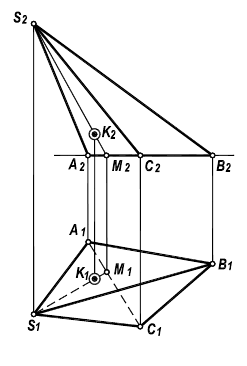
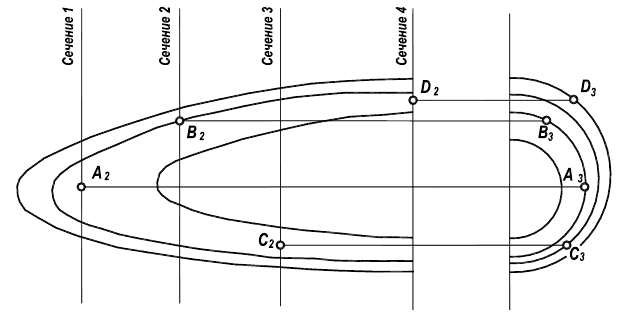
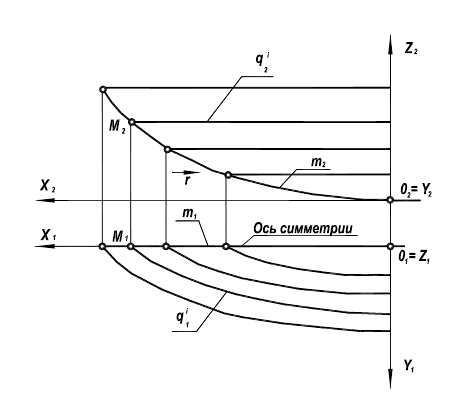
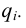
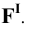
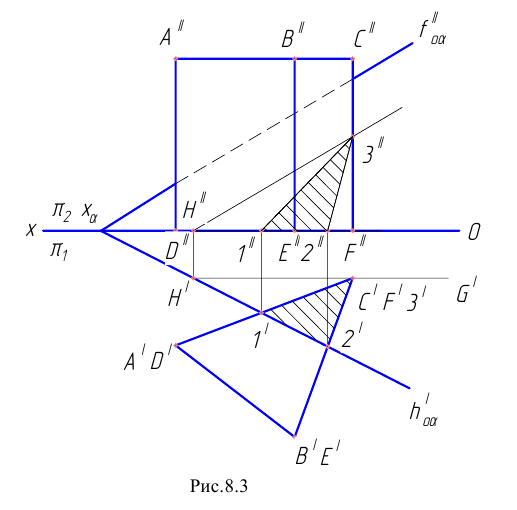
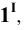
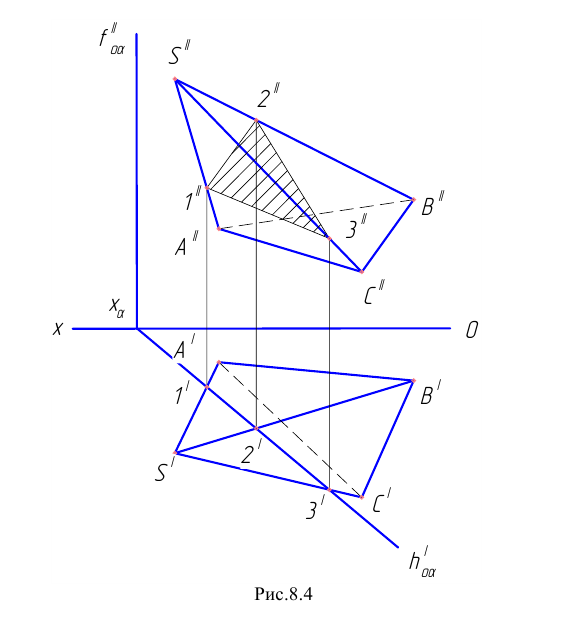
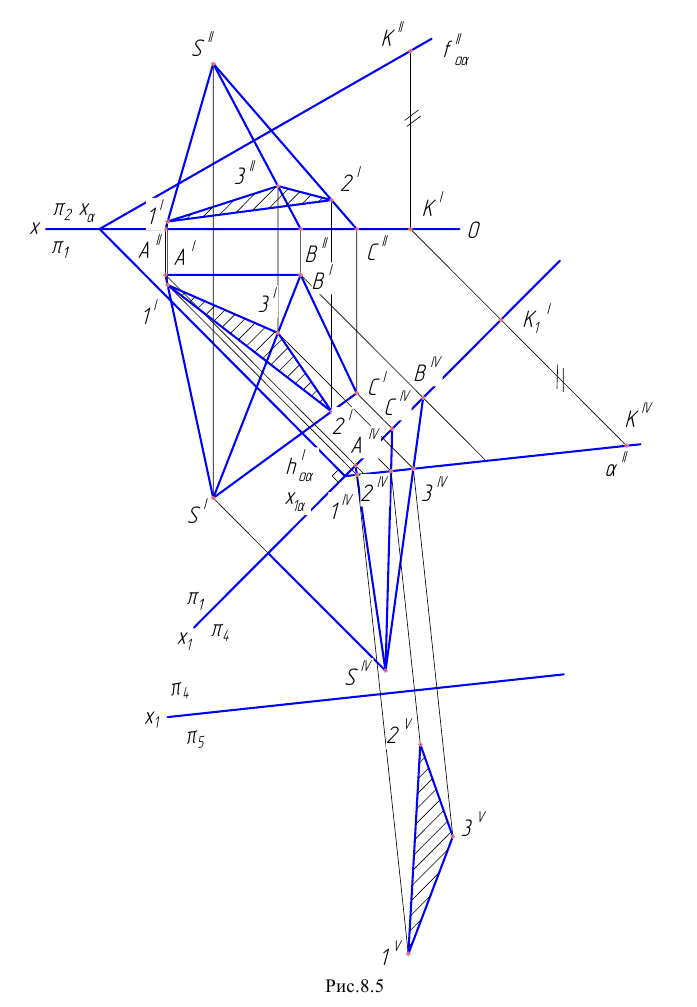
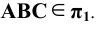
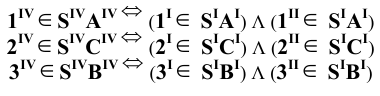
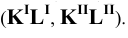
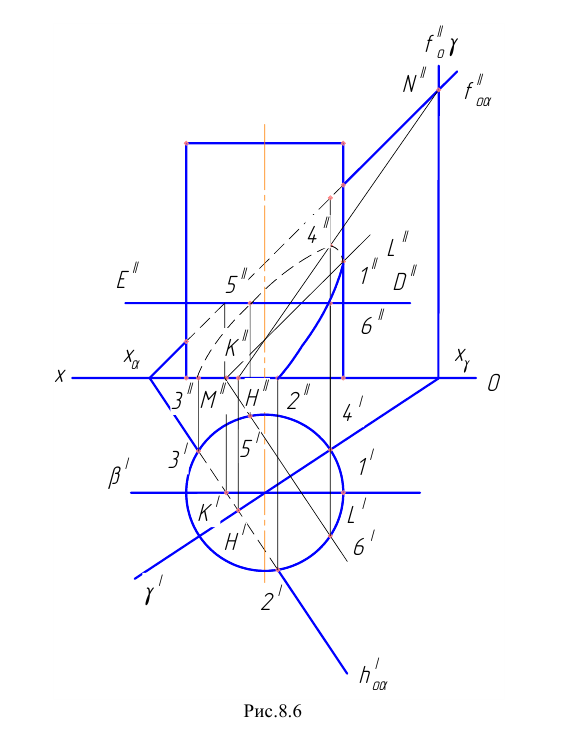
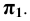
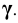
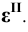
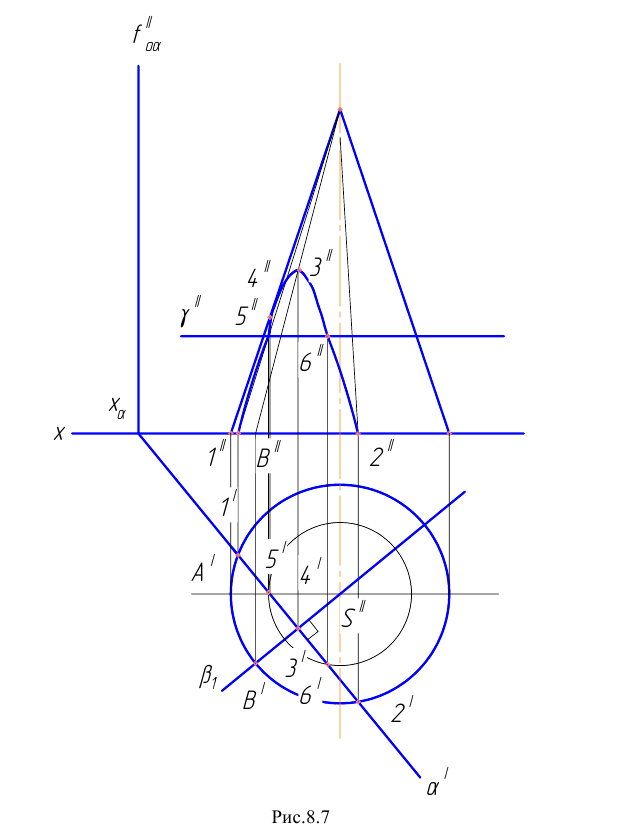
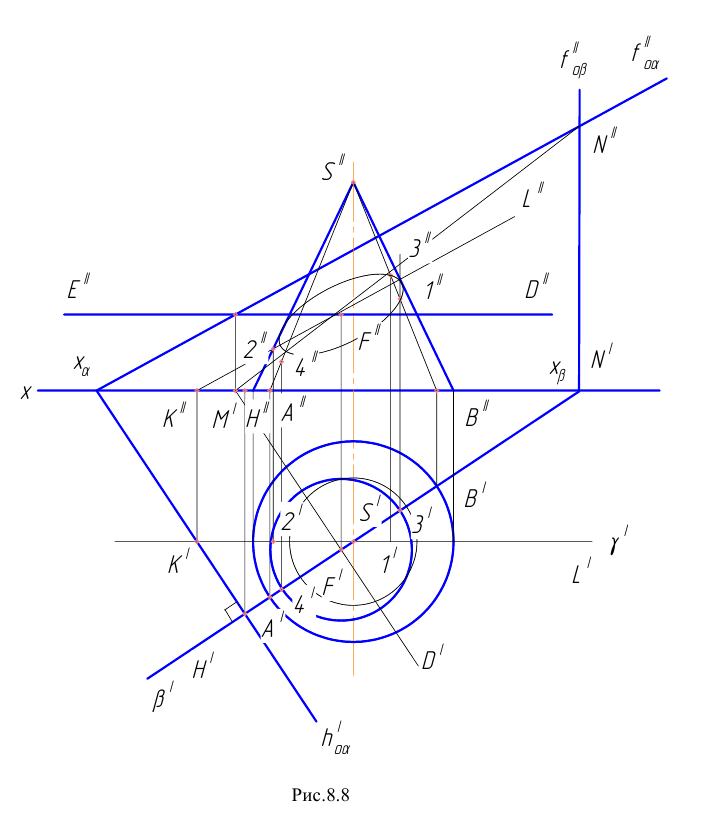
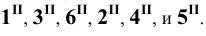
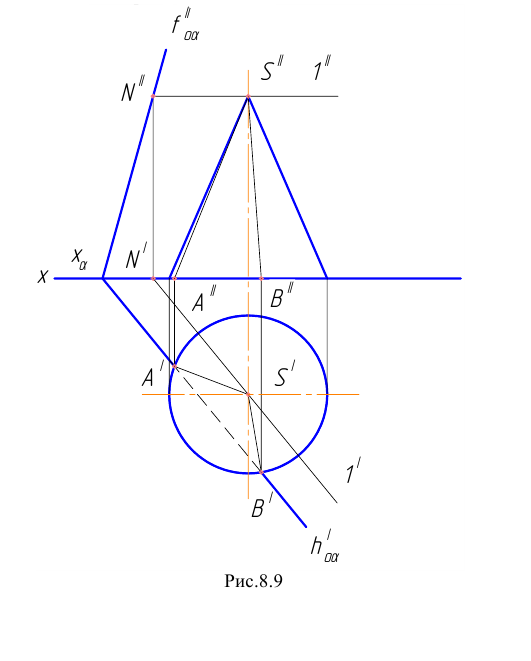
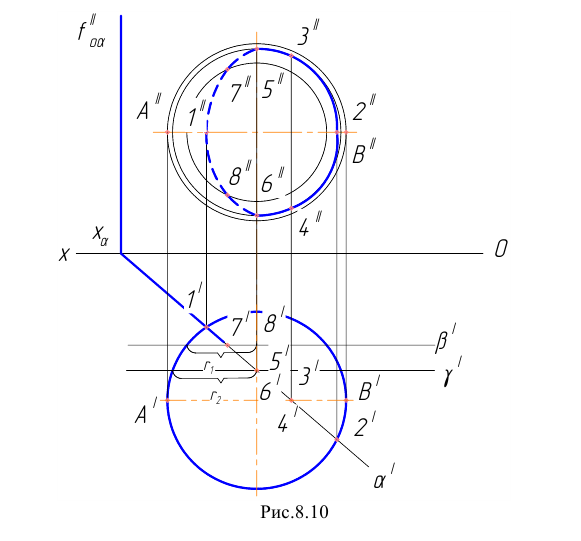
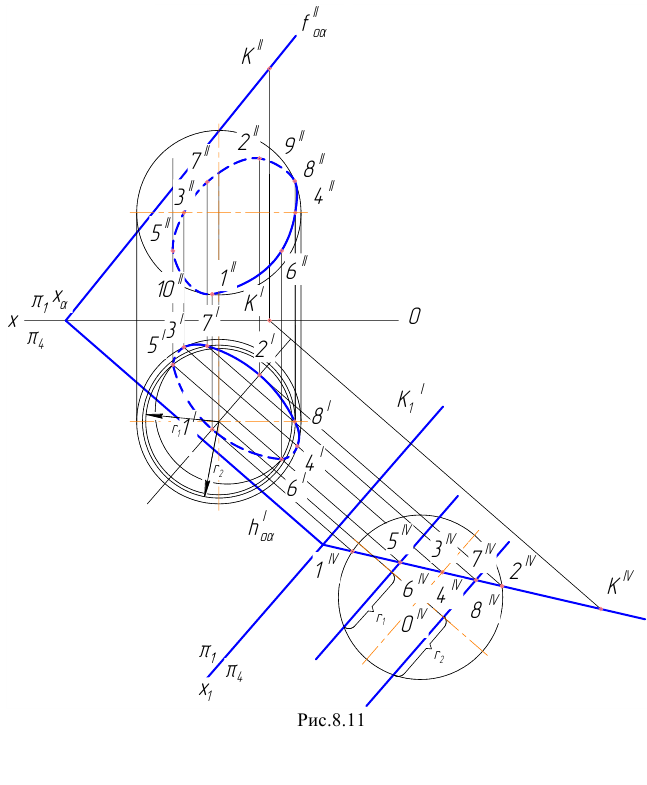
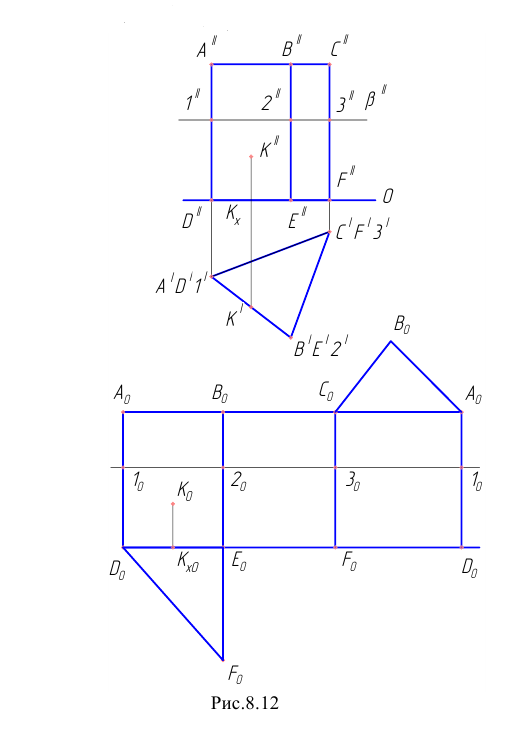
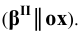
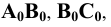
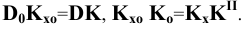
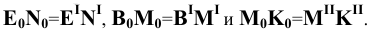
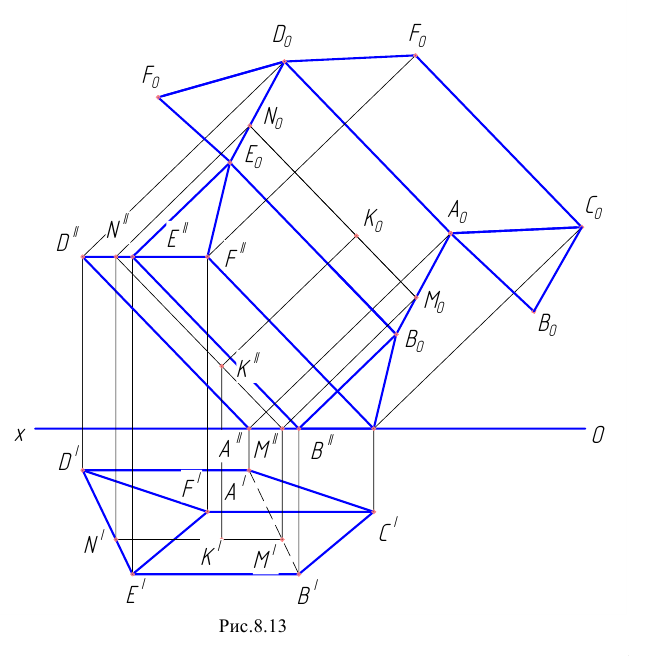
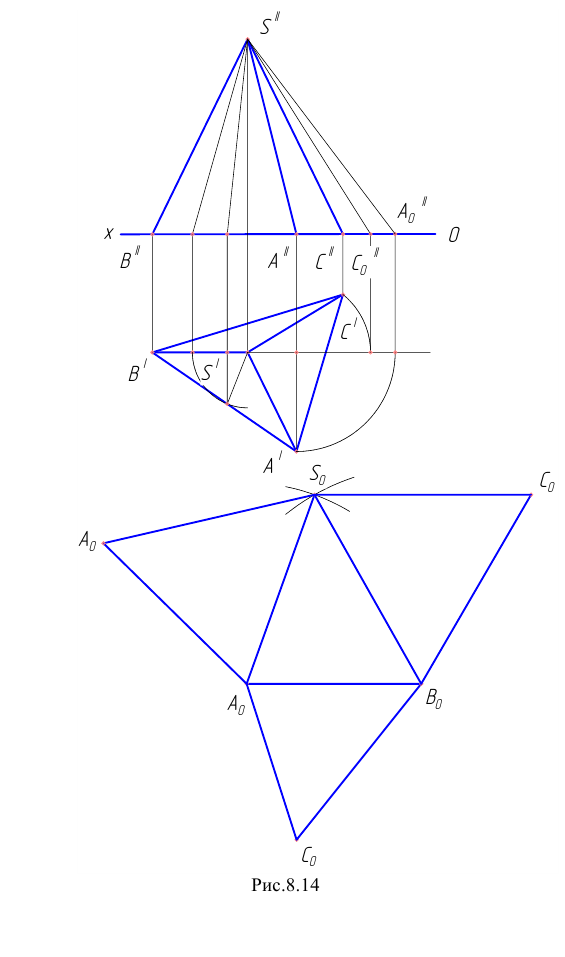
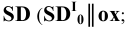
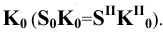
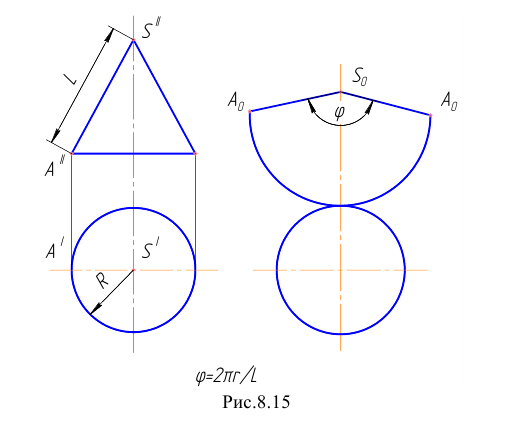
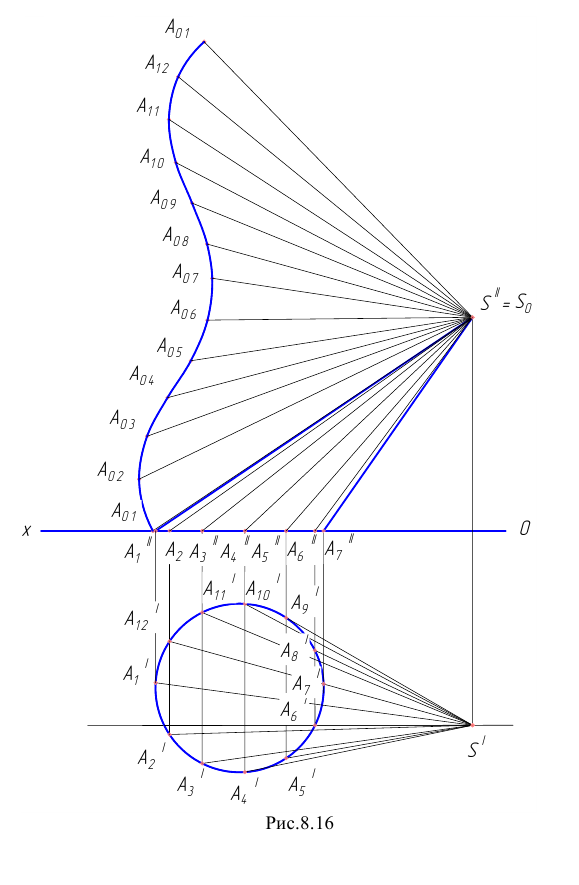

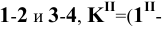
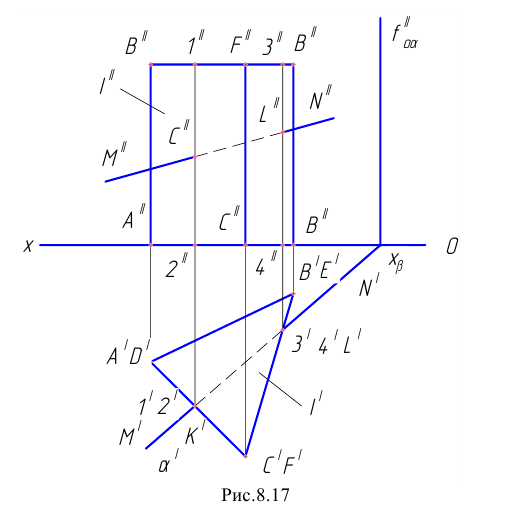
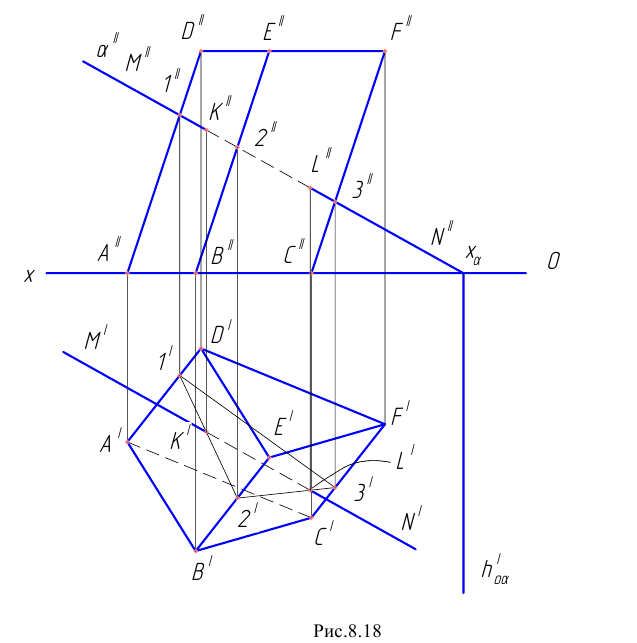
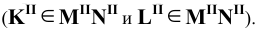
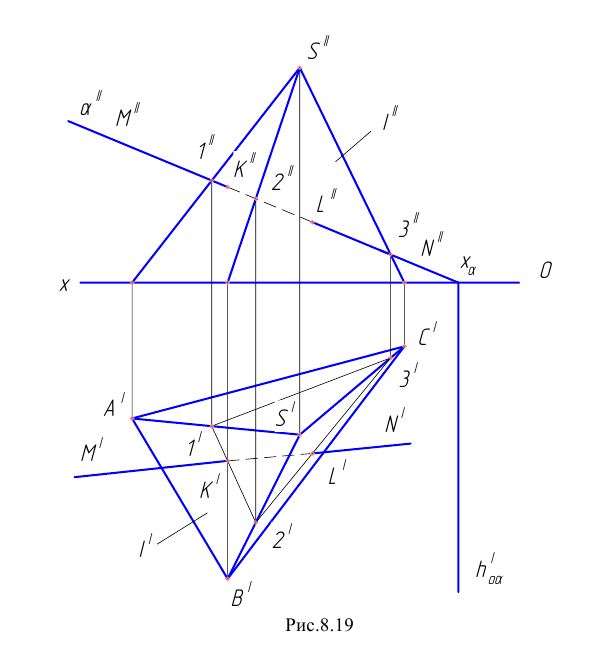
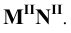
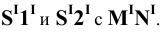
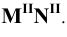
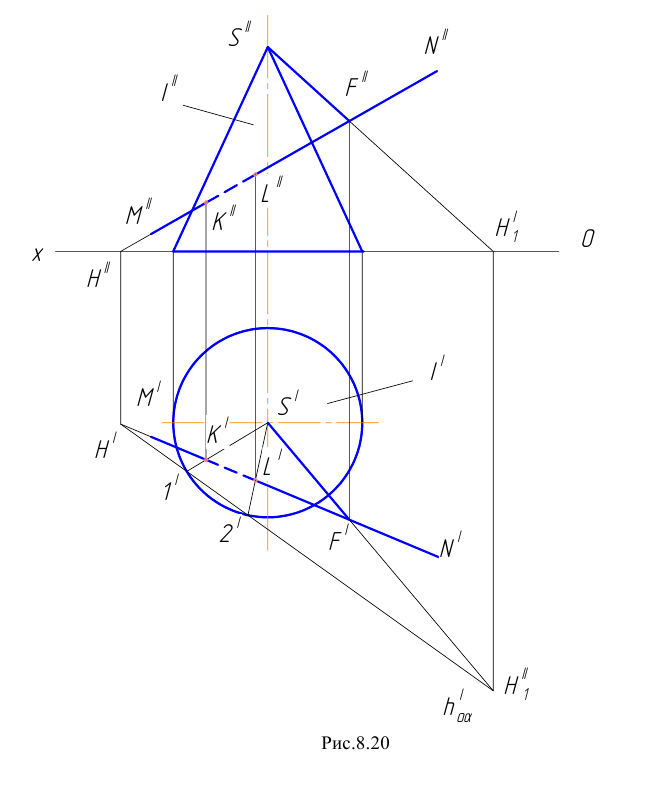
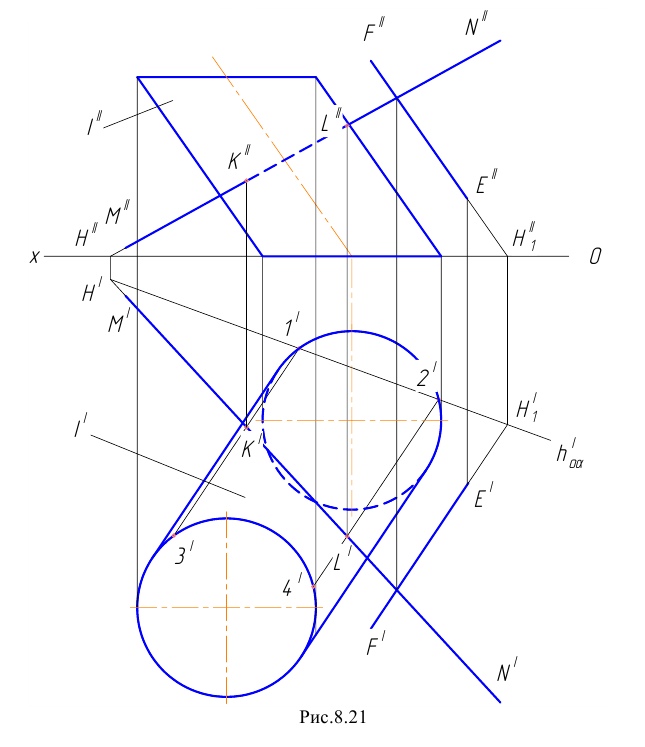
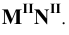
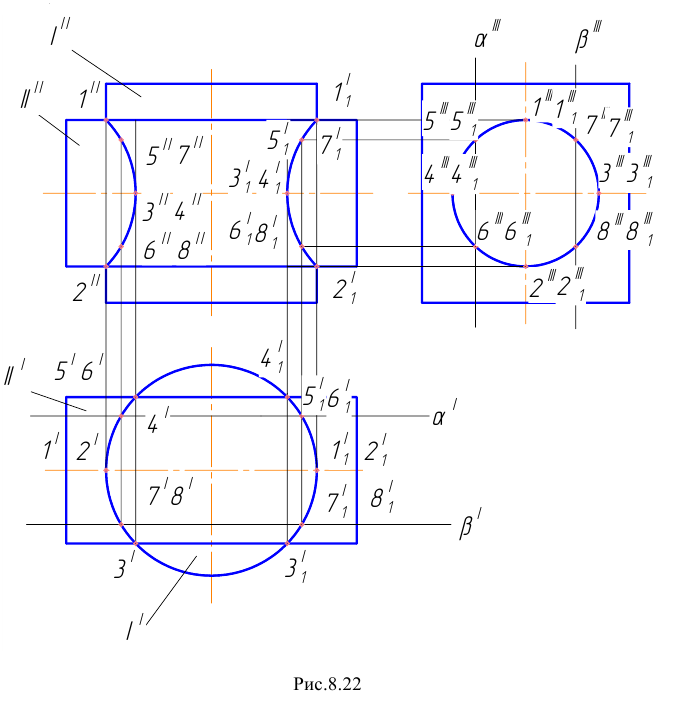
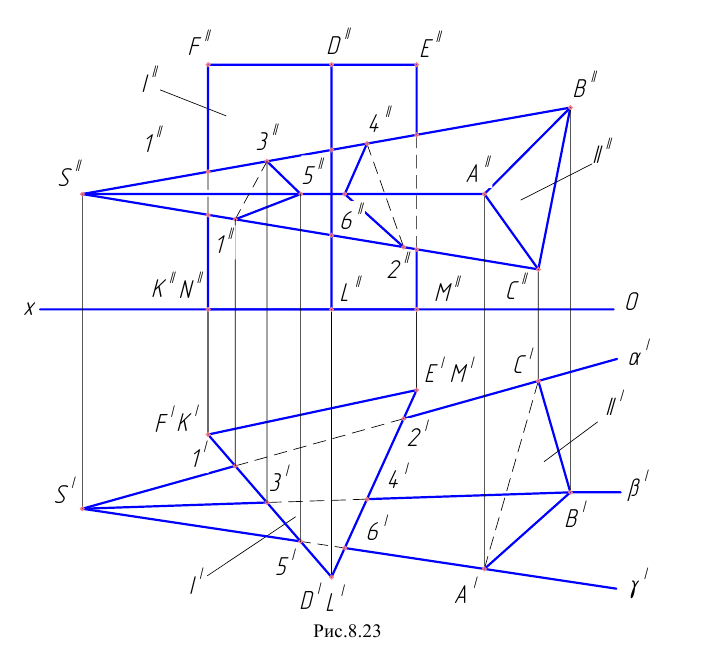
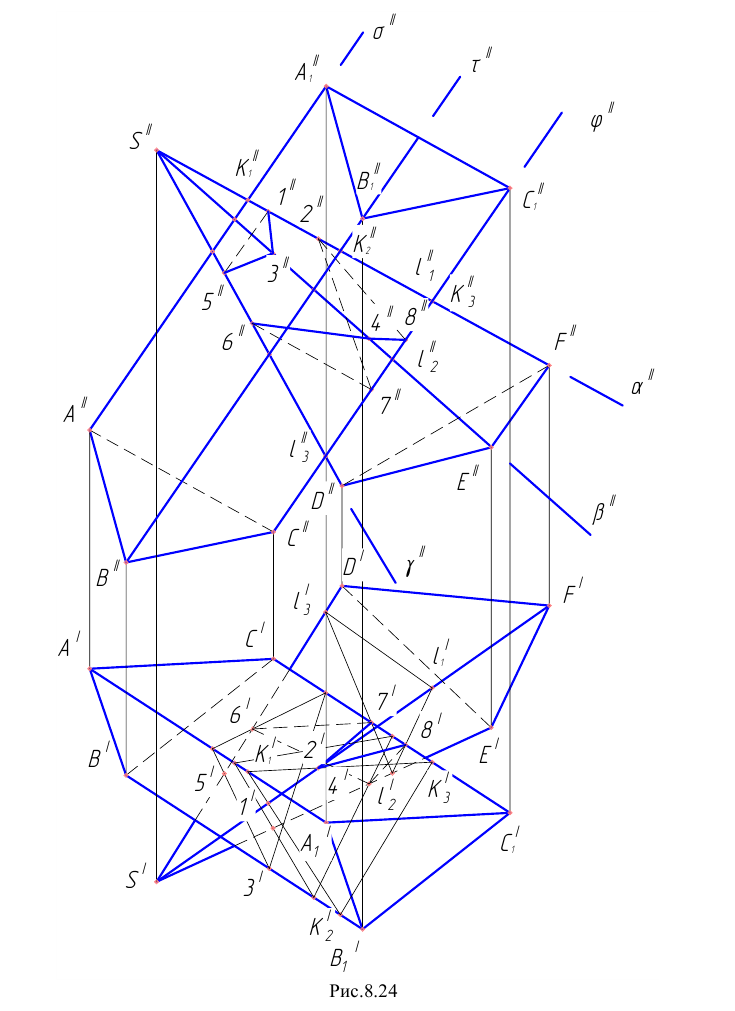
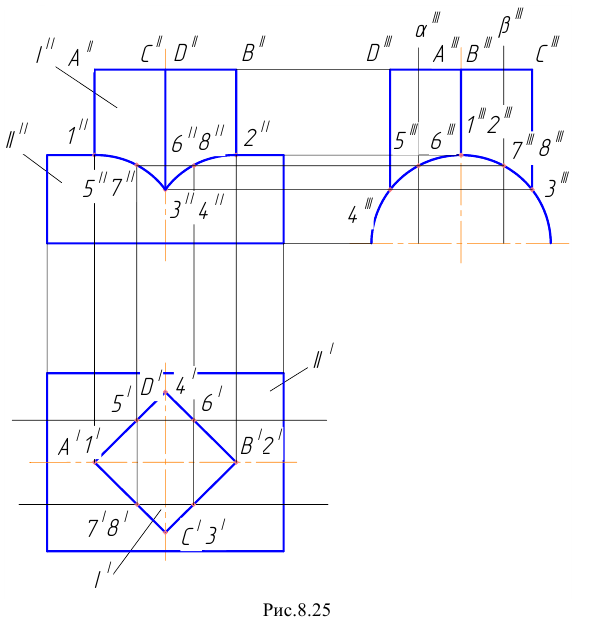
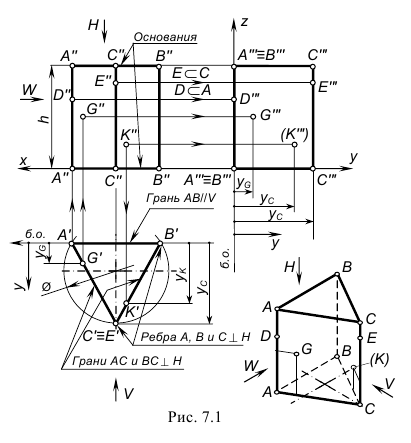
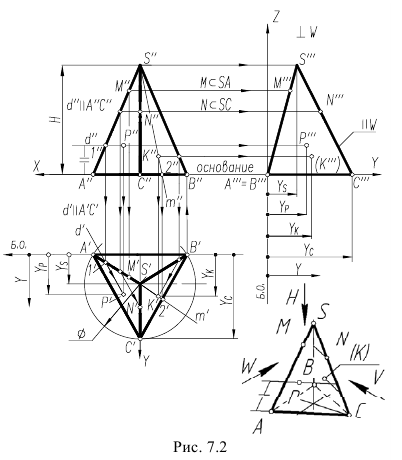
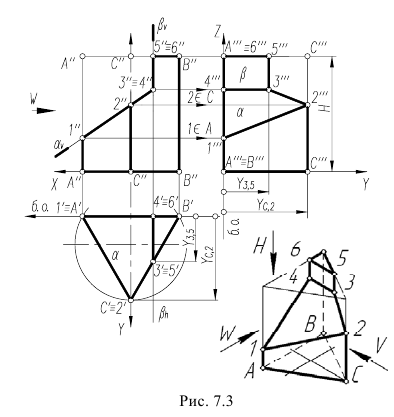
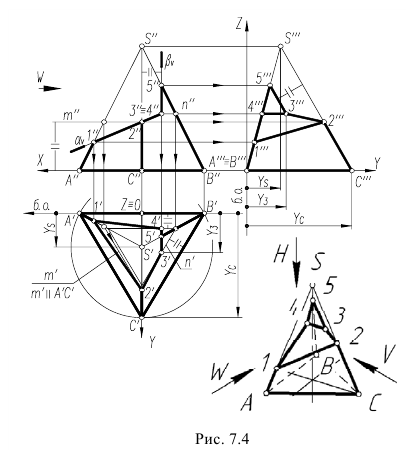
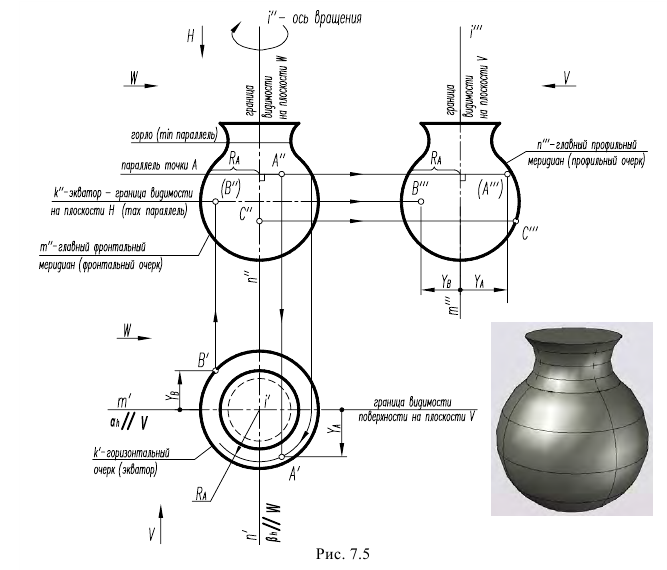
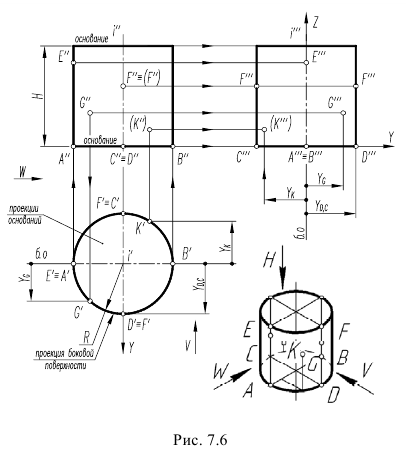
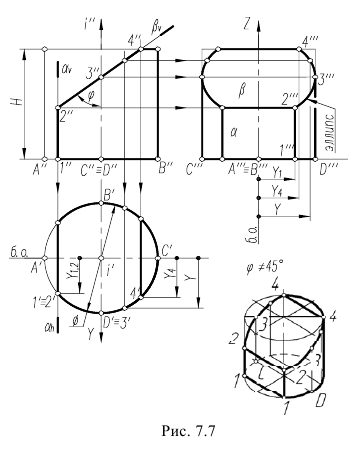
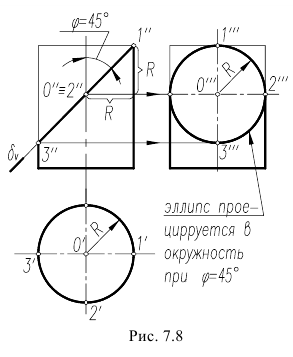
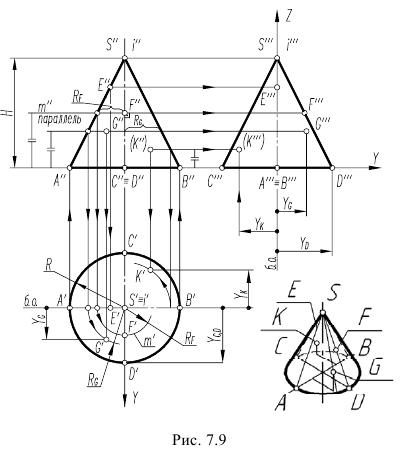
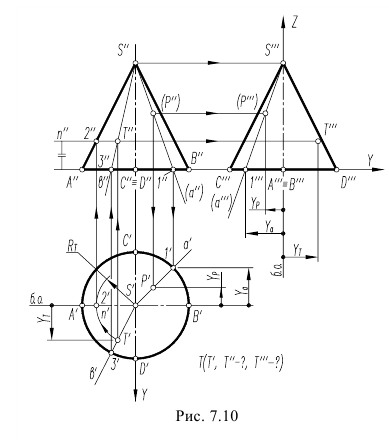
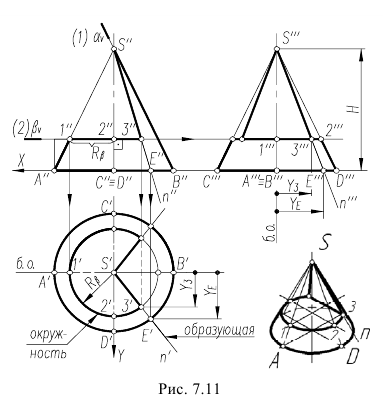
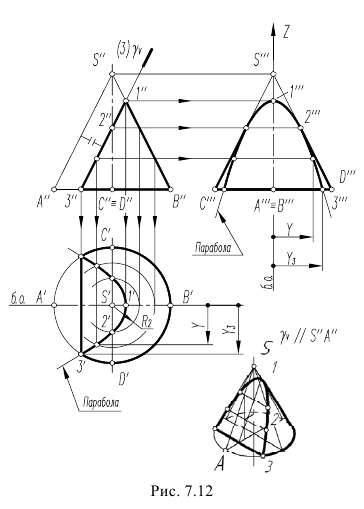
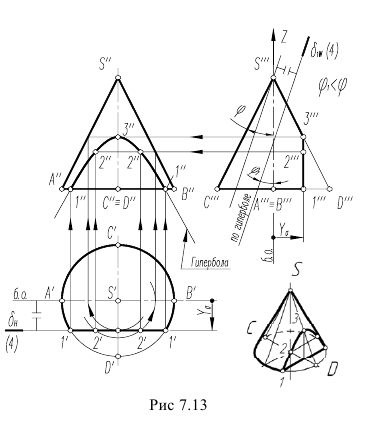
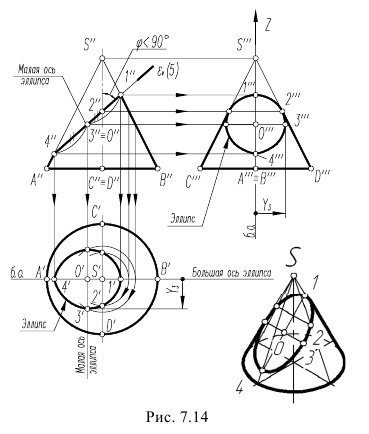
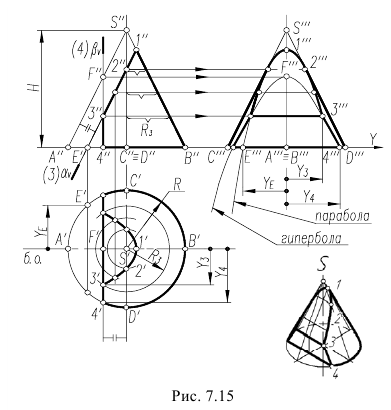
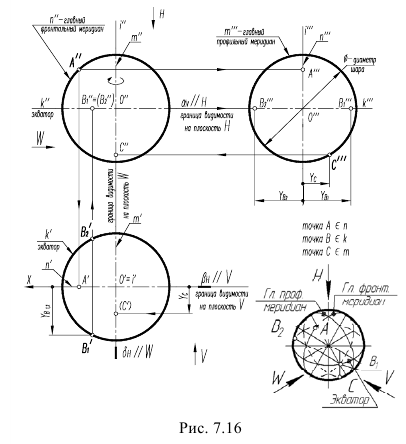
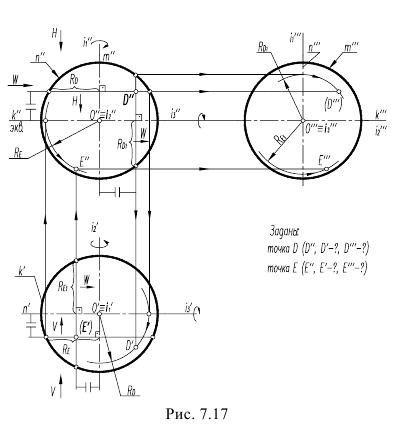
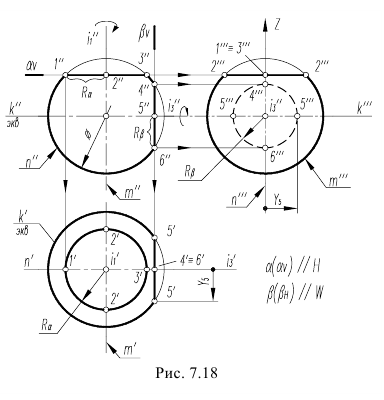
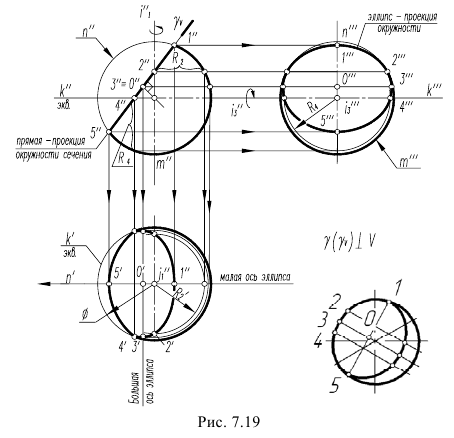

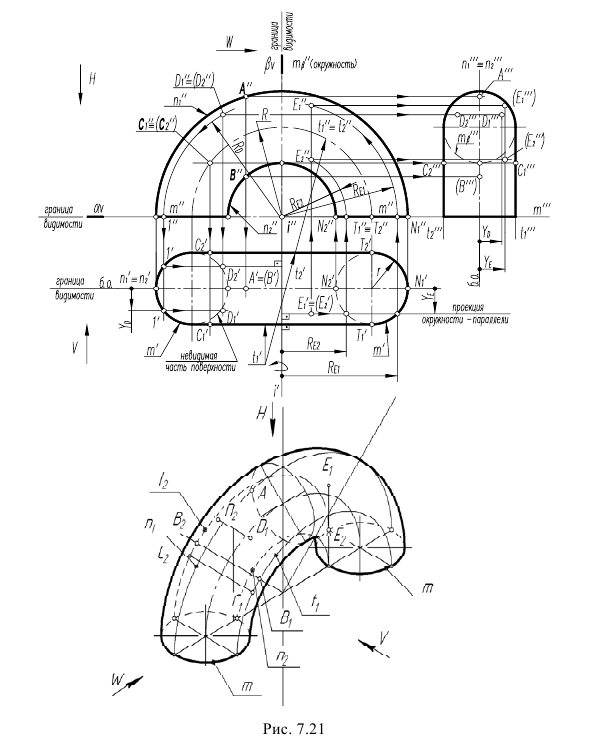
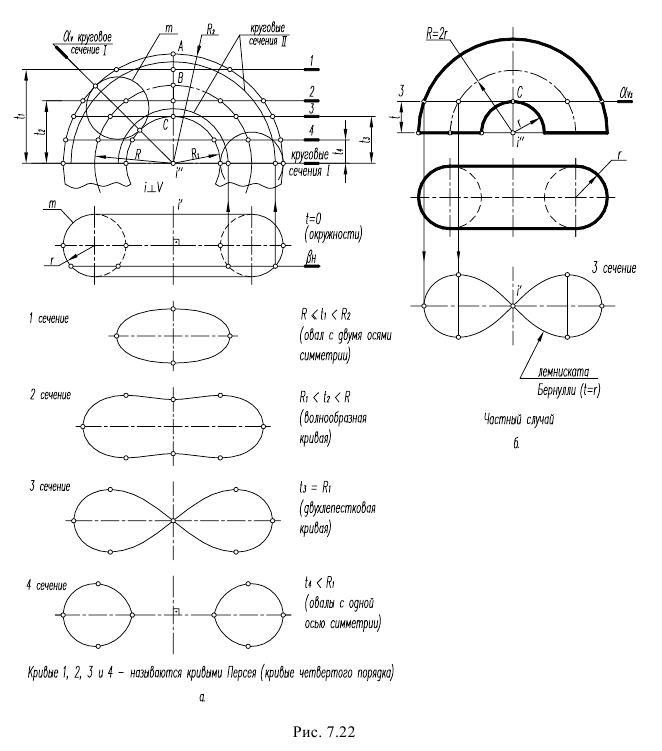
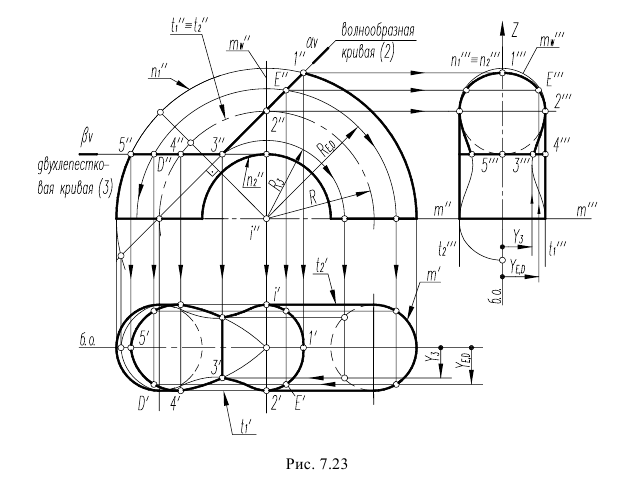
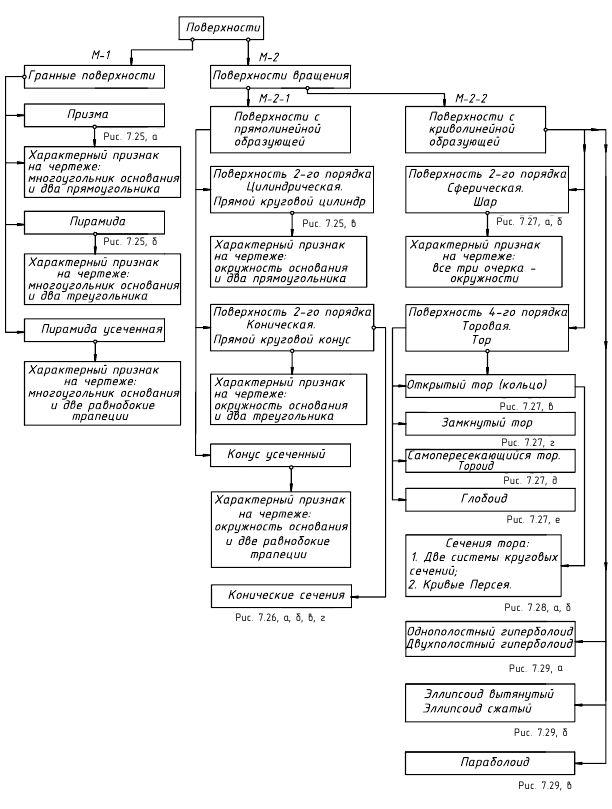
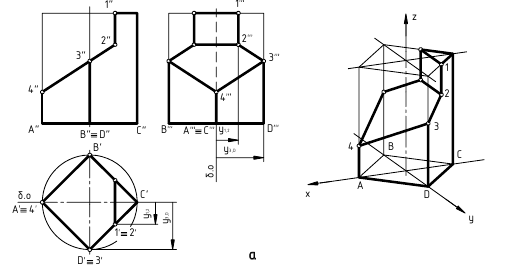
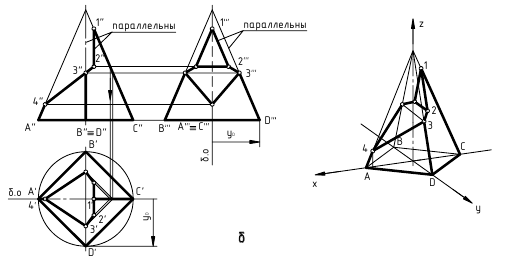
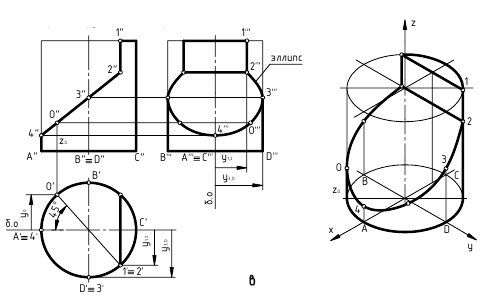
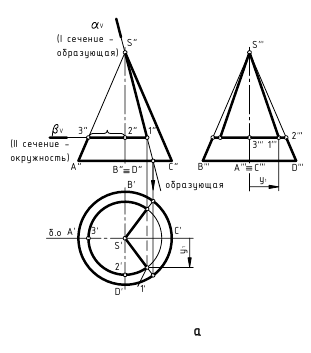
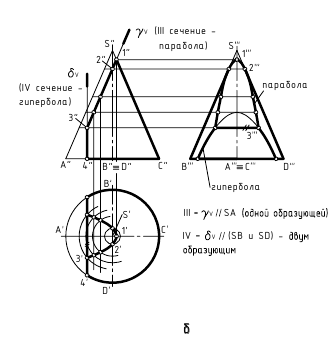
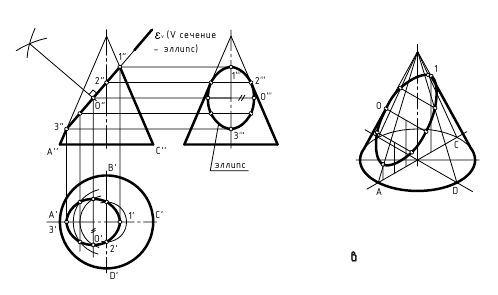
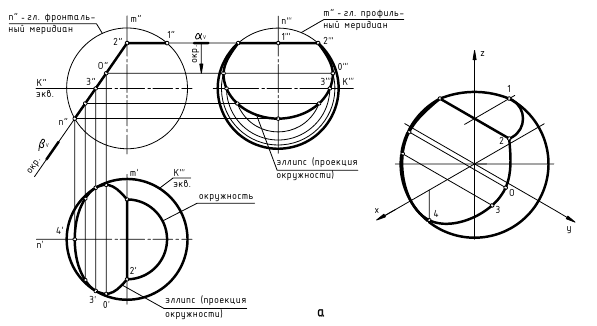
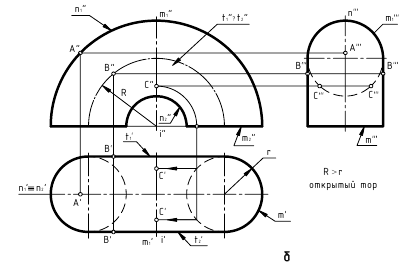
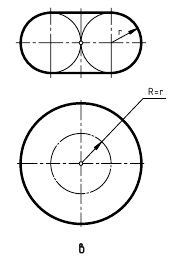
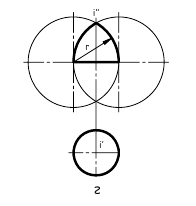
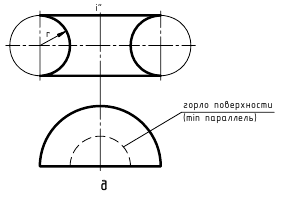
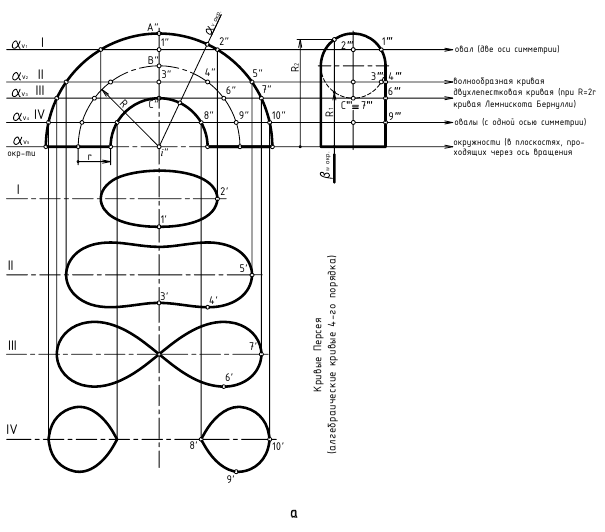
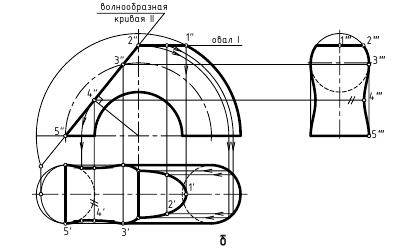
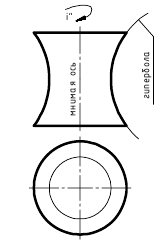
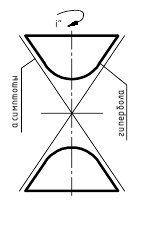
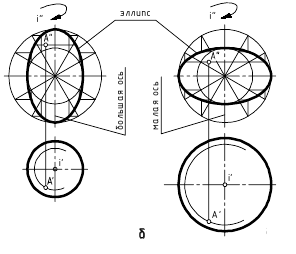
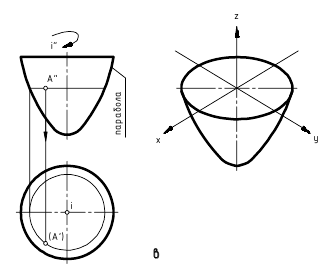
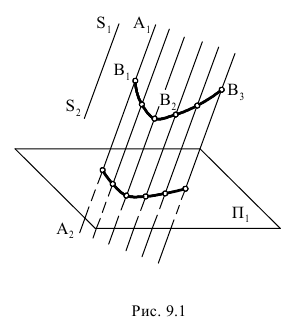
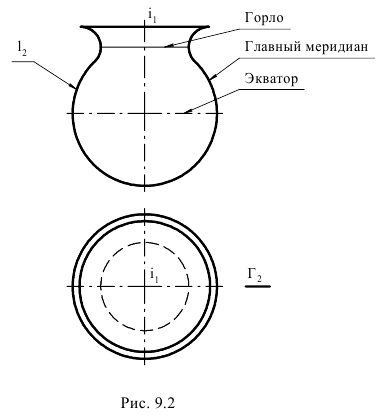
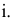
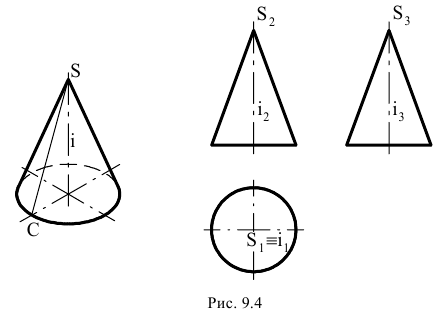
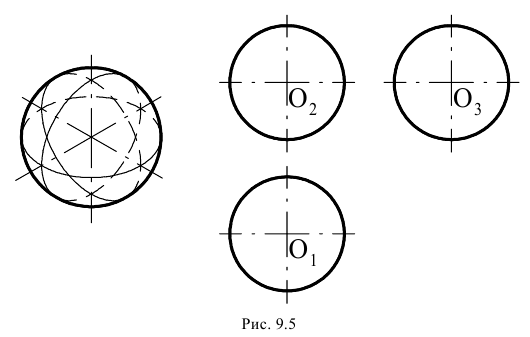
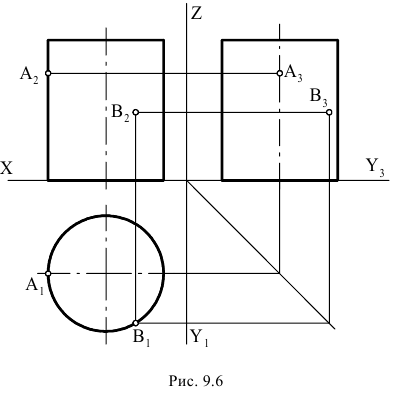
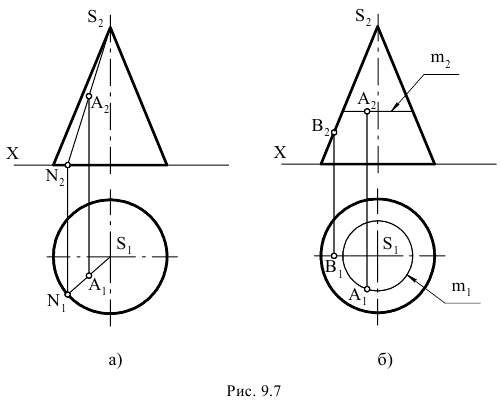
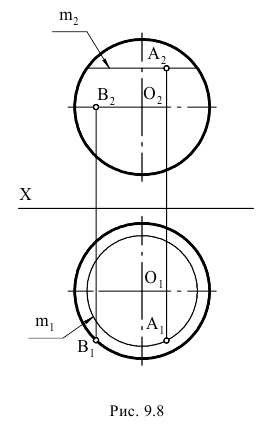
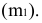
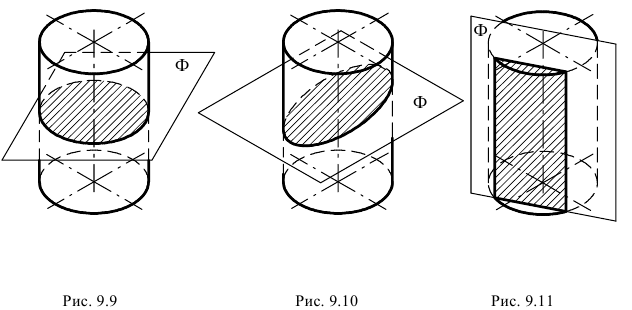
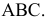
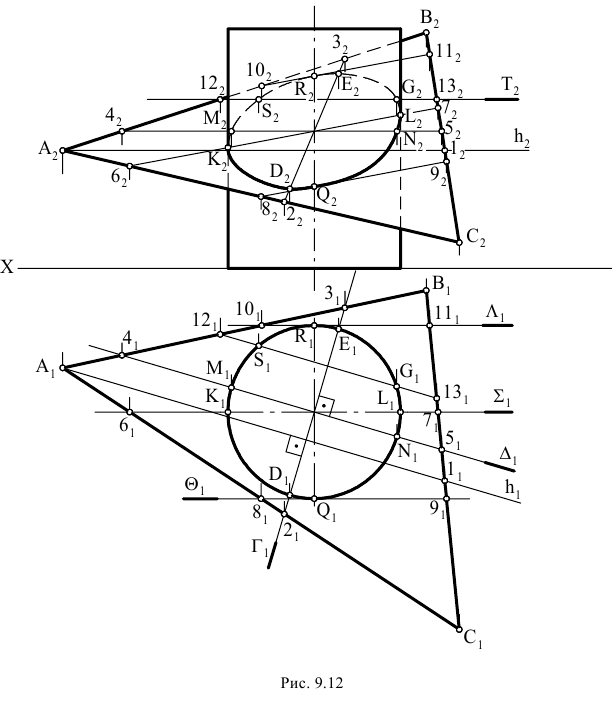
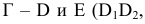
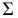
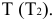
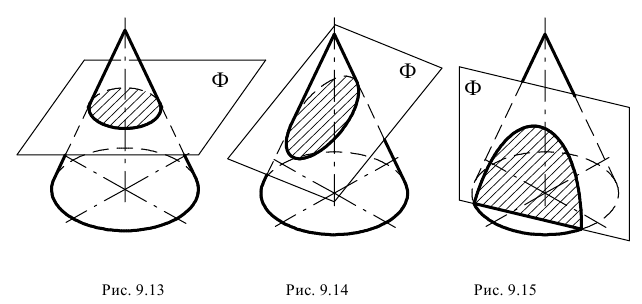
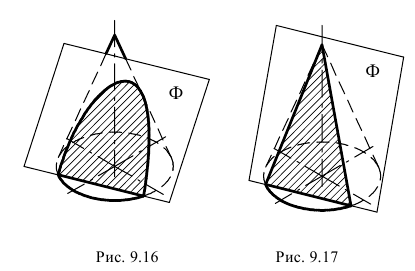
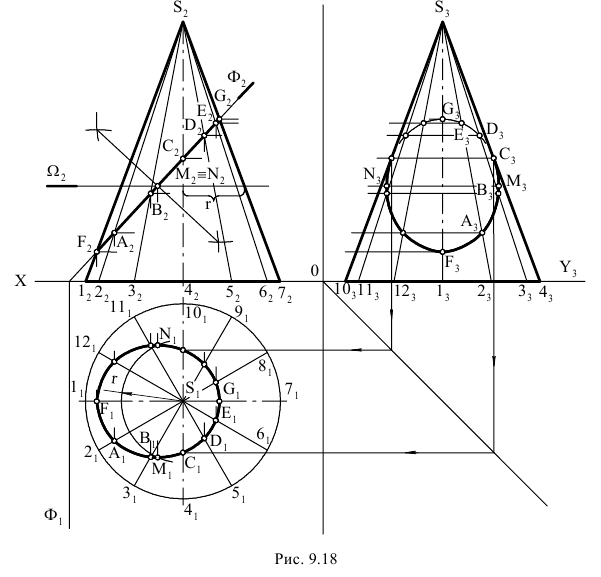
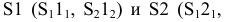
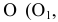
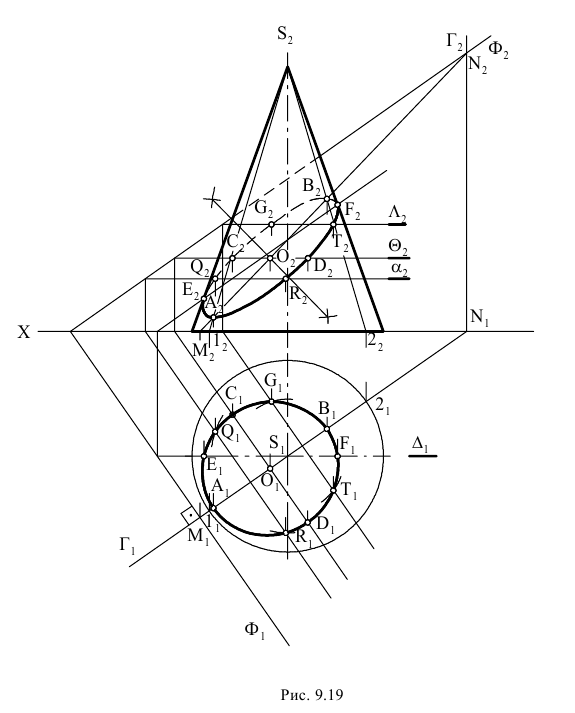
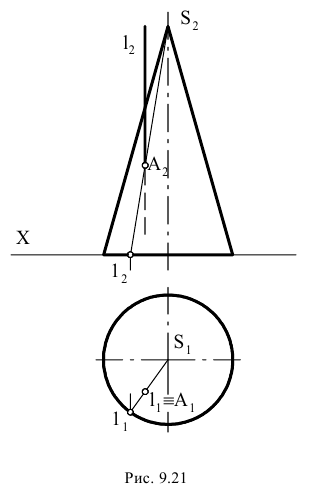
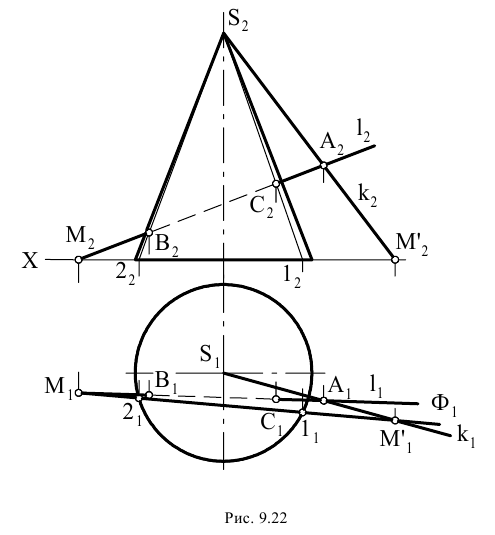
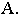
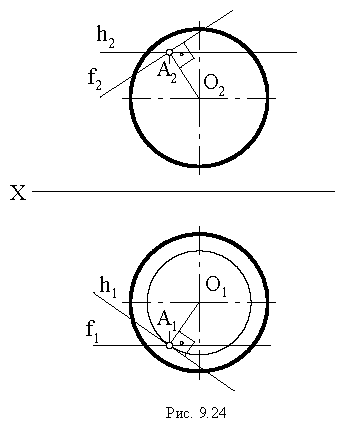
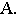
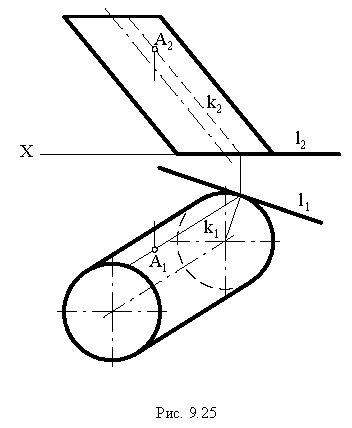
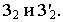
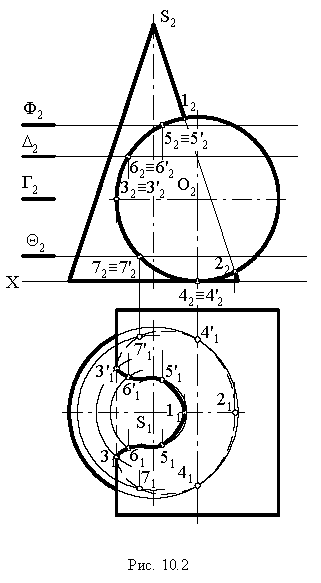
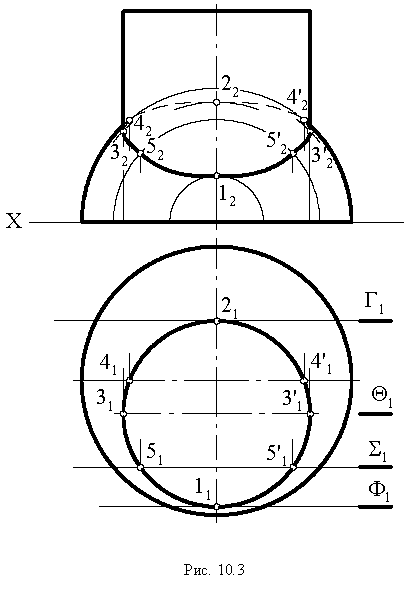
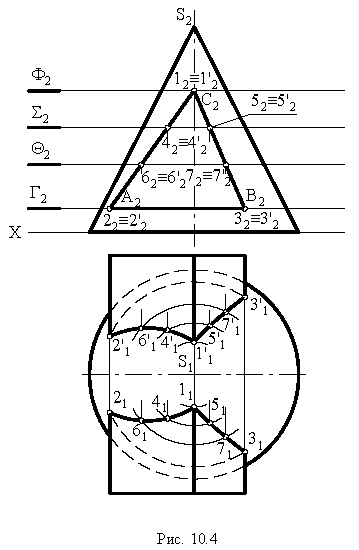
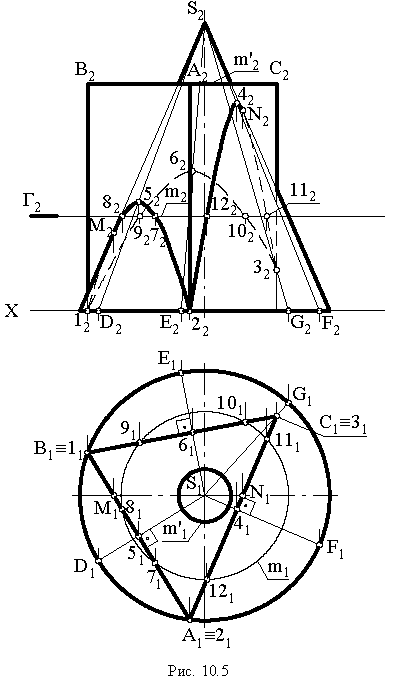
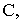
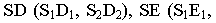
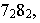
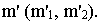
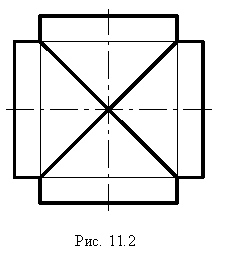
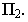
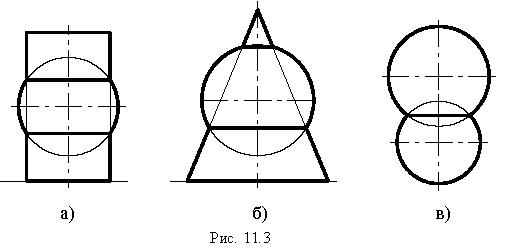
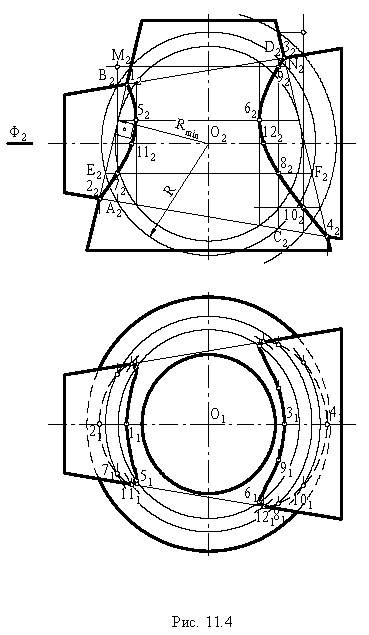
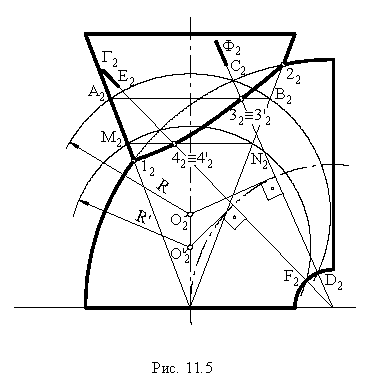
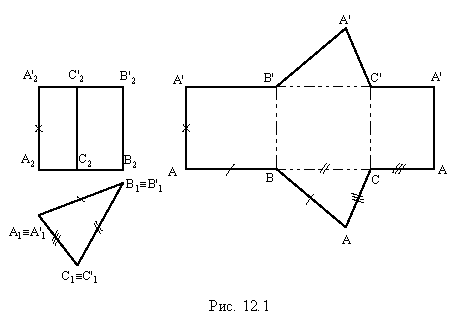
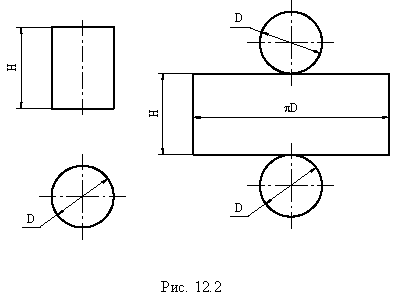
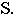
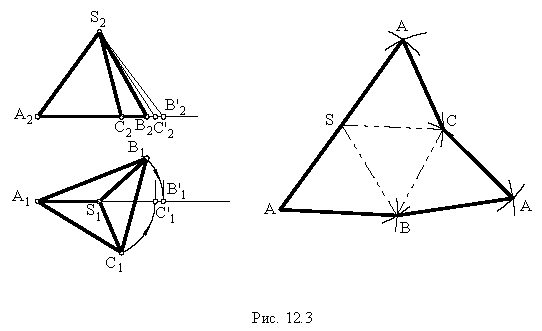
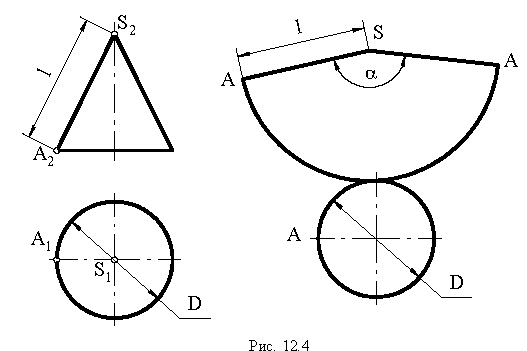
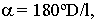
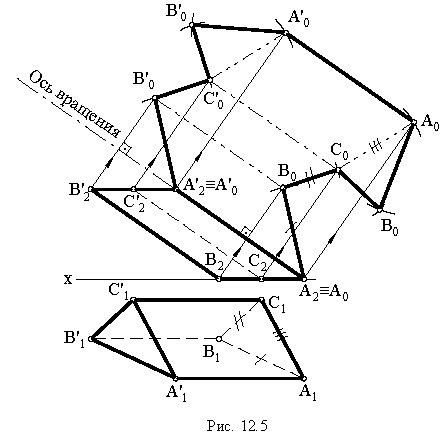
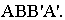
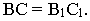
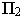 на новую
на новую  выбирая ее так, чтобы образующие цилиндра на новую плоскость проекций проецировались в натуральную величину. Для этого новую ось проекций проводят параллельно образующим цилиндра;
выбирая ее так, чтобы образующие цилиндра на новую плоскость проекций проецировались в натуральную величину. Для этого новую ось проекций проводят параллельно образующим цилиндра;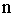 равных частей (см. рис. 12.6);
равных частей (см. рис. 12.6);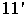 призмы, которое будет являться осью вращения граней призмы Дальнейшие построения аналогичны выполненным на рис. 12.5.
призмы, которое будет являться осью вращения граней призмы Дальнейшие построения аналогичны выполненным на рис. 12.5.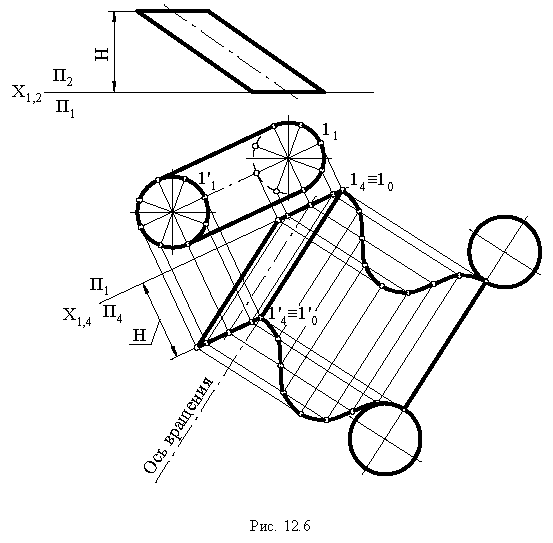
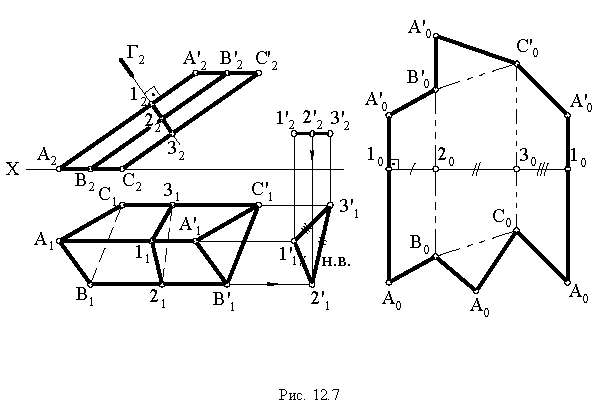
 Так как ребра призмы параллельны фронтальной плоскости проекций и на нее проецируются в натуральную величину, то нормальная плоскость будет являться фронтально-проецирующей плоскостью;
Так как ребра призмы параллельны фронтальной плоскости проекций и на нее проецируются в натуральную величину, то нормальная плоскость будет являться фронтально-проецирующей плоскостью;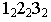 совпадает со следом плоскости
совпадает со следом плоскости 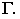 Натуральную величину фигуры сечения
Натуральную величину фигуры сечения 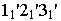 строят способом плоскопараллельного перемещения. Для этого плоскость
строят способом плоскопараллельного перемещения. Для этого плоскость 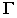 располагают параллельно горизонтальной плоскости проекций, чтобы фигура сечения проецировалась на плоскость проекций
располагают параллельно горизонтальной плоскости проекций, чтобы фигура сечения проецировалась на плоскость проекций 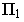 в натуральную величину;
в натуральную величину;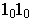 и через вершины сечения перпендикулярно линии
и через вершины сечения перпендикулярно линии 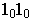 проводят прямые;
проводят прямые;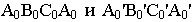 соединяют отрезками прямых;
соединяют отрезками прямых;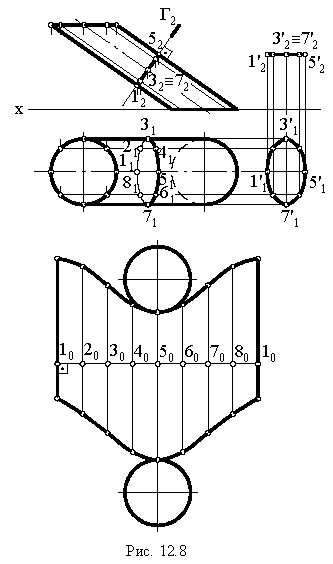
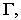 перпендикулярную к образующим цилиндра;
перпендикулярную к образующим цилиндра;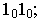
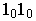 отрезки, на которых откладывают длины образующих от линии сечения до оснований. Длину образующих берут на фронтальной плоскости проекций;
отрезки, на которых откладывают длины образующих от линии сечения до оснований. Длину образующих берут на фронтальной плоскости проекций;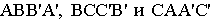 разбивают диагоналями на два треугольника. Затем определяют натуральную величину всех сторон треугольников, одной из сторон любого треугольника будет являться ребро призмы, второй – диагональ, а третьей -сторона основания наклонной призмы. Основание призмы принадлежит плоскости проекций
разбивают диагоналями на два треугольника. Затем определяют натуральную величину всех сторон треугольников, одной из сторон любого треугольника будет являться ребро призмы, второй – диагональ, а третьей -сторона основания наклонной призмы. Основание призмы принадлежит плоскости проекций 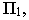 поэтому проецируется на нее в натуральную величину;
поэтому проецируется на нее в натуральную величину;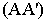 призмы любым из способов преобразования В данном случае применяют способ вращения вокруг прямой, перпендикулярной плоскости проекций
призмы любым из способов преобразования В данном случае применяют способ вращения вокруг прямой, перпендикулярной плоскости проекций 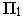 и проходящей через точку
и проходящей через точку 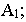
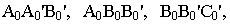
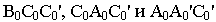 по трем сторонам;
по трем сторонам;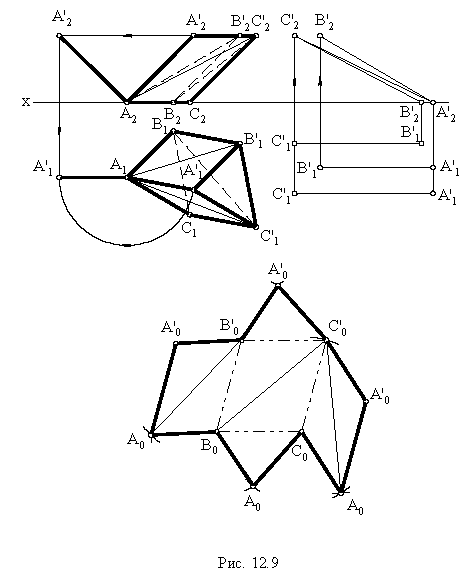
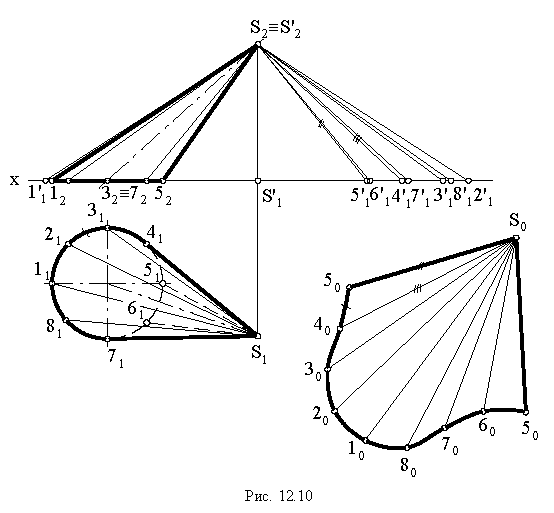
 таким образом, часть сферы заменяют частью цилиндрической поверхности. На горизонтальную плоскость проекций она проецируется в виде треугольника
таким образом, часть сферы заменяют частью цилиндрической поверхности. На горизонтальную плоскость проекций она проецируется в виде треугольника 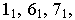 а на фронтальную – в виде дуги окружности;
а на фронтальную – в виде дуги окружности;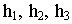 будет натуральной на плоскости проекций
будет натуральной на плоскости проекций  Строят горизонтальные проекции образующих, проходящих через соответствующие точки деления;
Строят горизонтальные проекции образующих, проходящих через соответствующие точки деления;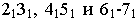 на плоскости проекций
на плоскости проекций 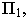 так как образующие параллельны горизонтальной плоскости проекций;
так как образующие параллельны горизонтальной плоскости проекций;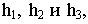 а через полученные точки откладывают вправо и влево отрезки, равные
а через полученные точки откладывают вправо и влево отрезки, равные 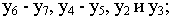
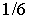 части поверхности сферы. Полная развертка поверхности сферы будет состоять из шести одинаковых долей.
части поверхности сферы. Полная развертка поверхности сферы будет состоять из шести одинаковых долей.