Как определить напряжение на батарее( источнике) ?
На этой странице вы найдете ответ на вопрос Как определить напряжение на батарее( источнике) ?. Вопрос
соответствует категории Физика и уровню подготовки учащихся 5 – 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.

В этой главе…
- Исследуем движение электронов и электрический ток
- Вычисляем напряжение и сопротивление по закону Ома
- Оцениваем мощность электрического тока
- Разбираемся с параллельными и последовательными цепями
- Знакомимся с правилами Кирхгофа
Статическое электричество возникает при избытке либо недостатке электронов, т.е. когда имеются отрицательно или положительно заряженные тела. А в привычном электричестве, т.е. в текущем по проводам электрическом токе, избыточного заряда нет, и, следовательно, нет и общего заряда. Есть лишь напряжение, подобное тому, которое создается батарейкой или настенной розеткой. Оно создается в проводах электрическим полем, в ответ на которое возникает движение электронов — электрический ток. (Более подробно о напряжении рассказывается в главе 16.)
Эта глава посвящена электронам, т.е. заряженным частицам, движущимся в электрических контурах, с которыми вы уже знакомы. В главе 16 рассказывается о статическом, а в этой — только о динамическом проявлении электричества. Здесь описываются сходства и различия между ними, носители и источники электрического тока, закон Ома, мощности электрического тока и, наконец, электрические контуры и их элементы.
Содержание
- Марширующие электроны: ток
- Знакомимся с силой тока
- Вычисляем силу тока, идущего через батарейку
- Оцениваем сопротивление: закон Ома
- Вычисляем силу тока
- Проверка удельного сопротивления
- Измеряем мощность: ватт
- От одного к другому: последовательные цепи
- Разделение тока: параллельные цепи
- Создаем электрические цепи по правилам Кирхгофа
- Используем правило контуров
- Исследуем многоконтурные цепи
- Разбираемся с параллельно и последовательно соединенными конденсаторами
- Конденсаторы в параллельных цепях
- Конденсаторы в последовательных цепях
- Соединяем резисторы с конденсаторами: RC-цепи
Марширующие электроны: ток
Электрический ток возникает при направленном движении электронов. Но как заставить их двигаться именно так, чтобы получился электрический ток? Ответ: нужно создать и поддерживать электродвижущую силу, или э.д.с. Э.д.с. обеспечивает разность потенциалов (напряжение), благодаря которой электроны чувствуют силовое воздействие.
Итак, чем именно создается э.д.с.? Батарейкой? Или настенной розеткой? Э.д.с. — это то, что дает напряжение, ведь напряжение — это все, что нужно для создания электрического поля в проводе, которое заставляет электроны двигаться. (В главе 16 говорится, что электрическое поле характеризуется своей напряженностью ( E ), которая равна отношению силы ( F ) и заряда ( q ): ( Е = F/q ).)
В физике величина электрического тока (сила тока) обозначается буквой ( I ) и измеряется в амперах (А).
Знакомимся с силой тока
Как правильно определить силу тока? Это величина заряда, проходящего через некоторую часть контура за некоторое время. А вот то же самое определение, но в виде формулы:
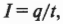
где ( q ) и ( t ) — это соответственно электрический заряд и время. Если за 1 с через контур проходит заряд в 1 Кл, то величина электрического тока равна 1 А.
Вычисляем силу тока, идущего через батарейку
Зная величину заряда в контуре с батарейкой и время, можно вычислить силу тока, идущего через батарейку: ( I=q/t ). Посмотрите на рис. 17.1; две вертикальные черты, расположенные сверху, означают батарейку. (Эти линии напоминают о разных металлических пластинах в первых батарейках, которые подвергались воздействию химических веществ и соединялись вместе.)
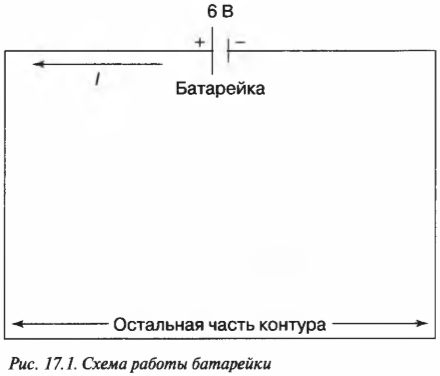
Батарейка обеспечивает электродвижущую силу величиной 6 В, которая гонит ток по контуру. Если за 30 с по контуру проходит заряд 19 Кл, то чему равна сила тока?
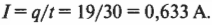
В данном случае по контуру течет 0,633 ампера. Обратите внимание, что ток идет от положительной части батарейки, обозначаемой на значке батарейки более длинной чертой, к отрицательной части, обозначаемой на значке батарейки более короткой линией.
Полезно считать, что в цепи батарейка является ступенькой напряжения. Иначе говоря, батарейка как бы “поднимает” ток, поступающий в ее отрицательную часть (в случае рис. 17.1 на уровень 6 В), а затем электрический ток снова “спускается” и течет по контуру.
Хотя ток всегда изображается движущимся по контуру от положительного к отрицательному знаку батарейки, но в действительности электроны движутся в противоположном направлении. Почему возникло такое различие? Причина здесь историческая: первые исследователи думали, что по контуру текут именно положительные заряды, но на самом деле все происходит наоборот. Впрочем, это не проблема, если вы будете придерживаться единообразия и всегда считать, что ток выходит с положительного конца батарейки.
Оцениваем сопротивление: закон Ома
Сопротивление — это величина, которая связывает приложенное напряжение с созданной им силой тока. Вот как выглядит формула, которая связывает напряжение, силу тока и сопротивление:
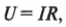
где ( U ), ( I ) и ( R ) — это соответственно напряжение, сила тока и сопротивление. Сопротивление измеряется в омах (Ом), 1 Ом = 1 В/1 А. Таким образом, прикладывая напряжение ( U ) на участке цепи с некоторым сопротивлением ( R ), получим силу тока ( I ). Это и есть закон Ома, названный так по фамилии своего открывателя Георга Симона Ома (сделавшего свое открытие в XIX веке).
Вычисляем силу тока
С помощью закона Ома можно найти силу тока, идущего от положительной к отрицательной клемме батарейки. Посмотрите на цепь, показанную на рис. 17.2, где батарейка с напряжением 6 В создает электрический ток, идущий через резистор ( R ) с сопротивлением 2 Ом.
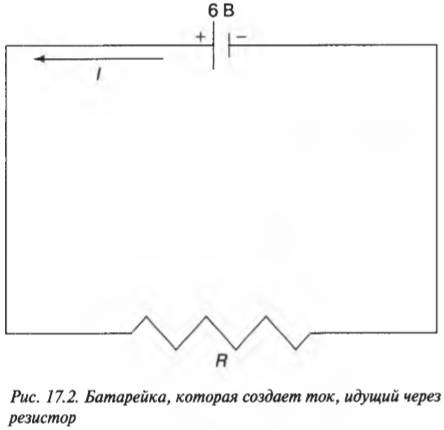
Из закона Ома следует, что:
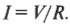
Подстановка числовых значений дает:
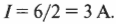
Итак, ток силой 3 А течет по контуру против часовой стрелки.
Проверка удельного сопротивления
При изучении электричества часто приходится иметь дело с величиной ( rho ) называемой удельным сопротивлением, т.е. сопротивлением на единицу длины и площади, и измеряемой в Ом·м. Зная силу тока через определенный материал, можно с помощью удельного сопротивления материала узнать его сопротивление. Физики вычислили значения удельного сопротивления многих распространенных материалов; некоторые из этих значений перечислены в табл. 17.1.
Сопротивление материала ( R ) можно найти, умножив его удельное сопротивление ( rho ) на его длину ( L ) (чем она больше, тем большее сопротивление вызывает) и поделив на площадь ( A ) поперечного сечения этого материала (чем больше площадь, которую должен пересекать ток, тем сопротивление меньше):
Измеряем мощность: ватт
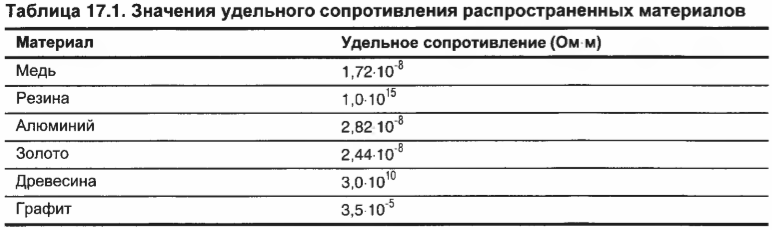
Некоторые предметы домашнего обихода, например, лампочки накаливания или сушилки для волос, используют электроэнергию. Мощность таких электроприборов измеряется в ваттах (Вт). Как определить ее величину? Работа по перемещению заряда ( q ) по цепи равна ( qU ), где ( U ) — это электродвижущая сила. Если поделить эту работу на время ее выполнения, получится мощность:
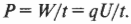
Впрочем, заряд ( q ), деленный на время ( t ), равняется силе тока ( I ), таким образом:
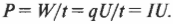
Мощность, которая обеспечивается в цепи источником э.д.с., в частности батарейкой, вычисляется по формуле ( P = IU ). Например, батарейка при 10 В создает в лампочке накаливания силу тока 0,5 А. Какова мощность этой лампочки? ( P = IU ), т.е. мощность равна 0,5·10 = 5 Вт. Впрочем, ( I = U/R ), поэтому мощность, обеспечиваемую в цепи определенным напряжением, можно вычислять несколькими способами:
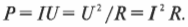
От одного к другому: последовательные цепи
В предыдущих разделах этой главы говорилось о токе, идущем через один резистор; впрочем, как показано на рис. 17.3, в цепи может быть и два резистора.
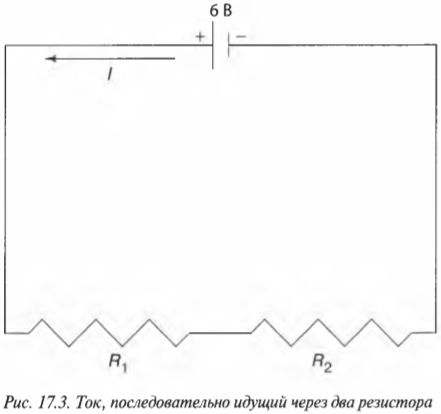
Два резистора могут быть подключены последовательно, когда, перед тем как вернуться к источнику электродвижущей силы (см. первый раздел этой главы), ток в цепи течет сначала через один из них, а затем — через другой. Рассмотрим последовательное подключение двух резисторов с сопротивлениями ( R_1 ) и ( R_2 ), когда один и тот же ток, перед тем как вернуться к батарейке, должен пройти через оба резистора. Тогда общее сопротивление ( R ) должно равняться сумме этих двух сопротивлений:
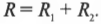
Итак, чтобы получить общее сопротивление двух последовательно соединенных резисторов, надо сложить их сопротивления ( R_1 ) и ( R_2 ). Например, если ( R_1 ) = 10 Ом и ( R_2 ) = 20 Ом, батарейка создает напряжение 6 В, то ток какой силы будет проходить через цепь? Общее сопротивление должно равняться 30 Ом, тогда:
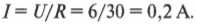
Разделение тока: параллельные цепи
Если в одной и той же цепи имеется множество резисторов, то совсем не обязательно, чтобы у них было только последовательное соединение (см. предыдущий раздел), когда ток идет от одного резистора к другому. Два резистора ( R_1 ) и ( R_2 ) можно соединить таким образом, чтобы ток разветвлялся, как на рис. 17.4. Какая-то часть тока идет через первый резистор, а другая — через второй.
Резисторы на рис. 17.4 являются параллельными, т.е. на концах каждого из них одно и то же напряжение, но ток, идущий через эти резисторы, не обязательно одинаковый.
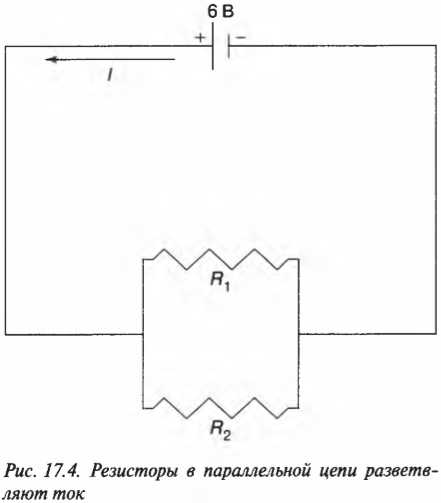
Напряжение на концах каждого из параллельных резисторов одинаково и равно 6 В, т.е. напряжению, создаваемому батарейкой. Этим и отличаются последовательно и параллельно соединенные резисторы. Через последовательно соединенные резисторы идет один и тот же ток. А когда резисторы соединены параллельно, на концах каждого из них одинаковое напряжение.
Итак, чему равно общее сопротивление резисторов ( R_1 ) и ( R_2 ) соединенных параллельно? Общая сила тока ( I ) — это сила тока, идущего через два резистора:
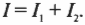
И поскольку ( I=U/R ) (см. выше раздел о законе Ома), то можно записать:
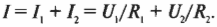
Дело в том, что при параллельном соединении ( U_1=U_2 ), поэтому если обозначить это общее напряжение как ( U ), то можно сказать, что:
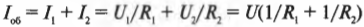
Это равенство еще записывается как ( I=U/R ), и в итоге мы получаем:
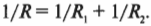
Эта формула показывает, как надо вычислять общее сопротивление двух параллельно соединенных резисторов. Если говорить о произвольном количестве резисторов, то получится такой способ вычисления общего сопротивления:
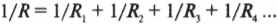
Например, если на рис. 17.4 ( R_1 ) = 10 Ом и ( R_2 ) = 30 Ом, а напряжение батарейки составляет 6 В, то ток какой силы идет через эту цепь? Величина, обратная общему сопротивлению цепи, равна
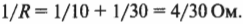
Чтобы найти общее сопротивление при параллельном соединении, надо сложить величины, обратные значениям сопротивления, а затем взять величину, обратную полученному результату. Таким образом, общее сопротивление равно 30/4 Ом, т.е. сила тока равна 6/(30/4) = 0,8 А.
Создаем электрические цепи по правилам Кирхгофа
К сожалению, электрические цепи не всегда можно разбить на последовательные и параллельные составляющие, поэтому важную роль играют правила Кирхгофа, названные так в честь своего открывателя, Густава Кирхгофа. Эти два простых правила позволяют анализировать цепи самой разной сложности, поскольку представляют собой неизменные соотношения целостности, которые выполняются между токами и напряжениями на участках любой электрической цепи. (Для корректной формулировки этих правил в цепи выделяются узлы, т.е. точки соединения трех и более проводников, и контуры, т.е. замкнутые пути из проводников. — Примеч. ред.)
- Правило соединения. Общий ток, притекающий в любой узел цепи, должен равняться общему току, вытекающему из него.
- Правило контуров. В любом замкнутом контуре сети сумма увеличений потенциала (например, от батарейки) должна равняться сумме падений потенциала (например, от резистора). (Иначе говоря, суммарная э.д.с. равна суммарному напряжению. — Примеч. ред.)
Правило соединения достаточно легко понять: сила тока, входящего в любой узел, должна равняться силе тока, выходящего из этого узла. Ну а как насчет правила контуров, которое гласит, что в любом замкнутом контуре суммарное увеличение и суммарное падение потенциала должны быть равны? Правило контуров означает, что насколько движущиеся по контуру электроны “спускаются”, настолько они и “поднимаются”, и приходят туда, откуда пришли. Например, увеличение потенциала выполняется батарейками; когда электроны входят в ее отрицательную часть и выходят из положительной, напряжение батарейки возрастает. С другой стороны, когда электрон входит в резистор, требуется определенное усилие для того, чтобы провести его через этот резистор (вот почему резистор еще называют сопротивлением), отсюда и понижение потенциала при выходе из него электрона.
Используем правило контуров
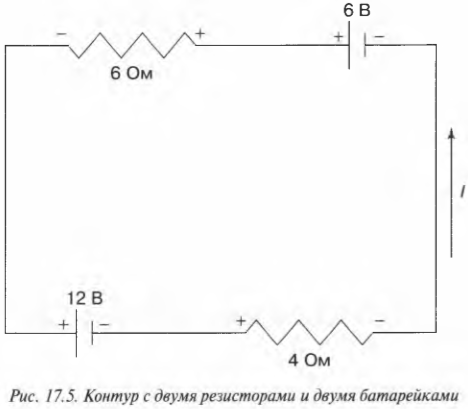
На рис. 17.5 показан пример использования правила контуров для цепи из двух резисторов и двух батареек. Ток какой силы идет по этой цепи?
Правило контуров гласит, что вдоль всего контура:
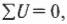
где ( sum!U ) — это сумма напряжений вдоль всего контура. Как можно использовать это правило?
Чтобы решить эту задачу, выберите направление тока, начертив стрелку, как показано на рис. 17.5. В действительности ток может идти в противоположном направлении, но здесь нет ничего плохого, ведь тогда полученная отрицательная сила тока будет показывать, что ток идет не в том направлении, которое было выбрано. Выбор направления тока — в данном примере против часовой стрелки — помогает начертить знаки + и — там, где ток соответственно заходит в резистор и выходит из него (эти действия в правило Кирхгофа не входят; я просто использую приемы, которые считаю полезными).
Известно, что вдоль всего контура ( sum!U ) = 0 и что в резисторе падение потенциала ( U = IR ). Остается только двигаться вдоль контура в одном направлении (не имеет значения, по часовой или против часовой стрелки), и когда встретится знак “+” или “-” (на резисторе или батарейке), нужно записать этот знак, а за ним — соответствующее ему падение или возрастание потенциала. Если, к примеру, начать с батарейки с э.д.с. 6 В и идти по часовой стрелке, то в соответствии с правилом контуров получим следующее равенство:
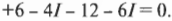
Сгруппировав его члены, получим:
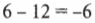
и
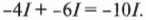
Таким образом:
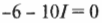
или
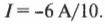
Итак, сила тока равна —0,6 А.
Из того, что сила тока имеет отрицательную величину, следует, что на самом деле ток идет в направлении, противоположном тому, которое выбрано сначала и показано на рис. 17.4.
Исследуем многоконтурные цепи
Если вам кажется, что правила Кирхгофа исчерпали все свои возможности уже на одноконтурных цепях, то попробуйте решить новую задачу, показанную на рис. 17.6.
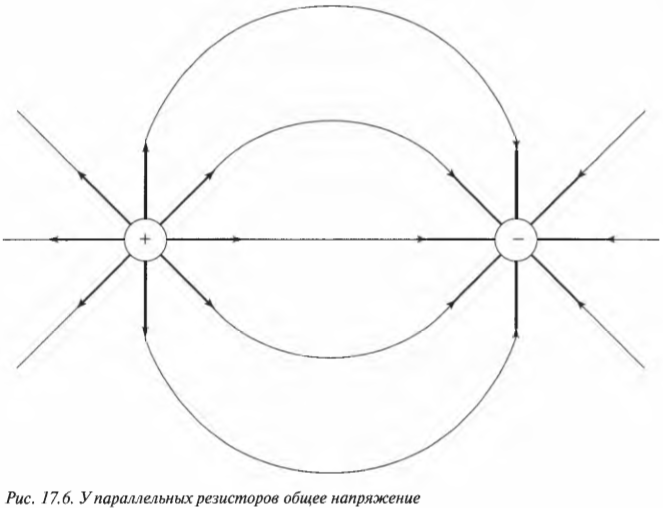
На рисунке показаны три ответвления цепи и три разных тока. Найдите соответствующие значения сил тока ( I_1 ), ( I_2 ) и ( I_3 ) с применением обоих правил Кирхгофа. Правило соединения гласит, что в любом узле ( sum!I ) = 0, где ( sum!I ) — это сумма всех сил токов (втекающих и вытекающих). Рассмотрим точку А, которая находится в левой части рис. 17.6. Токи, соответствующие значениям ( I_1 ) и ( I_2 ), в нее втекают, а ток, соответствующий значению ( I_3 ), из нее вытекает, поэтому:
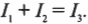
Теперь обратимся к правилу контуров, которое гласит, что ( sum!I ) = 0. В нашем примере три контура: два внутренних и один внешний, т.е. огибающий контур. Так как неизвестных у нас три (это значения силы тока ( I_1 ), ( I_2 ) и ( I_3 )), то все, что нам нужно, — это три уравнения. Согласно правилу ( sum!I ) = 0, одно из них у нас уже есть. Поэтому, чтобы получить два оставшихся уравнения, надо разобраться с двумя внутренними контурами. Верхний контур дает:
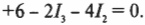
А из нижнего контура получается:
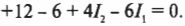
Итак, получено три уравнения с тремя неизвестными:
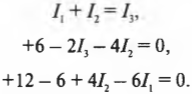
Если значение ( I_3 ), полученное из первого уравнения, подставить во второе, тогда можно получить:
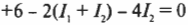
и
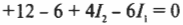
или
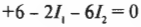
и
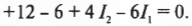
Используя первое из этих уравнений, можно ( I_1 ) выразить через ( I_2 ):
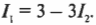
Подставив это значение ( I_1 ) во второе уравнение, получим:
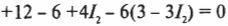
или
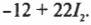
Таким образом:
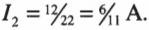
Теперь у нас есть одно из значений силы тока: ( I_2 ) = 6/11 А. Эту дробь можно вставить в уравнение:
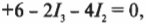
чтобы получить:
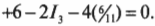
После деления на 2 получим:
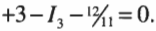
Тогда:
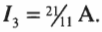
Теперь нам известны два значения сил токов ( I_2 ) и ( I_3 ). А как насчет ( I_1 )? Так как:
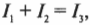
то:
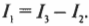
Отсюда легко получить, что:
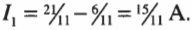
Итак, благодаря правилам Кирхгофа, теперь нам известны все значения силы тока: ( I_1 ) = 15/11 А, ( I_2 ) = 6/11 А и ( I_3 ) = 21/11 А.
В подобных задачах доя поиска решения часто требуется потратить много времени и выполнить много вычислений, но, справившись с ними, можно полностью определить значения основных параметров электрических цепей.
Разбираемся с параллельно и последовательно соединенными конденсаторами
Параллельные и последовательные цепи можно создавать не только из резисторов, но и из конденсаторов. Как известно (подробнее см. главу 16), конденсатор — это физическая система, способная сохранять электрический заряд. Чтобы найти общую емкость конденсаторов, используемых в параллельной цепи, надо просто сложить их емкости:
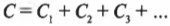
Конденсаторы в параллельных цепях
Когда конденсаторы подключены параллельно, то напряжение, создаваемое батарейкой, будет одинаковым для всех этих конденсаторов. Посмотрите на рис. 17.7, где показаны два конденсатора, подключенные в параллельную цепь.
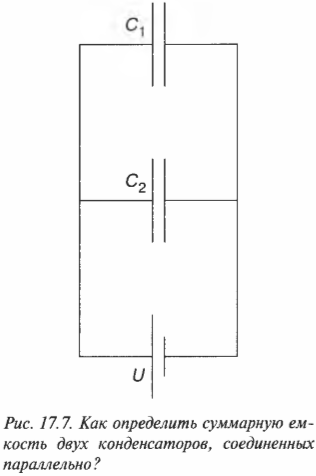
Что же делать в подобной ситуации? Найдите общий заряд ( Q ), хранящийся на обоих конденсаторах ( C_1 ) и ( C_2 ); он равен сумме зарядов, хранящихся на каждом из них:
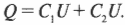
Так как батарейка подает на концы каждого конденсатора одно и то же напряжение ( U ), оно у конденсаторов одинаково, поэтому предыдущее равенство можно переписать как бы для одного конденсатора с емкостью ( C_1+C_2 ):
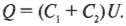
Иначе говоря, если заменить два конденсатора ( C_1 ) и ( C_2 ) одним ( C ), имеющим емкость ( C_1+C_2 ), то значение ( Q ) не изменится:
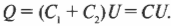
Конденсаторы в последовательных цепях
Когда конденсаторы включены параллельно, батарейка поддерживает одинаково напряжение на концах обоих конденсаторов.
На рис. 17.8 показаны два конденсатора в последовательной цепи. Что же делать в такой ситуации?
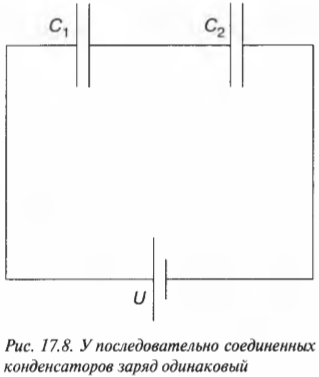
Как видно на рис. 17.8, самая правая пластина конденсатора ( C_1 ) и самая левая пластина конденсатора ( C_2 ) соединены друг с другом, но не с остальной цепью. Иначе говоря, две пластины от остальной цепи изолированы, и вначале они электрически нейтральны (с суммарным общим зарядом, равным нулю).
Любой отрицательный заряд ( -q ), появившийся на самой правой пластине конденсатора ( C_1 ), должен быть равен по величине любому положительному заряду ( q ), появившемуся на самой левой пластине конденсатора ( C_2 ), поскольку суммарный заряд на обеих этих пластинах должен быть равен нулю. А так как суммарный заряд на двух пластинах одного конденсатора тоже должен быть равен нулю, то заряд на самой левой пластине конденсатора ( C_1 ) и на самой правой пластине конденсатора ( C_2 ) должен быть равен соответственно ( q ) и ( -q ). Поэтому величины зарядов (хоть отрицательных, хоть положительных) на каждой пластине одинаковы и равны ( q ).
Итак, заряд на каждом конденсаторе одинаковый. Кроме того, известно, что общее напряжение на концах двух конденсаторов вычисляется по формуле:
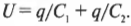
Так как заряд на каждом конденсаторе один и тот же, то это равенство принимает следующий вид:
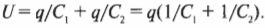
Если вписать в равенство общую емкость ( C ), то получится:
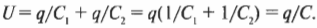
Иначе говоря, последовательно подключенные емкости складываются так же, как и параллельно подключенные резисторы (см. выше раздел о параллельно подключенных резисторах): складываются обратные значения и берется значение .обратное результату:
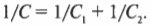
Если конденсаторов больше двух, то сложение для них надо делать следующим образом:
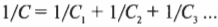
Соединяем резисторы с конденсаторами: RC-цепи
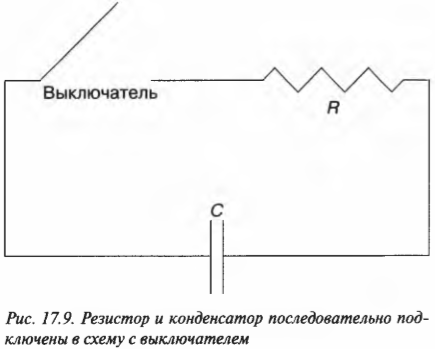
В предыдущих разделах этой главы речь шла о работающих отдельно друг от друга резисторах (электронных компонентах, затрудняющих движение тока в электрической цепи) и конденсаторах (телах, которые хранят заряд, держа его положительные и отрицательные компоненты отдельно, чтобы те притягивали друг друга, но при этом не могли самостоятельно соединиться). Теперь настало время собрать воедино резисторы и конденсаторы. Посмотрите на резистор и конденсатор, показанные на рис. 17.9. Допустим, что конденсатор в исходном состоянии имел напряжение ( U_0 ). Посмотрим, что произойдет после замыкания цепи с помощью выключателя. Может в цепи появится постоянный ток?
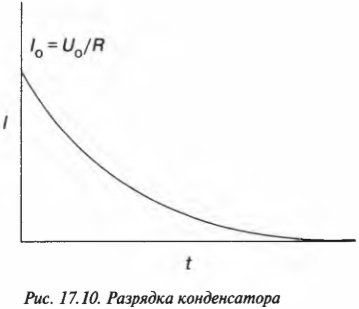
Но на самом деле ток ведет себя иначе: так, как показано на графике (рис. 17.10). Исходное значение силы тока равно (как и положено) ( U_0/R ) (где ( R ) означает сопротивление), но затем сила тока уменьшается. Что же происходит?
Дело в том, что с течением времени заряд конденсатора уменьшается и соответственно уменьшается ток. Конденсатор не является батарейкой и может подавать ток только тогда, когда на нем остается хоть какой-то заряд. Начальное значение силы тока равно ( U_0/R ), так как у конденсатора напряжение равно ( U_0 ), а ток идет через резистор ( R ). Но со временем ток слабеет по следующей формуле:
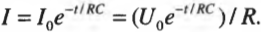
Здесь ( I ) — сила тока, ( e ) — основание натуральных логарифмов, равное 2,71828 (клавишу для вычисления значения функции ( e^{x} ) всегда можно найти на инженерном калькуляторе), ( t ) — время, ( R ) — сопротивление и ( C ) — это емкость. Подобно кривой, показанной на рис. 17.10, ведет себя и заряд конденсатора:
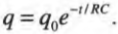
Глава 17. Летим вслед за электронами по проводам
3 (60%) 1 vote
$begingroup$
If voltage is calculated using the formula V=IR, how can the voltage be calculated of a battery if it is not connected to anything (i.e. no current)? I am not 100% sure about this, but neither do I think there is a resistance. Thus, how can V be calculated when both I (current) and R (resistance) are unknown?
asked Apr 4, 2018 at 19:08
$endgroup$
3
$begingroup$
The open-circuit voltage of a battery is based on the electrochemical potentials of the constituent materials. The theoretical voltage is determined by the Nernst Equation. You can look up the half-cell potentials. There is a temperature dependence which the Nernst Equation will predict.
Here is a simple undergrad lab where the students are asked to work this out for an ordinary lead-acid battery.
In practice electrical engineers are usually going to refer to the battery or cell datasheet for the range of voltages and the (usually more important) characteristics under various discharge conditions (and charge conditions, where applicable).
answered Apr 4, 2018 at 19:37
![]()
Spehro PefhanySpehro Pefhany
365k17 gold badges313 silver badges817 bronze badges
$endgroup$
$begingroup$
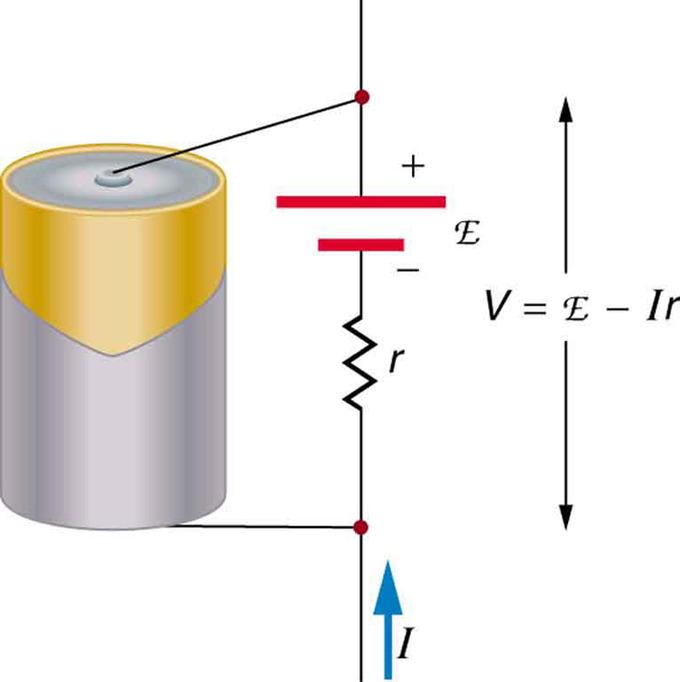
If the battery is not connected to anything, no current is flowing but voltage still exists across its positive and negative terminals. It is called EMF of the battery. It’s related by standard reduction potentials of its electrodes in chemistry as:
$$ E = E_{cathode} – E_{anode} $$
When the battery is connected to a resistor R, some current I will flow through R, as well as through a small series resistance r, which is the internal resistance of the battery. So effectively, we will get a terminal voltage, V across R, which is lesser than the EMF of the battery. Relations will look like:
$$ V = E – Ir = IR$$
answered Apr 4, 2018 at 19:42
![]()
Mitu RajMitu Raj
10.8k6 gold badges23 silver badges45 bronze badges
$endgroup$
$begingroup$
Voltage of a battery cannot be “calculated”, it is a given, inherent property of the electrical element. The potential V exists regardless of load or no load.
But if you connect a load R, then the current across the R will be I = V/R.
answered Apr 4, 2018 at 19:28
Ale..chenskiAle..chenski
38.6k2 gold badges35 silver badges100 bronze badges
$endgroup$
2
$begingroup$
V=IR is not a universal way to calculate voltage. It is for the special case where you have a known resistance (R) and a known current thru that resistance (I). Neither of these apply to “calculating the voltage of a battery”, whatever that is supposed to mean.
To a first approximation, you can model a battery as a voltage source in series with a resistance. Put another way, you model it like a Thevenin source. To find the value of the voltage source, simply measure the battery with nothing connected. Since there is no current (the current drawn by the voltmeter is so small that it can be ignored in this application) thru the resistor, the voltage across it is 0. The battery’s open circuit voltage is therefore the voltage of the internal voltage source.
To find the series resistance, apply a modest load on the battery, and measure the external voltage drop. You assume that the internal voltage source remains the same, and that the drop in external voltage is due to the drop across the resistance. You find the resistance by Ohm’s law: Ω = V / A, where V is the voltage drop across the internal resistance and A the battery current in Amps.
answered Apr 4, 2018 at 19:32
Olin LathropOlin Lathrop
310k36 gold badges422 silver badges908 bronze badges
$endgroup$
$begingroup$
If voltage is calculated using the formula V=IR, how can the voltage be calculated of a battery if it is not connected to anything (i.e. no current)?
We don’t calculate voltage, we measure it. To do so generally requires that we draw some current from the battery but only a tiny amount. Most digital multimeters have an input impedance of about 10 MΩ and hooking this up to a 9 V battery would cause a current draw of $ frac {V}{R} = frac {9}{10M} = 0.9 µA $. This is unlikely to cause a problem in most cases.

Figure 1. The ICE Supertester 680R analogue multimeter showing the DC and AC loading. The author had one of these for many years.
The old analog multimeters were typically 20 kΩ/V and the user had to take this into account when making a reading. For example, when on the 10 V DC range the load on the circuit would be 20k * 10 = 200 kΩ and this could load a high impedance circuit significantly.
answered Apr 4, 2018 at 19:31
![]()
TransistorTransistor
168k12 gold badges185 silver badges378 bronze badges
$endgroup$
Как определить напряжение на батарее (источнике) ?
Найдите правильный ответ на вопрос ✅ «Как определить напряжение на батарее (источнике) ? …» по предмету 📘 Физика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Формула напряжения в физике — это представление электрической потенциальной энергии на единицу заряда. Если ток был размещен в определенном месте, напряжение указывает на ее потенциальную энергию в этой точке. Другими словами, это измерение силы, содержащейся в электрическом поле или цепи в данной точке. Он равен работе, которую нужно было бы выполнить за единицу заряда против электрического поля, чтобы переместить его из одной точки в другую.
Напряжение является скалярной величиной, у него нет направления. Закон Ома гласит, что интенсивность равна текущему временному сопротивлению.
Единицы измерения в формуле
 Вам будет интересно:Антиклиналь + синклиналь – это складчатые горы
Вам будет интересно:Антиклиналь + синклиналь – это складчатые горы
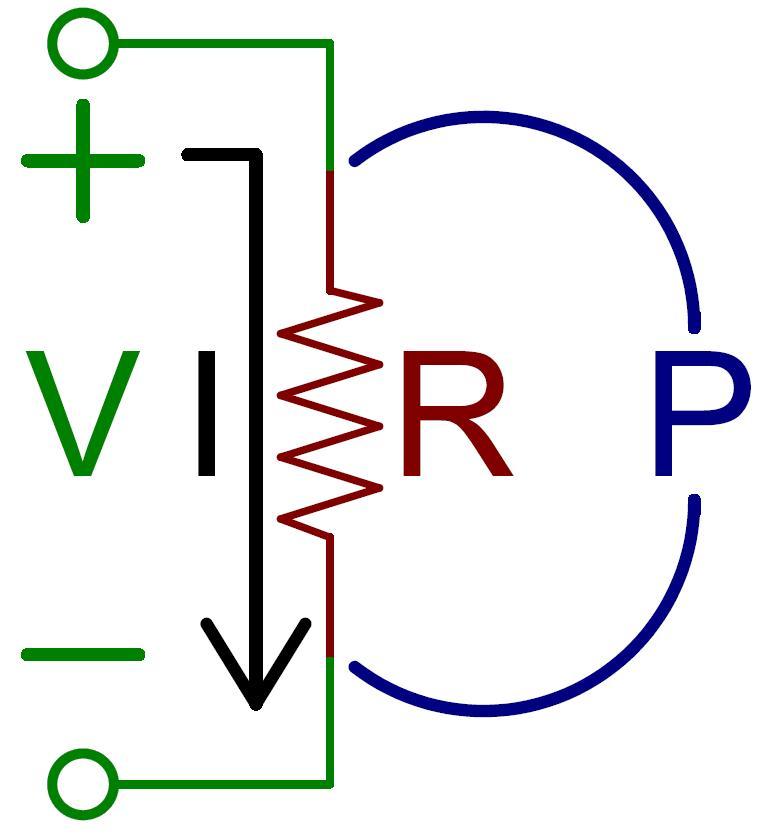
В формуле, определяющей напряжение, значением СИ является вольт. Таким образом, что 1В = 1 джоуль/кулон. Вольт назван в честь итальянского физика Алессандро Вольта, который изобрел химическую батарею.
Это означает, что в формуле напряжения в физике один кулон заряда получит один джоуль потенциальной энергии, когда он будет перемещен между двумя точками, где разность электрических потенциалов составляет один вольт. При напряжении 12, один кулон заряда получит 12 джоулей потенциальной энергии.
 Вам будет интересно:Ликвидация гетманства на Украине: история и интересные факты
Вам будет интересно:Ликвидация гетманства на Украине: история и интересные факты
Батарея на шесть вольт имеет потенциал для одного кулона заряда, чтобы получить шесть джоулей потенциальной энергии между двумя местоположениями. Батарея на девять вольт имеет потенциал для одного кулона заряда, чтобы получить девять джоулей потенциальной энергии.
Как работает закон в реальной жизни
Формулу напряжения в физике иногда очень сложно понять. Более конкретным примером из реальной жизни является резервуар для воды со шлангом, идущим снизу. Жидкость представляет собой накопленный заряд. Требуется работа, чтобы наполнить бак водой. Это создает запас жидкости. Как разделение заряда в батарее. Чем больше ее в резервуаре, тем сильнее давление – и вода может выходить через шланг с большей энергией. Если бы в аквариуме было меньше жидкости, она вышла бы с минимальным количеством интенсивности.
Пример с обычной водой
Этот потенциал давления эквивалентен напряжению. Чем больше воды в баке, тем сильнее воздействие. Чем мощнее заряд хранится в батарее, тем выше напряжение.
 Вам будет интересно:Что такое щелочь, в какие реакции вступают самые известные из них
Вам будет интересно:Что такое щелочь, в какие реакции вступают самые известные из них
Когда открываешь шланг, течет поток воды. Давление в резервуаре определяет, насколько быстро он вытекает. Электрический ток измеряется в амперах. Чем больше вольт, тем сильнее А тока. Значит, чем сильнее давление воды, тем быстрее она вытечет из бака.
Тем не менее ток также зависит от сопротивления. В случае шланга – это его ширина. Широкая труба позволяет пропускать больше воды за меньшее время, а узкая – противостоит потоку жидкости. С электрическим током также может быть сопротивление, измеренное в Омах.
По какой формуле определяется напряжение
Закон Ома гласит, что U равно текущему временному сопротивлению.
V=I*R
Если это 12-вольтовая батарея, то ее значение составляет два Ом, а ток составит шесть ампер. Если сопротивление было одним Ом, ток был бы 12 ампер.
Формула напряжения в физике гласит, что интенсивность, разница электрического потенциала и давления — это различие между двумя точками. Отличие в данном случае между двумя объектами (т. е. их напряжением) в статическом электрическом поле определяется как работа, необходимая на единицу заряда для перемещения испытательного резерва между точками. В Международной системе единиц полученный блок называется напряжением.
Различные используемые величины
В СИ работа выражается в джоулях на кулон, где 1 вольт = 1 джоуль за 1 кулон. Официальное определение СИ для вольта использует мощность и ток, где 1 вольт = 1 ватт (мощности) на 1 ампер (тока). Это определение эквивалентно более часто используемому «джоулю на кулон». Напряжение или разность электрических потенциалов обозначается символически DV, но чаще просто как V, например, в контексте Ома или Правилах Кирхгофа.
Различия электрического потенциала между точками могут быть вызваны зарядом, током через магнитное поле или некоторой комбинацией этих трех составляющих.
Вольтметр может быть использован для измерения напряжения (или разности потенциалов) между двумя точками в системе; часто в качестве одного объекта используется общий опорный потенциал, такой как заземление системы. Напряжение может представлять собой либо источник энергии (электродвижущая сила) либо потерянную, использованную или накопленную (падение потенциала) энергию.
Существует несколько полезных способов узнать какая формула напряжения в конкретном случае необходима.
Грубо говоря, сила определяется так, что отрицательно заряженные объекты притягиваются к более высоким напряжениям, а положительно – к более низким. Поэтому обычный ток в проводе или резисторе всегда течет от меньшего к большему.
 Вам будет интересно:Где находится Рейкьявик: страна, координаты, описание
Вам будет интересно:Где находится Рейкьявик: страна, координаты, описание
Исторически формула закона напряжения упоминалась с использованием такого термина, как давление. Даже сегодня «натяжение» все еще применяется в таком контексте, например, в термине «высокое напряжение», которое обычно употребляется в электронике на основе термоэлектронных клапанов (вакуумных трубок).
Как найти напряжение, формула. Потенциал электрического поля
Увеличение напряжения с некоторой точки xA в какой-то момент xB дан кем-то.
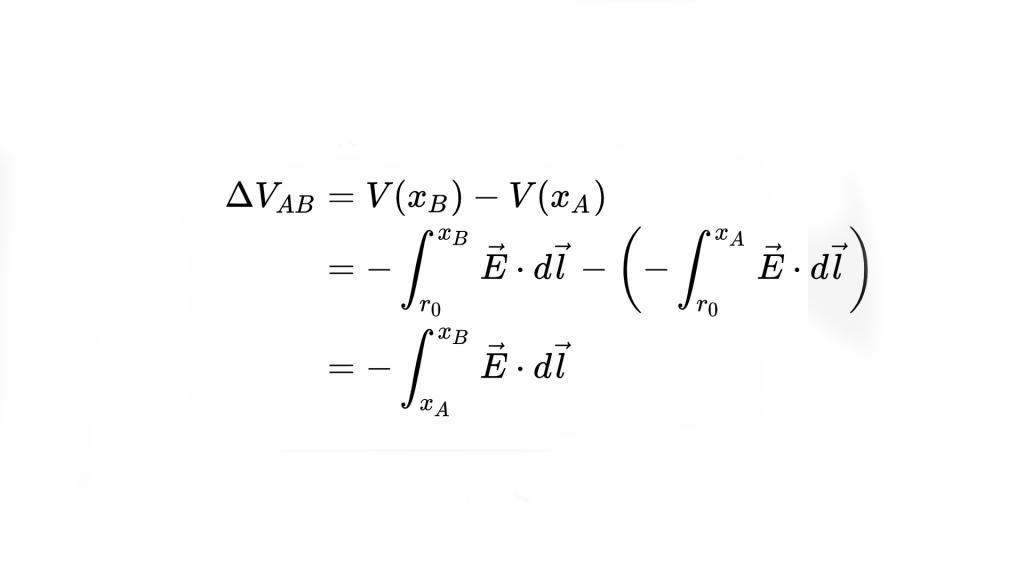
В этой формуле для вычисления напряжения увеличение от точки A до B равно работе, которую нужно было бы выполнить за единицу заряда, против электрического поля, чтобы переместить частицу с A на B, не вызывая какого-либо ускорения. Математически это выражается как криволинейный интеграл от электрического поля вдоль этого пути. Согласно данному определению, разность напряжений между двумя точками не формируется однозначно, когда существуют изменяющиеся во времени магнитные поля, поскольку электрическая сила не является консервативной в таких случаях.
Если используется это определение напряжения, любая цепь, в которой существуют изменяющиеся во времени магнитные поля, например, ряды, содержащие индукторы, не будет иметь четко определенного напряжения между узлами в цепи. Однако если магнитные поля надлежащим образом содержатся в каждом компоненте, то электрическое является консервативным во внешней области, и составляющие хорошо определены в ней. В этом случае напряжение на индукторе, если смотреть со стороны, оказывается.
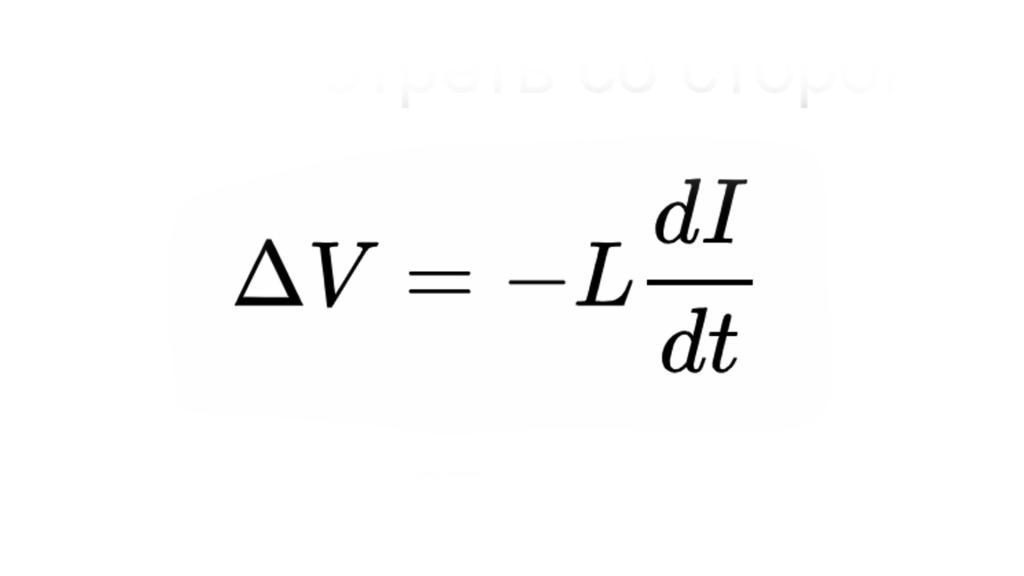
Несмотря на то, что внутреннее электрическое поле в катушке равно нулю (при условии, что это идеальный проводник). Существует еще несколько способов, чтобы узнать, какая формула напряжения необходима в конкретном случае.
Определение через разложение электрического поля
Используя приведенное выше понятие, потенциал не находится на одном месте, когда магнитные поля меняются со временем. В физике иногда полезно обобщать электрическое значение, рассматривая только консервативную часть поля. Это делается с помощью следующего разложения, используемого в электродинамике.

В показанной выше формуле Е – индуцированный – вращательное электрическое поле, обусловленное изменяющимися во времени магнитными фонами. В этом случае сила между точками всегда определяется однозначно.
Еще один способ
Разберем формулу механического напряжения в физике, теории цепей.
В схемотехническом анализе и электротехнике сила на катушке индуктивности не считается нулевым или неопределенным, как предполагает стандартное определение. Это связано с тем, что инженеры-электрики используют модель с сосредоточенными элементами для представления и анализа цепей.
При этом предполагается, что в области окружающего ряда нет магнитных полей, и их влияние содержится в «сосредоточенных элементах», которые являются идеализированными и автономными составляющими схемы, используемыми для моделирования физических компонентов. Если предположение о незначительных утечках полей является слишком неточным, их эффекты могут быть смоделированы паразитными компонентами.
Однако в случае физического индуктора идеальное представление с сосредоточенными параметрами часто является точным. Это связано с тем, что поля утечки в индуктивности, как правило, незначительны, особенно если заряд представляет собой тороид. Если протекшие поля небольшие, можно найти, что является независимым от пути, и на клеммах индуктора имеется четко определенное напряжение. Это причина того, что измерения с помощью вольтметра на катушке часто в достаточной степени не зависят от расположения измерительных проводов.
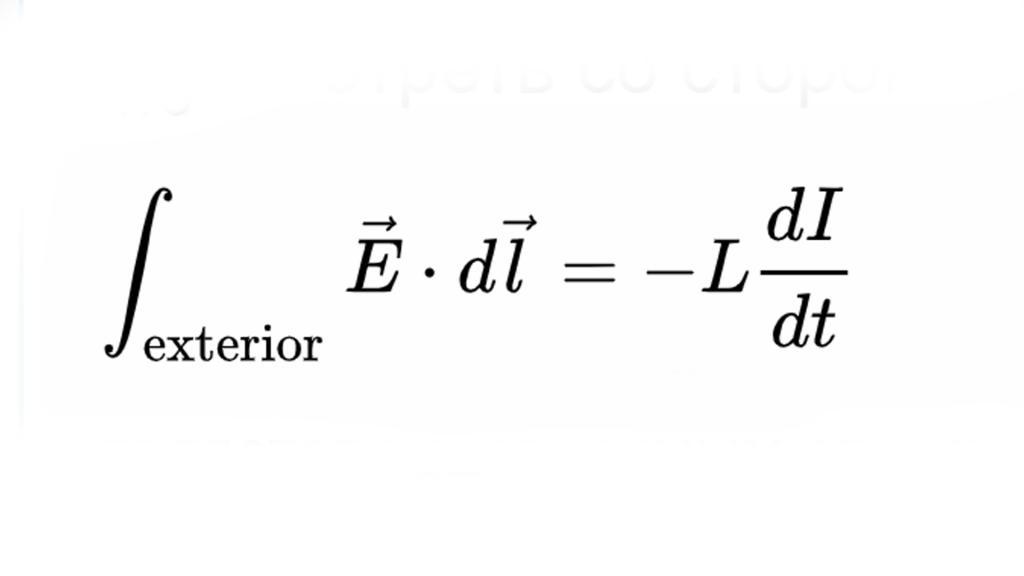
Гидравлическая аналогия
Простая параллель для электрического контура в формуле изменения напряжения — вода, протекающая по замкнутому трубопроводу, приводимая в действие механическим насосом. Это можно назвать «водным контуром». Разность потенциалов между двумя точками соответствует отличием давлений между ними. Если насос создает перепад напора, то вода, текущая из одной колбы в другую, сможет выполнять работу, например, приводить турбину в движение. Точно так же работа может выполняться электрическим током, управляемым разностью потенциалов, обеспечиваемой батареей. Например, напряжение, которое достаточно заряжено автомобильным аккумулятором, может «проталкивать» большой ток через обмотки стартерного двигателя. Если насос не работает, он не создает разности давлений, и турбина не вращается. Аналогично если аккумуляторная батарея машины очень слаба или разряжена, то она не будет вращать стартер.
Гидравлическая аналогия является полезным способом понимания многих электрических концепций. В такой системе напряжение вычисляется по формуле давления, умноженного на объем перемещаемого заряда. В электрической цепи работа, выполняемая для передвижения частиц или других носителей, равна «электрическому давлению», умноженному на количество перемещенных электрочастиц. Чем больше перепад давления между двумя точками в отношении потока (разность потенциалов или перепад давления воды), тем больше расстояние между ними (электрический ток или поток воды).
Измерительные приборы
Инструментарий для определения напряжения включает в себя вольтметр, потенциометр и осциллограф. Первый работает путем измерения тока через фиксированный резистор, который, согласно закону Ома, пропорционален напряжению. Потенциометр работает путем балансировки неизвестного напряжения с известным в мостовой цепи. Катодно-лучевой осциллограф вычисляет, усиливая U и используя его для отклонения электронного луча от прямой траектории.
Типичные напряжения
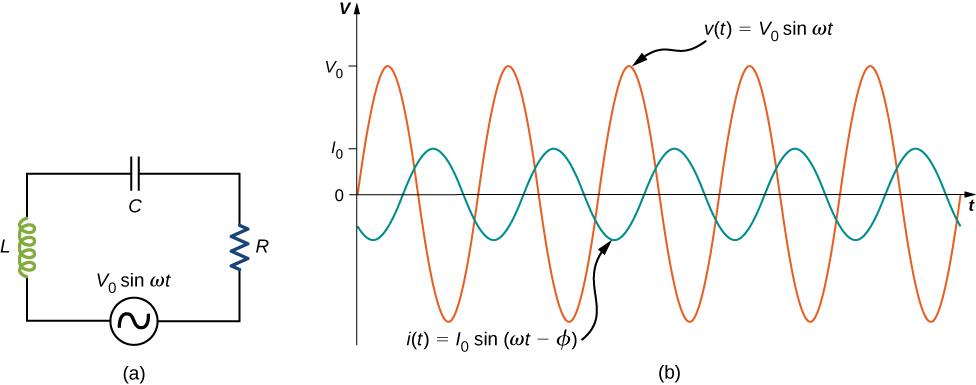
Общий поток для батарей фонарика составляет 1,5 V. А совместное напряжение для автомобильных аккумуляторов – 12 вольт.
Общая сила, поставляемая большими энергокомпаниями потребителю, составляет от 110 до 120 вольт и от 220 до 240 вольт. Напряжения в передаче энергии, используемые для распределения всего тока от электростанций, может быть в несколько сотен раз больше, чем любые потребительские напряжения, как правило, от 110 до 1200 кВ (переменного тока).
Сила, которая используется в воздушных линиях для питания всех железнодорожных локомотивов, составляет от 12 кВ до 50 кВ (переменного тока) или от 1,5 кВ до 3 кВ (постоянного тока).
Потенциал Гальвани
Внутри проводящего материала на энергию электрона влияют не только средние возможности, но и конкретная тепловая и атомная среда, в которой он находится. Когда вольтметр подключен между двумя различными типами металла, он не измеряет разность электростатического потенциала.
Величина, измеренная с помощью вольтметра, является отрицательной и обычно называется разностью напряжений. В то время как чистая нескорректированная электростатическая возможность (неизмеряемая с помощью вольтметра) иногда называется Гальванической. Термины «напряжение» и «электрический потенциал» неоднозначны в том смысле, что на практике они могут относиться к любому из них в различных контекстах.