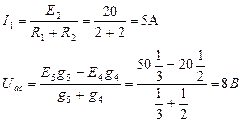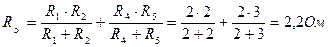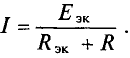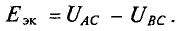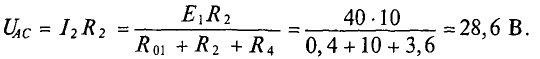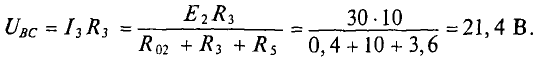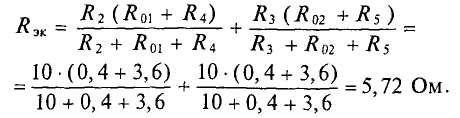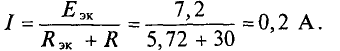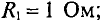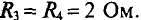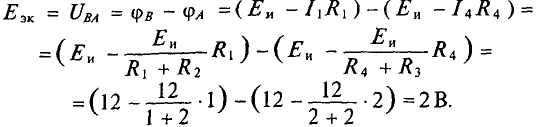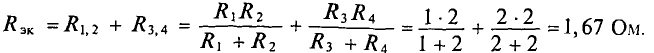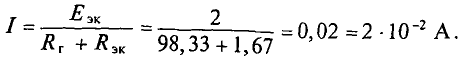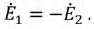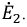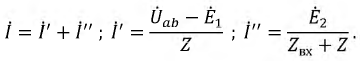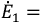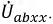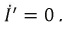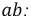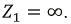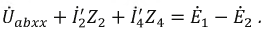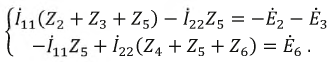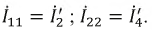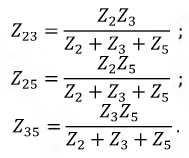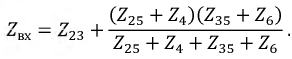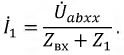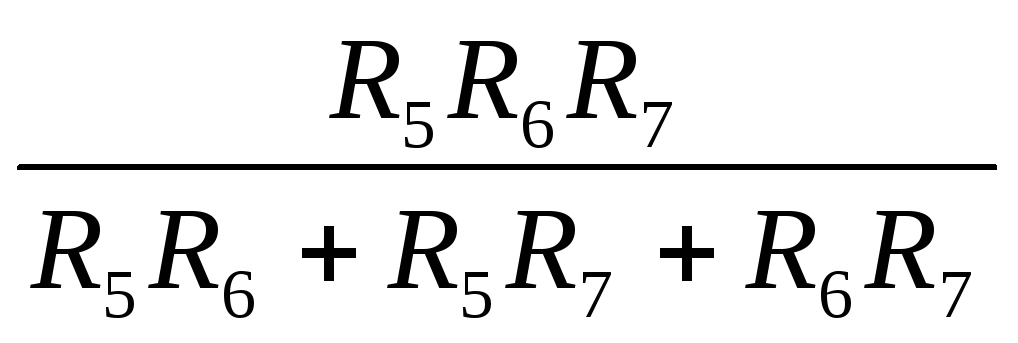Этот
метод обычно применяется в тех случаях,
когда требуется найти ток в какой-то
одной ветви при различных значениях
сопротивления этой ветви и неизменных
остальных параметрах цепи.
Пусть
в схеме на рис. 6.1, а нам
необходимо найти ток I1.
Тогда всю цепь относительно зажимов
первой ветви (узлов b и c)
мы представляем как активный двухполюсник
(рис. 6.1, б),
который, в свою очередь, заменяем
эквивалентным генератором (рис. 6.1, в).
ЭДС
эквивалентного генератора Eэ равна
напряжению холостого хода Uх на
разомкнутых зажимах двухполюсника
(рис. 6.2, а):
,
а его внутреннее сопротивление в
соответствии со схемой рис.
6.3,а определяется
по формуле
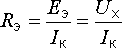
где –
ток короткого замыкания двухполюсника.

Рис.
6.1. Замена части электрической цепи
эквивалентным генератором
Рис.
6.2. Холостой ход активного двухполюсника
После
определения и
интересующий
нас ток находится из схемы рис. 6.1,в по
формуле

Заменяя
активный двухполюсник эквивалентным
генератором, ЭДС последнего мы можем
направлять произвольно – например, на
рис. 6.1, в ее
можно направить и вниз (при этом следует
поменять и знак перед вформуле
(6.2)). Но в схемах на рис. 6.2, в и
6.3, в этот
произвол исключен.
Рис.
6.3. Короткое замыкание двухполюсника
Если
на рис. 6.1, в мы
направили вверх,
от c к b,
то в режиме холостого хода точка b имеет
положительный потенциал, а c –
отрицательный (рис. 6.2, а).
Поэтому стрелка в
схемах рис. 6.2 направляется от b к c (от
плюса к минусу). Точно так же, от b к c,
т. е. в сторону действия ЭДС ,
должен быть направлен и ток (рис.
6.3).
Итак,
для того чтобы найти параметры
эквивалентного генератора, необходимо
рассмотреть два режима – холостого
хода и короткого замыкания.
Рассчитать
эти режимы можно любым методом. По
заданию требуется применить здесь метод
наложения.
6.1. Расчет режима холостого хода
В
соответствии с принципом наложения
(суперпозиции) напряжение холостого
хода может быть найдено как сумма
напряжений от действия каждой ЭДС в
отдельности:
,
где –
напряжение холостого хода, создаваемое
ЭДС (рис.
6.4, а); –
напряжение
холостого
хода от действия ЭДС (рис.
6.4, б).
Знаки
в правой части последнего уравнения
определяются взаимными направлениями
стрелок ,
и
(рис.
6.2. и 6.4).
Как следует направлять ,
мы только что выяснили.
Напряженияи
рекомендуется
направлять в ту же сторону, хотя это
необязательно. Если мы решили
направитьи
в
разные стороны, тобудет
равно их разности.
Токи
от действия каждой ЭДС в отдельности,
называемые частичными токами, на схемах
рис. 6.4, а и
6.4, б направляются
уже не произвольно, а в соответствии с
действующей в цепи единственной ЭДС –
по её стрелке.
Для
облегчения понимания структуры цепи
рекомендуется представить ее в более
удобном виде. Схему рис. 6.4, а,
например, можно изобразить так, как
показано на рис. 6.5.
Рис.
6.4. Схемы для расчета напряжения холостого
хода
Рис.
6.5. Упрощенная схема
Порядок
расчета схемы рис. 6.5 следующий.
Определяем
общее сопротивление цепи относительно
зажимов источника:
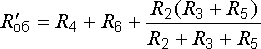
Находим
ток, протекающий по ветви с ЭДС:
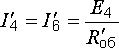
Рассчитываем
напряжение на
зажимах параллельно соединенных ветвей:
.
И
наконец, находим токи в параллельных
ветвях:


Последние
два тока можно рассчитать, и не находя
напряжения .
Рассмотрим
часть электрической цепи, состоящей из
двух параллельно соединенных сопротивлений
(рис.6.6).
Требуется
по известному току найти
токи и
.
Сначала определяем напряжение на
участке ab:
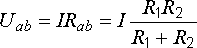
Затем
по закону Ома находим токи:

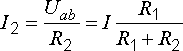
Полученные
формулы дают следующее простое правило.
Ток
в одной из параллельных ветвей равен
произведению общего тока и сопротивления
соседней ветви, деленному на сумму
сопротивлений параллельных ветвей.
Рис.6.6.
Определение токов в параллельных ветвях
В
соответствии с этим правилом для схемы
рис. 6.5 имеем:


Напряжение находим
по схеме рис. 6.4,а из
уравнения, составленного по второму
закону Кирхгофа для контура, включающего
в себя это напряжение. Например, контур,
отмеченный дугообразной пунктирной
стрелкой 1, состоит из двух ветвей (шестой
и пятой) и стрелки .
ЭДС в этом контуре нет, поэтому в
соответствии со вторым законом Кирхгофа
.
Отсюда
.
Можно
воспользоваться и контуром 2. Для него
,
откуда
.
Схема
рис. 6.4, б рассчитывается
аналогично:


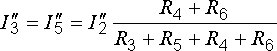
или
.
Если
в результате расчета ЭДС окажется
отрицательной, то во все формулы ее
значение следует подставлять со знаком
минус, не меняя, конечно, самих формул
и схем.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Очевидно, что
образовавшаяся петля – это замкнутый контур, который не оказывает влияния на
токораспределение между точками a и b, и его можно вовсе удалить из схемы (Рис. 14.4).
Рис. 14.4
Вышеприведенные
рассуждения позволяют сделать следующий вывод: любое сопротивление в любой
ветви схемы можно заменить эквивалентной ЭДС, численно равной падению напряжения
на этом сопротивлении и направленной навстречу току.
Очевидно, что
эту теорему можно сформулировать и следующим образом: любое сопротивление в
любой ветви схемы можно заменить эквивалентным источником тока. Ток источника
численно равен току через сопротивление и направлен в ту же сторону.
15. МЕТОД
ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА
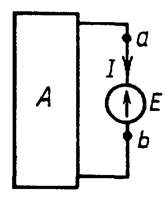
Рассмотрим
произвольную электрическую цепь, представив ее в виде активного двухполюсника и
ветви (Рис. 15.1).
Рис. 15.1
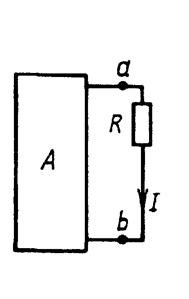
Как и в
предыдущей задаче, мы можем включить в ветвь две равных и противоположно направленных
ЭДС. Это не изменит токораспределения в схеме (Рис. 15.2).
Рис. 15.2
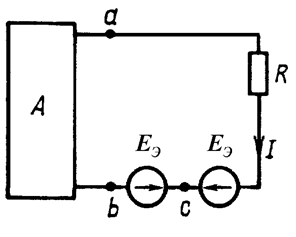
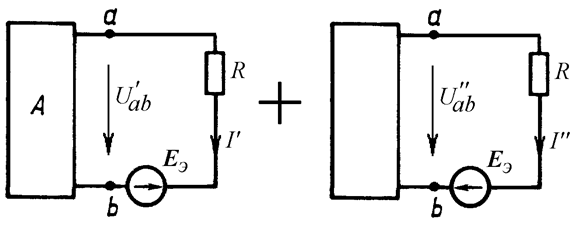
Воспользовавшись
методом наложения, разобьем получившуюся цепь на две: в одной из них оставим
лишь одну ЭДС Eэ (при этом
двухполюсник станет пассивным), в другой оставим все остальные источники (Рис. 15.3).
Рис. 15.3
Реальный ток
ветви есть сумма двух составляющих:
. (15.1)
По закону Ома
можно определить ток :
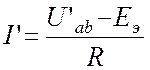
Так как ЭДС Eэ можно выбрать произвольно, выберем ее так,
чтобы дробь (15.2) обращалась в нуль.
При
. (15.3)
Соотношение
(15.3) означает, что активный двухполюсник на Рис. 15.3 работает в
режиме холостого хода, то есть ветвь с сопротивлением R
разомкнута или вообще удалена из схемы (Рис. 15.4). Напряжение называют напряжением холостого хода.
Рис. 15.4
Любой
пассивный двухполюсник всегда можно свернуть в одно эквивалентное сопротивление.
Тогда исходная схема принимает вид (Рис. 15.5):
Рис. 15.5
Ток в ветви
определяется по закону Ома:
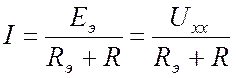
где Eэ
– ЭДС эквивалентного генератора;
Rэ
– сопротивление эквивалентного генератора;
R
– сопротивление ветви с искомым током.
Как видно из
предыдущих рассуждений ЭДС эквивалентного генератора численно равна напряжению
в разрыве ветви с искомым током и направлена в сторону тока. Сопротивление эквивалентного
генератора – это сопротивление цепи, из которой удалены все источники энергии,
свернутой относительно ветви с искомым током.
ЭДС и сопротивление
эквивалентного генератора можно определить как экспериментально, так и
аналитически.
Алгоритм экспериментального
определения параметров эквивалентного генератора
- Разрывают ветвь с искомым
током. Этот режим называется режимом холостого хода. Измеряют напряжение в
разрыве. Оно направлено в ту же сторону, что и искомый ток и численно
равно ЭДС эквивалентного генератора. - Закорачивают ветвь с искомым
током. Этот режим называется режимом короткого замыкания. Измеряют ток в
закоротке. Этот ток называется током короткого замыкания. - Сопротивление эквивалентного
генератора равно отношению напряжения холостого хода к току короткого
замыкания:
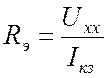
Алгоритм
аналитического расчета цепи методом эквивалентного генератора
- Ветвь с искомым током удаляется
из схемы и заменяется двумя зажимами. Исходная цепь значительно
упрощается. В дальнейшем ни в коем случае нельзя терять зажимы сворачиваемой
схемы. - Любым известным методом
определяется напряжение между зажимами Uхх.
Оно направлено в ту же сторону, что и искомый ток. ЭДС эквивалентного
генератора равна этому напряжению. - Вся цепь делается пассивной, то
есть источники удаляются и заменяются своими внутренними сопротивлениями.
Получившаяся пассивная цепь сворачивается в одно сопротивление Rэ относительно зажимов. - Искомый ток определяется по
закону Ома:
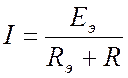
Метод
эквивалентного генератора наиболее эффективен, когда требуется определить ток в
одной ветви с переменным сопротивлением.
Пример 15.1
Определить ток
I3 методом эквивалентного генератора
(Рис. 15.6).
Рис. 15.6
Формируем
схему режима холостого хода. Ветвь с искомым током удаляем из схемы. Заменяем
ее двумя зажимами. Между зажимами обозначаем напряжение холостого хода. Оно направлено
в ту же сторону, что и искомый ток (Рис. 15.7).
Рис. 15.7
По второму
закону Кирхгофа для левого контура
.
По закону Ома
находим ток:
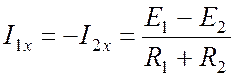
После чего
можно найти напряжение холостого хода:
.
ЭДС
эквивалентного генератора равна напряжению холостого хода:
.
Определяем
сопротивление эквивалентного генератора относительно зажимов (Рис. 15.8):
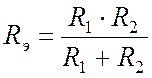
Рис. 15.8
Находим ток I3:
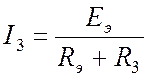
16. ЭЛЕКТРИЧЕСКИЕ
ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Синусоидальный
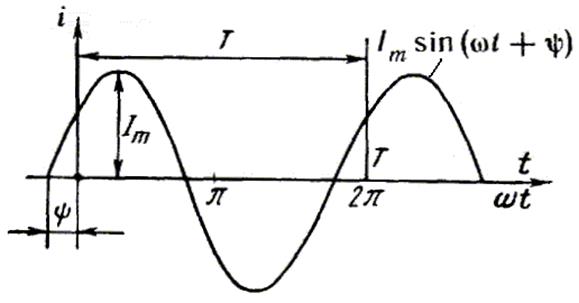
ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рис. 16.1):
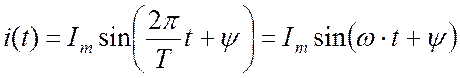
Рис. 16.1
Максимальное
значение функции называют амплитудой. Амплитуду тока обозначают Im.
Период Т
– это время, за которое совершается одно полное колебание.
Частота равна
числу колебаний в одну секунду (единица частоты – герц (Гц) или с-1):
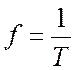
Угловая
частота (единица угловой частоты – рад/с или с-1):
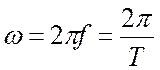
Аргумент
синуса, то есть , называют
фазой, слагаемое –
начальной фазой.
Любая
синусоидально изменяющаяся функция определяется тремя величинами: амплитудой,
угловой частотой и начальной фазой.
Значение
функции (16.1) в любой произвольный момент времени называют мгновенным
значением.
№9 Метод эквивалентного генератора.
Этот метод основан на сформулированной выше теореме (См. предыдущую лекцию) и применяется в тех случаях, когда требуется рассчитать ток в какой-либо одной ветви при нескольких значениях ее параметров (сопротивления и ЭДС) и неизменных параметрах всей остальной цепи.
Сущность метода заключается в следующем. Вся цепь относительно зажимов интересующей нас ветви представляется как активный двухполюсник, который заменяется эквивалентным генератором, к зажимам которого подключается интересующая нас ветвь. В итоге получается простая неразветвленная цепь, ток в которой определяется по закону Ома.
ЭДС ЕЭ эквивалентного генератора и его внутреннее сопротивление RЭ находятся из режимов холостого хода и короткого замыкания двухполюсника.
Порядок решения задачи этим методом рассмотрим на конкретном числовом примере.
Пример 1.5. В цепи, показанной на рис. 9.1, а, требуется рассчитать ток I3 при шести различных значениях сопротивления R3 и по результатам расчета построить график зависимости I3(R3).
Числовые значения параметров цепи: Е1 = 225 В; Е3 = 30 В; R1 = 3 Ом; R2 = 6 Ом.
Рис. 9.1 — Схема решения задачи
а) Расчет режима холостого хода.
Убираем третью ветвь, оставляя зажимы m и n разомкнутыми (рис. 9.2, а). Напряжение между ними, равное UX, находится как падение напряжения на сопротивлении R2:
б) Расчет режима короткого замыкания. Замыкаем накоротко зажимы m и n (рис. 9.2, б). Ток короткого замыкания: Ik=E1/R1=75 (A)
Внутреннее сопротивление эквивалентного генератора: Rэ=Ux/Ik=2 (Oм).
Рис. 9.2 — Режимы холостого хода (а) и короткого замыкания (б)
Величину Rэ можно найти и другим способом. Оно равно входному сопротивлению двухполюсника при равенстве нулю всех его ЭДС. Если на рис. 1.21, а мысленно закоротить зажимы ЭДС Е1, то сопротивления R1 и R2 окажутся соединенными параллельно, и входное сопротивление цепи относительно зажимов m и n будет равно:
Ток в полученной неразветвленной цепи (рис. 9.1, б) определяется по закону Ома:
Подставляя в последнюю формулу требуемые значения сопротивления R3, вычисляем ток и строим график (рис. 9.3).
Рис. 9.3 — Зависимость тока от сопротивления
Данную задачу целесообразно решать именно методом эквивалентного генератора. Применение другого метода, например метода контурных токов, потребует решать систему уравнений столько раз, сколько значений тока необходимо найти. Здесь же всю цепь мы рассчитываем только два раза, определяя Еэ и Rэ, а многократно используем лишь одну простую формулу (1.13).
Источник
Метод эквивалентного генератора (метод холостого хода и короткого замыкания)
На практике часто бывает необходимо изучить режим работы только одной из ветвей сложной электрической схемы, при этом не следует производить расчет всей схемы, а целесообразно воспользоваться методом эквивалентного генератора. Согласно этому методу в схеме выделяется исследуемая ветвь и расчет производится в следующем порядке:
1) произвольно выбираем направление тока в исследуемой ветви;
2) определяем напряжение холостого хода Uхх на зажимах разомкнутой исследуемой ветви;
3) находим входное (эквивалентное) сопротивление схемы со стороны зажимов разомкнутой ветви Rэ’ если известен ток короткого замыкания Iк.э., то 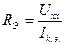
4) находим ток в исследуемой ветви:
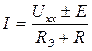
где: R – сопротивление ветви, в которой определяется ток;
Е – э.д.с. в исследуемой ветви, если ветвь не содержит э.д.с, то Е = 0.
Знаки «плюс» или «минус» в последнем выражении выбираются в соответствии с законом Ома для участка цепи, содержащего э.д.с.
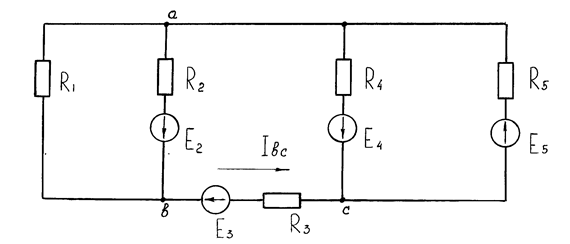
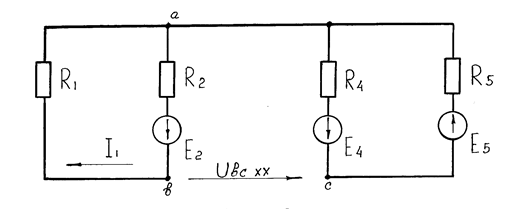
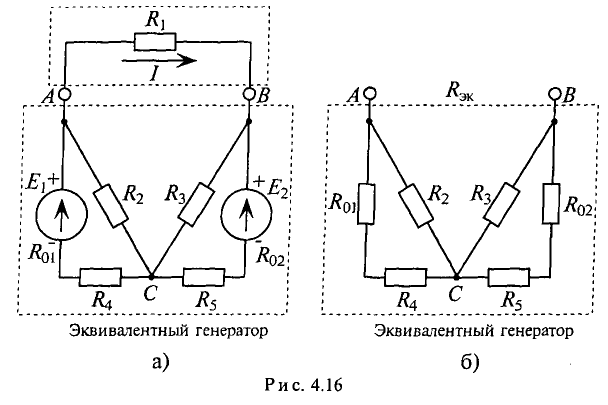
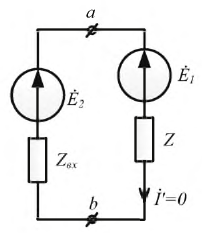
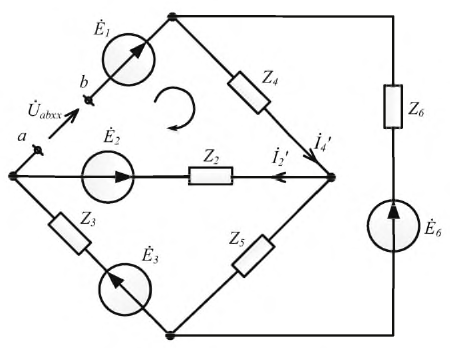
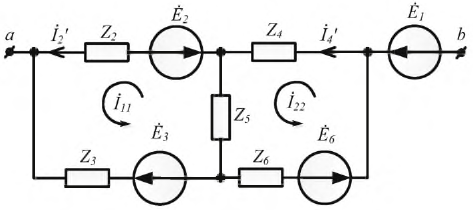
Рассмотрим применение метода эквивалентного генератора на примере схемы рис. 1.29, допустим Е2 = Е3 = Е4 = 20 В, Е5 = 50 В, R1 = R2 = R3 = R4 = 2 Ом; R5 = 3 Ом, требуется определить ток в ветви bс.
Рис. 1.29. Схема трехконтурной электрической цепи с четырьмя источниками э. д. с.
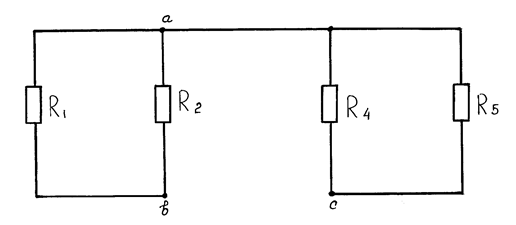
Указываем направление тока в ветви bс и определяем напряжение холостого хода Ubcxx на зажимах ветви bс. Схема в этом случае имеет вид, показанный на рис. 1.30.
Для нахождения Ubcxx вначале находим ток I1 и напряжение Uac по методу двух узлов:
Рис. 1.30. Схема для определения напряжения холостого хода Ubcxx по методу эквивалентного генератора
Напряжение Ubcxx определяется по второму закону Кирхгофа, обходя контур bасb:
Определяем эквивалентное сопротивление относительно зажимов bc, схема в этом случае имеет вид, показанный на рис. 1.31:
Рис. 1.31. Схема для определения эквивалентного сопротивления
относительно зажимов bс no методу эквивалентного генератора
Находим ток в исследуемой ветви bс :
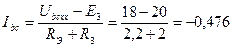
т.е. ток Ibc в схеме имеет направление, противоположное выбранному.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Как найти напряжение холостого хода в цепи с источником тока
Метод эквивалентного генератора, основанный на теореме об активном двухполюснике (называемой также теоремой Гельмгольца-Тевенена), позволяет достаточно просто определить ток в одной (представляющей интерес при анализе) ветви сложной линейной схемы, не находя токи в остальных ветвях. Применение данного метода особенно эффективно, когда требуется определить значения тока в некоторой ветви для различных значений сопротивления в этой ветви в то время, как в остальной схеме сопротивления, а также ЭДС и токи источников постоянны.
Теорема об активном двухполюснике формулируется следующим образом: если активную цепь, к которой присоединена некоторая ветвь, заменить источником с ЭДС, равной напряжению на зажимах разомкнутой ветви, и сопротивлением, равным входному сопротивлению активной цепи, то ток в этой ветви не изменится.
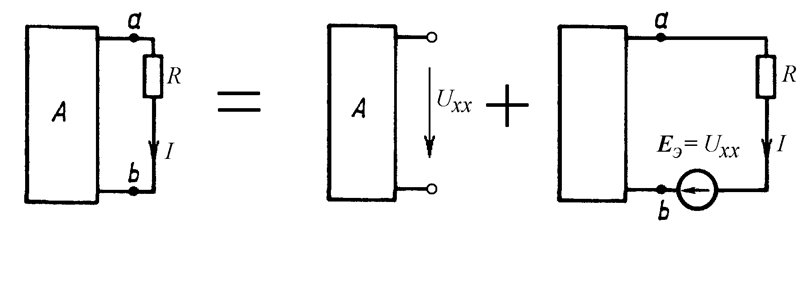
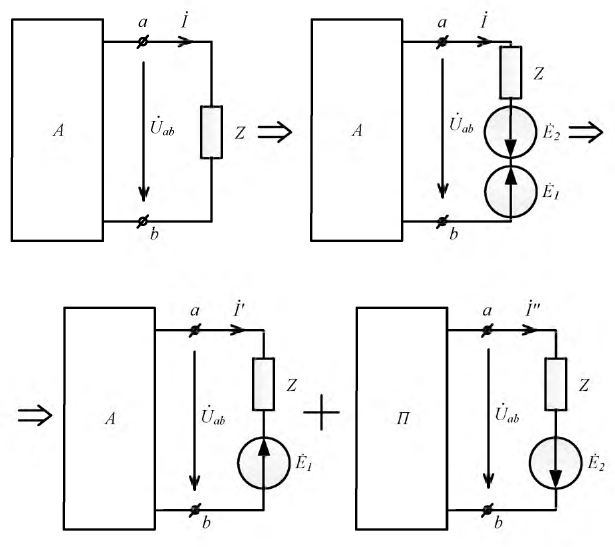
Ход доказательства теоремы иллюстрируют схемы на рис. 1.
Пусть в схеме выделена некоторая ветвь с сопротивлением Z, а вся оставшаяся цепь обозначена как активный двухполюсник А (рис. 1,а). Разомкнем эту ветвь между точками 1 и 2 (рис. 1,б). На зажимах этой ветви имеет место напряжение 






Указанные в теореме ЭДС и сопротивление можно интерпретировать как соответствующие параметры некоторого эквивалентного исходному активному двухполюснику генератора, откуда и произошло название этого метода.
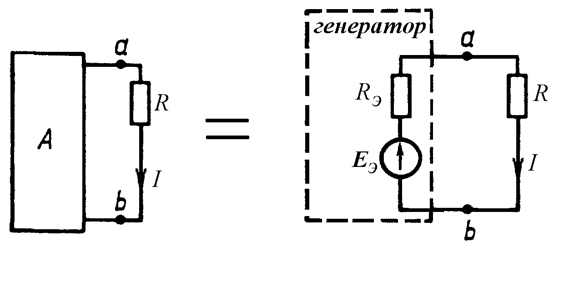
Таким образом, в соответствии с данной теоремой схему на рис. 2,а, где относительно ветви, ток в которой требуется определить, выделен активный двухполюсник А со структурой любой степени сложности, можно трансформировать в схему на рис. 2,б.
Отсюда ток 
 , , |
(1) |
где 
Уравнение (1) представляет собой аналитическое выражение метода эквивалентного генератора.
Параметры эквивалентного генератора (активного двухполюсника) могут быть определены экспериментальным или теоретическим путями.
В первом случае, в частности на постоянном токе, в режиме холостого хода активного двухполюсника замеряют напряжение 



В принципе аналогично находятся параметры активного двухполюсника и при синусоидальном токе; только в этом случае необходимо определить комплексные значения 

При теоретическом определении параметров эквивалентного генератора их расчет осуществляется в два этапа:
1. Любым из известных методов расчета линейных электрических цепей определяют напряжение на зажимах a-b активного двухполюсника при разомкнутой исследуемой ветви.
2. При разомкнутой исследуемой ветви определяется входное сопротивление активного двухполюсника, заменяемого при этом пассивным. Данная замена осуществляется путем устранения из структуры активного двухполюсника всех источников энергии, но при сохранении на их месте их собственных (внутренних) сопротивлений. В случае идеальных источников это соответствует закорачиванию всех источников ЭДС и размыканию всех ветвей с источниками тока.
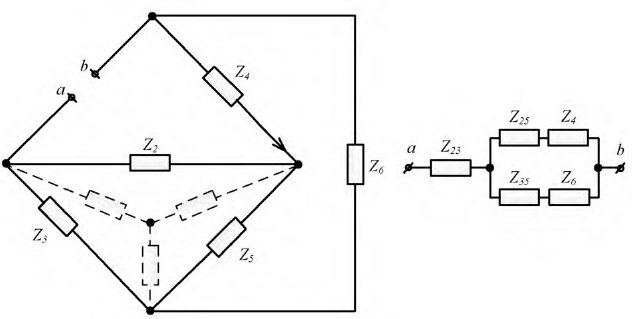
Сказанное иллюстрируют схемы на рис. 3, где для расчета входного (эквивалентного) сопротивления активного двухполюсника на рис. 3,а последний преобразован в пассивный двухполюсник со структурой на рис. 3,б. Тогда согласно схеме на рис. 3,б

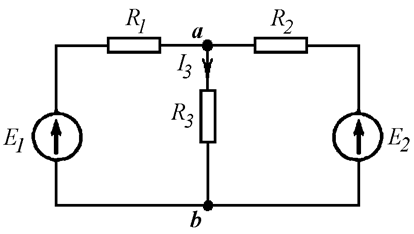
В качестве примера использования метода эквивалентного генератора для анализа определим зависимость показаний амперметра в схеме на рис. 4 при изменении сопротивления R переменного резистора в диагонали моста в пределах 
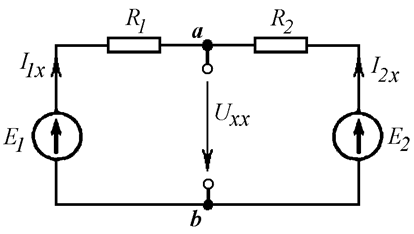
В соответствии с изложенной выше методикой определения параметров активного двухполюсника для нахождения значения 



Для определения входного сопротивления активного двухполюсника трансформируем его в схему на рис. 6.
Со стороны зажимов 1-2 данного пассивного двухполюсника его сопротивление равно:

Таким образом, для показания амперметра в схеме на рис. 4 в соответствии с (1) можно записать
 . . |
(2) |
Задаваясь значениями R в пределах его изменения, на основании (2) получаем кривую на рис.7.
В качестве примера использования метода эквивалентного генератора для анализа цепи при синусоидальном питании определим, при каком значении нагрузочного сопротивления 
Параметры цепи: 

В соответствии с теоремой об активном двухполюснике обведенная пунктиром на рис. 8 часть схемы заменяется эквивалентным генератором с параметрами
В соответствии с (1) для тока 

откуда для модуля этого тока имеем

Анализ полученного выражения (3) показывает, что ток I, а следовательно, и мощность будут максимальны, если 




Данные соотношения аналогичны соответствующим выражениям в цепи постоянного тока, для которой, как известно, максимальная мощность на нагрузке выделяется в режиме согласованной нагрузки, условие которого 
Таким образом, искомые значения 

Теорема вариаций применяется в тех случаях, когда требуется рассчитать, насколько изменятся токи или напряжения в ветвях схемы, если в одной из ветвей этой схемы изменилось сопротивление.
Выделим на рис. 9,а некоторые ветви с токами 



Пусть сопротивление n-й ветви изменилось на 







Для этой цепи можно записать


Полученные соотношения позволяют определить изменения токов в m-й и n-й ветвях, вызванные изменением сопротивления в n-й ветви.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В каких случаях эффективно применение метода эквивалентного генератора?
- Как можно экспериментально определить параметры эквивалентного генератора?
- Как можно определить параметры активного двухполюсника расчетным путем?
- Как необходимо преобразовать исходную схему активного двухполюсника для расчета его входного сопротивления?
- В каких задачах используется теорема вариаций?
- В цепи на рис. 4 источник ЭДС Е замене на источник тока J=10 А. Определить показание амперметра, если R=0.
Ответ: 
Для полученного значения 

Ответ: 
Источник
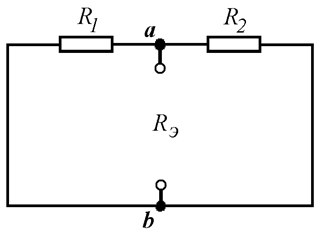
Метод эквивалентного генератора:
Метод эквивалентного генератора рационально применять в случае необходимости определения тока (напряжения, мощностн и др.) только одной ветви сложной электрической цепи.
Для этой цели разбивают сложную электрическую цепь на две части — на сопротивление R, ток которого
Активным этот двухполюсник называют потому, что в нем имеется источник ЭДС. Этот активный двухполюсник обладает определенной ЭДС
Ток в резисторе с сопротивлением R определяют по закону Ома
Таким образом, определение тока 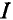
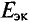
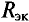
Величина ЭДС 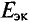
Внутреннее сопротивление эквивалентного генератора 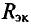
Практически для определения внутреннего сопротивления эквивалентного генератора измеряют амперметром ток между точки А и В работающего двухполюсника при коротком замыкании так как сопротивление амперметра настолько мало, что им можно пренебречь. Тогда
где 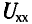
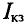
Такой метод практического определения внутреннего сопротивления эквивалентного генератора 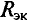
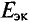
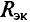
Пример 4.12
Определить ток в сопротивлении 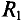
Решение
Для определения тока 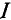
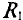
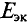
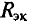
Знак «минус» обусловлен тем, что источники в схеме включены встречно и потенциал в точке А больше потенциала в точке В, так как 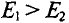
Напряжение
Напряжение
Следовательно, 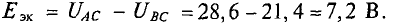
Искомый ток
Такой же ток получен в примере 4.6 на сопротивлении
Пример 4.13
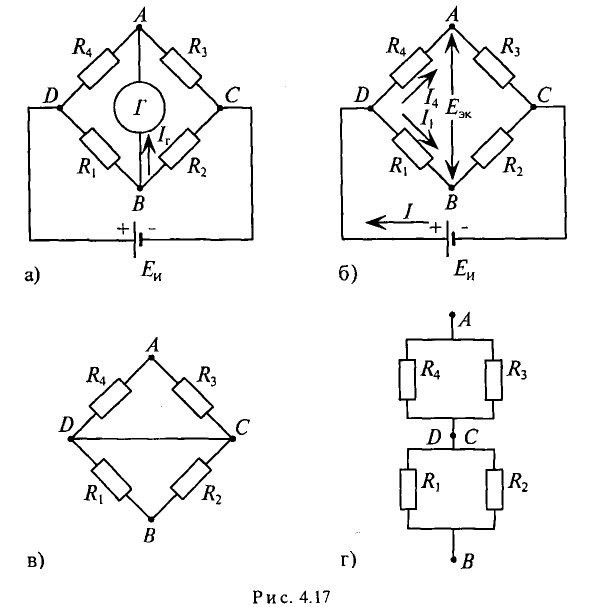
В схеме рис. 4.17а сопротивления плеч моста равны
Сопротивление гальванометра Rr = 98,33 Ом, ЭДС источника 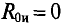
Решение
Для определения тока в цепи гальванометра 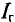
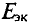
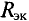
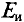
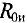
Для определения ЭДС эквивалентного генератора 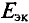
Тогда
При замене источника ЭДС 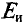
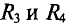
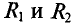
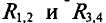
Тогда ток в ветви с гальванометром, который направлен из точки В в точку А, т. е. из точки с большим потенциалом в точку с наименьшим потенциалом (рис. 4.17а), будет равен
Метод эквивалентного генератора (активного двухполюсника)
Все методы, рассмотренные ранее, предполагали расчет токов одновременно во всех ветвях цепи. Однако в ряде случаев бывает необходимым контролировать ток в одной отдельно взятой ветви. В этом случае применяют для расчета метод эквивалентного генератора.
Пусть дана некоторая электрическая цепь, которую заменим активным двухполюсником (рис. 3.10), оставив только ветвь 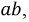
Сначала, введем в ветвь 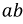
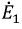
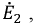
Затем, используя принцип наложения, данную цепь представим суммой двух цепей. В первой оставим все источники активного двухполюсника и источник ЭДС 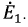
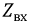
Рис. 3.10. Преобразование исходного двухполюсника в сумму двух цепей
На основании принципа наложения ток ветви
Поскольку 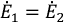
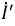
Напряжение на зажимах источника в режиме холостого хода численно равно его ЭДС. Тогда активный двухполюсник с источником 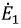
Рис. 3.11. Схема замещения активного двухполюсника
В этой схеме ЭДС 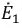
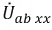
Таким образом, ток в ветви
Пусть дана цепь (рис. 3.12), в которой необходимо рассчитать ток 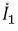
Рис. 3.12. Исходная цепь
Последовательность расчета:
1. Разомкнем ветвь с сопротивлением 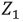
2. Зададим положительное направление 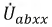
3. Токи 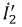
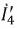
Тогда
4. Определим эквивалентное сопротивление пассивного двухполюсника. Для этого мысленно закоротим все источники ЭДС исходной цепи, оставляя в схеме для реальных источников их внутренние сопротивления.
В образовавшейся схеме пассивного двухполюсника невозможно определить эквивалентное сопротивление относительно зажимов 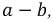
Преобразуем, например, «треугольник» сопротивлений 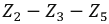
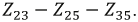
Рис. 3.14. Схема пассивного двухполюсника
Сопротивления этой схемы будут:
Входное сопротивление цепи 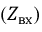
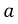
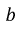
Окончательно имеем:
- Теоремы теории цепей
- Теорема обратимости (или взаимности)
- Теорема компенсации
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
- Метод свертывания электрической цепи
- Метод преобразования схем электрических цепей
- Параллельное соединение генераторов
- Метод узловых и контурных уравнений
Содержание
- Режимы электрических цепей
- Режим работы электрической цепи, то есть ее электрическое состояние, определяется значениями токов, напряжений и мощностей ее отдельных элементов. Номинальный режим. Рабочий режим. Режим холостого хода, режим короткого замыкания, холостой ход, короткое замыкание
- 1.6. Холостой ход и короткое замыкание тока.
- 1.7. Расчет сложных электрических цепей постоянного тока.
- 1.7.1. Метод непосредственного применения законов Кирхгофа
- Холостой ход электродвигателя
- Подписка на рассылку
- Параметры холостого хода электродвигателя
- Основы электротехники и электроники: Курс лекций , страница 10
Режимы электрических цепей
Режим работы электрической цепи, то есть ее электрическое состояние, определяется значениями токов, напряжений и мощностей ее отдельных элементов. Номинальный режим. Рабочий режим. Режим холостого хода, режим короткого замыкания, холостой ход, короткое замыкание
Номинальный режим. Источники и приемники электрической энергии, провода, а также вспомогательные аппараты и приборы характеризуются номинальными величинами тока Iн, напряжения Uн, мощности Pн, на которые эти устройства рассчитаны заводами-изготовителями для нормальной работы. Номинальные величины обычно указываются в паспорте устройства.
Режим работы, при котором действительные токи, напряжения, мощности элементов электрической цепи соответствуют их номинальным значениям, называется номинальным (нормальным).
Рабочий режим. Режимы электрической цепи по различным причинам могут отличаться от номинального.
Если в электрической цепи действительные характеристики режима отличаются от номинальных величин ее элементов, но отклонения находятся в допустимых пределах, то режим называется рабочим.
Рисунок 1 – Схема цепи с переменным сопротивлением приемника электрической энергии
Уравнение баланса напряжений
где U — внутреннее падение напряжения в источнике; U — напряжение на внешних зажимах источника.
Напряжение U на внешних зажимах источника, равное в этом случае напряжению на приемнике, меньше ЭДС источника на величину внутреннего падения напряжения
Общее определение коэффициента полезного действия
Отношение мощности Pпр приемника к мощности Pист источника называется коэффициентом полезного действия (КПД) источника
КПД источника можно определить отношением напряжения на зажимах источника к его ЭДС
Также КПД источника можно определить отношением сопротивления нагрузки к полному сопротивлению цепи
Из последней формулы видно, что чем меньше внутреннее сопротивление R, тем выше КПД источника.
Режимы холостого хода и короткого замыкания
При R = ∞ тока в цепи не будет. Этот случай соответствует размыканию цепи. Режим электрической цепи или отдельных источников, при котором ток в них равен нулю, называется режимом холостого хода.
При холостом ходе напряжение на внешних зажимах источника равно его ЭДС
При R = 0, согласно выражению (1),
а напряжение на зажимах приемника и источника равно нулю
Режим электрической цепи, при котором накоротко замкнут участок с одним или несколькими элементами, в связи с чем, напряжение на этом участке равно нулю, называется режимом короткого замыкания. Соответственно ток Iк в цепи называется током короткого замыкания.
Напряжение на зажимах источника уменьшается от U = Е до U = 0, если ток нагрузки увеличивается от 0 до тока короткого замыкания Iк (рисунок 2).
Рисунок 2 – Графики зависимости напряжения U на зажимах источника, мощности источника Pист, мощности приемника Pпр, КПД η источника, мощности потерь внутри источника P от тока в цепи при изменении сопротивления нагрузки от R = ∞ (холостой ход) до R = 0 (короткое замыкание), считая ЭДС источника постоянной
Задача Источник электрической энергии имеет в качестве нагрузки реостат с переменным сопротивлением R. ЭДС источника E = 24 В, а его внутреннее сопротивление R = 1 Ом. Построить графики зависимости напряжения U на зажимах источника, мощности источника Pист, мощности приемника Pпр, КПД η источника, мощности потерь внутри источника P от тока в цепи при изменении сопротивления нагрузки от R = ∞ (холостой ход) до R = 0 (короткое замыкание), считая ЭДС источника постоянной.
Решение
Для решения задачи воспользуемся схемой рисунок 1.
Например, для сопротивления нагрузки R = 11 Ом:
Для других значений сопротивления R результаты расчетов приведены в таблице 1.
Источник
1.6. Холостой ход и короткое замыкание тока.
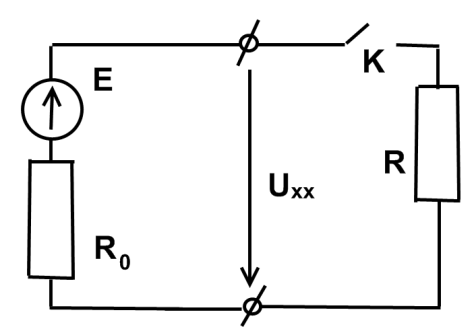
Рис. 1.8. Режим холостого хода
В режиме холостого хода внешняя цепь разомкнута (рис. 1.8.) При этом ее сопротивление равно бесконечности, а величина тока в цепи равна нулю. Следовательно, напряжение на зажимах генератора: Uxx= E.
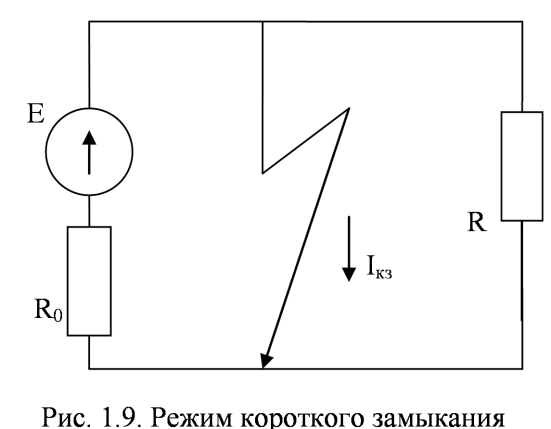
Короткое замыкание возникает обычно в результате повреждения изоляции соединительных проводов. При этом зажимы генератора оказываются замкнуты проводником с ничтожно малым сопротивлением (рис. 1.9).
Рис. 1.9 Режим короткого замыкания.
Практически напряжение на зажимах генератора в режиме короткого замыкания равно нулю, и сопротивление цепи равно внутреннему сопротивлению генератора R. Так как R обычно мало, величина тока короткого замыкания Iкз= 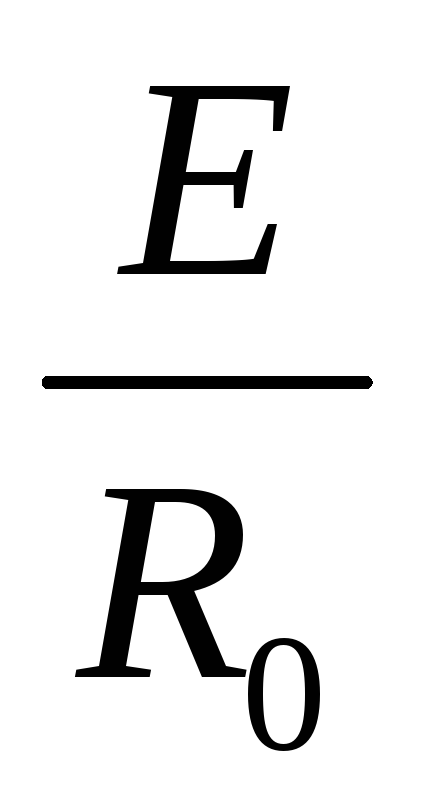
Короткое замыкание является аварийным режимом работы и представляет собой большую опасность для электрических установок, т.к. может повлечь за собой их разрушение, вследствие перегрева, вызванного большими токами.
1.7. Расчет сложных электрических цепей постоянного тока.
Приведем основные понятия сложной цепи. Несколько последовательно соединенных элементов цепи, по которым проходит один и тот же ток, образуют ветвь. В общем случае ветвь может содержать как сопротивления, так и ЭДС.
Точка соединения трех и более ветвей называют узловой точкой или узлом.
Несколько ветвей, образующих замкнутую электрическую цепь называют контуром.
1.7.1. Метод непосредственного применения законов Кирхгофа
Универсальным методом расчета токов в сложных цепях постоянного тока с несколькими источниками электрической энергии, является метод непосредственного применения I и II законов Кирхгофа.
К узловым точкам схемы применяется I закон Кирхгофа, согласно которому сумма токов, притекающих к узлу равна сумме токов уходящих от него, т.е. алгебраическая сумма токов в узле равна нулю. ∑I =0
К контурам применяется II закон Кирхгофа, согласно которому алгебраическая сумма ЭДС, действующих в контуре, равна сумме падений напряжений на всех сопротивлениях контура.
По первому и второму законам Кирхгофа составляют столько уравнений, сколько неизвестных токов в цепи. По первому закону Кирхгофа составляют n-1 уравнений, где n – число узлов в цепи. Недостающие уравнения составляют по второму закону Кирхгофа.
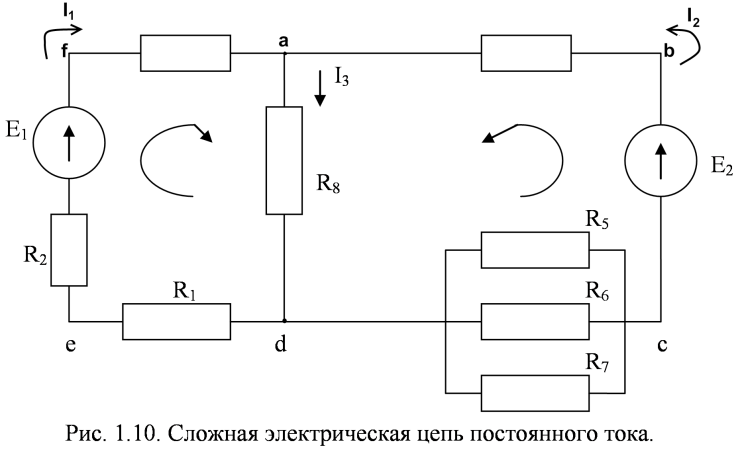
Рассмотрим применение метода на примере сложной электрической цепи, схема которой представлена на рис. 1.10
Рис. 1.10. Сложная электрическая цепь постоянного тока.
Расчет токов, протекающих в ветвях сложной цепи, проводят по следующим правилам:
По возможности упрощают схему, заменяя параллельно соединенные сопротивления одним эквивалентным. Для рассматриваемой схемы имеем
R567 =
Определяют количество искомых токов в цепи и произвольно задают их направления. Количество искомых токов равно количеству ветвей в цепи. В рассматриваемой цепи после упрощения остается три ветви abcd, ad, afed, следовательно, требуется найти значения трех токов I1, I2, I3, для чего необходимо составить три уравнения по законам Кирхгофа.
Определяют количество узлов в цепи и для всех узловых точек, кроме одной составляют уравнения по первому закону Кирхгофа. В рассматриваемой цепи две узловые точки a и d. Поэтому, по первому закону Кирхгофа составляется одно уравнение для узловой точки a, в соответствии с заданными направлениями токов
Выбирают произвольное направление обхода контуров по или против часовой стрелки и по второму закону Кирхгофа составляют недостающие уравнения. Для рассматриваемой цепи необходимо составить еще два уравнения. Они составляются по второму закону Кирхгофа, для контуров adef и abcd в соответствии с выбранными направлениями их обхода. При этом ЭДС и токи, совпадающие с направлением обхода контура, принимают со знаком плюс, а ЭДС и токи, противоположные этому направлению, со знаком минус. В результате получаем
5. Определяют неизвестные токи в ветвях, решая полученную систему уравнений (1.11), (1.12), (1.13). Если какие-то значения при расчете получаются со знаком минус, то это означает, что направления реальных токов противоположны заданным в начале расчета.
Проверку решения задачи осуществляют путем расчета уравнения баланса мощностей: алгебраическая сумма мощностей развиваемых всеми источниками ЭДС равна сумме мощностей, потребляемых всеми сопротивлениями нагрузки. В общем виде уравнение баланса мощностей записывается как ∑EI=∑I 2 R.
Применительно к рассматриваемой цепи, уравнение баланса мощностей принимает вид:
E1I1+E2I2 = I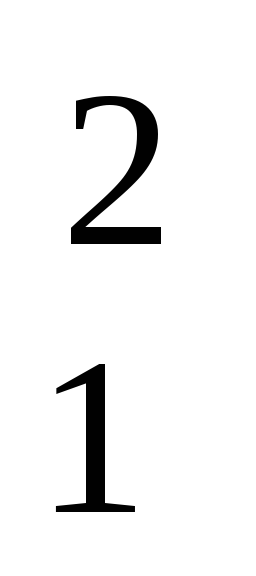
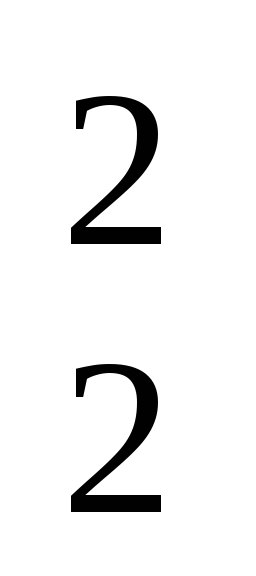
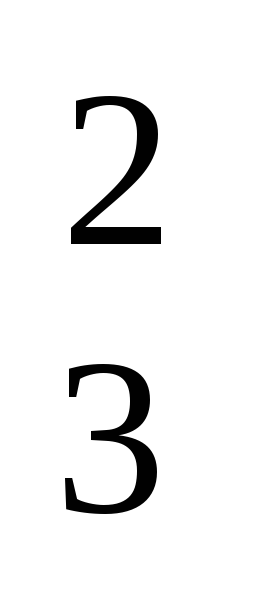
Если направление ЭДС совпадает с направлением тока в ветви, то их произведение включается в левую часть уравнения со знаком плюс, а если не
с
Источник
Холостой ход электродвигателя
Подписка на рассылку
- ВКонтакте
- ok
- YouTube
- Яндекс.Дзен
- TikTok
Электродвигатель переходит в режим холостого хода, когда с его вала снимают рабочую нагрузку. В этом случае можно определить такие важные параметры функционирования устройства, как намагничивающий ток, мощность и коэффициент потерь в элементах конструкции привода. Но главное – в режиме холостого хода можно определить исправность устройства.
Так, электродвигатель на холостом ходу греться не должен. Но в некоторых случаях температура привода повышается – и это сигнализирует о неполадках, которые впоследствии могут проявить себя.
Параметры холостого хода электродвигателя
Как было сказано выше, холостой ход – это режим работы асинхронного электродвигателя, при котором на валу нет нагрузки. В этом случае устройство с точки зрения электротехники схоже с трансформатором. Но главное – оно потребляет меньше электроэнергии, что особенно важно для контроля правильности работы мотора.
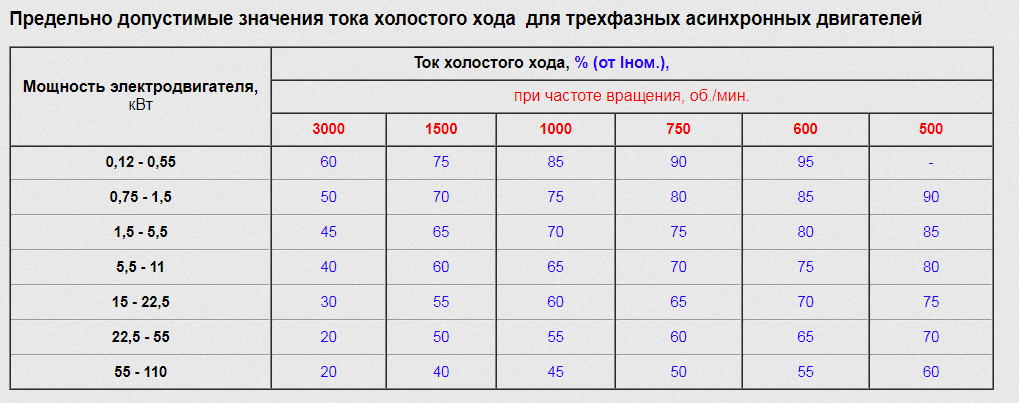
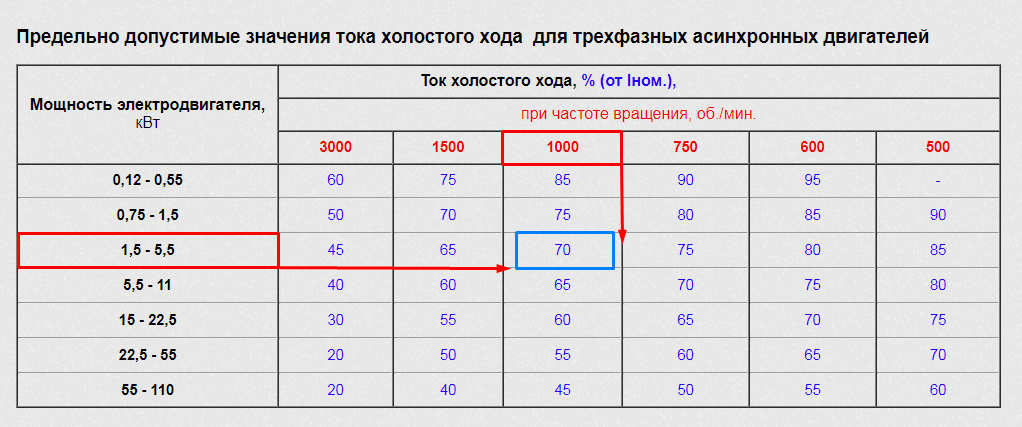
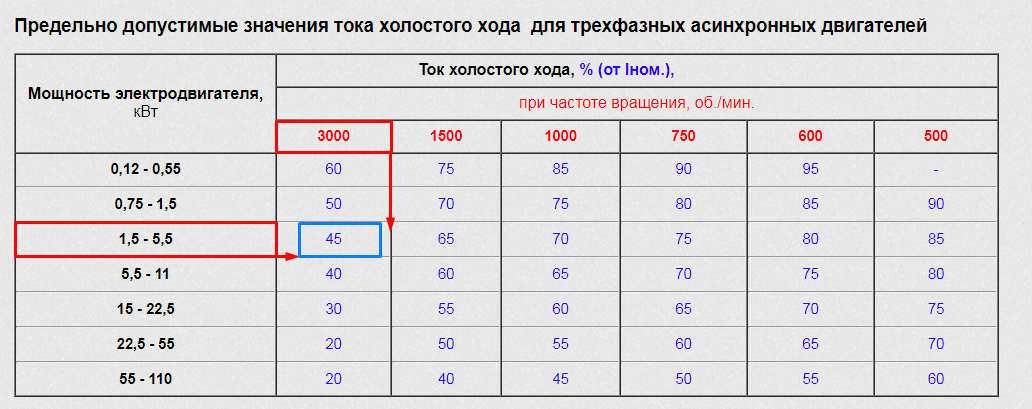
В частности, ток холостого хода асинхронного электродвигателя в зависимости от мощности и частоты вращения составляет в среднем 20-90% от номинального. Существует таблица, в которой указаны данные значения.
Так, например, ток холостого хода электродвигателя на 5 кВт при частоте вращения в 1000 оборотов в минуту составляет 70% от номинального (см. рис. 2). При частоте вращения 3000 оборотов в минуту – всего 45% от номинального (см. рис. 3). Это важно учесть, так как если фактическая сила тока значительно расходится с расчётной, то это сигнализирует о неполадках.
Стоит отметить, что параметры работы двигателя обычно указаны в прилагаемой к нему документации или могут быть получены посредством расчётов.
Что делать, если греется электродвигатель на холостом ходу
Электродвигатель на холостом ходу греться не должен. Допускается лишь незначительное увеличение температуры, обусловленное естественными причинами – появление трения в подшипниках на валу ротора и сопротивление в обмотке. А вот заметный нагрев сигнализирует в первую очередь о неполадках в устройстве.
Чаще всего нагревается асинхронный электродвигатель на холостом ходу из-за межвиткового замыкания в обмотках. Это требует срочного ремонта. Ведь при повышении нагрузок межвитковое замыкание может привести к перегреву и выгоранию обмотки – и, как следствие, повреждению как самого ЭД, так и конструкции, в которую он установлен.
Ещё одна возможная причина нагрева ЭД в этом режиме – эксплуатация в нештатных условиях. Например, превышение напряжения. В этом случае необходимо срочно отключить питание двигателя, так как из-за перегрева может возникнуть межвитковое замыкание в обмотках или замыкание обмотки на корпус двигателя.
Реже нагрев ЭД наблюдается из-за затруднённого движения ротора. Стоит убедиться, что подшипники работают нормально, а между обмотками ротора и статора не попали загрязнения.
Источник
Основы электротехники и электроники: Курс лекций , страница 10
Очевидно, что образовавшаяся петля – это замкнутый контур, который не оказывает влияния на токораспределение между точками a и b, и его можно вовсе удалить из схемы (Рис. 14.4).
Вышеприведенные рассуждения позволяют сделать следующий вывод: любое сопротивление в любой ветви схемы можно заменить эквивалентной ЭДС, численно равной падению напряжения на этом сопротивлении и направленной навстречу току.
Очевидно, что эту теорему можно сформулировать и следующим образом: любое сопротивление в любой ветви схемы можно заменить эквивалентным источником тока. Ток источника численно равен току через сопротивление и направлен в ту же сторону.
15. МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА
Рассмотрим произвольную электрическую цепь, представив ее в виде активного двухполюсника и ветви (Рис. 15.1).
Как и в предыдущей задаче, мы можем включить в ветвь две равных и противоположно направленных ЭДС. Это не изменит токораспределения в схеме (Рис. 15.2).
Воспользовавшись методом наложения, разобьем получившуюся цепь на две: в одной из них оставим лишь одну ЭДС Eэ (при этом двухполюсник станет пассивным), в другой оставим все остальные источники (Рис. 15.3).
Реальный ток ветви есть сумма двух составляющих:
По закону Ома можно определить ток :
Так как ЭДС Eэ можно выбрать произвольно, выберем ее так, чтобы дробь (15.2) обращалась в нуль.
Соотношение (15.3) означает, что активный двухполюсник на Рис. 15.3 работает в режиме холостого хода, то есть ветвь с сопротивлением R разомкнута или вообще удалена из схемы (Рис. 15.4). Напряжение называют напряжением холостого хода.
Любой пассивный двухполюсник всегда можно свернуть в одно эквивалентное сопротивление. Тогда исходная схема принимает вид (Рис. 15.5):
Ток в ветви определяется по закону Ома:
где Eэ – ЭДС эквивалентного генератора;
Rэ – сопротивление эквивалентного генератора;
R – сопротивление ветви с искомым током.
Как видно из предыдущих рассуждений ЭДС эквивалентного генератора численно равна напряжению в разрыве ветви с искомым током и направлена в сторону тока. Сопротивление эквивалентного генератора – это сопротивление цепи, из которой удалены все источники энергии, свернутой относительно ветви с искомым током.
ЭДС и сопротивление эквивалентного генератора можно определить как экспериментально, так и аналитически.
Алгоритм экспериментального определения параметров эквивалентного генератора
- Разрывают ветвь с искомым током. Этот режим называется режимом холостого хода. Измеряют напряжение в разрыве. Оно направлено в ту же сторону, что и искомый ток и численно равно ЭДС эквивалентного генератора.
- Закорачивают ветвь с искомым током. Этот режим называется режимом короткого замыкания. Измеряют ток в закоротке. Этот ток называется током короткого замыкания.
- Сопротивление эквивалентного генератора равно отношению напряжения холостого хода к току короткого замыкания:
Алгоритм аналитического расчета цепи методом эквивалентного генератора
- Ветвь с искомым током удаляется из схемы и заменяется двумя зажимами. Исходная цепь значительно упрощается. В дальнейшем ни в коем случае нельзя терять зажимы сворачиваемой схемы.
- Любым известным методом определяется напряжение между зажимами Uхх. Оно направлено в ту же сторону, что и искомый ток. ЭДС эквивалентного генератора равна этому напряжению.
- Вся цепь делается пассивной, то есть источники удаляются и заменяются своими внутренними сопротивлениями. Получившаяся пассивная цепь сворачивается в одно сопротивление Rэ относительно зажимов.
- Искомый ток определяется по закону Ома:
Метод эквивалентного генератора наиболее эффективен, когда требуется определить ток в одной ветви с переменным сопротивлением.
Определить ток I3 методом эквивалентного генератора (Рис. 15.6).
Формируем схему режима холостого хода. Ветвь с искомым током удаляем из схемы. Заменяем ее двумя зажимами. Между зажимами обозначаем напряжение холостого хода. Оно направлено в ту же сторону, что и искомый ток (Рис. 15.7).
По второму закону Кирхгофа для левого контура
По закону Ома находим ток:
После чего можно найти напряжение холостого хода:
ЭДС эквивалентного генератора равна напряжению холостого хода:
Определяем сопротивление эквивалентного генератора относительно зажимов (Рис. 15.8):
Находим ток I3:
16. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рис. 16.1):
Максимальное значение функции называют амплитудой. Амплитуду тока обозначают Im.
Период Т — это время, за которое совершается одно полное колебание.
Частота равна числу колебаний в одну секунду (единица частоты – герц (Гц) или с -1 ):
Угловая частота (единица угловой частоты – рад/с или с -1 ):
Аргумент синуса, то есть , называют фазой, слагаемое – начальной фазой.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.
Значение функции (16.1) в любой произвольный момент времени называют мгновенным значением.
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им. Даля 166
- ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им. Дегтярева 174
- КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им. Макарова 543
- НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им. Герцена 123
- РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им. Гагарина 114
- СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им. Каразина 305
- ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Полный список ВУЗов
- О проекте
- Реклама на сайте
- Правообладателям
- Правила
- Обратная связь
Чтобы распечатать файл, скачайте его (в формате Word).
Источник