Для школьников.
В предыдущих статьях рассмотрены цепи переменного тока, содержащие только активное сопротивление и содержащие только емкостное сопротивление.
Сейчас рассмотрим случай, когда в цепи переменного тока находится только катушка индуктивности (индуктивное сопротивление), а активным и емкостным сопротивлениями цепи можно пренебречь.
Начнём с опыта, позволяющего понять, когда появляется и от чего зависит индуктивное сопротивление в цепи переменного тока.
Две маленькие одинаковые электрические лампочки подключались к источникам одинакового напряжения. Но одна (правая) подключалась к источнику постоянного тока (аккумуляторной батарее), а другая (левая) – к источнику переменного тока.
Лампочки светили одинаково, так как количество выделяющегося тепла не зависит от того, какой ток протекает по нитям лампочек (постоянный или переменный).
Затем к лампочкам последовательно подключили катушки индуктивности, сделанные из толстой медной проволоки, содержащей большое число витков. Внутри катушек находятся железные сердечники.
Катушками индуктивности называются катушки, имеющие большую индуктивность и малое активное сопротивление (изготовлены из толстой проволоки). Часто активным сопротивлением такой катушки можно пренебречь.
Опыт показал, что в случае постоянного тока лампочка горит ярко, а в случае переменного тока она светит тускло. Как это объяснить?
В случае постоянного тока лампочка горит ярко, потому что сопротивление катушки мало.
Но почему катушка индуктивности очень сильно ослабляет переменный ток? Продолжаем рассматривать опыт.
Если из катушки (рис. б) постепенно вытягивать железный сердечник, то нить лампочки будет накаляться всё сильнее. При полном вытягивании сердечника лампочка будет светить довольно ярко. Убрав железный сердечник, во много раз уменьшили индуктивность катушки, значит дело в индуктивности.
Так как сила переменного тока быстро меняется, то в катушке возникает ЭДС самоиндукции.
В цепи только с индуктивным сопротивлением приложенное к цепи напряжение в каждый момент времени равно и противоположно ЭДС самоиндукции.
ЭДС самоиндукции по правилу Ленца направлена так, что стремится препятствовать изменению тока, то есть оказывает току сопротивление. Чем больше индуктивность катушки, тем большая ЭДС самоиндукции в ней возникает, тем больше индуктивное сопротивление. Индуктивное сопротивление зависит ещё от частоты тока, чем больше частота, тем больше это сопротивление.
При нарастании тока ЭДС самоиндукции препятствует этому нарастанию, поэтому ток позже достигает максимума, чем в отсутствие самоиндукции.
При убывании тока ЭДС самоиндукции стремится поддерживать ток. Поэтому нулевые значения тока достигаются в более поздний момент, чем в отсутствие самоиндукции.
Таким образом, при наличие индуктивности ток отстаёт по фазе от тока в отсутствие индуктивности, а следовательно, отстаёт по фазе от своего напряжения.
Можно сказать так: из-за явления самоиндукции ток в катушке индуктивности не может меняться скачком и отстаёт от напряжения.
Чем больше частота тока, тем больше будет ЭДС самоиндукции, стремящейся противодействовать изменению тока и тем больше будет сопротивление переменному току.
Индуктивное сопротивление находится по формуле, которая получена теоретически и подтверждена опытом:
Напряжение на индуктивном сопротивлении (индуктивное напряжение) :
Ток в цепи, содержащей только индуктивность, равен отношению напряжения на зажимах источника к индуктивному сопротивлению цепи:
В цепи, содержащей только индуктивное сопротивление, напряжение опережает ток на четверть Т/4 периода (или ток отстаёт от напряжения на четверть периода):
Из рисунка видно, когда ток ещё только проходит через нулевое положение, напряжение уже проходит через максимум, то есть мгновенные значения напряжения и тока меняются согласно уравнениям:
Разность фаз между током и напряжением, равная “пи” пополам, величина отрицательная.
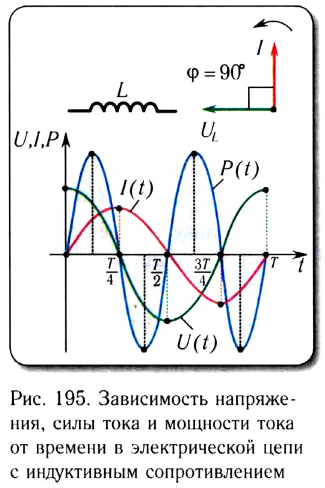
На следующем рисунке показано, как меняются во времени мгновенные значения тока, напряжения и мощности в цепи переменного тока, содержащей только индуктивное сопротивление:
Мгновенные значения мощности находятся через произведение мгновенных значений напряжения и тока, уравнения для которых записаны выше.
Видим, что мгновенная мощность в цепи, обладающей только индуктивностью, изменяется по синусоидальному закону с двойной частотой и имеет равные по модулю положительные и отрицательные значения.
В первую и третью части периода, когда ток в цепи растёт, мощность имеет положительное значение. В эти части периода магнитное поле вокруг электрической цепи усиливается за счёт энергии источника.
Убыванию тока соответствует отрицательное значение мощности. В эти части периода (второй и четвёртый) магнитное поле ослабевает, его энергия идёт обратно к источнику тока.
Таким образом, в цепи, содержащей только катушку индуктивности, происходит периодическая перекачка энергии от источника в энергию магнитного поля катушки индуктивности и возвращение её источнику.
Положительные и отрицательные значения мощности по модулю равны, поэтому средняя мощность за период в такой цепи равна нулю.
Эта мощность не расходуется во внешней части цепи, поэтому называется реактивной индуктивной мощностью:
Она образуется при работе электроприборов (трансформаторов, двигателей, электромагнитов и др., обладающих большой индуктивностью.)
Реактивная мощность в промышленных электрических цепях увеличивает нагрузку на провода и снижает коэффициент мощности цепи, поэтому реактивную нагрузку в электрической цепи на предприятиях снижают (об этом будет сказано в последующих статьях.)
Пример.
Катушка с индуктивностью 0,01 Гн включена в цепь переменного тока напряжением 120 В и частотой 50 Гц. Определить силу тока в катушке, индуктивное напряжение в ней и её реактивную мощность, если активным сопротивлением катушки можно пренебречь.
Используем формулы:
Ответ: 38,2 А; 120 В; 1460 Вт.
Из полученного ответа видим, что всё приложенное к катушке напряжение является индуктивным.
Итак, присутствие индуктивности в цепи переменного тока приводит к сдвигу фаз между током и напряжением в сети (колебания тока отстают от колебаний напряжения).
Емкостная мощность не совершает механической работы, не нагревает проводники.
Катушка индуктивности лишь периодически накапливает энергию магнитного поля и возвращает её обратно источнику тока.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Предыдущая запись : Конденсатор в цепи переменного тока. Емкостное сопротивление.
Следующая запись: Занятие 71. Последовательное соединение сопротивлений. Резонанс напряжений.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58 .
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
В электрической цепи сопротивление,
индуктивность и емкость относятся к
категории так называемых пассивных
двухполюсных элементов.
Между напряжением uи вызываемым им токомiвсопротивленииR
имеет место соответствие, определяемое
законом Ома:
![]() (2.1)
(2.1)
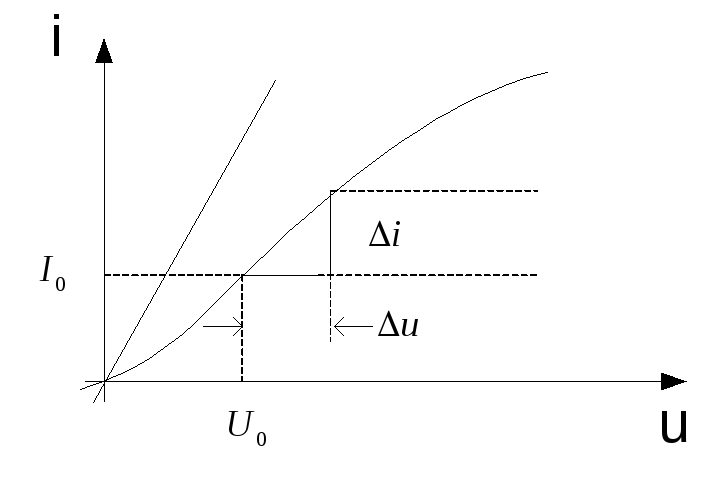
Рис. 2.2
Полагается, что Rне
зависит от протекающего через сопротивление
тока и внешних воздействий (температуры
и др.), а также от времени. Такое
сопротивление называется линейным.
Изображаемое на схемах в виде удлиненного
прямоугольника (рис. 2.1,а) сопротивление
R в реальной
цепи не всегда имеет вид отделяемого
от других элементов устройства в форме,
например, реостата или резистора. Чаще
оно учитывает, моделирует энергетические
потери и другие явления в цепи. Так, в
частности, реальная катушка индуктивности
часто представляется на схемах в виде
последовательно соединенныхL
иR, гдеR
– сопротивление проводов катушки.
ОтделитьR от
катушки физически невозможно, но при
анализе это, однако, допускается.
На схеме изображаются отдельно –
«чистое» (без индуктивности) сопротивление
R и «чистая» (без
сопротивления) индуктивностьL.
Такого рода несмешанные элементы цепиR,L,
а такжеCназываютсяидеальными. Речь, по существу, идет
омоделях, которыми заменяются
истинные устройства и элементы цепи на
электрических схемах.
23
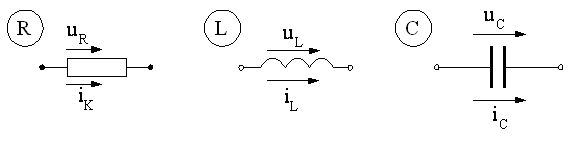
Рис. 2.1
Формально из (2.1) сопротивление Rпредставляет отношение напряжения к
возбуждаемому току. К такому пониманию
сопротивления (не только в отношенииR) при внешне сходных
обстоятельствах неоднократно будем
прибегать в дальнейшем.
И линейные и нелинейные сопротивления
можно характеризовать посредством
вольтамперных характеристик (рис. 2.2),
подобных рассмотренным в теме 1 по
отношению к источникам. У линейного
сопротивления (прямая на рис. 2.2)
зависимость u(i)
– линейная при всех значенияхi, положительных и отрицательных, а у
нелинейного она может иметь любой
непрямолинейный вид. В усилительных и
других устройствах приходится иметь
дело, как отмечалось в теме 1, не только
с абсолютными значениями напряженияuи токаi, но и с их
приращениями. На кривой зависимостиuотiвыбирается
некотораярабочая точкас координатамиU0,I0(рис. 2.2), относительно которой отсчитывают
приращениеΔi=i–I0
и Δu=u–
U0. При
небольшихΔiиΔuи приближенно линейном рабочем участке
кривойu(i)можно считать отношение
24
![]() в некоторых пределах величиной постоянной,
в некоторых пределах величиной постоянной,
не зависящей отuиi.
Определенное таким путем сопротивление![]() называется
называется
динамическим или дифференциальным.
С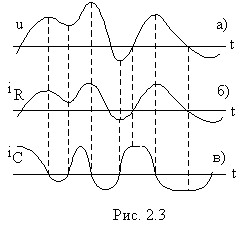 опротивлениеRнаделяется в теории
опротивлениеRнаделяется в теории
(близко к практике) тем свойством, что,
как бы причудливо ни менялось напряжение
на нем в функции времени (рис. 2.3,а), ток
изменяется аналогично, следуя за
напряжением. Кривые напряжения и тока
подобны, знаки уu(t)иi(t)
одинаковы. Вследствие этого, мгновеннаяp(t)
и средняяPмощности
неизменно положительны.
Сопротивление необратимо потребляет
электрическую энергию извне, преобразуя
ее в другие виды энергии: тепловую,
химическую, механическую, излучения и
пр.
Электрическая мощность Pпри постоянном токе определяется в
соответствии с законом Джоуля-Ленца
равенствами:
![]() (2.2)
(2.2)
Отсюда эквивалентное в энергетическом
отношении сопротивление Rпри известной потребляемой объектом
мощностиPнаходится
по формулам
![]() (2.3)
(2.3)
25
где U– напряжение иI– ток, потребляемый объектом.
Сопротивление Rможет
быть полной моделью отдельного физического
устройства (резистора, электрической
лампы) или составной частью модели более
сложных устройств (например, катушки
индуктивности), учитывающей потребление,
потери энергии. Величина сопротивления
может зависеть от частоты сигнала (за
счет поверхностного эффекта), температуры
окружающей среды и других факторов,
если их влияние необходимо учесть в
модели.
В связи с необратимым потреблением
энергии сопротивление R
называютактивным. Иначе обстоит
дело в случаереактивныхэлементов
цепейLиC.
Между зарядом емкостиqи напряжением на нейuCимеет место известное соотношение
![]() (2.4)
(2.4)
Токчерез емкость определяется
скоростью притока или убывания заряда
в ней и выражается равенством
![]() (2.5)
(2.5)
Поскольку iCзависит не от абсолютного значенияuC,
а от производной напряжения на емкости
по времени, при одном и том жеuCток может быть и положительным, и
отрицательным. На рис. 2.3,в показана
зависимость токаiCот времени для того же напряженияu(t)
(рис. 2.3,а), что и в случае сопротивленияR. Обращает на себя
внимание несхожесть кривойiC(t)
сu(t),
а так же сiR(t).
Напряжениена емкости определяется
равенством:
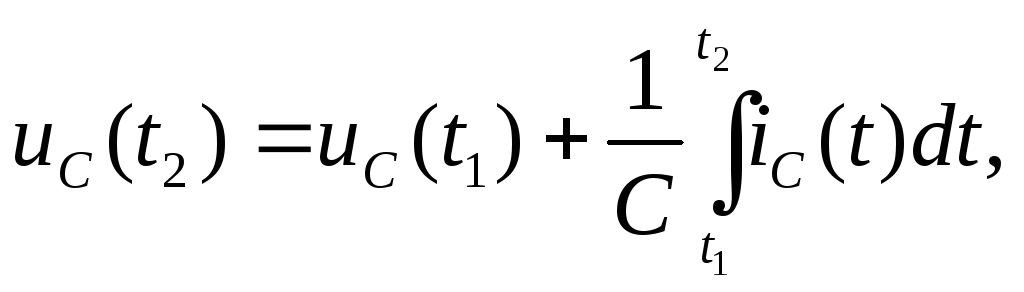 (2.6)
(2.6)
26
где uC(t1)– начальное напряжение на конденсаторе
к моменту начала наблюдения зарядного
процессаt1,
интеграл представляет дополнение к
начальному заряду конденсатора за счет
тока в интервале отt1до рассматриваемого момента времениt2. При нулевом
начальном заряде (напряжении)
![]() .
.
(2.7)
Заключенная в емкости зависящая от t
энергия выражается равенством
![]() (2.8)
(2.8)
В зависимости от функции uC(t)энергия может нарастать или убывать с
течением времени.
Третий элемент – индуктивностьL– дуален по отношению к емкостиC.
Это означает, что выражение для напряжения
на индуктивности может быть получено
из формулы для тока через емкость (2.5)
путем заменыCнаLиuнаi:
![]() (2.9)
(2.9)
Формула (2.9) представляет собой закон
электромагнитной индукции Фарадея –
Максвелла. Ток через индуктивность как
функция от tопределяется
дуальной по отношению к (2.6) формулой
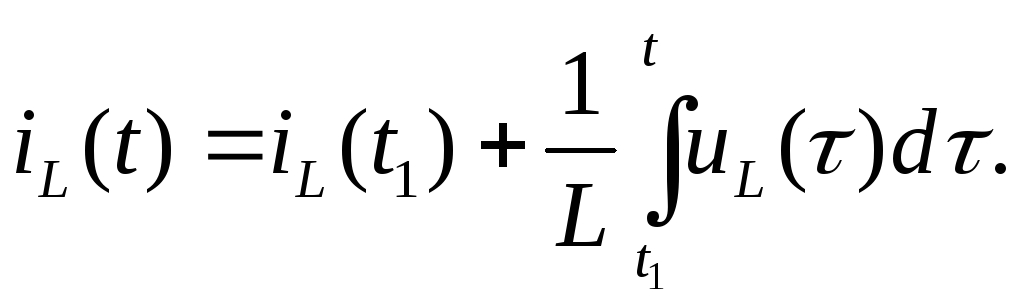 (2.10)
(2.10)
27
При нулевом к моменту t1токеiL(t1)
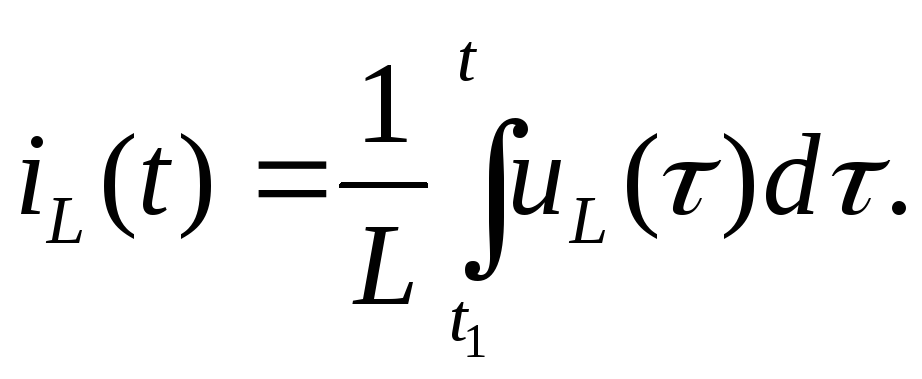 (2.11)
(2.11)
Энергия, заключенная в индуктивности
(в ее электромагнитном поле) в зависимости
от tопределяется
равенством
![]() (2.12)
(2.12)
Реактивные элементы моделируют процессы
накопления энергии электрического поля
в емкости Cили
магнитного поля в индуктивностиL.
Они либо забирают энергию из внешней
цепи, сохраняя и не преобразуя ее в
другие виды энергии, либо возвращают в
цепь ранее накопленную энергию. В первом
случае мгновенная мощность
![]() (2.13)
(2.13)
положительна, а во втором – отрицательна.
Для емкости и индуктивности соответственно
можно записать
![]() (2.14)
(2.14)
а для индуктивности
![]() (2.15)
(2.15)
28
Например, если напряжение емкости
положительно и возрастает, то pC(t)>0и происходит заряд емкости, то есть она
запасает энергию, поступающую за счет
тока внешней цепи (источника).
КОНТРОЛЬНЫЕ ВОПРОСЫ
При ответах на вопросы данной темы и
решении задач потребуется осуществлять
дифференцирование и интегрирование
простейших функций времени, заданных
в графическом виде. Достаточные для
этого справочные данные приведены ниже
в табл. 2.1.
Таблица 2.1.
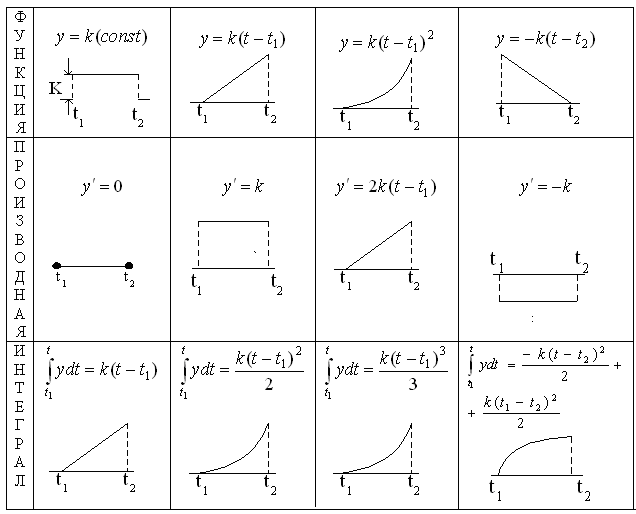
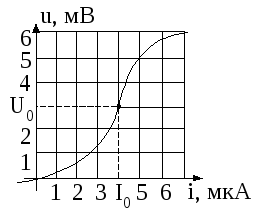
Рис. 2.6
29
1. Какими свойствами наделяется
сопротивление Rв
теории? Какие физические явления,
процессы скрываются за активным
сопротивлением, наносимым на схеме в
условленной форме (в виде удлиненного
прямоугольника (рис. 2.5))? Всегда ли
сопротивлениеRотделимо физически от других элементов
цепи?
2. По какой формуле можно найти сопротивление
Rдля эквивалентной
замены электродвигателя (рис. 2.5) при
напряженииU, развивающем
электрическую мощность в ваттах, равнуюP?
Чему равно сопротивление RAантенныAрадиопередатчика
(рис. 2.6) при излучаемой в пространство
мощности электромагнитных колебанийPA=100
Вт и действующем значении тока на ее
входеI=1А?
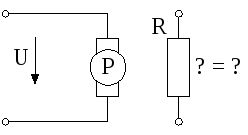
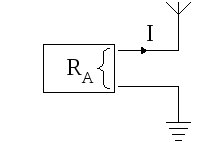
Рис.2.4
Рис. 2.5
3. Какое значение
![]() следует принять в расчетах в случае
следует принять в расчетах в случае
вольтамперной характеристики, приведенной
на рис. 2.6, при рабочей точке с координатамиU0,I0?
Оцените приближенно, чему оно равно
численно?
4. Чем принципиально отличается
сопротивление Rот
реактивных элементов цепейLиC? Почему со-
30
п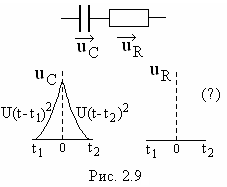 ротивлениеRназывается активным?
ротивлениеRназывается активным?
Каким соотношением связаны напряжениеuR(t)и ток через сопротивлениеiR(t)?
Зависит ли это соотношение от закона
изменения напряжения или тока в функции
времени при линейном сопротивленииR?
Может ли ток через сопротивление быть
отрицательным при положительном
напряжении или наоборот, при однонаправленных
ориентирных стрелках?
5. Какими соотношениями определяются
зависимости тока от напряжения и
напряжения от тока в случае индуктивности
L, емкостиC?
Может ли ток через индуктивность или
емкость быть отрицательным, когда
напряжение положительно и наоборот?
При каких условиях это имеет место?
6. При трапецеидальной форме изменения
напряжения u(t)(рис.2.7,
вверху) какая из функций времениi(t)(1,2 или 3) соответствует току через
сопротивлениеR?
7. Какая из функций времени i(t)на рис. 2.7 соответствует току через
индуктивностьL, через
емкостьC?
8. Истолкуйте зависимость напряжения
на индуктивности uL(t)
и мгновенной мощностиpL(t),
изображенных на рис. 2.8 (б и в) при законе
изменения тока во времени, приведенном
на рис. 2.8,а.
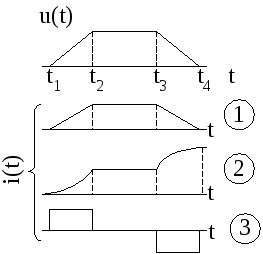
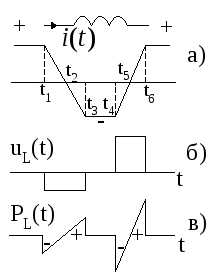
Рис. 2.7 Рис. 2.8
31
Почему мгновенная мощность в одних
интервалах времени положительна, в
других отрицательна? Как это связано
с энергетическими процессами в
индуктивности (накоплением или отдачей
энергии в ее магнитном поле)?
9. Импульс напряжения на емкости в
интервале от t1доt2 имеет
вид двух (нарастающей и спадающей)
ветвей параболы (рис.2.9). Какого вида
напряжение в том же интервале времени
покажет осциллограф, подключенный к
сопротивлениюR,
присоединенному последовательно к
емкости?
ЗАДАЧИ
2.1.(3 балла). Через последовательно
соединенные сопротивлениеR,
индуктивностьLи
емкостьCпротекает
одинаковый, линейно нарастающий ток
(рис. 2.10), определяемый уравнениями:
![]()
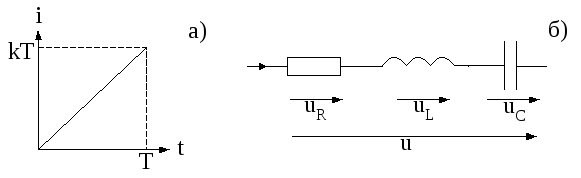
Рис. 2.10
32
Значения k,T,C,RиLпримите равными:
k=100/G А/с,T=G/3
мс,
![]() кОм,
кОм,
![]() нФ,
нФ,
![]() Гн,
Гн,
аргумент синуса – в радианах.
Напишите, используя индивидуальные
данные, уравнения для напряжений uR(t),
uL(t),
uC(t).Рассчитайте и изобразите одну под другой
в одинаковом масштабе времени исходную
функциюi(t)и функцииuR(t),
uL(t),
uC(t).
Построениям кривых должны предшествовать
расчетные таблицы значений функций в
выбранных для вычислений точках.
Количество расчетных точек должно быть
по возможности небольшим, но достаточным
для уверенного графического воспроизведения
исследуемых функций.
Просмотрите кривые. Обратите внимание
на существенно разный характер напряжений
на R,LиCпри одинаковом
токе.
Определите по кривым или рассчитайте
значения напряжений uR(t),
uL(t),
uC(t)
в момент времени
![]()
Сложите полученные таким путем три
напряжения и внесите их сумму в вольтах
(напряжение на трех последовательно
соединенных элементах, рис.2.10,б) в АКОС
для проверки.
2.2.(2 балла). Ток через катушку
индуктивностиLпри
подсоединении ее через сопротивлениеR(рис. 2.11,а) к источнику
постоянной ЭДСe(t)=E(замыкании ключаk) устанавливается
не мгновенно, а возрастает по закону:
![]()
33
где
![]() .
.
Функция эта применительно к некоторымE,R,
иизображена на рис. 2.11,б. Определите:
а) как изменяется напряжение uR(t)на сопротивленииRв
процессе установления тока в интервале
отt=0 доt=5
;
б) по какому закону изменяется напряжение
на индуктивности в том же интервале
времени?
Представьте результаты в аналитическом
и графическом виде в форме построенных
в одном масштабе по оси абсцисс функций
времени e(t),
i(t),
uR(t),
uL(t)при следующих данных:
![]() В,L=(G+1)мГн,R=(5+20N)кОм.
В,L=(G+1)мГн,R=(5+20N)кОм.
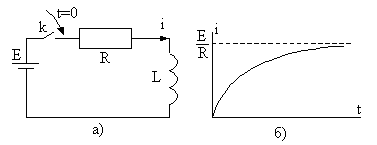
Рис. 2.11
Найдите напряжение на индуктивности
uL(t)=uв момент времениt=7/(N + G).
Внесите величину u
в вольтах для проверки в АКОС.
2.3.(2 балла). Ток через емкостьCпо мере ее заряда от источника постоянной
ЭДСE(рис. 2.12,а) через
сопротивлениеRуменьшается по закону
![]()
Зависимость iC(t)при некоторыхE,R
иCизображена
34
на рис. 2.12,б. Установите, по какому закону
возрастает напряжение на конденсаторе
uC(t)в процессе его заряда. К чему стремитсяuC(t)
с увеличением времени зарядаt.
Изобразите кривуюuC(t)в интервале времени отt=0
доt=3RC.
Определите энергию
![]() ,
,
переданную конденсатору источником по
истечении времени зарядаtпри
![]()
![]() мкФ,
мкФ,
![]() В.
В.
Внесите величину W
в мДж для проверки в АКОС!
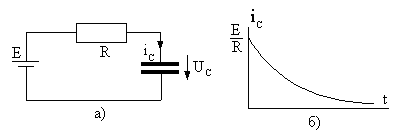
Рис. 2.12
2.4.(2 балла). ТокiL(t)через отклоняющую катушку системы
магнитной развертки телевизора изменяется
по периодическому закону (рис. 2.13);T
– период повторения. Уравнение
процесса в рамках одного периода отt=0
доt=Tможет
быть записано в виде
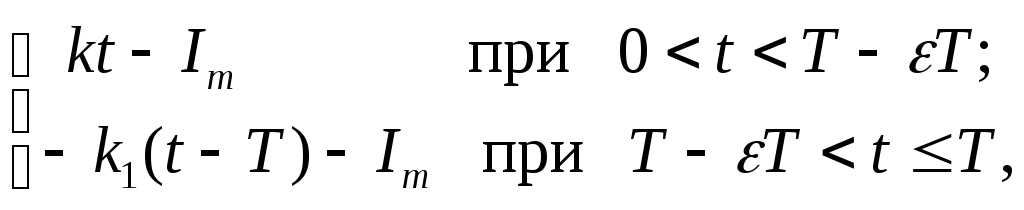
где k,k1– угловые коэффициенты прямых на рис.
2.13, задаваемые равенствами:
35
![]() А/с,
А/с,
![]() А/с.
А/с.
Найдите и изобразите графически, как
изменяется во времени напряжение uL(t)на катушке индуктивности при заданной
кривой изменения тока (рис.2.13) при
значении индуктивности
![]() Гн.
Гн.
Найдите разность между максимальным (положительным) и
минимальным (отрицательным) значениями
напряжения на катушке в интервале
периода.
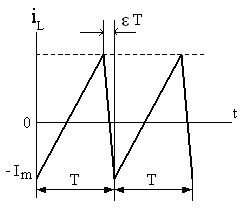
Рис. 2.13
Внесите величину в вольтах в АКОС для проверки.
2.5.(1 балл). Напряжение на конденсатореuC(t),
включенном (рис. 2.14,а) между зажимамиa,bисточника переменной,
так называемойгармонической
(синусоидальной) ЭДС, в интервале
периода изменяется по закону (рис.2.14,б).
Определите, по какому закону в этом
интервале времени изменяется ток iC(t)через конденсатор при следующих данных:
36
![]() В,
В,
![]() нФ,
нФ,![]() мкс.
мкс.
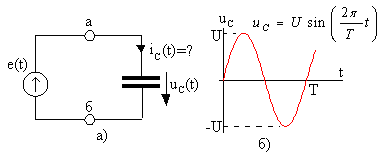
Рис. 2.14
Найти значение
![]() ,
,
мА, в момент времени
![]() мкс, внесите его в АКОС.
мкс, внесите его в АКОС.
2.6.(2 балла). При условиях предыдущей
задачи найдите выражение для мгновенной
мощностиpC(t),
постройте график в том же масштабе, что
и кривая рис. 2.14,б.
Истолкуйте кривую с физической точки
зрения – в каких интервалах времени
происходит накопление энергии в емкости
(заряд), в каких – отдача энергии источнику
(разряд).
Найдите значение мгновенной мощности
![]() в момент времени
в момент времени
![]() мкс.
мкс.
Внесите величину p,
мВт, для проверки в АКОС.
ДЛЯ ПЫТЛИВЫХ
2.1. Какой формы напряжение от источника
u(t)=e(t)следует подать на отклоняющие катушки
телевизионного ки-
37
нескопа (рис. 2.15) в интервале времени от
t1доt2для получения линейно нарастающего
тока (и напряженности магнитного поля
) в этом интервале?
2.2. Чему равно напряжение u1на индуктивностиLв
интервале времени отt1доt2(рис.
2.16), если известно, что напряжение на
емкости в этом интервале времени
возрастает по линейному закону?
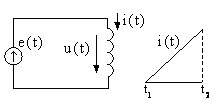
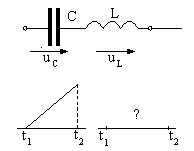
Рис. 2.15.
Рис. 2.16.
ОСНОВНЫЕ ФОРМУЛЫ
|
R |
C |
L |
|
|
|
|
|
|
|
|
|
|
|
|
ЛИТЕРАТУРА
[1, с. 16 – 28]; [2, с. 27 – 38].
38
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Катушка индуктивности: параметры и характеристики.
Индуктивность в цепи постоянного тока
Для лучшего понимания происходящих процессов в катушке, рассмотрим, что происходит в катушке при подаче на нее постоянного напряжения.
 При подключении источника питания к катушке в ней начинает протекать ток, который создает вокруг неё магнитное поле.
При подключении источника питания к катушке в ней начинает протекать ток, который создает вокруг неё магнитное поле.
Магнитные силовые линии поля распространяются через витки катушки наружу пересекая их, и образуют при этом ЭДС самоиндукции.
Эта ЭДС, согласно правилу Ленца, будет препятствовать мгновенному нарастанию тока в катушке. Нарастание тока происходит постепенно, по экспоненциальному закону.
Через небольшой промежуток времени переходной процесс заканчивается, и ток достигает своего нормального значения.
Продолжительность нарастания тока в секундах определяется по формуле:
где L — индуктивность катушки в генри , а R — общее сопротивление всей цепи в омах .
Если, к примеру, индуктивность катушки L=0,6 Г, а сопротивление цепи R=60 Ом, тогда длительность переходного процесса будет равна:
t=3•0,6/60=0,03 сек.
При отключении батареи от катушки индуктивность тоже происходит переходный процесс (такой опыт с первичной обмоткой трансформатора показан на странице «Электромагнетизм» рис.е).
В этом случае силовые магнитные линии будут приближаться к центру катушки опять пересекая ее витки. Создается ЭДС самоиндукции, которая уже направлена не против тока, а (опять же по правилу Ленца) совпадающая с направлением прерванного тока.
Если катушка имеет большую индуктивность (в нашем опыте катушкой является первичная обмотки трансформатора с большим количеством витков и значительным железным сердечником) и через нее протекал большой ток, то тогда ЭДС самоиндукции, появляющая на концах катушки индуктивности, может достигать величины во много раз больше напряжения источника питания.
Это объясняется тем, что при размыкании питающей сети энергия, запасенная в магнитном поле катушки, не исчезает, а превращается в ток.
Напряжение между концами катушки индуктивности может достигать таких значений, которое способно привести к пробою между обмотками, а так же выводу из строя полупроводниковых приборов. Это надо надо учитывать на практике при работе с приборами, имеющие катушки с большой индуктивностью через которые проходит значительный ток.
Индуктивность в цепи переменного тока
Для опытов с постоянным током катушка индуктивности намотана тонким проводом с большим количеством витков.
Это делается для того, чтобы при подаче на нее напряжения с мощного источника питания витки катушки не перегорели, т.к. при намотке витков толстым проводом сопротивление будет маленьким, а ток через нее большой (по закону Ома для постоянного тока I=U/R) и она может сгореть.
Сопротивление катушки индуктивности постоянному току (которое можно измерить мультиметром) называется активным сопротивлением.
Будет иначе, если в цепь катушки подать переменный ток.
При этом магнитное поле катушки индуктивности становится тоже переменным.
На рисунке показано, как меняется магнитное поле при синусоидальном токе. Во время периода магнитное поле меняет как свою силу, так и свое направление по синусоидальному закону. А это значит, что при этом возникает ЭДС самоиндукции, которая, согласно правилу Ленца, будет препятствовать приложенному извне напряжению.

Рассмотрим график происходящих процессов в катушке индуктивности.
При включения катушки в цепь переменного тока в первую четверть периода ( 0º-90º ) на катушку поступает нарастающее напряжение и ее магнитное поле «расширяется», накапливая магнитную энергию. Ток, в этот момент, противодействующей ЭДС самоиндукции, максимальный и противоположный по знаку с напряжением на катушке.
За другую четверть периода ( 90º-180º ), когда напряжение на катушке индуктивности уменьшается, магнитное поле «сворачивается», индуцируя ЭДС самоиндукции, которое совпадает с направлением тока. Этот ток самоиндукции в катушке старается уже «помочь» уменьшающему переменному току сохранить достигнутый большой магнитный поток. В этот полупериод катушка индуктивности уже не потребляет, а отдает энергию обратно генератору.
Следовательно, происходит постоянный обмен энергий между генератором и катушкой. А это означает, что средняя мощность потребления катушки равна нулю.
Благодаря разнице фаз тока и напряжения в 90º, катушка индуктивности имеет реактивную мощность и, соответственно, реактивное сопротивление , как и конденсатор. Разница лишь в том, что в катушке индуктивности напряжение опережает ток, а в конденсаторе — наоборот.
Реактивное (индуктивное) сопротивление катушки, в отличии от ее активного сопротивления , не вызывает безвозвратных потерь энергии.
Допустим, возьмем идеальную катушку , в которой не учитываются сопротивления провода и другие потери.
Тогда катушка индуктивности окажет переменному напряжению индуктивное сопротивление XL ,которое измеряется в омах и вычисляется по формуле:

где f — частота тока в герцах (Гц), а L — индуктивность катушки в генри (Г).
Отсюда видно, что величина индуктивного сопротивления катушки зависит от частоты и индуктивности. Чем выше частота тока и больше индуктивность катушки, тем больше индуктивное сопротивление.
К примеру, найдем индуктивное сопротивление катушки индуктивностью 5Г на частоте 50Гц.
XL=2π•50•5=1570 Ом.
На частоте 1кГц эта катушка будет иметь индуктивное сопротивление 31кОм, а на 1МГц — 31МОм. На графике показана зависимость упомянутой катушки от частоты.
Теперь, зная значение индуктивного сопротивления, можно записать закон Ома при переменном токе через катушку: 
Например,найдем ток, который протекает через идеальную катушку с индуктивностью L=500 мкГ, если ее подключить к переменному напряжению U=0,4 В и частотой f=500 кГц.
I= 0,4/2•3,14•5•10 3 •500•10 -6 =0,25 мА
В реальной катушке нужно учитывать не только индуктивное сопротивление, но и сопротивление потерь Rпот.
На низких частотах Rпот равно только сопротивлению провода катушки. При повышении частоты на катушке сопротивление потерь будет возрастать за счет появления других потерь (вихревые токи, поверхностный эффект проводника и т.д.) (рис. а ).
Поэтому полное сопротивление катушки индуктивности переменному току на средних частотах равно: 
и называется импедансом.
На высоких частотах начинает оказывать еще влияние cобственная (паразитная) емкость катушки Спараз , которая шунтирует индуктивность (рис. b ).
Основными параметрами высокочастотных катушек индуктивности являются индуктивность, добротность и собственная емкость .
Индуктивность зависит от количества витков, размера катушки и наличия ферромагнитного сердечника. Чем больше намотано витков на катушке, тем больше ее индуктивность. А наличие сердечника увеличит индуктивность катушки.
Добротность определяет качество катушки индуктивности и равна отношению индукнивного сопротивления к сопротивлению потерь: 
Чем больше добротность, тем качественнее катушка. Катушкой хорошего качества считается катушка с добротностью от 50 до 200.
Чтобы достигнуть такого качества используют следующие средства:
— применением сердечников, при которых увеличивается индуктивность при меньшем числе витков катушки (т.е. уменьшается сопротивление провода);
— увеличение толщины провода, что, правда, увеличит габариты катушки;
— в диапазоне длинных и средних волн применение провода литцендрат, который состоит из определенного количества проволочек изолированных друг от друга.
Собственная емкость катушки индуктивности обусловлена емкостью обмотки и является нежелательной. Для ее уменьшения применяются различные способы намотки катушки.
Одним из способов является перекрестная намотка типа «универсаль» (рис. c ). Так же применяется намотка витков не плотно друг к другу, а на определенном расстоянии с принудительным шагом)(рис. d,e ).
Источник
№20 Самоиндукция. Индуктивность. Синусоидальный ток в индуктивности.
Если в катушке, изображенной на рис. 20.1, магнитное поле создается собственным током i, то магнитный поток называется потоком самоиндукции и обозначается ФL, а индуцируемая в катушке ЭДС еL – ЭДС самоиндукции. В соответствии с формулой (20.1) она равна:

где ψ – потокосцепление самоиндукции, величина, пропорциональная протекающему по катушке току: ψ = Li.
Коэффициент пропорциональности L между потокосцеплением и током называется собственной индуктивностью или просто индуктивностью катушки (контура). Она зависит от формы и размеров катушки, а также от магнитной проницаемости сердечника. Ее размерность В x с/А=Ом x с. Эта единица измерения называется генри (Гн).
Подставляя последнее выражение в (2.15) и полагая L = const, получаем следующую формулу, определяющую ЭДС самоиндукции:

На рис. 2.18 показано изображение индуктивности на электрической схеме; uL – напряжение на зажимах катушки, обусловленное электродвижущей силой самоиндукции, или другими словами, напряжение, наведенное в катушке собственным переменным магнитным полем.

Рис. 2.18 — Обозначение индуктивности
Все три стрелки на схеме (i, eL, uL) принято направлять в одну сторону. Раньше мы видели, что при одинаковых направлениях стрелок напряжения и ЭДС они имеют разные знаки. Поэтому:

Знак минус в правой части формулы (2.16) обусловлен принципом Ленца, определяющим направление индуцированной ЭДС. В рассматриваемом случае он может быть сформулирован следующим образом:
ЭДС самоиндукции направлена так, что своим действием препятствует причине, вызвавшей ее появление.
Причина появления ЭДС самоиндукции – изменение тока. Поэтому при возрастании тока она направлена ему навстречу, при уменьшении тока – в одну с ним сторону.
Препятствуя изменению тока, ЭДС самоиндукции оказывает ему сопротивление, которое называется индуктивным и обозначается хL. В соответствии с формулой (2.16) его величина определяется индуктивностью и скоростью изменения тока, т.е. частотой. Формула, определяющая индуктивное сопротивление, имеет вид:

В цепях постоянного тока такого понятия мы не встречали, так как при постоянных магнитных полях ЭДС самоиндукции не возникает. Пусть ток, протекающий по индуктивности, определяется выражением (2.13). Тогда напряжение на ее зажимах, в соответствии с формулой (2.17), равно:

Это – мгновенное значение напряжения. Его амплитуда равна:

Аналогичное выражение получается (после деления на √2) и для действующих значений:


где Bl — индуктивная проводимость.

Запишем соответствующие формулы в символической форме:




Аналогично для действующих значений

Уравнения, связывающие напряжение и ток в индуктивности, как в вещественных, так и в комплексных числах, представляют собой закон Ома для индуктивности.
Начальная фаза напряжения больше начальной фазы тока на 90° . В индуктивности ток отстает от напряжения на четверть периода. Выражение закона Ома, записанное в символическое форме, указывает на этот сдвиг фаз. Вспомним, что умножение вектора на j приводит к его повороту на угол 90° против часовой стрелки.

Рис. 2.19 — Векторная диаграмма напряжения и тока в индуктивности
Согласно уравнениям (2.18) UL получается путем умножения произведения IxL на j, в результате чего вектор UL оказывается повернутым относительно вектора I.
Пример 2.5. Мгновенное значение напряжения на индуктивности определяется выражением uL = 200 sin(ωt+60°)В. Записать выражение мгновенного значения тока, если L = 63,67 мГн, а частота питающего напряжения f = 50 Гц. Построить векторные диаграммы напряжения и тока.
Решение. При частоте f = 50 Гц циклическая частота ω = 314 с-1, и индуктивное сопротивление xL = ωL = 20 Ом. Амплитуда тока равна:

Так как в индуктивности ток отстает от напряжения на четверть периода, его начальная фаза меньше начальной фазы напряжения на 90° : ψi = ψu – 90° = 60–90–30°.
Итак, i = 10sin (ωt–30°). Векторная диаграмма показана на рис. 2.20.
Источник
Индуктивность катушки, её назначение, характеристики, формулы
 Индуктивность — это физическая величина, характеризующая магнитные свойства электрической цепи. В некоторых источниках её называют коэффициентом самоиндукции, так как она зависит от текущего в замкнутом контуре тока и создаваемого им магнитного потока. Для определения величины этого показателя применяют несколько вариантов расчёта, которые основываются на различных физических параметрах.
Индуктивность — это физическая величина, характеризующая магнитные свойства электрической цепи. В некоторых источниках её называют коэффициентом самоиндукции, так как она зависит от текущего в замкнутом контуре тока и создаваемого им магнитного потока. Для определения величины этого показателя применяют несколько вариантов расчёта, которые основываются на различных физических параметрах.
Общие сведения
Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.
Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).
 Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.
Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.
Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.
Среди основных свойств индуктивности выделяются:
- Величина параметра никогда не может быть меньше нуля.
- Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.
Способы расчёта
Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.
Через силу тока
Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:
- L — индуктивность контура (в генри);
- Ф — величина магнитного потока, измеряемого в веберах;
- I — сила тока в катушке (в амперах).
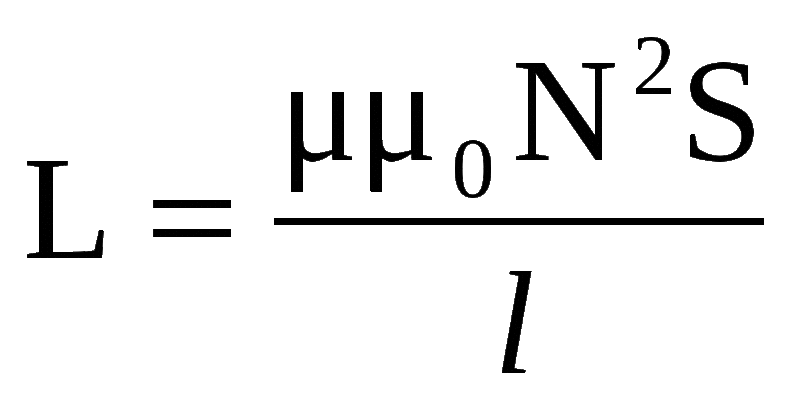
Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.
Соленоид конечной длины
Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:
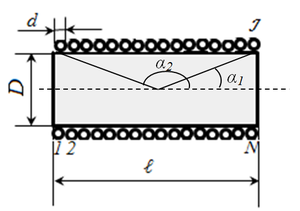 µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);- N — количество витков в катушке;
- S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
- l — длина соленоида в метрах.
Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:
- W — энергия магнитного потока, измеряемая в джоулях;
- I — сила тока в амперах.
Катушка с тороидальным сердечником
В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:
- N — число витков катушки;
- µ — относительная магнитная проницаемость;
- µ0 — магнитная постоянная;
- S — площадь сечения сердечника;
- π — математическая постоянная, равная 3,14;
- r — средний радиус тора.

Длинный проводник
Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:
 l — длина проводника в метрах;
l — длина проводника в метрах;- r — радиус сечения провода, измеряемый в метрах;
- µ0 — магнитная постоянная;
- µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
- µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
- π — число Пи;
- ln — обозначение логарифма.
Варианты измерения
Индуктивность катушки в физике определяется путём выполнения вычислений. Однако эту величину можно не только рассчитать, но и измерить. Делается это при помощи прямого или косвенного метода.
Прямой метод
Для измерения индуктивности катушки этим методом необходимо использовать специальные мостовые или прямопоказывающие устройства. С их помощью можно получить максимально точные данные, которые помогут выбрать требуемую катушку для схемы.
Порядок проведения измерений включает в себя следующие этапы:
- К прямопоказывающему приспособлению подключают катушку.
- После этого постепенно изменяют диапазоны измерений. Это делается до тех пор, пока получаемый результат не будет находиться примерно в середине интервала.
- Полученный результат фиксируют и высчитывают с учётом цены деления прибора, а также коэффициента, соответствующего положению переключателя.
Прямой метод измерения можно применить и при определении индуктивности с помощью мостового приспособления. Оно имеет более точную шкалу, поэтому позволяет получить достоверные данные.
Измерение выполняют путём проведения таких действий:
- Включённый мостовой прибор подсоединяют к катушке, индуктивность которой необходимо определить.
- Аналогично прямопоказывающему устройству проводят переключение интервалов измерений.
- После каждого такого действия ручку регулятора балансировки моста поочерёдно перемещают в одно и другое предельное положение.
- Как только удалось определить диапазон, в котором мост будет сбалансирован, можно выполнять дальнейшие действия.
- На следующем этапе измерений выполняется постепенное перемещение стрелочного индикатора.
- После того как в динамике прибора исчезнет звук, необходимо зафиксировать показатели.
- Затем их рассчитывают в соответствии с ценой деления шкалы и предусмотренным коэффициентом.
Косвенное определение
Для того чтобы измерить коэффициент самоиндукции, необходимо провести несколько подготовительных мероприятий. В первую очередь нужно собрать измерительную цепь по стандартной схеме, а также подготовить все необходимые приспособления (генератор синусоидального напряжения, частотомер, а также миллиамперметр и вольтметр, рассчитанные на переменный ток).
Порядок определения параметра:
- К выходу генератора параллельно подключают вольтметр. Он должен быть переключён в режим, при котором верхнее предельное значение будет соответствовать напряжению в 3−5 вольт.
 Аналогично подсоединяют и частотомер.
Аналогично подсоединяют и частотомер.- Отдельно собирают вторую цепь. В ней последовательно соединяют миллиамперметр и катушку, индуктивность которой нужно определить.
- Затем обе цепи подключают параллельно друг к другу.
- Подключённый генератор устанавливают в режим выработки синусоидального напряжения.
- Путём изменения частоты добиваются такой работы приборов, при которой вольтметр будет показывать примерно 2 вольта. При этом сила тока на миллиамперметре будет постепенно уменьшаться.
- После этого ручку частотомера перемещают в положение, соответствующее частоте измерений.
- Как только эти действия будут выполнены, можно фиксировать значения.
Полученные данные переводятся в СИ, а затем выполняются все необходимые расчёты. Первым делом определяется индуктивное сопротивление. Для этого значения приборов подставляются в следующую зависимость: X=U/I, где U — напряжение, а I — сила тока. Результат расчётов будет выражен в омах.
После этого вычисляется индуктивность по формуле L=X/2 πF. В ней используются такие условные обозначения:
- X — индуктивное сопротивление;
- π — математическая постоянная (примерно 3,14);
- F — частота в герцах, при которой проводились измерения.
Индуктивность — это важный физический параметр, позволяющий определить магнитные свойства электроцепи. При точном его измерении и правильном проведении предусмотренных расчётов можно получить достоверные данные, которые понадобятся при выборе катушки.
Источник
Индуктивность
Время на прочтение
9 мин
Количество просмотров 19K
Выше мы рассматривали два основных понятия в электротехнике — идеальный генератор напряжения и идеальный генератор тока.
Идеальный генератор напряжения выдает заданное напряжения U (давление в водопроводной аналогии) на любой нагрузке (сопротивлении внешней цепи).
При этом в соответствии с законом Ома I=U/R, даже если R стремится к нулю, а ток возрастает до бесконечности.
Внутренне сопротивление идеального генератора напряжения равно 0.Идеальный генератор тока выдает заданный ток I (поток в водопроводной аналогии), даже если сопротивление внешней цепи стремится к бесконечности. Напряжение на нагрузке при этом также стремится к бесконечности U=I*R.
Внутреннее сопротивление идеального генератора тока равно ∞.
Тут можно увидеть определенную симметрию, дуализм.
Мы рассматривали конденсатор С который может накапливать заряд (потому и называется — емкость) С=Q/U. Чем больше емкость, тем медленнее растет напряжение (давление) при закачке в конденсатор заряда U=Q/C.
Если емкость заряда очень большая (стремится к бесконечности), то такой конденсатор бесконечной емкости будет являться идеальным генератором напряжения. Он никогда не разрядится и при этом может выдать ток любой величины, и напряжение на нем будет оставаться постоянным.
Симметричным (дуальным) к конденсатору элементом будет являться индуктивность. Индуктивность обозначается буквой L (см схему ниже).
Обычно сам электронный компонент называется катушка индуктивности, а его параметр — индуктивность L.

Если конденсатор является генератором напряжения, то индуктивность является генератором тока. Индуктивность стремиться поддерживать ток в цепи постоянным, то есть препятствует изменению тока в цепи.
Индуктивность бесконечной величины является идеальным генератором тока, то есть будет бесконечно гнать заданный ток I независимо от сопротивления нагрузки.
Как хорошо сказано в wiki – “При сопоставлении силы электрического тока со скоростью в механике и электрической индуктивности с массой в механике ЭДС самоиндукции сходна с силой инерции.”
Это похоже как если вы подойдете к стоящей на рельсах вагонетке и станете ее толкать (приложите к ней силу). Вагонетка начнет медленно разгоняться и «ток все быстрее и быстрее побежит по проводам». А потом попробуйте вагонетку тормозить и она будет медленно останавливаться.
Так и в индуктивности, после подачи напряжения ток будет постепенно расти (вагонетка разгоняется), а при подаче напряжения другой полярности — постепенно уменьшаться (вагонетка тормозится).
Отсюда следует вывод «
Поезд мгновенно остановить нельзя!»
«Ток в индуктивности мгновенно остановить нельзя!»
То есть даже если щелкнуть выключателем S4 на схеме и разомкнуть цепь, ток в первый момент после этого будет продолжать идти! На практике это приводит к тому, что в момент размыкания контактов в выключателе между ними будет проскакивать искра.
Сопротивление при размыкании контактов увеличивается до бесконечности (в реальности до очень больших величин) и протекающий ток создаст на этом сопротивлении напряжение очень большой величины, так что воздушный промежуток между контактами будет пробит.
В водопроводной аналогии этому явлению можно сопоставить гидравлический удар, когда масса воды в водопроводе набирает скорость, и при резком закрытии крана вода, продолжая двигаться по инерции, создает высокое давление, что может привести к разрыву трубы.
Причины по которой индуктивность имеет такие свойства (поддержание тока в цепи) хорошо описаны в wiki –
https://ru.wikipedia.org/wiki/Самоиндукция
“При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это явление называется самоиндукцией. Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока.”
По отношению к конденсатору , основным отличием индуктивности, если говорить простыми словами, является то, что конденсатор пропускает переменный ток и не пропускает постоянный, а индуктивность наоборот — пропускает постоянный ток и не пропускает переменный.
Тут есть некий момент — постоянный ток это ток, который не меняется со временем, то, что называется «постоянная составляющая» частотой равной 0 Гц. Ее конденсатор не пропускает. Совсем.
А вот индуктивность совсем не пропускает переменный ток бесконечной частоты. А просто переменный ток любой конечной частоты немножко пропускает.
Но к понятию напряжения переменного тока мы вернемся позже.
Рассмотрим цепь на рис. 13 – подключение катушки индуктивности к генератору напряжения.
Ниже представлен график тока в индуктивности при подаче на нее постоянного напряжения от генератора напряжения.
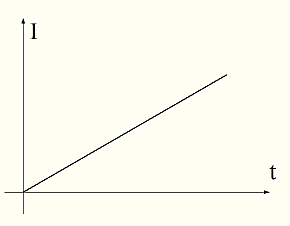
При подаче на индуктивность постоянного напряжения ток в ней линейно возрастает со временем.
Мы помним аналогичную картину для конденсатора.
Напряжение на конденсаторе линейно возрастает при его заряде постоянным током.
А что будет, если запитать индуктивность от генератора тока?

Ну тут из серии «кто кого заборет — слон или кит».
Попробуйте проанализировать работу схемы (hint – вообще схема изображена с ошибкой. В чем она заключается? Как нарисовать схему правильно?)
Цепи, содержащие конденсатор и индуктивность
Как было отмечено выше, индуктивность в электротехнике играет ту же роль, что масса в механике. А что является аналогом конденсатора в механике? Конденсатор является генератором напряжения, то есть создает силу, которая двигает поток заряда по проводам. Выше мы приводили аналог конденсатора в виде водонапорной башни, которая заполняется водой (зарядом) и давление (напряжение) в ней увеличивается.
Но можно также представить конденсатор в виде пружины — при заряде пружина сжимается и сила сжатия (напряжение) увеличивается. Емкость в этом случае величина обратная жесткости пружины. Чем пружина жестче, тем быстрее возрастает сила при сжатии. То есть соединение конденсатора и индуктивности эквивалентно вагонетке закрепленной на пружине. )
Что же будет происходить, если конденсатор соединить с индуктивностью, например как в схеме на рис. 16

Пусть конденсатор С заряжен до напряжения U. Ключ S2 замыкается и в цепи начинает течь ток. Это эквивалентно тому, как если бы мы сжали пружину и затем в какой-то момент отпустили (замкнули ключ S2).
В первый момент после замыкания ключа ток в цепи будет равен 0, так как индуктивность препятствует изменению тока. К вагонетке приложили силу, но в первый момент времени ее скорость равна 0. Затем ток начинает возрастать (вагонетка разгоняется). Пружина разжимается все больше и больше, скорость вагонетки (ток) растет и в какой-то момент времени пружина оказывается не сжата. Конденсатор разрядился до 0. Но. Мы помним что «ток в индуктивности мгновенно остановить нельзя!» Вагонетка разогналась и даже если мы не будем ее толкать, она будет двигаться по инерции. То есть индуктивность будет поддерживать ток и при этом заряжать конденсатор, но уже в другой полярности – заряды теперь будут скапливаться на другой обкладке конденсатора. Растущее напряжение противоположного знака на конденсаторе будет препятствовать движению зарядов, и в конце концов ток в цепи станет равным нулю. Но при этом конденсатор уже зарядился напряжением U другой полярности!
То есть цепь пришла в состояние когда конденсатор заряжен, ток в ней равен нулю.
Хм.. но это то же состояние, с которого мы начали, только полярность напряжения противоположная. Следовательно процесс повторится, только ток потечет уже в другую сторону и система вернется в исходное состояние. Вагонетка поедет обратно, проедет положение равновесия и по инерции снова сожмет пружину.
Возникнет колебательный процесс. То есть вагонетка на пружине так и будет кататься туда-сюда и в отсутствие потерь энергии (трения) этот процесс будет длиться бесконечно.
Таким образом соединение конденсатора с индуктивностью образует колебательное звено. Такие звенья широко используются в электротехнике для создания генераторов и фильтров напряжения переменного тока.
Понятие переменного тока рассмотрим в следующей статье.
UPD.
Поскольку возник диспут экспоненциально ли растет ток при подключении катушки индуктивности к генератору напряжения или линейно, скажу еще пару слов по этому вопросу.
Откуда же берется экспонента роста тока в схеме на рис.13?
Ответ- ниоткуда. Ее там нет. Ток растет линейно и зависимость тока от напряжения описывается формулой
![]()
ЭДС самоиндукции в цепи прямо пропорциональна скорости изменения силы тока в этой цепи.
Чтобы обеспечить U=const (а U – это производная от тока в катушке), ток должен линейно расти.
А откуда тогда вообще зашел разговор об экспоненте? А зашел он потому, что ток линейно растет только в идеальном случае — в схеме с идеальным генератором напряжения (бесконечной мощности и с нулевым внутренним сопротивлением) и идеальной индуктивностью (с нулевым внутренним сопротивлением).
В реальном случае с учетом внутреннего сопротивления схема будет выглядеть так.
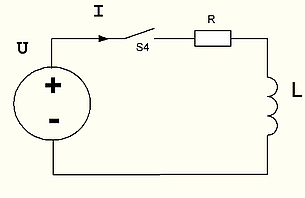
На схеме рис.17 R символизирует собой внутреннее сопротивление генератора и катушки индуктивности. (они все равно включены последовательно, поэтому можно обойтись одним R, как суммой этих сопротивлений)
В этом случае процесс разворачивается следующим образом. При замыкании ключа S4 цепь замкнется и должен был бы пойти ток. Однако, катушка индуктивности препятствует изменению тока, и в первый момент времени после замыкания ключа ток останется равным 0! По сути дела катушка в этот момент представляет собой разрыв цепи с бесконечным сопротивлением. Поэтому напряжение U будет приложено к катушке целиком. Можно и по другому подойти – Ur=I*R. Падение напряжения на резисторе равно I*R, I у нас равен 0, поэтому напряжение на резисторе тоже равно 0, и к катушке будет приложено полное напряжение U. Дальше ток в катушке будет расти. В области 0 линейно кстати (см рис 19 «Переход Суворова через Альпы» «Экспонента проходит через 0 под углом 45 градусов»). Ток будет расти и падение напряжения на резисторе тоже будет расти. А на катушке соответственно падать, потому что часть напряжения будет забирать на себя резистор. Поэтому со временем линейность роста тока в цепи будет нарушаться. Когда падение напряжения на резисторе I*R сравняется с напряжением генератора U рост тока прекратится совсем, потому что напряжение на катушке будет равно 0 (все напряжение будет падать на резисторе).
Вот в этом случае и получится такой экспоненциальный график роста тока в индуктивности.
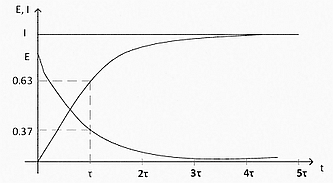

зы. В интернете столько разнообразной ереси на тему катушек индуктивности. Просто диву даешься.
«Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение. Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения.»
Ну.. поскольку про резистор в цепи ничего не сказано, то не на короткий промежуток, а пока входное напряжение не будет снято. Вторая часть звучит бредово, но направление верное — ток с цепи растет от нуля до.. без резистора до бесконечности, с резистором до I=Uвх/R.
Предположим, что обычная катушка индуктивности подключена к источнику напряжения через ключ. При замыкании ключа на индуктивность подается напряжение, вызывающее быстрое изменение протекающего через нее тока. Когда приложенное напряжение увеличивается от нуля до пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение, противоположное по полярности приложенному напряжению. Индуцированное напряжение при подаче питания на катушку индуктивности называется обратной ЭДС и определяется по формуле 1:
VL = – L*(di/dt), (1)
где:
VL – напряжение (обратная ЭДС), индуцированная на катушке;
L – индуктивность катушки;
di/dt – скорость изменения тока во времени. Видимо здесь попытались описать начальный момент возникновения ЭДС самоиндукции, но получилась ерунда. Говорить, что «индуцированное напряжение противоположно по полярности приложенному напряжению» это то же самое, что “падение напряжения на резисторе противоположно по полярности приложенному напряжению.” Ага, точно, приложенное напряжение сложили с падением напряжения и после резистора получили 0. Так и есть, лол.
«ЭДС самоиндукции» в катушке это аналог «падения напряжения» на резисторе. Только в резисторе электрическая энергия рассеивается, переходит в тепло, а в индуктивности — накапливается, переходит в энергию магнитного поля. В водопроводной аналогии индуктивность это такая турбинка, вставленная в водопроводную трубу, и которая имеет момент инерции. Турбинка пропускает воду только когда вращается. И вот крантель открыли, давление к турбинке приложили, она начала вращаться и пошел ток дальше по трубе. И чем быстрее турбинка вращается, тем больше ее пропускная способность. Турбинка раскручивается, ток возрастает и так до бесконечности. Это если нет потерь энергии — резистора. А если есть резистор (трение), то часть давления расходуется на преодоление трения. И когда вся входная энергия будет расходоваться на трение, турбинка перестанет ускоряться и ток достигнет максимальной величины.
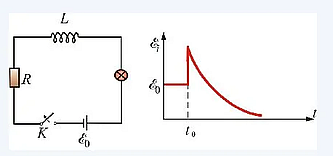
Картинка неправильная. В правильном варианте при отключении источника, подключался резистор и цепь оставалась замкнутой.
Рассмотрим следующую цепь
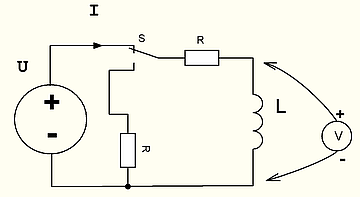
Вопрос на засыпку: Чему будет равно напряжение на индуктивности в первый момент после переключения ключа S из верхнего положения в нижнее?
Hint: Не надо выносить себе мозг, пытаясь сообразить с каким там знаком возникнет ЭДС самоиндукции и что с ней будет дальше. Надо применять простое правило:
Ток в индуктивности в первый момент времени после переключения сохраняется неизменным.
Дальше применять закон Ома.
Переменный электрический ток:
До сих пор рассматривались электрические цепи, содержащие в различных сочетаниях резисторы, конденсаторы и катушки, с источником постоянного тока либо без него. Теперь рассмотрим подключение таких цепей к источнику переменного тока.
Пусть источник тока создает переменное гармоническое напряжение (рис. 194)

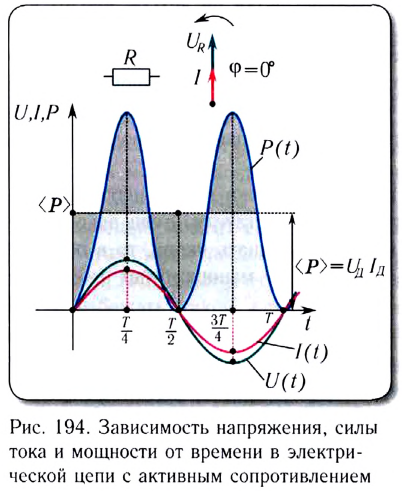
Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
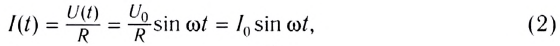
где 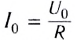 — амплитудное значение силы тока в цепи.
— амплитудное значение силы тока в цепи.
Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.
Величины 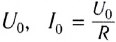 называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.
называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.
Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность 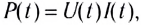 которая, в отличие от цепей постоянного тока, изменяется с течением времени.
которая, в отличие от цепей постоянного тока, изменяется с течением времени.
С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде
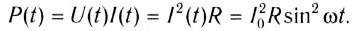
Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно.
Перепишем формулу для мощности по-другому:
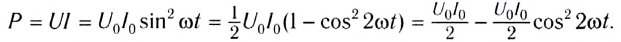
Первое слагаемое не зависит от времени. Второе слагаемое — переменная составляющая — функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (см. рис. 194).
Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле

Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.
Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Поскольку для постоянного тока 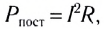 то с учетом ранее полученного выражения для среднего значения мощности переменного тока действующее значение силы тока
то с учетом ранее полученного выражения для среднего значения мощности переменного тока действующее значение силы тока

Аналогично можно ввести действующее значение и для напряжения

Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
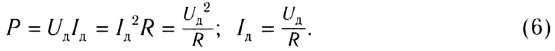
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе (см. рис. 194).
Таким образом, резисторы оказывают сопротивление как постоянному, так и переменному току, при этом в обоих случаях в них происходит превращение электрической энергии во внутреннюю. Вследствие этого сопротивление резисторов R получило название активного или омического сопротивления.
Катушка индуктивности в цепях переменного тока
Реальный соленоид (катушка индуктивности) обладает активным сопротивлением R и индуктивностью L. В цепях постоянного тока главную роль играет его сопротивление R, тогда как в цепях переменного тока — его индуктивность L.
Рассмотрим физические процессы, происходящие в идеальной катушке, у которой отсутствует активное сопротивление (R=0), при включении ее в цепь переменного тока.
В катушке индуктивностью L переменный ток 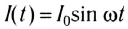 вызывает появление ЭДС самоиндукции:
вызывает появление ЭДС самоиндукции:
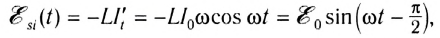 где
где 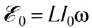 — амплитудное значение ЭДС самоиндукции (рис. 195).
— амплитудное значение ЭДС самоиндукции (рис. 195).
При возрастании силы тока ЭДС самоиндукции согласно правилу Ленца будет препятствовать его увеличению. Для идеальной катушки, активное сопротивление которой равно нулю (R=0), согласно закону Ома для полной цепи 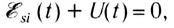 где U(t) напряжение на концах катушки.
где U(t) напряжение на концах катушки.
Следовательно, в любой момент времени внешнее напряжение на концах катушки равно по модулю и противоположно по знаку ЭДС самоиндукции в катушке:
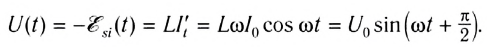
Сравнивая выражения для мгновенных значений силы тока I(t) и напряжения U(t), видим, что для их амплитудных значений можно записать закон Ома в виде 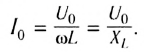
Величину 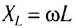 называют индуктивным сопротивлением катушки. Оно пропорционально индуктивности катушки и частоте переменного тока в цепи
называют индуктивным сопротивлением катушки. Оно пропорционально индуктивности катушки и частоте переменного тока в цепи 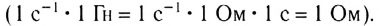
Обратите внимание на то, что фазы колебаний силы тока и напряжения не совпадают. Наличие сдвига фаз означает, что мгновенное значение напряжения U на катушке индуктивности опережает мгновенное значение силы I переменного тока по фазе на 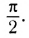 Такой сдвиг фаз между колебаниями силы тока и напряжения характерен в целом для цепей переменного тока, содержащих элементы, обладающие индуктивностью.
Такой сдвиг фаз между колебаниями силы тока и напряжения характерен в целом для цепей переменного тока, содержащих элементы, обладающие индуктивностью.
Закон Ома для цепи переменного тока, содержащей только катушку индуктивности, выполняется и для действующих значении силы тока 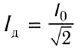 и напряжения
и напряжения 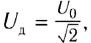 так как
так как 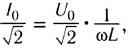 тогда
тогда 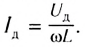
Таким образом, если в цепь переменного тока включена катушка индуктивности, то закон Ома выполняется для амплитудных и действующих значений силы тока и напряжения, но не выполняется для их мгновенных значений, так как мгновенные значения силы тока и напряжения не совпадают по фазе (см. рис. 195).
Мгновенная мощность, потребляемая катушкой индуктивности от источника переменного тока, определяется по формуле
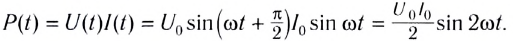
Поскольку среднее за период значение функции 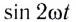 равно нулю, то и средняя мощность за период также равна нулю:
равно нулю, то и средняя мощность за период также равна нулю:
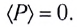
Как видно из рисунка 195, цепь с идеальной катушкой индуктивности в течение первой и третьей четвертей периода работает в режиме потребителя, запасая энергию магнитного поля 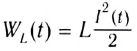 в катушке, а в течение второй и четвертой — в режиме генератора, возвращая источнику запасенную энергию.
в катушке, а в течение второй и четвертой — в режиме генератора, возвращая источнику запасенную энергию.
Поскольку потерь энергии в этом случае не происходит, то индуктивное сопротивление называют реактивным.
- Конденсатор в цепях переменного тока
- Электрический ток в различных средах
- Электромагнитная индукция в физике
- Правило Ленца для электромагнитной индукции
- Потенциал электрического поля
- Постоянный электрический ток
- Законы постоянного тока
- Переменный электрический ток
