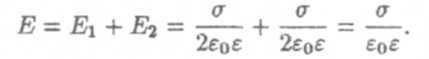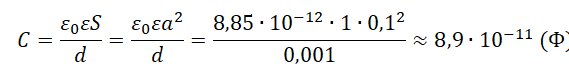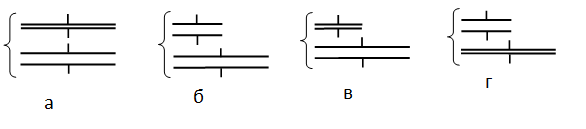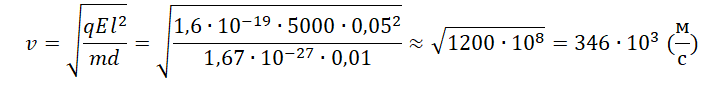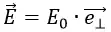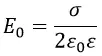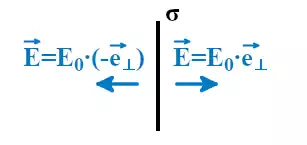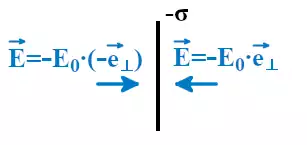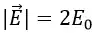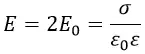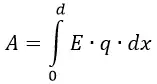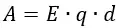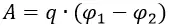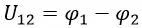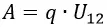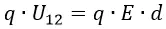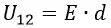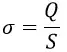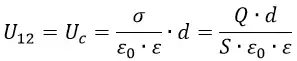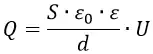Как найти напряжение между двумя пластинами

ДОМОСТРОЙСантехника и строительство

Если размеры пластин значительно превосходят расстояние между ними, то электрическое поле каждой из пластин можно считать близким к полю бесконечной равномерно заряженной плоскости.

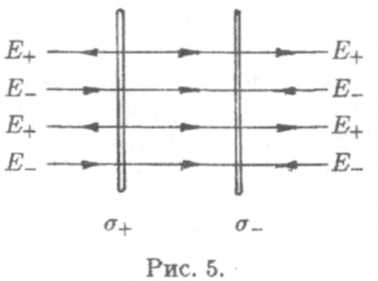
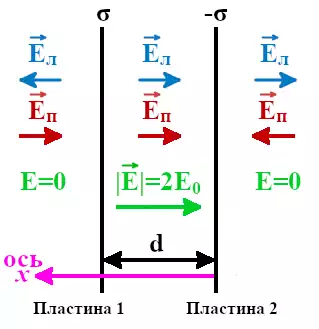
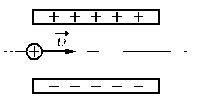
На рис. 5 показано поле системы разноименно заряженных плоскостей. Между пластинами:

Так как σ = q/S, то напряженность поля между пластинами

Все эти выражения справедливы для больших заряженных пластин, когда напряженность определяется в точке, расположенной далеко от краев.

Дата добавления: 2015-08-11 ; просмотров: 2800 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Решить предыдущую задачу при условии, что заряд второй пластины отрицательный.

СЗТУ, 2006 год, методичка. Задачи 311 и 312.

версия для печати
Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Изображаем пластины, так как σ > 0, то заряды на платинах положительные. Изображаем линии электрического поля: начинаются на положительных зарядах и уходят в бесконечность (на отрицательные заряды). Теперь посмотрим на рисунок: линии поля внутри между пластинами направлены навстречу друг другу, за пределами пластин линии напряженностей совпадают по направлению.

Далее находим результирующую напряженность внутри и вне платин: внутри — разность, вне — сумма.

Напряжение равно Ed, строим график.

Войдите или зарегистрируйтесь, чтобы отправлять комментарии

На основании чего Вы сделали такой вывод и причём здесь сигма?

За пределами пластин линии напряженностей совпадают по направлению. Почему?

Один нюанс. Чтобы решить 312 задачу, сначала нужно решить задачу 311.

Войдите или зарегистрируйтесь, чтобы отправлять комментарии

2. С таким подходом задачу не решить. Начните решение задачи с изучения вопроса теории: напряженность плоскости. И поправьте размерность в числовых данных условия задачи.

Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Запишем уравнения (1) в проекциях на ось OХ:

С учетом уравнений (2) получаем:

Не совсем понятно с графиком. Что значит «график изменения напряженности»? Напряженность будет скачком изменяться на пластинах, на остальных участках изменение напряженности будет равно нулю, и график будет состоять из трех точек.

Может, надо построить график зависимости напряженности от координаты вдоль оси, перпендикулярной пластинам?

Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Для задачи 312:

Как быть с графиками понятия не имею, что значит графики изменения напряжённости, есть понятие зависимость напряжённости от координаты?

ЭЛЕКТРИЧЕСКИЙ ЗАРЯД. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ.

Электрический заряд q — физическая величина, определяющая интенсивность электромагнитного взаимодействия.

Атомы состоят из ядер и электронов. В состав ядра входят положительно заряженные протоны и не имеющие заряда нейтроны. Электроны несут отрицательный заряд. Количество электронов в атоме равно числу протонов в ядре, поэтому в целом атом нейтрален.

Заряд любого тела: q = ±Ne , где е = 1,6*10 -19 Кл — элементарный или минимально возможный заряд (заряд электрона), N — число избыточных или недостающих электронов. В замкнутой системе алгебраическая сумма зарядов остается постоянной:

Точечный электрический заряд — заряженное тело, размеры которого во много раз меньше расстояния до другого наэлектризованного тела, взаимодействующего с ним.

Два неподвижных точечных электрических заряда в вакууме взаимодействуют с силами, направленными по прямой, соединяющей эти заряды; модули этих сил прямо пропорциональны произведению зарядов и обратно пропорциональны квадрату расстояния между ними:

где — электрическая постоянная.

где ₁₂ — сила, действующая со стороны второго заряда на первый, а ₂₁ — со стороны первого на второй.

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. НАПРЯЖЕННОСТЬ

Факт взаимодействия электрических зарядов на расстоянии можно объяснить наличием вокруг них электрического поля — материального объекта, непрерывного в пространстве и способного действовать на другие заряды.

Поле неподвижных электрических зарядов называют электростатическим.

Характеристикой поля является его напряженность.

Напряженность электрического поля в данной точке — это вектор, модуль которого равен отношению силы, действующей на точечный положительный заряд, к величине этого заряда, а направление совпадает с направлением силы.

Напряженность поля точечного заряда Q на расстоянии r от него равна

Принцип суперпозиции полей

Напряженность поля системы зарядов равна векторной сумме напряженностей полей каждого из зарядов системы:

Диэлектрическая проницаемость среды равна отношению напряженностей поля в вакууме и в веществе:

Она показывает во сколько раз вещество ослабляет поле. Закон Кулона для двух точечных зарядов q и Q , расположенных на расстоянии r в среде c диэлектрической проницаемостью :

Напряженность поля на расстоянии r от заряда Q равна

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРО-СТАТИЧЕСКОМ ПОЛЕ

Между двумя большими пластинами, заряженными противоположными знаками и расположенными параллельно, поместим точечный заряд q .

Так как электрическое поле между пластинами с напряженностью однородное, то на заряд во всех точках действует сила F = qE , которая при перемещении заряда на расстояние вдоль совершает работу

Эта работа не зависит от формы траектории, то есть при перемещении заряда q вдоль произвольной линии L работа будет такой же.

Работа электростатического поля по перемещению заряда не зависит от формы траектории, а определяется исключительно начальным и конечным состояниями системы. Она, как и в случае с полем сил тяжести, равна изменению потенциальной энергии, взятому с противоположным знаком:

Из сравнения с предыдущей формулой видно, что потенциальная энергия заряда в однородном электростатическом поле равна:

Потенциальная энергия зависит от выбора нулевого уровня и поэтому сама по себе не имеет глубокого смысла.

ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И НАПРЯЖЕНИЕ

Потенциальным называется поле, работа которого при переходе из одной точки поля в другую не зависит от формы траектории. Потенциальными являются поле силы тяжести и электростатическое поле.

Работа, совершаемая потенциальным полем, равна изменению потенциальной энергии системы, взятой с противоположным знаком:

Потенциал — отношение потенциальной энергии заряда в поле к величине этого заряда:

Потенциал однородного поля равен

где d — расстояние, отсчитываемое от некоторого нулевого уровня.

Потенциальная энергия взаимодействия заряда q с полем равна .

Поэтому работа поля по перемещению заряда из точки с потенциалом φ₁ в точку с потенциалом φ₂ составляет:

Величина называется разностью потенциалов или напряжением.

Напряжение или разность потенциалов между двумя точками — это отношение работы электрического поля по перемещению заряда из начальной точки в конечную к величине этого заряда:

НАПРЯЖЕННОСТЬ ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ

При перемещении заряда q вдоль силовой линии электрического поля напряженностью на расстояние Δ d поле совершает работу

Так как по определению, то получаем:

Отсюда и напряженность электрического поля равна

Итак, напряженность электрического поля равна изменению потенциала при перемещении вдоль силовой линии на единицу длины.

Если положительный заряд перемещается в направлении силовой линии, то направление действия силы совпадает с направлением перемещения, и работа поля положительна:

Тогда , то есть напряженность направлена в сторону убывания потенциала.

Напряженность измеряют в вольтах на метр:

Напряженность поля равна 1 В/м, если напряжение между двумя точками силовой линии, расположенными на расстоянии 1 м, равна 1 В.

Если независимым образом измерять заряд Q , сообщаемый телу, и его потенциал φ, то можно обнаружить, что они прямо пропорциональны друг другу:

Величина С характеризует способность проводника накапливать электрический заряд и называется электрической емкостью. Электроемкость проводника зависит от его размеров, формы, а также электрических свойств среды.

Электроёмкостъ двух проводников — отношение заряда одного из них к разности потенциалов между ними:

Емкость тела равно 1 Ф , если при сообщении ему заряда 1 Кл оно приобретает потенциал 1 В.

Конденсатор — два проводника, разделенные диэлектриком, служащие для накопления электрического заряда. Под зарядом конденсатора понимают модуль заряда одной из его пластин или обкладок.

Способность конденсатора накапливать заряд характеризуется электроемкостью, которая равна отношению заряда конденсатора к напряжению:

Емкость конденсатора равна 1 Ф, если при напряжении 1 В его заряд равен 1 Кл.

Емкость плоского конденсатора прямо пропорциональна площади пластин S , диэлектрической проницаемости среды , и обратно пропорциональна расстоянию между пластинами d:

ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА.

Точные эксперименты показывают, что W=CU 2 /2

Плотность энергии электрического поля

где V = Sd — объем, занимаемый полем внутри конденсатора. Учитывая, что емкость плоского конденсатора

а напряжение на его обкладках U=Ed

Пример. Электрон, двигаясь в электрическом поле из точки 1 через точку 2, увеличил свою скорость от 1000 до 3000 км/с. Определите разность потенциалов между точками 1 и 2.

Так как электрон увеличил свою скорость, то ускорение и сила Кулона сонаправлены со скоростью. Значит, электрон движется против силовых линий поля. Изменение кинетической энергии электрона равно работе поля :

Ответ: разность потенциалов равна — 22,7 В.

Источник

Как найти напряжение между пластинами конденсатора

Одним из разделов физики, лежащих в основе знания, посвященного процессам, связанным с электричеством, является электростатика. Она изучает взаимодействие неподвижных электрических зарядов. Поэтому одной из типичных задач, которую может потребоваться решить школьникам и студентам младших курсов ВУЗ-ов, является нахождение напряжения между пластинами конденсатора на основании знания различных параметров.

Вам понадобится

– знание емкости или геометрических и физических параметров конденсатора;
– знание энергии или заряда на конденсаторе.

Инструкция

Найдите напряжение между пластинами конденсатора, если известна текущая величина накопленной им энергии, а также его емкость. Энергия, запасенная конденсатором, может быть вычислена по формуле W=(C∙U²)/2, где C – емкость, а U – напряжение между пластинами. Таким образом, значение напряжения может быть получено как корень из удвоенного значения энергии, деленного на емкость. То есть, оно будет равно: U=√(2∙W/C).

Энергия, запасенная конденсатором, также может быть вычислена на основании значения содержащегося в нем заряда (количества электричества) и напряжения между обкладками. Формула, задающая соответствие между этими параметрами, имеет вид: W=q∙U/2 (где q – заряд). Следовательно, зная энергию и заряд конденсатора, можно вычислить напряжение между его пластинами по формуле: U=2∙W/q.

Поскольку заряд на конденсаторе пропорционален как приложенному к его пластинам напряжению, так и емкости устройства (он определяется формулой q=C∙U), то, зная заряд и емкость, можно найти и напряжение. Соответственно, для проведения расчета используйте формулу: U=q/C.

Для получения значения напряжения на конденсаторе с известными геометрическими и физическими параметрами, сначала рассчитайте его емкость. Для простого плоского конденсатора, состоящего из двух проводящих пластин, разделенных диэлектриком, расстояние между которыми пренебрежимо мало по сравнению с их размерами, емкость может быть вычислена по формуле: C=(ε∙ε0∙S)/d. Здесь d – расстояние между пластинами, а S – их площадь. Значение ε0 – электрическая постоянная (константа, равная 8,8542•10^-12 Ф/м), ε – относительная диэлектрическая проницаемость пространства между пластинами (ее можно узнать из физических справочников). Вычислив емкость, рассчитайте напряжение одним из методов, приведенных в шагах 1-3.

Обратите внимание

Для получения корректных результатов при вычислении напряжений между обкладками конденсаторов, перед проведением расчетов приводите значения всех параметров в систему СИ.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Определение

Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.

Плоский конденсатор — система двух разноименно заряженных пластин.

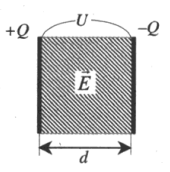
Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:

U=Ed

Электроемкость конденсатора

Определение

Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.

Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).

Электроемкость конденсатора определяется формулой:

C=ε0εSd

ε0 — диэлектрическая постоянная, равная 8,85∙10^–12 Кл²/(Н∙м²);
ε — диэлектрическая проницаемость среды;
S (м²) — площадь каждой пластины.

Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.

Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:

C=QU=qU

Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.

Энергия конденсатора

Формула энергии конденсатора

Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:

Wэ=q22C=CU22

Подсказки к задачам

Конденсатор отключен от источника	q = q′
Конденсатор подключен к источнику	U = U′
Количество теплоты и энергия конденсатора	Q = ∆W_э

Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.

10 см = 0,1 м

1 мм = 0,001 м

Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.

Площадь квадратной пластины равна квадрату ее стороны:

S = a²

Соединения конденсаторов

	Последовательное соединение	Параллельное соединение
Схема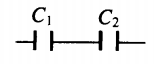
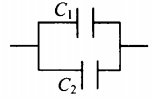Напряжение	U=U1+U2	U=U1=U2
Заряд	q=q1=q2	q=q1+q2
Электроемкость	1C=1C1+1C2	C=C1+C2

Подсказки к задачам

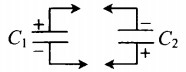
Два конденсатора, электроемкости которых C₁и C₂, заряжены до напряжения U₁и U₂. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами.

Схема соединения конденсаторов одноименными полюсами:

Заряд системы после соединения:

q′
=C1U1+C2U2

Электрическая емкость системы:

C′
=C1+C2

Напряжение:

U′
=q′C′=C1U1+C2U2C1+C2

Два конденсатора, электроемкости которых C₁и C₂, заряжены до напряжения U₁и U₂. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами.

Схема соединения конденсаторов разноименными полюсами:

Заряд системы после соединения:

q′
=C1U1−C2U2

Электрическая емкость системы:

C′
=C1+C2

Напряжение:

U′
=q′C′=C1U1−C2U2C1+C2

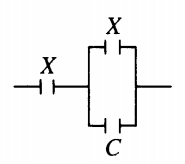
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.

Электрическая емкость параллельного соединения равна:

Cпарал=X+C

Электроемкость последовательного соединения:

1Cпослед=1Cпарал+1X=1X+C+1X

Учтем, что суммарная электроемкость равна C:

1C=1X+C+1X

Преобразуем, умножим выражение на CX(X+C):

X(X+C)=CX+C(X+C)

Раскроем скобки:

X2+XC=CX+CX+C2

X2−CX−C2=0

Решив уравнение, получим: X = 25,9 пФ.

Разбор задач на тему «Заряженная частица в поле конденсатора»

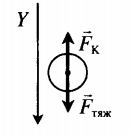
Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρ_ш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U?	Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−FA=0 ρ_ш > ρ, поэтому −Fтяж> −FA. В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так: Проекция второго закона Ньютона на ось ОУ: FK+FA=Fтяж Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения: Fтяж=ρш43πr3g Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения: FА=ρ43πr3g Сила Кулона: FK=qUd qUd+ρ43πr3g=ρш43πr3g q=(ρш43πr3g−ρ43πr3g)dU=4πr3gd(ρш−ρ)3U
Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l?	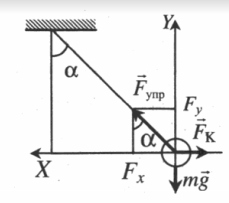Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−Fупр=0 Проекции на оси ОХ и ОУ соответственно: Fупрsinα−FK=0 Fупрcosα−mg=0 Отсюда: kΔlsinα=qUd kΔlcosα=mg Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их: (kΔl)2sin2α+(kΔl)2cos2α=(qUd)2+(mg)2 (kΔl)2(sin2α+cos2α)=(qUd)2+(mg)2 sin2α+cos2α=1 (kΔl)2=(qUd)2+(mg)2 U=dq√(kΔl)2−(mg)2
Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь.	Второй закон Ньютона в векторной форме: −Fтяж+−FK=0 Проекция на вертикальную ось: Fтяж−FK=0 Fтяж=mg FK=qUd mg=qUd d=qUmg
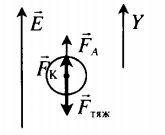
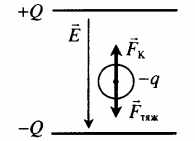
Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью −E, направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли?	Второй закон Ньютона в векторной форме: −Fтяж+−FK=m−a Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок: Если F_тяж> F_K, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны: a=mg−qEm s=b Если F_тяж< F_K, то шарик движется с ускорением верх. Ускорение и перемещение в этом случае равны: a=qE−mgm s=d Начальная скорость шарика равна нулю. Поэтому перемещение также равно: s=at22 Сделаем вычисления для случая F_тяж> F_K: at22=b mg−qEmt22=b t=√2bmmg−qE Выполняя вычисления для случая Сделаем вычисления для случая F_тяж< F_K, получим: t=√2bmqE−mg
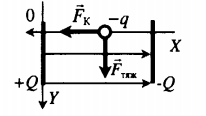
Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого −E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер.	Второй закон Ньютона в векторной форме: −Fтяж+−FK=m−a Если сила Кулона направлена вправо, то s_x = d. Если сила Кулона направлена вправо, то s_x = b. Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево. Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно: ax=qEm ay=g Проекции перемещений на эти же оси: sx=axt22 sx=Δh=gt22 axt22=b Или: qEmt22=b Так как время движения шарика по вертикали и горизонтали одинаково: t2=2Δhg=2mbqE Δh=mbgqE

Задание EF17979

Введите ответ в поле ввода
Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?

Для каждой величины определите соответствующий характер изменения:

увеличится
уменьшится
не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

1.Определить, от чего зависит емкость конденсатора, и как она изменится при уменьшении зазора между его обкладками.

2.Определить, от чего зависит величина заряда конденсатора, и как она изменится после уменьшения зазора между его обкладками.

3.Определить, от чего зависит разность потенциалов между обкладками конденсатора, и как она изменится при уменьшении зазора.

Решение

Емкость конденсатора определяется формулой:

C=ε0εSd

Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.

Вот как взаимосвязана электроемкость и заряд конденсатора:

C=qU

Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.

С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.

Ответ: 113

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18574

Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.

Алгоритм решения

1.Проанализировать каждый этап эксперимента.

2.Установить, от чего зависит угол отклонения стрелки электрометра.

3.Выяснить, что поменяется при смещении одной пластины конденсатора относительно другой, и что при этом произойдет со стрелкой электрометра.

Решение

На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.

На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:

C=ε0εSd

S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.

Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.

На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:

C=qU

Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.

Ответ: Увеличатся

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18695

Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?

Алгоритм решения

Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.

Решение

Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18703

Протон влетает в электрическое поле конденсатора параллельно его пластинам в точке, находящейся посередине между пластинами (см. рисунок). Найдите минимальную скорость υ, с которой протон должен влететь в конденсатор, чтобы затем вылететь из него. Длина пластин конденсатора 5 см, расстояние между пластинами 1 см, напряжённость электрического поля конденсатора 5000 В/м. Поле внутри конденсатора считать однородным, силой тяжести пренебречь.

Ответ записать в км/с, округлив до десятков.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

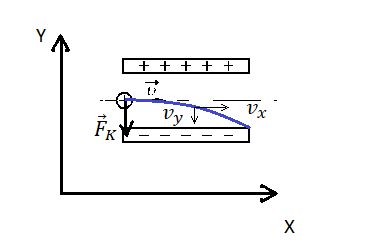
2.Выполнить рисунок. Указать направление движения протона и силы, действующие на него.

3.Выяснить, при каком условии протон успеет вылететь из конденсатора.

4.Выполнить решение в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса протона: m = 1,67∙10^–27 кг.

• Заряд протона: q = 1,6∙10^–19 Кл.

• Расстояние между обкладками конденсатора: d = 1 см.

• Длина пластин конденсатора: l = 5 см.

• Напряженность однородного поля внутри конденсатора: E = 5000 В/м.

1 см = 0,01 м

5 см = 0,05 м

Сделаем рисунок:

Изначально протон обладает только горизонтальной скоростью v, равной v_x. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.

Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью v_x:

t=lvx=lv

Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):

0,5d=at22

Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:

t=√da

Приравняем правые части уравнений времени и получим:

lv=√da

Отсюда скорость равна:

v=√al2d

Ускорение выразим из второго закона Ньютона:

FK=ma=qUd

a=qUmd

Но известно, что:

U=Ed

Поэтому:

a=qEdmd=qEm

Отсюда:

Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙10³ м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.

Ответ: 350

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 5.9k

Источник

Заряд на обкладках конденсатора: физика процессов и формула расчёта

Конденсатор — фундаментальный электронный компонент (наряду с резистором и катушкой индуктивности), предназначенный для накопления электрической энергии. Лучшей аналогией его работы будет сравнение с аккумуляторной батареей. Однако основой устройства последней являются обратимые химические реакции, а накопление заряда на обкладках конденсатора имеет исключительно электрическую природу.
В простейшем варианте конструкция состоит из двух электродов в форме проводящих пластин (называемых обкладками), разделённых диэлектриком, толщина которого ничтожно мала по сравнению с размерами обкладок.

Практически применяемые радиоэлектронные компоненты содержат много слоёв диэлектрика и электродов. В качестве обозначения конденсатора на схеме используются два параллельных отрезка с пространством между ними.

Они символизируют металлические пластины обкладок физического прибора, электрически разделённые между собой.

Многие считают Майкла Фарадея автором изобретения, но на самом деле это не так. Но он сделал главное — продемонстрировал первые практические примеры и способы использования этого прибора для хранения электрического заряда в своих экспериментах. Благодаря Фарадею человечество получило способ измерять возможность накапливать заряд. Эта величина называется ёмкостью и измеряется в Фарадах.

Работу конденсатора можно проиллюстрировать на примере событий, проходящих во вспышке цифровой фотокамеры за отрезок времени между нажатием кнопки и тем моментом, когда вспышка погаснет. Основой электронной схемы этого осветительного устройства является конденсатор, в котором происходит следующее:

Зарядка. После нажатия кнопки поток электронов приходит в конденсатор и останавливается на одной из его пластин благодаря диэлектрику. Этот поток называется зарядным током.
Накопление. Поскольку под действием электродвижущей силы всё больше и больше электронов будут поступать на обкладку и распределяться по ней, отрицательный заряд обкладки может расти до момента, пока накопленный потенциал не будет отталкивать поступающий избыточный поток электронов. Вторая пластина из-за дефицита электронов приобретает положительный заряд, по модулю равный отрицательному на первой. Зарядный ток будет протекать до тех пор, пока напряжение на обеих пластинах не сравняется с приложенным. Сила или скорость тока зарядки будет находиться на максимальном уровне в момент, когда пластины полностью разряжены, и приблизится к нулю в момент, когда напряжение на обкладках и источнике будут равны.
Сохранение. Поскольку обкладки заряжены противоположно, ионы и электроны будут притягиваться друг к другу, но не смогут соединиться из-за диэлектрической прослойки, создавая электростатическое поле. Благодаря этому полю конденсатор удерживает и сохраняет заряд.
Разряд. Если в цепи появляется возможность для электронов протечь другим путём, то напряжение, накопленное между положительными и отрицательными зарядами обкладок, мгновенно реализуется в электрический ток, импульс которого в лампе вспышки преобразуется в световую энергию.

Таким образом в фотовспышке реализуется способность конденсатора накопить для импульса энергию из батареи питания. Аккумулятор фотокамеры также является устройством, накапливающим энергию, но из-за химической природы накопления генерирует и отдаёт её медленно.

Ёмкость, заряд и напряжение

Свойство конденсатора сохранять заряд на пластинах в виде электростатического поля называется ёмкостью.

Чем больше площадь обкладок и меньше расстояние между ними, тем большее количество заряда они способны накопить и, соответственно, обладают большей ёмкостью.

При подаче напряжения на конденсатор отношение заряда Q к напряжению V даст значение ёмкости С. Формула заряда конденсатора будет выглядеть так:

Q=C*V.

Мера электрической ёмкости — фарад (Ф). Эта единица всегда положительная и не имеет отрицательных значений. 1 Ф равен ёмкости конденсатора, который способен сохранить заряд в 1 кулон на пластинах с напряжением в 1 вольт.

Фарад — очень большая единица измерения, для удобства использования применяют в основном её дольные меры:

Микрофарад (мкФ): 1мкФ=1/1000000 Ф.
Нанофарад (нФ): 1нФ=1/1000000000 Ф.
Пикофарад (пФ): 1пФ=1/000000000000 Ф.

Значение диэлектрика

Кроме общего размера обкладок и расстояния между ними, существует ещё один параметр, влияющий на ёмкость — используемый тип изолятора. Фактор, по которому определяется способность диэлектрика повышать ёмкость конденсатора в сравнении с вакуумом, называется диэлектрической проницаемостью и описывается для разных материалов постоянной величиной от 1 и до бесконечности (теоретически):

вакуум: 1,0000;
воздух: 1,0006;
бумага: 2,5—3,5;
стекло: 3—10;
оксиды металлов 6—20;
электротехническая керамика: до 80.

Кроме конденсаторов с твёрдым диэлектриком (керамических, бумажных, плёночных) существуют также электролитические. В последних используют алюминиевые или танталовые пластины с оксидным изолирующим слоем в качестве одного электрода и раствор электролита в качестве другого.

Главные особенности этой конструкции состоят в том, что она позволяет накапливать сравнительно внушительный заряд при небольших габаритах и является полярным электрическим накопителем. То есть включается в электрическую цепь с соблюдением полярности.

Энергия, которую способны накопить большинство конденсаторов, обычно невелика — не больше сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда.

Поэтому конденсаторы не могут заменить, например, аккумуляторные батареи в качестве источника питания. И хотя они способны эффективно выполнять только одну работу (сохранение заряда), их применение весьма многообразно в электрических цепях.

Конденсаторы используются как фильтры, для сглаживания сетевого напряжения, в качестве устройств синхронизации и для других целей.

Источник: https://220v.guru/elementy-elektriki/kondensatory/nakoplenie-zaryada-na-obkladkah-kondensatora.html

Формула электрического напряжения между пластинами

Как найти напряжение между пластинами конденсатора
Одним из разделов физики, лежащих в основе знания, посвященного процессам, связанным с электричеством, является электростатика. Она изучает взаимодействие неподвижных электрических зарядов. Поэтому одной из типичных задач, которую может потребоваться решить школьникам и студентам младших курсов ВУЗ-ов, является нахождение напряжения между пластинами конденсатора на основании знания различных параметров. Статьи по теме:

Как найти напряжение между пластинами конденсатора
Как найти диэлектрическую проницаемость
Как найти емкость конденсатора

— знание емкости или геометрических и физических параметров конденсатора;
— знание энергии или заряда на конденсаторе.

Инструкция 1 Найдите напряжение между пластинами конденсатора, если известна текущая величина накопленной им энергии, а также его емкость. Энергия, запасенная конденсатором, может быть вычислена по формуле W=(C∙U²)/2, где C — емкость, а U — напряжение между пластинами. Таким образом, значение напряжения может быть получено как корень из удвоенного значения энергии, деленного на емкость. То есть, оно будет равно: U=√(2∙W/C). 2 Энергия, запасенная конденсатором, также может быть вычислена на основании значения содержащегося в нем заряда (количества электричества) и напряжения между обкладками. Формула, задающая соответствие между этими параметрами, имеет вид: W=q∙U/2 (где q — заряд). Следовательно, зная энергию и заряд конденсатора, можно вычислить напряжение между его пластинами по формуле: U=2∙W/q. 3 Поскольку заряд на конденсаторе пропорционален как приложенному к его пластинам напряжению, так и емкости устройства (он определяется формулой q=C∙U), то, зная заряд и емкость, можно найти и напряжение. Соответственно, для проведения расчета используйте формулу: U=q/C. 4 Для получения значения напряжения на конденсаторе с известными геометрическими и физическими параметрами, сначала рассчитайте его емкость. Для простого плоского конденсатора, состоящего из двух проводящих пластин, разделенных диэлектриком, расстояние между которыми пренебрежимо мало по сравнению с их размерами, емкость может быть вычислена по формуле: C=(ε∙ε0∙S)/d. Здесь d — расстояние между пластинами, а S — их площадь. Значение ε0 — электрическая постоянная (константа, равная 8,8542•10^-12 Ф/м), ε — относительная диэлектрическая проницаемость пространства между пластинами (ее можно узнать из физических справочников). Вычислив емкость, рассчитайте напряжение одним из методов, приведенных в шагах 1-3. Обратите внимание Для получения корректных результатов при вычислении напряжений между обкладками конденсаторов, перед проведением расчетов приводите значения всех параметров в систему СИ. Статьи по теме:

Электроемкость. Конденсатор . урок. Физика 10 Класс

На этом уроке мы начнем изучение нового прибора – конденсатора – и новой физической величины – электроемкости. Исходя из опытов, мы рассмотрим количественную неодинаковость электризации разных тел одинаковыми зарядами, познакомимся с прибором для накопления зарядов и его основными характеристиками.

Тема: Основы электродинамики Урок: Электроёмкость. Конденсаторы

На предыдущих уроках мы знакомились с элементарными электрическими понятиями и принципами, в частности, мы говорили об электризации – явлении перераспределения заряда. Разговор о более глубоком исследовании этого явления начнем с опыта.

Изначально пусть нам даны две разные по размеру изолированные банки, подключенные к электроскопу (рис. 1):

Рис. 1

Теперь к каждой из банок поднесли одинаково заряженное тело. Естественно, с каждой банкой произойдет процесс электризации, и стрелки обоих электроскопов разойдутся. Однако оказалось, что электроскоп большей банки показал меньшее отклонение (рис. 2):

Рис. 2

Данный опыт доказывает, что различные тела электризуются одним и тем же зарядом по-разному (конкретно большая банка одним и тем же зарядом зарядилась до меньшего потенциала). И существует некоторая величина, которая показывает способность тела накапливать электрический заряд. Собственно, о ней и пойдет речь.

Определение. Электроемкость (емкость) – величина, равная отношению заряда переданного проводнику к потенциалу этого проводника.

Здесь: – емкость; – переданный заряд; – потенциал, до которого зарядился проводник.

Теперь непосредственно познакомимся со специализированными приборами для накопления зарядов.

Определение. Конденсатор – набор проводников, служащий для накопления электрического заряда. Конденсаторы состоят из двух проводников и разделяющего их диэлектрика, причем толщина диэлектрического слоя много меньше размеров проводников (рис. 3).

Рис. 3. Схематическое изображение конденсатора (Источник)

Особое внимание мы будем уделять так называемым плоским конденсаторам (слой диэлектрика расположен между двумя плоскими пластинами проводника). На электрической схеме конденсатор обозначается следующим образом (рис. 4):

Рис. 4. Условное обозначение конденсатора на электрической схеме

Емкость конденсатора определяется так же, как и любая другая электроемкость, однако с небольшим отличием (так как речь идет о системе проводников, а не о отдельно взятом проводнике, в формуле фигурирует не потенциал, а разность потенциалов или напряжение)

Здесь: – заряд на обкладках конденсатора (так называются проводники, из которых состоит конденсатор); – напряжение между обкладками конденсатора.

Единица измерения емкости: Ф – фарад

Однако, конечно же, емкость конденсатора – не постоянная величина, она зависит от конструкторских особенностей самого конденсатора. В случае плоского конденсатора эта зависимость имеет следующий вид:

Здесь: – диэлектрическая проницаемость среды; – электрическая постоянная; – площадь обкладки конденсатора; – расстояние между обкладками.

В конденсаторах роль диэлектрической прослойки, как правило, выполняет пропитанная соответствующим составом бумага, расположенная между двумя тонкими листами металла (рис. 5).

Рис. 5. Устройство конденсатора (Источник)

Конденсаторы можно разделить на три основных типа:

Конденсатор постоянной емкости – это свернутая в рулон упомянутая выше трехслойная лента (две ленты проводника и лента диэлектрика между ними).

Конденсаторы переменной емкости – приборы, используемые в радиотехнике, позволяющие регулировать параметры, от которых зависит емкость – ширина пластин и расстояние между ними (рис. 6).

Батарея же конденсаторов – это несколько конденсаторов, связанных по определенной схеме.

Рис. 6. Модель конденсатора переменной емкости (Источник)

Конденсатор – прибор для накопления заряда, и проводники, на которых накапливается заряд, создают между собой электрическое поле, а значит, конденсатор обладает некоторой энергией. Энергия конденсатора, по закону сохранения энергии, должна быть равна работе, выполненной по разделению зарядов.

Как мы уже знаем, работа по перемещению заряда в поле равна:

Здесь: – заряд; – напряженность; – модуль перемещения.

И теперь, если рассмотреть наш случай поля конденсатора, получается, что напряженность создается одновременно двумя обкладками, и для рассмотрения одной обкладки мы должны записать

Рис. 7. Однородное поле конденсатора

Воспользовавшись теперь формулой связи напряженности и напряжения из прошлого урока:

Формула для энергии конденсатора принимает вид:

Использовав в этой формуле формулу определения емкости конденсатора, можно получить еще две формы записи для энергии:

или

Этот урок завершает тему электростатики. Следующий будет посвящен уже электрическому току.

Дополнение 1. Электроемкость шара.

Для того чтобы оценить насколько велика емкость в 1 Ф, возьмем в качестве накапливающего заряд тела проводящий шар и выведем зависимость его емкости от его размеров.

Из предыдущего урока мы знаем формулу для определения потенциала шара:

Подставим теперь её в определение емкости:

Давайте рассмотрим случай в вакууме или же в воздухе (). Каковы же должны быть размеры шара, чтобы его емкость равнялась 1 Ф?

Для сравнения радиус Земли равен:

Дополнение 2. Соединение конденсаторов.

Иногда не получается найти конденсатор нужной конфигурации, тогда приходится составлять блоки из нескольких конденсаторов. Соединить два или более конденсатора можно двумя различными способами: параллельно или последовательно.

Параллельное соединение (рис. 8):

Рис. 8. Параллельное соединение конденсаторов

Так как выходы источника питания подсоединены одновременно к обкладкам всех конденсаторов, то потенциалы всех обкладок равны, металл является эквипотенциальной поверхностью:

Заряды на обкладках параллельно соединенных конденсаторов суммируются:

Разделив второе равенство на напряжение (любое, так как они равны) и воспользовавшись определением емкости конденсатора, получим:

Последовательное соединение (рис. 9):

Рис. 9. Последовательное соединение конденсаторов

Так как две обкладки соседних конденсаторов являются одной деталью, отрезанной от остальных проводников, по закону сохранения заряда, сумма их зарядов должна оставаться равной нулю, а значит, они равны по модулю, но противоположны по знаку, поэтому:

Падение же напряжения на всем участке складывается из падений напряжения на каждом конденсаторе:

Теперь, разделив второе равенство на заряд (любой, так как они равны) и воспользовавшись определением емкости конденсатора, получим:

Список литературы

Тихомирова С.А., Яворский Б.М. Физика (базовый уровень) – М.: Мнемозина, 2012.
Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Илекса, 2005.
Касьянов В.А. Физика 10 класс. – М.: Дрофа, 2010.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

Стр. 96-98: № 750–755. Физика. Задачник. 10-11 классы. Рымкевич А.П. – М.: Дрофа, 2013. (Источник)
Во сколько раз изменится емкость конденсатора, если листовую слюду заменить парафином той же толщины?
Какую площадь должны иметь пластины плоского конденсатора, для того чтобы его электроемкость была равна 1 пФ? Расстояние между пластинами – 0,5 мм.
Емкость одного конденсатора больше емкости другого в 4 раза, на какой конденсатор нужно подать большее напряжение, чтобы их энергии стали одинаковыми, во сколько раз больше?
*Почему большой заряд не может удержаться на сфере маленького радиуса?

Источник: https://interneturok.ru/lesson/physics/10-klass/osnovy-elektrodinamiki-2/elektroemkost-kondensator-variant-1-eryutkin-e-s

��

�� , �� . �� . 1 �� . �� . �� . �� .�

�� . �� , �� . �. �. ��: U� = �.

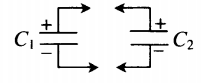
�� , �� , �� (+q), � �� (-q).

�� q �� : q = CUc

P��. 1. ��

�� , ��, �� , � �� . �� , � �� , �� , �� I��.�

�� , �� , �� . �. �. ��.

�� . 2,�, �� , �� Uc �� , �� , � �� , �� . �. �.

�� . �� .

��. 2. ��

�� , �� . �� . 2,�. � �� , �� , � �� io�� = E/Ri, �� . �. �. �� Ri.

�� , �. �. �� , �� . �� , �� . �. �. �� , �. �. �� – U �. �� i�� = (E-U�)/Ri

�� , �� U� �� i�� U� = E �� .

�� : ��

�� :�

1) �� Ri,�

2) �� .�

�� . 2 �� 10 ��: �� 1 �� . �. �. � = 100 � � � �� Ri�= 10 ��, �� 2 �� . �. �, �� : Ri = 5 ��.�

�� , �� , � �� .

��. 2. ��

�� . 3 �� . �. �. � = 100 � � �� Ri�= 10 �� : 10 �� (�� 1) � 20 �� (�� 2).�

�� io�� = �/Ri = 100/10 = 10�� , �� , �� , � �� .

��. 3. ��

��

�� .�

�� U�, �� , �� i��.�

�� . �� , �� . �� , �� , �. �. �� : Uc=0.�

�� . 4, � �� Uc� =100 � �� , �� , � �� .�

�� . 4,� �� . �� R � �� i�� = Uc/R

��. 4. ��

� �� , �� , �� , � � �� Uc � �� . �� Uc=0 �� .�

�� :�

1) �� Ѡ

2) �� R, �� .�

�� R, �� . �� , �� .�

�� , �� 10 �� 100 �, �� (��. 5): �� 1 � �� R =�40 ��, i�� = Uc�/R = 100/40 = 2,5 � � �� 2 – �� 20 �� i�� = 100/20 = 5 �.

��. 5. ��

�� , �� . �� , �� (�� ) � �� .

�� , �� 100 � � �� R�=40 �� (��. 6: �� 1 � �� 10 �� 2 � �� 20 ��).

��. 6. ��

�� , �� , �� .

�� , �� , � �� , �. �. �� . �� , �� .�

��

� �� , �� . �� , �. �.

�� , �� . �� , �� .

�� , �� , �� U, ��: W = W� = �U2/2

��. �� =10 �� U� = 500 �. �� , �� , �� .

��. �p� �� , �� , �� . �� W = W� = �U2/2 = (10 � 10-6 � 500)/2 = 1,25 ��.

Источник: https://ElectricalSchool.info/main/osnovy/1414-zarjad-i-razrjad-kondensatora.html

Зарядка конденсатора от источника постоянной ЭДС

Рассмотренный в предыдущем разделе процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теоретический интерес, как метод расчета энергии конденсатора. Реально конденсаторы заряжают, подключая их к источнику ЭДС, например, к гальванической батарее.

Пусть конденсатор емкостью C подключен к источнику, ЭДС которого равна e

(Рис. 145). Полное электрическое сопротивление цепи (включающее и внутренне сопротивление источника) обозначим
R
.

При замыкании ключа в цепи пойдет электрический ток, благодаря которому на обкладках конденсатора будет накапливаться электрический заряд.

По закону Ома сумма напряжений на конденсаторе и резисторе UR

=
IR
равна ЭДС источника , что приводит к уравнению

. (1)

В этом уравнении заряд конденсатора и сила тока зависят от времени. Скорость изменения заряда конденсатора по определению равна силе тока в цепи , что позволяет получить уравнение, описывающее изменение заряда конденсатора с течением времени

. (2)

Можно также получить уравнение, непосредственно описывающее изменение силы тока в цепи с течением времени. Для этого на основании уравнения (1) запишем уравнения для малых изменений входящих величин

Формально эту операцию можно описать следующим образом: уравнение (1) следует записать для двух моментов времени t

и (
t
+ Delta
t
), а затем из второго уравнения вычесть первое.

Так как ЭДС источника постоянна, то ее изменение равно нулю Delta e

= 0, сопротивление цепи и емкость конденсатора постоянны, поэтому их можно вынести из под знака изменения Delta, поэтому полученное уравнение приобретает вид

Наконец разделим его на промежуток времени, в течение которого произошли эти изменения, в результате получаем искомое уравнение (с учетом связи между силой тока и изменения заряда)

. (3)

Математический смысл этого уравнения указывает, что скорость уменьшения тока пропорциональна самой силе тока. Для однозначного решения этого уравнения необходимо задать начальное условие – значение силы тока в начальный момент времени I

0 = I(0).

С уравнениями такого типа мы познакомились в «математическом отступлении», поэтому здесь его анализ проведем кратко.

В начальный момент времени, когда заряд конденсатора равен нулю, скорость возрастания заряда (то есть сила тока) максимальна и равна .

Затем по мере накопления заряда сила тока будет уменьшаться, когда напряжение на конденсаторе станет равным ЭДС источника, заряд конденсатора достигнет максимального стационарного значения и ток в цепи прекратится.

Схематически зависимости заряда конденсатора и силы тока в цепи от времени показаны на рис. 146. Для оценки времени зарядки конденсатора можно принять, что заряд возрастает до максимального значения с постоянной скоростью, равной силе тока в начальный момент времени. В этом случае

. (4)

Аналогичная оценка исчезновения тока, полученная на основании уравнения (3) приводит к этому же результату.

Строго говоря, время зарядки конденсатора, описываемой уравнением (2) равно бесконечности. Это парадокс можно исключить, если принять во внимание дискретность электрического заряда.

Кроме того, заряд конденсатора, подключенного к батарее с течением времени случайным образом изменяется, флуктуирует, поэтому рассматриваемое уравнение описывает некоторые усредненные характеристики процесса.

Тем не менее, полученная оценка времени RC широко применяется в приближенных расчетах, часто ее называют просто временем зарядки конденсатора

Рассмотрим теперь превращения различных форм энергии в данном процессе. Понятно, что причиной тока в цепи и как следствие зарядки конденсатора являются сторонние силы источника.

На первый взгляд, энергетический баланс включает определенное противоречие: если источник сообщил конденсатору заряд q

, то сторонние силы совершили при этом работу
A
0 =
qe
, при этом энергия конденсатора стала равной , что в два раза меньше работы совершенной источником. Противоречие исчезает, если принять во внимание, что в процессе зарядки по цепи течет электрический ток, поэтому на резисторе выделяется некоторое количество теплоты, то есть часть энергии источника переходит в тепловую. Мысленно разобьем время зарядки на малые промежутки Delta
t
i (
i
= 1,2,3…). Перепишем уравнение (1) в виде

, (5)

и умножим его на величину малой порции заряда, переносимого за малый промежуток времени Delta t

i, Delta
q
i =
I
i Delta
t
i . В результате получим

. (6)

Здесь обозначено q

i – заряд конденсатора перед перенесением рассматриваемой порции заряда. Каждый член полученного уравнения имеет явный физический смысл:

– работа сторонних сил по перемещению порции заряда ?q

i; – увеличение энергии конденсатора при увеличении его заряда на Delta
q
i; – количество теплоты, выделившееся на резисторе, при протекании

порции заряда Delta q

Таким образом, закон сохранения энергии, выражаемый уравнением баланса (6) для малого промежутка времени оказывается выполненным, следовательно, он будет выполнен и для всего процесса зарядки. Просуммируем выражение (5) по всем промежуткам времени зарядки, в результате чего получим:

– полная работа сторонних сил по перенесению электрического заряда, равного стационарному заряду конденсатора; – энергия заряженного конденсатора; наконец, – количество выделившейся на резисторе теплоты.

Принимая во внимание уравнение (3) и формулы из «математического отступления», последнюю сумму можно выразить в виде

. (6)

Эта сумма же может быть вычислена графически. Формула (1) задает зависимость напряжения на резисторе UR

=
IR
от заряда конденсатора. Эта зависимость линейна, ее график (Рис. 147) является отрезком прямой линии.

За малый промежуток времени через резистор протечет малый заряд Delta q

i, при этом выделится количество теплоты , которое численно равно площади узкой полоски, выделенной на рисунке.

Полное количество теплоты, выделившейся при прохождении всего заряда численно равно площади треугольника под графиком зависимости U

R(
q
), то есть

. (7)

Таким образом, энергетический баланс полностью сходится и для всего процесса целиком: работа, совершенная источником равна сумме энергии конденсатора и количества выделившейся теплоты A

=
WC
+
Q
. Схематически преобразование энергии в этом процессе показано на рис. 148.

Интересно заметить, что количество теплоты, выделяющееся при зарядке, не зависит о сопротивления цепи и в точности равно энергии конденсатора.

То есть, половина энергии источника переходит в энергию электрического поля, а вторая в тепловую энергию, выделяющуюся в цепи: природа требует своеобразный пятидесятипроцентный налог в виде тепловых потерь, не зависимо от сопротивления цепи и емкости конденсатора[1].

Примечания

Но эти параметры цепи определяют время процесса.

Источник: https://scorcher.ru/art/electronica/electronica1.php

Заряд и напряжение на конденсаторе

§ 10. Заряд и разряд конденсатора

Конденсатор накапливает электрические заряды — заряжается. Накопление зарядов происходит в том случае, если конденсатор подключить к источнику электрической энергии. Процесс заряда конденсатора

(рис. 6). При установке ключа на контакт
1
пластины конденсатора окажутся подключенными к батарее и на них появятся противоположные по знаку электрические заряды («+» и «-»). Произойдет заряд конденсатора и между его пластинами возникнет электрическое поле. При заряде конденсатора свободные электроны правой пластины переместятся по проводнику в направлении положительного полюса батареи и на этой пластине останется недостаточное количество электронов, в результате чего она приобретет положительный заряд.

Свободные электроны с отрицательного полюса батареи переместятся на левую пластину конденсатора и на ней появится избыток электронов — отрицательный заряд. Таким образом, в проводах, соединяющих пластины конденсатора с батареей, будет протекать электрический ток, измеряемый миллиамперметром. Если между конденсатором и батареей не включено большое сопротивление, то время заряда конденсатора очень мало и ток в проводах протекает кратковременно. При заряде конденсатора энергия, сообщаемая батареей, переходит в энергию электрического поля, возникающего между пластинами конденсатора. Процесс разряда конденсатора

(см. рис. 6). Если ключ установить на контакт
2
, пластины заряженного конденсатора окажутся соединенными между собой и стрелка миллиамперметра мгновенно отклонится и затем вновь установится на нулевом делении. Произойдет разряд конденсатора и исчезнет электрическое поле между его пластинами. При разряде конденсатора «лишние» электроны с левой пластины переместятся по проводам к правой пластине, где их недостает, и когда количество электронов на пластинах конденсатора станет одинаковым, процесс разряда закончится и ток в проводах исчезнет. Энергия электрического поля конденсатора при его разряде расходуется на работу, связанную с перемещением зарядов — на создание электрического тока. Время разряда конденсатора через провода, обладающие малым сопротивлением, также весьма мало. Процесс заряда и разряда конденсатора широко используется в различных устройствах. Наиболее широко распространены бумажные, слюдяные и электролитические конденсаторы постоянной емкости.

Бумажный конденсатор КБГ.

Бумажный конденсатор (рис. 7) представляет собой металлический корпус
1
, в котором герметически закрыт пакет
2
, состоящий из пластин, выполненных в виде алюминиевой фольги
5
и изолированных одна от другой тонкой бумагой
4
, пропитанной изоляционным материалом (церезином, галоваксом). Пластины конденсатора присоединяются к выводным лепесткам
3
, изолированным ог корпуса.
Слюдяной конденсатор КСО.
Слюдяной конденсатор (рис. 7, б) состоит из двух пакетов металлических пластин и слюдяных прокладок. Между каждой парой пластин, принадлежащих разным пакетам, помещается тонкая прокладка из слюды. Собранные таким образом конденсаторы запрессовываются в пластмассу, из которой выходят наружу два лепестка по одному от каждого пакета пластин. Они служат для включения конденсатора в схему.
Электролитический конденсатор КЭ-2М.
Электролитический конденсатор (рис. 7, в) представляет собой алюминиевый стакан
6
, в котором помещаются две алюминиевые ленты, скатанные в рулон. Между лентами проложена фильтровальная бумага, пропитанная электролитом. Одна алюминиевая лента соединяется с корпусом стакана, а вторая — с контактом
7
, укрепленным на его верхней крышке. При заряде конденсатора на поверхности алюминиевых лент, подключаемых к положительному полюсу источника тока, образуется пленка окиси алюминия, являющаяся диэлектриком. Так как эта пленка очень тонкая, то емкость электролитических конденсаторов относительно велика. Электролитические конденсаторы изготовляют емкостью до 2000
мкф
при рабочем напряжении до 500
в
.
Конденсаторы переменной емкости.
Конденсаторы, емкость которых можно изменять, называются
конденсаторами переменной емкости
(рис. 8, а). Такой конденсатор состоит из неподвижных пластин (статора) и подвижных пластин (ротора), укрепленных на оси. При плавном повороте оси подвижные пластины в большей или меньшей степени входят в промежутки между неподвижными пластинами, не касаясь их, и емкость конденсатора плавно увеличивается. Когда подвижные пластины полностью входят в промежутки между неподвижными пластинами, емкость конденсатора достигает наибольшей величины.

Разновидностью конденсатора переменной емкости является конденсатор полупеременной емкости

(рис. 8, б). Такой конденсатор имеет неподвижную (статор) и подвижную (ротор) пластины. Основание пластин изготовлено из керамики, а на него нанесен слой серебра. Ротор укреплен с помощью винта. Поворачивая винт, перемещают ротор и при этом изменяется емкость конденсатора в пределах 2 — 30
пф
.

§
6. Заряд и разряд конденсатора
Чтобы зарядить конденсатор, надо, чтобы свободные электроны перешли из одной обкладки на другую. Переход электронов с одной обкладки конденсатора на другую происходит под действием напряжения источника по проводам, соединяющим этот источник с обкладками конденсатора.

В момент включения конденсатора зарядов на его обкладках нет и напряжение на нем равно нулю μ с =0. Поэтому зарядный ток определяется внутренним сопротивлением источника r в и имеет наибольшую величину:

I З max =E/ r в.

По мере накопления зарядов на обкладках конденсатора напряжение на нем увеличивается и падение напряжения на внутреннем сопротивлении источника будет равно разности ЭДС источника и напряжения на конденсаторе (Е- μ с). следовательно, зарядный ток

i з =(Е- μ с)/ r в.

Таким образом, с увеличением напряжения на конденсаторе ток заряда снизится и при μ с =Е становится равным нулю. Процесс изменения напряжения на конденсаторе и тока заряда во времени изображен на рис. 1. В самом начале заряда напряжение на конденсаторе резко возрастает, так как зарядный ток имеет наибольшее значение и накопление зарядов на обкладках конденсатора происходит интенсивно. По мере повышения напряжения на конденсаторе зарядный ток уменьшается и накопление зарядов на обкладках замедляется. Продолжительность заряда конденсатора зависит от его емкости и сопротивления цепи, увеличение которых приводит к возрастанию продолжительности заряда. С увеличением емкости конденсатора, возрастает количество зарядов, накапливаемых на его пластинах, а если увеличить сопротивление цепи уменьшится и зарядный ток, а это замедляет процесс накопления зарядов на этих обкладках.

Если обкладки заряженного конденсатора подключить к какому-либо сопротивлению R , то за счет напряжения на конденсаторе будет протекать разрядный ток конденсатора. При разряде конденсатора электронысодной пластины (при их избытке) будут переходить на другую (при их недостатке) и будет продолжается до тех пор, пока потенциалы обкладок не выравняются, т. е. напряжение на конденсаторе станет равным нулю. Изменение напряжения в процессе разряда конденсатора изображено на рис. 2. Ток разряда конденсатора пропорционален напряжению на конденсаторе (i р =μ с /R ), и его изменение во времени подобно изменению напряжения.

В начальный момент разряда напряжение на конденсаторе наибольшее (μ с =Е) и разрядный ток максимальный (I р max =E /R ), так что разряд происходит быстро. При понижении напряжения, ток разряда снижается и процесс перехода зарядов с одной обкладки на другую затормаживается.

Время процесса разряда конденсатора зависит от сопротивления цепи и емкости конденсатора, причем возрастание как сопротивления, так и емкости увеличивает продолжительность разряда. С увеличением сопротивления разрядный ток снижается, замедляется процесс переноски зарядов с одной на другую обкладок; с увеличением емкости конденсатора повышается заряд на обкладках.

Таким образом, в цепи, содержащей конденсатор, ток проходит только в процессе его заряда и разряда, т. е. когда напряжение на обкладках претерпевает изменение во времени. При постоянстве напряжения ток через конденсатор не проходит, т. е. конденсатор не пропускает постоянный ток, так как между его обкладками помещен диэлектрик и в результате этого цепь разомкнута.

При зарядке конденсатора, последний способен накапливать электрическую энергию, потребляя ее от энергоисточника. Накопленная энергия сохраняется определенное время. При разряде конденсатора эта энергия переходит к разрядному резистору, нагревая его, т. е. энергию электрического поля превращается в тепловую. Чем выше емкость конденсатора и напряжение на его обкладках, тем будет больше энергии, запасенной на нем. Энергия электрического поля конденсатора определяется следующим выражением

W=CU 2 /2.

Если конденсатор емкостью 100 мкФ заряжен до напряжения 200 В, то энергия, запасенная в электрическом поле конденсатора, W =100· 10 -6 · 200 2 /2=2 Дж.

Присоединим цепь, состоящую из незаряженного конденсатора емкостью С и резистора с сопротивлением R, к источнику питания с постоянным напряжением U (рис. 16-4).

Так как в момент включения конденсатор еще не заряжен, то напряжение на нем Поэтому в цепи в начальный момент времени падение напряжения на сопротивлении R равно U и возникает ток, сила которого

Рис. 16-4. Зарядка конденсатора.

Прохождение тока i сопровождается постепенным накоплением заряда Q на конденсаторе, на нем появляется напряжение и падение напряжения на сопротивлении R уменьшается:

как и следует из второго закона Кирхгофа. Следовательно, сила тока

уменьшается, уменьшается и скорость накопления заряда Q, так как ток в цепи

С течением времени конденсатор продолжает заряжаться, но заряд Q и напряжение на нем растут все медленнее (рис. 16-5), а сила тока в цепи постепенно уменьшается пропорционально разности — напряжений

Рис. 16-5. График изменения тока и напряжения при зарядке конденсатора.

Через достаточно большой интервал времени (теоретически бесконечно большой) напряжение на конденсаторе достигает величины, равной напряжению источника питания, а ток становится равным нулю — процесс зарядки конденсатора заканчивается.

Процесс зарядки конденсатора тем продолжительней, чем больше сопротивление цепи R, ограничивающее силу тока, и чем больше емкость конденсатора С, так как при большой емкости должен накопиться больший заряд. Скорость протекания процесса характеризуют постоянной времени цепи

чем больше , тем медленнее процесс.

Постоянная времени цепи имеет размерность времени, так как

Через интервал времени с момента включения цепи, равный , напряжение на конденсаторе достигает примерно 63% напряжения источника питания, а через интервал процесс зарядки конденсатора можно считать закончившимся.

Напряжение на конденсаторе при зарядке

т. е. уменьшается по закону показательной функции (рис. 16-7).

Разрядный ток конденсатора

т. е. он, так же как и напряжение, уменьшается по тому же закону (рис. 6-7).

Вся энергия, запасенная при зарядке конденсатора в его электрическом поле, при разряде выделяется в виде тепла в сопротивлении R.

Электрическое поле заряженного конденсатора, отсоединенного от источника питания, не может долго сохраняться неизменным, так как диэлектрик конденсатора и изоляция между его зажимами обладают некоторой проводимостью.

Разряд конденсатора, обусловленный несовершенством диэлектрика и изоляции, называется саморазрядом. Постоянная времени при саморазряде конденсатора не зависит от формы обкладок и расстояния между ними.

Процессы зарядки и разряда конденсатора называются переходными процессами.

Заряд конденсатора

Для того чтобы зарядить конденсатор, необходимо включить его в цепь постоянного тока. На рис. 1 показана схема заряда конденсатора. Конденсатор С присоединен к зажимам генератора. При помощи ключа можно замкнуть или разомкнуть цепь. Рассмотрим подробно процесс заряда конденсатора.

Генератор обладает внутренним сопротивлением. При замыкании ключа конденсатор зарядится до напряжения между обкладками, равного э. д. с. генератора: Uс = Е. При этом обкладка, соединенная с положительным зажимом генератора, получает положительный заряд (+q ), а вторая обкладка получает равный по величине отрицательный заряд (-q ). Величина заряда q прямо пропорциональна емкости конденсатора С и напряжению на его обкладках: q = CUc

P ис. 1

Для того чтобы обкладки конденсатора зарядились, необходимо, чтобы одна из них приобрела, а другая потеряла некоторое количество электронов. Перенос электронов от одной обкладки к другой совершается по внешней цепи электродвижущей силой генератора, а сам процесс перемещения зарядов по цепи есть не что иное, как электрический ток, называемый зарядным емкостным током I зар.

Зарядный ток в цени протекает обычно тысячные доли секунды до тех пор, пока напряжение на конденсаторе достигнет величины, равной э. д. с. генератора. График нарастания напряжения на обкладках конденсатора в процессе его заряда представлен на рис. 2,а, из которого видно, что напряжение Uc плавно увеличивается, сначала быстро, а затем все медленнее, пока не станет равным э. д. с. генератора Е. После этого напряжение на конденсаторе остается неизменным.

Рис. 2. Графики напряжения и тока при заряде конденсатора

Пока конденсатор заряжается, по цепи проходит зарядный ток. График зарядного тока показан на рис. 2,б. В начальный момент зарядный ток имеет наибольшую величину, потому что напряжение на конденсаторе еще равно нулю, и по закону Ома io зар = E/ Ri , так как вся э. д. с. генератора приложена к сопротивлению Ri.

По мере того как конденсатор заряжается, т. е. возрастает напряженно на нем, для зарядного тока уменьшается. Когда напряженно па конденсаторе уже имеется, падение напряжения на сопротивление будет равно разности между э. д. с. генератора и напряжением на конденсаторе, т. е. равно Е — U с. Поэтому i зар = (E-Uс)/Ri

Отсюда видно, что с увеличением Uс уменьшается i зар и при Uс = E зарядный ток становится равным нулю.

Продолжительность процесса заряда конденсатора зависит от двух величии:

1) от внутреннего сопротивления генератора Ri ,

2) от емкости конденсатора С.

На рис. 2 показаны графики нарядных токов для конденсатора емкостью 10 мкф: кривая 1 соответствует процессу заряда от генератора с э. д. с. Е = 100 В и с внутренним сопротивлением Ri = 10 Ом, кривая 2 соответствует процессу заряда от генератора с такой же э. д. с, но с меньшим внутренним сопротивлением: Ri = 5 Ом.

Из сравнения этих кривых видно, что при меньшем внутреннем сопротивлении генератора сила нарядного тока в начальный момент больше, и поэтому процесс заряда происходит быстрее.

Рис. 2. Графики зарядных токов при разных сопротивлениях

На рис. 3 дается сравнение графиков зарядных токов при заряде от одного и того же генератора с э. д. с. Е = 100 В и внутренним сопротивлением Ri = 10 ом двух конденсаторов разной емкости: 10 мкф (кривая 1) и 20 мкф (кривая 2).

Величина начального зарядного тока io зар = Е/Ri = 100/10 = 10 А одинакова для обоих конденсаторов, по так как конденсатор большей емкости накапливает большее количество электричества, то зарядный его ток должен проходить дольше, и процесс заряда получается более длительным.

Рис. 3. Графики зарядных токов при разных емкостях

Разряд конденсатора

Отключим заряженный конденсатор от генератора и присоединим к его обкладкам сопротивление.

На обкладках конденсатора имеется напряжение U с, поэтому в замкнутой электрической цепи потечет ток, называемый разрядным емкостным током i разр.

Ток идет от положительной обкладки конденсатора через сопротивление к отрицательной обкладке. Это соответствует переходу избыточных электронов с отрицательной обкладки на положительную, где их недостает. Процесс рам ряда происходит до тех пор, пока потенциалы обеих обкладок не сравняются, т. е. разность потенциалов между ними станет равном нулю: Uc=0 .

На рис. 4, а показан график уменьшения напряжения на конденсаторе при разряде от величины Uc о =100 В до нуля, причем напряжение уменьшается сначала быстро, а затем медленнее.

На рис. 4,б показан график изменения разрядного тока. Сила разрядного тока зависит от величины сопротивления R и по закону Ома i разр = Uc /R

Рис. 4. Графики напряжения и токов при разряде конденсатора

В начальный момент, когда напряжение па обкладках конденсатора наибольшее, сила разрядного тока также наибольшая, а с уменьшением Uc в процессе разряда уменьшается и разрядный ток. При Uc=0 разрядный ток прекращается.

Продолжительность разряда зависит:

1) от емкости конденсатора С

2) от величины сопротивления R , на которое конденсатор разряжается.

Чем больше сопротивление R , тем медленнее будет происходить разряд. Это объясняется тем, что при большом сопротивлении сила разрядного тока невелика и величина заряда на обкладках конденсатора уменьшается медленно.

Это можно показать на графиках разрядного тока одного и того же конденсатора, имеющего емкость 10 мкф и заряженного до напряжения 100 В, при двух разных величинах сопротивления (рис. 5): кривая 1 — при R = 40 Ом, i оразр = Uc о/R = 100/40 = 2,5 А и кривая 2 — при 20 Ом i оразр = 100/20 = 5 А.

Рис. 5. Графики разрядных токов при разных сопротивлениях

Разряд происходит медленнее также тогда, когда емкость конденсатора велика. Получается это потому, что при большей емкости на обкладках конденсатора имеется большее количество электричества (больший заряд) и для стекания заряда потребуется больший промежуток времени. Это наглядно показывают графики разрядных токов для двух конденсаторов раиной емкости, заряженных до одного и того же напряжения 100 В и разряжающихся на сопротивление R =40 Ом (рис. 6 : кривая 1 — для конденсатора емкостью 10 мкф и кривая 2 — для конденсатора емкостью 20 мкф).

Рис. 6. Графики разрядных токов при разных емкостях

Из рассмотренных процессов можно сделать вывод, что в цепи с конденсатором ток проходит только в моменты заряда и разряда, когда напряжение на обкладках меняется.

Объясняется это тем, что при изменении напряжения изменяется величина заряда на обкладках, а для этого требуется перемещение зарядов по цепи, т. е. по цепи должен проходить электрический ток. Заряженный конденсатор не пропускает постоянный ток, так как диэлектрик между его обкладками размыкает цепь.

Энергия конденсатора

В процессе заряда конденсатор накапливает энергию, получая ее от генератора. При разряде конденсатора вся энергия электрического поля переходит в тепловую энергию, т. е. идет на нагрев сопротивления, через которое разряжается конденсатор. Чем больше емкость конденсатора и напряжение на его обкладках, тем больше будет энергия электрического поля конденсатора. Величина энергии, которой обладает конденсатор емкостью С, заряженный до напряжения U, равна: W = W с = СU 2 /2

Пример. Конденсатор С=10 мкф заряжен до напряжении U в = 500 В. Определить энергию, которая выделится в вило тепла на сопротивлении, через которое разряжается конденсатор.

Решение. Пpи разряде вся энергия, запасенная конденсатором, перейдет в тепловую. Поэтому W = W с = СU 2 /2 = (10 х 10 -6 х 500)/2 = 1,25 дж.
Facebook

Конденсатор

Конденсатор – электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики – емкости. Емкость конденсатора (С) определяется как соотношение количества электрического заряда (Q) к напряжению (U).

Емкость конденсатора измеряется в фарадах (F) – единицах, названых в честь британского ученого физика Майкла Фарадея. Емкость в один фарад (1F) равняется количеству заряда в один кулон (1C), создающему напряжение на конденсаторе в один вольт (1V). Вспомним, что один кулон (1С) равняется величине заряда, прошедшего через проводник за одну секунду (1sec) при силе тока в один ампер (1A).

Однако кулон, это очень большое количество заряда относительно того, сколько способно хранить большинство конденсаторов. По этой причине, для измерения емкости обычно используют микрофарады (µF или uF), нанофарады (nF) и пикофарады (pF).

1nF = 0.000000001 = 10-9 F

1pF = 0.000000000001 = 10-12 F

Плоский конденсатор

Существует множество типов конденсаторов различной формы и внутреннего устройства. Рассмотрим самый простой и принципиальный — плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин проводника (обкладок), электрически изолированных друг от друга воздухом, или специальным диэлектрическим материалом (например бумага, стекло или слюда).

Заряд конденсатора. Ток

По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.

Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов.

Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора.

Поэтому в цепи идет электрический ток.

В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.

Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют переходным периодом заряда конденсатора.

Заряд конденсатора. Напряжение

В самом начале переходного периода зарядки, напряжение между обкладками конденсатора равняется нулю. Как только на обкладках начинают появляться заряженные частицы, между разноименными зарядами возникает напряжение. Причиной этому является диэлектрик между пластинами, который «мешает» стремящимся друг к другу зарядам с противоположным знаком перейти на другую сторону конденсатора.

На начальном этапе зарядки, напряжение быстро растет, потому что большой ток очень быстро увеличивает количество заряженных частиц на обкладках. Чем больше заряжается конденсатор, тем меньше ток, и тeм медленнее растет напряжение. В конце переходного периода, напряжение на конденсаторе полностью прекратит рост, и будет равняться напряжению на источнике питания.

Как видно на графике, сила тока конденсатора напрямую зависит от изменения напряжения.

Формула для нахождения тока конденсатора во время переходного периода:

ΔVc/Δt – Изменение напряжения на конденсаторе за отрезок времени

Разряд конденсатора

После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания.

Нагрузка R образовала проход между пластинами.

Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.

В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.

Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.

Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R.

Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки ( ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.

Продукт RC (сопротивление, умноженное на емкость) формирует временную константу τ (тау). За один τ конденсатор заряжается или разряжается на 63%. За пять τ конденсатор заряжается или разряжается полностью.

Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:

Устройство конденсатора. От чего зависит емкость?

Емкость плоского конденсатора зависит от трех основных факторов:

Расстояние между пластинами – d

Относительная диэлектрическая проницаемость вещества между пластинами — ɛ

Площадь пластин

Чем больше площадь пластин конденсатора, тем больше заряженых частиц могут на них разместится, и тем больше емкость.

Расстояние между пластинами

Емкость конденсатора обратно пропорциональна расстоянию между пластинами. Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).

Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине.

Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах.

Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.

Относительная диэлектрическая проницаемость

Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость ɛ. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.

Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.

Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.

Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.

Порошки оксидов металлов – от 6 до 20

Номинальное напряжение

Второй по значимости характеристикой после емкости является максимальное номинальное напряжение конденсатора.

Данный параметр обозначает максимальное напряжение, которое может выдержать конденсатор. Превышение этого значения приводит к «пробиванию» изолятора между пластинами и короткому замыканию.

Номинальное напряжение зависит от материала изолятора и его толщины (расстояния между обкладками).

Следует отметить, что при работе с переменным напряжением нужно учитывать именно пиковое значение (наибольшее мгновенное значение напряжения за период). Например, если эффективное напряжение источника питания будет 50В, то его пиковое значение будет свыше 70В.

Соответственно необходимо использовать конденсатор с номинальным напряжением более 70В.

Однако на практике, рекомендуется использовать конденсатор с номинальным напряжением не менее в два раза превышающим максимально возможное напряжение, которое будет к нему приложено.

Плоский конденсатор: емкость, напряжение, напряженность и прочее

В этой статье мы начнем разбирать конденсаторы “по косточкам”. Мы узнаем, как зависит напряжение на конденсаторе от расстояния между пластин, в чем отличие поведения конденсатора в случаях, когда он подключен к источнику и когда нет. В последующих статьях – продолжение.

Задача 1. Найти емкость сферического конденсатора, состоящего из двух концентрических сфер радиусами м и м. Пространство между сферами заполнено маслом. Какого радиуса должен быть изолированный шар, чтобы он имел емкость, равную емкости такого конденсатора?

Как известно,

Запишем потенциалы сфер:

Разность потенциалов:

Тогда емкость конденсатора равна (диэлектрическая проницаемость масла равна ):

А радиус шара был бы равен

Ответ: пФ, м. Задача 2. Найти емкость плоского конденсатора, состоящего из двух круглых пластин диаметром см, разделенных парафиновой прослойкой толщиной мм.

Диэлектрическая проницаемость парафина .

По формуле

Ответ: 556 мкФ

Задача 3. Площадь каждой пластины плоского конденсатора см. На каком расстоянии друг от друга надо расположить в воздухе пластины, чтобы емкость конденсатора была пФ?

Диэлектрическая проницаемость воздуха .

Из формулы

«вытащим» :

Ответ: 1 см

Задача 4. Расстояние между обкладками плоского конденсатора увеличивают. Как изменится: а) электроемкость конденсатора; б) напряженность электрического поля; в) напряжение? Рассмотреть два случая: 1) конденсатор заряжен и отключен от источника тока; 2) конденсатор подключен к источнику тока.

Здесь необходимо запомнить: если конденсатор заряжен и после этого отключен, то заряд на нем сохраняется. Действительно, куда ему деваться? А если начать что-либо менять, то будут меняться емкость и напряжение.

Если же конденсатор подключен к источнику, то напряжение на нем постоянно, и при любых вмешательствах (раздвинули пластины, вложили диэлектрик) будет меняться емкость и заряд.

Тогда в первом случае (заряд постоянен!): так как зависимость емкости от обратная, то емкость будет падать при увеличении расстояния между пластинами. Напряженность – никак не зависит от расстояния между обкладками, она не изменится; напряжение – увеличится, оно от величины зависит прямо.

Во втором случае (напряжение постоянно): напряженность поля уменьшится; емкость уменьшится.

Задача 5. Плоский конденсатор состоит из двух пластин, площадью см каждая, расположенных на расстоянии мм друг от друга, между которыми находится слой слюды. Какой наибольший заряд можно сообщить конденсатору, если допустимое напряжение кВ?

Диэлектрическая проницаемость слюды .

Ответ: 1,59 мкКл

Задача 6. Плоский воздушный конденсатор, расстояние между пластинами которого мм, заряжен до напряжения В и отключен от источника. Каким будет напряжение , если пластины раздвинуть до расстояния мм?

Если конденсатор заряжен и после этого отключен, то заряд на нем сохраняется. Тогда

Ответ: В

Задача 7. С какой силой взаимодействуют пластины плоского воздушного конденсатора площадью м, если напряжение на пластинах В и расстояние между ними м?

Сила взаимодействия пластин может быть вычислена как произведение заряда пластины на напряженность поля пластины: – делим пополам, потому что напряженность поля одной пластины вдвое меньше напряженности поля конденсатора – там пластин две штуки.

Ответ: мН.

Источник

В статье поле плоской пластины была выведена формула напряжённости электрического поля бесконечной плоской пластины. Если эту пластину рассмотреть в разрезе и ввести понятие поверхностной плотности заряда σ, то согласно указанной статьи в любой точке пространства напряжённость электрического поля направлена перпендикулярно плоскости пластины и по величине равно:

E₀ здесь жёстко определяется поверхностной плотностью заряда σ:

где σ – поверхностная плотность заряда;
ε₀ – диэлектрическая проницаемость для вакуума;
ε – относительная диэлектрическая проницаемость для вещества, которая для вакуума равна 1.

Формулы показывают, что величина напряжённости электрического поля плоской пластины, имеющей бесконечные размеры, не зависит от расстояния до неё.

Если σ положительная, то напряжённость электрического поля будет направлена от пластины и поле отталкивает положительные заряды.

Если σ отрицательная, то напряжённость электрического поля направлена к пластине и поле притягивает положительные заряды.

Плоским конденсатором будем называть пару параллельных плоских пластин с плотностью заряда одинаковой по модулю, но противоположной по знаку.

Расчёт и вывод формулы ёмкости плоского конденсатора

Напряжённость электрического поля конденсатора

Для расчёта плоского конденсатора расположим две пластины бесконечных размеров параллельно друг другу на некотором расстоянии d. Пусть одна пластина будет иметь поверхностную плотность заряда σ, а другая -σ. По модулю величины поверхностных плотностей зарядов будут равны. В такой ситуации общее поле плоского конденсатора по принципу суперпозиции равно сумме полей.

Обозначим напряжённости электрического поля от левой пластины плоского конденсатора как E_л, при этом положительные заряды будут отталкиваться от пластины.

Напряжённость электрического поля от правой пластины плоского конденсатора обозначим как E_п, при этом поле пластины будет притягивать к себе положительные заряды.

При равной плотности заряда напряжённость поля во всех точках пространства и от левой, и от правой пластин конденсатора будут равны по модулю. Это приведёт к тому, что слева и справа от пары пластин поля взаимно компенсируются и их сумма будет равна нулю. При этом поля между пластинами плоского конденсатора будут складываться.

где E₀ – напряжённость поля при положительной σ.

Суммарная напряжённость электрического поля плоского конденсатора будет направлена от пластины с положительной σ к пластине с отрицательной σ.

Электрическая энергия плоского конденсатора отсутствует вне его пластин и вся накоплена в пространстве между пластинами.

Работа по перемещению заряда

Для перемещения заряда от отрицательно заряженной пластины в направлении к положительно заряженной придётся совершить работу против электрической силы:

При вычислении этой работы видно, что величина заряда q и напряжённость поля E постоянны, поэтому формула примет вид:

В электрическом поле можно ввести понятие потенциала ϕ и выразить работу по перемещению заряда в точку 2 из точки 1 через разность потенциалов ϕ₁-ϕ₂.

Напряжение между пластинами плоского конденсатора

Разность электрических потенциалов между двумя точками называют напряжением и обозначают U₁₂:

Таким образом, сравнивая две формулы для работы мы получим:

В реальном конденсаторе площадь пластин ограничена по естественным причинам, поэтому, как правило, мы не имеем возможности знать плотность заряда, а знаем только заряд пластины. В этом случае плотность заряда σ мы можем вычислить по формуле:

где Q – заряд пластины;
S – площадь пластины.

Если пластины плоского конденсатора находятся достаточно близко друг к другу, то краевыми эффектами можно пренебречь и считать, что поле внутри конденсатора реальных размеров подобно полю внутри конденсатора с пластинами бесконечных размеров.

В таком случае имеем следующее выражение:

Напряжение между пластинами пропорционально полному заряду этих пластин:

Электрическая ёмкость плоского конденсатора

Коэффициент пропорциональности между зарядом на обкладках плоского конденсатора и напряжением между ними носит название ёмкости плоского конденсатора и обозначается буквой C:

Подробности венецианская штукатурка для внутренней отделки цена на сайте.

Источник

ДОМОСТРОЙСантехника и строительство

Комментарии

Как найти напряжение между пластинами конденсатора

Электроемкость конденсатора

Энергия конденсатора

Подсказки к задачам

Соединения конденсаторов

Подсказки к задачам

Разбор задач на тему «Заряженная частица в поле конденсатора»

Заряд на обкладках конденсатора: физика процессов и формула расчёта

Ёмкость, заряд и напряжение

Значение диэлектрика

Формула электрического напряжения между пластинами

Электроемкость. Конденсатор . урок. Физика 10 Класс

Дополнение 1. Электроемкость шара.

Дополнение 2. Соединение конденсаторов.

��

Зарядка конденсатора от источника постоянной ЭДС

Заряд и напряжение на конденсаторе

Конденсатор

Плоский конденсатор

Заряд конденсатора. Ток

Заряд конденсатора. Напряжение

Разряд конденсатора

Устройство конденсатора. От чего зависит емкость?

Площадь пластин

Расстояние между пластинами

Относительная диэлектрическая проницаемость

Номинальное напряжение

Плоский конденсатор: емкость, напряжение, напряженность и прочее

Расчёт и вывод формулы ёмкости плоского конденсатора

Напряжённость электрического поля конденсатора

Работа по перемещению заряда

Напряжение между пластинами плоского конденсатора

Электрическая ёмкость плоского конденсатора

Добавить комментарий Отменить ответ

ДОМОСТРОЙСантехника и строительство

Комментарии

Как найти напряжение между пластинами конденсатора

Электроемкость конденсатора

Энергия конденсатора

Подсказки к задачам

Соединения конденсаторов

Подсказки к задачам

Разбор задач на тему «Заряженная частица в поле конденсатора»

Заряд на обкладках конденсатора: физика процессов и формула расчёта

Ёмкость, заряд и напряжение

Значение диэлектрика

Формула электрического напряжения между пластинами

Электроемкость. Конденсатор . урок. Физика 10 Класс

Дополнение 1. Электроемкость шара.

Дополнение 2. Соединение конденсаторов.

����� � ������ ������������

Зарядка конденсатора от источника постоянной ЭДС

Заряд и напряжение на конденсаторе

Конденсатор

Плоский конденсатор

Заряд конденсатора. Ток

Заряд конденсатора. Напряжение

Разряд конденсатора

Устройство конденсатора. От чего зависит емкость?

Площадь пластин

Расстояние между пластинами

Относительная диэлектрическая проницаемость

Номинальное напряжение

Плоский конденсатор: емкость, напряжение, напряженность и прочее

Расчёт и вывод формулы ёмкости плоского конденсатора

Напряжённость электрического поля конденсатора

Работа по перемещению заряда

Напряжение между пластинами плоского конденсатора

Электрическая ёмкость плоского конденсатора

Вам также может понравиться

Как установить найти в пуске

Как составить тесты в конструкторе

Как найти эндер корабль в майнкрафте

Добавить комментарий Отменить ответ

��