Эта
задача при расчете электрических цепей
встречается очень часто. Пусть, например,
в цепи на рис. 2.1 требуется найти напряжение
между точками m и n.
Прежде
всего необходимо показать на схеме или
мысленно представить стрелку этого
напряжения. Её направление определяется
порядком следования индексов у буквы 
.
Для напряжения 
она
направлена отточки m к
точке n.
Если мы меняем местами индексы у буквы 
,
то следует изменить и направление
стрелки на схеме. При этом при расчете
меняется знак полученного напряжения,
так как 
.
Дальше
записываются уравнения по второму
закону Кирхгофа для любого контура,
включающего в себя эту стрелку, как было
сделано при расчете напряжений 
и 
.
Так, для контура m31nm при
обходе его по часовой стрелке
.
Отсюда
. (7.1)
При
соответствующем навыке последняя
формула может быть записана сразу, без
составления уравнения второго закона
Кирхгофа.
В
указанном контуре напряжение 
складывается
из трех напряжений:
. (7.2)
Порядок
индексов у букв U соответствует
порядку, в котором мы проходим участок
электрической цепи, идя от точки m к
точке n по
элементам 
, 
и 
.
Теперь
находим значение каждого слагаемого в
последнем уравнении.
Величина 
,
определяющая напряжение между точками m и
3, представляет собой падение напряжения
на сопротивлении 
,
которое мы должны взять со знаком минус,
так как от точки m к
точке 3 мы идем против тока 
:
.
Аналогично
.
Здесь
в правой части уравнения стоит плюс,
так как мысленная стрелка напряжения 
и
ток 
направлены
в одну сторону.
Третье
слагаемое 
представляет
собой напряжение на зажимах источника.
Если внутреннее сопротивление последнего
равно нулю, то это напряжение по величине
равно ЭДС, а знак его зависит от взаимного
направления стрелок напряжения и ЭДС
(рис. 7.1).
Рис.
7.1. Напряжение на зажимах источника
Рассмотрим
рис. 7.1.
При
указанной на схеме полярности зажимов
источника потенциал точки b выше
потенциала точки a на
величину ЭДС:
.
Поэтому
при одинаковых направлениях
стрелок 
и 
(рис.
7.1, а)
.
Если
направления стрелок 
и 
противоположны
друг другу
(рис. 7.1, б),
то
.
С
учетом сказанного напряжение на участке
1n (см.
рис. 2.1) равно
.
Подставляя
найденные значения напряжений на
участках в формулу (7.2), приходим к
выражению (7.1).
То
же самое напряжение, определяемое по
участку m2n,
будет равно
.
Разумеется,
вычисление одного и того же напряжения
по двум различным формулам должно
привести к одинаковым результатам.
8. Построение графиков
8.1. Общие требования к оформлению графиков. Зависимость мощности от тока
Правила
построения графиков рассмотрим на
примере зависимости мощности Р1, выделяющейся
в сопротивлении первой ветви, от тока I1 в
этой ветви. Эта зависимость определяется
уравнением баланса мощностей в схеме
рис. 6.1, в:
.
Так
как 
,
то
. (8.1)
Это
– уравнение параболы со смещенной
вершиной и направленными вниз ветвями
(рис. 8.1).
Значения
тока, при которых парабола пересекает
горизонтальную ось, находятся из
уравнения
и
соответственно равны
и 
.
По
смыслу 
–
это ток, протекающий в схеме рис.
6.1, в при
закороченном сопротивлении 
.
При токе, равном половине этого значения,
мощность 
максимальна:
.
Предположим,
что параметры цепи на рис. 6.1, в имеют
следующие численные значения:
=
72,4 В; 
=
130 В; 
=
43,6 Ом.
Прежде
всего находим максимальные значения
абсциссы и ординаты, которые будут
определять размеры графика. В нашем
примере – это значения 
и 
:
;
.
Исходя
из этих величин и предполагаемых размеров
графика, выбираем масштаб, который
указываем на каждой оси графика в виде
равномерной шкалы.
В
одной единице длины (сантиметре,
миллиметре) может содержаться m × 10n именованных
единиц. Здесь n –
целое число, положительное или
отрицательное, а для mрекомендуются
числа 1, 2, 5.
Положительные
значения величин откладываются вправо
по оси абсцисс и вверх по оси ординат.
В
конце каждой оси ставится буквенное
обозначение откладываемой величины и
через запятую – ее единица измерения.
Если
график строится на белой (нелинованной)
бумаге, то чертится масштабная сетка.
Данные
для построения графика рассчитываем
по формуле (8.1) и сводим их в таблицу
(табл. 8.1).
Таблица
8.1
Данные
для построения графика
|
|
0 |
0,2 |
0,4 |
0,5 |
0,6 |
0,66 |
0,8 |
0,9 |
1 |
1,2 |
1,32 |
|
|
0 |
9,78 |
16,1 |
17,9 |
18,9 |
19 |
18,2 |
16,5 |
14 |
6,34 |
0 |
,Абсциссы
точек, выбираемых для построения графика,
желательно располагать по оси равномерно.
Но вблизи характерных областей кривой
(в нашем случае у вершины параболы) точки
можно взять чаще. В таблицу внесены
также значения максимальной мощности
и тока, которому эта мощность соответствует.
При построении графика числа из таблицы
на осях не показываются (рис. 8.2).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
7. Определение напряжения между двумя точками электрической цепи
Эта задача при расчете электрических цепей встречается очень часто. Пусть, например, в цепи на рис. 2.1 требуется найти напряжение между точками m и n.
Прежде всего необходимо показать на схеме или мысленно представить стрелку этого напряжения. Её направление определяется порядком следования индексов у буквы . Для напряжения она направлена отточки m к точке n. Если мы меняем местами индексы у буквы , то следует изменить и направление стрелки на схеме. При этом при расчете меняется знак полученного напряжения, так как .
Дальше записываются уравнения по второму закону Кирхгофа для любого контура, включающего в себя эту стрелку, как было сделано при расчете напряжений и . Так, для контура m31nm при обходе его по часовой стрелке
.
. (7.1)
При соответствующем навыке последняя формула может быть записана сразу, без составления уравнения второго закона Кирхгофа.
В указанном контуре напряжение складывается из трех напряжений:
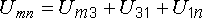. (7.2)
Порядок индексов у букв U соответствует порядку, в котором мы проходим участок электрической цепи, идя от точки m к точке n по элементам , и .
Теперь находим значение каждого слагаемого в последнем уравнении.
Величина , определяющая напряжение между точками m и 3, представляет собой падение напряжения на сопротивлении , которое мы должны взять со знаком минус, так как от точки m к точке 3 мы идем против тока :
.
.
Здесь в правой части уравнения стоит плюс, так как мысленная стрелка напряжения и ток направлены в одну сторону.
Третье слагаемое представляет собой напряжение на зажимах источника. Если внутреннее сопротивление последнего равно нулю, то это напряжение по величине равно ЭДС, а знак его зависит от взаимного направления стрелок напряжения и ЭДС (рис. 7.1).
Рис. 7.1. Напряжение на зажимах источника
При указанной на схеме полярности зажимов источника потенциал точки b выше потенциала точки a на величину ЭДС:
.
Поэтому при одинаковых направлениях стрелок и (рис. 7.1, а)
.
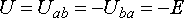Если направления стрелок 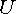и противоположны друг другу (рис. 7.1, б), то
.
С учетом сказанного напряжение на участке 1n (см. рис. 2.1) равно
.
Подставляя найденные значения напряжений на участках в формулу (7.2), приходим к выражению (7.1).
То же самое напряжение, определяемое по участку m2n, будет равно
.
Разумеется, вычисление одного и того же напряжения по двум различным формулам должно привести к одинаковым результатам.
8. Построение графиков
8.1. Общие требования к оформлению графиков. Зависимость мощности от тока
Правила построения графиков рассмотрим на примере зависимости мощности Р1, выделяющейся в сопротивлении первой ветви, от тока I1 в этой ветви. Эта зависимость определяется уравнением баланса мощностей в схеме рис. 6.1, в:
.
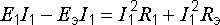Так как 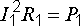, то
. (8.1)
Это – уравнение параболы со смещенной вершиной и направленными вниз ветвями (рис. 8.1).
Значения тока, при которых парабола пересекает горизонтальную ось, находятся из уравнения
и .
По смыслу – это ток, протекающий в схеме рис. 6.1, в при закороченном сопротивлении . При токе, равном половине этого значения, мощность максимальна:
.
Предположим, что параметры цепи на рис. 6.1, в имеют следующие численные значения:
= 72,4 В; = 130 В; = 43,6 Ом.
Прежде всего находим максимальные значения абсциссы и ординаты, которые будут определять размеры графика. В нашем примере – это значения и :
;
.
Исходя из этих величин и предполагаемых размеров графика, выбираем масштаб, который указываем на каждой оси графика в виде равномерной шкалы.
В одной единице длины (сантиметре, миллиметре) может содержаться m × 10 n именованных единиц. Здесь n – целое число, положительное или отрицательное, а для mрекомендуются числа 1, 2, 5.
Положительные значения величин откладываются вправо по оси абсцисс и вверх по оси ординат.
В конце каждой оси ставится буквенное обозначение откладываемой величины и через запятую – ее единица измерения.
Если график строится на белой (нелинованной) бумаге, то чертится масштабная сетка.
Данные для построения графика рассчитываем по формуле (8.1) и сводим их в таблицу (табл. 8.1).
Данные для построения графика
, А
Источник
Напряжение участке электрической цепи
Участок электрической цепи, по которому проходит ток одного и того же значения называют ветвью .
Место соединения трех и более ветвей называют узлом .
Замкнутую электрическую цепь, образованную одной или несколькими ветвями называют контуром .
Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.
На рис. 2.1 изображен участок цепи, содержащий только резистивный элемент, крайние точки которого обозначены буквами a и b. Пусть ток 
направлен от точки a к точке b (от более высокого потенциала к более низкому).
Следовательно, потенциал точки а (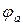
) выше потенциала точки b (
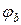) на значение, равное произведению тока на сопротивление R:
.
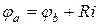В соответствии с определением напряжение между точками а и b
.
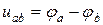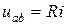
т. е. напряжение на сопротивлении равно произведению тока, протекающего по резистивному элементу, на значение его сопротивления. Последнее выражение называют законом Ома для участка цепи.
В электротехнике разность потенциалов на концах резистивного элемента (сопротивления) называют либо напряжением на сопротивлении, либо падением напряжения. Положительное направление падения напряжения на каком-либо участке (направление отсчета этого напряжения), указываемое на рисунках стрелкой, совпадает с положительным направлением отсчета тока, протекающего по данному сопротивлению.
Рассмотрим вопрос о напряжении на участке цепи, содержащем не только резистивный элемент, но и ЭДС. На рис. 2.2 показан участок цепи, в которой существует ток . Найдем разность потенциалов (напряжение) между точками a и c для этих участков. По определению,
.
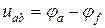Выразим потенциал точки а через потенциал точки f. При перемещении от точки f к точке d встречно направлению ЭДС источника Е2 (рис. 2.2) потенциал точки d оказывается ниже (меньше), чем потенциал точки f, на значение ЭДС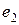 
источника Е2. При перемещении от точки d к точке c согласно направлению ЭДС источника Е1 (рис. 2.2) потенциал точки c оказывается выше (больше), чем потенциал точки d, на значение ЭДС 
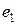источника Е1. При перемещении от точки c к точке b и далее к точке a потенциал точки a оказывается выше (больше) на величину падения напряжения на резисторах R2 и R1, соответственно, т.е.
.
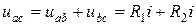Таким образом с учетом вышеизложенного:
,
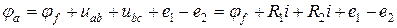напряжение на участке цепи между точками a и f равно:
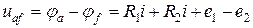
В общем случае напряжение на участке цепи равно сумме падений напряжения на резистивных элементах цепи и сумме ЭДС источников.
Положительное направление напряжения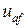 
показывают стрелкой от а к f. Согласно определению 
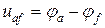, поэтому 
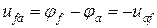т.е. изменение чередования (последовательности) индексов равносильно изменению знака этого напряжения.
Законы Кирхгофа
Первый закон Кирхгофа (уравнение электрического состояния для узла) можно сформулировать двояко:
1) алгебраическая сумма токов, входящих в любой узел схемы (рис.2.3,а), равна нулю:
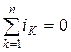
2) сумма токов, входящих в любой узел схемы (рис.2.3,б), равна сумме токов выходящих из этого узла:
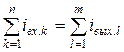
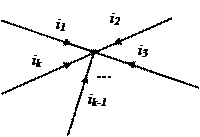
Физически первый закон Кирхгофа означает, что движение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.
Второй закон Кирхгофа (уравнение электрического состояния контура) также можно сформулировать двояко:
1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:
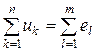
(в каждую из сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним);
2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю:
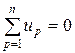
Напряжения участков цепи включают и падения напряжения на резистивных элементах и напряжения на источниках ЭДС.
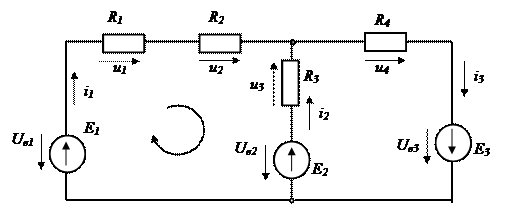
Для левого контура схемы рис.2.4
.
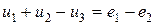
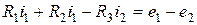Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.
Параллельное и последовательное соединение двухполюсников
Последовательное соединение резистивных элементов
Результирующее падение напряжения на цепи (рис. 2.5) из n последовательно включенных резистивных элементов:
.
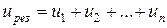В цепи существует общий ток .
Для линейных резистивных элементов:
,
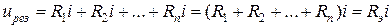где эквивалентное сопротивление цепи из n последовательно соединенных резистивных элементов:
.
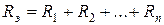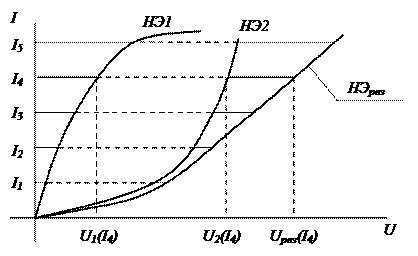
Для нелинейных резистивных элементов НЭ1 и НЭ2 результирующая ВАХ эквивалентного резистивного элемента определяется графическим способом (рис. 2.6).
В интересующем диапазоне токов (соответствующем участку ВАХ нелинейного элемента) задаются несколькими значениями токов (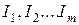
). Для каждого из выбранных значений тока, например 
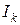, определяют результирующее напряжение на последовательно включенных элементах:
.
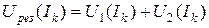На уровне каждой из ординат откладывают найденные значения абсцисс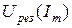 
. Результирующую ВАХ получают, проводя линию через найденные точки.
Параллельное соединение резистивных элементов
При параллельном соединении двухполюсных элементов (рис. 2.7) на их полюсах будет общее падение напряжения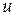 
.
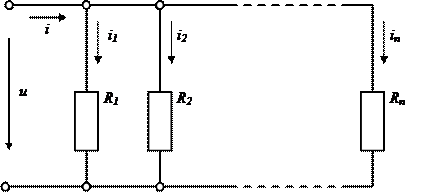
Общий ток , для n параллельно включенных двухполюсных элементов
.
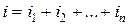Для линейных двухполюсных элементов ток через k-тый резистивный элемент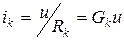 
, где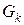 
– проводимость k-того резистивного элемента. Таким образом общий ток
,
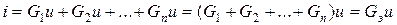где эквивалентная проводимость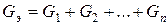 
равна сумме проводимости параллельно включенных двухполюсных элементов.
В частном случае для двух элементов эквивалентная проводимость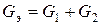 
, или эквивалентное сопротивление
.
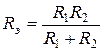Для нелинейных резистивных элементов НЭ1 и НЭ2 результирующая ВАХ эквивалентного резистивного элемента определяется графическим способом (рис. 2.8).
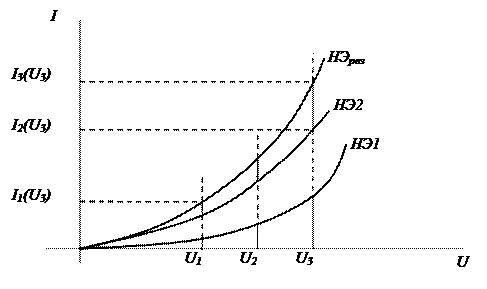
В интересующем диапазоне напряжений (соответствующем участку ВАХ нелинейного элемента) задаются несколькими значениями напряжений (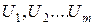
). Для каждого из выбранных значений напряжения, например 
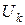, определяют результирующий (суммарный) ток через параллельно включенные элементы:
.
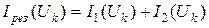На уровне каждой из абсцисс откладывают найденные значения ординат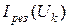 
. Результирующую ВАХ получают проводя линию через найденные точки.
Последовательное и параллельное соединение линейных индуктивных элементов
При последовательном соединении n линейных индуктивных элементов их результирующая индуктивность определяется
.
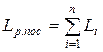При параллельном соединении n линейных индуктивных элементов их результирующая индуктивность определяется
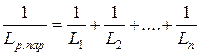, или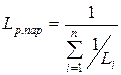 
.
Последовательное и параллельное соединение линейных емкостных элементов
При последовательном соединении n линейных емкостных элементов их результирующая емкость определяется
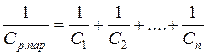, или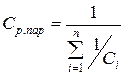 
.
При параллельном соединении n линейных емкостных элементов их результирующая емкость определяется
Источник
Напряжение электрического тока
4.2
Средняя оценка: 4.2
Всего получено оценок: 134.
4.2
Средняя оценка: 4.2
Всего получено оценок: 134.
Электрическое напряжение между двумя точками электрической цепи или электрического поля равно разности потенциалов в этих точках. Эта величина эквивалентна работе, которую производит электрическое поле при перемещении единичного электрического заряда из начальной точки в конечную. В зависимости от вида приложенного напряжения (постоянного или переменного) в электрической цепи формируется ток, величина которого определяется по формуле закона Ома.
Закон Ома
Электрическая цепь состоит из отдельных участков — однородных и неоднородных. Участки цепи, на которых отсутствует действие сторонних сил, т.е.участки, без источников тока, называются однородными. Участки цепи, на которых имеются источники тока, называются неоднородными.
Формула закона Ома для однородного участка цепи выглядит так:
$ I = {U over R} $ (1).
Полностью формулировка закона Ома звучит следующим образом: сила тока I для проводника на однородном участке цепи прямо пропорциональна напряжению U на этом участке и обратно пропорциональна сопротивлению проводника R.
Для неоднородного участка цепи, содержащего источник тока с электродвижущей силой Еэдс ,закон Ома записывается в следующем виде:
$ I = {E_{эдс} over R + r} $ (2),
где: R — сопротивление цепи, r — сопротивление источника тока. Уравнение (2) называется законом Ома для полной цепи: сила тока в полной цепи равна ЭДС источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Виды напряжений
В электрических цепях используются два основных напряжения электрического тока: постоянное и переменное.
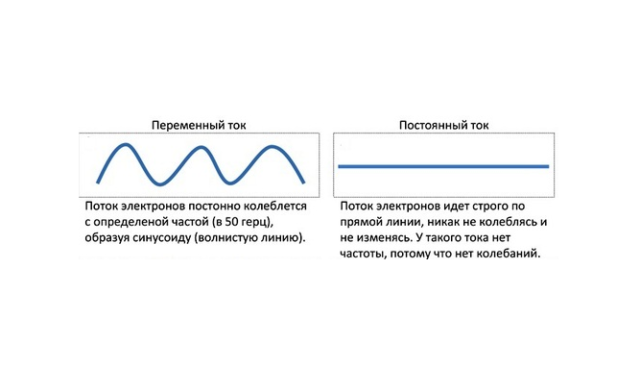
Постоянное во времени напряжение создается источниками тока (батареи, аккумуляторы), на концах которых долгое время сохраняется одна и та же разность потенциалов (ЭДС).
Электрический ток в этом случае тоже постоянен во времени и течет в одном направлении. Постоянное напряжение используется, когда не требуется транспортировать электроэнергию на большие расстояния: в электрических схемах, на транспорте, в военной и космической технике и т.д.
При изменении полярности потенциалов на клеммах источника, электрический ток тоже будет менять свое направление (колебаться), следуя по закону Ома за временными изменениями напряжения. Количество таких колебаний за определенный промежуток времени (период) называется частотой. Чаще всего используется синусоидальная зависимость тока от времени.
В России стандартная частота составляет 50 Герц, что соответствует изменениям полярности напряжения (и направления тока) 50 раз в секунду. Эти мерцания (пульсации) человеческий глаз не чувствует при использовании в системах освещения. Но в телевизорах и дисплеях компьютеров эту частоту повышают (от 85 Гц и выше), так как при долгом, пристальном рассматривании глаза начинают уставать.
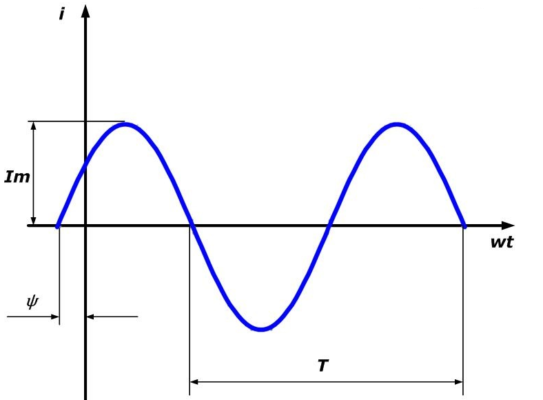
Переменный ток применяется при передаче электроэнергии на большие расстояния. Для этих целей лучше всего подходят трехфазные сети, которые подключены к электростанциям (тепловым, атомным, гидро-), где турбины генерируют такой переменный вид напряжения электрического тока.
Единицы измерения
В международной системе единиц (системе СИ) единица измерения напряжения (В) названа в честь итальянского исследователя Алессандро Вольта (1745-1827г.). Так как работа измеряется в джоулях (Дж), а заряд в кулонах (К), то:
$$ [1В] ={ [1 Дж]over [1 К] } $$
Единица измерения тока — ампер. Это одна из семи базовых единиц в системе СИ. Ток может изменяться (и измеряться) в широчайших пределах, поэтому часто используются такие внесистемные единицы, как:
- 1 наноампер (нА) = 10-9 А;
- 1 микроампер (мкА) = 0,000001 А;
- 1 миллиампер (мА) = 0,001 А;
- 1 килоампер (кА) = 1000 А.
Что мы узнали?
Итак, мы узнали, что величина напряжения равна работе, которую производит электрическое поле при перемещении единичного электрического заряда из начальной точки в конечную. В электрических цепях находят применение два основных вида напряжения электрического тока: постоянное и переменное. Передача электроэнергии на большие расстояния осуществляется с помощью переменного тока.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 134.
А какая ваша оценка?
Разводка электрических схем
Добавлено 18 октября 2020 в 18:13
До сих пор мы анализировали схемы с одной батареей и одним резистором, не учитывая соединительные провода между компонентами при формировании полной цепи. Имеет ли значение для наших расчетов длина провода или «форма» цепи? Давайте посмотрим на несколько принципиальных схем и выясним это.
Когда мы рисуем провода, соединяющие точки в электрической цепи, мы обычно предполагаем, что эти провода имеют незначительное сопротивление. Таким образом, они не вносят заметного влияния в общее сопротивление цепи, и поэтому единственное сопротивление, с которым нам приходится иметь дело, – это сопротивление компонентов. В приведенных выше схемах единственное сопротивление вносится резисторами 5 Ом, поэтому это всё, что мы будем учитывать в наших расчетах. В реальной жизни металлические провода на самом деле также обладают сопротивлением (как и источники питания!), но эти сопротивления, как правило, намного меньше, чем сопротивление других компонентов схемы, и поэтому их можно без опасений игнорировать. Исключения из этого правила составляют разводка мощных систем, где даже очень небольшое сопротивление проводника может вызвать значительные падения напряжения при обычных (в этом случае высоких) уровнях силы тока.
Электрически общие точки в цепи
Если сопротивление соединительного провода очень мало или отсутствует, мы можем рассматривать соединенные этим проводом точки в цепи как электрически общие. То есть точки 1 и 2 в приведенных выше цепях могут быть физически близко друг к другу или далеко друг от друга, но это не имеет значения для любых измерений напряжения или сопротивления относительно этих точек. То же самое касается точек 3 и 4. Это как если бы выводы резистора были подключены непосредственно к клеммам батареи для всего, что касается наших расчетов по закону Ома и измерений напряжения. Это полезно знать, потому что это означает, что вы можете заново нарисовать принципиальную схему или повторно развести схему, по желанию сокращая или удлиняя провода, не оказывая заметного влияния на работу схемы. Важно только то, что компоненты соединяются друг с другом в одинаковой последовательности.
Это также означает, что измерения напряжения между наборами «электрически общих» точек будут одинаковыми. То есть напряжение между точками 1 и 4 (непосредственно на батарее) будет таким же, как напряжение между точками 2 и 3 (непосредственно на резисторе). Внимательно посмотрите на следующую схему и попытайтесь определить, какие точки являются общими друг для друга:
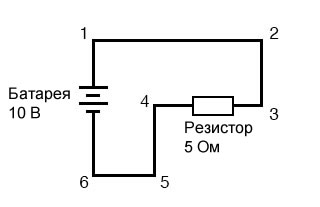
Здесь у нас есть только 2 компонента, не считая проводов: батарея и резистор. Хотя соединительные провода образуют законченную цепь извилистым путем, на пути тока есть только несколько электрически общих точек. Точки 1, 2 и 3 являются общими друг для друга, потому что они напрямую связаны между собой проводом. То же самое и с точками 4, 5 и 6.
Напряжение между точками 1 и 6 составляет 10 вольт, идущее прямо от батареи. Однако, поскольку точки 5 и 4 являются общими для 6, а точки 2 и 3 являются общими для 1, те же 10 вольт также присутствуют и между этими другими парами точек:
Между точками 1 и 4 = 10 вольт
Между точками 2 и 4 = 10 вольт
Между точками 3 и 4 = 10 вольт (непосредственно на резисторе)
Между точками 1 и 5 = 10 вольт
Между точками 2 и 5 = 10 вольт
Между точками 3 и 5 = 10 вольт
Между точками 1 и 6 = 10 вольт (непосредственно на батарее)
Между точками 2 и 6 = 10 вольт
Между точками 3 и 6 = 10 вольтПоскольку электрически общие точки соединены вместе проводом (нулевого сопротивления), между ними нет значительного падения напряжения, независимо от величины тока, проводимого через этот соединительный провод от одной физической точки к другой. Таким образом, если бы мы измеряли напряжения между общими точками, мы должны были бы измерить (практически) ноль:
Точки 1, 2 и 3 электрически общие
между точками 1 и 2 = 0 вольт
между точками 2 и 3 = 0 вольт
между точками 1 и 3 = 0 вольт
Точки 4, 5 и 6 электрически общие
между точками 4 и 5 = 0 вольт
между точками 5 и 6 = 0 вольт
между точками 4 и 6 = 0 вольтРасчет падения напряжения по закону Ома
Это также имеет смысл математически. С батареей на 10 В и резистором 5 Ом ток в цепи будет 2 ампера. Если сопротивление провода равно нулю, падение напряжения на любом непрерывном участке провода можно определить с помощью закона Ома:
(E=IR)
(E=(2 А)(0 Ом))
(E = 0 В)
Должно быть очевидно, что рассчитанное падение напряжения на любом непрерывном отрезке провода в цепи, где предполагается, что провод имеет нулевое сопротивление, всегда будет равно нулю, независимо от величины тока; поскольку ноль, умноженный на что-либо, равен нулю. Поскольку общие точки в цепи будут показывать одинаковые результаты измерений напряжения и сопротивления, то провода, соединяющие общие точки, часто имеют одно и то же обозначение. Это не означает, что точки подключения клемм имеют одинаковую маркировку, только соединительные провода. Возьмем для примера эту схему:
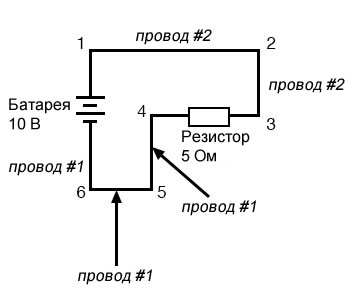
Точки 1, 2 и 3 являются общими друг для друга, поэтому провод между точками 1 и 2 обозначен так же (провод #2), как провод, соединяющий точки 2 и 3 (провод #2). В реальной схеме провод, тянущийся от точки 1 до 2, может даже быть не того же цвета или размера, что и провод, соединяющий точки 2 и 3, но они должны иметь одинаковые метки. То же самое касается проводов, соединяющих точки 6, 5 и 4.
Падение напряжения между общими точками должно равняться нулю
Знание того, что электрически общие точки имеют нулевое падение напряжения, является ценным принципом поиска и устранения неисправностей. Если я измеряю напряжение между точками в цепи, которые должны быть общими друг для друга, я должен получить значение ноль. Однако если я обнаружил значительное напряжение между этими двумя точками, то я могу с уверенностью сказать, что они не могут быть соединены вместе напрямую. Если эти точки должны быть электрически общими, но показания вольтметра говорят другое, то я знаю, что в схеме есть неисправность, а именно «разрыв» между этими точками.
Нулевое напряжение технически означает незначительное напряжение
Последнее замечание: для большинства практических целей можно предположить, что проводники имеют нулевое сопротивление. Однако в действительности по длине провода всегда будет присутствовать какое-то небольшое сопротивление, если только это не провод из сверхпроводника. Зная это, мы должны иметь в виду, что изученные здесь принципы в отношении общих электрических точек корректны в значительной степени, но не в абсолютной. То есть правило, согласно которому электрически общие точки гарантированно имеют нулевое напряжение между ними, более точно сформулировано следующим образом: электрически общие точки будут иметь очень маленькое падение напряжения между ними. Это небольшое, практически неизбежное сопротивление, обнаруживаемое в любом куске соединительного провода, при прохождении тока должно создавать маленькое падение напряжения по всей его длине. Пока вы понимаете, что эти правила основаны на идеальных условиях, вы не будете недоумевать, когда столкнетесь с каким-либо условием, которое может показаться исключением из правила.
Резюме
- Предполагается, что соединительные провода в цепи имеют нулевое сопротивление, если не указано иное.
- Провода в цепи можно укорачивать или удлинять, не влияя на работу схемы; всё, что имеет значение, – это то, что компоненты подключены друг к другу в одинаковой последовательности.
- Точки, напрямую соединенные в цепь нулевым сопротивлением (проводом), считаются электрически общими.
- Электрически общие точки с нулевым сопротивлением между ними будут иметь нулевое падение напряжения между ними, независимо от величины тока (в идеале).
- Показания напряжения или сопротивления между наборами электрически общих точек будут одинаковыми.
- Эти правила применимы к идеальным условиям, когда предполагается, что соединительные провода имеют абсолютно нулевое сопротивление. В реальной жизни это, вероятно, не так, но сопротивление проводов должно быть достаточно низким, чтобы общие принципы, изложенные здесь, оставались в силе.
Теги
Закон ОмаПроводникСопротивлениеСхемотехникаЭлектричество
Закон Ома для участка цепи — одна из основ электротехники. Данный закон указывает на соотношение между током, напряжением и сопротивлением.
Сам Закон Ома для участка цепи гласит так:
Сила тока в проводнике (участке электрической цепи) прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника (участка электрической цепи)
[Г.С. Ом, 1826]
Из этого определения Георг Ом вывел следующую формулу:
I = U/R или U = R*I
Формула, вытекающая из закона Ома, также известна в просторечии как формула URI. Такое название появилось от последовательности букв в формуле:
U = R*I
- R — сопротивление проводника (Ом);
- I — сила тока в проводнике (Ампер);
- U — напряжение приложенное к проводнику (Вольт).
Электрическая цепь и закон Ома
Три величины — напряжение, электрический ток и сопротивление — могут быть четко представлены в электрической цепи. В простейшем случае она состоит из источника постоянного напряжения и резистора. Резистор подключен к источнику напряжения, а для упрощения возьмем, что сопротивление проводов равно 0 Ом.
Направление электрического тока.
В электротехнике ток течет от плюса до минуса (смотрите рисунок 1). Другими словами, как только возникает замкнутая цепь, ток начинает течь от положительного полюса к отрицательному полюсу источника напряжения. Мы говорим о замкнутой цепи, когда два полюса источника напряжения соединены друг с другом сопротивлением.
Как и чем измерять ток и напряжение?
Есть два способа определения силы тока и напряжения. С одной стороны, их можно определить арифметически с помощью закона Ома для участка цепи. С другой стороны, две переменные также могут быть определены путем измерения.
Однако для арифметического определения тока или напряжения должны быть известны две другие величины (напряжение и сопротивление либо ток и сопротивление).
С другой стороны, метрологический метод также работает с любой электрической цепью. Для этого в электрическую цепь необходимо вставить амперметр и вольтметр . Они используются для измерения силы тока и напряжения. Но здесь также применяется закон Ома, поскольку сопротивление нельзя измерить напрямую, но его можно будет рассчитать, когда будут измерены значения тока и напряжения.
Итак, ток измеряется так амперметром, который последовательно подключается к потребителю (резистору, лампе накаливания и т. д.), Через который нужно определять ток. На принципиальной схеме он изображен как A внутри круга (см. рисунок 1). Амперметр имеет очень низкое внутреннее сопротивление, чтобы не влиять на ток, который должен протекать через потребителя. В идеале, внутреннее сопротивление амперметра принимается равным 0 Ом и поэтому просто опускается.
Измерение напряжения производится с помощью вольтметра, который замеряет разность потенциалов между двумя его точками подключения. На электрической схеме он обозначен буквой V внутри круга (см. рисунок 1). В отличие от амперметра, вольтметр подключается параллельно нагрузке, на которой измеряется напряжение. Добавление вольтметра параллельно некоторому потребителю (например, резистору) создает току еще один «обходной» путь, что резко изменяет параметры цепи. Чтобы избежать этих нежелательных последствий, надо применять вольтметры с максимально большим сопротивлением.
Вольт-амперная характеристика (ВАХ).
Вольт-амперная характеристика или характеристика UI резистора может быть записана путем приложения к нему различных напряжений и последующего измерения тока. Обычно при омическом сопротивлении достаточно одной точки измерения, которая затем соединяется с началом системы координат. Однако на практике, для целей контроля, выполняют серию измерений с тремя точками измерения.
Затем эти точки измерения отмечаются в системе координат и соединяются. Напряжение откладывают по оси абсцисс, а ток — по оси ординат. Пример ВАХ смотрите на рисунке ниже
ВАХ может быть использована для определения тока через резистор при определенном напряжении.
«Треугольник Ома»
Связь между отдельными величинами из закона Ома может быть показана в так называемом «треугольнике Ома».
Вверху треугольника вы найдете напряжение U, слева — сопротивление R, а справа — ток I.
Если вы хотите определить недостающую величину, то прикройте эту величину мысленно или пальцем, а затем посмотрите на две другие величины. Если две «не закрытые» величины находятся рядом друг с другом, то они умножаются. С другой стороны, если они расположены друг над другом, то верхняя величина делится на нижнюю.
Например, вы «закрываете» напряжение U в вершине «треугольника Ома». Две оставшиеся величины, то есть сопротивление R и ток I, находятся рядом. Соответственно, чтобы получить напряжение U, нужно умножить сопротивление R на ток I. Это в точности соответствует формуле закона Ома для участка электрической цепи.
Калькулятор, который основан на законе Ома
Используйте этот калькулятор, который основан на законе Ома для расчета соотношений между током, напряжением, сопротивлением и мощностью в электрических цепях. Чтобы воспользоваться калькулятором, введите значения в 2 любых поля и нажмите кнопку «рассчитать».
Таблица-шпаргалка
Используя закон Ома для участка цепи, а также формулу для мощности электрического тока: P = U*I – я подготовил для вас полезную таблицу-шпаргалку, которая позволяет соотносить между собой сопротивление (R), силу тока (I), напряжение (U) и мощность электрического тока (P). Будет точно полезно не только школьникам!
| Известные величины | R (сопротивление) | I (сила тока) | U (напряжение) | P (мощность) |
| Ток и сопротивление | U = I × R | P = I2 × R | ||
| Напряжение и ток | R = U / I | P = U × I | ||
| Мощность и ток | R = P / I2 | U = P / I | ||
| Напряжение и сопротивление | I = U / R | P = U2 / R | ||
| Мощность и сопротивление | I = P / R | |||
| Напряжение и мощность | R = U2 / R | I = P / U |
Пример применения закона Ома
В этом примере лампочка накаливания подключена к источнику постоянного напряжения с U=12 В. Цель – определить сопротивление лампочки. Для измерения силы тока также имеется амперметр.
Первая часть задачи – определить силу тока с помощью амперметра. Для этого его необходимо правильно вставить в цепь. Поскольку мы будем вычислять электрический ток, который протекает через лампочку, амперметр должен быть подключен последовательно с ней.
Непосредственно после включения источника напряжения измеряется ток I, равный 1A. Сопротивление лампочки можно рассчитать по закону Ома:
R = U / I = 12В / 1А = 12 Ом.
Через некоторое время вы снова смотрите на амперметр и замечаете, что ток упал до 200 мА.
Сопротивление лампочки изменилось. Почему так произошло? Это связано с разной температурой в момент включения и во время обычной работы, так как лампочка нагревается. Поэтому сопротивление холодной лампы ниже, чем теплой. Именно поэтому лампочку часто называют терморезистором.
Список использованной литературы
- Физика, 8 класс. Л.А. Исаченкова, Ю.Д. Лещинский, В.В. Дорофейчик. Издательство «Народная асвета»
- Физика. 8 класс. Учебник для общеобразовательных учреждений. Перышкин А.В.
