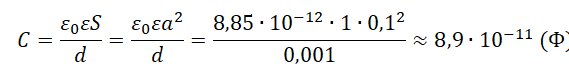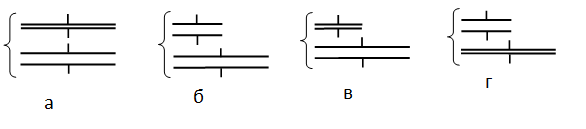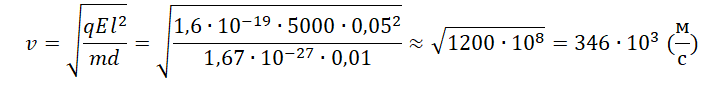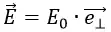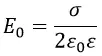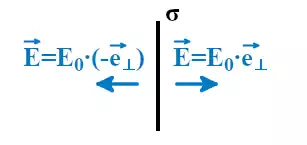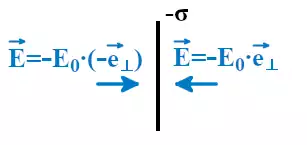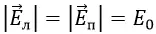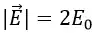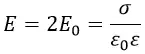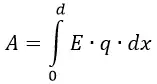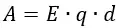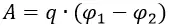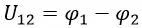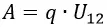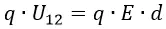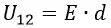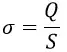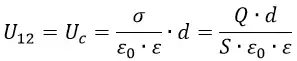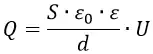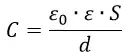Как найти напряжение между пластинами конденсатора
Одним из разделов физики, лежащих в основе знания, посвященного процессам, связанным с электричеством, является электростатика. Она изучает взаимодействие неподвижных электрических зарядов. Поэтому одной из типичных задач, которую может потребоваться решить школьникам и студентам младших курсов ВУЗ-ов, является нахождение напряжения между пластинами конденсатора на основании знания различных параметров.

Вам понадобится
- – знание емкости или геометрических и физических параметров конденсатора;
- – знание энергии или заряда на конденсаторе.
Инструкция
Найдите напряжение между пластинами конденсатора, если известна текущая величина накопленной им энергии, а также его емкость. Энергия, запасенная конденсатором, может быть вычислена по формуле W=(C∙U²)/2, где C – емкость, а U – напряжение между пластинами. Таким образом, значение напряжения может быть получено как корень из удвоенного значения энергии, деленного на емкость. То есть, оно будет равно: U=√(2∙W/C).
Энергия, запасенная конденсатором, также может быть вычислена на основании значения содержащегося в нем заряда (количества электричества) и напряжения между обкладками. Формула, задающая соответствие между этими параметрами, имеет вид: W=q∙U/2 (где q – заряд). Следовательно, зная энергию и заряд конденсатора, можно вычислить напряжение между его пластинами по формуле: U=2∙W/q.
Поскольку заряд на конденсаторе пропорционален как приложенному к его пластинам напряжению, так и емкости устройства (он определяется формулой q=C∙U), то, зная заряд и емкость, можно найти и напряжение. Соответственно, для проведения расчета используйте формулу: U=q/C.
Для получения значения напряжения на конденсаторе с известными геометрическими и физическими параметрами, сначала рассчитайте его емкость. Для простого плоского конденсатора, состоящего из двух проводящих пластин, разделенных диэлектриком, расстояние между которыми пренебрежимо мало по сравнению с их размерами, емкость может быть вычислена по формуле: C=(ε∙ε0∙S)/d. Здесь d – расстояние между пластинами, а S – их площадь. Значение ε0 – электрическая постоянная (константа, равная 8,8542•10^-12 Ф/м), ε – относительная диэлектрическая проницаемость пространства между пластинами (ее можно узнать из физических справочников). Вычислив емкость, рассчитайте напряжение одним из методов, приведенных в шагах 1-3.
Обратите внимание
Для получения корректных результатов при вычислении напряжений между обкладками конденсаторов, перед проведением расчетов приводите значения всех параметров в систему СИ.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Наряду с резисторами одними из наиболее часто используемых электронных компонентов являются конденсаторы. И в этой статье мы разберемся, из чего они состоят, как работают и для чего применяются! Давайте, в первую очередь, рассмотрим устройство и принцип работы конденсаторов. А затем плавно перейдем к основным свойствам и характеристикам — заряду, энергии и, конечно же, емкости конденсатора. Как видите, нам сегодня предстоит изучить много интересных моментов 🙂
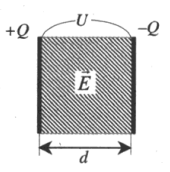
Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:
Такое устройство называется плоским конденсатором, а пластины — обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).
А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.
Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:
Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:
Здесь sigma — это поверхностная плотность заряда: sigma = frac
, а varepsilon — диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:
Но направления векторов разные — внутри конденсатора вектора направлены в одну сторону, а вне — в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:
А какая же будет величина напряженности вне конденсатора? А все просто — слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0 🙂
Процессы зарядки и разрядки конденсаторов.
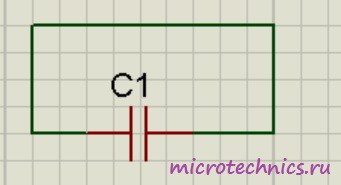
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:
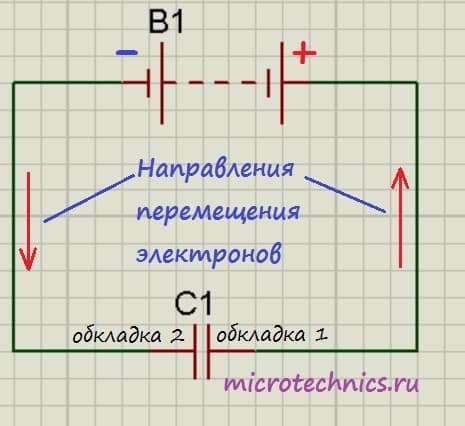
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?
Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.
При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.
Как видите, здесь нет ничего сложного 🙂
Емкость и энергия конденсатора.
Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда конденсатора q одного из проводников к разности потенциалов между проводниками:
Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:
Здесь у нас d — это расстояние между пластинами конденсатора, а q — заряд конденсатора. Подставим эту формулу в выражение для емкости:
Если в качестве диэлектрика у нас выступает воздух, то во всех формулах можно подставить varepsilon = 1 .
Для запасенной энергии конденсатора справедливы следующие выражения:
Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.
Итак, мы сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики! Так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку. Не пропустите!
Источник
Конденсаторы
теория по физике 🧲 электростатика
Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.
Плоский конденсатор — система двух разноименно заряженных пластин.
Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:
Электроемкость конденсатора
Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.
Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).
Электроемкость конденсатора определяется формулой:
- ε 0 — диэлектрическая постоянная, равная 8,85∙10 –12 Кл 2 /(Н∙м 2 );
- ε — диэлектрическая проницаемость среды;
- S (м 2 ) — площадь каждой пластины.
Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.
Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:
Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.
Энергия конденсатора
Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:
Подсказки к задачам
| Конденсатор отключен от источника | q = q′ |
| Конденсатор подключен к источнику | U = U′ |
| Количество теплоты и энергия конденсатора | Q = ∆Wэ |
Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.
Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.
Площадь квадратной пластины равна квадрату ее стороны:
Соединения конденсаторов
Подсказки к задачам
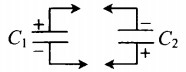
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами. | Схема соединения конденсаторов одноименными полюсами: 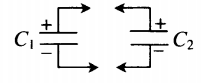 Заряд системы после соединения: Заряд системы после соединения: |
Электрическая емкость системы:
U′ = q ′ C ′ . . = C 1 U 1 + C 2 U 2 C 1 + C 2 . .
Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами.
Схема соединения конденсаторов разноименными полюсами:
Заряд системы после соединения:
Электрическая емкость системы:
U′ = q ′ C ′ . . = C 1 U 1 − C 2 U 2 C 1 + C 2 . .
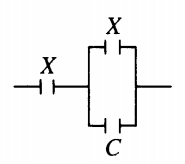
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.
Электрическая емкость параллельного соединения равна:
Электроемкость последовательного соединения:
1 C п о с л е д . . = 1 C п а р а л . . + 1 X . . = 1 X + C . . + 1 X . .
Учтем, что суммарная электроемкость равна C:
Преобразуем, умножим выражение на CX(X+C):
Решив уравнение, получим: X = 25,9 пФ.
Разбор задач на тему «Заряженная частица в поле конденсатора»
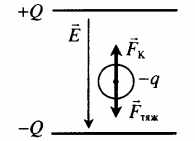
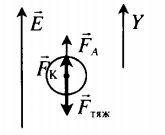
| Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U? | Условие равновесия исходит из второго закона Ньютона: |
ρш > ρ, поэтому − F т я ж > − F A . В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так:
Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения:
F т я ж = ρ ш 4 3 . . π r 3 g
Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения:
q U d . . + ρ 4 3 . . π r 3 g = ρ ш 4 3 . . π r 3 g
q = ( ρ ш 4 3 . . π r 3 g − ρ 4 3 . . π r 3 g ) d U . . = 4 π r 3 g d ( ρ ш − ρ ) 3 U . .
Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l? 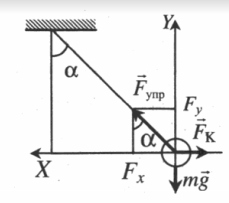
Условие равновесия исходит из второго закона Ньютона:
− F т я ж + − F K + − F у п р = 0
Проекции на оси ОХ и ОУ соответственно:
Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их:
( k Δ l ) 2 sin 2 . α + ( k Δ l ) 2 cos 2 . α = ( q U d . . ) 2 + ( m g ) 2
( k Δ l ) 2 ( sin 2 . α + cos 2 . α ) = ( q U d . . ) 2 + ( m g ) 2
( k Δ l ) 2 = ( q U d . . ) 2 + ( m g ) 2
U = d q . . √ ( k Δ l ) 2 − ( m g ) 2
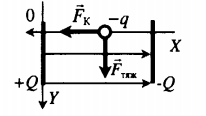
Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь. Второй закон Ньютона в векторной форме:
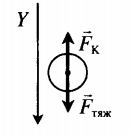
Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью − E , направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли? Второй закон Ньютона в векторной форме:
Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок:
Если Fтяж > FK, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны:
Начальная скорость шарика равна нулю. Поэтому перемещение также равно:
Выполняя вычисления для случая Сделаем вычисления для случая Fтяж t = √ 2 b m q E − m g . .
Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого − E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер. Второй закон Ньютона в векторной форме:
Если сила Кулона направлена вправо, то sx = d.
Если сила Кулона направлена вправо, то sx = b.
Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево.
Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно:
Проекции перемещений на эти же оси:
Так как время движения шарика по вертикали и горизонтали одинаково:
t 2 = 2 Δ h g . . = 2 m b q E . .
Введите ответ в поле ввода Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Емкость конденсатора определяется формулой:
Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.
Вот как взаимосвязана электроемкость и заряд конденсатора:
Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.
С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.
Алгоритм решения
На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.
На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:
S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.
Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.
На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:
Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?
Алгоритм решения
- Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
- Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.
Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.
pазбирался: Алиса Никитина | обсудить разбор | оценить
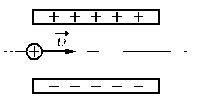
Ответ записать в км/с, округлив до десятков.
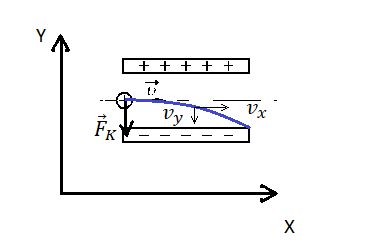
Алгоритм решения
Изначально протон обладает только горизонтальной скоростью v, равной vx. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.
Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью vx:
Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):
Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:
Приравняем правые части уравнений времени и получим:
Ускорение выразим из второго закона Ньютона:
Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙10 3 м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Источник
E0 здесь жёстко определяется поверхностной плотностью заряда σ:
где σ – поверхностная плотность заряда;
ε0 – диэлектрическая проницаемость для вакуума;
ε – относительная диэлектрическая проницаемость для вещества, которая для вакуума равна 1.
Формулы показывают, что величина напряжённости электрического поля плоской пластины, имеющей бесконечные размеры, не зависит от расстояния до неё.
Если σ положительная, то напряжённость электрического поля будет направлена от пластины и поле отталкивает положительные заряды.
Если σ отрицательная, то напряжённость электрического поля направлена к пластине и поле притягивает положительные заряды.
Плоским конденсатором будем называть пару параллельных плоских пластин с плотностью заряда одинаковой по модулю, но противоположной по знаку.
Расчёт и вывод формулы ёмкости плоского конденсатора
Напряжённость электрического поля конденсатора
Для расчёта плоского конденсатора расположим две пластины бесконечных размеров параллельно друг другу на некотором расстоянии d. Пусть одна пластина будет иметь поверхностную плотность заряда σ, а другая -σ. По модулю величины поверхностных плотностей зарядов будут равны. В такой ситуации общее поле плоского конденсатора по принципу суперпозиции равно сумме полей.
Обозначим напряжённости электрического поля от левой пластины плоского конденсатора как Eл, при этом положительные заряды будут отталкиваться от пластины.
Напряжённость электрического поля от правой пластины плоского конденсатора обозначим как Eп, при этом поле пластины будет притягивать к себе положительные заряды.
При равной плотности заряда напряжённость поля во всех точках пространства и от левой, и от правой пластин конденсатора будут равны по модулю. Это приведёт к тому, что слева и справа от пары пластин поля взаимно компенсируются и их сумма будет равна нулю. При этом поля между пластинами плоского конденсатора будут складываться.
где E0 – напряжённость поля при положительной σ.
Суммарная напряжённость электрического поля плоского конденсатора будет направлена от пластины с положительной σ к пластине с отрицательной σ.
Электрическая энергия плоского конденсатора отсутствует вне его пластин и вся накоплена в пространстве между пластинами.
Работа по перемещению заряда
Для перемещения заряда от отрицательно заряженной пластины в направлении к положительно заряженной придётся совершить работу против электрической силы:
При вычислении этой работы видно, что величина заряда q и напряжённость поля E постоянны, поэтому формула примет вид:
В электрическом поле можно ввести понятие потенциала ϕ и выразить работу по перемещению заряда в точку 2 из точки 1 через разность потенциалов ϕ1-ϕ2.
Напряжение между пластинами плоского конденсатора
Разность электрических потенциалов между двумя точками называют напряжением и обозначают U12:
Таким образом, сравнивая две формулы для работы мы получим:
В реальном конденсаторе площадь пластин ограничена по естественным причинам, поэтому, как правило, мы не имеем возможности знать плотность заряда, а знаем только заряд пластины. В этом случае плотность заряда σ мы можем вычислить по формуле:
где Q – заряд пластины;
S – площадь пластины.
Если пластины плоского конденсатора находятся достаточно близко друг к другу, то краевыми эффектами можно пренебречь и считать, что поле внутри конденсатора реальных размеров подобно полю внутри конденсатора с пластинами бесконечных размеров.
В таком случае имеем следующее выражение:
Напряжение между пластинами пропорционально полному заряду этих пластин:
Электрическая ёмкость плоского конденсатора
Коэффициент пропорциональности между зарядом на обкладках плоского конденсатора и напряжением между ними носит название ёмкости плоского конденсатора и обозначается буквой C:
Подробности венецианская штукатурка для внутренней отделки цена на сайте.
Проводники электричества — это вещества и материалы, которые хорошо проводят электричество. Схема из двух проводящих пластин, расположенных параллельно друг другу, называется плоским конденсатором.
Однако конденсаторы — это не только искусственные устройства. Часто в природе мы встречаем системы, которые можно рассматривать как плоские конденсаторы. Примером такого «конденсатора» являются клеточные мембраны внутри вашего тела (рис. 1). Знаете ли вы, какова напряженность электрического поля внутри такой мембраны?
Клеточная мембрана: биологическая мембрана, функция которой заключается в отделении внутренней части клетки от внешней среды. Эта мембрана состоит из двух липидных слоев. Между его стенками существует разность потенциалов. Это позволяет ему реагировать на внешние раздражители.
Что такое плоский конденсатор?
Плоский конденсатор — это расположение двух параллельных друг другу металлических пластин, называемых обкладками конденсатора. Пусть площадь каждой из этих пластин равна S, а расстояние между крышками равно d. На рисунке 2 показана схема заряженного плоского конденсатора.
Линии электрического поля обозначены на рис. 2. В каждой точке вектор напряженности электрического поля одинаков, т.е. поле однородно.
Согласно закону Гаусса, значение напряженности поля от каждой обкладки составляет: E+/- = σ / 2ε0 .
Закон Гаусса (для электричества):
Закон Гаусса (для электричества): уравнение, связывающее электрическое поле и его источник. Оно гласит, что поток ФE напряженности электрического поля Е, проникающий через любую замкнутую поверхность S, равен суммарному заряду q внутри этой поверхности, деленному на диэлектрическую проницаемость вакуума.
Напротив, результирующая напряженность поля от обоих покрытий составляет:
E = E+ + E— = 2 * σ / 2ε0 = σ / ε0 , где
σ — плотность поверхностного заряда, определяемая как отношение заряда q, накопленного на поверхности, к величине площади поверхности S: σ = q / S ,
ε0 — диэлектрическая проницаемость вакуума, ε0 = 8,85 · 10-12 Ф · м−1 .
Таким образом:
E = q / S * ε0
Из приведенной выше формулы мы можем определить единицу напряженности поля — [ В / м ].
Таким образом, единицей напряженности электрического поля, помимо ньютона на кулон, является вольт на метр.
Расчет разности потенциалов между обкладками плоского конденсатора
Итак, мы уже знаем, как выглядит поле между обкладками плоского конденсатора. Теперь рассмотрим, существует ли связь между разностью потенциалов и напряженностью электростатического поля в конденсаторе. В конце концов, и напряженность, и потенциал являются величинами, характеризующими электростатическое поле.
По определению, разность потенциалов ΔV между точками A и B электрического поля равна отношению работы, необходимой для переноса пробного заряда между этими точками (WAB), к величине этого заряда.
ΔV = WAB / q
Единицей измерения потенциала является вольт, который мы обозначаем символом В.
В случае плоского конденсатора, когда мы перемещаем заряд в однородном электрическом поле, работа WAB равна скалярному произведению вектора силы, действующей на образец заряда, и вектора смещения с длиной, равной расстоянию между обкладками d, и возвратом, соответствующим возврату вектора напряженности электрического поля (рис. 3).
WAB = F * d
Из определения напряженности электрического поля следует, что: F = E * q
То есть:
WAB = F * d = E * q * d = q * E * d * cos α
Где α (угол между вектором напряженности электрического поля и вектором смещения) равен 0, т.е. cosα = 1. Поэтому:
WAB = E * d * q
Подставляя приведенную выше формулу для: ΔV = WAB / q = q * E * d / q = E * d
Эта формула определяет связь между разностью потенциалов и напряженностью электрического поля в плоском конденсаторе.
Теперь преобразуем эту формулу, чтобы получить зависимость напряженности поля от разности потенциалов:
E = ΔV / d
Эта формула говорит нам, что величина напряженности поля в плоском конденсаторе равна отношению разности потенциалов между обкладками этого конденсатора к расстоянию между этими обкладками. Таким образом, мы видим, что напряженность поля в плоском конденсаторе E прямо пропорциональна разности потенциалов между его обкладками ∆V. Это означает, что если разность потенциалов между обкладками конденсатора увеличится (например, в два раза), то значение напряженности поля между обкладками также увеличится (также в два раза).
Формула для напряженности поля:
E = q / S * ε0
справедлива для вакуумного конденсатора. Если у нас есть диэлектрик между обкладками конденсатора, мы все равно должны учитывать его относительную электрическую проницаемость εr, которая является безразмерной величиной.
Тогда формула принимает вид:
E = q / S * ε0 * εr
Конденсатор. Энергия электрического поля
-
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
-
Ёмкость уединённого проводника
-
Ёмкость плоского конденсатора
-
Энергия заряженного конденсатора
-
Энергия электрического поля
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.
Но прежде введём понятие электрической ёмкости.
к оглавлению ▴
Ёмкость уединённого проводника
Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.
Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать
, так что
Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:
(1)
Например, потенциал уединённого шара в вакууме равен:
где — заряд шара,
— его радиус. Отсюда ёмкость шара:
(2)
Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в
раз:
Соответственно, ёмкость шара в раз увеличивается:
(3)
Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.
Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.
В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.
Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.
Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.
мкФ.
Как видите, Ф — это очень большая ёмкость.
Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим
из формулы (2):
Следовательно, диэлектрическая постоянная может измеряться в Ф/м:
Ф.
Так легче запомнить, не правда ли?
к оглавлению ▴
Ёмкость плоского конденсатора
Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.
Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.
Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.
Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух
Пусть заряды обкладок равны и
. Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина
— заряд положительной обкладки — называется зарядом конденсатора.
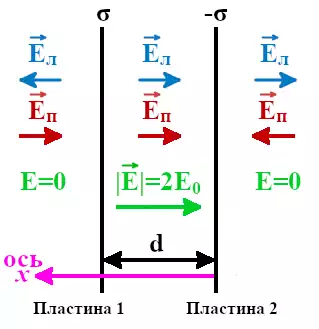
Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.
Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:
Здесь — напряжённость поля положительной обкладки,
— напряженность поля отрицательной обкладки,
— поверхностная плотность зарядов на обкладке:
На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.
Рис. 1. Электрическое поле плоского конденсатора
Согласно принципу суперпозиции, для результирующего поля имеем:
Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):
Внутри конденсатора поле удваивается:
или
(4)
Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:
Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.
Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.
Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов
между обкладками равна произведению
на
(вспомните связь напряжения и напряжённости в однородном поле!):
(5)
Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:
(6)
Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.
Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:
(7)
Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?
Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:
(8)
Соответственно, напряжение на конденсаторе:
(9)
Отсюда ёмкость плоского конденсатора с диэлектриком:
(10)
Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.
Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.
к оглавлению ▴
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.
Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.
Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.
Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок
.
Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
где — напряжённость поля первой обкладки:
Следовательно,
Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).
Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил
, с которыми притягиваются к первой обкладке всевозможные маленькие заряды
второй обкладки. При этом суммировании постоянный множитель
вынесется за скобку, а в скобке просуммируются все
и дадут
. В результате получим:
(11)
Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины
. Сила притяжения пластин совершает при этом работу:
Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины
, то работа силы притяжения получается отрицательной, как и должно быть.
С учётом формул (11) и (7) имеем:
где
Это можно переписать следующим образом:
где
(12)
Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины
. Это как раз и означает, что
— потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.
Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):
(13)
(14)
Особенно полезными являются формулы (12) и (14).
Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в
раз, и вместо (11) получим:
При вычислении работы силы , как нетрудно видеть, величина
войдёт в ёмкость
, и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).
Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
к оглавлению ▴
Энергия электрического поля
Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.
Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:
Но — объём конденсатора. Получаем:
(15)
Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме
.
Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.
Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.
Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:
(16)
В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.
Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:
(17)
(18)
Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Конденсатор. Энергия электрического поля» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023