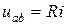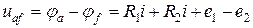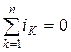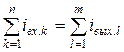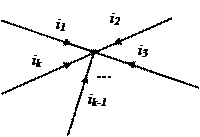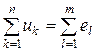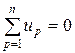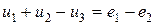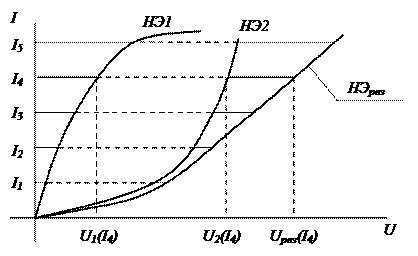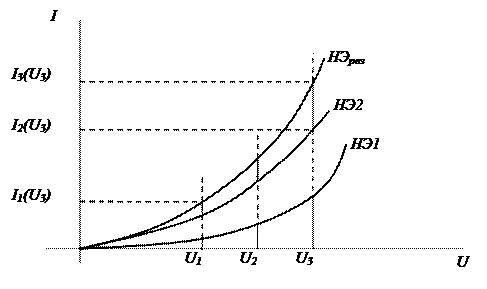Эта
задача при расчете электрических цепей
встречается очень часто. Пусть, например,
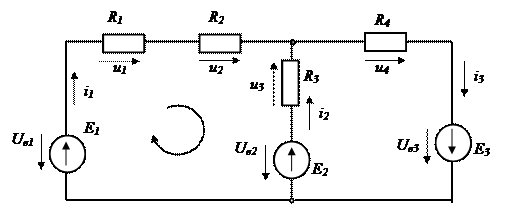
в цепи на рис. 2.1 требуется найти напряжение
между точками m и n.
Прежде
всего необходимо показать на схеме или
мысленно представить стрелку этого
напряжения. Её направление определяется
порядком следования индексов у буквы 
.
Для напряжения 
она
направлена отточки m к
точке n.
Если мы меняем местами индексы у буквы 
,
то следует изменить и направление
стрелки на схеме. При этом при расчете
меняется знак полученного напряжения,
так как 
.
Дальше
записываются уравнения по второму
закону Кирхгофа для любого контура,
включающего в себя эту стрелку, как было
сделано при расчете напряжений 
и 
.
Так, для контура m31nm при
обходе его по часовой стрелке
.
Отсюда
. (7.1)
При
соответствующем навыке последняя
формула может быть записана сразу, без
составления уравнения второго закона
Кирхгофа.
В
указанном контуре напряжение 
складывается
из трех напряжений:
. (7.2)
Порядок
индексов у букв U соответствует
порядку, в котором мы проходим участок
электрической цепи, идя от точки m к
точке n по
элементам 
, 
и 
.
Теперь
находим значение каждого слагаемого в
последнем уравнении.
Величина 
,
определяющая напряжение между точками m и
3, представляет собой падение напряжения
на сопротивлении 
,
которое мы должны взять со знаком минус,
так как от точки m к
точке 3 мы идем против тока 
:
.
Аналогично
.
Здесь
в правой части уравнения стоит плюс,
так как мысленная стрелка напряжения 
и
ток 
направлены
в одну сторону.
Третье
слагаемое 
представляет
собой напряжение на зажимах источника.
Если внутреннее сопротивление последнего
равно нулю, то это напряжение по величине
равно ЭДС, а знак его зависит от взаимного
направления стрелок напряжения и ЭДС
(рис. 7.1).
Рис.
7.1. Напряжение на зажимах источника
Рассмотрим
рис. 7.1.
При
указанной на схеме полярности зажимов
источника потенциал точки b выше
потенциала точки a на
величину ЭДС:
.
Поэтому
при одинаковых направлениях
стрелок 
и 
(рис.
7.1, а)
.
Если
направления стрелок 
и 
противоположны
друг другу
(рис. 7.1, б),
то
.
С
учетом сказанного напряжение на участке
1n (см.
рис. 2.1) равно
.
Подставляя
найденные значения напряжений на
участках в формулу (7.2), приходим к
выражению (7.1).
То
же самое напряжение, определяемое по
участку m2n,
будет равно
.
Разумеется,
вычисление одного и того же напряжения
по двум различным формулам должно
привести к одинаковым результатам.
8. Построение графиков
8.1. Общие требования к оформлению графиков. Зависимость мощности от тока
Правила
построения графиков рассмотрим на
примере зависимости мощности Р1, выделяющейся
в сопротивлении первой ветви, от тока I1 в
этой ветви. Эта зависимость определяется
уравнением баланса мощностей в схеме
рис. 6.1, в:
.
Так
как 
,
то
. (8.1)
Это
– уравнение параболы со смещенной
вершиной и направленными вниз ветвями
(рис. 8.1).
Значения
тока, при которых парабола пересекает
горизонтальную ось, находятся из
уравнения
и
соответственно равны
и 
.
По
смыслу 
–
это ток, протекающий в схеме рис.
6.1, в при
закороченном сопротивлении 
.
При токе, равном половине этого значения,
мощность 
максимальна:
.
Предположим,
что параметры цепи на рис. 6.1, в имеют
следующие численные значения:
=
72,4 В; 
=
130 В; 
=
43,6 Ом.
Прежде
всего находим максимальные значения
абсциссы и ординаты, которые будут
определять размеры графика. В нашем
примере – это значения 
и 
:
;
.
Исходя
из этих величин и предполагаемых размеров
графика, выбираем масштаб, который
указываем на каждой оси графика в виде
равномерной шкалы.
В
одной единице длины (сантиметре,
миллиметре) может содержаться m × 10n именованных
единиц. Здесь n –
целое число, положительное или
отрицательное, а для mрекомендуются
числа 1, 2, 5.
Положительные
значения величин откладываются вправо
по оси абсцисс и вверх по оси ординат.
В
конце каждой оси ставится буквенное
обозначение откладываемой величины и
через запятую – ее единица измерения.
Если
график строится на белой (нелинованной)
бумаге, то чертится масштабная сетка.
Данные
для построения графика рассчитываем
по формуле (8.1) и сводим их в таблицу
(табл. 8.1).
Таблица
8.1
Данные
для построения графика
|
|
0 |
0,2 |
0,4 |
0,5 |
0,6 |
0,66 |
0,8 |
0,9 |
1 |
1,2 |
1,32 |
|
|
0 |
9,78 |
16,1 |
17,9 |
18,9 |
19 |
18,2 |
16,5 |
14 |
6,34 |
0 |
,Абсциссы
точек, выбираемых для построения графика,
желательно располагать по оси равномерно.
Но вблизи характерных областей кривой
(в нашем случае у вершины параболы) точки
можно взять чаще. В таблицу внесены
также значения максимальной мощности
и тока, которому эта мощность соответствует.
При построении графика числа из таблицы
на осях не показываются (рис. 8.2).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
7. Определение напряжения между двумя точками электрической цепи
Эта задача при расчете электрических цепей встречается очень часто. Пусть, например, в цепи на рис. 2.1 требуется найти напряжение между точками m и n.
Прежде всего необходимо показать на схеме или мысленно представить стрелку этого напряжения. Её направление определяется порядком следования индексов у буквы . Для напряжения она направлена отточки m к точке n. Если мы меняем местами индексы у буквы , то следует изменить и направление стрелки на схеме. При этом при расчете меняется знак полученного напряжения, так как .
Дальше записываются уравнения по второму закону Кирхгофа для любого контура, включающего в себя эту стрелку, как было сделано при расчете напряжений и . Так, для контура m31nm при обходе его по часовой стрелке
.
. (7.1)
При соответствующем навыке последняя формула может быть записана сразу, без составления уравнения второго закона Кирхгофа.
В указанном контуре напряжение складывается из трех напряжений:
. (7.2)
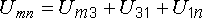
Порядок индексов у букв U соответствует порядку, в котором мы проходим участок электрической цепи, идя от точки m к точке n по элементам , и .
Теперь находим значение каждого слагаемого в последнем уравнении.
Величина , определяющая напряжение между точками m и 3, представляет собой падение напряжения на сопротивлении , которое мы должны взять со знаком минус, так как от точки m к точке 3 мы идем против тока :
.
.
Здесь в правой части уравнения стоит плюс, так как мысленная стрелка напряжения и ток направлены в одну сторону.
Третье слагаемое представляет собой напряжение на зажимах источника. Если внутреннее сопротивление последнего равно нулю, то это напряжение по величине равно ЭДС, а знак его зависит от взаимного направления стрелок напряжения и ЭДС (рис. 7.1).
Рис. 7.1. Напряжение на зажимах источника
При указанной на схеме полярности зажимов источника потенциал точки b выше потенциала точки a на величину ЭДС:
.
Поэтому при одинаковых направлениях стрелок и (рис. 7.1, а)
.
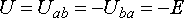
Если направления стрелок 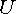и противоположны друг другу (рис. 7.1, б), то
.
С учетом сказанного напряжение на участке 1n (см. рис. 2.1) равно
.
Подставляя найденные значения напряжений на участках в формулу (7.2), приходим к выражению (7.1).
То же самое напряжение, определяемое по участку m2n, будет равно
.
Разумеется, вычисление одного и того же напряжения по двум различным формулам должно привести к одинаковым результатам.
8. Построение графиков
8.1. Общие требования к оформлению графиков. Зависимость мощности от тока
Правила построения графиков рассмотрим на примере зависимости мощности Р1, выделяющейся в сопротивлении первой ветви, от тока I1 в этой ветви. Эта зависимость определяется уравнением баланса мощностей в схеме рис. 6.1, в:
.
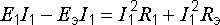
Так как 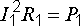, то
. (8.1)
Это – уравнение параболы со смещенной вершиной и направленными вниз ветвями (рис. 8.1).
Значения тока, при которых парабола пересекает горизонтальную ось, находятся из уравнения
и .
По смыслу – это ток, протекающий в схеме рис. 6.1, в при закороченном сопротивлении . При токе, равном половине этого значения, мощность максимальна:
.
Предположим, что параметры цепи на рис. 6.1, в имеют следующие численные значения:
= 72,4 В; = 130 В; = 43,6 Ом.
Прежде всего находим максимальные значения абсциссы и ординаты, которые будут определять размеры графика. В нашем примере – это значения и :
;
.
Исходя из этих величин и предполагаемых размеров графика, выбираем масштаб, который указываем на каждой оси графика в виде равномерной шкалы.
В одной единице длины (сантиметре, миллиметре) может содержаться m × 10 n именованных единиц. Здесь n – целое число, положительное или отрицательное, а для mрекомендуются числа 1, 2, 5.
Положительные значения величин откладываются вправо по оси абсцисс и вверх по оси ординат.
В конце каждой оси ставится буквенное обозначение откладываемой величины и через запятую – ее единица измерения.
Если график строится на белой (нелинованной) бумаге, то чертится масштабная сетка.
Данные для построения графика рассчитываем по формуле (8.1) и сводим их в таблицу (табл. 8.1).
Данные для построения графика
, А
Источник
Напряжение участке электрической цепи
Участок электрической цепи, по которому проходит ток одного и того же значения называют ветвью .
Место соединения трех и более ветвей называют узлом .
Замкнутую электрическую цепь, образованную одной или несколькими ветвями называют контуром .
Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.
На рис. 2.1 изображен участок цепи, содержащий только резистивный элемент, крайние точки которого обозначены буквами a и b. Пусть ток 
направлен от точки a к точке b (от более высокого потенциала к более низкому).
Следовательно, потенциал точки а (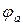
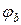
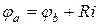
) выше потенциала точки b (
) на значение, равное произведению тока на сопротивление R:
.
В соответствии с определением напряжение между точками а и b
.
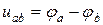
т. е. напряжение на сопротивлении равно произведению тока, протекающего по резистивному элементу, на значение его сопротивления. Последнее выражение называют законом Ома для участка цепи.
В электротехнике разность потенциалов на концах резистивного элемента (сопротивления) называют либо напряжением на сопротивлении, либо падением напряжения. Положительное направление падения напряжения на каком-либо участке (направление отсчета этого напряжения), указываемое на рисунках стрелкой, совпадает с положительным направлением отсчета тока, протекающего по данному сопротивлению.
Рассмотрим вопрос о напряжении на участке цепи, содержащем не только резистивный элемент, но и ЭДС. На рис. 2.2 показан участок цепи, в которой существует ток . Найдем разность потенциалов (напряжение) между точками a и c для этих участков. По определению,
.
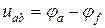
Выразим потенциал точки а через потенциал точки f. При перемещении от точки f к точке d встречно направлению ЭДС источника Е2 (рис. 2.2) потенциал точки d оказывается ниже (меньше), чем потенциал точки f, на значение ЭДС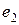 
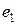
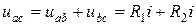
источника Е2. При перемещении от точки d к точке c согласно направлению ЭДС источника Е1 (рис. 2.2) потенциал точки c оказывается выше (больше), чем потенциал точки d, на значение ЭДС 
источника Е1. При перемещении от точки c к точке b и далее к точке a потенциал точки a оказывается выше (больше) на величину падения напряжения на резисторах R2 и R1, соответственно, т.е.
.
Таким образом с учетом вышеизложенного:
,
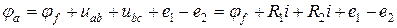
напряжение на участке цепи между точками a и f равно:
В общем случае напряжение на участке цепи равно сумме падений напряжения на резистивных элементах цепи и сумме ЭДС источников.
Положительное направление напряжения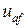 
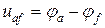
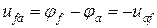
показывают стрелкой от а к f. Согласно определению 
, поэтому 
т.е. изменение чередования (последовательности) индексов равносильно изменению знака этого напряжения.
Законы Кирхгофа
Первый закон Кирхгофа (уравнение электрического состояния для узла) можно сформулировать двояко:
1) алгебраическая сумма токов, входящих в любой узел схемы (рис.2.3,а), равна нулю:
2) сумма токов, входящих в любой узел схемы (рис.2.3,б), равна сумме токов выходящих из этого узла:
Физически первый закон Кирхгофа означает, что движение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.
Второй закон Кирхгофа (уравнение электрического состояния контура) также можно сформулировать двояко:
1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:
(в каждую из сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним);
2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю:
Напряжения участков цепи включают и падения напряжения на резистивных элементах и напряжения на источниках ЭДС.
Для левого контура схемы рис.2.4
.
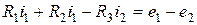
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.
Параллельное и последовательное соединение двухполюсников
Последовательное соединение резистивных элементов
Результирующее падение напряжения на цепи (рис. 2.5) из n последовательно включенных резистивных элементов:
.
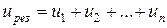
В цепи существует общий ток .
Для линейных резистивных элементов:
,
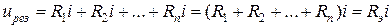
где эквивалентное сопротивление цепи из n последовательно соединенных резистивных элементов:
.
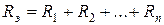
Для нелинейных резистивных элементов НЭ1 и НЭ2 результирующая ВАХ эквивалентного резистивного элемента определяется графическим способом (рис. 2.6).
В интересующем диапазоне токов (соответствующем участку ВАХ нелинейного элемента) задаются несколькими значениями токов (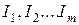
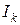
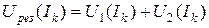
). Для каждого из выбранных значений тока, например 
, определяют результирующее напряжение на последовательно включенных элементах:
.
На уровне каждой из ординат откладывают найденные значения абсцисс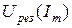 
. Результирующую ВАХ получают, проводя линию через найденные точки.
Параллельное соединение резистивных элементов
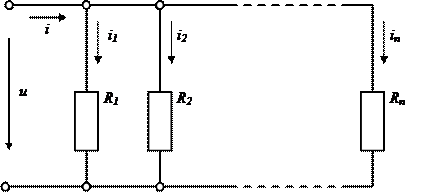
При параллельном соединении двухполюсных элементов (рис. 2.7) на их полюсах будет общее падение напряжения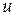 
.
Общий ток , для n параллельно включенных двухполюсных элементов
.
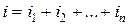
Для линейных двухполюсных элементов ток через k-тый резистивный элемент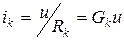 
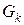
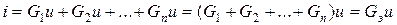
, где 
– проводимость k-того резистивного элемента. Таким образом общий ток
,
где эквивалентная проводимость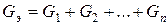 
равна сумме проводимости параллельно включенных двухполюсных элементов.
В частном случае для двух элементов эквивалентная проводимость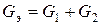 
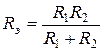
, или эквивалентное сопротивление
.
Для нелинейных резистивных элементов НЭ1 и НЭ2 результирующая ВАХ эквивалентного резистивного элемента определяется графическим способом (рис. 2.8).
В интересующем диапазоне напряжений (соответствующем участку ВАХ нелинейного элемента) задаются несколькими значениями напряжений (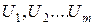
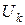
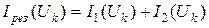
). Для каждого из выбранных значений напряжения, например 
, определяют результирующий (суммарный) ток через параллельно включенные элементы:
.
На уровне каждой из абсцисс откладывают найденные значения ординат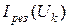 
. Результирующую ВАХ получают проводя линию через найденные точки.
Последовательное и параллельное соединение линейных индуктивных элементов
При последовательном соединении n линейных индуктивных элементов их результирующая индуктивность определяется
.
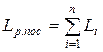
При параллельном соединении n линейных индуктивных элементов их результирующая индуктивность определяется
, или 
.
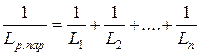
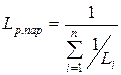
Последовательное и параллельное соединение линейных емкостных элементов
При последовательном соединении n линейных емкостных элементов их результирующая емкость определяется
, или 
.
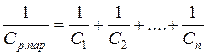
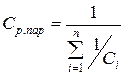
При параллельном соединении n линейных емкостных элементов их результирующая емкость определяется
Источник
2017-11-29 23:05
Мы видели (§ 24), что в случае равновесия зарядов напряжение между любыми точками проводника равно нулю. Наоборот, если по проводнику течет ток, то между различными точками проводника должно существовать напряжение. Исследуем распределение напряжения в проводнике с током.
Прикрутим к концам деревянного изолированного стержня (в точках
и
, рис. 76) проволоки и соединим их с полюсами работающей электрической машины. Так как дерево является проводником, хотя и плохим, то в стержне возникает ток. (Этот ток настолько слаб, что его можно обнаружить и измерить, только применяя чувствительный гальванометр.) Присоединив листки и корпус электрометра к каким-либо двум точкам стержня
и
, мы обнаружим, что между ними существует некоторое напряжение. Напряжение это тем больше, чем дальше друг от друга отстоят вдоль стержня сравниваемые точки, и достигает наибольшего значения между крайними точками стержня.
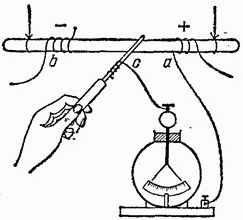
Рис. 76. Распределение напряжения в деревянном стержне 
, по которому идет ток. Присоединяя электрометр к точкам
и
стержня, можно убедиться, что напряжение тем больше, чем ближе к точке
взята точка
То же самое можно показать, пользуясь вместо электрической машины гальваническими элементами и создавая ток не в деревянном стержне, а в металлическом проводнике. Для этого можно взять кусок железной проволоки и замкнуть ее на батарею из нескольких элементов, соединенных последовательно. Ток в проволоке будет намного сильнее, чем в деревянном стержне, и его можно легко измерить, введя последовательно в цепь амперметр. Однако напряжение между различными точками проволоки будет в этом опыте невелико, и для его измерения нужно применить вместо обычного школьного электрометра более чувствительный прибор. И в этом опыте мы найдем, что между различными точками проволоки существует напряжение, которое достигает наибольшего значения между концами проволоки. При наличии в проводнике электрического тока между концами любого его участка существует электрическое напряжение.
Существование разности потенциалов между точками проводника с током совершенно аналогично существованию разности давлений в струе жидкости при ее течении с трением по трубам, с которым мы познакомились в томе I. Это сходство можно проследить на приборе, изображенном на рис. 77 и понятном без дальнейших пояснений. Если закрыть конец горизонтальной трубки краном, то тока жидкости не будет, при этом во всех манометрах 1,2,…
жидкость устанавливается на одной и той же высоте (обозначенной штрих-пунктирной линией), т. е. между различными точками трубки нет разности давлений, точно так же, как между точками проводника, по которому не течет ток, нет разности потенциалов. При открывании крана возникает более или менее сильный ток жидкости, и уровни манометров располагаются по наклонной линии, указывая на падение давления вдоль трубки.
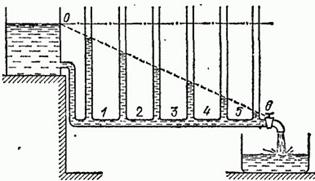
Рис. 77. Распределение давления жидкости в трубке аналогично падению электрического напряжения в цепи
Правило напряжений Кирхгофа (второй закон Кирхгофа)
Добавлено 14 января 2021 в 05:47
Что такое правило напряжений Кирхгофа (второй закон Кирхгофа)?
Принцип, известный как правило напряжений Кирхгофа (открытое в 1847 году немецким физиком Густавом Р. Кирхгофом), можно сформулировать следующим образом:
«Алгебраическая сумма всех напряжений в замкнутом контуре равна нулю»
Под алгебраической я подразумеваю, помимо учета величин, учет и знаков (полярностей). Под контуром я подразумеваю любой путь, прослеживаемый от одной точки в цепи до других точек в этой цепи, и, наконец, обратно в исходную точку.
Демонстрация закона напряжений Кирхгофа в последовательной цепи
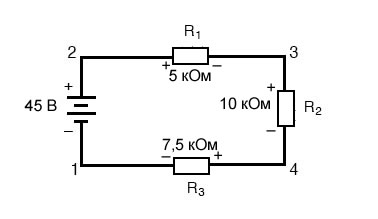
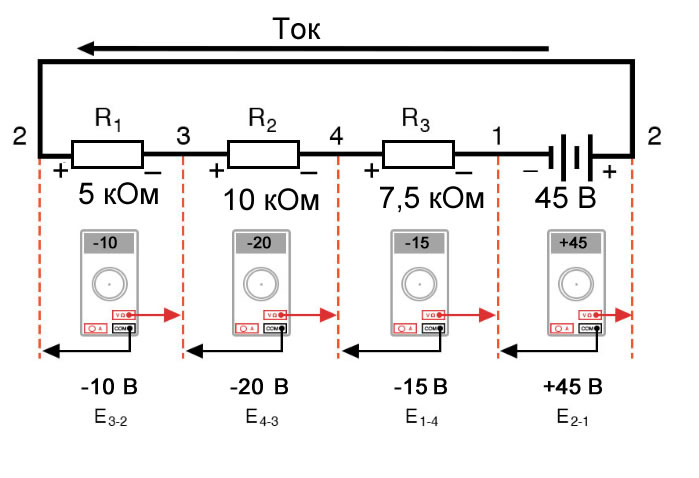
Давайте еще раз посмотрим на наш пример последовательной схемы, на этот раз нумеруя точки цепи для обозначения напряжений:
Если бы мы подключили вольтметр между точками 2 и 1, красный измерительный провод к точке 2 и черный измерительный провод к точке 1, вольтметр зарегистрировал бы значение +45 вольт. Для положительных показаний на дисплеях цифровых счетчиков знак «+» обычно не отображается, а скорее подразумевается. Однако для этого урока полярность показаний напряжений очень важна, поэтому я буду явно показывать положительные числа:
E2-1 = +45 В
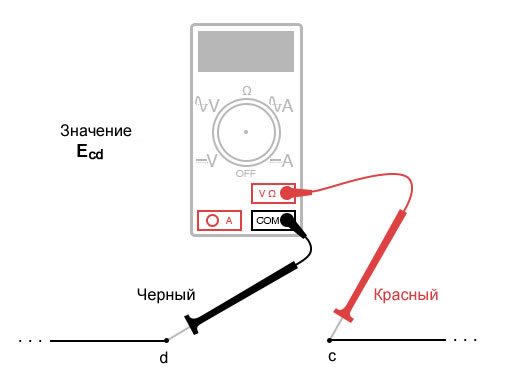
Когда напряжение указывается с двойным нижним индексом (символы «2-1» в обозначении «E2-1»), это означает напряжение в первой точке (2), измеренное по отношению ко второй точке (1). Напряжение, указанное как «Ecd», будет означать значение напряжения, показанное цифровым мультиметром с красным измерительным проводом в точке «c» и черным измерительным проводом в точке «d»: напряжение в точке «c» относительно точки «d».
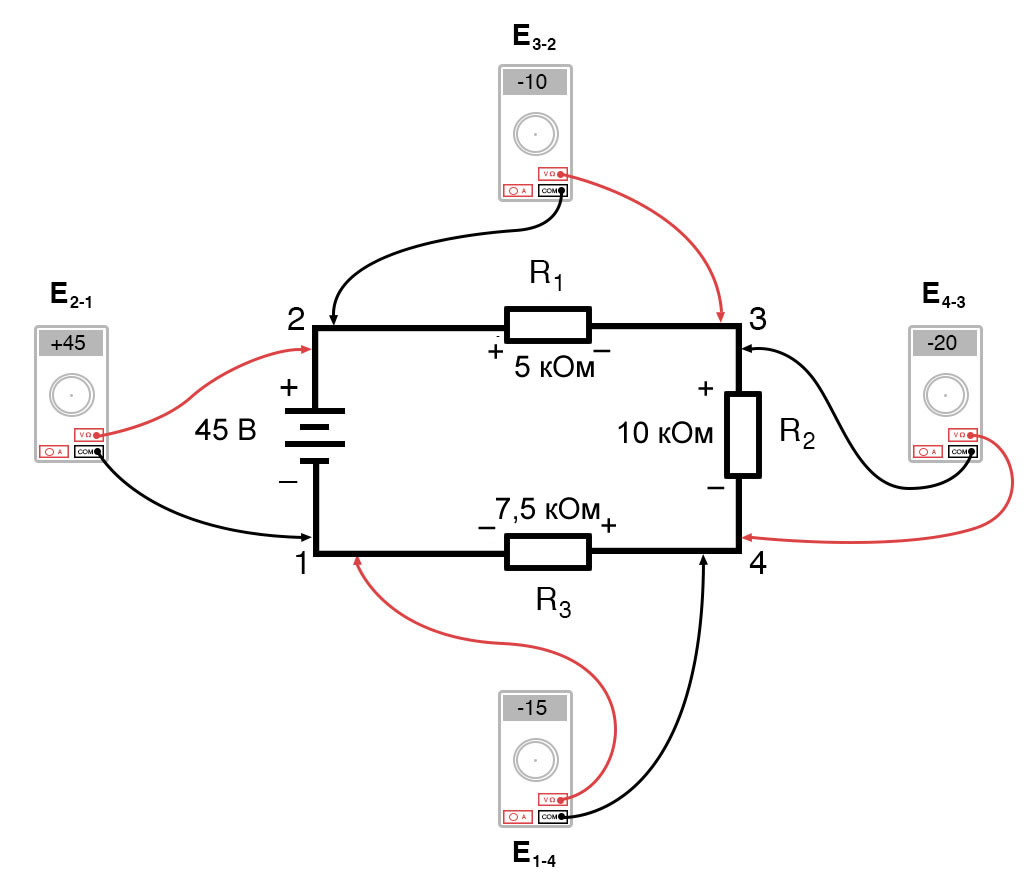
Если бы мы взяли тот же вольтметр и измерили падение напряжения на каждом резисторе, обходя цепь по часовой стрелке с красным измерительным проводом нашего мультиметра на точке впереди и черным измерительным проводом на точке позади, мы получили бы следующие показания:
E3-2 = -10 В
E4-3 = -20 В
E1-4 = -15 В
Нам уже должен быть знаком общий для последовательных цепей принцип, утверждающий, что отдельные падения напряжения в сумме составляют общее приложенное напряжение, но измерение падения напряжения таким образом и уделение внимания полярности (математическому знаку) показаний открывает еще один аспект этого принципа: все измеренные напряжения в сумме равны нулю:
[begin{matrix} E_{2-1} = & +45 В &text{напряжение в точке 2 относительно точки 1} \ E_{3-2} = & -10 В & text{напряжение в точке 3 относительно точки 2} \ E_{4-3} = & -20 В & text{напряжение в точке 4 относительно точки 3} \ E_{1-4} = & -15 В & text{напряжение в точке 1 относительно точки 4} \ hline \ & 0 В end{matrix}]
В приведенном выше примере контур образован следующими точками в следующем порядке: 1-2-3-4-1. Не имеет значения, с какой точки мы начинаем или в каком направлении движемся при следовании по контуру; сумма напряжений по-прежнему будет равна нулю. Чтобы продемонстрировать это, мы можем той же цепи подсчитать напряжения в контуре 3-2-1-4-3:
[begin{matrix} E_{2-3} = & +10 В &text{напряжение в точке 2 относительно точки 3} \ E_{1-2} = & -45 В & text{напряжение в точке 1 относительно точки 2} \ E_{4-1} = & +15 В & text{напряжение в точке 4 относительно точки 1} \ E_{3-4} = & +20 В & text{напряжение в точке 3 относительно точки 4} \ hline \ & 0 В end{matrix}]
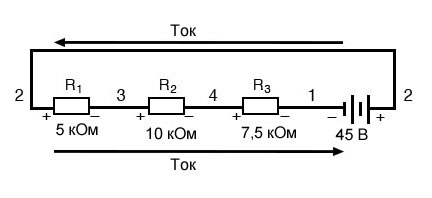
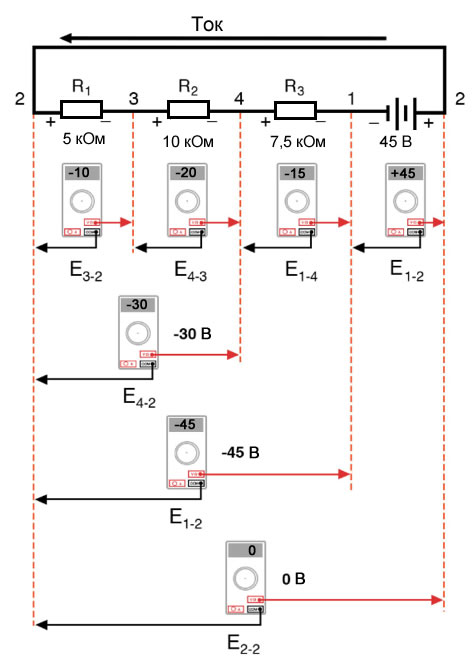
Этот пример может быть более понятен, если мы перерисуем нашу последовательную схему так, чтобы все компоненты были представлены на одной прямой линии:
Это всё та же последовательная схема, только с немного перераспределенными компонентами. Обратите внимание на полярность падений напряжения на резисторах по отношению к напряжению батареи: напряжение батареи отрицательное слева и положительное справа, тогда как все падения напряжения на резисторах ориентированы в другую сторону (положительное слева и отрицательное справа). Это потому, что резисторы сопротивляются потоку электрического заряда, проталкиваемого батареей. Другими словами, «толкание», прилагаемое резисторами против потока электрического заряда, должно происходить в направлении, противоположном источнику электродвижущей силы.
Здесь мы видим, что цифровой вольтметр покажет на каждом компоненте в этой цепи, если черный провод будет слева, а красный провод – справа:
Если бы мы взяли тот же вольтметр и измерили напряжение между комбинациями компонентов, начиная с единственного R1 слева и продвигаясь по всей цепочке компонентов, мы увидели бы, как напряжения складываются алгебраически (до нуля):
Тот факт, что последовательные напряжения складываются, не должен быть тайной, но мы заметили, что полярность этих напряжений имеет большое значение в том, как эти значения складываются. При измерении напряжения на R1 – R2 и R1 – R2 – R3 (я использую символ «двойное тире» «–» для обозначения последовательного соединения между резисторами R1, R2 и R3), мы видим, как измеряются бо́льшие значения напряжений (хотя и отрицательные), потому что полярности отдельных падений напряжения имеют одинаковую ориентацию (плюс слева, минус справа).
Сумма падений напряжения на R1, R2 и R3 равна 45 вольт, что соответствует выходному напряжению батареи, за исключением того, что полярность напряжения батареи (минус слева, плюс справа) противоположна падениям напряжения на резисторах, поэтому при измерении напряжения на всей цепочке компонентов мы получаем 0 вольт.
То, что мы должны получить ровно 0 вольт на всей линии, тоже не должно быть тайной. Глядя на схему, мы видим, что крайняя левая часть линии (левая сторона R1, точка номер 2) напрямую соединена с крайней правой частью линии (правая сторона батареи, точка номер 2), что необходимо для завершения схемы.
Поскольку эти две точки соединены напрямую, они являются электрически общими друг с другом. Таким образом, напряжение между этими двумя электрически общими точками должно быть равно нулю.
Демонстрация закона напряжений Кирхгофа в параллельной цепи
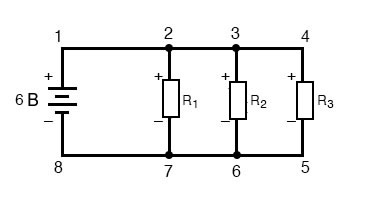
Правило напряжений Кирхгофа (второй закон Кирхгофа) будет работать вообще для любой конфигурации схемы, а не только для простых последовательных цепей. Обратите внимание, как это работает для следующей параллельной схемы:
При параллельной схеме напряжение на каждом резисторе равно напряжению питания: 6 вольт. Суммируя напряжения вдоль контура 2-3-4-5-6-7-2, мы получаем:
[begin{matrix} E_{3-2} = & 0 В &text{напряжение в точке 3 относительно точки 2} \ E_{4-3} = & 0 В & text{напряжение в точке 4 относительно точки 3} \ E_{5-4} = & -6 В & text{напряжение в точке 5 относительно точки 4} \ E_{6-5} = & 0 В & text{напряжение в точке 6 относительно точки 5} \ E_{7-6} = & 0 В & text{напряжение в точке 7 относительно точки 6} \ E_{2-7} = & +6 В & text{напряжение в точке 2 относительно точки 7} \ hline \ E_{2-2} = & 0 В end{matrix}]
Обратите внимание, что конечное (суммарное) напряжение я обозначил как E2-2. Поскольку мы начали наше пошаговое прохождение по контуру в точке 2 и закончили в точке 2, алгебраическая сумма этих напряжений будет такой же, как напряжение, измеренное между той же точкой (E2-2), которое, конечно, должно быть равно нулю.
Справедливость закона Кирхгофа о напряжениях независимо от топологии цепи
Тот факт, что эта цепь является параллельной, а не последовательной, не имеет ничего общего со справедливостью закона Кирхгофа о напряжениях. В этом отношении схема может быть «черным ящиком» (конфигурация ее компонентов полностью скрыта от нашего взгляда) с набором открытых клемм, между которыми мы можем измерить напряжение, – и правило напряжений Кирхгофа всё равно останется верным:
Попробуйте на приведенной выше диаграмме выполнить обход в любом порядке, начиная с любого вывода, и вернувшись к исходному выводу, и вы обнаружите, что алгебраическая сумма напряжений всегда равна нулю.
Более того, «контур», который мы отслеживаем для второго закона Кирхгофа, даже не обязательно должен быть реальным путем протекания тока в прямом смысле этого слова. Всё, что нам нужно сделать, чтобы соответствовать правилу напряжений Кирхгофа, – это начинать и заканчивать в одной и той же точке цепи, подсчитывая падения напряжения и полярности при переходе между точками. Рассмотрим следующий абсурдный пример, проходя по «контуру» 2-3-6-3-2 в той же параллельной резисторной цепи:
[begin{matrix} E_{3-2} = & 0 В &text{напряжение в точке 3 относительно точки 2} \ E_{6-3} = & -6 В & text{напряжение в точке 6 относительно точки 3} \ E_{3-6} = & +6 В & text{напряжение в точке 3 относительно точки 6} \ E_{2-3} = & 0 В & text{напряжение в точке 2 относительно точки 3} \ hline \ E_{2-2} = & 0 В end{matrix}]
Использование закона Кирхгофа о напряжениях в сложной цепи
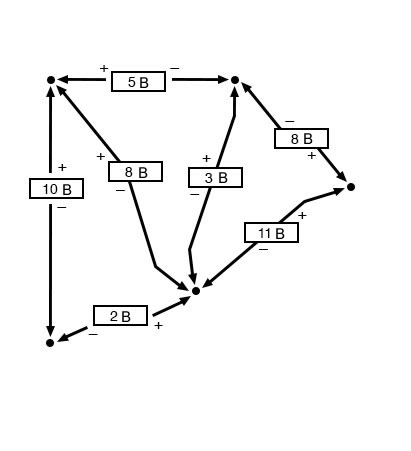
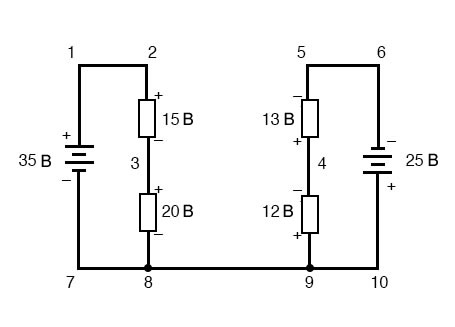
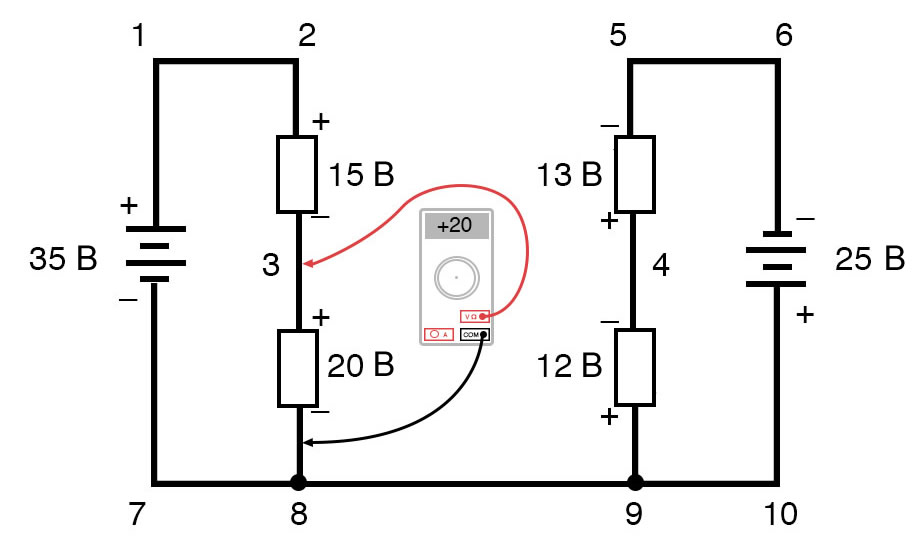
Закон Кирхгофа о напряжениях можно использовать для определения неизвестного напряжения в сложной цепи, где известны все другие напряжения вдоль определенного «контура». В качестве примера возьмем следующую сложную схему (на самом деле две последовательные цепи, соединенные одним проводом внизу):
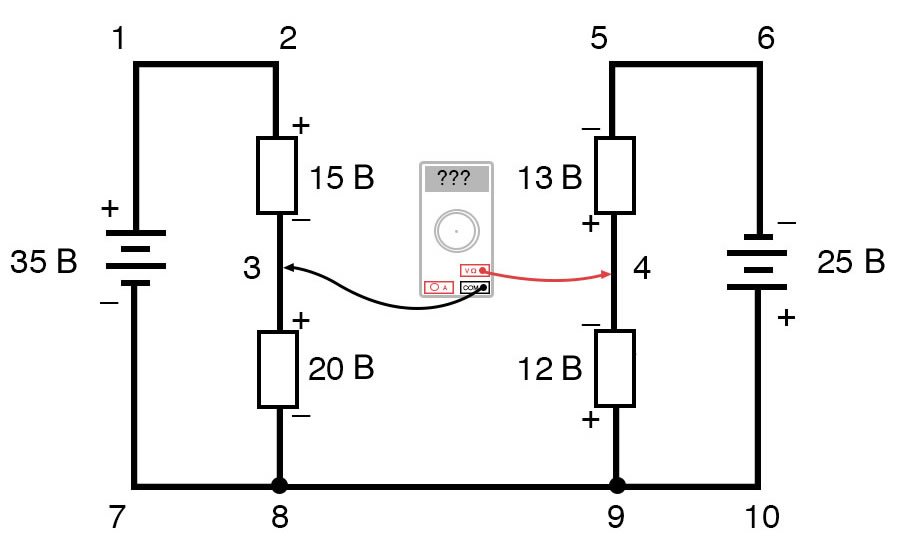
Чтобы упростить задачу, я опустил значения сопротивлений и просто указал падение напряжения на каждом резисторе. Две последовательные цепи имеют между собой общий провод (провод 7-8-9-10), что делает возможными измерения напряжения между этими двумя цепями. Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение правила напряжений Кирхгофа с напряжением между этими точками как неизвестным:
E4-3 + E9-4 + E8-9 + E3-8 = 0
E4-3 + 12 + 0 + 20 = 0
E4-3 + 32 = 0
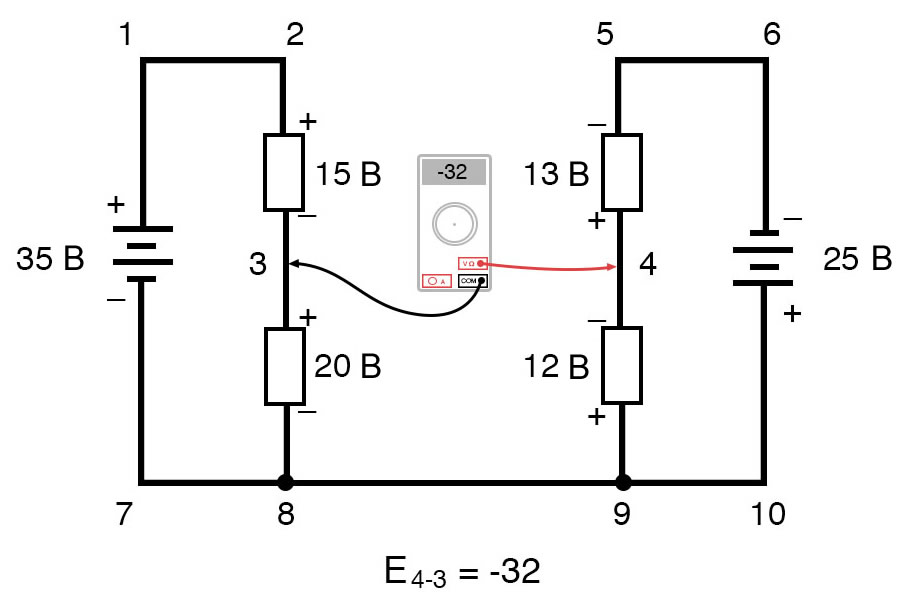
E4-3 = -32 В
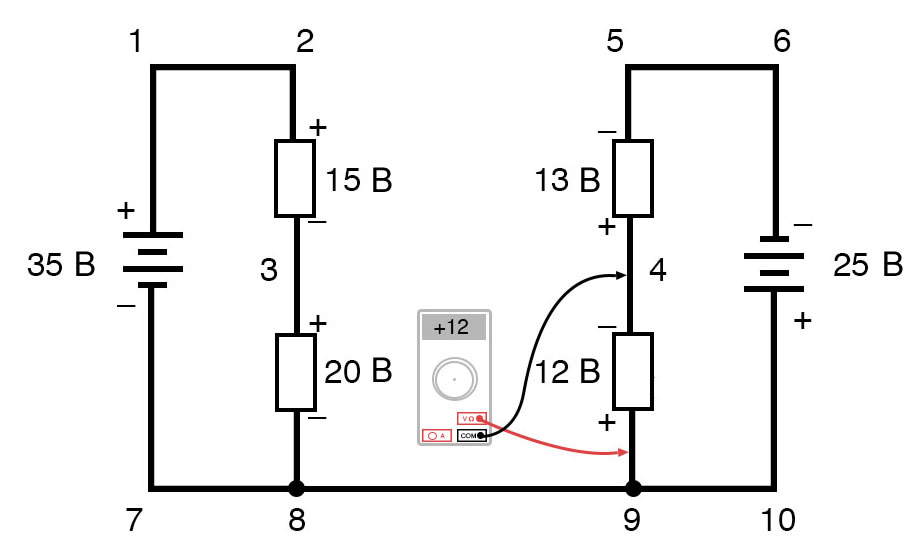
Обойдя контур 3-4-9-8-3, мы записываем значения падений напряжения так, как их регистрировал бы цифровой вольтметр, измеряя с красным измерительным проводом в точке впереди и черным измерительным проводом на точке позади, когда мы продвигаемся вперед по контуру. Следовательно, напряжение в точке 9 относительно точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» – в точке 4.
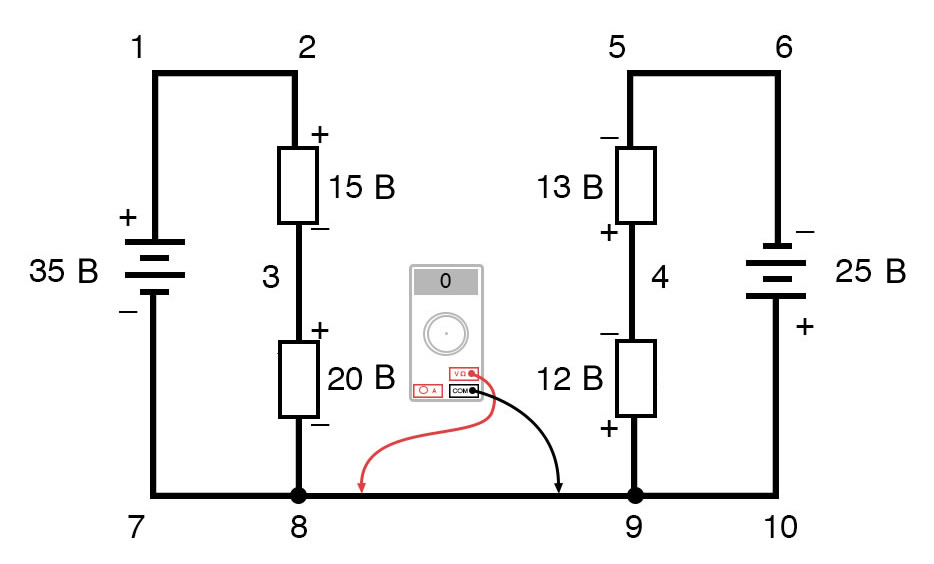
Напряжение в точке 3 относительно точки 8 составляет положительные (+) 20 вольт, потому что «красный провод» находится в точке 3, а «черный провод» – в точке 8. Напряжение в точке 8 относительно точки 9, конечно, равно нулю, потому что эти две точки электрически общие.
Наш окончательный ответ для напряжения в точке 4 относительно точки 3 – это отрицательные (-) 32 вольта, говорящие нам, что точка 3 на самом деле положительна относительно точки 4, именно это цифровой вольтметр показал бы при красном проводе в точке 4 и черном проводе в точке 3:
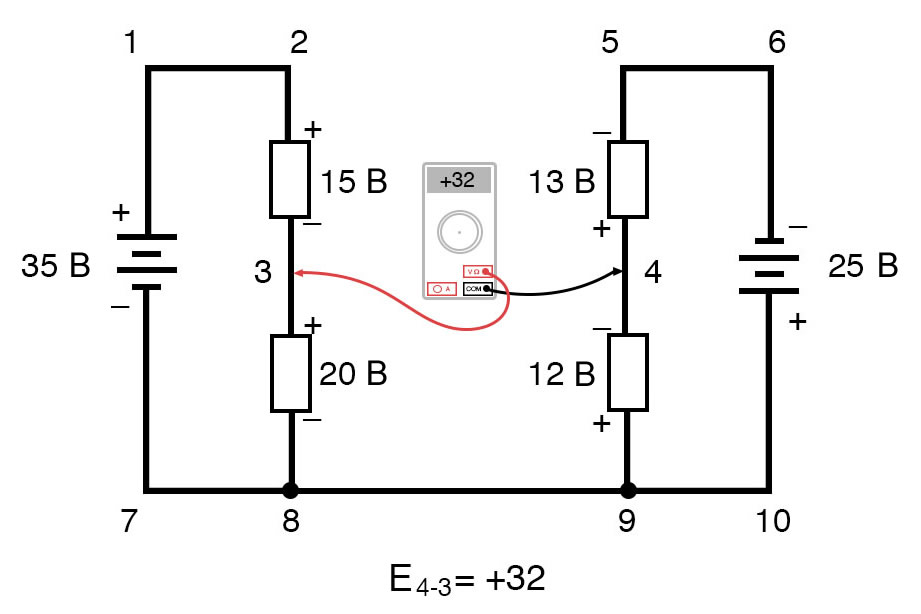
Другими словами, первоначальное размещение наших «измерительных щупов» в этой задаче правила напряжений Кирхгофа было «обратным». Если бы мы сформировали наше уравнение второго закона Кирхгофа, начиная с E3-4, вместо E4-3, обходя тот же контур с противоположной ориентацией измерительных проводов, окончательный ответ был бы E3-4 = +32 вольта:
Важно понимать, что ни один из подходов не является «неправильным». В обоих случаях мы приходим к правильной оценке напряжения между двумя точками 3 и 4: точка 3 положительна по отношению к точке 4, а напряжение между ними составляет 32 вольта.
Резюме
- Правило напряжений Кирхгофа (второй закон Кирхгофа): «Алгебраическая сумма всех напряжений в контуре равна нулю».
Теги
Анализ цепейДля начинающихОбучениеПараллельная цепьПолярностьПоследовательная цепьПравило напряжений Кирхгофа / Второй закон КирхгофаЭлектрическое напряжение
На прошлом уроке мы рассмотрели последовательное соединение проводников. При нем сила тока на всех участках цепи одинакова ($I = I_1 = I_2 = … = I_n$), а сопротивление всей цепи складывается из сопротивлений всех проводников, составляющих ее ($R = R_1 + R_2 + … + R_n$). Напряжение (подобно сопротивлению) всей цепи рассчитывается сложением напряжений на концах всех элементов, составляющих такую электрическую цепь ($U = U_1 + U_2 + … + U_n$).
На данном уроке мы рассмотрим другой вид соединения проводников — параллельный. Так мы подсоединяли вольтметр, когда измеряли напряжение на каком-либо участке цепи. Сейчас же мы рассмотрим закономерности для силы тока, сопротивления и напряжения в цепи для такого типа соединения.
Параллельное включение элементов в электрическую цепь
Какое соединение проводников называют параллельным?
Соберем электрическую цепь с таким соединением. Цепь будет состоять из источника тока, ключа и двух электроламп. Электролампы включены в цепь параллельно (рисунок 1).
Схема этой электрической цепи изображена на рисунке 2.
На схеме обозначены две точки A и B. Важный момент:
При параллельном соединении все входящие в него проводники одним своим концом присоединяются к точке A, а вторым концом — к другой точке B.
Так мы можем подключить еще несколько ламп или некоторое количество других потребителей электроэнергии. Поэтому все закономерности, которые мы рассмотрим далее, будут справедливы для любого количества параллельно подключенных в цепь проводников между точками A и B.
Напряжение в цепи при параллельном соединении проводников
Вольтметр подсоединяется в цепь параллельно. Взгляните на рисунок 3.
Можно ли сказать, что мы измеряем напряжение только на одной из ламп? Нет. Получается, что одновременно мы измеряем напряжения и на одной, и на другой лампе. Мы приходим к следующему заключению.
Напряжение на участке цепи AB и на концах всех параллельно соединенных проводников одно и то же:
$U = U_1 = U_2 = … = U_n$.
Значит, напряжение — это электрическая величина, которая одинакова для всех проводников, соединенных параллельно.
По этой причине в быту и технике очень удобно применять параллельный тип соединения проводников. Почему?
Во-первых, в таком случае все потребители электроэнергии изготавливаются в расчете на одну и ту же величину напряжения. Во-вторых, если исключить из цепи один потребитель, то другие продолжат работать. Цепь останется замкнутой.
Сила тока в цепи при параллельном соединении проводников
Теперь рассмотрим, что происходит с силой тока при параллельном подключении.
Взгляните на рисунок 4, а. В точке B ток разветвляется на два тока: $I_1$ и $I_2$.
Эти два тока сходятся снова в точке A. По смыслу этот момент очень похож на разветвление реки (рисунок 4, б) на два потока воды, которые через какое-то расстояние вновь сходятся в одно русло.
Как выражается сила тока в цепи до ее разветвления через силы токов в отдельных ветвях разветвления?
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединенных проводниках:
$I = I_1 + I_2 + … + I_n$.
Сопротивление в цепи при параллельном соединении проводников
Перейдем к сопротивлению. При параллельном соединении можно представить все проводники как один. Этот один проводник будет явно больше в диаметре, чем каждый из них по отдельности. Получается, что площадь поперечного сечения проводника как бы увеличивается при таком соединении.
Сопротивление рассчитывается по формуле $R = frac{rho l}{S}$. Чем больше поперечное сечение, тем меньше сопротивление.
Значит, общее сопротивление цепи уменьшается. Оно становится меньше сопротивления каждого из проводников, которые входят в такую электрическую цепь.
В цепи на рисунке 1 у нас две одинаковые лампы с сопротивлениями $R_1$. Общее сопротивление цепи $R$ будет в два раза меньше сопротивления каждой лампы: $R = frac{R_1}{2}$.
Общее сопротивление цепи при параллельном соединении проводников рассчитывается по формуле:
$frac{1}{R} = frac{1}{R_1} + frac{1}{R_2} + … + frac{1}{R_n}$.
Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
Очевидно, что чем больше проводников будет в разветвлении, тем меньше будет общее сопротивление цепи.
Пример параллельного соединения проводников
Взгляните на рисунок 5. Здесь изображена часть схемы электрической цепи. Здесь параллельно включены электрические лампы, нагревательные приборы и электродвигатель.
Где может использоваться такая схема соединения?
Например, в жилых помещениях. В точках A и B провода вводятся в квартиру.
Также в наших квартирах все стандартные розетки находятся под одинаковым напряжением в $220 space В$. Большинство производителей техники изготавливают приборы как раз под это напряжение.
Использовать параллельное подключение к одной и той же цепи очень удобно, поскольку в нее могут быть включены самые разные потребители энергии (рисунок 6).
Благодаря такому способу подключения, выключая свет в своей квартире, мы не выключаем его и у наших соседей. Любые электроприборы могут работать независимо от подключения или отключения в сеть других.
На практике также часто можно увидеть смешанное соединение проводников. В таких цепях присутствует и последовательный тип соединении, и параллельный.
Пример задачи
В осветительную сеть комнаты включены две электрические лампы, сопротивления которых равны $200 space Ом$ и $300 space Ом$. Напряжение в сети составляет $120 space В$. Определите силу тока в каждой лампе, силу тока в проводящих проводах (то есть силу тока до разветвления), общее сопротивление участка, состоящего из двух ламп.
Подразумевается, что лампы подключены в сеть параллельно. Запишем условие задачи и решим ее.
Дано:
$R_1 = 200 space Ом$
$R_2 = 300 space Ом$
$U = 120 space В$
$I_1 — ?$
$I_2 — ?$
$I — ?$
$R — ?$
Решение:
Запишем закон Ома для участка цепи с первой лампой:
$I_1 = frac{U_1}{R_1}$.
Значение сопротивления нам известно. Что с напряжением на этом участке?
Так как лампы подсоединены параллельно, то напряжение на каждой будет равно напряжению во всей цепи:
$U_1 = U_2 = U = 120 space В$
Тогда мы можем рассчитать силу тока в каждой лампе.
Сила тока в первой лампе:
$I_1 = frac{U}{R_1}$,
$I_1 = frac{120 space В}{200 space Ом} = 0.6 space А$.
Сила тока во второй лампе:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{120 space В}{300 space Ом} = 0.4 space А$.
Сила тока до разветвления будет равна сумме сил этих двух токов в лампах:
$I = I_1 + I_2$,
$I = 0.6 space А + 0.4 space А = 1 space А$.
Общее сопротивление цепи мы можем определить двумя способами.
Способ №1
Используя закон Ома для участка цепи, состоящего из двух параллельно соединенных ламп:
$I = frac{U}{R}$,
$R = frac{U}{I}$,
$R = frac{120 space В}{1 space А} = 120 space Ом$.
Способ №2
Используя формулу для расчета сопротивления при параллельном соединении проводников:
$frac{1}{R} = frac{1}{R_1} + frac{1}{R_2}$,
$frac{1}{R} = frac{1}{200 space Ом} + frac{1}{300 space Ом} = frac{5}{600 space Ом} = frac{1}{120 space Ом}$.
Отсюда, $R = frac{1}{frac{1}{120 space Ом}} = 120 space Ом$.
При решении этой задачи мы убедились, что общее сопротивление цепи меньше сопротивления каждого из параллельно подключенных проводников: $R < R_1 < R_2$.
Ответ: $I_1 = 0.6 space А$, $I_2 = 0.4 space А$, $I = 1 space А$, $R = 120 space Ом$.
Упражнения
Упражнение №1
Два проводника сопротивлением $10 space Ом$ и $15 space Ом$ соединены параллельно и подключены к напряжению в $12 space В$. Определите силу тока в каждом проводнике и силу тока до разветвления.
Дано:
$R_1 = 10 space Ом$
$R_2 = 15 space Ом$
$U = 12 space В$
$I_1 — ?$
$I_2 — ?$
$I — ?$
Показать решение и ответ
Скрыть
Решение:
Напряжение будет одинаковое как во всей цепи, так и на концах каждого из двух проводников.
Запишем закон Ома для первого проводника и рассчитаем силу тока в нем:
$I_1 = frac{U}{R_1}$,
$I_1 = frac{12 space В}{10 space Ом} = 1.2 space А$.
То же самое сделаем для второго проводника:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{12 space В}{15 space Ом} = 0.8 space А$.
Сила тока до разветвления в цепи будет равна сумме сил тока в каждом проводнике:
$I = I_1 + I_2$,
$I = 1.2 space А + 0.8 space А = 2 space А$.
Ответ: $I_1 = 1.2 space А$, $I_2 = 0.8 space А$, $I = 2 space А$.
Упражнение №2
Почему бытовые приборы в помещении необходимо соединять параллельно?
Потому что бытовые приборы рассчитаны на то же напряжение, которое подается от городской сети — $220 space В$. При параллельном соединении это напряжение будет одинаковым на всех участках цепи.
Также параллельное соединение позволяет включать и выключать приборы независимо друг от друга, что невозможно при последовательном соединении.
Упражнение №3
Три потребителя с сопротивлениями $20 space Ом$, $40 space Ом$ и $24 space Ом$ соединены параллельно. Напряжение на концах этого участка цепи равно $24 space В$. Определите силу тока в каждом потребителе, общую силу тока в участке цепи и сопротивление участка цепи.
Дано:
$R_1 = 20 space Ом$
$R_2 = 40 space Ом$
$R_3 = 24 space Ом$
$U = 24 space В$
$I_1 — ?$
$I_2 — ?$
$I_3 — ?$
$I — ?$
$R — ?$
Показать решение и ответ
Скрыть
Решение:
Напряжение на концах этого участка цепи будет равно напряжению на концах каждого потребителя, так как они соединены параллельно: $U_1 = U2 = U_3 = U = 24 space В$.
Используя закон Ома для участка цепи, рассчитаем силу тока на каждом потребителе электроэнергии.
Для первого потребителя:
$I_1 = frac{U}{R_1}$,
$I_1 = frac{24 space В}{20 space Ом} = 1.2 space А$.
Для второго потребителя:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{24 space В}{40 space Ом} = 0.6 space А$.
Для третьего потребителя:
$I_3 = frac{U}{R_3}$,
$I_3 = frac{24 space В}{24 space Ом} = 1 space А$.
Сила тока до разветвления в цепи будет равна сумме сил тока в каждом потребителе электроэнергии:
$I = I_1 + I_2 + I_3$,
$I = 1.2 space А + 0.6 space А + 1 space А = 2.8 space А$.
Теперь используем закон Ома, представляя участок цепи с тремя потребителями как единый участок цепи:
$I = frac{U}{R}$,
$R = frac{U}{I}$,
$R = frac{24 space В}{2.8 space А} approx 8.6 space Ом$.
Ответ: $I_1 = 1.2 space А$, $I_2 = 0.6 space А$, $I_3 = 1 space А$, $I = 2.8 space А$, $R approx 8.6 space Ом$.
Упражнение №4
Два проводника имеют сопротивления, равные $5 space Ом$ и $500 space Ом$. Почему при последовательном соединении этих проводников их общее сопротивление будет больше $500 space Ом$, а при параллельном соединении меньше $5 space Ом$?
При последовательном соединении проводников общее сопротивление цепи будет равно сумме сопротивлений составляющих ее проводников.
Общее сопротивление при последовательном соединении:
$R = R_1 + R_2 = 5 space Ом + 500 space Ом = 505 space Ом$.
Это значение действительно больше, чем $500 space Ом$.
При параллельном соединении общее сопротивление мы рассчитываем следующим образом:
$frac{1}{R} = frac{1}{R_1} + frac{1}{R_2}$,
$frac{1}{R} = frac{1}{5 space Ом} + frac{1}{500 space Ом} = frac{101}{500 space Ом}$,
$R = frac{1}{frac{101}{500 space Ом}} = frac{500 space Ом}{101} approx 5 space Ом$.
Согласитесь, что $5 space Ом$ намного меньше, чем $500 space Ом$.
Можно посмотреть на этот вопрос и с другой стороны. Сопротивление рассчитывается по формуле $R = frac{rho l}{S}$. Оно прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения.
При последовательном соединении проводников мы можем сказать, что длина проводника увеличивается. Значит, увеличивается и сопротивление. Общее сопротивление будет больше, чем сопротивление каждого отдельного проводника.
А при параллельном соединении увеличивается площадь поперечного сечения. Значит, сопротивление будет уменьшаться. Получается, что общее сопротивление такой цепи будет меньше сопротивления каждого из проводников.
Упражнение №5
На рисунке 7 изображена схема смешанного соединения проводников, сопротивления которых: $R_1 = 4 space Ом$, $R_2 = 6 space Ом$, $R_3 = 12 space Ом$, $R_4 = 2 space Ом$. Амперметр показывает силу тока $1 space А$. Определите напряжение между точками В и С и силу тока в каждом проводнике.
Дано:
$R_1 = 4 space Ом$
$R_2 = 6 space Ом$
$R_3 = 12 space Ом$
$R_4 = 2 space Ом$
$I_3 = 1 space А$
$U — ?$
$I_1 — ?$
$I_2 — ?$
$I_4 — ?$
Показать решение и ответ
Скрыть
Решение:
Амперметр подсоединен последовательно с проводником $R_3$. Он показывает силу тока $I_3 = 1 space А$. Это сила тока после разветвления.
Используя закон Ома для этого проводника, рассчитаем напряжение на его концах:
$I_3 = frac{U_3}{R_3}$,
$U_3 = I_3R_3$,
$U_3 = 1 space А cdot 12 space Ом = 12 space В$.
Так как проводники $R_3$ и $R_2$ подключены в цепь параллельно, то напряжение на каждом из этих проводников будет равно напряжению на участке цепи, который их включает. Это и есть напряжение между точками B и C:
$U = U_3 = 12 space В$.
По закону Ома рассчитаем силу тока на проводнике $R_2$:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{12 space В}{6 space Ом} = 2 space А$.
Теперь мы можем рассчитать силу тока до его разветвления — на проводниках $R_1$ и $R_4$. При этом $I_1 = I_4 = I$, потому что эти проводники включены в цепь последовательно. Это значит, что сила тока в любом участке такой цепи будет одинаковой. В нашем случае на проводнике $R_1$ и $R_4$.
Рассчитаем эту силу тока, используя величины, полученные с параллельно соединенных проводников. Сила тока до разветвления будет равна сумме сил тока в каждом проводнике после разветвления:
$I = I_2 + I_3$,
$I = 1 space А + 2 space А = 3 space А$.
Ответ: $U = 12 space В$, $I_1 = I_4 = I = 3 space А$, $I_2 = 2 space А$, $I_3 = 1 space А$.
