Применение закона Ома к расчету линейных электрических цепей постоянного тока
1. Найти ток ветви (рисунок 3), если: U=10 В, Е=20 В, R=5 Ом.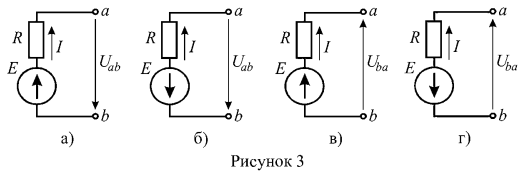
Решение:
Так как все схемы рисунка 3 представляют собой активные ветви, то для определения токов в них используем закон Ома обобщенный закон Ома. Рассмотрим рисунок 3 а: направление ЭДС совпадает с произвольно выбранным условно положительным направлением тока, следовательно, в формуле обобщенного закона Ома величина ЭДС учитывается со знаком «плюс». Направление напряжения ![]() не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;
не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;
![]()
Аналогично определяются токи в схемах б, в, г рисунка 3:
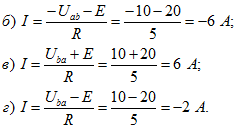
2. Найти напряжение между зажимами нетвей (рисунок 4).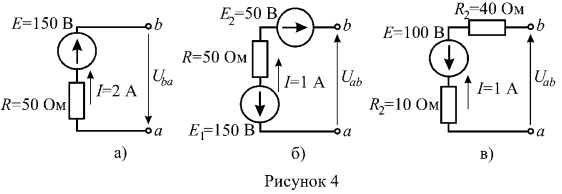
Решение:
Участок цепи, изображенный на рисунке 4 а содержит источник ЭДС, т.е. является активным, поэтому воспользуемся обобщенным законом Ома:
![]()
откуда выразим напряжение на зажимах:
![]()
Аналогично определяются напряжения на зажимах участков, изображенных на рисунках 4 б и 4 в.
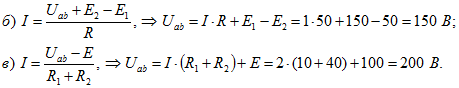
3. Определить неизвестные потенциалы точек участка цени (рисунок 5).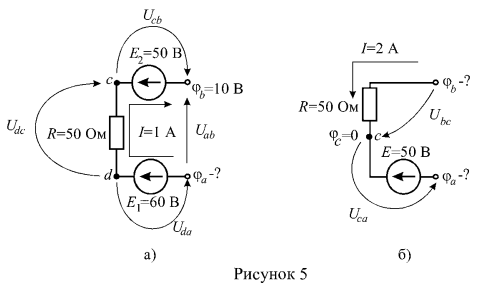
Решение:
Для схемы рисунка 5 а запишем обобщенный закон Ома:
![]()
откуда выразим напряжение на зажимах ветви:
![]()
Если представить напряжение ![]() как разность потенциалов:
как разность потенциалов:
![]()
тогда при известных параметрах цепи, токе и потенциале ![]() определим потенциал
определим потенциал ![]() :
:
![]()
Эту же задачу можно решить другим способом. Напряжение на зажимах источника ЭДС ![]() , без учета внутреннего сопротивления источника, по величине равно
, без учета внутреннего сопротивления источника, по величине равно ![]() и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):
и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):
![]()
и тогда, зная потенциал ![]() , определим потенциал точки С:
, определим потенциал точки С:
![]()
Потенциал точки d больше потенциала точки С на величину падения напряжения на сопротивлении R:
![]()
тогда
![]()
Потенциал точки а определяем с учетом направления напряжения ![]() на зажимах источника ЭДС
на зажимах источника ЭДС ![]() . Напряжение
. Напряжение ![]() направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):
направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):
![]()
откуда следует, что
![]()
или
![]()
Рассмотрим решение задачи для схемы рисунка 5 б. При известном потенциале точки С, параметрах элементов и токе, определим потенциалы крайних точек участка цепи ![]() . Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:
. Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:
![]()
откуда следует
![]()
Напряжение на участке с — а, равное по величине Е, направлено от точки с большим потенциалом к точке с меньшим потенциалом:
![]()
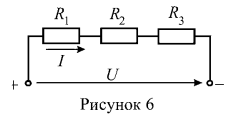
4. В цепи (рисунок 6) известны величины сопротивлений резистивных элементов: ![]() , входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением
, входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением ![]() . Определить величину сопротивления резистора
. Определить величину сопротивления резистора ![]() .
.
 Решение:
Решение:
Согласно закону Джоуля-Ленца, мощность на резистивном элементе определяется:
![]()
или, согласно закону Ома:
![]()
По известному значению мощности на резистивном элементе ![]() и величине сопротивления этого элемента определим ток в ветви:
и величине сопротивления этого элемента определим ток в ветви:
![]()
По закону Ома напряжение на зажимах определится:
![]()
тогда величина сопротивления резистивного элемента:
![]()
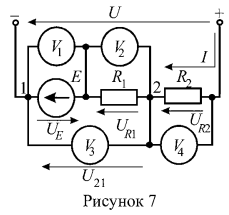
5. Определить показания вольтметров цепи (рисунок 7), если ![]() .
.
 Решение:
Решение:
Ток в цепи определим по закону Ома:
![]()
Вольтметр ![]() показывает напряжение на источнике ЭДС Е:
показывает напряжение на источнике ЭДС Е:
![]()
Вольтметры ![]() показывают величину падения напряжения на резистивных элементах
показывают величину падения напряжения на резистивных элементах ![]() :
:
![]()
Вольтметр ![]() , показывает напряжение на участке 2 — 1
, показывает напряжение на участке 2 — 1 ![]() , которое определим как алгебраическую сумма напряжений
, которое определим как алгебраическую сумма напряжений ![]() :
:
![]()
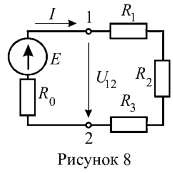
6. Ток симметричной цепи (рисунок 8) ![]() , внутреннее сопротивлении источника ЭДС
, внутреннее сопротивлении источника ЭДС ![]() . Определить ЭДС Е и мощность источника энергии.
. Определить ЭДС Е и мощность источника энергии.
 Решение:
Решение:
Напряжение на зажимах 1 — 2 определим по закону Ома для пассивной ветви:
![]()
Величину ЭДС источника энергии определим из выражения закона Ома для активной ветви:
![]()
Мощность, развиваемая источником энергии, определится:
![]()
7. Определение напряжения между двумя точками электрической цепи
Эта задача при расчете электрических цепей встречается очень часто. Пусть, например, в цепи на рис. 2.1 требуется найти напряжение между точками m и n.
Прежде всего необходимо показать на схеме или мысленно представить стрелку этого напряжения. Её направление определяется порядком следования индексов у буквы  . Для напряжения
. Для напряжения  она направлена отточки m к точке n. Если мы меняем местами индексы у буквы
она направлена отточки m к точке n. Если мы меняем местами индексы у буквы  , то следует изменить и направление стрелки на схеме. При этом при расчете меняется знак полученного напряжения, так как
, то следует изменить и направление стрелки на схеме. При этом при расчете меняется знак полученного напряжения, так как  .
.
Дальше записываются уравнения по второму закону Кирхгофа для любого контура, включающего в себя эту стрелку, как было сделано при расчете напряжений  и
и  . Так, для контура m31nm при обходе его по часовой стрелке
. Так, для контура m31nm при обходе его по часовой стрелке
 .
.
 . (7.1)
. (7.1)
При соответствующем навыке последняя формула может быть записана сразу, без составления уравнения второго закона Кирхгофа.
В указанном контуре напряжение  складывается из трех напряжений:
складывается из трех напряжений:
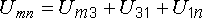 . (7.2)
. (7.2)
Порядок индексов у букв U соответствует порядку, в котором мы проходим участок электрической цепи, идя от точки m к точке n по элементам  ,
,  и
и  .
.
Теперь находим значение каждого слагаемого в последнем уравнении.
Величина  , определяющая напряжение между точками m и 3, представляет собой падение напряжения на сопротивлении
, определяющая напряжение между точками m и 3, представляет собой падение напряжения на сопротивлении  , которое мы должны взять со знаком минус, так как от точки m к точке 3 мы идем против тока
, которое мы должны взять со знаком минус, так как от точки m к точке 3 мы идем против тока  :
:
 .
.
 .
.
Здесь в правой части уравнения стоит плюс, так как мысленная стрелка напряжения  и ток
и ток  направлены в одну сторону.
направлены в одну сторону.
Третье слагаемое  представляет собой напряжение на зажимах источника. Если внутреннее сопротивление последнего равно нулю, то это напряжение по величине равно ЭДС, а знак его зависит от взаимного направления стрелок напряжения и ЭДС (рис. 7.1).
представляет собой напряжение на зажимах источника. Если внутреннее сопротивление последнего равно нулю, то это напряжение по величине равно ЭДС, а знак его зависит от взаимного направления стрелок напряжения и ЭДС (рис. 7.1).

Рис. 7.1. Напряжение на зажимах источника
При указанной на схеме полярности зажимов источника потенциал точки b выше потенциала точки a на величину ЭДС:
 .
.
Поэтому при одинаковых направлениях стрелок  и
и  (рис. 7.1, а)
(рис. 7.1, а)
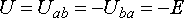 .
.
Если направления стрелок 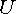 и
и  противоположны друг другу (рис. 7.1, б), то
противоположны друг другу (рис. 7.1, б), то
 .
.
С учетом сказанного напряжение на участке 1n (см. рис. 2.1) равно
 .
.
Подставляя найденные значения напряжений на участках в формулу (7.2), приходим к выражению (7.1).
То же самое напряжение, определяемое по участку m2n, будет равно
 .
.
Разумеется, вычисление одного и того же напряжения по двум различным формулам должно привести к одинаковым результатам.
8. Построение графиков
8.1. Общие требования к оформлению графиков. Зависимость мощности от тока
Правила построения графиков рассмотрим на примере зависимости мощности Р1, выделяющейся в сопротивлении первой ветви, от тока I1 в этой ветви. Эта зависимость определяется уравнением баланса мощностей в схеме рис. 6.1, в:
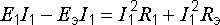 .
.
Так как 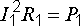 , то
, то
 . (8.1)
. (8.1)
Это – уравнение параболы со смещенной вершиной и направленными вниз ветвями (рис. 8.1).

Значения тока, при которых парабола пересекает горизонтальную ось, находятся из уравнения

 и
и  .
.
По смыслу  – это ток, протекающий в схеме рис. 6.1, в при закороченном сопротивлении
– это ток, протекающий в схеме рис. 6.1, в при закороченном сопротивлении  . При токе, равном половине этого значения, мощность
. При токе, равном половине этого значения, мощность  максимальна:
максимальна:
 .
.
Предположим, что параметры цепи на рис. 6.1, в имеют следующие численные значения:
 = 72,4 В;
= 72,4 В;  = 130 В;
= 130 В;  = 43,6 Ом.
= 43,6 Ом.
Прежде всего находим максимальные значения абсциссы и ординаты, которые будут определять размеры графика. В нашем примере – это значения  и
и  :
:
 ;
;
 .
.
Исходя из этих величин и предполагаемых размеров графика, выбираем масштаб, который указываем на каждой оси графика в виде равномерной шкалы.
В одной единице длины (сантиметре, миллиметре) может содержаться m × 10 n именованных единиц. Здесь n – целое число, положительное или отрицательное, а для mрекомендуются числа 1, 2, 5.
Положительные значения величин откладываются вправо по оси абсцисс и вверх по оси ординат.
В конце каждой оси ставится буквенное обозначение откладываемой величины и через запятую – ее единица измерения.
Если график строится на белой (нелинованной) бумаге, то чертится масштабная сетка.
Данные для построения графика рассчитываем по формуле (8.1) и сводим их в таблицу (табл. 8.1).
Данные для построения графика
 , А
, А
Источник
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ МЕЖДУ ДВУМЯ ТОЧКАМИ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Эта задача при расчете электрических цепей встречается очень часто. Пусть, например, в цепи на рис. 2.1 требуется найти напряжение между точками m и n.
Прежде всего необходимо показать на схеме или мысленно представить стрелку этого напряжения. Её направление определяется порядком следования индексов у буквы 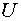 . Для напряжения
. Для напряжения 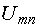 она направлена отточки m к точке n. Если мы меняем местами индексы у буквы
она направлена отточки m к точке n. Если мы меняем местами индексы у буквы 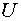 , то следует изменить и направление стрелки на схеме. При этом при расчете меняется знак полученного напряжения, так как
, то следует изменить и направление стрелки на схеме. При этом при расчете меняется знак полученного напряжения, так как  .
.
Дальше записываются уравнения по второму закону Кирхгофа для любого контура, включающего в себя эту стрелку, как было сделано при расчете напряжений 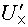 и
и 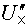 . Так, для контура m31nm при обходе его по часовой стрелке
. Так, для контура m31nm при обходе его по часовой стрелке
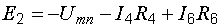 .
.
 . (7.1)
. (7.1)
При соответствующем навыке последняя формула может быть записана сразу, без составления уравнения второго закона Кирхгофа.
В указанном контуре напряжение 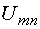 складывается из трех напряжений:
складывается из трех напряжений:
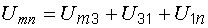 . (7.2)
. (7.2)
Порядок индексов у букв U соответствует порядку, в котором мы проходим участок электрической цепи, идя от точки m к точке n по элементам 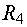 ,
, 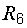 и
и 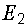 .
.
Теперь находим значение каждого слагаемого в последнем уравнении.
Величина 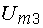 , определяющая напряжение между точками m и 3, представляет собой падение напряжения на сопротивлении
, определяющая напряжение между точками m и 3, представляет собой падение напряжения на сопротивлении 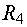 , которое мы должны взять со знаком минус, так как от точки m к точке 3 мы идем против тока
, которое мы должны взять со знаком минус, так как от точки m к точке 3 мы идем против тока 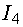 :
:
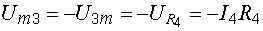 .
.
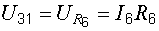 .
.
Здесь в правой части уравнения стоит плюс, так как мысленная стрелка напряжения 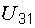 и ток
и ток 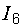 направлены в одну сторону.
направлены в одну сторону.
Третье слагаемое 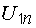 представляет собой напряжение на зажимах источника. Если внутреннее сопротивление последнего равно нулю, то это напряжение по величине равно ЭДС, а знак его зависит от взаимного направления стрелок напряжения и ЭДС (рис. 7.1).
представляет собой напряжение на зажимах источника. Если внутреннее сопротивление последнего равно нулю, то это напряжение по величине равно ЭДС, а знак его зависит от взаимного направления стрелок напряжения и ЭДС (рис. 7.1).
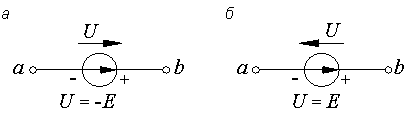
Рис. 7.1. Напряжение на зажимах источника
При указанной на схеме полярности зажимов источника потенциал точки b выше потенциала точки a на величину ЭДС:
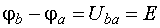 .
.
Поэтому при одинаковых направлениях стрелок 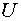 и
и  (рис. 7.1, а)
(рис. 7.1, а)
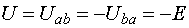 .
.
Если направления стрелок 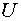 и
и  противоположны друг другу
противоположны друг другу
(рис. 7.1, б), то
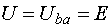 .
.
С учетом сказанного напряжение на участке 1n (см. рис. 2.1) равно
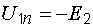 .
.
Подставляя найденные значения напряжений на участках в формулу (7.2), приходим к выражению (7.1).
То же самое напряжение, определяемое по участку m2n, будет равно
 .
.
Разумеется, вычисление одного и того же напряжения по двум различным формулам должно привести к одинаковым результатам.
ПОСТРОЕНИЕ ГРАФИКОВ
Общие требования к оформлению графиков. Зависимость мощности от тока
Правила построения графиков рассмотрим на примере зависимости мощности Р1,выделяющейся в сопротивлении первой ветви, от тока I1 в этой ветви. Эта зависимость определяется уравнением баланса мощностей в схеме рис. 6.1, в:
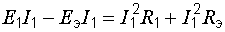 .
.
Так как 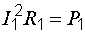 , то
, то
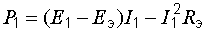 . (8.1)
. (8.1)
Это – уравнение параболы со смещенной вершиной и направленными вниз ветвями (рис. 8.1).
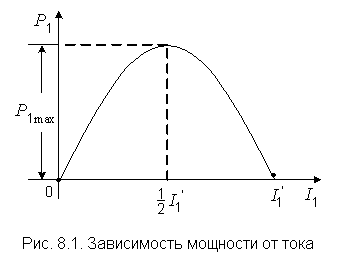
Значения тока, при которых парабола пересекает горизонтальную ось, находятся из уравнения
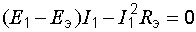
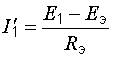 и
и 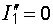 .
.
По смыслу 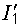 – это ток, протекающий в схеме рис. 6.1, в при закороченном сопротивлении
– это ток, протекающий в схеме рис. 6.1, в при закороченном сопротивлении 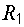 . При токе, равном половине этого значения, мощность
. При токе, равном половине этого значения, мощность 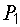 максимальна:
максимальна:
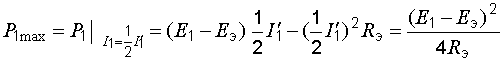 .
.
Предположим, что параметры цепи на рис. 6.1, в имеют следующие численные значения:
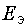 = 72,4 В;
= 72,4 В; 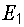 = 130 В;
= 130 В; 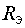 = 43,6 Ом.
= 43,6 Ом.
Прежде всего находим максимальные значения абсциссы и ординаты, которые будут определять размеры графика. В нашем примере – это значения 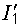 и
и 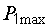 :
:
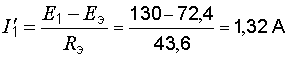 ;
;
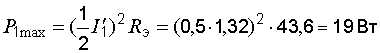 .
.
Исходя из этих величин и предполагаемых размеров графика, выбираем масштаб, который указываем на каждой оси графика в виде равномерной шкалы.
В одной единице длины (сантиметре, миллиметре) может содержаться m × 10 n именованных единиц. Здесь n – целое число, положительное или отрицательное, а для mрекомендуются числа 1, 2, 5.
Положительные значения величин откладываются вправо по оси абсцисс и вверх по оси ординат.
В конце каждой оси ставится буквенное обозначение откладываемой величины и через запятую – ее единица измерения.
Если график строится на белой (нелинованной) бумаге, то чертится масштабная сетка.
Данные для построения графика рассчитываем по формуле (8.1) и сводим их в таблицу (табл. 8.1).
Данные для построения графика
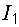 , А , А |
0 | 0,2 | 0,4 | 0,5 | 0,6 | 0,66 | 0,8 | 0,9 | 1 | 1,2 | 1,32 |
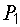 , Вт , Вт |
0 | 9,78 | 16,1 | 17,9 | 18,9 | 19 | 18,2 | 16,5 | 14 | 6,34 | 0 |
Абсциссы точек, выбираемых для построения графика, желательно располагать по оси равномерно. Но вблизи характерных областей кривой (в нашем случае у вершины параболы) точки можно взять чаще. В таблицу внесены также значения максимальной мощности и тока, которому эта мощность соответствует. При построении графика числа из таблицы на осях не показываются (рис. 8.2).
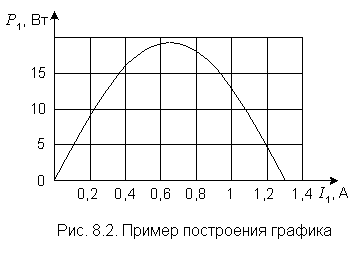
8.2. Зависимость тока от сопротивления
Зависимость тока в первой ветви от сопротивления этой ветви строим по уравнению (6.2), которое при выбранных значениях 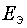 ,
, 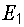 и
и 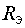 принимает вид:
принимает вид:
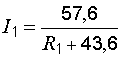 .
.
Подставляя сюда различные значения сопротивления 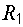 , приходим к результатам, представленным на рис. 8.3.
, приходим к результатам, представленным на рис. 8.3.
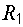 , Ом , Ом |
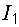 , А , А |
| 0 | 1,32 |
| 10 | 1,07 |
| 20 | 0,91 |
| 30 | 0,78 |
| 40 | 0,69 |
| 50 | 0,62 |
| 60 | 0,56 |
| 70 | 0,51 |
| 80 | 0,47 |
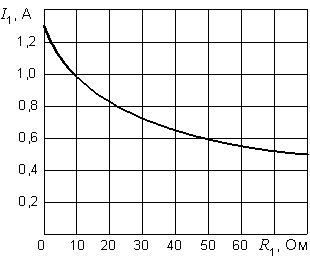
Рис. 8.3. Зависимость тока от сопротивления
Дата добавления: 2019-07-17 ; просмотров: 1719 ; Мы поможем в написании вашей работы!
Источник
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования – «Оренбургский государственный университет»
Кафедра теоретической и общей электротехники
Н.И.ДОБРОЖАНОВА, В.Н.ТРУБНИКОВА
Применение законов Ома и Кирхгофа к расчету линейных электрических цепей постоянного тока
ПРАКТИКУМ ПО ТЕОРЕТИЧЕСКИМ ОСНОВАМ ЭЛЕКТРОТЕХНИКИ
Рекомендовано к изданию Редакционно-издательским советом государственного образовательного учреждения высшего профессионального образования – «Оренбургский государственный университет»
Оренбург 2003
5
ББК 31.211я7 Д 56
УДК 621.3.011.7(076.5)
Рецензент кандидат технических наук, доцент Л.В.Быковская
Доброжанова Н.И., Трубникова В.Н.
Д56 Применение законов Ома и Кирхгофа к расчету линейных
электрических цепей постоянного тока: Практикум по ТОЭ. – Оренбург: ГОУ ОГУ, 2003. – 20 с.
Практикум предназначен для самостоятельной подготовки студентов по разделу «Цепи постоянного тока». Содержит теоретические сведения и примеры расчета цепей с использованием законов Ома и Кирхгофа, а также задачи для самостоятельного решения.
ББК 31.211я7
©Доброжанова Н.И., Трубникова В.Н., 2003
©ГОУ ОГУ, 2003
6
Введение
Физическое действие электрического тока проявляется в нагреве и механическом воздействии на токоведущие элементы электротехнического устройства. В конечном итоге это влияет на долговечность и надежность его работы. Перегрев токоведущих элементов устройства в первую очередь вызывает интенсивный износ изоляции, что, в конечном счете, приводит к короткому замыканию сопровождаемому, как правило, электрической дугой. Превышение механических усилий своего допустимого значения приводит к разрушению устройства, затем – к короткому замыканию. Поэтому первым этапом расчета электротехнического устройства, ставится задача определения величин токов в элементах устройства. При этом считается, что конфигурация и параметры элементов схемы электрической цепи устройства известны.
Наиболее общими, универсальными законами, позволяющими рассчитать любую электрическую цепь, являются законы Кирхгофа.
В данном практикуме по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием законов Ома и Кирхгофа, а также задачи для самостоятельного решения.
Практикум предназначен для глубокой самостоятельной проработки и самоконтроля усвоения курса ТОЭ. Материал подобран и расположен таким образом, что позволяет студентам эффективно и с минимальными затратами времени усвоить все вопросы, рассматриваемые на лекциях и лабораторно-практических занятиях.
7

1 Применение законов Ома и Кирхгофа к расчету линейных электрических цепей постоянного тока
1.1 Законы Ома Закон Ома для участка цепи (в пределах ветви) позволяет найти ток
участка по известной разности потенциалов (напряжению) на зажимах участка.
|
I |
R |
I = U ab |
= ϕa −ϕb |
– Закон Ома для участка цепи, не |
||||
|
a |
b |
|||||||
|
Uab |
R |
R |
содержащего |
источник |
ЭДС |
|||
|
(рисунок 1) |
||||||||
|
Рисунок 1 |
||||||||
|
I |
R |
E |
||||||
|
b |
||||||||
|
a |
±U ab ± E |
±(ϕa −ϕb )± E |
||||||
|
I = |
= |
– Закон |
Ома |
|||||
|
Uab |
R |
R |
||||||
|
для участка цепи, содержащего источник ЭДС |
|
Рисунок 2 |
(активная ветвь) (рисунок 2). |
Если положительные направления напряжения и ЭДС совпадают с произвольно выбранным положительным направлением тока ветви, то в приведенной формуле они учитываются со знаком плюс, и со знаком минус, если их направления не совпадают с направлением тока.
Задача 1.1.1 Найти ток ветви (рисунок 3), если: U =10 В, E =20 В,
R =5 Ом.
|
a |
a |
a |
a |
||||||||
|
R |
I |
R |
I |
R |
I |
R |
I |
||||
|
E |
Uab E |
Uab E |
Ubа E |
Ubа |
|||||||
|
b |
b |
b |
b |
||||||||
|
a) |
б) |
в) |
г) |
Рисунок 3
Решение:
Так как все схемы рисунка 3 представляют собой активные ветви, то для определения токов в них используем закон Ома обобщенный закон Ома. Рассмотрим рисунок 3 а: направление ЭДС совпадает с произвольно выбранным условно положительным направлением тока, следовательно, в формуле обобщенного закона Ома величина ЭДС учитывается со знаком
8
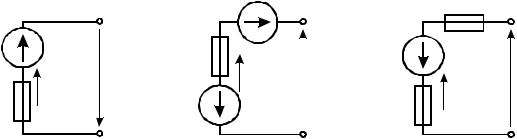
«плюс». Направление напряжения U ab не совпадает с направлением тока,
и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»:
|
а) |
I = |
−U ab + E |
= −10 +20 |
=2 А; |
||||||||||||||||
|
R |
5 |
|||||||||||||||||||
|
Аналогично определяются токи в схемах б, в, г рисунка 3: |
||||||||||||||||||||
|
б) |
I = |
−U ab − E |
= −10 −20 |
=-6 А; |
||||||||||||||||
|
R |
5 |
|||||||||||||||||||
|
в) |
I = |
U ba + E |
= |
10 +20 |
=6 А; |
|||||||||||||||
|
R |
5 |
|||||||||||||||||||
|
г) |
I = |
Uba − E |
= |
10 −20 |
=-2 А. |
|||||||||||||||
|
R |
5 |
|||||||||||||||||||
|
Задача 1.1.2 Найти напряжение между зажимами ветвей (рисунок 4). |
||||||||||||||||||||
|
E=150 В |
b |
E =50 В |
R2=40 Ом |
|||||||||||||||||
|
2 |
b |
E=100 В |
b |
|||||||||||||||||
|
Uba |
R=50 Ом |
Uab |
Uаb |
|||||||||||||||||
|
I=1 А |
I=1 А |
|||||||||||||||||||
|
R=50 Ом |
I=2 А |
R =10 Ом |
||||||||||||||||||
|
a |
E1=150 В |
2 |
||||||||||||||||||
|
a |
a |
|||||||||||||||||||
|
a) |
б) |
в) |
Рисунок 4
Решение:
Участок цепи, изображенный на рисунке 4 а содержит источник ЭДС, т.е. является активным, поэтому воспользуемся обобщенным законом Ома:
I = −Uba + E ,
R
откуда выразим напряжение на зажимах:
Uba = E − I R =150 −2 50 =50 В.
Аналогично определяются напряжения на зажимах участков, изображенных на рисунках 4 б и 4 в.
|
б) I = |
U ab + E2 − E1 |
, |
U |
ab |
= I R + E − E |
2 |
=1 50 +150 −50 =150 В; |
||||
|
R |
1 |
||||||||||
|
в) |
I = |
U ab − E |
, U |
ab |
= I (R + R |
2 |
)+ E = 2 (10 +40)+100 =200 В. |
||||
|
R1 + R2 |
1 |
||||||||||
9
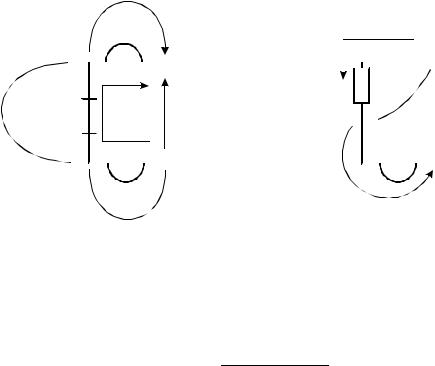
Задача 1.1.3 Определить неизвестные потенциалы точек участка цепи (рисунок 5).
Uсb
E2=50 В
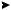 с
с

 ϕb=10 В
ϕb=10 В
Udc R=50 Ом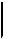
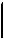 I=1 А Uab
I=1 А Uab
d

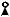 ϕa -?
ϕa -?
E1=60 В
Uda
I=2 А
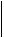

 ϕb -?
ϕb -?
R=50 Ом Ubc
ϕс=0  с
с
E=50 В
 ϕa -?
ϕa -?
Uca
Рисунок 5
Решение:
Для схемы рисунка 5 а запишем обобщенный закон Ома:
I = U ab + E1 − E2 , R
откуда выразим напряжение на зажимах ветви:
U ab = I R − E1 + E2 .
Если представить напряжениеU ab как разность потенциалов:
U ab =ϕa −ϕb ,
тогда при известных параметрах цепи, токе и потенциале ϕb определим потенциал ϕa :
ϕa = I R − E1 + E2 +ϕb =1 50 +100 −60 +10 =10 В.
Эту же задачу можно решить другим способом. Напряжение на зажимах источника ЭДС E2 , без учета внутреннего сопротивления источни-
ка, по величине равно E2 и направлено от точки с большим потенциалом
(точка c ) к точке с меньшим потенциалом (точка b ):
Ucb = E2 =ϕc −ϕb ,
и тогда, зная потенциал ϕb , определим потенциал точки c :
ϕc =ϕb + E2 .
Потенциал точки d больше потенциала точки c на величину падения напряжения на сопротивлении R :
Ucd =ϕc −ϕd = I R ,
тогда
ϕd =ϕc + I R =ϕb + E2 + I R .
10
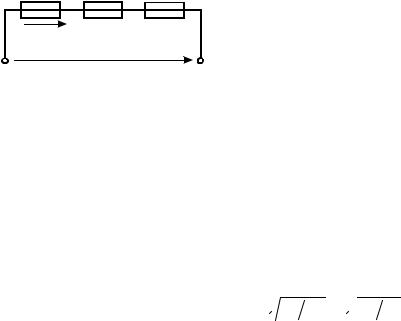
Потенциал точки a определяем с учетом направления напряжения U da на зажимах источника ЭДС E1. Напряжение U da направлено от точки
с большим потенциалом (точка d ) к точке с меньшим потенциалом (точка a ):
U da = E1 =ϕd −ϕa ,
откуда следует, что
ϕa =ϕd − E1
или
ϕa =ϕb + E2 + I R − E1 .
Рассмотрим решение задачи для схемы рисунка 5 б. При известном потенциале точки c , параметрах элементов и токе, определим потенциалы крайних точек участка цепи ϕa и ϕb . Напряжение на участке b −c , выра-
женное через разность потенциалов, определим по закону Ома:
Ubc =ϕb −ϕc = I R ,
откуда следует
ϕb =ϕc + I R = 0 +2 50 =100 В.
Напряжение на участке c −a , равное по величине E , направлено от точки с большим потенциалом к точке с меньшим потенциалом:
Uca = E =ϕc −ϕa
ϕa =ϕc − E = 0 −50 =-50 В.
Задача 1.1.4 В цепи (рисунок 6) известны величины сопротивлений
|
R1 |
R2 |
R3 |
резистивных |
элементов: |
R1 =10 Ом, |
|||
|
R2 =20 Ом, входное напряжение U =100 В и |
||||||||
|
мощность, выделяемая на резистивном эле- |
||||||||
|
I |
||||||||
|
U |
_ менте с сопротивлением R1 : P1=40 Вт. Оп- |
|||||||
|
+ |
||||||||
|
ределить величину сопротивления резистора |
Согласно закону Джоуля-Ленца, мощность на резистивном элементе определяется:
P =U I ,
или, согласно закону Ома:
P = I 2 R
По известному значению мощности на резистивном элементе R1 и величине сопротивления этого элемента определим ток в ветви:
P1 = I 2 R1 I =  P1 R1 =
P1 R1 = 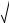 40 10 =2 А.
40 10 =2 А.
По закону Ома напряжение на зажимах определится:
U = I (R1 + R2 + R3 ),
11

|
тогда величина сопротивления резистивного элемента: |
||||||||||||||||||||||||||
|
R |
= |
U − I (R1 + R2 ) |
= |
100 −2(10 +20) |
=20 Ом. |
|||||||||||||||||||||
|
3 |
I |
2 |
||||||||||||||||||||||||
|
Задача 1.1.5 Определить показания вольтметров цепи (рисунок 7), |
||||||||||||||||||||||||||
|
если R1 =50 Ом, R2 =150 Ом, U =150 В, E =50 В. |
||||||||||||||||||||||||||
|
_ |
U |
+ |
Решение: |
|||||||||||||||||||||||
|
Ток в цепи определим по закону Ома: |
||||||||||||||||||||||||||
|
V |
V |
U + E |
150 +50 |
|||||||||||||||||||||||
|
1 |
2 |
I |
||||||||||||||||||||||||
|
I = R1 + R2 |
= 50 +150 =1 А. |
|||||||||||||||||||||||||
|
E |
R |
R |
||||||||||||||||||||||||
|
1 |
1 |
2 |
2 |
|||||||||||||||||||||||
|
Вольтметр V1 показывает напряжение |
||||||||||||||||||||||||||
|
UR2 |
||||||||||||||||||||||||||
|
UR1 |
||||||||||||||||||||||||||
|
UE |
V |
на источнике ЭДС E : |
||||||||||||||||||||||||
|
V |
V1 =U E = E =50 В. |
|||||||||||||||||||||||||
|
3 |
4 |
|||||||||||||||||||||||||
|
U |
21 |
Вольтметры V2 |
и V4 показывают ве- |
|||||||||||||||||||||||
|
личину |
падения напряжения на |
резистив- |
||||||||||||||||||||||||
|
Рисунок 7 |
||||||||||||||||||||||||||
|
ных элементах R1 и R2 : |
||||||||||||||||||||||||||
|
V2 =U R1 = I R1 =1 50 =50 В; |
||||||||||||||||||||||||||
|
V4 =U R2 = I R2 =1 150 =150 В. |
||||||||||||||||||||||||||
|
Вольтметр V3 , показывает напряжение на участке 2-1 U 21, которое |
||||||||||||||||||||||||||
|
определим как алгебраическую сумма напряжений U E и U R1: |
||||||||||||||||||||||||||
|
V3 =U 21 =U R1 −U E = 50 −50 =0. |
||||||||||||||||||||||||||
|
Задача 1.1.6 |
Ток симметричной |
цепи |
(рисунок 8) |
I =2,5 А, |
||||||||||||||||||||||
|
R1 =2,4 Ом, |
R2 =4,8 Ом, R3 =7,2 Ом, внутреннее сопротивлении источника |
|||||||||||||||||||||||||
|
ЭДС R0 =0,6 Ом. Определить ЭДС E и мощность источника энергии. |
||||||||||||||||||||||||||
|
I 1 |
R1 |
Решение: |
||||||||||||||||||||||||
|
E |
Напряжение на зажимах 1-2 определим по |
|||||||||||||||||||||||||
|
R2 |
закону Ома для пассивной ветви: |
|||||||||||||||||||||||||
|
R0 |
U12 |
U12 = I (R1 + R2 |
+ R3 )= 2,5 (2,4 +4,8 +7,2)=36 В. |
|||||||||||||||||||||||
|
R |
||||||||||||||||||||||||||
|
3 |
Величину ЭДС источника энергии опреде- |
|||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||
|
лим из выражения закона Ома для активной ветви: |
||||||||||||||||||||||||||
|
Рисунок 8 |
I = |
−U + E , |
E = I R |
+U = 2,5 0,6 +36 =37, |
||||||||||||||||||||||
|
R0 |
0 |
|||||||||||||||||||||||||
5 В.
Мощность, развиваемая источником энергии, определится:
PИ = E I = 37,5 2,5 =93,75 Вт.
12
1.2Законы Кирхгофа
Пе р в ы й з а к о н К и р х г о ф а является следствием закона сохранения заряда, согласно которому в узле заряд одного знака не может ни накапливаться, ни убывать, и формулируется следующим образом:
Алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю
∑Ik = 0 .
При этом токи, направленные к узлу, берут с одним произвольно выбранным знаком, а токи, направленные от узла – с противоположным.
В т о р о й з а к о н К и р х г о ф а является следствием закона сохранения энергии, в силу которого изменение потенциала в замкнутом контуре равно нулю.
При обходе замкнутого контура по отдельным участкам потенциал конечного узла этого участка повышается относительно потенциала его начального узла на величину напряжения, если направление обхода противоположно направлению напряжения, и понижается, когда направление обхода контура и направление напряжения совпадают. Поэтому изменения потенциала в замкнутом контуре можно определить суммированием напряжений с учетом их знаков. Согласно второму закону Кирхгофа: алгеб-
раическая сумма напряжений участков замкнутого контура равна нулю
∑U k = 0 .
При этом напряжения, положительные направления которых совпадают с направлением обхода контура, берутся с положительными знаками, а напряжения, положительные направления которых противоположны на-
|
правлению обхода – с отрицательными знаками. |
|||||||||||||||||
|
Uab |
Уравнение |
по второму |
закону |
||||||||||||||
|
Кирхгофа для |
замкнутого |
контура |
|||||||||||||||
|
а |
R |
b |
abcda (рисунок 9): |
||||||||||||||
|
1 |
−Uba +Ubc +U cd −U ad =0 |
||||||||||||||||
|
R4 |
I |
I1 |
|||||||||||||||
|
U |
4 |
I2 |
R |
Существует другое определение |
|||||||||||||
|
E |
|||||||||||||||||
|
ad |
4 |
2 |
Ubc второго закона Кирхгофа: алгебраиче- |
||||||||||||||
|
I3 |
ская сумма падений напряжений на |
||||||||||||||||
|
d |
c |
элементах замкнутого контура равна |
|||||||||||||||
|
R3 |
алгебраической сумме ЭДС, дейст- |
||||||||||||||||
|
Ucd |
вующих в этом контуре. |
||||||||||||||||
|
Рисунок 9 |
∑Ik Rk = ∑Ek |
Падения напряжения входят в сумму со знаком «плюс», если направления тока и обхода контура совпадают, и со знаком «минус» – если не совпадают. Аналогично учитывают знаки, суммируя величины электродвижущих сил источников ЭДС:
13
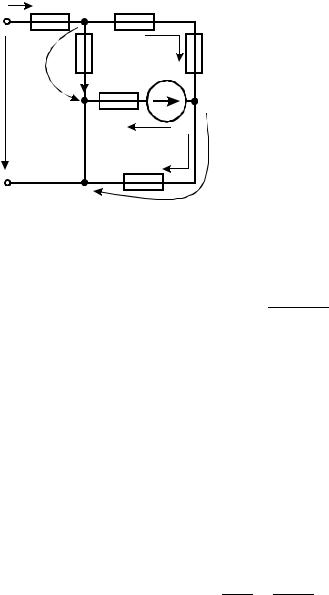
|
− I1R1 + I2 R2 + I3 R3 − I4 R4 = −E4 |
|||||||||||||||||||
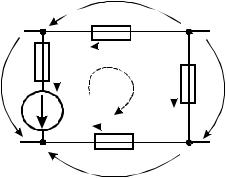
|
Задача 1.2.1 В цепи (рисунок 10) известны значения токов I6 =2 А, |
|||||||||||||||||||
|
I2 =1,25 А, |
I5 =0,8 |
А; |
величины |
сопротивлений R1 =2 Ом, R2 =3 Ом, |
|||||||||||||||
|
R3 =2 Ом, R4 =2 Ом, |
R5 =5 Ом. Определить напряжение U на входных за- |
||||||||||||||||||
|
жимах цепи, сопротивление R6 и величину E источника ЭДС. |
|||||||||||||||||||
|
I |
R1 |
R2 |
U13 |
Решение: |
|||||||||||||||
|
1 |
1 |
По закону Ома определим напря- |
|||||||||||||||||
|
I2 |
жение между узлами 3-2: |
||||||||||||||||||
|
U12 |
R6 |
R3 |
U32 = I5 R5 = 0,8 5 =4 В. |
||||||||||||||||
|
R4 E |
|||||||||||||||||||
|
I |
|||||||||||||||||||
|
U |
6 |
3 |
Из уравнения, составленного по |
||||||||||||||||
|
2 |
|||||||||||||||||||
|
I4 |
первому закону Кирхгофа для узла 3: |
||||||||||||||||||
|
I2 − I4 − I5 = 0 |
|||||||||||||||||||
|
R5 I5 |
|||||||||||||||||||
|
определим ток I4 : |
|||||||||||||||||||
|
2 |
U32 |
||||||||||||||||||
Рисунок 10 I4 = I2 − I5 =1,25-0,8=0,45 А.
Тогда, по закону Ома для ветви с
сопротивлением R4 :
I4 = U32 − E , R4
откуда выражаем величину E источника ЭДС:
E =U32 − I4 R4 = 4 −0,45 2 =3,1 В.
Напряжение U12 можно выразить из уравнения, записанного по II закону Кирхгофа для контура 1-3-2-1:
U13 +U 23 −U12 = 0 ,
U12 =U13 +U32 = I2 (R2 + R3 )+U32 =1,25 (3 +2)+4 =10,25 В.
Зная величины напряжения U12 и тока I6 , определим величину сопротивления R6 :
R6 = U12 =10,25 =6,8 Ом.
I6 1,5
Напряжение на входных зажимах цепи определится:
U =U R1 +U12 = I1 R1 +U12 .
14
«Потери» в проводах. Всякая цепь состоит обычно из каких-либо приборов (например, лампочек накаливания, нагревательных приборов, электролитических ванн и т. д.) и подводящих проводов. Эти приборы и провода обладают сопротивлением. Поэтому между концами любого участка цепи, который представляют эти приборы или провода, имеется напряжение.
Если в цепи идет ток
![]()
и сопротивления последовательно соединенных участков цепи равны
![]()
, то между концами каждого участка имеются соответственно напряжения
![]()
, определяемые по формуле (46.2):
![]()
,
![]()
,
![]()
, ….
Сумма этих напряжений представляет собой полное напряжение
![]()
, приложенное к концам всей цепи:
![]()
.
Таким образом, распределение напряжения между отдельными последовательно соединенными участками цепи зависит только от соотношения сопротивлений этих участков:
![]()
.
Пусть, например, генератор электростанции создает, на вводах, т. е. на концах проводов, введенных в квартиру, напряжение
![]()
(обычно
![]()
В). От вводов провода ведут к лампочке. Пусть сопротивление проводов равно
![]()
, сопротивление лампочки равно
![]()
, а сила тока, накаливающего лампочку, равна
![]()
. В таком случае напряжение, приходящееся на лампочку,
![]()
, а напряжение, приходящееся на подводящие провода,
![]()
. Так как напряжение
![]()
, то
![]()
. Другими словами, чем больше напряжение
![]()
, приходящееся на провода, тем меньшее напряжение остается на долю лампочки. Поэтому напряжение на проводах называется потерянным. Оно тем больше, чем больше сопротивление проводов и чем больше ток, идущий по линии.
Чтобы напряжение, потерянное в линии, не превышало допустимого предела, скажем
![]()
, сопротивление линии не должно превышать величины
![]()
, где
![]()
– допустимая потеря, а
![]()
– сила тока. Чем больше ток в линии, тем меньше должно быть ее сопротивление, а значит, тем толще должны быть провода. Этим объясняется, что для проводки сетей различного назначения применяются различные проводники: для электрических звонков и телефонов (слабые токи) вполне пригодны тонкие провода, имеющие диаметр несколько десятых долей миллиметра, а для промышленных сетей, питающих крупные электромоторы (сильные токи), необходимы медные шины и кабели с сечением, равным нескольким квадратным сантиметрам. Особенно велики могут быть потери в очень длинных линиях, например в линиях электропередачи от гидростанций к отдельным районам.
52.1.
Для нормального свечения автомобильной лампочки напряжение на концах ее нити должно равняться 12 В. Сколько таких лампочек нужно взять и как их нужно соединить для питания от источника тока, имеющего напряжение 120 В? Начертите схему соединения лампочек.
52.2.
В осветительную сеть с напряжением 220 В включены лампочка, имеющая сопротивление 400 Ом, и амперметр, измеряющий ток, текущий через лампочку. Чему равно напряжение на концах нити лампочки? Сопротивление амперметра и соединительных проводов равно 5 Ом.
52.3.
В осветительную сеть с напряжением 220 В включены электрическая печка и лампочка накаливания, соединенные последовательно. Сопротивление печки равно 20 Ом, сопротивление лампочки равно 240 Ом. Какое напряжение будет на печке и какое на лампочке? Начертите схему включения.
52.4.
Для освещения новогодних елок в продаже имеются гирлянды из нескольких последовательно соединенных маленьких лампочек, каждая из которых рассчитана на напряжение 6 или 8 В. Сколько 6-вольтовых и 8-вольтовых лампочек нужно взять для гирлянды, рассчитанной на напряжение 220 В? Если одна из лампочек гирлянды перегорит, будут ли гореть остальные? Что нужно сделать в этом случае, чтобы исправить гирлянду? Почему в инструкции к пользованию гирляндами сказано, что этим способом нельзя починить гирлянду, если перегорело больше трех-четырех лампочек.
52.5.
Реостат со скользящим контактом иногда употребляют как потенциометр (делитель напряжения). Концы обмотки (рис. 88) присоединяют к источнику напряжения, а в рабочей цепи пользуются напряжением между зажимами 8 и 5. Объясните смысл такого включения прибора. Найдите напряжение между этими зажимами при напряжении в сети 220 В, если движок расположен: а) посредине обмотки; б) ближе к зажиму 8 на расстоянии от него, равном 0,1 длины реостата; в) ближе к зажиму 9, на расстоянии от него, равном 0,2 длины реостата. Обмотка навита равномерно.
52.6.
Длина медных проводов линии электропередачи, соединяющей электростанцию с квартирой, равна 2 км, а их сечение равно 15 мм2. Чему равно напряжение на лампочках в этой квартире после включения электрического утюга, потребляющего ток 3 А, если до его включения оно было равно 220 В?
52.7.
Длина медных проводов линии электропередачи равна 1 км, а их сечение равно 10 мм2. Найдите напряжение, теряемое в линии, если ток в ней равен 5 А.
52.8.
Почему при включении в квартире каких-нибудь приборов, потребляющих большой ток (например утюга), горящие лампочки внезапно уменьшают свою яркость? Обратите внимание, что особенно велико уменьшение яркости в первый момент; затем яркость несколько возрастает, хотя и остается меньше, чем до включения утюга. Объясните явление.
52.9.
Уменьшение яркости горящей лампочки можно наблюдать, если включить где-нибудь в квартире очень сильную лампочку, потребляющую ток, равный нескольким амперам. И в этом случае наблюдается особо резкое уменьшение яркости в первый момент. Если взять в качестве второй лампочки старинную лампочку с угольным волоском вместо металлического, то особо резкого спада яркости в первый момент при этом не наблюдается. Почему?
Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
→
1.1 Методы анализа, основанные на законах Ома и Кирхгофа
1.1 Методы анализа, основанные на законах Ома и Кирхгофа
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
1.1 Методы анализа, основанные на законах Ома и законах Кирхгофа
Закон Ома устанавливает зависимость между напряжением и током на пассивной ветви, а также позволяет определить ток по известным потенциалам на концах ветви с источником напряжения.
Законы Кирхгофа применяют для нахождения токов в ветвях линейных и нелинейных схем при любом законе изменения во времени токов и напряжений.
Метод эквивалентных преобразований. При эквивалентных преобразований отдельные участки электрической цепи заменяются более простыми. Эквивалентность преобразования состоит в том, что токи и напряжения в непреобразованной части схемы не изменяются.
Последовательное упрощение схемы продолжается до ее преобразования в одноконтурную схему, после чего для расчета используется закон Ома.
Метод эквивалентных преобразований используется для нахождения внутреннего сопротивления эквивалентного генератора.
При помощи метода эквивалентных преобразований облегчают расчет расчет нелинейной цепи, упростив линейную часть цепи эквивалентными преобразованиями.
Принято пользоваться приведенным ниже алгоритмом метода законов Кирхгофа.
1. Произвольно выбирают положительные направления токов в ветвях и обозначают их на схеме.
2. Составляют уравнения по первому закону Кирхгофа: на одно уравнение меньше числа узлов (для последнего узла уравнение будет зависимым от предыдущих уравнений).
3. Выбирают независимые (главные) контуры и направление их обхода. Удобно для всех контуров выбрать одинаковое направление обхода.
4. Записывают уравнения по второму закону Кирхгофа для выбранных контуров.
5. Решая полученную систему уравнений, определяют искомые токи.
Решение задач на закон Ома и законы Кирхгофа
Задача 1.1. Определить эквивалентное сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К методом эквивалентных преобразований (рис. 1.1, a).
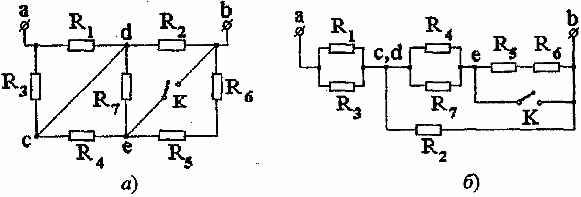
Рис. 1.1
Решение. Сохраняя топологию схемы, трансформируем ее к виду, удобному для анализа (отправная точка — потенциалы узлов c и d равны между собой).
Из рис. 1.1, б следует:
1. При разомкнутом ключе К
R ab = R 1 ⋅ R 3 R 1 + R 3 + ( R 47 + R 5 + R 6 )⋅ R 2 ( R 47 + R 5 + R 6 )+ R 2 .
2. При замкнутом ключе К
R 47 = R 1 ⋅ R 3 R 1 + R 3 + R 47 ⋅ R 2 R 47 + R 2 ,
где
R 47 = R 4 ⋅ R 7 R 4 + R 7 .
Задача 1.2. Определить методом эквивалентных преобразований сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К для схемы, изображенной на рис. 1.2.
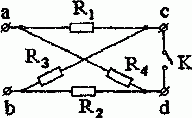
Рис. 1.2
Решение. Совершим поворот части схемы относительно зажимов c и d. В результате получим (рис. 1.3):
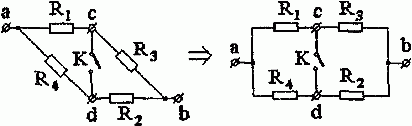
Рис. 1.3
1. При разомкнутом ключе К
R ab = ( R 1 + R 3 )⋅ ( R 2 + R 4 ) ( R 1 + R 3 )+ ( R 2 + R 4 ) .
2. При замкнутом ключе К
R ab = R 1 ⋅ R 4 R 1 + R 4 + R 2 ⋅ R 3 R 2 + R 3 .
Задача 1.3. Найти сопротивление между зажимами a и b для схемы, изображенной на рис. 1.4.
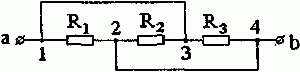
Рис. 1.4
Решение. К точке 2 подходят условные «начало» сопротивления R2 и «концы» сопротивлений Rl и R3.
К точке 3 подходят «начала» сопротивлений R1 и R3 и «конец» сопротивления R2.
Но тогда, все «начала» сопротивлений и все их «концы» соединяются соответственно в одни точки. А значит, по определению, имеем параллельное соединение приемников (рис. 1.5).
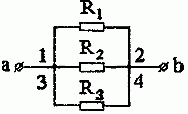
Рис. 1.5
Таким образом, сопротивление между зажимами a и b:
R ab = 1 Y ab = 1 1 R 1 + 1 R 2 + 1 R 3 .
Задача 1.4. Найти сопротивление R13, R14, R17 между различными парами вершин куба, ребра которого имеют заданное сопротивление R (рис. 1.6).
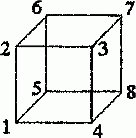
Рис. 1.6
Решение. Задачу проще всего решить методом амперметра и вольтметра. Суть метода заключается в следующем. Если к фиксированным точкам схемы a и b подвести условно известное напряжение Uab и определить ток I во внешней цепи, то искомое сопротивление Rab = Uab/I. При этом напряжение Uab (показание вольтметра) в соответствии с законами Кирхгофа определяется как функция тока I (показание амперметра).
1. Расчетная схема для определения сопротивления R13 имеет вид, представленный на рис. 1.7.
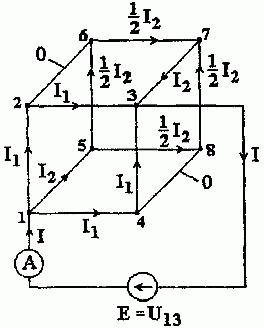
Рис. 1.7
В силу симметрии потенциалы точек 2 и 6 (4 и 8) равны между собой. Поэтому токи в ребрах. 2 — 6 и 4 — 8 отсутствуют.
Перераспределение токов I1 и I2 легко находится из первого закона Кирхгофа и соответствует рисунку 1.7.
Соотношение между токами найдем из второго закона Кирхгофа:
U 14 = U 15 + U 58 + U 84 ; I 1 ⋅R= I 2 ⋅R+ 1 2 I 2 ⋅R+0= 3 2 I 2 ⋅R.
Откуда:
I 1 = 3 2 I 2 ; I 2 = 2 3 I 1 .
А значит, общий ток
I=2 I 1 + I 2 =2 I 1 + 2 3 I 1 = 8 3 I 1 .
Но
U 13 =I⋅ R 13 = 8 3 I 1 ⋅ R 13 = U 12 + U 23 =2 I 1 ⋅R.
Откуда, сокращая на I1, имеем 8/3·R13 = 2R. Или, что-то же, искомое R13 = 3/4·R.
2. Расчетная схема для определения сопротивления R14 имеет вид, представленный на рис. 1.8.
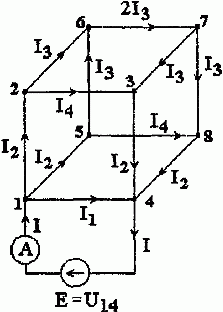
Рис. 1.8
В силу симметрии токи в ребрах 1 — 2, 1 — 4, 2 — 3 и 4 — 3 равны между собой. А значит, в соответствии с первым законом Кирхгофа, токи в ребрах 2 — 6 и 4 — 8 отсутствуют.
Перераспределение неизвестных токов I1, I2, I3, I4 находится из первого закона Кирхгофа (и симметрии цепи) и соответствует рис. 1.8.
Поскольку падение напряжения
U 23 = U 26 + U 67 + U 73 ; I 4 ⋅R= I 3 ⋅R+2 I 3 ⋅R+ I 3 ⋅R=4 I 3 ⋅R,
то, сокращая на R, имеем:
I 4 =4 I 3
или
I 3 = 1 4 I 4 .
Ток
I 2 = I 3 + I 4 = 1 4 I 4 + I 4 = 5 4 I 4
или
I 4 = 4 5 I 2 .
Но
U 14 = U 15 + U 58 + U 84 ; I 1 ⋅R= I 2 ⋅R+ I 4 ⋅R+ I 2 ⋅R= I 2 ⋅R+ 5 4 I 2 ⋅R+ I 2 ⋅R= 14 5 I 2 ⋅R.
Откуда, сокращая на R, имеем:
I 1 = 14 5 I 2
или
I 2 = 5 14 I 1 .
Но
U 14 =I⋅ R 14 = ( I 1 +2 I 2 )⋅ R 14 = ( I 1 + 10 14 I 1 )⋅ R 14 = 24 14 I 1 ⋅ R 14 = I 1 ⋅R.
Или, что то же, искомое R14 = 14/24·R = 7/12·R.
3. Расчетная схема для определения сопротивления R17 имеет вид, представленный на рис. 1.9.
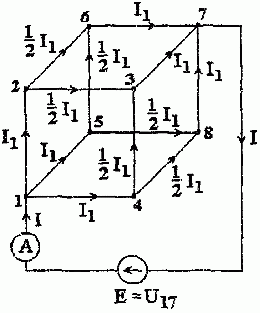
Рис. 1.9
В силу диагональной симметрии схемы полный ток I = 3I1.
Падение напряжения
U 17 = U 14 + U 43 + U 37 ; I⋅ R 17 = I 1 ⋅R+ 1 2 I 1 ⋅R+ I 1 ⋅R= 5 2 I 1 ⋅R.
Откуда искомое сопротивление R17 = 5/6·R.
Задача 1.5. Определить методом эквивалентных преобразований токи в ветвях цепи (рис. 1 10, а) и показание вольтметра, включенного между точками c и d, считая, что его сопротивление во много раз превышает сопротивление каждого из элементов цепи.
Чему равно показание амперметра, включенного между точками c и d, сопротивление которого считать равным нулю?
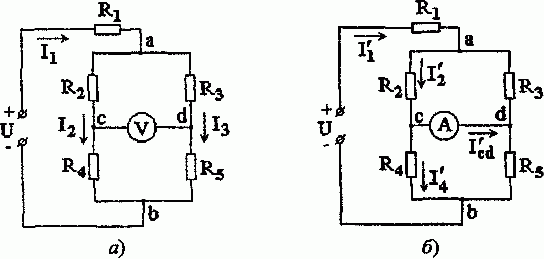
Рис. 1.10
Сопротивления элементов цепи: R1 =10 Ом, R2 = R3 = R5 = 25 Ом и R4 = 50 Ом, а приложенное к ней напряжение U = 120 В.
Решение. Расчет показания вольтметра. Из условия вытекает, что его включение не оказывает влияния на распределение токов в цепи. Для расчета токов сначала определяем эквивалентное сопротивление всей цепи (рис. 1.10, а):
R= R 1 + ( R 2 + R 4 )⋅ ( R 3 + R 5 ) ( R 2 + R 4 )+ ( R 3 + R 5 ) =10+ 75⋅50 125 =40 Ом.
В неразветвленной части цепи протекает ток
I 1 = U R = 120 40 =3 A.
Токи, протекающие через сопротивления (R2 + R4) и (R3 + R5) можно найти различными способами.
1. В параллельных ветвях токи распределяются обратно пропорционально их сопротивлениям (формула разброса токов):
I 2 = I 1 ⋅ R 3 + R 5 ( R 2 + R 4 )+ ( R 3 + R 5 ) =3⋅ 50 125 =1,2 A; I 3 = I 1 ⋅ R 2 + R 4 ( R 2 + R 4 )+ ( R 3 + R 5 ) =3⋅ 75 125 =1,8 A.
2. Найдем напряжение на зажимах параллельных ветвей:
U ab = I 1 ⋅ ( R 2 + R 4 )⋅ ( R 3 + R 5 ) ( R 2 + R 4 )+ ( R 3 + R 5 ) =3⋅ 75⋅50 125 =90 B.
Токи в ветвях с сопротивлениями R2 + R4 и R3 + R5 равны:
I 2 = U ab R 2 + R 4 = 90 75 =1,2 A; I 3 = U ab R 3 + R 5 = 90 50 =1,8 A.
Напряжение на зажимах параллельных ветвей может быть найдено как разность между приложенным напряжением и падением напряжения на сопротивлении R1: Uab = U — R1·I1.
Найдем показание вольтметра, равное напряжению между точками с и d:
U V = U cd =− I 2 ⋅ R 2 + I 3 ⋅ R 3 =−1,2⋅25+1,8⋅25=15 B.
Наконец, вычислим ток, проходящий через амперметр; он равен току короткого замыкания I’cd (рис. 1.10, б). Для его нахождения вычислим токи:
I ′ 1 = U R 1 + R 2 ⋅ R 3 R 2 + R 3 + R 4 ⋅ R 5 R 4 + R 5 = 144 47 A; I ′ 2 = I ′ 1 ⋅ R 3 R 2 + R 3 = 72 47 A; I ′ 4 = I ′ 1 ⋅ R 5 R 4 + R 5 = 48 47 A.
Искомый ток, проходящий через амперметр,
I A = I ′ cd = I ′ 2 − I ′ 4 = 24 47 =0,51 A.
Задача 1.6. В схеме рис. 1.11 заданы сопротивления приемников, величины ЭДС и источника тока отдельных ветвей. Рассчитать неизвестные токи, ЭДС E2 и сопротивление R5, пользуясь законами Кирхгофа.
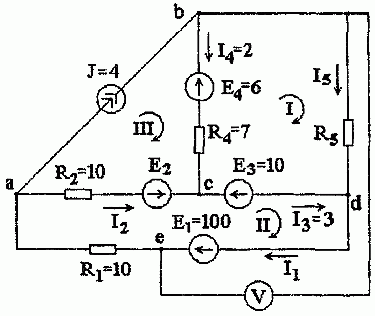
Рис. 1.11
Правильность решения проверить по балансу мощностей. Для наружного контура построить потенциальную диаграмму и определить показание вольтметра.
Решение
1. Всего в схеме пять ветвей, неизвестных токов I1, I2, I5 — три, неизвестных величин E2 и R5 — две, для нахождения которых составам три уравнения по первому закону Кирхгофа и два – по второму закону Кирхгофа:
для узла b: J= I 4 + I 5 ; для узла d: − I 5 − I 3 + I 1 =0; для контура I: I 5 R 5 − I 4 R 4 = E 3 + E 4 ; для контура II: I 1 R 1 + I 2 R 2 = E 1 + E 2 − E 3 .
Из первых трех уравнений находим токи:
I 5 =J− I 4 =4−2=2 A; I 1 = I 5 + I 3 =2+3=5 A; I 2 =−J+ I 1 =−4+5=1 A.
из четвертого уравнения
R 5 = E 3 + E 4 + I 4 ⋅ R 4 I 5 = 10+6+14 2 =15 Ом.
Величину E2 определяем из последнего уравнения:
E 2 = I 1 ⋅ R 1 + I 2 ⋅ R 2 − E 1 + E 3 =5⋅10+10⋅1−100+10=−30 B.
2. Для построения потенциальной диаграммы найдем потенциалы всех точек контура abcdea, приняв исходный потенциал точки a равным нулю:
φ e = φ a − I 1 ⋅ R 1 =0+5⋅10=50 B; φ d = φ e − E 1 =50−100=−50 B; φ b = φ d + I 5 ⋅ R 5 =−50+2⋅15=−20 B.
3. По найденным потенциалам строим потенциальную диаграмму, откладывая по оси ординат потенциалы точек, а по оси абсцисс — сопротивления участков (рис. 1.12).
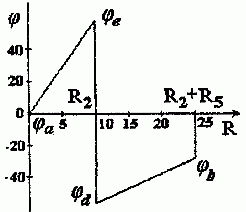
Рис. 1.12
3. Из потенциальной диаграммы легко определить разность потенциалов между точками b и c Ubc = 70 В, что и будет показывать вольтметр.
4. Произведем проверку баланса мощностей:
P источников = E 1 ⋅ I 1 + E 2 ⋅ I 2 + E 3 ⋅ ( − I 3 )+ E 4 ⋅ ( − I 4 )+ U ba ⋅J; P потребителей = I 1 2 ⋅ R 1 + I 2 2 ⋅ R 2 + I 4 2 ⋅ R 4 + I 5 2 ⋅ R 5 .
В этом уравнении нам неизвестно напряжение на зажимах источника тока Uba, которое легко найти из потенциальной диаграммы: Uba = –20 В. С учетом этого
P источников =100⋅5+ ( −30 )⋅1+10⋅ ( −3 )+6⋅ ( −2 )+ ( −20 )⋅4=348 Вт; P потребителей = 5 2 ⋅10+ 1 2 ⋅10+ 3 2 ⋅0+ 2 2 ⋅7+ 2 2 ⋅15=348 Вт; P источников = P потребителей =348 Вт.
Закон Ома, законы Кирхгофа в статье ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачи
 закон Ома,
закон Ома,
Законы Кирхгофа,
первый закон Кирхгофа,
второй закон Кирхгофа
