Как найти напряжение момента

Техническая механика

Сопротивление материалов

Напряжения при изгибе

Нормальные напряжения при чистом изгибе

Как было установлено ранее, в поперечных сечениях балки при чистом изгибе возникают только нормальные напряжения растяжения и сжатия. Вопрос о распределении этих напряжений по поперечному сечению решается путем рассмотрения деформаций волокон балки.

Рассмотрим участок балки, подверженный деформации чистого изгиба. Двумя поперечными сечениями АВ и СD выделим элемент балки бесконечно малой длины ds (рис 1) . Радиус кривизны нейтрального слоя балки обозначим ρ .

Рассмотрим слой волокон mn, находящийся на расстоянии y от нейтрального слоя NN . Это волокно в результате деформации изгиба удлинилось на величину nn₁ . Ввиду малости расстояния ds заштрихованные треугольники будем считать прямолинейными; эти треугольники подобны (n₁F || mE) :

Из подобия треугольников запишем равенство:

Так как левая часть этого равенства есть относительное удлинение, т. е. nn₁ / ds = ε , то y / ρ = ε .

Применив закон Гука при растяжении и сжатии σ = Еε , получим:

Из этой формулы видно, что нормальные напряжения при изгибе распределены по высоте сечения неравномерно: максимальные напряжения возникают в волокнах, наиболее удаленных от нейтральной оси. По ширине сечения нормальные напряжения не меняются.
Распределение нормальных напряжений изображено на рис. 2 .

Полученная формула для определения нормальных напряжений неудобна, так как в нее входит радиус кривизны нейтрального слоя.
Для вывода формулы, связывающей нормальные напряжения с изгибающим моментом, применим метод сечений и рассмотрим равновесие части балки, изображенной на рис. 3 .
В плоскости поперечного сечения выделим бесконечно малую площадку dA , в пределах которой будем считать нормальные напряжения σ постоянными; тогда нормальная сила dN , действующая на площадку dA , будет равна:

Составим уравнения равновесия:

1. Σ Z = 0; ∫dN = 0, или: ∫σ dA = ∫Еy / ρ dA = Е / ρ ∫y dA = 0 .

( ρ для данного сечения, а также модуль упругости Е – величины постоянные, поэтому вынесены за знак интеграла). Поскольку ρ и Е не равны нулю, значит, ∫y dA = 0 . Этот интеграл представляет собой статический момент площади сечения относительно оси x, т. е. нейтральной оси бруса (балки). Равенство нулю статического момента инерции означает, что при изгибе нейтральная ось проходит через центр тяжести площади поперечного сечения;

Так как при чистом изгибе изгибающий момент равен внешнему моменту М_и = m , то

М_и = ∫y dN = ∫y dA = ∫y Еy / ρ dA = Е / ρ ∫y 2 dA ,

где: I = ∫y 2 dA – момент инерции поперечного сечения относительно нейтральной оси; ЕI – жесткость сечения при изгибе.

Так как при чистом изгибе балки постоянного сечения М_и = const, то:

Следовательно, изогнутая ось такой балки представляет собой дугу окружности. Выражение радиуса кривизны подставим в формулу для определения нормальных напряжений; тогда:

σ = Еy / ρ = Ey / EI / М_и = М_и y / I .

Максимальное значение нормальные напряжения будут иметь у волокон, наиболее удаленных от нейтральной оси:

где W = I / y_max – момент сопротивления изгибу (или осевой момент сопротивления).
Момент сопротивления изгибу есть отношение осевого момента инерции поперечного сечения относительно нейтральной оси к расстоянию от этой оси до наиболее удаленного волокна.
Единица момента сопротивления сечения изгибу [W] = м 3 .

Итак, наибольшие нормальные напряжения при чистом изгибе вычисляются по формуле

Нетрудно заметить, что эта формула по своей структуре аналогична формулам для определения напряжений при растяжении, сжатии, сдвиге и кручении.

Касательные напряжения при изгибе

Очевидно, что при поперечном изгибе, вызванном приложением к балке поперечной силы, в сечениях балки должны возникнуть касательные напряжения.
Определением зависимости между внешними нагрузками, геометрическими и физическими параметрами балок и касательными напряжениями, возникающими в них, занимался русский мостостроитель Д. И. Журавский , который в 1855 году предложил следующую формулу:

Эта формула называется формулой Журавского и читается так:
касательные напряжения в поперечном сечении балки равны произведению поперечной силы Q на статический момент S относительно центральной оси части сечения, лежащей выше рассматриваемого слоя волокон, деленному на момент инерции I всего сечения относительно нейтральной оси и на ширину b рассматриваемого слоя волокон.

По формуле Журавского можно вывести зависимости для определения касательных напряжений в балках, имеющих разную форму поперечного сечения (прямоугольную, круглую и т. п.).
Например, для балки круглого сечения формула Журавского в результате преобразований выглядит так:

где Q – поперечная сила, вызывающая изгиб, А – площадь сечения балки.

Большинство балок в конструкциях рассчитывается только по нормальным напряжениям, и только три вида балок проверяют по касательным напряжениям:

— деревянные балки, т. к. древесина плохо работает на скалывание;
— узкие балки (например, двутавровые), поскольку максимальные касательные напряжения обратно пропорциональны ширине нейтрального слоя;
— короткие балки, так как при относительно небольшом изгибающем моменте и нормальных напряжениях у таких балок могут возникать значительные поперечные силы и касательные напряжения.
Максимальное касательное напряжение в двутавровой балке определяется по формуле Журавского, при этом геометрические характеристики таких балок берутся из справочных таблиц .

Расчеты на прочность при изгибе

Условие на прочность при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превышать допускаемое.
Полагая, что гипотеза о не надавливании волокон справедлива не только при чистом, но и при поперечном изгибе, мы можем нормальные напряжения при поперечном изгибе определять по такой же формуле, что и при чистом изгибе, при этом расчетная формула выглядит так:

и читается так: нормальное напряжение в опасном сечении, определенное по формуле σ_max = Ми_max / W ≤ [σ] не должно превышать допускаемое.
Допускаемое нормальное напряжение при изгибе выбирают таким же, как при растяжении и сжатии.
Максимальный изгибающий момент определяют по эпюре изгибающих моментов или расчетом.
Так как момент сопротивления изгибу W в расчетной формуле стоит в знаменателе, то чем больше W , тем меньшие напряжения возникают в сечении бруса.

Ниже приведены моменты сопротивления изгибу для наиболее часто встречающихся сечений:

1. Прямоугольное сечение размером b x h: W_пр = bh 2 / 6 .

2. Круглое сечение диаметром d: W_круг = π d 3 / 32 ≈ 0,1d 3

3. Кольцо размером D x d: W_кольца = ≈ 0,1 (D 4 – d 4 ) / D ; (момент сопротивления кольцевого сечения нельзя определять, как разность моментов сопротивления большого и малого кругов) .

Источник

Вычисление напряжении от изгибающего момента.

Вычисление напряжении от изгибающего момента.

• Расчет напряжения изгибающего момента. Изгибающий момент L4 может быть уравновешен только нормальным напряжением в виде прямой балки, а задача нахождения закона и формулы распределения напряжений на рабочей плоскости внешней силы, противоположной направлению, и для тех расчетов, которые больше момента L4, необходима и неопределенна для статики, необходимо

изучить изгиб мы опускаем такие расчеты при определении напряжения,§ 187] расчет напряжения от изгибающего момента 585 Поскольку вы уже используете готовое решение, необходимо учитывать нормальное напряжение балансировки изгибающего момента 7I, которое описано при определении

вертикального напряжения прямоугольной балки. Рассмотрим равновесное Людмила Фирмаль

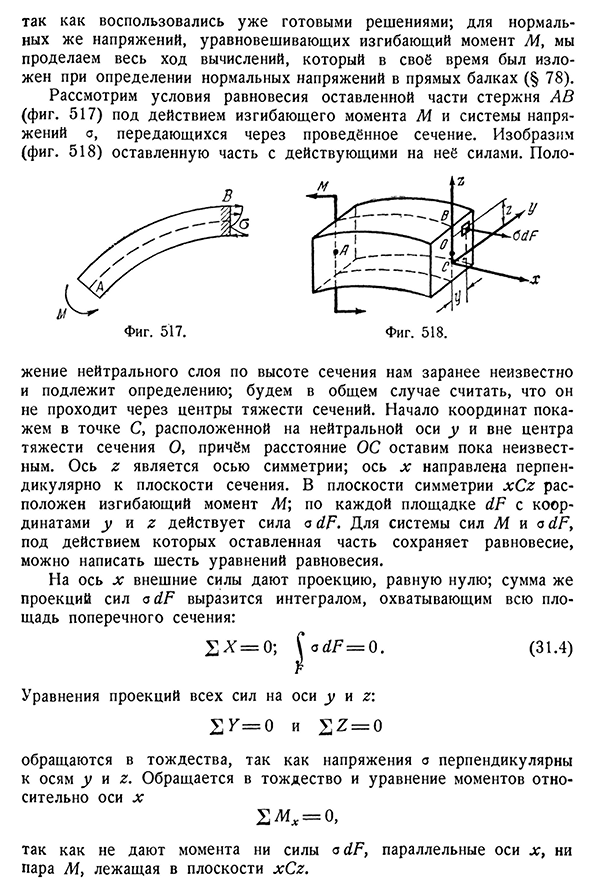
состояние левой части стержня АВ (рис. 517) передача через секции производится под действием изгибающего момента M и напряжения системы o. Нарисуйте (рис. 518) левая часть с действующей на нее силой. Поло- Фигура. 517 рис. Пятьсот восемнадцать Расположение нейтрального слоя на высоте поперечного сечения нам заранее не известно и подлежит определению. Начало координат появляется в точке C, расположенной вне центра тяжести на нейтральной оси

y и участке O, а расстояние до оси остается неизвестным. Ось Z является осью симметрии, а ось x перпендикулярна плоскости поперечного сечения. Плоскость симметрии xC z имеет изгибающий момент M. Для системы сил M и o dF можно записать шесть уравнений равновесия под действием левой части, удерживающей равновесие. Внешняя сила дает проекцию, равную нулю; сумма

• проекции силы dF представляется интегралом, охватывающим всю площадь поперечного сечения:^X=0;^d F=0. (31.4) Уравнение проекции всех сил на ось Y и ось z:% Y=0 и S-Z=0 становится одинаковым, поскольку напряжение o перпендикулярно оси y и оси Z.%M x = 0, потому что ни сила adF, параллельная оси x, ни пара L4 в плоскости xcz не дают момента.586 криволинейный стержень[глава XXXI по той же причине момент VS L4 относительно оси z также равен нулю; для силы adF эти моменты относительно этой оси являются

интегральными adFy. (31.5) Однако этот Интеграл равен нулю из-за симметрии поперечного сечения относительно оси Z. Остается обнулить сумму моментов всех сил относительно оси Y. Это уравнение записывается как^m y=0 -, M — adFz=0. Ф (31.6) Поэтому в условиях статики необходимо рассматривать два уравнения: Если AdF = 0, Но (31.4) М — ^Д Ф з=0. Ф (31.6) Закон изменения нормального напряжения оставался неизвестным.

Это подводит нас к высоте раздела для рассмотрения Ворота возникают Это деформация. Для Людмила Фирмаль

случая изгиба прямого стержня используют гипотезу плоского поперечного сечения, которая подтверждается экспериментами и криволинейными стержнями. Будем считать, что под действием сечения, перпендикулярного изгибающему моменту оси, я остаюсь плоским и повторяю только одно за другим(рис. 519). Поскольку, согласно приведенному выше предположению(§ 184), ось балки остается в той же плоскости во время деформации, которую она ставит перед деформацией, вокруг этих po-нейтральных осей QCI и C2C2, напряжение на волокнах, разнесенных на одинаковое расстояние от оси, перпендикулярной внешней силе, а затем растянутых и укороченных, таким образом, становится одинаковым по ширине отношения между относительным углом поворота двух соседних участков и деформацией волокна, уточняется. Выберите

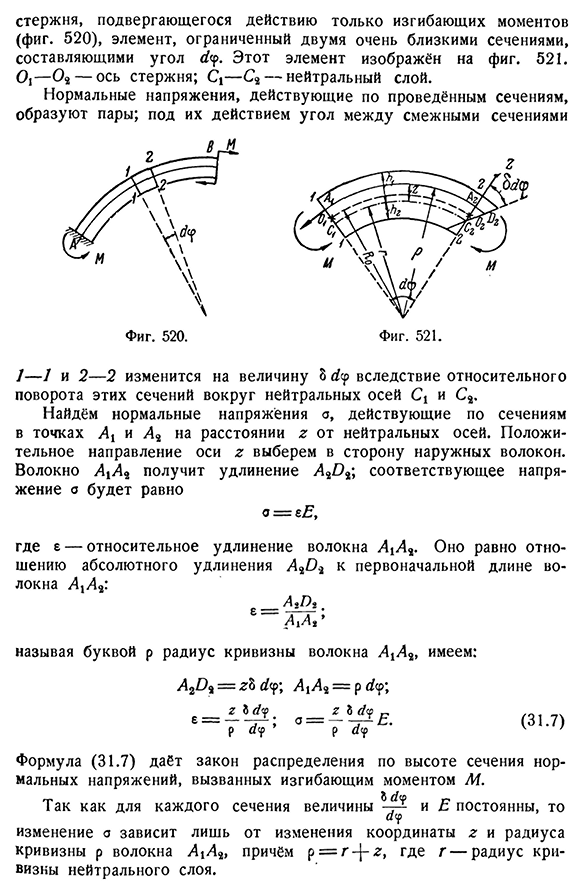
из кривой§ 187] расчет напряжения от изгибающего момента 587 Изгибающий момент (рис. 520), два очень близких сечения ограниченных элементов, которые составляют угол rfcp. Этот элемент показан на рисунке. 521 01-О2-ось стержня; — С2-нейтральный слой. Нормальное напряжение, действующее на пару проводимых секционных форм; угол между соседними секциями под действием 7-7 и 2-2 изменяются на величину 3dy за счет относительного вращения этих участков вокруг нейтральных осей CX и C2. Найдем нормальное напряжение o, действующее на сечение точек Ai и D2 на расстоянии z от нейтральной оси. Положительное направление оси Z выбирается

в направлении внешнего волокна. Волокно L1L2 получает удлинение L2T) 2;соответствующее напряжение a равно ми£, Здесь e-удлинение волокна D L2. Он равен абсолютному отношению удлинения D2O2 к исходной длине волокна^jX2: _2^2, Один Радиус кривизны волокна, называемого буквой p A i a Где M-изгибающий момент, а Интеграл охватывает всю площадь поперечного сечения. Интегралы, входящие в это уравнение, преобразуются следующим образом: зд Ф=^З Д Ф-Р^Д Ф F F F Последний из двух полученных интегралов равен нулю на основании (31.8), первый-это статический отрезок S площади поперечного сечения относительно нейтральной оси. Это значение

может быть вычислено как расстояние от его центра тяжести до нейтральной оси, то есть произведение площади поперечного сечения F на z^. 522): С=ФЗ*. (31.11)поэтому уравнение (31.10) принимает вид: И так оно и есть. Я^Ы=М; Б dy _ м

Е> (31.12) (31.13) И формулы для нормальных напряжений записывается следующим образом: Зет_ — • п (31.14) В Формуле (31.12) здесь мы находим, что статический момент S площади поперечного сечения относительно нейтральной оси не равен нулю, то есть поперечному сечению, когда нейтральная ось изгибает изогнутый стержень. 522 мы нарисовали этот сдвиг к центру кривизны стержня. Результат определения

величины g по формуле для различных сечений (31.9) показывает, что нейтральная ось фактически движется в указанном направлении. Это смещение обусловлено условиями равенства суммы сжимающих и растягивающих напряжений, действующих на поперечное сечение. Потому что напряжение от изгибающего момента на внешней кромке сечения невелико, а на внутренней-больше, чем на соответствующих волокнах прямого стержня того же сечения (рис. 522), для равенства указанной суммы нейтральная ось должна быть смещена от центра тяжести сечения к внутреннему волокну.590 изогнутый стержень[гл.

XXXI В дополнение к полученному напряжению мы получаем формулу для вычисления полного нормального напряжения изогнутого стержня, применяя напряжение, замеченное в предыдущем пункте, от вертикальной силы: (31.15)) Максимальные растягивающие и сжимающие напряжения абсолютной величины находятся в крайних волокнах 1 и 2(рис. Пятьсот двадцать два),

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.

Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки

Расчет напряжений

Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент M_x

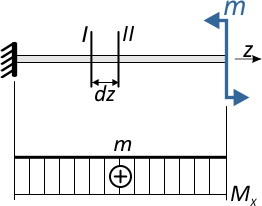
представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.

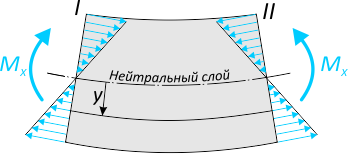
Закон распределения нормальных напряжений по высоте сечения выражается формулой:

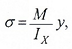
где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
I_x — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.

Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.

По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.

Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.

Например, для симметричного относительно нейтральной оси сечения, где y₁=y₂=h/2:

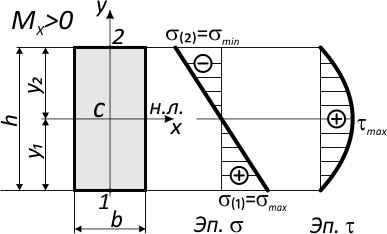
Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.

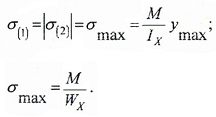
Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2:

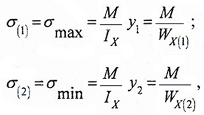
где:

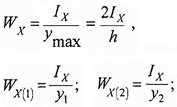
W_X — осевой момент сопротивления симметричного сечения;
W_X(1) и W_X(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.

Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.

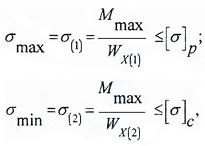
Здесь:
M_max — максимальное значение изгибающего момента, определяемого по эпюре M_x;
[σ], [σ]_р, [σ]_с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [σ]_с>[σ]_р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

1. Проверка прочности
   
2. Подбор сечений
   
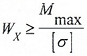
3. Определение максимально допустимой нагрузки
   

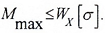
Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского

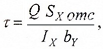
где
S_{x отс} — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
b_y — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Другие видео

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Q_max:

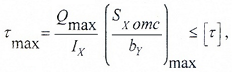
где [τ] – допустимое значение касательных напряжений для материала балки.

Полная проверка прочности

Полную проверку прочности балки производят в следующей последовательности:

1. По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
2. По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
3. По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда M_max и Q_max действуют в одном и том же сечении балки).

При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид:

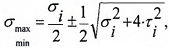
так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.

Другие видео

Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:

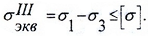
Деформации при изгибе >
Угловые и линейные перемещения в балках >
Примеры решения задач >
Лекции по сопромату >