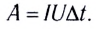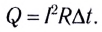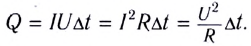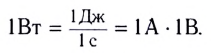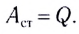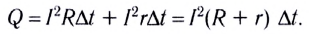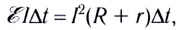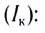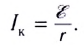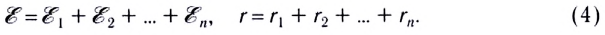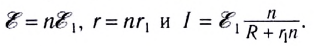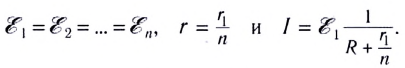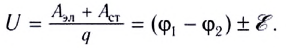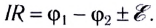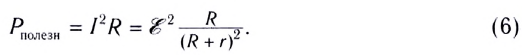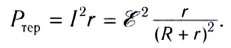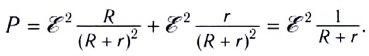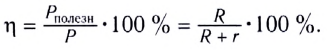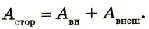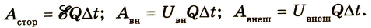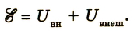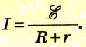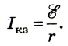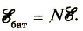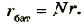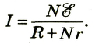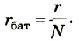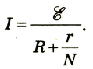Как найти напряжение на клеммах источника тока

Закон Ома для полной цепи

Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!

Идеальный источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.

Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?

Внутреннее сопротивление источника ЭДС

Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.

Выглядит все это в аккумуляторе примерно вот так:

Итак, что у нас получается в чистом виде?

Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:

Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.

На резисторе R падает напряжение U_R , а на внутреннем резисторе r падает напряжение U_r .

Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.

Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Закон Ома для полной цепи

Итак, последнее выражение носит название «закон Ома для полной цепи»

Е — ЭДС источника питания, В

R — сопротивление всех внешних элементов в цепи, Ом

r — внутреннее сопротивление источника питания, Ом

Просадка напряжения

Итак, знакомьтесь, автомобильный аккумулятор!

Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус

Наш подопечный готов к бою.

Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.

Первым делом давайте замеряем напряжение на клеммах аккумулятора

12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.

Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:

Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!

А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:

Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.

Смотрим на показания приборов:

Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.

Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла

Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.

Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.

Как найти внутреннее сопротивление источника ЭДС

Давайте снова вернемся к этой фотографии

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе U_r тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение U_R=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило U_r=E-U_R=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r

Вывод

Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.

Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.

Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.

Источник

Последовательное и параллельное соединение

Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей — проводников.

Для начала давайте вспомним, что такое проводник? Проводник — это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:

ρ – это удельное сопротивление, Ом × м

R – сопротивление проводника, Ом

S – площадь поперечного сечения, м 2

Более подробно об этом я писал здесь.

Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.

Последовательное соединение проводников

Сопротивление при последовательном соединении проводников

Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

последовательное соединение резисторов

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

формула при последовательном соединении резисторов

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор R_AB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор R_AB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R₁ , R₂ , R₃ , то получится, что через них течет та же самая сила тока, которая текла через резистор R_AB .

сила тока через последовательное соединение проводников

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R₁ течет такая же сила тока, как и через резистор R₂ и такая же сила тока течет через резистор R₃ .

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае R_AB =R₁ + R₂ + R₃ = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения U_R1 , U_R2 , U_R3 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.

параллельное соединение резисторов

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление R_AB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников

Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.

Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что

Если бы у нас еще были резисторы, соединенные параллельно, то для них

В этом случае, сила тока в цепи будет равна:

Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Воспользуемся формулами, которые приводили выше.

Если бы у нас еще были резисторы, соединенные параллельно, то для них

Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи

2-ой способ найти I

Чтобы найти R_общее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть R_общее = 1,25 Ом.

Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.

Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.

Источник

Измерения
показывают, что напряжение на зажимах источника тока, замкнутого на внешнюю
цепь, зависит от силы отбираемого тока (от «нагрузки») и изменяется с
изменением последнего. Пользуясь законом Ома, мы можем сейчас разобрать этот
вопрос точнее.

Из
формулы (80.1) имеем

,                (81.1)

где
 –
сопротивление внешней цепи, а  – внутреннее сопротивление
источника. Но к внешней цепи мы вправе применить закон Ома для участка цепи:

.                      (81.2)

Здесь
 –
напряжение во внешней цепи, т. е. разность потенциалов на зажимах источника.
Оно может быть выражено на основании (81.1), (81.2) следующей формулой:

.                 (81.3)

Мы
видим, что при замкнутой цепи напряжение  на зажимах источника тока всегда
меньше э. д. с. .
Напряжение  зависит
от силы тока  и
только в предельном случае разомкнутой цепи, когда сила тока , напряжение на
зажимах равно э. д. с.

Уменьшение
напряжения на зажимах источника при наличии тока  легко наблюдать на опыте. Для этого
нужно замкнуть какой-либо гальванический элемент на реостат и подключить к
зажимам элемента вольтметр (рис. 127). Перемещая движок реостата, можно видеть,
что чем меньше сопротивление внешней цепи, т. е. чем больше ток, тем меньше
напряжение на зажимах источника. Если сопротивление внешней цепи сделать очень
малым по сравнению с внутренним сопротивлением источника («вывести» реостат),
т. е. сделать «короткое замыкание», то напряжение на зажимах делается равным
нулю.

Рис. 127. С уменьшением
сопротивления внешней цепи напряжение на зажимах источника тока уменьшается: а)
схема опыта; б) общий вид экспериментальной установки, 1 – источник тока, 2 –
реостат, 3 – амперметр, 4 – вольтметр

Что
же касается тока, то он при коротком замыкании достигает своего максимального
значения .
Сила этого «тока короткого замыкания» получается из закона Ома (80.1), если в
нем положить  (т.
е. пренебречь сопротивлением  по сравнению с ):

.                   (81.4)

Отсюда
видно, что ток короткого замыкания зависит не только от э. д. с., но также и от
внутреннего сопротивления источника. Поэтому короткое замыкание представляет
различную опасность для разных источников тока.

Короткие
замыкания гальванического элемента сравнительно безвредны, так как при небольшой
э. д. с. элементов их внутреннее сопротивление велико, и поэтому токи короткого
замыкания малы. Такие токи не могут вызвать серьезные разрушения, и поэтому к
изоляции проводов в целях, питаемых элементами (звонки, телефоны и т. п.), не
предъявляют особо высоких требований. Иное дело силовые или осветительные цепи,
питаемые мощными генераторами. При значительной э. д. с. (100 и более вольт)
внутреннее сопротивление этих источников ничтожно мало, и поэтому ток короткого
замыкания может достигнуть огромной силы. В этом случае короткое замыкание
может привести к расплавлению проводов, вызвать пожар и т. д. Поэтому к
устройству и изоляции таких цепей предъявляют строгие технические требования,
которые ни в коем случае нельзя нарушать без риска вызвать опасные последствия.
Такие цепи всегда снабжаются предохранителями (§ 63) и притом нередко в
различных местах: общий предохранитель (при главном вводе), групповые и
штепсельные предохранители.

81.1. Внутреннее сопротивление
элемента Даниеля с э. д .с. 1,1 В равно 0,5 Ом. Вычислите ток короткого
замыкания этого элемента.

81.2. Элемент из предыдущей задачи
замкнут на сопротивление 0,6 Ом. Чему равно напряжение на зажимах элемента?

81.3. Э. д. с. генератора постоянного
тока равна 220 В, а внутреннее сопротивление равно 0,02 Ом. Какой ток возникает
при коротком замыкании?

81.4. При измерении э. д. с.
источников при помощи вольтметра мы всегда допускаем некоторую погрешность, так
как через вольтметр течет некоторый, хотя и очень малый, ток, и поэтому
источник, строго говоря, не разомкнут, а замкнут на вольтметр. Пусть внутреннее
сопротивление элемента равно 1 Ом, его э. д. с. равна 1,8 В, а сопротивление
вольтметра равно 179 Ом. Какую погрешность при измерении э. д. с. мы допускаем?

81.5. Можно ли точно измерить э. д. с.
при помощи электрометра? Как нужно присоединить электрометр к элементу для
измерения его э. д. с.?

81.6. Изменяется ли показание
электрометра, соединенного с гальваническим элементом, если параллельно с ним
включить конденсатор, как показано на рис. 128? Будет ли иметь значение емкость
конденсатора?

Рис. 128. К упражнению 81.6

81.7. Э. д. с. некоторого элемента
измеряют при помощи электрометра с конденсатором (рис. 129,а). Электрометр,
отсоединенный от элемента, после снятия диска показывает 500 В (рис. 129,б).
При этом известно, что емкость конденсатора при удалении диска уменьшается в
250 раз. Чему равно напряжение элемента?

Рис. 129. К упражнению 81.7

1. Источники
   напряжения и тока, их свойства,
   характеристики и схемы замещения.
   Законы Ома и Кирхгофа.

Источник ЭДС (идеальный
источник напряжения) — двухполюсник, напряжение на
зажимах которого постоянно (не зависит
от тока в цепи). Напряжение может быть
задано как константа, как функция
времени, либо как внешнее управляющее
воздействие.

В
простейшем случае напряжение определено
как константа, то есть напряжение
источника ЭДС постоянно.

Реальные
источники напряжения

Рисунок
2

Идеальный
источник напряжения (источник ЭДС)
является физической абстракцией, то
есть подобное устройство не может
существовать. Если допустить существование
такого устройства, то электрический
ток I,
протекающий через него, стремился бы к
бесконечности при подключении нагрузки,
сопротивление R_H которой
стремится к нулю. Но при этом получается,
что мощность источника
ЭДС также стремится к бесконечности,
так как .
Но это невозможно, по той причине, что
мощность любого источника энергии
конечна.

В
реальности, любой источник напряжения
обладает внутренним сопротивлением r,
которое имеет обратную зависимость от
мощности источника. То есть, чем больше
мощность, тем меньше сопротивление (при
заданном неизменном напряжении источника)
и наоборот. Наличие внутреннего
сопротивления отличает реальный источник
напряжения от идеального. Следует
отметить, что внутреннее сопротивление —
это исключительно конструктивное
свойство источника энергии. Эквивалентная
схема реального источника напряжения
представляет собой последовательное
включение источника ЭДС — Е
(идеального
источника напряжения) и внутреннего
сопротивления — r.

где

 —
падение напряжения
на внутреннем сопротивлении;

 —
падение напряжения
на нагрузке.

При
коротком замыкании (),
то есть вся мощность источника энергии
рассеивается на его внутреннем
сопротивлении. В этом случае токбудет
максимальным для данного источника
ЭДС. Зная напряжение холостого хода и
ток короткого замыкания, можно вычислить
внутреннее сопротивление источника
напряжения:

Исто́чник
то́ка (также генератор
тока) — двухполюсник,
который создаёт ток ,
не зависящий от сопротивления нагрузки,
к которой он присоединён. В быту
«источником тока» часто неточно называют
любой источник электрического напряжения
(батарею, генератор, розетку), но в строго
физическом смысле это не так, более
того, обычно используемые в быту источники
напряжения по своим характеристикам
гораздо ближе к источнику
ЭДС,
чем к источнику тока.

Свойства:

Идеальный источник тока

Напряжение на
клеммах идеального источника тока
зависит только от сопротивления внешней
цепи:

Мощность,
отдаваемая источником тока в сеть,
равна:

Так
как для источника тока ,
напряжение и мощность, выделяемая им,
неограниченно растут при росте
сопротивления..

Реальный источник тока

Реальный
источник тока, так же как и источник
ЭДС,
в линейном приближении может быть описан
таким параметром, как внутреннее
сопротивление .
Отличие состоит в том, что чем больше
внутреннее сопротивление, тем ближе
источник тока к идеальному (источник
ЭДС, наоборот, чем ближе к идеальному,
тем меньше его внутреннее сопротивление).
Реальный источник тока с внутренним
сопротивлением эквивалентен
реальному источнику ЭДС, имеющему
внутреннее сопротивление и
ЭДС .

Напряжение
на клеммах реального источника тока
равно:

Сила
тока в цепи равна:

Мощность,
отдаваемая реальным источником тока в
сеть, равна:

Схемы
замещения источников энергии

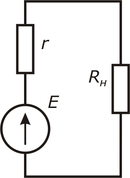
Простейшая
электрическая цепь и ее схема замещения,
как указывалось, состоят из одного
источника энергии с ЭДС Е и внутренним
сопротивлением rвт и
одного приемника с сопротивлением r.
Ток
во внешней по отношению к источнику
энергии части цепи, т. е. в приемнике с
сопротивлением r,
принимается направленным от точки а с
большим потенциалом к
точке b с
меньшим потенциалом .
Направление
тока будем обозначать на схеме стрелкой
с просветом или указывать двумя индексами
у буквы I, такими
же, как и у соответствующих точек схемы.
Так, для схемы рис. 1.3 ток в приемнике I = Iаb,
где индексы а и b обозначают направление
тока от точки а к точке b.
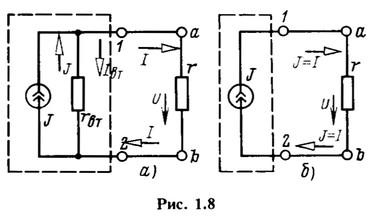
Покажем,
что источник энергии с известными
ЭДС E и
внутренним сопротивлением rвт,
может быть представлен двумя
основными схемами замещения (эквивалентными
схемами).
Как
уже указывалось, с одной стороны,
напряжение на выводах источника энергии
меньше ЭДС на падение напряжения внутри
источника:

 

с
другой стороны, напряжение на
сопротивлении r 

 

Ввиду
равенства из
(1.5а) и (1.56) получается или 

 

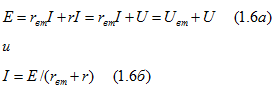
В
частности, при холостом ходе (разомкнутых
выводах а и b)
получается E=Uх,
т. е. ЭДС равна напряжению холостого
хода. При коротком замыкании (выводов
а и b)
ток 

 

Из
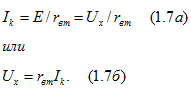
(1.7 6)
следует, что rвт источника
энергии, так же как и сопротивление
приемника, ограничивает ток.
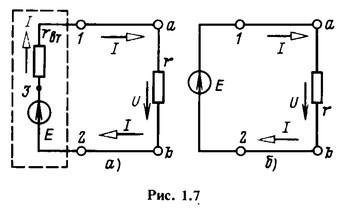
На
схеме замещения можно показать элемент
схемы с rвт,
соединенным последовательно с элементом,
обозначающим ЭДС E (рис.
1.7, а). Напряжение U зависит от тока
приемника и равно разности между
ЭДС E источника
энергии и падением напряжения rвтI (1.6а).
Схема источника энергии, показанная на
рис. 1.7, а, называется первой
схемой замещения или
схемой с источником ЭДС.
Если rвт<<r и
напряжение Uвт<<U,
т. е. источник электрической энергии
находится в режиме, близком к холостому
ходу, то можно практически пренебречь
внутренним падением напряжения и
принять Uвт = rвт =
0.
В этом случае для источника энергии
получается более простая эквивалентная
схема только с источником ЭДС, у которого
в отличие от реального источника
исключается режим короткого замыкания
(U =0). Такой источник энергии без внутреннего
сопротивления (rвт =
0),
обозначенный кружком со стрелкой внутри
и буквой E (рис.
1.7,6), называют идеальным
источником ЭДС или источником
напряжения (источником
с заданным напряжением). Напряжение на
выводах такого источника не зависит от
сопротивления приемника и всегда равно
ЭДС E.
Его внешняя характеристика – прямая,
параллельная оси абсцисс (штриховая
прямая ab на
рис. 1.4).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Закон Ома для полной цепи:

Работа тока на участке цепи равна произведению силы тока, напряжения па этом участке и промежутка времени, в течение которого совершалась работа:

Закон Джоуля — Ленца:

• количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени прохождения тока по проводнику:

Для однородного участка цепи количество выделившейся теплоты можно вычислить по любой из трех эквивалентных формул:

Мощность, идущая на нагревание проводника, равна работе, которая совершается током за единицу времени:

Единицей мощности электрического тока, так же как и механической мощности, является ватт (1 Вт):

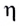
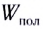
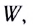
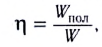
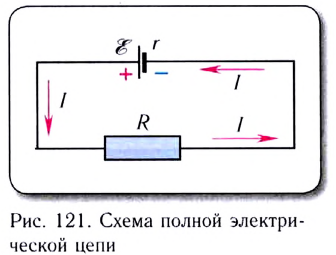
Коэффициент полезного действия (КПД) определяется отношением полезно использованной энергии  к полной энергии полученной системой:  и  является характеристикой эффективности работы системы.

Рассмотрим полную электрическую цепь, содержащую источник ЭДС 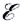с внутренним сопротивлением r и подключенный к ним резистор сопротивлением R (рис. 121).

Из определения ЭДС источника тока следует, что совершаемая источником работа

Из закона сохранения энергии следует, что в такой цепи происходит превращение энергии, запасенной источником тока, только в теплоту. При этом работа сторонних сил за промежуток времени 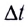равна выделившемуся в цепи количеству теплоты:

По закону Джоуля — Ленца

Таким образом,

откуда

Полученное выражение представляет собой закон Ома для полной цепи:
сила тока в полной цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна полному сопротивлению цепи.
Заметим, что максимально возможный ток в цепи с данным источником тока возникает в том случае, если сопротивление внешней части цепи стремится к нулю.

Максимально возможный ток через источник называют также током короткого замыкания

Короткое замыкание представляет серьезную опасность для мощных источников тока, поскольку может вывести их из строя.

У гальванических элементов (батареек) сила тока короткого замыкания небольшая, поэтому оно для них не очень опасно.

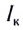
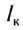
Внутреннее сопротивление свинцовых аккумуляторов имеет значение от r = 0,1 Ом до r = 0,01 Ом, и сила тока короткого замыкания в них может быть от = 20 А до  = 200 А. А поскольку при этом возможно разрушение пластин аккумуляторов, то следует соблюдать меры безопасности при работе с ними.
В быту, в осветительных сетях, на распределительных станциях ЭДС имеет величины свыше 100 В, а внутреннее сопротивление цепи очень мало, и согласно закону Ома для замкнутой цепи сила тока короткого замыкания может доходить до 1000 А. Вследствие этого короткое замыкание может привести к пожару. Для зашиты от пожаров в электрические цепи включаются плавкие предохранители, которые плавятся при определенной силе тока и размыкают цепь.

Короткое замыкание может возникнуть из-за плохой изоляции, когда два токоведущих провода соединяются между собой (закорачиваются). Внешнее сопротивление цепи в этом случае стремится к нулю, и сила тока резко возрастает.

Короткое замыкание электропроводки в быту может стать причиной пожара, поэтому ни в коем случае не занимайтесь ремонтом электрических сетей самостоятельно!

Закон Ома для полной цепи можно записать в следующем виде:

Таким образом, ЭДС источника равна сумме падений напряжений на внешнем и внутреннем участках замкнутой цепи.

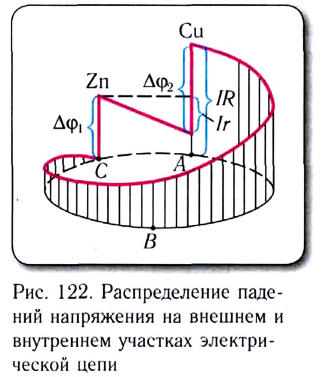
Закон Ома для полной цепи наглядно можно показать с помощью рисунка 122, где в качестве источника тока взят гальванический элемент Вольта (Сu—Zn).
Потенциал клеммы у цинковой пластины условно принят за нуль. Длина перпендикуляра к проводнику АВС в данной точке цепи пропорциональна ее потенциалу.

Падение напряжения на внешнем участке цепи равно IR, внутри источника — Ir.
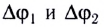
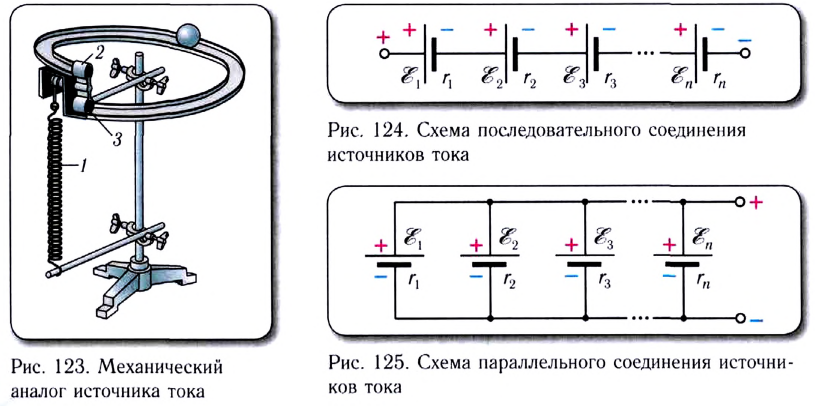
Скачки потенциалов на цинковой и медной пластинах соответственно обусловлены химическими процессами.
Для лучшего понимания процессов, происходящих в замкнутой электрической цепи рассмотрим аналогичную механическую модель (рис. 123).

Подобно тому как шарик скатывается по винтовой наклонной плоскости под действием силы тяжести из положения 2 в положение 3, так электроны движутся на внешнем участке цепи под действием сил электрического поля.
Для того чтобы поднять шарик в исходное положение 2, необходимо совершить работу против силы тяжести, которая в случае электрической цепи аналогична работе сторонних сил внутри источника тока.

В данном случае пружинное устройство 1, совершающее работу за счет энергии упругой деформации, является механическим аналогом источника ЭДС в замкнутой цепи.

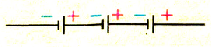
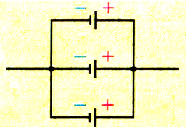
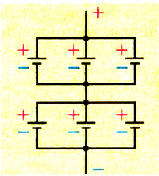
Для работы различных устройств мы используем батарейки (гальванические элементы), которые включаем последовательно с соблюдением полярности.
При последовательном соединении n источников тока, когда «минус» первого источника соединяется с «плюсом» второго и т. д. (рис. 124), их ЭДС и внутренние сопротивления суммируются:

В частном случае, если 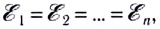 то

Параллельное соединение источников тока, когда «плюсы» всех источников соединяются в один узел, а «минусы» — в другой (рис. 125), используется значительно реже для повышения надежности электропитания. Можно показать, что при параллельном соединении п одинаковых источников тока суммарная ЭДС батареи равна ЭДС одного источника, а внутреннее сопротивление рассчитывается по законам параллельного соединения:

Работа по перемещению зарядов на неоднородном участке цепи равна сумме работ, совершаемых сторонними силами источника тока и силами электрического поля.

Поскольку напряжение на участке цепи равно отношению работы к перенесенному заряду 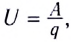то

Знак перед берется положительный, если ЭДС увеличивает потенциал в цепи в направлении прохождения тока, и отрицательный — если уменьшает.

С учетом того, что U = IR (R — полное сопротивление резисторов и источников ЭДС на участке цепи), находим силу тока на участке цепи:

Эта формула выражает закон Ома для неоднородного участка цепи: падение напряжения на неоднородном участке цепи — произведение силы тока I и сопротивления участка цепи R:

Отметим, что падение напряжения пропорционально суммарной работе всех сил, в то время как напряжение U пропорционально работе только электростатических сил.

Мощность, выделяемая на внешнем участке цепи, в которую включены тепловые потребители энергии, называется полезной мощностью. Для ее вычисления используются формулы:

Мощность, выделяемая на внутреннем сопротивлении источника тока, называется теряемой мощностью и вычисляется по формулам:

Сумма полезной и теряемой мощностей равна полной мощности источника тока, которая учитывает выделение энергии как на внешнем, так и на внутреннем участках цепи:

 

Коэффициент полезного действия источника тока, определяемый как отношение полезной мощности к полной, зависит от сопротивления нагрузки и внутреннего сопротивления источника тока:

Наибольшую полезную мощность от данного источника можно получить тогда, когда внешнее сопротивление равно внутреннему (R = r), и в этом случае максимальный КПД 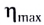= 50 % (докажите это).

• Заказать решение задач по физике

Закон Ома для полной цепи

Открытый Г. Омом закон для участка цени в общем случае справедлив и для полной цепи, если принимать во внимание как внешнюю, так и внутреннюю части цепи. Математическую запись закона Ома для этого случая можно получить на основании закона сохранения энергии, универсального для всех процессов в природе.

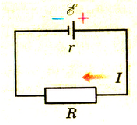
Пусть электрическая цепь состоит из источника тока, имеющего ЭДС и внутреннее сопротивление г, и проводника сопротивлением R (рис. 1.51).

Pиc. 151. Замкнутая электрическая цепь

Согласно закону сохранения энергии работа сторонних сил равна сумме работ электрического тока во внешней и внутренней частях цепи:

По определению

Отсюда

Если учесть, что по закону Ома для участка цепи U =IR, то получим формулу этого закона для полной цепи:

Таким образом, сила тока в полной цепи пропорциональна электроднижущей силе источника и обратно пропорциональна полному сопротивлению цепи.

Сила тока в полной цепи пропорциональна электродвижущей силе источника и обратно пропорциональна полному сопротивлению цепи:

Пользуясь законом Ома для полной цепи, можно рассчитать два экстремальных случая н электрической цепи – короткое замыкание и разомкнутую цепь. Если сопротивление внешней цепи стремится к нулю (короткое замыкание), то сила тока в цепи

Это будет максимальное значение силы тока для данной цепи.
Если цепь разорвана (R→∞ ), то ток в цени прекращается при любых значениях ЭДС и внутреннего сопротивления. В последнем случае напряжение нм полюсах источника тока будет равно электродвижущей силе. Поэтому иногда дают упрощенное определение ЭДС: это величина, равная напряжению на клеммах источника при разомкнутой цепи.

Источники тока могут соединяться в батареи. Существуют несколько способов соединения источников тока.

Последовательным называют соединение, при котором соединяются друг с другом разноименные полюса источников: положительный предыдущего с отрицательным следующего и т. д. (рис. 1.52). Чаще всего соединяют источники с одинаковыми характеристиками, поэтому при последовательном соединении N источников ЭДС батареи будет в N раз больше, чем ЭДС одного источника:

Внутреннее сопротивление такой батареи будет также в N раз больше:

Рис. 152. Схема последовательного соединения источников тока

Для последовательного соединения источников тока закон Ома для полной цепи будет записываться:

Последовательное соединение источников τoιca удобно в том случае, когда сопротивление потребителя значительно больше внутреннего сопротивления одного источника тока.
Параллельным является соединение, при котором все одноименные полюса соединяется в один узел (рис. 1.53).

Pиc. 153. Схема параллельного соединения источников тока

Параллельное соединение применяют тогда, когда в цепи необходимо получить большое значение силы тока при небольшом напряжении.

Электродвижущая сила батареи параллельно соединенных одинаковых источников равна ЭДС одного источника:

Формула закона Ома для параллельного соединения источников имеет вид:

Параллельное соединения удобно тогда» когда сопротивление внешней части цепи значительно меньше внутреннего сопротивления одного источника.

При смешанном соединении батареи источников тока (параллельно или последовательно) в свою очередь соединяют последовательно или параллельно (рис. 1.54).

Pиc. 1.54. Смешанное соединение источников тoκa

Научная статья
на тему:  “Напряжение на клеммах и напряжение холостого хода“

«Напряжение на
клеммах» источника напряжения – это напряжение, которое прикладывается между
двумя клеммами (соединениями, полюсами) источника напряжения; это напряжение
идентично напряжению, которое падает на внешнем сопротивлении цепи.

Напряжение на
клеммах принимает максимальное значение, когда внешнее сопротивление бесконечно
велико: в этом случае почти все напряжение на внешнем сопротивлении падает и
почти отсутствует напряжение на внутреннем сопротивлении. Однако, поскольку ток
не может протекать с бесконечно большим внешним сопротивлением, это
максимальное значение напряжения также называется «напряжением холостого хода» .

Напряжение
холостого хода соответствует значению напряжения источника напряжения при
отсутствии подключенного потребителя. Это значение можно приблизительно
измерить с помощью вольтметра, поскольку он не имеет бесконечного значения
сопротивления, но имеет очень большое значение сопротивления.

Диаграмма зависимости
напряжения на клеммах источника напряжения от внутреннего сопротивления и протекающего тока .

Если к источнику
напряжения подключен потребитель с конечным сопротивлением, устанавливается
сила тока , протекающая как через
потребителя, так и через источник напряжения. При внутреннем сопротивлении источника напряжения, напоминающем по закону Ома,
напряжение от; таким образом,
напряжение на клеммах уменьшается на эту величину по сравнению с напряжением
холостого хода. В этом случае к напряжению на клеммах
применимо следующее:

(1)

Чем меньше
внешнее сопротивление цепи, тем выше сила тока ; это приводит к снижению
напряжения на клеммах  .

Пример:

●      Насколько велико напряжение на клеммах источника
напряжения по сравнению с его напряжением холостого хода, если
внешнее сопротивление такое же, как внутреннее
сопротивление источника напряжения?
Если ,
то следующая сила тока :

Вставка этого значения в приведенную выше формулу (1) приводит к
напряжению на клеммах :

В этом случае напряжение на клеммах упало до половины напряжения холостого
хода.

В случае
короткого замыкания внешнее сопротивление падает почти до нуля; сила тока тогда
ограничивается только обычно очень низким внутренним сопротивлением источника
напряжения. Сила тока, возникающая здесь, может быть настолько велика, что
источник напряжения может быть разрушен тепловым воздействием тока; в случае
короткого замыкания существует опасность возгорания.

В случае
короткого замыкания батареи и аккумуляторы могут высвободить всю накопленную
химическую энергию в течение нескольких минут. В практических приложениях,
например , в автомобилях, риск возникновения пожара в случае короткого
замыкания часто предотвращен тонкими предохранители:
Провод , встроенный в них светится быстро , когда тока слишком высоки, тем
самым прерывая цепь.

В случае
источников питания производитель должен указать предел нагрузки, в котором
указывается сила тока, которую источник питания может обеспечивать в течение
длительного периода времени. Если предел нагрузки превышен в течение
длительного периода времени или в течение короткого времени и, следовательно,
очень очевидно, могут возникнуть короткие замыкания в блоке питания из-за
перегрева, которые могут вывести блок питания из строя и вызвать главный
предохранитель в распределительной сети. коробка (выключатель или
предохранитель ФИ) “вылететь”. Поэтому в определенных приложениях
рекомендуется использовать блок питания, который также рассчитан на несколько
более высокие токи.