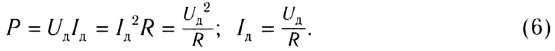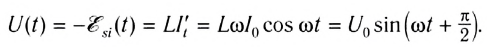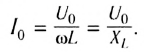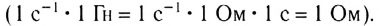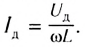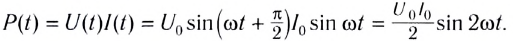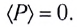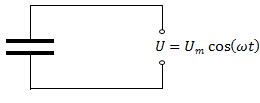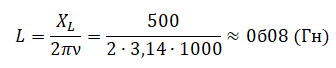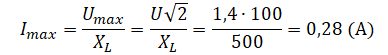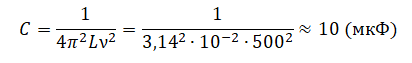Переменный электрический ток:
До сих пор рассматривались электрические цепи, содержащие в различных сочетаниях резисторы, конденсаторы и катушки, с источником постоянного тока либо без него. Теперь рассмотрим подключение таких цепей к источнику переменного тока.
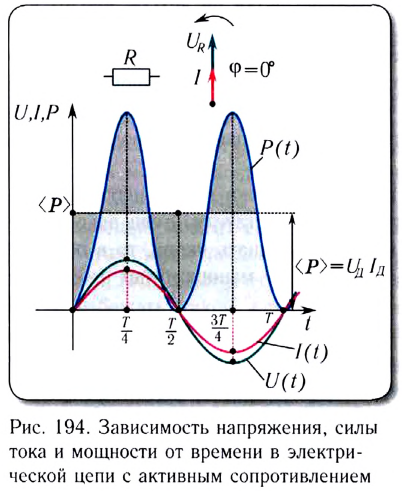
Пусть источник тока создает переменное гармоническое напряжение (рис. 194)
Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
где 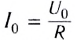
Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.
Величины 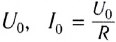
Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность 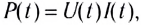
С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде
Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно.
Перепишем формулу для мощности по-другому:
Первое слагаемое не зависит от времени. Второе слагаемое — переменная составляющая — функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (см. рис. 194).
Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле
Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.
Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Поскольку для постоянного тока 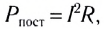
Аналогично можно ввести действующее значение и для напряжения
Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе (см. рис. 194).
Таким образом, резисторы оказывают сопротивление как постоянному, так и переменному току, при этом в обоих случаях в них происходит превращение электрической энергии во внутреннюю. Вследствие этого сопротивление резисторов R получило название активного или омического сопротивления.
Катушка индуктивности в цепях переменного тока
Реальный соленоид (катушка индуктивности) обладает активным сопротивлением R и индуктивностью L. В цепях постоянного тока главную роль играет его сопротивление R, тогда как в цепях переменного тока — его индуктивность L.
Рассмотрим физические процессы, происходящие в идеальной катушке, у которой отсутствует активное сопротивление (R=0), при включении ее в цепь переменного тока.
В катушке индуктивностью L переменный ток 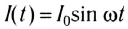
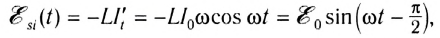
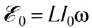
При возрастании силы тока ЭДС самоиндукции согласно правилу Ленца будет препятствовать его увеличению. Для идеальной катушки, активное сопротивление которой равно нулю (R=0), согласно закону Ома для полной цепи 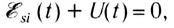
Следовательно, в любой момент времени внешнее напряжение на концах катушки равно по модулю и противоположно по знаку ЭДС самоиндукции в катушке:
Сравнивая выражения для мгновенных значений силы тока I(t) и напряжения U(t), видим, что для их амплитудных значений можно записать закон Ома в виде
Величину 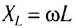
Обратите внимание на то, что фазы колебаний силы тока и напряжения не совпадают. Наличие сдвига фаз означает, что мгновенное значение напряжения U на катушке индуктивности опережает мгновенное значение силы I переменного тока по фазе на 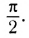
Закон Ома для цепи переменного тока, содержащей только катушку индуктивности, выполняется и для действующих значении силы тока 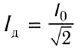
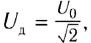
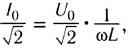
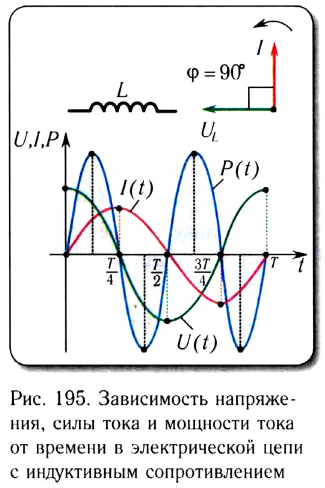
Таким образом, если в цепь переменного тока включена катушка индуктивности, то закон Ома выполняется для амплитудных и действующих значений силы тока и напряжения, но не выполняется для их мгновенных значений, так как мгновенные значения силы тока и напряжения не совпадают по фазе (см. рис. 195).
Мгновенная мощность, потребляемая катушкой индуктивности от источника переменного тока, определяется по формуле
Поскольку среднее за период значение функции 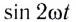
Как видно из рисунка 195, цепь с идеальной катушкой индуктивности в течение первой и третьей четвертей периода работает в режиме потребителя, запасая энергию магнитного поля 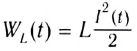
Поскольку потерь энергии в этом случае не происходит, то индуктивное сопротивление называют реактивным.
- Конденсатор в цепях переменного тока
- Электрический ток в различных средах
- Электромагнитная индукция в физике
- Правило Ленца для электромагнитной индукции
- Потенциал электрического поля
- Постоянный электрический ток
- Законы постоянного тока
- Переменный электрический ток
Катушка индуктивности в цепи переменного тока
Рассмотрим цепь, содержащую в себе катушку индуктивности , и предположим, что активное сопротивление цепи, включая провод катушки, настолько мало, что им можно пренебречь. В этом случае подключение катушки к источнику постоянного тока вызвало бы его короткое замыкание, при котором, как известно, сила тока в цепи оказалась бы очень большой.
Иначе обстоит дело, когда катушка присоединена к источнику переменного тока. Короткого замыкания в этом случае не происходит. Это говорит о том. что катушка индуктивности оказывает сопротивление проходящему по ней переменному току .
Каков характер этого сопротивления и чем оно обусловливается?
Чтобы ответить ил этот вопрос, вспомним явление самоиндукции. Всякое изменение тока в катушке вызывает появление в ней ЭДС самоиндукции, препятствующей изменению тока. Величина ЭДС самоиндукции прямо пропорциональна величине индуктивности катушки и скорости изменения тока в ней. Но так как переменный ток непрерывно изменяется, то непрерывно возникающая в катушке ЭДС самоиндукции создает сопротивление переменному току.
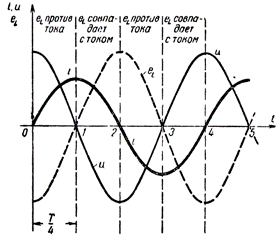
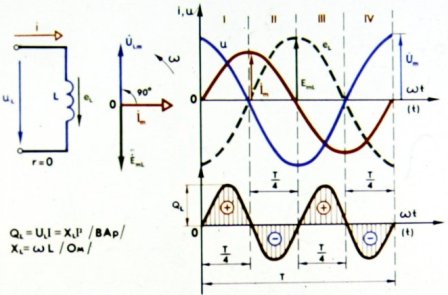
Для уяснения процессов, происходящих в цепи переменного тока с катушкой индуктивности, обратимся к графику. На рисунке 1 построены кривые линии, характеризующие соответственно тик в цепи, напряжение на катушке и возникающую в ней ЭДС самоиндукции. Убедимся в правильности произведенных па рисунке построений.
Цепь переменного тока с катушкой индуктивности
С момента t = 0, т. е. с начального момента наблюдения за током, он начал быстро возрастать, но по мере приближения к своему максимальному значению скорость нарастания тока уменьшалась. В момент, когда ток достиг максимальной величины, скорость его изменения на мгновение стала равной нулю, т. е. прекратилось изменение тока. Затем ток начал сначала медленно, а потом быстро убывать и по истечении второй четверти периода уменьшился до нуля. Скорость же изменения тока за эту четверть периода, возрастая от пуля, достигла наибольшей величины тогда, когда ток станет равным нулю.
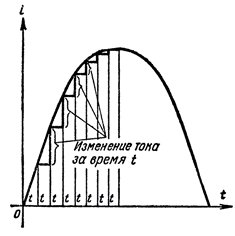
Рисунок 2. Характер изменений тока во времени в зависимости от величины тока
Из построений на рисунке 2 видно, что при переходе кривой тока через ось времени увеличение тока за небольшой отрезок времени t больше, чем за этот же отрезок времени, когда кривая тока достигает своей вершины.
Следовательно, скорость изменения тока уменьшается по мере увеличения тока и увеличивается по мере его уменьшения, независимо от направления тока в цепи.
Очевидно, и ЭДС самоиндукции в катушке должна быть наибольшей тогда, когда скорость изменения тока наибольшая, и уменьшаться до нуля, когда прекращается его изменение. Действительно, на графике кривая ЭДС самоиндукции e L за первую четверть периода, начиная от максимального значения, упала до нуля (см. рис. 1).
На протяжении следующей четверти периода ток от максимального значения уменьшался до нуля, однако скорость его изменения постепенно возрастала и была наибольшей в момент, когда ток стал равным нулю. Соответственно и ЭДС самоиндукции за время этой четверти периода, появившись вновь в катушке, постепенно возрастала и оказалась максимальной к моменту, когда ток стал равным нулю.
Однако направление свое ЭДС самоиндукции изменила на обратное, так как возрастание тока в первой четверти периода сменилось во второй четверти его убыванием.
Продолжив дальше построение кривой ЭДС самоиндукции, мы убеждаемся в том, что за период изменения тока в катушке и ЭДС самоиндукции совершит в ней полный период своего изменения. Направление ее определяется законом Ленца: при возрастании тока ЭДС самоиндукции будет направлена против тока (первая и третья четверти периода), а при убывании тока, наоборот, совпадать с ним по направлению (вторая и четвертая четверти периода).
Таким образом, ЭДС самоиндукции, вызываемая самим переменным током, препятствует его возрастанию и , наоборот, поддерживает его при убывании .
Обратимся теперь к графику напряжения на катушке (см. рис. 1). На этом графике синусоида напряжения на зажимах катушки изображена равной и противоположной синусоиде ЭДС самоиндукции. Следовательно, напряжение на зажимах катушки в любой момент времени равно и противоположно ЭДС самоиндукции, возникающей в ней. Напряжение это создается генератором переменного тока и идет на то, чтобы погасить действие в цепи ЭДС самоиндукции.
Таким образом, в катушке индуктивности, включенной в цепь переменного тока, создается сопротивление прохождению тока. Но так как такое сопротивление вызывается в конечном счете индуктивностью катушки , то и называется оно индуктивным сопротивлением.
Индуктивное сопротивление обозначается через X L и измеряется, как и активное сопротивление, в омах.
Индуктивное сопротивление цепи тем больше, чем больше частота источника тока, питающего цепь, и чем больше индуктивность цепи. Следовательно, индуктивное сопротивление цепи прямо пропорционально частоте тока и индуктивности цепи; определяется оно по формуле X L = ω L , где ω — круговая частота, определяемая произведением 2π f . — индуктивность цепи в гн.
Закон Ома для цепи переменного тока, содержащей индуктивное сопротивление, звучит так: величина тока прямо пропорциональна напряжению и обратно пропорциональна индуктивному сопротивлению це п и , т. е. I = U / X L , где I и U — действующие значения тока и напряжения, а X L — индуктивное сопротивление цепи.
Рассматривая графики изменения тока в катушке. ЭДС самоиндукции и напряжения на ее зажимах, мы обратили внимание на то, что изменение этих в еличин не совпадает по времени. Иначе говоря, синусоиды тока, напряжения и ЭДС самоиндукции оказались для рассматриваемой нами цепи сдвинутыми по времени одна относительно другой. В технике переменных токов такое явление принято называть сдвигом фаз .
Если же две переменные величины изменяются по одному и тому же закону (в нашем случае по синусоидальному) с одинаковыми периодами, одновременно достигают своего максимального значения как в прямом, так и в обратном направлении, а также одновременно уменьшаются до нуля, то такие переменные величины имеют одинаковые фазы или, как говорят, совпадают по фазе.
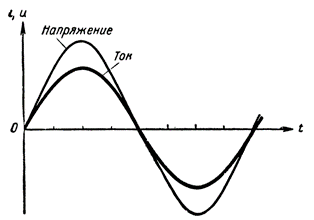
В качестве примера на рисунке 3 приведены совпадающие по фазе кривые изменения тока и напряжения. Такое совпадение фаз мы всегда наблюдаем в цепи переменного тока, состоящей только из активного сопротивления.
В том случае, когда цепь содержит индуктивное сопротивление, фазы тока и напряжения, как это видно из рис. 1 не совпадают, т. е. имеется сдвиг фаз между этими переменными величинами. Кривая тока в этом случае как бы отстает от кривой напряжения на четверть периода.
Следовательно, при включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между током и напряжением, причем ток отстает по фазе от напряжения на четверть периода . Это значит, что максимум тока наступает через четверть периода после того, как наступил максимум напряжения.
ЭДС же самоиндукции находится в противофазе с напряжением на катушке, отставая, в свою очередь, от тока на четверть периода. При этом период изменения тока, напряжения, а также и ЭДС самоиндукции не меняется и остается равным периоду изменения напряжения генератора, питающего цепь. Сохраняется также и синусоидальный характер изменения этих величин.
Рисунок 3. Совпадение по фазе тока и напряжения в цепи с активным сопротивлением
Выясним теперь, каково отличие нагрузки генератора переменного тока активным сопротивлением от нагрузки его индуктивным сопротивлением.
Когда цепь переменного тока содержит в себе лишь одно активное сопротивление, то энергия источника тока поглощается в активном сопротивлении, нагревая проводник.
Когда же цепь не содержит активного сопротивления (мы условно считаем его равным нулю), а состоит лишь из индуктивного сопротивления катушки, энергия источника тока расходуется не на нагрев проводов, а только на создание ЭДС самоиндукции, т. е. она превращается в энергию магнитного поля. Однако переменный ток непрерывно изменяется как по величине, так и по направлению, а следовательно, и магнитное поле катушки непрерывно изменяется в такт с изменением тока. В первую четверть периода, когда ток возрастает, цепь получает энергию от источника тока и запасает ее в магнитном поле катушки. Но как только ток, достигнув своего максимума, начинает убывать, он поддерживается за счет энергии, запасенной в магнитном поле катушки посредством ЭДС самоиндукции.
Таким образом, источник тока, отдав в течение первой четверти периода часть своей энергии в цепь, в течение второй четверти получает ее обратно от катушки, выполняющей при этом роль своеобразного источника тока. Иначе говоря, цепь переменного тока, содержащая только индуктивное сопротивление, не потребляет энергии : в данном случае происходит колебание энергии между источником и цепью. Активное же сопротивление, наоборот, поглощает в себе всю энергию, сообщенную ему источником тока.
Говорят, что катушка индуктивности, в противоположность омическому сопротивлению, не активна по отношению к источнику переменного тока, т. е. реактивна . Поэтому индуктивное сопротивление катушки называют также реактивным сопротивлением .
Источник
Какое напряжение возникает между концами катушки
1) Какой индуктивностью обладает контур, если при силе тока 20 А магнитный поток в контуре равен 10^-2 Вб?
2) Какое напряжение возникает между концами катушки с индуктивностью 1 Гн при равномерном убывании силы тока в ней от 1 до 0 А за 10^-3 с?
3) Вычислите индуктивность цилиндрической катушки, имеющей 1000 витков, длину 50 см и диаметр 10 см.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
1) Ф=L*I, L=Ф/I=10⁻²/2=0.005 Гн
2) ε=-L*ΔI/Δt= 1Гн*1А/10⁻³с=1000 В
3) L=μ₀N²S/l, S=πd²/4, L=4π*10⁻⁷ *10⁶ *π*0.01/4*0.5=0.02 Гн
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Физика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.
Источник
Какое напряжение возникает между концами катушки
«Физика — 11 класс»
Индуктивность в цепи влияет на силу переменного тока.
Есть цепь из катушки с большой индуктивностью и электрической лампы накаливания.
При подключении с помощью переключателя цепи к источнику постоянного напряжения или к источнику переменного напряжения постоянное напряжение и действующее значение переменного напряжения будут равны.
Однако лампа светится ярче при постоянном напряжении.
Значит действующее значение силы переменного тока в цепи меньше силы постоянного тока.
Это объясняется явлением самоиндукции.
При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно.
Возникающее при этом вихревое электрическое поле тормозит движение электронов.
По прошествии некоторого времени сила тока достигает наибольшего (установившегося) значения, соответствующего данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не будет успевать достигнуть тех значений, которые она приобрела бы с течением времени при постоянном напряжении.
Максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю.
Иначе сила тока, согласно закону Ома, была бы бесконечно большой.
Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля 

Из равенства 

Так как удельная работа кулоновского поля равна напряжению на концах катушки, можно записать:
При изменении силы тока по гармоническому закону
i = Im sin ωt
еi = —Li’ = —LωIm cos ωt
Так как u = —ei напряжение на концах катушки оказывается равным
где
Um = LωIm — амплитуда напряжения.
Колебания напряжения на катушке опережают по фазе колебания силы тока на 

Амплитуда силы тока в катушке равна:
и действующие значения силы тока и напряжения, то получим:
Величину XL, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.
Действующее значение силы тока связано с действующим значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.
Индуктивное сопротивление зависит от частоты ω.
Постоянный ток вообще «не замечает» индуктивности катушки.
При ω = 0 индуктивное сопротивление равно нулю (XL = 0).
Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока.
Итак,
Катушка индуктивности оказывает сопротивление переменному току.
Это сопротивление, называемое индуктивным, равно произведению циклической частоты на индуктивность.
Колебания силы тока в цепи с индуктивностью отстают по фазе от колебаний напряжения на 
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика
Источник
Опишем колебания, которые происходят в цепи переменного тока при включении в нее конденсатора и катушки индуктивности. А также рассмотрим условия, при выполнении которых в цепи переменного тока наступает резонанс. Получим формулы для вычисления амплитуд напряжений, введем понятия емкостного и индуктивного сопротивления и выясним, какую роль играют эти величины.
Конденсатор в цепи переменного тока
Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см. рисунок ниже).
Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться.
Найдем, как меняется сила тока в цепи, содержащей только конденсатор, если сопротивление проводов и обкладок конденсатора можно пренебречь (см. рис. выше). Напряжение на конденсаторе будет равно:
u=φ1−φ2=qC
Учтем, что напряжение на конденсаторе равно напряжению на концах цепи:
qC=Umaxcosωt
Следовательно, заряд конденсатора меняется по гармоническому закону:
q=CUmaxcosωt
Тогда сила тока, представляющая собой производную заряда по времени, будет равна:
i=q´=−CUmaxsinωt=CUmaxcos(ωt+π2)
Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на π2 (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.
Амплитуда силы тока равна:
Imax=UmaxCω
Примем, что:
1Cω=XC
Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что:
Определение
I=UXC
Величина XC, равная обратному произведению циклической частоты на электрическую емкость конденсатора, называется емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть.
Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура qmax=10−6 Кл. Амплитудное значение силы тока в контуре Imax=10−3 А. Определите период колебания (потерями на нагревание проводника пренебречь).
Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки:
q2max2C=LI2max2
Отсюда:
LC=q2maxI2max
√LC=qmaxImax
T=2π√LC=2πqmaxImax=2·3,1410−610−3≈6,3·10−3 (с)
Катушка индуктивности в цепи переменного тока
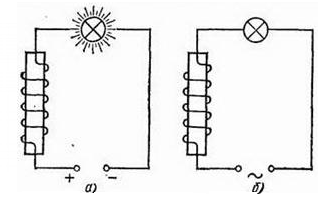
Соберем две электрических цепи, состоящих из лампы накаливания, катушки индуктивности и источника питания: в первом случае постоянного, во втором — переменного (см. рисунки «а» и «б» ниже).
Опыт покажет, что в цепи постоянного тока лампа светится ярче по сравнению с той, что включена в цепь переменного тока. Это говорит о том, что сила тока в цепи постоянного тока выше действующего значения силы тока в цепи переменного тока.
Результат опыта легко объясняется явлением самоиндукции. При подключении катушки к постоянному источнику тока сила тока нарастает постепенно. Возрастающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь спустя какое-то время сила тока достигает наибольшего значения, соответствующему данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не успевает достигнуть максимального значения. Поэтому максимальное значение силы тока в цепи переменного тока с катушкой индуктивности ограничивается индуктивность. Чем больше индуктивность и чем больше частота приложенного напряжения, тем меньше амплитуда силы переменного тока.
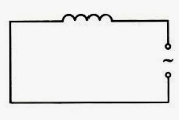
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (см. рисунок ниже). Для этого найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна равняться нулю. Иначе, согласно закону Ома, сила тока была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля →Ei, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля →Eк, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства →Ei=−→Eк следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции ei) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Учитывая, что удельная работа кулоновского поля равна напряжения на концах катушки, можно записать:
ei=−u
Напомним, что сила переменного тока изменяется по гармоническому закону:
i=Imaxsinωt
Тогда ЭДС самоиндукции равна:
ei=−Li´=−LωImaxcosωt
Так как u=−ei, то напряжение на концах катушки оказывается равным:
u= LωImaxcosωt=LωImaxsin(ωt+π2)=Umax(ωt+π2)
Амплитуда напряжения равна:
Umax=LωImax
Следовательно, колебания напряжения на катушке опережают колебания силы тока на π2, или колебания силы тока отстают от колебаний напряжения на π2, что одно и то же.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (см. график ниже).
Но в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Амплитуда силы тока в катушке равна:
Imax=UmaxLω
Введем обозначение:
Lω=XL
Также будем использовать вместо амплитуд действующие значения силы тока и напряжения. Тогда получим:
Определение
I=UXL
Величина XL, равная произведению циклической частоты на индуктивность, называется индуктивным сопротивлением. Индуктивное сопротивление зависит от частоты. Поэтому в цепи постоянного тока, в котором отсутствует частота, индуктивное сопротивление катушки равно нулю.
Пример №2. Катушка с индуктивным сопротивлениемXL=500 Ом присоединена к источнику переменного напряжения, частота которого ν = 1000 Гц. Действующее значение напряжения U = 100 В. Определите амплитуду силы тока Imax в цепи и индуктивность катушки L. Активным сопротивлением пренебречь.
Индуктивное сопротивление катушки выражается формулой:
XL=Lω=2πνL
Отсюда:
Так как амплитуда напряжения связана с его действующим значением соотношением Umax=U√2, то для амплитуды силы тока получаем:
Резонанс в электрической цепи
Механические и электромагнитные колебания имеют разную природу, но процессы, происходящие при этом, идентичны. Поэтому можно предположить, что резонанс в электрической цепи так же реален, как резонанс в колебательной системе, на которую действует периодическая сила.
Напомним, что в механической системе резонанс тем более заметен, чем меньше в колебательной системе трение между ее элементами. Роль трения в электрической цепи играет активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника, который при этом нагревается. Следовательно, резонанс в электрической цепи будет отчетливо наблюдаться при малом активном сопротивлении R.
Если активное сопротивление мало, то собственная частота колебаний в колебательном контуре определяется формулой:
ω0=1√LC
Сила тока при вынужденных колебаниях должна достигать максимальных значений, когда частота переменного напряжения, приложенного к контуру равна собственной частоте колебательного контура:
ω=ω0=1√LC
Определение
Резонанс в электрическом колебательном контуре — явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
После включения внешнего переменного напряжения резонансное значение силы тока в цепи устанавливается не моментально, а постепенно. Амплитуда колебаний силы тока возрастает до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:
I2maxR2=UmaxImax2
Упростив это уравнение, получим:
ImaxR=Umax
Следовательно, амплитуда установившихся колебаний силы тока при резонансе определяется уравнением:
Imax=UmaxR
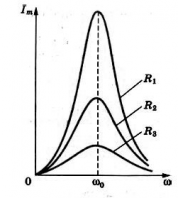
При сопротивлении, стремящемся к нулю, сила тока возрастает до бесконечно больших значений. При большом сопротивлении сила тока возрастает незначительно. Это хорошо видно на графике ниже.
Пример №3. В цепь переменного тока с частотой ν = 500 Гц включена катушка индуктивностью L = 10 мГн. Какой емкости конденсатор надо включить в эту цепь, чтобы наступил резонанс?
Электрическая цепь, описываемая в условии, представляет собой колебательный контур. Резонанс в этой цепи наступит, когда частота переменного тока будет равна собственной частоте колебательного контура (ν = ν0).
Но:
ν0=12π√LC
Тогда:
ν=12π√LC
Отсюда:
Задание EF22579
К колебательному контуру подсоединили источник тока, на клеммах которого напряжение гармонически меняется с частотой ν.
Индуктивность L катушки колебательного контура можно плавно менять от максимального значения Lmax до минимального Lmin, а ёмкость его конденсатора постоянна.
Ученик постепенно уменьшал индуктивность катушки от максимального значения до минимального и обнаружил, что амплитуда силы тока в контуре всё время возрастала. Опираясь на свои знания по электродинамике, объясните наблюдения ученика.
Алгоритм решения
1.Установить, что вызывает увеличение амплитуды силы тока.
2.Объяснить, какие изменения вызвало уменьшение индуктивности.
3.Объяснить, при каком условии в течение всего эксперимента амплитуда силы тока может только расти.
Решение
В колебательном контуре источником тока возбуждаются вынужденные колебания. Частота этих колебаний равна частоте источника — ν. Амплитуда колебаний зависит от того, как соотносятся между собой внешняя частота и частота собственных электромагнитных колебаний, которая определяется формулой:
ν0=12π√LC
По мере увеличения внешней частоты от нуля до ν0 амплитуда растет. Она достигает максимума тогда, когда происходит резонанс. При этом внешняя частота равна частоте собственных электромагнитных колебаний: ν = ν0. Затем амплитуда начинает убывать.
В данном случае, ученик меняет не внешнюю частоту, а частоту собственных электромагнитных колебаний. При плавном уменьшении индуктивности контура от максимального значения Lmax до минимального Lmin частота возрастает от ν0min до ν0max. Причем:
ν0min=12π√LminC
ν0max=12π√LmaxC
Из того факта, что амплитуда всё время увеличивалась, можем сделать вывод, что частота ν0 всё время приближалась к частоте источника тока, при этом ν > ν0max. В противном случае наблюдалось бы уменьшений амплитуды силы тока.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22785
В колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят свободные незатухающие электромагнитные колебания.
Из приведённого ниже списка выберите две величины, которые остаются постоянными при этих колебаниях.
Ответ:
а) период колебаний силы тока в контуре
б) фаза колебаний напряжения на конденсаторе
в) заряд конденсатора
г) энергия магнитного поля катушки
д) амплитуда колебаний напряжения на катушке
Алгоритм решения
- Определить, от чего зависит каждая из перечисленных величин.
- Установить, какие величины меняются, а какие нет.
Решение
В колебательном контуре происходят гармонические колебания. Поэтому период колебаний силы тока в контуре — величина постоянная.
Фаза — это величина, которая определяет положение колебательной системы в любой момент времени. Поскольку в системе происходят колебания, фаза меняется.
Заряд конденсатора — колебания происходят за счет постоянной перезарядки конденсатора. Следовательно, эта величина тоже меняется.
Энергия магнитного поля катушки — в колебательном контуре происходят взаимные превращения энергии магнитного поля катушки в энергию электрического поля конденсатора, и обратно. Поэтому энергия магнитного поля катушки постоянно меняется.
В условии задачи сказано, что колебания незатухающие. Это значит, что полная механическая энергия колебательной системы сохраняется. Поскольку именно от нее зависит амплитуда колебаний напряжения на катушке, то эта величина также остается постоянной.
Ответ: ад
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18656
Алгоритм решения
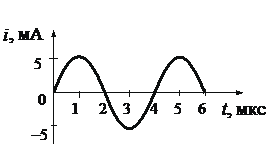
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2=4π√LC2π√LC=2
Отсюда:
T2=T12=4·10−62=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 9.9k
как найти напряжение на катушке и на конденсаторах??? Нужны формулы
юлия калиткина
Профи
(862),
закрыт
9 лет назад
Петро Хрiн
Гений
(95078)
11 лет назад
На катушке U = I * XL (B), где индуктивное сопротивление XL = 2 *Пи * f *L, где f – частота переменного тока, Гц; L – индуктивность катушки, Гн.
На конденсаторе U = I * Xс (B), где ёмкостное сопротивление Хс = 1 / 2 *2*Пи*f *C (C – ёмкость конденсатора, Ф.
Катушка индуктивности в цепях переменного тока – формулы и определение с примерами
Переменный электрический ток:
До сих пор рассматривались электрические цепи, содержащие в различных сочетаниях резисторы, конденсаторы и катушки, с источником постоянного тока либо без него. Теперь рассмотрим подключение таких цепей к источнику переменного тока.
Пусть источник тока создает переменное гармоническое напряжение (рис. 194)
Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону: 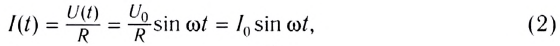
где 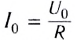
Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.
Величины 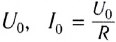
Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность 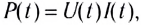
С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде
Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно.
Перепишем формулу для мощности по-другому: 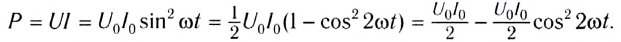
Первое слагаемое не зависит от времени. Второе слагаемое — переменная составляющая — функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (см. рис. 194).
Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле 
Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.
Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Поскольку для постоянного тока 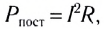

Аналогично можно ввести действующее значение и для напряжения
Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе (см. рис. 194).
Таким образом, резисторы оказывают сопротивление как постоянному, так и переменному току, при этом в обоих случаях в них происходит превращение электрической энергии во внутреннюю. Вследствие этого сопротивление резисторов R получило название активного или омического сопротивления.
Катушка индуктивности в цепях переменного тока
Реальный соленоид (катушка индуктивности) обладает активным сопротивлением R и индуктивностью L. В цепях постоянного тока главную роль играет его сопротивление R, тогда как в цепях переменного тока — его индуктивность L.
Рассмотрим физические процессы, происходящие в идеальной катушке, у которой отсутствует активное сопротивление (R=0), при включении ее в цепь переменного тока.
В катушке индуктивностью L переменный ток 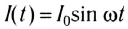
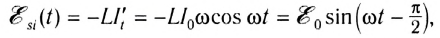
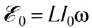
При возрастании силы тока ЭДС самоиндукции согласно правилу Ленца будет препятствовать его увеличению. Для идеальной катушки, активное сопротивление которой равно нулю (R=0), согласно закону Ома для полной цепи 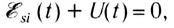
Следовательно, в любой момент времени внешнее напряжение на концах катушки равно по модулю и противоположно по знаку ЭДС самоиндукции в катушке:
Сравнивая выражения для мгновенных значений силы тока I(t) и напряжения U(t), видим, что для их амплитудных значений можно записать закон Ома в виде
Величину 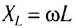
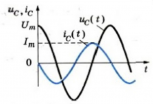
Обратите внимание на то, что фазы колебаний силы тока и напряжения не совпадают. Наличие сдвига фаз означает, что мгновенное значение напряжения U на катушке индуктивности опережает мгновенное значение силы I переменного тока по фазе на 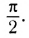
Закон Ома для цепи переменного тока, содержащей только катушку индуктивности, выполняется и для действующих значении силы тока 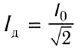
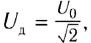
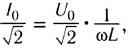
Таким образом, если в цепь переменного тока включена катушка индуктивности, то закон Ома выполняется для амплитудных и действующих значений силы тока и напряжения, но не выполняется для их мгновенных значений, так как мгновенные значения силы тока и напряжения не совпадают по фазе (см. рис. 195).
Мгновенная мощность, потребляемая катушкой индуктивности от источника переменного тока, определяется по формуле
Поскольку среднее за период значение функции 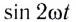
Как видно из рисунка 195, цепь с идеальной катушкой индуктивности в течение первой и третьей четвертей периода работает в режиме потребителя, запасая энергию магнитного поля 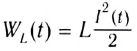
Поскольку потерь энергии в этом случае не происходит, то индуктивное сопротивление называют реактивным.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Конденсатор в цепях переменного тока
- Электрический ток в различных средах
- Электромагнитная индукция в физике
- Правило Ленца для электромагнитной индукции
- Потенциал электрического поля
- Постоянный электрический ток
- Законы постоянного тока
- Переменный электрический ток
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Катушка индуктивности. Описание, характеристики, формула расчета
Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.
Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:
где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
где ω является угловой частотой резонансной частоты F:
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:
где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей
Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Последовательное соединение индуктивностей
Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
Добротность катушки индуктивности
На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.
Добротность катушки индуктивности может быть найдена через следующую формулу:
где R является собственным сопротивлением обмотки.
Катушка индуктивности. Формула индуктивности
Базовая формула индуктивности катушки:
- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
- l = длина катушки в метрах (м)
Индуктивность прямого проводника:
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
Индуктивность катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
Индуктивность многослойной катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
Индуктивность плоской катушки:
- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
Конденсатор, катушка и резонанс в цепи переменного тока
теория по физике 🧲 колебания и волны
Опишем колебания, которые происходят в цепи переменного тока при включении в нее конденсатора и катушки индуктивности. А также рассмотрим условия, при выполнении которых в цепи переменного тока наступает резонанс. Получим формулы для вычисления амплитуд напряжений, введем понятия емкостного и индуктивного сопротивления и выясним, какую роль играют эти величины.
Конденсатор в цепи переменного тока
Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см. рисунок ниже).
Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться.
Найдем, как меняется сила тока в цепи, содержащей только конденсатор, если сопротивление проводов и обкладок конденсатора можно пренебречь (см. рис. выше). Напряжение на конденсаторе будет равно:
u = φ 1 − φ 2 = q C . .
Учтем, что напряжение на конденсаторе равно напряжению на концах цепи:
q C . . = U m a x cos . ω t
Следовательно, заряд конденсатора меняется по гармоническому закону:
q = C U m a x cos . ω t
Тогда сила тока, представляющая собой производную заряда по времени, будет равна:
i = q ´ = − C U m a x sin . ω t = C U m a x cos . ( ω t + π 2 . . )
Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на π 2 . . (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.
Амплитуда силы тока равна:
I m a x = U m a x C ω
Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что:
Величина X C , равная обратному произведению циклической частоты на электрическую емкость конденсатора, называется емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть.
Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура q m a x = 10 − 6 Кл. Амплитудное значение силы тока в контуре I m a x = 10 − 3 А. Определите период колебания (потерями на нагревание проводника пренебречь).
Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки:
q 2 m a x 2 C . . = L I 2 m a x 2 . .
L C = q 2 m a x I 2 m a x . .
√ L C = q m a x I m a x . .
T = 2 π √ L C = 2 π q m a x I m a x . . = 2 · 3 , 14 10 − 6 10 − 3 . . ≈ 6 , 3 · 10 − 3 ( с )
Катушка индуктивности в цепи переменного тока
Соберем две электрических цепи, состоящих из лампы накаливания, катушки индуктивности и источника питания: в первом случае постоянного, во втором — переменного (см. рисунки «а» и «б» ниже).
Опыт покажет, что в цепи постоянного тока лампа светится ярче по сравнению с той, что включена в цепь переменного тока. Это говорит о том, что сила тока в цепи постоянного тока выше действующего значения силы тока в цепи переменного тока.
Результат опыта легко объясняется явлением самоиндукции. При подключении катушки к постоянному источнику тока сила тока нарастает постепенно. Возрастающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь спустя какое-то время сила тока достигает наибольшего значения, соответствующему данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не успевает достигнуть максимального значения. Поэтому максимальное значение силы тока в цепи переменного тока с катушкой индуктивности ограничивается индуктивность. Чем больше индуктивность и чем больше частота приложенного напряжения, тем меньше амплитуда силы переменного тока.
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (см. рисунок ниже). Для этого найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна равняться нулю. Иначе, согласно закону Ома, сила тока была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля → E i , порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля → E к , создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства → E i = − → E к следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции e i ) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Учитывая, что удельная работа кулоновского поля равна напряжения на концах катушки, можно записать:
Напомним, что сила переменного тока изменяется по гармоническому закону:
i = I m a x sin . ω t
Тогда ЭДС самоиндукции равна:
e i = − L i ´ = − L ω I m a x cos . ω t
Так как u = − e i , то напряжение на концах катушки оказывается равным:
u = L ω I m a x cos . ω t = L ω I m a x sin . ( ω t + π 2 . . ) = U m a x ( ω t + π 2 . . )
Амплитуда напряжения равна:
U m a x = L ω I m a x
Следовательно, колебания напряжения на катушке опережают колебания силы тока на π 2 . . , или колебания силы тока отстают от колебаний напряжения на π 2 . . , что одно и то же.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (см. график ниже).
Но в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Амплитуда силы тока в катушке равна:
I m a x = U m a x L ω . .
Также будем использовать вместо амплитуд действующие значения силы тока и напряжения. Тогда получим:
Величина X L , равная произведению циклической частоты на индуктивность, называется индуктивным сопротивлением. Индуктивное сопротивление зависит от частоты. Поэтому в цепи постоянного тока, в котором отсутствует частота, индуктивное сопротивление катушки равно нулю.
Пример №2. Катушка с индуктивным сопротивлением X L = 500 Ом присоединена к источнику переменного напряжения, частота которого ν = 1000 Гц. Действующее значение напряжения U = 100 В. Определите амплитуду силы тока I m a x в цепи и индуктивность катушки L. Активным сопротивлением пренебречь.
Индуктивное сопротивление катушки выражается формулой:
X L = L ω = 2 π ν L
Так как амплитуда напряжения связана с его действующим значением соотношением U m a x = U √ 2 , то для амплитуды силы тока получаем:
Резонанс в электрической цепи
Механические и электромагнитные колебания имеют разную природу, но процессы, происходящие при этом, идентичны. Поэтому можно предположить, что резонанс в электрической цепи так же реален, как резонанс в колебательной системе, на которую действует периодическая сила.
Напомним, что в механической системе резонанс тем более заметен, чем меньше в колебательной системе трение между ее элементами. Роль трения в электрической цепи играет активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника, который при этом нагревается. Следовательно, резонанс в электрической цепи будет отчетливо наблюдаться при малом активном сопротивлении R.
Если активное сопротивление мало, то собственная частота колебаний в колебательном контуре определяется формулой:
Сила тока при вынужденных колебаниях должна достигать максимальных значений, когда частота переменного напряжения, приложенного к контуру равна собственной частоте колебательного контура:
Резонанс в электрическом колебательном контуре — явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
После включения внешнего переменного напряжения резонансное значение силы тока в цепи устанавливается не моментально, а постепенно. Амплитуда колебаний силы тока возрастает до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:
I 2 m a x R 2 . . = U m a x I m a x 2 . .
Упростив это уравнение, получим:
I m a x R = U m a x
Следовательно, амплитуда установившихся колебаний силы тока при резонансе определяется уравнением:
I m a x = U m a x R . .
При сопротивлении, стремящемся к нулю, сила тока возрастает до бесконечно больших значений. При большом сопротивлении сила тока возрастает незначительно. Это хорошо видно на графике ниже.
Пример №3. В цепь переменного тока с частотой ν = 500 Гц включена катушка индуктивностью L = 10 мГн. Какой емкости конденсатор надо включить в эту цепь, чтобы наступил резонанс?
Электрическая цепь, описываемая в условии, представляет собой колебательный контур. Резонанс в этой цепи наступит, когда частота переменного тока будет равна собственной частоте колебательного контура (ν = ν0).
ν 0 = 1 2 π √ L C . .
К колебательному контуру подсоединили источник тока, на клеммах которого напряжение гармонически меняется с частотой ν.
Индуктивность L катушки колебательного контура можно плавно менять от максимального значения Lmax до минимального Lmin, а ёмкость его конденсатора постоянна.
Ученик постепенно уменьшал индуктивность катушки от максимального значения до минимального и обнаружил, что амплитуда силы тока в контуре всё время возрастала. Опираясь на свои знания по электродинамике, объясните наблюдения ученика.
Алгоритм решения
Решение
В колебательном контуре источником тока возбуждаются вынужденные колебания. Частота этих колебаний равна частоте источника — ν. Амплитуда колебаний зависит от того, как соотносятся между собой внешняя частота и частота собственных электромагнитных колебаний, которая определяется формулой:
ν 0 = 1 2 π √ L C . .
По мере увеличения внешней частоты от нуля до ν0 амплитуда растет. Она достигает максимума тогда, когда происходит резонанс. При этом внешняя частота равна частоте собственных электромагнитных колебаний: ν = ν0. Затем амплитуда начинает убывать.
В данном случае, ученик меняет не внешнюю частоту, а частоту собственных электромагнитных колебаний. При плавном уменьшении индуктивности контура от максимального значения Lmax до минимального Lmin частота возрастает от ν0min до ν0max. Причем:
ν 0 m i n = 1 2 π √ L m i n C . .
ν 0 m a x = 1 2 π √ L m a x C . .
Из того факта, что амплитуда всё время увеличивалась, можем сделать вывод, что частота ν0 всё время приближалась к частоте источника тока, при этом ν > ν0max. В противном случае наблюдалось бы уменьшений амплитуды силы тока.
pазбирался: Алиса Никитина | обсудить разбор | оценить
В колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят свободные незатухающие электромагнитные колебания.
Из приведённого ниже списка выберите две величины, которые остаются постоянными при этих колебаниях.
а) период колебаний силы тока в контуре
б) фаза колебаний напряжения на конденсаторе
в) заряд конденсатора
г) энергия магнитного поля катушки
д) амплитуда колебаний напряжения на катушке
Алгоритм решения
- Определить, от чего зависит каждая из перечисленных величин.
- Установить, какие величины меняются, а какие нет.
Решение
В колебательном контуре происходят гармонические колебания. Поэтому период колебаний силы тока в контуре — величина постоянная.
Фаза — это величина, которая определяет положение колебательной системы в любой момент времени. Поскольку в системе происходят колебания, фаза меняется.
Заряд конденсатора — колебания происходят за счет постоянной перезарядки конденсатора. Следовательно, эта величина тоже меняется.
Энергия магнитного поля катушки — в колебательном контуре происходят взаимные превращения энергии магнитного поля катушки в энергию электрического поля конденсатора, и обратно. Поэтому энергия магнитного поля катушки постоянно меняется.
В условии задачи сказано, что колебания незатухающие. Это значит, что полная механическая энергия колебательной системы сохраняется. Поскольку именно от нее зависит амплитуда колебаний напряжения на катушке, то эта величина также остается постоянной.
pазбирался: Алиса Никитина | обсудить разбор | оценить

[spoiler title=”источники:”]
http://fornk.ru/1970-katushka-induktivnosti-opisanie-xarakteristiki-formula-rascheta/
[/spoiler]