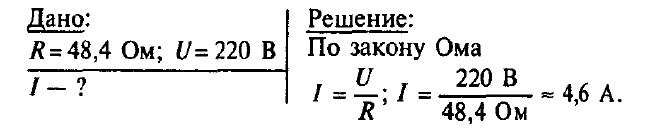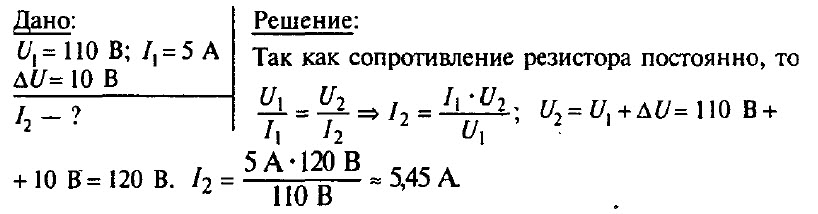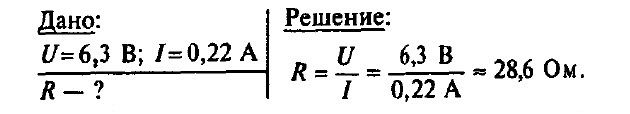Задачи на Закон Ома с решениями
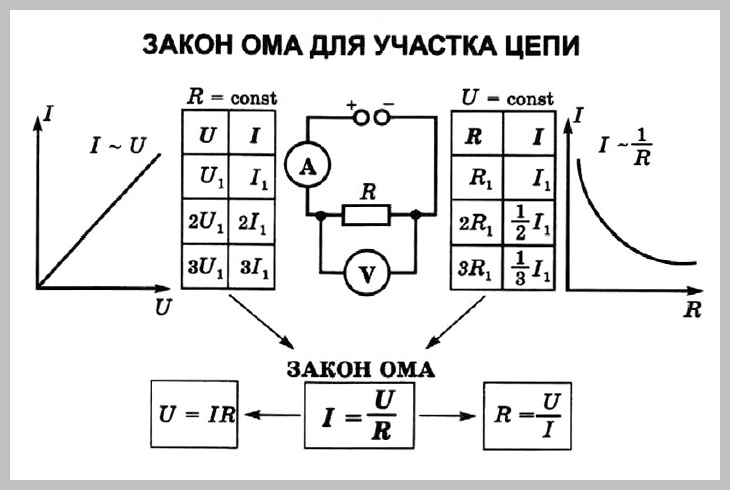
Формулы, используемые на уроках физики «Задачи на Закон Ома» в 8 классе, а также для подготовки к ОГЭ.
Название величины |
Обозначение |
Единица измерения |
Формула |
Сила тока |
I |
А |
I = U / R |
Напряжение |
U |
В |
U = IR |
Сопротивление |
R |
Ом |
R = U/I |
Решение задач на уроках физики в 10-11 классах и при подготовке к ЕГЭ смотрите в следующих конспектах:
ЕГЭ: Закон Ома для участка цепи
ЕГЭ: Закон Ома для всей цепи
Задачи на Закон Ома.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
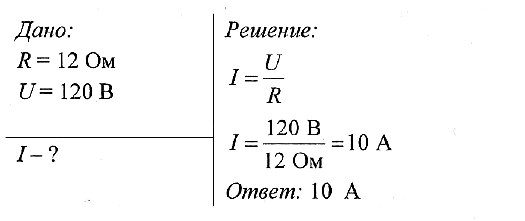
Задача № 1.
Какова сила тока в резисторе, если его сопротивление 12 Ом, а напряжение на нем 120 В?
Задача № 2.
Сопротивление проводника 6 Ом, а сила тока в нем 0,2 А. Определите напряжение на концах проводника.
Задача № 3.
Определите сопротивление проводника, если при напряжении 110 В сила тока в нем 2 А.
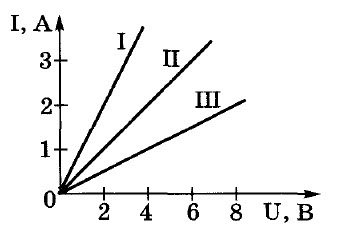
Задача № 4.
По графикам зависимости силы тока от напряжения определите сопротивление каждого проводника.
Решение:
Задача № 5.
Чему равна сила тока в электрической лампе карманного фонаря, если сопротивление нити накала 16,6 Ом и лампа подключена к батарейке напряжением 2,5 В?
Задача № 6.
Электрический утюг включен в сеть с напряжением 220 В. Какова сила тока в нагревательном элементе утюга, если сопротивление его равно 48,4 Ом?
Задача № 7.
При напряжении 110 В, подведенном к резистору, сила тока в нем равна 5 А. Какова будет сила тока в резисторе, если напряжение на нем увеличить на 10 В?
Задача № 8.
Чему равно сопротивление спирали электрической лампы в рабочем состоянии, у которой на цоколе написано 6,3 В, 0,22 А?
Задача № 9.
Показание вольтметра, присоединенного к горящей электрической лампе накаливания, равно 120 В, а амперметра, измеряющего силу тока в лампе, 0,5 А. Чему равно сопротивление лампы? Начертите схему включения лампы, вольтметра и амперметра.
Задача № 10.
ОГЭ
Источник постоянного тока с ЭДС E = 12 В и внутренним сопротивлением г = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить силу тока в цепи I, падение напряжения UR на внешнем участке и падение напряжения Ur на внутреннем участке цепи.
Краткая теория для решения Задачи на Закон Ома.
Это конспект по теме «ЗАДАЧИ на Закон Ома». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на сопротивление проводника
- Посмотреть конспект по теме Закон Ома. Соединение проводников
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Download Article
Download Article
Before you can calculate the voltage across a resistor, you’ll first have to determine what kind of circuit you are using. If you need a review of the basic terms or a little help understanding circuits, start with the first section. Otherwise, jump ahead to the type of circuit you have to solve.
-
1
Learn about current. Let’s think about current by using an analogy: imagine you pour a bag of corn kernels into a bowl. Each corn kernel is an electron, and the stream of kernels flowing into the bowl is the current.[1]
When talking about the flow, you describe it by saying how many kernels are flowing each second. When talking about a current, you measure it in amperes (amps), or a certain (very large) number of electrons flowing per second. -
2
Think about electrical charge. Electrons have a “negative” electrical charge. This means they attract (or flow toward) objects with a positive charge, and repel (or flow away from) objects with a negative charge. Since they’re all negative, electrons are always trying to push away from other electrons, spreading out wherever they can.
Advertisement
-
3
Understand voltage. Voltage measures the difference in electrical charge between two points. The greater the difference, the more energetically the two sides attract each other. Here’s an example with an everyday battery:
- Inside a battery, chemical reactions happen that produces a buildup of electrons. The electrons go to the negative end, while the positive end stays mostly empty. (These are called the negative and positive terminals.) The longer this goes on, the larger the voltage between the two ends.
- When you connect a wire between the negative and positive ends, the electrons at the negative end suddenly have somewhere to go. They shoot toward the positive end, creating a current. The larger the voltage, the more electrons move to the positive end each second.
-
4
Figure out resistance. Resistance is exactly what it sounds like. The more resistance something has, the harder it is for the electrons to push through. This slows the current, since fewer electrons can push through each second.
- A resistor is anything in the circuit that adds resistance. You can buy an actual “resistor” at an electronics store, but in a circuits problem it might represent a light bulb or anything else with resistance.
-
5
Memorize Ohm’s Law. There’s a very simple relationship between current, voltage, and resistance.[2]
Write this down or memorize it; you’ll use it often when solving circuit problems:- Current = voltage divided by resistance
- This is usually written: I = V / R
- Think about what happens when you increase V (voltage) or R (resistance). Does this match what you learned in the explanations above?
Advertisement
-
1
Understand a series circuit. A series circuit is easy to identify. It’s just one loop of wire, with everything arranged in a row. The current flows around the entire loop, going through each resistor or element in order.
- The current is always the same at any point along the circuit.[3]
- When calculating voltage, it doesn’t matter where the resistor is on the circuit. You can pick up the resistors and move them around, and you’ll still have the same voltage across each one.
- We’ll use an example circuit with three resistors in series: R1, R2, and R3. This is powered by a 12 volt battery. We’ll find the voltage across each one.
- The current is always the same at any point along the circuit.[3]
-
2
Calculate the total resistance. Add together all resistance values on the circuit. The answer is the total resistance of the series circuit.
- For example, the three resistors R1, R2, and R3 have resistances of 2 Ω (ohms), 3 Ω, and 5 Ω respectively. The total resistance is 2 + 3 + 5 = 10 ohms.
-
3
Find the current. Use Ohm’s Law to find the current of the entire circuit. Remember, the current is the same anywhere on a series circuit. Once we calculate the current this way, we can use it for all our calculations.
- Ohm’s Law says that the current I = V / R. The voltage across the whole circuit is 12 volts, and the total resistance is 10 ohms. The answer is I = 12 / 10 = 1.2 amperes.
-
4
Adjust Ohm’s Law to solve for voltage. With basic algebra, we can change Ohm’s Law to solve for voltage instead of current:[4]
- I = V / R
- IR = VR / R
- IR = V
- V = IR
-
5
Calculate the voltage across each resistor. We know the resistance, we know the current, and we have our equation. Plug in the numbers and solve. Here’s our example problem solved for all three resistors:
- Voltage across R1 = V1 = (1.2A)(2Ω) = 2.4 volts.
- Voltage across R2 = V2 = (1.2A)(3Ω) = 3.6 volts.
- Voltage across R3 = V3 = (1.2A)(5Ω) = 6.0 volts.
-
6
Check your answer. In a series circuit, the sum of all your answers must equal the total voltage.[5]
Add up every voltage you calculated and see if you get the voltage of the entire circuit. If you didn’t, go back and check for mistakes.- In our example, 2.4 + 3.6 + 6.0 = 12 volts, the voltage across the whole circuit.
- If your answer is slightly off (for instance, 11.97 instead of 12), you probably rounded a number at some point. Your answer is still correct.
- Remember, voltage measures the differences in charge, or numbers of electrons. Imagine counting the number of new electrons you see as you travel along the circuit. If you count them correctly, you’re going to end up with the total change in electrons from the beginning to the end.
Advertisement
-
1
Understand parallel circuits. Imagine a wire leaving one end of a battery, then splitting into two separate wires. These two wires run parallel to each other, then join up again before they reach the other end of the battery. If there’s a resistor on the left wire and a resistor on the right wire, those two resistors are connected “in parallel.”[6]
- You can have any number of wires in a parallel circuit. These instructions will still work for a circuit that splits into one hundred wires and comes back together.
-
2
Think about how the current flows. In a parallel circuit, the current flows across each path available to it. Current will flow through the wire on the left, cross the left resistor, and reach the other end. At the same time, current will flow through the wire on the right, cross the right resistor, and reach the end. No part of the current doubles back or flows through two parallel resistors.
-
3
Use the total voltage to find the voltage across each resistor. If you know the voltage across the whole circuit, the answer is surprisingly easy. Each parallel wire has the same voltage as the entire circuit.[7]
Let’s say a circuit with two parallel resistors is powered by a 6 volt battery. The voltage across the left resistor is 6 volts, and the voltage across the right resistor is 6 volts. It doesn’t even matter how much resistance there is. To understand why, think back to the series circuits described above:- Remember that adding voltage drops in a series circuit always results in the total voltage across the circuit.
- Think of each path the current takes as a series circuit. The same holds true for this: if you count up all the voltage drops, you’ll end up with the total voltage.
- Since the current through each of the two wires only passes through one resistor, the voltage across that resistor must equal the total voltage.
-
4
Calculate the total current of the circuit. If the problem doesn’t tell you what the total voltage of the circuit is, you’ll need to complete a few more steps. Start by finding the total current passing through the circuit. In a parallel circuit, the total current is equal to the sum of the current running through each parallel path.[9]
- In mathematical terms: Itotal = I1 + I2 + I3…
- If you’re having trouble understanding this, imagine a water pipe split into two paths. The total amount of water flow is just the amount of water flow in each pipe, added together.
-
5
Compute the total resistance of the circuit. Resistors are not as effective in a parallel circuit, because they only block the current going along one wire. In fact, the more wires there are, the easier it is for the current to find a way through. To find the total resistance, solve for Rtotal in this equation:[9]
- 1 / Rtotal = 1 / R1 + 1 / R2 + 1 / R3 …
- For example, a circuit has a 2 ohm and a 4 ohm resistor in parallel. 1 / Rtotal = 1/2 + 1/4 = 3/4 → 1 = (3/4)Rtotal → Rtotal = 1/(3/4) = 4/3 = ~1.33 ohms.
-
6
Find the voltage from your answers. Remember, once we find the total voltage of the circuit, we have found the voltage across any one of the parallel wires. Solve for the whole circuit using Ohm’s law.[10]
Here’s an example:- A circuit has 5 amperes of current running through it. The total resistance is 1.33 ohms.
- According to Ohm’s Law, I = V / R, therefore V = IR
- V = (5A)(1.33Ω) = 6.65 volts.
Advertisement
Add New Question
-
Question
What is the percentage of applied voltage that will be dropped across r3=70 if r1=80 and r2=50?
It would be 35%. The higher the resistance, the higher the voltage drop. The ratio of resistances here is 80:50:70. Solving for 70 ohms, we get 35%.
-
Question
What is the voltage of a 60 ohm resistor if the circuit voltage is 150 volts with two parallel 30 ohm resistors and one 60 ohm resister in the series?
Assuming you intend to ask what is the voltage drop across the 60 ohm resistor, the answer is 120v. The two parallel 30 ohm resistors have an equivalent resistance of 15 ohms. 1/(1/30 + 1/30) = 15. The total resistance appears as 75 ohms to the 150v source. Find the circuit current by I = E/R or I = 150/75 = 2 amps. Find the voltage drop for the 60 ohm resistor with E = I x R or E = 2 x 60 = 120V drop across the 60 Ohm resistor.
-
Question
What becomes the Voltage if we use 2 resistors of 4W in parallel?
As any other data is not provided, the voltage across two resistors of 4w in parallel is the same.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If you have a complicated circuit that involves resistors in series and resistors in parallel, pick two nearby resistors. Find the total resistance across them using the rules for resistors in parallel or in series, as appropriate. Now you can treat them as a single resistor. Keep doing this until you have a simple circuit with resistors either in parallel or in series.[11]
-
The voltage across a resistor is often called a “voltage drop.”
-
Understand the terminology:
- Circuit – composed of elements (e.g. resistors, capacitors, and inductors) connected by wires and wherein current can pass through
- Resistors – elements that can reduce or resist current
- Current – flow of charge into wires; unit: Ampere, A
- Voltage – work done per unit charge; unit: Voltage, V
- Resistance – measurement of the opposition of an element to electric current; unit: Ohm, Ω
Advertisement
References
About This Article
Article SummaryX
To calculate voltage across a resistor in a series circuit, start by adding together all of the resistance values in the circuit. Then, divide the voltage across the circuit by the total resistance to find the current. Once you have the current, calculate voltage for the individual resistors by multiplying the current by the resistance. For example, in a series circuit with 3 resistors of 2, 3 and 5 Ohms, and a voltage of 12 volts, the current would be 12 divided by 10, or 1.2 amperes. For the 2 Ohm resistor, the voltage would be 1.2 times 2, or 2.4 volts. If you want to learn how to calculate voltage in a parallel circuit, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 913,934 times.
Reader Success Stories
-
Mohd Rodzi Mohamad
Aug 26, 2016
“This article is very neatly and clearly explained with illustrations of pictures for better comprehension. Very…” more
Did this article help you?
Загрузить PDF
Загрузить PDF
Если вам необходимо найти напряжение на сопротивлении (резисторе), первым делом необходимо определить тип электрической цепи. Для лучшего понимания основных терминов, используемых в физике и электротехнике, начните с первого раздела. Если же вы знакомы с терминологией, пропустите его и перейдите к описанию типа электрической цепи.
-
1
Рассмотрим понятие электрического тока. Воспользуемся аналогией: представьте, что вы поместили несколько зерен кукурузы в воду, текущую по трубе. Поток эквивалентен электрическому току, а зерна служат аналогией электронов.[1]
Говоря о потоке, мы описываем его количеством зерен, пересекших поперечное сечение трубы за одну секунду. При рассмотрении электрического тока мы измеряем его в амперах, соответствующих определенному (очень большому) количеству электронов, пересекающих сечение провода за одну секунду. -
2
Рассмотрим понятие электрического заряда. Каждый электрон имеет “отрицательный” электрический заряд. Это означает, что электроны притягиваются, или движутся по направлению к положительному заряду и отталкиваются, или движутся от отрицательного заряда. Каждый электрон обладает отрицательным зарядом, поэтому они отталкиваются друг от друга, стремясь разойтись в стороны.
-
3
Ознакомьтесь с понятием напряжения. Напряжение между двумя точками соответствует разности электрических зарядов, размещенных в этих точках. Чем больше эта разница, тем сильнее данные точки притягиваются друг к другу. Рассмотрим понятие напряжения на примере обычной электрической батарейки:
- Внутри батарейки происходят химические реакции, в результате которых образуются свободные электроны. Эти электроны движутся к отрицательному полюсу батарейки, удаляясь от ее положительного полюса (эти полюса соответствуют отрицательной и положительной клеммам батарейки). Чем дольше длится данный процесс, тем большее напряжение возникает между полюсами.
- Если вы соедините проволокой отрицательный и положительный полюса, у скопившихся электронов появится возможность покинуть отрицательный полюс. Они начнут перетекать к положительному полюсу, создавая электрический ток. Чем выше напряжение, тем больше электронов переместится к положительному полюсу за единицу времени.
-
4
Рассмотрим понятие электрического сопротивления. Его название точно отображает смысл. Чем выше сопротивление какого-либо объекта, тем тяжелее электронам пройти через него. В результате уменьшается ток, поскольку за единицу времени через проводник проходит меньшее число электронов.
- Сопротивлением, или резистором называется что-либо, увеличивающее сопротивление электрической цепи. “Резистор” можно приобрести в магазине электротоваров, но в цепи его роль может выполнять и любой другой объект, обладающий сопротивлением, например, лампа накаливания.
-
5
Запомните закон Ома. Он представляет собой простое соотношение между током, напряжением и сопротивлением. Запишите или запомните это соотношение — оно пригодится вам при расчете электрических цепей:
- Ток равен напряжению, поделенному на сопротивление
- Это записывается следующим образом: I = V / R
- Подумайте о том, что происходит, если вы увеличиваете V (напряжение) или R (сопротивление). Соответствует ли это приведенным выше объяснениям?
Реклама
-
1
Ознакомьтесь с понятием последовательного соединения. Такое соединение легко определить — оно представляет собой набор расположенных в ряд сопротивлений. Ток течет по этим сопротивлениям, последовательно проходя через каждое из них.
- Величина тока одинакова в любой точке цепи.[2]
- При расчете напряжения неважно, где именно в цепи расположен тот или иной резистор. Можно поменять их местами, напряжение на каждом из них останется неизменным.
- В качестве примера рассмотрим цепь, состоящую из трех последовательно соединенных сопротивлений: R1, R2 и R3. Пусть цепь питается от 12-вольтовой батарейки. Найдем напряжение на каждом сопротивлении.
- Величина тока одинакова в любой точке цепи.[2]
-
2
Сначала рассчитаем общее сопротивление. Сложим все сопротивления, включенные в цепь. В результате получим общее сопротивление резисторов, соединенных последовательно.
- Пусть три резистора R1, R2 и R3 имеют сопротивления 2 Ома, 3 Ома и 5 Ом соответственно. Тогда общее сопротивление составит 2 + 3 + 5 = 10 Ом.
-
3
Найдем ток. Используем закон Ома для всей цепи. Как мы помним, при последовательном соединении ток одинаков в любой точке цепи. Поэтому достаточно один раз определить ток и использовать найденную величину во всех последующих расчетах.
- Согласно закону Ома, I = V / R. Напряжение в цепи составляет 12 вольт, а общее сопротивление – 10 Ом. Отсюда находим I = 12 / 10 = 1,2 ампера.
-
4
Применим закон Ома, чтобы найти напряжение на резисторах. При помощи простых преобразований можно выразить напряжение через ток и сопротивление, переписав закон Ома следующим образом:
- I = V / R
- IR = VR / R
- IR = V
- V = IR
-
5
Рассчитаем напряжение на каждом резисторе. Нам известны их сопротивления, протекающий через них ток, и в нашем распоряжении есть равенство, связывающее ток и сопротивление с напряжением. Подставляя в это равенство численные значения, находим ответ. Для нашего примера это выглядит следующим образом:
- Напряжение на резисторе R1 = V1 = (1,2A)(2Ома) = 2,4 вольта.
- Напряжение на резисторе R2 = V2 = (1,2A)(3Ома) = 3,6 вольта.
- Напряжение на резисторе R3 = V3 = (1,2A)(5Ом) = 6,0 вольт.
-
6
Проверим полученный ответ. При последовательном соединении сумма напряжений на каждом сопротивлении должна равняться общему напряжению в цепи.[3]
Сложите найденные напряжения, проверив, равна ли их сумма полному напряжению. Если нет, проверьте решение и найдите ошибку.- В нашем примере 2,4 + 3,6 + 6,0 = 12 вольт, что соответствует общему напряжению в цепи.
- Если ответ немного не совпадает с точным значением (например, 11,97 вместо 12), это, вероятно, вызвано тем, что вы на каком-то этапе округлили полученные величины. В этом случае ответ верен.
- Помните о том, что напряжение соответствует разности зарядов или количества электронов. Представьте себе, что вы подсчитываете число электронов, продвигаясь вдоль цепи. Если вы правильно сосчитаете их, то в результате получите разность зарядов между начальной и конечной точками цепи.
Реклама
-
1
Ознакомьтесь с понятием параллельного соединения. Представьте себе, что вы подсоединили провод к одному полюсу батарейки и расщепили его вдоль на две половины. Эти две части провода идут параллельно друг другу и затем вновь соединяются в один провод перед вторым полюсом батарейки. Если разместить на обеих ветках провода по резистору, они будут соединены «параллельно».[4]
- Параллельно можно соединить любое количество сопротивлений. Данное описание годится и для цепи, состоящей из сотни параллельных проводов.
-
2
Рассмотрим, как течет ток. При параллельном соединении он проходит через все ветки цепи. Ток будет течь через левый провод, пересекая расположенный на нем резистор; одновременно ток будет проходить и через правый провод с резистором. Пройдя через обе ветки, ток достигнет положительного полюса; ни на каком участке цепи ток не будет течь в обратном направлении.
-
3
Зная общее напряжение, найдем напряжение на каждом резисторе. Сделать это очень просто, если известно общее напряжение в цепи. При параллельном соединении напряжение на каждой ветке будет равно общему напряжению в цепи.[5]
Предположим, что наша цепь состоит из двух параллельно соединенных сопротивлений и питается 6-вольтовой батарейкой. В этом случае напряжение и на левом, и на правом сопротивлении составит 6 вольт. При этом каждая ветка может содержать любое число резисторов. Чтобы понять это, вернемся к последовательному соединению, рассмотренному выше:- Как мы помним, при последовательном соединении общее напряжение представляет собой сумму напряжений на каждом сопротивлении.
- Будем считать, что каждая ветка цепи представляет собой набор резисторов, соединенных последовательно. Таким образом, вычислив сумму напряжений на всех сопротивлениях одной из веток, мы найдем общее напряжение.
- Поскольку в нашем случае ток, текущий по каждой ветке, проходит через один резистор, напряжение на этом резисторе и будет общим напряжением в цепи.
-
4
Найдем общий ток в цепи. Если в условии задачи не указано общее напряжение, понадобятся некоторые дополнительные вычисления. Начнем с нахождения общего тока, протекающего по цепи. При параллельном соединении общий ток равен сумме токов, проходящих через каждую ветку цепи.[6]
- В математической записи это означает: Iобщий = I1 + I2 + I3…
- Для лучшего понимания представьте себе водопроводную трубу, разделенную на два рукава. Общее количество воды равно сумме воды, протекающей по каждому рукаву.
-
5
Найдем общее сопротивление цепи. При параллельном соединении резисторы не так сильно снижают ток через цепь, поскольку каждый из них вносит вклад в сопротивление лишь своей ветки цепи. Фактически чем больше ответвлений цепи, тем легче току пройти через нее. Чтобы найти общее сопротивление, необходимо решить относительно Rобщее следующее уравнение:
- 1 / Rобщее = 1 / R1 + 1 / R2 + 1 / R3 …
- Предположим, что цепь состоит из двух резисторов сопротивлением 2 Ома и 4 Ома, соединенных параллельно. Тогда 1 / Rобщее = 1/2 + 1/4 = 3/4 → 1 = (3/4)Rобщее → Rобщее = 1/(3/4) = 4/3 = ~1,33 Ома.
-
6
Вычислим напряжение. Как мы помним, общее напряжение в цепи равно напряжению на одной из ее веток. Воспользуемся законом Ома. Рассмотрим конкретный случай:
- Через цепь течет ток силой 5 ампер. Общее сопротивление цепи равно 1,33 Ома.
- Согласно закону Ома, I = V / R, откуда V = IR
- V = (5A)(1,33Ом) = 6,65 вольт.
Реклама
Советы
- Если вы имеете дело со сложной цепью, состоящей из последовательно и параллельно соединенных сопротивлений, рассмотрите сначала два соседних резистора. Найдите их общее сопротивление, пользуясь правилами для последовательного или параллельного соединения, в соответствии с тем, как соединены данные резисторы. После этого можно рассматривать два данных резистора как одно сопротивление. Продолжайте таким образом объединять резисторы до тех пор, пока у вас не получится простая цепь, состоящая из параллельно либо последовательно соединенных сопротивлений.[7]
- Напряжение на сопротивлении часто называют «падением напряжения».
- Усвойте терминологию:
- Цепь — набор элементов (например, резисторов, конденсаторов и катушек), соединенных проводами так, что через них может проходить электрический ток.
- Резисторы — элементы, оказывающие сопротивление протекающему через них току и понижающие его силу
- Ток — поток электрического заряда через проволоку и элементы цепи, измеряется в амперах (А)
- Напряжение — работа, затрачиваемая на перемещение единичного заряда, измеряется в вольтах (В)
- Сопротивление — мера сопротивления прохождению электрического тока, измеряется в омах (Ом)
Реклама
Об этой статье
Эту страницу просматривали 167 087 раз.
Была ли эта статья полезной?
Последовательное соединение проводников .
( I_{общ}=I_1=I_2=I_3 )
( U_{общ}=U_1+U_2+U_3 )
( R_{общ}=R_1+R_2+R_3 )
Пройти тест на эту тему
Задача 1. (Последовательное соединение проводников)
Сопротивления (R_1=2 Ом ) и (R_2=3 Ом ) соединены последовательно.
Найти сопротивление цепи.
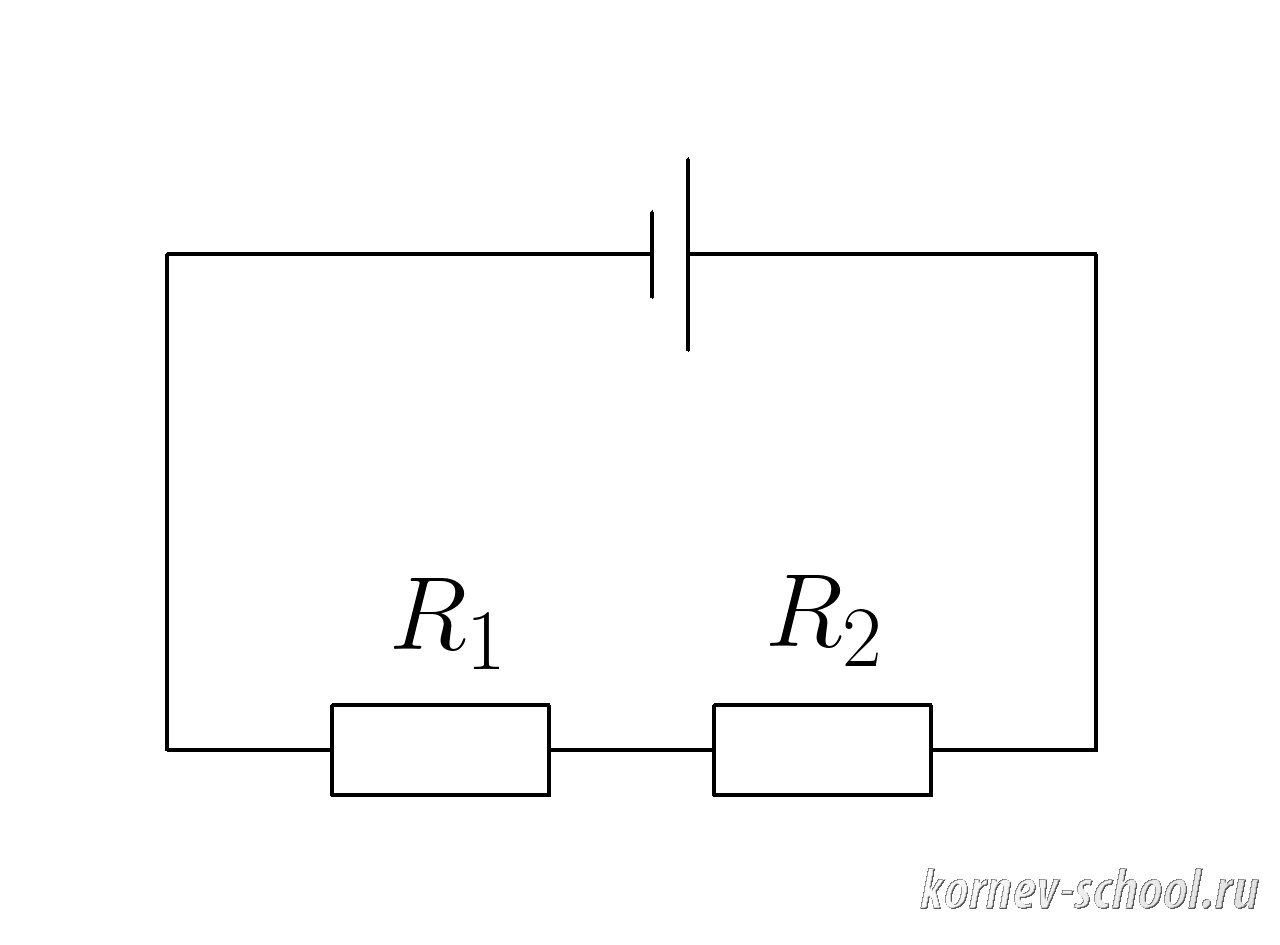
Показать ответ
Показать решение
Видеорешение
Задача 2. (Последовательное соединение проводников)
Напряжение на контактах батарейки (U_{общ}=15 В ; ), (R_1=2 Ом ), (R_2=3 Ом ).
Вычислить силу тока цепи.

Показать ответ
Показать решение
Видеорешение
Задача 3. (Последовательное соединение проводников)
Напряжение на контактах батарейки (U_{общ}=15 В ; ), (R_1=2 Ом ), (R_2=3 Ом ).
Вычислить напряжение на каждом из сопротивлений.

Показать ответ
Показать решение
Видеорешение
Задача 4. (Последовательное соединение проводников)
Напряжение на контактах батарейки (U_{общ}=12 В ; ), (R_1=1 Ом ), (R_2=2 Ом ,;;;R_3=3 Ом ).
Вычислить напряжение на каждом из сопротивлений.
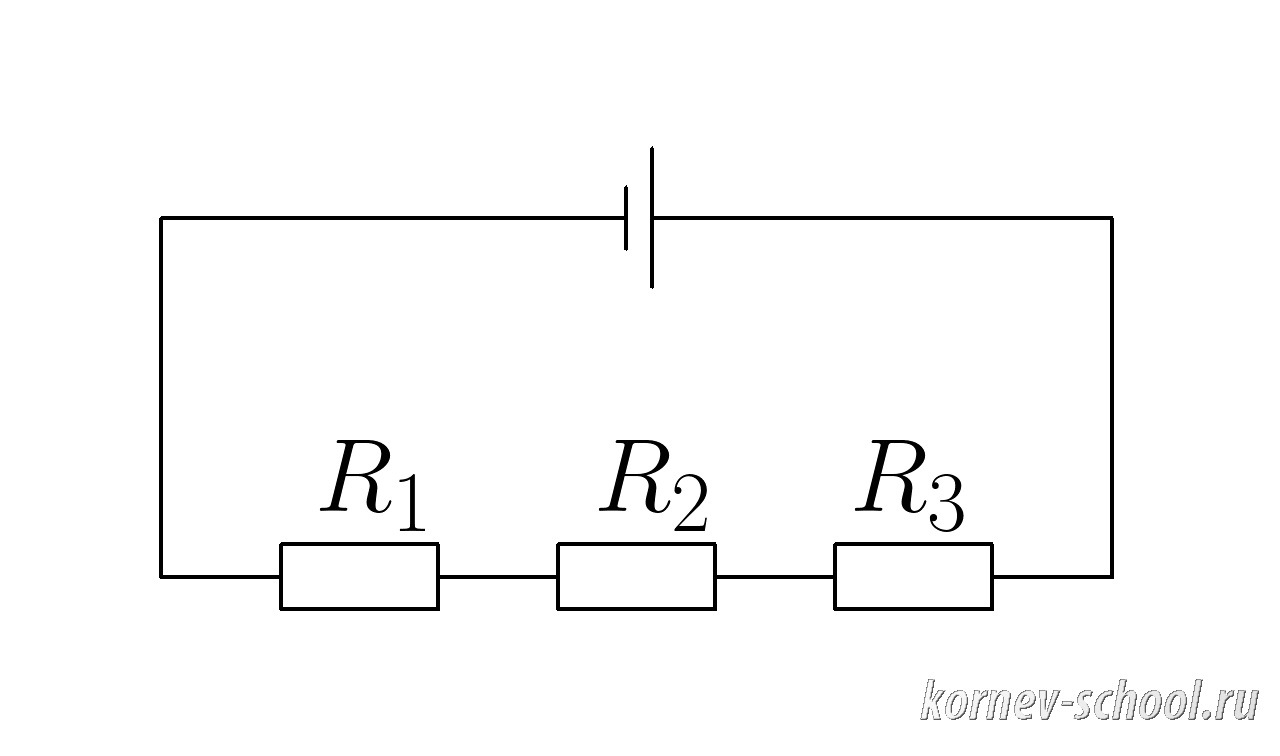
Показать ответ
Показать решение
Видеорешение
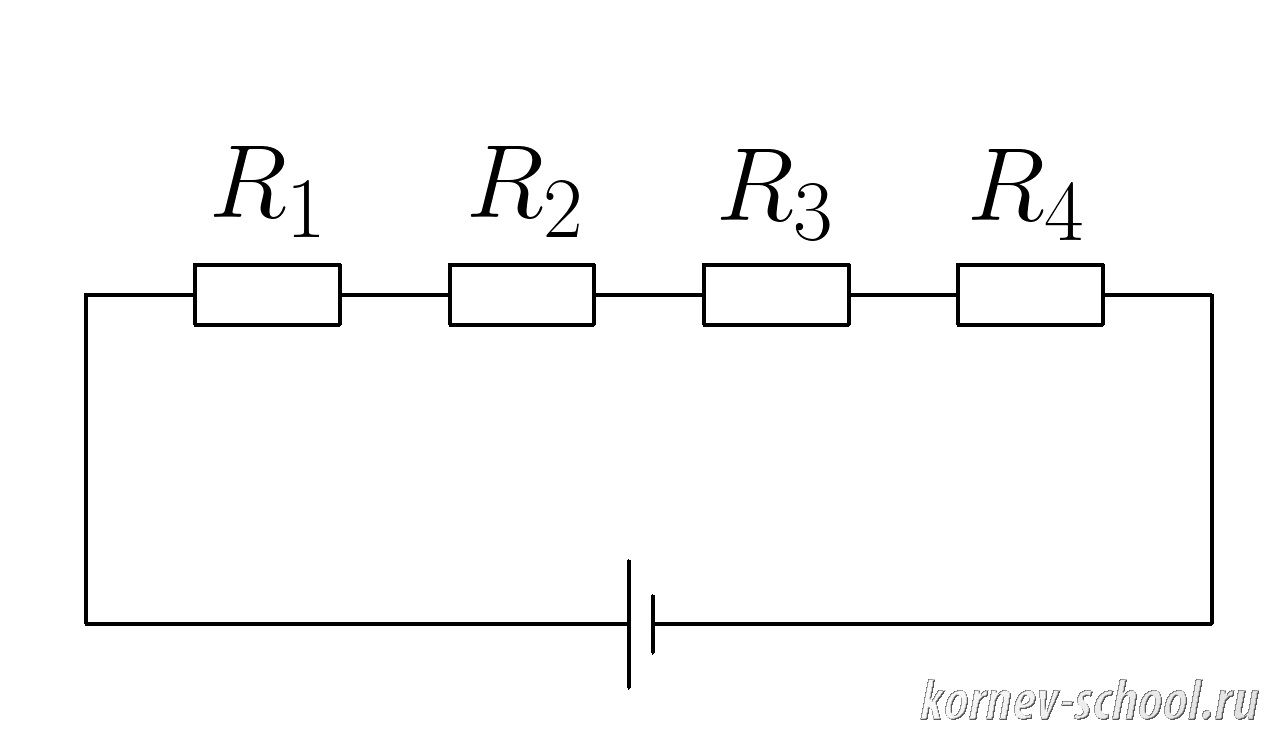
Задача 5. (Последовательное соединение проводников)
Напряжение на контактах батарейки (U_{общ}=12 В ; ), (R_1=0,5 Ом ), (R_2=1,5 Ом ,;;;R_3=1 Ом,;;;R_4=2 Ом ).
Вычислить напряжение на резисторе (R_1 ) .
Показать ответ
Показать решение
Видеорешение
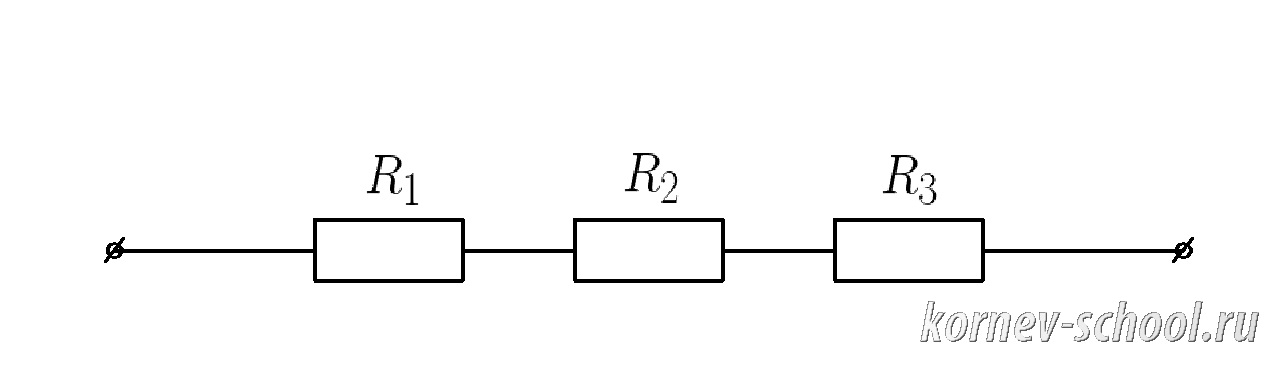
Задача 6. (Последовательное соединение проводников)
Напряжение цепи (U_{цепи}=120 В ; ), (R_1=2,5 Ом ), (R_2=1,5 Ом ,;;;R_3=1 Ом ).
Вычислить напряжение на резисторе (R_2 ) .
Показать ответ
Показать решение
Видеорешение
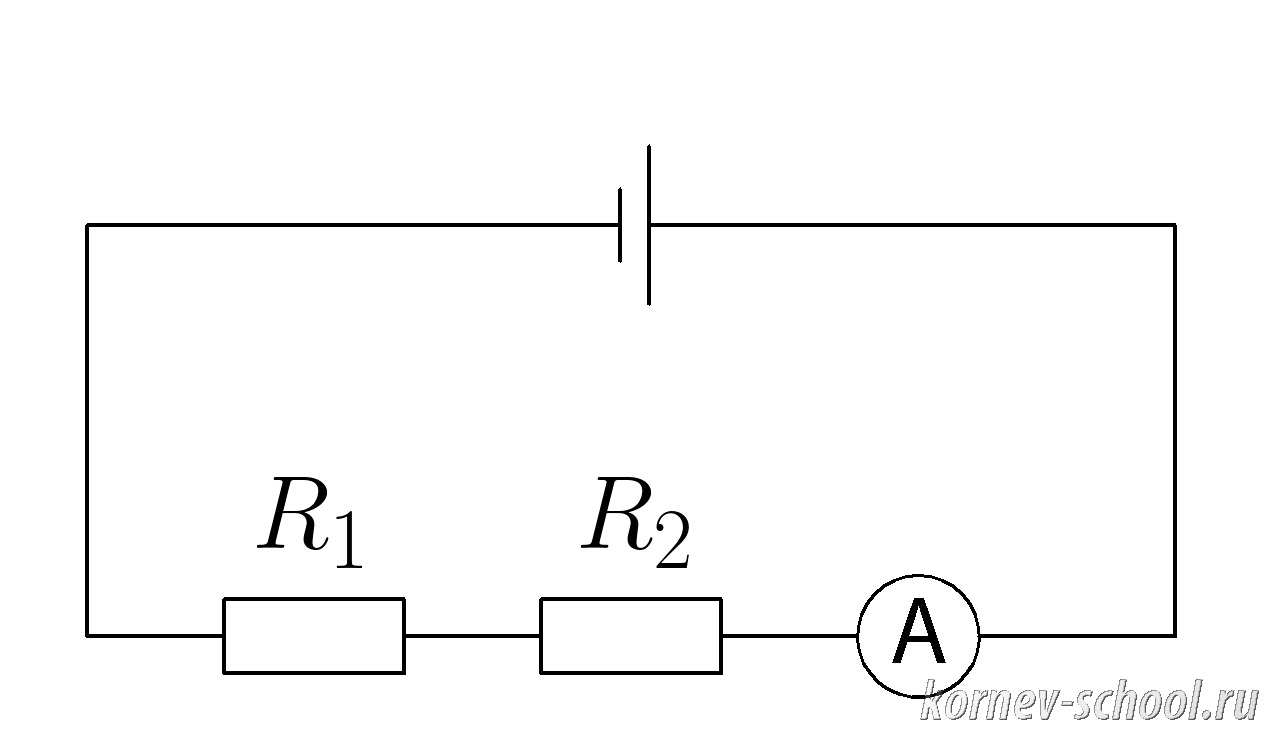
Задача 7. (Последовательное соединение проводников)
Амперметр А показывает силу тока (I_{общ}=4 А ; ), (R_1=1,5 Ом ), (R_2=2,5 Ом ).
Вычислить напряжение на каждом из сопротивлений и напряжение цепи (общее)
Показать ответ
Показать решение
Видеорешение
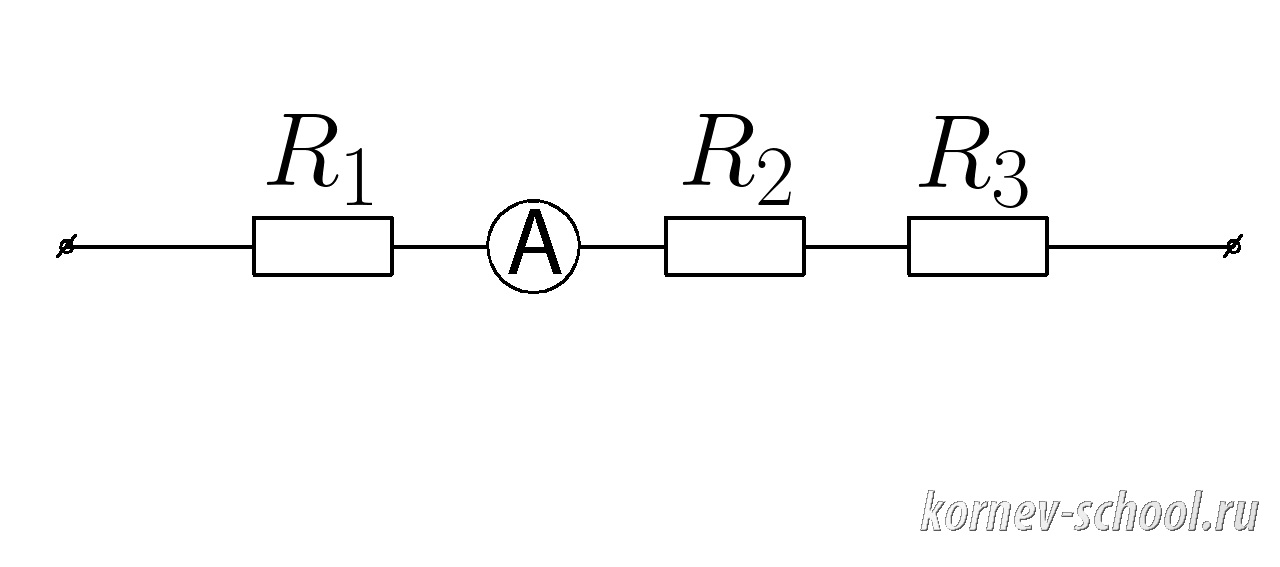
Задача 8. (Последовательное соединение проводников)
Амперметр А показывает силу тока (I_{общ}=0,7 А ; ), (R_1=1,5 Ом, ;R_2=2,5 Ом , ;R_3=3 Ом ).
Вычислить напряжение цепи (общее)
Показать ответ
Показать решение
Видеорешение
Задача 9. (Последовательное соединение проводников)
Амперметр показывает силу тока (I_{общ}=1,7 А ; ), (R_1=1 Ом, ;R_2=2,5 Ом , ;R_3=31 Ом ).
Вычислить напряжение на резисторе ( R_2 )
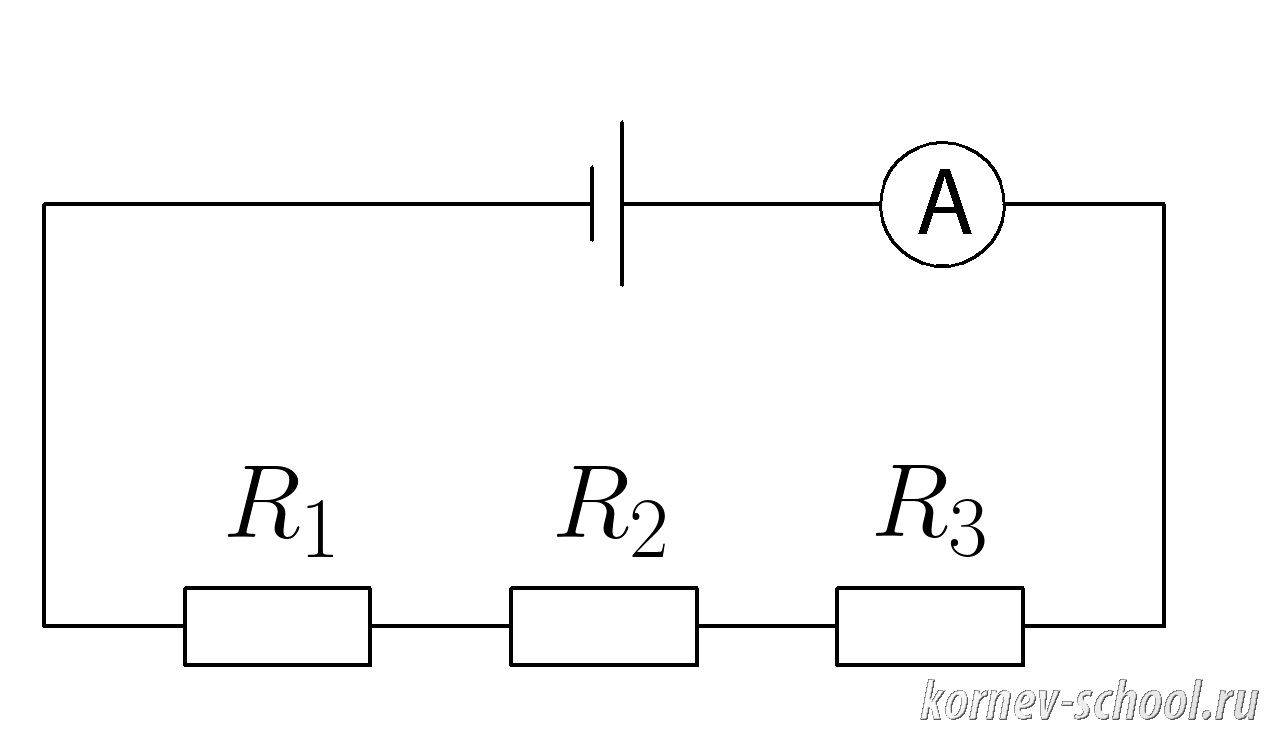
Показать ответ
Показать решение
Видеорешение
Задача 10. (Последовательное соединение проводников)
Амперметр показывает силу тока (I_{общ}=1,7 А ; ), (R_1=1 Ом, ;R_2=2,5 Ом , ;R_3=31 Ом ).
Какое напряжение показывает вольтметр ( V ; ) ?
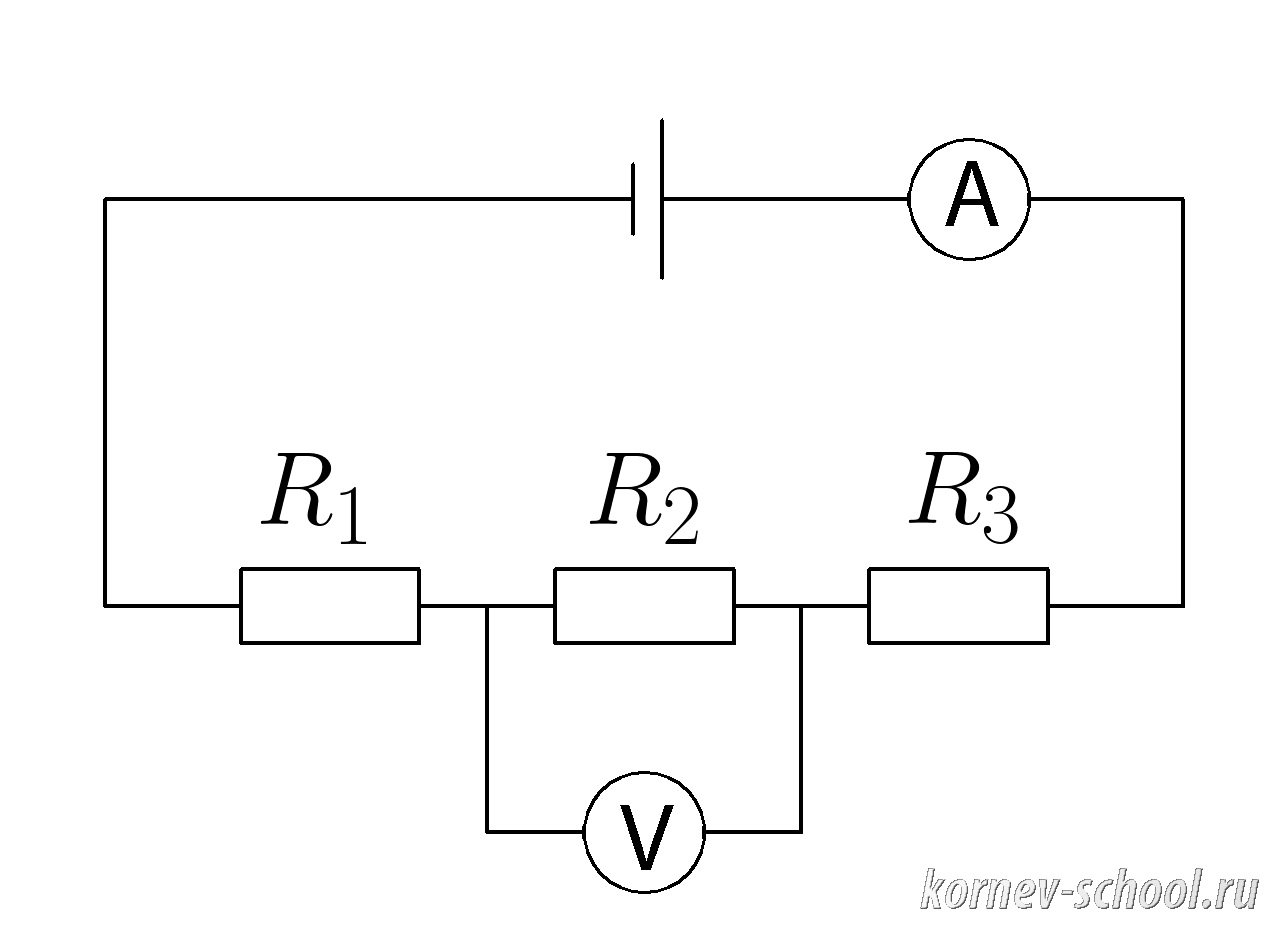
Показать ответ
Показать решение
Видеорешение
Задача 11. (Последовательное соединение проводников)
Амперметр показывает силу тока (I_{общ}=1,7 А ; ), (R_1=1 Ом, ;R_2=2,5 Ом , ;R_3=31 Ом ).
Какое напряжение показывает вольтметр ( V ; ) ?
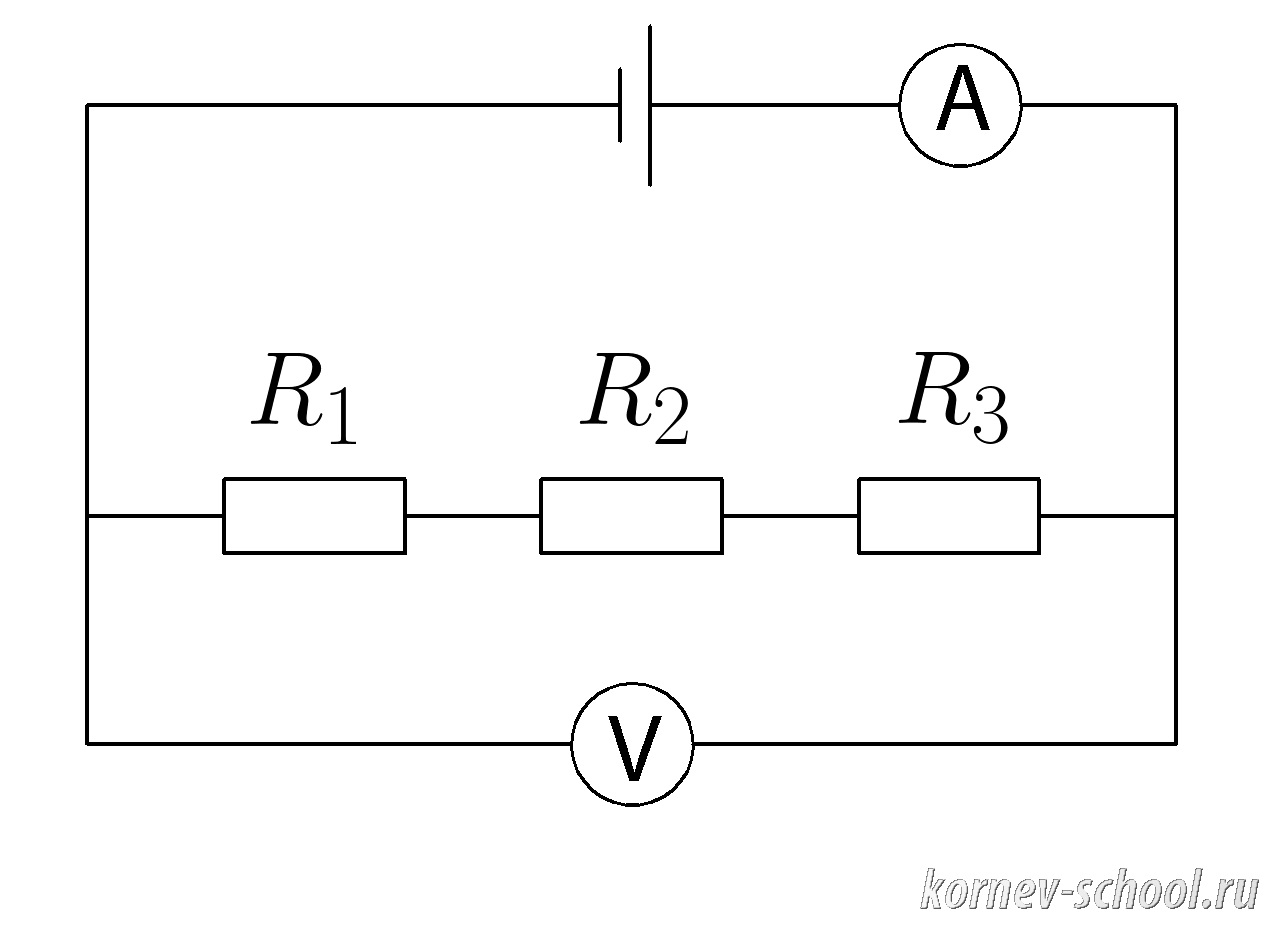
Показать ответ
Показать решение
Видеорешение
Задача 12. (Последовательное соединение проводников)
Амперметр показывает силу тока (I_{общ}=3 А ; ), (R_1=1 Ом, ;R_2=2 Ом , ;R_3=3 Ом ).
Какое напряжение показывает вольтметр ( V ; ) ?
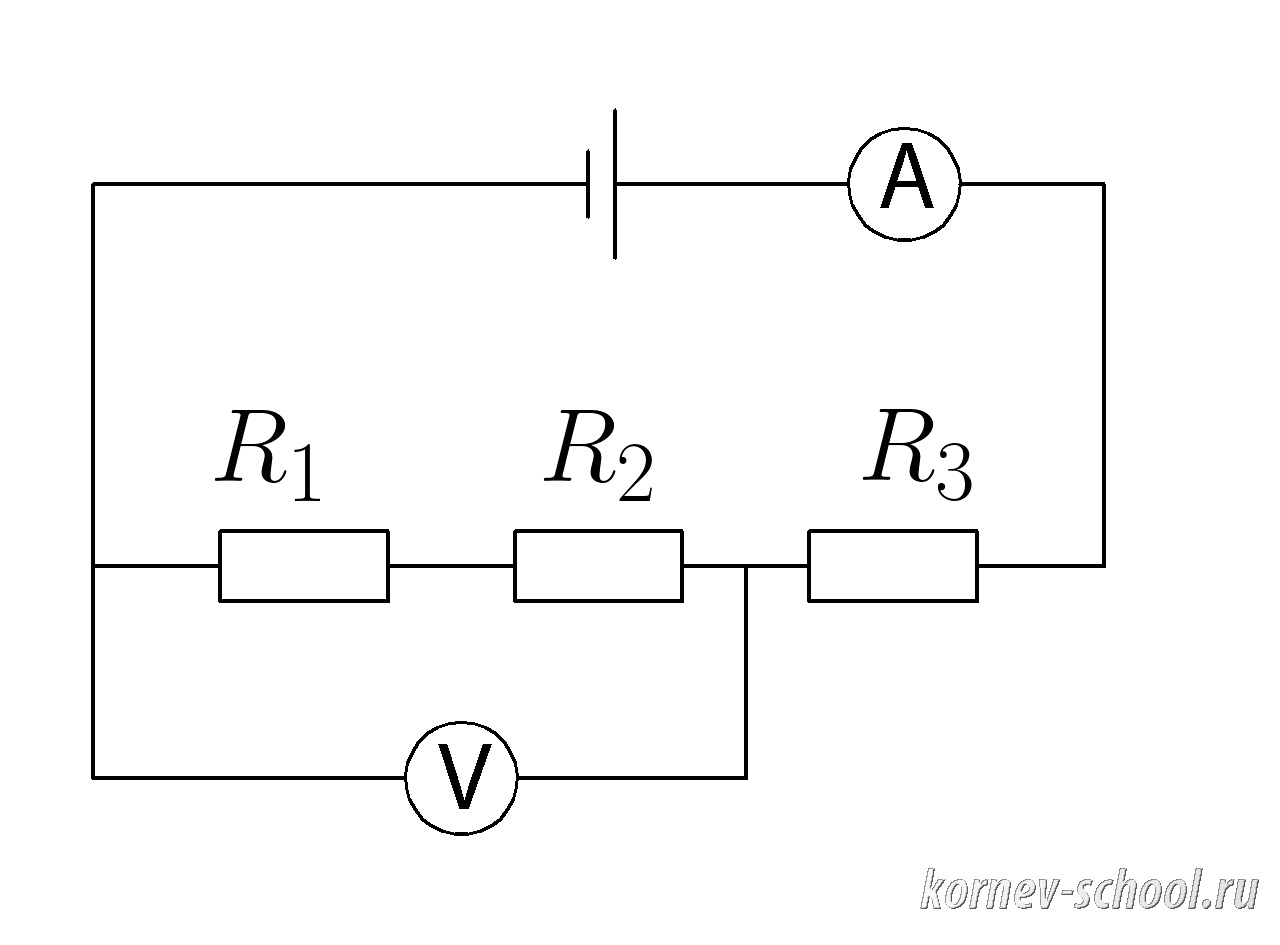
Показать ответ
Показать решение
Видеорешение
Задача 13. (Последовательное соединение резисторов)
Сила тока цепи, изображенной на рисунке (I_{общ}=0,3 А ; ), а
ее напряжение (U_{общ}=9 В . )
Сопротивления резисторов
(R_1=12 Ом, ;R_2=2 Ом . )
Найти сопротивление третьего резистора.

Показать ответ
Показать решение
Видеорешение
1. Контрольный 4,4А
Напряжение на контактах батарейки (U_{общ}=22 В ; ), (R_1=2 Ом ), (R_2=3 Ом ).
Найти силу тока цепи.
2. Контрольный 8,8В
Напряжение на контактах батарейки (U_{общ}=22 В ; ), (R_1=2 Ом ), (R_2=3 Ом ).
Найти напряжение на первом резисторе.
3. Контрольный 18В
Напряжение на контактах батарейки (U_{общ}=42 В ; ), (R_1=2 Ом ), (R_2=3 Ом ), (R_3=2 Ом )
Найти напряжение на резисторе (R_2).
4. Контрольный 33В
Напряжение на контактах батарейки (U_{общ}=66 В ; ), (R_1=1 Ом ), (R_2=1 Ом ;; R_3=1 Ом;;
R_4=3 Ом. )
Найти напряжение на резисторе (R_4).
5. Контрольный 1,6В
Амперметр А показывает силу тока (I_{общ}=0,2 А ; ), (R_1=3,5 Ом ), (R_2=4,5 Ом ).
Вычислить напряжение цепи (общее)
6. Контрольный 0,2В
Амперметр А показывает силу тока (I_{общ}=2 мА ; ), (R_1=35 Ом ), (R_2=45 Ом ),(R_3=20 Ом ).
Вычислить напряжение цепи (общее)
7. Контрольный 24,5В
Амперметр А показывает силу тока (I_{общ}=700 мА ; ), (R_1=20 Ом ), (R_2=5 Ом ),(R_3=10 Ом ).
Вычислить напряжение цепи (общее)
Задача
N10.2
Расчет
погрешности измерения в цепи переменного
тока
1.
Цель задачи.
Целью
данной задачи является научиться
рассчитывать методическую и инструментальную
погрешности измерения напряжения в
цепи переменного тока. Студенты должны
оценить влияние входного сопротивления
и входной емкости вольтметра на
методическую погрешность.
2.
Состав условия задачи
Имеется
делитель напряжения, состоящий из
последовательно включенных резисторов
R1 и R2, как это показано на рисунке 1
Рисунок 1. Электрическая схема делителя
напряжения
На
делитель напряжения подано переменное
напряжение с действующим значением U
и частотой f.
К резистору R2 подключен аналоговый
многопредельный вольтметр с внутренним
сопротивлением RV
на пределе измерения Uпр,
как показано на рисунке 2.
Рисунок 2. Электрическая схема делителя
напряжения с подключенным вольтметром
В
условии задачи приводятся также значения
входной емкости вольтметра и соединительных
проводов С, а также класса точности
вольтметра Кт.
Студенту
предлагается определить среднеквадратическую
относительную погрешность измерения
напряжения на резисторе R2,
обусловленную классом точности вольтметра
и методической погрешностью.
3. Порядок решения задачи
Решение задачи будет состоять из
следующих этапов:
1) расчет значения напряжения на резисторе
R2 для случая, когда к
делителю напряжения не подключен
вольтметр;
2) составление эквивалентной схемы
делителя напряжения с подключенным
вольтметром;
3) расчет эквивалентного сопротивления
нижней части делителя напряжения с
подключенным вольтметром;
4) расчет значения напряжения на резисторе
R2 для случая, когда к
делителю напряжения подключен вольтметр;
5) расчет методической погрешности
измерения напряжения на резисторе R2
для случая, когда к делителю напряжения
подключен вольтметр;
6) расчет погрешности измерения напряжения
на резисторе R2, обусловленной
классом точности вольтметра;
7)
расчет среднеквадратической относительной
погрешности измерения напряжения на
резисторе R2,
обусловленной классом точности вольтметра
и методической погрешностью.
Рассмотрим
указанные этапы более подробно.
3.1.1. Определим ток, протекающий по
резисторам R1 и R2,
когда к схеме не подключен вольтметр.
, (1)
где IR1nV
– ток, протекающий по резисторам R1
и R2, когда к схеме не
подключен вольтметр;
U
– напряжение, поданное на делитель
напряжения.
3.1.2. Определим падение напряжения на
резисторе R2, когда к схеме
делителя напряжения не подключен
вольтметр.
UR2nV=
IR1nV
·R2, (2)
где UR2nV
– падение напряжения на резисторе R2,
когда к схеме не подключен вольтметр.
Решая совместно уравнения (1) и (2), получим
. (3)
3.2. Составление эквивалентной схемы делителя напряжения с подключенным вольтметром;
Согласно условию задачи к резистору R2
подключен вольтметр. Электрическая
схема делителя напряжения с подключенным
вольтметром показана на рисунке 2.
Идеальный
вольтметр (вольтметр с бесконечно
большим входным сопротивлением и
бесконечно малой входной ёмкостью)
показал бы значение напряжения, равное
UR2nV.
Однако в данной задаче вольтметр имеет
входное сопротивление RV
и входную емкость С. В этом случае
параллельно резистору R2
подключаются активное и реактивное
сопротивления вольтметра, как показано
на рисунке 3.
Рисунок 3. Эквивалентная схема делителя
напряжения с подключенным вольтметром
Анализ схемы, представленной на рисунке
3, говорит о том, что в схеме присутствуют
активные сопротивления (резисторы R1,
R2 и входное сопротивление
вольтметра RV)
и реактивное сопротивление (входная
емкость вольтметра и емкость подводящих
проводов С). Это обстоятельство необходимо
учитывать в дальнейших расчетах.
3.3. Расчет эквивалентного сопротивления нижней части делителя напряжения с подключенным вольтметром
Для расчета полного сопротивления
нижней части делителя напряжения с
учетом того, что в сопротивлении
вольтметра присутствует реактивная
составляющая используем следующую
методику.
3.3.1. Определим эквивалентное активное
сопротивление параллельно включенных
резистора R2 и входного
активного сопротивления вольтметра RV
Rэ
= R2·RV/(R2+RV).
3.3.2. Определим круговую частоту источника
переменного напряжения
ω=2·π·f.
3.3.3. Определим эквивалентное полное
комплексное сопротивление нижней части
делителя напряжения с подключенным
вольтметром.
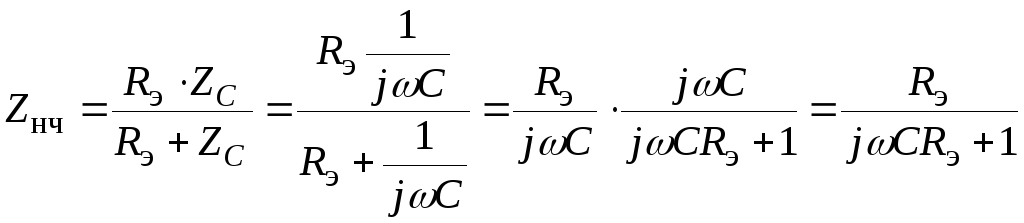
где ZC=1/(jωC)
– комплексное сопротивление конденсатора
С на частоте f.
Чтобы выделить действительную и мнимую
части полученного выражения, умножим
числитель и знаменатель на число,
сопряженное со знаменателем
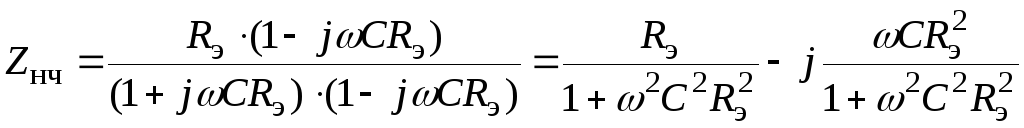
Чтобы упростить выражение (4), введем
вспомогательные коэффициенты:
,

В результате эквивалентное полное
комплексное сопротивление нижней части
делителя напряжения с подключенным
вольтметром будет иметь вид
Zнч=F–jG.
3.4. Расчет значения напряжения на резисторе r2 для случая, когда к делителю напряжения подключен вольтметр
3.4.1. Определим эквивалентное полное
комплексное сопротивление делителя
напряжения с подключенным вольтметром.
Zдн=R1+Zнч=(R1+F)-jG.
Обозначим действительную часть
полученного выражения через коэффициент
А, т.е.
A=R1+F.
В результате эквивалентное полное
комплексное сопротивление делителя
напряжения с подключенным вольтметром
будет иметь вид
Zдн=А-jG.
3.4.2. Определим комплексное значение
тока, протекающего по делителю напряжения
с подключенным к нему вольтметром
. (6)
Чтобы упростить выражение (7), введем
вспомогательные коэффициенты:
,
.
В результате комплексное значение тока,
протекающего по делителю напряжения с
подключенным к нему вольтметром, будет
иметь вид
Iдн=М+jN.
3.4.3 Определим падение напряжения на
резисторе R2, когда к схеме
делителя напряжения подключен вольтметр.
UR2V=
Iдн·Zнч=(M+jN)·(F–jG)=(FM+GN)+j(NF–GM).
3.4.4. Определим модуль напряжения на
резисторе R2, когда к схеме
делителя напряжения подключен вольтметр.
.
Соседние файлы в папке задачи
- #
- #
- #