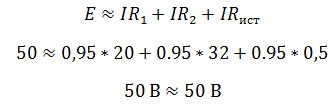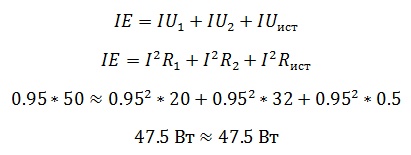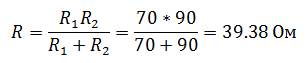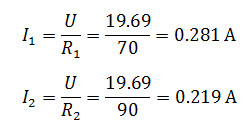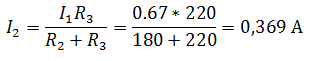Как найти напряжение на входе схемы

Как найти напряжение на входе схемы

НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Занятие1

Цели занятия:

1.Научиться находить рабочую точку графическим методом в неразветвленной цепи с одним нелинейным элементом.

2.Научиться находить рабочую точку графическим методом в разветвленной цепи с одним нелинейным элементом.

3.Научиться находить рабочую точку графическим методом в разветвленной цепи с несколькими нелинейными элементами.

Для цепи с двумя последовательно соединенными элементами, один из которых – линейный (рис. 6.1), рационально отыскание рабочей точки на пересечении вольт-амперной характеристики (ВАХ) нелинейного элемента (НЭ) с зеркальным отображением ВАХ линейного элемента.

I

НЭ1

R

U

U 1

U 2

Рис.6.1

Решение этим методом поясняет рис.

6.2. Строим ВАХ НЭ I(U1). В

рабочей точке на основании

второго

закона Кирхгофа

напряжение

U1 =U −U2 . Построим график

I(U −U2 ),

который является

зеркальным

отображением графика I(U2 ) , смещенного вправо на величину входного

напряжения U . Так как ВАХ линейного элемента является прямой линией, то для построения графика I(U −UЛЭ) нужны только две точки, одна из

которых с координатами (U,0). Очевидно, что графики пересекаются в рабочей точке А. Находим соответствующие ей значения тока I и напряжений U1 и U2 .

Для разветвленной схемы с одним нелинейным элементом, ток в котором и надо найти, в решении как промежуточный можно использовать метод эквивалентного генератора. Делим схему на две части: НЭ и всю остальную часть схемы, которая является активным двухполюсником.

Активный двухполюсник заменим эквивалентным ему генератором. Активный двухполюсник является линейной цепью, расчет которой намного проще, чем нелинейной. ЭДС генератора Ег равна напряжению холостого

хода на зажимах активного двухполюсника. Сопротивление Rг – это

эквивалентное сопротивление пассивного двухполюсника относительно входных зажимов. Пассивный двухполюсник получаем из активного, закорачивая источники ЭДС и разрывая источники тока. Полученная схема представляет собой последовательное соединение нелинейного и линейного элементов.

I

I(U–U2)

I(U1 )

I(U-U2 )

I

A

Рис. 6.2

Рабочую точку рационально найти на пересечении ВАХ НЭ и зеркального изображения ВАХ линейного элемента (рис. 6.2). График I(Ег −URг ) является прямой линией, зеркально отображающей график

I (URг ), смещенный вправо на величину Ег. Для его построения нужны две

точки. Одна из них с координатами (Ег,0).

Для построения второй точки можно задаться произвольным значением тока I j . Соответствующее ему напряжение U R j = RгI j отложим от

значения Ег влево. Отыскав рабочую точку А, найдем соответствующее ей значение тока I.

Задача1

Вычислить сопротивление R линейного элемента в схеме рис. 6.3, если входное напряжение U =120 В, напряжение на лампочке Uл = 75 В, ВАХ

лампочки задана табл. 6.1.

I R

U

Рис.6.3

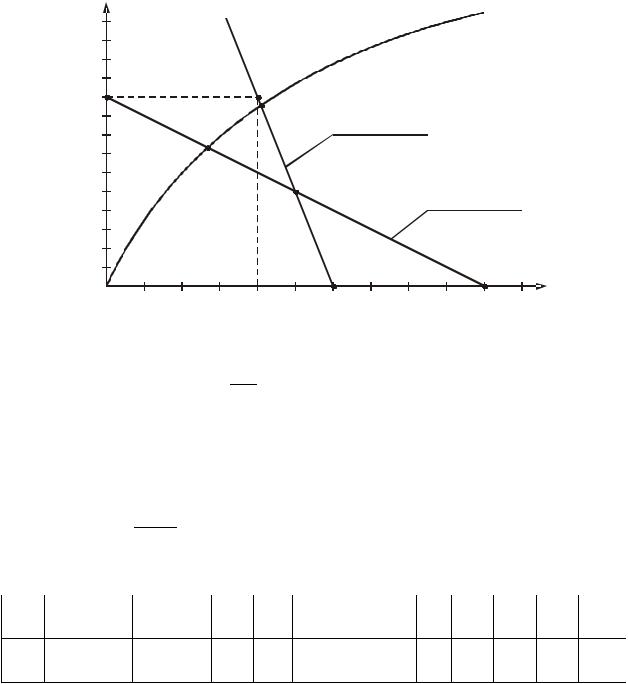
Решение

1. Построим ВАХ лампочки (рис. 6.4).

I, А

ВАХ лампочки

0,7

0,6

0,5

2

2

B

A

К задаче 5

0,4

0,3

0,2

К задаче 2

0,1

1

1

40

80

120

160

200 U, В

Рис.6.4

2. Сопротивление R = U R .

3. По

второму

I

закону

Кирхгофа

напряжение

U R =U −Uл =120 −75 = 45 В.

Uл = 75 В

ток

4. Найдем

ток

схемы

по

ВАХ

лампочки. При

I ≈ 0,425 А.

Тогда R =

45

=106 Ом.

0,425

Таблица 6.1

U,

0

1

20

40

60

80

10

120

14

160

18

200

220

240

260

B

0

0

0

0

I,

0

0,

0,

0,

0,3

0,4

0,5

0,5

0,6

0,6

0,

0,7

0,7

0,7

0,75

A

1

18

3

8

5

5

5

7

2

3

4

Задача2

Найти ток в схеме рис. 6.3, если U = 200 В, R = 400 Ом.

Решение

Отыщем рабочую точку на пересечении ВАХ лампочки и зеркального отображения ВАХ линейного элемента, которое можно построить по двум точкам. Первая из них с координатами (200 В; 0). Для построения второй точки зададимся произвольным значением тока, например I j = 0,5 А. Тогда

UR j = R I j = 400 0,5 = 200 В. Отложим напряжение UR j от U = 200 В

влево. Получим вторую точку с координатами (0; 0,5 А). Рабочая точка А находится на пересечении двух графиков (см. рис. 6.4). Ей соответствует значение тока I ≈ 0,38 А.

Задачи 3 и 4 решите самостоятельно.

Задача3

Вычислить входное напряжение в схеме рис. 6.5, если ток I = 0,18 А.

I

U

Рис.6.5

Ответ: U = 40 В.

Задача4

Вычислить мощность, потребляемую лампочкой в схеме рис. 6.3 при входном напряжении U =180 В, если при входном напряжении U = 220 В напряжение на лампочке Uл =127 В.

Ответ: Рл = 50 Вт.

Задача5

Вычислить мощность, потребляемую лампочкой в схеме рис. 6.6, если U =150 В, R1 =100 Ом, R2 = 400 Ом, ВАХ лампочки приведена на рис. 6.4.

Решение

1. Заменим схему эквивалентной ей одноконтурной с помощью метода эквивалентного генератора. Разделим схему на две части: лампочку и всю остальную схему – активный двухполюсник (рис. 6.7), который заменим эквивалентным ему генератором. ЭДС генератора

Eг =Uхх = R2 Iхх .

Ток Iхх = R1 U+ R2 = 0,3 А.

Тогда Ег = 400 0,3 =120 В.

Iхх

R1

a

R2

U

Uхх

b

Рис.6.7

Схема пассивного двухполюсника приведена на рис. 6.8.

Сопротивление

R = R = R1 R2

= 100 400 = 80 Ом.

г

ab

R1

+ R2

100 + 400

R1

I Л

а

R2

Ег

b

Rг

Рис.6.8

Рис.6.9

Получившаяся одноконтурная схема изображена на рис. 6.9.

2. Найдем рабочую точку на пересечении ВАХ лампочки с зеркальным отображением ВАХ линейного резистора. Одна точка для построения графика I (Eг −U Rг ) – с координатами (120 В; 0). Для построения второй

точки зададимся значением тока I j = 0,5 А. Тогда URj = Rг I j = 0,5 80 = 40

В. Отложим 40 В от 120 В влево и получим точку с координатами (80 В; 0,5 А). Проведем прямую через эти две точки (см. рис. 6.4). Рабочая точка В позволяет определить Uл ≈83 В и Iл ≈ 0,45 А.

Мощность, потребляемая лампочкой,

Pл =Uл Iл =83 0,45 ≈ 37,4 Вт.

Задачу 6 решите самостоятельно.

Задача6

Найти все токи в схеме рис. 6.6, если U = 380 В, R1 =300 Ом, R2 = 600

Ом.

Ответ: I1 = 0,8 А; I2 = 0,22 А; Iл = 0,58 А.

Задача7

Вычислить напряжение на входе схемы рис. 6.6, если R1 =50 Ом, R2 =100Ом, ток Iл = 0,2 А, ВАХ лампочки приведена на рис. 6.10.

II,, AА

0,30,3

0,20,2

0,10,1

50 100100 150150 200200 U,U, ВВ

РисРис.6..106.10

Решение

1. По ВАХ лампочки найдем напряжение между двумя узлами, равное напряжению на лампочке:

U12 =Uл =100 В.

2. Вычислим ток I2 по закону Ома

I2 = U12 =100 =1 А.

R2 100

3. Вычислим ток I1 по первому закону Кирхгофа

I1 = I2 + Iл =1+ 0,2 =1,2 А.

4. Вычислим входное напряжение по второму закону Кирхгофа

U = R1 I1 +U12 =50 1,2 +100 =160 В.

Задача8

Найти ток в неразветвленной части цепи схемы рис. 6.11, если U =100 В, все лампочки одинаковые. ВАХ лампочки приведена на рис. 6.12.

I

U

Рис. 6.11

Решение

1.По ВАХлампочки найдемток I2 = 0,6 А.

2.В ветви с последовательным соединением двух одинаковых

лампочек на каждой лампочке напряжение Uл = U2 = 50 В.

3.По ВАХ лампочки найдем ток I1 = 0,4 А.

4.По первому закону Кирхгофа найдем ток

I = I1 + I2 = 0,4 + 0,6 =1 А.

Задачи 9–11 решите самостоятельно.

I, А

0,8

0,6

0,4

0,2

50

100

150

U, B

Рис. 6.12

Задача9

Найти напряжение на входе схемы рис. 6.11, если ток I1 = 0,4 А и все

лампочки одинаковые. ВАХ лампочки приведена на рис. 6.12. Ответ: U =100 В.

Задача10

Вычислить ток в неразветвленной части схемы рис. 6.11, если ток I1 = 0,4 А и все лампочки одинаковые. ВАХ лампочки приведена на рис. 6.12.

Ответ: I =1 А.

Задача11

Найти напряжение на входе схемы рис. 6.13, если ток I1 = 0,2 А и все лампочки одинаковые. ВАХ лампочки приведена на рис. 6.14.

U

Рис. 6.13

I, А

0,6

0,4

0,2

50 100 150 200 U,В

Рис. 6.14

Ответ: U = 200 В.

Занятие2

Цель занятия:

1. Научиться вычислять ток в нелинейном элементе методом итерации (последовательных приближений).

Сущность метода итерации (последовательных приближений) заключается в аналитическом решении системы алгебраических нелинейных уравнений. Статическое сопротивление нелинейного элемента должно быть задано в функции от тока или напряжения.

Пусть в схеме один нелинейный элемент (НЭ), ток в котором и надо найти. Остальную часть схемы (активный двухполюсник) заменим эквивалентным ему генератором (рис. 6.15).

Графическая иллюстрация решения методом итерации приведена на рис. 6.16.

Напряжение на нелинейном элементе U = Eг − RгI . Ток зависит от

статического сопротивления НЭ, которое, в свою очередь, зависит от напряжения, поэтому это уравнение является нелинейным: U = F(U ) .

Пусть напряжение в нулевом приближении U0 = Eг. На ВАХ НЭ

находим соответствующую рабочую точку b. Так как ток в схеме один, то току I0 на графике I(Eг − RгI) соответствует точка с. Напряжение на НЭ

U = Eг − RгI , поэтому переходим из точки с в точку d. Повторяя этот

процесс, получаем рабочую точку А.

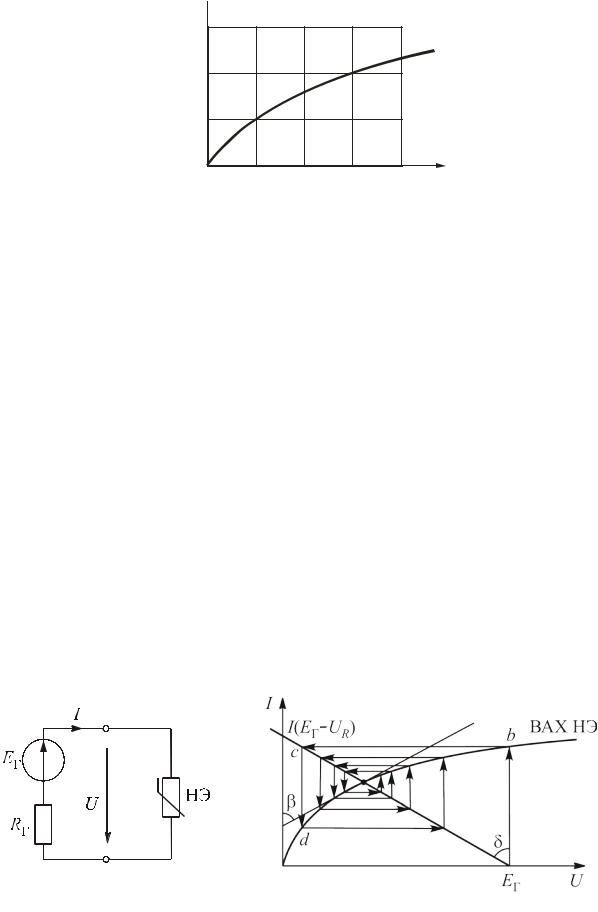
Итерационный процесс может быть организован различными методами. Наиболее эффективным считается метод Ньютона – Рафсона.

Пусть нелинейное уравнение

f (x) = 0 имеет единственный корень x = xk +1.

В окрестности этого корня функция f (xk +1) разлагается в ряд Тейлора:

f (xk+1) = f (xk

+∆xk ) ≈f (x k ) +∆xk

f ′(xk ) =0

Отсюда следует xk +1 = xk + ∆xk , где ∆xk

= h = −

f (xk)

– поправка

f ′(xk )

к предыдущему решению. Из приведенных соотношений следует алгоритм метода Ньютона – Рафсона:

1. Задаем начальное приближенное значение искомого решения x0

(k = 0).

2. Определяем поправку h0 . Для ее вычисления по выражению функции находим производную.

3.Определяем уточненное значение корня x1 = x0 + h0 .

4.Повторяем процесс на следующем шаге и уточняем предыдущее решение до необходимой точности.

Геометрическая интерпретация метода приведена на рис. 6.17. В

качестве начального приближения примем U0 = Eг . В точке a проводим касательную к ВАХ НЭ, по касательной переходим на график I(Eг − RгI) в

точку b, далее в точку c на ВАХ НЭ, снова проводим касательную и т. д. Из рисунка видно, что число шагов, необходимых для нахождения решения в случае применения метода Ньютона – Рафсона, значительно меньше, чем при обычном итерационном процессе (рис. 6.16).

I

a

ВАХ НЭ

b

d

c

A

I (Eг −U )

Eг U

Рис.6.17

Соседние файлы в папке ТОЭ3

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Содержание

  1. Электрический ток. Закон Ома для цепей постоянного и переменного тока.
  2. Напряжение цепи переменного тока
  3. В помощь изучающему электронику
  4. — Цепь переменного тока —
  5. Входное и выходное сопротивление
  6. Предисловие
  7. Входное сопротивление
  8. Как измерить входное сопротивление
  9. Измерение входного сопротивления на практике
  10. Выходное сопротивление
  11. Измерение выходного сопротивления на практике
  12. Заключение

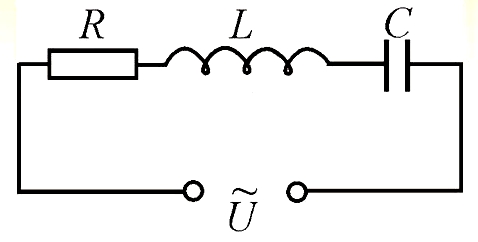
Электрический ток. Закон Ома для цепей постоянного и переменного тока.

Онлайн расчёт электрических величин напряжения, тока и мощности для участка цепи,
полной цепи, цепи с резистивными, ёмкостными и индуктивными элементами.
Теория и практика для начинающих.

Начнём с терминологии.
Электрический ток — это направленное движение заряженных частиц, при котором происходит перенос заряда из одной области электрической цепи в другую.
Силой электрического тока (I) является величина, которая численно равна количеству заряда Δq, протекающего через заданное поперечное сечение проводника S за единицу времени Δt: I = Δq/Δt.
Напряжение электрического тока между точками A и B электрической цепи — физическая величина, значение которой равно работе эффективного электрического поля, совершаемой при переносе единичного пробного заряда из точки A в точку B.
Омическое (активное) сопротивление — это сопротивление цепи постоянному току, вызывающее безвозвратные потери энергии постоянного тока.
Теперь можно переходить к закону Ома.

Закон Ома был установлен экспериментальным путём в 1826 году немецким физиком Георгом Омом и назван в его честь. По большому счёту, Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, определяющих зависимость между электрическими величинами, такими как: напряжение, сопротивление и сила тока исключительно для проводников, обладающих постоянным сопротивлением. При расчёте напряжений и токов в нелинейных цепях, к примеру, таких, которые содержат полупроводниковые или электровакуумные приборы, этот закон в простейшем виде уже использоваться не может.

Тем не менее, закон Ома был и остаётся основным законом электротехники, устанавливающим связь силы электрического тока с сопротивлением и напряжением.
Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:
I=U/R,

Закон Ома для участка цепигде
I – сила тока в проводнике, измеряемая в амперах [А];
U – электрическое напряжение (разность потенциалов), измеря- емая в вольтах [В];
R – электрическое сопротивление проводника, измеряемое в омах [Ом].

Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.

Зная любые два из трёх приведённых параметров можно произвести и расчёт величины мощности, рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:
P(Вт) = U(В)×I(А) = I 2 (А)×R(Ом) = U 2 (В)/R(Ом)

Формулы, описывающие закон Ома, настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта.

Не заслуживают, так не заслуживают. Деревянные счёты Вам в помощь, уважаемые дамы и рыцари!
Считайте, учитывайте размерность, не стирайте из памяти, что:

Единицы измерения напряжения: 1В=1000мВ=1000000мкВ;
Единицы измерения силы тока:1А=1000мА=1000000мкА;
Единицы измерения сопротивления:1Ом=0.001кОм=0.000001МОм;
Единицы измерения мощности:1Вт=1000мВт=100000мкВт.

Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.

ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.

Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.

Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения rвнутр .
Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = Rвнешн + rвнутр , после чего закон приобретает солидное название — закон Ома для полной цепи:
I=U/(R+r) .

Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду:

Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/Rll = 1/R4+1/R5 .
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице ссылка на страницу.

Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.
Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока — под значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.

А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
Приведём диаграммы для нескольких различных форм сигнала.

Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов — это максимальное значение, которого достигает амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.

Рассчитываем действующее значение напряжение интересующей нас формы:

Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.

С этим разобрались!

Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.
В общем случае смотреться это будет так:

Закон Ома для переменного тока

А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид: Закон Ома для переменного тока
Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами: XC = 1/(2πƒС) , XL = 2πƒL .

Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии индуктивного или емкостного элемента — необходимо указать значение частоты f !

КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.

Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем простенький бестрансформаторный источник питания.

Токозадающими цепями в данной схеме являются элементы R1 и С1.

Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом — 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в — 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока нагрузки.
Зададимся номиналами R1 — 30 Ом, С1 — 1 Мкф, частотой сети f — 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет — надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости — 3,18 Мкф, при котором Z = 1,04кОм.

Всё — закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!

Источник

Напряжение цепи переменного тока

ads

Напряжение в цепи переменного тока

Переменное напряжение — это напряжение, которое изменяется с течением времени. Далее будем рассматривать только гармоническое переменное напряжение (изменяется по синусоиде).

u = Umsin(2πt + Ψ ) = Umsin(ωt + Ψ )

Где u = u(t) — мгновенное значение переменного напряжения [В].

Um — максимальное значение напряжения (амплитудное значение) [В].

f — частота равная числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с -1 )

ω — угловая частота (омега) (единица угловой частоты — рад/с или с -1 )

ω = 2πf = 2π/T

Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.

U — Действующее значение напряжения [В]:Действующее значение напряжения

Рассмотрим параметры напряжения в бытовой электросети.

Все мы знаем, что у нас дома в розетке поступает переменный ток, с напряжением 220 вольт и частотой 50 герц (в идеальных условиях) на самом деле допускается не большая погрешность как в меньшую, так и в большую сторону так, что не удивляйтесь если ваш вольтметр покажет не 220, а например 210 или даже 230 В.).

Большинство приборов измеряет не амплитудное, а действующее значение переменного напряжения, тока, мощности так, что если мы говорим что у нас напряжение сети 220, 380 В и т. д. то имеется виду именно действующие значения.

  • Действующее значение напряжения U = 220 В.
  • Амплитудное значение напряжения цепи переменного токаUm = U*√2 = 220 *√2 = 311 В.
  • Угловая частота ω = 2πf = 3,14*2*50 = 314рад/с.
  • Начальная фаза Ψ = 0град.
  • Мгновенное значениеu= 311sin(314t)В.

Источник

В помощь изучающему электронику

Формулы, вычисления, .

— Цепь переменного тока —

Данный справочник собран из разных источников. Но на его создание подтолкнула небольшая книжка «Массовой радиобиблиотеки» изданная в 1964 году, как перевод книги О. Кронегера в ГДР в 1961 году. Не смотря на такую ее древность, она является моей настольной книгой (наряду с несколькими другими справочниками). Думаю время над такими книгами не властно, потому что основы физики, электро и радиотехники (электроники) незыблемы и вечны.

Основные понятия
Сопротивление в цепи переменного тока
В омическом (активном) сопротивлении ток совпадает по фазе с напряжением (фазовый угол равен нулю), поэтому расчет сопротивления конструктивных элементов РЭА в цепях переменного тока производится по формулам, выведенным для цепи постоянного тока. По мере повышения частоты начинает проявляться так называемый поверхностный эффект, сопротивление проводника увеличивается, так как происходит вытеснение тока к поверхности проводника. Этот эффект характеризуется глубиной проникновения тока δ. Величина δ численно равна такому расстоянию от поверхности (проводника), на котором плотность тока составляет 36% от плотности тока на поверхности (уменьшается в e раз). Существенно, что, хотя сопротивление проводника увеличивается с ростом частоты, оно по-прежнему остается активным, ток и напряжение в проводнике совпадают по фазе.
Глубина проникновения тока вычисляется по формуле
где:
Конденсатор в цепи переменного тока
Индуктивность в цепи переменного тока

С — емкость конденсатора С при настройке контура в резонанс на частоту генератора;
ΔС = СВ — СН — соответственно большее и меньшее, чем С, значения емкости конденсатора С, соответствующие уменьшению напряжения на контуре до 0,707 от резонансного значения.

При ω в 1/сек, и ΔС в ф,

8—длина воздушного зазора, см;
В — индукция, тл (обычно выбирают 5 = 0,7 тл);
I — ток, а.

Мощность переменного тока

Pa = U I cosφ [ва];

Pp = U I sinφ [ва];

Оглавление.

Основные понятия. Замкнутая и разветвленная цепи постоянного тока

Основные понятия, Сопротивление в цепи переменного тока , Конденсатор в цепи переменного тока, Индуктивность в цепи переменного тока, Мощность переменного тока

Основные зависимости, Последовательный колебательный контур, Параллельный колебательный контур

Входная цепь приемника

RC и LC фильтры — общие положения, RC фильтры, LC фильтры

Аттенюаторы, Согласование источника с нагрузкой по мощности, току и напряжению

Основные параметры передающих антенн, Параметры приемных антенн, Вибраторные антенны, Рамочные антенны, Приемные ферритовые антенны, Формулы для расчета вибраторных антенн

РАСПРОСТРАНЕНИЕ РАДИОВОЛН В СВОБОДНОМ ПРОСТРАНСТВЕ — Общие положения, ИОНОСФЕРА И ЕЕ ВЛИЯНИЕ НА РАСПРОСТРАНЕНИЕ РАДИОВОЛН, Преломление и отражение радиоволн в ионосфере, Особенности распространения сверхдлинных и длинных волн, Особенности распространения средних волн, Особенности распространения коротких волн, РАСПРОСТРАНЕНИЕ УЛЬТРАКОРОТКИХ ВОЛН В ПРИЗЕМНОМ ПРОСТРАНСТВЕ, Распространения радиоволн над поверхностью земли, дальний прием

Источник

Входное и выходное сопротивление

Входное и выходное сопротивление является очень важным в электронике.

Предисловие

Ладно, начнем издалека… Как вы знаете, все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и тд. В нашей статье будем использовать понятие “блок”. Например, источник питания, собранный по этой схеме:

состоит из двух блоков. Я их пометил в красном и зеленом прямоугольниках.

В красном блоке мы получаем постоянное напряжение, а в зеленом блоке мы его стабилизируем. То есть блочная схема будет такой:

Блочная схема – это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод “от простого к сложному” полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем – готовое устройство, например, телевизор.

Ладно, что-то отвлеклись. Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.

– Ага! Так что же получается? Я могу просто тупо взять готовые блоки и изобрести любое электронное устройство, которое мне придет в голову?

Да! Именно на это нацелена сейчас современная электроника 😉 Микроконтроллеры и конструкторы, типа Arduino, добавляют еще больше гибкости в творческие начинания молодых изобретателей.

На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.

Думаю, все помнят, что такое сопротивление и что такое резистор. Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением. Но что такое входное и выходное сопротивление? Это уже что-то новенькое. Если прислушаться к этим фразам, то входное сопротивление – это сопротивление какого-то входа, а выходное – сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления? А вот “прячутся” они в самих блоках радиоэлектронных устройств.

Входное сопротивление

Итак, имеем какой-либо блок. Как принято во всем мире, слева – это вход блока, справа – выход.

Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение Uвх от другого блока или от источника питания, а на его выходе появится напряжение Uвых (или не появится, если блок является конечным).

Но раз уж мы подаем напряжение на вход (входное напряжение Uвх), следовательно, у нас этот блок будет кушать какую-то силу тока Iвх.

Теперь самое интересное… От чего зависит Iвх ? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи :

Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от… СОПРОТИВЛЕНИЯ. Но где нам его найти? А прячется оно в самом каскаде и называется входным сопротивлением.

То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет). Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока. Скажем так, совокупное сопротивление.

Как измерить входное сопротивление

Как мы знаем, на каждый блок подается какой-либо сигнал от предыдущего блока или это может быть даже питание от сети или батареи. Что нам остается сделать?

1)Замерить напряжение Uвх, подаваемое на этот блок

2)Замерить силу тока Iвх, которую потребляет наш блок

3) По закону Ома найти входное сопротивление Rвх.

Если у вас входное сопротивление получается очень большое, чтобы замерить его как можно точнее, используют вот такую схему.

Мы с вами знаем, что если входное сопротивление у нас большое, то входная сила тока в цепи у нас будет очень маленькая (из закона Ома).

Падение напряжения на резисторе R обозначим, как UR

Входное и выходное сопротивление

Входное и выходное сопротивление

Из всего этого получаем…

Входное и выходное сопротивление

Когда мы проводим эти измерения, имейте ввиду, что напряжение на выходе генератора не должно меняться!

Итак, давайте посчитаем, какой же резистор нам необходимо подобрать, чтобы как можно точнее замерять это входное сопротивление. Допустим, что у нас входное сопротивление Rвх=1 МегаОм, а резистор взяли R=1 КилоОм. Пусть генератор выдает постоянное напряжение U=10 Вольт. В результате, у нас получается цепь с двумя сопротивлениями. Правило делителя напряжения гласит: сумма падений напряжений на всех сопротивлениях в цепи равняется ЭДС генератора.

В результате получается цепь:

Высчитываем силу тока в цепи в Амперах

Входное и выходное сопротивление

Получается, что падение напряжения на сопротивлении R в Вольтах будет:

Входное и выходное сопротивление

Грубо говоря 0,01 Вольт. Вряд ли вы сможете точно замерить такое маленькое напряжение на своем китайском мультиметре.

Какой отсюда вывод? Для более точного измерения высокого входного сопротивления надо брать добавочное сопротивление также очень большого номинала. В этом случае работает правило шунта: на бОльшем сопротивлении падает бОльшее напряжение, и наоборот, на меньшем сопротивлении падает меньшее напряжение.

Измерение входного сопротивления на практике

Ну все, запарка прошла ;-). Давайте теперь на практике попробуем замерить входное сопротивление какого-либо устройства. Мой взгляд сразу упал на Транзистор-метр. Итак, выставляем на блоке питания рабочее напряжение этого транзистор-метра, то есть 9 Вольт, и во включенном состоянии замеряем потребляемую силу тока. Как замерить силу тока в цепи, читаем в этой статье. По схеме все это будет выглядеть вот так:

А на деле вот так:

Итак, у нас получилось 22,5 миллиАмпер.

Теперь, зная значение потребляемого тока, можно найти по этой формуле входное сопротивление:

Входное и выходное сопротивление

Выходное сопротивление

Яркий пример выходного сопротивления – это закон Ома для полной цепи, в котором есть так называемое “внутреннее сопротивление”. Кому лень читать про этот закон, вкратце рассмотрим его здесь.

Что мы имели? У нас был автомобильный аккумулятор, с помощью которого мы поджигали галогенную лампочку. Перед тем, как цеплять лампочку, мы замеряли напряжение на клеммах аккумулятора:

И как только подсоединяли лампочку, у нас напряжение на аккумуляторе становилось меньше.

Входное и выходное сопротивление

Разница напряжения, то есть 0,3 Вольта (12,09-11,79) у нас падало на так называемом внутреннем сопротивлении r 😉 Оно же и есть ВЫХОДНОЕ СОПРОТИВЛЕНИЕ. Его также называют еще сопротивлением источника или эквивалентным сопротивлением.

У всех аккумуляторов есть это внутреннее сопротивление r, и “цепляется” оно последовательно с источником ЭДС (Е).

Но только ли аккумуляторы и различные батарейки обладают выходным сопротивлением? Не только. Выходным сопротивлением обладают все источники питания. Это может быть блок питания, генератор частоты, либо вообще какой-нибудь усилитель.

В теореме Тевенина (короче, умный мужик такой был) говорилось, что любую цепь, которая имеет две клеммы и содержит в себе туеву кучу различных источников ЭДС и резисторов разного номинала можно привести тупо к источнику ЭДС с каким-то значением напряжения (Eэквивалентное) и с каким-то внутренним сопротивлением (Rэквивалентное).

Eэкв – эквивалентный источник ЭДС

Rэкв – эквивалентное сопротивление

То есть получается, если какой-либо источник напряжения питает нагрузку, значит, в источнике напряжения есть ЭДС и эквивалентное сопротивление, оно же выходное сопротивление.

В режиме холостого хода (то есть, когда к выходным клеммам не подцеплена нагрузка) с помощью мультиметра мы можем замерить ЭДС (E). С замером ЭДС вроде бы понятно, но вот как замерить Rвых ?

В принципе, можно устроить короткое замыкание. То есть замкнуть выходные клеммы толстым медным проводом, по которому у нас будет течь ток короткого замыкания Iкз.

В результате у нас получается замкнутая цепь с одним резистором. Из закона Ома получаем, что

Входное и выходное сопротивление

Но есть небольшая загвоздка. Теоретически – формула верна. Но на практике я бы не рекомендовал использовать этот способ. В этом случае сила тока достигает бешеного значения, да вообще, вся схема ведет себя неадекватно.

Измерение выходного сопротивления на практике

Есть другой, более безопасный способ. Не буду повторяться, просто скопирую со статьи закон Ома для полной цепи, где мы находили внутреннее сопротивление аккумулятора. В той статье, мы к акуму цепляли галогенную лампочку, которая была нагрузкой R. В результате по цепи шел электрический ток. На лампочке и на внутреннем сопротивлении у нас падало напряжение, сумма которых равнялась ЭДС.

Итак, для начала замеряем напряжение на аккумуляторе без лампочки.

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае E=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем резисторе падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r:

Заключение

Входное и выходное сопротивление каскадов (блоков) в электронике играют очень важную роль. В этом мы убедимся, когда начнем рассматривать статью по согласованию узлов радиоэлектронных схем. Все качественные вольтметры и осциллографы также стараются делать с очень высоким входным сопротивлением, чтобы оно меньше сказывалось на замеряемый сигнал и не гасило его амплитуду.

С выходным сопротивлением все намного интереснее. Когда мы подключаем низкоомную нагрузку, то чем больше внутреннее сопротивление, тем больше напряжение падает на внутреннем сопротивлении. То есть в нагрузку будет отдаваться меньшее напряжение, так как разница осядет на внутреннем резисторе. Поэтому, качественные источники питания, типа блока питания либо генератора частоты, пытаются делать как можно с меньшим выходным сопротивлением, чтобы напряжение на выходе “не проседало” при подключении низкоомной нагрузки. Даже если сильно просядет, то мы можем вручную подкорректировать с помощью регулировки выходного напряжения, которые есть в каждом нормальном источнике питания. В некоторых источниках это делается автоматически.

Источник

Источник

Электроника

учебно-справочное пособие

Входное и выходное сопротивление

Все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и т.д. Например, (рис. 1) состоит из двух блоков.

Рис. 1 — Схема источника питания

На рисунке 1 в левом блоке мы получаем постоянное напряжение, а в правом блоке его стабилизируем (рис. 2).

Рис. 2 — Блочная схема источника питания

Блочная схема — это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод «от простого к сложному» полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем — готовое устройство, например, телевизор.

Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.

На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.

Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением.

Если прислушаться фразам, то входное сопротивление — это сопротивление какого-то входа, а выходное — сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления? А вот «прячутся» они в самих блоках радиоэлектронных устройств.

Входное сопротивление

В блочной схеме вход блока располагается слева, выход — справа.

Рис. 3 — Входы и выходы в блочной схеме

Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение Uвх от другого блока или от источника питания, а на его выходе появится напряжение Uвых (или не появится, если блок является конечным).

Рис. 4 — Входное и выходное напряжения

Но раз уж мы подаем напряжение на вход (входное напряжение Uвх), следовательно, у нас этот блок будет потреблять какую-то силу тока Iвх.

Рис. 5 — Сила тока на входе

От чего зависит Iвх ? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи:

Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от. СОПРОТИВЛЕНИЯ. Но где нам его найти? А прячется оно в самом каскаде и называется входным сопротивлением.

Рис. 6 — Входное сопротивление

То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет. Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока.

Измерение входного сопротивления

Как мы знаем, на каждый блок подается какой-либо сигнал от предыдущего блока или это может быть даже питание от сети или батареи. Что нам остается сделать?

  1. Замерить напряжение Uвх , подаваемое на блок.
  2. Замерить силу тока Iвх , которую потребляет блок.
  3. По закону Ома найти входное сопротивление Rвх .

Если у вас входное сопротивление получается очень большое, чтобы замерить его как можно точнее, используют вот такую схему.

Рис. 7 — Измерение входного сопротивления

Мы с вами знаем, что если входное сопротивление у нас большое, то входная сила тока в цепи у нас будет очень маленькая (из закона Ома).

Падение напряжения на резисторе R обозначим, как

Когда мы проводим эти измерения, имейте ввиду, что напряжение на выходе генератора не должно меняться!

Итак, давайте посчитаем, какой же резистор нам необходимо подобрать, чтобы как можно точнее замерять это входное сопротивление. Допустим, что у нас входное сопротивление Rвх=1 МОм, а резистор взяли R = 1 КОм. Пусть генератор выдает постоянное напряжение U=10 В. В результате, у нас получается цепь с двумя сопротивлениями. Правило делителя напряжения гласит: сумма падений напряжений на всех сопротивлениях в цепи равняется ЭДС генератора.

Рис. 8 — Делитель напряжения

Рассчитываем силу тока в цепи в амперах:

Получается, что падение напряжения на сопротивлении R в вольтах будет:

Грубо говоря 0,01 В. Вряд ли вы сможете точно замерить такое маленькое напряжение на своем мультиметре.

Какой отсюда вывод? Для более точного измерения высокого входного сопротивления надо брать добавочное сопротивление также очень большого номинала. В этом случае работает правило шунта: на бОльшем сопротивлении падает бОльшее напряжение, и наоборот, на меньшем сопротивлении падает меньшее напряжение.

Давайте теперь на практике попробуем замерить входное сопротивление какого-либо устройства. Итак, выставляем на блоке питания рабочее напряжение этого транзистор-метра, то есть 9 В, и во включенном состоянии замеряем потребляемую силу тока. По схеме все это будет выглядеть вот так:

Итак, у нас получилось 22,5 миллиАмпер.

Теперь, зная значение потребляемого тока, можно найти по этой формуле входное сопротивление:

Выходное сопротивление

Яркий пример выходного сопротивления — это закон Ома для полной цепи, в котором есть так называемое «внутреннее сопротивление».

Что мы имели? У нас был автомобильный аккумулятор, с помощью которого мы поджигали галогеновую лампочку. Перед тем, как цеплять лампочку, мы замеряли напряжение на клеммах аккумулятора:

И как только подсоединяли лампочку, у нас напряжение на аккумуляторе становилось меньше.

Разница напряжения, то есть 0,3 В (12,09 -11,79) у нас падало на так называемом внутреннем сопротивлении r . Оно же и есть ВЫХОДНОЕ СОПРОТИВЛЕНИЕ. Его также называют еще сопротивлением источника или эквивалентным сопротивлением.

У всех аккумуляторов есть это внутреннее сопротивление r, и «цепляется» оно последовательно с источником ЭДС ( Е ).

Рис. 13 — Внутреннее сопротивление аккумулятора

Выходным сопротивлением обладают все источники питания. Это может быть блок питания, генератор частоты, либо вообще какой-нибудь усилитель.

В теореме Тевенина говорилось, что любую цепь, которая имеет две клеммы и содержит в себе много различных источников ЭДС и резисторов разного номинала можно привести к источнику ЭДС с каким-то значением напряжения ( Eэкв ) и с каким-то внутренним сопротивлением ( Rэкв ).

Eэкв — эквивалентный источник ЭДС

Rэкв — эквивалентное сопротивление

То есть получается, если какой-либо источник напряжения питает нагрузку, значит, в источнике напряжения есть ЭДС и эквивалентное сопротивление, оно же выходное сопротивление.

В режиме холостого хода (то есть, когда к выходным клеммам не подцеплена нагрузка) с помощью мультиметра мы можем замерить ЭДС ( E ). С замером ЭДС вроде бы понятно, но вот как замерить Rвых ?

В принципе, можно устроить короткое замыкание. То есть замкнуть выходные клеммы толстым медным проводом, по которому у нас будет течь ток короткого замыкания Iкз .

Рис. 15 — Ток короткого замыкания

В результате у нас получается замкнутая цепь с одним резистором. Из закона Ома получаем, что

Но есть небольшая загвоздка. Теоретически — формула верна. Но на практике я бы не рекомендовал использовать этот способ. В этом случае сила тока достигает бешенного значения, да вообще, вся схема ведет себя неадекватно.

Есть другой, более безопасный способ. Не буду повторяться, просто скопирую со статьи закон Ома для полной цепи, где мы находили внутреннее сопротивление аккумулятора. В той статье, мы к акуму цепляли галогеновую лампочку, которая была нагрузкой R. В результате по цепи шел электрический ток. На лампочке и на внутреннем сопротивлении у нас падало напряжение, сумма которых равнялась ЭДС.

Итак, для начала замеряем напряжение на аккумуляторе без лампочки (рис. 17).

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае E = 12,09 В.

Как только мы цепанули нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение

следовательно, на внутреннем резисторе падение напряжения составило

Сила тока в цепи равняется I =4,35 Ампер. ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи вычисляем, чему у нас будет равняться внутреннее сопротивление r:

r = (12,09 — 11,79)/4,35 = 0,069 [Ом]

Выводы

Входное и выходное сопротивление каскадов (блоков) в электронике играют очень важную роль при согласовании узлов радиоэлектронных схем. Все качественные вольтметры и осциллографы также стараются делать с очень высоким входным сопротивлением, чтобы оно меньше сказывалось на замеряемый сигнал и не гасило его амплитуду.

С выходным сопротивлением все намного интереснее. Когда мы подключаем низкоомную нагрузку, то чем больше внутреннее сопротивление, тем больше напряжение падает на внутреннем сопротивлении. То есть в нагрузку будет отдаваться меньшее напряжение, так как разница осядет на внутреннем резисторе. Поэтому, качественные источники питания, типа блока питания либо генератора частоты, пытаются делать как можно с меньшим выходным сопротивлением, чтобы напряжение на выходе «не проседало» при подключении низкоомной нагрузки. Даже если сильно просядет, то мы можем вручную подкорректировать с помощью регулировки выходного напряжения, которые есть в каждом нормальном источнике питания. В некоторых источниках это делается уже автоматически.

Источники:

Электроника © ЦДЮТТ • Марсель Арасланов • 2019

Источник

Найти входное напряжение

Найти входное напряжение
Есть задача и примерное решение. Как я понял, остаётся только U входное найти. Как это сделать?

Найти входное напряжение и ток четырехполюсника
Всем привет Дали задачу, помогите пожалуйста ее решить Rn — это нагрузка на резисторе? Как от.

Найти входное напряжение в параллельном диодном ключе
Определить величину входного напряжения в параллельном диодном ключе, представленный на схеме при.

Найти входное сопротивление цепи и напряжение катушки
Сопротивления всех элементов равны 2 Ом. Входное напряжение 10 В. Не могу разобраться как сложить.

Добавлено через 2 минуты
Схему нужно будет перерисовать. Назвать резисторы. И те 2 резистора, которые по 30(Ом) их объединить в 1 по формуле параллельных резисторов. R = (R1*R2)/(R1 + R2).

Ну так ты это сделай сначала.

Добавлено через 28 минут
Сопротивления могут включаться последовательно. Общее сопротивление — это сумма этих сопротивлений.

Добавлено через 24 минуты
В общем-то последние(крайние правые) 2 сопротивления тоже соединены параллельно и их нужно объединить в 1.

Входное напряжение
Здраствуйте. Помогите с задачей, надо определить входное напряжение и построить топографическую.

входное напряжение
Здравствуйте, подскажите пожалуйста какое будет входное напряжение двухполюсника, если P=1 кВт, Q=.

Входное напряжение цепи
Входное НАПРЯЖЕНИЕ на схеме так определяется ? U=I1*Rэкв, где Rэкв=R1+R2*R3/(R2+R3) ?

Входное напряжение в последовательной цепи
Дано: R = 5 Ом Xc = 4 Ома XL = 6 Ом Uc = 40В. цепь еще дана.. последовательно включены.

Каким будет входное и выходное напряжение
Каким в данной схеме будут входное и выходное напряжение. Формулы. Не могу понять, как их выразить.

Входное напряжение. Направление токов в цепи
Здравствуйте! Помогите пожалуйста разобраться с направлением токов в цепи. Верно ли они.

Источник

Источник

Что такое входное сопротивление и как его измерить

При работе со сложными схемами нужно уметь определять характеристики их отдельных блоков и элементов. В частности, входное и выходное сопротивление. Важно знать, что они из себя представляют, как определяются и какую роль играют в работе устройства.

Пример сложной цепи

Понятие входного сопротивления для постоянного тока

Радиоэлектронные устройства могут быть не только относительно, но и очень сложными, состоящими из многих блоков. Однако независимо от сложности устройства, количества используемых в нем деталей, схему можно рассматривать в качестве совокупности простых частей с определенной разностью потенциалов на входе. На выходе блока имеется ещё два контакта, на которых также присутствует напряжение. В первом случае его называют входным, в другом — выходным. Сказанное можно пояснить следующим рисунком.

Упрощённое изображение блока

Входное сопротивление цепи можно легко измерить с помощью вольтметра. Также нетрудно определить силу тока, протекающего между контактами. Для этого достаточно к схеме последовательно подключить амперметр. Получив эти два параметра, по закону Ома можно определить сопротивление схемы. Его называют входным. Иногда при этом рассматривают входное сопротивление длинной линии. Его определяющим свойством является то, что при подключении нагрузки к клеммам источника питания электрические характеристики не меняются.

Устройство блока может быть достаточно сложным, но в рассматриваемом случае не принимаются во внимание особенности его конструкции. Фактически можно представить, что внутри как бы находится резистор с определенным активным сопротивлением, соответствующим измеренному.

Мнимый резистор

Входное электрическое сопротивление рассматривается как общая характеристика конкретного блока. Напряжение на вход может поступать с выхода другого блока или, например, с клемм аккумулятора или батареи.

Что такое внутреннее сопротивление при переменном токе

В предыдущем разделе было рассмотрено чисто активное сопротивление. При наличии в цепи только активного сопротивления фазы напряжения и тока совпадают. В реальных схемах обязательно присутствует реактивное сопротивление, которое делится еще на ёмкостное и индуктивное. Для постоянного тока его значение принято считать пренебрежимо малым и не принимать во внимание при расчёте параметров.

Блок, через который проходит переменный ток

Если используется переменное напряжение на входе, тогда рассматривается полное сопротивление, состоящее из активного и реактивного. Их суммируют, используя правило прямоугольного треугольника. В этом случае один катет соответствует активному сопротивлению, второй — реактивному, а гипотенуза — полному или импедансу.

Важно учитывать, что в цепи с переменным током фаза напряжения сдвигается относительно фазы тока. Сдвиг фаз зависит от соотношения активного и реактивного сопротивлений конкретной цепи.

При отсутствии конденсаторов и катушек индуктивности в цепи емкостным и индуктивным сопротивлениями можно пренебречь и учитывать только активное. В этом случае ток будет следовать за напряжением, одновременно принимая нулевые и максимальные значения.

Если же в цепь включить катушку или конденсатор, создающих индуктивное или емкостное сопротивление настолько большого значения, что активное становится пренебрежимо малым, то сдвиг фаз будет равен π/2.

Сдвиг фаз между током и напряжением

Так как реактивное сопротивление зависит от частоты поступающего сигнала, то чтобы более точно определить импеданс, необходимо узнать нужные параметры при двух различных частотах.

Следует принимать во внимание, что входное полное сопротивление линии может быть различным в отличающихся температурных условиях. Характер и величина отличий зависит от конкретного устройства рассматриваемого блока. Также требуется учитывать обратное влияние самой процедуры измерения на электрические параметры схемы.

Входное сопротивление зависит еще и от того, каким способом вводится в цепь сигнал обратной связи (ОС). Если этот сигнал отсутствует, то входное сопротивление определяется напряжением и током, присутствующими на входе. В том случае, когда обратную связь вводят по последовательной схеме, сопротивление на входе увеличивается при отрицательной ОС и уменьшается при положительной ОС.

При использовании параллельной схемы введения ОС входное сопротивление уменьшается и при отрицательной, и при положительной ОС. При небольшом сопротивлении в цепи ОС оно может составлять десятые, и даже тысячные доли Ома.

Как измерить

При определении входных параметров блока его устройство не рассматривается, но при этом может возникнуть необходимость провести измерение входного сопротивления. Блок выглядит как чёрный ящик, имеющий две входных и две выходных клеммы. Наиболее простым решением является определение входного напряжения и силы тока. Для простоты можно предположить, что рассматривается постоянный ток. Определить входное электрическое сопротивление в этом случае можно способом, который описан далее.

Пример разделения схемы на отдельные блоки

Найти входное сопротивление можно, разделив напряжение на силу тока. Однако в рассматриваемом случае нужно понимать, что если напряжение подаётся с батареи, то на показания будет влиять внутреннее сопротивление источника тока.

Если в блоке используется конденсатор, то нужно учитывать, что через него ток проходить не будет. С другой стороны, для переменного тока он помехой не является. Для переменного тока в качестве входного сопротивления цепи рассматривается полное сопротивление (импеданс). Оно представляет собой векторную сумму активного (омического) и реактивного (индуктивного и ёмкостного) сопротивлений. Однако его значение будет отличаться при различных частотах. Поэтому процедура измерения является более сложной по сравнению с постоянным током. В этом случае может быть использована следующая схема.

Схема измерения

В данной схеме применён генератор переменного тока, который расположен слева. Его соединяют с исследуемым блоком, подавая на него переменный ток. На одном из соединительных проводов ставится резистор с известным сопротивлением R.

Напряжение измеряют дважды — перед резистором и после него. Пусть его значение будет равно U1 и U2 соответственно. Как известно, при переменном входном токе I(вх) падение напряжения на этой детали составит U2 – U1. С другой стороны оно будет равно I(вх) × R. В результате может быть получена следующая формула:

Из этой формулы можно определить величину входного тока:

I(вх) = ( U2 − U1 ) / R.

На вход исследуемого блока поступает напряжение U2:

Входное сопротивление R(вх) найдем, используя формулу:

( U2 − U1 ) / R = U2 / R(вх).

Определяем значение сопротивления:

R(вх) = R × U2 / ( U2 − U1 ).

Все величины в правой части равенства являются известными или были измерены. Подставив их формулу, можно определить величину входного сопротивления схемы.

Применение описанного здесь способа позволяет точно вычислять входное сопротивление даже в тех случаях, когда оно очень велико.

Выходное напряжение

При рассмотрении упрощённой схемы блока видно, что у него имеется выходное напряжение. Оно появляется на контактах, указанных на изображении справа.

Схема для выходного сопротивления

На рисунке показан идеальный источник тока, который, как предполагается, не имеет внутреннего сопротивления. Это означает, что может быть создан сколько угодно большой ток. Имеющийся на схеме резистор нарушает определенную идеальность, ограничивая величину тока при коротком замыкании.

Измерение выходного тока может быть выполнено следующим образом. Напряжение U является известной величиной. При коротком замыкании может быть измерен проходящий по контактам ток. Выходное сопротивление R(вых) определяется по закону Ома. Для его вычисления необходимо напряжение разделить на ток.

Однако этот способ неудобен, так как большой ток нарушает условия функционирования схемы и может привести к поломкам. Поэтому на практике между клеммами ставят дополнительный резистор с известной величиной сопротивления R и только после этого измеряют значение силы тока I и напряжения U2. Предварительно следует определить разность потенциалов U1 с помощью вольтметра. Исходя из закона Ома, получают следующую формулу:

R(вых) = ( U2 – U1 ) / ( U2 / R ).

Практическое применение

Понятие входного сопротивления играет важную роль при согласовании характеристик соединённых между собой блоков. Сказанное можно пояснить на следующем примере.

Предположим, что первым блоком является источник питания. Если к его клеммам присоединён следующий блок, то при практическом определении его входного сопротивления станет понятно, что оно немного меньше расчётной величины.

Это связано с наличием внутреннего сопротивления аккумулятора. Чем оно больше, тем искажение заметнее. Аналогичная ситуация наблюдается при соединении двух любых других блоков. Чтобы передача сопротивления проходила с минимальными потерями, необходимо, чтобы выходное сопротивление предыдущего блока было намного меньше входного у последующего.

С учетом этого обстоятельства необходимо уметь определять рассматриваемые величины, а при создании схемы обеспечивать их правильное соотношение. Если оно будет нарушено, то произойдёт значительное падение напряжения при передаче.

На практике обычно сталкиваются с очень большими значениями входных сопротивлений. В некоторых случаях они могут достигать 1 МОм. Это часто происходит при относительно небольшом входном напряжении. В результате сила рассматриваемого тока получается также небольшой.

В электронике входное и выходное сопротивление играют важную роль. Все качественные измерительные приборы стараются делать с очень высоким входным сопротивлением, чтобы оно минимально сказывалось на измеряемом сигнале и не гасило его амплитуду.

Что касается качественных источников питания, то их выпускают с очень небольшим выходным сопротивлением, чтобы при подключении низкоомной нагрузки напряжение на выходе «не проседало». Но даже если это случится, его можно подкорректировать вручную, используя регулировку выходного напряжения, присутствующую в каждом нормальном источнике питания.

Калькулятор напряжения – расчет по току, сопротивлению, мощности

Расчет электрического напряжения по току, сопротивлению, мощности с помощью калькулятора – рассчитайте напряжение онлайн и по формулам.

  • Расчёт
  • Скачать

Используйте калькулятор напряжения для расчета вольтажа сети по известным значениям силы тока, сопротивления, мощности. Алгоритм программы выполняет подсчеты по формулам закона Ома для участка цепи. Чтобы получить результат, выберите необходимый тип операции, заполните поля и нажмите кнопку «Рассчитать».

Смежные нормативные документы:

  • СП 256.1325800.2016 «Электроустановки жилых и общественных зданий. Правила проектирования и монтажа»
  • СП 31-110-2003 «Проектирование и монтаж электроустановок жилых и общественных зданий»
  • СП 76.13330.2016 «Электротехнические устройства»
  • ГОСТ 31565-2012 «Кабельные изделия. Требования пожарной безопасности»
  • ГОСТ 10434-82 «Соединения контактные электрические. Классификация»
  • ГОСТ Р 50571.1-93 «Электроустановки зданий»

Формулы расчета напряжения

Электрическое напряжение (U) — это скалярная физическая величина, которая равна работе электрического поля по перемещению заряда из одной точки цепи к другой. Международная единица измерения — Вольт (В / V).

— Напряжение по току и сопротивлению: U = I × R
— Напряжение по току и мощности: U = P / I
— Напряжение по мощности и сопротивлению: U = √(P × R)

Делитель напряжения. Расчет делителя напряжения.

Делитель напряжения, одна из широко используемых схем соединения резисторов. Делитель напряжения позволяет уменьшить выходное напряжение. Например, на вход делителя подается 12 Вольт, а на выходе 3 Вольта, или сколько нужно, но не больше входного напряжения делителя. Схема соединения резисторов, о которой мы говорим, может использоваться только для слаботочной нагрузки, чуть позже я объясню почему. Вот собственно и сама схема делителя:

Расчет делителя напряжения

Делитель напряжения вы все ни один раз видели, например, регулятор громкости. Регулятором громкости является переменный резистор, соединенный по схеме потенциометра.

Потенциометр и реостат Потенциометр, можно представить как два резистора, соединённых последовательно, при вращении рукоятки один резистор уменьшает свое сопротивление, другой увеличивает.

В делителе напряжения, входное напряжение полностью падает на двух резисторах. Например, входное напряжение 40 Вольт и если на одном резисторе падает 3 Вольта, то на другом 37 Вольт.

Делитель напряжения_1

Расчет делителя напряжения.

Сразу скажу одно правило, ток, протекающий через резистор R1 и R2 должен быть как минимум в 10 раз больше, чем ток нагрузки (иначе будет просадка напряжения на выходе). Например, если к нашему девайсу будет подсоединена лампа, потребляющая ток 40 мА, то делитель нужно рассчитывать так, чтобы ток, текущий через резисторы R1 и R2 был минимум 400 мА (в 10 и более раз больше).

И еще один нюанс. Ток делителя не только должен быть больше тока нагрузки в 10 раз, но и должен быть меньше тока, выдаваемого источником тока. Вот пример, мы посадили на выход делителя напряжения лампу, потребляющую 200 мА, соответственно ток через делитель потечет как минимум в 10 раз больше (2 Ампер), но если источник тока у нас рассчитан выдавать 1 Ампер, то он просто напросто не вытянет и сгорит, либо сработает защита.

Поэтому есть правило. При расчете делитель напряжения нужно рассчитывать так, чтобы ток через него был как минимум в 10 раз больше тока нагрузки и меньше максимального тока источника. Отсюда делитель напряжения используют для слаботочных нагрузок.

Входной ток (ток делителя) ищется по такой формуле:

Например, у меня входное напряжение 12 Вольт (10 Ампер), мне нужен делитель напряжения, у которого на выходе нагрузка напряжением 3 Вольта и током потребления 20 мА (зацеплю светодиод).

Делитель напряжения_2

Ток делителя Iвх должен быть минимум в 10 раз больше тока нагрузки, возьму в 20 раз. Получается Iвх = 20 мА*20=400мА.

Найдем теперь сумму резисторов R1 и R2 (Rобщ) зная ток, текущий через них 0,4 Ампер и напряжение на них 12 Вольт. Rобщ=12 Вольт/0,4 Ампер = 30 Ом.

Далее нахожу номинал резистора R2 по следующей формуле:

R2 = (3 Вольта*30 Ом)/12 Вольт = 7,5 Ом.

Теперь нахожуу R1, R1 = Rобщ – R2 = 30 – 7,5 = 22,5 Ом.

Давайте проверим по этой формуле:

Iвх = 3 Вольт / 7,5 Ом = 0,4 Ампер.

Iвх = 12 Вольт / 30 Ом = 0,4 Ампер.

Рассчитаем мощность резисторов. Напряжение на R2 = 3 Вольт, значит напряжение на R1 = Uвх-Uвых = 9 Вольт (я уже говорил, если на одном падает 3 Вольта, то на втором резисторе делителя падает остальное напряжение).

Мощность ищется по следующей формуле:

Формула расчета мощности

P1 = 9 Вольт* 0,4 Ампер = 3,6 Вт (из стандартного ряда 5 Вт);

P2 = 3 Вольт* 0,4 Ампер = 1,2 Вт (из стандартного ряда 2 Вт);

Вот еще несколько формул, вы их можете использовать для расчета делителя напряжение в зависимости от того, какими известными значениями вы владеете.

Делитель_4

  • Проверка расчета практически.

Делитель напряжения_2

При расчете мы получили следующие номиналы резисторов, R1 = 22,5 Ом (из стандартного рядя 22 Ом), R2 = 7,5 Ом.

По мощности у меня оба резистора 2 Вт, поэтому R1 у меня сильно греется.

DSC06308

Входное напряжение делителя 12 Вольт.

DSC06295

Напряжение, которое падает на R1 = 22 Ом почти 9 Вольт.

DSC06299

Напряжение, которое падает на R2 = 7,5 Ом (наше выходное напряжение делителя) = 3 Вольта.

DSC06298

Ток, текущий через R1 и R2 (входной ток делителя) = 430 мА.

DSC06305

Светодиод загорается и горит в нормальном режиме, не перегорая.

Источник

Расчет простых цепей постоянного тока

В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.  

Пример 1


  Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов  R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.

Схема простой электрической цепи 

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи. 

Формула 1Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов. 

Формула 2

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем. 

Формула 3

Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.

В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками. 

Формула 4

Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.

Формула 5

Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.

Пример 2


  Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Схема для примера 2

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов. 

Токи в резисторах Формула 6

В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Формула 7

Если у вас возникли затруднения, прочтите статью законы Кирхгофа.

Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи 

Формула 8

А затем напряжение 

Формула 9

Зная напряжения, найдем токи, протекающие через резисторы 

Формула 10

Как видите, токи получились теми же.

Пример 3

  В электрической цепи, изображенной на схеме R1=50 Ом, R2=180 Ом, R3=220 Ом. Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.

Схема для примера 3 

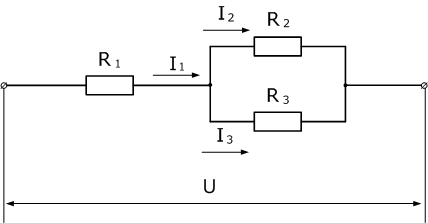
Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.

Эквивалентное сопротивление и ток в цепи 

Формула 11Отсюда мощность, выделяемая на R1 

Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим 

Формула 13

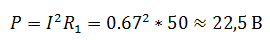
Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3, как напряжение на резисторе R2 

Формула 14

Таким образом производится расчет простых цепей постоянного тока.

  • Просмотров: 102106
    • Источник

    Добавить комментарий