Измерения показывают, что напряжение на зажимах источника тока, замкнутого на внешнюю цепь, зависит от силы отбираемого тока (от «нагрузки») и изменяется с изменением последнего. Пользуясь законом Ома, мы можем сейчас разобрать этот вопрос точнее.
Из формулы (80.1) имеем
![]()
, (81.1)
где
![]()
– сопротивление внешней цепи, а
![]()
– внутреннее сопротивление источника. Но к внешней цепи мы вправе применить закон Ома для участка цепи:
![]()
. (81.2)
Здесь
![]()
– напряжение во внешней цепи, т. е. разность потенциалов на зажимах источника. Оно может быть выражено на основании (81.1), (81.2) следующей формулой:
![]()
. (81.3)
Мы видим, что при замкнутой цепи напряжение
![]()
на зажимах источника тока всегда меньше э. д. с.
![]()
. Напряжение
![]()
зависит от силы тока
![]()
и только в предельном случае разомкнутой цепи, когда сила тока
![]()
, напряжение на зажимах равно э. д. с.
Уменьшение напряжения на зажимах источника при наличии тока
![]()
легко наблюдать на опыте. Для этого нужно замкнуть какой-либо гальванический элемент на реостат и подключить к зажимам элемента вольтметр (рис. 127). Перемещая движок реостата, можно видеть, что чем меньше сопротивление внешней цепи, т. е. чем больше ток, тем меньше напряжение на зажимах источника. Если сопротивление внешней цепи сделать очень малым по сравнению с внутренним сопротивлением источника («вывести» реостат), т. е. сделать «короткое замыкание», то напряжение на зажимах делается равным нулю.
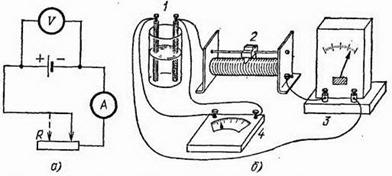
Рис. 127. С уменьшением сопротивления внешней цепи напряжение на зажимах источника тока уменьшается: а) схема опыта; б) общий вид экспериментальной установки, 1 – источник тока, 2 – реостат, 3 – амперметр, 4 – вольтметр
Что же касается тока, то он при коротком замыкании достигает своего максимального значения
![]()
. Сила этого «тока короткого замыкания» получается из закона Ома (80.1), если в нем положить
![]()
(т. е. пренебречь сопротивлением
![]()
по сравнению с
![]()
):
![]()
. (81.4)
Отсюда видно, что ток короткого замыкания зависит не только от э. д. с., но также и от внутреннего сопротивления источника. Поэтому короткое замыкание представляет различную опасность для разных источников тока.
Короткие замыкания гальванического элемента сравнительно безвредны, так как при небольшой э. д. с. элементов их внутреннее сопротивление велико, и поэтому токи короткого замыкания малы. Такие токи не могут вызвать серьезные разрушения, и поэтому к изоляции проводов в целях, питаемых элементами (звонки, телефоны и т. п.), не предъявляют особо высоких требований. Иное дело силовые или осветительные цепи, питаемые мощными генераторами. При значительной э. д. с. (100 и более вольт) внутреннее сопротивление этих источников ничтожно мало, и поэтому ток короткого замыкания может достигнуть огромной силы. В этом случае короткое замыкание может привести к расплавлению проводов, вызвать пожар и т. д. Поэтому к устройству и изоляции таких цепей предъявляют строгие технические требования, которые ни в коем случае нельзя нарушать без риска вызвать опасные последствия. Такие цепи всегда снабжаются предохранителями (§ 63) и притом нередко в различных местах: общий предохранитель (при главном вводе), групповые и штепсельные предохранители.
81.1.
Внутреннее сопротивление элемента Даниеля с э. д.с. 1,1 В равно 0,5 Ом. Вычислите ток короткого замыкания этого элемента.
81.2.
Элемент из предыдущей задачи замкнут на сопротивление 0,6 Ом. Чему равно напряжение на зажимах элемента?
81.3.
Э. д. с. генератора постоянного тока равна 220 В, а внутреннее сопротивление равно 0,02 Ом. Какой ток возникает при коротком замыкании?
81.4.
При измерении э. д. с. источников при помощи вольтметра мы всегда допускаем некоторую погрешность, так как через вольтметр течет некоторый, хотя и очень малый, ток, и поэтому источник, строго говоря, не разомкнут, а замкнут на вольтметр. Пусть внутреннее сопротивление элемента равно 1 Ом, его э. д. с. равна 1,8 В, а сопротивление вольтметра равно 179 Ом. Какую погрешность при измерении э. д. с. мы допускаем?
81.5.
Можно ли точно измерить э. д. с. при помощи электрометра? Как нужно присоединить электрометр к элементу для измерения его э. д. с.?
81.6.
Изменяется ли показание электрометра, соединенного с гальваническим элементом, если параллельно с ним включить конденсатор, как показано на рис. 128? Будет ли иметь значение емкость конденсатора?
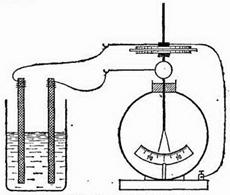
Рис. 128. К упражнению 81.6
81.7.
Э. д. с. некоторого элемента измеряют при помощи электрометра с конденсатором (рис. 129, а). Электрометр, отсоединенный от элемента, после снятия диска показывает 500 В (рис. 129, б). При этом известно, что емкость конденсатора при удалении диска уменьшается в 250 раз. Чему равно напряжение элемента?
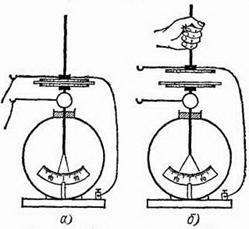
Рис. 129. К упражнению 81.7
Электроника
учебно-справочное пособие
Расчет простых цепей постоянного тока
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1
Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r=0,5 Ом. Сопротивления резисторов R1 = 20 и R2 = 32 Ом (рис. 1). Определить ток в цепи и напряжения на резисторах.

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.

Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.
Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
50 = 0,95·20 + 0,95·32 + 0,95·0,5
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей. В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
0,95·50 = 0,95 2 ·20 + 0,95 2 ·32 + 0,95 2 ·0,5
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2
Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА (рис. 2). Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах:

В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.
Решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи:

А затем напряжение:
Зная напряжения, найдем токи, протекающие через резисторы

Токи получились теми же.
Пример 3
В электрической цепи, изображенной на рис. 3 R1=50 Ом, R2=180 Ом, R3=220 Ом. Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.

Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.
Эквивалентное сопротивление и ток в цепи

Отсюда мощность, выделяемая на R1:
Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим

Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3 , как напряжение на резисторе R2:
Пример 4
Имеется лампочка на напряжение 12 В мощностью 20 Вт и источник 17 В, к которому нам нужно подключить эту лампочку. Рассчитать резистор, который понизит напряжение 17 В до 12 В (рис. 4).

При последовательном соединении элементов напряжения на них могут отличаться, но ток всегда одинаковый на любом участке цепи. Вычислим ток, потребляемый лампочкой:

Значит, через резистор протекает такой же ток. В качестве напряжения берем падение напряжения на гасящем резисторе, ведь это действительно то самое напряжение, которое действует на этом резисторе ( Uобщ=UR1+UR2 )

Из приведенного примера совершенно очевидно, что  . Причем это относится не только к резисторам, но и, например, к динамикам, если мы вычисляем какое напряжение нужно подвести к динамику с заданной мощностью и сопротивлением, чтобы он развил эту мощность.
. Причем это относится не только к резисторам, но и, например, к динамикам, если мы вычисляем какое напряжение нужно подвести к динамику с заданной мощностью и сопротивлением, чтобы он развил эту мощность.

Источники:
Электроника © ЦДЮТТ • Марсель Арасланов • 2019
Источник
Резистивные электрические цепи
Содержание:
Расчёт резистивных электрических цепей в статическом режиме:
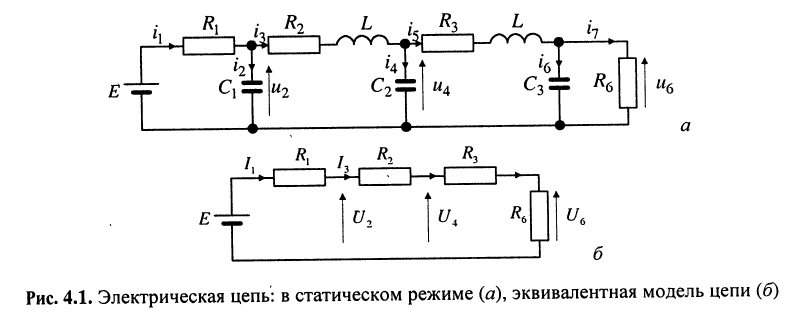
Электрическая цепь характеризуется режимом работы, который определяет характер действующих в ней напряжений и токов. Наиболее просто задача составления уравнений решается для цепей, находящихся в статическом режиме. Говорят, что цепь находится в статическом режиме, если все действующие в ней токи и напряжения являются постоянными. Статический режим соответствует постоянному току (рис. 4.1, а). В этом случае схема замещения индуктивности представляет собой короткозамкнутую цепь, а схема замещения ёмкости — разрыв цепи <см. разд. 3.1.1). Поэтому в эквивалентной модели цепи (рис. 4.1, б), находящейся в статическом режиме, содержатся только резистивные элементы.
Иначе говоря, в статическом режиме имеем резистивную модель цепи, что позволяет ограничиться анализом только резистивной цепи. Тем не менее, результаты, полученные для этого случая, в последующем будут распространены на анализ линейных цепей общего вида.
Расчёт последовательных электрических цепей (делители напряжений)
Рассмотрим последовательную электрическую цепь, состоящую из п рези-стивных элементов и одного источника напряжения
(рис. 4.2).
Задача 4.1.
Определить ток 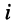
Решение. Согласно закону Ома для выбранных направлений отсчётов тока и напряжений получим:
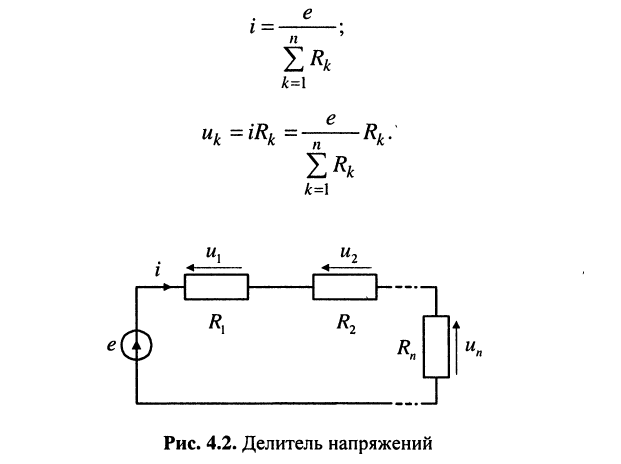
Вывод: для определения напряжения на любом элементе последовательной цепи необходимо заданное напряжение источника разделить на сумму сопротивлении всех резистивных элементов и умножить на сопротивление данного элемента.
Полученное положение часто называют правилом деления напряжений, а саму цепь — делителем напряжений.
Расчёт параллельных электрических цепей (делители токов)
Рассмотрим параллельную электрическую цепь, состоящую из 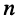 резистивных элементов и одного источника тока (рис. 4.3).
резистивных элементов и одного источника тока (рис. 4.3).
Задача 4.2.
Определить напряжение и на зажимах цепи и токи 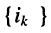 в резистивных элементах.
в резистивных элементах.
Решение. Согласно закону Ома для выбранных направлений отсчёта тока и напряжений получим:
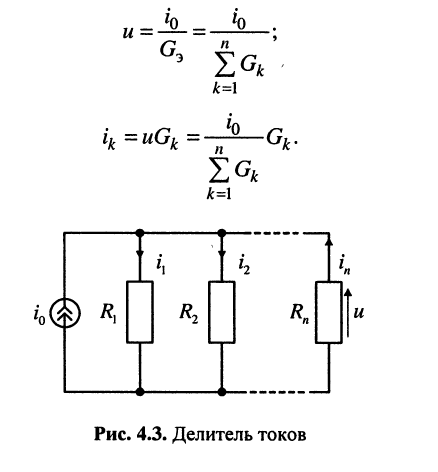
Вывод: для определения тока в любом резистивном элементе параллельной цепи необходимо задающий ток i0 источника разделить на сумму проводимостей всех элементов и умножить на проводимость того элемента, по которому протекает искомый ток.
Полученное положение часто называют правилом деления токов, а саму цепь — делителем токов.
Расчёт параллельно-последовательных электрических цепей
Определение:
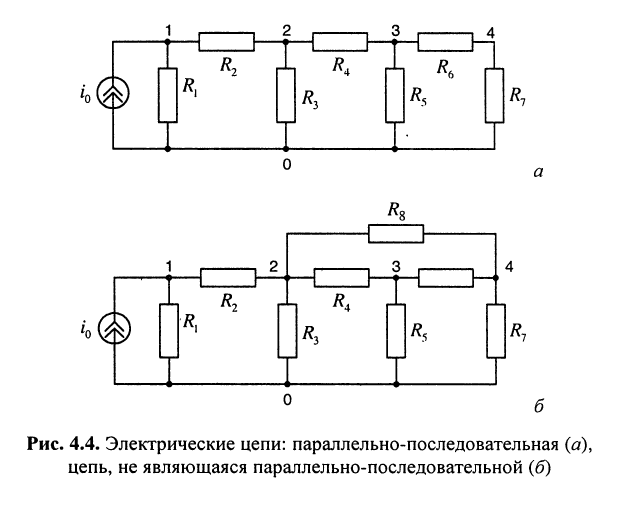
Параллельно-последовательной электрической цепью называется цепь, которая представляет собой совокупность ветвей, связанных между собой только параллельно или последовательно.
Пример такой цепи приведён на рис. 4.4, а, где резистивные элементы 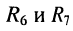 включены последовательно; параллельно к ним подключён элемент
включены последовательно; параллельно к ним подключён элемент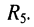 . Последовательно с двухполюсником из элементов
. Последовательно с двухполюсником из элементов 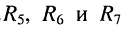 подключён элемент
подключён элемент 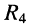 и т. д. вплоть до элемента
и т. д. вплоть до элемента 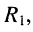 соединённого параллельно с источником тока и двухполюсником, образуемым всеми остальными элементами цепи.
соединённого параллельно с источником тока и двухполюсником, образуемым всеми остальными элементами цепи.
Если цепь рис. 4.4, а дополнить резистивным элементом или каким-либо источником, включённым не между смежными узлами, то полученная цепь уже не будет параллельно-последовательной; такая цепь получается, например, при включении элемента 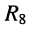 между узлами 2 и 4 (рис. 4.4, б).
между узлами 2 и 4 (рис. 4.4, б).
Расчёт параллельно-последовательных электрических цепей с одним источником
Напряжения и токи в параллельно-последовательных резистивных цепях с одним источником находятся путём эквивалентных преобразований схемы заданной цепи в направлении к источнику тока 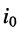 или источнику напряжения
или источнику напряжения 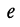 по следующему правилу:
по следующему правилу:
- анализируется структура цепи и выделяется самый удалённый от источника воздействия элемент, от которого и начинаются эквивалентные преобразования;
- резистивные элементы, соединённые только последовательно или только параллельно, заменяются их эквивалентами;
- эквивалентные замены проводятся до тех пор, пока схема заданной цепи не преобразуется в схему последовательной или параллельной цепи;
- для полученной эквивалентной цепи по закону Ома находится ток, протекающий через источник напряжения, или напряжение на зажимах источника задающего тока;
- исходная схема цепи восстанавливается в обратном порядке и на основании правил, установленных в разд. 4.1 и 4.2, находятся токи, протекающие в элементах, и напряжения на этих элементах.
Пример 4.1.
Найти напряжения на элементах параллельно-последовательной цепи, изображённой на рис. 4.5, а.
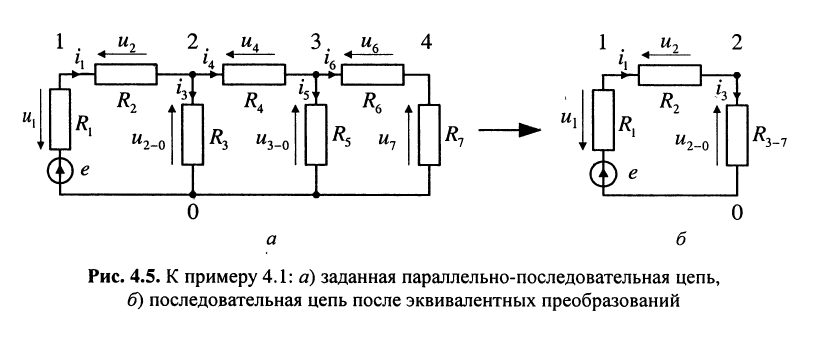
а) последовательно соединённые элементы 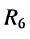 и
и 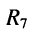 , заменяются двухполюсником
, заменяются двухполюсником
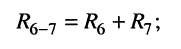
б) параллельно соединённые элемент 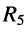 и двухполюсник
и двухполюсник 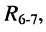 включённые между узлами 3 — 0, заменяются двухполюсником
включённые между узлами 3 — 0, заменяются двухполюсником
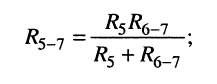
в) последовательно соединённые элемент 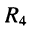 и двухполюсник
и двухполюсник 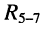 заменяются двухполюсником
заменяются двухполюсником
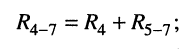
г) параллельно соединённые элемент 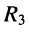 и двухполюсник
и двухполюсник 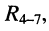 включённые между узлами 2 — 0, заменяются двухполюсником
включённые между узлами 2 — 0, заменяются двухполюсником
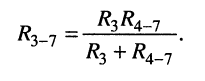
На этом эквивалентные преобразования завершаются, поскольку полученная эквивалентная цепь (рис. 4.5, б) представляет собой последовательное соединение источника напряжения 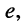 элементов
элементов 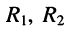 и двухполюсника
и двухполюсника 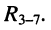
Вычисление токов и напряжений на элементах схемы эквивалентной цепи:
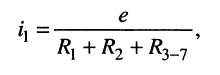
по правилу деления напряжений получаем:
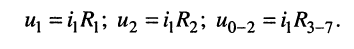
Вычисление токов и напряжений на резистивных элементах схемы исходной цепи (в обратном порядке для восстановления цепи):
а) по правилу деления токов находим ток 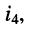 протекающий через элемент
протекающий через элемент 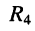 и двухполюсник
и двухполюсник 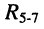
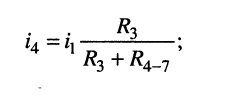
б) по правилу деления напряжений вычисляем напряжение на элементе 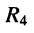 и на двухполюснике
и на двухполюснике 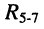 (между узлами 3-0)
(между узлами 3-0)
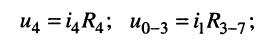
в) аналогично определяем токи 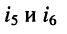
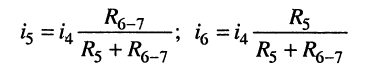
и напряжения на элементах 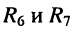
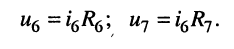
Расчёт параллельно-последовательных электрических цепей с несколькими источниками
Для нахождения токов и напряжений в цепи с несколькими независимыми источниками применяется свойство аддитивности линейной цепи (1.2), называемое часто принципом наложения или суперпозиции, который обычно формулируют в виде теоремы:
Реакция линейной электрической цепи на совокупность воздействий равна сумме реакций, вызываемых в той же цепи каждым из воздействий в отдельности.
Смысл принципа наложения состоит в том, что если к линейной электрической цепи подведено 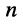 воздействий, например, в виде ЭДС
воздействий, например, в виде ЭДС 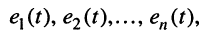 то реакция в любом из элементов цепи, например ток
то реакция в любом из элементов цепи, например ток 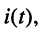 будет представлять сумму токов
будет представлять сумму токов 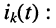
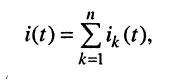
где 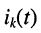 — ток в рассматриваемом элементе цепи, вызываемый воздействием ЭДС
— ток в рассматриваемом элементе цепи, вызываемый воздействием ЭДС 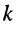 -го источника
-го источника 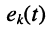 при условии, что ЭДС остальных источников положены равными нулю.
при условии, что ЭДС остальных источников положены равными нулю.
Принцип наложения является следствием линейности оператора, с помощью которого описывается электрическая цепь
(см. разд. 1.4). Именно этот принцип может быть использован для практического определения линейности цепи: если в результате эксперимента над некоторой электрической цепью окажется, что реакция цепи на сумму воздействий равна сумме реакций на каждое из воздействий в отдельности, то исследуемая цепь является линейной.
Пример 4.2.
Найти напряжения на резистивном элементе 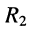 параллельно-последовательной цепи с двумя независимыми источниками, изображённой на рис. 4.6, а.
параллельно-последовательной цепи с двумя независимыми источниками, изображённой на рис. 4.6, а.
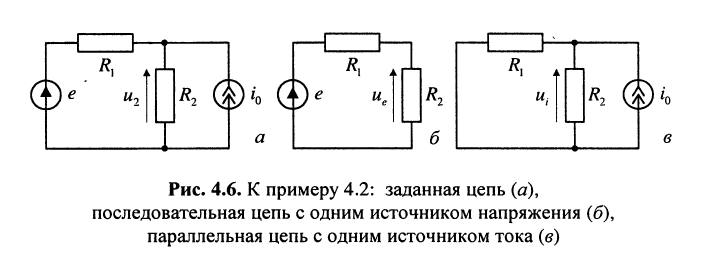
Решение. Согласно принципу наложения напряжение 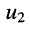 равно сумме напряжений
равно сумме напряжений 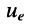 и
и 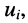 создаваемых соответственно источником напряжения и источником тока в отдельности
создаваемых соответственно источником напряжения и источником тока в отдельности
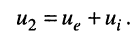
1. Положим, что в цепи имеется только источник напряжения, а задающий ток источника тока равен нулю; в этом случае ветвь, содержащая источник тока, оказывается разомкнутой (рис. 4.6, б); тогда образуется последовательная цепь, в которой
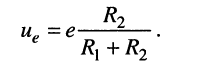 (4.1)
(4.1)
2. Положим, что в цепи имеется только источник тока, а задающее напряжение источника напряжения равно нулю; в этом случае ветвь, содержащая источник напряжения, оказывается замкнутой накоротко (рис. 4.6, в); тогда образуется параллельная цепь, в которой
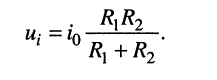 (4.2)
(4.2)
Складывая (4.1) и (4.2), окончательно получаем
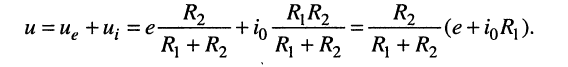 (4.3)
(4.3)
Расчёт электрических цепей методами уравнений Кирхгофа
На практике электрические цепи являются не столь простыми, нежели рассмотренные, и далеко не всегда представляют собой комбинацию последовательно и параллельно соединённых ветвей. Примером часто используемой цепи является удлинитель
(рис. 4.7). Расчёт (анализ) таких цепей осуществляются на основании прямого применения законов Кирхгофа (см. лекцию 2).
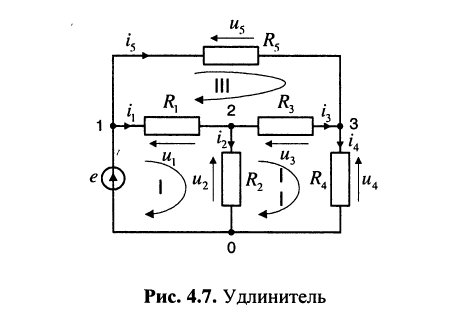
В зависимости от того, что подлежит определению, различают два метода: метод токов ветвей и метод напряжений ветвей, которые обычно называют прямыми методами расчёта цепей.
Метод уравнений Кирхгофа заключается в составлении и решении трёх групп уравнений:
- уравнений по первому закону Кирхгофа для узлов;
- уравнений по второму закону Кирхгофа для замкнутых контуров;
- уравнений по закону Ома для каждого элемента цепи.
4.4.1. Метод токов ветвей
В методе токов ветвей неизвестными, подлежащими определению, являются токи ветвей. Существо метода состоит в следующем.
Пусть цепь содержит 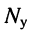 узлов и
узлов и 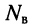 ветвей, включая источники напряжения. Поскольку неизвестными являются токи в ветвях, число необходимых независимых уравнений должно быть равно
ветвей, включая источники напряжения. Поскольку неизвестными являются токи в ветвях, число необходимых независимых уравнений должно быть равно 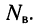 По первому закону Кирхгофа можно составить только
По первому закону Кирхгофа можно составить только
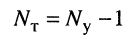
независимых уравнений (2.4).
По второму закону Кирхгофа можно составить только
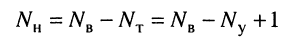
независимых уравнений (2.6).
На основании полученных зависимостей можно сформулировать порядок расчёта цепи рассматриваемым методом:
- На схеме цепи выбираются положительные направления токов в ветвях и напряжений на элементах.
- Составляется
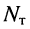 независимых уравнений относительно токов в узлах по первому закону Кирхгофа.
независимых уравнений относительно токов в узлах по первому закону Кирхгофа. - Составляется
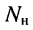 независимых уравнений относительно контурных токов по второму закону Кирхгофа.
независимых уравнений относительно контурных токов по второму закону Кирхгофа. - Напряжения на резистивных элементах, входящие в уравнения п. 3, выражаются через токи по закону Ома.
- Полученная система из
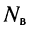 уравнений решается относительно искомых величин.
уравнений решается относительно искомых величин.
Пример 4.3.
Рассчитать токи всех ветвей удлинителя (см. рис. 4.7).
Решение. Для однозначного составления уравнений выберем направления токов и напряжений такими, как показано на рисунке.
Удлинитель имеет 4 узла и 6 ветвей, поэтому по первому закону Кирхгофа можно составить
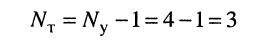
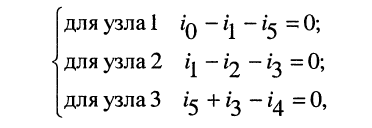 (4.4)
(4.4)
и по второму закону Кирхгофа можно составить также
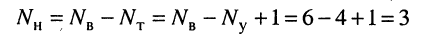
независимых уравнения; при выбранных направлениях обхода контуров получаем:
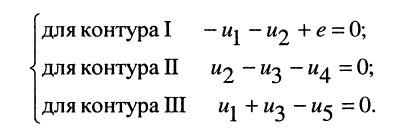 (4.5)
(4.5)
Выразим напряжения 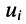 , на резисторах
, на резисторах 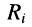 через токи
через токи 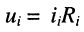 ; и полученные выражения подставим в систему уравнений для напряжений в контурах:
; и полученные выражения подставим в систему уравнений для напряжений в контурах:
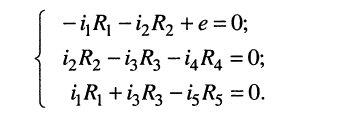 (4.6)
(4.6)
Объединение систем уравнений 4.4 и 4.6 даёт систему (4.7), в которой переменными являются токи ветвей (элементов).
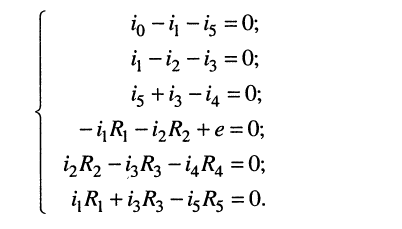 (4.7)
(4.7)
Объединённая система уравнений является неоднородной системой из шести алгебраических уравнений относительно такого же числа неизвестных 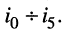
Метод напряжений ветвей
В методе напряжений ветвей неизвестными, подлежащими определению, являются напряжения на элементах цепи. Метод подобен методу, рассмотренному в разд. 4.4.1, а именно: так же, как и в предыдущем случае, составляются две системы уравнений по первому и второму законам Кирхгофа, однако теперь все токи ветвей выражаются через напряжения и проводимости резисторов по закону Ома. Две полученные системы объединяются в одну, результатом решения которой оказываются напряжения на резисторах.
Пример 4.3.
Рассчитать напряжения на элементах удлинителя (см. рис. 4.7) при выбранных на рисунке направлениях токов и напряжений.
Решение. Составляются системы уравнений (4.4) и (4.5), после чего в системе
(4.4) токи 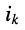 выражаются через напряжения
выражаются через напряжения 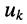 на резисторах
на резисторах 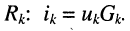 В результате получаем систему
В результате получаем систему
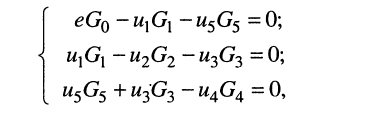 (4.8)
(4.8)
где 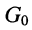 является эквивалентной проводимостью всей цепи. Объединением
является эквивалентной проводимостью всей цепи. Объединением
(4.5) и (4.8) получаем систему
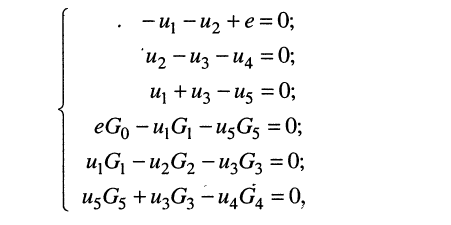 (4.9)
(4.9)
в которой неизвестными являются напряжения на резисторах.
Видно, что метод напряжений ветвей является дуальным по отношению к методу токов ветвей, т. к. для получения системы (4.9) достаточно в системе (4.7) произвести простую замену токов на напряжения и сопротивлений на проводимости.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гармонические напряжения и токи
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Электрические цепи синусоидального тока
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Электрические цепи с распределенными параметрами
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник
Чему равно напряжение на зажимах источника тока?
Напряжение на зажимах источника тока равно падению напряжения на внешнем сопротивлении цепи: V=IR, где I=ε/(R+r) отсюда r=R(e-V)/V=4 Ом.
Как найти напряжение на зажимах цепи?
- или E = I (r + r0), (23)
- т. е. напряжение на участке цепи равно произведению силы тока на сопротивление этого участка. …
- где I r — падение напряжения в сопротивлении r, т. е. …
- Из формулы (26) следует, что напряжение на зажимах источника энергии (генератора) равно разности между э. д.
Чему равно напряжение на зажимах источника эдс работающего в режиме генератора?
Итак, напряжение на зажимах источника, работающего в режиме потребителя, равно сумме ЭДС и внутреннего падения напряжения. Следовательно, напряжение на зажимах источника, отдающего энергию, или генератора, равно разности ЭДС и внутреннего падения напряжения.
Почему напряжение на зажимах источника тока меньше эдс?
Напряжение на зажимах источника меньше ЭДС на величину падения напряжения на внутреннем сопротивлении источника (1): … Очевидно, что напряжение на зажимах источника ЭДС тем больше, чем меньше его внутреннее сопротивление. В идеальном источнике ЭДС R0=0, U=E (напряжение не зависит от величины нагрузки).
Почему напряжение на полюсах источника тока зависит от?
Напряжение на полюсах источника тока зависит от величины отбираемого тока (“от нагрузки”), оно всегда меньше электродвижущей силы источника. … Величина тока, текущего по внешней цепи, зависит от напряжения источника тока и сопротивления, оказываемого этой цепью.
Что показывает вольтметр подключенный к источнику тока?
Идеальный вольтметр, подключенный к зажимам работающего источника тока, показывает напряжение , как это следует из закона Ома для однородного участка цепи – в данном случае для сопротивления нагрузки. … В пределе при напряжение на зажимах разомкнутого источника равно его ЭДС.
Что показывает вольтметр подключенный к источнику тока при разомкнутой цепи?
Вольтметр показывает падение напряжение на его клеммах. Если цепь разомкнута и Вы подсоединили клеммы вольтметра к батарее, то, собственно говоря, сам вольтметр и замкнул цепь, и весь возможный ток проходит через него. Но сопротивление вольтметра очень велико, так что ток получается ничтожный.
Чем опасен режим короткого замыкания для источника?
Опасность короткого замыкания При большой мощности источника ток достигнет очень большой величины, который может повредить источник, потребитель, соединительные провода. Перегрев соединительных проводов может привести к пожару. … Очень опасно КЗ мощных электрохимических источников электричества, — особо аккумуляторов.
Почему при коротком замыкании напряжение равно нулю?
Потому что напряжение на клеммах источника соответствует напряжению на внешней цепи. А при коротком замыкании ток по внешней цепи практически не течет (на то оно и короткое замыкание!). Раз не течет, значит, и напряжение близко к нулю.
Почему падает напряжение при коротком замыкании?
И чем больше будет нагрузка, тем сильнее будет падение напряжения. Так как при коротком замыкании сопротивление цепи практически равно нулю, а сила тока при этом будет максимально возможной, то и падение напряжение на источнике питания также будет максимальной (около нуля).
Какая сила тока возникает при коротком замыкании?
Как раз на последнее и стоит обращать в данном случае пристальное внимание. В связи с тем, что сопротивление проводки очень мало, его принято считать равным «0». При коротком замыкании мгновенно увеличивается сила тока, которая приводит к сильному выделению тепла, происходит перегрев аппаратов и проводов.
Что происходит с силой тока при коротком замыкании?
Ток при коротком замыкании может превысить номинальный ток в цепи во много раз. … При коротких замыканиях резко возрастают токи в короткозамкнутой цепи и снижается напряжение, что представляет большую опасность для электрического оборудования и может вызвать перебои в электроснабжении потребителей.
Как определить силу тока при коротком замыкании?
Методика расчета тока кз
- Определяем полное сопротивление питающей линии до точки короткого замыкания: Zл = √(R2л+X2л), Ом …
- Определяем сопротивление питающего трансформатора …
- Рассчитываем ток короткого замыкания
Чем можно объяснить что при коротком замыкании сила тока в цепи может достигнуть огромного значения?
Причиной короткого замыкания может быть ремонт проводки под током или случайное соприкосновение с открытыми контактами. 4. Чем объяснить, что при коротком замыкании сила тока в цепи может достигнуть огромного значения? При коротком замыкании сопротивление цепи незначительно.
Как происходит пожар при коротком замыкании?
При коротком замыкании мгновенно увеличивается сила тока, которая приводит к сильному выделению тепла. Это – в свою очередь – может привести к расплавлению проводки и её последующему возгоранию.
В каком случае происходит короткое замыкание?
Короткое замыкание может возникать в результате нарушения изоляции токоведущих элементов или механического соприкосновения неизолированных элементов. Также коротким замыканием называют состояние, когда сопротивление нагрузки меньше внутреннего сопротивления источника питания.
Что такое короткое замыкание и как с ним бороться?
Короткое замыкание – это соединение провода заземления или нулевого с фазовым либо двух фазовых проводов. Получается взаимодействие двух проводников с отличающимися потенциалами. Коротким контакт называется, потому что он произошел без электроприбора. При соединении таких проводов происходит маленький взрыв.
Что такое короткое замыкание простыми словами?
Если же говорить простым языком, короткое замыкание – это любое незапланированное, нештатное соединение электрических проводников с разным потенциалом, например, фазы и ноля, при котором образуются разрушительные токи. …
Что такое короткое замыкание и чем оно опасно?
Короткое замыкание является одной из самых опасных неисправностей электрической цепи. … В лучшем случае замыкание просто испортит прибор и сделает его непригодным, но ведь может возникнуть и пожар. Самым опасным считается короткое замыкание электрической сети, потому что она имеет низкое сопротивление.
Как не допустить короткого замыкания?
Чтобы избежать короткого замыкания следует соблюдать определенные правила: Не использовать старые провода с несоответствующей изоляцией. Быть внимательным при проведении электромонтажных работ. Снимать изоляцию при монтаже крайне аккуратно, не резать провод ножом вдоль жил.
Что делать в случае короткого замыкания?
Если место замыкания хорошо видно
- Сразу же идите к щитку, выключайте на автомате выключатель, который отвечает за данный участок электрической цепи. …
- После отключения внимательно следите за точкой, чтобы не было воспламенения. …
- Когда всё закончилось, и опасность миновала, можете вызывать профильного специалиста.
Как работает защита от короткого замыкания?
Так вот, когда большой ток протекает через автомат, в катушке возникает сильный магнитный поток, который приводит в движение механизм расцепителя автомата. … Таким образом, получается, что одна защита (индуктивная) работает на токи короткого замыкания, а вторая на токи, длительно протекающие по кабелю.
Как защиты от возгорания электропроводки?
Меры защиты
- На этапе монтажа или замены электропроводки необходимо предусматривать запас по сечению кабеля. …
- Обеспечить изоляцию проводов от горючих материалов прокладкой из негорючих. …
- При замене проводки стоит применять медный кабель, специально предназначенный для бытовых помещений. …
- Не допускать соединения проводов внутри стен.
Чем тушить проводку в домашних условиях?
Обесточенную проводку можно тушить, по сути, уже всеми доступными средствами – водой, песком, снегом или любым огнетушителем. Сложнее потушить, если проводку по каким-то причинам отключить не удается или у того, кто тушит, нет уверенности в том, что вся проводка надежно обесточена.
Что делать если загорелся щиток?
Когда горит проводка, первое, что нужно сделать – это обесточить объект. Сделать это в частной квартире или доме можно выкрутив пробки счетчика, или же специальным реле-переключателем (автомат защиты). Только после обесточивания можно начать тушить, иначе велик риск получить электрическое поражение.
Чем опасны оголенные провода?
Если поврежден провод, питающий устройство непосредственно от сети 220В, то случайное замыкание «на себя» может вызвать поражение электрическим током. Например, при случайном касании оголенных концов провода. Такая ситуация может стать причиной ожога, проблем со здоровьем или даже привести к смерти.
Что будет если не изолировать провода?
Итак: Прежде всего, при обнаружении оголенных проводов не включайте свет и не включайте никаких электрических приборов. Это может привести к подаче напряжения на поврежденный участок и короткому замыканию. … Если же напряжения нет, то это совсем не значит, что проводка повреждена.
Что будет если помочиться на оголенный провод?
Ничего. Струя мочи слишком разделена и не составляет достаточно цельного потока, чтобы электрический ток, даже высоковольтный, смог через нее пройти и ударить человека.
Что будет если тронуть оголенный провод?
Это очень опасно. Если задеть оголенный провод включенного прибора, можно получить поражение током. … Если вы прикасаетесь к включенному электроприбору мокрыми руками, то рискуете получить удар током. Перед тем как включать, выключать или еще что-либо делать с электроприбором, руки надо вытереть насухо!১৪ মে, ২০১৯
Что такое оголенный провод?
«Оголённый провод» (англ. The Living End) — кинофильм Грегга Араки о нескольких днях жизни вне закона двух ВИЧ-положительных геев, находящихся «в бегах».
Физический смысл закона
Потребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребитель, проходит и через источник тока, а значит, току кроме сопротивления проводника оказывается сопротивление самого источника. Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.
Физический смысл зависимости тока от ЭДС источника и сопротивления цепи заключается в том, что чем больше ЭДС, тем больше энергия носителей зарядов, а значит больше скорость их упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.
Зависимость можно показать на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения в цепи идет ток, наблюдаемый по амперметру, двигая ползунок реостата, увидим, что при изменении внешнего сопротивления ток будет меняться.
Примеры задач на применение закона Ома для замкнутой цепи
К источнику ЭДС 10 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 4 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
| Дано: | Решение: |
|
|
При подключении к батарее гальванических элементов резистора сопротивлением 20 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 10 Ом сила тока стала 1,5 А. Найти ЭДС и внутреннее сопротивление батареи.
1.8. Электрический ток. Закон Ома
Если изолированный проводник поместить в электрическое поле то на свободные заряды q в проводнике будет действовать сила В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю (см. § 1.5).
Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.
Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда Δq, переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени Δt, к этому интервалу времени:
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.
Рисунок 1.8.1.
Упорядоченное движение электронов в металлическом проводнике и ток I. S – площадь поперечного сечения проводника, – электрическое поле
В Международной системе единиц СИ сила тока измеряется в амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током (см. § 1.16).
Постоянный электрический ток может быть создан только в замкнутой цепи, в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю (см. § 1.4). Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.
Цепь постоянного тока можно разбить на отдельные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными. Участки, включающие источники тока, называются неоднородными.
При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов Δφ12 = φ1 – φ2 между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе 12, действующей на данном участке. Поэтому полная работа равна
Величину U12 принято называть напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:
Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
где R = const.
Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
IR = U12 = φ1 – φ2 + = Δφ12 + .
Это соотношение принято называть обобщенным законом Ома или законом Ома для неоднородного участка цепи.
На рис. 1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи (cd) является однородным.
Рисунок 1.8.2.
Цепь постоянного тока
По закону Ома
Участок (ab) содержит источник тока с ЭДС, равной .
По закону Ома для неоднородного участка,
Сложив оба равенства, получим:
I (R + r) = Δφcd + Δφab + .
Но Δφcd = Δφba = – Δφab. Поэтому
Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Сопротивление r неоднородного участка на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока. В этом случае участок (ab) на рис. 1.8.2 является внутренним участком источника. Если точки a и b замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (R <<� r), тогда в цепи потечет ток короткого замыкания
Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику последовательно подсоединяется некоторое внешнее сопротивление. Тогда сопротивление r равно сумме внутреннего сопротивления источника и внешнего сопротивления, и при коротком замыкании сила тока не окажется чрезмерно большой.
Если внешняя цепь разомкнута, то Δφba = – Δφab = , т. е. разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС.
Если внешнее нагрузочное сопротивление R включено и через батарею протекает ток I, разность потенциалов на ее полюсах становится равной
На рис. 1.8.3 дано схематическое изображение источника постоянного тока с ЭДС равной и внутренним сопротивлением r в трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к. з.). Указаны напряженность электрического поля внутри батареи и силы, действующие на положительные заряды: – электрическая сила и – сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.
Рисунок 1.8.3.
Схематическое изображение источника постоянного тока: 1 – батарея разомкнута; 2 – батарея замкнута на внешнее сопротивление R; 3 – режим короткого замыкания
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры.
Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB. Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 1.8.4, это условие записывается в виде:
Это условие означает, что ток IB = Δφcd / RB, протекающий через вольтметр, много меньше тока I = Δφcd / R1, который протекает по тестируемому участку цепи.
Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение.
Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением RA. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 1.8.4 сопротивление амперметра должно удовлетворять условию
чтобы при включении амперметра ток в цепи не изменялся.
Измерительные приборы – вольтметры и амперметры – бывают двух видов: стрелочные (аналоговые) и цифровые. Цифровые электроизмерительные приборы представляют собой сложные электронные устройства. Обычно цифровые приборы обеспечивают более высокую точность измерений.
Рисунок 1.8.4.
Включение амперметра (А) и вольтметра (В) в электрическую цепь
Применение закона Ома к расчету линейных электрических цепей постоянного тока
1. Найти ток ветви (рисунок 3), если: U=10 В, Е=20 В, R=5 Ом.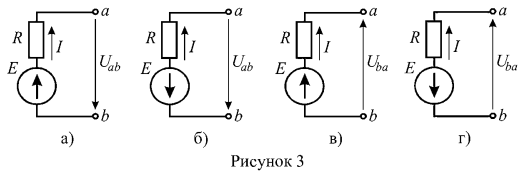
Решение:
Так как все схемы рисунка 3 представляют собой активные ветви, то для определения токов в них используем закон Ома обобщенный закон Ома. Рассмотрим рисунок 3 а: направление ЭДС совпадает с произвольно выбранным условно положительным направлением тока, следовательно, в формуле обобщенного закона Ома величина ЭДС учитывается со знаком «плюс». Направление напряжения ![]() не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;
не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;
![]()
Аналогично определяются токи в схемах б, в, г рисунка 3:
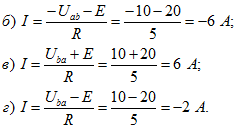
2. Найти напряжение между зажимами нетвей (рисунок 4).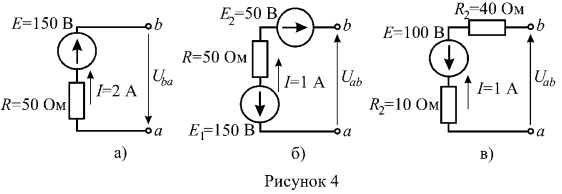
Решение:
Участок цепи, изображенный на рисунке 4 а содержит источник ЭДС, т.е. является активным, поэтому воспользуемся обобщенным законом Ома:
![]()
откуда выразим напряжение на зажимах:
![]()
Аналогично определяются напряжения на зажимах участков, изображенных на рисунках 4 б и 4 в.
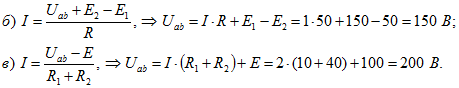
3. Определить неизвестные потенциалы точек участка цени (рисунок 5).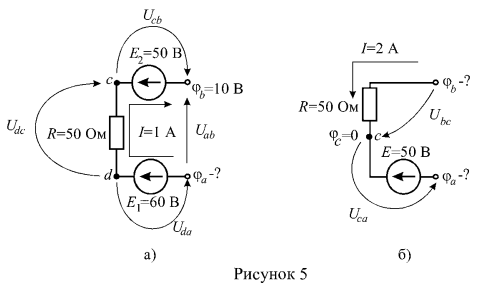
Решение:
Для схемы рисунка 5 а запишем обобщенный закон Ома:
![]()
откуда выразим напряжение на зажимах ветви:
![]()
Если представить напряжение ![]() как разность потенциалов:
как разность потенциалов:
![]()
тогда при известных параметрах цепи, токе и потенциале ![]() определим потенциал
определим потенциал ![]() :
:
![]()
Эту же задачу можно решить другим способом. Напряжение на зажимах источника ЭДС ![]() , без учета внутреннего сопротивления источника, по величине равно
, без учета внутреннего сопротивления источника, по величине равно ![]() и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):
и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):
![]()
и тогда, зная потенциал ![]() , определим потенциал точки С:
, определим потенциал точки С:
![]()
Потенциал точки d больше потенциала точки С на величину падения напряжения на сопротивлении R:
![]()
тогда
![]()
Потенциал точки а определяем с учетом направления напряжения ![]() на зажимах источника ЭДС
на зажимах источника ЭДС ![]() . Напряжение
. Напряжение ![]() направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):
направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):
![]()
откуда следует, что
![]()
или
![]()
Рассмотрим решение задачи для схемы рисунка 5 б. При известном потенциале точки С, параметрах элементов и токе, определим потенциалы крайних точек участка цепи ![]() . Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:
. Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:
![]()
откуда следует
![]()
Напряжение на участке с — а, равное по величине Е, направлено от точки с большим потенциалом к точке с меньшим потенциалом:
![]()
4. В цепи (рисунок 6) известны величины сопротивлений резистивных элементов: ![]() , входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением
, входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением ![]() . Определить величину сопротивления резистора
. Определить величину сопротивления резистора ![]() .
.
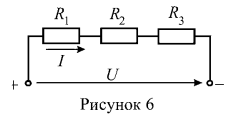 Решение:
Решение:
Согласно закону Джоуля-Ленца, мощность на резистивном элементе определяется:
![]()
или, согласно закону Ома:
![]()
По известному значению мощности на резистивном элементе ![]() и величине сопротивления этого элемента определим ток в ветви:
и величине сопротивления этого элемента определим ток в ветви:
![]()
По закону Ома напряжение на зажимах определится:
![]()
тогда величина сопротивления резистивного элемента:
![]()
5. Определить показания вольтметров цепи (рисунок 7), если ![]() .
.
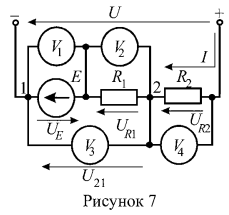 Решение:
Решение:
Ток в цепи определим по закону Ома:
![]()
Вольтметр ![]() показывает напряжение на источнике ЭДС Е:
показывает напряжение на источнике ЭДС Е:
![]()
Вольтметры ![]() показывают величину падения напряжения на резистивных элементах
показывают величину падения напряжения на резистивных элементах ![]() :
:
![]()
Вольтметр ![]() , показывает напряжение на участке 2 — 1
, показывает напряжение на участке 2 — 1 ![]() , которое определим как алгебраическую сумма напряжений
, которое определим как алгебраическую сумма напряжений ![]() :
:
![]()
6. Ток симметричной цепи (рисунок 8) ![]() , внутреннее сопротивлении источника ЭДС
, внутреннее сопротивлении источника ЭДС ![]() . Определить ЭДС Е и мощность источника энергии.
. Определить ЭДС Е и мощность источника энергии.
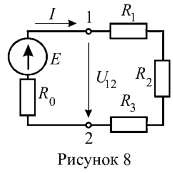 Решение:
Решение:
Напряжение на зажимах 1 — 2 определим по закону Ома для пассивной ветви:
![]()
Величину ЭДС источника энергии определим из выражения закона Ома для активной ветви:
![]()
Мощность, развиваемая источником энергии, определится:
![]()
