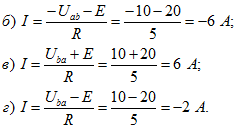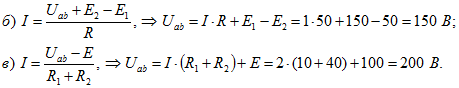Измерения
показывают, что напряжение на зажимах источника тока, замкнутого на внешнюю
цепь, зависит от силы отбираемого тока (от «нагрузки») и изменяется с
изменением последнего. Пользуясь законом Ома, мы можем сейчас разобрать этот
вопрос точнее.
Из
формулы (80.1) имеем
, (81.1)
где
–
сопротивление внешней цепи, а – внутреннее сопротивление
источника. Но к внешней цепи мы вправе применить закон Ома для участка цепи:
. (81.2)
Здесь
–
напряжение во внешней цепи, т. е. разность потенциалов на зажимах источника.
Оно может быть выражено на основании (81.1), (81.2) следующей формулой:
. (81.3)
Мы
видим, что при замкнутой цепи напряжение на зажимах источника тока всегда
меньше э. д. с. .
Напряжение зависит
от силы тока и
только в предельном случае разомкнутой цепи, когда сила тока , напряжение на
зажимах равно э. д. с.
Уменьшение
напряжения на зажимах источника при наличии тока легко наблюдать на опыте. Для этого
нужно замкнуть какой-либо гальванический элемент на реостат и подключить к
зажимам элемента вольтметр (рис. 127). Перемещая движок реостата, можно видеть,
что чем меньше сопротивление внешней цепи, т. е. чем больше ток, тем меньше
напряжение на зажимах источника. Если сопротивление внешней цепи сделать очень
малым по сравнению с внутренним сопротивлением источника («вывести» реостат),
т. е. сделать «короткое замыкание», то напряжение на зажимах делается равным
нулю.
Рис. 127. С уменьшением
сопротивления внешней цепи напряжение на зажимах источника тока уменьшается: а)
схема опыта; б) общий вид экспериментальной установки, 1 – источник тока, 2 –
реостат, 3 – амперметр, 4 – вольтметр
Что
же касается тока, то он при коротком замыкании достигает своего максимального
значения .
Сила этого «тока короткого замыкания» получается из закона Ома (80.1), если в
нем положить (т.
е. пренебречь сопротивлением по сравнению с
):
. (81.4)
Отсюда
видно, что ток короткого замыкания зависит не только от э. д. с., но также и от
внутреннего сопротивления источника. Поэтому короткое замыкание представляет
различную опасность для разных источников тока.
Короткие
замыкания гальванического элемента сравнительно безвредны, так как при небольшой
э. д. с. элементов их внутреннее сопротивление велико, и поэтому токи короткого
замыкания малы. Такие токи не могут вызвать серьезные разрушения, и поэтому к
изоляции проводов в целях, питаемых элементами (звонки, телефоны и т. п.), не
предъявляют особо высоких требований. Иное дело силовые или осветительные цепи,
питаемые мощными генераторами. При значительной э. д. с. (100 и более вольт)
внутреннее сопротивление этих источников ничтожно мало, и поэтому ток короткого
замыкания может достигнуть огромной силы. В этом случае короткое замыкание
может привести к расплавлению проводов, вызвать пожар и т. д. Поэтому к
устройству и изоляции таких цепей предъявляют строгие технические требования,
которые ни в коем случае нельзя нарушать без риска вызвать опасные последствия.
Такие цепи всегда снабжаются предохранителями (§ 63) и притом нередко в
различных местах: общий предохранитель (при главном вводе), групповые и
штепсельные предохранители.
81.1. Внутреннее сопротивление
элемента Даниеля с э. д .с. 1,1 В равно 0,5 Ом. Вычислите ток короткого
замыкания этого элемента.
81.2. Элемент из предыдущей задачи
замкнут на сопротивление 0,6 Ом. Чему равно напряжение на зажимах элемента?
81.3. Э. д. с. генератора постоянного
тока равна 220 В, а внутреннее сопротивление равно 0,02 Ом. Какой ток возникает
при коротком замыкании?
81.4. При измерении э. д. с.
источников при помощи вольтметра мы всегда допускаем некоторую погрешность, так
как через вольтметр течет некоторый, хотя и очень малый, ток, и поэтому
источник, строго говоря, не разомкнут, а замкнут на вольтметр. Пусть внутреннее
сопротивление элемента равно 1 Ом, его э. д. с. равна 1,8 В, а сопротивление
вольтметра равно 179 Ом. Какую погрешность при измерении э. д. с. мы допускаем?
81.5. Можно ли точно измерить э. д. с.
при помощи электрометра? Как нужно присоединить электрометр к элементу для
измерения его э. д. с.?
81.6. Изменяется ли показание
электрометра, соединенного с гальваническим элементом, если параллельно с ним
включить конденсатор, как показано на рис. 128? Будет ли иметь значение емкость
конденсатора?
Рис. 128. К упражнению 81.6
81.7. Э. д. с. некоторого элемента
измеряют при помощи электрометра с конденсатором (рис. 129,а). Электрометр,
отсоединенный от элемента, после снятия диска показывает 500 В (рис. 129,б).
При этом известно, что емкость конденсатора при удалении диска уменьшается в
250 раз. Чему равно напряжение элемента?
Рис. 129. К упражнению 81.7
Применение закона Ома к расчету линейных электрических цепей постоянного тока
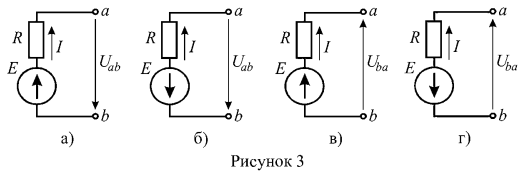
1. Найти ток ветви (рисунок 3), если: U=10 В, Е=20 В, R=5 Ом.
Решение:
Так как все схемы рисунка 3 представляют собой активные ветви, то для определения токов в них используем закон Ома обобщенный закон Ома. Рассмотрим рисунок 3 а: направление ЭДС совпадает с произвольно выбранным условно положительным направлением тока, следовательно, в формуле обобщенного закона Ома величина ЭДС учитывается со знаком «плюс». Направление напряжения не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;
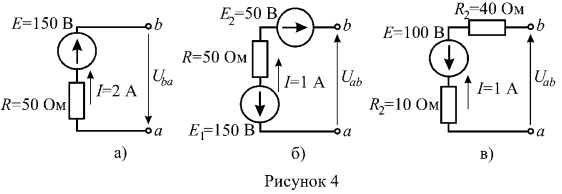
Аналогично определяются токи в схемах б, в, г рисунка 3:
2. Найти напряжение между зажимами нетвей (рисунок 4).
Решение:
Участок цепи, изображенный на рисунке 4 а содержит источник ЭДС, т.е. является активным, поэтому воспользуемся обобщенным законом Ома:
откуда выразим напряжение на зажимах:
Аналогично определяются напряжения на зажимах участков, изображенных на рисунках 4 б и 4 в.
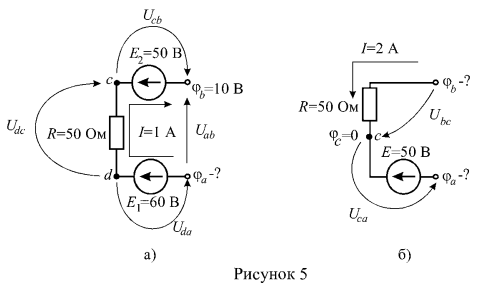
3. Определить неизвестные потенциалы точек участка цени (рисунок 5).
Решение:
Для схемы рисунка 5 а запишем обобщенный закон Ома:
откуда выразим напряжение на зажимах ветви:
Если представить напряжение как разность потенциалов:
тогда при известных параметрах цепи, токе и потенциале определим потенциал
:
Эту же задачу можно решить другим способом. Напряжение на зажимах источника ЭДС , без учета внутреннего сопротивления источника, по величине равно
и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):
и тогда, зная потенциал , определим потенциал точки С:
Потенциал точки d больше потенциала точки С на величину падения напряжения на сопротивлении R:
тогда
Потенциал точки а определяем с учетом направления напряжения на зажимах источника ЭДС
. Напряжение
направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):
откуда следует, что
или
Рассмотрим решение задачи для схемы рисунка 5 б. При известном потенциале точки С, параметрах элементов и токе, определим потенциалы крайних точек участка цепи . Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:
откуда следует
Напряжение на участке с — а, равное по величине Е, направлено от точки с большим потенциалом к точке с меньшим потенциалом:
4. В цепи (рисунок 6) известны величины сопротивлений резистивных элементов: , входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением
. Определить величину сопротивления резистора
.
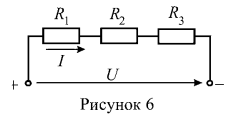
Согласно закону Джоуля-Ленца, мощность на резистивном элементе определяется:
или, согласно закону Ома:
По известному значению мощности на резистивном элементе и величине сопротивления этого элемента определим ток в ветви:
По закону Ома напряжение на зажимах определится:
тогда величина сопротивления резистивного элемента:
5. Определить показания вольтметров цепи (рисунок 7), если .
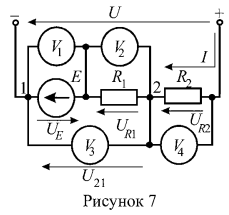
Ток в цепи определим по закону Ома:
Вольтметр показывает напряжение на источнике ЭДС Е:
Вольтметры показывают величину падения напряжения на резистивных элементах
:
Вольтметр , показывает напряжение на участке 2 — 1
, которое определим как алгебраическую сумма напряжений
:
6. Ток симметричной цепи (рисунок 8) , внутреннее сопротивлении источника ЭДС
. Определить ЭДС Е и мощность источника энергии.
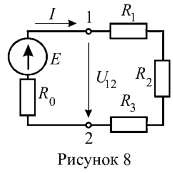
Напряжение на зажимах 1 — 2 определим по закону Ома для пассивной ветви:
Величину ЭДС источника энергии определим из выражения закона Ома для активной ветви:
Мощность, развиваемая источником энергии, определится:
Помогите с решинием, не могу разобраться
Ученик
(233),
закрыт
12 лет назад
Виктор Томин
Знаток
(270)
12 лет назад
Ответ: E=I*r+I*R, где E-ЭДС, r-внутреннее сопротивление, R-сопр. нагрузки.
Отсюда получаем I=E/(R+r).
После подстановки I=0.4
U источника = r*I=0.2
U нагрузки = R*I=1.8
Источник: Мозг
goggens
Гуру
(3066)
12 лет назад
До подключения внешнего сопротивления цепь не замкнута, падения напряжения от внутреннего сопротивления нет, и напряжение на зажимах так и будет 2 вольта.
После подключения внешнего сопротивления напряжение на зажимах
будет 2В минус ток*внутреннее сопротивление, т. е. 2 – 2/(4.5+0.5)*0.5 = 2 – 0.4*0.5 = 1.8 вольт.
Физический смысл закона
Потребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребитель, проходит и через источник тока, а значит, току кроме сопротивления проводника оказывается сопротивление самого источника. Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.
Физический смысл зависимости тока от ЭДС источника и сопротивления цепи заключается в том, что чем больше ЭДС, тем больше энергия носителей зарядов, а значит больше скорость их упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.
Зависимость можно показать на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения в цепи идет ток, наблюдаемый по амперметру, двигая ползунок реостата, увидим, что при изменении внешнего сопротивления ток будет меняться.
Примеры задач на применение закона Ома для замкнутой цепи
К источнику ЭДС 10 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 4 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
| Дано: | Решение: |
|
|
При подключении к батарее гальванических элементов резистора сопротивлением 20 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 10 Ом сила тока стала 1,5 А. Найти ЭДС и внутреннее сопротивление батареи.
1.8. Электрический ток. Закон Ома
Если изолированный проводник поместить в электрическое поле то на свободные заряды q в проводнике будет действовать сила В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю (см. § 1.5).
Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.
Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда Δq, переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени Δt, к этому интервалу времени:
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.
Рисунок 1.8.1.
Упорядоченное движение электронов в металлическом проводнике и ток I. S – площадь поперечного сечения проводника, – электрическое поле
В Международной системе единиц СИ сила тока измеряется в амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током (см. § 1.16).
Постоянный электрический ток может быть создан только в замкнутой цепи, в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю (см. § 1.4). Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.
Цепь постоянного тока можно разбить на отдельные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными. Участки, включающие источники тока, называются неоднородными.
При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов Δφ12 = φ1 – φ2 между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе 12, действующей на данном участке. Поэтому полная работа равна
Величину U12 принято называть напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:
Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
где R = const.
Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
IR = U12 = φ1 – φ2 + = Δφ12 + .
Это соотношение принято называть обобщенным законом Ома или законом Ома для неоднородного участка цепи.
На рис. 1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи (cd) является однородным.
Рисунок 1.8.2.
Цепь постоянного тока
По закону Ома
Участок (ab) содержит источник тока с ЭДС, равной .
По закону Ома для неоднородного участка,
Сложив оба равенства, получим:
I (R + r) = Δφcd + Δφab + .
Но Δφcd = Δφba = – Δφab. Поэтому
Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Сопротивление r неоднородного участка на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока. В этом случае участок (ab) на рис. 1.8.2 является внутренним участком источника. Если точки a и b замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (R <<� r), тогда в цепи потечет ток короткого замыкания
Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику последовательно подсоединяется некоторое внешнее сопротивление. Тогда сопротивление r равно сумме внутреннего сопротивления источника и внешнего сопротивления, и при коротком замыкании сила тока не окажется чрезмерно большой.
Если внешняя цепь разомкнута, то Δφba = – Δφab = , т. е. разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС.
Если внешнее нагрузочное сопротивление R включено и через батарею протекает ток I, разность потенциалов на ее полюсах становится равной
На рис. 1.8.3 дано схематическое изображение источника постоянного тока с ЭДС равной и внутренним сопротивлением r в трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к. з.). Указаны напряженность электрического поля внутри батареи и силы, действующие на положительные заряды: – электрическая сила и – сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.
Рисунок 1.8.3.
Схематическое изображение источника постоянного тока: 1 – батарея разомкнута; 2 – батарея замкнута на внешнее сопротивление R; 3 – режим короткого замыкания
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры.
Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB. Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 1.8.4, это условие записывается в виде:
Это условие означает, что ток IB = Δφcd / RB, протекающий через вольтметр, много меньше тока I = Δφcd / R1, который протекает по тестируемому участку цепи.
Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение.
Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением RA. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 1.8.4 сопротивление амперметра должно удовлетворять условию
чтобы при включении амперметра ток в цепи не изменялся.
Измерительные приборы – вольтметры и амперметры – бывают двух видов: стрелочные (аналоговые) и цифровые. Цифровые электроизмерительные приборы представляют собой сложные электронные устройства. Обычно цифровые приборы обеспечивают более высокую точность измерений.
Рисунок 1.8.4.
Включение амперметра (А) и вольтметра (В) в электрическую цепь
Физический смысл закона
Потребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребитель, проходит и через источник тока, а значит, току кроме сопротивления проводника оказывается сопротивление самого источника. Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.
Физический смысл зависимости тока от ЭДС источника и сопротивления цепи заключается в том, что чем больше ЭДС, тем больше энергия носителей зарядов, а значит больше скорость их упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.
Зависимость можно показать на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения в цепи идет ток, наблюдаемый по амперметру, двигая ползунок реостата, увидим, что при изменении внешнего сопротивления ток будет меняться.
Что такое напряжение
Электрическое напряжение (обозначается как U) – это физическая величина, которая отражает количественную характеристику работы электрического поля по переносу заряда из точки А в точку В. Соответственно напряжение может быть между двумя точками цепи, но в отличии от ЭДС оно может быть между двумя выводами какого-то из элементов цепи. Напомним, что ЭДС характеризует работу, выполненную сторонними силами, то есть работу самого источника тока или ЭДС по переносу заряда через всю цепь, а не на конкретном элементе.
Это определение можно выразить простым языком. Напряжение источников постоянного тока – это сила, которая перемещает свободные электроны от одного атома к другому в определенном направлении.
Для переменного тока используют следующие понятия:
- мгновенное напряжение — это разность потенциалов между точками в данный промежуток времени;
- амплитудное значение – представляет максимальную величину по модулю мгновенного значения напряжения за промежуток времени;
- среднее значение – постоянная составляющая напряжения;
- среднеквадратичное и средневыпрямленное.
Напряжение участка цепи зависит от материала проводника, сопротивления нагрузки и температуры. Так же как и электродвижущая сила измеряется в Вольтах.
Часто для понимания физического смысла напряжения, его сравнивают с водонапорной башней. Столб воды отождествляют с напряжением, а поток с током.
При этом столб воды в башне постепенно уменьшается, что характеризует понижение напряжения и уменьшения силы тока.
Постоянный ток: источники тока 2
Расчет падений напряжений между различными точками, определение токов и напряжений в цепи в том числе с использованием законов Кирхгофа – вот что нас ждет в этой статье.
Задача 1. В батарее, изображенной на рисунке, В, Ом, В‚ Ом‚ В, Ом; Ом‚ Ом. Найти ЭДС и внутреннее сопротивление этой батареи.
Внутренние сопротивления просто сложим (соединены последовательно):
Чтобы найти ЭДС, обратим внимание, что источники включены «неправильно», поэтому ЭДС будет равна
Ответ: Ом, В.
Задача 2. Вычислить ЭДС и внутреннее сопротивление батареи, состоящей из трех источников ЭДС (рис.), если ЭДС источников соответственно 10 В, 20 В, 30 В, а их внутренние сопротивления одинаковы и равны 1 Ом. При параллельном соединении источников их можно пересчитать в один по следующим формулам:
К задаче 2
Тогда
Теперь пересчитаем последовательное соединение двух источников:
Ответ: Ом, В. Задача 3. В некоторой цепи имеется участок, изображенный на рисунке, Ом, Ом‚ Ом, В, В‚ В. Найти силу тока в каждом сопротивлении и потенциал .
По первому закону Кирхгофа .
Пусть
Тогда:
Тогда сила тока в ветвях:
Задача 4. Определить разность потенциалов между клеммами в схеме, изображенной на рисунке, если В, Ом, Ом.
Сопротивления ветвей равны
Так как сопротивления ветвей равны, то общее сопротивление обеих ветвей
А ток в неразветвленной части цепи равен
Этот ток разделится ровно пополам в точке – опять же по причине равенства сопротивлений ветвей. Таким образом, токи в ветвях равны 1 A.
Эти токи создадут падения напряжений В, В.
Из рисунка можем записать по второму закону Кирхгофа:
Ответ: В.
Задача 5. Найти разность потенциалов на зажимах каждого источника тока, если Ом, Ом, Ом, В.
К задаче 5
Определим ток в цепи, для этого сначала определим суммарную ЭДС:
Ток в цепи равен:
Такой ток создаст падение напряжения на :
На :
Тогда на зажимах первого источника
На зажимах второго источника
Ответ: B, B.
Задача 6. В цепь включены три источника ЭДС и два резистора (рис.) Определить ЭДС и внутреннее сопротивление эквивалентного источника‚ действующего в цепи, а также разность потенциалов между точками А и В, если В, В, В, Ом, Ом, Ом, Ом, Ом.
Вcе сопротивления просто сложим (соединены последовательно):
Чтобы найти ЭДС, обратим внимание, что источники включены «неправильно», поэтому ЭДС будет равна
Ток в цепи будет равен:
Такой ток создаст падения напряжений:
По второму закону Кирхгофа запишем:
Ответ: В.
Задача 7. В схему включены три батареи (рис. 12.62) В, В, В, Ом, Ом, Ом. Найти напряжение на зажимах первой батареи.
К задаче 7
Вcе сопротивления просто сложим (соединены последовательно):
Чтобы найти ЭДС, обратим внимание, что источники включены «неправильно», поэтому ЭДС будет равна
Ток в цепи будет равен:
Такой ток создаст падение напряжения:
Искомое напряжение равно
Ответ: В.
Примеры задач на применение закона Ома для замкнутой цепи
К источнику ЭДС 10 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 4 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
| Дано: | Решение: |
|
|
При подключении к батарее гальванических элементов резистора сопротивлением 20 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 10 Ом сила тока стала 1,5 А. Найти ЭДС и внутреннее сопротивление батареи.
§ 5. Электродвижущая сила и напряжение источника электрической энергии
При соединении проводником двух разноименно заряженных тел а и б (рис. 11, а), т. е. таких тел, между которыми действует некоторая разность потенциалов, свободные электроны в этих телах и в соединительном проводнике придут в движение и возникнет электрический ток. Этот ток будет протекать по проводнику до тех пор, пока потенциалы обоих тел не станут равными.
Можно, однако, обеспечить и непрерывное движение электронов по проводнику, соединяющему два разноименно заряженных тела, т.е. непрерывное прохождение электрического тока. Для этого надо каким-то образом возвращать электроны обратно на отрицательно заряженное тело, другими словами, поддерживать постоянными заряды этих тел. Это означает, что для прохождения постоянного тока по металлическому проводнику необходимо все время обеспечивать на его концах разность потенциалов, или напряжение. Для этого проводник надо подключить к источнику электрической энергии и создать замкнутую электрическую цепь (рис. 11, б). В проводнике положительные заряды движутся от точек с более высоким потенциалом к точкам с более низким потенциалом, т. е. от положительного зажима источника электрической энергии к отрицательному. Но внутри источника эти заряды должны перемещаться от отрицательного зажима к положительному, т. е. от точки с низшим потенциалом к точке с высшим потенциалом. Такое перемещение зарядов внутри источника совершается благо-
даря электродвижущей силе (э. д. с), которая возбуждается в источнике. Э. д. с. поддерживает разность потенциалов на зажимах источника электрической энергии, обеспечивая прохождение тока по электрической цепи. Эта разность потенциалов определяет собой напряжение источника электрической энергии. Э. д. с. обозначается буквой Е (е) и численно равна работе, которую нужно затратить на перемещение единицы положительного заряда от одного зажима источника к другому. Э. д. с. и напряжение источника тесно связаны друг с другом. Если в источнике не возбуждается э. д. с, то будет отсутствовать и напряжение на его зажимах.
Следует отметить, что э. д. с. и напряжение источника могут существовать независимо от наличия тока в цепи. Если электрическая цепь постоянного тока разомкнута, то ток по цепи не проходит, но при работающем генераторе или аккумуляторе в них возбуждается э. д. с. и между их зажимами действует напряжение.
За единицу э. д. с, также как и напряжения, принят вольт. В разных источниках электрической энергии э. д. с. возникает по различным физическим причинам. Например, в электрических генераторах э. д. с. получается в результате электромагнитной индукции, в химических источниках тока (аккумуляторах, гальванических элементах) — вследствие электрохимических реакций.
Количественная разница между э. д. с. и напряжением источника будет рассмотрена в § 9.