На канале, в статье №25 “Потеря нулевого проводника, в чём опасность”, с помощью специальной программы были смоделированы и рассмотрены ситуации, когда в жилом доме на три квартиры терялась нейтраль (нулевой рабочий проводник N) при различной загруженности фаз.
В статье №29 ” Куда отъехала нейтраль”, показано почему и куда смещается нейтральная точка при неравномерной нагрузке и нарушении целостности нейтрального проводника. Рассмотрим последнюю ситуацию, описанную в статье №29 (рис. 1), когда обрыв нейтрального проводника (отключен S4) произошёл при неравномерной нагрузке в квартирах.
Результаты таковы: на лампе R1 напряжение 335 В; утюг R2 под напряжением 103 В; на условной электроплитке R3 – 300 В (вместо номинальных 230 В). Разность потенциалов между нулевыми точками источника и потребителя электрической энергии или напряжение смещения нейтрали Un′n = 134 В (вольтметр 10). Лампа с сопротивлением R1 выйдет из строя, схема изменится: сопротивления R2 и R3 включатся последовательно на линейное напряжение Ubc = 399 В. В цепи потечёт ток равный I = Ubc/(R1+R2). I = 399/229,2 = 1,74 А. Напряжение Ur2 = I R2 = 1,74 х 52,9 =92 В, напряжение Ur3 = I R3 = 1,74 х 176,3 = 307 В. В реальной жизни в многоквартирном доме данная ситуация будет развиваться стремительно и непредсказуемо: автоматически включаются и отключаются холодильники, электрообогреватели и кондиционеры; жильцы включают – отключают утюги, стиральные машинки, освещение и прочие электрооборудование; отключаются вышедшие из строя электроприборы. Происходит постоянное перераспределение нагрузки в фазах, что в свою очередь приводит к колебаниям напряжения в широких пределах.
Напряжение между нейтральными точками потребителя и источника Un′n, может быть рассчитано методом узловых потенциалов.
Ůn′n = ŮaYa+ŮbYb+ŮcYc / Ya+Yb+Yc+Yn, где Ya, Yb, Yc – комплексные проводимости фаз приемника, Yn – комплексная проводимость нейтрального провода. Проводимость величина обратная сопротивлению: Ya =1/Za, Yb = 1/Zb, Yc = 1/Zc, Yn = 1/Zn. Za, Zb, Zc – комплексные сопротивления нагрузки. Zn – комплексное сопротивление нейтрального проводника. Ůa, Ůb, Ůc – фазные напряжения на обмотках трансформатора.
При симметричной нагрузке Za = Zb = Zc, а следовательно и Ya = Yb = Yc =Y. Ůn′n = Y(Ůa+Ůb+Ůc) / 3Y+Yn. Фазные напряжения на обмотках трансформатора одинаковые по амплитуде и частоте, сдвинутые по фазе одна от другой на угол 120°. Сумма их мгновенных значений и сумма векторов амплитуд (и векторов действующих значений), в любой момент времени равны нулю (рис. 4). Ůa+Ůb+Ůc = 0.
Числитель в формуле равен нулю, поэтому Ůn′n = 0. Таким образом, независимо от того имеется нейтральный проводник или его нет, при симметричной нагрузке отсутствует разность потенциалов между нулевыми точками источника и потребителя электрической энергии. Фазные напряжения приемника не искажаются и остаются симметричными, равными фазным напряжениям источника. При симметричной нагрузке нейтральный провод можно удалить и это не повлияет на фазные напряжения приемника. Так без нулевого рабочего проводника N работают, например, трёхфазные электродвигатели или электрические котлы.
Когда нагрузка несимметрична (Za ≠ Zb ≠ Zc), а сопротивление нейтрального проводника мало (Zn стремится к 0), тогда проводимость Yn стремится к бесконечности, напряжение Uńn, в соответствии с формулой, стремится к нулю. Фазные напряжения приемника остаются практически симметричными, однако с возрастанием сопротивления нейтрального проводника напряжение Un′n также возрастает и фазные напряжения на нагрузке искажаются. Как уже отмечалось, Uńn прямо пропорционально зависит от сопротивления Zn (его длины, сечения и материала), а также от величины тока в нейтральном проводнике, который тем больше, чем больше неравномерность нагрузок в фазах (см. на канале статью 29).
Если нейтральный провод отсутствует или оборван, то его сопротивление Zn можно принять бесконечно большим, а проводимость Yn равной нулю. При несимметричной нагрузке (Za ≠ Zb ≠ Zc) формула для расчёта смещения нейтрали будет выглядеть так: Ůn′n = ŮaYa+ŮbYb+ŮcYc / Ya+Yb+Yc. Напряжение смещения нейтрали оказывается максимальным, искажения фазных напряжений приемника также максимальны.
Рассчитаем напряжение смещения нейтрали, напряжения и токи в нагрузке в схеме рис. 1 и сравним полученные результаты с показаниями приборов. Любой вектор может быть описан с помощью комплексных выражений (рис. 5).
ċ = a + jb = c cos e + jc sin e, где с = Ѵ (а² + b²).
Напряжения в фазах трансформатора равны по амплитуде и отличаются по фазе друг относительно друга на угол 120 градусов. Когда начальная фаза вектора Ůa равна 0 градусов (как на рис. 4), то этот вектор совмещен с осью вещественных величин комплексной плоскости (рис. 6).
Ůa = Ua = 230 B.
Вектор Ůb отстаёт, а вектор Ůc опережает вектор Ůa на 120 градусов. Ůb = – Ub cos 60° – j Ub sin60° = – 230 х 0,5 – j 230 х 0.866 = – 115 – j 199,2. Ůc = – Uc cos 60° + j Uc sin 60° = – 230 x 0,5 + j 230 x 0,866 = – 115 + j 199,2.
Сопротивления в фазах приёмника чисто активные: R1 = 529 Ом; R2 = 52,9 Ом; R3 = 176,3 Ом. Проводимости: Y1 = 1/R1 = 1/529 = 0,0019 См; Y2 = 1/R2 = 1/52,9 = 0,019 См; Y3 = 1/R3 = 1/176,3 = 0,0057 См. Сименс – единица измерения проводимости [См = 1/Ом].
ŮaY1 = 230 x 0,0019 = 0,437; ŮbY2 = (- 115 – j 199,2) x 0,019 = – 2,185 – j 3,785; ŮcY3 = (- 115 + j 199,2) x 0,0057 = – 0,656 + j 1,135.
Ůn′n = (0,437 – 2,185 – j 3,785 – 0,656 + j 1,135) / 0,0019 + 0,019 + 0,0057. Ůn′n = (- 2,4 – j 2,65) / 0,0266 = – 90,2 – j 99,6. tgφ = 90,2/99,6 = 0,9056, φ = 42,18 гр.
Действующее значение (модуль) Un′n = Ѵ (90,2² + 99,6²) = 134,38 B.
Напряжения на нагрузке R1, R2, R3. Ůr1 = Ůa – Ůn′n = 230 – (- 90,2 – j 99,6) = 320,2 + j 99,6. Ur1 =Ѵ (320,2² + 99,6²) = 335,3 B. Ůr2 = Ůb – Ůn′n = (- 115 – j 199,2) – (- 90,2 – j 99,6) = – 24,8 – j 99,6. Ur2 =Ѵ (24,8² + 99,6²) = 102,6 B. Ůr3 = Ůc – Ůn′n = (- 115 + j 199,2) – (- 90,2 – j 99,6) = – 24,8 + j 298,8. Ur3 =Ѵ (24,8² + 298,8²) = 299,8 B.
Токи в фазах: Ir1 = Ur1/R1 = 335,3/529 = 0,634 A; Ir2 = Ur2/R2 = 102,6/52,9 = 1,94 A; Ir3 = Ur3/R3 = 299,8/176,3 = 1,7 A. Полученные результаты расчётов совпадают с показаниями вольтметров и амперметров в схеме рис. 1.
Содержание:
Трехфазные несимметричные цепи:
Трехфазная цепь несимметрична, если комплексы сопротивлений ее фаз неодинаковы.
Несимметричной может быть действующая в цепи система э. д. с. (не равны модули э. д. с. или фазовые сдвиги между каждой парой э. д. с.). .
Для расчета несимметричной цепи применяются различные методы в зависимости от ее схемы и вида несимметрии.
Расчет несимметричной трехфазной цепи при соединении источника и приемника звездой
На схеме (см. рис. 20.4) видно, что при соединении звездой трехфазная система представляет собой электрическую цепь с двумя узлами — нейтральными точками N и N’. Наиболее удобным методом расчета в данном случае является метод узлового напряжения.
Определение токов
Рассмотрим сначала общий случай расчета цепи с нулевым проводом, сопротивление которого ZN. При этом сделаем некоторые упрощения: сопротивления линейных проводов и фаз источников будем полагать равными нулю. Если указанные сопротивления нельзя считать равными нулю, их можно отнести к приемнику, прибавив к сопротивлениям последнего по правилам сложения комплексов.
При таком упрощении потенциалы линейных зажимов источника и приемника (например, точек А и А’) можно считать одинаковыми.
Напряжение между нулевыми точками N и N’, или узловое напряжение
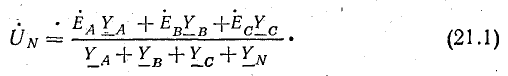
Смещение нейтрали
На рис. 21.1 изображена топографическая диаграмма цепи рис. 20.4, а при несимметричной нагрузке.
При наличии сопротивления в нулевом проводе (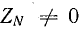 ) нулевая точка приемника на топографической диаграмме не совпадает с нулевой точкой источника. Поэтому напряжение UN называют напряжением смещения нейтрали. Вследствие смещения нейтрали напряжения на фазах приемника оказываются неодинаковыми, несмотря на симметрию фазных напряжений источника (см. решение задачи 21.3).
) нулевая точка приемника на топографической диаграмме не совпадает с нулевой точкой источника. Поэтому напряжение UN называют напряжением смещения нейтрали. Вследствие смещения нейтрали напряжения на фазах приемника оказываются неодинаковыми, несмотря на симметрию фазных напряжений источника (см. решение задачи 21.3).
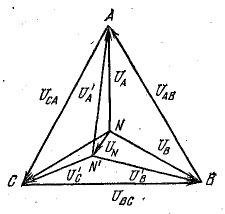
Рис. 21.1. Топографическая диаграмма при несимметричной нагрузке (соединение звездой)
Из формулы (21.1) видно, что симметрия фазных напряжений на нагрузке, когда UN = 0, достигается в двух частных случаях.
1. При симметричной нагрузке, когда комплексы проводимостей фаз равны: 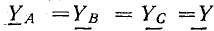 . В этом случае в числителе проводимость
. В этом случае в числителе проводимость 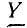 можно вынести за скобку, внутри которой складывается три вектора э. д. с. источника, равных по величине и сдвинутых по фазе на 120°; эта сумма равна нулю (см. рис. 20.8, б) и UN = 0. Поэтому ток в нулевом проводе равен нулю [см. формулу (21.4)] и необходимость в этом проводе отпадает, а электроснабжение симметричных приемников осуществляется по трехпроводной системе.
можно вынести за скобку, внутри которой складывается три вектора э. д. с. источника, равных по величине и сдвинутых по фазе на 120°; эта сумма равна нулю (см. рис. 20.8, б) и UN = 0. Поэтому ток в нулевом проводе равен нулю [см. формулу (21.4)] и необходимость в этом проводе отпадает, а электроснабжение симметричных приемников осуществляется по трехпроводной системе.
2. В четырехпроводной системе, когда сопротивление нулевого провода равно нулю (YN = ∞.)
Роль нулевого провода
Нулевой провод является уравнительным. Потенциалы нейтрали источника и приемника с помощью этого провода принудительно уравнены, а поэтому звезда векторов фазных напряжений приемника точно совпадает со звездой фазных напряжений источника.
Четырехпроводная система применяется в электрических сетях с напряжением 380/220 В при электроснабжении от общего источника силовой (электродвигатели) и осветительной (электролампы) нагрузки.
При несимметричной нагрузке обрыв нулевого провода (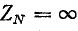 ) вызывает значительное изменение токов и фазных напряжений, что в большинстве случаев недопустимо. Поэтому в нулевой провод предохранители не устанавливаются.
) вызывает значительное изменение токов и фазных напряжений, что в большинстве случаев недопустимо. Поэтому в нулевой провод предохранители не устанавливаются.
Определение мощности
При несимметричной нагрузке нужно определить мощность каждой фазы. Например, для фазы А:
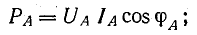
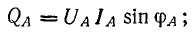
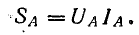
Аналогично определяются мощности других фаз.
Активная мощность всей трехфазной цепи равна сумме мощностей фаз:

Реактивная мощность цепи равна алгебраической сумме реактивных мощностей фаз:

В этой сумме реактивная мощность катушки считается положительной, а реактивная мощность конденсатора — отрицательной.
Задача 21.1.
При соединении звездой с нулевым проводом определить фазные напряжения и токи в приемнике энергии, сопротивления которого заданы комплексами:
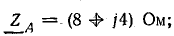
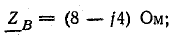
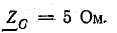
Действующая величина симметричной трехфазной системы э. д. с. 220 В. Сопротивление нулевого провода 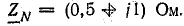
Построить векторную диаграмму.
Сопротивлениями линейных проводов и внутренними сопротивлениями источника э. д. с. пренебречь.
Решение. Схема, соответствующая условию задачи, показана на рис. 21.2, а.
Проводимости ветвей между узловыми точками NN’:
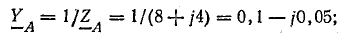
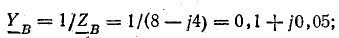
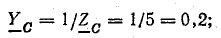
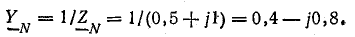
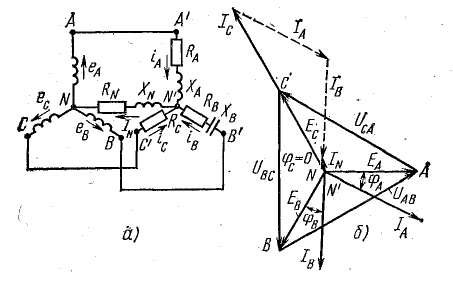
Рис. 21.2. К задаче 21.1
Комплексы э. д. с. источника:
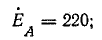
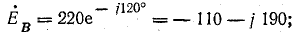
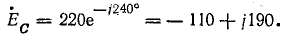
Узловое напряжение
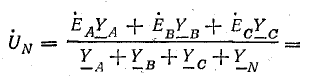
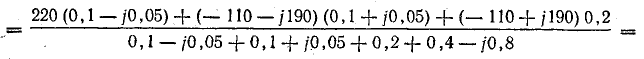
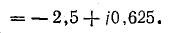
Фазные напряжения приемника:
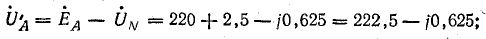
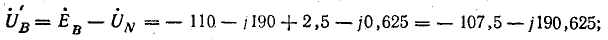
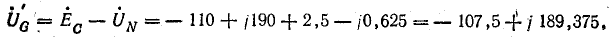
Токи в фазах и нулевом проводе:
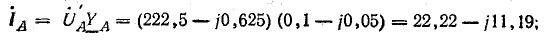
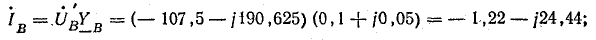
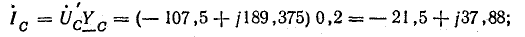
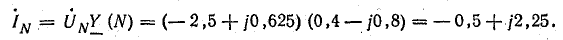
Векторная диаграмма напряжений и токов показана на рис. 21.2, б.
Задача 21.3.
Электрические лампы включены звездой в трехфазную сеть с линейным напряжением 380 В. В каждую фазу включены по 50 ламп с номинальной мощностью 60 Вт каждая, номинальным напряжением 220 В. Как изменяются фазные напряжения и токи при изменении нагрузки одной фазы от холостого хода до короткого замыкания при обрыве нулевого провода?
В каждом выбранном случае нагрузки построить векторную диаграмму, определить мощность всей трехфазной цепи.
Решение. Условию задачи соответствует схема рис. 21.3, а, на которой группа ламп в каждой фазе условно показана двумя лампами.
Оставляя постоянным число ламп в фазах В и С, будем менять его в фазе А. Подсчеты по условию задачи выполним для таких нагрузок в фазе А: 50, 25, 100 ламп, короткое замыкание, холостой ход.
1. При включении в каждую фазу по 50 одинаковых ламп нагрузка симметрична. Поэтому фазные напряжения на нагрузке равны фазным напряжениям в сети:
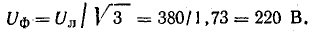
Напряжение на лампах равно номинальному. В этом случае лампы работают с номинальной мощностью.
Это даёт право определить фазные токи по заданной мощности ламп:
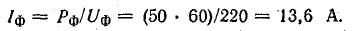
При соединении звездой IФ = IЛ, поэтому Iл = 13,6 А. Общая мощность трехфазной цепи
Р = ЗРФ = 3 • 60 • 50 = 9000 Вт.
2. В фазе А включено 25 ламп.
При несимметричной нагрузке напряжения на лампах отличаются от фазных напряжений в сети. Поэтому определить токи по заданной мощности ламп нельзя, так как действительная мощность ламп и фазные напряжения их неизвестны. При решении задачи будем считать, что сопротивление ламп в накаленном состоянии нити практически не меняется при некотором изменении их мощности.
Сопротивление лампы в номинальном режиме
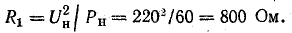
Сопротивление фаз В и С при включении 50 ламп
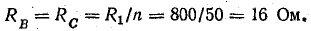
Сопротивление фазы А
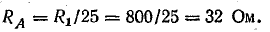
Комплексы фазных напряжений в сети:
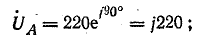
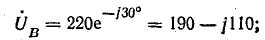

Проводимости ветвей:
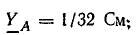
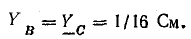
Смещение нейтрали
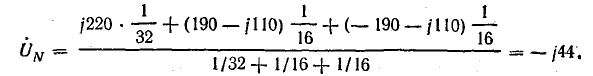
Напряжения фаз:
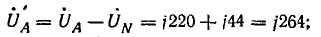
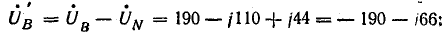
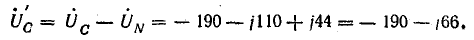
Токи в фазах:
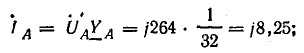
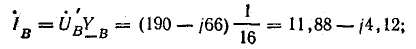
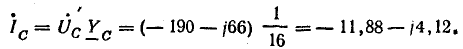
Мощность всех ламп в фазах:
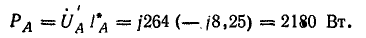
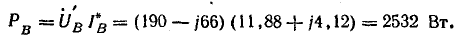
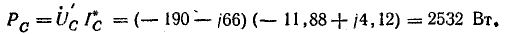
Мощность одной лампы:
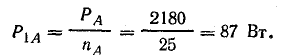
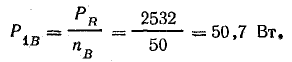
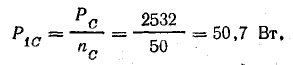
Общая мощность в трехфазной системе
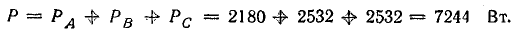
Векторная диаграмма напряжений для различной нагрузки фазы А показана на рис. 21.3, д.
Положение нулевой точки на диаграмме соответствует такой нагрузке фазы А: 1 — симметричная нагрузка (во всех фазах по 50 ламп); 2 — в фазе А 25 ламп; 3 — фаза А разомкнута (холостой ход); 4 — в фазе А 100 ламп; 5 — в фазе А короткое замыкание.
Выполните расчет трехфазной цепи для случаев нагрузки 3, 4, 5 подобно приведенному расчету для случая нагрузки 2, проверьте соответствие результатов расчета векторной диаграмме рис. 21.3, д.
Как видно, нулевая точка нагрузки при изменении проводимости фазы А перемещается на прямой АD, которая является перпендикуляром, опущенным из точки А к вектору линейного напряжения UBC. При холостом ходе фазы А (обрыв линейного провода в этой фазе) нулевая точка перемещается в точку D и напряжения на двух других фазах UB и UC по величине оказываются равными половине линейного напряжения UBC (рис. 21.3, б).
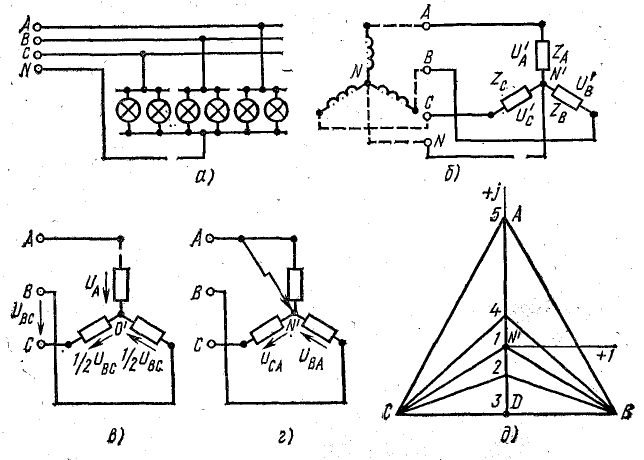
Рис. 21.3. К задаче 21.3
То же следует из схемы рис. 21.3, в. В рассматриваемом случае сопротивления фаз В и С оказываются включенными последовательно на линейное напряжение UBC.
Сопротивления эти равны, поэтому линейное напряжение делится между двумя фазами поровну.
При коротком замыкании фазы А линейный провод этой фазы подводится непосредственно к нулевой точке нагрузки (рис. 21.3, г). Поэтому лампы, включенные в фазы В и С, оказываются под линейным напряжением.
Расчет несимметричной трехфазной цепи при соединении треугольником
Трехфазная цепь при соединении приемника треугольником и любой схеме соединения фаз источника имеет разветвленную многоконтурную схему (см., например, рис. 20.8, а; 21.5).
Расчет такой цепи выполняется одним из известных методов с учетом состава ее элементов и схемы соединения.
Соединение источника и приемника треугольником
Расчет сложной цепи (см. рис. 20.8, а) значительно упрощается, если не принимать во внимание сопротивление проводов. В этом случае напряжения на фазах приемника равны соответствующим напряжениям источника и, как правило, представляют собой симметричную систему.
Если трехфазная система напряжений, приложенных к приемнику, известна, то фазные токи 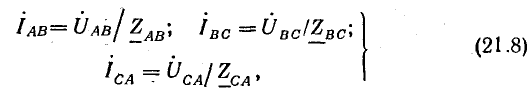
где 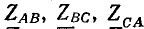 — полные сопротивления фаз.
— полные сопротивления фаз.
Линейные токи можно определить графически, как показано на рис. 21.4. Если задача решается в комплексной форме, линейные токи находят по формулам (20.7).
Мощность в несимметричной трехфазной цепи при соединении треугольником определяют по тем же формулам, что и при соединении звездой (21.6), (21.7).
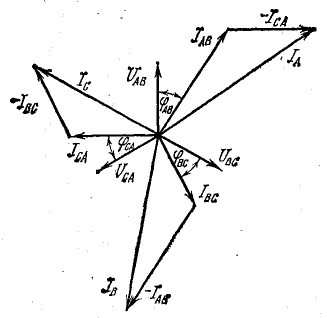
Рис. 21.4. Векторная диаграмма токов при несимметричной нагрузке (соединение треугольником)
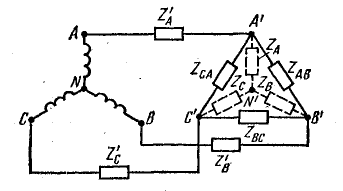
Рис. 21.5. К вопросу о преобразовании треугольника сопротивлений в эквивалентную звезду в трехфазной цепи
Преобразование звезды и треугольника сопротивлений в трехфазных цепях
Расчет трехфазных цепей при смешанном соединении (звездой и треугольником), с учетом сопротивлений проводов линии представляет значительные трудности.
В этих случаях упрощения достигаются благодаря применению метода взаимного преобразования звезды и треугольника.
На рис. 21.5 приемник энергии соединен треугольником. С учетом сопротивлений проводов линии (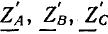 ) расчет такой цепи удобно выполнить, заменив треугольник сопротивлений эквивалентной звездой. Общее сопротивление фазы определяется сложением сопротивлений проводов линии и эквивалентной звезды приемника.
) расчет такой цепи удобно выполнить, заменив треугольник сопротивлений эквивалентной звездой. Общее сопротивление фазы определяется сложением сопротивлений проводов линии и эквивалентной звезды приемника.
Если в ходе расчета схемы со смешанным соединением приемников — звездой и треугольником (рис. 21.6) — необходимо определить общее сопротивление фазы, это делается преобразованием звезды в треугольник или треугольника в звезду.
При симметричной нагрузке можно преобразовать треугольник в звезду, а затем две звезды заменить одной. Последняя операция возможна только при симметричной нагрузке, когда фазные напряжения у этих «звезд» одинаковы (смещение нейтрали отсутствует). При несимметричной нагрузке звезду следует преобразовать в эквивалентный треугольник, а затем сложением соответствующих проводимостей определить общую проводимость каждой фазы.
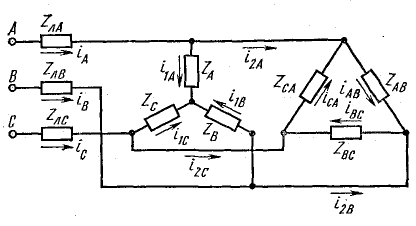
Рис. 21.6. к расчету трехфазной цепи при соединении приемников звездой и треугольником
Если в последнем случае требуется учесть сопротивление проводов, то общий треугольник еще раз приходится преобразовать в звезду и к сопротивлениям звезды прибавить сопротивления проводов линии.
Задача 21.4.
Сопротивления фаз приемника 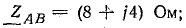
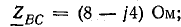
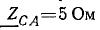 подключены треугольником к трехфазному генератору, обмотки которого также соединены треугольником. Действующие значения симметричной системы э. д. с. генератора 220 В. Пренебрегая сопротивлениями линейных проводов и обмоток генератора, определить фазные и линейные токи, активную, реактивную и полную мощности каждой фазы и всей цепи. Построить векторную диаграмму.
подключены треугольником к трехфазному генератору, обмотки которого также соединены треугольником. Действующие значения симметричной системы э. д. с. генератора 220 В. Пренебрегая сопротивлениями линейных проводов и обмоток генератора, определить фазные и линейные токи, активную, реактивную и полную мощности каждой фазы и всей цепи. Построить векторную диаграмму.
Решение. Схема рис. 20.8, а соответствует условию задачи. Если сопротивления линейных проводов и обмоток генератора считать равными нулю, то фазные напряжения приемника равны соответствующим э. д. с.:
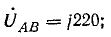
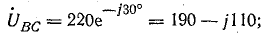
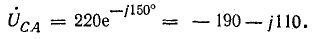
Фазные токи в приемнике:
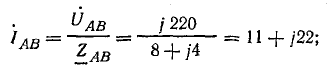
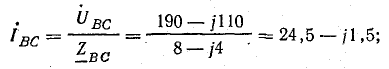
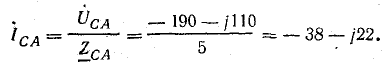
Линейные токи:
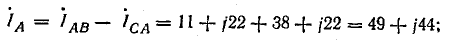
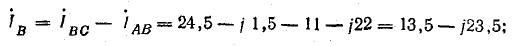
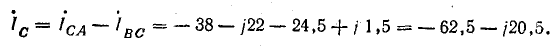
Сумма линейных токов
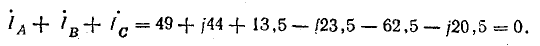
Равенство нулю суммы линейных токов является общим свойством трехфазных трехпроводных цепей при соединении звездой и треугольником при симметричной и несимметричной нагрузках.
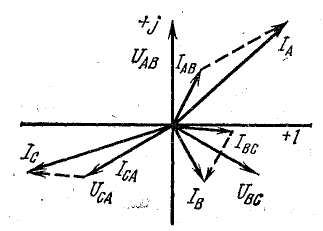
Рис. 21.7. К задаче 21.4
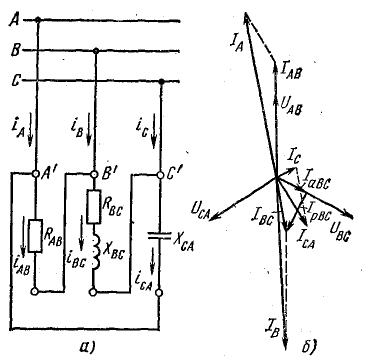
Рис. 21.8. К задаче 21.5
Мощности фаз:
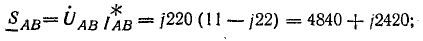
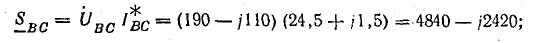
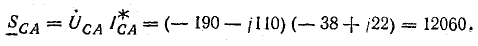
Общая мощность системы:
активная
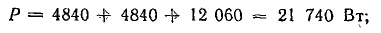
реактивная
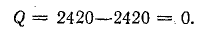
Векторная диаграмма построена на рис. 21.7.
Задача 21.5.
Приемник электрической энергии, соединенный треугольником, включен в сеть с линейным напряжением 120 В. Сопротивления фаз: 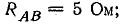
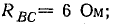
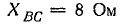 (инд.);
(инд.); 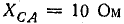 (емк.).
(емк.).
Начертить схему по условию задачи. Определить фазные и линейные токи, активную, реактивную и полную мощности в каждой фазе и всей цени. Построить векторную диаграмму.
Решение. Схема цепи изображена на рис. 21.8, а.
Решим задачу без применения комплексных чисел. Токи в фазах:
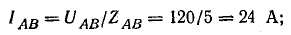
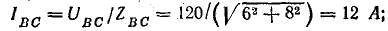
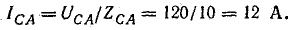
Линейные токи определим графически с помощью векторной диаграммы. Для этого найдем активные и реактивные токи фаз.
В фазе АВ включено активное сопротивление, поэтому
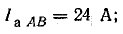
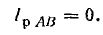
В фазе ВС последовательно соединены R и ХL, поэтому
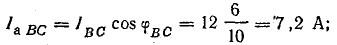
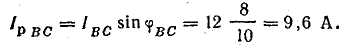
В фазе CA включено емкостное сопротивление, следовательно,
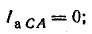
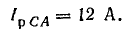
Векторная диаграмма цепи показана на рис. 21.8, б. Для определения линейных токов постройте векторную диаграмму на листе миллиметровой бумаги в масштабах: 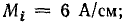
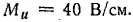
Линейные токи: 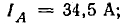
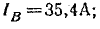
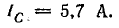
Мощности фаз:
активные
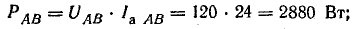
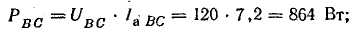
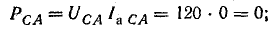
реактивные
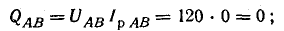
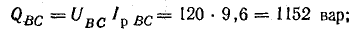
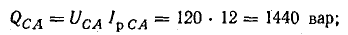
полные
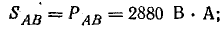
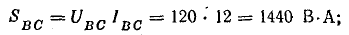
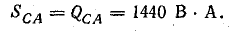
Мощность всей цепи:
активная
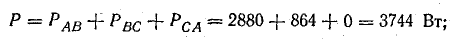
реактивная
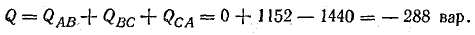
Знак минус указывает на емкостный характер реактивной мощности цепи.
Симметричные составляющие несимметричной трехфазной системы
Несимметричную трехфазную систему токов (напряжений или других синусоидальных величин) можно представить в виде суммы трех симметричных систем.
Разложение несимметричной системы векторов на симметричные составляющие применяется для расчета и анализа несимметричных режимов в трехфазных цепях: при симметричной нагрузке, но несимметричной системе э. д. с., при однофазных и двухфазных коротких замыканиях, при обрыве линейных проводов в цепях с симметричной системой э. д. с.
Комплексы симметричных составляющих
Первая симметричная система имеет прямую последовательность фаз (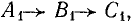 рис. 21.9, а), вторая — обратную (
рис. 21.9, а), вторая — обратную (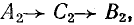 рис. 21.9, б). Третья система, называемая системой нулевой последовательности, состоит из трех равных величин, совпадающих по фазе (
рис. 21.9, б). Третья система, называемая системой нулевой последовательности, состоит из трех равных величин, совпадающих по фазе (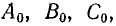 рис. 21.9, в).
рис. 21.9, в).
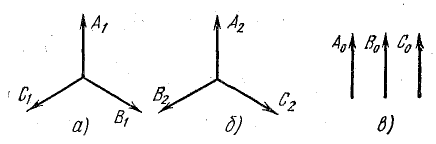
Рис. 21.9. Симметричные составляющие несимметричной системы
Система величин:
прямой последовательности
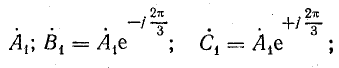
обратной последовательности
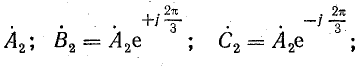
нулевой последовательности
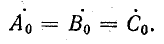
Умножение на 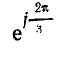 означает поворот вектора на 120″ против движения часовой стрелки. Обозначим
означает поворот вектора на 120″ против движения часовой стрелки. Обозначим 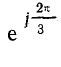 через а и будем называть это выражение поворотным множителем.
через а и будем называть это выражение поворотным множителем.
Поворот вектора против часовой стрелки на 240° можно выразить умножением его на а2.
Умножение вектора на а3 не меняет его положения:
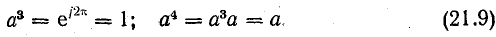
С помощью поворотного множителя а системы прямой и обратной последовательности можно записать так:
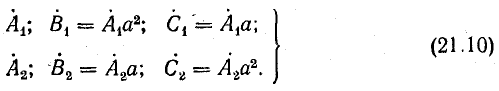
Сумма синусоидальных величин симметричной системы равна нулю, поэтому

Разложение несимметричной системы на симметричные составляющие
Выразим комплексы несимметричной системы через симметричные составляющие:
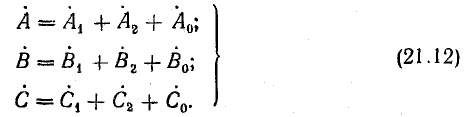
Если из этой системы уравнений можно однозначно определить симметричные составляющие через известные величины 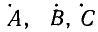 несимметричной системы, то этим будет доказана возможность разложения несимметричной системы на три симметричные — прямой, обратной и нулевой последовательности.
несимметричной системы, то этим будет доказана возможность разложения несимметричной системы на три симметричные — прямой, обратной и нулевой последовательности.
Используя выражения (21.10), запишем систему уравнений (21.12) в таком виде:
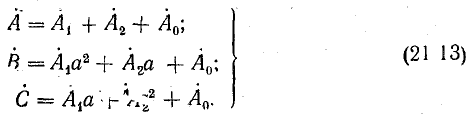
Решение системы уравнений (21.13) позволяет найти симметричные составляющие 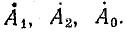
Сложим уравнения:
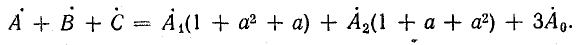
Учитывая формулу (21.11), найдем

Умножим второе уравнение в системе (21.13) на 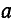 , а третье — на
, а третье — на 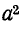 и сложим все уравнения:
и сложим все уравнения:
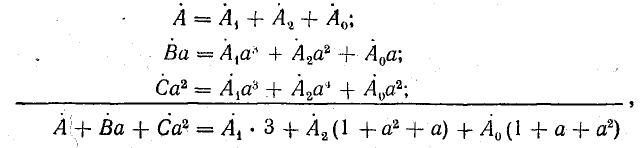
откуда
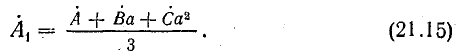
Умножим второе уравнение в системе (21.13) на 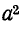 , а третье на
, а третье на 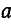 и сложим все уравнения:
и сложим все уравнения:
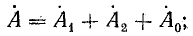
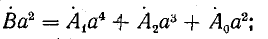
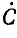
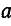 =
= 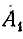
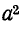 +
+ 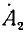
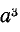 +
+ 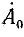
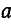

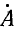 +
+ 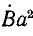 +
+ 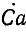 =
= 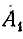 (1 +
(1 + 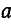 +
+ 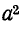 ) +
) + 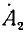 • 3 +
• 3 + 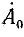 (1 +
(1 + 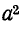 +
+ 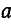 )
)
откуда
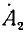 =
= 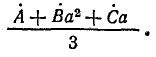 (21.16)
(21.16)
Свойства трехфазных цепей
Отметим некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений.
Степень несимметрии линейных напряжений оценивается коэффициентом несимметрии, т.е. отношением составляющей обратной последовательности напряжений к составляющей прямой последовательности.
ε = 100 • Uоп/Uпп.
Отсюда следует, что ток в нулевом проводе можно найти, если утроить величину составляющей тока нулевой последовательности.
В трехпроводной системе сумма линейных токов равна нулю. Из формулы (21.14) следует, что линейные токи в этом случае не содержат составляющей нулевой последовательности. Это справедливо и для линейных напряжений трехфазной системы, сумма которых тоже равна нулю.
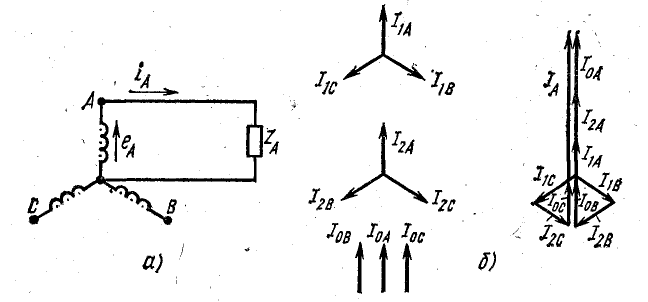
Рис. 21.10. Симметричные составляющие токов трехфазной цепи при разомкнутых двух фазах
Отсутствие тока в одной или двух фазах при несимметричном режиме означает, что сумма трех симметричных составляющих токов в этих фазах равна нулю.
Например, на схеме рис. 21.10, а фазы В и С разомкнуты. Поэтому 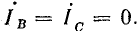
Согласно формулам (21.14) — (21.16), симметричные составляющие токов имеют следующие выражения:
прямой последовательности
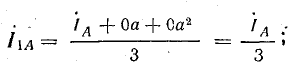
обратной последовательности
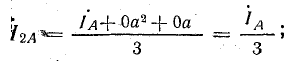
нулевой последовательности
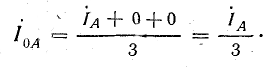
На рис. 21.10, б показаны симметричные составляющие прямой, обратной и нулевой последовательности и их геометрическое сложение; в результате сложения получаем:
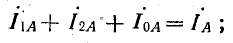
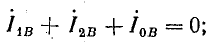
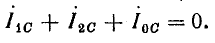
Задача 21.8.
В результате неправильной маркировки концов обмоток трехфазного трансформатора (начало фазы А вторичной обмотки помечено как конец) система линейных напряжений несимметрична. Определить симметричные составляющие линейных напряжений при соединении звездой, если фазные напряжения во вторичной обмотке 220 В.
Решение. Запишем комплексы фазных напряжений во вторичной обмотке:
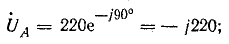
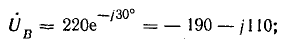
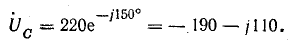
Вектор напряжения 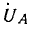 в соответствии с условием задачи повернут на 180°.
в соответствии с условием задачи повернут на 180°.
Комплексы линейных напряжений:
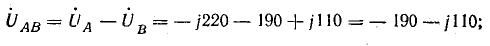
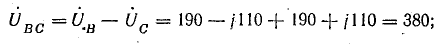
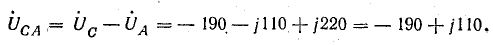
Составляющие:
нулевой последовательности
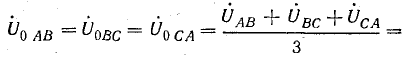
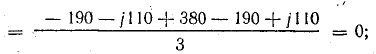
прямой последовательности
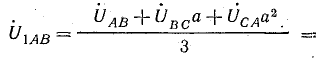
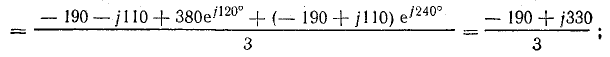
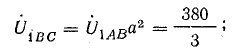

обратной последовательности
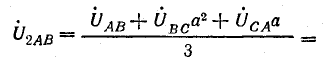
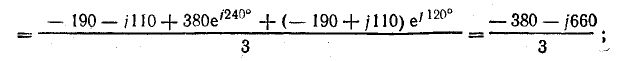
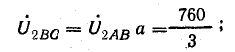
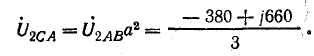
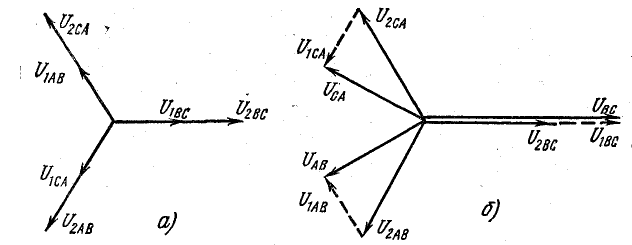
Рис. 21.11. К задаче 21.8
На рис. 21.11, а, б показаны векторы систем прямой и обратной последовательности и их сумма — система трех исходных векторов линейных напряжений.
Задача 21.9.
Трехфазный электродвигатель, включенный в сеть с линейным напряжением 380 В при соединении звездой, имеет мощность на валу Р2 = 14 кВт; соsφ = 0,8; к. п. д. η = 0,85.
Определить симметричные составляющие токов в обмотке двигателя при обрыве линейного провода в фазе В.
Решение. При нормальной работе ток в фазе двигателя
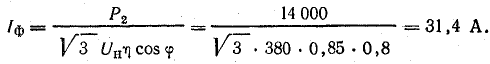
При симметричной системе напряжений токи в фазах двигателя образуют симметричную систему (рис. 21.12, а). При обрыве линейного провода В векторная диаграмма фазных напряжений и токов показана на рис. 21.12, б.
Ток в фазах В равен нулю (IB = 0).
Токи в фазах А и С равны по величине, но находятся в противофазе: IА = IC.
Для определения величины токов IА и IC найдем расчетное сопротивление фазы двигателя при нормальном режиме, которое будем считать неизменным:
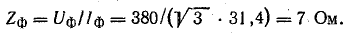
При обрыве линейного провода фазы В обмотки двух других фаз двигателя с одинаковым сопротивлением включены последовательно на линейное напряжение UCA. Поэтому ток в фазах А и С
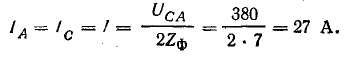
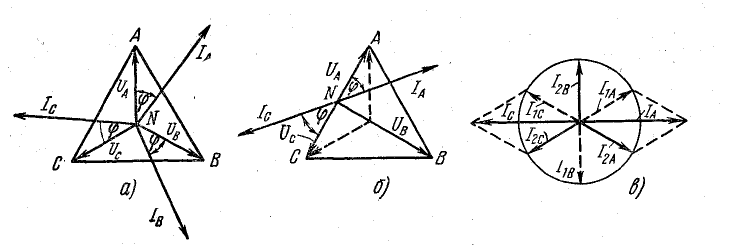
Рис. 21.12. к задаче 21.9
Выразим токи в комплексной форме, полагая ток IA совпадающим с положительным направлением действительной оси:

Токи:
нулевой последовательности
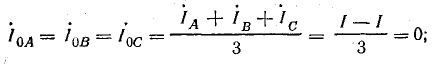
прямой последовательности
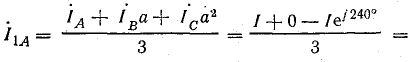
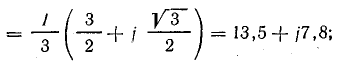
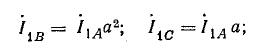
обратной последовательности
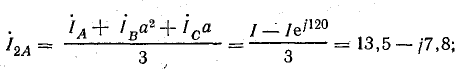
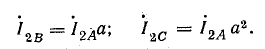
На рис. 21.12, в изображены симметричные составляющие токов в двигателе при обрыве фазы.
Несимметричный режим работы трехфазной цепи
Несимметрия в трехфазной цепи может быть вызвана различными причинами: 1) неодинаковым сопротивлением фаз (несимметричная нагрузка); 2) несимметричным коротким замыканием (например, между двумя фазами или фазой и нейтралью); 3) размыканием фазы; 4) неравенством э. д. с. и т. п.
Расчет токов и напряжений в трехфазной цепи при несимметричном режиме может производиться теми же
методами, которые применяются для расчета однофазных цепей.
Рассмотрим несколько простейших вариантов (без взаимной индукции между фазами).
1. Несимметричная трехфазная цепь, соединенная звездой, с нейтральным проводом (рис. 12-13).
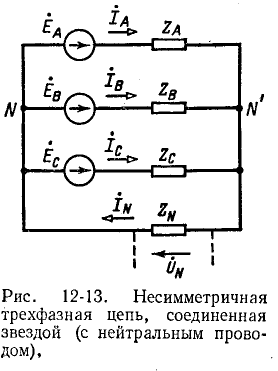
Несимметричная трехфазная цепь, показанная на рис. 12-13, может рассматриваться как трехконтурная цепь с тремя э. д. с. Такая цепь может быть рассчитана методами контурных токов, узловых напряжений и другими. Поскольку в схеме имеются только два узла, наиболее целесообразно в данном случае определить узловое напряжение (напряжение смещения) между нейтральными точками N’ и N по формуле,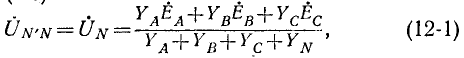
где 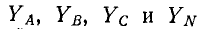 — проводимости соответствующих ветвей.
— проводимости соответствующих ветвей.
После этого найдем токи:
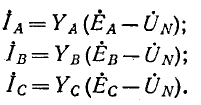
В симметричной трехфазной цепи 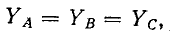 и поэтому при
и поэтому при 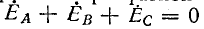 узловое напряжение равно нулю.
узловое напряжение равно нулю.
Стучаю размыкания какой-либо фазы или нейтрального провода соответствует равенство нулю проводимости данной фазы или нейтрального провода. j
При отсутствии нейтрального провода, полагая в (12-1)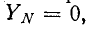 , имеем:
, имеем:
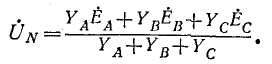
2. Несимметричная трехфазная нагрузка, соединенная звездой (без нейтрального провода), с заданными линейными напряжениями на выводах (рис. 12-14).
Если заданы линейные напряжения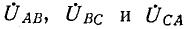 на выводах нагрузки, соединенной звездой, то токи в фазах звезды определяются следующим образом.
на выводах нагрузки, соединенной звездой, то токи в фазах звезды определяются следующим образом.
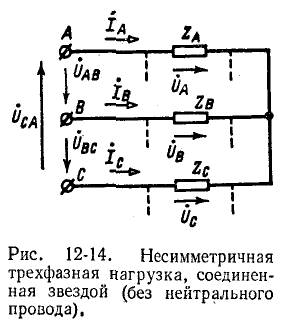
Обозначив фазные напряжения на выводах нагрузки через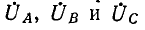 (рис. 12-14), получим
(рис. 12-14), получим
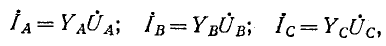
где 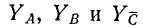 — проводимости фаз нагрузки.
— проводимости фаз нагрузки.
Равенство нулю суммы токов трех фаз записывается в виде:
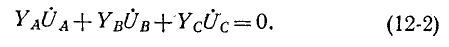
Фазные напряжения 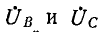 могут быть выражены через
могут быть выражены через 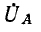 и заданные линейные напряжения:
и заданные линейные напряжения:
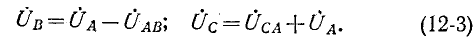
Подстановка (12-3) в (12-2) дает:
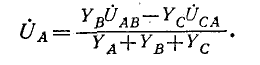
Круговой заменой индексов (с порядком следования АВСА и т. д.) находятся:
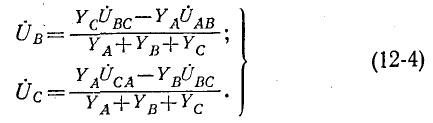
По фазным напряжениям нагрузки находятся фазные токи.
В Случае симметричной нагрузки 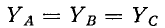 вектор фазного напряжения равен одной трети диагонали параллелограмма, построенного на соответствующих линейных напряжениях. Фазные напряжения в этом случае определяются векторами, соединяющими центр тяжести треугольника напряжений (точка пересечения медиан) с вершинами треугольника.
вектор фазного напряжения равен одной трети диагонали параллелограмма, построенного на соответствующих линейных напряжениях. Фазные напряжения в этом случае определяются векторами, соединяющими центр тяжести треугольника напряжений (точка пересечения медиан) с вершинами треугольника.
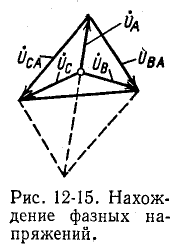
На рис. 12-15 построение сделано для фазы А по формуле (12-4)1
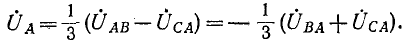
В качестве примера рассмотрим схему фазоуказателя, используемую для определения чередования фаз по времени, состоящую из конденсатора и двух одинаковых электрических ламп, соединенных звездой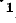 .
.
Положим, что конденсатор присоединен к фазе А, лампы — к фазам В и С; емкостное сопротивление конденсатора берется равным по модулю сопротивлению лампы, т. е. 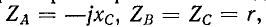 причем
причем 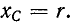
Неравенство напряжений на лампах проявится в том, что накал ламп будет разным.
1 Для определения чередования фаз на практике обычно пользуются специальным прибором, в котором создается вращающееся магнитное поле, увлекающее за собой диск в ту или другую сторону.
Отношение напряжений согласно выведенным выше выражениям (12-4) равно при симметрии линейных напряжений:
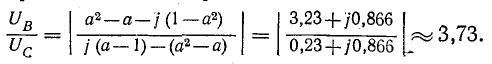
Следовательно, лампа, присоединенная к фазе В (т. е. к фазе, опережающей ту, к которой присоединена вторая лампа), будет светить ярко, а лампа, присоединенная к отстающей фазе, — тускло.
Вместо конденсатора можно применить индуктивную катушку, подобрав ее индуктивное сопротивление приблизительно равным по модулю сопротивлению лампы. В этом случае ярче будет светить лампа, присоединенная к отстающей фазе. Эти соотношения также могут быть получены непосредственно из векторной диаграммы.
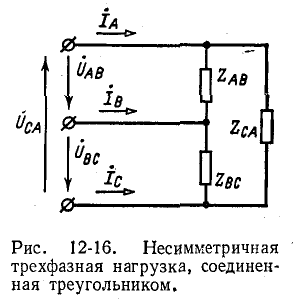
3. Несимметричная трехфазная нагрузка, соединенная треугольником, с заданными напряжениями на выводах Рис. 12-16. Несимметричная (рис. 12-16). Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы линейные напряжения 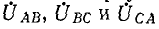 (рис. 12-16), то токи в сопротивлениях нагрузки равны:
(рис. 12-16), то токи в сопротивлениях нагрузки равны:
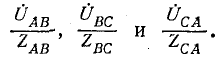
Токи в линии определяются как разности соответствующих токов нагрузки, например: 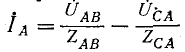 и т. д.
и т. д.
Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы фазные напряжения 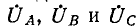 источника, соединенного в звезду, то линейные напряжения на выводах нагрузки находятся как разности соответствующих фазных напряжений, в результате чего задача сводится к только что рассмотренному случаю(рис. 12-16).
источника, соединенного в звезду, то линейные напряжения на выводах нагрузки находятся как разности соответствующих фазных напряжений, в результате чего задача сводится к только что рассмотренному случаю(рис. 12-16).
Пример 12-2. Сопротивления фаз нагрузки, соединенной звездной
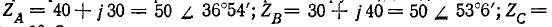
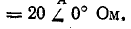
Сопротивление нейтрального провода
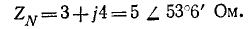
Напряжения на цепи представляют собой симметричную звезду: 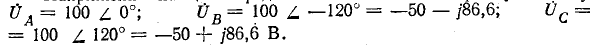
Требуется определить фазные напряжения нагрузки.
Проводимости фаз нагрузки и нейтрального провода
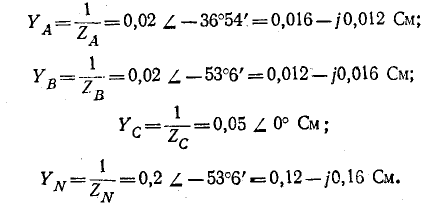
На основании формулы (12-1)
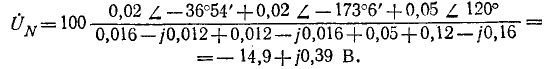
Искомые фазные напряжения нагрузки:
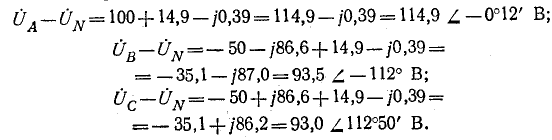
Мощность несимметричной трехфазной цепи
Пользуясь комплексной формой записи мощности, можно написать общее выражение для мощности трехфазной цепи:
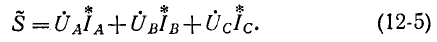
Действительная часть этого выражения представляет собой активную мощность
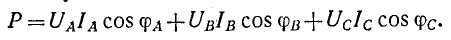
Суммарная активная мощность, потребляемая несимметричной трехфазной цепью, может быть в соответствии с этим измерена при помощи трех ваттметров, включенных на подведенные к данной цепи фазные напряжения относительно нейтрали и одноименные с ними токи. Активная мощность равна сумме показаний трех ваттметров. Такой метод измерения применяется при наличии нейтрального провода (рис. 12-17) или искусственно созданной нейтральной точки.
В случае отсутствия нейтрального провода измерение может быть произведено с помощью двух ваттметров
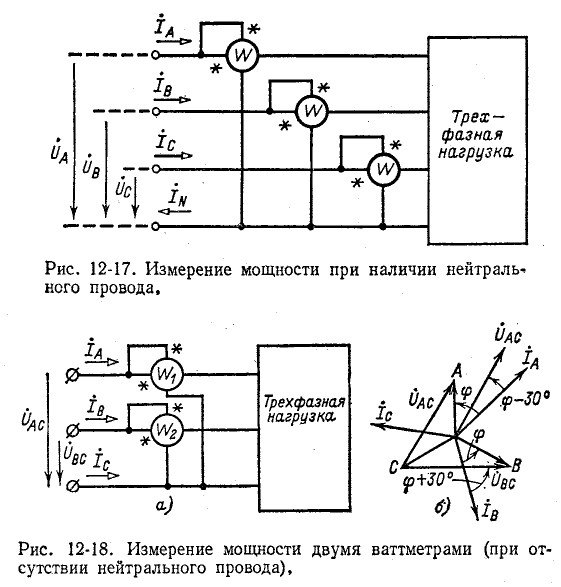
(рис. 12-18). В этом случае выражение (12-5) преобразуется следующим образом: исключая ток 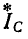 с помощью условия
с помощью условия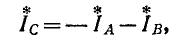
получаем: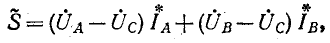
или
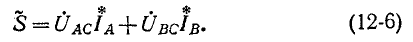
В соответствии с (12-6) при измерении активной мощности двумя ваттметрами к одному из них подводятся напряжение 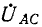 и ток
и ток 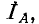 а ко второму — напряжение
а ко второму — напряжение 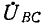 и ток
и ток 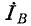 (рис. 12-18, а). Показания ваттметров складываются алгебраически.
(рис. 12-18, а). Показания ваттметров складываются алгебраически.
Круговой заменой А, В. и С в выражении (12-6) можно получить выражения для других равноценных вариантов включения двух ваттметров.
Следует иметь в виду’, что если стрелка одного ваттметра отклоняется по шкале в обратную сторону, то, изменив направление напряжения или тока, подводимого к данному ваттметру, записывают полученное показание со знаком минус. При симметричном режиме работы трехфазной цепи такое положение имеет место при
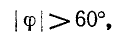
что видно непосредственно из векторной диаграммы (рис. 12-18, б).
При симметричном режиме показания двух ваттметров в схеме рис. 12-18, б будут следующие:
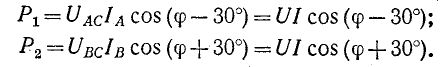
Сумма и разность показаний ваттметров соответственно равны:
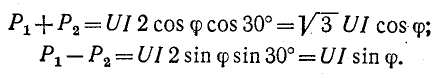
Следовательно, при симметричном режиме работы трехфазной цепи тангенс угла сдвига фаз может быть вычислен по формуле
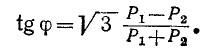
- Вращающееся магнитное поле
- Электрические цепи синусоидального тока
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Метод симметричных составляющих
- Цепи периодического несинусоидального тока
- Резонанс токов
- Трехфазные симметричные цепи
4.4.1 Расчет трехфазной
цепи не отличается от расчета однофазных
цепей с несколькими источниками
электроэнергии, имеющими различные
начальные фазы. Используя для расчета
метод узловых потенциалов, можно
определить важные для потребителя
электрической энергии величины – фазные
напряжения, фазные и линейные токи,
напряжение на нейтрали при несимметричных
нагрузках, обрыве нулевого провода.
4.4.2 Порядок решения
задачи рассмотрен на примере расчета
трехфазной четырехпроводной цепи,
линейное напряжение которой Uл.
= 660 В. Сопротивления нагрузки соединены
в звезду и имеют следующие данные: RA
= 8 Ом; XLA
= 6 Ом; RB
= 6 Ом; XBC
= 8 Ом;
RC
= 23 Ом; XCL
= 15,3 Ом. Нулевой провод имеет только
активное сопротивление R0
=1 Ом.
Определить:
1) Напряжение смещения нейтрали:
а) при наличии
нулевого провода;
б) при его обрыве;
2) Напряжения на каждой фазе:
а) при наличии
нулевого провода;
б) при его обрыве;
3) Фазные, линейные токи и ток в нулевом проводе:
а) при наличии
нулевого провода;
б) при обрыве
нулевого провода
4) При наличии нулевого провода:
а) полную, активную
и реактивную мощности каждой фазы и
всей цепи;
б) коэффициенты
мощности каждой фазы и всей цепи.
Сопротивления
обмоток источника питания и фазных
проводов не учитывать. Схема включения
приемников электрической энергии дана
на рис. 14.
Построить векторные
диаграммы токов и напряжений:
а) для случая с
неповрежденным нулевым проводом;
б) при обрыве
нулевого провода;
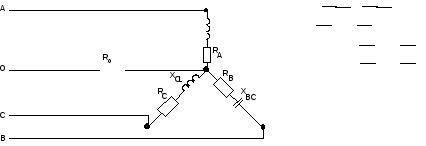
Рис. 14. Схема
включения приемников электрической
энергии в трехфазную
четырехпроводную
цепь.
Решение.
1) Определение напряжения смещения нейтрали.
Напряжение
смещения нейтрали U0
может быть найдено методом узловых
потенциалов
![]() 0
0
= (![]() А
А
YA
+
![]() В
В
YВ
+
![]() С
С
YС)/(YА
+ YВ
+ YС
+ Y0),
(4.4.1)
где
![]() А,
А,
![]() В,
В,
![]() С
С
– фазные напряжения фаз А, В и С;
YА,
YВ,
YС
и Y0
– проводимости
фаз А, В, С и нулевого провода.
Все величины
должны быть записаны в комплексном виде
в алгебраической и показательной формах.
При соединении
фаз звездой действующие значения фазных
Uф.
и линейных Uл.
напряжений связаны соотношением
Uф.
= Uл./![]() (4.4.2)
(4.4.2)
Таким образом,
UА
= UВ
= UС
= 660/
![]()
= 380 В.
Комплексы
напряжений, сопротивлений и проводимостей
в показательной и алгебраической формах:
![]() А
А
= 380 е![]() =
=
(380 +j0)
В;
![]() В
В
= 380 е![]() =
=
(-190 –j328)
В;
![]() С
С
= 380 е![]() =
=
(-190 +j328)
В;
ZА
= 8 + j6
= 10 е![]() Ом;
Ом;
YА
= 1/ ZА
= 1/ 10 е![]() =
=
0,1 е![]() =
=
(0,08 –j0,06)
См;
ZВ
= 6 – j8
= 10 е![]() Ом;
Ом;
YВ
= 1/ ZВ
= 1/10 е![]() =
=
0,1 е![]() =
=
(0,06 +j0,08)
См;
ZС
= 23 + j15,3
= 27,6 е![]() Ом;
Ом;
YС
= 1/ZС
= 1/27,6 е![]() =
=
0,0362 е![]() =
=
(0,03 –j0,02)
См;
Z0
= 1 + j0
= 1 Ом;
Y0
= 1/ Z0
= 1/1 = 1 См.
Напряжение смещения
нейтрали по (4.4.1)
а) при наличии
нулевого провода
![]() 0
0
= (380
е![]() 0,1
0,1
е![]() +
+
380 е![]() 0,1
0,1
е![]() +
+
380 е![]() 0,0362
0,0362
е![]() )/
)/
/(0,08
– j0,06
+ 0,06 + j0,08
+ 0,03 – j0,02
+ 1) = (38 е![]() + 38 е
+ 38 е![]() +
+
+ 13,7е![]() )/
)/
1,17 = 32,48 е![]() +
+
32,48 е![]() +
+
11,75 е![]() =
=
= 26 –j19,5
+12,7 – j30
+ 0,752 + j11,75
= 39,45 – j37,75
= 54 е![]() .
.
б) при обрыве
нулевого провода
![]() 0=(380е
0=(380е![]() 0,1
0,1
е![]() +
+
380е![]() 0,1
0,1
е![]() +
+
380е![]() 0,0362
0,0362
е![]() )/
)/
/(0,08
– j0,06
+ 0,06 + j0,08
+ 0,03 – j0,02)
= (38 е![]() + 38 е
+ 38 е![]() +
+
+ 13,7 е![]() )/
)/
0,17 = 223,5 е![]() + 223,5 е
+ 223,5 е![]() +
+
80,9 е![]() =
=
= 178 – j134
+ 87 – j205
+ 5,17 + j80,74
= 270 – j258
= 372е![]() .
.
Напряжение смещения нейтрали определяется по следующей формуле:
- Еа, Ев, Ес — ЭДС источника питания
- Уа, Ув, Ус — проводимости фаз потребителя, напомним, что проводимость — величина обратная полному сопротивлению, то есть У=1/Z
- 00’ — эти точки соответствуют нулю нагрузки и нулю генератора (трансформатора), питающего данную нагрузку
Под смещением нейтрали понимают, что между нулевым проводом источника и нагрузки возникает напряжение, а по нулевому проводу течет ток. Но, это в случае, если нулевые провода соединены. Если же нулевой провод источника и нагрузки не соединен, то смещение нейтрали может вызвать нарушение магнитного равновесия в трансформаторе.

Напряжение смещения нейтрали при различных типах нагрузок
Как видно, такие проблемы происходят из-за неправильных действий “электриков” либо из-за самопроизвольного обрыва (отгорания) нулевого провода в старом жилом фонде.

Мнение эксперта
It-Technology, Cпециалист по электроэнергетике и электронике
Задавайте вопросы “Специалисту по модернизации систем энергогенерации”
Назначение нулевого провода Произошло очень неприятное вернувшись домой вечером, люди обнаружили, что у них погорели телевизоры, холодильники, зарядки, и т. Спрашивайте, я на связи!
Нулевой провод
Случай 3 — нагрузка по трем фазам разнородная
В случае с разнородной неравномерной нагрузкой нейтральная точка нагрузки (0’) вышла за пределы треугольника. Значения же фазных напряжений на нагрузке превышают это значение на источнике питания в несколько раз. Однако, не следует забывать, что это смещение происходит только на нагрузке, а не на источнике питания.
Неоднородность нагрузки будет влиять на источник питания (трансформатор или генератор), только, если относительно источника эта нагрузка будет велика. В этом случае может произойти нарушение магнитной устойчивости трансформатора.
Следует помнить, чем выше нагрузка, тем большее влияние на систему она может оказывать, аналогично, как большие двигатели серьезнее просаживают напряжение на шинах при перерывах питания на электростанциях.

Последствия обрыва нуля в трехфазной сети
- Электрики ремонтировали ввод в подъезд. И во время ремонта на несколько секунд был отключен рабочий ноль. Произошло очень неприятное: вернувшись домой вечером, люди обнаружили, что у них погорели телевизоры, холодильники, зарядки, и т.п. – то, что у нас постоянно включено в розетки. Хорошо, что ещё не произошел пожар.
- Пришёл по вызову, жалоба – плавает напряжение. Меряю напряжение (всё выключено) – почти 300 вольт. Затем при включении лампы накаливания напряжение падает до 70В… Оказалось, в этажном щитке выгорел болт, на который приходит ноль. Произошел обрыв нуля, перекос фаз, напряжения пошли вразнос. Заменил болт, восстановил контакт, напряжение нормализовалось.

Болт нуля. Ржавый, периодически не контачит. Если его менять без отключения, 100% в подъезде погорит техника!
Нулевой провод отгорел от второго болта. Видно, как он отвалился под натяжением. Прежде, чем отвалиться, он ПОЧТИ переплавил изоляцию фазных проводов (вертикальные, красный и белый).
Какое освещение Вы предпочитаете
ВстроенноеЛюстра
Сервер ещё не включали, возможно, интеллектуальный ущерб будет больше…
На месте этой трагедии я установил трехфазное реле напряжения Барьер, читайте статью по ссылке.
Как видно, такие проблемы происходят из-за неправильных действий “электриков” либо из-за самопроизвольного обрыва (отгорания) нулевого провода в старом жилом фонде.
В этой статье подробно расскажу, почему такое бывает и как с этим бороться.
Перекос фаз в трехфазной сети
В первую очередь нужно понять, что же такое фаза, и что ноль, и только после этого – как их найти.

Мнение эксперта
It-Technology, Cпециалист по электроэнергетике и электронике
Задавайте вопросы “Специалисту по модернизации систем энергогенерации”
Отгорание нуля в трехфазной сети: современные проблемы электросетей Замыкание одной из фаз с рабочей нейтралью нулем и несработка по каким-либо причинам автомата защиты неисправность, большая длина участка линии между местом КЗ и автоматом и пр. Спрашивайте, я на связи!
Фаза и ноль в электрике — назначение фазного и нулевого провода
Обрыв нуля во входном щитке дома или квартиры.
Во входном щитке дома или квартиры нулевой провод может оборваться на вводном автоматическом выключателе или на нулевой шине. Как правило, ослабляется винтовое соединение, из-за чего теряется контакт между проводом и зажимом, или, в редких случаях, нулевой провод обламывается на зажиме и повисает в воздухе.
Также из-за плохого контакта между зажимом и проводом происходит нагрев и обгорание провода и, как следствие, между ними образуется большое переходное сопротивление в виде нагара

При отсутствии нуля все электрические приборы в доме работать не будут. Но если останется включенный в розетку хоть один бытовой прибор или останется включенный выключатель света, фаза через радиокомпоненты блока питания
бытовой техники или
нить накала
лампы беспрепятственно пройдет на нулевую шину, а с шины на все нулевые провода электрической проводки. И как следствие, на обоих гнездах розеток и контактах выключателей будет присутствовать фаза. Это объясняется тем, что все нулевые провода электрической проводки соединяются вместе на нулевой шине.
Для определения такой неисправности достаточно отключить из розеток все бытовые приборы и отключить все выключатели света или выкрутить лампочки. После этих действий вторая фаза из розеток и контактов выключателей пропадет. Лечится неисправность восстановлением контактов на зажимах вводного автомата или на нулевой шине.
Роль нулевого провода при соединении звездой
Звезда — это особый способ соединения концов обмоток генератора, при котором все они соединяются в одну точку, называемую нейтралью.
При этом провода на выходе у потребителя также соединяются в аналогичную точку, а провод, соединяющий две нейтрали, называется нулевым. Провода же, соединяющие начало фазы у потребителя и генератора называются линейными.
Готовые работы на аналогичную тему
В случае подключения трёхфазного двигателя нагрузка для всех трёх фазовых проводов будет одинаковая, соответственно, возвращение остаточного тока на генератор возможно по одному из фазовых проводов, на котором фазовое напряжение в данный момент времени равно нулю.
Если же нагрузки на стороне потребителя неодинаковые, остаточный ток после каждой нагрузки будет выходить разным и, соответственно, фазовое напряжение тоже будет разное.
Если говорить упрощённо, в каждый момент времени оно будет равно напряжению между проводом, который в данный момент времени не является несущим фазовый ток, и фазовым проводом — то есть оно будет разным.
Использование же нулевого провода в таком случае поможет предотвратить эти перепады и таким образом исключить возникновение неисправностей в сети.
Рисунок 1. Роль нулевого провода в трехфазной цепи при соединении звездой
На рисунке представлена схема подключения трёхфазной цепи при подключении звездой.
Ток по нейтральному проводу, соединяющему между собой две нейтрали, будет течь только при включении (или выключении) всей системы и старте работы первой из обмоток генератора.
В остальное время он будет возвращаться на генератор по фазовым проводам по очереди.
Фазовое напряжение на рисунке обозначено с помощью букв $U_A$, $U_C, U_B$, ЭДС на обмотках генератора — $E_C, E_A$ и $E_B$, а ток, текущий по фазовым проводам — буквами $I_C, I_A$ и $I_B$.
Сам генератор обозначен буквой $G$, а потребитель буквой $M$. Сопротивления у потребителя обозначены буквами $Z_A, Z_B$ и $Z_C$.
Линейные напряжения — то есть напряжения между фазами — обозначены соответственно $U_CA, U_AB, U_BC$. На рисунке стрелками показаны провода, к которым нужно подключить вольтметр для измерения линейного напряжения.


Мнение эксперта
It-Technology, Cпециалист по электроэнергетике и электронике
Задавайте вопросы “Специалисту по модернизации систем энергогенерации”
Нулевой провод: роль и обозначение, классификация, отличие от фазного Важно понимать, что возникновение электрического тока возможно исключительно при наличии замкнутой электрической сети рисунок 2. Спрашивайте, я на связи!
Случай 2 — нагрузка однородная и неравномерная по трем фазам
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно,
все рассмотренные ранее методы расчета и анализа в символической форме в полной
мере распространяются на них. Анализ трехфазных систем удобно осуществлять с
использованием векторных диаграмм, позволяющих достаточно просто определять
фазовые сдвиги между переменными. Однако определенная специфика многофазных
цепей вносит характерные особенности в их расчет, что, в первую очередь, касается
анализа их работы в симметричных режимах.
Расчет симметричных режимов работы трехфазных систем
Многофазный приемник и вообще многофазная цепь называются симметричными,
если в них комплексные сопротивления соответствующих фаз одинаковы, т.е.
если ![]() . В противном случае они являются
. В противном случае они являются
несимметричными. Равенство модулей указанных сопротивлений не является
достаточным условием симметрии цепи. Так, например трехфазный приемник на рис.
1,а является симметричным, а на рис. 1,б – нет даже при условии: ![]() .
.

Если к симметричной трехфазной цепи приложена симметричная трехфазная система
напряжений генератора, то в ней будет иметь место симметричная система токов.
Такой режим работы трехфазной цепи называется симметричным. В этом режиме
токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг
по отношению к другу на угол ![]() . Вследствие указанного расчет
. Вследствие указанного расчет
таких цепей проводится для одной – базовой – фазы, в качестве которой
обычно принимают фазу А. При этом соответствующие величины в других фазах получают
формальным добавлением к аргументу переменной фазы А фазового сдвига ![]() при сохранении неизменным ее модуля.
при сохранении неизменным ее модуля.
Так для симметричного режима работы цепи на рис. 2,а при известных линейном
напряжении и сопротивлениях фаз ![]() можно записать
можно записать
 ,
,
где ![]()
определяется характером нагрузки ![]() .
.
Тогда на основании вышесказанного
![]() ;
;
![]() .
.

Комплексы линейных токов можно найти с использованием векторной диаграммы на
рис. 2,б, из которой вытекает:

При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется
с помощью двух основных приемов:
Все треугольники заменяются эквивалентными звездами. Поскольку треугольники
симметричны, то в соответствии с формулами преобразования «треугольник-звезда»
 .
.
Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы
их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи
их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется
базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам
которого определяются соответствующие величины в других фазах.
Пусть, например, при заданном фазном напряжении ![]() необходимо определить линейные
необходимо определить линейные
токи ![]() и
и ![]() в схеме на рис. 3, все сопротивления
в схеме на рис. 3, все сопротивления
в которой известны.
В соответствии с указанной методикой выделим расчетную фазу А, которая представлена
на рис. 4. Здесь ![]() ,
, ![]() .
.
Тогда для тока  можно записать
можно записать
 ,
,
и соответственно ![]() .
.


Расчет несимметричных режимов работы трехфазных систем
Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет
место несимметричный режим работы. Такие режимы при наличии в цепи только статической
нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для
всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные
напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить,
что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес
также потенциалы узлов, чаще других для расчета сложных схем применяется метод
узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей
с электрическими машинами в основном применяется метод симметричных составляющих,
который будет рассмотрен далее.
При заданных линейных напряжениях наиболее просто рассчитываются трехфазные
цепи при соединении в треугольник. Пусть в схеме на рис. 2,а ![]() . Тогда при известных комплексах
. Тогда при известных комплексах
линейных напряжений в соответствии с законом Ома
 ;
;  ;
;  .
.
По найденным фазным токам приемника на основании первого закона Кирхгофа определяются
линейные токи:
![]() .
.
Обычно на практике известны не комплексы линейных напряжений, а их модули.
В этом случае необходимо предварительное определение начальных фаз этих напряжений,
что можно осуществить, например, графически. Для этого, приняв ![]() , по заданным модулям напряжений,
, по заданным модулям напряжений,
строим треугольник (см. рис.5), из которого (путем замера) определяем значения
углов a и b.

Тогда

Искомые углы a и b могут быть также найдены аналитически
на основании теоремы косинусов:

При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода
с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям
на фазах источника. В этом случае фазные токи легко определяются по закону Ома,
т.е. путем деления известных напряжений на фазах потребителя на соответствующие
сопротивления. Однако, если сопротивление нейтрального провода велико или он
отсутствует, требуется более сложный расчет.
Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной
нагрузке ![]() ей в общем случае будет соответствовать
ей в общем случае будет соответствовать
векторная диаграмма напряжений (см. рис. 6,б), на которой нейтральные точки
источника и приемника занимают разные положения, т.е. ![]() .
.
Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением
смещения нейтральной точки (обычно принимается, что ![]() ) или просто напряжением смещения
) или просто напряжением смещения
нейтрали. Чем оно больше, тем сильнее несимметрия фазных напряжений на нагрузке,
что наглядно иллюстрирует векторная диаграмма на рис. 6,б.
Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали.
Если оно известно, то напряжения на фазах нагрузки равны:
![]() .
.

Тогда для искомых токов можно записать:
![]() .
.
Соотношение для напряжения смещения нейтрали, записанное на основании метода
узловых потенциалов, имеет вид
 . . |
(1) |
При наличии нейтрального провода с нулевым сопротивлением ![]() , и из (1)
, и из (1) ![]() . В случае отсутствия нейтрального
. В случае отсутствия нейтрального
провода ![]() . При симметричной нагрузке
. При симметричной нагрузке ![]() с учетом того, что
с учетом того, что ![]() , из (1) вытекает
, из (1) вытекает ![]() .
.

В качестве примера анализа несимметричного
режима работы цепи с использованием соотношения (1) определим, какая из ламп
в схеме на рис. 7 с прямым чередованием фаз источника будет гореть ярче, если
![]() .
.
Запишем выражения комплексных сопротивлений фаз нагрузки:

Тогда для напряжения смещения нейтрали будем иметь

Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника
опускается)

Таким образом, наиболее ярко будет гореть лампочка в фазе С.
В заключение отметим, что если при соединении в звезду задаются линейные напряжения
(что обычно имеет место на практике), то с учетом того, что сумма последних
равна нулю, их можно однозначно задать с помощью двух источников ЭДС, например,
![]() и
и ![]() . Тогда, поскольку при этом
. Тогда, поскольку при этом ![]() , соотношение (1) трансформируется
, соотношение (1) трансформируется
в формулу
 . . |
(2) |
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Какой многофазный приемник является симметричным?
- Какой режим работы трехфазной цепи называется симметричным?
- В чем заключается специфика расчета симметричных режимов работы трехфазных
цепей? - С помощью каких приемов трехфазная симметричная схема сводится к расчетной
однофазной? - Что такое напряжение смещения нейтрали, как оно определяется?
- Как можно определить комплексы линейных напряжений, если заданы их модули?
- Что обеспечивает нейтральный провод с нулевым сопротивлением?
- В цепи на рис. 6,а
 ;
;  ;
;  ;
;  . Линейное напряжение равно 380
. Линейное напряжение равно 380
В. - В схеме предыдущей задачи
 ;
;  . Остальные параметры те же.
. Остальные параметры те же. - В задаче 8 нейтральный провод оборван.
- В задаче 9 нейтральный провод оборван.
Определить ток в нейтральном проводе.
Ответ: ![]() .
.
Определить ток в нейтральном проводе.
Ответ: ![]() .
.
Определить фазные напряжения на нагрузке.
Ответ: ![]() ;
; ![]() ;
; ![]() .
.
Определить фазные напряжения на нагрузке.
Ответ: ![]() ;
; ![]() ;
; ![]() .
.
