σ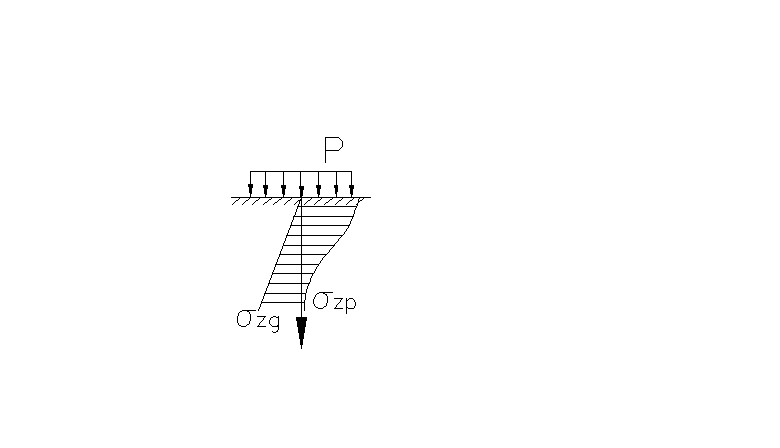
zр
– напряжения от внешней нагрузки.
σzg
– напряжения от собственного веса
грунта.
1
.)
основание однородное:
NL– отметка природного
рельефа;
σzg=γ*z
γ– удельный вес грунта (кН/м3)
γ=ρ*g
2.) основание слоистое (неоднородное):
σ
zg
= Σγi*hi
= γ1*h1+ γ2*h2+
γ3*(z–h1–h2)
3
.)
основание однородно, грунт водонепроницаемый,
есть УГВ.
σzg
= Σγi*hi
= γ*dw+
γsb*(z–
dw)
γsb –
удельный вес грунта с учетом взвешивающего
действия воды (определяется для
водопроницаемых грунтов, залегающих
ниже уровня грунтовых вод).
γsb= (ρsb*g)=
(γs–
γw)/(1+e).
γs– удельный
вес твердых частиц;
γw– удельный
вес воды = 10 кН/м3.
е– коэф-т пористости.
γ– удельный вес грунта, определяется
для всех грунтов, залегающих выше УГВ,
для водонепроницаемых грунтов, залегающих
ниже УГВ (водонепроницаемый грунт –
глина).
4
.)
основание однородное, грунт
водонепроницаемый, есть УГВ:
σzg=γ*z
5.) основание неоднородное, есть УГВ.:
σzg
= Σγi*hi
= γ1*h1+ γ2*h2+
γ3*(z–h1–h2)
+ γsb3*(h1+h2+h3–dw)+
+ γsb4*h4+
γ5*(z–h1-h2-h3-h4)+
γw*hw
γw– удельный
вес воды = 10 кН/м3.
hw– расстояние от УГВ до водонепроницаемого
слоя.
hw
= h1+h2+h3+h4-dw
6.) верхний грунт насыпной:
Давление насыпи не учитывается.
Насыпной слой рассматривается до3-х
метров и более 3-х м.
Слои рассчитываются как в предыдущих
случаях.
NL– отметка природного
рельефа;
DL– планировочная отметка.
10.) Определение осадки фундамента методом послойного суммирования.
Этот метод универсальный. Расчетные
осадки обычно занижены за исключением
полутвердых и твердых глин. Расчетная
схема – линейно-деформ. полупространство
с условным ограничением сжимаемой
толщи.
Допущения:
1.) грунт является линейно-деформ.телом.
2.) деформации развиваются под действием
только нормальных вертикальных напряжений
σz.
3.) Боковое расширение грунта невозможно.
4.) Нормальное вертикальное внешнее
давление σzропределяется под центром фундамента.
5.) Фундамент не обладает жесткостью.
6.) Деформации учитываются только в
пределах сжимаемой толщи Нс.
7.) Коэф-т β=0,8.
На схеме:
1
.)
Все основание делится на слои толщинойhi <0,4b(b-ширина
фундамента).
2.) Определяются расстояния zi–
это расстояния от подошвы фундамента
до поверхностиi-го слоя.
3.) Определяется Si-осадка поверхностиi-го
слоя:
Si=(σzpi*hi)/Ei,гдеσzpi– среднее значение вертикального
нормального напряжения я вi-слое
грунта равное полусумме указанных
напряжений на верхних и нижних границах
слоя.
4.) Определяется осадка фундамента
S=βΣ(σzpi*hi)/Ei=βΣSi.
Чтобы определить сжимаемую толщу,
необходимо построить 3 эпюры:σzg-от
собственного веса грунта,σzp-эпюра
напряжений от внешнего давления
(σzp=α*Р0),0,2σzg(Е>5МПа)
или0,1σzg(если
Е<5МПа). Считается что, ниже точки
пересечения грунт не сжимается и осадки
= 0; расстояние от подошвы фундамента до
точки пересечения называетсямощностью
сжимаемой толщи (слоев)Нс.
11.) Определение осадки фундамента методом эквивалентного слоя.
Этот метод используется, если площадь
подошвы фундамента не превышает 50м2.
Допущения:
а.) грунт является линейно-деформируемым
материалом.
б.) грунт однороден на всю глубину
сжимаемой толщи.
1.) основание однородное:
S=he*mυ*PО
he– толщина эквивалентного
слояhe=Aυw*b,
гдеb– ширина подошвы
фундамента,Aυw
– коэф-т эквивалентного слоя,
определяется по таблицам справочников
в зависимости от вида грунта и формы
фундамента.
mυ– коэф-т относительной сжимаемости.mυ=m0*(1+e),
гдее– коэф-т пористости грунта,
залегающего под подошвой фундамента,m0– коэф-т
сжимаемости.
РО = РmII
– σzg0,
гдеРО– дополнительное
давление на подошве фундамента,РmII– среднее давление под подошвой
фундамента. σzg0– напряжение от собственного веса
грунта на уровне подошвы фундамента.
2.) основание неоднородное:
S=he*mυm*P0,
гдеmυm=
(1/2he2)*Σ(zi*hi*mυi),
где mυi– коэф-т относительной сжимаемостиi-го слоя.
Соседние файлы в папке Шпоры к госам_Грунты
- #
- #
- #
- #
- #
- #
- #
В практике проектирования неоднородность основания учитывается в следующих случаях:
- – слой сжимаемого грунта залегает на практически несжимаемом (например, скальном) основании;
- – под сравнительно малосжимаемым слоем залегает более сжимаемый грунт.
На рис. 5.12 приведены схематические эпюры вертикальных нормальных напряжений под центром прямоугольной площадки, загруженной равномерно распределенной нагрузкой при жестком (кривая 2) и слабом (кривая 3) подстилающих слоях. Кривая 1 показывает распределение напряжений в однородном основании. Как видно из рис. 5.12, при жестком подстилающем слое напряжения на границе слоев увеличиваются, а при слабом подстилающем слое уменьшаются.
Значения σz/p на кровле несжимаемого слоя, расположенного на глубине Н, под центром равномерно загруженной площади приведены в табл. 5.7.
Напряжения при слабом подстилающем слое определяются в зависимости от E1/E2 (где E1 и E2 — модули деформации верхнего и подстилающего слоя). В табл. 5.8 приведены значения σz/p на контакте со слабым подстилающим слоем по оси полосы, загруженной равномерно распределенной нагрузкой, при отсутствии трения по контактной плоскости.
ТАБЛИЦА 5.7. ЗНАЧЕНИЯ σz/p НА КОНТАКТЕ С НЕСЖИМАЕМЫМ СЛОЕМ
| H/b1 | σz/p для площадки | |||||
| круглой (r = b1) | прямоугольной с отношением сторон η = l/b | полосовой (η = ∞) | ||||
| 1 | 2 | 3 | 10 | |||
| 0 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| 0,25 | 1,009 | 1,009 | 1,009 | 1,009 | 1,009 | 1,009 |
| 0,5 | 1,064 | 1,053 | 1,033 | 1,033 | 1,033 | 1,033 |
| 0,75 | 1,072 | 1,082 | 1,059 | 1,059 | 1,059 | 1,059 |
| 1 | 0,965 | 1,027 | 1,039 | 1,026 | 1,025 | 1,025 |
| 2 | 0,473 | 0,541 | 0,717 | 0,769 | 0,761 | 0,761 |
| 3 | 0,249 | 0,298 | 0,474 | 0,549 | 0,560 | 0,560 |
| 5 | 0,098 | 0,125 | 0,222 | 0,287 | 0,359 | 0,359 |
| 10 | 0,025 | 0,032 | 0,064 | 0,093 | 0,181 | 0,185 |
Рис. 5.12. Схема распределения вертикальных нормальных напряжений в основании под центром равномерно загруженной, прямоугольной площадки
1 — однородном; 2 — с жестким подстилающим слоем; 3 — со слабым подстилающим слоем
ТАБЛИЦА 5.8. ЗНАЧЕНИЯ σz/p ПО ОСИ ПОЛОСЫ НА КОНТАКТЕ СО СЛАБЫМ ПОДСТИЛАЮЩИМ СЛОЕМ (ПО ДАННЫМ А.А. КУЛАГИНА)
| H/b1 | σz/p при E1/E2 | |||
| 1 | 2 | 5 | 10 | |
| 0 | 1,000 | 1,000 | 1,000 | 1,000 |
| 1 | 0,818 | 0,755 | 0,639 | 0,541 |
| 2 | 0,550 | 0,478 | 0,378 | 0,307 |
| 3 | 0,396 | 0,339 | 0,262 | 0,206 |
| 4 | 0,306 | 0,258 | 0,194 | 0,148 |
| 5 | 0,248 | 0,206 | 0,150 | 0,113 |
5.2.3. Напряжения от собственного веса грунта
Вертикальное нормальное напряжение σz от собственного веса грунта определяется по формуле
,
(5.20)
где n — число слоев грунта, расположенных выше рассматриваемой глубины; γi — удельный вес грунта i-го слоя; hi — толщина i-го слоя грунта.
Удельный вес грунтов, залегающих ниже уровня подземных вод, но выше водоупора, определяется с учетом взвешивающего действия воды по формуле
γsb = (γs – γω)/(1 + e),
(5.21)
где γs — удельный вес частиц грунта; γω — удельный вес воды, принимаемый равным 10 кН/м3; е — коэффициент пористости грунта.
Если удельный вес грунта определен при его полном водонасыщении (степень влажности Sr = 1, γ = γsat), то
γsb = γsat – γω.
(5.22)
При определении σz от собственного веса грунта в водоупорном слое необходимо учитывать давление столба воды, расположенного выше водоупора.
Горизонтальные нормальные напряжения от собственного веса грунта
σx = σy = ξσz,
(5.23)
где ξ = v/(1 – v) — коэффициент бокового давления грунта (здесь v принимается по табл. 1.15).
Пример 5.3. Определить вертикальное нормальное напряжение σz от собственного веса грунта на глубине z = 9 м при грунтовых напластованиях, показанных на рис. 5.13.
Рис. 5.13. К примеру 5.3 (значении σz даны в кПа)
Слой 1 — суглинок (толщина слоя h1 = 2 м, удельный вес γ1 = 17,8 кН/м3); слой 2 — песок средней крупности (h2 = 2 м, удельный вес частиц γs = 26,6 кН/м3, γ2 = 18,3 кН/м3, коэффициент пористости е = 0,61, влажность ω = 0,11); слой 3 — тот же песок ниже уровня подземных вод (h3 = 3 м, γ3 = 20,3 кН/м3 при степени влажности Sr = 1); слой 4 — глина, служащая водоупором (γ4 = 20,2 кН/м3).
Решение, по формуле (5.22) удельный вес грунта слоя 3
γsb = 20,3 – 10 = 10,3 кН/м3.
По формуле (5.20) на глубине z = 9 м получаем: σz = 17,8 × 2+ 18,3 × 2 + 10,3 × 3 + 20,2 × 2 + 10 × 3 = 173,6 кПа.
Значения ординат эпюры σz приведены на рис. 5.13.
5.3. НАГРУЗКИ И ВОЗДЕЙСТВИЯ, УЧИТЫВАЕМЫЕ В РАСЧЕТАХ ОСНОВАНИЙ
Нагрузки и воздействия, передаваемые фундаментами сооружений на основания, как правило, должны устанавливаться расчетам исходя из рассмотрения совместной работы сооружения и основания или фундамента и основания. Учитываемые при этом нагрузки и воздействия на сооружение или отдельные его элементы, а также возможные их сочетания применяются согласно требованиям норм [3].
Характер и степень перераспределения нагрузок на основание, а следовательно, и дополнительные усилия в конструкциях сооружения зависят от вида, состояния и свойства грунтов, характера их напластования, статической схемы сооружения, его пространственной жесткости и многих других факторов.
Нагрузки на основание допускается определять без учета их перераспределения над фундаментной конструкцией при расчете:
а) оснований зданий и сооружений III класса;
б) общей устойчивости массива грунта основания совместно с рассматриваемым сооружением;
в) средних значений деформаций основания;
г) деформаций основания в стадии привязки типовых проектов к местным грунтовым условиям.
Все расчеты оснований должны производиться на расчетные значения нагрузок, которые определяются как произведение их нормативных значений на коэффициент надежности по нагрузке γf. Этот коэффициент, учитывающий возможное отклонение нагрузок в неблагоприятную сторону, принимается при расчете оснований по несущей способности по указаниям [3], а при расчете оснований по деформациям равным единице.
Расчет оснований по деформациям производится на основное сочетание нагрузок, по несущей способности — на основное сочетание, а при наличии особых нагрузок и воздействий — на основное и особое сочетания. Нагрузки на перекрытия зданий и снеговые нагрузки, которые согласно нормам [3] могут относиться как к длительным, так и к кратковременным, при расчете оснований по несущей способности считаются кратковременными, а при расчете по деформациям — длительными. Нагрузки от подвижного подъемно-транспортного оборудования в обоих случаях считаются кратковременными.
В расчетах оснований необходимо учитывать нагрузки от складируемого материала и оборудования, размещаемого вблизи фундаментов.
Усилия в конструкциях, вызываемые климатическими температурными воздействиями, при расчете оснований по деформациям допускается не учитывать, если расстояния между температурно-усадочными швами не превышают значений, указанных в нормах проектирования соответствующих конструкций. Технологические температурные воздействия учитываются в расчетах оснований по деформациям при соответствующем обосновании в зависимости от продолжительности этих воздействий.
Напряжения от действия собственного веса грунта
Для нахождения вертикального напряжения от действия веса грунта на глубине z мысленно вырежем столб грунта до этой глубины с единичной площадью основания (рис. 3.16) и найдем суммарное напряжение szg от веса этого столба:
, (3.28)
где n – число разнородных слоев грунта в пределах глубины z ; gi – удельный вес грунта i — го слоя; hi – толщина i — го слоя.
Эпюра напряжений от собственного веса грунта в пределах однородного слоя имеет вид треугольника, при слоистом залегании эпюра изображается ломаной линией.
Удельный вес водопроницаемых грунтов (пески, супеси), залегающих ниже уровня грунтовых вод, принимается с учетом взвешивающего действия воды по формуле
, (3.29)
где gs – удельный вес твердых частиц грунта; gw – удельный вес воды; е – коэффициент пористости грунта.
Если водопроницаемый слой подстилается водоупорным слоем в виде плотных глин, на кровлю водоупора передается гидростатическое давление воды gw× h3 и на эпюре давления появляется уступ (рис. 3.16).
Рис. 3.16. Эпюра напряжений szg от собственного веса грунта:
1 – суглинок; 2 – песок; 3 – глина
Горизонтальные напряжения от собственного веса грунта определяются как
, (3.30)
где x – коэффициент бокового давления грунта в состоянии покоя.
Касательных напряжений в массиве от действия собственного веса грунта не возникает (txy = txz = tyz = 0). Значение коэффициента бокового давления грунта находится из выражения
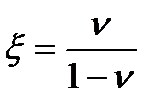. (3.31)
Здесь n – коэффициент Пуассона грунта.
3.6. Распределение напряжений на подошве фундамента
(контактная задача)
При решении всех ранее рассмотренных задач о распределении напряжений в грунтах считалось, что нагрузка передается непосредственно на поверхность грунтового массива без использования какой-либо конструкции. Такая схема передачи нагрузки характерна при возведении на основании земляных сооружений, например, насыпей, при передаче нагрузки через гибкую плиту и т.п. Нагрузка на основание от сооружений чаще всего передается через фундаменты, представляющие собой достаточно жесткие конструкции. При взаимодействии фундамента сооружения с основанием на поверхности контакта возникают напряжения. Напряжения на контакте поверхности основания с нижней поверхностью конструкции, через которую передаются нагрузки, называются контактными напряжениями. Характер распределения этих напряжений зависит от жесткости, формы, размеров сооружения и жесткости грунтов основания.
Критерием оценки жесткости сооружения может служить показатель гибкости по М.И. Горбунову-Посадову:
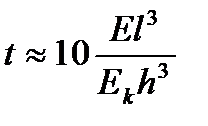; (3.32)
где Е – модуль деформации грунта; Ек – модуль упругости конструкции;
l и h — длина и толщина конструкции.
1 – абсолютно жесткие (t ≤ 1) , когда деформируемость сооружения ничтожно мала по сравнению с деформируемостью основания. Пример – фундаменты под дымовые трубы, элеваторы, массивные фундаменты мостовых опор и др.;
2 – абсолютно гибкие (t ≥ 10), когда деформируемость сооружения настолько велика, что оно свободно следует за деформациями сооружения. Пример – насыпи, днища металлических резервуаров;
3 – сооружения конечной жесткости (1
Источник
Напряжение в грунте от собственного веса
Напряжение – это средняя величина непрерывно распределенных в сечении внутренних сил, приходящихся на единицу площади сечения.
При горизонтальной поверхности и отсутствии бокового расширения грунта для определения компонентов напряжений от его собственного веса используются зависимости
При однородной толще грунтов
где ξ – коэффициент бокового давления;
Напряжение в грунте от сосредоточенной силы.
Решение задачи о распределении напряжений от действия вертикальной сосредоточенной силы, приложенной в точке на поверхности однородного изотропного линейно-деформируемого полупространства (задача Буссинеска), получено в виде
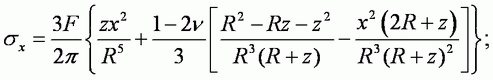
Сумма главных напряжений в любой точке основания
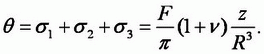
Перемещения, параллельные осям координат,
При многих оснований важно определение вертикальных составляющих напряжений σz:
где 
Для определения k в зависимости от отношения r/z используется график:
На рисунке показаны изобары (линии равных напряжений) вертикальных напряжений при действии сосредоточенной силы.
Анализируя формулу (*), можно сказать, что:
1 В точке приложения силы А напряжения σz будут бесконечно большими.
2 Полностью напряжения σz затухают на глубине z, равной бесконечности.
Напряжения в грунте от распределенной нагрузки.
В случае действия распределенной по части поверхности грунта нагрузки произвольной интенсивности напряжения можно определять по приведенным выше выражениям, используя принцип суперпозиции (независимости действия сил).
Область загружения делится на ряд элементов, распределенная нагрузка на которых заменяется равнодействующими в центрах их тяжести.
Вертикальное сжимающее напряжение на глубине z от поверхности на любой горизонтальной площадке в произвольной точке А определится как
или 
При одинаковой интенсивности нагрузки
Для более строгого решения задачи переходят к интегрированию по всей площади загружения, принимая стороны элементов разбивки как дифференциалы dx и dy.
Для сложной формы нагрузки и любой формы площади загружения строгого решения для определения напряжений в грунте пока нет. Есть строгое решение для равномерно распределенной нагрузки при квадратной, прямоугольной и круглой форме площади загружения.
Напряжения от действия внешней нагрузки под центром фундамента.
Решение для определения σz под центром площадки выглядит как:
где b – ширина подошвы фундамента;
a – длина подошвы фундамента;
z – глубина, на которой определяется σz;
Значение этой сложной функции f приведены в СНиП 2.02.01- 83 * в виде таблиц.
В них по двум параметрам 
и 
определяется значение этой функции: 
Cогласно СНиП: 
Метод угловых точек.
В результате сравнения численных решений, оказалось, что напряжение под центром и под углом площадки связаны следующим образом:
При использовании метода угловых точек для определения напряжений σz напряжения под центом площадки загружения (подошвы фундамента) находят по той же таблице СНиП, но коэффициент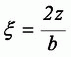 
берут в виде: 
где b – ширина подошвы фундамента;
коэффициент η – не меняется.
Коэффициент α1 находим, пользуясь соотношениями:
и
Коэффициент α2 находим, пользуясь соотношениями:
и 
Напряжения σz на горизонтальной площадке под углом А на любой глубине можно определять из простого соотношения:
Пользуясь методом угловых точек можно находить вертикальные нормальные напряжения σz в любой точке углового массива:
Источник
5.2.2. Неоднородное основание
В практике проектирования неоднородность основания учитывается в следующих случаях:
- – слой сжимаемого грунта залегает на практически несжимаемом (например, скальном) основании;
- – под сравнительно малосжимаемым слоем залегает более сжимаемый грунт.
На рис. 5.12 приведены схематические эпюры вертикальных нормальных напряжений под центром прямоугольной площадки, загруженной равномерно распределенной нагрузкой при жестком (кривая 2) и слабом (кривая 3) подстилающих слоях. Кривая 1 показывает распределение напряжений в однородном основании. Как видно из рис. 5.12, при жестком подстилающем слое напряжения на границе слоев увеличиваются, а при слабом подстилающем слое уменьшаются.
Значения σz/p на кровле несжимаемого слоя, расположенного на глубине Н , под центром равномерно загруженной площади приведены в табл. 5.7.
Напряжения при слабом подстилающем слое определяются в зависимости от E1/E2 (где E1 и E2 — модули деформации верхнего и подстилающего слоя). В табл. 5.8 приведены значения σz/p на контакте со слабым подстилающим слоем по оси полосы, загруженной равномерно распределенной нагрузкой, при отсутствии трения по контактной плоскости.
ТАБЛИЦА 5.7. ЗНАЧЕНИЯ σz/p НА КОНТАКТЕ С НЕСЖИМАЕМЫМ СЛОЕМ
| H/b1 | σz/p для площадки | |||||
| круглой ( r = b1 ) | прямоугольной с отношением сторон η = l/b | полосовой ( η = ∞) | ||||
| 1 | 2 | 3 | 10 | |||
| 0 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| 0,25 | 1,009 | 1,009 | 1,009 | 1,009 | 1,009 | 1,009 |
| 0,5 | 1,064 | 1,053 | 1,033 | 1,033 | 1,033 | 1,033 |
| 0,75 | 1,072 | 1,082 | 1,059 | 1,059 | 1,059 | 1,059 |
| 1 | 0,965 | 1,027 | 1,039 | 1,026 | 1,025 | 1,025 |
| 2 | 0,473 | 0,541 | 0,717 | 0,769 | 0,761 | 0,761 |
| 3 | 0,249 | 0,298 | 0,474 | 0,549 | 0,560 | 0,560 |
| 5 | 0,098 | 0,125 | 0,222 | 0,287 | 0,359 | 0,359 |
| 10 | 0,025 | 0,032 | 0,064 | 0,093 | 0,181 | 0,185 |
ТАБЛИЦА 5.8. ЗНАЧЕНИЯ σz/p ПО ОСИ ПОЛОСЫ НА КОНТАКТЕ СО СЛАБЫМ ПОДСТИЛАЮЩИМ СЛОЕМ (ПО ДАННЫМ А.А. КУЛАГИНА)
| H/b1 | σz/p при E1/E2 | |||
| 1 | 2 | 5 | 10 | |
| 0 | 1,000 | 1,000 | 1,000 | 1,000 |
| 1 | 0,818 | 0,755 | 0,639 | 0,541 |
| 2 | 0,550 | 0,478 | 0,378 | 0,307 |
| 3 | 0,396 | 0,339 | 0,262 | 0,206 |
| 4 | 0,306 | 0,258 | 0,194 | 0,148 |
| 5 | 0,248 | 0,206 | 0,150 | 0,113 |
5.2.3. Напряжения от собственного веса грунта
Вертикальное нормальное напряжение σz от собственного веса грунта определяется по формуле
где n — число слоев грунта, расположенных выше рассматриваемой глубины; γi — удельный вес грунта i -го слоя; hi — толщина i -го слоя грунта.
Удельный вес грунтов, залегающих ниже уровня подземных вод, но выше водоупора, определяется с учетом взвешивающего действия воды по формуле
где γs — удельный вес частиц грунта; γω — удельный вес воды, принимаемый равным 10 кН/м 3 ; е — коэффициент пористости грунта.
Если удельный вес грунта определен при его полном водонасыщении (степень влажности Sr = 1, γ = γsat ), то
При определении σz от собственного веса грунта в водоупорном слое необходимо учитывать давление столба воды, расположенного выше водоупора.
Горизонтальные нормальные напряжения от собственного веса грунта
где ξ = v/(1 – v) — коэффициент бокового давления грунта (здесь v принимается по табл. 1.15).
Пример 5.3. Определить вертикальное нормальное напряжение σz от собственного веса грунта на глубине z = 9 м при грунтовых напластованиях, показанных на рис. 5.13.
Слой 1 — суглинок (толщина слоя h1 = 2 м, удельный вес γ1 = 17,8 кН/м 3 ); слой 2 — песок средней крупности ( h2 = 2 м, удельный вес частиц γs = 26,6 кН/м 3 , γ2 = 18,3 кН/м 3 , коэффициент пористости е = 0,61, влажность ω = 0,11); слой 3 — тот же песок ниже уровня подземных вод ( h3 = 3 м, γ3 = 20,3 кН/м 3 при степени влажности Sr = 1); слой 4 — глина, служащая водоупором ( γ4 = 20,2 кН/м 3 ).
Решение, по формуле (5.22) удельный вес грунта слоя 3
По формуле (5.20) на глубине z = 9 м получаем: σz = 17,8 × 2+ 18,3 × 2 + 10,3 × 3 + 20,2 × 2 + 10 × 3 = 173,6 кПа.
Значения ординат эпюры σz приведены на рис. 5.13.
5.3. НАГРУЗКИ И ВОЗДЕЙСТВИЯ, УЧИТЫВАЕМЫЕ В РАСЧЕТАХ ОСНОВАНИЙ
Нагрузки и воздействия, передаваемые фундаментами сооружений на основания, как правило, должны устанавливаться расчетам исходя из рассмотрения совместной работы сооружения и основания или фундамента и основания. Учитываемые при этом нагрузки и воздействия на сооружение или отдельные его элементы, а также возможные их сочетания применяются согласно требованиям норм [3].
Характер и степень перераспределения нагрузок на основание, а следовательно, и дополнительные усилия в конструкциях сооружения зависят от вида, состояния и свойства грунтов, характера их напластования, статической схемы сооружения, его пространственной жесткости и многих других факторов.
Нагрузки на основание допускается определять без учета их перераспределения над фундаментной конструкцией при расчете:
а) оснований зданий и сооружений III класса;
б) общей устойчивости массива грунта основания совместно с рассматриваемым сооружением;
в) средних значений деформаций основания;
г) деформаций основания в стадии привязки типовых проектов к местным грунтовым условиям.
Все расчеты оснований должны производиться на расчетные значения нагрузок, которые определяются как произведение их нормативных значений на коэффициент надежности по нагрузке γf . Этот коэффициент, учитывающий возможное отклонение нагрузок в неблагоприятную сторону, принимается при расчете оснований по несущей способности по указаниям [3], а при расчете оснований по деформациям равным единице.
Расчет оснований по деформациям производится на основное сочетание нагрузок, по несущей способности — на основное сочетание, а при наличии особых нагрузок и воздействий — на основное и особое сочетания. Нагрузки на перекрытия зданий и снеговые нагрузки, которые согласно нормам [3] могут относиться как к длительным, так и к кратковременным, при расчете оснований по несущей способности считаются кратковременными, а при расчете по деформациям — длительными. Нагрузки от подвижного подъемно-транспортного оборудования в обоих случаях считаются кратковременными.
В расчетах оснований необходимо учитывать нагрузки от складируемого материала и оборудования, размещаемого вблизи фундаментов.
Усилия в конструкциях, вызываемые климатическими температурными воздействиями, при расчете оснований по деформациям допускается не учитывать, если расстояния между температурно-усадочными швами не превышают значений, указанных в нормах проектирования соответствующих конструкций. Технологические температурные воздействия учитываются в расчетах оснований по деформациям при соответствующем обосновании в зависимости от продолжительности этих воздействий.
Сорочан Е.А. Основания, фундаменты и подземные сооружения
Источник
