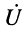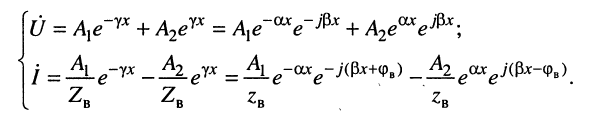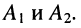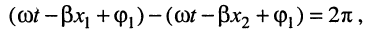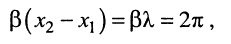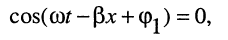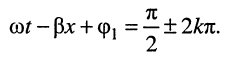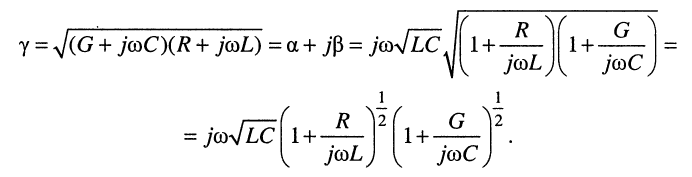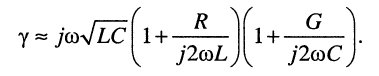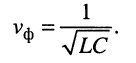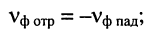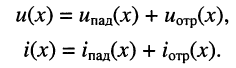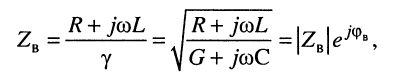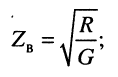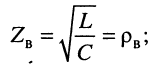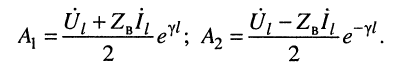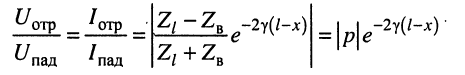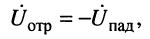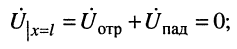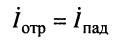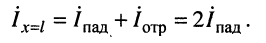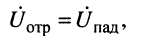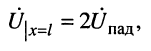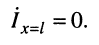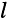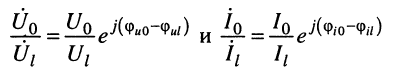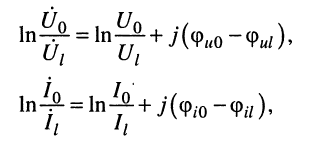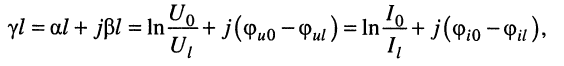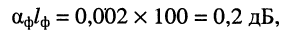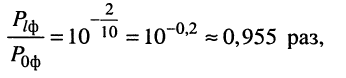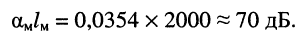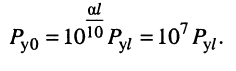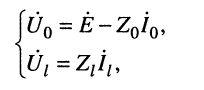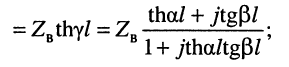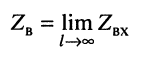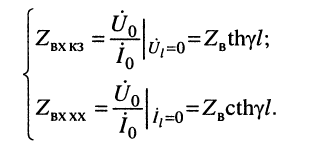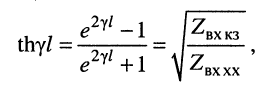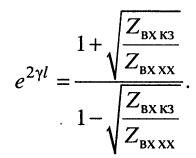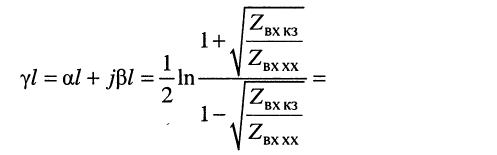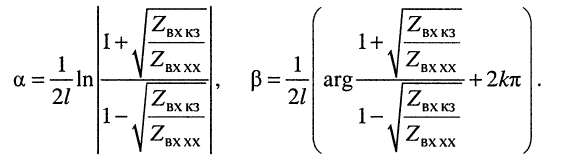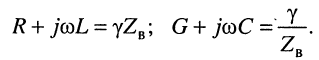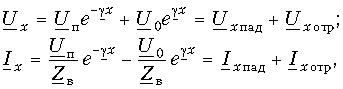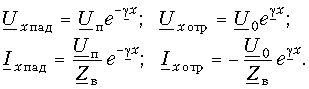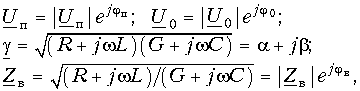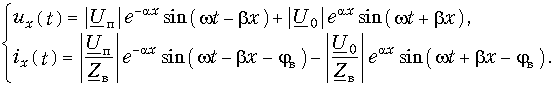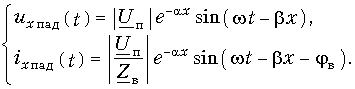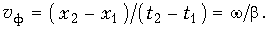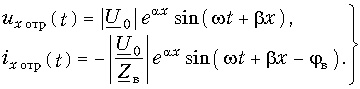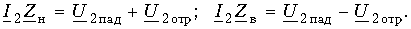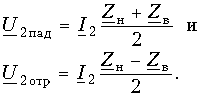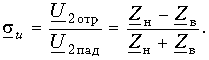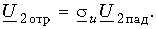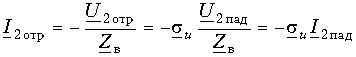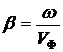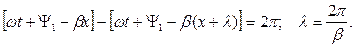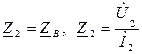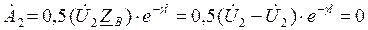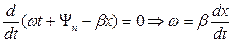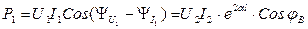Как найти напряжение падающей волны

Подставим в фор­мулу (5.13) A₂e^jyп вместо , A₁e^jyо вместо , заме­ним на a + jb, получим:

.

(5.28)

Аналогичную операцию проделаем с формулой (5.16), причем в дополнение заменим Z_в на z_вe^jjв [см. формулу (5.17)]:

.

(5.29)

Для перехода от комплексов напряжения и тока к функциям времени умножим правые части формул (5.28) и (5.29) на и от произведений возьмем мнимую часть:

;

(5.30)

.

(5.31)

Падающей электромагнитной волной (рис. 5.4) называют процесс перемещения электромагнитного состояния (электромагнитной волны) от источника энергии к приемнику, т.е. в на­шем случае в направлении уве­личения координаты х. Элек­тромагнитное состояние опре­деляется совокупностью электрического и магнитного полей. Падающая волна, распростра­няясь от источника энергии к приемнику, несет энергию, за­ключенную в ее электрическом и магнитном полях.

Отраженной электромагнитной волной (рис. 5.5) называют процесс пере­мещения электромагнитного состояния (электромагнитной волны) от приемника к источнику энергии, т.е. в нашем случае в сторону уменьшения координаты х.

Падающая электромагнитная волна образована падающей волной напряжения [второе слагаемое формулы (5.30)] и падающей волной тока [второе слагаемое формулы (5.31)]. Отраженная электромагнит­ная волна образована отраженной волной напряжения [первое сла­гаемое формулы (5.30)] и отраженной волной тока [первое слагаемое формулы (5.31)].

Знак «минус» у отраженной волны то­ка свидетельствует о том, что поток энергии, который несет с собой отражен­ная электромагнитная волна, движется в обратном направлении по сравнению с потоком энергии, который несет с со­бой падающая волна.

Каждая компонента падающей вол­ны (волна напряжения или волна то­ка) представляет собой синусоидальное колебание, амплитуда которого уменьшается по мере роста х (множитель е^—ax), а аргумент является функ­цией времени и координаты х.

Каждая компонента отраженной электромагнитной волны за­тухает по мере продвижения волны от конца линии к началу (множитель е^ax).

Физически эффект умень-шения амплитуд падающей и отражен­ной волн по мере их продвижения по линии объясняется наличием по­терь в линии.

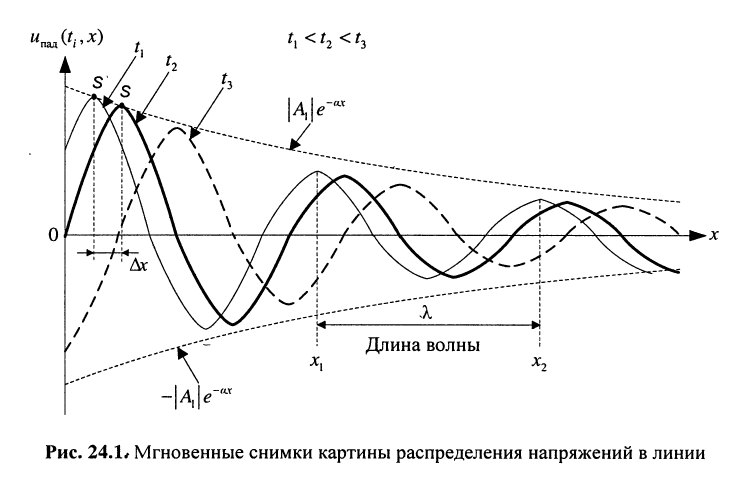
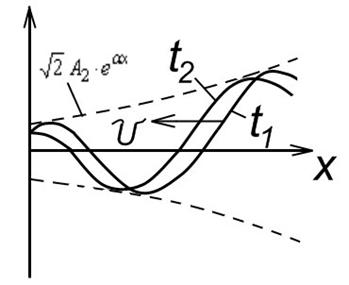
На рис. 5.4 изображены графики распределения падающей волны напря­жения вдоль линии (в функции x) для двух смежных моментов времени: t₁ и t₂ > t₁. Падающая волна распростра­няется слева направо. При построении принято wt₁ + y_п = 0.

На рис. 5.5 представлены графики распределения отраженной волны напряжения для двух смежных моментов времени: t₁ и t₂ > t₁

Отраженная волна распространяется справа налево.

Коэффициент отражения

Отношение напряжения отра­женной волны в конце линии к напряжению падающей волны в конце линии называют коэффициентом отражения по напряжению и обоз­начают К_и. В соответствии с формулой (5.13)

.

При согласованной нагрузке К_и = 0, при холостом ходе К_и = 1.

Коэффициент отражения по току К_i = -К_и

Фазовая скорость

Фазовой скоростью (u_ф) называют ско­рость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу колебания, или иначе: фазовая скорость-это скорость перемещения по линии неизменного фазового состояния. Если фаза падающей волны напряжения неизменна, то в соответствии с фор­мулой (5.28)

wt + y_{п –} b x = const.

Возьмем производную по времени от обеих частей последнего равенства:

(wt + y_{п –} b x) = 0, или w – b = 0.

Отсюда

u_ф = dx / dt = w /b.

(5.32)

Длина волны

Под длиной волны (c) понимают расстояние, на которое распространяется волна за один период T = 1/f:

c = uT = u / f.

(5.33)

Содержание:

Волновые параметры длинной линии:

Полученные в предыдущей лекции уравнения передачи длинной линии (23.8) описывают комплексные амплитуды напряжения

Тогда для мгновенных значений напряжений и токов в линии получаем:

        (24.1)

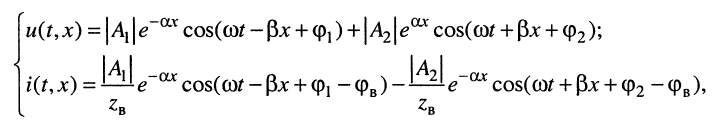
где — аргументы комплексных величин

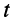
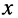
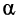
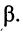
Решения (24.1) подтверждают, что напряжения и токи в длинной.линии являются функциями как времени , так и координаты (расстояния) . Каждое из уравнений представляет собой сумму двух слагаемых, структуры которых тождественны, но отличаются только знаками перед коэффициентами затухания и фазы Сначала рассмотрим левые слагаемые уравнений (24.1)

напряжений и токов, которые назовём падающими волнами напряжения и тока (смысл такого названия будет ясен из дальнейшего):

           (24.2)

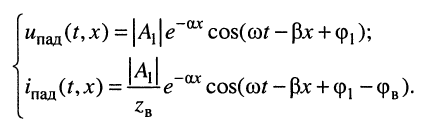
Из этих выражений следует:

Сказанное демонстрируется на рис. 24.1, где представлено графическое распределение мгновенных значений напряжений по линии для трёх последовательных моментов времени: Эти графики можно рассматривать как последовательные мгновенные снимки картины распределения напряжений в указанные моменты времени. Они отображают волну, распространяющуюся от начала линии к концу. Например, рассматривая графики в моменты и , замечаем, что в момент фаза напряжения в каждой точке линии изменится на величину Огибающая процесса изображена пунктиром. Аналогичная картина имеет место и для тока.

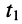
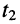
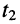
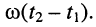
Определение:

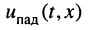
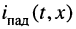
Совокупность волн напряжения и тока называется падающей волной.

Найдём длину 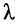и скорость распространения падающей волны в линии.

Под длиной волны понимают расстояние между смежными сечениями линии, фаза колебаний волны на которых отличается на 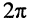(рис. 24.1):

откуда имеем равенство

из которого получаем формулу для вычисления длины волны:

               (24.3)

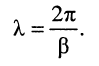
Определение:

Скоростью распространения, или фазовой скоростью, называют скорость 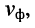с которой распространяется в линии состояние равной фазы волны; например, скорость, с которой перемещается вдоль линии нуль напряжения или тока.

Нуль напряжения достигается в точках, где функция косинуса равна нулю, поэтому условие состояния равной фазы можно записать в виде равенства:

при этом аргумент имеет значения:

Продифференцировав обе части полученного равенства по переменной t, найдём скорость распространения нуля

           (24.4)

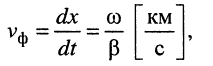
т. е. скорость распространения состояния равной фазы.

Фазовая скорость показывает, какое расстояние проходит точка в единицу времени (см. рис. 24.1), и равна отношению частоты колебания к коэффициенту фазы.

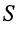
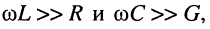
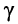
Рассмотрим, чему будет равен коэффициент фазы в наиболее характерной для практики области частот, когда  для чего разложим коэффициент распространения на вещественную и мнимую части:

Разложение в ряды полученных в правой части биномиальных сомножителей и удержание в разложениях лишь по два слагаемых даёт:

Раскрывая скобки и пренебрегая в произведении величиной второго порядка малости, получаем приближённое выражение для коэффициента распространения:

                     (24.5)

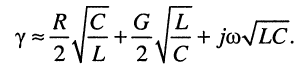
В линиях с хорошим диэлектриком проводимость чрезвычайно мала, поэтому второе вещественное слагаемое в выражении (24.5) оказывается очень малым по сравнению с первым, что позволяет записать формулы для коэффициентов затухания и фазы с хорошей степенью приближения:

                     (24.6)

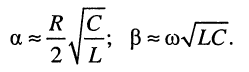
Тогда в указанной выше области частот фазовая скорость (24.4) согласно (24.6) оказывается равной

Подставляя сюда формулы значений первичных параметров длинной линии L и С (табл. 23.1), получаем:

                (24.7)

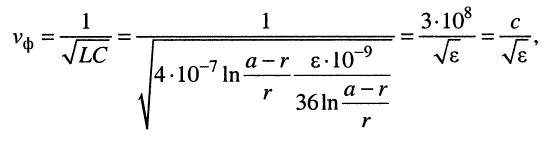
где с — скорость света.

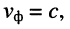
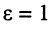
Из (24.7) ясно, что для воздушных линий  поскольку в этом случае можно считать . Для коаксиального кабеля, у которого всегда , фазовая скорость меньше скорости света в вакууме (например, при типовом значении имеем с).

Интересно, что в области низких частот значение фазовой скорости убывает с уменьшением частоты. Это объясняется меньшим проявлением скин-эффекта: волна больше проникает в проводник, и колеблющиеся частицы внутри проводника возбуждают вторичные волны. Поскольку частицы обладают некоторой инерцией, образуемые ими вторичные волны запаздывают по фазе относительно вынуждающей колебания волны, поэтому происходит запаздывание фазы результирующей волны и, как следствие, уменьшение фазовой скорости.

Обратимся теперь ко вторым слагаемым уравнений (24.1), которые назовём отражёнными волнами напряжения и тока:

                 (24.8)

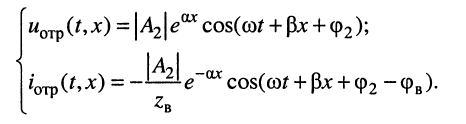
Проведя анализ этих слагаемых подобно тому, как это сделано для падающих волн, нетрудно убедиться, что они описывают затухающую волну такого же характера, как и падающая, но распространяющуюся в обратном направлении: от конца к началу линии.

Определение:

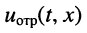
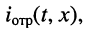
Волна напряжения и тока распространяющаяся от конца к началу линии, называется отражённой волной.

Соотношения между комплексными амплитудами падающих и отражённых волн

Из анализа, выполненного в разд. 24.1, следует:

• фазовая скорость отражённой волны совпадает с точностью до знака с фазовой скоростью падающей волны

Волновое сопротивление

Прежде всего отметим, что при любом jc, т. е. в любой точке линии согласно (24.9) справедливы равенства:

       (24.10)

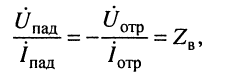
которое говорит о том, что в любом сечении линии .отношение комплексных амплитуд напряжения и тока падающей (отражённой) волны равно волновому сопротивлению линии

Свойства волнового сопротивления можно определить из выражений (24.10) и (23.6):

из которых следует:

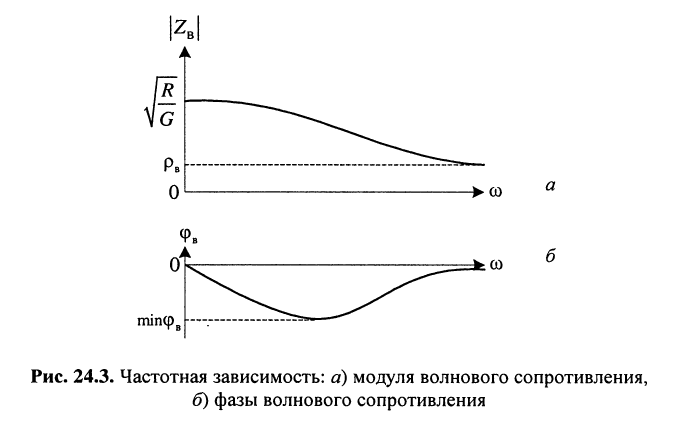
модуль волнового сопротивления 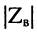представляет собой отношение амплитуды напряжения к амплитуде тока падающей (отражённой) волны;

фаза (угол) 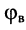волнового сопротивления представляет собой разность между фазами напряжения и тока падающей (отражённой) волны;

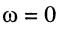
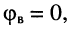
на частоте фаза а само волновое сопротивление чисто активно

при стремлении частоты  к бесконечности   фаза  и волновое сопротивление как и в предыдущем случае чисто активно 

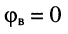
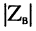
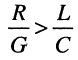
модуль волнового сопротивления | с увеличением частоты уменьшается, поскольку для реальных линий (рис. 24.3, а);

изменение фазы от нулевого значения при 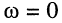до нулевого значения при говорит о том, что на одной из частот фаза будет минимальна (рис. 24.3, б), поскольку на всех частотах она является отрицательной.

Коэффициент отражения

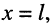
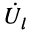
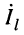
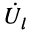
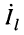
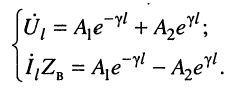
Что касается соотношения между комплексными амплитудами напряжения (тока) падающей и отражённой волн, то оно оказывается различным в различных сечениях линии. Установить эти соотношения можно из системы (23.8), положив при условии, что напряжение и ток  в конце линии известны. При этих условиях из (23.7) находятся два уравнения относительно комплексных амплитуд напряжения тока :

           (24.11)

Из системы (24.11) согласно правилу Крамера получаем значения постоянных 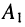и

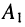
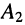
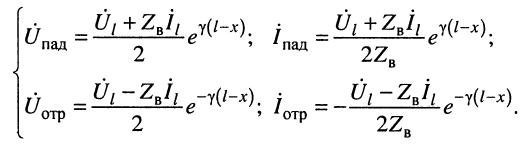
 Подстановка найденных значений i и в (24.9) приводит к частному решению:

            (24.12)

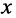
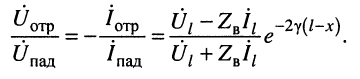
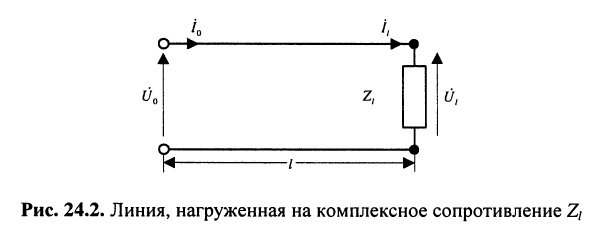
Система уравнений (24.12) позволяет записать отношение комплексных амплитуд напряжений и токов отражённой и падающей волн в сечении линии, расположенном на расстоянии от её начала:

         (24.13)

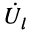
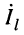
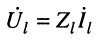
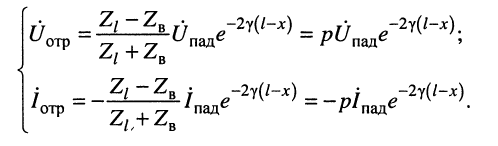
Но при выбранных направлениях отсчётов (рис. 24.2) напряжения  и тока имеет место равенство   поэтому из (24.13) окончательно получаем:

         (24.14)

Определение:

Отношение

          (24.15)

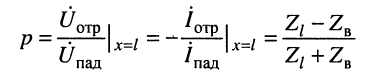
комплексной амплитуды напряжения отражённой волны к комплексной амплитуде напряжения падающей волны называется коэффициентом отражения.

Анализ соотношений (24.14) и (24.15) приводит к следующим выводам:

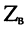
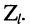
1.    Коэффициент отражения является комплексной величиной и полностью зависит от волнового сопротивления линии и сопротивления нагрузки .

2.    Коэффициент отражения по току отличается от коэффициента отражения по напряжению только знаком.

3.    При 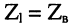коэффициент отражения равен нулю р = 0, поэтому отражённая волна отсутствует. Линия, сопротивление нагрузки которой равно её волновому сопротивлению, называется нагруженной согласованно, а сопротивление нагрузки — согласованным сопротивлением. Любая другая нагрузка приводит к появлению в линии отражённой волны.

4.    Отношение амплитуд отражённой и падающей волн (см. (24.14) и (24.15))

убывает с удалением от конца линии к её началу
 

5.    В режиме короткого замыкания, когда 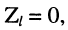коэффициент отражения по напряжению р = -1, а коэффициент отражения по току
р = 1. Это означает, что напряжения отражённой и падающей волн в конце линии находятся в противофазе:

а результирующее напряжение равно нулю

при этом токи падающей и отражённой волн оказываются в фазе

и результирующий ток равен удвоенному току падающей волны

6.    В режиме холостого хода, когда 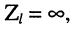коэффициент отражения по напряжению р = 1, поэтому имеет место ситуация, противоположная относительно вывода, указанного в п. 5: напряжения отражённой и падающей волн в конце линии находятся в фазе:

и результирующее напряжение равно удвоенному напряжению падающей волны

а ток равен нулю

Уравнения передачи согласованно нагруженной длинной линии

Ранее (см. разд. 23.3) были получены уравнения передачи длинной линии (23.8), которые представляют собой общее решение телеграфных уравнений и описывают закон распределения напряжений и токов по всей линии. Для решения же большинства практических задач достаточно знать соотношения лишь между напряжениями и токами на внешних зажимах линии и вовсе не интересоваться законом распределения напряжений и токов по длине линии. Иначе говоря, на практике вполне достаточно рассматривать линию как согласованно нагруженный четырёхполюсник, полностью описываемый соответствующими уравнениями передачи.

Поставим задачу найти уравнения передачи согласованно нагруженной линии, которые связывают комплексные амплитуды напряжений и токов на её внешних зажимах.

Воспользуемся уравнениями (24.12) для комплексных амплитуд напряжений и токов падающей и отражённой волн и подставим их в систему (24.9):

                             (24.16)

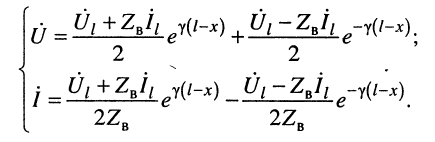
Если в систему (24.9) подставить выражения (24.14), получим

                         (24.17)

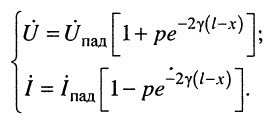
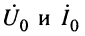
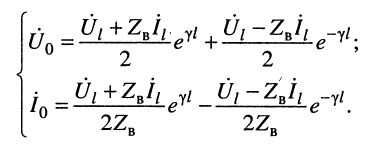
Системы (24.16) и (24.17) представляют собой системы уравнений передачи длинной линии. Обычно комплексные амплитуды напряжения и тока на входных зажимах линии (х = 0) обозначают через (см. рис. 24.2); при таких обозначениях из системы (24.16) получаем наиболее удобную форму записи уравнений передачи линии:

         (24.18)

В большинстве случаев уравнения (24.8) записывают в более компактном виде:

         (24.19)

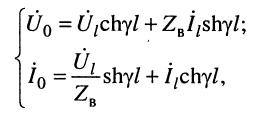
где
   —   гиперболический косинус

     —    гиперболический синус.
 

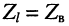
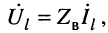
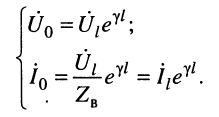
Для режима согласованной нагрузки, когда и т. е. когда отсутствует отражённая волна, из (24.18) получаем уравнения передачи согласованно нагруженной линии:

      (24.20)

Именно в такой режим и стремятся поставить линию связи, поскольку отражённые волны вызывают ряд нежелательных явлений, о чём речь пойдёт далее.

Постоянная передачи и частотные характеристики длинной линии

Постоянная передачи длинной линии:

Определение

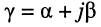
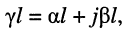
Безразмерная комплексная величина, равная произведению коэффициента распространения на длину линии

   (24.21)

называется постоянной передачи линии.

Вещественная часть постоянной передачи 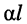называется собственным, волновым или характеристическим затуханием линии, а мнимая часть — собственной, волновой или характеристической фазой.

Постоянная передачи и входящие в неё параметры характеризуют линию как таковую и не зависят от свойств генератора и нагрузки, между которыми линия может быть включена.

Поскольку режим согласованной нагрузки для линии является типовым, найдём указанные ранее параметры только для этого режима.

В таком случае постоянную передачи можно получить, прологарифмировав уравнения (24.20):

       (24.22)

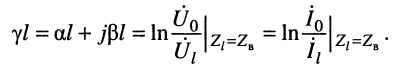
Подставляя отношения комплексных амплитуд

под знак логарифма, получаем:

на основании чего можно записать два равноправных выражения для коэффициента распространения

откуда имеем:

собственное затухание линии

      (24.3)

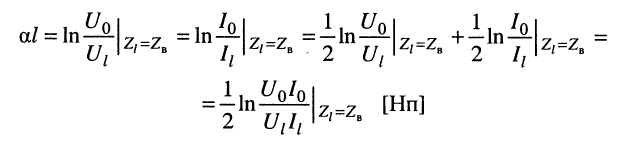
    и её собственную фазу

       (24.24)

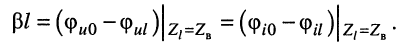
Из выражений (24.23) и (24.24) следует, что для согласованно нагруженной линии:

    собственное затухание линии 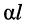 [Нп] равно натуральному логарифму отношения амплитуд или действующих значений напряжений (токов) на входе и выходе; оно равно также половине натурального логарифма отношения полных мощностей на входе и выходе;

    собственная фаза линии равна разности начальных фаз колебаний напряжений (токов) на входе и выходе.

Собственное затухание линии часто оценивается в децибелах:

         (24.25)

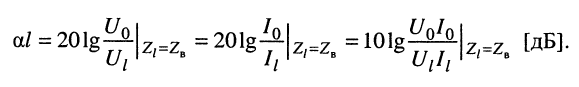
В этом случае нетрудно переформулировать зависимость собственного затухания, выраженного в децибелах, через десятичные логарифмы отношений амплитуд напряжений (токов) или полных мощностей.

Пример 24.1.

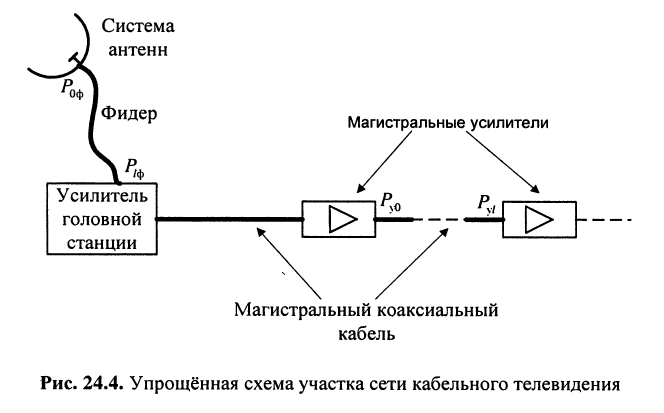
Оценим потери мощности телевизионного сигнала при распространении его в фидере’ от системы антенн до усилителя головной станции и в коаксиальном кабеле сети кабельного телевидения на отрезках магистральной линии между магистральными усилителями (рис. 24.4).

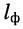
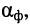
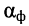
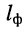
Решение. Затухание фидера зависит от его конструкции, длины и коэффициента затухания который измеряется на средней частоте частотного диапазона фидера. Обычный фидерный тракт имеет длину 50—150 м. Типовым кабелем, используемом при конструировании фидерных трактов, является кабель РК-75-24-51, имеющий полосу пропускания 50—600 МГц и коэффициент затухания = 0,002 дБ/м на частоте 300 МГц. Тогда при средней длине фидера = 100 его собственное затухание (24.25) оказывается равным

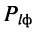
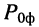
а отношение мощности сигнала на выходе фидера к мощности сигнала на входе фидера составляет

 т. е. потери мощности в фидере невелики.

 Фидер — линия для передачи электрических колебаний высокой частоты от радиопередатчика к антенне и от антенны к радиоприёмнику.

В то же время типовой магистральный коаксиальный кабель QR 540 JCA имеет полосу пропускания 5—1000 МГц и коэффициент затухания 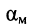= 0,0354 дБ/м на частоте 300 МГц.

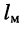
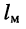
Расстояние между смежными усилителями магистрали обычно составляет до = 2 км. Следовательно, собственное затухание отрезка магистрального кабеля равно

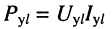
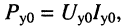
Последнее означает, что полная мощность на входе последующего усилителя меньше полной мощности которая отдаётся в линию предшествующим усилителем, в десятки миллионов раз, поскольку согласно (24.25)

Частотные характеристики (АЧХ и ФЧХ) согласованно нагруженной длинной линии

Исходя из уравнений передачи согласованно нагруженной линии (24.20) запишем её комплексную частотную характеристику через постоянную передачи линии:

        (24.26)

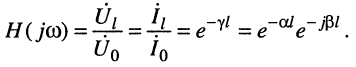
Отсюда нетрудно получить постоянную передачи через КЧХ линии:

        (24.27)

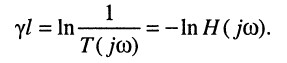
Амплитудно-частотная и фазочастотная характеристики определяются из (24.26): 

       (24.28)

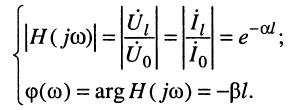
Для несогласованной нагруженной линии КЧХ можно найти из её уравнений передачи (24.18), подставив в них равенства:

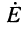
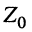
где и — комплексная амплитуда ЭДС и комплексное внутреннее сопротивление генератора, подключённого к линии.

Входное сопротивление длинной линии

Определение:

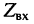
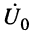
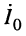
Входным сопротивлением линии называется отношение комплексной амплитуды напряжения к комплексной амплитуде тока , действующих на входе линии.

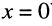
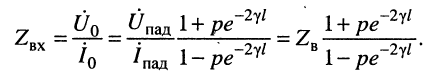
Формулу входного сопротивления для линии с произвольной нагрузкой можно получить из уравнений (24.17), если положить расстояние   и разделить первое уравнение на второе:

      (24’29)

Анализ формулы (24.29) показывает:

    при согласованной нагрузке входное сопротивление равно волновому, поскольку в данном случае 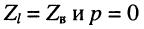(24.15);

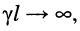
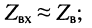
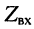
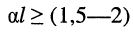
    если постоянная передачи линии стремится к бесконечности то входное и волновое сопротивления весьма близки по величине считают, что не зависит от нагрузки при собственном затухании линии Нп;

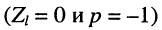
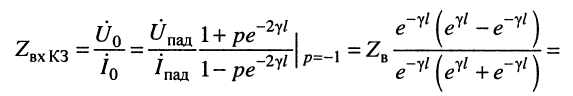
    в режиме КЗ получаем

         (24.30)

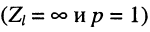
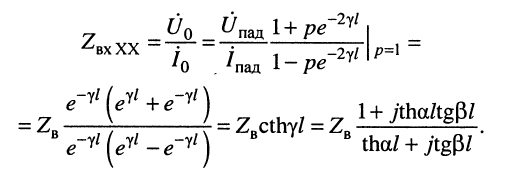
в режиме XX  имеем

          (24.31)

Вывод:

волновое сопротивление линии представляет собой предел, к которому стремится входное сопротивление при безграничном увеличении длины линии:

Этот факт объясняется тем, что при большом затухании линии значительная часть мощности, подводимой к её входу, рассеивается в самой линии и лишь небольшой остаток мощности поступает в нагрузку (см. пример 24.1). По этой причине энергетические соотношения на входе линии пренебрежимо мало зависят от энергетических соотношений на её выходе и, в частности, от сопротивления нагрузки линии.

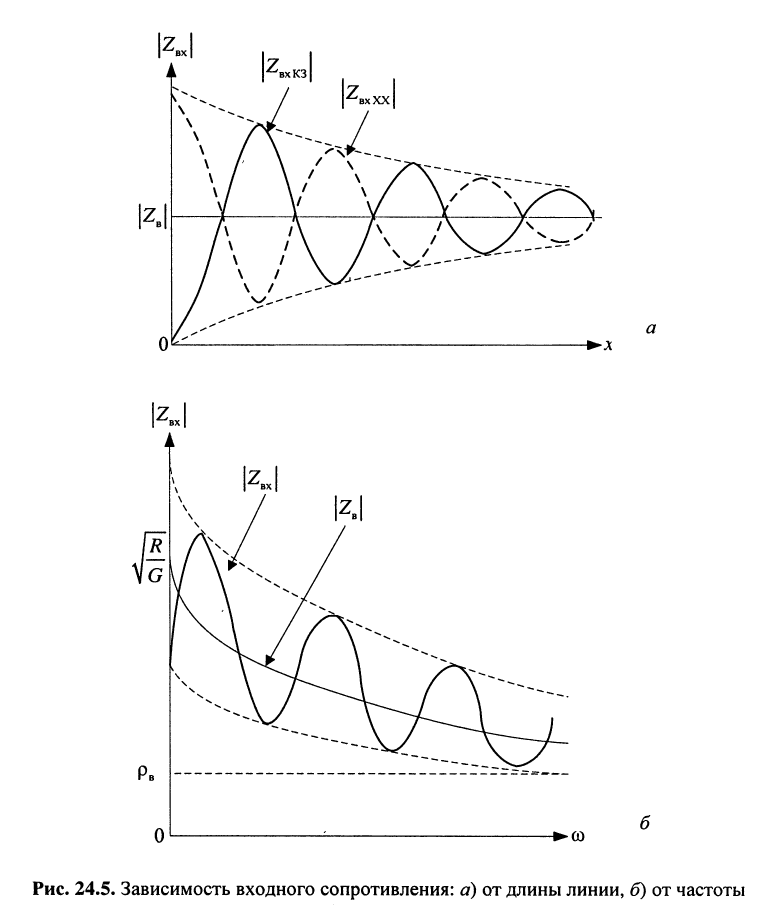
С увеличением длины линии увеличивается и её затухание, а потому уменьшается амплитуда отражённой волны на входе линии, что, в свою очередь, приводит к уменьшению отклонения входного сопротивления линии от её волнового сопротивления как по модулю, так и по фазе. В пределе входное сопротивление линии стремится к волновому сопротивлению. На рис. 24.5, а показаны зависимости модулей входных сопротивлений в режимах XX и КЗ. Колебательный характер волнового сопротивления при несогласованной нагрузке объясняется наличием падающих и отражённых волн.

Входное сопротивление зависит не только от длины линии, но и от частоты (рис. 24.5, б). С ростом частоты увеличиваются как собственное затухание так и собственная фаза линии. Это приводит к весьма сложному волнообразному характеру изменения входного сопротивления линии относительно её волнового сопротивления.

Допустимые отклонения входного сопротивления линии от её волнового сопротивления строго нормированы, и при эксплуатации длинных линий необходимо придерживаться указываемых для линии обычно весьма жёстких норм.

Определение параметров линии методом холостого хода и короткого замыкания

Определение первичных и вторичных параметров линии наиболее просто осуществлять с помощью измерений входного сопротивления линии при двух граничных сопротивлениях нагрузки: холостом ходе и коротком замыкании.

Из уравнений (24.19) в режимах 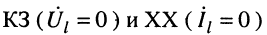 имеем

Совместное решение этих уравнений позволяет найти значения волновых параметров линии: волнового сопротивления и постоянной передачи.

Волновое сопротивление

      (24.32)

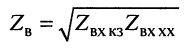
равно среднему геометрическому из входных сопротивлений короткозамкнутой и разомкнутой линии. Это выражение можно рассматривать как ещё одно определение волнового сопротивления длинной линии.

Гиперболический тангенс постоянной передачи

      (24.33)

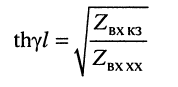
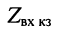
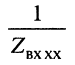
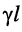
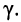
равен среднему геометрическому из сопротивления короткозамкнутой линии и проводимости — разомкнутой линии. Найдём из (24.33) постоянную передачи и коэффициент распространения Поскольку

то

Логарифмируя обе части последнего равенства, получаем постоянную передачи:
 

          (24.34)

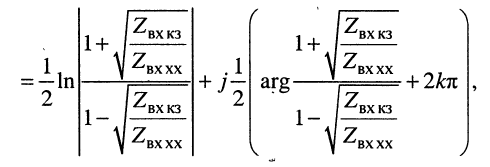
откуда легко находятся коэффициенты затухания и фазы:

Коэффициент 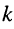равен целому числу волн, укладывающихся по длине линии.

Во всех формулах необходимо брать только арифметические корни.

Зная волновые параметры линии, нетрудно вычислить её первичные параметры путём приравнивания вещественных и мнимых частей равенств:

Замечание:

Метод холостого хода и короткого замыкания целесообразно применять в том случае, когда затухание линии не превышает
1 Нп (8,69 дБ), что характерно для большинства длинных линий.

Обозначим в уравнениях передачи (13.8) Uп = (U1 + I1Zв)/2 и U0 = (U1 – I1Zв)/2. С учетом этих обозначений запись уравнений передачи однородной длинной линии упростится и будет иметь вид

где

Напряжение и ток состоят из сумм двух слагаемых. Первые слагаемые уменьшаются с увеличением расстояния от начала ли­нии х, вторые – возрастают. Создается впечатление о существова­нии в линии двух типов волн: падающей и отраженной. Чтобы убе­диться в этом, рассмотрим мгновенные значения напряжения и тока.

Помня, что в (13.10) все величины в общем случае комплексные

можно по известным правилам перейти от (13.10) для комплексных значений к уравнениям передачи для мгновенных значений напряжений и токов. Для простоты положим jп = j0 = 0. Тогда

Проанализируем сначала первые слагаемые этих уравнений, которые обозначим

В каждом сечении линии (т. е. в каждой точке х) колебания напряжения и тока являются гармоническими. Амплитуда этих колебаний уменьшается по мере удаления от начала линии по за­кону е–aх. В каждой последующей точке линии колебания отстают по фазе от колебаний в предыдущей точке (на это указывает знак «минус» перед bх).

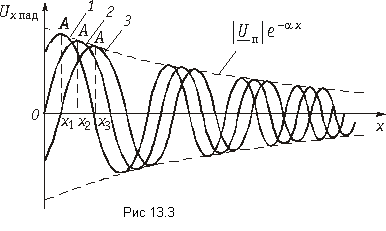
Если в момент времени t1 сделать фотографию распределения, например, напряжения uxпад вдоль линии, то она будет иметь вид кривой 1 (рис. 13.3). В следующий момент t2 фаза напряжения в каждой точке линии изменится на величину w(t2 – t1), и вся кар­тина как бы сместится вдоль оси х вправо (кривая 2 на рис. 13.3). Аналогичная ситуация будет наблюдаться и в момент времени t3 > t2 (кривая 3 на рис. 13.3).

Если сделать последовательно ряд мгновенных фотографий и затем их проецировать на экран, то создается впечатление движу­щейся волны напряжения вдоль цепи. Фактически же вдоль цепи распространяется состояние равной фазы. Например, можно взять точку цепи х1, соответствующую максимуму напряжения в момент времени t1 (точка А на рис. 13.3) и определить скорость ее пере­мещения. Скорость распространения вдоль цепи состояния равной фазы называется фазовой скоростью распространения

В момент времени t1 в точке х1 имеется определенное фазовое состояние wt1 – bх1. Это же фазовое состояние будет наблюдаться в точке х2, но уже в момент времени t2 wt2 – bх2. Приравнивая их получаем wt1– bх1= wt2– bх2

Фазовую скорость распространения (км/с) найдем как отно­ше­ние расстояния х2– х1, пройденного точкой A, ко времени t2 – t1

Таким образом, уравнения (13.12) описывают волны напряже­ния и тока, распространяющиеся от начала к концу линии. Такие волны называются падающими

Обратимся ко вторым слагаемым выражений (13.11), которые обозначим

Эти слагаемые описывают волны точно такого же характера, как и падающие, но распространяющиеся в обратном направлении, т. е. от конца линии к началу. Эти волны называются отражен­ными волнами напряжения и тока. Амплитуды отраженных волн убывают от конца линии к началу, наибольшая амплитуда наблю­дается в конце линии.

В соответствии с рассмотренной картиной можно сказать, что в установившемся режиме гармонических колебаний напряжение и ток в любой точке линии складываются из падающих и отражен­ных волн напряжения и тока, т. е. ux = uxпад + uxотр; ix = ixпад + + ixотр. Отраженные волны возникают в конце линии.

Складывая эти равенства и вычитая из первого второе, имеем:

Отношение комплексной амплитуды отраженной волны к ком­плексной амплитуде падающей волны называется коэффициентом отражения по напряжению

Отсюда

Коэффициент отражения по напряжению показывает, какую часть амплитуды падающей волны в конце линии составляет ампли­туда отраженной волны. Амплитуда отраженной волны тока

В то же время I2отр = siI2пад, где si – коэффициент отражения по току. Отсюда видно, что si = —su, т. е. коэффициент отражения по току равен по значению и противоположен по знаку коэффициенту отражения по напряжению.

Рассмотрим некоторые частные режимы работы линии. Если линия замкнута накоротко на конце (короткое замыкание (КЗ)), т. е. Zн = 0, то коэффициент su= —1, а коэффициент si= 1. Падаю­щая и отраженная волны напряжения в конце линии имеют рав­ные амплитуды и сдвинуты по отношению друг к другу на 180°. Амплитуда результирующей волны напряжения в конце линии бу­дет равна нулю. В то же время падающая и отраженная волны тока будут иметь равные амплитуды, что приведет к увеличению тока в конце короткозамкнутой линии.

При холостом ходе (XX) в конце линии Zн = ¥ коэффициент su = 1 и si=—1, т. е. картина изменится на противоположную: ток в нагрузке будет равен нулю, а напряжение увеличится вдвое. Случай, когда Zн = Zв, рассмотрен ниже.

Переходя
от комплексных действующих значений
напряжения и тока (3.3) к мгновенным,
получаем

где  
 –
начальная фаза, 
, 
.

Первые
слагаемые в этих уравнениях описывают
падающие волны напряжения и тока
соответственно, т.е. волны, двигающиеся
от начала линии к её концу. Падающие
волны убывают с увеличением 
,
что объясняется потерями при распространении
волны по линии. Вторые слагаемые описывают
обратные или отражённые волны напряжения
и тока, которые движутся от конца линии
к её началу и при этом убывают тоже из-за
потерь в линии (рис. 3.2).

Таким
образом, мгновенное значение напряжения
в любой точке линии определяется суммой
падающей и отражённой волн напряжения,
а мгновенное значение тока в любой точке
линии определяется разностью падающей
и отражённой волн тока.

Из
уравнений (3.7) следует, что напряжение
и ток в длинной линии зависят не только
от волновых параметров линии 
 и 
  в
явной форме, но и от внешних параметров
(сопротивления нагрузки или внутреннего
сопротивления источника эдс) через
коэффициенты 
 и 
 в
неявной форме.

Рис.
3.2. Падающая (а) и отражённая (б) волны
напряжения в длинной линии при
гармоническом напряжении на входе

Величина 
 характеризует
убывание амплитуды на единице длины
линии как падающей, так и отражённой
волн и поэтому носит название коэффициента
затухания. Коэффициент фазы 
 характеризует
изменение фазы, приходящееся на единицу
длины линии, и носит название коэффициента
фазы.

Длиной
волны 
 называют
расстояние между двумя точками, фазы
которых отличаются на 
,
то есть

Отсюда                

Скорость
перемещения падающей волны называют
фазовой и определяют как скорость
перемещения точки, фаза колебаний в
которой остаётся постоянной:

Отсюда 
 и
фазовая скорость получается равной

Следовательно, 
.
Подставляя эту зависимость в выражение
для 
 в
формуле (3.9), получаем известное уравнение

где 
 –
период гармонического колебания.

Запишем
выражения (3.3) через падающие и отражённые
волны:

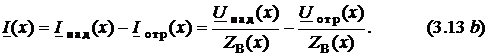
Отсюда
получаем соотношения

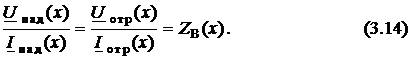
Для
однородной длинной линии выполняется
условие 
,
и отношения (3.14) не зависят от координаты.

Пусть
известны значения напряжения 
 и
тока 
 в
начале длинной линии (точки 1 и 
),
то есть при 
.

Уравнения
(3.3) в этом случае преобразуются в

Решая
совместно, получаем

Обычно
начало линии передачи бывает недоступно
для непосредственных измерений. Например,
у лабораторных генераторов оно находится
внутри корпуса прибора, у телевизионных
приёмников – в точке соединения
коаксиального кабеля с антенной, то
есть, как правило, на крыше здания. В то
же время конец линии практически всегда
доступен. Поэтому весьма часто расстояния
в линии отмеряют от конца, вводя
координату 
,
где 
 –
длина линии передачи (рис. 3.1).

При 
 или 
 уравнения
(3.3) преобразуются в

Преобразуя
уравнение (3.17 b)
относительно 
 и
подставляя полученное выражение в
уравнение (3.17 a),
находим постоянные интегрирования
через параметры на конце длинной линии

В
этих выражениях напряжение 
 и
ток 
 можно
считать известными, так как они доступны
для измерений. Кроме того, они связаны
друг с другом по закону Ома:

Также
известно волновое сопротивление 
,
а неизвестной является длина линии 
.

Подставляя
коэффициенты 
 и 
 из
(3.18) в формулы (3.3) и переходя к координате 
,
получаем запись уравнений через известные
величины:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Падающие и отраженные волны

Если в уравнение для напряжения

Подставив вместо 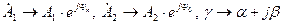, получим:

И перейдем к синусоидальным функциям:

Из этих уравнений можно сформулировать следующие определения:

Падающей электромагнитной волной называют процесс перемещения электромагнитного состояния (электромагнитной волны) от источника энергии к приемнику, т.е. в направлении увеличения координаты х.

Электромагнитное состояние определяется совокупностью электрического и магнитного полей.

Падающая волна, распространяясь от источника энергии к приемнику, несет энергию, заключенную в ее электрических и магнитных полях.

Отраженной электромагнитной волной называют процесс перемещения электромагнитного состояния (электромагнитной волны) от приемника к источнику энергии, т.е. в сторону уменьшении координаты х.

Падающая электромагнитная волна образована падающей волной напряжения и падающей волной тока.

Отраженная электромагнитная волна образована отраженной волной напряжения и отраженной волной тока.

Минус у отраженной волны тока свидетельствует о том, что поток энергии, который несет с собой отраженная волна, движется в обратном направлении по сравнению с потоком энергии, который несет падающая волна.

Каждая компонента падающей волны представляет синусоидальной колебание, амплитуда которого уменьшается по мере роста х (е -αх ), а аргумент является функцией времени и координаты х.

Каждая компонента отраженной электромагнитной волны затухает по мере продвижения волны от конца линии к началу (е αх ). Физически эффект уменьшения амплитуд падающей и отраженной волн, по мере их продвижения по линии, объясняется наличием потерь в линии.

Падающая волна распространяется слева направо. При построении принято .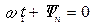

Отраженная волна распространяется справа налево.

Отношение напряжения отраженной волны в конце линии к напряжению падающей волны в конце линии называют коэффициентом отражения по напряжению:

При холостом ходе k_U = 1.

Величина характеризует изменение амплитуды волны на единицу длины линии (коэффициент ослабления)

Коэффициент фазы равен изменению фазы на единицу длины.

Убывание амплитуды волны вдоль линии обуславливается потерями в линии, а изменение фазы – конечной скоростью распространения электромагнитных колебаний.

λ – длина волны, равная расстоянию между двумя точками линии, в которых фазы рассматриваемой слагающей отличаются на 2π, т.е.

При согласованной нагрузке k_U = 0

Режимом согласованной нагрузки называют такой режим, при котором сопротивление нагрузки равно волновому сопротивлению, т.е.

При этом отраженная волна будет отсутствовать, т.е.

Коэффициент отражения по току:

Фазовой скоростью называют скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу колебания или иначе фазовая скорость – это скорость перемещения по линии несинусоидального фазового состояния.

Если фаза падающей волны напряжения неизменна, то

Взяв производные по времени от обеих частей, получим:

При постоянном токе (ω = 0) понятия коэффициента фазы β и фазовой скорости теряют физический смысл.

Фазовая скорость обратной волны:

Знак минус указывает, что обратная волна движется в направлении, противоположном направлению прямой волны

Т.е. за время, равное одному периоду, падающие и отраженные волны перемещаются на расстояние, равное длине волны.

Линии, физическая длина которых соизмерима с длиной волны считаются длинными линиями.

Линия без потерь

Независимо от того, соблюдается ли оптимальное соотношение параметров или не соблюдается, во всех случаях желательно, чтобы активные сопротивления R₀ и проводимости G₀ были по возможности малы, т.е.

В первом приближении рассматривают линию, не имеющую потерь (строго говоря таких линий не существует), т.е. полагают, что R₀ = G₀ = 0, тогда вторичные параметры линии (как указывалось выше) имеют вид:

(чисто активное)

,

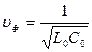
Т.е. отсутствуют также фазовые искажения.

Выражения для коэффициента фазы β, фазовой скорости V_Ф и волн сопротивлением Z_B совпадают с выражениями, полученными для линии без искажений.

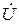
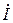
Для определения и в точке линии обратимся к известным формулам

Т.к. = 0, то

Линия без искажений

Неискаженной или линией без искажений называют такую линию, вдоль которой волны всех частот распространяются с одинаковой фазовой скоростью и затухают в равной степени.

Неодинаковое затухание на разных частотах создают так называемые амплитудные искажения, а неодинаковая скорость волн – фазовые искажения.

Для того, чтобы линия была неискажающей коэффициент затухания α и фазовая скорость V_Ф не должны зависеть от частоты. Такое условие будет выполняться, если между параметрами линиями будет иметь место следующее соотношение:

Обозначим

Из полученных формул следует, что коэффициент затухания α и фазовая скорость в линии без искажений зависит от частоты.

Волновое сопротивление в линии без искажений

является действительным числом и так же не зависит от частоты.

Для устранения искажений, вызванных несогласованностью сопротивления приемника с сопротивлением линии, применяют режим согласованной нагрузки, т.е. Z₂ = Z_B.

Ток и напряжение в линии при согласованной нагрузке определяется следующим образом:

При :

В начале линии при y = l:

U₂ – модуль, Ψ_U2 – аргумент 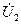; I₂ – модуль, Ψ_I2 – аргумент

Коэффициент полезного действия в линии без искажений имеет наиболее возможное значение e -2α l , как и при согласованной нагрузке:

Т.к. при согласованной нагрузке угол между и также равен φ_В

Ввиду того, что Z_B линии без искажений является активным, при согласованной нагрузке напряжение и ток в любой точке линии совпадают по фазе, т.е.

Следовательно, на любом отрезке линии без искажений, нагруженной согласованно, энергия магнитного поля равна энергии электрического поля.

Следует заметить, что на практике , для того, чтобы приблизить линию к линии без искажений изменяют первичные параметры линии L₀, C₀, R₀, G₀.

Наилучшим средством приближения первичных параметров является искусственное увеличение L₀.

5.6. Падающие и отраженные волны в линии

Подставим в фор­мулу (5.13) A₂e j y п вместо , A₁e j y о вместо , заме­ним на a + jb, получим:

.

Аналогичную операцию проделаем с формулой (5.16), причем в дополнение заменим Z_в на z_вe j j в [см. формулу (5.17)]:

.

Для перехода от комплексов напряжения и тока к функциям времени умножим правые части формул (5.28) и (5.29) на и от произведений возьмем мнимую часть:

;

.

Падающей электромагнитной волной (рис. 5.4) называют процесс перемещения электромагнитного состояния (электромагнитной волны) от источника энергии к приемнику, т.е. в на­шем случае в направлении уве­личения координаты х. Элек­тромагнитное состояние опре­деляется совокупностью электрического и магнитного полей. Падающая волна, распростра­няясь от источника энергии к приемнику, несет энергию, за­ключенную в ее электрическом и магнитном полях.

Отраженной электромагнитной волной (рис. 5.5) называют процесс пере­мещения электромагнитного состояния (электромагнитной волны) от приемника к источнику энергии, т.е. в нашем случае в сторону уменьшения координаты х.

Падающая электромагнитная волна образована падающей волной напряжения [второе слагаемое формулы (5.30)] и падающей волной тока [второе слагаемое формулы (5.31)]. Отраженная электромагнит­ная волна образована отраженной волной напряжения [первое сла­гаемое формулы (5.30)] и отраженной волной тока [первое слагаемое формулы (5.31)].

Знак «минус» у отраженной волны то­ка свидетельствует о том, что поток энергии, который несет с собой отражен­ная электромагнитная волна, движется в обратном направлении по сравнению с потоком энергии, который несет с со­бой падающая волна.

Каждая компонента падающей вол­ны (волна напряжения или волна то­ка) представляет собой синусоидальное колебание, амплитуда которого уменьшается по мере роста х (множитель е — a x ), а аргумент является функ­цией времени и координаты х.

Каждая компонента отраженной электромагнитной волны за­тухает по мере продвижения волны от конца линии к началу (множитель е a x ).

Физически эффект умень-шения амплитуд падающей и отражен­ной волн по мере их продвижения по линии объясняется наличием по­терь в линии.

На рис. 5.4 изображены графики распределения падающей волны напря­жения вдоль линии (в функции x) для двух смежных моментов времени: t₁ и t₂ > t₁. Падающая волна распростра­няется слева направо. При построении принято wt₁ + y_п = 0.

На рис. 5.5 представлены графики распределения отраженной волны напряжения для двух смежных моментов времени: t₁ и t₂ > t₁

Отраженная волна распространяется справа налево.

Коэффициент отражения

Отношение напряжения отра­женной волны в конце линии к напряжению падающей волны в конце линии называют коэффициентом отражения по напряжению и обоз­начают К_и. В соответствии с формулой (5.13)

.

При согласованной нагрузке К_и = 0, при холостом ходе К_и = 1.

Коэффициент отражения по току К_i = -К_и

Фазовая скорость

Фазовой скоростью (u_ф) называют ско­рость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу колебания, или иначе: фазовая скорость-это скорость перемещения по линии неизменного фазового состояния. Если фаза падающей волны напряжения неизменна, то в соответствии с фор­мулой (5.28)

Возьмем производную по времени от обеих частей последнего равенства:

(wt + y_{п –} b x) = 0, или w – b = 0.

Длина волны

Под длиной волны (c) понимают расстояние, на которое распространяется волна за один период T = 1/f:

Переходные процессы в цепях с распределенными параметрами

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

В цепях с распредпараметрами, например, в высоковольтных ЛЭП, обмотках электрических машин и трансформаторов и т. д. также могут возникать переходные процессы (ПП). Однако они могут возникать не только из-за коммутации, но и при изменении внешних электрических и магнитных полей. Так, если вблизи ЛЭП расположено заряженное облако (рис.9.1) и в результате молнии оно разрядилось на землю (а не на линию), то электроны, индуктированные на проводах линии теперь не будут притягиваться зарядами облака и начинают растекаться по ЛЭП в обе стороны – при этом возник переходный процесс. Аналогичная картина имеет место при изменении внешнего магнитного поля. По указанной причине расстраивается электросвязь во время магнитных бурь. ПП в ЛРП возникают и при передаче телефонных и телеграфных сигналов, телемеханических и специальных импульсов (например, для проверки линии или выявления места её повреждения). ПП в цепях с распредпараметрами имеют существенное значение для электроэнергетики, электросвязи, счетно-решающей техники, радиотехники и т. д.

Так как высоковольтные ЛЭП являются наиболее яркими представителями цепей с распредпараметрами, то в дальнейшем будем вести речь о ПП именно в них.

При расчете ПП в ЛЭП будем исходить из основных дифуравнений

где R0, L0, g0, C0 – первичные параметры линии; x – расстояние от начала линии до рассматриваемой точки; u, i – напряжение и ток в последней. Решение этих уравнений в общем виде пока не найдено, поэтому в ТОЭ переходные процессы изучаются в линиях без потерь, т. е. в линиях с R0 = 0 и g0 = 0. Это допущение практически вполне оправданно, т. к. реальные линии обычно отличаются малыми потерями. Изучение ПП при R0 = 0 и g0 = 0 дает возможность качественно исследовать основные черты процесса. В количественном отношении неучет R0 и g0 для начальных стадий ПП существенного влияния обычно не оказывает, однако для последующих стадий учет R0 и g0 желателен.

При R0 = 0 и g0 = 0 дифуравнения ЛРП принимают вид

Продифиринцировав первое уравнение по х, а второе по t, получим

откуда

или (1)

т. к. фазовая скорость в линии без потерь

Уравнение (1) – это дифуравнение второго порядка в частных производных. В математике оно известно под названием уравнения колебания струны. Его решение дано Даламбером и имеет вид: u=f1(x-vt)+f2(x+vt), где f1 и f2 –это с позиций математики функции, которые должны быть дважды дифференцируемыми и при подстановке в уравнение давать тождество, а с позиций электротехники – это напряжение падающей и отраженной волны.

Убедимся в том, что f1 действительно представляет собой напряжение падающей волны, т. е. волны, перемещающейся в сторону возрастания х. Для всех зачений х, при которых х-vt=const, она имеет одно и тоже значение. Допустим в некоторый момент времени t=t1 распределение волны вдоль линии может быть представлено графиком f1(x-vt1) (рис.9.2). Тогда для t = t1+Dt распределение f1 вдоль линии будет f1(x-vt1-vDt)= f1(x-Dx-vt1), где Dx= vDt. Из этого выражения следует, что кривая f1(t1+Dt) смещена на расстояние Dx относительно кривой f1(t1), причем смещена в сторону больших х. Таким образом, f1 представляет собой волну напряжения, перемещающуюся от начала линии к её концу, т. е. падающую волну. Начальный участок волны, первый перемещающийся по линии, называется её фронтом. Различают крутой и пологий фронт волны. Точка линии, для которой справедливо условие: при х>xф uпад=0, а при х хф uотр¹0.

Напомним, что в воздушных линиях скорость движения волн равна скорости света, а в кабельных – в два раза меньше.

Таким образом, во время ПП u = uпад + uотр. Для определения тока во время ПП используем формулу , откуда (1)

т. к. и

Проинтегрировав (1), получим

Выражения называются законом Ома для падающих и отраженных волн.

Итак во время ПП напряжение и ток в любой точке линии можно определять так:

Распространение прямоугольной волны вдоль линии бех потерь

Для выяснения физической стороны явлений, возникающих при движении волны, рассмотрим незаряженную линию, которая при t=0 подключается к идеальному источнику постоянной ЭДС. Сразу после замыкания рубильника по линии начнет перемещаться падающая электромагнитная волна, причем uпад=Е, iпад=Е/ZC. Эта волна создает электромагнитное поле. За время dt она переместится на расстояние dx=vdt и на фронте волны будет иметь место приращение потокосцепления dy = iL0dx. Согласно закону электромагнитной индукции это приведет к возникновению ЭДС

Таким образом, на фронте волны возникает ЭДС, в точности равная напряжению падающей волны и противоположная ему по знаку. Она то и придает напряжение (заряжает) последующие участки линии.

При движении волны по линии на поверхности верхнего провода накапливаются заряды одного знака, а на нижнем проводе – происходит накопление зарядов противоположного знака. За время dt, когда волна пройдет расстояние dx, приращение заряда составит величину dq = C0dxuпад = С0dxE. Это приведет к возникновению тока на всем протяжении участков линии, по которым волна прошла

Это соотношение говорит о том, что ток падающей волны – это ток заряда линии.

Электромагнитная волна, продвигаясь по линии, каждой единице её длины сообщает энергию электрического поля и энергию магнитного поля , которые равны друг другу. Действительно, поскольку , то

Схемы замещения для расчета падающих волн

Для расчета падающих волн используется схема замещения, составление которой проиллюстрируем на ряде примеров. Пусть ЛЭП, имеющая характеристическое сопротивление ZC, подключается к идеальному источнику постоянной ЭДС (рис.9.4,а).

Схема замещения имеет вид, приведенный на рис.9.4,б. В соответствии с этой схемой имеем , uпад = Е.

Если последовательно с источником включено активное сопротивление R0 (рис.9.5,а), то схема замещения имеет чуть более сложный вид (рис.9.5,б). По схеме замещения можно записать .

Когда последовательно с источником включена индуктивность L (рис.9.6,а), схема замещения принимает вид, приведенный на рис.9.6,б.

В отличие от двух предыдущих примеров в данной схеме замещения возникает переходный процесс, который может быть рассчитан любым известным методом, например, классическим. Правда в данном случае имеет место включение цепи, состоящей из активного сопротивления (ZC) и индуктивности, и формула для тока ПП нам известна: А uпад = ZC iпад . В данном случае падающая волна является функцией времени и по этому закону она изменяется в начале линии. Для того, чтобы получить выражение падающей волны для других точек линии, необходимо в полученном выражении заменить t на Такая замена учитывает процесс перемещения падающей волны от начала линии к концу со скоростью v. Тогда .

Рассмотрим еще один пример составления схемы замещения для расчета падающей волны, который отражен на рис.9.7,а. Отличие данного примера от всех предыдущих заключается в том, что в схеме замещения (рис.9.7,б) имеет место три тока, но для определения падающей волны необходимо определить ток в ветви с ZC, который может быть рассчитан любым известным методом. Полученное выражение будет функцией времени и определяет падающую волну в начале линии. Для того, чтобы получить выражение падающей волны для других точек линии, необходимо в полученном выражении заменить t на

Таким образом, падающую волну можно рассчитать по схеме замещения, в которой линия представлена своим ZC и для её определения необходимо рассчитать либо ток либо напряжение именно на ZC.

Схема замещения для расчета отраженных и преломленных волн

Когда падающая волна достигнет конца линии, к которой присоединена нагрузка или другая линия, то часть падающей волны проникнет в нагрузку, а часть отразится и возникнет отраженная волна. Для определения отраженной волны и волны, проникающей в нагрузку, применяется расчетная схема, которую принято называть схемой замещения для расчета отраженных и преломленных волн. Чтобы выяснить как составляется эта схема, обратимся к рис.9.8, на котором изображена ЛЭП, в конце которой включена нагрузка.

Пусть по линии движется падающая волна, которую будем считать известной. С того момента времени, когда она дойдет до конца линии, по нагрузке начнет протекать ток iн и на ней будет действовать напряжение uн. Напряжение и ток в любой точке линии можно представить как результат наложения падающих и отраженных волн. Это справедливо и для напряжения и тока вконце линии, т. е. uн = uпад + uотр ; iн = iпад – iотр , причем

Тогда или откуда .

Последнему уравнению удовлетворяет схема с сосредоточенными параметрами (рис.9.9), которая и является схемой замещения для расчета отраженных и преломленных волн. Эта схема состоит из последовательно соединенных ZС и сопротивления нагрузки линии, а главной её отличительной особенностью является то, что ЭДС равна 2uпад.

Для определения отраженной волны необходимо в схеме замещения любым методом произвести расчет либо тока нагрузки, либо напряжения uн во время ПП. Если по схеме замещения был рассчитан ток нагрузки, то iн(t) = iпад(t) – iотр(t), откуда iотр(t) = iпад(t) — iн(t). Если по схеме замещения определено uн, то uн(t) = uпад(t) + uотр(t), откуда uотр(t) = uн(t) — uпад(t). Кроме того uотр(t) = ZС iотр(t). Полученные выражения uотр(t) и iотр(t) являются функциями времени и по такому закону они изменябются в конце линии. Для получения общего выражения отраженных волн как в функции времени, так и в функции координаты, необходимо учесть процесс их перемещения от конца линии со скоростью v, а именно вместо t подставить t=t—y/v , т. е. uотр(t,y) = [uотр(t)]t=t—y/v.

В заключение напомним, что в воздушных линиях скорость движения волн равна скорости света, а в кабельных – в два раза ниже.

Отражение электромагнитной волны от активного сопротивления нагрузки

Если в конце линии, по которой перемещается известная падающая волна, подключено активное сапротивление нагрузки, то отраженную волну можно определить по схеме замещения с сосредоточенными параметрами (рис.9.10). В этой схеме как ZC, так и Rн являются чисто активными, поэтому uн и iн от времени не зависят и имеют следующие значения

Тогда где — есть коэффициент отражения.

Таким образом, при чисто активной нагрузке uотр = nuпад , eсли это выражение поделить на ZC, то получим iотр = niпад, т. е. отраженную волну легко рассчитать через коэффициент отражения.

Из формулы для n следует, что он может быть как положительным (при Rн > ZC), так и отрицательным (при Rн