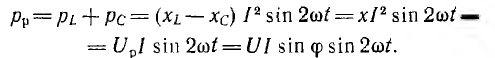Векторная диаграмма токов и напряжений
Процессы, протекающие в электроцепи переменного тока с активным сопротивлением и реактивной индуктивностью, можно наглядно выразить в графическом виде.

Статья даст описание, что такое векторные диаграммы, где и для чего они используются. Также будет описана временная диаграмма и ее назначение. В конце будет дан пример построения простой диаграммы для электроцепи с последовательным соединением элементов.
Определение
Векторная диаграмма токов и напряжений — это геометрическое изображение всех процессов, величин и амплитуд синусоидального тока. Все имеющиеся величины располагаются на плоскости в виде векторов.
Построение векторной диаграммы использует физика и электротехника. Благодаря созданию такой диаграммы можно значительно упростить выполняемые расчеты, а так же в наглядном и доступном виде отобразить происходящие процессы.
Метод векторных диаграмм позволяет также увидеть в цепи переменного тока возникающие короткие и межфазовые замыкания, а также вычислить возможные потери мощности.

Обычно такая диаграмма строится вместе с временной. Временная диаграмма — это графическое изображение входа и выхода в электрической цепи. Временные диаграммы помогают определить временной промежуток между началом, протеканием и окончанием сигнала. Например, при нажатии на кнопку возникает сигнал, который поступает к приемнику и запускает процесс его работы.
Временные диаграммы также применимы к синусоидальной электрической цепи, так как этот ток имеет начальную точку отсчета (включение питания) и время движения от источника тока к потребителю. Такие диаграммы представляют собой график, на котором изображается начальная точка отсчета, вектор времени и углы смещения фаз.
Разновидности
Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:
- Точными. Векторная точная диаграмма — это отображение выполненного численного расчета в соответствующем масштабе. С помощью нее определяют параметры фаз и амплитудные значения строго геометрическим способом.
- Качественные. Такие гистограммы строят для наблюдения взаимосвязи между электровеличинами без использования числовых характеристик. Такой способ позволяет экспериментировать с различными параметрами и моделировать процессы в электроцепях.
Векторную диаграмму токов можно построить 2 разными способами:
- Круговым. В ее принципе лежит вектор, который описывает изменение характеристик путем образования круга или полукруга на плоскости. При таком варианте учитывается направление движения с учетом направления положения вектора.

- Линейным. Такой векторной диаграмме при изменении характеристик направление изменяется строго прямолинейно.

Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.
Построение
Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.
- Катушка индуктивности UL с напряжением 15 вольт. Ток в индуктивном сопротивлении имеет сдвиг фазы 90°.
- Конденсатор UC с напряжением 20 вольт и опережением на 90 градусов.
- Напряжение резистора UR 10 вольт, его направление совпадает с током I.
- Сила тока в цепи I равняется 3 ампера.
Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.
- Отложить на плоскости I в виде горизонтальной линии с масштабом 1 A/см (масштаб может быть любым, главное — выполнять все элементы диаграммы одного типа в одном масштабе). Сам ток равен 3 ампера, поэтому его длина будет равна 3 см.

- Теперь необходимо отложить вертикальный вектор UL в масштабе 5 В/см. Он отображает напряжение катушки индуктивности и равен 15 вольт. Его длина на плоскости составит в данном масштабе так же 3 см.

- Далее нужно графически обозначить вектор напряжения активного сопротивления. Его точка отсчета располагается на окончании вертикального вектора UL. Для принятого масштаба 5 В/см ему соответствует вектор длиной 2 см. Линия должна быть строго параллельна горизонтальному вектору I.

- Теперь нужно отобразить на данной диаграмме напряжение конденсатора UC. Его началом будет конечная точка вектора UR, а конец данного вектора будет расположен ниже горизонтального вектора I. В масштабе 5 В/см ему соответствует вектор длиной 4 см.

- Чтобы определить соответствующее такой схеме общение напряжение U надо будет сделать следующее. Начало вектора расположено в принятой точке отсчета, а конец его будет расположен в конечной точке вектора UC.

Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.
Способ 2
Построение векторных диаграмм с учетом всех известных значений для цепи переменного тока с последовательным соединением конденсатора, резистора и катушки индуктивности. При таком построении нам так же известно напряжение самой цепи. Цепь состоит из:
- Резистора UR;
- Конденсатора UC;
- Катушки UL.
Далее надо:
- На плоскости Im откладывается вектор UR (резистор). Его направление точно совпадает с током, поэтому это будет горизонтальная линия.

- От точки отсчета откладывается вниз вектор UC (конденсатор). Вектор откладывается под углом 90 градусов вниз, так как он имеет указанное ранее опережение 90°.

- От этой же точки отсчета откладывается вектор UL (катушка индуктивности). Ее значение откладывается ровно на 90 градусов вертикально, так как есть сдвиг фазы на 90 градусов.

Данная диаграмма может использоваться для контроля и расчета влияния всех известных параметров цепи и элементов, а также их взаимосвязи между собой.
- Показать результат сложения вектора UL и UC.

- При увеличении величины сопротивления определить разницу между напряжением и сопротивлением можно, используя новый вектор Um.

- Кроме того можно определить угол сдвига фазы φ в цепи.

Основное преимущество векторной диаграммы заключается в следующем — простое и быстрое сложение, вычитание двух параметров во время расчета электрических цепей.
Понятие о векторах и векторных диаграммах также подразумевает расчет цепи питания трехфазной сети, подключенной по методу звезды. Она строится с учетом сразу 3 отложенных векторов от 0 оси ординат. Такое построение определяет вектор от источника тока к приемнику. Строится вектор со следующими значениями:
- На оси ОХ откладываются настоящие значения величин, а на оси OY мнимые значения.
- Угловая величина обозначается как W.
- Также присутствует сам вектор Im и угол сдвига фаз φ.
Далее нужно сделать:
- На плоскости выбрать точку отсчета.
- От нее отложить вектор Im, учитывая угол сдвига фаз равный 90°.
- Длина вектора Im равна значению его напряжения и откладывается в выбранном масштабе.

Таким же образом на плоскость накладываются еще две прямые линии. Общая диаграмма покажет симметричность фаз или их сдвиг при появлении короткого замыкания. Такая диаграмма может стать примером для расчета напряжения, тока или нагрузки на каждую фазу с моделированием различных параметров.
Заключение
Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.
Видео по теме
Токи
ветвей находятся сразу:
![]()
Для
определения общего тока необходимо
построить векторную диаграмму (рис.
23.1, б). Построение начинаем с вектора
напряжения, так как оно является общим
для всех ветвей. Из векторной диаграммы
имеем:

![]()
Разность
индуктивной и емкостной проводимостей
представляет собой общую реактивную
проводимость цепи B=BL-BC.

Векторы
токов на диаграмме образуют треугольник
токов. Его горизонтальный катет,
представляющий проекцию вектора тока
на вектор напряжения, называется активной
составляющей тока и равен току в активном
элементе цепи: Ia=Ig=GU
(рис. 23.2, а). Проекция вектора тока на
направление, перпендикулярное напряжению,
– это реактивная составляющая тока.
Она равна суммарному току реактивных
элементов:

Разделив
все стороны треугольника токов на U,
получим треугольник проводимостей
(рис. 23.2, б), стороны которого связаны
следующими соотношениями:

2. Символический метод.
Раньше
были получены следующие формулы:
![]()
Подставляя
их в уравнение первого закона Кирхгофа,
получаем:

№24
Пассивный двухполюсник в цепи
синусоидального тока. Эквивалентные
сопротивления и проводимости.
![]()
На
рис. 24.1 показан пассивный двухполюсник,
состоящий из активных и реактивных
элементов. Действующие значения
напряжения U, тока I и угол сдвига фаз
между ними φ известны.
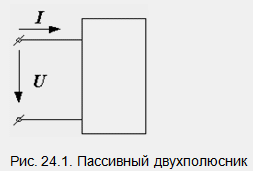
Построим
по этим значениям векторную диаграмму
и, спроектировав вектор напряжения на
вектор тока и перпендикулярное к нему
направление, получим треугольник
напряжений, образованный сторонами Ua,
Up,
U (рис. 24.2 а).
Схема
называется последовательной схемой
замещения или последовательной
эквивалентной схемой пассивного
двухполюсника, а ее параметры R , X и Z –
эквивалентными сопротивлениями
двухполюсника.

Треугольник,
образованный сторонами R, X, Z и подобный
треугольнику напряжений, представляет
собой треугольник сопротивлений
Теперь
разложим вектор тока на две составляющие
Ia – активную , направленную по вектору
напряжения, и реактивную Ip, перпендикулярную
к нему (рис. 24.3, а). Такой векторной
диаграмме соответствует параллельная
схема замещения двухполюсника (рис.
24.3, б). Ее параметры G, B и Y называются
эквивалентными проводимостями. Токи в
элементах G и B мы и представляем как
активную и реактивную составляющие
общего тока: Ia=GU, Ip=BU. Из треугольника
токов (рис. 24.3, а) получается треугольник
проводимостей.

Получим
условия эквивалентности приведенных
схем.
Для
последовательной цепи U=IZ, для параллельной
I=YU, а так как токи и напряжения в обеих
схемах одинаковы, то: Y=1/Z и Z=1/Y
т.е.
в любой электрической цепи полная
проводимость есть величина, обратная
полному сопротивлению.
Формулы
перехода от последовательной эквивалентной
схемы к параллельной:

Формулы
перехода от параллельной эквивалентной
схемы к последовательной:
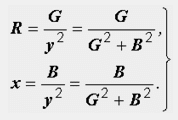
Обращаем
внимание на то, что каждая из проводимостей
G и B зависит от обоих сопротивлений –
активного и реактивного. В свою очередь,
каждое из сопротивлений определяется
обеими проводимостями. Соотношения G =
1/R и B = 1/x справедливы только в частном
случае, первое – при х = 0, второе – при
R = 0.
Следует
отметить, что активная и реактивная
составляющие напряжения и тока физически
не существуют, измерить их нельзя. Они
относятся только к соответствующим
эквивалентным схемам замещения и
находятся расчетом. Более того, проектируя,
например, вектор тока на различные
напряжения, мы получим для него разные
составляющие.
№25
Закон Ома в символической форме для
произвольной цепи.
![]()
Пусть
мгновенные значения напряжения и тока
на зажимах произвольного пассивного
двухполюсника определяются выражениями,
комплексы действующих значений которых
соответственно равны :

а
их отношение определяет комплексное
сопротивление двухполюсника:

Величина,
обратная комплексному сопротивлению
– комплексная проводимость:

Сопротивления
z, R, x и проводимости y, G и B, входящие в
два последних выражения, есть не что
иное, как эквивалентные параметры
двухполюсника.
№26
О расчете цепей синусоидального тока.
![]()
Как
следует из изложенного теоретического
материала и приведенных примеров, при
анализе цепей синусоидального тока
широко применяются векторные диаграммы
и комплексные числа. Сами по себе
векторные диаграммы зачастую служат
для иллюстрации результатов теоретических
исследований и решения задач. Они
помогают лучше понять сущность изучаемых
процессов и наглядно представить
соотношения и связи напряжений и токов
на различных участках с параметрами
цепи.
Во
многих случаях векторные диаграммы,
построенные предварительно по изложенным
выше правилам без каких-либо вычислений,
являются основой для вывода из них
конкретной методики решения данной
задачи. Возможны также привязка векторной
диаграммы к комплексным осям, выражение
векторов комплексными числами и
дальнейший расчет в символической
форме. Принципиального отличия между
методом векторных диаграмм и символическим
нет. Как мы видели раньше, за аналитическими
действиями с комплексными числами
кроются определенные геометрические
операции с векторами.
Следует
также помнить, что никакого физического
содержания векторы и комплексные числа
в себе не несут. Это чисто математические
абстракции, необходимые для анализа.
Символический
метод базируется на законах Ома и
Кирхгофа, которые в символической форме
записываются точно так же, как в цепях
постоянного тока. Поэтому все изложенные
ранее методы расчета цепей постоянного
тока, вытекающие из этих законов,
применимы и для расчета в символической
форме цепей синусоидального тока.
№27
Явление резонанса в электрических
цепях.
![]()
Резонансом
называют режим, когда в цепи, содержащей
индуктивности и емкости, ток совпадает
по фазе с напряжением. Входные реактивные
сопротивление и проводимость равны
нулю: x = ImZ
= 0 и B = ImY
= 0. Цепь носит чисто активный характер:
Z = R; сдвиг фаз отсутствует (φ=0).
В
цепи, содержащей последовательно
соединенные участки с индуктивным и
емкостным характерами сопротивлений,
резонанс называется резонансом
напряжений. Рассмотрим простейшую цепь,
которую часто называют последовательным
контуром. Для нее резонанс наступает
при x = xL – xC = 0 или xL = xC, откуда:

Напряжения
на индуктивности и емкости в этом режиме
равны по величине и, находясь в противофазе,
компенсируют друг друга. Все приложенное
к цепи напряжение приходится на ее
активное сопротивление (рис. 27.1, а).

Напряжения
на индуктивности и емкости могут
значительно превышать напряжения на
входе цепи. Их отношение, называемое
добротностью контура Q, определяется
величинами индуктивного (или емкостного)
и активного сопротивлений:

Добротность
показывает, во сколько раз напряжения
на индуктивности и емкости при резонансе
превышают напряжение, приложенное к
цепи. В радиотехнических цепях она может
достигать нескольких сотен единиц.
Из
условия выше следует, что резонанса
можно достичь, изменяя любой из параметров
– частоту, индуктивность, емкость. При
этом меняются реактивное и полное
сопротивления цепи, а вследствие этого
– ток, напряжение на элементах и сдвиг
фаз. Не приводя анализа формул, показываем
графические зависимости некоторых из
этих величин от емкости (рис. 27.2). Емкость
С0,
при которой наступает резонанс, можно
определить из формулы: С0=1/(ω2L).

Аналогичные
рассуждения можно провести и для цепи,
состоящей из параллельно соединенных
R, L и C. Векторная диаграмма ее резонансного
режима приведена на рис. 27.1, б. Рассмотрим
теперь более сложную цепь с двумя
параллельными ветвями, содержащими
активные и реактивные сопротивления
(рис. 27.3, а).
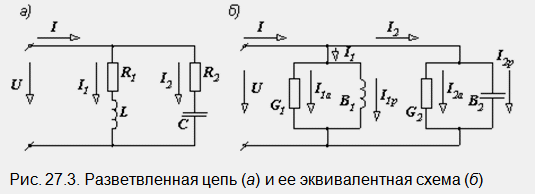
Для
нее условием резонанса является равенство
нулю ее реактивной проводимости: ImY = 0.
Это равенство означает, что мы должны
мнимую часть комплексного выражения Y
приравнять к нулю.
Определяем
комплексную проводимость цепи. Она
равна сумме комплексных проводимостей
ветвей:

Приравнивая
к нулю выражение, стоящее в круглых
скобках, получаем:

Левая
и правая части последнего выражения
представляют собой не что иное, как
реактивные проводимости первой и второй
ветвей B1 и B2. Заменяя схему на рис. 27.3, а
эквивалентной (рис. 27.3, б), параметры
которой вычисляем по формулам, и используя
условие резонанса (B = B1 – B2 = 0), снова
приходим к конечному выражению.
Схеме
на рис. 27.3, б соответствует векторная
диаграмма, приведенная на рис. 27.4

Резонанс
в разветвленной цепи называется
резонансом токов. Реактивные составляющие
токов параллельных ветвей противоположны
по фазе, равны по величине и компенсируют
друг друга, а сумма активных составляющих
токов ветвей дает общий ток.
№28
Энергия и мощность в цепи синусоидального
тока.
![]()
Пусть
на некотором участке цепи, напряжение
на зажимах которого равно u,
током i за
время dt переносится электрический заряд
dq = idt. Затрачиваемая источником энергия
равна при этом dw = udq = uidt, а развиваемая
мощность p = dw/dt = ui. Эта величина называется
мгновенной мощностью и определяет
скорость и направление движения энергии
на рассматриваемом участке. Если энергия
поступает в цепь и накапливается в ней,
функция w(t) возрастает, и мгновенная
мощность положительна как производная
возрастающей функции. Напряжение u и
ток i в
эти моменты времени имеют одинаковые
знаки. Процесс накопления энергии в
цепи наблюдается, например, при заряде
конденсатора. В те моменты времени,
когда u и i имеют
разные знаки, мгновенная мощность
отрицательна, функция w(t), определяющая
энергию, поступающую в цепь, убывает,
так как только убывающая функция имеет
отрицательную производную. Убыль энергии
в электрической цепи означает возврат
ее источнику. Такая ситуация возникает
при разряде конденсатора.
Энергия,
поступающая в цепь, может не возвращаться
к источнику, а необратимо преобразовываться
в тепло или механическую работу.
Количество этой энергии определяется
законом Джоуля–Ленца и за время, равное
периоду синусоидального тока, равно:

Эта
величина, отнесенная ко времени Т,
определяет среднее значение мгновенной
мощности за период и называется активной
мощностью:

Физически
активная мощность представляет собой
энергию, выделяющуюся в виде тепла или
механической работы в единицу времени.
Пусть
ток и напряжение на входе произвольного
пассивного двухполюсника описываются
выражениями:
![]()
Подставляя
их в формулу ранее и интегрируя, получаем:
P=UIcos(φ)
Используя
соотношения между сторонами в треугольниках
напряжений и токов, сопротивлений и
проводимостей, можно написать цепочку
формул для вычисления активной мощности:
![]()
Рассмотрим
теперь энергетические процессы,
происходящие в отдельно взятых элементах.
В
активном сопротивлении напряжение и
ток совпадают по фазе (φ = 0); в любой
момент времени их знаки одинаковы,
мгновенная мощность положительна, т.е.
в него постоянно поступает энергия
электрического тока, преобразуясь в
тепловую или механическую. Активная
мощность равна:
![]()
В
реактивных элементах угол сдвига фаз
по величине равен 90°. В индуктивности,
при отстающем токе, он положителен, в
емкости, при опережающем токе, –
отрицателен. Подставляя φ = +- 90° в
выражение напряжения на входе цепи,
получим u = Um sin (ωt+-90°) = +-Um cos(ωt). При таком
напряжении мгновенная мощность колеблется
с двойной частотой, изменяясь по
синусоидальному закону:
![]()
т.е.
дважды за полпериода меняет знак.
Подстановка этого выражения приводит
к результату: P = 0. Равенство нулю активной
мощности означает, что в реактивных
элементах не происходит необратимого
преобразования электромагнитной энергии
в тепловую и механическую.
Можно
показать, что в индуктивности в течение
первой четверти периода, при возрастании
тока от нуля до Im, в магнитном поле
индуктивности накапливается энергия
WM=(LI2m)/2.
В течение следующей четверти периода,
когда ток уменьшается до нуля, эта
энергия из магнитного поля возвращается
во внешнюю цепь.
В
емкости – аналогично: в течение одной
четверти периода, когда напряжение на
обкладках конденсатора возрастает от
нуля до Um, конденсатор заряжается, в его
электрическом поле накапливается
энергия: Wэ=(СU2m)/2.
В следующую четверть периода конденсатор
разряжается, его напряжение уменьшается
до нуля, и накопленная в электрическом
поле энергия возвращается в цепь.
Энергию, которой электрическое поле
конденсатора и магнитное поле катушки
обмениваются с цепью, будем называть
энергией обмена.
Для
энергии магнитного поля WM и
электрического поля WЭ можно
записать следующие формулы:
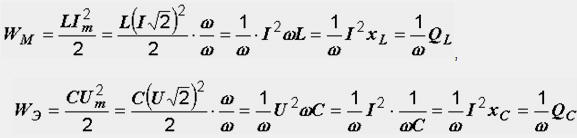
Величины
QL=I2XL и
QC=I2XC имеющие
размерность мощности, называются
соответственно реактивной мощностью
индуктивности и реактивной мощностью
емкости. К работе, совершаемой переменным
током, они отношения не имеют, а являются
величинами, пропорциональными энергии
магнитного и электрического полей:
QL=ωWM,
QC=ωWЭ.
В
цепи, содержащей одновременно и
индуктивность и емкость, колебания
энергии происходят таким образом, что
в те моменты времени, когда магнитное
поле индуктивности накапливает энергию,
электрическое поле емкости энергию
отдает, и наоборот. Т.е., когда энергия
магнитного поля положительна, энергия
электрического поля отрицательна.
Суммарная энергия электрического и
магнитного полей за четверть периода
равна:

где
Q – реактивная мощность цепи, она
пропорциональна суммарной энергии
электрического и магнитного полей и
может быть определена через реактивные
сопротивления:
![]()
При
резонансе, когда XL=XC ,
равны реактивные мощности QL и
QC и
энергии WM и
WЭ ,
накапливаемые в магнитном и электрическом
полях. В этом случае обмен энергией
между индуктивностью и емкостью
происходит без участия источника.
Для
вычисления реактивной мощности можно
написать цепочку формул:
![]()
При
анализе электрических цепей часто
используется треугольник мощностей,
который можно получить, умножив стороны
треугольника сопротивлений на квадрат
тока (рис. 28.1). Для него справедливы
следующие соотношения:

Буквой
S, стоящей рядом с гипотенузой треугольника,
обозначается полная мощность. Ее можно
вычислить по одной из следующих формул:

Полная
мощность определяется той электрической
энергией, которая вырабатывается
генератором и отдается в цепь. Она
характеризует габариты электрических
машин и аппаратов. Величина напряжения
определяет уровень изоляции – ее толщину
и расстояние между токоведущими
частотами, а ток – поперечное сечение
проводника, условия охлаждения машины.
При
cosφ = 1 полная мощность равна наибольшему
значению активной мощности, которую
можно получить при заданных напряжении
и токе.
Единицы
измерения мощности, имея одну и ту же
размерность, называются по-разному.
Единица активной мощности – ватт (Вт),
реактивной – вольт-ампер реактивный
(вар), полной – вольт-ампер (ВА).
Комплексная
мощность определяется произведением
комплекса напряжения и сопряженного
комплекса тока:
![]()
№29
Явление взаимной индукции.
![]()
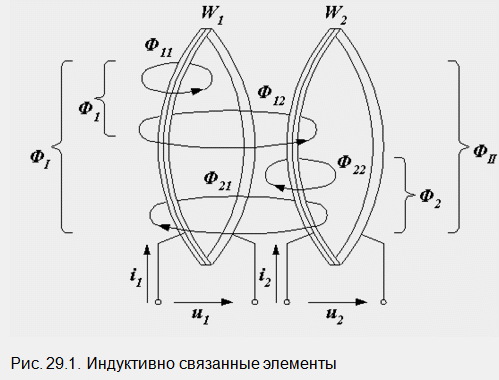
Пусть
имеются две катушки, намотанные в виде
тонких колец. Их активные сопротивления
равны нулю, числа витков W1 и W2. Катушки
находятся достаточно близко друг от
друга, так что магнитное поле каждой из
них какой-то своей частью охватывает
соседнюю. Схематическая картина магнитных
потоков, создаваемых токами i1 и
i2,
показана на рис. 29.1. Каждый поток изображен
в виде одной силовой линии, обозначенной
буквой Ф с двумя индексами. Первый –
указывает номер катушки, током которой
он создается (происхождение магнитного
потока), второй – номер катушки,
охватываемой этим потоком (объект его
воздействия). Рассмотрим магнитные
потоки первой катушки. Ток создает поток
Ф1,
называемый потоком самоиндукции. Его
часть Ф11 охватывает
только первую катушку, а WЭ захватывает
и витки второй. В сумме они равны Ф1.
Кроме того, витки первой катушки
охватываются потоком Ф21,
называемым потоком взаимной индукции
и составляющим часть потока Ф2,
создаваемого током второй катушки i2.
Суммарный магнитный поток ФI,
пронизывающий первую катушку, складывается
из потоков самоиндукции Ф1 и
взаимной индукции Ф21.
Сумма берется алгебраическая ФI=Ф1+-Ф21,
так как эти потоки могут быть направлены
одинаково, либо противоположно друг
другу. Изображение на рис. 29.1 соответствует
второму случаю.
При
принятой форме катушки можно считать,
что все ее витки охватываются одним и
тем же магнитным потоком. Умножив
последний на число витков W1, получим
полное потокосцепление первой катушки:
![]()
где
ψ1=W1Ф1 –
собственное потокосцепление первой
катушки (потокосцепление самоиндукции);
ψ21=W1Ф21 –
потокосцепление взаимной индукции.
Каждое
из этих потокосцеплений пропорционально
создающему его току: ψ1=L1i1 и
ψ21=Mi2 .
Поэтому ψI=L1i1+-Mi2.
При изменении магнитного потока в
катушке индуцируется эдс электромагнитной
индукции, и на ее зажимах появляется
напряжение:

Аналогичное
уравнение можно записать и для второй
катушки.
Первое
слагаемое в правой части последнего
уравнения U1L представляет
собой напряжение, обусловленное током
самой катушки (напряжение самоиндукции),
а второе U1M –
напряжение, наведенное на зажимах первой
катушки изменяющимся магнитным полем
второй катушки (напряжение взаимной
ииндукции). Эти напряжения имеют
одинаковые знаки при согласном направлении
магнитных потоков и разные – при
встречном.
Для
решения задачи о характере включения
катушек и о направлении их магнитных
потоков вводят понятие одноименных
зажимов, отмечая их на схеме одинаковыми
значками. Разметку делают руководствуясь
следующим определением.
Одноименными
зажимами двух катушек называются такие
зажимы, когда при одинаковых направлениях
токов относительно этих зажимов магнитные
потоки самоиндукции и взаимной индукции
в каждой катушке складываются.
Другими
словами, если мы имеем две катушки, у
которых отмечены начала и концы намотки,
и если токи в них протекают одинаково,
например от начала к концу в обеих
катушках, то оба магнитные потока в
каждой из них будут направлены согласно.
Наличие
магнитной связи между катушками
обозначается на схемах двухсторонней
дугообразной стрелой, рядом с которой
ставится буква i1.
№30
Последовательное соединение индуктивно
связанных элементов.
![]()
Пусть
две катушки, обладающие сопротивлениями
R1 и R2 , индуктивностями L1 и L2 и взаимной
индуктивностью M, соединены последовательно
(рис. 30.1).

Возможны
два вида их соединения – согласное и
встречное. Если считать, что звездочками
отмечены начала обмоток, то при согласном
включении начало второй подключается
к концу первой (рис. 30.1, а). Токи в обеих
катушках направлены одинаково относительно
одноименных зажимов: от начала к концу.
При встречном включении катушек конец
второй присоединяется к концу первой
(рис. 30.1, б).
Напряжение
на каждой из катушек содержит три
составляющих: падение напряжения на
активном сопротивлении, напряжение
самоиндукции и напряжение взаимной
индукции:

Последние
имеют одинаковые знаки при согласном
включении и разные при встречном.
Напряжение на входе цепи равно сумме
этих двух напряжений:
![]()
Входное
комплексное сопротивление цепи получим
из совместного рассмотрения трех
последних уравнений:

где
Z1 и Z2 – комплексные сопротивления
катушек, а ZM –
комплексное сопротивление взаимной
индукции:

Из
формулы выше вытекают формулы, определяющие
общую индуктивность цепи и суммарное
индуктивное сопротивление:

Можно
определить результирующее индуктивное
сопротивление каждой катушки. У первой
оно равно X1+-XM.
И здесь при согласном включении оно
больше чем при встречном. Физически это
объясняется тем, что в первом случае
магнитный поток, охватывающий каждую
катушку, больше чем во втором; например,
для первой катушки ФIсогл=Ф1+Ф21,
а ФIвстр=Ф1-Ф21.
Вследствие этого ЭДС электромагнитной
индукции, оказывающая току индуктивное
сопротивление, при согласном включении
больше, чем при встречном.
На
рис. 30.1 изображены векторные диаграммы,
построенные по уравнениям (30.1) и (30.2).
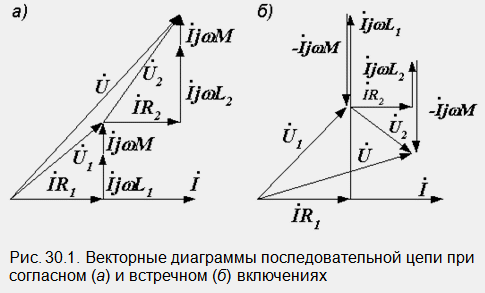
При
встречном включении возможен так
называемый “емкостный” эффект,
когда у одной из катушек напряжение на
зажимах отстает по фазе от тока (напряжение
на рис. 30.1, б). Это имеет место, когда
индуктивность катушки меньше величины
взаимной индуктивности. В этом случае
результирующая индуктивность
рассматриваемой катушки (с учетом
взаимной индукции) отрицательна: L2-M<0.
Для всей цепи такой эффект невозможен.
Ее индуктивность всегда положительна,
и цепь носит активно-индуктивный
характер.
№31
Параллельное соединение индуктивно
связанных элементов.
![]()
разноименных. Пусть
две индуктивно связанные катушки с
параметрами R1, R2, L1, L2 и M соединены
параллельно (рис. 3.5). Оба вида соединения
будем рассматривать одновременно.
Согласное соединение получается при
подключении к одному и тому же узлу
одноименных зажимов, встречное

точками.
Запишем уравнения Кирхгофа для
рассматриваемой цепи и решая их, получим
выражения, определяющие токи: Первый
случай отмечен на схеме звездочками,
второй

Входное
комплексное сопротивление цепи равно
отношению напряжения к току на ее
зажимах:
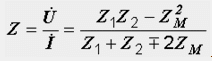
При
отсутствии магнитной связи между
катушками, полагая ZM=0,
получаем известную формулу для определения
общего сопротивления двух параллельных
ветвей:
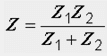
Во
всех приведенных выражениях у слагаемых
с двойным знаком верхний знак относится
к согласному соединению, нижний к
встречному.
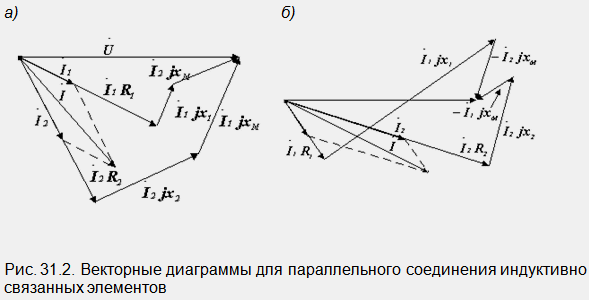
На
рис. 31.2 представлены векторные диаграммы
рассматриваемой цепи при согласном (а)
и встречном (б) соединениях катушек. При
построении векторы I1jX1 и
I1jXM проводятся
перпендикулярно току I1,
а векторы I2jX2 и
I2jXM перпендикулярно
току I2.
При согласном соединении напряжения
взаимной индукции опережают соответствующие
токи, при встречном отстают от них.
№32
Разметка зажимов индуктивно связанных
катушек.
![]()
Если
разметка осуществляется в процессе
изготовления катушек, то одноименные
зажимы можно указать, проследив
направления намотки. Для двух катушек
это сделать очень легко (рис. 32.1, а).

Поступаем
следующим образом. Отмечаем один из
зажимов первой катушки каким-либо
значком, например, звездочкой. Предположим,
что это – начало обмотки. Направим ток
в ней от начала к концу и, пользуясь
правилом правой руки, определяем
направление магнитного потока: правой
рукой охватываем катушку так, чтобы
четыре пальца показали направление
тока в ее витках, тогда отогнутый большой
палец покажет направление магнитного
потока. Во второй катушке ток направляем
так, чтобы его магнитный поток имел то
же самое направление. Зажим, от которого
ток уходит в катушку, также является
началом. Его тоже отмечаем звездочкой.
Более
сложный случай показан на рис. 32.1, б.
Оказывается, здесь невозможно указать
одноименные зажимы сразу для всех трех
катушек. Приходится рассматривать их
попарно и действовать так, как только
что описано. При этом, рассматривая
отдельно какую-то пару катушек, на
стержень магнитопровода с третьей
катушкой не обращаем внимания.
Рекомендуем
самостоятельно проверить правильность
разметки зажимов, выполненной на рис.
32.1, б.
В
том случае, когда направление намотки
катушек неизвестно и установить его
без разрушения катушки невозможно,
прибегают к помощи электроизмерительных
приборов.
Один
из возможных способов заключается в
следующем. Обе катушки поочередно
собирают в схемы, показанные на рис.
3.8, и подключают к источнику синусоидального
напряжения одной и той же величины.

Очевидно,
что в одном случае получается согласное
соединение, в другом – встречное. Вид
соединения определяем по показаниям
амперметра. Вспомним, что при согласном
соединении катушек их полное сопротивление
больше, а, следовательно, при одной и
той же величине входного напряжения
ток меньше, чем при встречном. А определив
вид соединения, легко делаем разметку:
при согласном последовательном соединении
катушки подключаются друг к другу
разноименными зажимами (начало второй
к концу первой). Если на рис. 33.2 при
одинаковых показаниях вольтметров
амперметр показывает 1,5 А в левой схеме
и 1,1 А – в правой, то слева имеем встречное
соединение, справа согласное, и поэтому
одноименными зажимами являются первый
и четвертый, а также второй и третий.
Покажем
еще один способ разметки. Первую катушку
присоединяем через ключ к источнику
постоянного напряжения, например, к
аккумуляторной батарее; к зажимам второй
катушки подключаем гальванометр (или
вольтметр) магнитоэлектрической системы
(рис. 32.3, а).

Зажим
первой катушки, подключаемый к
положительному полюсу источника,
помечаем каким-нибудь способом, например,
прикрепляем к нему бирку. Затем замыкаем
ключ. Если стрелка прибора при этом
отбрасывается на шкалу, вешаем такую
же бирку на тот зажим второй катушки,
который присоединен к положительной
клемме прибора (зажим 3). Если стрелка
отклоняется влево, за пределы шкалы, то
одноименным с зажимом 1 является зажим
4.
С
целью теоретического обоснования метода
проведем этот опыт с катушками, направления
намотки и одноименные зажимы которых
известны (рис. 32.3, б).
При
замыкании ключа в первой катушке
возникает возрастающий по величине ток
i1,
который создает магнитный поток Ф1,
также возрастающий по величине. Последний
индуцирует во второй катушке ЭДС
электромагнитной индукции. Создаваемый
ею ток i2 возбуждает
магнитный поток Ф2,
направление которого противоположно
направлению Ф1,
так как попринципу Ленца он должен
противодействовать его возрастанию. А
магнитный поток такого направления
создается током, направление которого
показано на схеме. Напоминаем, что
направления тока в катушке и создаваемого
им магнитного потока связаны правилом
правой руки. Ток i2 в
рассматриваемой схеме протекает через
гальванометр от его плюсовой клеммы к
минусовой. При таком направлении тока
через прибор его стрелка отбрасывается
на шкалу.
Результатом
проведенных рассуждений является
следующее практическое правило: если
в процессе эксперимента при замыкании
ключа стрелка прибора магнитоэлектрической
системы отклоняется в сторону шкалы,
то одноименными являются зажимы,
присоединенные к плюсу батареи и плюсу
прибора.
№33
Сложная цепь с взаимной индуктивностью.
![]()
Пусть
задана двухконтурная цепь, содержащая
индуктивно связанные элементы (рис.
3.10). Для ее расчета необходимо составить
три (по числу неизвестных токов) уравнения
по законам Кирхгофа. Первое уравнение,
для верхнего узла, затруднений не
вызывает: I1+I2-I3=0
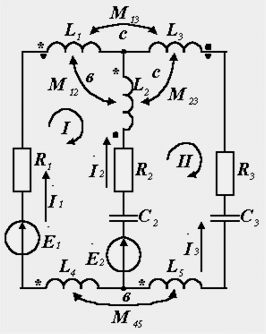
Рис.
33.1. Сложная цепь с взаимной индуктивностью
Еще
два уравнения напишем по второму закону
Кирхгофа для контуров, обозначенных
закругленными стрелками I и II, показывающими
направление обхода контура при написании
уравнений. Но предварительно необходимо
определить вид включения катушек. Для
каждой их пары одноименные зажимы
отмечены своими значками. Предположим,
что это начала обмоток. Первая и вторая
катушки, одноименные зажимы которых
отмечены звездочками, включены встречно,
так как в первой ток протекает от начала
к концу, а во второй от конца к началу.
Поставим для памяти рядом со стрелкой
M12 букву
в (встречное включение). У второй и
третьей катушек начала обмоток обозначены
точками. В обеих катушках токи протекают
одинаково относительно этих зажимов –
от начала к концу, значит катушки включены
согласно; ставим рядом со стрелкой букву
с (согласное включение). Аналогично
поступаем и с остальными катушками.
Записываем
уравнение для первого контура:
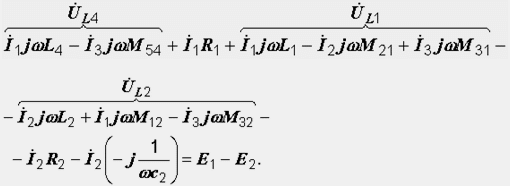
Дадим
некоторые пояснения. Напряжение на
зажимах катушки, индуктивно связанной
с другой катушкой, складывается из
напряжения самоиндукции (IjωL) и напряжения
взаимной индукции (IjωM). При согласном
включении эти напряжения имеют одинаковые
знаки, при встречном – разные. Для
лучшего восприятия индексы у буквы M
поставлены так, чтобы они указывали
катушку, создающую магнитное поле
(первый индекс), и катушку, в которой
наводится ЭДС (второй индекс). Например,
обозначение M32 показывает,
что мы определяем влияние третьей
катушки на вторую. Рассмотрим составляющие
напряжения на элементе L2.
В уравнении (3.4) они объединены фигурной
скобкой UL2.
Первое слагаемое -I2jωL – это напряжение
самоиндукции. Оно записано с минусом,
так как при обходе контура мы идем по
этому элементу против тока. Второе
слагаемое I1jωM12 –
это напряжение, наведенное на зажимах
второй катушки магнитным потоком,
создаваемым током первой катушки. Его
знак (плюс) из-за встречного включения
противоположен знаку напряжения
самоиндукции. Напряжение, которое
наводится во второй катушке со стороны
третьей (I3jωM32),
имеет тот же знак (минус), что и напряжение
самоиндукции, так как вторая и третья
катушки соединены согласно.
Приводим
уравнение, записанное для второго
контура:

№34
Эквивалентная замена индуктивных
связей.
![]()
Имеется
возможность избежать составления таких
сложных уравнений, как в предыдущем
подразделе. Для этого нужно произвести
так называемую развязку электрической
цепи, заменив схему с индуктивно
связанными элементами эквивалентной
схемой без индуктивных связей. Делается
это по следующему правилу: если два
элемента L1 и
L2,
имеющие взаимную индуктивность ,
присоединены к узлу электрической цепи
одноименными зажимами, то при переходе
к эквивалентной схеме к этим элементам
добавляется –M, а в третью, отходящую
от узла, ветвь включается M (рис. 34.1, а).
Если
характер подключения катушек меняется,
т.е. они присоединяются к узлу разноименными
зажимами, то в эквивалентной схеме знак
перед M меняется на противоположный
(рис. 34.1, б).
Для
доказательства приведенных утверждений
необходимо в каждой паре схем произвольно
указать направления токов (одинаковые
для одной и той же ветви) и записать
выражения напряжений Uab,
Ubc и
Uca.
Для обеих схем они оказываются одинаковыми,
что подтверждает их эквивалентность.

№35
Трансформатор без стального сердечника.
![]()
Простейший
трансформатор представляет собой
совокупность двух обмоток, размещенных
на общем магнитопроводе (рис. 35.1, а).

К
его первичной обмотке подводится
напряжение источника питания, а ко
вторичной – подключается нагрузка.
Одноименными зажимами обмоток являются
их верхние выводы. Ток первичной обмотки
I1 создает в магнитопроводе магнитный
поток Ф1, который в свою очередь во
вторичной обмотке вызывает появление
тока I2. Создаваемый им магнитный поток
Ф2 в соответствии с принципом Ленца
препятствует потоку Ф1, т.е. направлен
ему навстречу. Направление тока I2,
соответствующее показанному на схеме
потоку Ф2, определяем по правилу правой
руки.
Мы
будем рассматривать трансформатор, не
имеющий ферромагнитного сердечника.
Такие трансформаторы применяются при
высоких частотах и в специальных
электроизмерительных устройствах.
Катушки с ферромагнитными сердечниками
имеют нелинейные характеристики и здесь
не рассматриваются.
Электрическая
схема замещения трансформатора изображена
на рис. 35.1, б. На схеме указаны: R1, X1, R2, X2
и – сопротивления первичной и вторичной
обмоток трансформатора, RН и
XH –
сопротивления нагрузки. Введем
обозначения: R22=R2+RH и
X22=X2+XH –
суммарные активное и реактивное
сопротивления вторичной цепи
трансформатора, Z1=R1+jX1, Z2=R2+jX2, ZH=RH+jXH,
Z22=R22+jX22 – комплексные сопротивления
соответствующих участков.
Запишем
уравнения второго закона Кирхгофа для
первичной и вторичной цепей трансформатора,
учитывая, что его обмотки имеют встречное
включение:

Обозначив
I1jXM=E2M,
второе уравнение системы (35.1) можно
записать так:
E2M=I2Z2+I2Z=
Физически
E2M –
это ЭДС, которая наводится во вторичной
обмотке переменным магнитным полем
первичной обмотки. С учетом этого
уравнение можно прочитать так: ЭДС,
наведенная во вторичной обмотке
трансформатора, равна сумме падений
напряжений на всех элементах его
вторичного контура. Подставляя I2ZH=U2 ,
получим: U2=E2M-I2Z2 .
Смысл последнего уравнения заключается
в следующем: напряжение на вторичных
зажимах трансформатора меньше эдс,
наведенной во вторичной обмотке, на
величину падения напряжения на ее
сопротивлении.
На
рис. 35.2 изображена векторная диаграмма
трансформатора. Ее построение начинаем
со вторичного тока I2. Ориентируясь на
его направление, проводим векторы
напряжений на всех элементах вторичной
цепи. Их сумма равна ЭДС E2M.
Так как в формуле, определяющей ее
величину, присутствует множитель j,
поворачивающий вектор на четверть
оборота, то ток проводим под углом 90° к
E2M в
сторону отставания. Определив направление
I1, строим векторы I1R1 и I1jX1 , которые в
сумме с I2jXM –
дают U1.

Для
анализа работы трансформатора применяют
различные эквивалентные схемы. Рассмотрим
некоторые из них.
Соединив
между собой два нижних зажима трансформатора
(режим его работы при этом не изменится)
и произведя развязку индуктивных связей,
придём к Т-образной эквивалентной схеме
(рис. 35.3).

Из
второго уравнения системы выразим ток
I2 и подставим в первое уравнение той же
системы:

Последнему
выражению соответствует схема,
изображенная на рис. 35.3. Соединенное
последовательно с Z1 сопротивление
ZBH называется
вносимым (из вторичной цепи трансформатора
в первичную).
Как
следует из формулы, оно равно:

Его
активная и реактивная составляющие
соответственно равны:

Появление
в первичном контуре активного
сопротивления, вносимого из первичного
контура, физически означает следующее.
Энергия, подводимая к трансформатору,
потребляется не только сопротивлением
R1, но и сопротивлениями вторичной цепи
R2 и RH,
куда она передается через переменное
магнитное поле между обмотками.
Из-за
минуса в формуле вносимого реактивного
сопротивления общее реактивное
сопротивление всей цепи, равное сумме
X1 и XBH,
оказывается меньше индуктивного
сопротивления первичной обмотки.
Это
хорошо согласуется со сказанным ранее.
При встречном соединении обмоток
трансформатора поток Ф2, направленный
противоположно потоку Ф1, уменьшает
последний, что приводит к уменьшению
общего индуктивного сопротивления.
№36
Трехфазная система.
![]()
Многофазной
системой называется совокупность,
состоящая из ”n” отдельных одинаковых
электрических цепей или электрических
схем, режимные параметры в которых (е,
u, i) сдвинуты во времени на равные отрезки
Δt=T/n или по фазе Δωt=2π/n=360°/n.
Отдельные
части системы называются фазами. Термин
”фаза” в электротехнике имеет два
смысловых значения: первое – как момент
времени для синусоидальной функции
тока или напряжения, второе – как часть
многофазной системы. В технике нашли
применение 2-х, 3-х, 6-и и более фазные
системы. В электроэнергетике наибольшее
распространение получила трехфазная
система, обладающая рядом преимуществ
перед системами с другим числом фаз.
Трехфазная
система состоит из трех электрических
цепей или электрических схем (фаз),
параметры режима (u,i) в которых сдвинуты
во времени на Δωt=2π/3=360°/3=120°. Отдельные
фазы трехфазной системы согласно ГОСТ
обозначаются (именуются) заглавными
латинскими буквами А, В, С (основное
обозначение), или цифрами 1, 2, 3 (допустимое
обозначение), или заглавными латинскими
буквами R, S, T (международное обозначение).

Не
имеет значения, какую из трех фаз
именовать какой буквой А, В или С,
существенным является их порядок
следования друг за другом во времени.
Прямым порядком следования фаз называется
А→В→С→А,
при котором параметры режима (u, i) в фазе
В отстают от аналогичных параметров в
фазе А на 120°, а в фазе С – опережают на
120°. При обратном порядке следования
фаз А→С→В→А
параметры режима в фазе С отстают от
аналогичных пара¬метров в фазе А на
120°, а в фазе В – опережают на 120°.
Если
отдельные фазы системы работают
изолировано и независимо друг от друга,
то система называется несвязанной.
Рассмотрим работу простейшей несвязанной
трехфазной системы (рис. 36.1). Мгновенные
значения фазных ЭДС генератора сдвинуты
во времени на 120° в порядке следования
фаз A→B→C→A:
eA=Emsinωt
↔
EA=Eej0°
eB=Emsin(ωt-120°)
↔
EB=Ee-j120°
eC=Emsin(ωt-240°)=Emsin(ωt+120°)
↔
EC=Eej120°
Графические
диаграммы этих функций показаны на рис.
36.2, а векторные – на рис. 36.3.
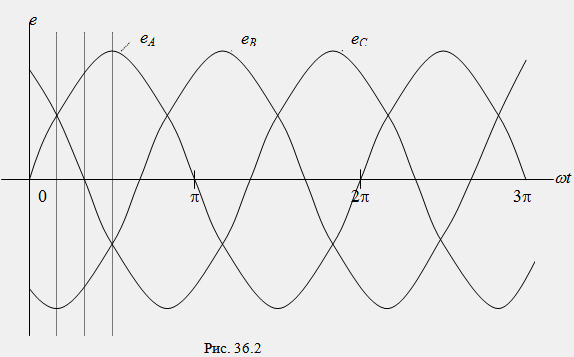

Основное
свойство любых переменных функций (е,
u, i) в симметричной трехфазной системе
состоит в том, что сумма их мгновенных
значений в любой момент времени равна
нулю, например,
еА +
еВ +
еС =
0. Найдем эту сумму для разных моментов
времени:

Если
нагрузка отдельных фаз равна между
собой, т.е. ZA=ZB=ZC=Zejφ,
то фазные токи будут равны по модулю и
сдвинуты по фазе относительно своих
ЭДС (напряжений ) на один и тот же угол
φ, а между собой, как и ЭДС, будут сдвинуты
по фазе на 120°. Следовательно, фазные
токи iА,
iВ,
iСобразуют
симметричную трехфазную систему и для
них будут справед-ливы полученные ранее
выводы: iА +
iВ +
iС =
0; IА +
IВ +
IС =
0.
Преобразуем
несвязанную трехфазную систему в
связанную путем объединения трех
обратных приводов в один общий привод.
Согласно 1-ому закону Кирхгофа в общем
проводе должен протекать суммарный ток
iN =
iА +
iВ +
iC =
0. Это означает, что потребность в обратном
проводе вообще отпадает, благодаря чему
достигается значительная экономия
проводов при передаче энергии от
трехфазного генератора к приемнику.
Достоинства
(преимущества) трехфазной системы:
1)
Передача энергии от генератора к
потребителям трехфазным током наиболее
выгодна экономически, чем при любом
другом числе фаз. Например, по сравнению
с двухпроводной системой достигается
экономия проводов в два раза (3 провода
вместо 6), соответственно уменьшаются
потери энергии в проводах линии.
2)
Трехфазная система позволяет технически
просто получить круговое вращающееся
поле, которое лежит в основе работы всех
трехфазных машин (генераторов и
двигателей).
3)
Элементы трехфазной системы (генераторы,
трансформаторы, двигатели) просты по
конструкции, надежны в работе, имеют
хорошие массогабаритные показатели,
сравнительно дешевы, долговечны.
4)
На выходе трехфазных генераторов имеется
два уровня выходного напряжения –
линейное и фазное, отличающиеся в √3
раз (Uл /Uф = √3), что позволяет подключать
к такому генератору приемники с различными
номинальными напряжениями.
Благодаря
своим достоинствам трехфазная система
применяется в электроэнергетике для
производства, передачи, распределения
и потребления электрической энергии.
Трехфазная
система и ее основные звенья – генератор,
трансформатор, линия элек¬тропередачи,
двигатель – были разработаны в 1889 году
инженером Доливо-Добровольским (фирма
Сименс и Шукерт). Создание этой системы
явилось важным событием в истории
развития теоретической и прикладной
электротехники.
№37
Способы соединения обмоток трехфазных
генераторов.
![]()
В
обмотках трехфазного генератора
индуктируются синусоидальные ЭДС,
сдвину¬тые по фазе на 120°:
eA=Emsinωt
↔
EA=Eфej0°
eB=Emsin(ωt-120°)
↔
EB=Eфe-j120°
eC=Emsin(ωt-240°)=Emsin(ωt+120°)
↔
EC=Eфej120°
Между
собой фазные обмотки генератора могут
соединяться по двум различным схемам:
звездой (у) и треугольником (Δ).
При
соединении в звезду концы фазных обмоток
(фаз) генератора соединяются в общую
точку N, которая называется нулевой или
нейтральной, а начала обмоток служат
линейными выводами генератора А, В, С
(рис. 37.1).
Векторная
диаграмма напряжений трехфазного
генератора при соединении его фазных
обмоток в звезду показана на рис. 37.2 а,
б.
В
трехфазном генераторе различают фазные
и линейные напряжения. Фазными называются
напряжения между началами и концами
фазных обмоток или между одним из
линейных выводов А, В, С и нулевым выводом
N. Фазные напряжения равны фазным ЭДС:
UА=ЕА,
UВ=ЕВ,
UС=ЕС (индекс
N при фазных напряжениях опускается,
так как φN =
0). Линейными называются напряжения
между двумя линейными выводами А, В, С.
Линейные напряжения равны векторной
разности двух фазных напряжений:
UАВ =UА –
UВ;
UВС =UВ –
UС;
UСА =UС –
UА .

При
расчете трехфазных цепей комплексным
методом фазные и линейные напряжения
генератора представляются в комплексной
форме, при этом один из векторов системы
принимают за начальный и совмещают его
с вещественной осью, а остальные вектора
получают начальные фазы согласно их
углам сдвига по отношению к начальному
вектору. На рис. 37.2 а показан вариант
представления напряжений трехфазного
генератора в комплексной форме, когда
за начальный вектор принимается фазное
напряжение фазы А. В этом случае фазные
напряжения генератора в комплексной
форме получат вид : UA=Uфej0°,
UB=Uфe-j120°,
UC=Uфej120°,
линейные напряжения: UAB=Uлej30°,
UBC=Uлe-j90°,
UCA=Uлej150°.
На
рис. 37.2 б показан другой вариант
представления напряжений трехфазного
генератора в комплексной форме, когда
за начальный вектор принимается линейное
напряжение UAB.
В этом случае фазные напряжения генератора
в комплексной форме получат вид:
UA=Uфe-j30°,
UB=Uфe-j150°,
UC=Uфej90°,
линейные напряжения: UAB=Uлej0°,
UBC=Uлe-j120°,
UCA=Uлej120°.
Из
геометрии получаем соотношение между
модулями линейного и фазного напряжений:
UЛ =
2UФ cos
30° =2UФ √(3)/2 =√(3) UФ.
Обмотки
трехфазного генератора теоретически
можно включать по схеме треуголь¬ника.
В такой схеме конец каждой предыдущей
фазы соединяется с началом последующей,
а точки соединения служат линейными
выводами генератора (рис. 37.3).

При
соединении фаз в треугольник в его
контуре действует сумма фазных ЭДС: ∑e
= еАВ +
еВС +
еСА.
В реальных трехфазных генераторах
технически невозможно обеспечить
равенство нулю для суммарной ЭДС. Так
как собственные сопротивления обмоток
генератора малы, то даже незначительная
по величине суммарная ЭДС ∑e > 0 может
вызвать в контуре треугольника
уравнительный ток, соизмеримый с
номинальным током генератора, что
привело бы к дополнительным потерям
энергии и снижению КПД генератора. По
этой причине обмотки трехфазных
генераторов запрещается соединять по
схеме треугольника.
Номинальным
напряжением в трехфазной системе
называется линейное напряжение.
Номинальное напряжение принято выражать
в киловольтах (кВ). Шкала номинальных
трехфазных напряжений, применяемых на
практике, имеет вид: 0,4; 1,1; 3,5; 6,3; 10,5; 22;
35; 63; 110; 220; 330; 500; 750. На потребительском
уровне номинальное трехфазное напряжение
может указываться в виде отношения
UЛ⁄UФ,
например: UЛ/UФ =
380 ⁄ 220 В.
№38
Способы соединения фаз трехфазных
приемников.
![]()
Приемники
трехфазного тока могут подключаться к
генератору по двум схемам – звезды (y)
и треугольника (Δ). Как известно, на
выходе трехфазного генератора получаются
два напряжение (линейное и фазное),
отличающиеся в Uл/Uф = √3 раз. С другой
стороны каждый приёмник энергии рассчитан
на работу при определенном напряжении,
которое называется номинальным. Схема
соединения фаз приемника должна
обеспечить подключение его фаз номинальное
фазное напряжение. Таким образом, выбор
схемы соединения фаз трехфазного
приемника зависит от соотношения
номинальных напряжений приемника и
генератора (сети).
Схема
звезды применяется в том случае, если
номинальное напряжение приемника
соответствует (равно) фазному напряжению
генератора. При соединении в звезду
концы фаз приемника объединяются в одну
точку “n”, называемую нулевой или
нейтральной, а начала фаз подключаются
к линейным выводам трехфазного генератора
А, В, С линейными проводами. Если нулевая
точка приемника “n” соединена с нулевой
точкой генератора “N” нулевым проводом,
то схема получила название звезды с
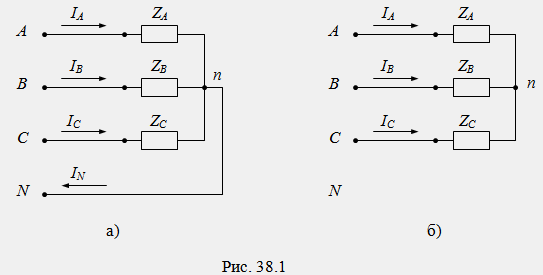
нулевым проводом (рис. 38.1а). При отсутствии
нулевого провода схема носит название
звезды без нулевого провода (рис. 38.1б).
Токи,
протекающие в линейных проводах по
направлению от генератора к приемнику,
называются линейными.
Токи,
протекающие в фазах приемника по
направлению от начал к концам, называются
фазными. В схеме звезды фазы приемника
включены последовательно с линейными
проводами и по ним протекают одни и те
же токи (IA,
IB,
IC).
Поэтому для схемы звезды понятия линейные
и фазные токи тождественны: IЛ =
IФ.
Ток,
протекающий в нулевом проводе от
приемника к генератору, называется
нулевым или нейтральным (IN).
Напряжения
между началами и концами фаз приемника
называются фазными (UAn,
UBn,
UCn),
а напряжения между началами фаз –
линейными (UAB,
UBC,
UCA).
Линейные напряжения приемника и
генератора тождественно равны.
В
схеме звезды с нулевым проводом (рис.
38.1а) к каждой фазе приемника подводится
непосредственно фазное напряжение
генератора (UAN =
UAn =
UA,
UBN =
UBn =
UB,
UCN =
UCn =
UC),
каждая из фаз при этом работает независимо
друг от друга, а линейные (фазные) токи
определяются по закону Ома:

Ток
в нулевом проводе в соответствии с
первым законом Кирхгофа равен
геометрической сумме линейных (фазных)
токов:
IN=IA+IB+IC
При
симметричной нагрузке ZA=ZB=ZC ток
в нулевом проводе IN=0
и, следовательно, надобность в нeм
отпадает. Симметричные трехфазные
приемники (например, трехфазные
электродвигатели) включаются по схеме
звезды без нулевого провода.
При
несимметричной нагрузке относительная
величина тока в нулевом проводе зависит
от характера и степени не симметрии
фазных токов. Как правило, трехфазные
приёмники стремятся спроектировать по
возможности близкими к симметричным,
поэтому ток в нулевом проводе в реальных
условиях значительно меньше линейных
(фазных) токов.
схеме
звезды без нулевого провода (рис. 38.1б)
при любой нагрузке фаз должно выполняться
условие первого закона Кирхгофа:
IA+IB+IC=0
Из
уравнения следует вывод, что изменение
одного из токов влечет изменение двух
других токов, то есть отдельные фазы
работают в зависимом друг от друга
режиме. При несимметричной нагрузке
потенциал нулевой точки приемника Un
становится не равным нулю, он “смещается”
на комплексной плоскости с нулевого
положения, при этом фазные напряжения
приемника (UAn,
UBn,
UCn)
не равны соответствующим фазным
напряжениям генератора (UA,
UB,
UC),
происходит так называемый перекос
фазных напряжений приемника (рис. 38.2).

Расчет
токов и напряжений в схеме звезды без
нулевого провода выполняется в следующей
последовательности.
Определяется
напряжение (потенциал) нейтральной
точки приемника по методу двух узлов:

где
ZN –
комплексное сопротивление нулевого
провода, при его отсутствии ZN=∞.
Фазные
напряжения приемника определяются как
разности потенциалов соответствующих
точек:
UAn=UA-Un,
UBn=UB-Un ,
UCn=UC-Un.
Фазные
токи приемника определяются по закону
Ома:

Комплексные
мощности фаз приемника:

Режим
работы приемника с перекосом фазных
напряжений является ненормальным и
может привести его к выходу из строя.
По этой причине несимметричную трехфазную
нагрузку запрещается включать по схеме
звезды без нулевого провода (например,
осветительную нагрузку).
Схема
треугольника применяется в том случае,
если номинальное фазное напряжение
приемника соответствует (равно) линейному
напряжению генератора. При соединении
в треугольник конец каждой фазы
соединяется с началом последующей, а
точки соединения (вершины треугольника)
подключаются к линейным выводам
трехфазного генератора А, В, С линейными
проводами (рис.38.3).
Токи,
протекающие в фазах приемника по
направлению от их начал к концам,
называются фазными (IAB,
IBC,
ICA).
Токи, протекающие в линейных проводах
по направлению от генератора к приемнику,
называются линейными (IA,
IB,
IC).

В
схеме треугольника фазные и линейные
напряжения приемника тождественно
равны (UAB,
UBC,
UCA).
В этой схеме к каждой фазе приемника
подводится непосредственно линейное
напряжение генератора, при этом отдельные
фазы работают независимо друг от друга.
Фазные токи определяются по закону Ома:

Линейные
токи определяются из уравнений первого
закона Кирхгофа для вершин треугольника,
они равны геометрической разности
фазных токов:
IA=IAB-ICA;
IB=IBC-IAB;
IC=ICA-IBC.
В
симметричном режиме фазные и линейные
токи симметричны, при этом отношение
их модулей составляет IЛ/IФ = √3 .
При
несимметричной нагрузке соотношение
между линейными и фазными токами
определяется уравнениями первого закона
Кирхгофа. На рис. 38.4 показана векторная
диаграмма токов и напряжений для
произвольной трехфазной цепи при
соединении фаз в треугольник.

№38
Способы соединения фаз трехфазных
приемников.
![]()
Приемники
трехфазного тока могут подключаться к
генератору по двум схемам – звезды (y)
и треугольника (Δ). Как известно, на
выходе трехфазного генератора получаются
два напряжение (линейное и фазное),
отличающиеся в Uл/Uф = √3 раз. С другой
стороны каждый приёмник энергии рассчитан
на работу при определенном напряжении,
которое называется номинальным. Схема
соединения фаз приемника должна
обеспечить подключение его фаз номинальное
фазное напряжение. Таким образом, выбор
схемы соединения фаз трехфазного
приемника зависит от соотношения
номинальных напряжений приемника и
генератора (сети).
Схема
звезды применяется в том случае, если
номинальное напряжение приемника
соответствует (равно) фазному напряжению
генератора. При соединении в звезду
концы фаз приемника объединяются в одну
точку “n”, называемую нулевой или
нейтральной, а начала фаз подключаются
к линейным выводам трехфазного генератора
А, В, С линейными проводами. Если нулевая
точка приемника “n” соединена с нулевой
точкой генератора “N” нулевым проводом,
то схема получила название звезды с
нулевым проводом (рис. 38.1а). При отсутствии
нулевого провода схема носит название
звезды без нулевого провода (рис. 38.1б).
Токи,
протекающие в линейных проводах по
направлению от генератора к приемнику,
называются линейными.
Токи,
протекающие в фазах приемника по
направлению от начал к концам, называются
фазными. В схеме звезды фазы приемника
включены последовательно с линейными
проводами и по ним протекают одни и те
же токи (IA,
IB,
IC).
Поэтому для схемы звезды понятия линейные
и фазные токи тождественны: IЛ =
IФ.
Ток,
протекающий в нулевом проводе от
приемника к генератору, называется
нулевым или нейтральным (IN).

Напряжения
между началами и концами фаз приемника
называются фазными (UAn,
UBn,
UCn),
а напряжения между началами фаз –
линейными (UAB,
UBC,
UCA).
Линейные напряжения приемника и
генератора тождественно равны.
В
схеме звезды с нулевым проводом (рис.
38.1а) к каждой фазе приемника подводится
непосредственно фазное напряжение
генератора (UAN =
UAn =
UA,
UBN =
UBn =
UB,
UCN =
UCn =
UC),
каждая из фаз при этом работает независимо
друг от друга, а линейные (фазные) токи
определяются по закону Ома:

Ток
в нулевом проводе в соответствии с
первым законом Кирхгофа равен
геометрической сумме линейных (фазных)
токов:
IN=IA+IB+IC
При
симметричной нагрузке ZA=ZB=ZC ток
в нулевом проводе IN=0
и, следовательно, надобность в нeм
отпадает. Симметричные трехфазные
приемники (например, трехфазные
электродвигатели) включаются по схеме
звезды без нулевого провода.
При
несимметричной нагрузке относительная
величина тока в нулевом проводе зависит
от характера и степени не симметрии
фазных токов. Как правило, трехфазные
приёмники стремятся спроектировать по
возможности близкими к симметричным,
поэтому ток в нулевом проводе в реальных
условиях значительно меньше линейных
(фазных) токов.
схеме
звезды без нулевого провода (рис. 38.1б)
при любой нагрузке фаз должно выполняться
условие первого закона Кирхгофа:
IA+IB+IC=0
Из
уравнения следует вывод, что изменение
одного из токов влечет изменение двух
других токов, то есть отдельные фазы
работают в зависимом друг от друга
режиме. При несимметричной нагрузке
потенциал нулевой точки приемника Un
становится не равным нулю, он “смещается”
на комплексной плоскости с нулевого
положения, при этом фазные напряжения
приемника (UAn,
UBn,
UCn)
не равны соответствующим фазным
напряжениям генератора (UA,
UB,
UC),
происходит так называемый перекос
фазных напряжений приемника (рис. 38.2).

Расчет
токов и напряжений в схеме звезды без
нулевого провода выполняется в следующей
последовательности.
Определяется
напряжение (потенциал) нейтральной
точки приемника по методу двух узлов:

где
ZN –
комплексное сопротивление нулевого
провода, при его отсутствии ZN=∞.
Фазные
напряжения приемника определяются как
разности потенциалов соответствующих
точек:
UAn=UA-Un,
UBn=UB-Un ,
UCn=UC-Un.
Фазные
токи приемника определяются по закону
Ома:

Комплексные
мощности фаз приемника:

Режим
работы приемника с перекосом фазных
напряжений является ненормальным и
может привести его к выходу из строя.
По этой причине несимметричную трехфазную
нагрузку запрещается включать по схеме
звезды без нулевого провода (например,
осветительную нагрузку).
Схема
треугольника применяется в том случае,
если номинальное фазное напряжение
приемника соответствует (равно) линейному
напряжению генератора. При соединении
в треугольник конец каждой фазы
соединяется с началом последующей, а
точки соединения (вершины треугольника)
подключаются к линейным выводам
трехфазного генератора А, В, С линейными
проводами (рис.38.3).
Токи,
протекающие в фазах приемника по
направлению от их начал к концам,
называются фазными (IAB,
IBC,
ICA).
Токи, протекающие в линейных проводах
по направлению от генератора к приемнику,
называются линейными (IA,
IB,
IC).

В
схеме треугольника фазные и линейные
напряжения приемника тождественно
равны (UAB,
UBC,
UCA).
В этой схеме к каждой фазе приемника
подводится непосредственно линейное
напряжение генератора, при этом отдельные
фазы работают независимо друг от друга.
Фазные токи определяются по закону Ома:

Линейные
токи определяются из уравнений первого
закона Кирхгофа для вершин треугольника,
они равны геометрической разности
фазных токов:
IA=IAB-ICA;
IB=IBC-IAB;
IC=ICA-IBC.
В
симметричном режиме фазные и линейные
токи симметричны, при этом отношение
их модулей составляет IЛ/IФ = √3 .
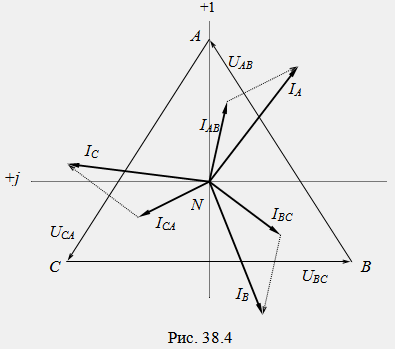
При
несимметричной нагрузке соотношение
между линейными и фазными токами
определяется уравнениями первого закона
Кирхгофа. На рис. 38.4 показана векторная
диаграмма токов и напряжений для
произвольной трехфазной цепи при
соединении фаз в треугольник.
№39
Расчет сложных трехфазных цепей.
![]()
Сложная
трехфазная цепь, например, объединенная
энергосистема, может содержать большое
число трехфазных генераторов, линий
электропередачи, приемников трехфазной
энергии. Схема такой цепи представляет
собой типичный пример сложной цепи
переменного тока. Установившейся режим
в такой схеме может быть описан системой
алгебраических уравнений с ком-плексными
коэффициентами, составленных по одному
из методов расчета сложных цепей (метод
законов Кирхгофа, метод контурных токов,
метод узловых потенциалов). Наиболее
рациональным методом расчета таких
трехфазных цепей является метод уз¬ловых
потенциалов, при этом составление
уравнений и их решение производится в
матричной форме.
В
более простых случаях возможно применение
любых методов расчета, позволяющих
получить экономичное решение задачи.
На рис. 39.1 представлена схема параллельного
подключения нескольких трехфазных
приемников с различными схемами
соединения фаз к одному генератору. В
представленной схеме расчет фазных и
линейных токов каждого из приемников
может выполняться индивидуально и
независимо друг от друга, а линейные
токи источника определяются как
геометрические суммы токов всех
приемников, например, IA=IA1+IA2+IA3.

Как
известно, объединенная трехфазная
энергосистема работает в режиме, близком
к симметричному. В симметричном режиме
токи и напряжения смежных фаз отличаются
только углом сдвига на ±120º. Расчет токов
и напряжений в установившемся симметричном
режиме производится только для одной
из фаз, например для фазы А, при этом
трехфазные цепи представляются
однофазными эквивалентными схемами.
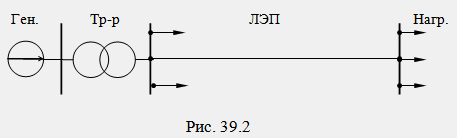
На рис. 39.2 представлена символьная схема
передачи энергии от трехфазного
генератора к удаленным приемникам, а
на рис. 39.3 – расчетная однофазная схема
для той же цепи. На расчетной схеме рис.
39.3 каждому звену электропередачи
соответствует его стандартная схема
замещения.

В
результате расчетов определяются токи
и напряжения во всех элементах схемы
для фазы А, например IA=Iejα.
Аналогичные токи и напряжения в фазе В
определяется умножением соответствующих
величин фазы А на поворотный множитель
e-j120°,
а для фазы С – на множитель ej120°.
№40
Мощность трехфазной цепи и способы ее
измерения.
![]()
Активная
и реактивная мощности трехфазной цепи,
как для любой сложной цепи, равны суммам
соответствующих мощностей отдельных
фаз:
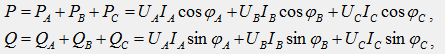
где
IA,
UA,
IB,
UB,
IC,
UC –
фазные значения токов и напряжений.
В
симметричном режиме мощности отдельных
фаз равны, а мощность всей цепи может
быть получена путем умножения фазных
мощностей на число фаз:
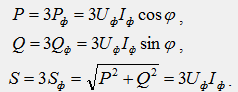
В
полученных выражениях заменим фазные
величины на линейные. Для схемы звезды
верны соотношения Uф/Uл/√3, Iф=Iл,
тогда получим:
![]()
Для
схемы треугольника верны соотношения:
Uф=Uл ; Iф=Iл / √3 , тогда получим:
![]()
Следовательно,
независимо от схемы соединения (звезда
или треугольник) для сим¬метричной
трехфазной цепи формулы для мощностей
имеют одинаковый вид:

В
приведенных формулах для мощностей
трехфазной цепи подразумеваются линейные
значения величин U и I, но индексы при их
обозначениях не ставятся.
Активная
мощность в электрической цепи измеряется
прибором, называемым ваттметром,
показания которого определяется по
формуле:
![]()
где
Uw,
Iw –
векторы напряжения и тока, подведенные
к обмоткам прибора.
Для
измерения активной мощности всей
трехфазной цепи в зависимости от схемы
соединения фаз нагрузки и ее характера
применяются различные схемы включения
измерительных приборов.
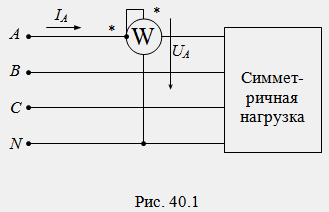
Для
измерения активной мощности симметричной
трехфазной цепи при-меняется схема с
одним ваттметром, который включается
в одну из фаз и измеряет активную мощность
только этой фазы (рис. 40.1). Активная
мощность всей цепи получается путем
умножения показания ваттметра на число
фаз: P=3W=3UфIфcos(φ).
Схема с одним ваттметром может быть
использована только для ориентированной
оценки мощности и неприменима для точных
и коммерческих измерений.
Для
измерения активной мощности в
четырехпроводных трехфазных цепях (при
на¬личии нулевого провода) применяется
схема с тремя приборами (рис. 40.2), в
которой произво¬дится измерение активной
мощности каждой фазы в отдельности, а
мощность всей цепи оп¬ределяется как
сумма показаний трех ваттметров:

Для
измерения активной мощности в трехпроводных
трехфазных цепях (при отсутствии нулевого
провода) применяется схема с двумя
приборами (рис. 40.3).

При
отсутствии нулевого провода линейные
(фазные) ток связаны между собой
урав¬нением 1-го закона Кирхгофа:
IA+IB+IC=0.
Сумма показаний двух ваттметров равна:


Таким
образом, сумма показаний двух ваттметров
равна активной трехфазной мощности,
при этом показание каждого прибора в
отдельности зависит не только величины
нагрузки но и от ее характера.
На
рис. 40.4 показана векторная диаграмма
токов и напряжений для сим¬метричной
нагрузки. Из диаграммы следует, что
показания отдельных ваттметров могут
быть определены по формулам:

Анализ
полученных выражений позволяет сделать
следующие выводы. При активной нагрузке
(φ = 0), показания ваттметров равны (W1 =
W2).
При
активно-индуктивной нагрузке(0 ≤ φ ≤
90°) показание первого ватт-метра меньше,
чем второго (W1 < W2), а при φ>60° показание
первого ваттметра становится отрицательным
(W1<0).
При
активно-емкостной нагрузке(0 ≥ φ≥ -90°)
показание второго ватт-метра меньше,
чем первого (W1 больше W2), а при φ(меньше)-60
° показание второго ватт-метра становится
отрицательным.
№41
Вращающееся магнитное поле.
![]()
Одним
из важнейших достоинств трехфазной
системы является возможность получения
с ее помощью кругового вращающегося
магнитного поля, которое лежит в основе
работы трехфазных машин (генераторов
и двигателей).
Для
получения кругового вращающегося
магнитного поля необходимо и достаточно
выполнить два условия. Условие первое:
необходимо 3p одинаковых катушки (p =1, 2,
3,….) расположить в пространстве так,
чтобы их оси были расположены в одной
плоскости и сдвинуты взаимно на равные
углы ∆α=360°/3p. Условие второе: необходимо
пропустить по катушкам равные по
амплитуде и сдвинутые во времени на
∆t=T/3 или ∆ωt = 360°/3=120° переменные токи
(симметричный трехфазный ток). При
соблюдении указанных условий в
пространстве вокруг катушек будет
создано круговое вращающееся маг-нитное
поле с постоянной амплитудой индукции
Вmax вдоль
его оси и с постоянной угловой скоростью
вращения ωп.
На
рис. 41.1 показано пространственное
расположение трех (p = 1) одинаковых
катушек под равными углами в 120° согласно
первому условию.
По
катушкам, по направлению от их начал
(A, B, C) к концам (X, Y, Z) протекает симметричный
трехфазный ток:

Магнитное
поле, создаваемое каждой катушкой в
отдельности, пропорционально току
катушки (B = k*i), следовательно магнитные
поля отдельных катушек в центре координат
образуют симметричную трехфазную
систему В(t):


Положительные
направления магнитных полей каждой
катушки (векторов BA,
BB,
BC)
в пространстве определяются по правилу
правоходового винта согласно принятым
положительным направлениям токов
катушек (рис. 41.1).
Результирующий
вектор индукции магнитного поля B для
любого момента времени может быть найден
путем пространственного сложения
векторов BA,
BB,
BC отдельных
катушек. Определим значение результирующего
вектора индукции магнитного поля B для
нескольких моментов времени ωt = 0°; 30°;
60°. Пространственное сложение векторов
вы¬полним графически (рис. 41.2а, б, в ).
Результаты расчета сведены в отдельную
таблицу:

Анализ
таблицы показывает, что результирующий
вектор индукции магнитного поля B(t,x,y)
имеет постоянную амплитуду (Вmax=3/2Bm)
и равномерно вращается в пространстве
в положительную сторону по направлению
катушки А к катушке В с угловой скоростью
ωп , равной угловой частоте тока ω. В
общем случае угловая скорость вращения
магнитного поля зависит еще и от числа
катушек:

В
технике для характеристики вращения
магнитного поля пользуются понятием
частоты вращения: n=60f/p [об/мин]
С
изменением числа p пространственная
картина магнитного поля изменяется:
при p=1 магнитное поле имеет два полюса
(или одну пару полюсов), при p=2 – четыре
полюса (или 2 пары полюсов) и т.д. (рис.
41.3). По этой причине число p = 1, 2, 3,…
называют числом пар полюсов магнитного
поля.
Частоту
вращения магнитного поля можно изменять
плавно изменением частоты питающего
тока f, и ступенчато – изменением числа
пар полюсов p. В промышленных условиях
оба способа регулирования частоты
вращения поля являются технически и
экономически малоэффективными. При
постоянной частоте промышленного тока
f=50 Гц шкала синхронных частот вращения
магнитного поля в функции числа пар
полюсов выглядит следующим образом:
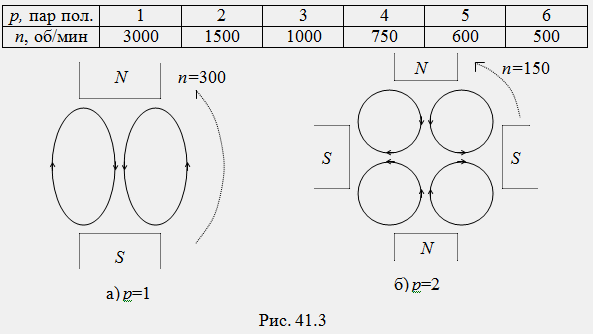
Для
изменения направления вращения магнитного
поля достаточно изменить порядок
следования фаз питающего тока или,
попросту, поменять местами две любые
фазы источника между собой.
№42
Теоретические основы метода симметричных
составляющих.
![]()
Метод
симметричных составляющих применяется
для расчета трехфазных цепей в
несимметричных режимах. Несимметричные
режимы в энергосистеме возникают при
различных видах коротких замыканий.
Расчет токов коротких замыканий –
важная инженерная задача в электроэнергетике,
которая решается методом симметричных
составляющих.
Математически
любая несимметричная трехфазная система
векторных величин (напряжений, токов и
др.) может быть представлена в виде суммы
(заменена суммой) из трех симметричных
трехфазных систем, а именно: а) системы
прямой последовательности с прямым
порядком следования фаз A→B→C→A;
б) системы обратной последовательности
с обратным порядком следования фаз
A→C→B→A;
в) системы нулевой последовательности,
ко¬торая состоит из трех равных векторов,
совпадающих по фазе. Отдельные
симмет-ричные системы векторов, на
которые раскладывается несимметричная
сис-тема, называются сим¬метричными
составляющими. Вектора симметричных
составляющих индексируются цифрами: 1
– для прямой последовательности, 2 – для
обратной последовательности и 0 – для
нулевой последовательности.
На
рис. 42.1 представлены симметричные
составляющие некоторой несимметричной
трехфазной системы напряжений UA,UB,UC.
В
методе симметричных составляющих для
упрощения формы записи уравнений
пользуются коэффициентом a=ej120° (поворотный
множитель), умножением на который
поворачивают вектор на угол в 120° без
изменения его модуля. Свойства поворотного
множителя: a2=ej240°=e-j120°,
a3=1,
a4=a,
1+a+a2=0.


Вектора
исходной несимметричной системы
определяются по принципу наложения как
геометрические суммы соответствующих
векторов симметричных составляющих:

Геометрическое
сложение векторов симметричных
составляющих согласно этим уравнениям
показано на рис. 42.2.
Используя
поворотный множитель “a” и “a2”,
выразим все слагаемые правой части
уравнений через симметричные составляющие
фазы А:

Умножим
все члены уравнения (2) на “a”, а все
члены уравнения (3) на “a2”,
сложим все три уравнения почленно и
получим:

Из
полученного уравнения следует формула
для выделения симметричной составляющей
прямой последовательности из несимметричной
системы векторов:

Умножим
все члены уравнения (2) на “a2”,
а все члены уравнения (3) на “a”, сложим
все три уравнения почленно и получим:

Из
полученного уравнения следует формула
для выделения симметричной составляющей
обратной последовательности из
несимметричной системы векторов:

Сложим
все три уравнения (1), (2) и (3) почленно и
получим:
![]()
Из
полученного уравнения следует формула
для выделения симметричной составляющей
нулевой последовательности из
несимметричной системы вектор:
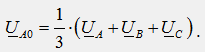
Полученные
формулы применяются на практике для
разложения несимметричных трехфазных
систем векторов на симметричные
составляющие.
№43
Расчет режима симметричной трехфазной
нагрузки при несимметричном напряжении.
![]()
Пусть
к симметричному трехфазному приемнику,
например электродвигателю, приложена
несимметричная система напряжений UA,
UB,
UC.
Для получения общих закономерностей
введем в схему нулевой провод с
сопротивлением ZN.
Схема цепи примет вид (рис. 43.1):
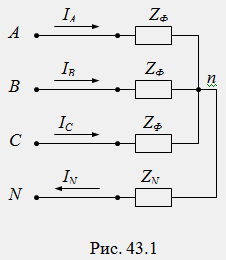
Разложим
несимметричную систему напряжений UA,
UB,
UC на
симметричные составляющие прямой,
обратной и нулевой последовательностей:

Применим
к расчету схемы метод наложения и
выполним расчет токов отдельно для
каждой симметричной составляющей
напряжения. Так как для каждой из
симметричных составляющих трехфазная
схема генератор-приемник полностью
симметрична, то расчет ре¬жима можно
выполнять только для одной фазы А,
соответственно трехфазную схему следует
заменить тремя однофаз¬ными отдельно
для каждой составляющей (рис. 43.2а, б, в).
В симметричном режиме для прямой и
обратной последовательностей ток в
нулевом проводе равен нулю и, следовательно,
напряжение UnN=0.
Это означает, что сопротивление в
нейтраль¬ном проводе ZN не
оказывает влияния на фазные токи и не
должно включаться в схемы для этих
последовательностей (рис. 43.2 а, б). Токи
нулевой последовательности во всех
фазах сов¬падают и могут замкнуться
только через нулевой провод: IN =
IA0 +
IB0 +
IC0 =
3IA0.
По 2-му закону Кирх¬гофа для нулевой
последовательности (рис. 43.1) получим:
UA0 =
IA0Z0 +
INZN =
IA0(Z0 +
3ZN)
Согласно
полученному уравнению схема замещения
для нулевой последовательности получит
вид (рис. 43.2 в), в которой последовательно
с сопротивлением фазы Z0 включается
утроенное сопротивление нейтрали 3ZN.
В
схемах для отдельных симметричных
составляющих (рис. 43.2 а, б, в) обозначены
Z1,
Z2,
Z0 –
комплексные сопротивления фазы приемника
для токов соответственно прямой, обратной
и нулевой последовательностей. Для
приемников с вращающимся магнитным
полем эти сопротивления существенно
отличаются.

По
закону Ома в каждой из схем рис. 43.2а, б,
в производится расчет токов прямой,
обратной и нулевой последовательностей:

Действительные
токи в исходной схеме (рис. 43.1) определяются
по методу наложения, как векторные суммы
токов прямой, обратной и нулевой
последовательностей:

Комплексные
сопротивления фаз статичных трехфазных
приемников (осветительная нагрузка,
нагревательные приборы и др.) не зависят
от вида последовательности, для таких
приемников Z1=Z2=Z0.
Расчет токов таких приемников может
выполняться обычными методами. Для
трехфазных приемников, в которых
существует вращающееся магнитное поле
(электродвигатели, генераторы),
сопротивления фаз для токов разных
последовательностей существенно
отличаются (Z1>Z0>Z2).
Расчет токов таких приемников при
несимметричном напряжении должен
производиться исключительно методом
симметричных составляющих.
Векторные диаграммы можно считать универсальным инструментом определения параметров не только наиболее распространенных трехфазных, но иных многофазных #электроцепей. В том числе шести и девятифазных.
Разберем пару примеров графическим способом определения #тока в нейтрали при соединении “#звездой”. Их решение будет аналогичным.
При строении диаграмм необходимо учитывать вид нагрузки каждой #фазы:
- Если в той или иной фазе присутствует только емкостная нагрузка Хс, то вектор тока будет опережать вектор напряжения на 90 градусов.
- Наличие только индуктивности Х l будет влиять противоположно – вектор напряжения в его движении против часовой стрелки будет опережать вектор тока на те же 90 градусов.
- Присутствие только активной резистивной нагрузки R обеспечивает полное согласованное движение вектора тока и напряжения – угол сдвига фаз между ними равен 0.
- Если в той или иной фазе присутствует одновременно емкость, индуктивность и активное сопротивление, то угол сдвига фи можно найти из результата расчета cos фи. И он будет за исключением случая резонанса меньше 90 градусов.
360 градусов полного оборота вращающегося против часовой стрелки вектора при построении векторной диаграммы трехфазной цепи предполагают распределение векторов напряжения 3 фаз А, В и С через 120 градусов.
Соответственно, в шестифазной цепи это будет 350 / 6 = 60 градусов и в девятифазной – 360 / 9 = 40 градусов.
Пример построения векторной диаграммы трехфазной цепи
Из диаграммы можно сделать несколько выводов:
- В фазе А присутствует активная и индуктивная нагрузка. Это следует из того, что угол сдвига по фазе не равен 90 град., но фи = 30 градусов и при вращении против часовой стрелки двух векторов Ua и Ia вектор напряжения фазы А будет идти впереди вектора тока.
- В фазе В ток (Ib) и напряжения (Ub) совпадают по фазе. угол фи между векторами равен 0, а cos фи равен 1.
- В фазе С наличествует активная и емкостная нагрузка. Мы видим, что угол фи между векторами Uc и Ic меньше 90 градусов и при вращении против часовой стрелки двух векторов Ua и Ia вектор тока фазы С будет идти впереди вектора напряжения.
Диаграмма недостроена. Нужно еще сложить вектора токов и получить значение тока в нулевом проводе.
Пример построения векторной диаграммы шестифазной цепи
Для схемы #6 фазной цепи с соединением “звезда” ток в нулевом проводе будет найден аналогично:
Содержание:
Цепи переменного тока:
Основное применение в электротехнике и радиотехнике имеют переменные напряжения и токи, являющиеся периодическими функциями времени. Мгновенные значения периодических напряжений u и токов i повторяются через промежуток времени Т, называемый периодом:
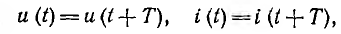
где t — время; число периодов в единицу времени 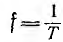
Электротехника сильных токов использует в основном низкие частоты. Промышленной частотой в СССР и Европе является 50 гц, в Америке 60 гц, в некоторых областях техники применяют частоты в сотни герц и выше. Техника проводной и радиосвязи использует широкий диапазон частот от долей герц до 1012 гц. Постоянные э.д. с. и токи можно рассматривать как частный случай переменных, частота которых равна нулю (f — 0).
Простейшими и широко применяемыми в электротехнических и радиотехнических устройствах являются периодические напряжения и токи, изменяющиеся по закону синуса. Для случая синусоидального закона изменения функций разработаны простые методы расчета цепей, подобные методам расчета цепей постоянного тока. Если закон изменения периодического напряжения u (t) или i (t) отличен от синусоиды, эти функции могут быть разложены в ряд Фурье, т. е. представлены в виде суммы синусоид, что позволит при расчетах линейных цепей применить метод наложения и свести расчеты к синусоидальным функциям.
Что такое цепь постоянного тока
Цепью постоянного тока называется такая цепь, в которой ЭДС, токи и напряжения остаются постоянными по величине и не зависят от времени.
Цепи делятся на два больших класса:
- линейные;
- нелинейные.
Электрические цепи, содержащие только элементы с линейными вольтамперными характеристиками, называются линейными цепями.
Генератор синусоидального напряжения
Для получения синусоидальных переменных токов в линейных цепях э. д. с. также должны изменяться по синусоиде. Простейшим генератором синусоидальной э. д. с. может служить прямоугольная катушка, вращающаяся с постоянной угловой скоростью в однородном магнитном поле вокруг оси, перпендикулярной к направлению линий магнитной индукции (рис. 6.1). При этом пронизывающий катушку магнитный поток изменяется, и в ней по закону электромагнитной индукции индуктируется э. д. с. Цепь нагрузки подключается к генератору с помощью щеток, наложенных на два кольца, соединенных с катушкой.
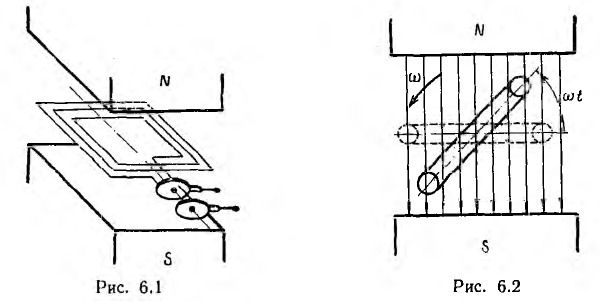
Пусть в начальный момент времени t=О плоскость катушки будет перпендикулярна магнитным линиям (пунктир на рис. 6.2). Тогда магнитный поток, пронизывающий катушку, будет иметь максимальное (амплитудное) значение Фm. Если угловая скорость вращения катушки с числом витков w равна ω, то в момент времени t катушка окажется повернутой на угол ωt, и мгновенные значения ее потока и потокосцепления будут равны
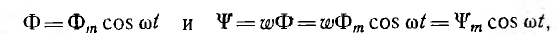
где 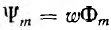 — максимальное значение потокосцепления.
— максимальное значение потокосцепления.
Тогда мгновенное значение э. д. с. катушки
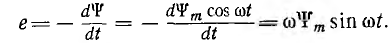
Величина 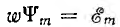 представляет собой максимальное значение
представляет собой максимальное значение
э. д. с., которое она получает, когда sinωt становится равным единице.
Следовательно, 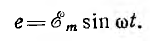
Временные диаграммы
Временная диаграмма магнитного потока и электродвижущей силы катушки показана на рис. 6.3, а. Максимальная э. д. с. индуктируется в моменты, когда поток, пронизывающий катушку, равен нулю, так как тогда скорость изменения потока достигает наибольшего значения. Э д. с. равна нулю в моменты, когда поток получает максимальное значение, так как при этом поток не меняет своей величины.
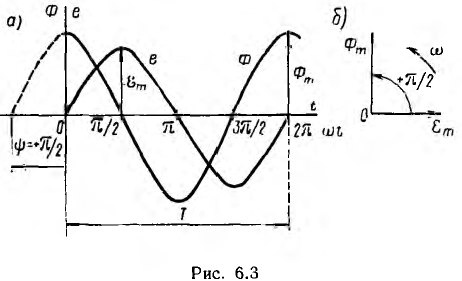
Как видно из рис. 6.3, а,
откуда 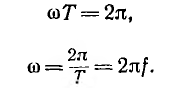
Величина ω, пропорциональная частоте f и равная в данном случае угловой скорости вращения катушки, называется угловой частотой.
Общее выражение для синусоидальной функции времени имеет вид:
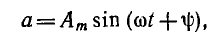
где а — мгновенное значение функции; Аm — ее максимальное значение (амплитуда); ω— угловая частота; угол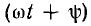 — фаза, а угол ψ — начальная фаза. Начальная фаза определяет значение функции для начального момента времени:
— фаза, а угол ψ — начальная фаза. Начальная фаза определяет значение функции для начального момента времени:
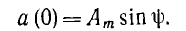
Так, для рассмотренного источника синусоидальной э. д. с.
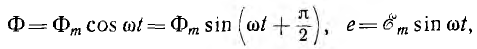
начальная фаза потока равна + π/2 , э. д. с. — нулю, т. е. магнитный поток и э. д. с. сдвинуты по фазе на π/2.
На временной диаграмме, как видно из рис. 6.3, а, положительная начальная фаза откладывается от начала координат влево, т. е. в сторону отрицательных значений ωt, а отрицательную начальную фазу следует откладывать в сторону положительных значений ωt.
Векторные диаграммы
Расчеты в цепях с синусоидальными напряжениями и токами весьма упрощаются, если вместо синусоид оперировать с их изображениями — вращающимися векторами.
Пусть NOM является прямоугольной системой осей координат и пусть положительные углы откладываются против направления вращения стрелки часов (рис. 6.4). Если нужно найти, например, мгновенные значения синусоиды э. д. с. 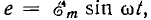 то для этого можно взять вектор ОА, длина которого равна в выбранном масштабе максимальному значению э. д. с.
то для этого можно взять вектор ОА, длина которого равна в выбранном масштабе максимальному значению э. д. с. 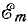 считать начальным положением вектора ОА0 такое, при котором он образует с осью ON угол, равный начальной фазе, т. е. в данном случае совпадает с 0N: вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. Тогда угол, который вектор образует с осью ON в момент времени е, будет равен ωt и мгновенное значение э. д. с. е
считать начальным положением вектора ОА0 такое, при котором он образует с осью ON угол, равный начальной фазе, т. е. в данном случае совпадает с 0N: вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. Тогда угол, который вектор образует с осью ON в момент времени е, будет равен ωt и мгновенное значение э. д. с. е
для этого момента времени будет равно проекции Оа вектора ОА на ось ОМ:
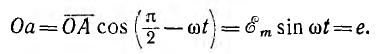
Проекция вектора ОА на ось ОМ для начального момента времени 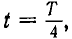
будет равна нулю, для момента времени, когда вектор повернется на угол π/2, проекция будет равна 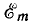 полный цикл изменений э. д. с. получится за один полный оборот вектора ОА.
полный цикл изменений э. д. с. получится за один полный оборот вектора ОА.
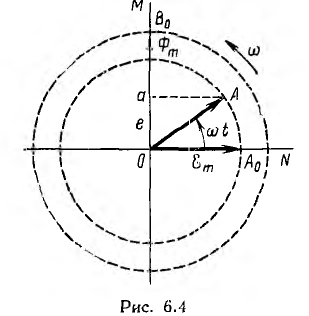
Таким же образом можно находить мгновенные значения потока 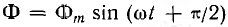 , с той разницей, что для начального момента
, с той разницей, что для начального момента
времени вектор ОВ0, изображающий в выбранном масштабе максимальное значение потока Фm, необходимо направить по оси ОМ, так как он должен образовать с осью ON угол + π/2, равный начальной фазе потока.
Таким образом, можно условиться изображать синусоидальную функцию вектором, длина которого определяется максимальным ее значением, а направление — ее начальной фазой, при этом положительная начальная фаза откладывается от горизонтальной оси в сторону вращения векторов. В результате получается векторная диаграмма, показанная для рассмотренного примера потока и э. д. с. на рис. 6.3, б.
Векторы, изображающие синусоидальные функции времени, имеют совсем другой смысл, чем векторы, изображающие, например, силы в механике. Вектор силы дает ее величину и направление в пространстве, вектор, изображающий синусоиду, является вращающимся вектором, дающим своей проекцией на неподвижную ось мгновенное значение синусоиды. Такой вектор чертится в начальном своем положении, которое дает начальную фазу синусоиды, но, конечно, не направление изображаемой величины впространстве. Подобным вектором можно изображать любую синусоидально изменяющуюся величину, в том числе скалярную — э. д. с., тон, поток и т. п.
Векторные диаграммы особенно удобны при сложении или вычитании синусоид одинаковой частоты. Как известно, результатом будет также синусоида той же частоты. При сложении нескольких синусоид нужно складывать их мгновенные значения, т. е. проекции векторов, изображающих эти синусоиды, но так как сумма проекций векторов на какую-либо ось равна проекции геометрической суммы этих векторов на ту же ось, то эга геометрическая сумма и будет вектором, изображающим результирующую синусоиду. Длина вектора даст амплитуду результирующей синусоиды, угол с горизонтальной осью — ее начальную фазу.
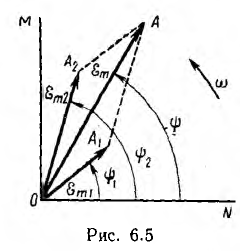
Так, например, для двух синусоид (рис. 6.5)
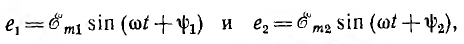
изображаемых векторами 0А1 и 0А2, вектор ОА, изображающий суммарную синусоиду
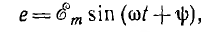
будет геометрической суммой векторов OA1 и ОА2. Он имеет величину 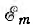 и составляет с осью ON угол ψ. Так как синусоиды е1 и е2 имеют одну и ту же частоту, изображающие их векторы вращаются с одинаковой угловой скоростью, углы между ними не изменяются, и результирующий вектор сохраняет постоянную длину, вращаясь с той же угловой скоростью.
и составляет с осью ON угол ψ. Так как синусоиды е1 и е2 имеют одну и ту же частоту, изображающие их векторы вращаются с одинаковой угловой скоростью, углы между ними не изменяются, и результирующий вектор сохраняет постоянную длину, вращаясь с той же угловой скоростью.
Аналогично, путем геометрического вычитания, может быть найден вектор, изображающий результирующую синусоиду разности двух синусоид. Следовательно, алгебраическому суммированию синусоид, т.е. суммированию их мгновенных значений, соответствуют геометрические действия над изображающими их векторами.
Особенности цепей переменного тока
Для цепей переменного тока справедливы законы Ома, Кирхгофа и Джоуля — Ленца применительно к мгновенным значениям напряжений, токов и мощностей для одного и того же момента времени. Однако в отличие от пассивной цепи постоянного тока, в которой ток определяется приложенным к ней напряжением и ее сопротивлением, в пассивной цепи переменного тока возникают внутренние переменные э. д. с. самоиндукции и э. д. с. емкости, которые должны, быть учтены, кроме приложенного напряжения, при составлении уравнений по основным законам.
Так же, как и в цепях постоянного тока, при составлении уравнений по этим законам для цепей переменного тока необходимо задаться условным положительным направлением напряжений и токов, хотя действительные их направления периодически меняются. По аналогии с цепями постоянного тока удобно принять, что положительные направления напряжения и тока всей цепи и каждого из ее элементов — резистора, катушки индуктивности и конденсатора — совпадают. Тогда мгновенная мощность р = ui всей цепи и каждого из ее элементов будет положительной, когда действительные направления их напряжения и тока совпадают, т. е. когда цепь или ее элементы являются потребителями энергии, что принято характеризовать положительной мощностью.
Выбранные положительные направления для мгновенных значений напряжений и токов сохраняются при переходе к векторам— сумме (разности) мгновенных значений соответствует геометрическая сумма (разность) изображающих их векторов.
Физические и энергетические процессы на участках цепи с сопротивлением, с индуктивностью, с емкостью весьма различны, поэтому предварительно они рассматриваются раздельно до изучения цепей с их сочетанием.
Цепь с сопротивлением
Постоянный ток распределяется по всему сечению проводника равномерно, т. е. во всех точках его сечения плотность тока одинакова.
Плотность переменного тока возрастает от оси проводника к его поверхности. Это явление называется поверхностным эффектом, рассматриваемым в ч. IV. Приближенно можно считать, что переменный ток в проводнике использует только часть s’ его сечения s. Следовательно, сопротивление R постоянному току, называемое обычно омическим, будет меньше сопротивления r переменному току:
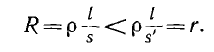
Сопротивление г получило название активного сопротивления проводника.
Поверхностный эффект проявляется тем сильней, чем больше частота, сечение, удельная проводимость и магнитная проницаемость проводника. При промышленной частоте (50 гц) и тонких медных или алюминиевых проводах поверхностным эффектом можно пренебречь и считать активное сопротивление равным омическому.
Пусть к активному сопротивлению (рис. 6.6, а) приложено синусоидальное напряжение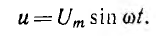
По закону Ома ток
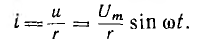
Ток получает максимальное значение 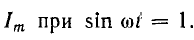 . Тогда
. Тогда
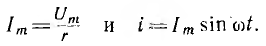
Следовательно, в цепи с сопротивлением r напряжение и ток совпадают по фазе (рис. 6.6, 6.) На векторной диаграмме вектор напряжении совпадает по направлению с вектором тока (рис. 6.6, в). Максимальные значения напряжения и тока также подчинены закону Ома.
Мгновенная мощность р равна произведению мгновенных значений напряжения и тока:
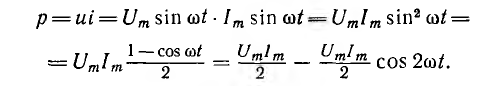
Как видно из этого выражения, мгновенная мощность имеет постоянную составляющую 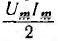 и переменную составляющую, изменяющуюся по косинусоиде двойной частоты
и переменную составляющую, изменяющуюся по косинусоиде двойной частоты 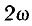 с амплитудой
с амплитудой 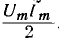
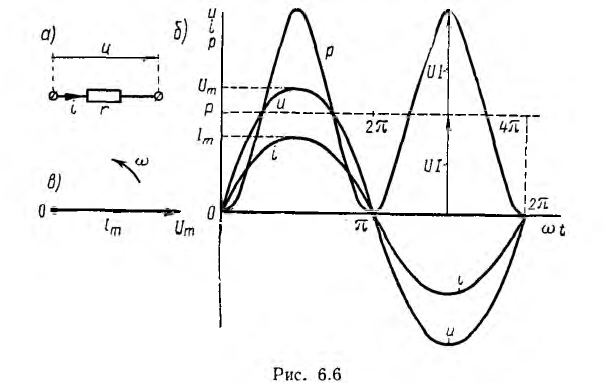
Кривая мощности также изображена на рис. 6.6, б. Мощность равна нулю при u = 0 и i = 0, всегда положительна и получает максимальное значение в те моменты, когда напряжение и ток также максимальны.
Среднее значение мощности за период — средняя мощность
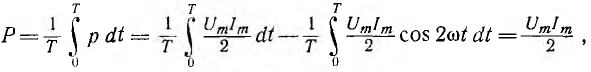
т. e. равна постоянной составляющей мгновенной мощности.
Пользуясь зависимостью между максимальными значениями напряжения и тока, выражение для средней мощности можно переписать следующим образом:
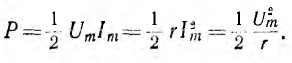
Обычно величина переменного тока характеризуется действующим значением. Так называется значение постоянного тока I, которое дает ту же мощность Р в том же сопротивлении r:
следовательно, 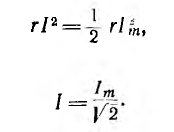
Аналогично, действующее значение напряжения
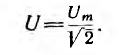
Следовательно, мгновенная мощность
средняя мощность 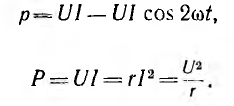
Энергия, поглощаемая активным сопротивлением,
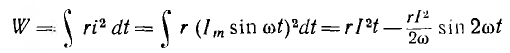
непрерывно растет. Эта энергия поставляется источником, питающим цепь.
Цепь с индуктивностью и цепь с емкостью
Цепь с индуктивностью и цепь с емкостью являются накопителями энергии соответственно электрического и магнитного поля. Чтобы подчеркнуть эту аналогию, цепь с индуктивностью и цепь с емкостью
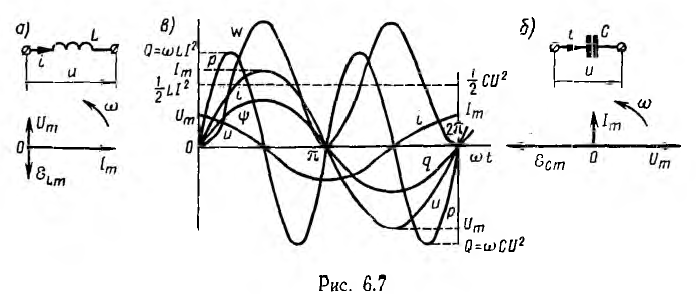
рассматриваются одновременно. Величины, определяющие процессы в них, — ток в цепи с индуктивностью и напряжение на цепи с емкостью — задаются с одинаковой фазой.
Пусть ток цепи с индуктивностью L (рис. 6.7, а)
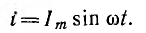
Тогда потокосцепление
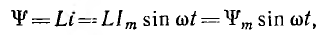
т. e. совпадает по фазе с током.
Пусть напряжение цепи с емкостью С (рис. 6.7, б)
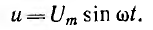
Тогда заряд
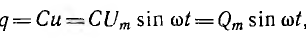
т. e. совпадает по фазе с напряжением.
Временная диаграмма этих и далее вычисляемых величин изображена на рис. 6.7, в, причем обозначения кривых показаны соответственно слева и справа.
Энергия, запасаемая в электрическом поле,
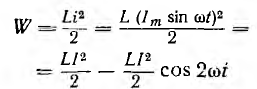
пульсирует с двойной частотой 2ω около среднего значения 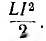 Увеличиваясь с ростом тока за счет энергии источника, энергия поля при уменьшении тока возвращается источнику.
Увеличиваясь с ростом тока за счет энергии источника, энергия поля при уменьшении тока возвращается источнику.
Энергия, запасаемая в магнитном поле,
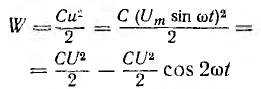
пульсирует с двойной частотой 2ω около среднего значенияя 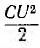 . Увеличиваясь с ростом напряжения за счет энергии источника, энергия поля при уменьшении напряжения возвращается источнику.
. Увеличиваясь с ростом напряжения за счет энергии источника, энергия поля при уменьшении напряжения возвращается источнику.
Мгновенная мощность, равная производной энергии по времени,

также изменяется с двойной частотой, будучи положительной, когда энергия поступает в приемник, и отрицательной, когда приемник возвращает энергию источнику.
Средняя мощность
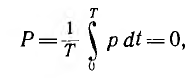
т. е. процесс колебаний энергии между источником и приемником не сопровождается потерями. Максимальное значение мощности
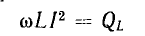 называется индуктивнои мощностью.
называется индуктивнои мощностью.
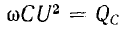 называется емкостной мощностью.
называется емкостной мощностью.
В системе СИ эти мощности измеряются в реактивных вольтамперах (вар).
Мгновенное значение напряжения
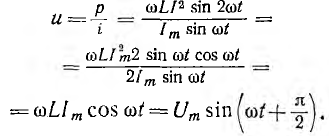
Векторная диаграмма цепи с L показана на рис. 6.7, а. Следовательно, в цепи с L ток отстает от напряжения пофазе на угол 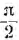 . Так как направление отсчета этого угла от вектора тока к вектору напряжения совпадает с направлением вращения векторов, этот угол считается положительным, т. е.
. Так как направление отсчета этого угла от вектора тока к вектору напряжения совпадает с направлением вращения векторов, этот угол считается положительным, т. е. 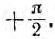
Максимальное значение напряжения
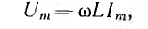 отсюда частные
отсюда частные 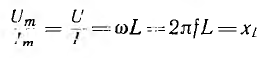
Мгновенное значение тока
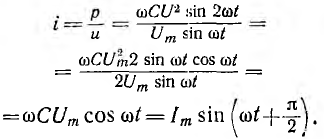
Векторная диаграмма цепи с С показана на рис. 6.7, б. Следовательно, в цепи с С ток опережает напряжение по фазе на угол 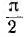 . Так как направление отсчета этого угла от вектора тока к вектору напряжения противоположно направлению вращения векторов, этот угол считается отрицательным, т. е. —
. Так как направление отсчета этого угла от вектора тока к вектору напряжения противоположно направлению вращения векторов, этот угол считается отрицательным, т. е. —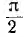 .
.
Максимальное значение тока
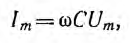 отсюда частные
отсюда частные 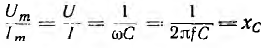
играют роль сопротивления применительно к максимальным и действующим значениям напряжения и тока. Они называются индуктивным сопротивлением емкостным сопротивлением и в системе единиц СИ измеряются в омах.
Емкостное сопротивление обратно пропорционально емкости и частоте; при постоянном напряжении оно равно бесконечности.
В цепи с емкостью величина
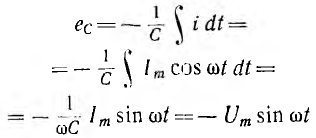
может быть названа э. д. с. емкости. Она равна и противоположна по фазе напряжению цепи.
Индуктивное сопротивление прямо пропорционально индуктивности и частоте; при постоянном токе оно равно нулю.
В цепи с индуктивностью возникает э. д. с. самоиндукции
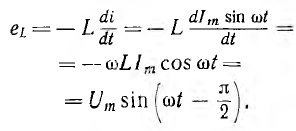
Она равна и противоположна по фазе напряжению цепи.
Отсюда видно, что применять индуктивное или емкостное сопротивления в соотношениях между мгновенными напряжениями и токами нельзя, так как

Соотношения u = —е, полученные в предположении их одинакового положительного направления, аналогичны соотношениям для напряжения U и э. д. с.  источника энергии без внутреннего сопротивления при выборе для них одинакового направления
источника энергии без внутреннего сопротивления при выборе для них одинакового направления 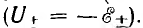
Итак, соотношения в цепи с индуктивностью и в цепи с емкостью аналогичны. От зависимостей в одной цепи к зависимостям в другой можно перейти, заменяя соответствующие величины по табл. 6.1.
Таблица 6.1
| Цепь с индуктивностью | L | ψ | u | i | ω | t | W | p |
| Цепь с емкостью | C | q | i | u | ω | t | W | p |
Измерения в цепях переменного тока
Для измерения переменного тока и напряжения могут быть применены амперметры и вольтметры электромагнитной и электродинамической систем, рассмотренные. При включении такого aмперметра в цепь переменного тока его мгновенный момент вращения mвр будет пропорционален квадрату мгновенного значения тока i, подвижная же часть прибора, очевидно, даст отклонение, пропорциональное среднему значению этого момента:
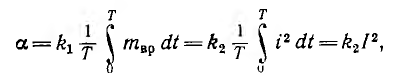
т. е. прибор измерит действующее значение тока. Аналогично, вольтметры этих двух систем измеряют действующее значение напряжения.
Для измерения мгновенных значений переменных токов и напряжений применяется осциллограф, основным элементом которого является вибратор — прибор магнитоэлектрической системы, подвижной частью которой является легкая петелька; ее момент вращения и угол отклонения пропорциональны измеряемой величине. Вместо стрелки на подвижной части укреплено зеркальце, отражающее луч света на движущуюся фотопленку, на которой записывается временная диаграмма тока или напряжения.
Для измерения средней мощности в цепях переменного тока применим ваттметр электродинамической системы. Как следует из , его мгновенный момент вращения mвр будет пропорционален мгновенной мощности р = ui. Тогда отклонение подвижней части пропорционально ее среднему значению:
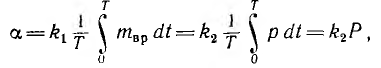
т. е. средней мощности.
Для получения положительного отклонения ваттметр следует включать по схеме рис. 2.9. В цепях только с индуктивностью и с емкостью ваттметр, очевидно, должен дать нулевое показание.
Анализ и расчет простых цепей переменного тока
Основной особенностью цепей переменного тока (по сравнению с цепями постоянного тока) является наличие в них реактивных элементов – емкостей и индуктивностей . Реактивные элементы, не рассеивая мощность электромагнитных колебаний, изменяют разность фаз между колебаниями электрического тока и напряжения на участке цепи. Вследствие этого амплитудные значения напряжения и силы тока достигаются не одновременно. При расчете электрической цепи переменного тока необходимо учитывать эту особенность, т.е. учитывать фазовые отношения между колебаниями токов и напряжений.
Цепь с последовательным соединением участков с сопротивлением, с индуктивностью и с емкостью
По закону Ома мгновенное значение тока в цепи с последовательно
включенными активным сопротивлением r, индуктивностью L и емкостью С (рис. 7.1, а) зависит не только от приложенного напряжения и, но и от возникающих в цепи э. д. с. индуктивности eL и э. д.с. емкости ес–
отсюда 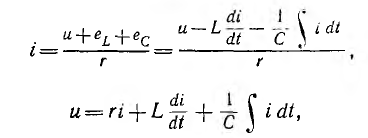
т. е. приложенное напряжение распадается на три напряжения, из которых первое Ua=ri преодолевает активное сопротивление цепи, второе 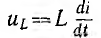
уравновешивает противоположную ему по знаку э. д. с. индуктивности eL и третье 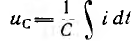 уравновешивает противоположную ему по знаку э. д.с емкости ес.
уравновешивает противоположную ему по знаку э. д.с емкости ес.
Задавшись током цепи
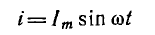
и подставив это выражение тока в уравнение напряжений:
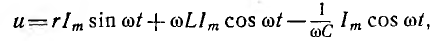
можно видеть, что отдельные составляющие напряжения представляют собой синусоиды и, следовательно, суммарное напряжение также будет синусоидой, вектор которой равен геометрической сумме векторов составляющих синусоид.
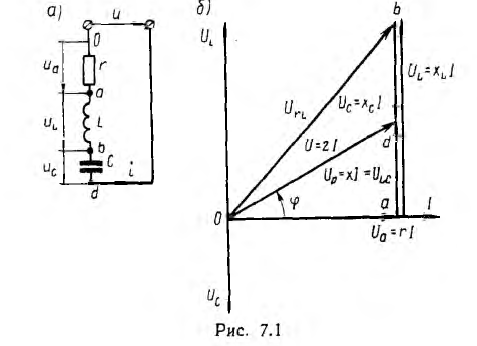
Это построение сделано на рис. 7.1, б для векторов, равных по величине действующим значениям. Вектор активного напряжения UB=rl совпадает по фазе с вектором тока I. Индуктивное напряжение
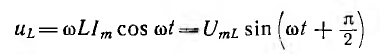
опережает ток на 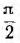 и, следовательно, вектор индуктивного напряжения
и, следовательно, вектор индуктивного напряжения
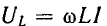 сдвинут относительно вектора тока по вращению векторов на тот же угол. Емкостное напряжение
сдвинут относительно вектора тока по вращению векторов на тот же угол. Емкостное напряжение
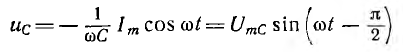
и его вектор 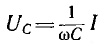 противоположен по фазе вектору UL. На рис. 7.1, б он отложен из конца вектора UL в противоположную сторону. Замыкающий вектор и есть вектор полного напряжения U. Необходимо отметить интересную особенность векторной диаграммы рис. 7.1, б.
противоположен по фазе вектору UL. На рис. 7.1, б он отложен из конца вектора UL в противоположную сторону. Замыкающий вектор и есть вектор полного напряжения U. Необходимо отметить интересную особенность векторной диаграммы рис. 7.1, б.
При ее построении векторы напряжений на участках цепи откладывались в той же последовательности, в какой эти участки включены в цепь рис. 7.1, а. Поэтому отдельным точкам векторной диаграммы (0, a, b, d) соответствуют одноименные точки цепи. Такая диаграмма может быть названа топографической. Она позволяет сразу найти векторы напряжений между любыми точками цепи, соединив их прямой линией. На рис. 7.1, б показаны векторы напряжений UrL и ULC на участках rL и LC.
В результате сложения векторов получается прямоугольный треугольник напряжений с гипотенузой, равной полному напряжению U, катетом, равным активному напряжению UB и катетом Up = UL — Uc; напряжение Up называется реактивным. На диаграмме рис. 7.1, б преобладает индуктивное напряжение (UL > Uс) и поэтому реактивное напряжение совпадает по фазе с индуктивным.
Из треугольника напряжений видно, что
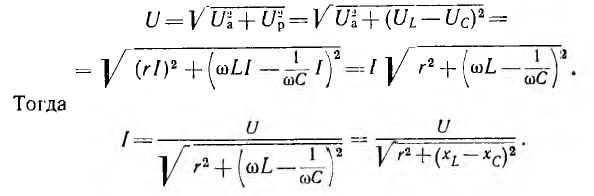
Сопротивление  называется реактивным и обозначается буквой х. Знаменатель выражения для тока
называется реактивным и обозначается буквой х. Знаменатель выражения для тока
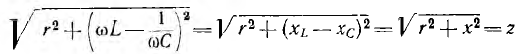
играет роль сопротивления и называется полным сопротивлением.
В системе единиц СИ z также измеряется в омах.
Следовательно,
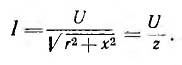
Полученные выражения могут рассматриваться как аналог закона Ома для переменного тока. Необходимо подчеркнуть, что закон Ома в таком виде справедлив только для максимальных и действующих значений переменного тока и напряжения. Для мгновенных значений но в таком виде неприменим; написать 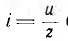 было бы грубой ошибкой, так как мгновенные значения тока и напряжения не находятся в линейной зависимости.
было бы грубой ошибкой, так как мгновенные значения тока и напряжения не находятся в линейной зависимости.
Здесь полезно сопоставить различные выражения закона Ома для этой цепи. Для мгновенных значений

для векторов, очевидно, можно было бы написать:

где 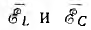 — векторы э. д. с. индуктивности и емкости, а для действующих значений аналог закона Ома:
— векторы э. д. с. индуктивности и емкости, а для действующих значений аналог закона Ома:

Отсюда видно, что физически существующие э. д. с. индуктивности и емкости, входящие в выражения (7.1) и (7.2), в выражении (7.3) формально учитываются через реактивные сопротивления xL и хс.
Вектор тока сдвинут по фазе относительно вектора напряжения на острый угол  ; на диаграмме рис. 7.1, б вектор тока отстает от век тора напряжения. Угол
; на диаграмме рис. 7.1, б вектор тока отстает от век тора напряжения. Угол  может быть определен из треугольника напряжений:
может быть определен из треугольника напряжений:
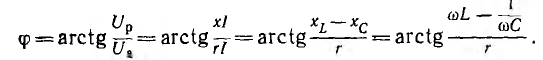
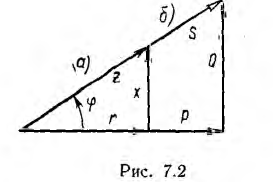
Если разделить все стороны треугольника напряжений на общий множитель I, получится подобный ему треугольник сопротивлений с гипотенузой z и
катетами r и х (рис. 7.2, а), откуда
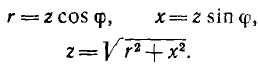
Мгновенная мощность цепи равна произведению мгновенных значений напряжения и тока:
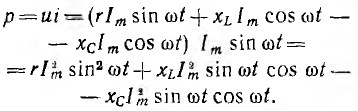
После подстановки значений 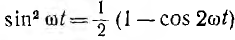 и
и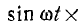
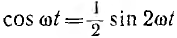
выражение для мгновенной мощности получает вид
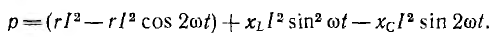
Первый член правой части есть мгновенная мощность активного сопротивления
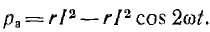
После подстановки соотношений из треугольника напряжений
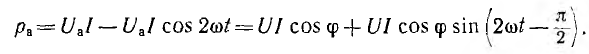
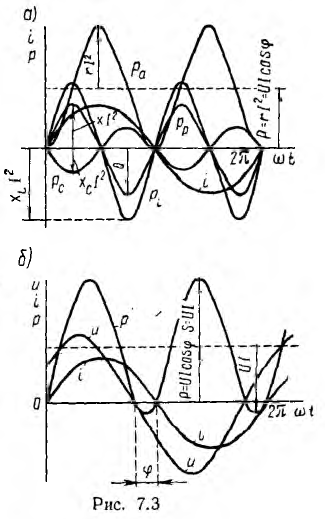
Эта мощность (рис. 7.3, a) имеет постоянную составляющую
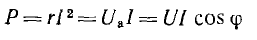
переменную — синусоиду двойной частоты с такой же амплитудой.
Величина Р является, очевидно, средней мощностью за период. Она называется активной мощностью. В системе СИ мгновенная и активная мощности измеряются в ваттах (вт).
Второй и третий член дают мгновенную мощность индуктивности и емкости (см. рис. 7.3, а):
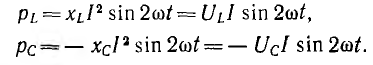
Эти мощности изменяются по синусоидам двойной частоты противоположным по фазе, т. е. когда индуктивность отдает энергию, емкость ее получает, и наоборот. Среднее значение pL и рс равно нулю. В сумме они дают мгновенную мощность реактивных участков цепи:
Амплитуда синусоиды этой мощности
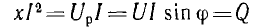
называется реактивной мощностью. В системе СИ реактивная мощность измеряется в реактивных вольт-амперах (вар).
Теперь выражение для мгновенной мощности всей цепи может быть
преобразовано:
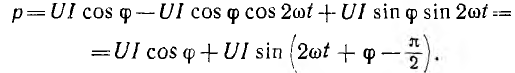
Таким образом, мгновенная мощность р всей цепи имеет постоянную составляющую UI cos ф и переменную составляющую — синусоиду с амплитудой UI (рис. 7.3, б); р равно нулю когда u = 0 или i = 0.
Так как амплитуда переменной части UI больше постоянной составля
ющей UI cosϕ, мощность в определенные промежутки времени становится отрицательной. Когда мощность положительна, цепь получает энергию от источника; когда мощность отрицательна, цепь отдает энергию источнику. Очевидно, возврат энергии источнику получается за счет энергии поля того из реактивных участков цепи, мощность которого больше (для рис. 7.3, б за счет индуктивности). Отдавая запасенную в своем поле энергию, индуктивность снабжает энергией емкость, отдает часть своей энергии безвозвратно активному сопротивлению, а остаток возвращает источнику. Промежутки времени, в течение которых мощность положительна, больше, чем те, при которых мощность отрицательна.
Амплитуда переменной части мгновенной мощности всей цепи
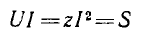
называется полной мощностью и измеряется в системе СИ в вольт-амперах (ва).
Если умножить все стороны треугольника сопротивлений на общий множитель I2, получается подобный ему прямоугольный треугольник мощностей (см. рис. 7.2, б) с углом у вершины, равным ϕ, гипотенузой, равной полной мощности 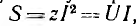 катетом равным активной мощности
катетом равным активной мощности 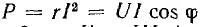 и другим катетом равным реактивной мощности
и другим катетом равным реактивной мощности 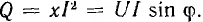 Из треугольник; мощностей видно, что
Из треугольник; мощностей видно, что
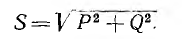
Полная мощность S является характерной величиной для всякой электрической установки, любой электрической машины, аппарата, линии передачи и т. п. Сечение их проводов рассчитывается на ток I таким образом, чтобы провода не перегревались от выделяемого в них тепла. Изоляция рассчитывается на напряжение U; сердечник и н. с. обмотки электромагнитных механизмов рассчитываются на магнитный поток, который также пропорционален напряжению (см., например, формулу для 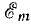 ). Другими словами, любая электрическая установка рассчитывается на напряжение и на ток, т. е. на полную мощность UI, средняя же мощность
). Другими словами, любая электрическая установка рассчитывается на напряжение и на ток, т. е. на полную мощность UI, средняя же мощность
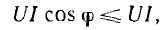
так как 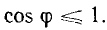 . Следовательно, полная мощность есть та максимальная активная мощность, которая может быть получена при данных действующих значениях напряжения и тока. Из-за сдвига фаз расчетная (полная) мощность установки используется неполностью. Отсюда ясна важность высокого cosϕ, называемого коэффициентом мощности.
. Следовательно, полная мощность есть та максимальная активная мощность, которая может быть получена при данных действующих значениях напряжения и тока. Из-за сдвига фаз расчетная (полная) мощность установки используется неполностью. Отсюда ясна важность высокого cosϕ, называемого коэффициентом мощности.
В общем случае напряжение и и ток i цепи записываются так:
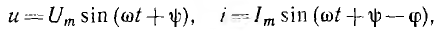
где ψ — начальная фаза напряжения;
ϕ — разность фаз напряжения и тока.
Если в рассмотренной цепи 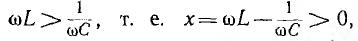 то
то 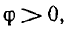 и ток отстает по фазе от напряжения. Если
и ток отстает по фазе от напряжения. Если 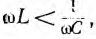 т.е.
т.е. 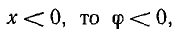 и ток опережает напряжение.
и ток опережает напряжение.
Для цепи с последовательным соединением сопротивления r и индуктивности L аналог закона Ома и сдвиг по фазе могут быть получены 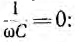
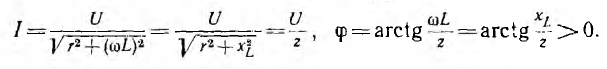
Аналогично, для цепи с последовательным соединением сопротивления r и емкости С, положив 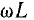 = 0:
= 0:
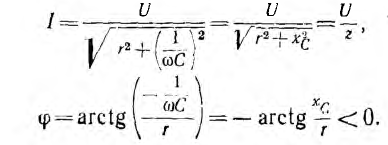
Резонанс напряжений
В электрических цепях, содержащих индуктивности и емкости, возможно явление резонанса, при котором напряжение и ток цепи совпадают по фазе. В цепи с последовательным соединением сопротивления, индуктивности и емкости (см. рис. 7.1, а) будет резонанс напряжений, когда
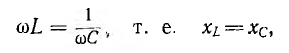
так как в этом случае ток и разность фаз напряжения и тока
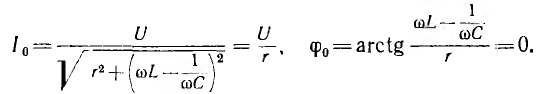
Напряжения на участках цепи при резонансе
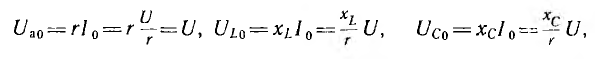
т. е. активное напряжение равно полному, а индуктивное напряжение — емкостному напряжению, так как индуктивное сопротивление xL равно емкостному хс. Если
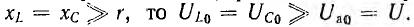
При резонансе, ограниченный лишь активным сопротивлением, при малом r также может получить большое значение.
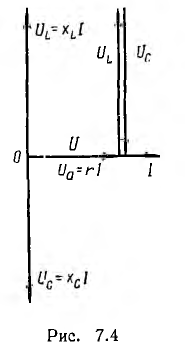
На рис. 7.4 показана векторная диаграмма для случая резонанса. Как видно из этой диаграммы и приведенных соотношений, при резонансе цепь, несмотря на наличие в ней индуктивности и емкости, ведет себя как активное сопротивление. Ток совпадает по фазе с напряжением и получает наибольшее значение. Реактивное напряжение
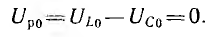
Так как условием резонанса является равенство 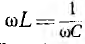 то для данных двух величин из трех (L, С, ω) резонанс может быть получен подбором третьей. Итак, резонанс будет при
то для данных двух величин из трех (L, С, ω) резонанс может быть получен подбором третьей. Итак, резонанс будет при
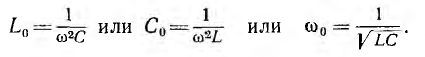
Индуктивное и емкостное сопротивления при резонансе
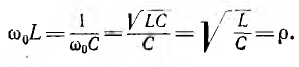
Величина р называется характеристическим сопротивлением цепи, а ее отношение к активному сопротивлению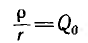 называется добротностью цепи (контура). Добротность равна также отношению индуктивного или емкостного напряжения при резонансе к напряжению всей цепи. Обратная величина
называется добротностью цепи (контура). Добротность равна также отношению индуктивного или емкостного напряжения при резонансе к напряжению всей цепи. Обратная величина
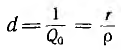
называется затуханием цепи. Чем меньше r, а следовательно, и d, тем при резонансе больше активная (средняя) мощность
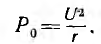
Мгновенные мощности индуктивности и емкости при резонансе равны по величине и обратны по знаку (рис. 7.5):
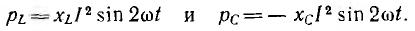
Индуктивная QL = xLP2 и емкостная Qc = ХсР2 мощности также равны друг другу. Следовательно, при резонансе мгновенная мощность рр и реактивная мощность Q всей цепи будут
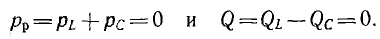
Этого следовало ожидать, так как при резонансе, как показано, цепь ведет себя как активное сопротивление.
Максимальное значение энергии индуктивности
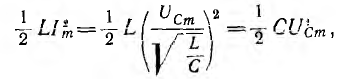
т. е. равно максимальному значению энергии емкости. Тогда, если
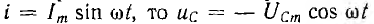 и мгновенное значение суммарной энергии индуктивности и емкости равно:
и мгновенное значение суммарной энергии индуктивности и емкости равно:
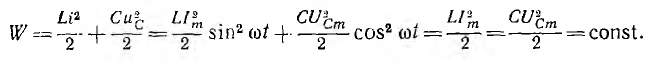
Отсюда видно, что при резонансе суммарная энергия, запасенная реактивными элементами цепи, постоянна и равна максимальной энергии индуктивности, равной, в свою очередь, максимальной энергии емкости. Колебания энергии индуктивности и емкости противоположны по фазе и в цепи происходит полный обмен энергиями между ними.
Источник не участвует в этом обмене и доставляет лишь энергию активному сопротивлению цепи.
Таким образом, при резонансе происходит взаимная компенсация индуктивных и емкостных сопротивлений, напряжений и мощностей.
Далее рассмотрен режим, когда напряжение на зажимах цепи постоянно, а частота изменяется от 0 до .
.
Ток I = 0 при ω = 0 и ω =  и максимален при резонансе, когда ω = ω0.
и максимален при резонансе, когда ω = ω0.
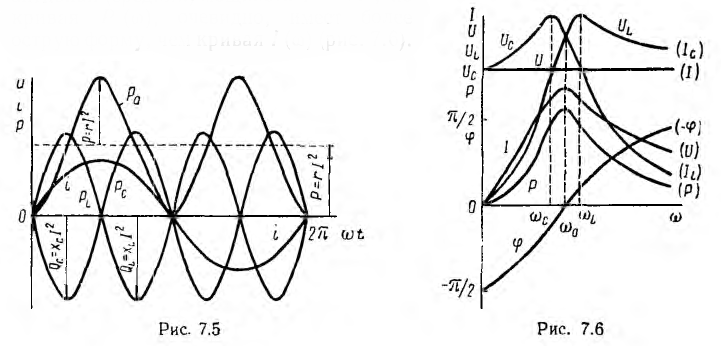
Аналогично изменяется активное напряжение Uа = rl и активная (средняя) мощность Р = rI2, но кривая Р (ω), очевидно, имеет более острую форму, чем кривая I(ω) (рис. 7.6). Индуктивное напряжение UL = 0 при ω = 0. При ω =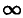 UL = U, при резонансе
UL = U, при резонансе  . Для определения частоты
. Для определения частоты 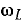 , при которой UL максимально, вместо исследования на максимум величины
, при которой UL максимально, вместо исследования на максимум величины
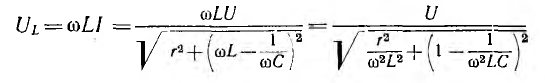
проще исследовать подрадикальное выражение на минимум, взяв его
производную по ω и приравняв нулю:
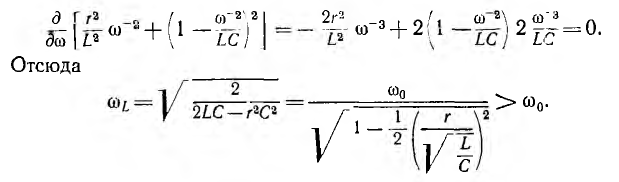
Значение ULmax получится после подстановки значения 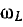 в общее выражение для UL:
в общее выражение для UL:
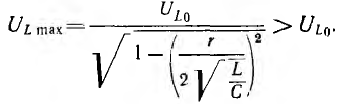
Емкостное напряжение Uc = U при ω=0, U=0 при ω= 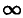 при резонансе
при резонансе 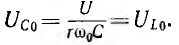
Определение частоты 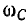 , при которой Uc проходит через максимум, и значение Ucmax можно провести аналогично предыдущему:
, при которой Uc проходит через максимум, и значение Ucmax можно провести аналогично предыдущему:
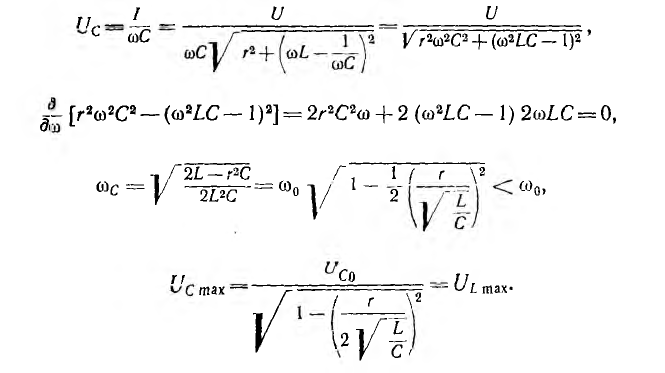
Таким образом, наибольшие значения напряжений на индуктивности и емкости равны между собой.
Графики зависимостей 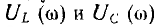 показаны также на рис. 7.6.
показаны также на рис. 7.6.
При увеличении активного сопротивления r цепи 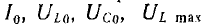
и Ucmax уменьшаются, а частоты ωL и ωс удаляются от резонансной частоты
ω0; при 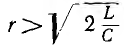 максимумов нет.
максимумов нет.
Кривые на рис. 7.6 называются резонансными кривыми или частотными характеристиками цепи.
Явление резонанса имеет широкое применение в радиотехнике.
Например, в ряде устройств используется зависимость режима работы
цепи с последовательным соединением L и С от частоты и повышение тока этой цепи при резонансе.
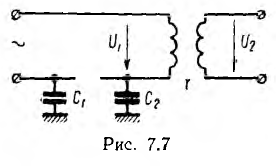
В электротехнике резонанс напряжений часто является аварийным режимом; так при обрыве линии передачи, питающей отключенный со вторичной стороны трансформатор Т (рис. 7.7), может наступить резонанс между емкостью
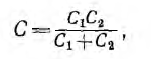
(С1 и С2 — емкости на землю двух участков линии передачи) и индуктивностью L первичной обмотки трансформатора, что вызовет недопустимое для изоляции и безопасности установки повышение напряжения U1 в первичной и, следовательно, U2 во вторичной обмотках трансформатора.
Цепь с параллельным соединением участков с сопротивлением, с индуктивностью и с емкостью. Резонанс токов
Основные соотношения:
При параллельном соединении сопротивления r, индуктивности L и емкости С (рис. 7.8, а) мгновенное значение тока i всей цепи, согласно первому закону Кирхгофа, равно алгебраической сумме мгновенных значений токов отдельных приемников:
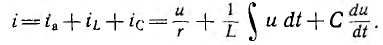
После подстановки в это выражение напряжения 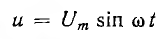 ток всей цепи представляется суммой ‘синусоид:
ток всей цепи представляется суммой ‘синусоид:
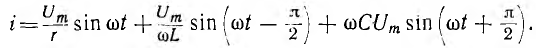
Следовательно, ток всей цепи также будет синусоидой, вектор которой может быть найден как геометрическая сумма векторов слагающих синусоид. Векторная диаграмма для действующих значений дана на рис. 7.8, б.
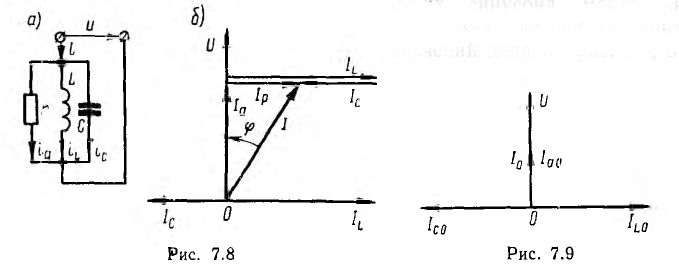
Активный ток 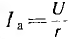 совпадает по фазе с напряжением U, индуктивный ток
совпадает по фазе с напряжением U, индуктивный ток 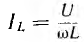 отстает отнапряжения на
отстает отнапряжения на 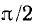 емкостный ток Iс = ωCU опережает напряжение на
емкостный ток Iс = ωCU опережает напряжение на 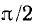 , реактивный ток
, реактивный ток 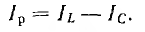
Тогда действующее значение тока всей цепи а разность фаз напряжения и тока
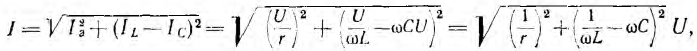
а разность фаз напряжения и тока
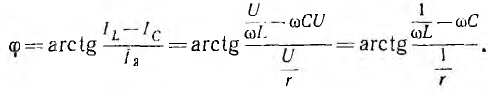
Резонанс токов наступит при
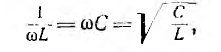
т. е. при условии, аналогичном условию резонанса напряжений.
Тогда
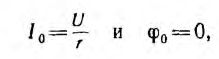
т. е. цепь будет вести себя как активное сопротивление.
Токи ветвей цепи при резонансе:
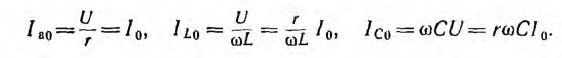
Векторная диаграмма для случая резонанса изображена на рис. 7.9.
Так как векторы 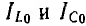 равны между собой и направлены противоположно, сумма их — реактивный ток — равна нулю. Ток цепи I0 равен активному току Iа0 и совпадает по фазе с напряжением.
равны между собой и направлены противоположно, сумма их — реактивный ток — равна нулю. Ток цепи I0 равен активному току Iа0 и совпадает по фазе с напряжением.
При 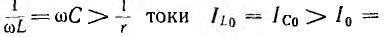 Ia0 т. е. токи в индуктивности и в
Ia0 т. е. токи в индуктивности и в
емкости будут больше тока всей цепи, равного току в активном сопротивлении.
Энергетическая сторона процесса здесь такая же, как и при резонансе напряжений: суммарная энергия, запасенная в полях цепи, постоянна и равна максимальной энергии емкости, равной в свою очередь максимальной индуктивности. Колебания энергии емкости и индуктивности противоположны по фазе, и в цепи происходит полный обмен энергиями между ними. Источник не участвует в этом обмене, он доставляет лишь энергию активному сопротивлению.
Если в рассматриваемой цепи поддерживать неизменным напряжение U и увеличивать частоту ω, активный ток 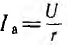 и активная мощность
и активная мощность 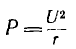 останутся неизменными, индуктивныи ток
останутся неизменными, индуктивныи ток 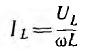 будет убывать, а емкостный ток
будет убывать, а емкостный ток 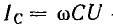 — возрастать; при резонансе
— возрастать; при резонансе 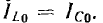 Частотные характеристики цепи показаны на рис 7.10.
Частотные характеристики цепи показаны на рис 7.10.
Ток всей цепи
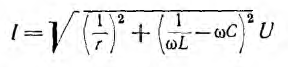
получает при резонансе, когда 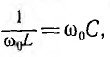 , минимальное значение
, минимальное значение 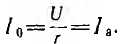 Фазный сдвиг
Фазный сдвиг  положителен при ω< ω0, равен нулю при ω = ω0 и отрицателен при ω > ω0.
положителен при ω< ω0, равен нулю при ω = ω0 и отрицателен при ω > ω0.
В высокочастотных генераторах, усилителях и других радиотехнических устройствах используется зависимость режимов работы от частоты в цепи с параллельным соединением L и С и повышение напряжения этой цепи при резонансе токов.
Дуальные цепи
При сравнении уравнения, написанного для цепи с параллельным соединением r, L и С (см. рис. 7.8, а) на основе первого закона Кирхгофа,
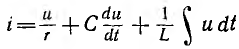
с уравнением для цепи с последовательным соединением r, L и С (см. рис. 7.1, а), написанного на основе второго закона Кирхгофа,
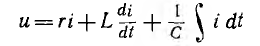
видно, что оба уравнения имеют в качестве независимой переменной время t и совершенно аналогичны, причем одно получается из другого при взаимной замене схемы и величин по табл. 7.1.
Таблица 7.1
| Парaллельное соединение | i | u | 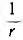 |
L | C |
| Последовательное соединение | u | i | r | C | L |
Две цепи, в которых напряжения первой цепи ведут себя, как токи второй и, наоборот, токи первой ведут себя, как напряжения второй, называются дуальными. Цепь с L и цепь с С, как видно, дуальны. Дуальными являются также цепи с последовательным и параллельным соединениями r, L и С, и все выводы, сделанные для последовательной схемы, можно перенести на параллельную, если заменить величины так, как указано в приведенной таблице. Взаимная замена напряжения и тока должна, очевидно, производиться
и для их действующих значений U и I, а частота ш для обеих схем должна быть одинакова.
Так, например, результаты исследования последовательной схемы при U = const и ω = var, изображенные на рис. 7.6, могут быть целиком перенесены на параллельную схему, работающую при I = const и ω= var, причем кривая, изображающая изменение тока I цепи, будет изображать кривую изменения напряжения U, кривая UL — кривую Iс и кривая Uc — кривую IL. Зависимость активной (средней) мощности 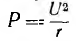 от частоты будет такой же, зависимость
от частоты будет такой же, зависимость  будет отличаться только знаком (рис. 7.6, обозначения кривых даны
будет отличаться только знаком (рис. 7.6, обозначения кривых даны
справа в скобках). Дуальными будут и векторные диаграммы, что можно видеть, например, из сравнения рис. 7.1, б и 7.3, б.
Общему выражению для емкостного напряжения последовательной схемы будет соответствовать общее выражение для индуктивного тока параллельной схемы:
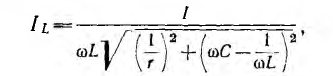
выражению для максимумов напряжений UL и Uc будет соответствовать выражение для максимумов токов Iс и IL:
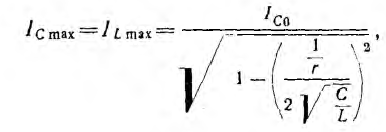
выражению для частоты 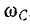 , при которой Uc проходит через максимум, будет соответствовать выражение
, при которой Uc проходит через максимум, будет соответствовать выражение 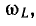 , при которой IL проходит через максимум:
, при которой IL проходит через максимум:
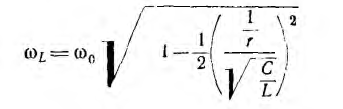
Совершенно аналогичны между собой и режимы работы параллельной цепи при ω = var и U = const (см. рис. 7.10) и последовательной — при ω = var и 1=const, если произвести указанную замену величин (обозначения кривых даны справа в скобках). Интересно отметить,что при неизменном токе напряжение U последовательной цепи при резонансе, когда 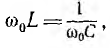 получает минимальное значение.
получает минимальное значение.
Повышение коэффициента мощности
Схема, в которой возможен резонанс токов, используется в электротехнике для повышения коэффициента мощности. Обычно приемники электрической энергии имеют активно-индуктивный характер, т. е. работают со сдвигом фаз 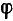 >0 между напряжением и током. Так, электрический двигатель переменного тока может быть представлен в виде схемы с параллельным соединением r и XL (рис. 7.11, а), где активная мощность Р, расходуемая в сопротивлении г, равна сумме полезной мощности двигателя и всех потерь в нем, а реактивная мощность Q индуктивного сопротивления XL равна индуктивной мощности двигателя, связанной с его магнитным полем.
>0 между напряжением и током. Так, электрический двигатель переменного тока может быть представлен в виде схемы с параллельным соединением r и XL (рис. 7.11, а), где активная мощность Р, расходуемая в сопротивлении г, равна сумме полезной мощности двигателя и всех потерь в нем, а реактивная мощность Q индуктивного сопротивления XL равна индуктивной мощности двигателя, связанной с его магнитным полем.
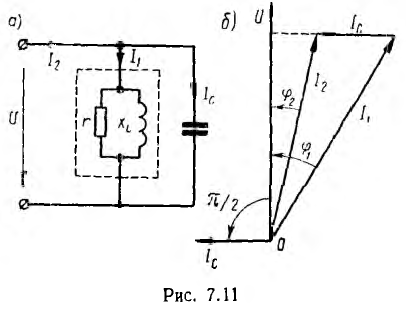
Источник энергии, питающий такой приемник, а также линия передачи должны быть рассчитаны на полную мощность S = UI, превышающую среднюю мощность приемника Р = UI cosϕ. Для меньшения полной мощности источника и линии передачи путем повышения коэффициента мощности часто применяется параллельное пюдключение к приемнику батареи конденсаторов, т. е. схема, в которой возможен резонанс токов.
На рис. 7.11, б показана векторная диаграмма этой цепи. Здесь r1 — ток нагрузки, ϕ1 — фазный сдвиг, / с — ток батареи конденсаторов, который при пренебрежении потерями в них опережает напряжение U по фазе на угол 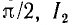 — ток источника, ϕ2 — новый фазный сдвиг. На основании этой диаграммы можно вычислить емкость С батареи конденсаторов, необходимой для уменьшения фазного сдвига ϕ1 до величины ϕ2:
— ток источника, ϕ2 — новый фазный сдвиг. На основании этой диаграммы можно вычислить емкость С батареи конденсаторов, необходимой для уменьшения фазного сдвига ϕ1 до величины ϕ2:
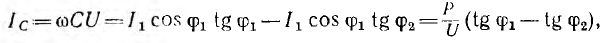
где Р — средняя мощность приемника.
Отсюда
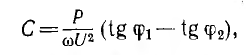
при ϕ2 = 0 емкость
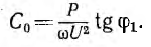
Элементарные методы расчета простых цепей переменного тока
Эквивалентные схемы:
При расчете цепи любой приемник может быть заменен эквивалентной схемой с сосредоточенными параметрами, имеющей равные ток и фазный сдвиг при том же напряжении и той же частоте. Если приемник (рис. 7.12, а) при напряжении U и частоте f потребляет ток I с фазным сдвигом 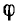 (рис. 7.12, б), то полное сопротивление r и полная мощность S этого приемника и его эквивалентной схемы будут:
(рис. 7.12, б), то полное сопротивление r и полная мощность S этого приемника и его эквивалентной схемы будут:
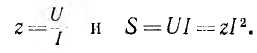
Первой простейшей эквивалентной схемой является последовательное соединение активного г и реактивного х сопротивлени, (рис. 7.12, в для случая преобладания индуктивного сопротивления)
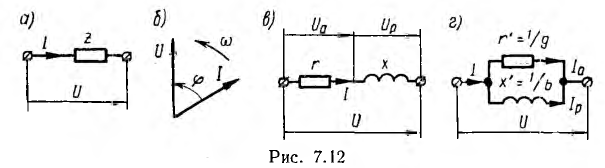
Тогда активные и реактивные сопротивления, напряжения и мощности этой эквивалентной схемы соответственно равны:
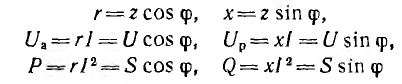
и могут быть представлены катетами подобных прямоугольных треугольников, гипотенузы которых равны полным величинам:
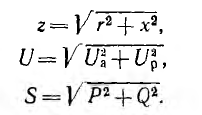
Треугольники сопротивлений, напряжений и мощностей изображены на рис. 7.13, а.
Второй простейшей эквивалентной схемой того же приемника является параллельное соединение активного r’ и реактивного x’ сопротивлений (рис. 7.12, г), не равных r и х эквивалентной ей последовательной схемы. Параллельную схему удобней характеризовать проводимостями: активной 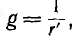 реактивной
реактивной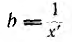 и полной у. Полная проводимость и полная мощность приемника и его параллельной эквивалентной схемы соответственно равны:
и полной у. Полная проводимость и полная мощность приемника и его параллельной эквивалентной схемы соответственно равны:
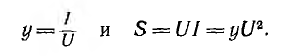
Токи ветвей параллельной эквивалентной схемы, называемые активным и реактивным:
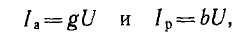
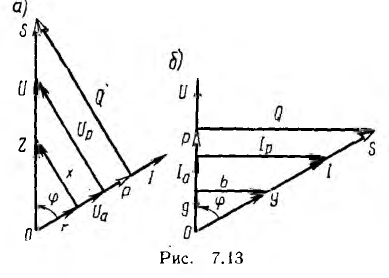
изображены на векторной диаграмме рис. 7.13, б. Так как они сдвинуты между собой по фазе на угол π/2, полный ток
откуда 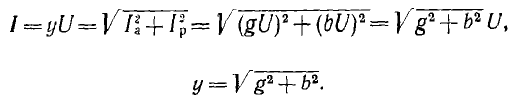
На рис. 7.13, б прямоугольный треугольник токов совмещен стреугольником проводимостей, а также с треугольником мощностей, гипотенуза которого равна полной мощности S, а катеты —активной и реактивной мощностям:

Все эти треугольники имеют у вершины угол 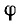 и подобны.
и подобны.
Сопротивления и проводимости часто называют параметрами приемников. Это определение полностью справедливо для и у, величины же r, х и g, b правильней называть параметрам и эквивалентных схем.
Так как последовательная и параллельная схемы эквивалентны между собой, активные, реактивные и полные мощности их должны быть также между собой равны:
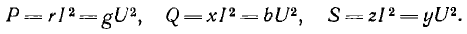
Отсюда могут быть получены переходные формулы зт сопротивлений последовательной схемы к проводимостям параллельной схемы:
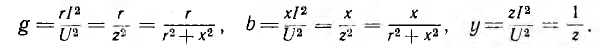
Аналогичным образом могут быть получены переходные формулы от проводимостей параллельной схемы к сопротивлениям последовательной:
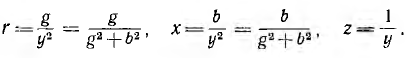
Таким образом, обратными друг другу являются только полные сопротивление г и проводимость у, активные и реактивные сопротивления и проводимости находятся в более сложной зависимости.
При анализе поведения какого-либо приемника при переменной частоте необходимо заменять его эквивалентной схемой, близкой физической сущности этого приемника, т. е. схемой, в которой сопротивления, индуктивности и емкости ее элементов могут быть приняты пастояинными. Так, в некотором диапазоне частот можно пренебречь поверхностным эффектом, и, например, для кольцевого соленоида считать сопротивление r и индуктивность L независящими от частоты, определяя их по формулам:
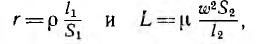
где l1 и l2 — соответственно длины провода обмотки и сердечника, S1, и S2 — их сечения. Пренебрегая током через межвитковые емкости соленоида, что допустимо только при низких частотах, следует представить соленоид в виде последовательной эквивалентной схемы постоянными параметрами r и L (см. рис. 7.12, в). Тогда при постоянном токе (ω = 0) соленоид и его эквивалентная схема будут иметь сопротивление r, а с ростом частоты ω его сопротивление z = 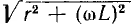 будет возрастать, что соответствует действительности, cопротивление параллельной схемы с постоянными параметрами r’ и L’ (см. рис. 7.12, г) при ω = 0 было бы равно нулю, при ω=
будет возрастать, что соответствует действительности, cопротивление параллельной схемы с постоянными параметрами r’ и L’ (см. рис. 7.12, г) при ω = 0 было бы равно нулю, при ω=  стало бы равным активному сопротивлению, что не соответствует действительности. Поэтому параметры г’ и L’ параллельной эквивалентно схемы должны изменяться с частотой.
стало бы равным активному сопротивлению, что не соответствует действительности. Поэтому параметры г’ и L’ параллельной эквивалентно схемы должны изменяться с частотой.
Цепи с последовательным и параллельным соединением приемников
При последовательном соединении нескольких приемников каждый из них удобно заменить эквивалентной схемой, состоящей из последовательного соединения активного г и реактивного х сопротивлений.
Ток всех приемников такой цепи одинаков, а мгновенное значение напряжения, согласие второму закону Кирхгофа, равно алгебраической сумме мгновенных значений напряжений отдельных приемников. При переходе к векторам алгебраическая сумма заменяется геометрической.
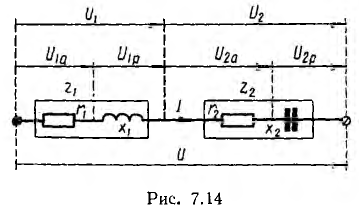
В качестве примера на рис. 7.15, а показана векторная диаграмма для цепи рис. 7.14, состоящей из последовательного соединения двух приемников —одного с индуктивным характером нагрузки и другого с емкостным. Векторы напряжения приемников и всей цени разлагаются на составляющие: активные Uа — по вектору тока и реактивные Uр — перпендикулярно вектору тока. Если разделить все напряжения (стороны треугольников напряжений: 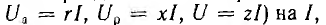 получится подобный рис. 7.15, а многоугольник сопротивлений (рис. 7.15, б). При умножении напряжений на I получится подобный рис. 7.15, а многоугольник мощностей со сторонами
получится подобный рис. 7.15, а многоугольник сопротивлений (рис. 7.15, б). При умножении напряжений на I получится подобный рис. 7.15, а многоугольник мощностей со сторонами 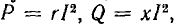
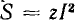 (рис. 7.15, в).
(рис. 7.15, в).
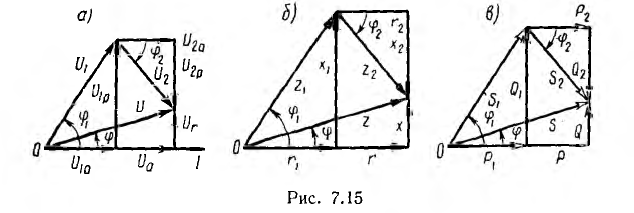
При параллельном соединении нескольких приемников каждый из них удобно заменить эквивалентной схемой, состоящей из параллельного соединения активной g и реактивной b проводимостей. Напряжение всех приемников такой цепи одинаково, а мгновенное значение тока цепи, согласно первому закону Кирхгофа, равно алгебраической сумме мгновенных значений токов отдельных приемников. При пере ходе к векторам алгебраическая сумма заменяется геометрической.
В качестве примера на рис. 7.17 дана векторная диаграмма для цепи, состоящей из параллельного соединения приемника с индуктивным характером нагрузки и приемника с емкостной нагрузкой (рис. 7.16). Векторы тока приемников и всей цепи разлагаются на составляющие:
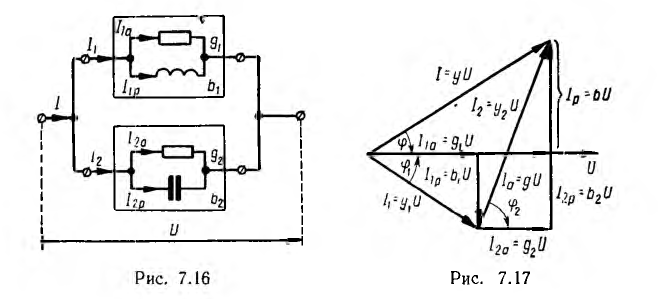
активные Iа по вектору напряжения U и реактивные Iр — перпендикулярно вектору напряжения. Если разделить все токи (стороны треугольников токов: 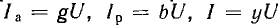 ) на U, получится подобный рис. 7.17 многоугольник проводимостей (g, b, у), а при умножении токов на U — подобный многоугольник мощностей (Р = gU2 , Q = bU2, , S = yU2).
) на U, получится подобный рис. 7.17 многоугольник проводимостей (g, b, у), а при умножении токов на U — подобный многоугольник мощностей (Р = gU2 , Q = bU2, , S = yU2).
Из многоугольников рис. 7.15 и 7.17 видно, что при последовательном соединении складываются сопротивления, напряжения и мощности, а при параллельном — проводимости, токи и тоже мощности. Активные величины складываются арифметически, реактивные — алгебраически, а полные — геометрически.
Расчет цепей со смешанным соединением приемников методами преобразования и пропорционального пересчета
При смешанном (параллельно-последовательном) соединении приемников с заданными параметрами, питаемых одним источником энергии, токи, напряжения и мощности ветвей цепи могут быть определены аналитически методом преобразования, заключающимся в постепенной замене сложной цепи более простой, ей эквивалентной. Ход решения подобной задачи показан на рис. 7.18.
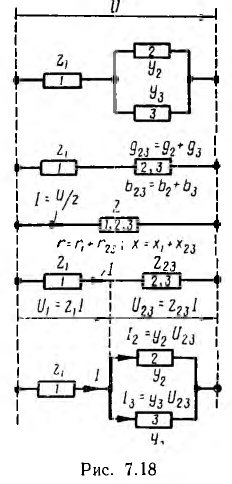
Группа приемников, соединенных параллельно, заменяется одним, активная проводимость которого равна арифметической сумме активных проводимостей приемников, а реактивная—алгебраической сумме реактивных. Группа приемников, соединенных последовательно, заменяется одним, активное сопротивление которого равно арифметической сумме активных сопротивлений отдельных приемников, а реактивное — алгебраической сумме. После замены всей цени одним приемником определяется ток при заданном напряжении или напряжение при заданном токе и сдвиг фаз между ними. Затем схема разворачивается в первоначальную цепь с постепенным определением напряжений, токов и фазных сдвигов в отдельных приемниках.
В процессе решения этой задачи несколько раз приходится при менять переходные формулы от сопротивлений к проводимостях и от проводимостей к сопротивлениям.
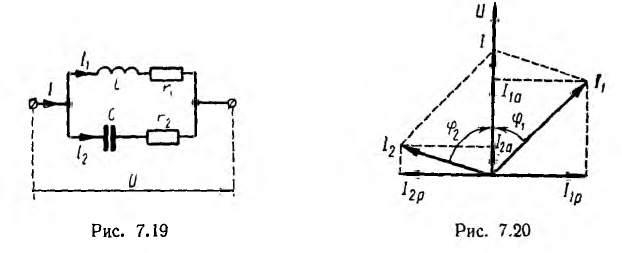
В качестве примера далее решается важная для электротехники задача определения частоты ω, при которой в схеме рис. 7.19 наступит резонанс токов, т. е. напряжение и ток всей цепи будут совпадать по фазе. Для этого, очевидно, реактивная проводимость всей цепи должна быть равна нулю:
откуда 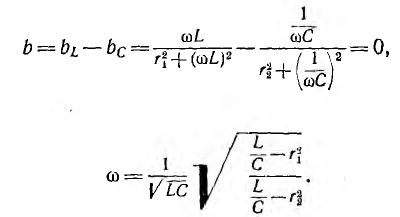
Таким образом, в общем случае, когда 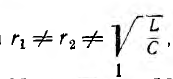 частота ω резонанса в этой цепи отличается от частоты
частота ω резонанса в этой цепи отличается от частоты 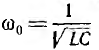 резонанс; при последовательном или параллельном соединении L и С. Векторная диаграмма для резонанса в цепи рис. 7.19 изображена на рис. 7.2G Реактивные составляющие токов ветвей в сумме дают нуль, и ток все цепи равен сумме активных составляющих.
резонанс; при последовательном или параллельном соединении L и С. Векторная диаграмма для резонанса в цепи рис. 7.19 изображена на рис. 7.2G Реактивные составляющие токов ветвей в сумме дают нуль, и ток все цепи равен сумме активных составляющих.
Так как в общем случае токи ветвей сдвинуты по фазе не на π/2, их мгновенные мощности, изменяющиеся с двойной частотой, будут сдвинуты по фазе на угол, отличный от π, т. е. они не находятся в противофазе. Это значит, что в общем случае резонанса полного обмена энергиями между индуктивной и емкостной ветвями не происходит.
Интересно отметить частные случаи:
1) при 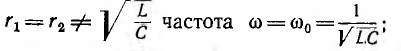
2) при 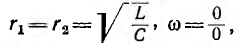 т. е. резонанс будет при любой частоте;
т. е. резонанс будет при любой частоте;
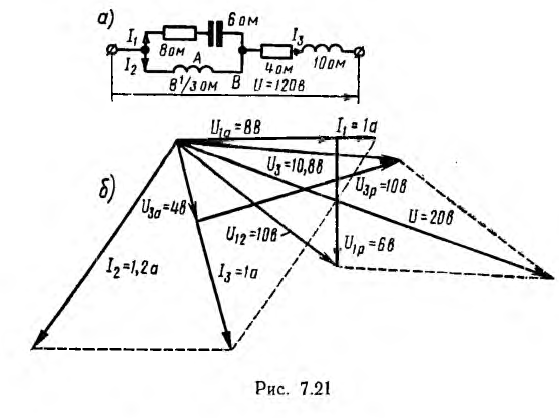
3) при  резонансная частота будет мнимым числом, а это значит, что резонанс в этой цепи невозможен.
резонансная частота будет мнимым числом, а это значит, что резонанс в этой цепи невозможен.
Расчет подобных цепей может быть произведен также графоаналитически — методом пропорционального пересчета. Он основан на том, что в линейной цепи токи пропорциональны напряжениям, следовательно, векторная диаграмма напряжений и токов, рассчитанная или построенная для одного значения питающего цепь напряжения, сохранит свой вид при изменении этого напряжения, и лишь масштабы для напряжения и тока изменятся во столько же раз.
Например, для цепи рис. 7.21, а, решая задачу графоаналитически, целесообразно строить векторную диаграмму, задавшись током первой ветви l1, = 1а. Затем последовательно вычисляются и в выбранном масштабе наносятся на диаграмму векторы в соответствии со своей фазой, после чего они складываются графически (рис. 7.21, б):
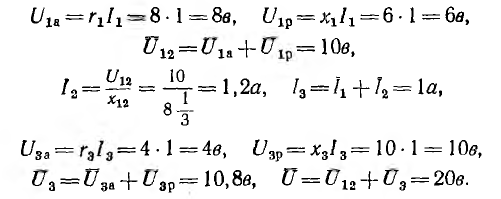
Таким образом, напряжение всей цепи оказалось равным 20 б вместо заданных 120 в. Следовательно, векторная диаграмма рис. 7.21, б остается действительной и для заданного напряжения, если увеличить масштабы для напряжений и токов в 120/20 = 6 раз.
Элементы и параметры электрических цепей переменного тока
Все реальные электротехнические устройства обладают электрическим сопротивлением R, индуктивностью L и емкостью С, которые являются параметрами электрической цепи переменного тока. Однако влияние каждого из параметров на ток в цепи различно, поэтому в некоторых случаях из расчетной схемы исключаются те, влияние которых незначительно.
Таким образом схема электрической цепи переменного тока характеризуется одним из указанных параметров R, L, C или комбинацией их при различных способах соединения элементов.
Цепь с активным сопротивлением
Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону
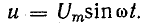
Требуется определить ток и мощность цепи.
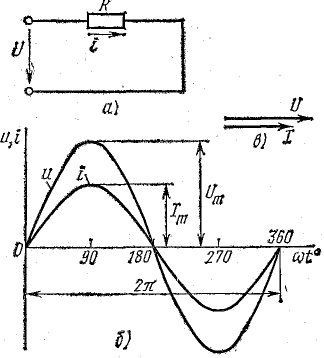
Рис. 13.1. К вопросу о цепи с активным сопротивлением
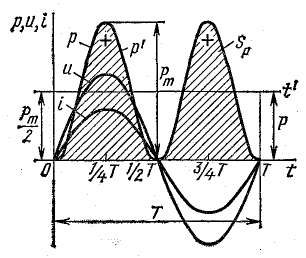
Рис. 13.2. График мгновенной мощности в цепи с активным сопротивлением
Ток в цепи
Выражение для мгновенного тока найдем по закону Ома:
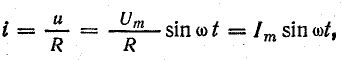
где 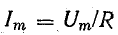 — амплитуда тока.
— амплитуда тока.
Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, в).
Действующий ток найдем, разделив амплитуду на 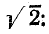
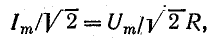
отсюда
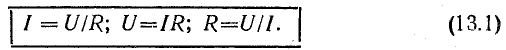
Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы (2.6) для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.
Мгновенная мощность
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока:
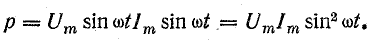
Из тригонометрии найдем
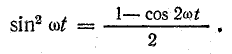
Учитывая это, запишем
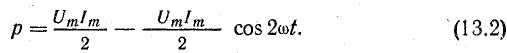
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2).
Если ось времени t поднять по чертежу на величину р = Рm/2 = UmIm/2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
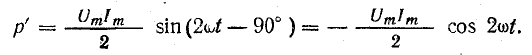
Таким образом, в первоначальной системе координат мгновенная мощность равна сумме постоянной величины 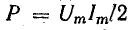 и переменной р’:
и переменной р’: 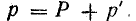
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Активная мощность
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2.
Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sр выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Рm.
В этом случае часть площади Sр, находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
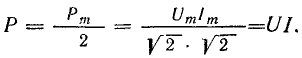
Активная мощность цепи с сопротивлением равна произведению действующих величин напряжения и тока:
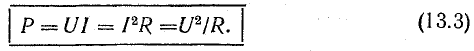
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности р(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
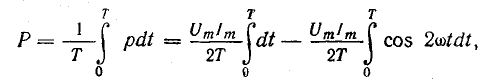
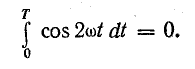
Поэтому
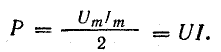
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
Цепь с индуктивностью
Исследуемая далее цепь, содержащая только индуктивность, является искусственной, так как катушки, линии электропередачи и другие устройства кроме индуктивности L имеют и активное сопротивление.
Однако рассмотрение идеальной катушки (при R = 0) необходимо для уяснения физических процессов в реальных цепях.
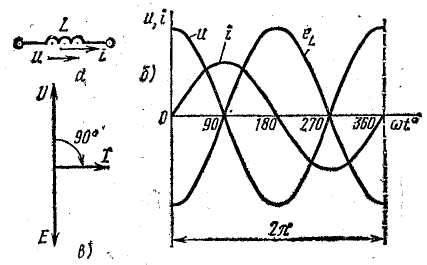
Рис. 13.4. К вопросу о цепи с индуктивностью
Это тем более важно, что в отдельных случаях активным сопротивлением и емкостью можно пренебречь из-за их малости. Например, ненагруженный трансформатор в схеме замещения в ряде случаев может быть представлен только своей индуктивностью.
Допустим, что для цепи (рис. 13.4, а) известны индуктивность L и ток, изменяющийся по закону

Требуется определить напряжение и мощность цепи.
Индуктивное напряжение
Переменный ток в катушке вызывает э. д. с. самоиндукции. При отсутствии активного сопротивления приложенное к катушке напряжение уравновешивается только э. д. с. самоиндукции, поэтому в соответствии со вторым законом Кирхгофа в любой момент времени 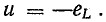
Э. д. с. самоиндукции пропорциональна скорости изменения тока [см. формулу (10.10)]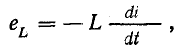
а напряжение
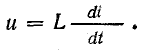
Уравнение приложенного напряжения можно найти, рассматривая векторную диаграмму на рис. 13.5, где ток изображен вектором Im, который предполагается вращающимся с угловой скоростью, равной угловой частоте ω. В начальном положении (при t = 0) вектор Im направлен по горизонтальной оси вправо. Это соответствует уравнению тока (13.4), если мгновенные величины i определять проекцией вращающегося вектора Im на вертикальную ось.
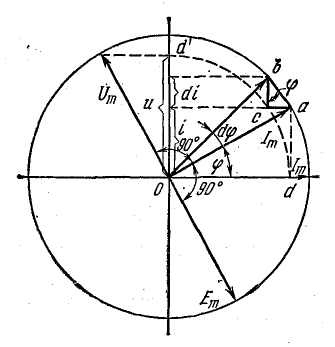
Рис. 13.5. Векторная диаграмма цепи с индуктивностью
Рассмотрим промежуточные положения вектора Im, отстоящие от начального на угол 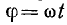 и
и 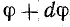 , где dφ — элементарный угол, на который вектор Im поворачивается за малый промежуток времени dt. За время dt ток изменился на di. Приращение тока выражается катетом прямоугольного треугольника abc, гипотенуза которого ab при весьма малом угле dφ может быть приравнена дуге окружности между точками а и b, а угол при вершине b равен φ. Поэтому отрезок ab в масштабе тока имеет значение
, где dφ — элементарный угол, на который вектор Im поворачивается за малый промежуток времени dt. За время dt ток изменился на di. Приращение тока выражается катетом прямоугольного треугольника abc, гипотенуза которого ab при весьма малом угле dφ может быть приравнена дуге окружности между точками а и b, а угол при вершине b равен φ. Поэтому отрезок ab в масштабе тока имеет значение 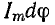 и
и 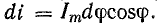
Уравнение напряжения
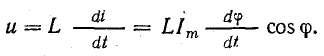
Но
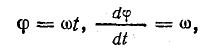
поэтому
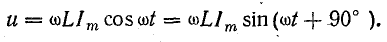
Это уравнение можно получить, дифференцируя уравнение тока:
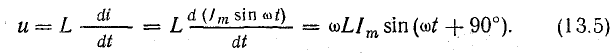
Индуктивное сопротивление
Действующая величина напряжения определяется из уравнения (13.5), где 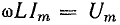 — амплитуда напряжения.
— амплитуда напряжения.
Разделив это выражение на 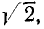 получим
получим
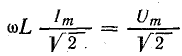
Отсюда
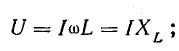

Коэффициент пропорциональности между действующими величинами напряжения и тока, равный произведению индуктивности и угловой частоты ωL, обозначают XL и называют реактивным сопротивлением индуктивности или индуктивным сопротивление е м.
Индуктивное сопротивление выражается в омах:
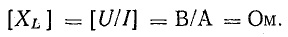
Действующая величина тока в цепи с индуктивностью равна отношению действующей величины напряжения к индуктивному сопротивлению.
Формула (13.6) похожа на формулу Ома. Это позволяет ток в цепи с индуктивностью определять так же, как ток в цепи с активным сопротивлением. Но нужно помнить, что индуктивное сопротивление с физической точки зрения ничего общего с обычным сопротивлением не имеет. Понятие об индуктивном сопротивлении, введенное для облегчения расчета, заменяет в расчете фактическое влияние э. д. с. самоиндукции на ток в цени, т. е. отражает инерционные свойства электрической цепи.
Векторная диаграмма цепи
Сопоставление уравнений тока (13.4) и напряжения (13.5) показывает, что в цепи с индуктивностью ток отстает от напряжения по фазе на четверть периода, или в угловой мере на π/2. Это видно также на рис. 13.5. Мгновенное напряжение выражается отрезком о-d в масштабе, отличающемся от масштаба тока в ωL раз. Перенесем этот отрезок на вертикальную ось (отрезок о-d’), где откладываются мгновенные величины тока. Этому мгновенному напряжению и соответствует вектор Um, опережающий вектор Im по ходу вращения на угол 90°. Э.д.с. самоиндукции, направленная против приложенного напряжения, имеет уравнение
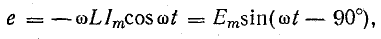
а на рис. 13.5 изображена вектором Еm, отстающим от вектора тока Im на 90°. На рис. 13.4 это показано отдельно на графике и векторной диаграмме (на векторной диаграмме отложены действующие величины).
Мгновенная и реактивная мощности
Мгновенная мощность 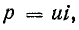 или
или
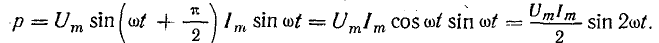
График изменения мощности (рис. 13.6) представляет собой синусоиду двойной частоты с амплитудой
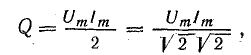
или

Наибольшая величина мощности в цепи с индуктивностью равна произведению действующих напряжения и тока.
Для выяснения физического смысла энергетических процессов обратим еще раз внимание на график мощности. Из него видно, что мгновенная мощность в течение периода четыре раза меняет знак (в моменты времени Т/4; Т/2; 3/4Т; Т). Изменение знака мощности означает, что направление потока энергии меняется.
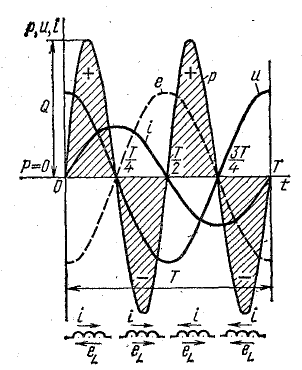
Рис. 13.6. График мгновенной мощности в цепи с индуктивностью
В первую четверть периода, когда ток в цепи увеличивается, энергия накапливается в магнитном поле катушки за счет энергии источника. Катушка в это время является приемником энергии, ток направлен против э. д. с. самоиндукции. Во вторую четверть периода, когда ток уменьшается, энергия возвращается в сеть (источнику).
Направления э. д. с. самоиндукции и тока в катушке совпадают — катушка является источником энергии. В следующую половину периода процесс повторяется. Нетрудно заметить, что количество энергии, накапливаемой в катушке за одну четверть периода (заштрихованная площадь «+»), точно равно количеству энергии, возвращаемой обратно в следующую четверть периода (заштрихованная площадь «—»).
Средняя (активная) мощность за период в цепи с индуктивностью равна нулю (Р = 0), так как в цепи с индуктивностью преобразования электрической энергии в другие виды энергии (тепловую, механическую) не происходит.
Скорость накопления и убыли энергии магнитного поля меняется по гармоническому закону. Амплитуда кривой мгновенной мощности Q является характеристикой этого процесса и называется реактивной мощностью.
Единицу мощности в этом случае называют вар — вольт-ампер реактивный — в отличие от единицы активной мощности — ватта.
Задача 13.4.
Катушка имеет индуктивность L = 15,9 мГн, активное сопротивление R = 0. Начертить график зависимости индуктивного сопротивления и тока в катушке от частоты приложенного напряжения, если действующее напряжение U = 100 В остается неизменным.
Решение. Нужно задаться несколькими величинами частоты, определить соответствующие индуктивные сопротивления, а затем величины тока.
Для частоты f = 50 Гц
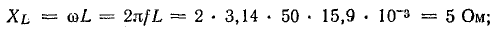
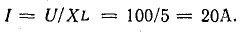
По результатам расчета для других частот (f = 0,25, 100, 500, 1000, 10 000 Гц) постройте в прямоугольной системе координат графики согласно условию задачи.
Цепь с емкостью
В конденсаторе с идеальным диэлектриком предполагается полное отсутствие тока проводимости и потерь энергии. Изменение напряжения между обкладками конденсатора сопровождается электрическим током смешения, величина которого зависит от емкости С. При напряжении на конденсаторе (рис. 13.7, а) 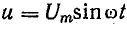 определим ток и мощность.
определим ток и мощность.
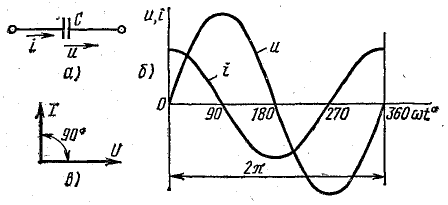
Рис. 13.7, К вопросу о цепи с емкостью
Электрический ток смещения
Внешнее электрическое поле вызывает поляризацию диэлектрика.
При всяком изменении электрического поля изменяется поляризованность диэлектрика, причем связанные заряженные частицы, входящие в состав атомов и молекул вещества, перемещаются, образуя электрический ток.
Явление движения связанных заряженных частиц в диэлектрике при изменении поляризации диэлектрика называют электрическим током поляризации.
Ток поляризации, согласно формуле (2.2),
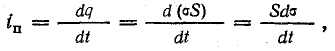
где σ —плотность электрического смещения заряда; отсюда
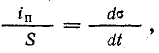
где 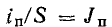 — плотность тока поляризации.
— плотность тока поляризации.
Учитывая формулу (7.20), найдем, что плотность тока поляризации равна скорости изменения поляризованности:
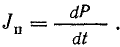
При изменении электрического поля меняется не только вектор поляризации Р, но и вектор электрического смещения в вакууме D0.Из выражений (7.22) и (7.24) следует
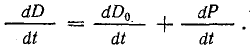
Второе слагаемое в правой части этого уравнения есть плотность тока поляризации, связанного с движением заряженных частиц диэлектрика. Первое слагаемое также имеет размерность плотности тока, но характеризует физический процесс в самом электрическом поле при его изменении во времени.
Величину 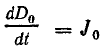 называют плотностью электрического смещения в вакууме. Плотность полного электрического тока смещения
называют плотностью электрического смещения в вакууме. Плотность полного электрического тока смещения
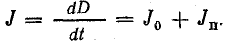
Введение понятия о токе смещения позволяет рассматривать электрическую цепь с конденсатором непрерывной: на участках из проводников имеется ток проводимости, а в диэлектрике — равный ему ток смещения.
Ток в цепи с емкостью
Заряд конденсатора пропорционален напряжению между его обкладками [см. формулу (7.28)], поэтому изменение напряжения сопровождается изменением заряда:
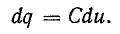
Скорость изменения заряда пропорциональна скорости изменения напряжения:
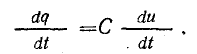
Но скорость изменения заряда равна электрическому току [см. формулу (2.2)]:

При этом во внешнем по отношению к конденсатору участке цепи происходит движение электронов (ток проводимости) через источник. Одновременно при увеличении напряжения совершается поляризация диэлектрика в конденсаторе и возникает ток смещения. При уменьшении напряжения диэлектрик деполяризуется.
Таким образом, ток в цепи с конденсатором пропорционален скорости изменения напряжения на его обкладках.
Уравнение (13.8) по форме подобно уравнению (13.5). Поэтому характер изменения тока при синусоидальном напряжении можно проследить на векторной диаграмме аналогично тому, как это сделано при рассмотрении цепи с индуктивностью (см. рис. 13.5), отнеся рассуждения к скорости изменения напряжения.
На диаграмме векторы тока и напряжения следует поменять местами . В связи с этим уравнение тока для цепи с емкостью можно записать аналогично уравнению для напряжения в цепи с индуктивностью:
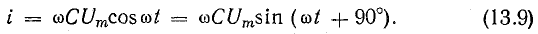
Уравнение тока можно получить, дифференцируя уравнение напряжения:
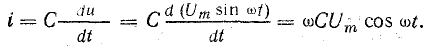
Емкостное сопротивление
Величина 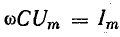 есть амплитуда тока. Разделив это выражение на
есть амплитуда тока. Разделив это выражение на 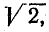 получим
получим

Величину 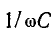 обозначают ХС и называют реактивным сопротивлением емкости или емкостным сопротивлением. Емкостное сопротивление — величина, обратная произведению емкости и угловой частоты.
обозначают ХС и называют реактивным сопротивлением емкости или емкостным сопротивлением. Емкостное сопротивление — величина, обратная произведению емкости и угловой частоты.
Действующий ток в цепи с емкостью равен отношению действующего напряжения к емкостному сопротивлению.
Формула (13.10) по форме совпадает с формулой Ома. Однако емкостное сопротивление физически ничего общего с обычным сопротивлением R не имеет.
Понятие о емкостном сопротивлении, введенное для облегчения расчетов, отражает в расчете противодействие заряженного конденсатора току в цепи.
Сопоставление уравнений напряжения и тока показывает, что в цепи с емкостью напряжение отстает от тока по фазе на четверть периода, или в угловой мере на π/2. На рис. 13.7, б, в это показано на графике и векторной диаграмме.
Мощность в цепи
Построение графика мгновенной мощности (рис. 13.8) выполняется точно так же, как и для цепи с индуктивностью, если иметь в виду, что мгновенная мощность выражается таким же произведением:
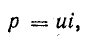
или
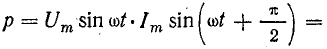
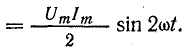
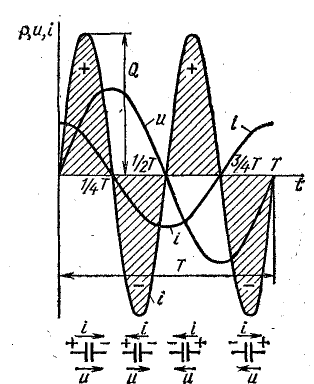
Рис. 13.8. График мгновенной мощности в цепи с емкостью
Из графика видно, что мгновенная мощность, как и в цепи с индуктивностью, четыре раза в течение периода меняет знак. В первую четверть периода, когда напряжение на конденсаторе увеличивается, энергия накапливается в электрическом поле конденсатора за счет работы источника. Конденсатор в это время заряжается, т. е. является приемником энергии: направления тока и приложенного напряжения совпадают. Во вторую четверть периода, когда напряжение уменьшается, энергия в том же количестве возвращается в сеть (к источнику), ток в цепи направлен против напряжения сети, т. е. конденсатор является источником энергии (разряжается).
Проведя рассуждения, аналогичные тем, какие были вделаны для цепи с индуктивностью, найдем, что активная мощность в цепи с емкостью равна нулю (Р = 0), а реактивная мощность равна произведению действующих величин напряжения и тока:

Таким образом, в цепи с емкостью, так же как и в цепи с индуктивностью, преобразования электрической энергии в другие виды энергии (тепловую, механическую) не происходит.
Задача 13.7. Конденсатор имеет емкость С = 637 мкФ. Начертить график зависимости емкостного сопротивления и тока в конденсаторе от частоты приложенного напряжения, действующее значение которого U = 100 В остается неизменным.
Решение. Для решения задачи нужно задаться несколькими значениями частоты. Определить соответствующие величины емкостного сопротивления, а затем тока.
Для частоты 50 Гц

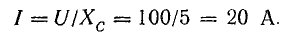
По результатам расчета для других частот (f = 0,25, 100, 500, 1000, 10 000 Гц) постройте и прямоугольной системе координат графики согласно условию задачи.
Цепь с реальной катушкой индуктивности
Реальная катушка отличается от идеальной тем, что переменный ток в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р , а изменение энергии в магнитном поле — реактивной мощностью Q .
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому в схеме замещения реальная катушка должна быть представлена активным и реактивным элементами.
Деление реальной катушки на два элемента искусственно, так как конструктивно оба элемента неразделимы. Однако такой же схемой замещения можно представить реальную цепь из двух конструктивно не совмещенных элементов, один из которых характеризуется только активной мощностью Р(Q = 0), а другой — реактивной (индуктивной) мощностью Q (Р = 0).
Схема замещения катушки с последовательным соединением элементов
В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.
Активное сопротивление определяется величиной мощности потерь
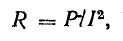
а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением 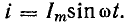 Требуется определить напряжение в цепи и мощность.
Требуется определить напряжение в цепи и мощность.
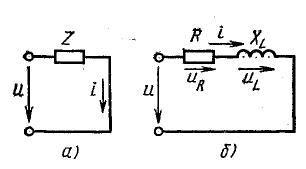
Рис. 13.9. Схема замещения реальной катушки индуктивности (цепь R, L)
При переменном токе в катушке возникает э. д. с. самоиндукции еL, поэтому ток зависит от действия приложенного напряжения и э. д. с. еL. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид
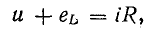
или
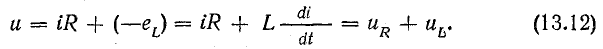
Приложенное к катушке напряжение состоит из двух слагаемых, одно из которых uR равно падению напряжения в активном сопротивлении, а другое 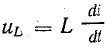 уравновешивает э. д. с. самоиндукции.
уравновешивает э. д. с. самоиндукции.
В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б).
Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам, полученным, uR совпадает по фазе с током, а uL опережает ток на 90°.
Поэтому
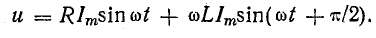
Векторная диаграмма напряжений. Полное сопротивление катушки
Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения
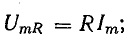
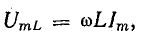
а действующие величины
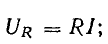
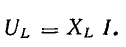
Вектор общего напряжения
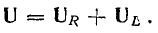
Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Мi и напряжения Мu.
За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока ψi = 0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.
Вектор UR по направлению совпадает с вектором тока I, а вектор UL направлен перпендикулярно вектору I с положительным углом.
Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ > 0, но <90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях UR и UL:

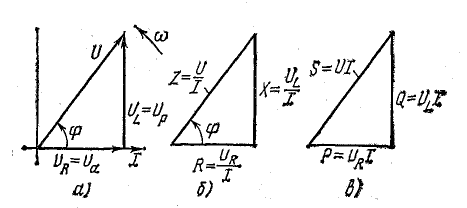
Рис. 13.10. Векторная диаграмма цепи, треугольники сопротивлений и мощностей
Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Для катушки по схеме рис. 13.9 при Uа = UR

Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается Uр. Для катушки Up = UL

При токе 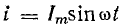 уравнение напряжения можно записать на основании векторной диаграммы в виде
уравнение напряжения можно записать на основании векторной диаграммы в виде
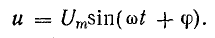
Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное 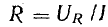 и индуктивное
и индуктивное 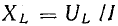 сопротивления, а гипотенузой — величина
сопротивления, а гипотенузой — величина 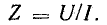
Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи. Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени.
Из треугольника сопротивлений следует

Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома (2.6):
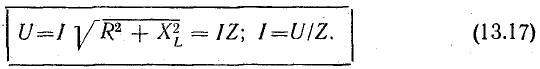
Из треугольников напряжений и сопротивлений определяются
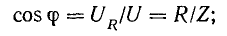
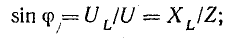
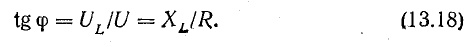
Мощность катушки
Мгновенная мощность катушки
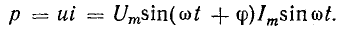
Из графика мгновенной мощности (рис. 13.11) видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется. Относительно некоторой оси t’, сдвинутой параллельно оси t на величину Р, график мгновенной мощности является синусоидальной функцией двойной частоты.
При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).
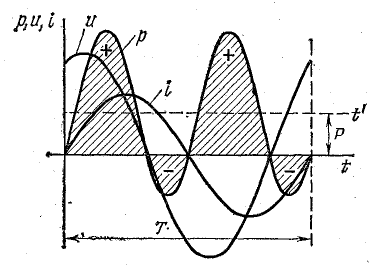
Рис. 13.11. График мгновенной мощности цепи
Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).
Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.
На основании выводов, в активном сопротивлении 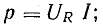
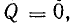 а в индуктивном
а в индуктивном 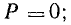
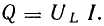
Активная мощность всей цепи равна активной мощности в сопротивлении R, а реактивная — реактивной мощности в индуктивном сопротивлении ХL . Подставляя значения 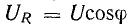 и
и 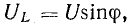 определяемые из треугольника напряжений по формулам (13.18), получим:
определяемые из треугольника напряжений по формулам (13.18), получим:


Кроме активной и реактивной мощностей пользуются понятием полной мощности S, которая определяется произведением действующих величин напряжения и тока цепи:

Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):
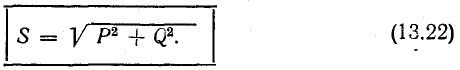
Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток.
Из треугольника мощностей можно определить
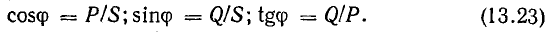
Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В • А).
Активная мощность Р меньше или равна полной мощности цепи. Отношение активной мощности цепи к ее полной мощности 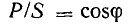 называют коэффициентом мощности.
называют коэффициентом мощности.
Назначение приемников электрической энергии — преобразование ее в другие виды энергии. Поэтому колебания энергии в цепи не только бесполезны, но и вредны, так как при этом в приемнике не совершается полного преобразования электрической энергии в работу или тепло, а в соединительных проводах она теряется.
Схема замещения катушки с параллельным соединением элементов
Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной ВL проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее.
Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.
Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством

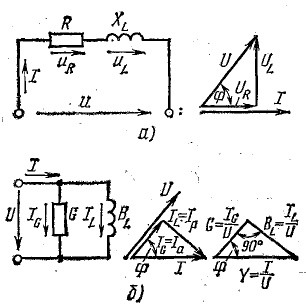
Рис. 13.12. Варианты схемы замещения катушки индуктивности
Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: IG — ток в ветви с активной проводимостью, по фазе совпадает с напряжением; IL — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.
Вектор тока I и его составляющие IG и ILобразуют прямоугольный треугольник, поэтому

Составляющая тока в активном элементе

Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается Iа. Для катушки по схеме на рис. 13.12, 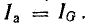
Составляющая тока в реактивном элементе

Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки Iр = IL .
Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная 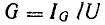 и индуктивная
и индуктивная 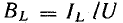 проводимости, а гипотенузой — величина
проводимости, а гипотенузой — величина 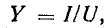 называемая полной проводимостью цепи.
называемая полной проводимостью цепи.
Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим
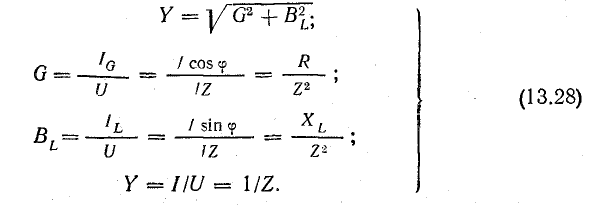
Кроме того,
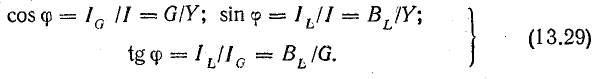
Задача 13.10.
Для определения параметров катушки R и L ее включили сначала в цепь постоянного тока, а затем в цепь переменного тока с частотой f = 50 Гц по схемам рис. 13.13, а, б.
При постоянном токе I1 = 4 А вольтметр показал U1 = 12 В, а при переменном I2 = 5А — U2 = 25 В. Определить активное сопротивление и индуктивность катушки и при переменном токе активную, реактивную и полную мощности. Построить векторную диаграмму и треугольник сопротивлений.
Решение. При постоянном токе э. д. с. самоиндукции в катушке не возникает. Поэтому индуктивное сопротивление ХL = 0. Ток определяется приложенным напряжением и активным сопротивлением.
По формуле Ома,
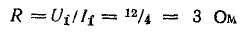
При переменном токе отношение напряжения к току даст величину полного сопротивления
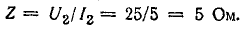
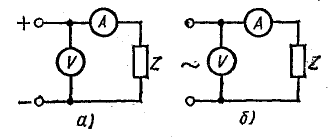
Рис. 13.13. к задаче 13.10
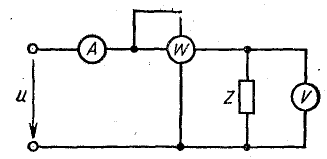
Рис. 13.14. К задачам 13.12, 13.13
Индуктивное сопротивление
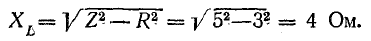
Индуктивность
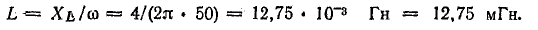
При разборе решения данной задачи на отдельном листе миллиметровой бумаги рекомендуется построить векторную диаграмму цепи и треугольники сопротивлений и мощностей, предварительно определив необходимые величины.
Задача 13.12.
В цепи переменного тока с активным сопротивлением и индуктивностью (рис. 13.14) при частоте f = 100 Гц измерительные приборы показывают: амперметр — 10 А, вольтметр — 200 В, ваттметр — 1600 Вт. Определить параметры схем замещения цепи с последовательным (R, XL) и параллельным (G, ВL) соединением элементов; реактивную и полную мощности цепи. Построить векторные диаграммы применительно к обеим схемам замещения.
Решение (для схемы замещения с последовательным соединением элементов).
Сопротивления:
активное
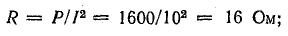
полное
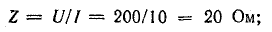
индуктивное
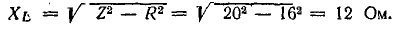
Мощности цепи:
реактивная
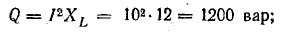
полная
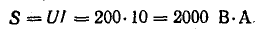
Для построения векторной диаграммы дополнительно определим активную и реактивную составляющие напряжения:
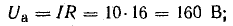
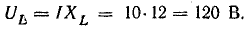
Векторная диаграмма показана на рис. 13.10, а.
Цепь с реальным конденсатором
При переменном напряжении на реальном конденсаторе кроме тока смещения имеются небольшие токи проводимости через толщу диэлектрика (объемный ток) и по поверхности (поверхностный ток). Токи проводимости и поляризацию диэлектрика сопровождают потери энергии.
Таким образом, в реальном конденсаторе наряду с изменением энергии электрического поля (это характеризует реактивная мощность Q) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в тепло, скорость которого выражается активной мощностью Р. Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами.
Деление реального конденсатора на два элемента — это расчетный прием, так как конструктивно их выделить нельзя. Однако такую же схему замещения имеет реальная цепь из двух элементов, один из которых характеризуется только активной мощностью Р (Q = 0), другой — реактивной (емкостной) мощностью Q(Р = 0).
Схема замещения конденсатора с параллельным соединением элементов
Реальный конденсатор (с потерями) можно представить эквивалентной схемой параллельного соединения активной G и емкостной Вс проводимостей (рис. 13.15), причем активная проводимость определяется мощностью потерь в конденсаторе 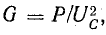 а емкость — конструкцией конденсатора .
а емкость — конструкцией конденсатора .
Предположим, что проводимости G и Вс для такой цепи известны, а напряжение имеет уравнение 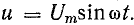
Требуется определить токи в цепи и мощность.
Исследование цепи с активным сопротивлением и цепи с емкостью показало, что при синусоидальном напряжении токи в них также синусоидальны.
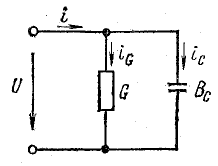
Рис. 13.15. Схема замещения реального конденсатора
При параллельном соединении ветвей G и Вс , согласно первому закону Кирхгофа, общий ток i равен сумме токов в ветвях с активной и емкостной проводимостями:

Учитывая, что ток iG совпадает по фазе с напряжением, а ток ic опережает напряжение на четверть периода, уравнение общего тока можно записать в следующем виде:
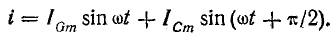
Так как
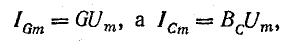
то
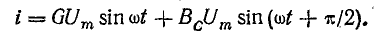
Векторная диаграмма токов
Для определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению
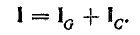
Действующие величины составляющих тока:


Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения 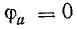 ).
).
Вектор IG совпадает по направлению с вектором U, а вектор Iс направлен перпендикулярно вектору U с положительным углом.
Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол φ, величина которого больше нуля, но меньше 90′.
Вектор I является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы IG и IC:
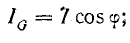
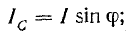
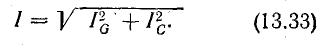
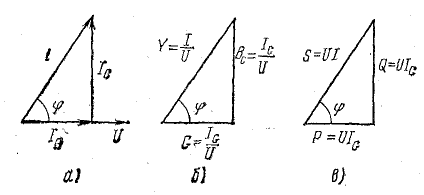
Рис. 13.16. Треугольники токов, проводимостей, мощностей
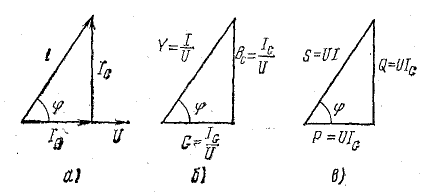
Рис. 13.17. График мгновенной мощности цепи
При напряжении  в соответствии с векторной диаграммой уравнение тока
в соответствии с векторной диаграммой уравнение тока
Треугольник проводимостей
Стороны треугольников токов, выраженные в единицах тока, разделим на напряжение U. Получим подобный треугольник проводимостей (рис. 13.16, б), катетами которого являются активная 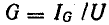 и емкостная
и емкостная 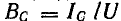 проводимости, а гипотенузой — полная проводимость цепи
проводимости, а гипотенузой — полная проводимость цепи 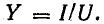
Из треугольника проводимостей

Связь между действующими величинами напряжения и тока выражается формулами
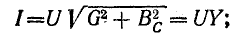
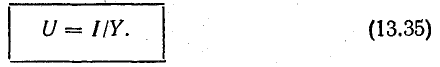
Из треугольников токов и проводимостей определяют величины
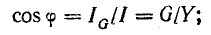
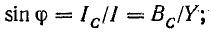
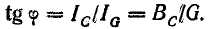
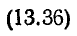
Мощность
Выражение мгновенной мощности реального конденсатора
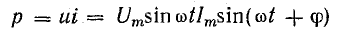
совпадает с выражением мгновенной мощности катушки.
Рассуждения, аналогичные тем, которые сделаны при рассмотрении графика мгновенной мощности катушки (см. рис.13. 11), можно провести и для реального конденсатора на основе графика рис. 13.17.
Величины активной, реактивной и полной мощностей выражаются теми же формулами, какие были получены для катушки [см. (13.19)— (13.22)].
Это нетрудно показать, если стороны треугольника токов, выраженные в единицах тока, умножить на напряжение U.
В результате умножения получится подобный треугольник мощностей (рис. 13.16, в), катетами которого являются мощности:
активная
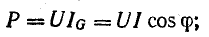
реактивная
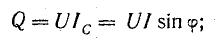
полная
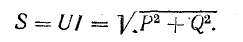
Схема замещения конденсатора с последовательным соединением элементов
Реальный конденсатор, так же как и катушка, на расчетной схеме может быть представлен последовательным соединением двух участков: с активным R и емкостным Хс сопротивлениями.
На рис. 13.18, а такая схема показана в сравнении со схемой параллельного соединения активной и емкостной проводимостей (рис.13.18, б). Все выводы и формулы, полученные для катушки, остаются в силе и для конденсатора при условии замены индуктивного сопротивления емкостным.
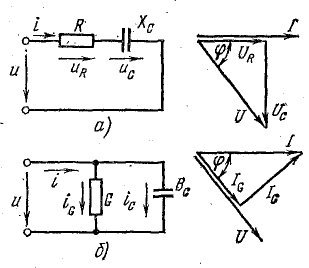
Рис. 13.18. Варианты схемы замещения реального конденсатора
Конденсаторы, применяемые на практике, имеют относительно малые потери энергии. Поэтому в схемах замещения они представлены чаще всего только реактивной частью, т. е. емкостью 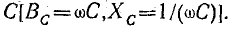
Участки цепи, где последовательно соединены отдельные элементы — резистор R и конденсатор С, имеют такую схему замещения, как показано на рис. 13.18, а.
Задача 13.13.
В цепи переменного тока с активным сопротивлением и емкостью (см. рис. 13.14) при частоте f = 100 Гц измерительные приборы показывают. амперметр — 6 А, вольтметр — 180 В, ваттметр — 360 Вт. Определите параметры схем замещения цепи с параллельным (G, ВL) и последовательным (R, ХC) соединением элементов: реактивную и полную мощности цепи. Постройте векторные диаграммы применительно к обеим схемам замещения.
Решение (для схемы замещения с параллельным соединением элементов). Проводимости:
активная
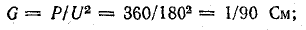
полная
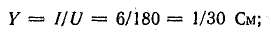
емкостная
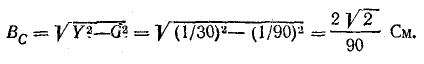
Мощности цепи
реактивная
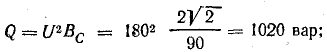
полная
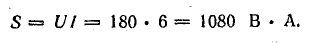
Для построения векторной диаграммы дополнительно определим активную и реактивную составляющие тока:
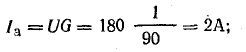
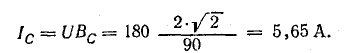
Векторная диаграмма показана на рис. 13.16, а.
Решить задачу для схемы с последовательным соединением элементов.
Расчет электрических цепей переменного тока с помощью векторных диаграмм
В данной главе будут рассмотрены электрические цепи переменного тока, содержащие три параметра R, L, С при последовательном, параллельном соединении резисторов, катушек и конденсаторов.
Расчет таких цепей можно вести на основе векторных диаграмм, из которых получаются расчетные формулы.
Последовательное соединение катушки и конденсатора
При последовательном соединении катушки и конденсатора на расчетной схеме каждый из этих элементов электрической цепи может быть представлен активным и реактивным сопротивлениями или активной и реактивной проводимостями.
Для расчета более простой является схема рис. 14.1, а, где элементы соединены последовательно, а в схеме рис. 14.1, б они соединены смешанно.
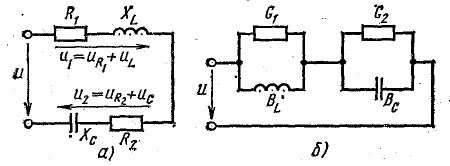
Рис. 14.1. Схемы замещения катушки и конденсатора при последовательном соединении
Предположим известными параметры катушки R1, L и конденсатора R2С; ток в цепи 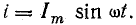
Требуется определить напряжение на участках цепи и мощность.
Векторная диаграмма и полное сопротивление цепи
Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:
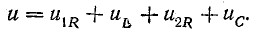
Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:
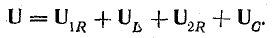
Для построения векторной диаграммы находим:
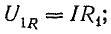
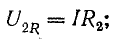
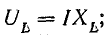
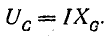
В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая.
1.  . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.
. Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.
Векторная сумма напряжений 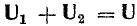 дает общее напряжение в цепи. Вместе с тем вектор UI является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения, цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются:
дает общее напряжение в цепи. Вместе с тем вектор UI является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения, цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: 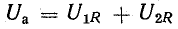 .
.
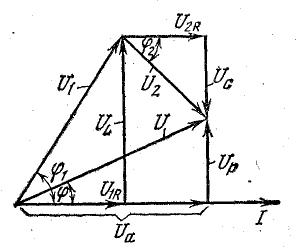
Рис. 14.2. Векторная диаграмма при ХL > ХC
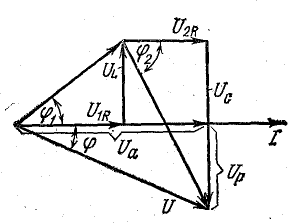
Рис. 14.3. Векторная диаграмма при ХL < X
Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: 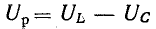
При одинаковом токе во всех элементах цепи 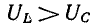 . Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует
. Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует
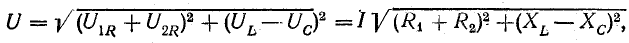
или
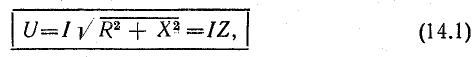
где 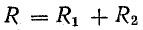 и
и 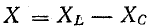 — общее активное и реактивное сопротивления цепи;
— общее активное и реактивное сопротивления цепи; 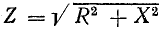 — полное сопротивление цепи.
— полное сопротивление цепи.
Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.
Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:
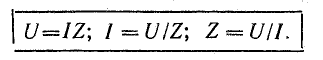
Из треугольников напряжения и сопротивлений определяют следующие величины:
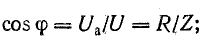
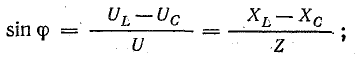
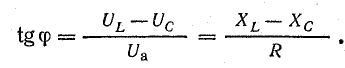
Угол сдвига по фазе между напряжением и током в цепи положительный (φ > 0) (фазовые углы отсчитываются от вектора тока).
2.  . Векторная диаграмма изображена на рис. 14.3, где UL < UC, поэтому общее напряжение отстает от тока на угол φ < 0.
. Векторная диаграмма изображена на рис. 14.3, где UL < UC, поэтому общее напряжение отстает от тока на угол φ < 0.
Реактивное сопротивление цепи носит емкостный характер. Расчетные формулы для первого случая остаются без изменения и для второго случая.
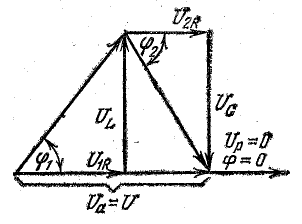
Рис. 14.4. Векторная диаграмма при XL = XC
3. 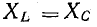 . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы:
. В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: 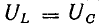 (рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R. Общее напряжение совпадает по фазе с током и равно по величине активной составляющей напряжения.
(рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R. Общее напряжение совпадает по фазе с током и равно по величине активной составляющей напряжения.
Угол φ сдвига фаз между током и общим напряжением равен нулю.
Ток в цепи и общее напряжение связаны формулой
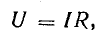 или
или 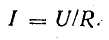
В случае ХL = ХC в цепи имеет место явление резонанса напряжений.
Энергетический процесс в цепи
Из треугольника напряжений легко получить треугольник мощностей, из которого следуют уже известные формулы:
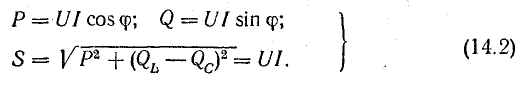
Реактивные мощности входят в расчеты также с разными знаками: индуктивная мощность положительна, а емкостная — отрицательна.
В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует и из формул (14.2).
При φ > 0 Q > 0; при φ < 0 Q < 0.
Активная мощность положительна при любом угле, так как 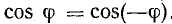
Полная мощность также всегда положительна.
На основании формул (14.2) можно сделать вывод, что в рассматриваемой цепи совершается преобразование электрической энергии 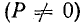 и обменный процесс между генератором и приемником
и обменный процесс между генератором и приемником 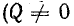 при
при 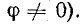
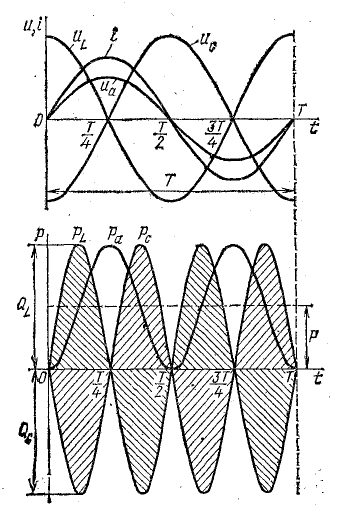
14.5. Графики u, i, p при XL = XC
Энергетические процессы в данном случае сложнее, чем в ранее рассмотренных простых цепях. Усложнение объясняется тем, что наряду с обменом энергией между генератором и приемником совершается обмен энергией внутри приемника, между катушкой и конденсатором.
Особенности энергетического процесса в цепи с последовательным соединением катушки и конденсаторов отражены на рис. 14.5, где показаны графики мгновенной мощности отдельных элементов и цепи в целом при 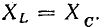
Катушка и конденсатор в течение полупериода накапливают равные количества энергии. Однако в первую четверть периода, когда ток увеличивается, а напряжение на конденсаторе уменьшается, энергия накапливается в магнитном поле катушки и уменьшается в электрическом поле конденсатора, причем скорость изменения энергии (мощность) в любой момент времени одинакова. Это дает основание считать, что обмен энергией происходит только в приемнике между катушками и конденсатором.
Для преобразования электрической энергии в другой вид приемник получает ее от генератора со средней скоростью (мощностью) Р.
Задача 14.1.
Конденсатор емкостью С = 3,4 мкФ и катушка с активным сопротивлением R = 50 Ом и индуктивностью L = 29,8 мГн подключены последовательно к генератору с напряжением U = 200 В (рис. 14.6). Определить ток, активную, реактивную и полную мощности катушки, конденсатора и всей цепи при неизменном напряжении генератора и трех значениях частоты: 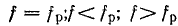 где fр — резонансная частота.
где fр — резонансная частота.
Решение. Для примера далее приведен расчет при частоте f = 250 Гц.
Реактивное сопротивление индуктивности
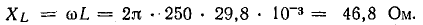
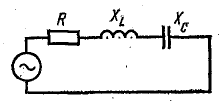
Рис. 14.6. К задаче 14.1
Реактивное сопротивление емкости
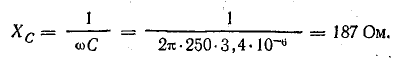
Полное сопротивление
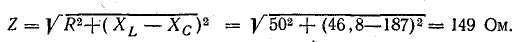
Ток в цепи
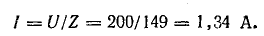
Угол сдвига фаз между током и напряжением
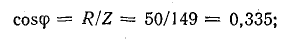

Активная мощность
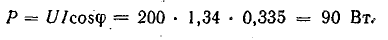
Реактивная мощность индуктивности
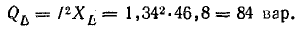
Реактивная мощность емкости
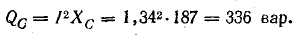
Реактивная мощность цепи
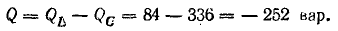
Сделать аналогичный подсчет для частот: f = fр; f < fр; f > fр.
Расчет неразветвленных цепей переменного тока
Порядок расчета, установленный для цепи при последовательном соединении катушки и конденсатора, можно применить и для цепи, содержащей произвольное число катушек и конденсаторов, соединенных последовательно.
На рис. 14.7, а для примера дана схема неразветвленной цепи, состоящей из пяти участков: конденсатора (R1, Х1) и катушки (R2, Х2), представленных активными и реактивными сопротивлениями; резистора R3; идеальных конденсатора Х4 и катушки Х5.
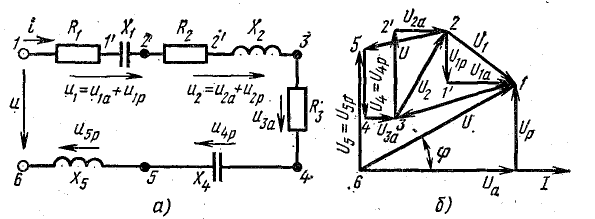
Рис. 14.7. Расчетная схема неразветвленной цепи и ее векторная диаграмма
Предположим, что кроме сопротивлений известен ток в цепи i = Imsinωt.
Требуется найти напряжения на участках, общее напряжение в цепи и мощность.
Векторная диаграмма
Выберем условно-положительное направление тока i, как указано на схеме. Для мгновенных величин в соответствии со вторым законом Кирхгофа уравнение напряжений
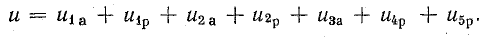
Переходя к действующим величинам напряжений, нужно написать векторную сумму:
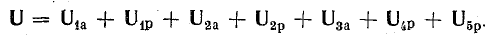
Численно векторы напряжений определяются произведением тока и сопротивления соответствующего участка.
На рис. 14.7, б построена векторная диаграмма, соответствующая этому уравнению. За исходный, как обычно при расчете неразветвленных цепей, принят вектор тока, а затем проведены векторы падения напряжения на каждом участке схемы, причем направления их относительно вектора тока выбраны в соответствии с характером сопротивления участков.
При построении диаграммы напряжений начальной точкой выбрана точка 6, совпадающая с началом вектора тока I. Из этой точки проведен вектор U5р реактивного напряжения индуктивности (по фазе опережает ток на 90°) между точками 5 и 6 цепи. Из конца его проведен вектор U4р реактивного напряжения емкости (по фазе отстает от тока на 90°) между точками 4 и 5 цепи. Затем отложен вектор U3a активного напряжения на резисторе (совпадает по фазе с током) между точками 3 и 4 цепи и т. д., если следовать по цепи против направления тока. Точки векторной диаграммы, где сходятся начало следующего вектора с концом предыдущего, обозначены теми же номерами, какими на схеме обозначены точки, отделяющие один элемент от другого.
При таком, построении напряжение между любыми двумя точками цепи можно найти по величине и фазе, проведя вектор на диаграмме между точками с теми же номерами. Например, напряжение U5.2 между точками 5 и 2 выражается вектором, проведенным из точки 2 в точку 5 (вектор U5.2 направлен в обратную сторону); напряжение U3.1 между точками 3 и 1 выражается вектором, проведенным из точки 1 в точку 3.
Векторная диаграмма, построенная в соответствии с чередованием элементов цепи, называется топографической, так как точки, отделяющие векторы друг от друга, соответствуют точкам, разделяющим элементы схемы.
Расчетные формулы
Из векторной диаграммы видно, что все активные составляющие векторов напряжений направлены одинаково — параллельно вектору тока, поэтому векторное сложение их можно заменить арифметическим и найти активную составляющую напряжения цепи: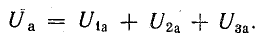
Реактивные составляющие векторов напряжений перпендикулярны вектору тока, причем индуктивные напряжения направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая напряжения цепи Uр определяется их алгебраической суммой, в которой индуктивные напряжения считаются положительными, а емкостные — отрицательными: 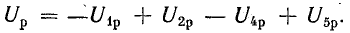
Векторы активного, реактивного и полного напряжений цепи образуют прямоугольный треугольник, из которого следует

Подставив падения напряжения, выраженные через ток и соответствующие сопротивления, получим:
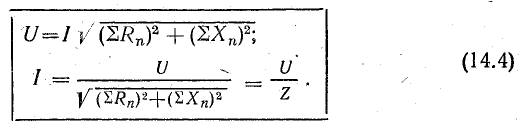
Таким образом снова получена знакомая уже формула, связывающая ток, напряжение и полное сопротивление цепи [ср. (14.4) и (14.1)].
В этой формуле 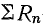 — общее активное сопротивление, равно арифметической сумме всех активных сопротивлений, входящих в неразветвленную цепь;
— общее активное сопротивление, равно арифметической сумме всех активных сопротивлений, входящих в неразветвленную цепь; 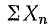 — общее реактивное сопротивление, равное алгебраической сумме всех реактивных сопротивлений, входящих в неразветвленную цепь. В этой сумме индуктивные сопротивления считаются положительными, а емкостные —отрицательными. Полное сопротивление неразветвленной цепи
— общее реактивное сопротивление, равное алгебраической сумме всех реактивных сопротивлений, входящих в неразветвленную цепь. В этой сумме индуктивные сопротивления считаются положительными, а емкостные —отрицательными. Полное сопротивление неразветвленной цепи
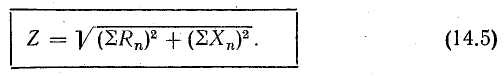
В общем случае полное сопротивление цепи определяется как гипотенуза прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активное и реактивное сопротивления всей цепи. Из треугольника сопротивлений следует:
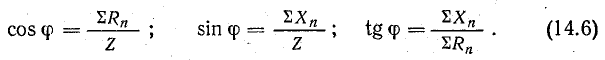
От треугольника напряжений можно перейти также к треугольнику мощностей и получить уже известные формулы для определения мощностей в цепи:
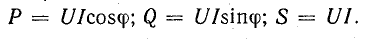
Вместе с тем активную мощность цепи можно представить как арифметическую сумму активных мощностей в элементах с активным сопротивлением. Реактивная мощность цепи равна алгебраической сумме мощностей реактивных элементов.
В этой сумме мощность индуктивных элементов считается положительной, а емкостных — отрицательной:
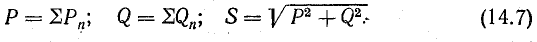
Формулы (14.2)—(14.7) являются общими; из них можно получить конкретное выражение для любой неразветвленной цепи.
Задача 14.3.
Определить ток и составить баланс мощностей для цепи, схема которой изображена на рис. 14.8. Построить топографическую диаграмму и по ней определить напряжение U8.5 между точками 8 и 5 и U6.1 между точками 6 и 1.
Дано:
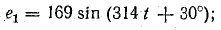
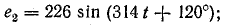
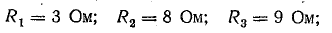
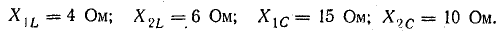
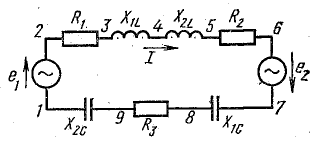
Рис. 14.8. К задаче 14.3
Решение. Согласно второму закону Кирхгофа, составим уравнение напряжений в векторной форме, предварительно выбрав условно-положительные направления э. д. с. и тока в схеме (их целесообразно выбрать одинаковыми независимо от того, в каком режиме работает источник э. д. с., так как фазовый угол сдвига, полученный в результате расчета, укажет истинный режим его работы):
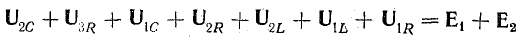
или
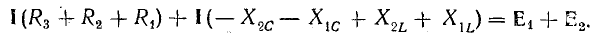
Общее активное сопротивление
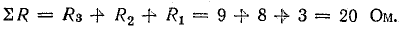
Общее реактивное сопротивление
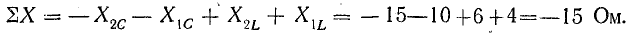
Как видно, общее реактивное сопротивление имеет емкостный характер. Полное сопротивление цепи
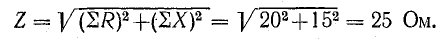
Действующие величины э. д. с.:
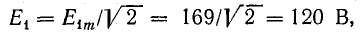
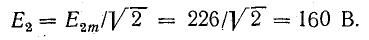
Для определения действующей величины суммы двух э. д. с. ( Е1 + Е2) построим векторную диаграмму (рис. 14.9, а) (рекомендуется построить на отдельном листе миллиметровой бумаги в масштабе Ми = 40 В/см).
Измерение вектора Е показывает, что величина суммарной э. д. с. Е = 200 В. Э. д. с. можно найти, учитывая, что ее составляющие взаимно перпендикулярны. В этом случае
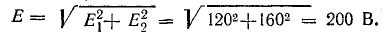
Ток
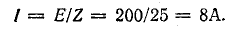
Напряжения на отдельных участках схемы:
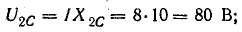
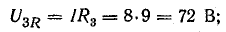
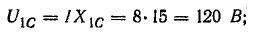
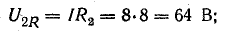
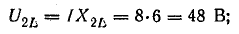
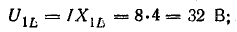
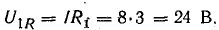
Для построения векторной топографической диаграммы (рис. 14.9, б) выберите масштабы Мi = 2 А/см; Ми = 40 В/см (рекомендуется построить на отдельном листе миллиметровой бумаги).
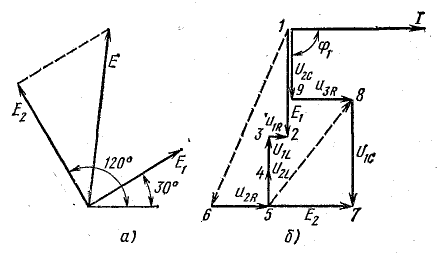
Рис. 14.9. К задаче 14.3
По векторной диаграмме найдены углы сдвига фаз между током и э. д. с. Е1 и Е2: φ1 = –90°, φ2 = 0.
Мощности участков приемника:
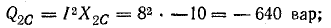
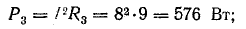
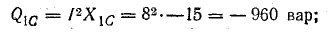
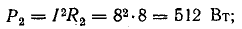
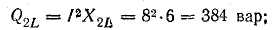
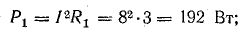
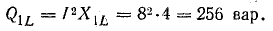
Мощности источников:
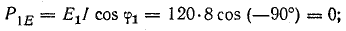
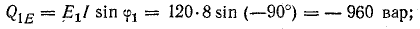
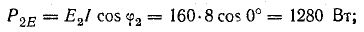
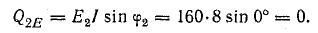
Баланс мощностей:
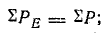
1280 = 192 + 576 + 512 = 1280;
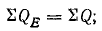
— 960 = — 640— 960 + 384 + 256 = — 960.
Реактивные мощности емкостного характера Q2С, Q1С и Q1E и отрицательны, так как между векторами напряжений и токов, определяющими их, углы отрицательны.
Для определения напряжений U8.5 и U6.1, проведем векторы между соответствующими точками топографической диаграммы. Вектор направляется к точке, стоящей первой в обозначении напряжения. Например, вектор U8.5 направлен в точку 8 из точки 5. Измерение векторов U8.5 и U6.1 дает:
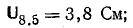
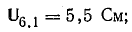
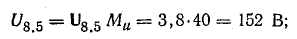
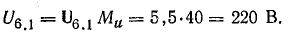
Параллельное соединение катушки и конденсатора
Для рассмотрения параллельного соединения катушки и конденсатора представим их на схеме активными и реактивными проводимостями (рис. 14.11, а).
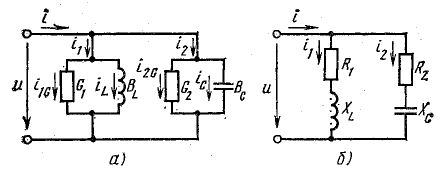
Рис. 14.11. Схемы замещения катушки и конденсатора при параллельном соединении
На схеме рис. 14.11, б те же катушки и конденсатор представлены активными и реактивными сопротивлениями. Первая схема имеет некоторое преимущество, так как в ней все элементы соединены параллельно, а в другой они соединены смешанно.
Считая известными параметры катушки G1, ВL и конденсатора G2, Вс, а также напряжение 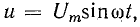 , определим токи в цепи и ее мощность.
, определим токи в цепи и ее мощность.
Векторная диаграмма цепи. Полная проводимость цепи
Согласно первому закону Кирхгофа, мгновенная величина общего тока равна сумме мгновенных токов отдельных ветвей:
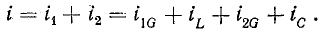
Имея в виду несовпадение по фазе активных и реактивных токов, величину общего тока найдем векторным сложением:
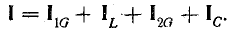
Для построения векторной диаграммы находим:
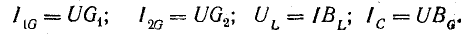
В зависимости от соотношения величин реактивных проводимостей ветвей с индуктивностью и емкостью можно отметить три случая.
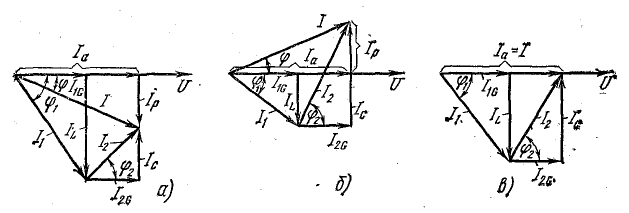
Рис. 14.12. Векторные диаграммы:
1.  Для этого случая векторная диаграмма представлена на рис. 14.12, а. На диаграмме построены треугольники токов для катушки и конденсатора и найдены векторы токов I1 и I2 в этих элементах:
Для этого случая векторная диаграмма представлена на рис. 14.12, а. На диаграмме построены треугольники токов для катушки и конденсатора и найдены векторы токов I1 и I2 в этих элементах:
Векторная сумма токов 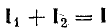 дает общий ток в цепи. Вместе с тем вектор I является гипотенузой прямоугольного треугольника токов, катеты которого — составляющие вектора тока по двум взаимно перпендикулярным осям:
дает общий ток в цепи. Вместе с тем вектор I является гипотенузой прямоугольного треугольника токов, катеты которого — составляющие вектора тока по двум взаимно перпендикулярным осям:
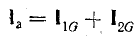 — активная составляющая;
— активная составляющая;
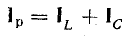 — реактивная составляющая.
— реактивная составляющая.
Векторы активных составляющих токов направлены в одну сторону, поэтому их численные значения складываются. Векторы реактивных составляющих токов направлены перпендикулярно вектору напряжения в противоположные стороны, поэтому им даются разные знаки: индуктивные токи считаются положительными, а емкостные — отрицательными. При одинаковом напряжении на всех элементах цепи  Общий ток отстает от общего напряжения по фазе на угол φ. Из треугольника токов следует
Общий ток отстает от общего напряжения по фазе на угол φ. Из треугольника токов следует
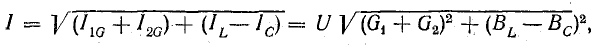
или
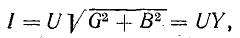
где 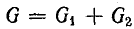 и
и 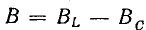 — общие активная и реактивная проводимости цепи;
— общие активная и реактивная проводимости цепи; 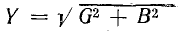 — полная проводимость цепи.
— полная проводимость цепи.
Эти три проводимости графически можно изобразить сторонами прямоугольного треугольника проводимостей, который получается уже известным способом из треугольника токов.
Полная проводимость цепи У является коэффициентом пропорциональности между действующими величинами общего тока и напряжения цепи:
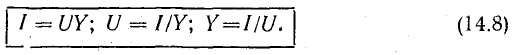
Из треугольников токов и проводимостей определяются величины:
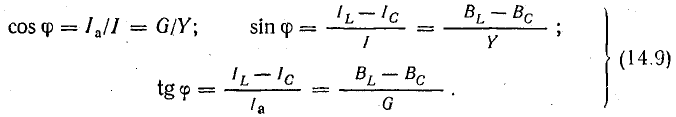
Угол сдвига по фазе между напряжением и общим током в цепи положительный (φ > 0) (фазовые углы отсчитываются от вектора тока).
2. 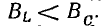 Векторная диаграмма изображена на рис. 14.12, б. Так как
Векторная диаграмма изображена на рис. 14.12, б. Так как 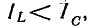 то напряжение отстает от общего тока на угол φ < 0.
то напряжение отстает от общего тока на угол φ < 0.
Реактивная проводимость цепи имеет емкостный характер. Расчетные формулы, полученные для случая 1, действительны и для этого случая.
3. 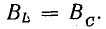 В этом случае реактивные составляющие токов катушки и конденсатора равны по величине:
В этом случае реактивные составляющие токов катушки и конденсатора равны по величине:  Реактивная составляющая общего тока и общая реактивная проводимость равны нулю. Общий ток совпадает по фазе с напряжением и равен по величине активной составляющей тока. Угол φ сдвига фаз между общим током и напряжением равен нулю.
Реактивная составляющая общего тока и общая реактивная проводимость равны нулю. Общий ток совпадает по фазе с напряжением и равен по величине активной составляющей тока. Угол φ сдвига фаз между общим током и напряжением равен нулю.
Общий ток в цепи и напряжение связаны формулой
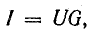 , или
, или 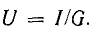
В случае 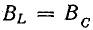 в цепи имеет место резонанс токов.
в цепи имеет место резонанс токов.
Энергетический процесс в цепи
Из векторной диаграммы токов легко получить треугольник мощностей, из которого следуют те же формулы (14.2), которые были получены для последовательного соединения катушки и конденсатора.
Реактивные мощности индуктивности и емкости входят в расчет с разными знаками: реактивная мощность индуктивности положительна, а реактивная мощность емкости отрицательна. В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует из формул (14.2).
Если φ > 0, то Q > 0; при φ < 0 Q < 0.
Активная мощность положительна при любом значении угла. Полная мощность тоже всегда положительна.
В рассматриваемой цепи активная мощность имеет определенную величину  следовательно, имеет место преобразование электрической энергии в другой вид. Кроме того, часть энергии, полученной от генератора, возвращается обратно в генератор
следовательно, имеет место преобразование электрической энергии в другой вид. Кроме того, часть энергии, полученной от генератора, возвращается обратно в генератор  при
при  Обмен энергией совершается также между катушкой и конденсатором.
Обмен энергией совершается также между катушкой и конденсатором.
Задача 14.5.
В цепи, схема которой изображена на рис. 14.13, определить ток, активную, реактивную и полную мощность катушки, конденсатора и всей цепи при неизменном напряжении U = 200 В и частоте источника f = 100 Гц. Параметры цепи: R1 = 10 Ом, L = 55,2 мГн, С = 138 мкФ, R2 = 0.
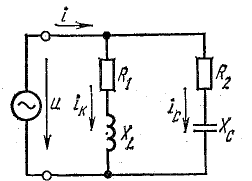
Рис. 14.13. К задаче 14.5
Решение. При частоте f = 100 Гц индуктивное сопротивление первой ветви
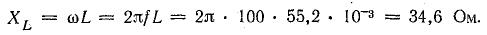
Проводимости:
активная
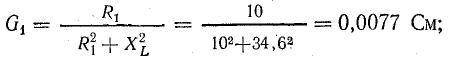
реактивная
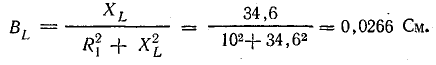
Полная проводимость катушки
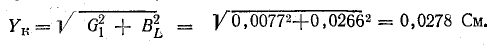
Проводимости второй ветви:
активная

реактивная
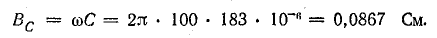
Полная проводимость цепи
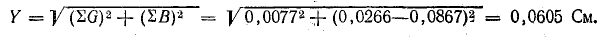
Токи:
в неразветвленной части цепи
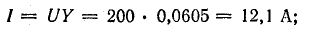
в конденсаторе
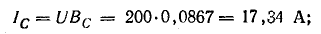
в катушке
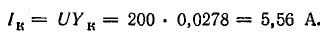
Коэффициент мощности цепи
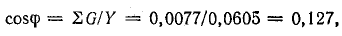
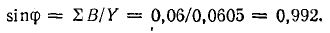
Реактивные мощности:
катушки
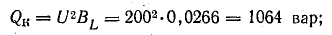
конденсатора
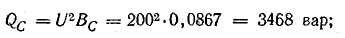
цепи
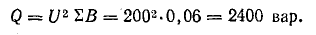
Активная мощность цепи
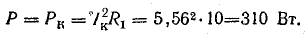
Полные мощности:
катушки
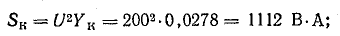
конденсатора
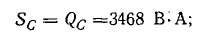
цепи
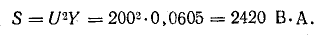
Задача 14.6.
Для схемы рис. 14.13 по данным условия задачи 14.5 найти резонансную частоту fр. Выполнить расчет цепи в порядке, изложенном при решении задачи 14.4, для двух значений частоты источника: 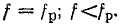
Решение. При резонансе 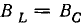 , т. е.
, т. е.
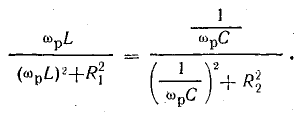
Решая относительно резонансной частоты, можно получить формулу
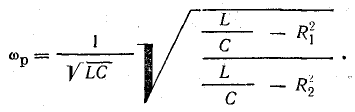
Учитывая, что R2 = 0, и подставляя другие данные, получим:
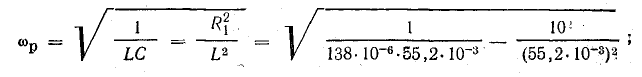
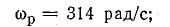
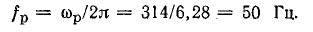
Далее расчет цепи по условию задачи выполните самостоятельно.
Расчет цепей с параллельным соединением ветвей
Расчет электрической цепи, рассмотренный в предыдущем параграфе, можно распространить на цепи, содержащие произвольное число приемников, соединенных параллельно.
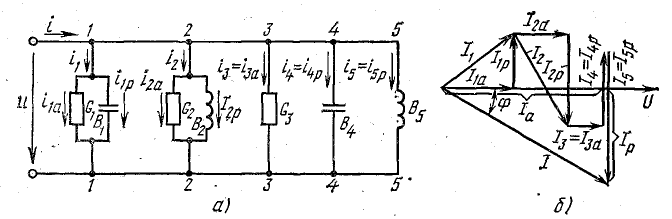
Рис. 14.14. Расчетная схема разветвленной цепи с двумя узлами и ее векторная диаграмма
На рис. 14.14, а параллельно соединены те же элементы цепи, были рассмотрены при последовательном соединении (см. рис. 14.7, а). Предположим, что для этой цепи известны напряжение 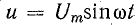 и параметры элементов цепи R, L, C. Требуется найти токи в цепи и мощность.
и параметры элементов цепи R, L, C. Требуется найти токи в цепи и мощность.
Векторная диаграмма
Для мгновенных величин в соответствии с первым законом Кирхгофа уравнение токов
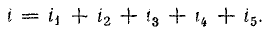
Представляя ток в каждой ветви суммой активной и реактивной составляющих, получим
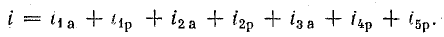
Для действующих токов нужно написать векторное уравнение
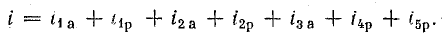
Численные значения векторов токов определяются произведением напряжения и проводимости соответствующей ветви.
На рис. 14.14, б построена векторная диаграмма, соответствующая этому уравнению. За исходный вектор принят, как обычно при расчете цепей с параллельным соединением ветвей, вектор напряжения U, а затем нанесены векторы тока в каждой ветви, причем направления их относительно вектора напряжения выбраны в соответствии с характером проводимости ветвей. Начальной точкой при построении диаграммы токов выбрана точка, совпадающая с началом вектора напряжения . Из этой точки проведен вектор I1а активного тока ветви I-I (по фазе совпадает с напряжением), а из конца его проведен вектор I1p реактивного тока той же ветви (опережает напряжение на 90°). Эти два вектора являются составляющими вектора I1 тока первой ветви. Далее в том же порядке отложены векторы токов других ветвей. Следует обратить внимание на то, что проводимость ветви 3-3 активная, поэтому реактивная составляющая тока в этой ветви равна нулю. В ветвях 4-4 и 5-5 проводимости реактивные, поэтому в составе этих токов нет активных составляющих.
Расчетные формулы
Из векторной диаграммы видно, что все активные составляющие векторов тока направлены одинаково — параллельно вектору напряжения, поэтому векторное сложение их можно заменить арифметическими найти активную составляющую общего тока: 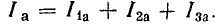
Реактивные составляющие векторов токов перпендикулярны вектору напряжения, причем индуктивные токи направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая общего тока в цепи определяется их алгебраической суммой, в которой индуктивные токи считаются положительными, а емкостные — отрицательными: 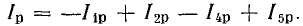
Векторы активного, реактивного и полного тока всей цепи образуют прямоугольный треугольник, из которого следует

Подставив величины токов в ветвях, выраженные через напряжение и соответствующие проводимости, получим
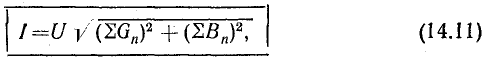
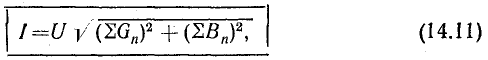
где 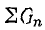 — общая активная проводимость, равная арифметической сумме активных проводимостей всех ветвей;
— общая активная проводимость, равная арифметической сумме активных проводимостей всех ветвей; 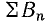 — общая реактивная проводимость, равная алгебраической сумме реактивных проводимостей всех ветвей (в этой сумме индуктивные проводимости считаются положительными, а емкостные — отрицательными); Y — полная проводимость цепи;
— общая реактивная проводимость, равная алгебраической сумме реактивных проводимостей всех ветвей (в этой сумме индуктивные проводимости считаются положительными, а емкостные — отрицательными); Y — полная проводимость цепи;
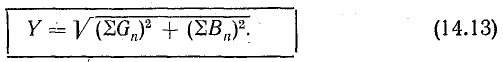
Таким образом получена знакомая уже формула (14.12), связывающая напряжение, ток и проводимость цепи [ср. (14.12) и (14.8)].
Следует обратить внимание на возможные ошибки при определении полной проводимости цепи по известным проводимостям отдельных ветвей: нельзя складывать арифметически проводимости ветвей, если токи в них не совпадают по фазе.
Полную проводимость цепи в общем случае определяют как гипотенузу прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активная и реактивная проводимости всей цепи:
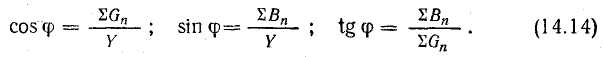
От треугольника токов можно перейти также к треугольнику мощностей и для определения мощности получить известные уже формулы
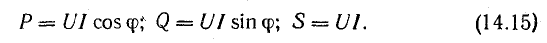
Активную мощность цепи можно представить как арифметическую сумму активных мощностей ветвей.
Реактивная мощность цепи равна алгебраической сумме мощностей ветвей. В этом случае индуктивная мощность берется положительной, а емкостная — отрицательной:
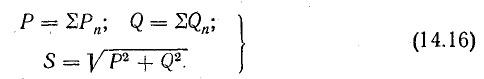
Расчет цепи без определения проводимостей ветвей
Расчет электрической цепи при параллельном соединении ветвей можно выполнить без предварительного определения активных и реактивных проводимостей, т. е. представляя элементы цепи в схеме замещения их активными и реактивными сопротивлениями (рис. 14.15, а).
Определяют токи в ветвях по формуле (14.4):
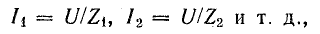
где Z1, Z2 и т. д. — полные сопротивления ветвей.
Полное сопротивление ветви, в которую входят несколько элементов, соединенных последовательно, определяют по формуле (14.5).
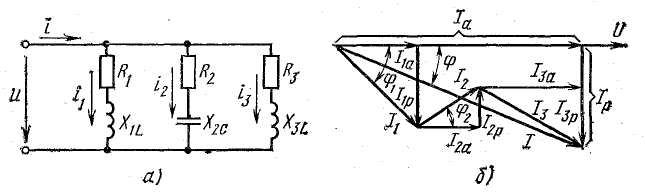
Рис. 14.15. Схема электрической цепи и ее векторная диаграмма
Для построения векторной диаграммы токов (рис. 14.15, б) можно определить активную и реактивную составляющие тока каждой ветви по формулам
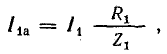
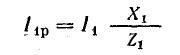
и т. д. для всех ветрей.
В этом случае отпадает необходимость определения углов φ1, φ2 и построения их на чертеже.
Ток в неразветвленной части цепи
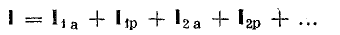
Общий ток и мощность цепи определяются далее в том же порядке, какой был показан ранее [см. формулы (14.10), (14.15), (14.16)].
Задача 14.7.
Определить ток в неразветвленной части цепи (рис. 14.16, а), активную, реактивную и полную мощности всей цепи. Построить векторную диаграмму токов и напряжений. Дано: R1 = 6 Ом, L1 = 25,5 мГн, R2 = 20 Ом, R2 = 15 Ом; L3 = 47,9 мГн, С3 = 159 мкФ, и 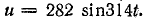
Решение. Реактивные сопротивления ветвей:
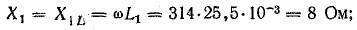
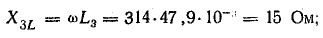
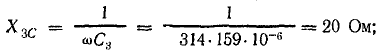
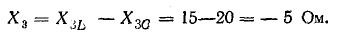
Полные сопротивления ветвей:
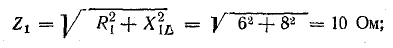
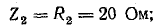
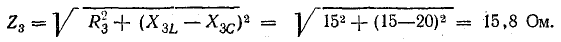
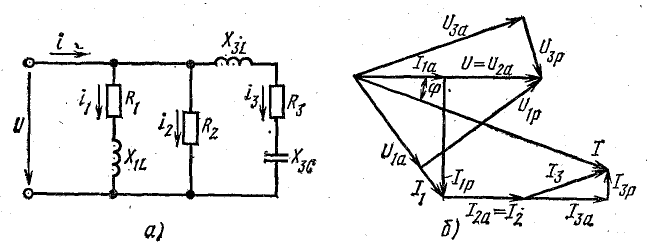
Рис. 14.16. к задаче 14.7
Действующее, напряжение
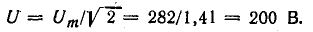
Токи в ветвях:
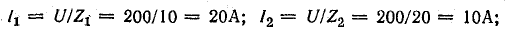
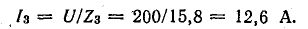
Составляющие токов ветвей:
активные
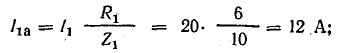
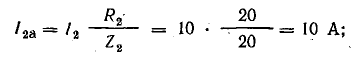
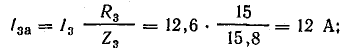
реактивные
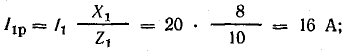
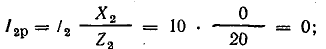
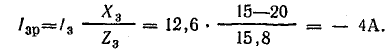
Общий ток:
активный
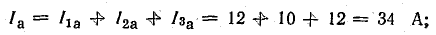
реактивный
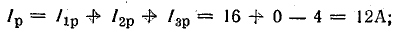
в неразветвленной части цепи
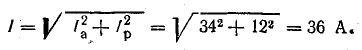
Активные мощности:
ветвей
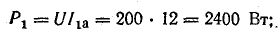
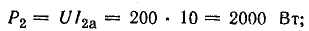
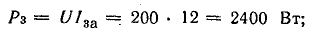
всей цепи
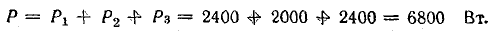
Реактивные мощности:
ветвей
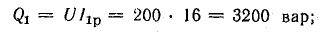
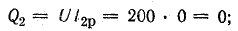
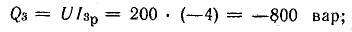
всей цепи
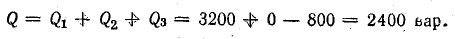
Полная мощность цепи
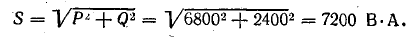
Проверка правильности подсчета мощности:
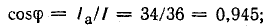
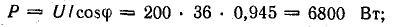
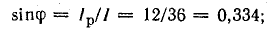
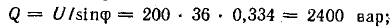
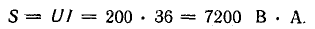
Для построения векторной диаграммы дополнительно определим активные и реактивные напряжения ветвей:
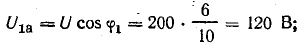
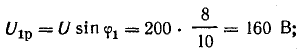
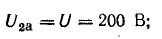
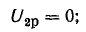
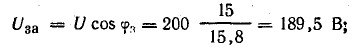
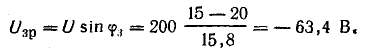
Векторная диаграмма показана на рис. 14.16, б.
- Символический метод расчета цепей
- Четырехполюсники
- Линейные диаграммы
- Круговые диаграммы
- Энергия в электрических цепях
- Линейные электрические цепи
- Нелинейные электрические цепи
- Магнитные цепи и их расчёт
При исследовании электрических цепей и моделировании часто пользуются векторными диаграммами токов и напряжений. Под векторной диаграммой понимается совокупность векторов, изображающих синусоидальные функции времени [1].
Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.
- Представление синусоидальных функций в виде комплексных чисел
- Закон Ома в комплексной форме
- Векторная диаграмма при последовательном соединении элементов
- Векторная диаграмма при параллельном соединении элементов
Представление синусоидальных функций в виде комплексных чисел
Векторная диаграмма – это удобный инструмент представления синусоидальных функций времени, коими являются, к примеру, напряжения и токи электрической цепи переменного тока.
Рассмотрим, например, произвольный ток, представленный в виде синусоидальной функции
$$ i(t) = 10 sin(omega t + 30 degree). $$
Данный синусоидальный сигнал можно представить в виде комплексной величины
$$ underline{I} = 10 angle 30 degree. $$
Для формирования комплексного числа используются модуль и фаза синусоидального сигнала.
Закон Ома в комплексной форме
Известно [1], что напряжение $ underline{U} $ на сопротивлении $ underline{Z} $ связано с током $ underline{I} $, протекающим через это сопротивление, согласно закону Ома:
$$ underline{U} = underline{Z} cdot underline{I}. $$
Кроме того, известны соотношения, определяющие активное сопротивление резистора, индуктивное сопротивление катушки и ёмкостное сопротивление конденсатора:
$$ underline{Z}_{R} = R, $$
$$ underline{Z}_{L} = jX_{L}, $$
$$ underline{Z}_{L} = -jX_{C}, $$
где $ X_{L} = omega L $, $ X_{C} = frac{1}{omega C} $, $ R $ – сопротивление резистора, $ L $ – индуктивность катушки, $ C $ – ёмкость конденсатора, $ omega = 2 pi f $ – циклическая частота, $ f $ – частота сети, $ j $ – мнимая единица.
Векторная диаграмма при последовательном соединении элементов
Для построения векторных диаграмм сперва составляют уравнения по законам Кирхгофа для рассматриваемой электрической цепи.
Рассмотрим электрическую цепь, представленную на рис. 1, и нарисуем для неё векторную диаграмму напряжений. Обозначим падение напряжение на элементах.
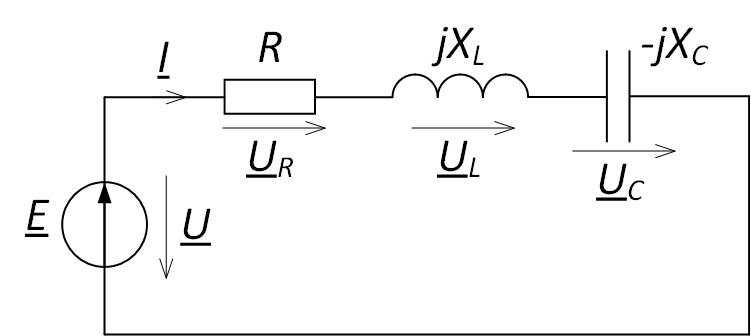 Рис. 1. Последовательное соединение элементов цепи
Рис. 1. Последовательное соединение элементов цепи
Составим уравнение для данной цепи по второму закону Кирхгофа:
$$ underline{U}_{R} + underline{U}_{L} + underline{U}_{C} = underline{E}. $$
По закону Ома падение напряжений на элементах определяется по следующим выражениям:
$$ underline{U}_{R} = underline{I} cdot R, $$
$$ underline{U}_{L} = underline{I} cdot jX_{L}, $$
$$ underline{U}_{C} = -underline{I} cdot jX_{C}. $$
Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости. Обычно вектора токов и напряжений отображаются в своих масштабах: отдельно для напряжений и отдельно для токов.
Из курса математики известно, что $ j = 1 angle 90 degree $, $ -j = 1 angle -90 degree $. Отсюда при построении векторной диаграммы умножение какого-либо вектора на мнимую единицу $ j $ приводит к повороту этого вектора на 90° против часовой стрелки, а умножение на $ -j $ приводит к повороту этого вектора на 90° по часовой стрелке.
При построении векторной диаграммы напряжений на комплексной плоскости сперва отобразим вектор тока $ underline{I} $, после чего относительного него будем отображать вектора падений напряжений (рис. 2) с учётом приведённых выше соотношений для мнимой единицы.
Падение напряжения на резисторе $ underline{U}_{R} $ совпадает по направлению с током $ underline{I} $ (т.к. $ underline{U}_{R} = underline{I} cdot R $, а $ R $ – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Падение напряжения на индуктивном сопротивлении опережает вектор тока на 90° (т.к. $ underline{U}_{L} = underline{I} cdot jX_{L} $, а умножение на $ j $ приводит повороту этого вектора на 90° против часовой стрелки). Падение напряжения на ёмкостном сопротивлении отстаёт от вектора тока на 90° (т.к. $ underline{U}_{C} = -underline{I} cdot jX_{C} $, а умножение на $ -j $ приводит повороту этого вектора на 90° по часовой стрелке).

Рис. 2. Векторная диаграмма напряжений при последовательном соединении элементов цепи
Следует обратить внимание, что на одной векторной диаграмме изображают только векторы тех величин, у которых частота совпадает!
Векторная диаграмма при параллельном соединении элементов
Рассмотрим электрическую цепь, представленную на рис. 3, и нарисуем для неё векторную диаграмму токов. Обозначим направление токов в ветвях.
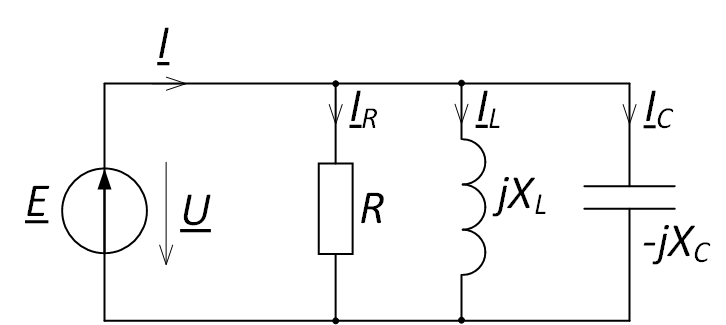
Рис. 3. Параллельное соединение элементов цепи
Составим уравнение для данной цепи по первому закону Кирхгофа:
$$ underline{I}- underline{I}_{R}- underline{I}_{L}- underline{I}_{C} = 0, $$
откуда
$$ underline{I} = underline{I}_{R} + underline{I}_{L} + underline{I}_{C} = 0. $$
Определим по закону Ома токи в ветвях по следующим выражениям, учитывая, что $ frac{1}{j} = -j $:
$$ underline{I}_{R} = frac{underline{E}}{R}, $$
$$ underline{I}_{L} = frac{underline{E}}{jX_{L}} = -j frac{underline{E}}{X_{L}}, $$
$$ underline{I}_{C} = frac{underline{E}}{-jX_{C}} = j frac{underline{E}}{X_{C}}. $$
Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости.
При построении векторной диаграммы токов на комплексной плоскости сперва отобразим вектор ЭДС $ underline{E} $, после чего относительного него будем отображать вектора токов токов (рис. 4) с учётом приведённых выше соотношений для мнимой единицы.
Ток в резисторе IR совпадает по направлению с ЭДС $ underline{E} $ (т.к. $ underline{I}_{R} = frac{underline{E}}{R} $, а $ R $ – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Ток в индуктивном сопротивлении отстаёт от вектора ЭДС на 90° (т.к. $ underline{I}_{L} = -j frac{underline{E}}{X_{L}} $, а умножение на $ -j $ приводит повороту этого вектора на 90° по часовой стрелке). Ток в ёмкостном сопротивлении опережает вектор ЭДС на 90° (т.к. $ underline{I}_{C} = j frac{underline{E}}{X_{C}} $, а умножение на $ j $ приводит повороту этого вектора на 90° против часовой стрелки). Результирующий вектор тока определяется после геометрического сложения всех векторов по правилу параллелограмма.
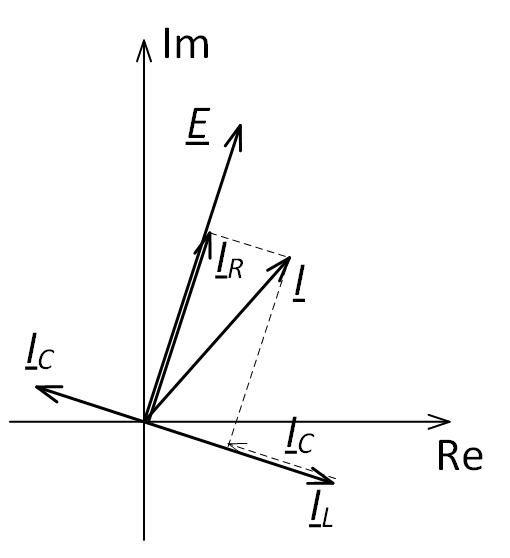
Рис. 4. Векторная диаграмма токов при параллельном соединении элементов цепи
Для произвольной цепи алгоритм построения векторных диаграмм аналогичен вышеизложенному с учётом протекаемых в ветвях токов и прикладываемых напряжений.
Обращаем ваше внимание, что на сайте представлен инструмент для построения векторных диаграмм онлайн для трёхфазных цепей.
Список использованной литературы
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.