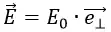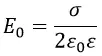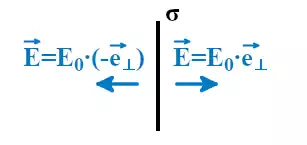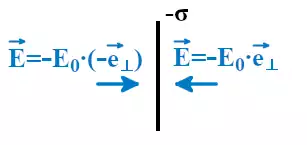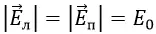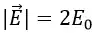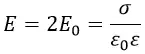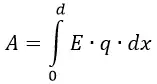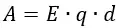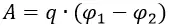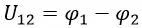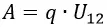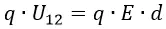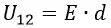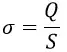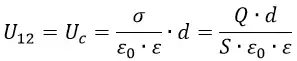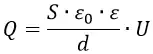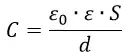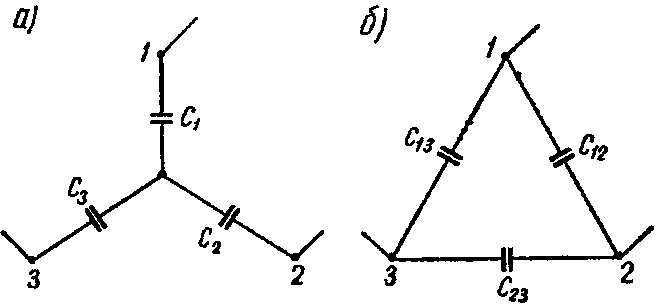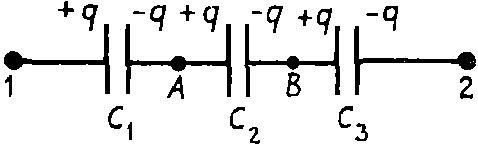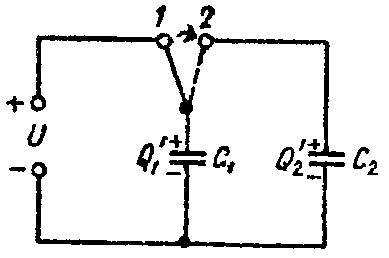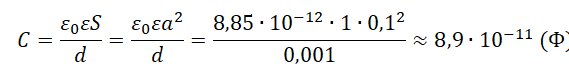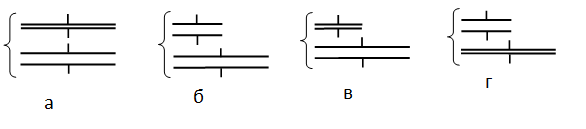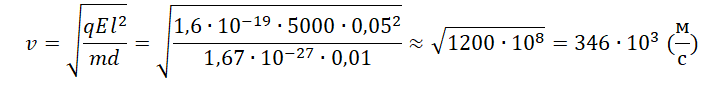Как найти напряжение поля конденсатора - Сайт, где вы сможете решить свои вопросы

Особенности конденсаторов

Конденсатор – один из самых важных элементов электрической цепи. Он накапливает внутри себя электрический заряд и передает его другим элементам электрической цепи. О том, что представляет собой конденсатор и как определить на нём напряжение, рассказывается ниже.

Что такое конденсатор

Конденсатор – это двухполюсное устройство, имеющее постоянное или переменное емкостное значение и малую проводимость. Это элемент цепи, служащий накопителем энергии, что формирует электрическое поле; пассивный электронный компонент любого подключения. Содержит в себе несколько металлических электродов или обкладок, между которыми находится диэлектрик. Может иметь пакетную, трубчатую, дисковую, литую секционированную и рулонную конструкцию.

Конденсатор имеет в плоскую или цилиндрическую форму. Плоское устройство состоит из относительно далеко расположенных друг от друга пластин, а цилиндрический – из нескольких полых коаксиальных проводящих цилиндров с радиусами r1 и r2 (основное условие – r1 > r2).

Термин из учебного пособия

Характеристики конденсаторов

Главной характеристикой прибора является емкость, то есть, количество энергии, которое он может накопить в виде электронов. Общее число зарядов на пластинах определяет величину емкости конденсатора.

Обратите внимание! Емкость зависит от площади обкладок и диэлектрической проницаемости материала. Чем больше площадь конденсаторных пластин, тем больше заряженных частиц могут поместиться на них и тем выше показатель емкости.

Из важнейших характеристик также можно назвать удельную емкость, плотность, номинальную силу заряда и полярность. Из дополнительных параметров можно указать количество фаз, метод установки конденсатора, рабочую температуру, активный электрический ток переменного или постоянного типа.

В электротехнике существуют также понятия негативных факторов, искажающих рабочие свойства колебательного контура. К ним относятся электрическое сопротивление и эквивалентная последовательная индуктивность. В качестве примера негативного критерия можно привести показатель, показывающий падение заряда после отключения электричества.

В чем измеряется напряжение конденсаторов

Напряжение отражается на корпусе оборудования и показывает то, при какой силе энергии оно работает. Измеряется напряжение конденсаторов в фарадах. Это единица, названная в честь Майкла Фарадея. Один фарад – это кулон, или заряд, прошедший через проводник за одну секунду при силе тока в один ампер. Как правило, фарады и кулоны не используются для измерения на практике, потому что чаще применяются дробные величины – микро-, нано- и пикофарады.

Измерение силы заряда двухполюсника

Что влияет на напряжение конденсаторов

Чтобы возник заряд, двухполюсник должен быть подключен к электрической цепи с постоянным током. Для этой цели может быть использован генератор, каждый из которых обладает внутренним сопротивлением. Во время короткого замыкания заряжается прибор, и между его обкладками появляется заряд. Поэтому на вольтаж конденсаторов влияет внутреннее сопротивление. Также, на него оказывают влияние температурные колебания – чем выше нагрев, тем ниже номинальный показатель напряжения.

Важно! На напряжение конденсаторов оказывает большое влияние ток утечки. Вопреки сложившемуся мнению, диэлектрик пропускает небольшое количество электротока, что приводит к потере начального заряда с течением времени, и напряжение в итоге незначительно падает.

Как вычислить напряжение и вольтаж

Чтобы определить мощность, напряжение и вольтаж двухполюсников, можно использовать мультиметр или специальную формулу для теоретических расчётов. Чтобы проверить мультиметром силу заряда и количество вольт, необходимо вставить щупы в измеряемое оборудование, переключить прибор на режим омметра, нажать на соответствующую клавишу проверки и получить запрашиваемый показатель.

Обратите внимание! Сила заряда при проверке быстро падает, поэтому правильной будет та цифра, которая появилась на индикаторе мультиметра в самом начале измерений.

Формулы измерения напряжения конденсаторов

Численный показатель напряжения равен электродвижущей силе. Также он определяется, как емкость, поделенная на величину заряда, исходя из формулы определения его величины. В соответствии с ещё одним правилом, напряжение равно току утечки, поделенному на изоляционное сопротивление.

В целом, конденсатор – это устройство для аккумулирования электрического заряда, состоящее из нескольких пластинчатых электродов, которые разделены с помощью диэлектриков. Устройство имеет электрод, измеряемый в фарадах. Один фарад равен одному кулону. На напряжение устройства влияет ток, показатели которого можно вычислить через описанные выше формулы.

Источник

Занятие 48. Напряжённость электростатического поля, создаваемого заряженной пластиной. Поле конденсатора

Получена формула для напряжённости электрического поля плоского конденсатора, широко применяемого в электрических цепях. Для этого надо применить теорему Гаусса и найти сначала формулу напряжённости для одной заряженной пластины, а затем для параллельных заряженных пластин.

Итак , рассмотрена теорема Гаусса и её применение для получения формул нахождения напряжённости электростатических полей, создаваемых протяжёнными заряженными телами. По ходу найдено выражения для напряжённости электрического поля плоского конденсатора.

Подумайте над решением следующих задач:

1. К вертикальной равномерно заряженной пластине с плотностью заряда 4 10 -7 Кл/м2 прикреплена нить. На нити подвешен заряженный шарик массой 1 г. Знаки заряда пластины и шарика одинаковы. Найти заряд шарика, если нить образует с вертикалью угол 30 градусов. Ответ: 2,5 10 -7 Кл

2. Электрон влетает в плоский горизонтально расположенный конденсатор длиной 5 см. При вылете из конденсатора электрон отклоняется от своего первоначального направления на 2 мм. Напряжённость электрического поля внутри конденсатора 20 кВ/м. Какую скорость и кинетическую энергию имел электрон перед влётом в конденсатор? Ответ: 4,7 10 7 м/с; 10 -15 Дж.

Отвечаю на вопрос о напряжённости электрического поля, создаваемого заряженной пластинкой конечных размеров :

На рисунке ниже показана тонкая заряженная пластинка конечных размеров и силовые линии электрического поля, создаваемого ею.

В этом случае полученная формула для напряжённости поля, создаваемого бесконечной заряженной плоскостью, справедлива только для точек, расположенных внутри области, ограниченной пунктирной линией.

В других точках, расположенных всё дальше от пластинки и всё ближе к её краям, будет всё более отличаться от поля, создаваемого бесконечной заряженной плоскостью.

На расстояниях значительно больших размера пластинки электрическое поле можно рассматривать как поле точечного заряда (заряд пластинки принимается за точечный заряд).

К.В. Рулёва. Подписывайтесь на канал. Оценивайте занятия.

Предыдущая запись: решение задач к занятию 47.

Следующая запись: Как поведёт себя электрон, влетевший в электрическое поле плоского конденсатора?

Ссылки на занятия до электростатики даны в Занятии 1 .

Ссылки на занятия, начиная с электростатики, даны в Занятии 45 .

Источник

Конденсатор. Энергия электрического поля

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.

Но прежде введём понятие электрической ёмкости.

Ёмкость уединённого проводника

Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать , так что

Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:

Например, потенциал уединённого шара в вакууме равен:

где — заряд шара, — его радиус. Отсюда ёмкость шара:

(2)

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:

Соответственно, ёмкость шара в раз увеличивается:

(3)

Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.

Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.

В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.

Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.

мкФ.

Как видите, Ф — это очень большая ёмкость.

Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2) :

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

Ф.

Так легче запомнить, не правда ли?

Ёмкость плоского конденсатора

Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.

Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.

Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух

Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора.

Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

Здесь — напряжённость поля положительной обкладки, — напряженность поля отрицательной обкладки, — поверхностная плотность зарядов на обкладке:

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля имеем:

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

Внутри конденсатора поле удваивается:

(4)

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4) . Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.

Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):

(5)

Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6) , таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:

(7)

Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?

Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:

(8)

Соответственно, напряжение на конденсаторе:

(9)

Отсюда ёмкость плоского конденсатора с диэлектриком:

(10)

Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.

Важное следствие формулы (10) : заполнение конденсатора диэлектриком увеличивает его ёмкость.

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.

Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.

Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.

Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .

Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

где — напряжённость поля первой обкладки:

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил , с которыми притягиваются к первой обкладке всевозможные маленькие заряды второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все и дадут . В результате получим:

(11)

Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины . Сила притяжения пластин совершает при этом работу:

Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины d_1)’ alt='(d_2 > d_1)’/> , то работа силы притяжения получается отрицательной, как и должно быть.

С учётом формул (11) и (7) имеем:

Это можно переписать следующим образом:

Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.

Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

Особенно полезными являются формулы (12) и (14) .

Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:

При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10) .

Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

Энергия электрического поля

Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

Но — объём конденсатора. Получаем:

(15)

Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.

Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:

(16)

В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.

Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:

(17)

(18)

Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.

Источник

Конденсатор. Энергия электрического поля

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Ёмкость уединённого проводника
Ёмкость плоского конденсатора
Энергия заряженного конденсатора
Энергия электрического поля

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Но прежде введём понятие электрической ёмкости.

к оглавлению ▴

Ёмкость уединённого проводника

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение varphi , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать 1/C , так что

$varphi = frac{displaystyle q}{displaystyle C vphantom{1^a}}.$

$C = frac{displaystyle q}{displaystyle varphi }.$ (1)

Например, потенциал уединённого шара в вакууме равен:

$varphi = frac{displaystyle kq}{displaystyle R vphantom{1^a}}=frac{displaystyle q}{displaystyle 4 pi varepsilon_0R vphantom{1^a}},$

где — заряд шара, — его радиус. Отсюда ёмкость шара:

(2)

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:

$varphi = frac{displaystyle q}{displaystyle 4 pi varepsilon_0 varepsilon R vphantom{1^a}}.$

Соответственно, ёмкость шара в раз увеличивается:

(3)

Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным 6400 км.

$C = 4 pi varepsilon_0 R approx 4 cdot 3,14 cdot 8,85 cdot 10^{-12} cdot 6400 cdot 10^3 approx 712$ мкФ.

Как видите, Ф — это очень большая ёмкость.

$varepsilon_0 = frac{displaystyle C} {displaystyle 4 pi R vphantom{1^a}}.$

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

$varepsilon_0 = 8,85 cdot 10^{-12}$ Ф.

Так легче запомнить, не правда ли?

к оглавлению ▴

Ёмкость плоского конденсатора

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух

Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

$E_+ = E_-=frac{displaystyle sigma }{displaystyle 2 varepsilon_0 vphantom{1^a}}.$

Здесь E_+ — напряжённость поля положительной обкладки, E_- — напряженность поля отрицательной обкладки, sigma — поверхностная плотность зарядов на обкладке:

$sigma =frac{displaystyle q}{displaystyle S vphantom{1^a}}.$

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля vec{E} имеем:

$vec{E} = vec{E}_+ + vec{E}_-$

Внутри конденсатора поле удваивается:

$E = E_+ + E_-= frac{displaystyle sigma }{displaystyle varepsilon_0},$

или

$E = frac{displaystyle q}{displaystyle varepsilon_0 S vphantom{1^a}}.$ (4)

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

$U=Ed=frac{displaystyle qd}{displaystyle varepsilon_0 S vphantom{1^a}}.$ (5)

$C=frac{displaystyle q}{displaystyle U vphantom{1^a}}.$ (6)

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:

$C=frac{displaystyle varepsilon_0 S}{displaystyle d vphantom{1^a}}.$ (7)

Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:

$E=frac{displaystyle q}{displaystyle varepsilon_0 varepsilon S vphantom{1^a}}.$ (8)

Соответственно, напряжение на конденсаторе:

$U=Ed=frac{displaystyle qd}{displaystyle varepsilon_0 varepsilon S vphantom{1^a}}.$ (9)

Отсюда ёмкость плоского конденсатора с диэлектриком:

$C=frac{displaystyle varepsilon_0 varepsilon S}{displaystyle d vphantom{1^a}}.$ (10)

Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.

к оглавлению ▴

Энергия заряженного конденсатора

Возьмём на второй обкладке настолько маленькую площадку, что заряд q_0 этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

где E_1 — напряжённость поля первой обкладки:

$E_1=frac{displaystyle sigma }{displaystyle 2 varepsilon _0 vphantom{1^a}}=frac{displaystyle q}{displaystyle 2varepsilon_0 S vphantom{1^a}}.$

Следовательно,

$F_0=frac{displaystyle q_0q}{displaystyle 2 varepsilon_0 S vphantom{1^a}}.$

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил F_0 , с которыми притягиваются к первой обкладке всевозможные маленькие заряды q_0 второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все q_0 и дадут . В результате получим:

$F=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 S vphantom{1^a}}.$ (11)

Предположим теперь, что расстояние между обкладками изменилось от начальной величины d_1 до конечной величины d_2 . Сила притяжения пластин совершает при этом работу:

Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины , то работа силы притяжения получается отрицательной, как и должно быть.

С учётом формул (11) и (7) имеем:

$A=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 S vphantom{1^a}}left ( d_1-d_2 right )=frac{displaystyle q^2d_1}{displaystyle 2varepsilon_0 S vphantom{1^a}}-frac{displaystyle q^2d_2}{displaystyle 2varepsilon_0 S vphantom{1^a}}=frac{displaystyle q^2}{displaystyle 2C_1 vphantom{1^a}}-frac{displaystyle q^2}{displaystyle 2C_2 vphantom{1^a}}=W_1-W_2,$

где
$W_1=frac{displaystyle q^2}{displaystyle 2C_1 vphantom{1^a}},$
$W_2=frac{displaystyle q^2}{displaystyle 2C_2 vphantom{1^a}}$

Это можно переписать следующим образом:

где

$W=frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}}.$ (12)

Используя соотношение q = CU , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

$W=frac{displaystyle qU}{displaystyle 2 vphantom{1^a}},$ (13)

$W=frac{displaystyle CU^2}{displaystyle 2 vphantom{1^a}}.$ (14)

Особенно полезными являются формулы (12) и (14).

$F=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 varepsilon S vphantom{1^a}}.$

к оглавлению ▴

Энергия электрического поля

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

$W=frac{displaystyle CU^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle varepsilon_0 S}{displaystyle d vphantom{1^a}} cdot frac{displaystyle (Ed)^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}Sd.$

Но Sd = V — объём конденсатора. Получаем:

$W=frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}V.$ (15)

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:

$omega =frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}.$ (16)

$W =frac{displaystyle varepsilon_0 varepsilon E^2}{displaystyle 2 vphantom{1^a}}V.$ (17)

$omega =frac{displaystyle varepsilon_0 varepsilon E^2}{displaystyle 2 vphantom{1^a}}.$ (18)

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Конденсатор. Энергия электрического поля» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

В статье поле плоской пластины была выведена формула напряжённости электрического поля бесконечной плоской пластины. Если эту пластину рассмотреть в разрезе и ввести понятие поверхностной плотности заряда σ, то согласно указанной статьи в любой точке пространства напряжённость электрического поля направлена перпендикулярно плоскости пластины и по величине равно:

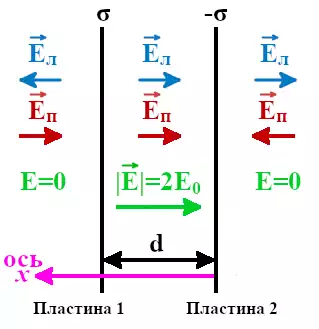
E₀ здесь жёстко определяется поверхностной плотностью заряда σ:

где σ – поверхностная плотность заряда;
ε₀ – диэлектрическая проницаемость для вакуума;
ε – относительная диэлектрическая проницаемость для вещества, которая для вакуума равна 1.

Формулы показывают, что величина напряжённости электрического поля плоской пластины, имеющей бесконечные размеры, не зависит от расстояния до неё.

Если σ положительная, то напряжённость электрического поля будет направлена от пластины и поле отталкивает положительные заряды.

Если σ отрицательная, то напряжённость электрического поля направлена к пластине и поле притягивает положительные заряды.

Плоским конденсатором будем называть пару параллельных плоских пластин с плотностью заряда одинаковой по модулю, но противоположной по знаку.

Расчёт и вывод формулы ёмкости плоского конденсатора

Напряжённость электрического поля конденсатора

Для расчёта плоского конденсатора расположим две пластины бесконечных размеров параллельно друг другу на некотором расстоянии d. Пусть одна пластина будет иметь поверхностную плотность заряда σ, а другая -σ. По модулю величины поверхностных плотностей зарядов будут равны. В такой ситуации общее поле плоского конденсатора по принципу суперпозиции равно сумме полей.

Обозначим напряжённости электрического поля от левой пластины плоского конденсатора как E_л, при этом положительные заряды будут отталкиваться от пластины.

Напряжённость электрического поля от правой пластины плоского конденсатора обозначим как E_п, при этом поле пластины будет притягивать к себе положительные заряды.

При равной плотности заряда напряжённость поля во всех точках пространства и от левой, и от правой пластин конденсатора будут равны по модулю. Это приведёт к тому, что слева и справа от пары пластин поля взаимно компенсируются и их сумма будет равна нулю. При этом поля между пластинами плоского конденсатора будут складываться.

где E₀ – напряжённость поля при положительной σ.

Суммарная напряжённость электрического поля плоского конденсатора будет направлена от пластины с положительной σ к пластине с отрицательной σ.

Электрическая энергия плоского конденсатора отсутствует вне его пластин и вся накоплена в пространстве между пластинами.

Работа по перемещению заряда

Для перемещения заряда от отрицательно заряженной пластины в направлении к положительно заряженной придётся совершить работу против электрической силы:

При вычислении этой работы видно, что величина заряда q и напряжённость поля E постоянны, поэтому формула примет вид:

В электрическом поле можно ввести понятие потенциала ϕ и выразить работу по перемещению заряда в точку 2 из точки 1 через разность потенциалов ϕ₁-ϕ₂.

Напряжение между пластинами плоского конденсатора

Разность электрических потенциалов между двумя точками называют напряжением и обозначают U₁₂:

Таким образом, сравнивая две формулы для работы мы получим:

В реальном конденсаторе площадь пластин ограничена по естественным причинам, поэтому, как правило, мы не имеем возможности знать плотность заряда, а знаем только заряд пластины. В этом случае плотность заряда σ мы можем вычислить по формуле:

где Q – заряд пластины;
S – площадь пластины.

Если пластины плоского конденсатора находятся достаточно близко друг к другу, то краевыми эффектами можно пренебречь и считать, что поле внутри конденсатора реальных размеров подобно полю внутри конденсатора с пластинами бесконечных размеров.

В таком случае имеем следующее выражение:

Напряжение между пластинами пропорционально полному заряду этих пластин:

Электрическая ёмкость плоского конденсатора

Коэффициент пропорциональности между зарядом на обкладках плоского конденсатора и напряжением между ними носит название ёмкости плоского конденсатора и обозначается буквой C:

Подробности венецианская штукатурка для внутренней отделки цена на сайте.

Источник

Главная
→
Примеры решения задач ТОЭ
→
Расчет электрической цепи постоянного тока с конденсаторами

Расчет электрической цепи постоянного тока с конденсаторами

Основные положения и соотношения

1. Общее выражение емкости конденсатора

C= Q U .

2. Емкость плоского конденсатора

C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d ,

здесь

S — поверхность каждой пластины конденсатора;

d — расстояние между ними;

ε_a = ε_r·ε₀ — абсолютная диэлектрическая проницаемость среды;

ε_r — диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);

ε 0 = 1 4π⋅ с 2 ⋅ 10 −7 ≈8,85418782⋅ 10 −12 Ф м – электрическая постоянная.

3. При параллельном соединении конденсаторов С₁, С₂, …, С_n эквивалентная емкость равна

C= C 1 + C 2 +…+ C n = ∑ k=1 n C k .

4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:

C= C 1 ⋅ C 2 C 1 + C 2 ,

а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:

U 1 =U⋅ C 2 C 1 + C 2 ; U 2 =U⋅ C 1 C 1 + C 2 .

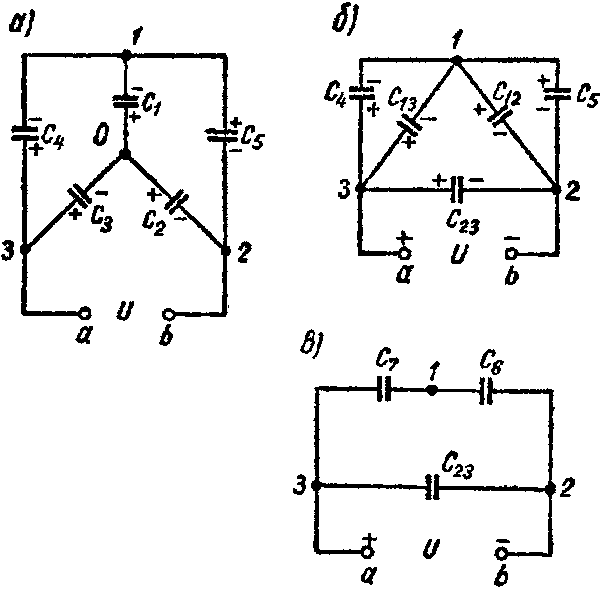
5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)

Рис. 0

осуществляется по формулам:

Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ; C 13 = C 1 ⋅ C 3 ΣC ; C 23 = C 2 ⋅ C 3 ΣC , где ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .

6. Энергия электростатического поля конденсатора:

W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .

7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:

1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:

ΣQ=Σ Q ′ .

2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:

∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k .

Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.

Решение задач на расчет электрической цепи постоянного тока с конденсаторами

Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).

Рис. 1

Решение

На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U₁₂, то на левую пластину конденсатора С₁ перейдет заряд +q, на правую пластину конденсатора С₃ заряд –q.

Вследствие электризации через влияние правая пластина конденсатора С₁ будет иметь заряд –q, а так как пластины конденсаторов С₁ и С₂ соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C₂ будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.

Найти эквивалентную емкость — это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.

Разность потенциалов U₁₂ = φ₁ — φ₂ складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов

U 12 = φ 1 − φ 2 =( φ 1 − φ A )+( φ A − φ B )+( φ B − φ 2 )= U 1A + U AB + U B2 .

Воспользовавшись формулой напряжения на конденсаторе

U= q C ,

запишем

q C = q C 1 + q C 2 + q C 3 .

Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов

1 C = 1 C 1 + 1 C 2 + 1 C 3 .

В общем случае эквивалентная емкость при последовательном соединении конденсаторов

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

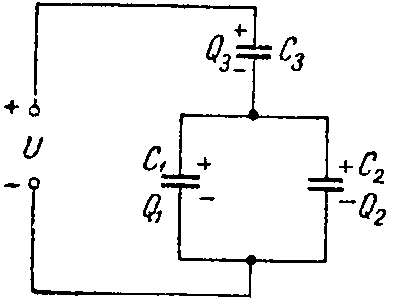
Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.

Рис. 2

Емкости конденсаторов: C₁ =50 мкФ; C₂ =150 мкФ; C₃ =300 мкФ.

Решение

Эквивалентная емкость конденсаторов C₁ и C₂, соединенных параллельно

C₁₂ = C₁ + C₂ = 200 мкФ,

эквивалентная емкость всей цепи равна

C= C 12 ⋅ C 3 C 12 + C 3 = 200⋅300 500 =120 мкФ.

Заряд на эквивалентной емкости

Q = C·U = 120·10^–6·240 = 288·10^–4 Кл.

Той же величине равен заряд Q₃ на конденсаторе C₃, т.е. Q₃ = Q = 288·10^–4 Кл; напряжение на этом конденсаторе

U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96 В.

Напряжение на конденсаторах C₁ и C₂ равно

U₁ = U₂ = U — U₃ = 240 — 96 = 144 В.

их заряды имеют следующие значения

Q₁ = C₁·U₁ = 50·10^–6·144 = 72·10^–4 Кл;

Q₂ = C₂·U₂ = 150·10^–6·144 = 216·10^–4 Кл.

Энергии электростатического поля конденсаторов равны

W 1 = Q 1 ⋅ U 1 2 = 72⋅ 10 −4 ⋅144 2 ≈0,52 Дж; W 2 = Q 2 ⋅ U 2 2 = 216⋅ 10 −4 ⋅144 2 ≈1,56 Дж; W 3 = Q 3 ⋅ U 3 2 = 288⋅ 10 −4 ⋅96 2 ≈1,38 Дж.

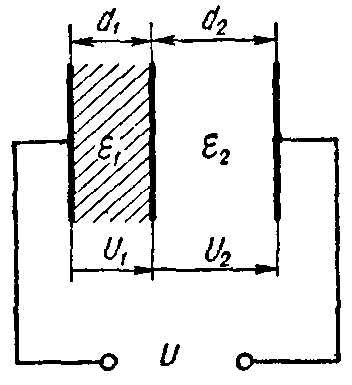
Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см², имеет диэлектрик, состоящий из слюды (ε_r₁ = 6) толщиною d₁ = 0,3 мм и стекла (ε_r₂ = 7) толщиною d₂ =0,4 мм.

Пробивные напряженности слюды и стекла соответственно равны E₁ = 77 кВ/мм, E₂ = 36 кВ/мм.

Рис. 3

Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.

Решение

Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов

C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .

Подставляя сюда числовые значения, предварительно заменив ε_a₁ = ε_r₁·ε₀ и ε_a₂ = ε_r₂·ε₀, получим

C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12 Ф.

Обозначим общее напряжение, подключаемое к слоистому конденсатору, через U_пр, при этом заряд конденсатора будет равен

Q = C·U_пр.

Напряжения на каждом слое будут равны

U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .

Напряженности электростатического поля в каждом слое

E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .

Здесь U’_np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U”_np — общее напряжение, при котором происходит пробой второго слоя.

Из последнего выражения находим

U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5 кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0 кВ.

Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное

27,0 кВ / 2 = 13,5 кВ.

Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d₁ = 1 см друг от друга. Площадь обкладок S = 50 см². Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.

Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d₂ = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.

Решение

Энергия заряженного плоского конденсатора равна

W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,

где С₁ — емкость до раздвижения обкладок.

Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения

Q = C₂·U₂,

где C₂ — емкость конденсатора после раздвижения обкладок, следует, что, так как C₂ = ε₀·S/d₂ стало меньше в 10 раз (d₂ увеличилось в 10 раз), то напряжение на конденсаторе U₂ увеличилось в 10 раз, т. е. U₂ = 10U.

Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d₂ будет больше первоначальной

W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .

Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.

Таким образом, надо совершить работу, равную

W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7 Дж.

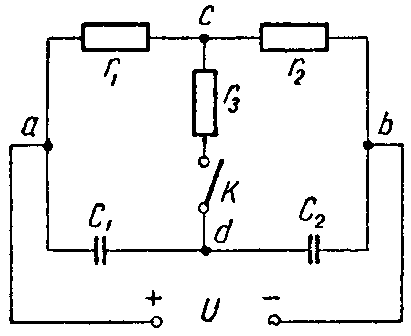
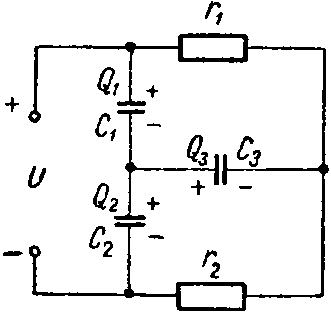
Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.

Даны: C₁ = 30 мкФ; C₂ = 20 мкФ; r₁ = 100 Ом. r₂ = 400 Ом. r₃ = 600 Ом, U = 20 В.

Решение

Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям

U 1 = C 2 C 1 + C 2 ⋅U= 20⋅ 10 −6 30⋅ 10 −6 +20⋅ 10 −6 ⋅20=8 В; U 2 =U− U 1 =20−8=12 В.

Рис. 4

Ключ К замкнут. Через сопротивления r₁ и r₂ протекает ток

I= U r 1 + r 2 = 20 500 =0,04 А,

а через сопротивление r₃ ток не протекает.

Поэтому точки c и d равнопотенциальны (φ_c = φ_d). Следовательно, напряжение между точками a и c (U_ac = φ_a — φ_c) равно напряжению между точками a и d (U_ad = φ_a — φ_d).

Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r₁

U_C₁ = I·r₁ = 0,04·100 = 4 В.

Аналогично напряжение на втором конденсаторе равно

U_C₂ = I·r₂ = 0,04·400 = 16 В.

Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C₁ = 5 мкФ; C₂ = 120 мкФ. Конденсатор C₂ предварительно не был заряжен.

Рис. 5

Решение

Когда рубильник находится в положении 1, то конденсатор C₁ заряжен до напряжения U и его заряд равен

Q = C₁·U = 5·10^–6·25 = 125·10^–6 Кл.

После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C₁ и C₂ (рис. 5). Обозначим эти заряды через Q’₁ и Q’₂.

На основании закона сохранения электричества имеем

Q = Q’₁ + Q’₂ = 125 10^–6 Кл. (1)

По второму закону Кирхгофа имеем

0= U C1 − U C2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,

или

Q ′ 1 5⋅ 10 −6 − Q ′ 2 120⋅ 10 −6 =0. (2)

Решая уравнения (1) и (2), найдем

Q’₁ = 5 10^–6 Кл; Q’₂ = 120 10^–6 Кл.

Доставка свежих и аппетитных японских суши в Новороссийске – ям ям..

Напряжение на зажимах конденсаторов станет равным

U C1 = Q ′ 1 C 1 = U C2 = Q ′ 2 C 2 = 5⋅ 10 −6 5⋅ 10 −6 =1 В.

Энергия обоих конденсаторов будет равна

W= C 1 ⋅ U C1 2 2 + C 2 ⋅ U C2 2 2 =62,5⋅ 10 −6 Дж.

Подсчитаем энергию, которая была запасена в конденсаторе С₁, при его подключении к источнику электрической энергии

W нач = C 1 ⋅U 2 = 5⋅ 10 −6 ⋅ 25 2 2 =1562,5⋅ 10 −6 Дж.

Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10^–6 — 62,5·10^–6 = 1500·10^–6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C₁ в конденсатор C₂ после перевода рубильника в положение 2.

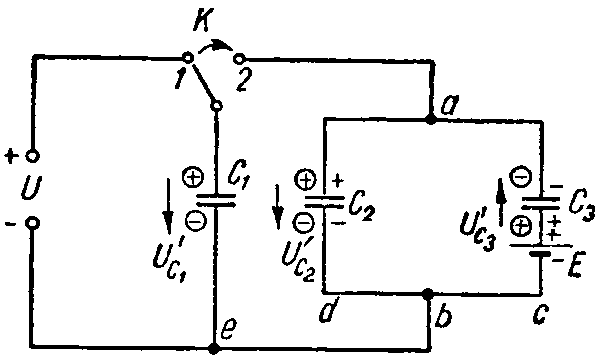
Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.

Емкости конденсаторов равны: C₁ = 10 мкФ; C₂ = 30 мкФ; C₃ = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.

Рис. 6

Решение

Рубильник находится в положении 1. Заряд конденсатора C₁ равен

Q₁ = C₁·U = 10·10^–6·30 = 0,3·10^–3 Кл.

В указанном положении рубильника конденсаторы C₂ и C₃ соединены последовательно друг с другом, поэтому их заряды равны: Q₂ = Q₃. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем

E= U C2 + U C3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,

откуда

Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅E= 30⋅ 10 −6 ⋅60⋅ 10 −6 90⋅ 10 −6 ⋅50=1⋅ 10 −3 Кл.

При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’₁, Q’₂ и Q’₃. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.

Для узла a

Q’₁ + Q’₂ — Q’₃ = Q₁ + Q₂ — Q₃. (1)

Для контура 2ebda2

0= U ′ C1 − U ′ C2 = Q ′ 1 C 1 − Q ′ 2 C 1 .

Для контура bcadb

E= U ′ C2 − U ′ C3 = Q ′ 2 C 2 + Q ′ 3 C 3 .

Уравнения (1) — (3), после подстановки числовых значений величин, примут вид

Q’₁ + Q’₂ — Q’₃ = 0,3·10^–3; (4)

3Q’₁ — Q’₂ = 0; (5)

2Q’₂ + Q’₃ = 3·10^–3. (6)

Решая совместно уравнения (4) — (6), получим

Q’₁ = 0,33·10^–3 Кл; Q’₂ = 0,99·10^–3 Кл; Q’₃ = 1,02·10^–3 Кл.

Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.

Напряжения на конденсаторах после перевода рубильника будут равны

U C1 = Q ′ 1 C 1 = 0,33⋅ 10 −3 10⋅ 10 6 =33 В; U C2 = Q ′ 2 C 2 = 0,99⋅ 10 −3 30⋅ 10 6 =33 В; U C3 = Q ′ 3 C 3 = 1,02⋅ 10 −3 60⋅ 10 6 =17 В.

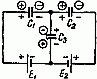
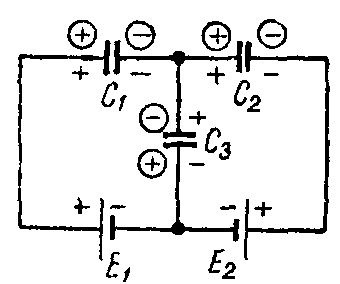
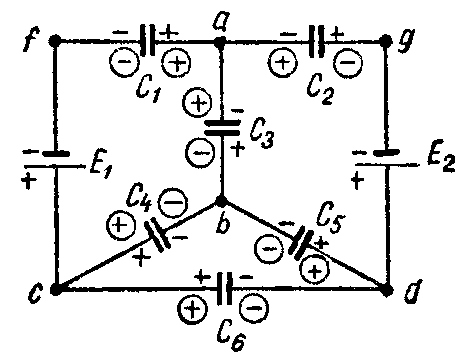
Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C₁ = 5 мкФ; C₂ = 4 мкФ; C₃ = 3 мкФ; э. д. с. источников E₁ = 20 В и E₂ = 5 В.

Рис. 7

Решение

Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках

− Q 1 + Q 2 − Q 3 =0; E 1 = U C1 − U C3 = Q 1 C 1 − Q 3 C 3 ; E 2 =− U C2 − U C3 =− Q 2 C 2 − Q 3 C 3 .

Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q₁ = 50 мкКл; Q₂ = 20 мкКл; Q₃ = –30 мкКл.

Таким образом, истинная полярность зарядов на обкладках конденсаторов C₁ и C₂ соответствует выбранной, а у конденсатора C₃ — противоположна выбранной.

Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C₁ = 2 мкФ; C₂ = 3 мкФ; C₃ = 5 мкФ; C₄ = 1 мкФ; C₅ = 2,4 мкФ.

Рис. 8

Индивидуалка Дана (34 лет) т.8 926 650-82-63 Москва, метро Сокол.

Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.

Решение

1-й способ. Звезду емкостей C₁, C₂ и C₃ (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)

C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 =0,6 мкФ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 =1,0 мкФ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 =1,5 мкФ.

Емкости C₁₂ и C₅ оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость

C₆ = C₁₂ + C₅ = 3 мкФ.

Аналогично

C₇ = C₁₃ + C₄ = 2 мкФ.

Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется

C ab = C 23 + C 6 ⋅ C 7 C 6 + C 7 =2,7 мкФ.

Вычислим напряжение на каждом из конденсаторов.

На конденсаторе C₇ напряжение равно

U 7 = C 6 C 6 + C 7 ⋅U=6 В.

Таково же напряжение и на конденсаторах C₄ и C₁₃

U₄ = U₃₁ = 6 В.

Напряжение на конденсаторе C₆ равно

U₆ = U — U₇ = 4 В;

U₅ = U₁₂ = 4 В.

Вычислим заряды

Q₄ = C₄·U₄ = 6·10^–6 Кл;

Q₅ = C₅·U₅ = 9,6·10^–6 Кл;

Q₁₂ = C₁₂·U₁₂ = 6·10^–6 Кл;

Q₁₃ = C₁₃·U₃₁ = 2,4·10^–6 Кл.

По закону сохранения электричества для узла 1 схем 8, а и б имеем

–Q₄ — Q₁ + Q₅ = –Q₄ — Q₁₃ + Q₁₂ + Q₅,

отсюда

Q₁ = Q₁₃ — Q₁₂ = 3,6·10^–6 Кл,

а напряжение на конденсаторе, емкостью C₁ составляет

U 1 = Q 1 C 1 =1,8 В.

Далее находим напряжения и заряды на остальных конденсаторах

U₃₁ = U₁ + U₃,

отсюда

U₃ = U₃₁ — U₁ = 4,2 В;

Q₃ = C₃·U₃ = 21·10^–6 Кл,

также

U₁₂ = U₂ — U₁ = 4,2 В,

откуда

U₂ = U₁₂ + U₁ = 5,8 В;

Q₂ = C₂·U₂ = 17,4·10^–6 Кл.

Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.

2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)

для узла 1

Q₅ — Q₁ — Q₄ = 0; (1)

для узла О

Q₁ + Q₂ — Q₃ = 0; (2)

для контура О13О

Q 1 C 1 − Q 4 C 4 + Q 3 C 3 =0; (3)

для контура О12О

Q 1 C 1 + Q 5 C 5 − Q 2 C 2 =0; (4)

для контура a3О2b

Q 3 C 3 + Q 2 C 2 =U. (5)

Система уравнений (1) — (5) — содержит пять неизвестных: Q₁, Q₂, Q₃, Q₄ и Q₅. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы С_ab можно найти из отношения

C ab = Q U ,

где Q = Q₃ + Q₄, или Q = Q₂ + Q₅.

Задача 9. В схеме рис. 9 найти распределение зарядов, если E₁ = 20 В; E₂ = 7 В; C₁ = 7 мкФ; C₂ = 1 мкФ; C₃ = 3 мкФ; C₄ = 4 мкФ; C₅ = C₆ = 5 мкФ.

Рис. 9

Решение

При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:

для узла а

Q₁ + Q₂ + Q₃ = 0;

для узла b

–Q₃ — Q₄ — Q₅ = 0;

для узла c

–Q₁ + Q₄ + Q₆ = 0;

для контура afcba

E 1 = U C1 + U C4 − U C3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;

ля контура gdbag

E 2 = U C5 − U C3 + U C2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;

для контура cbdc

0= U C4 − U C5 − U C6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .

Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды

Q₁ = 35 мкКл; Q₂ = –5 мкКл; Q₃ = –30 мкКл;

Q₄ = 20 мкКл; Q₅ = 10 мкКл; Q₆ = 15 мкКл.

Таким образом, истинные знаки зарядов Q₁, Q₄, Q₅ и Q₆ соответствуют выбранным, а знаки Q₂ и Q₃ противоположны выбранным.

Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.

Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C₁ = 6 мкФ; C₂ = 2 мкФ; C₃ = 3 мкФ; r₁ = 500 Ом; r₂ = 400 Ом; U = 45 В.

Рис. 10

Решение

Через сопротивления протекает ток

I= U r 1 + r 2 =0,05 А.

Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:

− Q 1 + Q 2 + Q 3 =0; U= U C1 + U C2 = Q 1 C 1 + Q 2 C 2 ; I⋅ r 1 = U C1 + U C3 = Q 1 C 1 + Q 3 C 3 ,

или

Q 1 = Q 2 + Q 3 ; 45= Q 1 6⋅ 10 −6 + Q 2 2⋅ 10 −6 ; 25= Q 1 6⋅ 10 −6 + Q 3 3⋅ 10 −6 .

Решив эту систему уравнений, найдем, что

Q₁ = 90 мкКл; Q₂ = 60 мкКл; Q₃ = 30 мкКл.

последовательное соединение конденсаторов,
параллельное соединение конденсаторов,
Расчет цепи конденсаторов,
Конденсатор в цепи постоянного тока,
Цепи с конденсаторами

Комментарии

Источник

Определение

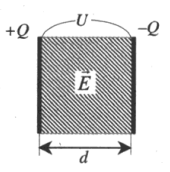
Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.

Плоский конденсатор — система двух разноименно заряженных пластин.

Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:

U=Ed

Электроемкость конденсатора

Определение

Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.

Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).

Электроемкость конденсатора определяется формулой:

C=ε0εSd

ε0 — диэлектрическая постоянная, равная 8,85∙10^–12 Кл²/(Н∙м²);
ε — диэлектрическая проницаемость среды;
S (м²) — площадь каждой пластины.

Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.

Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:

C=QU=qU

Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.

Энергия конденсатора

Формула энергии конденсатора

Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:

Wэ=q22C=CU22

Подсказки к задачам

Конденсатор отключен от источника	q = q′
Конденсатор подключен к источнику	U = U′
Количество теплоты и энергия конденсатора	Q = ∆W_э

Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.

10 см = 0,1 м

1 мм = 0,001 м

Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.

Площадь квадратной пластины равна квадрату ее стороны:

S = a²

Соединения конденсаторов

	Последовательное соединение	Параллельное соединение
Схема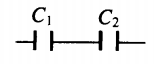
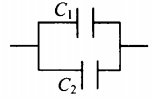Напряжение	U=U1+U2	U=U1=U2
Заряд	q=q1=q2	q=q1+q2
Электроемкость	1C=1C1+1C2	C=C1+C2

Подсказки к задачам

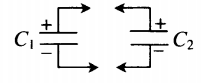
Два конденсатора, электроемкости которых C₁и C₂, заряжены до напряжения U₁и U₂. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами.

Схема соединения конденсаторов одноименными полюсами:

Заряд системы после соединения:

q′
=C1U1+C2U2

Электрическая емкость системы:

C′
=C1+C2

Напряжение:

U′
=q′C′=C1U1+C2U2C1+C2

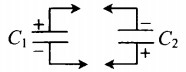
Два конденсатора, электроемкости которых C₁и C₂, заряжены до напряжения U₁и U₂. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами.

Схема соединения конденсаторов разноименными полюсами:

Заряд системы после соединения:

q′
=C1U1−C2U2

Электрическая емкость системы:

C′
=C1+C2

Напряжение:

U′
=q′C′=C1U1−C2U2C1+C2

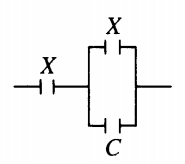
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.

Электрическая емкость параллельного соединения равна:

Cпарал=X+C

Электроемкость последовательного соединения:

1Cпослед=1Cпарал+1X=1X+C+1X

Учтем, что суммарная электроемкость равна C:

1C=1X+C+1X

Преобразуем, умножим выражение на CX(X+C):

X(X+C)=CX+C(X+C)

Раскроем скобки:

X2+XC=CX+CX+C2

X2−CX−C2=0

Решив уравнение, получим: X = 25,9 пФ.

Разбор задач на тему «Заряженная частица в поле конденсатора»

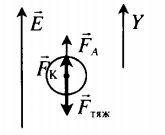
Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρ_ш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U?	Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−FA=0 ρ_ш > ρ, поэтому −Fтяж> −FA. В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так: Проекция второго закона Ньютона на ось ОУ: FK+FA=Fтяж Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения: Fтяж=ρш43πr3g Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения: FА=ρ43πr3g Сила Кулона: FK=qUd qUd+ρ43πr3g=ρш43πr3g q=(ρш43πr3g−ρ43πr3g)dU=4πr3gd(ρш−ρ)3U
Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l?	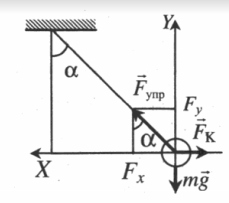Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−Fупр=0 Проекции на оси ОХ и ОУ соответственно: Fупрsinα−FK=0 Fупрcosα−mg=0 Отсюда: kΔlsinα=qUd kΔlcosα=mg Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их: (kΔl)2sin2α+(kΔl)2cos2α=(qUd)2+(mg)2 (kΔl)2(sin2α+cos2α)=(qUd)2+(mg)2 sin2α+cos2α=1 (kΔl)2=(qUd)2+(mg)2 U=dq√(kΔl)2−(mg)2
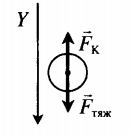
Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь.	Второй закон Ньютона в векторной форме: −Fтяж+−FK=0 Проекция на вертикальную ось: Fтяж−FK=0 Fтяж=mg FK=qUd mg=qUd d=qUmg
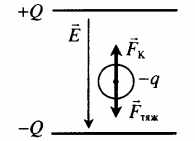
Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью −E, направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли?	Второй закон Ньютона в векторной форме: −Fтяж+−FK=m−a Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок: Если F_тяж> F_K, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны: a=mg−qEm s=b Если F_тяж< F_K, то шарик движется с ускорением верх. Ускорение и перемещение в этом случае равны: a=qE−mgm s=d Начальная скорость шарика равна нулю. Поэтому перемещение также равно: s=at22 Сделаем вычисления для случая F_тяж> F_K: at22=b mg−qEmt22=b t=√2bmmg−qE Выполняя вычисления для случая Сделаем вычисления для случая F_тяж< F_K, получим: t=√2bmqE−mg
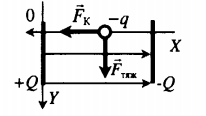
Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого −E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер.	Второй закон Ньютона в векторной форме: −Fтяж+−FK=m−a Если сила Кулона направлена вправо, то s_x = d. Если сила Кулона направлена вправо, то s_x = b. Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево. Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно: ax=qEm ay=g Проекции перемещений на эти же оси: sx=axt22 sx=Δh=gt22 axt22=b Или: qEmt22=b Так как время движения шарика по вертикали и горизонтали одинаково: t2=2Δhg=2mbqE Δh=mbgqE

Задание EF17979

Введите ответ в поле ввода
Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?

Для каждой величины определите соответствующий характер изменения:

увеличится
уменьшится
не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

1.Определить, от чего зависит емкость конденсатора, и как она изменится при уменьшении зазора между его обкладками.

2.Определить, от чего зависит величина заряда конденсатора, и как она изменится после уменьшения зазора между его обкладками.

3.Определить, от чего зависит разность потенциалов между обкладками конденсатора, и как она изменится при уменьшении зазора.

Решение

Емкость конденсатора определяется формулой:

C=ε0εSd

Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.

Вот как взаимосвязана электроемкость и заряд конденсатора:

C=qU

Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.

С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.

Ответ: 113

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18574

Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.

Алгоритм решения

1.Проанализировать каждый этап эксперимента.

2.Установить, от чего зависит угол отклонения стрелки электрометра.

3.Выяснить, что поменяется при смещении одной пластины конденсатора относительно другой, и что при этом произойдет со стрелкой электрометра.

Решение

На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.

На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:

C=ε0εSd

S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.

Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.

На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:

C=qU

Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.

Ответ: Увеличатся

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18695

Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?

Алгоритм решения

Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.

Решение

Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18703

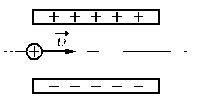
Протон влетает в электрическое поле конденсатора параллельно его пластинам в точке, находящейся посередине между пластинами (см. рисунок). Найдите минимальную скорость υ, с которой протон должен влететь в конденсатор, чтобы затем вылететь из него. Длина пластин конденсатора 5 см, расстояние между пластинами 1 см, напряжённость электрического поля конденсатора 5000 В/м. Поле внутри конденсатора считать однородным, силой тяжести пренебречь.

Ответ записать в км/с, округлив до десятков.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Выполнить рисунок. Указать направление движения протона и силы, действующие на него.

3.Выяснить, при каком условии протон успеет вылететь из конденсатора.

4.Выполнить решение в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

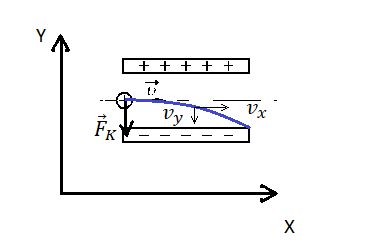
Запишем исходные данные:

• Масса протона: m = 1,67∙10^–27 кг.

• Заряд протона: q = 1,6∙10^–19 Кл.

• Расстояние между обкладками конденсатора: d = 1 см.

• Длина пластин конденсатора: l = 5 см.

• Напряженность однородного поля внутри конденсатора: E = 5000 В/м.

1 см = 0,01 м

5 см = 0,05 м

Сделаем рисунок:

Изначально протон обладает только горизонтальной скоростью v, равной v_x. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.

Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью v_x:

t=lvx=lv

Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):

0,5d=at22

Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:

t=√da

Приравняем правые части уравнений времени и получим:

lv=√da

Отсюда скорость равна:

v=√al2d

Ускорение выразим из второго закона Ньютона:

FK=ma=qUd

a=qUmd

Но известно, что:

U=Ed

Поэтому:

a=qEdmd=qEm

Отсюда:

Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙10³ м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.

Ответ: 350

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 5.9k

Источник

Особенности конденсаторов

Что такое конденсатор

Характеристики конденсаторов

В чем измеряется напряжение конденсаторов

Что влияет на напряжение конденсаторов

Как вычислить напряжение и вольтаж

Формулы измерения напряжения конденсаторов

Занятие 48. Напряжённость электростатического поля, создаваемого заряженной пластиной. Поле конденсатора

Конденсатор. Энергия электрического поля

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Ёмкость уединённого проводника

Ёмкость плоского конденсатора

Энергия заряженного конденсатора

Энергия электрического поля

Конденсатор. Энергия электрического поля

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Ёмкость уединённого проводника

Ёмкость плоского конденсатора

Энергия заряженного конденсатора

Энергия электрического поля

Расчёт и вывод формулы ёмкости плоского конденсатора

Напряжённость электрического поля конденсатора

Работа по перемещению заряда

Напряжение между пластинами плоского конденсатора

Электрическая ёмкость плоского конденсатора

Расчет электрической цепи постоянного тока с конденсаторами

Электроемкость конденсатора

Энергия конденсатора

Подсказки к задачам

Соединения конденсаторов

Подсказки к задачам

Разбор задач на тему «Заряженная частица в поле конденсатора»

Вам также может понравиться

Как можно найти скрытую игру

Как найти джинн в геншин импакт

Как найти стеклянные осколки варфрейм

Добавить комментарий Отменить ответ