Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники. И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей — проводников.
Для начала давайте вспомним, что такое проводник? Проводник — это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:
ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м2
l – длина проводника, м
Более подробно об этом я писал здесь.
Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.
Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.
Получается, можно записать, что
Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .
показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.
Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами
Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.
Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.
Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?
Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Следовательно,
UR1 = IR1 =1×2=2 Вольта
UR2 = IR2 = 1×3=3 Вольта
UR3 = IR3 =1×5=5 Вольт
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Получается
U=UR1+UR2+UR3
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.
Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле
Если же мы имеем только два параллельно соединенных проводника
То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.
Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn
Сила тока при параллельном соединении проводников
Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.
Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
I1 = U/R1
I2 = U/R2
I3 = U/R3
Если бы у нас еще были резисторы, соединенные параллельно, то для них
In = U/Rn
В этом случае, сила тока в цепи будет равна:
Задача
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.
Решение
Воспользуемся формулами, которые приводили выше.
I1 = U/R1
I2 = U/R2
I3 = U/R3
Если бы у нас еще были резисторы, соединенные параллельно, то для них
In = U/Rn
Следовательно,
I1 = U/R1 = 10/2=5 Ампер
I2 = U/R2 = 10/5=2 Ампера
I3 = U/R3 = 10/10=1 Ампер
Далее, воспользуемся формулой
чтобы найти силу тока, которая течет в цепи
I=I1 + I2 + I3 = 5+2+1=8 Ампер
2-ой способ найти I
I=U/Rобщее
Чтобы найти Rобщее мы должны воспользоваться формулой
Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.
I=U/Rобщее = 10/1,25=8 Ампер.
Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.
Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.
Подробное объяснение на видео:
Прикольный набор радиолюбителя по ссылке <<<
Похожие статьи по теме «последовательное и параллельное соединение»
Закон Ома
Проводник (электрический проводник)
Что такое резистор
Делитель напряжения
Делитель тока
Что такое напряжение
Что такое сила тока
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 января 2021 года; проверки требуют 16 правок.
Последовательное соединение проводников.
Параллельное соединение проводников.
Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.
При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включённых проводников.
Последовательное соединение[править | править код]
При последовательном соединении проводников сила тока в любых частях цепи одна и та же: 
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника питания, равно сумме напряжений на отдельных участках цепи: 
Резисторы[править | править код]

Катушка индуктивности[править | править код]

Электрический конденсатор[править | править код]
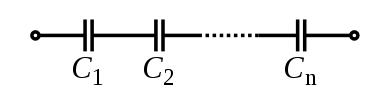
.
Мемристоры[править | править код]
Выключатели[править | править код]

Цепь замкнута, когда замкнуты все выключатели. Цепь разомкнута, когда разомкнут хотя бы один выключатель. (См.также Логическая операция И).
Параллельное соединение[править | править код]
Сила тока в неразветвлённой части цепи равна сумме сил тока в отдельных параллельно соединённых проводниках: 
Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же: 
Резисторы[править | править код]
При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость 

Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее (искомое) сопротивление.
Для двух параллельно соединённых резисторов их общее сопротивление равно: 
Если 

При параллельном соединении резисторов их общее сопротивление будет меньше наименьшего из сопротивлений.
Катушка индуктивности[править | править код]

Электрический конденсатор[править | править код]
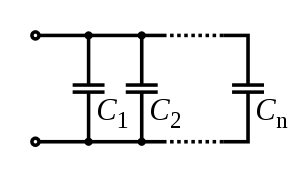
.
Мемристоры[править | править код]
Выключатели[править | править код]
Цепь замкнута, когда замкнут хотя бы один из выключателей. (См.также Логическая операция ИЛИ).
Примеры использования[править | править код]
- Батареи гальванических элементов или аккумуляторов, в которых отдельные химические источники тока соединены последовательно (для увеличения напряжения) или параллельно (для увеличения тока).
- Регулировка мощности электрического устройства, состоящего из нескольких одинаковых потребителей электроэнергии, путём их переключения с параллельного на последовательное соединение. Таким способом регулируется мощность конфорки электрической плиты, состоящей из нескольких спиралей; мощность (скорость движения) электровоза, имеющего несколько тяговых двигателей.
- Делитель напряжения
- Балласт
- Шунт
См. также[править | править код]
- Теория электрических цепей
- Измерительный мост
- Делитель напряжения
- Делитель тока
- Электрический импеданс
- Закон Ома
- Законы Кирхгофа
Литература[править | править код]
- Перышкин А. В. Учебник для общеобразовательных учреждений 10 класс. М.: 2011. С.121
- Перышкин А. В. Учебник для общеобразовательных учреждений 8 класс № 42
Ссылки[править | править код]
- Последовательное и параллельное соединение сопротивлений
- Соединение конденсаторов: руководство для начинающих
На прошлом уроке мы рассмотрели последовательное соединение проводников. При нем сила тока на всех участках цепи одинакова ($I = I_1 = I_2 = … = I_n$), а сопротивление всей цепи складывается из сопротивлений всех проводников, составляющих ее ($R = R_1 + R_2 + … + R_n$). Напряжение (подобно сопротивлению) всей цепи рассчитывается сложением напряжений на концах всех элементов, составляющих такую электрическую цепь ($U = U_1 + U_2 + … + U_n$).
На данном уроке мы рассмотрим другой вид соединения проводников — параллельный. Так мы подсоединяли вольтметр, когда измеряли напряжение на каком-либо участке цепи. Сейчас же мы рассмотрим закономерности для силы тока, сопротивления и напряжения в цепи для такого типа соединения.
Параллельное включение элементов в электрическую цепь
Какое соединение проводников называют параллельным?
Соберем электрическую цепь с таким соединением. Цепь будет состоять из источника тока, ключа и двух электроламп. Электролампы включены в цепь параллельно (рисунок 1).
Схема этой электрической цепи изображена на рисунке 2.
На схеме обозначены две точки A и B. Важный момент:
При параллельном соединении все входящие в него проводники одним своим концом присоединяются к точке A, а вторым концом — к другой точке B.
Так мы можем подключить еще несколько ламп или некоторое количество других потребителей электроэнергии. Поэтому все закономерности, которые мы рассмотрим далее, будут справедливы для любого количества параллельно подключенных в цепь проводников между точками A и B.
Напряжение в цепи при параллельном соединении проводников
Вольтметр подсоединяется в цепь параллельно. Взгляните на рисунок 3.
Можно ли сказать, что мы измеряем напряжение только на одной из ламп? Нет. Получается, что одновременно мы измеряем напряжения и на одной, и на другой лампе. Мы приходим к следующему заключению.
Напряжение на участке цепи AB и на концах всех параллельно соединенных проводников одно и то же:
$U = U_1 = U_2 = … = U_n$.
Значит, напряжение — это электрическая величина, которая одинакова для всех проводников, соединенных параллельно.
По этой причине в быту и технике очень удобно применять параллельный тип соединения проводников. Почему?
Во-первых, в таком случае все потребители электроэнергии изготавливаются в расчете на одну и ту же величину напряжения. Во-вторых, если исключить из цепи один потребитель, то другие продолжат работать. Цепь останется замкнутой.
Сила тока в цепи при параллельном соединении проводников
Теперь рассмотрим, что происходит с силой тока при параллельном подключении.
Взгляните на рисунок 4, а. В точке B ток разветвляется на два тока: $I_1$ и $I_2$.
Эти два тока сходятся снова в точке A. По смыслу этот момент очень похож на разветвление реки (рисунок 4, б) на два потока воды, которые через какое-то расстояние вновь сходятся в одно русло.
Как выражается сила тока в цепи до ее разветвления через силы токов в отдельных ветвях разветвления?
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединенных проводниках:
$I = I_1 + I_2 + … + I_n$.
Сопротивление в цепи при параллельном соединении проводников
Перейдем к сопротивлению. При параллельном соединении можно представить все проводники как один. Этот один проводник будет явно больше в диаметре, чем каждый из них по отдельности. Получается, что площадь поперечного сечения проводника как бы увеличивается при таком соединении.
Сопротивление рассчитывается по формуле $R = frac{rho l}{S}$. Чем больше поперечное сечение, тем меньше сопротивление.
Значит, общее сопротивление цепи уменьшается. Оно становится меньше сопротивления каждого из проводников, которые входят в такую электрическую цепь.
В цепи на рисунке 1 у нас две одинаковые лампы с сопротивлениями $R_1$. Общее сопротивление цепи $R$ будет в два раза меньше сопротивления каждой лампы: $R = frac{R_1}{2}$.
Общее сопротивление цепи при параллельном соединении проводников рассчитывается по формуле:
$frac{1}{R} = frac{1}{R_1} + frac{1}{R_2} + … + frac{1}{R_n}$.
Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
Очевидно, что чем больше проводников будет в разветвлении, тем меньше будет общее сопротивление цепи.
Пример параллельного соединения проводников
Взгляните на рисунок 5. Здесь изображена часть схемы электрической цепи. Здесь параллельно включены электрические лампы, нагревательные приборы и электродвигатель.
Где может использоваться такая схема соединения?
Например, в жилых помещениях. В точках A и B провода вводятся в квартиру.
Также в наших квартирах все стандартные розетки находятся под одинаковым напряжением в $220 space В$. Большинство производителей техники изготавливают приборы как раз под это напряжение.
Использовать параллельное подключение к одной и той же цепи очень удобно, поскольку в нее могут быть включены самые разные потребители энергии (рисунок 6).
Благодаря такому способу подключения, выключая свет в своей квартире, мы не выключаем его и у наших соседей. Любые электроприборы могут работать независимо от подключения или отключения в сеть других.
На практике также часто можно увидеть смешанное соединение проводников. В таких цепях присутствует и последовательный тип соединении, и параллельный.
Пример задачи
В осветительную сеть комнаты включены две электрические лампы, сопротивления которых равны $200 space Ом$ и $300 space Ом$. Напряжение в сети составляет $120 space В$. Определите силу тока в каждой лампе, силу тока в проводящих проводах (то есть силу тока до разветвления), общее сопротивление участка, состоящего из двух ламп.
Подразумевается, что лампы подключены в сеть параллельно. Запишем условие задачи и решим ее.
Дано:
$R_1 = 200 space Ом$
$R_2 = 300 space Ом$
$U = 120 space В$
$I_1 — ?$
$I_2 — ?$
$I — ?$
$R — ?$
Решение:
Запишем закон Ома для участка цепи с первой лампой:
$I_1 = frac{U_1}{R_1}$.
Значение сопротивления нам известно. Что с напряжением на этом участке?
Так как лампы подсоединены параллельно, то напряжение на каждой будет равно напряжению во всей цепи:
$U_1 = U_2 = U = 120 space В$
Тогда мы можем рассчитать силу тока в каждой лампе.
Сила тока в первой лампе:
$I_1 = frac{U}{R_1}$,
$I_1 = frac{120 space В}{200 space Ом} = 0.6 space А$.
Сила тока во второй лампе:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{120 space В}{300 space Ом} = 0.4 space А$.
Сила тока до разветвления будет равна сумме сил этих двух токов в лампах:
$I = I_1 + I_2$,
$I = 0.6 space А + 0.4 space А = 1 space А$.
Общее сопротивление цепи мы можем определить двумя способами.
Способ №1
Используя закон Ома для участка цепи, состоящего из двух параллельно соединенных ламп:
$I = frac{U}{R}$,
$R = frac{U}{I}$,
$R = frac{120 space В}{1 space А} = 120 space Ом$.
Способ №2
Используя формулу для расчета сопротивления при параллельном соединении проводников:
$frac{1}{R} = frac{1}{R_1} + frac{1}{R_2}$,
$frac{1}{R} = frac{1}{200 space Ом} + frac{1}{300 space Ом} = frac{5}{600 space Ом} = frac{1}{120 space Ом}$.
Отсюда, $R = frac{1}{frac{1}{120 space Ом}} = 120 space Ом$.
При решении этой задачи мы убедились, что общее сопротивление цепи меньше сопротивления каждого из параллельно подключенных проводников: $R < R_1 < R_2$.
Ответ: $I_1 = 0.6 space А$, $I_2 = 0.4 space А$, $I = 1 space А$, $R = 120 space Ом$.
Упражнения
Упражнение №1
Два проводника сопротивлением $10 space Ом$ и $15 space Ом$ соединены параллельно и подключены к напряжению в $12 space В$. Определите силу тока в каждом проводнике и силу тока до разветвления.
Дано:
$R_1 = 10 space Ом$
$R_2 = 15 space Ом$
$U = 12 space В$
$I_1 — ?$
$I_2 — ?$
$I — ?$
Показать решение и ответ
Скрыть
Решение:
Напряжение будет одинаковое как во всей цепи, так и на концах каждого из двух проводников.
Запишем закон Ома для первого проводника и рассчитаем силу тока в нем:
$I_1 = frac{U}{R_1}$,
$I_1 = frac{12 space В}{10 space Ом} = 1.2 space А$.
То же самое сделаем для второго проводника:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{12 space В}{15 space Ом} = 0.8 space А$.
Сила тока до разветвления в цепи будет равна сумме сил тока в каждом проводнике:
$I = I_1 + I_2$,
$I = 1.2 space А + 0.8 space А = 2 space А$.
Ответ: $I_1 = 1.2 space А$, $I_2 = 0.8 space А$, $I = 2 space А$.
Упражнение №2
Почему бытовые приборы в помещении необходимо соединять параллельно?
Потому что бытовые приборы рассчитаны на то же напряжение, которое подается от городской сети — $220 space В$. При параллельном соединении это напряжение будет одинаковым на всех участках цепи.
Также параллельное соединение позволяет включать и выключать приборы независимо друг от друга, что невозможно при последовательном соединении.
Упражнение №3
Три потребителя с сопротивлениями $20 space Ом$, $40 space Ом$ и $24 space Ом$ соединены параллельно. Напряжение на концах этого участка цепи равно $24 space В$. Определите силу тока в каждом потребителе, общую силу тока в участке цепи и сопротивление участка цепи.
Дано:
$R_1 = 20 space Ом$
$R_2 = 40 space Ом$
$R_3 = 24 space Ом$
$U = 24 space В$
$I_1 — ?$
$I_2 — ?$
$I_3 — ?$
$I — ?$
$R — ?$
Показать решение и ответ
Скрыть
Решение:
Напряжение на концах этого участка цепи будет равно напряжению на концах каждого потребителя, так как они соединены параллельно: $U_1 = U2 = U_3 = U = 24 space В$.
Используя закон Ома для участка цепи, рассчитаем силу тока на каждом потребителе электроэнергии.
Для первого потребителя:
$I_1 = frac{U}{R_1}$,
$I_1 = frac{24 space В}{20 space Ом} = 1.2 space А$.
Для второго потребителя:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{24 space В}{40 space Ом} = 0.6 space А$.
Для третьего потребителя:
$I_3 = frac{U}{R_3}$,
$I_3 = frac{24 space В}{24 space Ом} = 1 space А$.
Сила тока до разветвления в цепи будет равна сумме сил тока в каждом потребителе электроэнергии:
$I = I_1 + I_2 + I_3$,
$I = 1.2 space А + 0.6 space А + 1 space А = 2.8 space А$.
Теперь используем закон Ома, представляя участок цепи с тремя потребителями как единый участок цепи:
$I = frac{U}{R}$,
$R = frac{U}{I}$,
$R = frac{24 space В}{2.8 space А} approx 8.6 space Ом$.
Ответ: $I_1 = 1.2 space А$, $I_2 = 0.6 space А$, $I_3 = 1 space А$, $I = 2.8 space А$, $R approx 8.6 space Ом$.
Упражнение №4
Два проводника имеют сопротивления, равные $5 space Ом$ и $500 space Ом$. Почему при последовательном соединении этих проводников их общее сопротивление будет больше $500 space Ом$, а при параллельном соединении меньше $5 space Ом$?
При последовательном соединении проводников общее сопротивление цепи будет равно сумме сопротивлений составляющих ее проводников.
Общее сопротивление при последовательном соединении:
$R = R_1 + R_2 = 5 space Ом + 500 space Ом = 505 space Ом$.
Это значение действительно больше, чем $500 space Ом$.
При параллельном соединении общее сопротивление мы рассчитываем следующим образом:
$frac{1}{R} = frac{1}{R_1} + frac{1}{R_2}$,
$frac{1}{R} = frac{1}{5 space Ом} + frac{1}{500 space Ом} = frac{101}{500 space Ом}$,
$R = frac{1}{frac{101}{500 space Ом}} = frac{500 space Ом}{101} approx 5 space Ом$.
Согласитесь, что $5 space Ом$ намного меньше, чем $500 space Ом$.
Можно посмотреть на этот вопрос и с другой стороны. Сопротивление рассчитывается по формуле $R = frac{rho l}{S}$. Оно прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения.
При последовательном соединении проводников мы можем сказать, что длина проводника увеличивается. Значит, увеличивается и сопротивление. Общее сопротивление будет больше, чем сопротивление каждого отдельного проводника.
А при параллельном соединении увеличивается площадь поперечного сечения. Значит, сопротивление будет уменьшаться. Получается, что общее сопротивление такой цепи будет меньше сопротивления каждого из проводников.
Упражнение №5
На рисунке 7 изображена схема смешанного соединения проводников, сопротивления которых: $R_1 = 4 space Ом$, $R_2 = 6 space Ом$, $R_3 = 12 space Ом$, $R_4 = 2 space Ом$. Амперметр показывает силу тока $1 space А$. Определите напряжение между точками В и С и силу тока в каждом проводнике.
Дано:
$R_1 = 4 space Ом$
$R_2 = 6 space Ом$
$R_3 = 12 space Ом$
$R_4 = 2 space Ом$
$I_3 = 1 space А$
$U — ?$
$I_1 — ?$
$I_2 — ?$
$I_4 — ?$
Показать решение и ответ
Скрыть
Решение:
Амперметр подсоединен последовательно с проводником $R_3$. Он показывает силу тока $I_3 = 1 space А$. Это сила тока после разветвления.
Используя закон Ома для этого проводника, рассчитаем напряжение на его концах:
$I_3 = frac{U_3}{R_3}$,
$U_3 = I_3R_3$,
$U_3 = 1 space А cdot 12 space Ом = 12 space В$.
Так как проводники $R_3$ и $R_2$ подключены в цепь параллельно, то напряжение на каждом из этих проводников будет равно напряжению на участке цепи, который их включает. Это и есть напряжение между точками B и C:
$U = U_3 = 12 space В$.
По закону Ома рассчитаем силу тока на проводнике $R_2$:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{12 space В}{6 space Ом} = 2 space А$.
Теперь мы можем рассчитать силу тока до его разветвления — на проводниках $R_1$ и $R_4$. При этом $I_1 = I_4 = I$, потому что эти проводники включены в цепь последовательно. Это значит, что сила тока в любом участке такой цепи будет одинаковой. В нашем случае на проводнике $R_1$ и $R_4$.
Рассчитаем эту силу тока, используя величины, полученные с параллельно соединенных проводников. Сила тока до разветвления будет равна сумме сил тока в каждом проводнике после разветвления:
$I = I_2 + I_3$,
$I = 1 space А + 2 space А = 3 space А$.
Ответ: $U = 12 space В$, $I_1 = I_4 = I = 3 space А$, $I_2 = 2 space А$, $I_3 = 1 space А$.
Напряжение при параллельном и последовательном соединении
Напряжение при параллельном и последовательном соединении: в первом случае одинаково для всей цепи, а во втором – равно сумме значений для каждого потребителя.
Напряжение при параллельном соединении

В параллельном соединении все ветви потребителей энергии сходятся в двух точках цепи, что изображено на схеме.
При таком соединении напряжение U1, U2 и U3 для трех компонентов цепи одинаково. То есть общее равно напряжению для любой ветки цепи:
U = U1 = U2 = … = Un
Напряжение при последовательном соединении

При последовательном соединении потребители энергии соединены друг с другом в виде цепочки, как показано в схематическом рисунке.
При последовательном соединении общее напряжение будет равно сумме значений для каждого ее звена:
U = U1 + U2 + … + Un
Общие сведения о напряжении
Напряжение обозначается буквой U. Единица в системе СИ – Вольт. Измеряется специальным прибором – вольтметром. Формула напряжения:
U = I*R,
где I – сила тока, А;
R – сопротивление проводника, Ом.
Примеры вычисления напряжения при параллельном и последовательном соединении
Возьмем для примера цепь с двумя резисторами. Если их соединение параллельно, на вольтметре будут показаны одни и те же значения для любого участка цепи:
U = U1 = U2 = 10 Вольт
При последовательном соединении общее напряжение равно сумме показателей обоих приборов, т.е.
U = 10 + 10 = 20 Вольт.
Применение двух типов соединений на практике
Так как при параллельном соединении напряжение для любой ветки цепи одинаково, его часто применяют на практике. Например, чтобы включить сразу несколько приборов, которым требуется одинаковое напряжение, а работа каждого не зависит от остальных приборов: холодильник, утюг, микроволновая печь и другие. Выключение утюга или холодильника никак не скажется на работе микроволновки. При последовательном соединении выключение одного из участников цепи ведет к обесточиванию всех приборов. Например: в елочной гирлянде при перегорании одной лампочки перестает работать вся гирлянда.
Загрузить PDF
Загрузить PDF
В параллельной цепи резисторы соединены таким образом, что электрический ток в цепи делится между резисторами и проходит через них одновременно (сравните это с автодорогой, которая разделяется на две параллельные дороги и делит поток машин на два потока, движущихся параллельно друг другу). В этой статье мы расскажет вам, как вычислить напряжение, силу тока и сопротивление в параллельной цепи.
Шпаргалка
- Формула для вычисления общего сопротивления RT в параллельной цепи: 1/RT = 1/R1 + 1/R2 + 1/R3 + …
- Напряжение в параллельной цепи одинаковое на каждом ее элементе: VT = V1 = V2 = V3 = …
- Формула для вычисления общей силы тока в параллельной цепи: IT = I1 + I2 + I3 + …
- Закон Ома: V = IR
-
1
Определение. Параллельная цепь — это цепь, в которой ток течет из точки А в точку В одновременно по нескольким элементам цепи (то есть поток электронов разбивается на несколько потоков, которые на конечном участке цепи вновь объединяются в единый поток). В большинстве задач, в которых присутствует параллельная цепь, нужно вычислить напряжение, сопротивление и силу тока.
- Элементы, подключенные параллельно, находятся на отдельных ветвях цепи.
-
2
Сила тока и сопротивление в параллельных цепях. Представьте себе автостраду с несколькими полосами, на каждой из которых установлен пункт пропуска, замедляющий движение автомобилей. Построив новую полосу, вы увеличите скорость движения (даже если и на этой полосе вы поставите пункт пропуска). Аналогично с параллельной цепью — добавив новую ветвь, вы уменьшите общее сопротивление цепи и увеличите силу тока.
-
3
Общая сила тока в параллельной цепи равна сумме силы тока на каждом элементе этой цепи. То есть, если известна сила тока на каждом резисторе, сложите эти силы тока, чтобы найти общую силу тока в параллельной цепи: IT = I1 + I2 + I3 + …
-
4
Общее сопротивление в параллельной цепи. Оно вычисляется по формуле: 1/RT = 1/R1 + 1/R2 + 1/R3 + …, где R1, R2 и так далее — это сопротивление соответствующих элементов (резисторов) этой цепи.
- Например, параллельная цепь включает два резистора и сопротивление каждого равно 4 Ом. 1/RT = 1/4 + 1/4 → 1/RT = 1/2 → RT = 2 Ом. То есть общее сопротивление параллельной цепи с двумя элементами, сопротивления которых равны, в два раза меньше сопротивления каждого резистора.
- Если какая-либо ветвь параллельной цепи не имеет сопротивления (0 Ом), то весь ток пройдет именно через эту ветвь.[1]
-
5
Напряжение. Напряжение — это разность электрических потенциалов между двумя точками электрической цепи. Так как здесь рассматриваются две точки без учета пути движения тока по цепи, напряжение в параллельной цепи одинаково на каждом элементе этой цепи, то есть: VT = V1 = V2 = V3 = …
-
6
Вычислите значения неизвестных величин по закону Ома. Закон Ома описывает взаимосвязь между напряжением V, силой током I и сопротивлением R: V = IR. Если вам известны значения двух величин из этой формулы, вы можете найти значение третьей величины.
- Вы можете применить закон Ома для всей цепи (V = ITRT) или для одной ветви этой цепи (V = I1R1).
Реклама
-
1
Нарисуйте таблицу, чтобы облегчить решение задачи, особенно если неизвестны значения сразу нескольких величин в данной параллельной цепи.[2]
Рассмотрим пример электрической цепи с тремя параллельными ветвями. Обратите внимание, что здесь под ветвями подразумеваются резисторы с сопротивлениями R1, R2, R3.R1 R2 R3 Общее Единицы измерения V В I А R Ом -
2
Внесите в таблицу данные вам значения. Например, к электрической цепи подключена батарея, напряжение которой равно 12 В. Цепь включает три параллельные ветви с сопротивлениями 2 Ом, 4 Ом, 9 Ом.
R1 R2 R3 Общее Единицы измерения V 12 В I А R 2 4 9 Ом -
3
Заполните значения напряжения для каждого элемента цепи. Помните, что общее напряжение в параллельной цепи и напряжение на каждом резисторе этой цепи равны.
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I А R 2 4 9 Ом -
4
Вычислите силу тока на каждом резисторе по закону Ома. Так как теперь в каждом столбце вашей таблицы есть значения двух величин, вы с легкостью вычислите значение третей величины при помощи закона Ома: V = IR. В нашем примере нужно найти силу тока, поэтому перепишите формулу закона Ома следующим образом: I = V/R
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 12/2 = 6 12/4 = 3 12/9 = ~1,33 А R 2 4 9 Ом -
5
Вычислите общую силу тока. Помните, что общая сила тока в параллельной цепи равна сумме сил тока на каждом элементе этой цепи.
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 6 3 1,33 6 + 3 + 1,33 = 10,33 А R 2 4 9 Ом -
6
Вычислите общее сопротивление. Сделайте это одним из двух способов. Либо используйте формулу
1/RT = 1/R1 + 1/R2 + 1/R3, либо формулу закона Ома: R = V/I.R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 6 3 1.33 10,33 А R 2 4 9 12 / 10,33 = ~1,17 Ом Реклама
-
1
Вычислите мощность тока по формуле: P = IV. Если вам дана мощность тока на каждом участке цепи, то общая мощность вычисляется по формуле: PT = P1 + P2 + P3 + ….
-
2
Вычислите общее сопротивление в параллельной цепи, состоящей из двух ветвей (двух резисторов).
- RT = R1R2 / (R1 + R2)
-
3
Найдите общее сопротивление в параллельной цепи, если сопротивление всех резисторов одинаково: RT = R1 / N, где N — количество резисторов в цепи.[3]
- Например, если в параллельной цепи два резистора с одинаковым сопротивлением, то общее сопротивление цепи будет вдвое меньше сопротивления одного резистора. Если в цепи восемь одинаковых резисторов, то общее сопротивление будет в восемь раз меньше сопротивления одного резистора.
-
4
Вычислите силу тока на каждом резисторе, если напряжение неизвестно. Это можно сделать, воспользовавшись правилом Кирхгофа.[4]
Вам необходимо вычислить сопротивление каждого резистора и общую силу тока в цепи.- Два резистора в параллельной цепи: I1 = ITR2 / (R1 + R2)
- Несколько (более двух) резисторов в параллельной цепи. В этом случае для вычисления I1 найдите общее сопротивление всех резисторов за исключением R1. Для этого воспользуйтесь формулой для вычисления общего сопротивления в параллельной цепи. Затем используйте правило Кирхгофа, заменив R2 полученным значением.
Реклама
Советы
- В параллельной цепи напряжение одинаково на всех резисторах.
- Возможно, в вашем учебнике закон Ома представлен следующей формулой: E = IR или V = AR. Здесь присутствуют другие обозначения величин, но суть закона Ома не меняется.
- Общее сопротивление часто именуется эквивалентным сопротивлением.
- Если у вас нет калькулятора, найти общее сопротивление, используя значения R1, R2 и так далее, довольно проблематично. Поэтому воспользуйтесь законом Ома.
- Если в задаче дана параллельно-последовательная цепь, сделайте вычисления для ее параллельного участка, а затем для полученной последовательной цепи.
Реклама
Об этой статье
Эту страницу просматривали 172 541 раз.














































