Смешанное соединение резисторов. Расчет смешанного соединения
26 Ноя 2018г | Раздел: Радио и Электрика начинающим
Здравствуйте, уважаемые читатели сайта sesaga.ru. Смешанное соединение резисторов представляет собой сложную электрическую цепь, в которой часть резисторов соединена последовательно, а часть параллельно.

В радиолюбительской практике такое включение резисторов встретить трудно, так как нет смысла подбирать сопротивление таким сложным способом. Достаточно соединить два, ну максимум три резистора последовательно или параллельно, чтобы подобрать нужный номинал.
Смешанное соединение встречается в основном в учебниках физики или электротехники в виде задач. Мне вспоминается такая задачка из школьной программы, но тогда она мне показалась сложной и правильно решить ее не получилось.
И вот, исходя из полученного опыта, хочу рассказать Вам, как вычислить общее сопротивление смешанного соединения резисторов. Вдруг кому-нибудь в жизни да и пригодится.
Расчет смешанного соединения резисторов.
Расчет начинают от дальнего участка цепи по отношению к источнику питания.
Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.
Суть данного метода заключается в уменьшении количества элементов в цепи с целью упрощения схемы и, соответственно, упрощению расчета общего сопротивления.
Разберем схему смешанного соединения из семи резисторов:

Самым дальним участком схемы оказались резисторы R6 и R7, соединенные параллельно:

Вычисляем их общее сопротивление используя формулу параллельного соединения:

Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6 с суммарным сопротивлением равным 30, 709 кОм.

Продолжим расчет и следующим дальним участком схемы оказались резисторы R5 и R6, соединенные последовательно:

Вычисляем их общее сопротивление используя формулу последовательного соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):

Схема уменьшилась еще на один элемент и приняла вид:

Теперь дальним участком оказались резисторы R4 и R5 соединенные параллельно:

Вычисляем их общее сопротивление:

Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно. Таким образом мы максимально упростили схему и привели ее к удобному расчету.

Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного соединения, и получаем общее сопротивление всей цепи:

Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения.
Удачи!
Поделиться с друзьями:
Смешанное соединение резисторов. Расчет смешанного соединения
Здравствуйте, уважаемые читатели сайта sesaga.ru. Смешанное соединение резисторов представляет собой сложную электрическую цепь, в которой часть резисторов соединена последовательно, а часть параллельно.

В радиолюбительской практике такое включение резисторов встретить трудно, так как нет смысла подбирать сопротивление таким сложным способом. Достаточно соединить два, ну максимум три резистора последовательно или параллельно, чтобы подобрать нужный номинал.
Смешанное соединение встречается в основном в учебниках физики или электротехники в виде задач. Мне вспоминается такая задачка из школьной программы, но тогда она мне показалась сложной и правильно решить ее не получилось.
И вот, исходя из полученного опыта, хочу рассказать Вам, как вычислить общее сопротивление смешанного соединения резисторов. Вдруг кому-нибудь в жизни да и пригодится.
Расчет смешанного соединения резисторов.
Расчет начинают от дальнего участка цепи по отношению к источнику питания.
Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.
Суть данного метода заключается в уменьшении количества элементов в цепи с целью упрощения схемы и, соответственно, упрощению расчета общего сопротивления.
Разберем схему смешанного соединения из семи резисторов:

Самым дальним участком схемы оказались резисторы R6 и R7, соединенные параллельно:

Вычисляем их общее сопротивление используя формулу параллельного соединения:

Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6 с суммарным сопротивлением равным 30, 709 кОм.

Продолжим расчет и следующим дальним участком схемы оказались резисторы R5 и R6, соединенные последовательно:

Вычисляем их общее сопротивление используя формулу последовательного соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):

Схема уменьшилась еще на один элемент и приняла вид:

Теперь дальним участком оказались резисторы R4 и R5 соединенные параллельно:

Вычисляем их общее сопротивление:

Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно. Таким образом мы максимально упростили схему и привели ее к удобному расчету.

Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного соединения, и получаем общее сопротивление всей цепи:

Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения.
Удачи!
Источник
Соединение резисторов — как считать общее сопротивление
Применяются следующие соединения резисторов: параллельное, последовательное и смешанное.
Последовательное соединение резисторов
Последовательное соединение резисторов — это такое взаимное расположение компонентов, при котором ток движется в одном направлении и имеет общее значение для каждого резистора. При таком соединении напряжение на каждом участке будет пропорционально сопротивлению конкретного резистора в цепи.
Принципиальная схема последовательного соединения:
Для подсчета общего (эквивалентного) сопротивление при последовательном соединении нужно сложить все номинальные сопротивления резисторов входящих в цепь:
В представленной схеме для наглядности приведены напряжения на каждом из трех участков. И падение напряжения происходит в зависимости от сопротивления конкретного резистора. Сила тока в цепи общая для всех резисторов ( I = I1 = I2 = I3 ). Поэтому согласно закону Ома сила тока при известном напряжении источника питания (в данном случае U = 220 В) определяется по формуле:
I = U / R = U / (R1 + R2 + R3 + . + Rn) .
I = 220 / (20 + 70 + 10) = 220 / 100 = 2,2 A.
Формулы нахождения напряжения на участке цепи при известной силе тока (в данном случае I = I1 = I2 = I3 = 2,2 A):
Соответственно U1 = 2,2 × 20 = 44 В; U2 = 2,2 × 70 = 154 В; U3 = 2,2 × 10 = 22 В. В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи (220 В).
Рассмотренные три резистора в последовательной цепи можно заменить одним с сопротивлением 100 Ом:
Если можно несколько резисторов заменить одним, то возникает логичный вопрос, зачем применяется такое комбинирование. Простыми словами можно ответить, что иногда невозможно подобрать резистор с требуемыми параметрами или необходимо создать более сложные электронные схемы. В этом случае прибегают к последовательному, параллельному или смешанному соединению в цепи.
В цепи из последовательно соединенных резисторов главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление. К примеру, если соединить три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате получиться составной с сопротивлением 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом. А если убрать резистор на 10 Ом, то сопротивление незначительно уменьшиться до 101 Ом.
Параллельное соединение резисторов
Параллельное соединение резисторов — это такое взаимное соединение компонентов, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.
При таком соединении напряжение во всей цепи и на каждом участке одинаково и равно напряжению источника питания U = U1 = U2 = U3 = Un . По каждому резистору течет свой ток. Сумма токов всех резисторов дает общую силу тока цепи: I = I1 + I2 + I3 + . + In . Соответственно общая проводимость параллельной цепи равна сумме ее отдельных проводимостей. Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 + . + 1 / Rn . Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Рассчитаем общее сопротивление для приведенного выше примера с параллельным соединением резисторов:
1 / R = 1 / 20 + 1 / 70 + 1 / 10 ≈ 0,164.
Выделим основные особенности параллельного соединения резисторов:
- Общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора.
- Увеличение числа параллельно соединенных резисторов ведет к уменьшению общего сопротивления и увеличению общей силы тока в цепи.
- Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
- Если в цепи используются резисторы одного номинала, то формула общего сопротивления упрощается и принимает вид R = R1 / N (R1 – номинальное сопротивление резистора; N – количество резисторов с одинаковым номинальным сопротивлением).
Смешанное соединение резисторов
Смешанное соединение резисторов — это комбинация последовательного и параллельного соединения. Иногда такую комбинацию называют последовательно-параллельным соединением.
Пример цепи со смешанным соединением резисторов:
Для расчета эквивалентного сопротивления таких соединений всю цепь разбивают на простейшие участки и придерживаются следующего алгоритма:
Параллельное соединение резисторов используется для получения меньшего сопротивления из имеющихся простейших радиоэлектронных элементов. При таком способе соединения складываются проводимости. Поэтому чем больше параллельно включенных резисторов, тем ниже получается общее сопротивление или выше проводимость соответственного участка электрической цепи – носителям электрических зарядов легче его преодолеть.
Последовательное соединение резисторов используется с целью большего ограничения протеканию электрическому току, то есть приводит к повышению сопротивления соответственного участка электрической цепи или для снижения ее проводимости.
Важнейшим параметром резистора является мощность рассеивания. При любом способе соединения, не важно, при последовательном, при параллельном или при смешанном, происходит сложение мощностей рассеивания отдельных резисторов. Поэтому все вместе они способны рассеять больше тепла, а соответственно и пропустить большие токи не перегреваясь, что широко применяется в радиолюбительской практике.
Источник
Ток и напряжение при параллельном, последовательном и смешанном соединении проводников
 Реальные электрические цепи чаще всего включают в себя не один проводник, а несколько проводников, как-то соединенных друг с другом. В самом простом виде электрическая цепь имеет только «вход» и «выход», то есть два вывода для соединения с другими проводниками, через которые заряд (ток) имеет возможность втекать в цепь и из цепи вытекать. При установившемся токе в цепи, значения величин токов на входе и на выходе будут одинаковы.
Реальные электрические цепи чаще всего включают в себя не один проводник, а несколько проводников, как-то соединенных друг с другом. В самом простом виде электрическая цепь имеет только «вход» и «выход», то есть два вывода для соединения с другими проводниками, через которые заряд (ток) имеет возможность втекать в цепь и из цепи вытекать. При установившемся токе в цепи, значения величин токов на входе и на выходе будут одинаковы.
Если взглянуть на электрическую цепь, включающую в себя несколько разных проводников, и рассмотреть на ней пару точек (вход и выход), то в принципе остальная часть цепи может быть рассмотрена как одиночный резистор (по ее эквивалентному сопротивлению).
При таком подходе говорят, что если ток I – это ток в цепи, а напряжение U – напряжение на выводах, то есть разность электрических потенциалов между точками «входа» и «выхода», то тогда отношение U/I можно рассмотреть как величину эквивалентного сопротивления R цепи целиком.
Если закон Ома выполняется, то эквивалентное сопротивление можно вычислить довольно легко.
Ток и напряжение при последовательном соединении проводников

В простейшем случае, когда два и более проводников объединены друг с другом в последовательную цепь, ток в каждом проводнике окажется одним и тем же, а напряжение между «выходом» и «входом», то есть на выводах всей цепи, будет равным сумме напряжений на составляющих цепь резисторах. И поскольку закон Ома справедлив для любого из резисторов, то можно записать:

Итак, для последовательного соединения проводников характерны следующие закономерности:
Для нахождения общего сопротивления цепи, сопротивления составляющих цепь проводников складываются;
Ток через цепь равен току через любой из проводников, образующих цепь;
Напряжение на выводах цепи равно сумме напряжений на каждом из проводников, образующих цепь.
Ток и напряжение при параллельном соединении проводников
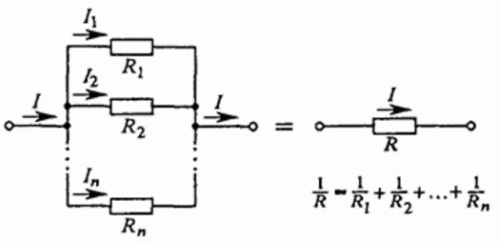
При параллельном соединении нескольких проводников друг с другом, напряжение на выводах такой цепи — это напряжение на каждом из проводников, составляющих цепь.
Напряжения на всех проводниках равны между собой и равны напряжению приложенному (U). Ток через всю цепь — на «входе» и «выходе» — равен сумме токов в каждой из ветвей цепи, параллельно объединенных и составляющих данную цепь. Зная, что I = U/R, получаем, что:
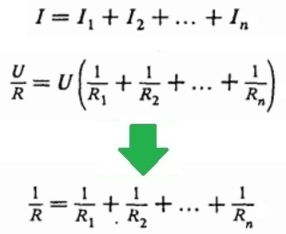
Итак, для параллельного соединения проводников характерны следующие закономерности:
Для нахождения общего сопротивления цепи — складываются обратные величины сопротивлений составляющих цепь проводников;
Ток через цепь равен сумме токов через каждый из проводников, образующих цепь;
Напряжение на выводах цепи равно напряжению на любом из проводников, образующих цепь.
Эквивалентные схемы простых и сложных (комбинированных) цепей
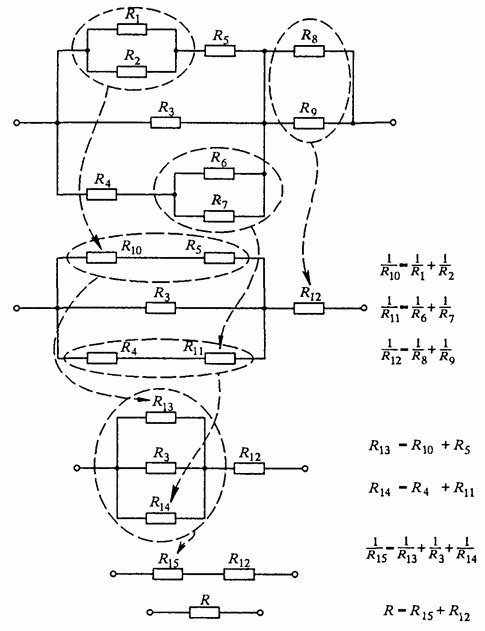
В большинстве случаев схемы цепей, являясь комбинированным соединением проводников, поддаются пошаговому упрощению.
Группы соединенных последовательно и параллельно частей цепи, заменяют эквивалентными сопротивлениями по приведенному выше принципу, шаг за шагом вычисляя эквивалентные сопротивления кусочков, затем приводя их к одному эквивалентному значению сопротивления всей цепи.
И если сначала схема выглядит довольно запутанной, то будучи упрощенной шаг за шагом, она может быть разбита на меньшие цепочки из последовательно и параллельно соединенных проводников, и так в конце концов сильно упрощена.
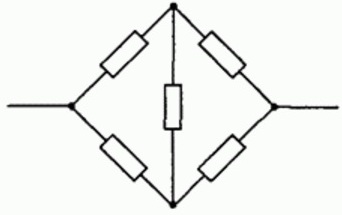
Между тем, не все схемы подаются упрощению таким простым путем. Простая с виду схема «моста» из проводников не может быть исследована таким образом. Здесь нужно применять уже несколько правил:
Для каждого резистора выполняется закон Ома;
В любом узле, то есть в точке схождения двух и более токов, алгебраическая сумма токов равна нулю: сумма токов втекающих в узел, равна сумме токов вытекающих из узла (первое правило Кирхгофа);
Сумма напряжений на участках цепи при обходе по любому пути от «входа» до «выхода» равна приложенному к цепи напряжению (второе правило Кирхгофа).
Мостовое соединение проводников
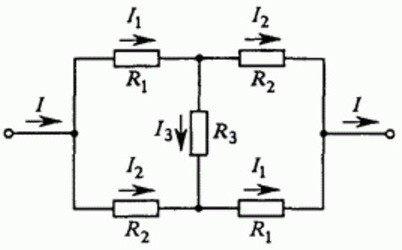
Дабы рассмотреть пример использования приведенных выше правил, рассчитаем цепь, собранную из проводников, объединенных в схему моста. Чтобы вычисления получились не слишком сложными, примем, что некоторые из сопротивлений проводников равны между собой.
Обозначим направления токов I, I1, I2, I3 на пути от «входа» в цепь — к «выходу» из цепи. Видно, что схема симметрична, поэтому токи через одинаковые резисторы одинаковы, поэтому обозначим их одинаковыми символами. В самом деле, если поменять у цепи местами «вход» и «выход», то схема будет неотличима от исходной.
Для каждого узла можно записать уравнения токов, исходя из того, что сумма токов втекающих в узел равна сумме токов вытекающих из узла (закон сохранения электрического заряда), получится два уравнения:
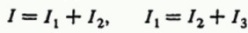
Следующим шагом записывают уравнения сумм напряжений для отдельных участков цепи при обходе цепи от входя к выходу различными путями. Так как схема является в данном примере симметричной, то достаточно двух уравнений:
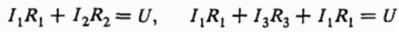
В процессе решения системы линейных уравнений, получается формула для нахождения величины тока I между зажимами «входным» и «выходным», исходя из заданного приложенного к цепи напряжения U и сопротивлений проводников:
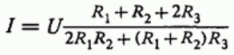
А для общего эквивалентного сопротивления цепи, исходя из того, что R = U/I, следует формула:
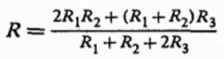
Можно даже проверить правильность решения, например приведя к предельным и к частным случаям величины сопротивлений:
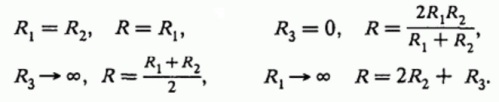
Теперь вы знаете, как находить ток и напряжение при параллельном, последовательном, смешанном, и даже при мостовом соединении проводников, применяя закон Ома и правила Кирхгофа. Эти принципы очень просты, и даже самая сложная электрическая цепь с их помощью в конце концов приводится к элементарному виду путем нескольких несложных математических операций.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Один из способов определения силы тока в резисторе – это ее прямое измерение мультиметром. Измерения следует проводить в разрыве цепи после резистора следующим образом:
– выставить на тестере максимально допустимый диапазон,
– присоединить щупы прибора к месту разрыва цепи.
Применив закон Ома, искомую величину можно также определить расчетным путем:
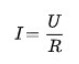
где I – сила тока, U – напряжение, R – сопротивление (единицы измерения ампер (А), вольт (В), ом (Ом) соответственно).
В приборостроении и электротехнике применяются различные типы соединения и подключения резисторов, что обеспечивает разнообразие электротехнических свойств электрических схем.
Типы соединений резисторов
Соединение элементов в одну цепь осуществляется следующими способами:
-
последовательно;
-
параллельно;
-
смешанно.
Общие схемы типов соединений представлены на рисунке 1.
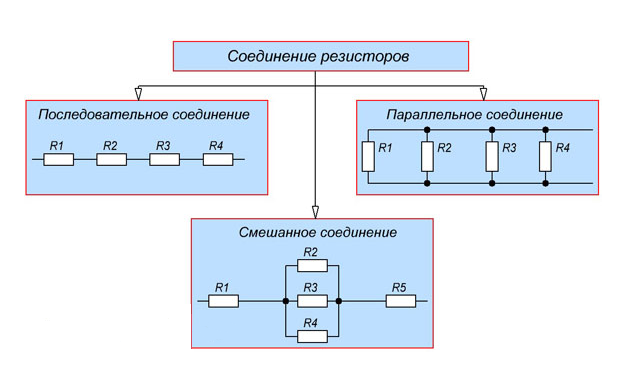
Рисунок 1. Типы соединений резисторов
Параллельным соединением принято считать соединение, при котором элементы цепи соединены так, что их начала могут соединиться в одной точке, а концы – в другой (см.рис.2)
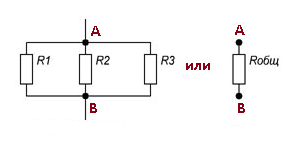
Рисунок 2. Параллельное соединение резисторов
Потоку заряженных частиц при прохождении участка АВ предоставлено несколько вариантов пути, поэтому на каждом участке с резистором будет протекать ток, величиной, обратно пропорциональной сопротивлению резистора.
При увеличении нагрузки параллельного соединения, в случае подключения большого числа резисторов способом параллельного соединения в электрическую цепь, общее сопротивление цепи значительно уменьшится, за счет увеличения числа путей, предоставленных потоку заряженных частиц. Увеличение количества возможных вариантов движения влечет за собой уменьшение противодействия движению тока.
Как найти сопротивление параллельно соединенных резисторов?
Общее сопротивление резисторов в случае параллельного соединения определено по закону Ома в следующем соотношении:
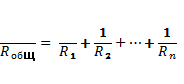
и рассчитывается по формуле:
![]()
Для примера произведем расчет общего сопротивления для цепи из двух резисторов, обладающих сопротивлением R1= R2=7Ом (см. рис.3а)
R12= 7*7/ (7+7) = 3,5Ом
Сопротивление на участке АВ
(1– 2) в 2 раза меньше R каждого из резисторов.
При параллельном подсоединении к рассматриваемой цепи еще одного резистора, также обладающего аналогичным сопротивлением R3=7Ом (см. рис.3б) общее сопротивление цепи рассчитывается с учетом предыдущих вычислений, где R12= 3,5Ом
Rобщ= 3,5*7/ (3,5+7) = 2,33 Ом
R123< R3
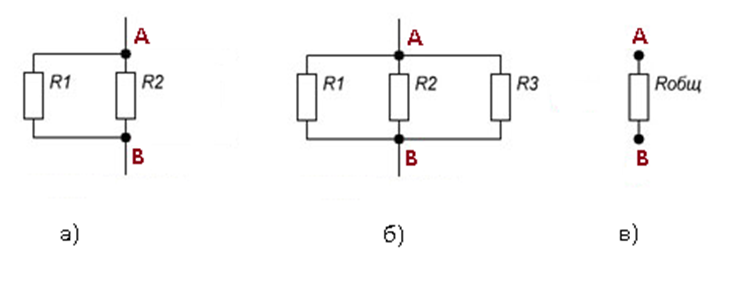
Рисунок 3. Увеличение цепи параллельного соединения резисторов
Из расчетов следует, что общее сопротивление (см. рис.3в) всегда будет меньше сопротивления любого параллельно включенного резистора. Такое условие обеспечивается равенством токов на входе и выходе узлов или групп параллельных резисторов и постоянством напряжения в сети.
Что такое последовательное соединение резисторов?
При последовательном соединении резисторы подсоединяются друг за другом, при этом конец предыдущего резистора соединен с началом последующего резистора (рисунок 4).
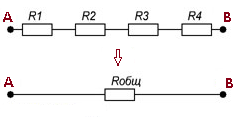
Рисунок 3. Последовательное соединение резисторов.
Потоку заряженных частиц при прохождении участка АВ предоставлен один путь, поэтому, чем больше резисторов подсоединено, тем большее сопротивление движущимся заряженным частицам они оказывают, то есть общее сопротивление участка цепи Rобщ возрастает.
Формула для расчета общего сопротивления при последовательном соединении имеет вид:
Как рассчитать напряжения на последовательно соединенных резисторах?
Последовательное соединение резисторов увеличивает общее сопротивление. Ток во всех частях схемы будет одинаковым, при этом будет определяться падение напряжения на каждом резисторе.
Общее напряжение питания на резисторах, соединенных последовательно, равно сумме разностей потенциалов на каждом резисторе:
URобщ =UR1+ UR2 + UR3+ UR4
Применив закон Ома, можно вычислить напряжение на каждом резисторе:
UR1=I*R1, UR2=I*R2, UR3=I*R3, UR4=I*R4
Напряжение на участке АВ рассчитывается по формуле:
UАВ=I* (R1
+ R2+R3+R4)
А ток в цепи:
![]()
Резисторы, соединенные последовательно, применяются в электротехнике в качестве делителя напряжения.
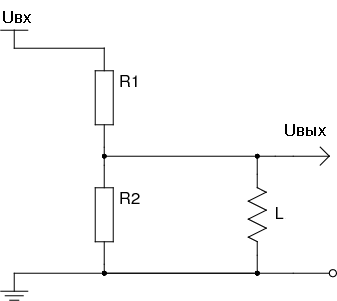
Рисунок 5. Схема простейшего делителя напряжения
Регулируя сопротивление обоих резисторов можно выделить требуемую часть входящего напряжения. При необходимости деления напряжения на несколько частей к источнику напряжения подключается несколько последовательно соединенных резисторов.
Смешанное соединение резисторов
В электротехнике наиболее распространено использование различных комбинаций параллельного и последовательного подключения. Силу тока при смешанном соединении резисторов определяют путем разделения цепи на последовательно соединенные части. Однако для определения общего сопротивления в случае параллельного сопротивления различных частей следует применять соответствующую формулу.
Алгоритм расчета смешанного подключения аналогичен правилу расчета базовой схемы последовательного и параллельного подключения резисторов. В этом нет ничего нового: нужно правильно разложить предложенное решение на пригодные для расчета части. Участки с элементами подключаются поочередно или параллельно. Гибридное резистивное соединение представляет собой комбинацию последовательного и параллельного. Эту комбинацию иногда называют последовательно-параллельным соединением.
На рисунке 6 представлена схема смешанного соединения резисторов.
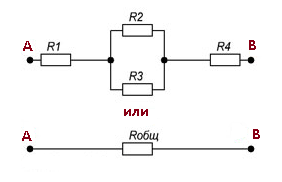
Рисунок 6. Смешанное соединение резисторов.
На рисунке показано, что резисторы R2 и R3
соединены параллельно, а R1, R23
и R4 последовательно.
Чтобы рассчитать сопротивление этого соединения, вся схема делится на простейшие части, начиная с параллельного или последовательного сопротивления. Тогда следующий алгоритм выглядит следующим образом:
1. Определите эквивалентное сопротивление части резистора, подключенной параллельно.
2. Если эти части содержат резисторы, включенные последовательно, сначала рассчитайте их сопротивление.
3. Вычислив эквивалентное сопротивление резистора, перерисовываем схему. Обычно схема получается из последовательного эквивалентного сопротивления.
4. Рассчитайте сопротивление цепи.
Другие способы подключения хорошо видны на примере, показанном на рисунке. Без специальных расчетов очевидно, что параллельное соединение резисторов создает несколько путей для тока. Следовательно, в одиночном контуре его сила будет меньше по сравнению с контрольными точками на входе и выходе. При этом напряжение на отметке остается неизменным.
Пример участка цепи для расчета сопротивления смешанного соединения показан на рисунке 5.
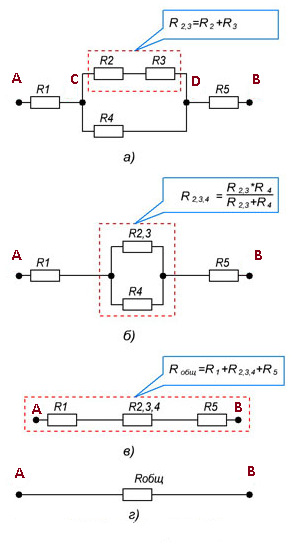
Рисунок 7. Общее сопротивление участка цепи со смешанным соединением резисторов.


При
решении задач на смешанное соединение проводников обычно составляют так
называемые эквивалентные схемы, выделяя участки с последовательным и
параллельным соединением.
Пример
1.

Сопротивление R1,2 заменило
выделенный участок цепи, в котором два проводника соединены параллельно.
Тогда
мы можем найти сопротивление этого участка с параллельным соединением
проводников:
![]()
А теперь видно,
что проводники R1,2 и R3 соединены
последовательно. Общее сопротивление равно R = R1,2 + R3 = 4 +
2 = 6.
Пример
2.

В данном случае
нужно развернуть схему, двигаясь от точки к точке. Видно, что в точке Б схема
разветвляется, а в точке В ветви соединяются. Таким образом,
эквивалентные схемы будут иметь вид:


R2, R3 и R4 соединены
последовательно. Поэтому R2,3,4 = R2 + R3 + R4 = 1 + 10
+ 1 = 12
R2,3,4 и R5 соединены
параллельно. Поэтому

И в последней
схеме проводники соединены последовательно. R = R2-5 + R1 + R6 = 1 + 4,8
+ 1 = 6,8.
Пример
3.
Найти распределение токов и напряжений в цепи.

Решение.
Так
как известны сила тока и сопротивление на первом участке, то можно найти
напряжение на нем: U1 = I1 R1 = 1 ∙ 10
= 10 B.
Первый
и второй проводники соединены параллельно. Значит, напряжение на них одинаково,
т.е. U1 = U2 = 10 В. Так
как первый и второй проводники имеют одинаковое сопротивление, то сила
тока на них одинакова: I2 = 1 А. При
параллельном соединении I1,2 = I1 + I2 = 2 А.
Участки
1-2, 3-4-5 и 6-7 соединены последовательно между собой, значит I3,4,5 = I6,7 = I1,2 = 2 A.
Найдем
общее сопротивление участка 3-4-5:

R3,4,5
= 3 Ом.
Тогда можно найти напряжение на 3-4-5, при параллельном соединении оно
одинаково на всех участках. U3,4,5 = I3,4,5 ∙R3,4,5 = 2 ∙ 3 =
6 В.
U3 = U4 = U5 = 6 В. Зная
напряжение на каждом из участков и сопротивление, можно найти силу тока на
каждом участке.

Смешаннымсоединением называют
сочетание последовательного и
параллельного соединений резисторов.
Большое разнообразие этих соединений
не позволяет вывести общую формулу для
определения эквивалентного сопротивления
цепи. Поэтому в каждом конкретном случае,
используя методы расчета при
последовательном и параллельном
соединениях, можно рассчитать
эквивалентное сопротивление при
смешанном соединении. Поясним это на
конкретном примере расчета электрической
цепи (рис. 1.20 а).
Электрическую цепь постепенно упрощают
и приводят к простейшему виду (рис. 1.20
б, в)
![]() ;
;![]() ;
;![]()
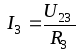 ;
;
![]()
![]() .
.
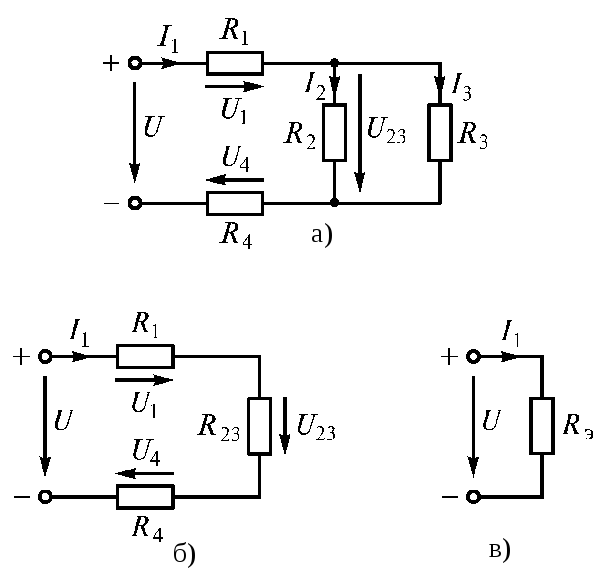
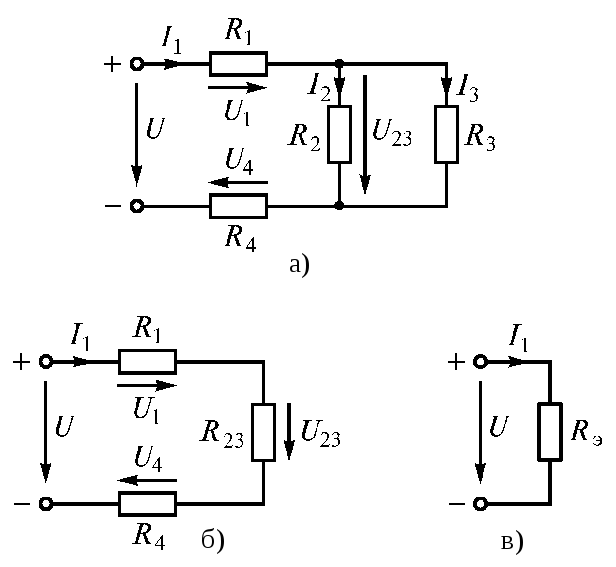
Рис. 1.20
Проверка: 1)![]() 2)
2)![]() .
.
1.8.4. Метод преобразований треугольника резисторов в эквивалентную звезду и наоборот
Рассмотрим
две электрические цепи (рис. 1.21). Одна
из них имеет вид треугольника, другая
– трехлучевой звезды. В дальнейшем
такие соединения будем называть
соответственно соединением в треугольник
и соединением звездой.
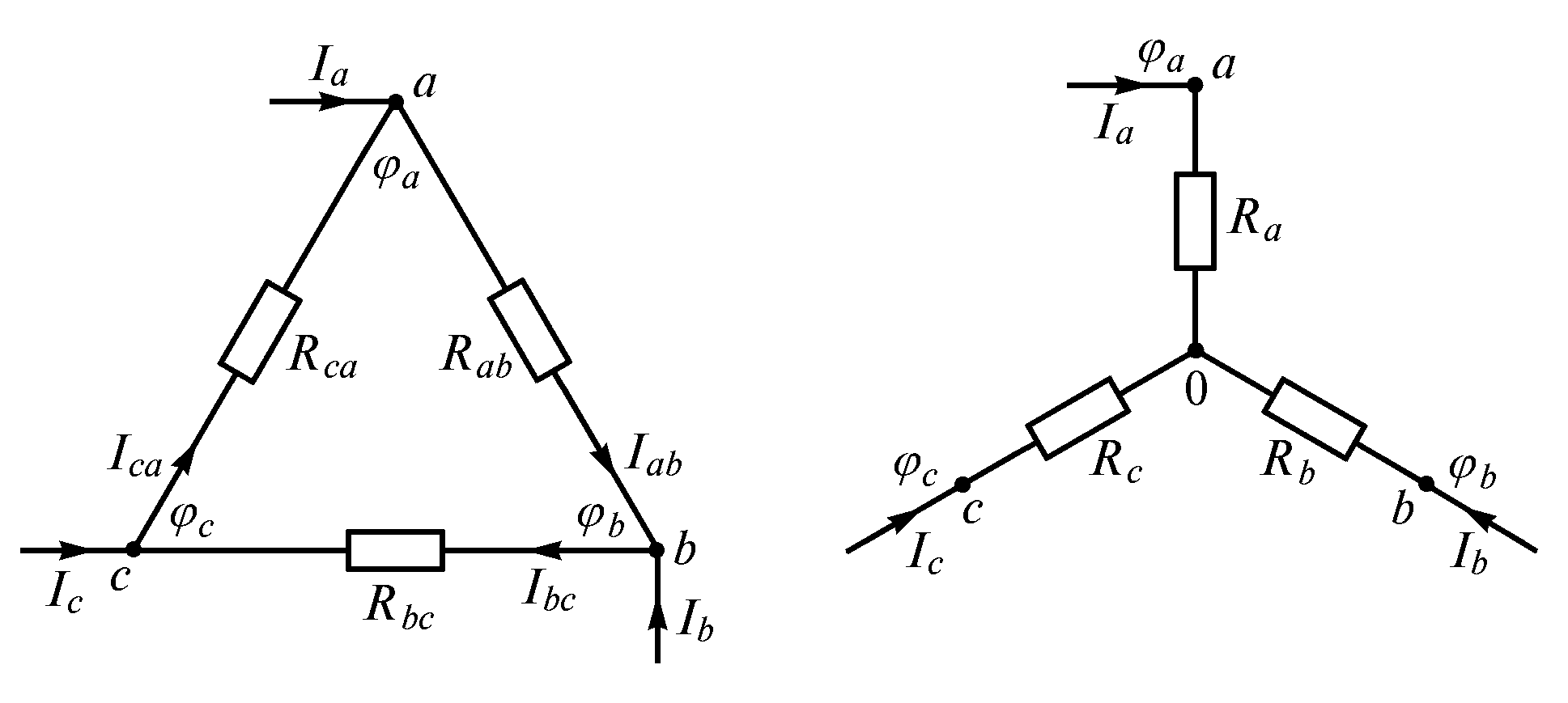
Рис. 1.21
Соединения такого вида очень распространены
в трехфазных цепях, в которых часто
возникает необходимость перехода от
одного вида соединения к другому
(эквивалентному). Эквивалентность
треугольника и звезды резисторов
заключается в том, что их замена не
изменяет потенциалов узловых точек
(φа,
φb
иφс),
являющихся вершинами треугольника и
эквивалентной звезды. Не изменяются
также токи, напряжения и мощности в
остальной части схемы, не затронутой
преобразованием.
Формулы пересчета без вывода сопротивлений
ветвей треугольника
![]() ,
,![]() ,
,![]() в эквивалентную звезду
в эквивалентную звезду![]() ,
,![]() ,
,![]() имеют вид
имеют вид
![]()
![]()
![]() (1.39)
(1.39)
При переходе от звезды к треугольнику
можно воспользоваться следующими
формулами
![]()
![]()
![]() (1.40)
(1.40)
Если сопротивления всех ветвей цепи
по схеме треугольник одинаковы, т.е.
![]() ,
,
сопротивления эквивалентной звезды
будут также одинаковые:![]() ,
,
причем
![]() .
.
1.8.5. Последовательное соединение источников энергии
В практике последовательное и согласное
включение источников применяют для
увеличения напряжения. Рассмотрим схему
с двумя согласно и одним встречно
включенными источниками (рис. 1.22).
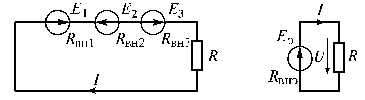
Рис. 1.22
По второму закону Кирхгофа запишем
![]() .
.
(1.41)
Отсюда
![]() ,
,
(1.42)
где
![]()
![]() .
.
Напряжения на зажимах источников и
приемника
![]()
![]()
![]()
![]() .
.
При последовательном соединении
![]() источников с одинаковыми параметрами
источников с одинаковыми параметрами
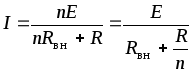 .
.
(1.43)
1.8.6. Параллельное соединение источников энергии
В тех случаях, когда номинальное
напряжение приемника равно напряжению
одного источника, а его ток больше
допустимого тока одного источника,
применяют параллельное соединение
источников (рис. 1.23 а).
При параллельном
соединении источников с одинаковыми
параметрами их общая ЭДС не изменится,
но уменьшатся токи через каждый источник
и внутреннее сопротивление общего
источника. Тогда эквивалентный источник
(рис. 1.23 б) имеет следующие параметры:
![]()
![]() .
.
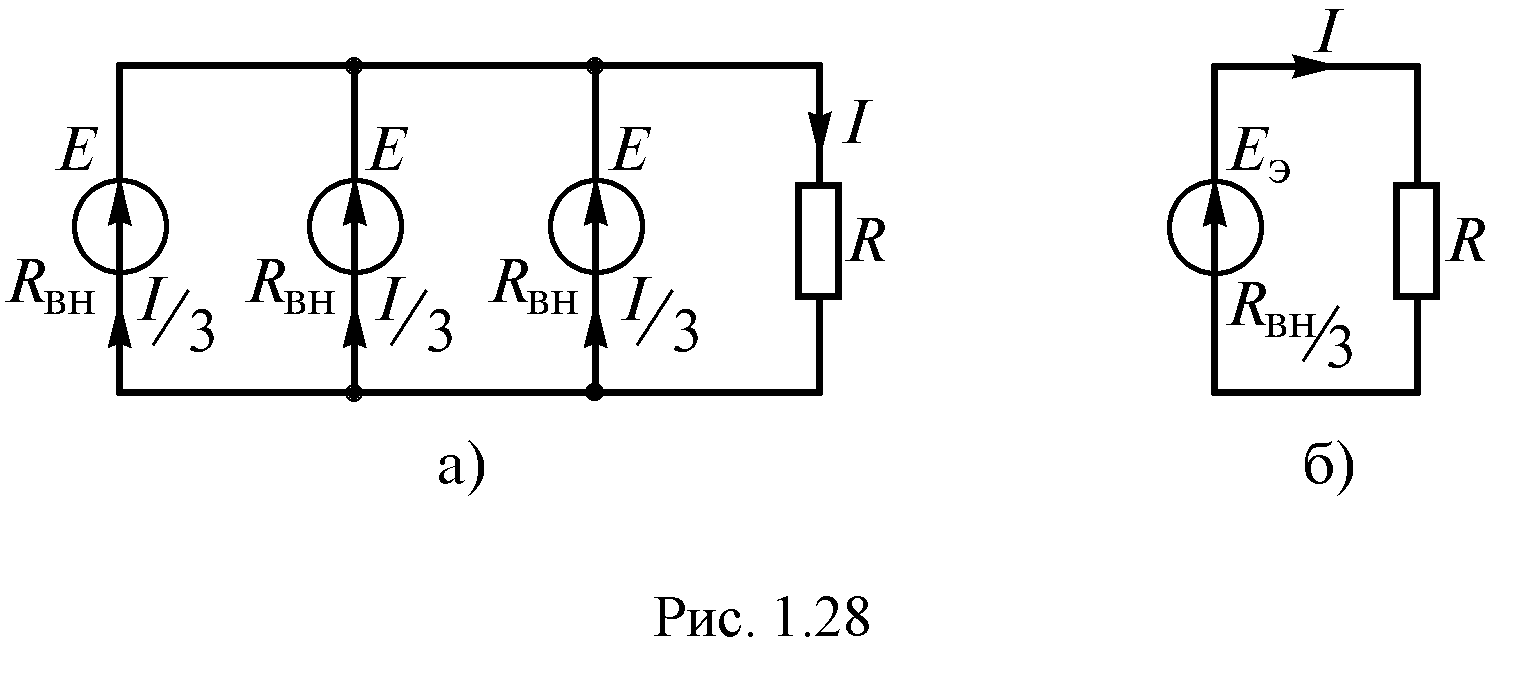
Рис. 1.23
При![]() источниках
источниках
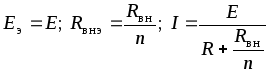 .
.
(1.44)
 Пример
Пример
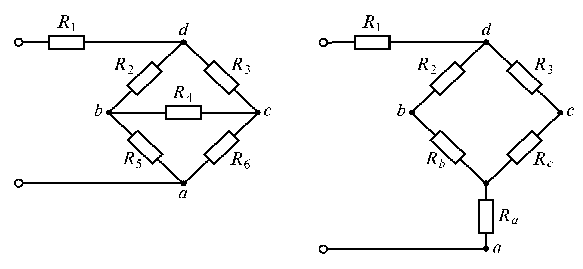
1.1. Определить
эквивалентное сопротивление цепи (рис.
1.24 а),
если
![]() 1Ом;
1Ом;
![]() 3Ом.
3Ом.
а) б)
в) г)
Рис. 1.24
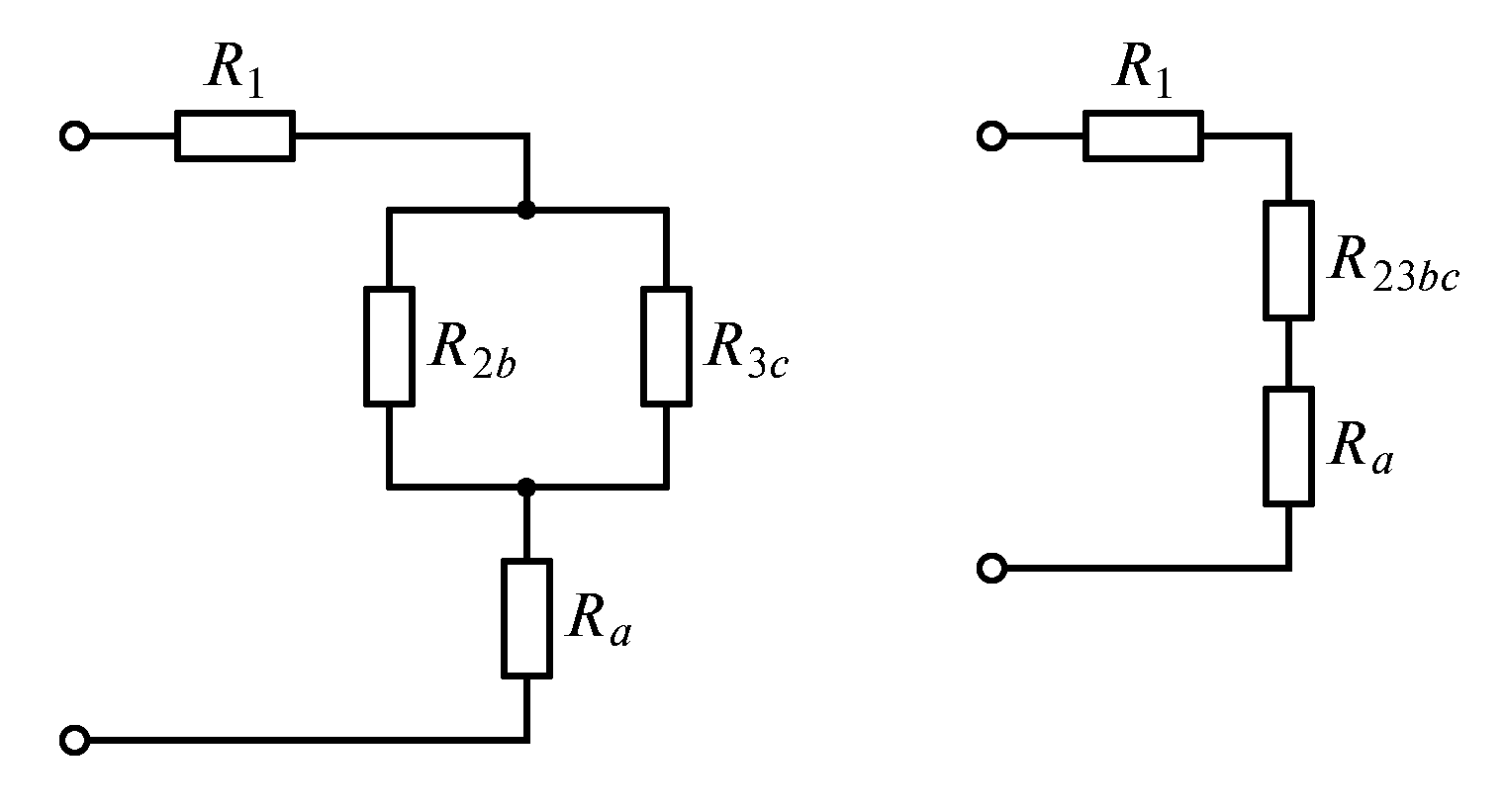
Решение. Преобразуем
треугольник сопротивлений
![]() в эквивалентную
в эквивалентную
звезду сопротивлений
![]() (рис. 1.24 б).
(рис. 1.24 б).
Так как
![]() ,
,
то
![]() Ом.
Ом.
Дальнейшее решение
выполним преобразованием последовательно
или параллельно
соединенных сопротивлений резисторов
их эквивалентными сопротивлениями
«свертыванием» схемы. Резисторы
![]() и
и![]() ,
,
а также![]() и
и![]() соединены последовательно, поэтому их
соединены последовательно, поэтому их
общие сопротивления
![]() Ом;
Ом;![]() Ом.
Ом.
Полученная
схема приведена на рис. 1.24 в.
Резисторы
![]() и
и![]() соединены параллельно, поэтому (рис.
соединены параллельно, поэтому (рис.
1.24 г)
![]() Ом.
Ом.
Эквивалентное сопротивление всей цепи
![]() Ом.
Ом.
Пример 1.2.Определить токи в ветвях
цепи (рис. 1.25 а), если задано:![]() Ом;
Ом;![]() = 6Ом;
= 6Ом;![]() Ом;
Ом;![]() = 2Ом;
= 2Ом;![]() = 100В.
= 100В.
Решение. Резисторы
![]() и
и![]() соединены последовательно и образуют
соединены последовательно и образуют
ветвь с током![]() .
.
Резисторы![]() и
и![]() включены параллельно, а относительно
включены параллельно, а относительно
резистора![]() – последовательно. Вычислим эквивалентные
– последовательно. Вычислим эквивалентные
сопротивления:
![]() Ом;
Ом;
![]() Ом.
Ом.
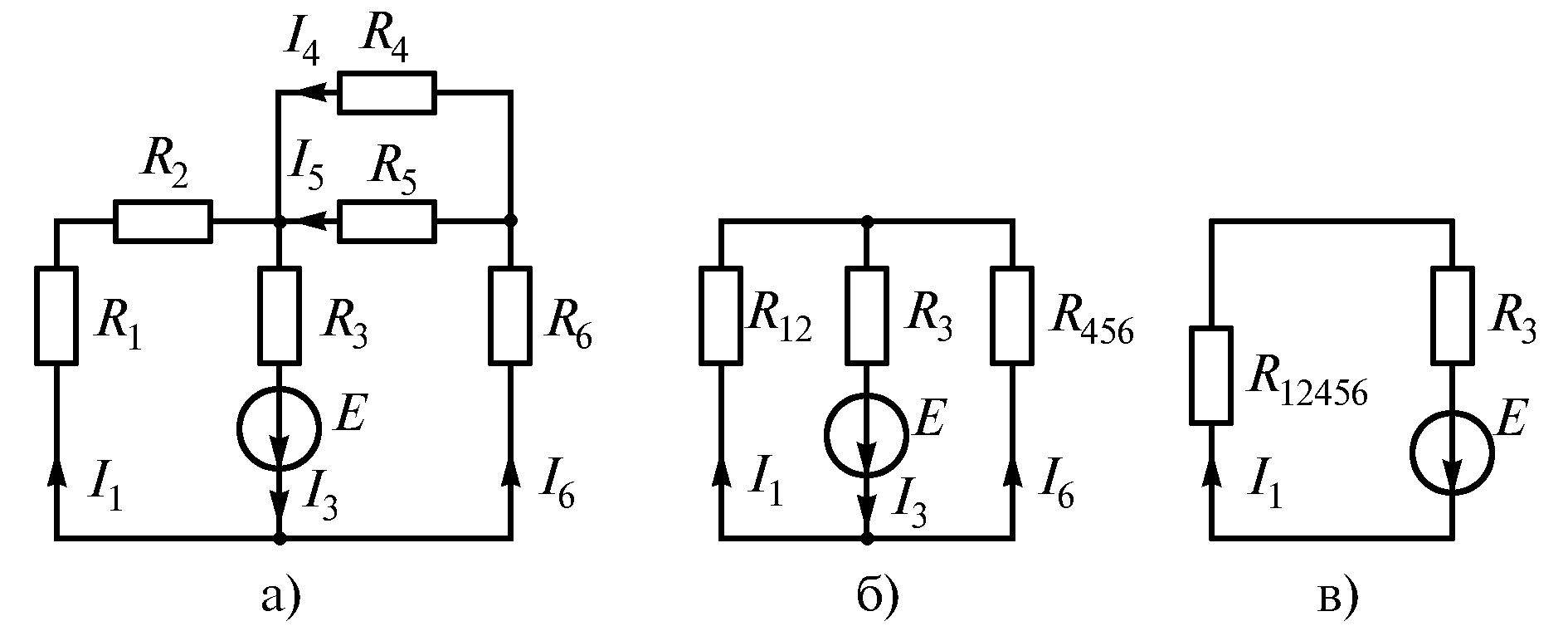
Рис. 1.25
Резисторы
![]() и
и![]() соединены параллельно, а по отношению
соединены параллельно, а по отношению
к![]() – последовательно, поэтому (рис. 1.25
– последовательно, поэтому (рис. 1.25
б, в)
![]() Ом.
Ом.
Эквивалентное сопротивление цепи
![]() Ом.
Ом.
Ток в ветви с источником
![]() А.
А.
Так как сопротивления резисторов
![]() и
и![]() одинаковы, то
одинаковы, то
![]() А.
А.
Аналогично, при
![]()
![]() А.
А.
