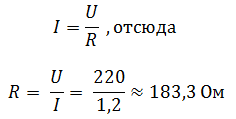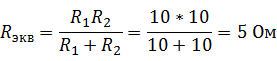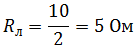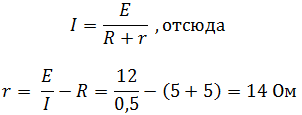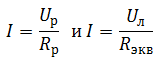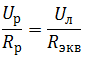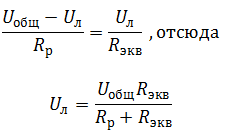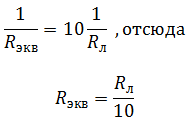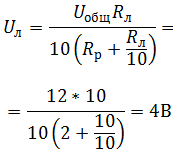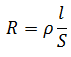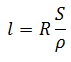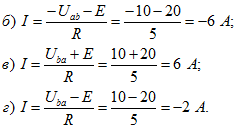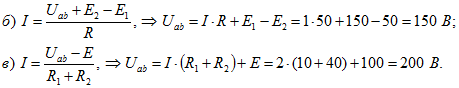Задачи на нахождение силы тока в цепи, напряжения. Как решать задачи на закон Ома.
Задачи на силу тока в основном касаются определения силы тока, напряжения и сопротивления. В данном разделе Вы найдете формулы для решения задач. Мы разберем решение типичных элементарных задач, используя закон Ома.
Задача 1. Сила тока
Через нить накаливания лампочки от карманного фонарика за 2 мин проходит электрический заряд, равный 30 Кл. Определите силу тока в этой лампочке.
| Дано: | CИ | Решение |
| q = 30 Кл | Сила тока I определяется по формуле | |
| t = 2 мин | 120 с | I= q/t |
| I – ? | I = 30Кл/120с = 0,25А = 250м А |
Сила тока. Решение задач
Задача 2. Напряжение в цепи
Электродвигатель включен в электрическую цепь с напряжением 24В. Определите заряд, прошедший через электродвигатель, если при этом была совершена работа, равная 84 кДж
| Дано: | CИ | Решение |
| U = 24 В | Напряжение на электродвигателе определяется по формуле | |
| А = 84 кДж | 84000 Дж | U=A/q q= A/U |
| q – ? | Q = 84000 Дж/24 В = 3500 Кл |
Напряжение в цепи. Решение задач
Задача 3. Закон Ома сила тока
Определите силу тока в кипятильнике, включенном в сеть с напряжением 220 В, если сопротивление спирали составляет 55 Ом.
| Дано: | CИ | Решение |
| U = 220 В | Силу тока в кипятильнике можно определить, воспользовавшись законом Ома | |
| R = 55 Ом | І=U/R | |
| І – ? | І = 220 B/55 Ом = 4 А |
Сила тока по закону Ома. Решение задач
Задача 4. Закон Ома напряжение
Какое напряжение нужно приложить к концам проводника сопротивлением 5 Ом, тобі по проводнику пошел ток с силой тока, равной 300 мА
| Дано: | CИ | Решение |
| R = 5 Ом | Необходимое напряжение можно определить, воспользовавшись законом Ома | |
| І = 300 мА | 0.3 A | І=U/R U = IR |
| U – ? | U = 0,3 А * 5 Ом = 1,5 В |
Напряжение в сети. Закон Ома
Задача 5. Сопротивление по закону Ома
Определите cопротивление резистора, если за время 10 мин через него проходит заряд 200 Кл. Напряжение на концах резистора равно 6 В.
Источник
Как найти напряжение сети задача
Решение задач на уроках физики в 10-11 классах и при подготовке к ЕГЭ смотрите в следующих конспектах:
Задачи на Закон Ома.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
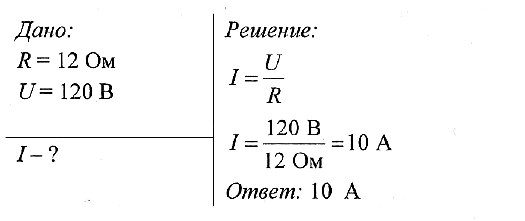
Задача № 1. Какова сила тока в резисторе, если его сопротивление 12 Ом, а напряжение на нем 120 В?
Задача № 2. Сопротивление проводника 6 Ом, а сила тока в нем 0,2 А. Определите напряжение на концах проводника.
Задача № 3. Определите сопротивление проводника, если при напряжении 110 В сила тока в нем 2 А.
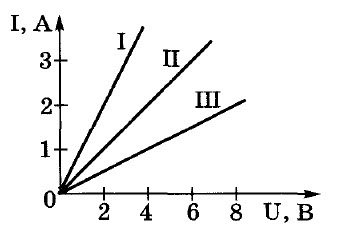
Задача № 4. По графикам зависимости силы тока от напряжения определите сопротивление каждого проводника.
Задача № 5. Чему равна сила тока в электрической лампе карманного фонаря, если сопротивление нити накала 16,6 Ом и лампа подключена к батарейке напряжением 2,5 В?
Задача № 6. Электрический утюг включен в сеть с напряжением 220 В. Какова сила тока в нагревательном элементе утюга, если сопротивление его равно 48,4 Ом?
Задача № 7. При напряжении 110 В, подведенном к резистору, сила тока в нем равна 5 А. Какова будет сила тока в резисторе, если напряжение на нем увеличить на 10 В?
Задача № 8. Чему равно сопротивление спирали электрической лампы в рабочем состоянии, у которой на цоколе написано 6,3 В, 0,22 А?
Задача № 9. Показание вольтметра, присоединенного к горящей электрической лампе накаливания, равно 120 В, а амперметра, измеряющего силу тока в лампе, 0,5 А. Чему равно сопротивление лампы? Начертите схему включения лампы, вольтметра и амперметра.
Задача № 10. ОГЭ Источник постоянного тока с ЭДС E = 12 В и внутренним сопротивлением г = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить силу тока в цепи I, падение напряжения UR на внешнем участке и падение напряжения Ur на внутреннем участке цепи.
Краткая теория для решения Задачи на Закон Ома.
Это конспект по теме «ЗАДАЧИ на Закон Ома». Выберите дальнейшие действия:
Источник
Сила тока и напряжение(решение задач).
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Практическая работа №3 : Расчет силы тока и напряжения. (8А ,В класс)
Цель урока : В ходе эксперимента установить связь между силой тока и напряжением;
обеспечить интерактивные возможности самостоятельной учебной работы за счет
использования активно-деятельных форм обучения.
Учащиеся должны знать, что такое сила тока и напряжение, какова связь между ними;
Знать устройство и принцип действия амперметра и вольтметра и уметь ими пользоваться;
формировать умение анализировать, видеть проблему и пути её решения;
формировать ИКТ-компетентность школьника.
Продолжить формирование научного мировоззрения посредством изучения нового материала;
Показать роль опыта, как источника новых знаний;
Способствовать воспитанию эстетических качеств личности посредством четких записей и чертежей; воспитать личностные качества ребят посредством справки об ученом
Способствовать развитию общеучебных умений и навыков;
Развивать логическое и абстрактное мышление учащихся;
Способствовать развитию наблюдательности, самостоятельной работы учащихся, решения проблемных ситуаций.
развивать умение сравнивать, строить доказательства, обобщать, выдвигать гипотезы, переносить знания в новую ситуацию;
выполнять задания творческого и поискового характера, применять знания и способы действий в изменённых условиях.
моделировать с помощью рисунков, схематичных рисунков, предметов;
развивать и поддерживать учебную мотивацию, познавательный интерес учащихся, в результате использования информационных технологий.
Организационный момент (2-3 мин)
Актуализация опорных знаний (5-7 мин)
Практическая работа (25 мин)
Актуализация опорных знаний
Что такое электрический ток?
Что принято за направление электрического тока?
Какая величина характеризует действия электрического тока?
Как найти силу тока? Формула.
Единицы измерения силы тока.
Каким прибором измеряется сила тока? Его условное обозначение.
Как и куда подключается амперметр?
Что можно сказать о силе тока, если в цепи есть разветвление (параллельное соединение)?
Что заставляет заряженные частицы двигаться в проводнике направленно?
Почему мы можем утверждать, что электрическое поле совершает работу?
Какая величина характеризует работу электрического поля?
Как найти напряжение? Формула.
Каким прибором измеряется напряжение? Условное обозначение.
Как и куда подключается вольтметр в цепи?
Чему равно общее напряжение всей цепи, если в ней несколько потребителей соединены последовательно?
1.Электрический ток представляет собой … (упорядоченное движении заряженных частиц)
За направление электрического тока принимают … (направление движения положительно заряженных частиц)
Сила тока обозначается буквой латинского алфавита … ( I)
Величина равная отношению электрического заряда, прошедшего через поперёчное сечение проводника, ко времени прохождения …(силой тока)
Единица измерения силы тока в СИ называется … (ампер)
Для измерения силы тока используют прибор … (амперметр)
Амперметр включается в электрическую цепь … с тем прибором, силу тока в котором измеряют.(последовательно)
Сила тока в неразветвлённой части цепи равна … в отдельных параллельно соединенных проводниках. (сумме)
Если есть ток, значит, есть движение зарядов, следовательно, есть сила, которая заставляет двигаться заряды, есть ток, которая направлена вдоль тока.
При перемещении заряда q в электрическом поле электрические силы совершают работу.
Напряжение показывает, работу тока при перемещении электрического заряда, равного 1 Кл.
Величина равная отношению работы тока на данном участке к электрическому заряду, прошедшему по этому участку называется … (напряжением)
За единицу напряжения принимают … (вольт)
Для измерения напряжения применяют прибор, называемый … (вольтметром)
Зажимы вольтметра присоединяют к тем точкам цепи, между которыми надо измерить напряжение, такое включение прибора называется … (параллельным)
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно … (сумме напряжений на отдельных участках цепи)
Практическая работа: Расчет силы тока и напряжения . (Работа в группах).
Сила тока и напряжение
1. . Сила тока в цепи электрической плитки равна 1,4 А. Какой электрический заряд проходит через поперечное сечение ее спирали за 20 мин?
2. Как на практике можно определить работу электрического тока в цепи? Какие для этого нужны приборы?
3.Сколько электронов должно пройти за 1с через поперечное сечение проводника,чтобы включенный в цепь амперметр показал 1мА?
1. По проводнику, к концам которого приложено напряжение 5 В, прошло 100 Кл электричества. Определите работу тока.
2. Электрическая лампочка включена в цепь напряжением 10 В. Током была совершена работа 150 Дж. Какое количество электричества прошло через нить накала лампочки?
1. Лампочка включена в сеть напряжением 110 В. Какое количество электричества прошло через нить накала лампочки, если работа тока 220 Дж?
2. Определите работу тока, если через проводник, находящийся под напряжением 30 В, прошло 75 Кл электричества.
1. Какую работу совершит ток силой 3 А за 10 мин при напряжении в цепи 15 В?
2. В лампочке карманного фонаря сила тока равна 0,2 А. Вычислите электрическую энергию, получаемую лампочкой за каждые 2 мин, если напряжение на лампочке составляет 3,6 В.
Две лампы включены в электрические цепи, в которых силы тока равны, но несмотря на это одна из ламп горит менее ярко, чем другая. О чём свидетельствует этот факт? Какой вывод о напряжении на лампе можно сделать?
На одном участке цепи при перемещении по нему 100 Кл электричества была совершена такая же работа, как и при перемещении 600 Кл электричества на другом участке. На концах какого участка напряжение больше и во сколько раз?
Начертите схему электрической цепи, состоящей из источника тока и двух последовательно соединенных ламп. Изобразите, как надо подключить амперметр и вольтметр для измерения силы тока в каждой лампе и напряжения на каждой лампе.
1. Башенный кран равномерно поднимает груз массой 0,5 т на высоту 30 м за 2 мин. Сила тока в электродвигателе равна 16,5 А при напряжении 220 В. Определите КПД электродвигателя крана.
2. Каков КПД электродвигателя, который за 20 с поднимает груз массой 150 кг на высоту 12 м? Напряжение в электрической сети 380 В, сила тока через двигатель 4 А.
3.При напряжении 1В сила тока в цепи равна 0,2А. Напряжение на концах цепи увеличивают сначала до 5В, а затем до 12В. Какой будет сила тока в цепи при этих напряжениях
5. Домашнее задание : на листках по уровням
1. Две лампы включены в электрические цепи, в которых силы тока равны, но,
несмотря на это одна из ламп горит менее ярко, чем другая. О чем свидетельствует
этот факт? Какой вывод о напряжении на лампах можно сделать?
2. На одном участке цепи при перемещении по нему 100 Кл электричества была
совершена такая же работа, как и при перемещении 600 Кл электричества на другом
участке. На концах, какого участка напряжение больше и во сколько раз?
1. Какие источники тока вы знаете?
2. По спирали электролампы проходит 540 Кл электричества за каждые 5 мин. Чему
1. Чему равно напряжение на участке цепи, на котором совершена работа 500 Дж
при прохождении 25 Кл электричества?
2. Вычислите работу, которая совершается при прохождении через спираль
электроплитки 15 Кл электричества, если она включена в сеть напряжением 220 В?
1. При электросварке сила тока достигает 200 А. Какой электрический заряд проходит
через поперечное сечение электрода за 1 мин?
2. Определите напряжение на участке цепи, если при прохождении по нему заряда в
15 Кл током была совершена работа 9 кДж.
1. При переносе 240 Кл электричества из одной точки электрической цепи в другую за
16 мин совершена работа в 1200 Дж. Определите напряжение и силу тока в цепи.
2. Какова сила тока в лампочке велосипедного фонарика, если при напряжении
4 В в ней за 1с расходуется 0,8 Дж электроэнергии?
1. По обмотке включенного в цепь прибора идет ток силой 5 мА. Какое количество
электричества пройдет через прибор в течение 1 ч?
2. Определите силу тока в осветительной сети, если при напряжении 220 В в ней за
Источник

где Эпол max max, max — определяется по годовому графику по продолжительности:
|
max |
∑ |
|||||||
|
2100 1 max0,7 4000 |
2400 |
0,5 6400 4000 |
0,3 8760 6400 |
5338 ч; |
||||
|
Эпол |
1 |
|||||||
|
100 |
5338 |
|||||||
|
533800 |
533800 МВт ч; |
|||||||
|
η |
100 % |
98,16 %. |
||||||
|
533800 |
9983,86 |
3.1. Общие положения
Электрическая сеть высокого напряжения для передачи и распределения электроэнергии относится к категории электрических цепей, поэтому для расчета ее режима применяются общие методы теории цепей. Пусть задана мощ-
|
ность некоторой нагрузки |
узла |
, которая должна быть учтена на- |
||
|
ряду с |
другими нагрузками |
при расчете |
режима сети. Ток этой нагрузки |
|
|
и, следовательно, может быть вычислен при известном напря- |
||||
|
жении |
на зажимах этой нагрузки. Однако именно напряжения в узлах сети |
|||
|
√3 |
являются искомыми величинами. Это обстоятельство препятствует непосредственному использованию законов Кирхгофа для получения однозначного решения, поэтому нашли применение и другие методы решения, в том числе метод последовательных приближений (итерационный метод).
Метод последовательных приближений основан на последовательном уточнении напряжений в узлах электрической сети, причем в качестве начального приближения может быть использовано разумное допущение о том, что напряжения во всех узлах в нормальном режиме не могут существенно отличаться от номинального напряжения данного класса сети. Введение такого допущения позволяет определить приближенно потери мощности на каждом участке сети, мощности в начале и конце каждого участка и токи нагрузок.
Значение тока на участке или мощности в начале участка, непосредственно связанного с узлом, где напряжение считается известным, является достаточным для того, чтобы определить напряжение в конце этого участка. В свою очередь, становится возможным расчет напряжения в конце следующего участка и т. д.
Процесс продолжается до тех пор, пока значения напряжений во всех узлах, полученные после выполнении данной итерации, не будут отличаться от напряжений, полученных на предыдущей итерации, менее чем на заданную величину точности расчета.
Все необходимые расчетные формулы приведены в [1, гл. 6].
16

3.2. Типовые задачи
Задача 1. Определить напряжение в конце воздушной линии 500 кВ в на-
грузочном режиме 800 300 и в режиме холостого хода, построить векторные диаграммы токов и напряжений. Схема сети приведена на рис. 3.1. Расчет выполнить без учета потерь на корону.
Решение задачи. Схема замещения сети с указанными на ней параметрами приведена на рис. 3.2.
Режим холостого хода. На первой итерации расчета начальное приближение напряжения в конце ЛЭП принимается равным напряжению в начале ли-
нии, 515 кВ. Каждая итерация состоит из двух частей. Сначала, двигаясь от конца ЛЭП к началу, находят потери мощности в продольных и поперечных элементах и потоки мощности в конце и начале ЛЭП (прямой ход итерации), затем определяют напряжение в конце ЛЭП (обратный ход).
|
1 |
2,5 |
38 |
2 |
|||||||||||||||||
|
1 |
250 км |
2 |
515 кВ |
н |
к |
|||||||||||||||
|
2АС–500 3 |
||||||||||||||||||||
|
515 кВ |
800 |
300 |
9,1 |
10 |
||||||||||||||||
|
Рис. 3.1. Схема сети |
Рис. 3.2. Схема замещения сети |
|||||||||||||||||||
|
∆ ш |
Определение потерь в шунте |
|||||||||||||||||||
|
515 |
9,1 10 |
241, |
5 МВ А |
|||||||||||||||||
|
Поскольку мощность нагрузки равна нулю, то3 |
при условном. |
направлении |
||||||||||||||||||
|
тока от узла 1 к узлу 2, |
241, |
5 МВ А. |
||||||||||||||||||
|
мощности в продольном сопротивлении: |
||||||||||||||||||||
|
∆ |
Определение потерьк |
∆ |
ш |
3 |
||||||||||||||||
|
к |
241,35 |
2,5 |
38 |
0,55 |
8,35 |
МВ А; |
||||||||||||||
|
к |
515 |
|||||||||||||||||||
|
н |
∆ |
241,35 |
0,55 |
8,35 |
0,55 233 |
МВ А. |
На этом прямой ход итерации закончен.
В соответствии с условным направлением тока напряжение в конце ЛЭП:
|
∆ |
, где |
515|0°, тогда |
∆ |
δ . |
Продольная и поперечная составляющие падения напряжения:
|
0,55 |
2,5 |
233 |
38 |
17,19 кВ, |
|
|
515 |
|||||
|
0,55 |
38 |
233 |
2,5 |
1,17 кВ. |
|
–
515
17

Теперь напряжение в узле 2 в конце первой итерации
|
515 |
17,19 |
1,17 532,19 |
1,17 532,19| 0,126°. |
Наибольшее рабочее напряжение на классе 500 кВ составляет 525 кВ. Полученное значение напряжения превышает допустимую величину, поэтому режим холостого хода линии недопустим. Для снижения напряжения в конце линии в режиме холостого хода необходима установка шунтирующих реакторов. Выбор регулирующих устройств будет рассматриваться ниже.
Векторная диаграмма токов и напряжений линии 500 кВ в режиме холостого хода показана на рис. 3.3, при ее построении в целях наглядности не соблюден масштаб векторов.
|
ш |
∆ |
δ |
+ |
||||||
|
δ |
|||||||||
|
Рис. 3.3. Векторная диаграмма сети |
|||||||||
|
Ток в шунте |
определяется следующим образом: |
||||||||
|
1 |
1 |
532,24| 0,126° |
0,279| 89,87°кА, |
||||||
|
ш |
√ |
√ |
0,91 |
10 |
|||||
|
3 |
3 |
то есть ток в шунте опережает вектор напряжения в конце ЛЭП на угол π⁄2.
Нагрузочный режим. Как и в предыдущем расчете, на первой итерации начальное приближение напряжения в конце ЛЭП принимается равным напряже-
|
нию в начале линии, |
515 кВ. |
|||||
|
Определение потерь в шунте |
||||||
|
∆ Потокш |
515 |
9,1 |
10 |
|||
|
мощности в конце линии равен |
241,35 МВ А. |
|||||
|
к |
∆ ш |
241,35 |
800 |
300 |
800 58,65 МВ А. |
Определение потерь мощности в продольном сопротивлении и потока в начале линии:
|
∆ |
к |
800 |
69,4 |
2,5 |
38 |
6,07 92,19 МВ А, |
|||
|
∆ |
|||||||||
|
503,4 |
|||||||||
|
н |
кМВ |
800 |
58,65 |
6,07 |
92,19 |
806,07 |
|||
|
150,84 |
А. |
На этом прямой ход итерации закончен.
В соответствии с условным направлением тока напряжение в конце ЛЭП:
|
∆ |
, где |
515|0°, тогда |
∆ |
δ . |
18

Продольная и поперечная составляющие падения напряжения:
|
∆ |
н |
н |
806,07 |
2,5 |
150,84 |
38 |
15 кВ, |
|||
|
515 |
||||||||||
|
н |
н |
806,07 |
38 |
150,84 |
2,5 |
|||||
|
δ |
58,7 кВ. |
|||||||||
|
515 |
||||||||||
|
Напряжение в узле 2 в первой итерации расчета |
||||||||||
|
515 |
15 |
58,7 500 |
58,7 503,4| 6,7°. |
Вторая итерация расчета отличается от первой только тем, что в качестве напряжения в конце ЛЭП используется его значение, полученное в первой итерации:
|
∆к ш |
503,4 |
9,1 |
10 |
230,6 |
МВ А; |
; |
|||||||||||
|
230,6 |
800 |
300 |
800 |
69,4 |
МВ А |
||||||||||||
|
∆ |
800 |
69,4 |
|||||||||||||||
|
2,5 |
38 |
6,36 |
96,7) МВ А; |
||||||||||||||
|
503,4 |
|||||||||||||||||
|
н |
800 |
69,4 |
6,36 |
96,7 |
806,36 |
166,1 МВ А; |
|||||||||||
|
806,36 |
2,5+166,1 |
38 |
806,36 |
38 |
166,1 |
2,5 |
|||||||||||
|
∆ |
|||||||||||||||||
|
16,2 |
515 |
кВ; |
515 |
||||||||||||||
|
58,7 |
6,7° кВ. |
||||||||||||||||
|
515 |
16,2 |
58.7 |
498,8 |
58,7 |
502,24| |
Как видно из результатов решения задачи, напряжение в конце линии 500 кВ в нагрузочном режиме не выходит за пределы длительно допустимых.
Задача 2. Построить векторные диаграммы токов и напряжений электрической сети без учета потерь мощности для сети, схема замещения которой приведена на рис. 3.4.
|
1 |
2 |
200| 0° |
3 |
|
|
1 |
8 |
1 |
20 |
Рис. 3.4. Схема замещения сети
|
100 |
50 |
100 |
50 |
||
|
1 |
2 |
3 |
|||
|
1 |
20 |
||||
|
200 |
100 |
100 |
50 |
Рис. 3.5. Потокораспределение без потерь мощности
Решение задачи. В соответствии с условием задачи потери мощности не учитываются и тогда потоки мощности в начале и конце участков ЛЭП одинаковы. Потоки мощности в сети показаны на рис. 3.5, знаки потоков соответствуют условным направлениям потоков. Векторная диаграмма приведена на рис. 3.6. Построение диаграммы начинается с узла 3, в котором задано напря-
19

жение 200 кВ, напряжение совмещается с вещественной осью комплексной плоскости. Ток узла 3:
|
100 |
50 |
0,289 0,145 кА. |
||||||
|
√ |
√ |
200 |
||||||
|
3 |
||||||||
|
3 |
||||||||
|
Направление тока |
указывает на наличие в узле 3 генератора, что и было |
задано в условиях задачи, ток опережает напряжение в узле 3.
δ δ δ
+
δ ∆
δ
∆
Рис. 3.6. Векторная диаграмма токов и напряжений
Напряжение в узле 2, кВ, в соответствии с условным направлением тока
|
∆ |
∆ |
δ100 |
1 |
50 |
20 |
100 |
20 |
50 1 |
||||||||||||||||||||||||||||||
|
200 |
||||||||||||||||||||||||||||||||||||||
|
200 |
| |
°. |
200 |
|||||||||||||||||||||||||||||||||||
|
200 |
5,5 |
9,75 |
194,5 |
9,75 |
194,7 |
2,87 |
||||||||||||||||||||||||||||||||
|
Таким образом, |
194,7 |
| |
2,87 . |
|||||||||||||||||||||||||||||||||||
|
Ток нагрузки в узле| δ2: |
° |
|||||||||||||||||||||||||||||||||||||
|
200 |
100 |
200 |
100 |
194,5 |
9,75 |
|||||||||||||||||||||||||||||||||
|
√ |
194,5 |
9,75 |
194,7 |
|||||||||||||||||||||||||||||||||||
|
3 |
3 |
|||||||||||||||||||||||||||||||||||||
|
√3 |
||||||||||||||||||||||||||||||||||||||
|
0,578 |
√0,326 кА. |
φ |
, где |
|||||||||||||||||||||||||||||||||||
|
напряжения в узле 2 на угол |
||||||||||||||||||||||||||||||||||||||
|
Ток нагрузки узла 2 отстает от |
1 |
⁄ |
2, |
φ |
26 . |
|||||||||||||||||||||||||||||||||
|
Тогда ток на |
tgφ |
⁄ |
° |
|||||||||||||||||||||||||||||||||||
|
участке 1 2 определяется по первому закону Кирхгофа |
||||||||||||||||||||||||||||||||||||||
|
0,578 |
0,326 0,289 |
0,145 |
0,289 |
181 кА. |
||||||||||||||||||||||||||||||||||
|
Напряжение в узле 1, кВ, определяется по отношению к напряжению узла |
||||||||||||||||||||||||||||||||||||||
|
2 по тому же принципу, как найдено |
по отношению к , при этом в качест- |
|||||||||||||||||||||||||||||||||||||
|
ве исходного используется |
модуль напряжения в узле 2: |
∆50 1, |
||||||||||||||||||||||||||||||||||||
|
194,7 |
100 1 |
50 8 |
100 8 |
|||||||||||||||||||||||||||||||||||
|
194,7∆ |
δ |
194,7 |
| |
|||||||||||||||||||||||||||||||||||
|
2,57 |
3,85 |
197,27 |
197,3 |
1,12 |
194,7 |
|||||||||||||||||||||||||||||||||
|
3,85 |
; |
|||||||||||||||||||||||||||||||||||||
|
° |
20

|
| δ |
197,3 |
| |
1,12 |
|||||||||
|
°. |
||||||||||||
|
Угол напряжения |
найден по отношению к напряжению |
, абсолютный |
||||||||||
|
угол напряжения |
по отношению к заданному напряжению |
определяется |
||||||||||
|
как алгебраическая сумма углов напряжений |
по отношению к |
и по от- |
||||||||||
|
ношению к , т. е. |
° |
° |
° |
| δ |
| |
°. |
||||||
|
δ |
δ |
δ |
1,12 |
2,87 |
197,3 |
1,75 |
||||||
|
1,75 ; |
||||||||||||
|
Задача 3. Определить напряжение в узле |
в сети с равномерно распре- |
|||||||||||
|
деленной нагрузкой, плотность нагрузки |
0,3 МВт/км. Схема сети пока- |
|||||||||||
|
зана на рис. 3.7, напряжение базисного узла |
3,3 кВ, нагрузка узла |
|||||||||||
|
2 |
1,6 МВ |
А, длины линий приведены на схеме. При решении принять |
||||||||||
|
0,1 Ом/км, |
0,2 Ом/км. Потерями мощности пренебречь. |
Решение задачи. Расчет параметров режима электрической сети с равномерно распределенной нагрузкой производится при замене распределенной нагрузки на суммарную сосредоточенную, включенную в центре питания распределенной нагрузки (точка ). Суммарная нагрузка ℓ 0,3 1 0,3 МВт.
|
1 |
2 |
1 км |
3 |
1 км |
|
0,5 км |
||||
|
3,3 кВ |
|
2 |
1,6 |
|||||||||||||||||||||
|
Рис. 3.7. Исходная схема |
||||||||||||||||||||||
|
Определение параметров схемы замещения: |
||||||||||||||||||||||
|
участок 1 2: |
0,1 |
0,5 |
0,05 Ом; |
0,2 |
0,5 |
0,1 Ом; |
||||||||||||||||
|
участок 3 : |
0,1 |
1 |
0,1 Ом; |
0,2 1 |
0,2 Ом; |
|||||||||||||||||
|
участок |
2 3, сопротивление линии с равномерно распределенной на- |
|||||||||||||||||||||
|
грузкой обычно принимается чисто активным, поэтому |
0,1 1 |
0,1 Ом. |
||||||||||||||||||||
|
Схема замещения сети показана на рис. 3.8, а, эквивалентная схема за- |
||||||||||||||||||||||
|
мещения — на рис. 3.8, б. |
||||||||||||||||||||||
|
а |
1 |
0,05 |
0,1 |
0,05 |
0,05 |
0,1 |
0,2 |
|||||||||||||||
|
3,3 кВ |
2 |
3 |
||||||||||||||||||||
|
0,3 |
2 |
1,6 |
||||||||||||||||||||
|
1 |
0,1 |
0,1 |
0,15 |
0,2 |
||||||||||||||||||
|
б |
||||||||||||||||||||||
|
3,3 кВ |
||||||||||||||||||||||
|
0,3 |
2 |
1,6 |
||||||||||||||||||||
|
Рис. 3.8. Схема замещения сети: |
||||||||||||||||||||||
|
а – исходная; б – эквивалентная |
21

Потери мощности не учитываются, поэтому потоки, МВ А, в сети зависят только от нагрузок:
|
2 |
1,6; |
2 |
1,6 |
0,3 |
2,3 |
1,6 |
|||||||||||||
|
Напряжение узла |
в соответствии с направлением мощности определяет. |
– |
|||||||||||||||||
|
ся как: |
∆ |
; |
2,3∆ |
∆ |
0,1δ |
; |
|||||||||||||
|
∆ |
0,1 |
1,6 |
|||||||||||||||||
|
0,118 |
кВ; |
||||||||||||||||||
|
2,3 |
0,13,31,6 |
0,1 |
|||||||||||||||||
|
δ |
0,021 |
кВ. |
|||||||||||||||||
|
3,3 |
|||||||||||||||||||
|
В сети с |
3 кВ поперечная составляющая падения напряжения мала |
||||||||||||||||||
|
и ею можно |
ном |
||||||||||||||||||
|
пренебречь, тогда |
|||||||||||||||||||
|
Напряжение в узле |
: |
∆ |
3,3 |
,0,118 |
3,182 кВ. |
||||||||||||||
|
∆ |
2 |
0,15 |
1,6 |
0,2 |
0,195∆кВ; |
3,182 |
0,195 |
2,987 кВ. |
|||||||||||
|
3,182 |
|||||||||||||||||||
Задача 4. Выполнить электрический расчет сети, показанной на рис. 3.9. Линия выполнена сечением 2АС 400, длина линии 100 км, два трансформатора
|
ТРДЦН 63000/220, нагрузка |
100 МВт, |
0,9, напряжение базисного |
|
|
узла 230 кВ. |
2 |
3 cosφ |
|
|
1 |
|||
|
б |
230 кВ |
100 48,4 МВ А |
|
Рис. 3.9. Исходная схема сети
Решение задачи. Расчет электрической сети, в которой заданы напряжение питающего (базисного) узла и мощность нагрузки, сводится к итерационному процессу. Схема замещения сети приведена на рис. 3.10. Параметры схемы замещения сети определены с использованием [2].
|
∆ кор |
0,15 |
∆ кор |
0,15 |
т |
⁄ |
||||||
|
2 |
2 |
230 |
11 |
||||||||
|
3,75 |
21к |
1,95 |
50 |
||||||||
|
1 |
н |
2 н |
к |
3 |
3 |
||||||
|
2,7 |
10 |
хх 0,16 |
100 |
48,43 |
|||||||
|
2 |
1 |
||||||||||
|
Рис. |
3.10. Схема замещения сети |
||||||||||
|
∆ |
22

|
1. |
Линия электропередачи (участок 1 2). |
||||||||||||||||||||||||||||||||
|
Для сечения АС 400: |
|||||||||||||||||||||||||||||||||
|
0,075 Ом/км; |
0,42 Ом/км; |
2,7 |
10 |
Ом/км; |
|||||||||||||||||||||||||||||
|
∆ кор max |
1,7 кВт/км; |
∆ кор min |
1,3 кВт/км; |
1 |
|||||||||||||||||||||||||||||
|
л |
∆ кор max |
ℓ |
1 |
0,75 |
0,42 |
100 |
3,75 |
21 |
Ом; |
||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||
|
1,7 |
1,3 |
||||||||||||||||||||||||||||||||
|
∆ кор ср |
2 |
∆ кор min |
1,5 кВт/км; |
||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||
|
∆ |
1кор срℓ |
1,5 |
100 |
2 |
0,3 МВт; |
||||||||||||||||||||||||||||
|
∆ кор |
1 |
||||||||||||||||||||||||||||||||
|
2л |
ℓ |
2,7 |
10 |
100 |
2 |
2,7 |
10 |
См. |
|||||||||||||||||||||||||
|
2 |
2 |
2 |
|||||||||||||||||||||||||||||||
|
2. |
|||||||||||||||||||||||||||||||||
|
Трансформатор (участок 2 3). |
|||||||||||||||||||||||||||||||||
|
Параметры трансформатора ТРДЦН 63000/220: |
|||||||||||||||||||||||||||||||||
|
∆ |
3,9 Ом; |
100,7 Ом; |
∆ |
0,082 МВт; |
∆ |
0,504 МВАр; |
МВ А; |
||||||||||||||||||||||||||
|
хх |
∆ |
ххт |
∆ хх |
∆ хх |
хх0,082 |
1 |
хх |
0,164 |
1,008 |
||||||||||||||||||||||||
|
т |
1 |
т |
1 |
0,504 2 |
|||||||||||||||||||||||||||||
|
т |
т |
т |
3,9 |
100,7 |
1,95 |
50,35 |
Ом. |
||||||||||||||||||||||||||
|
2 |
Итерационный процесс расчета установившегося режима сети складывается из прямого и обратного ходов. Прямой ход включает определение потокораспределения в сети с учетом потерь мощности, обратный связан с расчетом напряжений узлов сети.
Прямой ход первой итерации
Для выполнения расчета потокораспределения необходимо задать началь-
|
ные приближения напряжений в узлах сети. Пусть |
220 кВ, |
210 кВ. |
Расчет начинается с конца передачи (рис. 3.10). Поток в конце участка 2 3 , совпадает с нагрузкой, т. к. участок 3 3 является идеальным трансформатором,
|
к |
100 |
48,4 |
МВ А. |
||||||||||
|
Потери мощности на участке 2 3: |
|||||||||||||
|
∆ |
к |
к |
к |
||||||||||
|
100 |
48,4 |
1,95 |
50,35 |
0,55 |
14,1 МВ А; |
||||||||
|
н |
к |
210 |
|||||||||||
|
∆ |
100 |
48,4 |
; |
0,55 |
14,1 |
100,55 62,5 МВ А; |
|||||||
|
к |
н |
∆ хх |
∆ кор |
∆ ш |
|||||||||
|
2 |
23

|
∆ ш |
2,7 10 |
220 |
13,07 МВ А; |
||||||||
|
2 |
|||||||||||
|
к |
100,55 |
∆ |
62,5 |
0,16 |
1 0,15 |
13,07 |
100,86 50,43 МВ А; |
||||
|
н |
к |
; |
к |
к |
|||||||
|
∆ |
к |
||||||||||
|
100,86 |
50,43 |
3,75 |
21 |
0,99 5,52 МВ А; |
|||||||
|
н |
|||||||||||
|
220 |
|||||||||||
|
100,86 |
50,43 |
0,99 |
5,52 |
101,85 |
55,95 МВ А. |
На этом заканчивается прямой ход первой итерации. Учет потерь в шунте узла 1 в данном случае не требуется, так как они не влияют на уровни напряжений (узел 1 – шины бесконечной мощности).
Обратный ход первой итерации
Обратный ход позволяет уточнить напряжения узлов. В соответствии с условным направлением потока (в данном случае совпадает с действительным), напряжение узла 2 можно выразить через известное напряжение питающего уз-
|
ла |
б: |
, |
( |
δ |
) |
выражается через |
|||||||||||
|
Вектор падения |
напряжения на участке 1 2 |
||||||||||||||||
|
∆ |
∆ |
) |
∆ |
. |
|||||||||||||
|
продольную ( |
) |
и поперечную ( |
δ |
∆ |
ориентированные |
||||||||||||
|
составляющие, |
|||||||||||||||||
|
известного вектора |
. |
||||||||||||||||
|
относительно |
∆ |
∆ |
|||||||||||||||
|
Теперь |
δ |
. |
ω + |
||||||||||||||
|
δ |
|||||||||||||||||
|
δ |
∆ |
∆ |
|||||||||||||||
|
Рис. 3.11. Векторная диаграмма напряжений участка 1–2 |
|||||||||||||||||
|
Связь напряжений |
и |
показана на диаграмме напряжений (рис. 3.11), |
изображенной на вращающейся с частотой ω комплексной плоскости.
|
101,85 |
3,75 |
55,95 |
21 |
6,66 кВ; |
|||
|
230 |
|||||||
|
101,85 |
21 |
55,95 |
3,75 |
8,39 кВ. |
|||
|
230 |
|||||||
24

|
Угол |
δ |
вектора |
определяется по |
соотношению |
||||||||||||||
|
8,39 |
||||||||||||||||||
|
δ |
arctg |
δ |
arctg |
2,15°. |
||||||||||||||
|
230 |
6,66 |
|||||||||||||||||
|
Модуль вектора |
: |
∆ |
||||||||||||||||
|
∆ |
δ |
230 |
6,66 |
8,39 |
223,57 кВ. |
|||||||||||||
|
Таким образом, |
223,5 |
2,15 кВ. |
||||||||||||||||
|
Аналогично выполнен расчет| напряжения° |
узла 3 по отношению к |
: |
||||||||||||||||
|
Теперь |
∆ |
∆ |
, ∆, |
∆ |
δ |
. |
||||||||||||
|
н |
δ |
100,55 |
1,95 |
62,5 |
50,35 |
|||||||||||||
|
∆ |
н |
14,96 кВ; |
||||||||||||||||
|
н |
н |
223,5 |
||||||||||||||||
|
δ |
100,55 |
50,35 |
62,5 |
1,95 |
22,11 кВ. |
|||||||||||||
|
223,5 |
||||||||||||||||||
|
δ |
δ |
∆ |
∆ |
участка 2–3 |
|||||||||
|
Рис. 3.12. Векторная диаграмма напряжений |
|||||||||||||
|
ω |
|||||||||||||
|
Векторная диаграмма напряжений участка 2 3 показана на рис. 3.12 в но- |
|||||||||||||
|
вых осях |
; |
, совмещенных с вектором |
. |
||||||||||
|
Угол δ |
вектора |
по отношению к |
напряжению |
определяется как |
|||||||||
|
22,11 |
|||||||||||||
|
δ |
arctg |
δ |
arctg |
6,25°. |
|||||||||
|
223,5 |
14,96 |
||||||||||||
|
Модуль вектора |
∆ |
||||||||||||
|
∆ |
δ |
||||||||||||
|
201,94| |
223,5 |
14,96 |
22,11 |
208,6 кВ. |
|||||||||
|
6,25° кВ. |
Векторные диаграммы участков 1 2 и 2 3 совмещены на рис. 3.13, там же показаны абсолютные углы напряжений по отношению к заданному базисному напряжению. Сопоставление векторных диаграмм участков 1 2 и 2 3 и всей
25
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задачи на Закон Ома с решениями
Формулы, используемые на уроках физики «Задачи на Закон Ома» в 8 классе, а также для подготовки к ОГЭ.
Название величины |
Обозначение |
Единица измерения |
Формула |
Сила тока |
I |
А |
I = U / R |
Напряжение |
U |
В |
U = IR |
Сопротивление |
R |
Ом |
R = U/I |
Решение задач на уроках физики в 10-11 классах и при подготовке к ЕГЭ смотрите в следующих конспектах:
ЕГЭ: Закон Ома для участка цепи
ЕГЭ: Закон Ома для всей цепи
Задачи на Закон Ома.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Какова сила тока в резисторе, если его сопротивление 12 Ом, а напряжение на нем 120 В?
Задача № 2.
Сопротивление проводника 6 Ом, а сила тока в нем 0,2 А. Определите напряжение на концах проводника.
Задача № 3.
Определите сопротивление проводника, если при напряжении 110 В сила тока в нем 2 А.
Задача № 4.
По графикам зависимости силы тока от напряжения определите сопротивление каждого проводника.
Решение:
Задача № 5.
Чему равна сила тока в электрической лампе карманного фонаря, если сопротивление нити накала 16,6 Ом и лампа подключена к батарейке напряжением 2,5 В?
Задача № 6.
Электрический утюг включен в сеть с напряжением 220 В. Какова сила тока в нагревательном элементе утюга, если сопротивление его равно 48,4 Ом?
Задача № 7.
При напряжении 110 В, подведенном к резистору, сила тока в нем равна 5 А. Какова будет сила тока в резисторе, если напряжение на нем увеличить на 10 В?
Задача № 8.
Чему равно сопротивление спирали электрической лампы в рабочем состоянии, у которой на цоколе написано 6,3 В, 0,22 А?
Задача № 9.
Показание вольтметра, присоединенного к горящей электрической лампе накаливания, равно 120 В, а амперметра, измеряющего силу тока в лампе, 0,5 А. Чему равно сопротивление лампы? Начертите схему включения лампы, вольтметра и амперметра.
Задача № 10.
ОГЭ
Источник постоянного тока с ЭДС E = 12 В и внутренним сопротивлением г = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить силу тока в цепи I, падение напряжения UR на внешнем участке и падение напряжения Ur на внутреннем участке цепи.
Краткая теория для решения Задачи на Закон Ома.
Это конспект по теме «ЗАДАЧИ на Закон Ома». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на сопротивление проводника
- Посмотреть конспект по теме Закон Ома. Соединение проводников
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
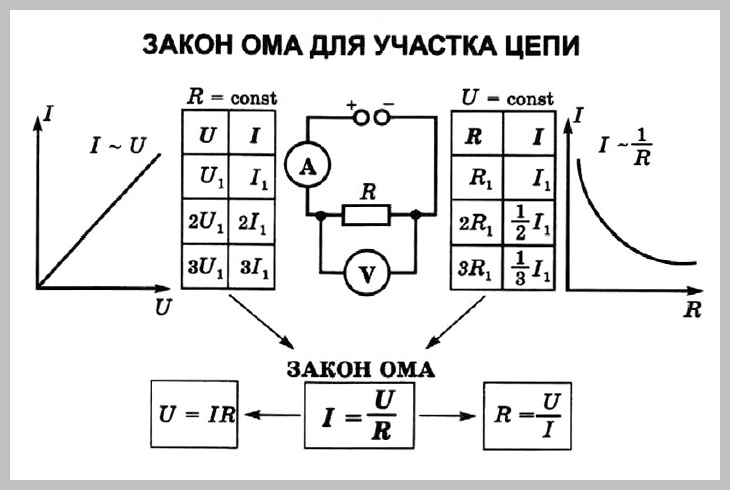
Решение задач на закон Ома для участка и полной цепи
Решение задач на закон Ома сводится к нахождению одной из трех неизвестных составляющих: тока, сопротивления или напряжения. Сам же закон описывает, как они соотносятся между собой.
Напомним, что согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
Формула закона Ома для участка цепи:
Формула закона Ома для полной цепи:
 Задача 1
Задача 1
Утюг включенный в сеть напряжением 220 В, потребляет ток 1,2 А. Определите сопротивление утюга.
|
Дано U = 220 В I = 1,2 А |
Решение Согласно закону Ома для участка цепи: |
|
Найти R – ? |
|
|
Ответ: R = 183,3 Ом. |
Задача 2
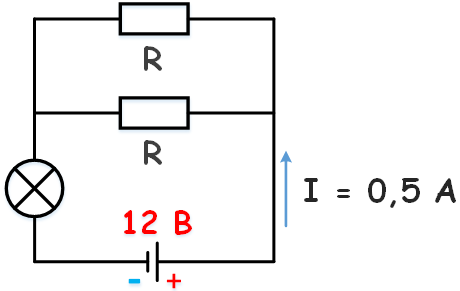
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.
|
Дано E = 12 В I = 0,5 А Rл = Rр/2 Rр = 10 Ом |
Решение Найдем экв. сопротивление двух параллельно соединённых резисторов: Сопротивление лампочки: Согласно закону Ома для полной цепи: |
|
Найти r – ? |
|
|
Ответ: r = 14 Ом. |
Задача 3
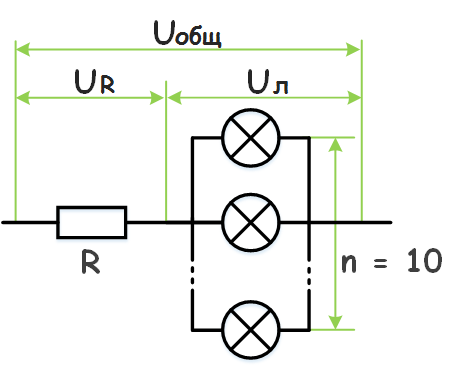
К участку цепи с напряжением 12 В через резистор сопротивлением 2 Ом подключены десять одинаковых лампочек сопротивлением 10 Ом. Найти напряжение на каждой лампочке.
|
Дано Uобщ = 10 В Rр = 2 Ом Rл = 10 Ом |
Решение Так как лампочки подключены параллельно, напряжение на них будет одинаковым, согласно закону Ома для участка цепи: При последовательном соединении ток в цепи общий: Выразим Uл через Uобщ: Найдем Rэкв: Окончательно получим: |
|
Найти Uл – ? |
|
|
Ответ: Uл = 4 В. |
Задача 4
Как определить длину мотка медной проволоки, не разматывая его?
Решение:
Для решения данной задачи необходимо воспользоваться формулой:
отсюда длина проволоки
В этой формуле, l – длина проволоки, R – сопротивление, S – площадь поперечного сечения, ρ – удельное сопротивление металлов, в данном случае ρ для меди равно 0.0175 Ом/м.
Сопротивление R проволоки можно измерить с помощью омметра, а площадь S с помощью штангенциркуля, измерив диаметр проволоки и по формуле Πr2 вычислив ее значение. Значение удельного сопротивления ρ не только для меди, но и других металлов можно найти в справочнике, или тут. Подставив все известные величины в формулу, приведенную выше, получим длину проволоки.
Задача 5
Начертите схему электрической цепи, состоящей из источника тока, выключателя и двух ламп, включенных параллельно. Что произойдет в цепи при перегорании одной лампы?
Решение:
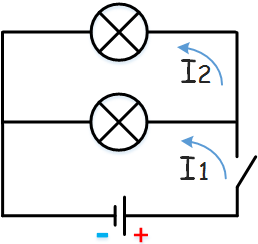
При перегорании одной из лампочек, вторая будет гореть, так как, при параллельном включении проводников токи I1 и I2 проходящие через них не зависят друг от друга и при разрыве параллельной цепочки ток продолжает протекать.
Применение закона Ома к расчету линейных электрических цепей постоянного тока
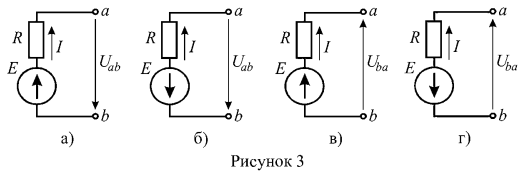
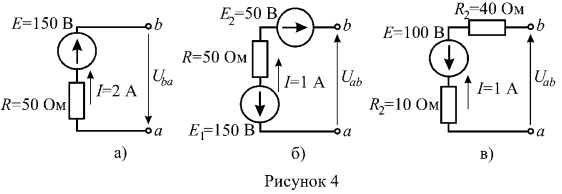
1. Найти ток ветви (рисунок 3), если: U=10 В, Е=20 В, R=5 Ом.
Решение:
Так как все схемы рисунка 3 представляют собой активные ветви, то для определения токов в них используем закон Ома обобщенный закон Ома. Рассмотрим рисунок 3 а: направление ЭДС совпадает с произвольно выбранным условно положительным направлением тока, следовательно, в формуле обобщенного закона Ома величина ЭДС учитывается со знаком «плюс». Направление напряжения не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;
Аналогично определяются токи в схемах б, в, г рисунка 3:
2. Найти напряжение между зажимами нетвей (рисунок 4).
Решение:
Участок цепи, изображенный на рисунке 4 а содержит источник ЭДС, т.е. является активным, поэтому воспользуемся обобщенным законом Ома:
откуда выразим напряжение на зажимах:
Аналогично определяются напряжения на зажимах участков, изображенных на рисунках 4 б и 4 в.
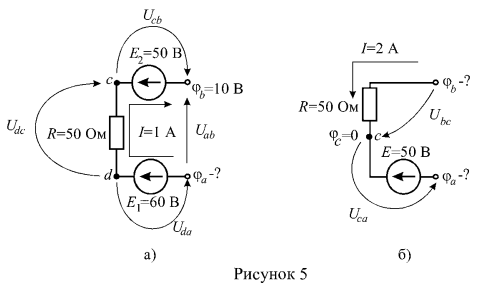
3. Определить неизвестные потенциалы точек участка цени (рисунок 5).
Решение:
Для схемы рисунка 5 а запишем обобщенный закон Ома:
откуда выразим напряжение на зажимах ветви:
Если представить напряжение как разность потенциалов:
тогда при известных параметрах цепи, токе и потенциале определим потенциал
:
Эту же задачу можно решить другим способом. Напряжение на зажимах источника ЭДС , без учета внутреннего сопротивления источника, по величине равно
и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):
и тогда, зная потенциал , определим потенциал точки С:
Потенциал точки d больше потенциала точки С на величину падения напряжения на сопротивлении R:
тогда
Потенциал точки а определяем с учетом направления напряжения на зажимах источника ЭДС
. Напряжение
направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):
откуда следует, что
или
Рассмотрим решение задачи для схемы рисунка 5 б. При известном потенциале точки С, параметрах элементов и токе, определим потенциалы крайних точек участка цепи . Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:
откуда следует
Напряжение на участке с — а, равное по величине Е, направлено от точки с большим потенциалом к точке с меньшим потенциалом:
4. В цепи (рисунок 6) известны величины сопротивлений резистивных элементов: , входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением
. Определить величину сопротивления резистора
.
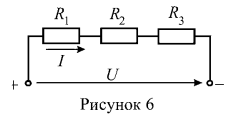
Согласно закону Джоуля-Ленца, мощность на резистивном элементе определяется:
или, согласно закону Ома:
По известному значению мощности на резистивном элементе и величине сопротивления этого элемента определим ток в ветви:
По закону Ома напряжение на зажимах определится:
тогда величина сопротивления резистивного элемента:
5. Определить показания вольтметров цепи (рисунок 7), если .
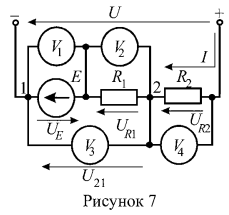
Ток в цепи определим по закону Ома:
Вольтметр показывает напряжение на источнике ЭДС Е:
Вольтметры показывают величину падения напряжения на резистивных элементах
:
Вольтметр , показывает напряжение на участке 2 — 1
, которое определим как алгебраическую сумма напряжений
:
6. Ток симметричной цепи (рисунок 8) , внутреннее сопротивлении источника ЭДС
. Определить ЭДС Е и мощность источника энергии.
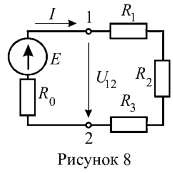
Напряжение на зажимах 1 — 2 определим по закону Ома для пассивной ветви:
Величину ЭДС источника энергии определим из выражения закона Ома для активной ветви:
Мощность, развиваемая источником энергии, определится:




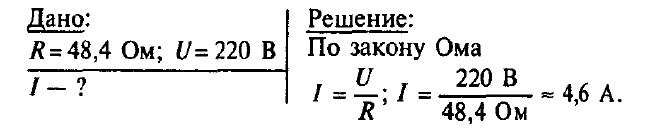
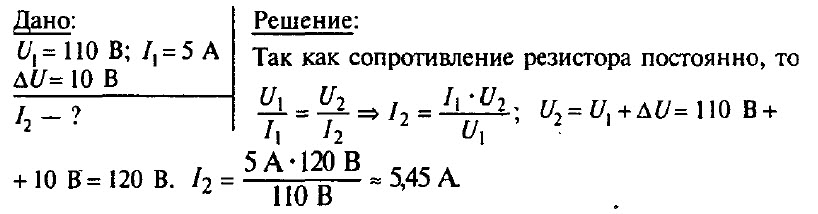
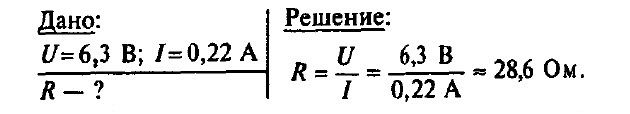


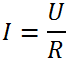
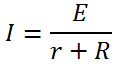 Задача 1
Задача 1